Stability evolution mechanisms and control strategies for lower and upper trapezoidal blocks in fully mechanized top-coal caving faces of extra-thick coal seams

In underground coal mining operations, particularly in fully mechanized top-coal caving (FMTC) faces of extra-thick coal seams, structural instability after key stratum fracturing will cause severe deformation and damage to the surrounding rock mass of the working face. The methods of field investigation, theoretical analysis, physical similarity simulation, and engineering tests were employed to investigate the instability characteristics and interaction laws of the lower and upper trapezoidal block structures in the FMTC face in extra-thick coal seams with dual key strata during periods of pressure. A mechanical model of the stability of the lower and upper trapezoidal blocks above the working face with severe and weak periodic pressures was established, and the stability transformation law, interaction relationship, and influencing factors of the stability of the lower and upper trapezoidal blocks with the dual key strata working face in the extra-thick coal seam were studied. The results show that (1) it is easy to induce the sliding instability of the lower and upper trapezoidal blocks with the advance of the working face. (2) The sliding instability coefficients of the lower and upper trapezoidal blocks are positively correlated, whereas the rotational deformation instability coefficients are negatively correlated. (3) An increase in the distance between the lower and upper key strata easily induces sliding instability in the upper trapezoidal block and sliding instability and rotational deformation instability in the lower trapezoidal block. (4) Increasing the mining height could improve the sliding stability of the lower and upper trapezoidal blocks and the rotational deformation stability of the upper trapezoidal block, but it is easy to induce rotational deformation instability of the lower trapezoidal block. (5) A higher support force on hydraulic supports improves sliding stability in lower and upper trapezoidal blocks but does not affect rotational deformation stability. Finally, the rationality and reliability of the study are verified by engineering applications in the 8309 working face of the Tongxin Coal Mine.

1 Introduction

Coal, a quintessential fossil fuel, holds a pivotal position in global energy consumption. The coal sector serves as a fundamental pillar of economic structure for numerous nations and regions around the world (Panaedova et al., 2023; Chen et al., 2023a; b; Liu et al., 2024; Lou et al., 2024). In China, reserves of extra-thick coal seams represent more than 20% of the nation’s total coal reserves, serving as the predominant mining seams for a significant number of mines with production capacities exceeding ten million tons (Lv et al., 2019; Xie et al., 2022; Lou et al., 2025). Fully mechanized top-coal caving mining technology (FMTCMT) is extensively employed in the extraction of extra-thick coal seams (Wei et al., 2022). This approach offers substantial benefits in terms of large-scale operations, high output, and enhanced efficiency. This technology has been extensively developed and applied in China, where it has demonstrated substantial economic potential and has attracted considerable attention from the international mining community (Zhang et al., 2019; Guo et al., 2024). The mining space of the working face with FMTCMT in the extra-thick coal seam is extremely large, and the movement of the surrounding rock is very complex and unprecedented, resulting in very severe mining pressure behavior (Kuang et al., 2019; Wu et al., 2024). The control of surrounding rock is extremely difficult, which severely affects the normal production of coal mines (Hao et al., 2022; Chai et al., 2024). Consequently, rigorous research on the failure mechanisms and control technologies of the surrounding rock in the fully mechanized mining faces of extra-thick coal seams is highly important.

Numerous experts and scholars have investigated the overburden structure and the laws of mine pressure behavior in overlying strata within fully mechanized top coal caving (FMTC) working faces of thick coal seams (Zhou and Yu, 2022; Jing et al., 2021; Shi et al., 2021; Vu, 2022; Wu et al., 2025; Li et al., 2025). In terms of the structural form of key strata, Tu et al. (2020) and Zhao et al. (2021) investigated the overburden structure and stress evolution characteristics of the FMTC face, determined the distribution range of the internal and external stress fields, and established the optimal layout positions for the roadway. Yu and Yan, (2020) provided a classification standard for the immediate and main roofs of extra-thick coal seam working faces through field measurements, numerical simulations, and other methods. The rock stratum existing in the form of a cantilever structure from bottom to top is termed the immediate roof, and the rock stratum existing in the form of a hinged structure above the immediate roof is termed the main roof. Liu et al. (2015) and Li et al. (2019) reported that in the FMTC working face of an extra-thick coal seam, the overlying strata manifest as a “upper main roof-masonry beam and lower main roof-inverted step combination cantilever beam” structure. Based on this structural characterization, they established the rated working resistance for hydraulic supports and thereby optimized the support system to accommodate site-specific geological and mechanical conditions. Furthermore, Yu, (2016) and Li et al. (2024) conducted a detailed analysis of the mechanism of periodic pressure and strong mining pressure formation in the thick coal seam of the Datong mining area and elucidated the influence of rock fracture and movement in the near and far fields on mining pressure behavior. In terms of the stability of key blocks, Wang et al. (2015) and Wang et al. (2024) reported that, during the periodic pressure period, the main roof of an extra-thick coal seam working face manifests a static three-hinged arch structure. They further elucidated the conditions for the sliding and rotational deformation instability of the main roof structure. Furthermore, Zhu et al. (2020) noted that the far-field key stratum (within 8–15 times the mining height from the coal seam) in the large space mining field of extra-thick coal seams forms a “transverse O-X” type initial fracture and a “transverse U-Y” type periodic fracture, whereas the near-field key strata (within 4–6 times the mining height from the coal seam) exhibit a “lengthwise O-X″ type fracture. Additionally, they proposed a stability discrimination method for arc-shaped triangular blocks of far-field key strata. In the study of the stability of overlying rock structures, Zhang et al. (2022) employed theoretical analysis, physical similarity simulation, and numerical simulation methods to demonstrate that with increasing mining height, the rotation angle of the “masonry beam” block continuously increases. This progressive increase in the rotation angle leads to destabilization of the structure, ultimately resulting in the formation of a “composite cantilever beam” structure. Yang et al. (2021) established a planar-hinged rock mass equilibrium mechanical model and analyzed the stability transformation law of key blocks. He et al. (2020) established a stability mechanical model for the arc-shaped triangular block above the gob-side roadway of an extra-thick coal seam and analyzed the stability transformation law. Qin et al. (2022) established a mechanical model of the main roof trapezoidal block and provided criteria for identifying instability. Lv et al. (2023) analyzed the stability of a right-angled trapezoidal block with a special-shaped load. These advancements offer valuable references and robust theoretical underpinnings for the control of the surrounding rock in FMTC faces of extra-thick coal seams. Notably, the above research mainly focuses on the stability of the surrounding rock in the working face with a single key stratum. The dynamic behaviors and interaction mechanisms after the dual key strata fractured during the advance of the working face in extra-thick coal seams with dual key strata are extremely complex, and the influence on the mining safety of the working face remains insufficiently addressed in current research.

To address this issue, this study integrates multiple methodologies, including field investigations, theoretical analyses, physically similar simulations and engineering tests. A novel mechanical model for the stability of lower and upper trapezoidal block structures in extra-thick coal seams was developed, incorporating the characteristics of severe and weak periodic pressure. Comprehensive analyses were conducted on three fundamental aspects: 1) the stability transformation trend of the lower and upper trapezoidal blocks, 2) the interaction relationship of the lower and upper trapezoidal blocks, and 3) the quantitative relationship of influencing factors and the dual trapezoidal blocks. The research conclusions derived from this research have been effectively utilized to guide the control of mining pressure behavior in the working face, and the effect was significant. These findings hold the potential to serve as a salient reference for the control of the surrounding rock in mining areas with analogous geological and production conditions.

2 Engineering background

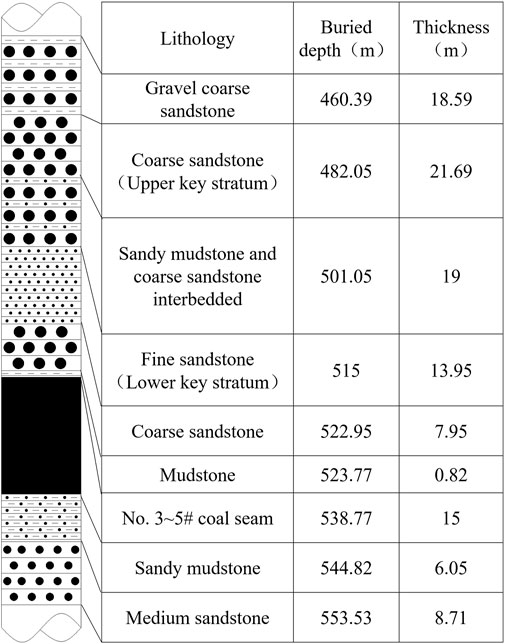
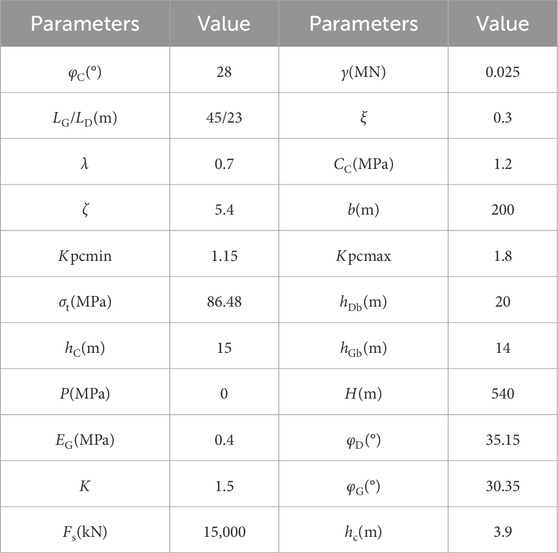
The Tongxin Coal Mine is located in northern Shanxi Province, China, and is a large and modern underground mining operation. The mine primarily exploits the No. 3-5 coal seams of the Carboniferous‒Permian system. The average thickness of the coal seam is 15 m, with an average dip angle of 1.5°. FMTCMT was adopted. The cutting height of the shearer is 3.9 m. The stratigraphic column of the working face is shown in Figure 1.

Figure 1

Figure 1. Histogram of coal and rock seams in Tongxin Coal Mine.

According to key strata theory (Chen et al., 2023a; b; Feng et al., 2023), dual key strata exist above working faces, controlling mining pressure behavior. The lower key stratum consists of fine sandstone, which is positioned 8.77 m above the coal seam and has a thickness of 13.95 m, whereas the upper key stratum consists of coarse sandstone, which is positioned 21.69 m above the coal seam and has a thickness of 41.72 m.

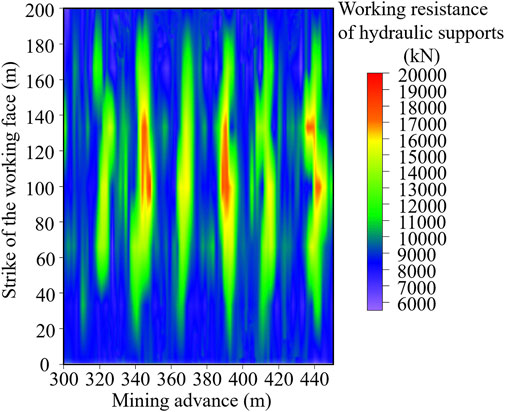
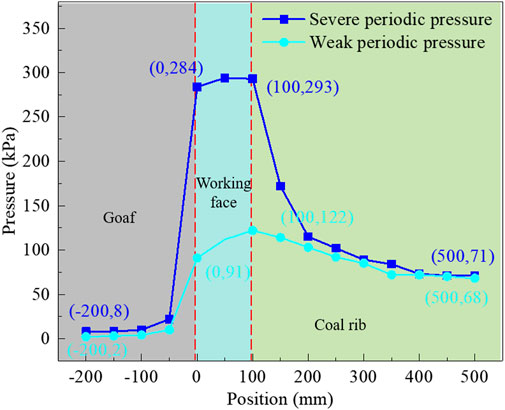
The final working resistance of the hydraulic supports for each cycle of movement during extraction in the Tongxin Coal Mine was analyzed, and the mining pressure behavior was obtained. As shown in Figure 2, when the mine pressure affects the working face, the final working resistance of each cycle in the middle position experiences a greater increase than those at the head and tail positions do. With the extraction of the working face, there is a phenomenon of cyclic alternation in the lower and upper final working resistance of each cycle for the hydraulic support, which indicates that the working face follows the law of severe and weak periodic pressure on the working face. The average step distances of the severe and weak periodic pressures are 45 m and 23 m, and the dynamic load coefficients are 2.01 and 1.74, respectively. Field investigations revealed that the severe periodic pressure exerted on the working face often leads to significant mining pressure. As illustrated in Figure 3, this pressure results in the breaking of the hydraulic support column, whereas the timber supports in front of the working face become compressed and deformed.

Figure 2

Figure 2. The law of periodic pressure of the FMTC face in the extra-thick seam.

Figure 3

Figure 3. The Documentation of support system failures during the severe periodic pressure. (A) Catastrophic fracture propagation in hydraulic support column assemblies; (B) Progressive deformation of timber supports.

3 Theory and methods

3.1 Fundamental assumptions

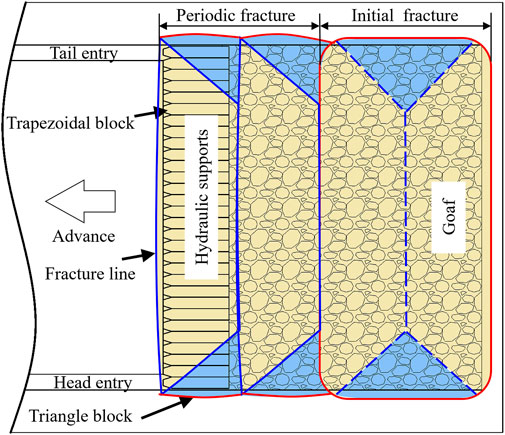
During extraction, the key strata undergo periodic fracturing, and the fracture line is in front of the working face (Yang et al., 2020). This progressive failure ultimately generates an approximately isosceles trapezoidal block structure above the working face, complemented by arc-shaped triangular block structures along both sides of the excavation (Chen et al., 2019). For analytical simplification, the arc-shaped triangular blocks are considered right-angled triangular blocks, as shown in Figure 4.

Figure 4

Figure 4. Fracture pattern of key stratum.

Following strata fracturing, the trapezoidal block rotates and forms a stable structure with the unbroken key stratum, and the trapezoidal block forms during the previous period of pressure. If a trapezoidal block experiences sliding or rotational deformation instability, severe mining pressure behavior and even working face instability can occur. For FMTC working faces in extra-thick coal seams with dual key strata, simultaneous fracturing and rotation occur in both the lower and upper key strata during severe periodic pressure episodes, with the lower trapezoidal block supporting its self-weight combined with overburden-transmitted loads (Figure 5A). Conversely, under weak periodic pressure conditions, only the lower key stratum fractures and rotates while the upper stratum remains continuous, resulting in the lower trapezoidal block bearing its self-weight plus loads transferred from the weakened interstrata rock mass (Figure 5B).

Figure 5

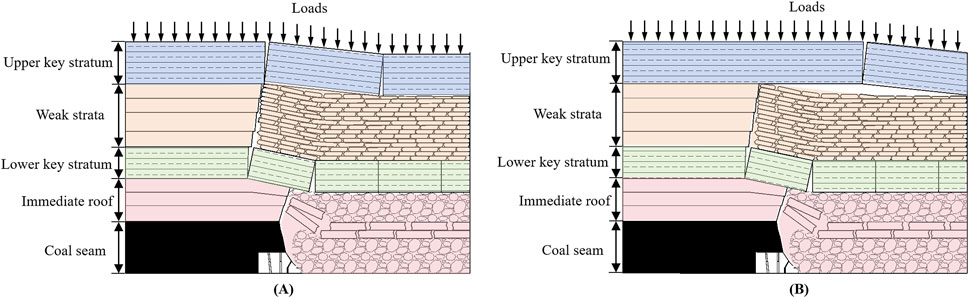
Figure 5. Distribution of overlying strata during the period of periodic pressure. (A) Severe periodic pressure; (B) Weak periodic pressure.

3.2 Mechanical model

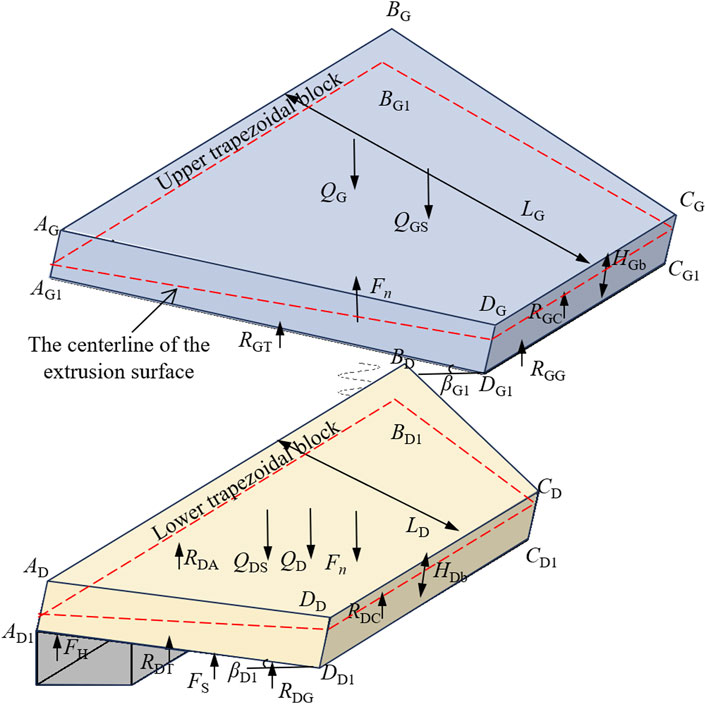
The position and attitude characteristics, geometric dimensions, and force conditions of the trapezoidal blocks were comprehensively considered during the period of periodic pressure. The lower and upper trapezoidal blocks were selected as the research objects, and a structural stability mechanical model was established, with a detailed schematic representation provided in Figure 6.

Figure 6

Figure 6. Mechanical model of lower and upper trapezoidal blocks.

3.2.1 Mechanical model of the lower trapezoidal block

As illustrated in Figure 6, the lower trapezoidal block experiences multiple axial constraints, including the support force of the coal body (F_H), the support force of the hydraulic support (F_S), the support force of the goaf gangue (R_DG), the shear stress (R_DA) and normal stress (T_DA) of the lower key stratum in front of the working face, the shear stress (R_DC) and normal stress (T_DC) of the lower trapezoidal block that has completed rotation, the shear stress (R_DT) and normal stress (T_DT) of the lower arc-shaped triangular blocks on both sides, the gravity (Q_D), the load of the weak rock strata between the lower and upper key strata (Q_DS), and the pressure exerted by the upper trapezoidal block (Fn). When the upper trapezoidal block forms a stable structure and the weak rock strata separate from the lower trapezoidal block, Fn is 0. When the upper trapezoidal block becomes unstable, Fn is the sum of the gravity and the normal stress of the weak rock strata on the upper key strata.

The governing horizontal force equilibrium equation for the lower trapezoidal block is mathematically expressed as:

$T_{\text{DA}}-T_{\text{DC}}-2T_{\text{DT}}\mathit{cos}{\theta }_{\mathrm{D}}=0$

where θ_D is the bottom angle of the arc-shaped triangle blocks on both sides of the lower key stratum, °.

$T_{\text{DC}}=\frac{\left(Q_{\text{DS}}+Q_{\mathrm{D}}+F_{\mathrm{n}}\right)L_{\mathrm{D}}}{2\left(h_{\text{Db}}-L_{\mathrm{D}}\mathit{tan}{\beta }_{\mathrm{D}1}\right)}$

where h_Db is the thickness of the lower trapezoidal block, m; L_D is the length of the lower trapezoidal block along the strike direction, m; and β_D1 is the rotation angle of the lower trapezoidal block, °.

${\beta }_{\mathrm{D}1}=\mathit{arctan}\frac{h_{\mathrm{c}}-\sum h_{\mathrm{i}}\left(K_{\text{pcmin}}-1\right)}{L_{\text{DT}}}$

where h_c is the mining height of the coal seam, m; ∑h_i is the distance between the lower key stratum and the working face, m; K_pcmin is the residual bulking coefficient of the immediate roof; and L_DT is the length of the lower triangular block along the dip direction of the working face, m.

$L_{\text{DT}}=L_{\mathrm{D}}\sqrt{{\left(L_{\mathrm{D}}/b\right)}^2+1.5}-L_{\mathrm{D}}/b$

where b is the length of the working face along the dip direction, m.

$T_{\text{DT}}=\frac{L_{\text{DT}}{Q}_{\text{DT}}}{2h_{\text{Db}}-L_{\text{DT}}\mathit{sin}{\beta }_{\mathrm{D}2}}$

where Q_DT is the sum of gravity and the overlying load of the lower triangular block, MPa; and β_D2 is the rotation angle of the lower triangular block, °

${\beta }_{\mathrm{D}2}=\mathit{arctan}\frac{h_{\mathrm{c}}-\sum h_{\mathrm{i}}\left(K_{\text{pcmin}}-1\right)}{L_{\text{DT}}}$

The governing vertical force equilibrium equation for the lower trapezoidal block is mathematically expressed as:

$Q_{\text{DS}}+Q_{\mathrm{D}}+F_{\mathrm{n}}-F_{\mathrm{H}}-R_{\text{DG}}-R_{\text{DC}}-2R_{\text{DT}}-F_{\mathrm{S}}-R_{\text{DA}}=0$

The support force exerted by the coal seam on the lower trapezoidal block is

$F_{\mathrm{H}}={\displaystyle {\int }_0^{L_{\mathrm{H}}}}\frac{C_{\mathrm{C}}}{\mathit{tan}{\phi }_{\mathrm{C}}}\left[e^{\frac{2\mathit{tan}{\phi }_{\mathrm{C}}\left(L_{\mathrm{H}}-x\right)}{h_c\lambda }}-1\right]\left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{D}}}\right)dx$

where L_H is the length of the coal body below the lower trapezoidal block along the strike direction, m; x is the horizontal distance between the selected position and the fracture line of the lower key stratum, m; C_C is the cohesion of the coal, MPa; φ_C is the friction of coal, °; and λ is the horizontal pressure coefficient of the coal rib.

The support force generated by the gangue within the goaf acting upon the lower trapezoidal block is

$R_{\text{DG}}=-{\displaystyle {\int }_{L_{\text{SD}}}^{L_{\mathrm{D}}}}\zeta \ln \frac{\left[\left(L_{\mathrm{D}}-x\right)\mathit{sin}{\beta }_{\mathrm{D}1}+h_{\text{pcmin}}-h_{\mathrm{Z}}{K}_{\text{pcmin}}\right]}{h_{\mathrm{Z}}\left(K_{\text{pcmax}}-K_{\text{pcmin}}\right)}\left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{D}}}\right)dx$

where L_SD is the horizontal distance between the hydraulic support and the lower key stratum fracture line, m; h_pcmin is the compression height of the goaf gangue, m; ζ is the coefficient of the rock seam load, h_Z, is the thickness of the immediate roof, m; and K_pcmax is the origin bulking coefficient of the goaf gangue.

The shear stress transmitted from the triangular blocks to the adjacent lower trapezoidal block is

$R_{\text{DT}}=\frac{\left[\begin{array}{c}{T}_{\text{DT}}\left(h_{\mathrm{b}}-L_{\text{DT}}\mathit{sin}{\beta }_{\mathrm{D}2}\right)\mathit{cos}{\theta }_{\mathrm{D}}+\\ {\displaystyle {\int }_0^{L_{\mathrm{T}1}}}2y\mathit{tan}{\theta }_{\mathrm{D}}\left[\left(\frac{C_{\mathrm{C}}}{\mathit{tan}{\phi }_{\mathrm{D}}}+\frac{P}{\lambda }\right)e^{\frac{2\mathit{tan}{\phi }_{\mathrm{D}}\left(L_{\mathrm{T}1}-y\right)}{h_c\lambda }}-\frac{C_{\mathrm{C}}}{\mathit{tan}{\phi }_{\mathrm{D}}}\right]\left(L_{\mathrm{T}}-y\right)dy+\\ {\displaystyle {\int }_{L_{\mathrm{T}1}}^{L_{\mathrm{T}2}}}\frac{\left\{2E_{\mathrm{G}}y\mathit{tan}{\theta }_{\mathrm{D}}\left(L_{\text{DT}}-y\right)\left[y\mathit{sin}{\beta }_{\mathrm{D}2}-h_{\mathrm{c}}+\left(h_{\mathrm{c}}-h_{\mathrm{C}}+h_{\mathrm{z}}\right)\left(K_{\text{pcmin}}-1\right)\right]\right\}}{\left(h_{\mathrm{c}}-h_{\mathrm{r}}+h_{\mathrm{z}}\right)K_{\text{pcmin}}}dy\\ +{\displaystyle {\int }_{L_{\mathrm{T}2}}^{L_{\text{DT}}}}\frac{\left\{2E_{\mathrm{G}}y\mathit{tan}{\theta }_{\mathrm{D}}\left(L_{\text{DT}}-x\right)\left[y\mathit{sin}{\beta }_{\mathrm{D}2}-h_{\mathrm{c}}+h_{\mathrm{z}}\left(K_{\text{pcmin}}-1\right)\right]\right\}}{h_{\mathrm{z}}{K}_{\text{pcmin}}}dy+\frac{Q_{\text{DT}}{L}_{\text{DT}}\mathit{cos}{\beta }_{\mathrm{D}2}}{3}\end{array}\right]}{L_{\text{DT}}\mathit{cos}{\beta }_{\mathrm{D}2}}$

where y is the distance from the selected position to the fracture line of the lower triangle blocks, m; L_T2 is the distance from the uncaved position of the working face head/tail to the fracture line of the lower triangle blocks, m; E_G is the support coefficient of gangue for lower trapezoidal blocks, MPa; h_C is the thickness of the coal seam, m; L_T1 is the distance from the coal rib of entry to the fracture line of the lower triangle blocks, m; and K_pcmin is the residual bulking coefficient of goaf gangue.

$L_{\mathrm{T}1}=\frac{\lambda h_{\mathrm{c}}}{2\mathit{tan}{\phi }_{\mathrm{C}}}\mathit{ln}\left[\frac{\lambda \left(\mathit{tan}{\phi }_{\mathrm{C}}K\gamma H+C_{\mathrm{C}}\right)}{\lambda C_{\mathrm{C}}+\mathit{tan}{\phi }_{\mathrm{C}}P}\right]$

where γ is the specific gravity of the overlying strata, kN/m³; H is the burial depth of the coal seam, m; P is the support resistance of the coal rib, MPa; and K is the coefficient of stress concentration.

The moment equilibrium equation governing the lower trapezoidal block can be expressed as

$\begin{array}{ll}\hfill R_{\text{DC}}L& -{\displaystyle {\int }_{L_{\mathrm{S}}}^{L_{\mathrm{D}}}}x\zeta \ln \frac{\left[\left(L_{\mathrm{D}}-x\right)\mathit{sin}{\beta }_{\mathrm{D}1}+h_{\text{pcmin}}-h_{\mathrm{Z}}{K}_{\text{pcmin}}\right]}{h_{\mathrm{Z}}\left(K_{\text{pcmax}}-K_{\text{pcmin}}\right)}\hfill \\ \hfill & \left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{D}}}\right)+{\displaystyle \underset{0}{\overset{L_{\mathrm{H}}}{\int }}}x\left[\frac{C_{\mathrm{C}}}{\mathit{tan}{\phi }_{\mathrm{C}}}{e}^{\frac{2\mathit{tan}\phi \left(L_{\mathrm{H}}-x\right)}{h_c\lambda }}-\frac{C_{\mathrm{C}}}{\mathit{tan}{\phi }_{\mathrm{C}}}\right]\hfill \\ \hfill & \left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{D}}}\right)dx+F_{\mathrm{S}}{L}_{\mathrm{S}}-\frac{T_{\text{DC}}\left(h_{\mathrm{b}}-L_{\mathrm{D}}\mathit{sin}{\beta }_{\mathrm{D}1}\right)}{2}\hfill \\ \hfill & -T_{\text{DT}}\mathit{sin}{\theta }_{\mathrm{D}}\mathit{cos}{\theta }_{\mathrm{D}}\left(h_{\mathrm{b}}-L_{\text{DT}}\mathit{sin}{\beta }_{\mathrm{D}2}\right)=\frac{\left(Q_{\text{DS}}+Q_{\mathrm{D}}+F_{\mathrm{n}}\right)L}{2}\hfill \end{array}$

3.2.2 Mechanical model of the upper trapezoidal block

As shown in Figure 6, the upper trapezoidal block experiences multiple axial constraints, including the shear stress (R_GA) and normal stress (T_GA) of the upper key stratum in front of the working face, the shear stress (R_GC) and normal stress (T_GC) of the upper trapezoidal block that has completed rotation, the shear stress (R_GT) and normal stress (T_GT) of the upper arc-shaped triangular blocks on both sides, gravity (Q_G), the load on the upper key stratum (Q_GS), the support force of the goaf gangue (R_GG), and the normal stress exerted by the lower trapezoidal block (-Fn).

The governing horizontal force equilibrium equation for the upper trapezoidal block is mathematically expressed as

$T_{\text{GA}}=\frac{\left(Q_{\text{GS}}+Q_{\mathrm{G}}-F_{\mathrm{n}}\right)L_G}{2\left(h_{\text{Gb}}-L_{\mathrm{G}}\mathit{tan}{\beta }_{\mathrm{G}1}\right)}+\frac{2L_{\text{GT}}{Q}_{\text{GT}}\mathit{cos}{\theta }_{\mathrm{G}}}{2h_{\text{Gb}}-L_{\text{GT}}\mathit{sin}{\beta }_{\mathrm{G}2}}$

where θ_G is the bottom angle of the arc-shaped key triangle blocks on both sides of the upper key stratum, °; L_G is the length of the upper trapezoidal block along the strike direction, m; h_Gb is the thickness of the upper trapezoidal block, m; β_G1 is the rotation angle of the upper trapezoidal block, °; Q_GT is the sum of gravity and the overlying load of the upper triangular block, MPa; and β_G2 is the rotation angle of the upper triangular block, °.

${\beta }_{\mathrm{G}1}=\mathit{arctan}\frac{h_{\mathrm{c}}-\sum h_{\mathrm{i}}\left(K_{\text{pcmin}}-1\right)}{L_{\mathrm{G}}}$

$L_{\text{GT}}=L_{\mathrm{G}}\sqrt{{\left(L_{\mathrm{G}}/b\right)}^2+1.5}-L_{\mathrm{G}}/b$

${\beta }_{\mathrm{G}2}=\mathit{arctan}\frac{h_{\mathrm{c}}-\sum h_{\mathrm{i}}\left(K_{\text{pcmin}}-1\right)}{L_{\text{GT}}}$

The governing vertical force equilibrium equation for the upper trapezoidal block is mathematically expressed as:

$\begin{array}{ll}\hfill Q_{\text{GS}}& +Q_{\mathrm{G}}-F_{\mathrm{n}}+{\displaystyle {\int }_{L_{\mathrm{D}}}^{L_{\mathrm{G}}}}\zeta \ln \frac{\left[\left(L_{\mathrm{G}}-x\right)\mathit{sin}{\beta }_{\mathrm{G}1}+h_{\text{pcmin}}-h_Z{K}_{\text{pcmin}}\right]}{h_Z\left(K_{\text{pcmax}}-K_{\text{pcmin}}\right)}\left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{G}}}\right)\hfill \\ \hfill & dx-R_{\text{GC}}-\frac{2\left[3T_{\text{GT}}\left(h_{\mathrm{b}}-L_{\text{GT}}\mathit{sin}{\beta }_{G2}\right)\mathit{cos}{\theta }_{\mathrm{G}}-Q_{\text{GT}}{L}_{\text{GT}}\mathit{cos}{\beta }_{\mathrm{G}2}\right]}{3L_{\text{GT}}\mathit{cos}{\beta }_{\mathrm{G}2}}-R_{\text{GA}}=0\hfill \end{array}$

The moment equilibrium equation governing the upper trapezoidal block can be expressed as

$\begin{array}{ll}\hfill R_{\text{GC}}L& -{\displaystyle {\int }_{L_{\mathrm{D}}}^{L_{\mathrm{G}}}}x\zeta \ln \frac{\left[\left(L_{\mathrm{G}}-x\right)\mathit{sin}{\beta }_{\mathrm{G}1}+h_{\text{pcmin}}-h_Z{K}_{\text{pcmin}}\right]}{h_{\mathrm{Z}}\left(K_{\text{pcmax}}-K_{\text{pcmin}}\right)}\hfill \\ \hfill & \left(b-\frac{2x}{\mathit{tan}{\theta }_{\mathrm{G}}}\right)\hspace{0.17em}dx+R_{\text{GT}}{L}_{\mathrm{G}}\hfill \\ \hfill & -\frac{T_{\text{GC}}\left(h_{\mathrm{b}}-L_{\mathrm{G}}\mathit{sin}{\beta }_{\mathrm{G}1}\right)}{2}-T_{\text{GT}}\mathit{sin}{\theta }_{\mathrm{G}}\mathit{cos}{\theta }_{\mathrm{G}}\hfill \\ \hfill & \left(h_{\mathrm{b}}-L_{\text{GT}}\mathit{sin}{\beta }_{\mathrm{G}2}\right)=\frac{\left(Q_{\text{GS}}+Q_{\mathrm{G}}-F_{\mathrm{n}}\right)L}{2}\hfill \end{array}$

3.2.3 Instability analysis of lower and upper trapezoidal blocks

Through the aforementioned calculations, the instability coefficients k_D1, k_D2, k_G1 and k_G2 are established. Specifically, k_D1 (k_G1) serves as the criterion for assessing the sliding instability of lower (uupper) trapezoidal blocks, with the condition for sliding instability being k_D1 (k_G1)≤1. Similarly, k_D2 (k_G2) is utilized as the criterion for evaluating the rotational deformation instability of lower (upper) trapezoidal blocks, where the condition for rotational deformation instability is k_D2 (k_G2) ≥1.

$\left\{\begin{array}{c}{k}_{\mathrm{D}1}=\frac{T_{\text{DA}}\mathit{tan}{\phi }_{\mathrm{D}}}{R_{\text{DA}}},k_{\mathrm{D}2}=\frac{T_{\text{DA}}}{S_{\mathrm{D}}\xi {\sigma }_{\mathrm{t}}}\\ k_{\mathrm{G}1}=\frac{T_{\text{GA}}\mathit{tan}{\phi }_{\mathrm{G}}}{R_{\text{GA}}},k_{\mathrm{G}2}=\frac{T_{\text{GA}}}{S_{\mathrm{G}}\xi {\sigma }_{\mathrm{t}}}\end{array}\right.$

where φ_D and φ_G are the internal friction angles of the lower and upper trapezoidal blocks, respectively, °; ξ is the squeezing coefficient of the trapezoidal blocks; σ_t is the ultimate compressive strength of the trapezoidal blocks, MPa; and S_D and S_G are the contact surface areas of the hinge interfaces of the lower and upper trapezoidal blocks, respectively, where S_D specifically represents the interface area between the lower trapezoidal blocks, whereas S_G corresponds to the interface area between the upper trapezoidal blocks.

4 Results and analysis

4.1 Parameters of the mechanical model

The parameters of the mechanical model for both the lower and upper trapezoidal blocks are detailed in Table 1, and the other parameters are shown in Figure 1.

Table 1

Table 1. Calculation parameter of mechanical model.

4.2 Stability transformation law of lower and upper trapezoidal blocks during extraction

The stability transformation characteristics of the lower and upper trapezoidal blocks under severe and weak periodic pressures are shown in Figure 7.

(1) Under severe periodic pressure, the k_D1 and k_G1 values tend to decrease as the distance from the fracture line decreases, with the rate of decrease gradually diminishing. This phenomenon suggests that with ongoing extraction, the support area of the intact coal seam beneath the trapezoidal blocks progressively decreases, leading to a reduction in the normal stress acting on the blocks and consequently increasing their susceptibility to sliding instability. When the working face is 18 m away from the fracture line, the k_G1 value reaches the critical value of 1. As the working face continues to be extracted, the upper trapezoidal block experiences sliding instability, whereas the lower trapezoidal block does not. Notably, at every mining position, k_D1>k_G1, indicating that, compared with the upper trapezoidal block, the lower trapezoidal block is not prone to sliding instability, which is very beneficial for the lower trapezoidal block to bear the load above. During weak periodic pressure, the decreasing trends of the k_D1 and k_G1 values are the same as those during severe periodic pressure.

(2) During periodic pressure, the k_D2 and k_G2 values remain invariant with respect to mining advance, consistently maintaining values below the critical threshold of 1.0. This effectively eliminates the potential for rotational deformation instability in both the lower and upper trapezoidal blocks throughout the mining process.

(3) Comparative analysis of the stability variation between severe and weak periodic pressure conditions reveals distinct behavioral patterns for the lower trapezoidal block. Within the range of 10 m $\ge$ L_H $\ge$ 0 m, the k_D1 value during severe periodic pressure is less than that during weak periodic pressure, indicating that the lower trapezoidal block is more stable during weak periodic pressure and is not prone to sliding instability. Conversely, in the range of 23 m $\ge$ L_H > 10 m, this trend reverses. The k_G1 value during severe periodic pressure is greater than that during weak periodic pressure, indicating that the lower trapezoidal block is less prone to rotary deformation instability during weak periodic pressure.

Figure 7

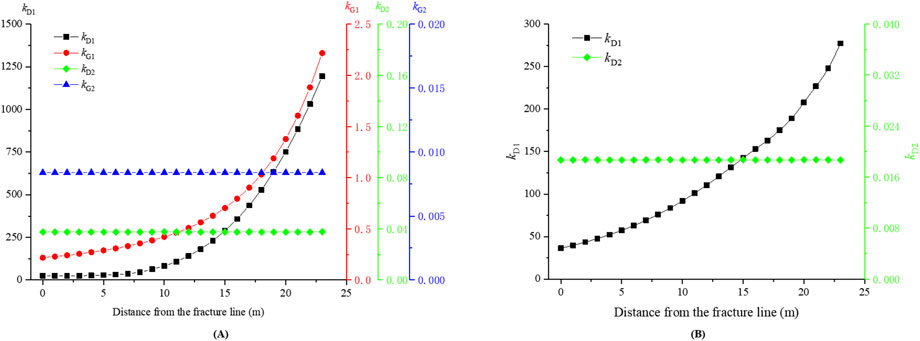
Figure 7. Stability transformation law of trapezoidal blocks. (A) Severe periodic pressure; (B) Weak periodic pressure.

4.3 Stability interaction law of lower and upper trapezoidal blocks

Through the integration of k_D1 and k_G1, F_n can be offset, and the sliding stability interaction relationship between the lower and upper trapezoidal blocks can be obtained. Analogously, with the integration of k_D2 and k_G2 in the formula, the rotary deformation stability interaction relationship between the lower and upper trapezoidal blocks can be obtained. Figure 8 illustrates these interaction laws through analysis conducted at three critical working face positions (0 m, 5 m, and 10 m) relative to the key stratum fracture line.

(1) The k_G1 value increases with increasing k_D1 value, but the rate of increase gradually diminishes, demonstrating that enhanced sliding stability in the lower trapezoidal block nonlinearly elevates the sliding stability of the upper trapezoidal block. Nevertheless, with the improvement in the sliding stability of the lower trapezoidal block, the influence on the sliding stability of the upper trapezoidal block gradually weakens.

(2) The k_G2 value decreases with increasing k_D2 value, and the rate of decrease gradually decreases, revealing that enhanced rotational deformation stability in the lower trapezoidal block inversely correlates with rotational deformation stability in the upper trapezoidal block. With increasing rotational deformation stability of the lower trapezoidal block, the impact on the rotational deformation stability of the upper trapezoidal block gradually weakens.

Figure 8

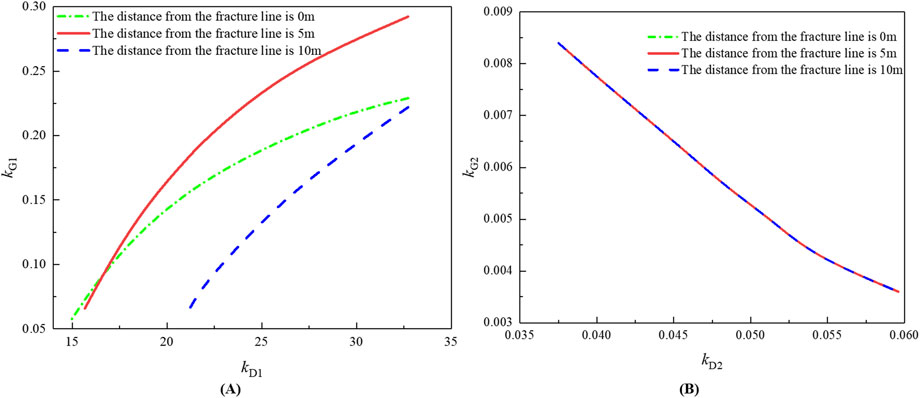
Figure 8. Stability interaction relationship of the lower and upper trapezoidal blocks. (A) k_D1 and k_G1; (B) k_D2 and k_G2.

4.4 Influence of the distance between the lower and upper key strata on the trapezoidal block

Figure 9 systematically illustrates the stability evolution of the lower and upper trapezoidal blocks with different distances between the lower and upper key strata, analyzed at three critical advance positions (0 m, 5 m, and 10 m) relative to the key stratum fracture line.

(1) As depicted in Figure 9A, the distance between the lower and upper key strata increases from 10 m to 100 m. When the working face is 0 m, 5 m, and 10 m away from the fracture line, the k_D1 values decrease from 41.12, 46.01 and 96.48 to 4.64, 20.71 and 69.39, and the k_G1 values decrease from 42.75, 2.21 and 0.83 to 0.01, 0.01 and 0.12, respectively. This phenomenon indicates that an increase in the distance between the lower and upper key strata significantly compromises the sliding stability of the lower and upper trapezoidal blocks, which can easily induce sliding instability in the lower and upper trapezoidal blocks, with the sliding instability of the lower trapezoidal block demonstrating heightened sensitivity to changes in the distance between the lower and upper key strata.

(2) As shown in Figure 9B, the k_G1 and k_G2 values do not change with increasing distance from the fracture line. When the distance from the fracture line is 0 m, 5 m, or 10 m, the variation laws of k_G1 and k_G2 with the distance between the lower and upper key strata are the same. The distance between the lower and upper key strata increases from 10 m to 70 m, k_G1 at 0 m, 5 m, and 10 m from the fracture line decreases from 0.0012 to 0.0001, whereas k_G2 increases from 0.0135 to 0.0300. Notably, this inverse proportionality suggests that enhanced rotational deformation stability in the lower trapezoidal block (by increasing the distance between the lower and upper key strata) occurs at the expense of rotational deformation stability in the upper trapezoidal block.

Figure 9

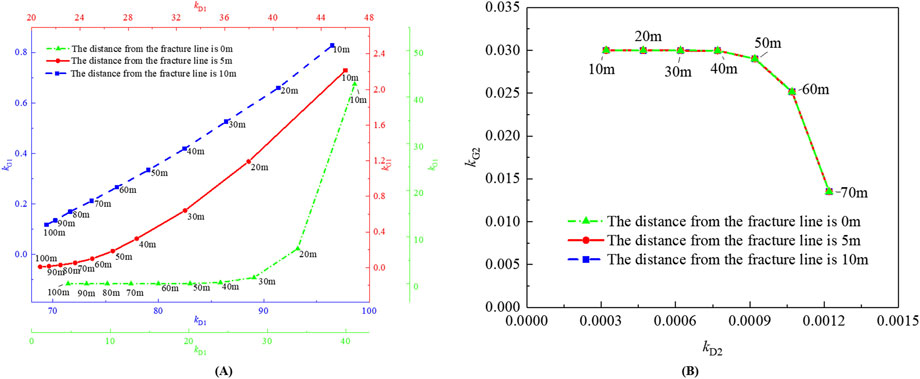
Figure 9. Influence of the distance between the lower and upper key strata on the stability of the lower and upper trapezoidal blocks. (A) k_D1 and k_G1; (B) k_D2 and k_G2.

In short, from both a technical perspective and application conditions, controlling the stability of trapezoidal blocks through changes in the distance between the lower and upper key strata has certain limitations in terms of technique and application. While interlayer distance adjustments partially influence the stability of trapezoidal blocks, they fail to holistically address the competing stability requirements of dual strata in practical engineering scenarios.

4.5 Influence of the mining height on a trapezoidal block

Figure 10 shows the stability evolution of the lower and upper trapezoidal blocks across mining height variations (4–15 m) at three critical advance positions (0 m, 5 m, and 10 m) relative to the key stratum fracture line.

(1) As shown in Figure 10A, an increase in the mining height from 4 m to 15 m increases the k_D1 values at 0 m, 5 m, and 10 m from the fracture line from 9.60, 14.40, and 41.36 to 24.90, 28.70, and 82.50, respectively, whereas the k_G1 values increase from 0.03, 0.19, and 0.33 to 0.22, 0.29, and 0.42, respectively. These results demonstrate that increasing the mining height of the working face can enhance the sliding stability of the lower and upper trapezoidal blocks. Furthermore, the mining height variation has a greater effect on the sliding instability of the lower trapezoidal block than on the sliding instability of the upper trapezoidal block.

(2) As demonstrated in Figure 10B, the k_G1 and k_G2 values exhibit position-independent behavior across the fracture line distance. When the distance from the fracture line is 0 m, 5 m, or 10 m, the variation laws of k_G1 and k_G2 with mining height are the same. The mining height increases from 4 m to 15 m, and the k_G1 value increases from 0.001 to 0.0375, whereas the k_G2 value decreases from 0.028 to 0.0084. This finding indicates that increasing the mining height can reduce the rotational deformation stability of the lower trapezoidal block and enhance the rotational deformation stability of the upper trapezoidal block.

Figure 10

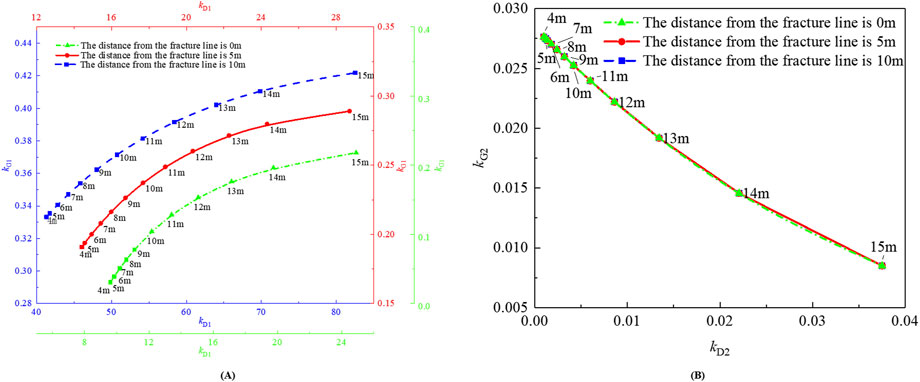
Figure 10. Influence of mining height on the stability of lower and upper trapezoidal blocks. (A) k_D1 and k_G1; (B) k_D2 and k_G2.

In summary, mining height escalation enhances the sliding stability of the lower and upper trapezoidal blocks and the rotational deformation stability of the upper trapezoidal block but significantly reduces the rotational deformation stability of the lower trapezoidal blocks. The lower trapezoidal block is prone to rotational deformation instability. Therefore, relying solely on mining height adjustments for stability control presents inherent limitations.

4.6 Influence of hydraulic support working resistance on the stability of lower and upper trapezoidal blocks

Figure 11 shows the stability evolution of the lower and upper trapezoidal blocks under different working resistances of the hydraulic supports when the working face is positioned 0 m, 5 m, and 10 m from the key stratum fracture line.

(1) Figure 11A shows that increasing the hydraulic support working resistance from 0 kN to 15,000 kN enhances the stability of the lower and upper trapezoidal blocks as follows: the k_D1 values at 0 m, 5 m, and 10 m from the fracture line increase from 13.27, 21.54, and 67.36 to 24.90, 28.70, and 82.50, respectively, whereas the k_G1 values increase from 0.05, 0.18, and 0.36 to 0.22, 0.29, and 0.42, respectively. This progression indicates that enhancing the working resistance simultaneously improves the sliding stability of both the lower and upper trapezoidal blocks, with hydraulic support variations exerting a more significant influence on the lower trapezoidal blocks’ sliding stability than on the upper trapezoidal blocks.

(2) As shown in Figure 11B, the working resistance of the hydraulic supports increases from 0 kN to 15,000 kN, and both the k_D2 and k_G2 values maintain constant values of 0.0375 and 0.0084, respectively. Therefore, the change in the working resistance of hydraulic supports does not affect the stability of the rotational deformation of the lower and upper trapezoidal blocks.

Figure 11

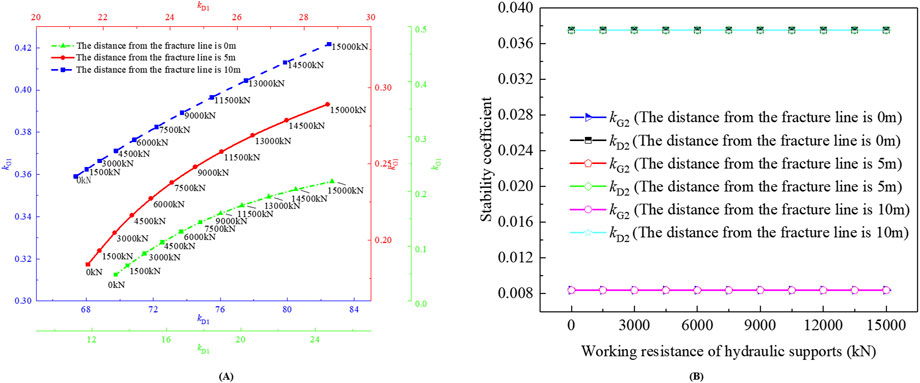
Figure 11. Influence of working resistance on the stability of the lower and upper trapezoidal blocks. (A) k_D1 and k_G1; (B) k_D2 and k_G2.

Notably, variations in working resistance exclusively influence the stability of dual trapezoidal blocks without inhibiting their rotational deformation. The stability of trapezoidal blocks can be adjusted by adjusting the working resistance of hydraulic supports, whereas the rotational behavior is governed by geological constraints.

5 Validation

5.1 Physical similarity simulation

5.1.1 Design and process

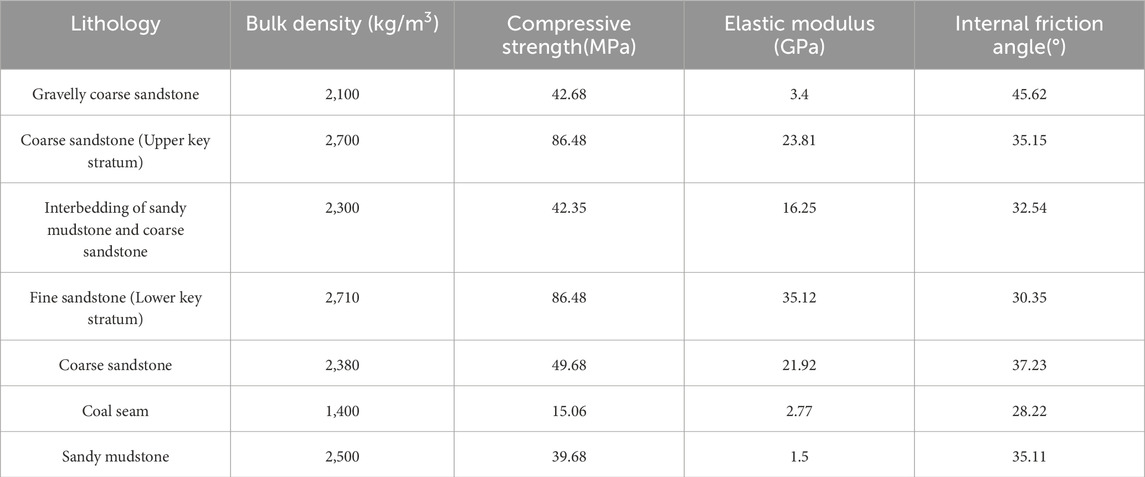
Based on the overlying strata characteristics of the typical FMTC face in the Tongxin coal mine, a physical similarity simulation experiment was conducted using a specifically designed experimental platform measuring 1.8 m in length, 0.16 m in width, and 1.4 m in height. The experimental setup was established with a geometric similarity ratio of 100:1 and a specific gravity similarity ratio of 1.6:1 while maintaining an overburden load of 0.048 MPa on the model surface. The mechanical parameters of the model are presented in Table 2. To monitor the subsidence of the strata accurately during working face extraction, the displacement measuring points were systematically arranged on the model, with horizontal and vertical spacings of 0.1 m, as illustrated in Figure 12A. The coal seam in the model was excavated unidirectionally, with the working face supported by a small-scale support structure fabricated from acrylic material. The model’s excavation time similarity ratio was maintained at 7.07:1.

Table 2

Table 2. Mechanical parameters of the similarity model.

Figure 12

Figure 12. Model building and mining: (A) The model of physical similarity simulation; (B) Layout characteristics of lower and upper key blocks during severe periodic pressure; (C) Layout characteristics of lower and upper key blocks during weak periodic pressure.

5.1.2 Fracture characteristics of rock strata

The fracture characteristics of the key strata under severe and weak periodic pressures are shown in Figures 12B,C.

Simultaneous fracturing of both the lower and upper key strata triggers concurrent collapse of the overlying strata above the upper key stratum and soft rock between the lower and upper key strata, as shown in Figure 12B. This results in the lower key block bearing the combined load from all collapsed overburden strata, inducing severe periodic pressure. In contrast, fracturing of the low-key stratum alone leads to destabilization of soft rock between the lower and upper key strata, as shown in Figure 12C. The low-key block becomes subjected to dual loading mechanisms: gravitational forces from collapsed soft rock and stress transfer caused by elastic deformation of the upper key stratum, manifesting as weak periodic pressure. A comparative analysis of the degree of fracture development of the immediate roof reveals significantly greater damage accumulation under severe periodic pressure conditions than under weak pressure scenarios, confirming enhanced strata pressure manifestation during severe periodic events.

Strain gauges were strategically positioned on the floor of the coal seam to monitor surrounding rock pressure variations following fractures in both the lower and upper key strata, with spatial distribution details illustrated in Figure 13.

Figure 13

Figure 13. Stress distribution of surrounding rock during periodic pressure.

The postfracture observations of the key strata revealed a substantial increase in the abutment stress at the working face. The quantitative analysis revealed that the floor pressure magnitudes at the hydraulic support heads and tails during simultaneous lower and upper key strata fracturing were 2.40 and 3.12 times greater, respectively, than those in the scenarios involving lower key stratum fractures. These measurements clearly reveal that severe and weak periodical pressure characteristics are present in the extraction.

When the distance between the lower and upper key strata approaches infinity, the fracture and spatial configurations of the lower and upper key blocks above the working face are shown in Figure 14A. Compared with Figure 12B, the thickness of the weak rock above the lower key stratum increases with increasing distance between the lower and upper key strata. When the distance reaches a certain value, the working face experiences periodic pressure, the upper key stratum no longer fractures, and the lower key stratum experiences slight sliding instability. The roof and rib of the working face are severely damaged. This phenomenon confirms that increasing the distance between the lower and upper key strata can reduce the sliding stability of lower key blocks.

Figure 14

Figure 14. Layout characteristics of lower and upper key blocks with different influencing factors: (A) Infinite distance between lower and upper key strata; (B) Mining height of 40 mm; (C) Absence of hydraulic supports.

The fracture and spatial configurations of the lower and upper key blocks with increasing mining height are shown in Figure 14B. Compared with Figure 12B, reducing the mining height from 150 mm to 40 mm results in marked sliding instability of the lower key blocks, which confirms the positive correlation between the mining height and sliding stability of the lower key block.

The fracture and spatial configurations of the lower and upper key blocks with changes in the working resistance of the hydraulic supports are shown in Figure 14C. Compared with Figure 12B, during severe periodic pressure, the hydraulic supports are removed, and the lower key block experiences significant sliding instability. The degree of plastic damage to the working face roof and rib increases, and the mining pressure behavior becomes severe. The finding that the sliding stability of lower key blocks increases with increasing working resistance of hydraulic supports has been verified.

5.2 Engineering test

The mine pressure behavior of the 0∼700 m mining advance in the 8309 working face of the Tongxin coal mine was comprehensively analyzed.

The extraction phase exhibited pronounced severe and weak periodic pressure alternations, characterized by key strata fracturing and notable compression deformation in the hydraulic support columns during periods of pressure. As documented in Figure 15A, five critical positions (254 m, 347 m, 394 m, 630 m, and 677 m in advance) initiated severe periodic pressure events, manifesting as (1) catastrophic roof fragmentation, (2) extensive coal rib spallation, (3) rapid surge in hydraulic support resistance, and (4) systematic activation of safety valves. The reasons are as follows: the upper trapezoidal block sliding instability occurred during severe periodic pressure, resulting in the obvious ground pressure behavior of the working face. In the above five mining advances, the lower and upper key strata sliding instabilities occurred at the same time, and the load of the lower key strata and its overlying strata was transmitted to the coal rib and hydraulic supports through the immediate roof, resulting in severe ground pressure behavior of the working face.

Figure 15

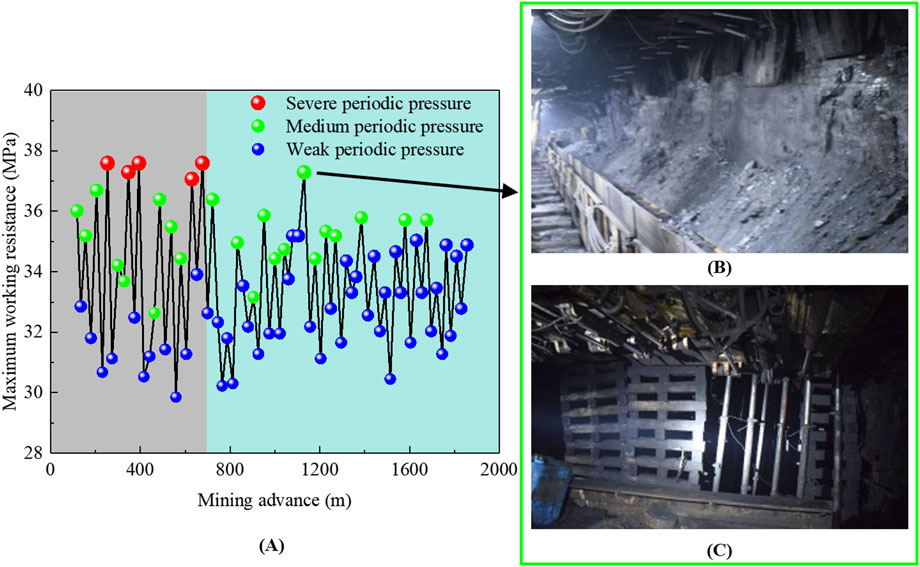
Figure 15. Mining pressure behavior analysis of 8309 working face: (A) Periodic pressure law; (B) Mining pressure behavior of coal rib; (C) Mining pressure behavior of tail entry.

Integrated mechanical modeling and physical similarity simulation analyses revealed that while elevated mining height enhances sliding stability in the lower and upper trapezoidal blocks above the working face, it concurrently elevates rotational deformation instability coefficients in lower blocks, predisposing them to rotational deformation instability. This relationship fundamentally precludes reliable trapezoidal block stabilization through mining height modulation alone. Based on the actual situation of the working face, field practice has introduced enhanced hydraulic support working resistance. Commencing at 700 m, hydraulic supports with a rated working resistance of 15,000 kN increased the initial working resistance from 7,400 kN to 12,800 kN; the effect comparison is shown in Figure 15A.

Postimplementation of enhanced hydraulic support measures, monitoring data confirmed the complete elimination of severe periodical pressure events with a reduction in medium periodical pressure events. As shown in Figures 15B,C, field documentation captured during periodic pressure empirically validates this stabilization strategy, and the roof and rib of the working face are intact, demonstrating that optimized hydraulic support working resistance effectively suppresses trapezoidal block instability.

6 Discussion

Severe periodic pressure, resulting from the simultaneous instability of lower and upper trapezoidal blocks, triggers the failure of the surrounding rock of the working face (Guo et al., 2024). To guarantee safe and smooth mining, implementing strategies to control the rock surrounding the working face becomes essential. The newly proposed stability mechanical model of lower and upper trapezoidal blocks offers a viable solution to such problems. Through comparative analysis of the effects of the distance between the lower and upper key strata, the mining height and the working resistance of hydraulic supports on the stability of the lower and upper trapezoidal blocks, the feasibility of the working face rock stability control method is confirmed. While stability control for working faces with a single key stratum performs well (Qin et al., 2022; Lv et al., 2023; Chen et al., 2023a; b), the complex ground pressure behavior in working faces with multiple key strata leads to poor control effectiveness. In contrast to the traditional single key stratum surrounding rock control method, our control approach provides quantitative guidance for dual key strata working face surrounding rock control, thereby enhancing the control effectiveness.

However, the overlying rock strata above the working face are complex, and the adaptability of idealized mechanical models to actual working conditions on site still needs to be improved. The variation patterns of the sliding instability coefficients and rotational deformation instability coefficients obtained in field instances provide valuable insights into the trends of stability changes in the lower and upper trapezoidal blocks. While these patterns deepen our understanding of the manifestation of mining pressure behavior during extraction, they are insufficient for precisely predicting the magnitudes of these changes. Effective guidance can only be achieved by integrating these insights with actual field observation data.

7 Conclusion

(1) Systematic monitoring of alternating severe and weak periodic pressure patterns in FMTC faces within an extra-thick coal seam enabled the development of a mechanical model for the stability of the lower and upper trapezoidal blocks. The analytical results demonstrate a progressive deterioration in the sliding stability of the lower and upper trapezoidal blocks as the face advances during periodic pressure, whereas the rotational deformation stability remains constant.

(2) The equations of stability interaction revealed the relationship between the sliding and rotational stability mechanisms of the lower and upper trapezoidal blocks. Under fixed advance, the sliding stability coefficient between the lower and upper trapezoidal blocks exhibits a strong positive correlation, whereas the rotational stability coefficient manifests negative interdependence.

(3) Based on mechanical modeling and physical similarity simulations, (i) increasing the distance between the lower and upper key strata decreases the sliding stability of the lower and upper trapezoidal blocks and the rotational deformation stability of the lower trapezoidal block while simultaneously enhancing the rotational deformation stability of the upper trapezoidal block. (ii) Increasing the mining height enhances the sliding stability of both the lower and upper trapezoidal blocks and the rotational deformation stability of the upper trapezoidal blocks but can easily induce instability in the rotational deformation of the lower trapezoidal blocks. (iii) Increasing the working resistance of hydraulic supports effectively enhances the sliding stability of both the lower and upper trapezoidal blocks without affecting their rotational deformation stability.

(4) Field implementation in the Tongxin 8309 working face through initial working resistance optimization of the hydraulic support successfully mitigated severe pressure behavior during periodic pressure. The successful implementation of this operational strategy validated the rationality and reliability of the mechanical model and physical similarity simulation for the stability of the lower and upper trapezoidal blocks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BQ: Writing – original draft, Writing – review and editing. FH: Writing – review and editing. QZ: Writing – review and editing. ZZ: Writing – original draft. GS: Writing – review and editing. XL: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the National Natural Science Foundation of China No. 61933013, and 52374149, and in part by Maoming Science and Technology Plan Project No. 2024009, and 2024021, and the Projects of Talents Recruitment of Guangdong University of Petrochemical Technology, No. 2023rcyj2022.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chai, Y., Dou, L., He, J., Ma, X., Lu, F., and He, H. (2024). Limitations of upper protective layers as pressure relief measures for extra-thick coal seam mining: insights from a case study. Energies 17 (6), 1446. doi:10.3390/en17061446

CrossRef Full Text | Google Scholar

Chen, D. D., He, F. L., and Xie, S. R. (2019). Time-space relationship between periodic fracture of plate structure of the main roof and rebound in the whole region with elastic foundation boundary. Chin. J. Rock Mech. Eng. 38 (06), 1172–1187. doi:10.13722/j.cnki.jrme.2018.0923

CrossRef Full Text | Google Scholar

Chen, D. D., Jiang, Z. S., and Xie, S. R. (2023a). Mechanism and key parameters of stress load-off by innovative asymmetric hole-constructing on the two sides of deep roadway. Int. J. Coal Sci. Technol. 10, 82. doi:10.1007/s40789-023-00635-z

CrossRef Full Text | Google Scholar

Chen, D. D., Zhu, J., Ye, Q., Ma, X., Xie, S., Guo, W., et al. (2023b). Application of gob-side entry driving in fully mechanized caving mining: a review of theory and technology. Energies 16 (6), 2691. doi:10.3390/en16062691

CrossRef Full Text | Google Scholar

Feng, J., Wang, W., Wang, Z., Lou, F., Wang, H., Wu, R., et al. (2023). Study on the mechanism and control of strong rock pressure in thick coal seam mining under the goaf of very close multiple coal seams. Processes 11 (5), 1320. doi:10.3390/pr11051320

CrossRef Full Text | Google Scholar

Guo, J., Huang, W., Feng, G., Bai, J., Li, L., Wang, Z., et al. (2024). Stability analysis of longwall top-coal caving face in extra-thick coal seams based on an innovative numerical hydraulic support model. Int. J. Min. Sci. TECHNO 34 (3), 491–505. doi:10.1016/j.ijmst.2024.04.011

CrossRef Full Text | Google Scholar

Hao, J., Chen, A. F., Li, X. L., Bian, H., Zhou, G. H., Wu, Z. G., et al. (2022). Analysis of surrounding rock control technology and its application on a dynamic pressure roadway in a thick coal seam. Energies 15 (23), 9040. doi:10.3390/en15239040

CrossRef Full Text | Google Scholar

He, W. R., He, F. L., and Chen, D. D. (2020). Pillar width and surrounding rock control of gob-side roadway with mechanical caved mining in extra-thick coal seams under hard-thick main roof. J. Min. & Saf. Eng. 37 (02), 349–358. doi:10.13545/j.cnki.jmse.2020.02.015

CrossRef Full Text | Google Scholar

Jing, H. W., Yin, Q., Yang, S. Q., and Chen, W. Q. (2021). Micro-mesoscopic creep damage evolution and failure mechanism of sandy mudstone. Int. J. Geomech. 21 (3), 04021010. doi:10.1061/(ASCE)GM.1943-5622.0001940

CrossRef Full Text | Google Scholar

Kuang, T. J., Li, Z., Zhu, W., Xie, J., Ju, J., Liu, J., et al. (2019). The impact of key strata movement on ground pressure behaviour in the Datong coalfield. Int. J. ROCK Mech. Min. 119, 193–204. doi:10.1016/j.ijrmms.2019.04.010

CrossRef Full Text | Google Scholar

Li, H. M., Wang, S., and Li, D. Y. (2019). Intelligent ground control at longwall working face. J. China Coal Soc. 44 (1), 127–140. doi:10.13225/j.cnki.jccs.2018.5039

CrossRef Full Text | Google Scholar

Li, Y., Tai, Y., Yu, B., Kuang, T., Gao, R., and Liu, J. (2024). Evolution and control technology of energy aggregation and dissipation of a high hard roof during breakage and destabilization. Int. J. Fract. 245, 1–23. doi:10.1007/s10704-023-00745-4

CrossRef Full Text | Google Scholar

Li, Z. X., Zhang, J. H., Li, Z. H., Heng, S., Wang, S. L., and Tian, Y. N. (2025). Failure characteristics and crack propagation process of coal-rock combinations under mine-induced stress. J. Appl. GEOPHYS 236, 105668. doi:10.1016/j.jappgeo.2025.105668

CrossRef Full Text | Google Scholar

Liu, C. Y., Yang, J. X., and Yu, B. (2015). Support resistance determination of fully mechanized top-coal caving face in extra thick seam under multi-layered hard strata. J. Min. Saf. Eng. 32 (01), 7–13. doi:10.13545/j.cnki.jmse.2015.01.002

CrossRef Full Text | Google Scholar

Liu, Y., Li, Y., and Pu, Y. (2024). Exploring the endogenous structure and evolutionary mechanism of the global coal trade network. ENERG Econ. 136, 107710. doi:10.1016/j.eneco.2024.107710

CrossRef Full Text | Google Scholar

Lou, Z., Wang, K., Kang, M., Zhao, W., Wei, G., Yue, J., et al. (2024). Plugging methods for underground gas extraction boreholes in coal seams: a review of processes, challenges and strategies. J. Nat. Gas. Sci. Eng. 122, 205225. doi:10.1016/j.jgsce.2024.205225

CrossRef Full Text | Google Scholar

Lou, Z., Wang, K., Yao, H. W., Zhao, W., Qin, H. J., Wu, Z. Q., et al. (2025). A novel dynamic filling material for plugging fractures around underground gas extraction boreholes: experimental and engineering performances. Energy 314, 134202. doi:10.1016/j.energy.2024.134202

CrossRef Full Text | Google Scholar

Lv, H., Wang, Z., and Tang, Y. (2019). Experimental study on top-coal breaking and moving rules during fully mechanized top-coal caving mining in extremely thick coal sea. Chin. J. Rock Mech. Eng. 38 (03), 476–486. doi:10.13722/j.cnki.jrme.2018.1276

CrossRef Full Text | Google Scholar

Lv, K., He, F. L., and Xu, X. H. (2023). Fracture characteristics and stability analysis of main roof plate structure with special-shaped load and elastic foundation. Chin. J. Rock Mech. Eng. 42 (4), 930–947. doi:10.13722/j.cnki.jrme.2022.0480

CrossRef Full Text | Google Scholar

Panaedova, G., Borodin, A., Zehir, C., Laptev, S., and Kulikov, A. (2023). Overview of the Russian coal market in the context of geopolitical and economic turbulence: the European embargo and new markets. Energies 16 (19), 6797. doi:10.3390/en16196797

CrossRef Full Text | Google Scholar

Qin, B. B., He, F. L., and Lv, K. (2022). Research on structural stability of main roof trapezoid block in the terminal mining period of fully mechanized top coal caving face of extra thick coal seam. J. Min. & Saf. Eng. 9 (03), 489–498. doi:10.13545/j.cnki.jmse.2021.0168

CrossRef Full Text | Google Scholar

Shi, X. S., Jing, H. W., Chen, W. Q., Gao, Y., and Zhao, Z. L. (2021). Investigation on the creep failure mechanism of sandy mudstone based on micromesoscopic mechanics. Geofluids 2021, 1–19. doi:10.1155/2021/5550733

CrossRef Full Text | Google Scholar

Tu, M., Bu, Q. W., Fu, B. J., and Wang, Y. (2020). Mechanical analysis of mining stress transfer on isolated island face in extra-thick fully mechanized top-coal caving mining. Geofluids 2020, 8834321–8834416. doi:10.1155/2020/8834321

CrossRef Full Text | Google Scholar

Vu, T. T. (2022). Solutions to prevent face spall and roof falling in fully mechanized longwall at underground mines, Vietnam. Min. Min. Depos. 16, 127–134. doi:10.33271/mining16.01.127

CrossRef Full Text | Google Scholar

Wang, J. C., Li, M., Wang, Z. H., Li, Z., Zhang, H., and Song, S. X. (2024). The influence of inter-band rock on rib spalling in longwall panel with large mining height. Int. J. Min. Sci. TECHNO 34 (4), 427–442. doi:10.1016/j.ijmst.2024.03.006

CrossRef Full Text | Google Scholar

Wang, J. C., Yang, S. L., Li, Y., and Wang, Z. (2015). A dynamic method to determine the supports capacity in longwall coal mining. Int. J. Min. Reclam. Env. 29 (4), 277–288. doi:10.1080/17480930.2014.891694

CrossRef Full Text | Google Scholar

Wei, W., Yang, S., Li, M., Jinwang, Z., and Chuanbo, W. (2022). Motion mechanisms for top coal and gangue blocks in longwall top coal caving (LTCC) with an extra-thick seam. Rock Mech. Rock Eng. 55, 5107–5121. doi:10.1007/s00603-022-02928-2

CrossRef Full Text | Google Scholar

Wu, J. Y., Yang, S., Williamson, M., Wong, H. S., Bhudia, T., Pu, H., et al. (2025). Microscopic mechanism of cellulose nanofibers modified cemented gangue backfill materials. Adv. COMPOS Hybrid. MA 8, 177. doi:10.1007/s42114-025-01270-9

CrossRef Full Text | Google Scholar

Wu, Z., Sun, Q., and Wang, Y. (2024). Evolution laws of water-flowing fracture zone and mine pressure in mining shallow-buried, hard, and extra-thick coal seams. Appl. Sci. 14, 2915. doi:10.3390/app14072915

CrossRef Full Text | Google Scholar

Xie, S. R., Wu, Y., Ma, X., Chen, D., Guo, F., Jiang, Z., et al. (2022). Reasonable stopping method and retracement channel support at fully mechanized top coal caving working face of 15 m extra-thick coal seam: a case study. Energy Sci. Eng. 10, 4336–4357. doi:10.1002/ese3.1301

CrossRef Full Text | Google Scholar

Yang, J. Z., Liu, Q. J., and Xu, G. (2021). Strata behavior regularity and overlying strata broken structure of super large mining-height working face with 8.8 m support. J. Min. & Saf. Eng. 38 (04), 655–665. doi:10.13545/j.cnki.jmse.2020.0083

CrossRef Full Text | Google Scholar

Yang, S. L., Wang, J. C., and Li, L. H. (2020). Analysis of deformation and fracture characteristics of key strata based on the medium thick plate theory. J. China Coal Soc. 45 (8), 2718–2727. doi:10.13225/j.cnki.jccs.2020.0366

CrossRef Full Text | Google Scholar

Yu, B. (2016). Behaviors of overlying strata in extra-thick coal seams using top-coal caving method. J. ROCK Mech. Geotech. 8 (2), 238–247. doi:10.1016/j.jrmge.2015.11.006

CrossRef Full Text | Google Scholar

Yu, L., and Yan, S. (2020). The basic principle of roof strata control in fully mechanized caving mining of extra thick coal seam. J. China Coal Soc. 45 (S1), 31–37. doi:10.13225/j.cnki.jccs.2020.0230

CrossRef Full Text | Google Scholar

Zhang, Q., Yue, J., Liu, C., Feng, C., and Li, H. (2019). Study of automated top-coal caving in extra-thick coal seams using the continuum-discontinuum element method. Int. J. ROCK Mech. Min. 122, 104033. doi:10.1016/j.ijrmms.2019.04.019

CrossRef Full Text | Google Scholar

Zhang, X., Zhao, X., and Luo, L. (2022). Structural evolution and motion characteristics of a hard roof during thickening coal seam mining. Front. EARTH SC-SWITZ 9, 794783. doi:10.3389/feart.2021.794783

CrossRef Full Text | Google Scholar

Zhao, Y. Q., Yang, Y. M., Li, X. B., and Wang, Z. Q. (2021). Overlying strata movement and abutment pressure evolution process of fully mechanized top coal caving mining in extra thick coal seam. Geofluids 2021, 1–11. doi:10.1155/2021/7839888

CrossRef Full Text | Google Scholar

Zhou, Y., and Yu, X. Y. (2022). Study of the evolution of water-conducting fracture zones in overlying rock of a fully mechanized caving face in gently inclined extra-thick coal seams. Appl. Sci. 12, 9057. doi:10.3390/app12189057

CrossRef Full Text | Google Scholar

Zhu, W. B., Yu, B., and Ju, J. F. (2020). Experimental study on horizontal “U-Y” periodical breakage characteristics of key strata in stope roof. Coal Sci. Technol. 48 (2), 36–43. doi:10.13199/j.cnki.cst.2020.02.004

CrossRef Full Text | Google Scholar