Joint response characteristics of AE and PSC in coal rheological-impact process

A combined monitoring experiment of pressure stimulated currents (PSC) and acoustic emission (AE) signals was conducted on coal samples under the coupled action of rheology and impact load. The temporal response characteristics of AE and PSC were analyzed, and a nonlinear fitting method was used to obtain the functional relationship between AE increment and the number of impacts. Based on the non-extensive statistical mechanics theory, the non-extensive parameter of the PSC decay process was calculated, and the decay law of PSC over time after impact loading was analyzed. The results show that AE and PSC signals can synchronously reflect the deformation and failure behavior of coal samples under rheological and impact loading conditions. During the impact loading stage, both AE counts and PSC signals exhibit a simultaneous surge, demonstrating distinct instantaneous response characteristics. In the subsequent rheological stage, the AE signal manifests as sporadic counts, while the PSC rapidly decays in a power law manner to a stable value. As the rheological stress level and the number of impacts increase, both the maximum and stable values of the PSC exhibit a gradual decreasing trend. The non-extensive statistical mechanics analysis indicates that PSC decay exhibits non-extensive characteristics, with a significant reduction in before impact failure, suggesting that q can be used to assess coal mass stability.

1 Introduction

During coal mining, rockburst is a common coal-rock dynamic disaster, often occurring several hours to dozens of hours after roadway excavation is completed, making it highly concealed and hazardous (He et al., 2005; Mishra and Verma, 2015; Li et al., 2017). The formation process involves the transition of coal deformation from steady state rheology to non-steady state abrupt failure under high geostress conditions and is often influenced by dynamic disturbances from activities such as mining and blasting (Zhu et al., 2016; 2019; Feng et al., 2022; Kong et al., 2022; Hu et al., 2024; Li et al., 2024a; Li et al., 2025). Therefore, conducting creep mechanical tests on rocks under dynamic load disturbances is a crucial approach to studying the mechanism and process of rockburst occurrence. Moreover, the failure process of coal and rock is accompanied by the release of various forms of energy, including elastic energy, acoustic energy, and electromagnetic energy. Using geophysical methods to monitor the energy release of rock rheological failure under dynamic load disturbance conditions is of great significance for the monitoring and early warning of rockburst disasters in coal mines (Wang and He, 2005; Wang et al., 2012; Wang et al., 2024; Li H. et al., 2021; Li et al., 2024 S.; Kong et al., 2024). This contributes to the sustainable and safe mining of coal, especially in the context of increasing mining depths and the frequent occurrence of dynamic disasters.

The loading of coal-rock materials can induce PSC signals, a phenomenon initially explored in studies on the electromagnetic radiation mechanism of rocks (Warwick et al., 1982). It was not until the early 21st century that PSC generated by loaded rocks gained widespread attention and became an emerging research field among scholars worldwide (Guo, 2015; Tsallis, 2023). Freund (2002), Freund et al. (2006), Freund (2011) conducted experimental studies on the PSC effects in granite, plagioclase, gabbro, limestone, marble, and other rock types under loading conditions. Their findings revealed that even at relatively low stress levels, the samples were capable of generating PSC. To further investigate the PSC response characteristics during rock material damage, many researchers have conducted uniaxial loading, graded loading, and cyclic loading tests on different types of rock materials. Uniaxial graded loading experiments on marble demonstrated that regardless of the stress level, the PSC always decreases to the background value within a short period (ranging from tens to two hundred seconds) (Stavrakas et al., 2003; Triantis et al., 2012). Under constant stress, the PSC decays to a stable value, which remains higher than the pre-loading PSC level. Moreover, this stable PSC value increases with increasing stress levels (Scoville et al., 2015; Stergiopoulos et al., 2015; Li et al., 2021a). Stergiopoulos et al. (2015) conducted three point bending tests on cement mortar samples to study the decay behavior of PSC. Their research verified that the PSC decay follows the principles of non-extensive statistical theory, with the non-extensive parameter gradually increasing as the stress level rises. It reaches its peak at approximately 85% of the peak stress before subsequently declining, confirming the feasibility of using the non-extensive parameter for predicting specimen instability and failure. Li (2020) conducted compression failure experiments on different types of rocks and observed their discharge characteristics. Their study explored the mechanisms of electric generation, discharge, and the ignition of gob gas disasters during the fracture process.

The research on the PSC response of rock materials under loading has so far been conducted primarily under quasi-static loading conditions, while studies on the PSC response during the deformation of rock materials under creep conditions remain largely unexplored. However, due to the characteristics of deep coal mines—such as high geostress, strong rheological behavior of coal-rock masses, and significant influence from dynamic load disturbances—conducting PSC experiments under dynamic load disturbance conditions would be more aligned with the evolutionary process of coal mine dynamic disasters.

Previous research results have consistently shown that the induced current is correlated with applied stress, damage, and deformation, which is highly similar to the AE response during coal-rock loading and failure. To investigate the correlation between AE and PSC during the damage process of rock materials, Triantis et al. (2012) conducted three point bending tests at different loading rates, simultaneously measuring AE and PSC signals. Their results demonstrated a high correlation between the two signals, both effectively reflecting the damage process of cement mortar samples. Subsequently, Kourkoulis et al. (2018) further studied the tensile failure of marble samples by integrating PSC, AE, and three dimensional digital image correlation (3D DIC) techniques. These studies provide a research foundation for the feasibility of using combined AE and PSC monitoring to assess coal mass damage and deformation.

AE is highly sensitive to the instant of coal-rock material fracture but has a weaker response during the phase from the onset of loading to failure, making it difficult to fully characterize the damage evolution process of rock. In contrast, the PSC has high sensitivity and enables continuous monitoring, providing a complementary advantage to AE. While extensive research has been conducted on the response patterns of either AE or PSC signals during conventional coal-rock loading and failure processes (Li et al., 2015; Li et al., 2021b; Li et al., 2023), studies on the synchronous response of AE and PSC during the creep process under dynamic disturbance conditions remain unexplored.

Therefore, considering the characteristics of deep coal mine roadways and surrounding rock—such as significant rheological behavior, susceptibility to mining-induced disturbances, and strong disaster concealment—this study conducts a combined AE-PSC monitoring experiment on coal under the combined action of rheological and impact loads. The temporal response characteristics of AE and PSC signals are analyzed, with a specific focus on PSC signals. Using a nonlinear fitting method, the functional relationship between PSC increments and the number of impacts is derived. Furthermore, based on non-extensive statistical mechanics theory, the non-extensive parameter q for the PSC decay process is calculated, and the decay law of PSC over time after impact loading is analyzed. The research findings provide valuable insights into the mechanism of PSC generation and enhance the applicability of this technology in coal mining safety monitoring.

2 Experimental equipment and testing scheme

2.1 Experimental equipment

2.1.1 Rheology-impact loading test system

The rheology-impact loading system integrates the ALT1000 static hydraulic system and the Hopkinson bar system to achieve synchronized axial static and impact dynamic loading. The ALT1000 static hydraulic system consists of a hydraulic cylinder, a hydraulic station control system, a pressure loading control system, a pressure operation display, and a static strain acquisition system. Through program control, the system can set the required loading speed for the experiment, enabling loading, unloading, and force maintenance at various force-control speeds.

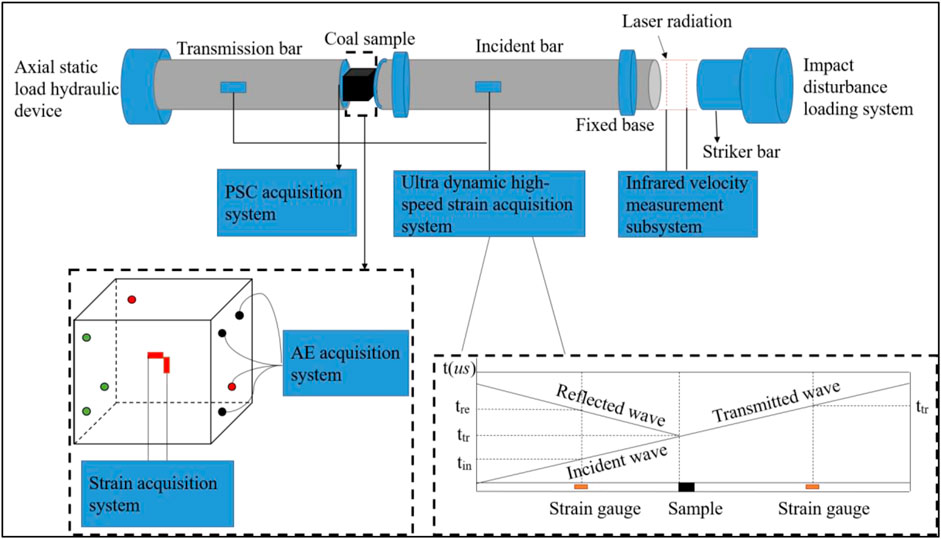
The static strain acquisition system consists of a static strain acquisition instrument, an acquisition system, and strain gauges. The dynamic impact tests are primarily conducted using the Hopkinson pressure bar system, which includes a high pressure chamber, an infrared velocimeter, an energy absorption device, a super dynamic strain acquisition instrument, and the main body of the pressure bar. The main body of the pressure bar consists of an impact bullet, an incident bar, and a transmission bar. The bars have a diameter of 100 mm and lengths of 400 mm, 5,000 mm, and 3,000 mm, respectively. They are all made of 30CrMoSiNi2A steel, with an elastic modulus of 210 GPa and a wave propagation speed of 5,100 m/s. During testing, the specimen is placed between the incident bar and the transmission bar. The data acquisition for the dynamic impact process is primarily achieved using strain gauges attached to the incident and transmission bars, strain bridge connection boxes, and a super dynamic strain acquisition instrument. The experimental system is illustrated in Figure 1.

Figure 1

Figure 1. Rheology-impact loading test system.

2.1.2 PSC acquisition system

The PSC signal acquisition system primarily consists of a Keithley 6517B electrometer, shielded connection cables, electrode sheets, a computer, and signal acquisition software. The Keithley 6517B electrometer has a current measurement range of 10^–12–20 mA and a reading rate of 425 readings per second. Electrode sheets are attached to both ends of the specimen, enabling the rapid and high precision real time acquisition of PSC response signals within high resistance materials such as coal and rock. A current signal acquisition program developed based on LabVIEW is used for real time display and storage of the acquired PSC data. The physical setup of the PSC signal acquisition system is shown in Figure 2.

Figure 2

Figure 2. PSC acquisition system.

2.1.3 AE acquisition system

The AE signals are acquired and stored using the Express-8, a 24-channel AE system produced by Physical Acoustics Corporation (PAC). This system includes AE sensors, preamplifiers, the AEwin RockTest for Express-8 software suite, and a main processing unit. In this experiment, seven NANO-30 AE sensors were used, with an operating frequency range of 150–400 kHz and a resonance frequency of 300 kHz. During testing, the sensors were tightly attached to the specimen’s surface. Based on the sensor sensitivity and environmental noise test results, the AE signal acquisition parameters were set as follows: the signal acquisition threshold was set to 30 dB, the sampling rate was 1 MSPS, and the preamplifier gain was 40 dB. The AE signal acquisition system is shown in Figure 3.

Figure 3

Figure 3. AE acquisition system.

2.2 Experimental scheme

The rheological test is conducted by applying a preset axial constant stress to the specimen using the static hydraulic system, while the SHPB impact loading system is used to apply an impact load with a preset impact velocity. The specific experimental steps include.

2.2.1 Specimen installation

The specimen is placed at the center of the end faces of the incident bar and the transmission bar. Square copper electrode sheets, measuring 80 mm × 80 mm with a thickness of 0.5 mm, are positioned between the specimen ends and the bar end faces. The electrode sheets are connected to a Keithley 6517B electrometer via shielded cables. Subsequently, the axial static hydraulic system is activated, and an initial stress of 0.1 MPa is applied to the specimen using a force-controlled mode to pre-tighten the specimen.

2.2.2 Connection and parameter configuration of the AE-PSC monitoring system

The AE monitoring system, Keithley 6517B electrometer, and TST3830 dynamic-static strain acquisition instrument are assembled and set up. The AE sensors, strain gauges, and electrode sheets attached to the specimen surface are then connected to their respective monitoring devices. Subsequently, the parameters of each instrument are adjusted and configured for data acquisition.

2.2.3 Experimental loading

The loading is controlled programmatically, applying stress at a rate of 0.05 MPa/s until reaching the preset axial constant stress value. Once the target stress is reached, the force is maintained, allowing the specimen to undergo rheological deformation under constant stress. Every 4 h during the rheological phase, the SHPB system is used to apply cyclic impact disturbances with the same impact velocity. Each cyclic impact consists of four shocks. If the specimen does not exhibit significant inertial fracture under the cyclic impact load, the rheology-impact test process is repeated. Throughout the application of rheological stress and impact load, strain, AE, and PSC signals are synchronously collected.

2.2.4 End of the experiment

When the specimen undergoes significant through-going fracture due to prolonged rheological deformation and multiple cyclic impacts, it is considered to have failed, marking the end of the experiment. At this point, the collection of strain, AE, and PSC signals is simultaneously stopped. The experimental process is shown in Figure 4.

Figure 4

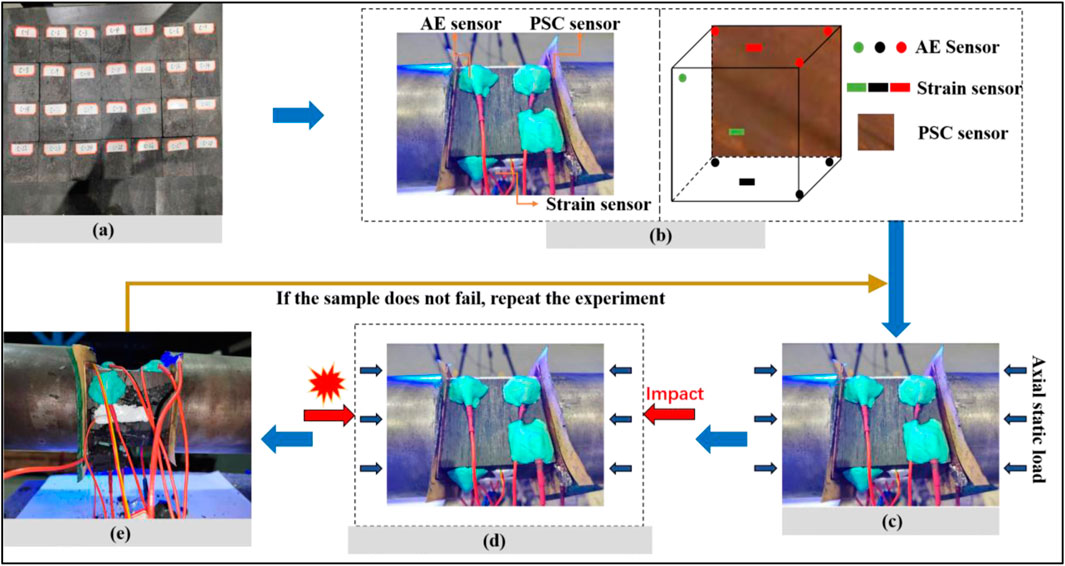
Figure 4. Flow chart of rheological-impact test. (a) Sample preparation. (b) Sensor installation. (c) 4-hour creep loading. (d) 4 impacts with the same vclonocity. (e) Sample failure.

3 Temporal response patterns of PSC and AE during the rheology-impact failure process

Figure 5 illustrates the variations in strain, AE counts, and PSC over time during the cyclic rheology-impact failure process of coal sample C9 under test conditions with a rheological stress of 60% and an impact velocity of 4.5 m/s. The results indicate that the coal body generates significant AE and PSC signals during the rheology-impact process, with distinct differences in response between the rheological and impact loading stages. Upon the application of impact load, the specimen undergoes an instantaneous increase in deformation, accompanied by a sudden surge in AE counts and a simultaneous enhancement in PSC intensity. Following the impact load, the specimen continues to experience rheological deformation under sustained rheological stress. After the first two impacts, the rheological deformation of the specimen remains nearly unchanged. However, with subsequent impact loads, the coal sample exhibits a gradual increase in rheological deformation. Eventually, after approximately 1.9 h following the fifth cyclic impact, the specimen undergoes abrupt failure.

Figure 5

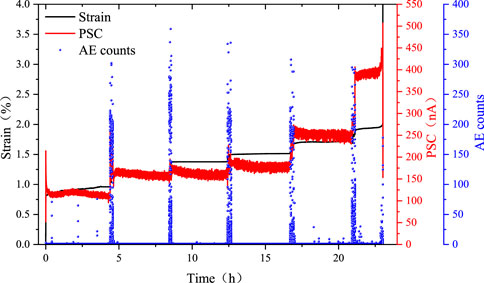
Figure 5. Time variation of AE and PSC during rheology-impact loading and failure of the coal sample.

During the rheological deformation process, the AE count does not show a significant increase. However, slight fluctuations in AE counts are observed during the first rheological stage and the 5th to 6th steady state rheological stages, just before failure. This indicates that under rheological stress, the coal sample undergoes crack compaction and crack propagation, leading to the release of internal elastic energy. The PSC signal is continuously monitored throughout the steady-state deformation process. As the rheological deformation gradually stabilizes, the PSC signal exhibits a macroscopic synchronization with the deformation pattern of the coal sample.

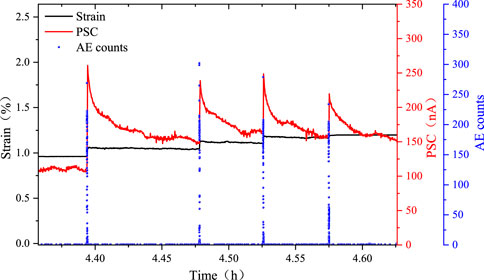
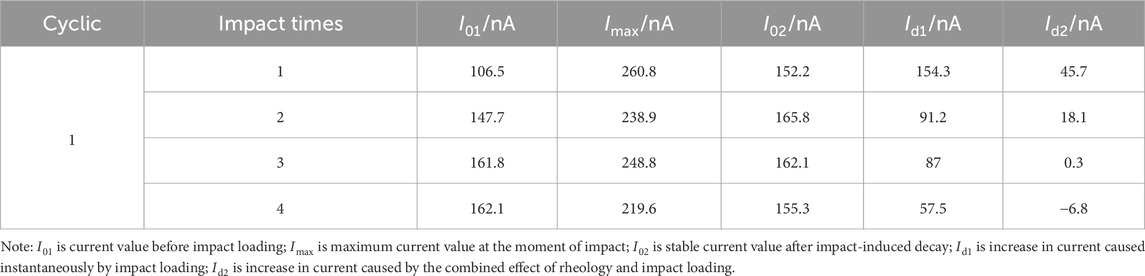
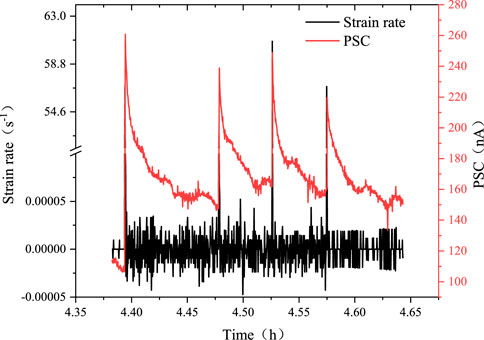
Specimen C9 underwent four tests with the same impact velocity during the first cyclic impact, with the variations in AE, PSC, and deformation under the combined effects of impact and rheological stress recorded in real-time, as shown in Figure 6. At the moment of impact loading, strain, AE, and PSC signals exhibit a simultaneous surge, with the PSC signal displaying a distinct peak. After reaching its peak value, the specimen remains under sustained rheological stress, causing the PSC to decay in a power law manner and gradually relax to a stable value. The stable current value after each impact varies slightly but remains higher than the pre-impact level. A statistical analysis of PSC parameter variations during the cyclic impact process is presented in Table 1, and based on this data, the curve of PSC increment versus impact count is plotted in Figure 7.

Figure 6

Figure 6. Time variation of strain, AE, and PSC during the first cyclic impact of specimen C9.

Table 1

Table 1. PSC variation of sample C9 under impact.

Figure 7

Figure 7. Variation of PSC increment with impact count.

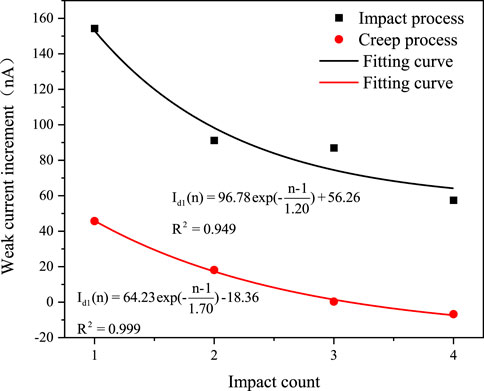
From the parameter statistics in Table 1 and the trend shown in Figure 7, it can be observed that under the same impact velocity and rheological stress conditions, the peak value of the PSC gradually decreases with an increasing number of impacts. Both the sudden surge amplitude and the increment after stabilizing also decrease progressively with each impact. This indicates that PSC exhibits a significant time-dependent effect during the initial damage and deformation process of the rock. Its variation pattern follows the equation:

$I_{d1}\left(n\right)=C·\exp \left(-\frac{n-1}{\lambda }\right)+B,n\in \mathrm{N}(1)$

Where, $\lambda$ is factor related to damage evolution, $n$ is number of loading cycles, C is factor representing the value approaching $n=1$.

Equation 1 describes the variation of the maximum PSC increment with the number of impacts under the same impact conditions but does not reflect the relationship between specimen deformation and PSC changes. From Figure 8, it is evident that strain and PSC increase simultaneously at the moment of impact. However, after the impact load is applied, the specimen remains under sustained rheological stress, leading to a gradual increase in strain, while the corresponding PSC gradually decays. This indicates that PSC and strain deformation do not exhibit a linear relationship. Observing the moment of impact, the specimen’s deformation process follows a pattern of instantaneous surge, slowed growth, and eventually no further increase. Correspondingly, the strain rate undergoes an instantaneous increase, followed by a gradual decrease, and eventually approaches 0. Based on this qualitative analysis, there is a positive correlation between PSC magnitude and strain rate.

Figure 8

Figure 8. Variation of PSC with strain rate.

After the impact load is applied, the specimen undergoes minor deformation fluctuations under the influence of rheological stress, but the overall deformation remains insignificant. Correspondingly, the AE signal remains relatively quiet, showing no significant fluctuations or increases, with only sporadic AE counts. To better visualize the temporal variations of AE and PSC at the moment of impact, a magnified plot of AE-PSC signals during impact was created, as shown in Figure 9. During each impact load event, PSC and specimen deformation increase simultaneously, while AE counts exhibit a distinct sudden peak. Prior to this peak, there is almost no significant AE signal. Subsequently, AE counts rapidly decay, accompanied by dense downward parabolic AE signals. Since this process lasts for more than 0.5 s, whereas dynamic impact loading typically occurs within 200–300 μs, which is significantly shorter than 0.5 s, the observed AE count variations must result from the combined effects of dynamic impact loading and static rheological stress.

Figure 9

Figure 9. Time Variation of AE and PSC under single impact and rheological stress.

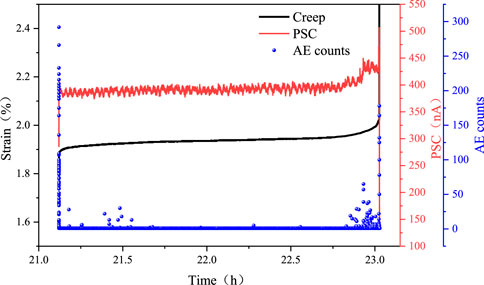
After experiencing both impact and rheological effects, the specimen undergoes sudden failure. Figure 10 illustrates the AE and PSC responses during the microrheological failure process. The results indicate that AE counts exhibit clear phase dependent characteristics during rheological deformation, which can be broadly divided into three distinct stages: (1) Initial active phase. After the application of impact load, the specimen quickly enters the decelerated rheological stage, where strain continues to increase, but the rate of strain increase gradually decreases and stabilizes. At this stage, the specimen is in the initial rheological phase, during which the instantaneous axial stress disrupts the pre-existing stress equilibrium within the coal. The coal matrix and particles undergo slip and dislocation, leading to further crack compaction and closure. The strain energy stored within the coal is released in the form of AE, making AE activity relatively high. (2) Short-term quiescent phase. As rheological deformation transitions into a steady growth phase, most of the weak crystalline units within the specimen are fractured, and cracks become further compacted, leading to an overall increase in coal strength. Consequently, AE activity enters a short-term stable and quiescent period, where minimal AE signals are observed. (3) Accelerated failure active phase. With the continuous accumulation of crack-induced damage, the total strain increases progressively, and internal coal damage becomes the dominant factor. During this stage, the cracks accumulated in the steady-state rheological phase begin to propagate and interconnect. The displacement and slippage of crystalline particles lead to the formation of more macroscale fractures, eventually causing the macroscopic instability and rupture of the coal body. The strain energy stored within the coal is released entirely during the accelerated rheological failure process, with AE signals reaching their peak intensity at the moment of failure. Regarding the corresponding PSC response, during the steady-state rheological deformation phase before failure, the PSC shows a slight increase but remains relatively stable. However, during the final accelerated phase, the PSC exhibits a significant surge, culminating in a sharp spike at the moment of failure.

Figure 10

Figure 10. AE and PSC response patterns during the rheological failure process.

4 PSC attenuation characteristics

By analyzing the deformation and PSC variation of the sample under the influence of rheological-impact forces, it is observed that each time an impact load is applied, it causes significant deformation and a sharp increase in PSC. Subsequently, under the action of rheological stress, the PSC signal generated by the sample gradually decays and eventually stabilizes. Previous studies have shown that after a major earthquake, multiple aftershocks (i.e., seismic events with smaller magnitudes) typically follow. As time passes after the main shock, the frequency of aftershocks gradually decreases and eventually ceases, exhibiting a clear attenuation characteristic (Chmel and Shcherbakov, 2012). Non-extensive statistical mechanics has been widely applied in studying system fluctuations and the process of reaching a stable state. Using non-extensive statistical theory to investigate the PSC decay pattern after an impact can reflect the process where energy, after suddenly accumulating in the coal, gradually dissipates and adjusts towards a balanced equilibrium state.

4.1 Non-extensive statistical mechanics theory

Non-extensive statistical mechanics was developed by Tsallis in 1988 as an extension of extensive statistical mechanics. The core idea involves modifying the classical Boltzmann-Gibbs (B-G) entropy by introducing a non-extensive parameter, leading to a probability distribution in the form of a power law. By leveraging certain relationships from B-G statistical mechanics, Tsallis derived the corresponding statistical mechanics framework for non-extensive entropy (Oghosian BM, 1996; Tsallis C, 2009; Guo, 2015; Stergiopoulos et al., 2015). Non-extensive statistical mechanics has been widely applied in studying system fluctuations and stability processes, particularly in complex systems exhibiting long-range interactions, fractal structures, and anomalous diffusion.

4.1.1 Tsallis entropy

In thermodynamics, entropy was introduced as a state function and later incorporated into statistical mechanics to describe the degree of disorder in a system. Boltzmann and Gibbs refined equilibrium statistical mechanics based on the principle of entropy, leading to the establishment of the Boltzmann-Gibbs (B-G) statistical theory (Tsallis C, 2009), which is defined as:

$S_{B-G}=-k_B{\displaystyle \sum _{i=1}^W}{p}_i\ln p_i(2)$

where, $k_B$ is Boltzmann constant; $W$ is total number of micro states in the system; $p_i$ is the probability of the system being in the $i_{th}$ state is denoted as $p_i$, which satisfies the normalization condition.

When the system is in an equal probability state, the probability of each state is given by $p_i=1/W,\forall i$:

$S_{\mathrm{B}-\mathrm{G}}=\ln W(3)$

However, the Boltzmann-Gibbs (BG) statistical theory is not universally applicable to all systems (Landsberg, 1984). To address this limitation, C. Tsallis extended the BG entropy formulation and proposed the Tsallis entropy, which generalizes the classical entropy definition (Tsallis, 2023).

According to the Boltzmann-Gibbs (BG) entropy formula (Equation 3), its fundamental form is a logarithmic function, which can be expressed as (Equation 4):

$\ln \left(x_A{x}_B\right)=\ln x_A+\ln x_B(4)$

This ensures that the Boltzmann-Gibbs (BG) entropy formula is extensive. Its inverse function is the exponential function, which can be expressed as:

$y=e^x(5)$

Equation 5 can be regarded as the solution to a differential equation under the initial condition y (0) = 1. Based on this, Tsallis proposed a more generalized differential equation (Equation 6) (Tsallis, 2023):

$\frac{\mathrm{d}y}{\mathrm{d}x}=y^q\left(\text{Initial\hspace{0.17em}condition}: y\left(0\right)=1,q\in R\right)(6)$

Solving the differential equation (Equation 7):

$y={\left[1+\left(1-q\right)x\right]}^{1/\left(1-q\right)}(7)$

When $q\to 1$, we obtain the Equation 8:

${\left[1+\left(1-q\right)x\right]}^{1/\left(1-q\right)}={\mathrm{e}}^x(8)$

From this, we obtain the generalized exponential function, given by (Equation 9):

${\mathrm{e}}_q^x\equiv {\left[1+\left(1-q\right)x\right]}^{1/\left(1-q\right)}\left(e_1^x=e^x\right)(9)$

The corresponding generalized logarithmic function is given by:

${\ln }_{q}x\equiv \frac{x^{1-q}-1}{1-q}x>0;{\ln }_{1}x=\ln x(10)$

Substituting Equation 10 into the Boltzmann-Gibbs entropy formula (Equation 2), we obtain the Tsallis q-entropy, expressed as Equation 11:

$S_q=k_B\frac{1-{\displaystyle {\sum }_{i=1}^W}{p}_i^q}{q-1}(11)$

Where, q is non-extensive parameter.

When $q\to 1$, we obtain the Equation 12:

$S_1\equiv \underset{q\to 1}{\lim }{S}_q=S_{\text{BG}}(12)$

When the system follows an equal probability distribution, the Tsallis q- entropy can be expressed as Equation 13:

$S_q^T=\frac{1-W·{\left(1/W\right)}^q}{q-1}={\ln }_{q}W(13)$

4.1.2 Reasons for using non-extensive statistical mechanics to study PSC signal attenuation patterns

Many physical phenomena, such as fractals and diffusion of materials (Cao and Wang, 2005; Guo, 2015), energy distribution, and fluctuations, can be effectively described using power law functions. Non-extensive statistical mechanics (NST) extends the traditional exponential probability distribution into a power law probability distribution, making it suitable for analyzing complex systems with various degrees of interactions and correlations. For different levels of system complexity, the non-extensive parameter q serves as a simple and effective characterization metric. It provides a quantitative measure of how much a system deviates from classical extensive behavior, making it widely applicable in multiscale, self-organized, and non-equilibrium physical processes.

Previous studies have shown that coal-rock deformation and fracture under loading generate PSC signals, and the process of crack propagation and evolution significantly affects these signals. Under long term loading, coal deformation typically exhibits nonlinear characteristics, with internal structures experiencing long range interactions and memory effects—both of which align well with the application scope of non-extensive statistical mechanics (NST) (Stergiopoulos et al., 2015). Applied NST to analyze the attenuation of PSC signals during bending fracture experiments on concrete specimens. By continuously recording PSC signals at different stages—including the instant of stress loading, continuous loading, and stress maintenance—they calculated the q values corresponding to different stress levels. Their findings demonstrated that: NST effectively describes the attenuation behavior of stimulated PSC with good fitting accuracy. Changes in the entropy index q provide a reliable evaluation indicator for fracture events. Similarly, Li et al. (2021a) applied NST to analyze PSC attenuation during coal deformation and failure under conventional uniaxial loading. His study successfully characterized PSC decay patterns using NST, achieving good predictive accuracy. These findings suggest that NST is a valid tool for analyzing PSC attenuation in coal-rock materials under conventional uniaxial loading conditions. However, in this study, a rheology-impact loading approach is used, with synchronously recorded PSC signals. A key question arises: Can non-extensive statistical mechanics still be applied to analyze PSC signals under rheology-impact loading conditions? To verify the applicability of this statistical method, it is first necessary to analyze the fundamental attenuation patterns of PSC signals during the rheology-impact loading experiment.

4.2 Non-extensive characteristics of PSC during the rheology-impact process

4.2.1 PSC attenuation law

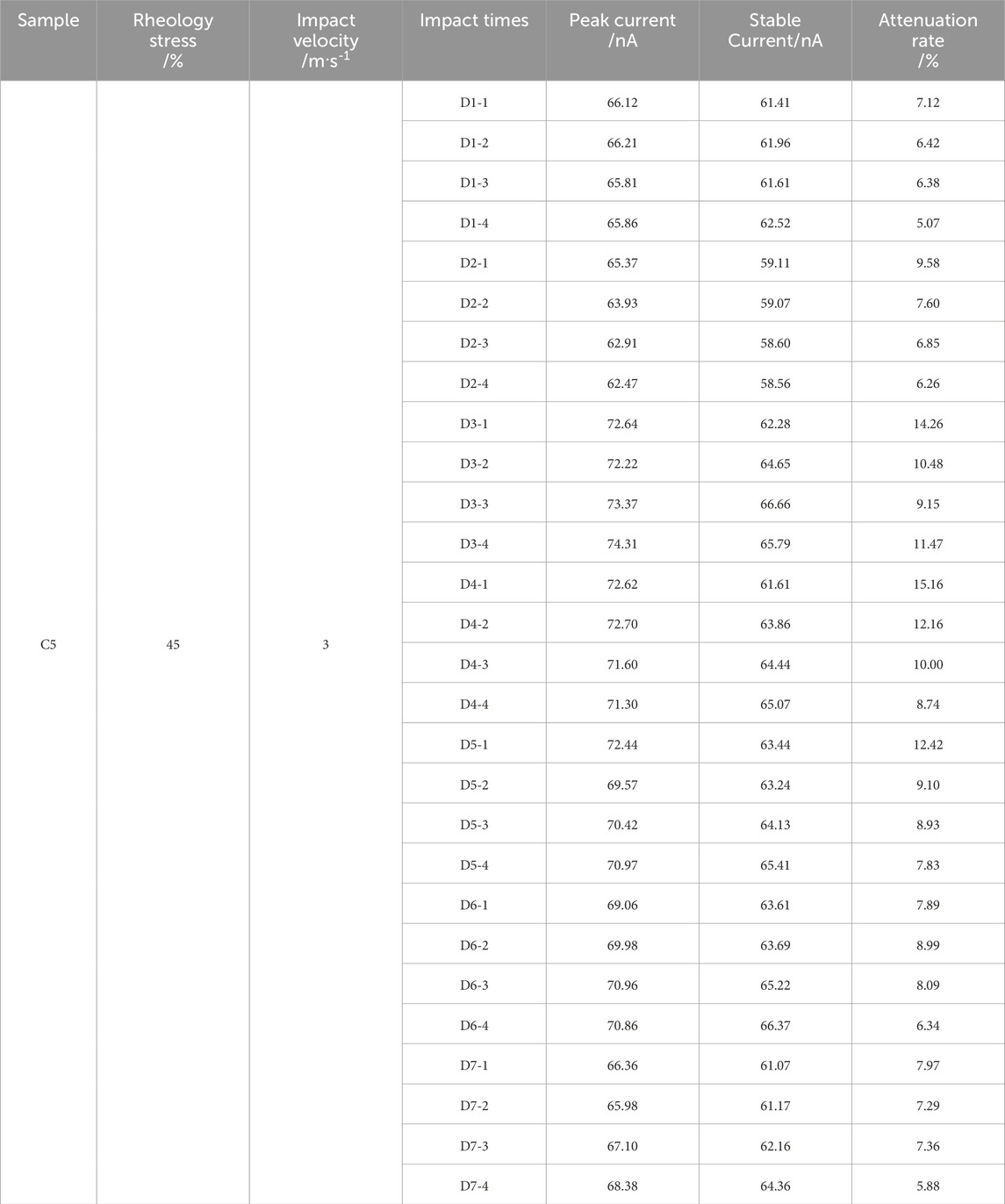
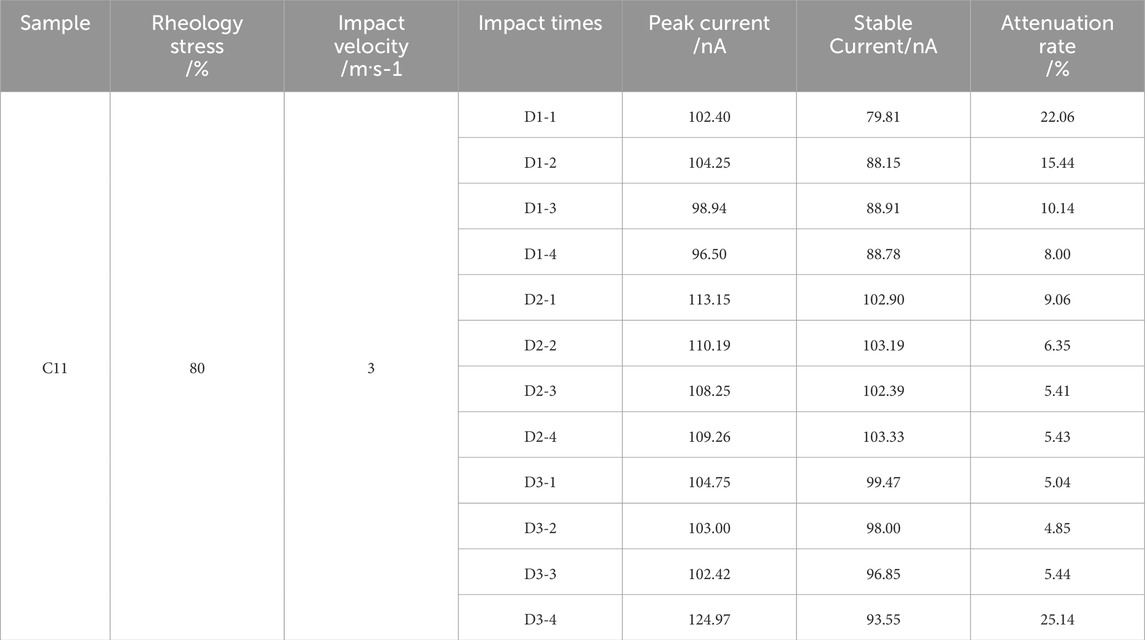
Figures 11, 12 show the PSC attenuation curves of coal samples C5 and C11 under the conditions of rheological stresses of 45% and 80%, respectively, and an impact velocity of 3 m/s during the cyclic rheology-impact process. To facilitate the analysis of the PSC attenuation pattern, the starting time of the PSC response in each rheology-impact process was zeroed. From the figures, it can be seen that after each impact, the PSC attenuation pattern is generally consistent: at the moment of impact loading, the PSC reaches its peak value, and then it gradually decays under the sustained action of rheological stress, ultimately stabilizing. Figures 11a, 12a show the changes in PSC during the initial loading rheological process for samples C5 and C11, where D represents a specific cyclic impact. At the moment of rheological stress loading, the PSC reaches 164 nA and 137 nA, respectively, and then rapidly decreases, stabilizing at around 67 nA and 72 nA after a decay of approximately 2000–2,600 s. Figures 11b–h and Figures 12b–d show the PSC decay process under impact disturbances for samples C5 and C11, where the PSC decay under impact disturbance is more gradual compared to the initial rheological stage. At the moment of each impact, the PSC increases slightly, with the increase amplitude being almost within 10 nA, and then it decays to a stable value after approximately 200–300 s.

Figure 11

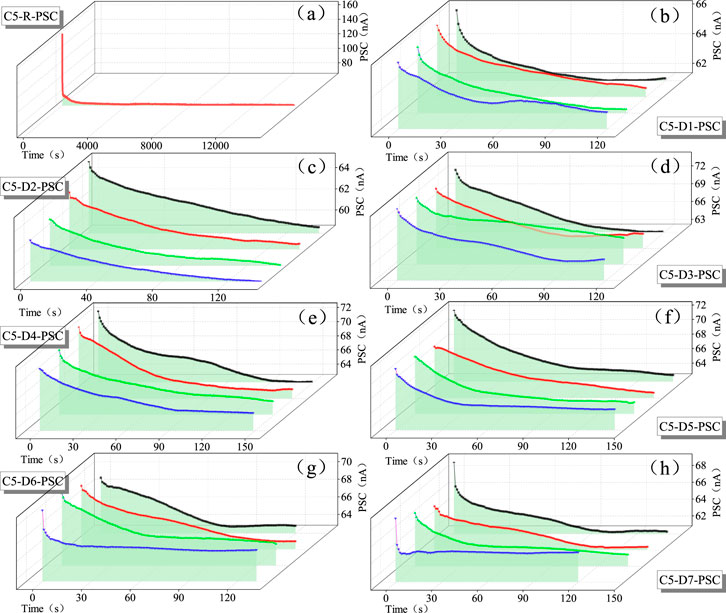
Figure 11. The PSC attenuation curve of the coal sample C5 under rheology-impact loading during the rheological process.

Figure 12

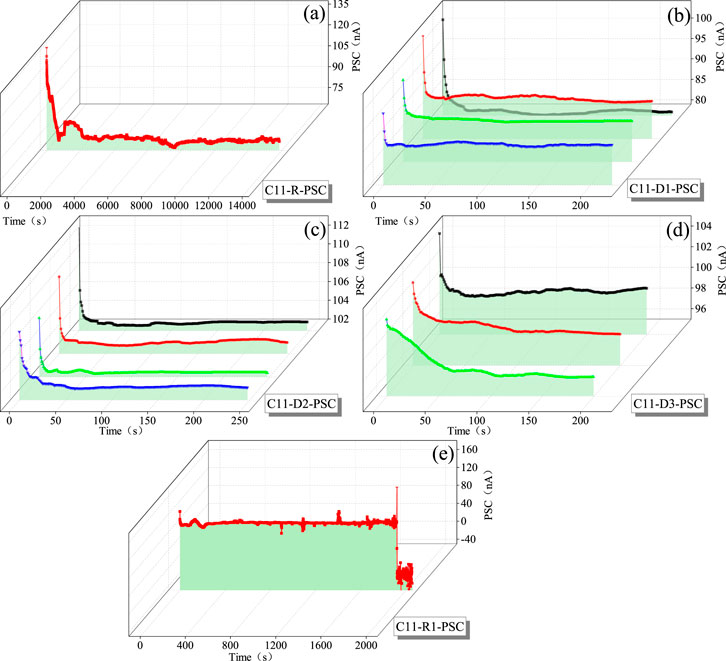
Figure 12. The PSC attenuation curve of the coal sample C11 under rheology-impact loading during the rheological process.

The highest value and the stable value of PSC attenuation in each cycle are defined as $I_H$ and $I_L$, respectively. After the impact, the PSC decays over a certain period and gradually stabilizes. The decay rate R is introduced to represent the extent of PSC decay. The decay rate is defined as the ratio of the decay value after stabilization to the peak PSC value, expressed as:

$R=\frac{I_H-I_L}{I_H}(14)$

Using Equation 14, the decay rates of PSC for coal samples C5 and C11 at different impact cycles are calculated, and the results are shown in Tables 2, 3.

Table 2

Table 2. PSC attenuation parameters of sample C5 under creep-impact conditions.

Table 3

Table 3. PSC attenuation parameters of sample C11 under creep-impact conditions.

Statistical analysis of the time variation of peak current, stable current, and decay rate R is shown in Figure 13. From Figure 13a, it can be observed that under the same rheological stress conditions, the peak current and stable current induced by impact differ, but as the number of impacts increases, their variation becomes less significant, remaining within the range of 60–75 nA. When observing the decay rate variation, it is evident that throughout the rheology-impact process, the decay rate stays below 15% and exhibits a trapezoidal trend: initially increasing steadily, followed by high fluctuations, and finally decreasing and stabilizing at a low level. As shown in Figure 13b, under high rheological stress levels (80%), the instantaneous peak current caused by impact is mostly in the range of 95–125 nA, with the stable current within 80–100 nA. This is significantly higher than the PSC levels observed for sample C5 under a 45% rheological stress condition. This indicates that the magnitude of PSC is closely related to the rheological stress level. As the rheological stress increases, both the instantaneous peak current and stable PSC also increase. As the number of impacts increases, the variations in instantaneous peak current and stable current become smaller, gradually stabilizing. Regarding the decay rate, the PSC decay trend of sample C11 differs from that of sample C5: before rheological failure occurs, the decay rate gradually decreases with each impact. However, during the last impact before rheological failure, the decay rate sharply increases from 5.4% to 21.1%. Despite this, the stable PSC remains almost unchanged, going from 96.85 to 93.55 nA, with a change rate of only 3.4%. This suggests that, under sustained rheological stress, impact loading causes an increase in instantaneous peak current but has a minimal impact on the stable PSC in the subsequent steady state.

Figure 13

Figure 13. The changes in PSC attenuation parameters for the specimen.

4.2.2 Non-Extensive Characteristics of PSC

As shown in Figures 11, 12, the PSC generated by the specimen after experiencing the combined effects of rheology and impact loading exhibits an approximately exponential decay over time. Therefore, non-extensive statistical mechanics can be used to analyze the PSC decay pattern:

$I\left(t\right)=\frac{I_t-I_L}{I_H-I_L}(15)$

Where, $I\left(t\right)$ is normalized PSC; $I_{\mathrm{t}}$ is the PSC at time t; $I_L$ is the stable PSC after decay; $I_H$ is the peak PSC value.

After impact disturbance, the PSC variation follows an exponential decay pattern, which can be expressed as Equation 16:

$\frac{dI\left(t\right)}{dt}=-\alpha I\left(t\right)(16)$

The general form of the PSC decay process, considering a more generalized expression, can be written as Equation 17:

$\frac{dI\left(t\right)}{dt}=-{\alpha }_q{I}^q\left(t\right)(17)$

From this, we can derive the general solution for the PSC attenuation process:

$I\left(t\right)={\left[1-\left(1-q\right)·{\alpha }_q·t\right]}^{1/1-q}=\exp \left(-{\alpha }_q·t\right)(18)$

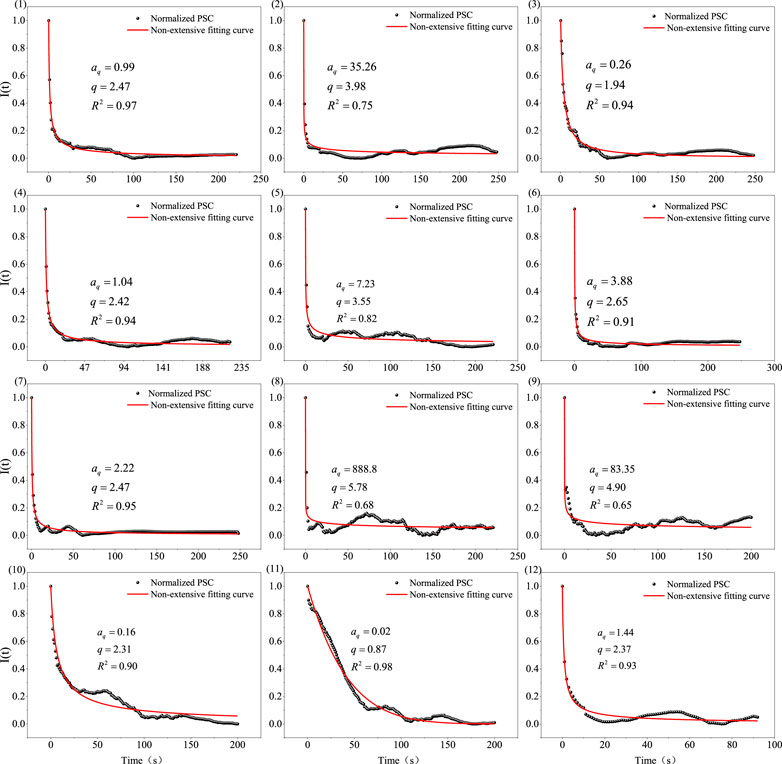
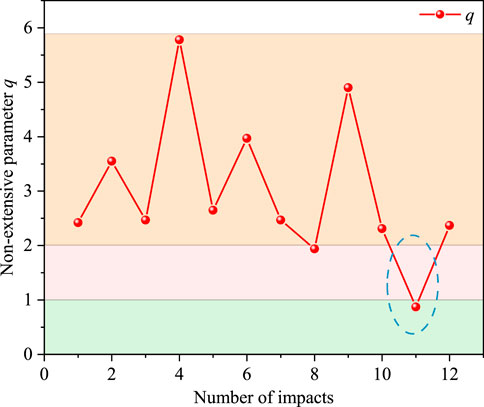
Using Equations 15, 18, the normalized PSC of the specimen under rheology-impact conditions was analyzed and fitted, with the results shown in Figure 14. From the figure, it is evident that non-extensive statistical mechanics performs well in characterizing the PSC decay pattern, indicating that the PSC decay exhibits non-extensive behavior. The non-extensive statistical mechanics fitting parameters for PSC decay under multiple impacts are shown in Table 4. From the table, it can be seen that under rheological stress, the PSC decay parameters vary for the same impact load. Figure 14 reveals that the q value significantly affects the concavity of the curve: the higher the q value, the greater the curvature of the PSC decay curve, and the faster the decay rate. To further understand the variation of the q value under rheology-impact loading, a curve representing the change in q value under multiple impacts is plotted in Figure 15. The figure shows that the q value increases initially and then decreases with the number of impacts. During the first 9 impact cycles, the q value increases overall with each impact. However, after the 10th impact, the q value drops sharply and remains at a lower level during subsequent impacts.

Figure 14

Figure 14. Fitting curves of PSC attenuation in different impact-creep processes.

Table 4

Table 4. Nonextensive parameter q values of PSC attenuation under cyclic impact.

Figure 15

Figure 15. The distribution pattern of the q value with respect to the number of impacts.

The above results indicate that under rheology-impact loading, the PSC exhibits exponential decay, and the decay process generally follows non-extensive statistical mechanics, meaning the PSC decay process after the impact is non-extensive.During the first 10 impact cycles, the non-extensive parameter $q>2$, indicating that the system exhibits non-extensive behavior with increasing complexity. However, after the 11th impact, there is a sharp drop in the q value, and at this point, $q<1$. This sharp decrease suggests the onset of a critical change in the material’s structure, leading to a more disordered state. Following this impact, the specimen undergoes rheological failure, marking the end of the experiment.Therefore, the q value can be used to assess the stability of the coal body, as it provides insight into the material’s structural integrity and failure threshold under cyclic loading.

5 Conclusion

This study investigates the PSC and AE signal responses of coal under the combined action of rheological and impact loads. Using a nonlinear fitting method, a functional relationship was established between the PSC increment and the number of impacts. Based on non-extensive statistical mechanics theory, the attenuation law of PSC signals after impact loading was discussed. The main conclusions are as follows:

(1) AE and PSC signals can synchronously reflect the deformation and failure behavior of coal samples under impact and rheological loading conditions. During the impact loading phase, both the AE count and PSC signals exhibit a sharp surge, demonstrating distinct instantaneous response characteristics. In the subsequent rheological phase, the AE signals show sporadic counts, while the PSC exhibits a decaying trend.

(2) After each impact, the PSC rapidly decays in a power law fashion to a stable value. This attenuation pattern is influenced by the release of impact kinetic energy and the stress wave propagation characteristics. As the rheological stress level and number of impacts increase, both the maximum PSC and the stable PSC show a gradual decreasing trend.

(3) Non-extensive statistical mechanics analysis indicates that the PSC decay exhibits non-extensive characteristics, with a significant decrease in the q value before impact failure. The q value can be used to assess the stability of the coal mass, providing a valuable tool for evaluating the risk of failure or instability in coal under dynamic loading conditions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DW: Conceptualization, Data curation, Investigation, Methodology, Project administration, Resources, Validation, Writing – original draft, Writing – review and editing. XH: Writing – review and editing, Conceptualization. EW: Writing – review and editing, Funding acquisition, Validation. CL: Resources, Writing – review and editing. DL: Formal Analysis, Writing – original draft. ZM: Supervision, Visualization, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52227901, 52204257).

Conflict of interest

Author CL was employed by Shandong Energy Group Luxi Mining Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JY declared a shared affiliation with the authors DW, EW, DL, ZM to the handling editor at time of review.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, K., and Wang, canjun (2005). Tsallis entropy and nonextensive statistical mechanics. J. Yunnan Univ. Nat. Sci. Ed. 27, 514–520.

Google Scholar

Chmel, A., and Shcherbakov, I. (2012). Acoustic, electromagnetic, and photon emission from dynamically fracturing granite. Pure Appl. Geophys. 169, 2139–2148. doi:10.1007/s00024-012-0470-z

CrossRef Full Text | Google Scholar

Feng, X., Ding, Z., Hu, Q., Zhao, X., Ali, M., and Banquando, J. T. (2022). Orthogonal numerical analysis of deformation and failure characteristics of deep roadway in coal mines: a case study. Minerals 12, 185. doi:10.3390/min12020185

CrossRef Full Text | Google Scholar

Freund, F. (2002). Charge generation and propagation in igneous rocks. J. Geodyn. 33, 543–570. doi:10.1016/s0264-3707(02)00015-7

CrossRef Full Text | Google Scholar

Freund, F. (2011). Pre-earthquake signals: underlying physical processes. J. Asian Earth Sci. 41, 383–400. doi:10.1016/j.jseaes.2010.03.009

CrossRef Full Text | Google Scholar

Freund, F. T., Takeuchi, A., and Lau, B. W. S. (2006). Electric currents streaming out of stressed igneous rocks – a step towards understanding pre-earthquake low frequency EM emissions. Phys. Chem. Earth Parts A/b/c 31, 389–396. doi:10.1016/j.pce.2006.02.027

CrossRef Full Text | Google Scholar

Guo, R. (2015). The basic problems and stochastic dynamical foundation of nonextensive statistical mechanics. Tianjin: Tianjin University.

Google Scholar

He, M. C., Xie, H. P., Peng, S. P., and Jiang, Y. D. (2005). Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 24, 2803–2813.

Google Scholar

Hu, J., He, M., Li, H., Tao, Z., Liu, D., Cheng, T., et al. (2024). Rockburst hazard control using the excavation compensation method (ECM): a case study in the qinling water conveyance tunnel. Engineering 34, 154–163. doi:10.1016/j.eng.2023.11.013

CrossRef Full Text | Google Scholar

Kong, X., He, D., Liu, X., Wang, E., Li, S., Liu, T., et al. (2022). Strain characteristics and energy dissipation laws of gas-bearing coal during impact fracture process. Energy 242, 123028. doi:10.1016/j.energy.2021.123028

CrossRef Full Text | Google Scholar

Kong, X., Zhan, M., Lin, H., Cai, Y., Ji, P., He, D., et al. (2024). Time-varying characteristics of acoustic emission and fractals based on information dimension during structural failure of coal subjected to uniaxial compression. Measurement 236, 115088. doi:10.1016/j.measurement.2024.115088

CrossRef Full Text | Google Scholar

Kourkoulis, S. K., Pasiou, E. D., Dakanali, I., Stavrakas, I., and Triantis, D. (2018). Mechanical response of notched marble beams under bending versus acoustic emissions and electric activity. J. Theor. Appl. Mech. 523, 523. doi:10.15632/jtam-pl.56.2.523

CrossRef Full Text | Google Scholar

Landsberg, P. T. (1984). Is equilibrium always an entropy maximum. J. Stat. Phys. 35, 159–169. doi:10.1007/bf01017372

CrossRef Full Text | Google Scholar

Li, D., Wang, E., Feng, X., Wang, D., Zhang, X., and Ju, Y. (2023). Weak current induced by coal deformation and fracture and its response to mine seismicity in a deep underground coal mine. Eng. Geol. 315, 107018. doi:10.1016/j.enggeo.2023.107018

CrossRef Full Text | Google Scholar

Li, D., Wang, E., Ju, Y., and Wang, D. (2021a). Laboratory investigations of a new method using pressure stimulated currents to monitor concentrated stress variations in coal. Nat. Resour. Res. 30, 707–724. doi:10.1007/s11053-020-09749-6

CrossRef Full Text | Google Scholar

Li, D., Wang, E., Li, Z., Ju, Y., Wang, D., and Wang, X. (2021b). Experimental investigations of pressure stimulated currents from stressed sandstone used as precursors to rock fracture. Int. J. Rock Mech. Min. Sci. 145, 104841. doi:10.1016/j.ijrmms.2021.104841

CrossRef Full Text | Google Scholar

Li, H., He, M., Qiao, Y., Cheng, T., and Han, Z. (2024a). Assessing burst proneness and seismogenic process of anisotropic coal via the realistic energy release rate (RERR) index. Rock Mech. Rock Eng. 58, 2999–3013. doi:10.1007/s00603-024-04281-y

CrossRef Full Text | Google Scholar

Li, H., He, M., Xiao, Y., Liu, D., Hu, J., and Cheng, T. (2025). Granite strainbursts induced by true triaxial transient unloading at different stress levels: insights from excess energy ΔE. J. Rock Mech. Geotech. Eng.

Google Scholar

Li, H., Qiao, Y., Shen, R., He, M., Cheng, T., Xiao, Y., et al. (2021c). Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: phenomenon and mechanism. Eng. Geol. 294, 106386. doi:10.1016/j.enggeo.2021.106386

CrossRef Full Text | Google Scholar

Li, M. (2020). Study on the mechanical-electrical signature and ignition properties of coal mine goaf roof. Xuzhou: China University of Mining and Technology.

Google Scholar

Li, S., He, D., Kong, X., Lin, H., Ma, Y., Li, X., et al. (2024b). Relationship between micro-pores fractal characteristics about NMR T2 spectra and macro cracks fractal laws based on box dimension method of coal under impact load from energy dissipation theory. Chaos, Solit. Fractals 189, 115685. doi:10.1016/j.chaos.2024.115685

CrossRef Full Text | Google Scholar

Li, X., Yang, C., Ren, T., Nie, B., Zhao, C., Liu, S., et al. (2017). Creep behaviour and constitutive model of coal filled with gas. Int. J. Min. Sci. Technol. 27, 847–851. doi:10.1016/j.ijmst.2017.07.017

CrossRef Full Text | Google Scholar

Li, Z. H., Wang, E. Y., and He, M. (2015). Laboratory studies of electric current generated during fracture of coal and rock in rock burst coal mine. J. Min. 2015, 1–9. doi:10.1155/2015/235636

CrossRef Full Text | Google Scholar

Mishra, B., and Verma, P. (2015). Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks. Int. J. Coal Geol. 137, 55–65. doi:10.1016/j.coal.2014.11.005

CrossRef Full Text | Google Scholar

Oghosian, B. M. (1996). Thermodynamic description of the relaxation of two-dimensional turbulence using Tsallis statistics. Phys. Rev. E 53, 4754–4763. doi:10.1103/physreve.53.4754

CrossRef Full Text | Google Scholar

Scoville, J., Sornette, J., and Freund, F. T. (2015). Paradox of peroxy defects and positive holes in rocks part II: outflow of electric currents from stressed rocks. J. Asian Earth Sci. 114, 338–351. doi:10.1016/j.jseaes.2015.04.016

CrossRef Full Text | Google Scholar

Stavrakas, I., Anastasiadis, C., Triantis, D., and Vallianatos, F. (2003). Piezo stimulated currents in marble samples: precursory and concurrent-with-failure signals. Nat. Hazards Earth Syst. Sci. 3, 243–247. doi:10.5194/nhess-3-243-2003

CrossRef Full Text | Google Scholar

Stergiopoulos, Ch., Stavrakas, I., Triantis, D., Vallianatos, F., and Stonham, J. (2015). Predicting fracture of mortar beams under three-point bending using non-extensive statistical modeling of electric emissions. Phys. A 419, 603–611. doi:10.1016/j.physa.2014.10.060

CrossRef Full Text | Google Scholar

Triantis, D., Stavrakas, I., Kyriazopoulos, A., Hloupis, G., and Agioutantis, Z. (2012). Pressure stimulated electrical emissions from cement mortar used as failure predictors. Int. J. Fract. 175, 53–61. doi:10.1007/s10704-012-9701-7

CrossRef Full Text | Google Scholar

Tsallis, C. (2009). Introduction to nonextensive statistical mechanics. New York: SpringerPress.

Google Scholar

Tsallis, C. (2023). Introduction to nonextensive statistical mechanics: approaching a complex world. Cham: Springer International Publishing.

CrossRef Full Text | Google Scholar

Wang, D., Ma, Y., Liu, X., Li, D., Liu, Q., Yang, H., et al. (2024). Improving mining sustainability and safety by monitoring precursors of catastrophic failures in loaded granite: an experimental study of acoustic emission and electromagnetic radiation. Sustainability 16, 1045. doi:10.3390/su16031045

CrossRef Full Text | Google Scholar

Wang, E., He, X., Liu, X., and Xu, W. (2012). Comprehensive monitoring technique based on electromagnetic radiation and its applications to mine pressure. Saf. Sci. 50, 885–893. doi:10.1016/j.ssci.2011.08.013

CrossRef Full Text | Google Scholar

Wang, E., He, X., and Yu, G. M. (2005). An experimental study of the electromagnetic emission memory effect during deformation and fracture of coal or rock. Chin. J. Geophys. 48, 419–426. doi:10.1002/cjg2.669

CrossRef Full Text | Google Scholar

Warwick, J. W., Stoker, C., and Meyer, T. R. (1982). Radio emission associated with rock fracture: possible application to the great chilean earthquake of May 22, 1960. J. Geophys. Res. Solid Earth 87, 2851–2859. doi:10.1029/jb087ib04p02851

CrossRef Full Text | Google Scholar

Zhu, W., Li, S., Li, S., and Niu, L. (2019). Influence of dynamic disturbance on the creep of sandstone: an experimental study. Rock Mech. Rock Eng. 52, 1023–1039. doi:10.1007/s00603-018-1642-7

CrossRef Full Text | Google Scholar

Zhu, W., Li, S., Niu, L., Liu, K., and Xu, T. (2016). Experimental and numerical study on stress relaxation of sandstones disturbed by dynamic loading. Rock Mech. Rock Eng. 49, 3963–3982. doi:10.1007/s00603-016-1049-2

CrossRef Full Text | Google Scholar