Study on the mechanical traits, failure mechanisms, energy responses, and influencing factors of columnar jointed basalts under direct and indirect tensile conditions

In this study, by merging mesoscopic damage mechanics, the probabilistic strength principle, and continuum mechanics, the visuals of columnar jointed basalts (CJBs) featuring various joint arrangement patterns are converted into inhomogeneous numerical models utilizing the digital visual analysis based on the digital image correlation (DIC)-enhanced rock failure process analysis (RFPA). The strength–deformation traits, rupture features, and energy progression trends of CJBs subjected to direct tension and indirect tension (Brazilian splitting) are explored and compared. The acoustic emission (AE) energy buildup linked to the specimen’s peak stress is defined as the micro-crack energy index (MCEI), and the impact of multiple factors on the MCEI is analyzed. A factor sensitivity analysis is conducted. The study reveals that compared to the Brazilian splitting condition (BSC), under the direct tensile condition (DTC), the tensile strength (TS) and equivalent deformation modulus (EDM) of specimens in directions I and II (perpendicular to the column axis) are higher. In the direction parallel to the column axis, compared to the DTC, the TS of the specimens under the BSC is lower at the column tilt angle β = 0°–60° and higher at β = 75°–90°. Under the BSC, damage and fracture occur on the joints and columns within a localized area along the longitudinal centerline of the specimen. Considering diverse influencing factors and compared to the DTC, the MCEI for β = 30° specimens appears at a later stage and exhibits a lower magnitude under the BSC. When subjected to the DTC, the sensitivity of the MCEI to diverse factors ranks, in decreasing order, as follows: joint strength, the secondary joint set, joint constitutive behavior, meso-rock strength, and the rock homogeneity index. However, under the BSC, the sensitivity of the MCEI to joint constitutive behavior is higher than that to the secondary joint set. These findings can function as an academic foundation for understanding the sequence of emergence and magnitude differences of MCEIs in CJBs under tensile conditions, thus providing a scientific basis for rock mass engineering monitoring, reinforcement, and operational maintenance.

1 Introduction

Columnar joints comprise primary tensile fracture structures that develop in volcanic rocks, with those occurring in basalt being particularly well-preserved and typical (Xiao et al., 2023). Columnar jointed basalts (CJBs) or columnar jointed rock masses (CJRMs) are located in numerous areas on Earth, including Brazil, Japan, South Korea, the United States, the United Kingdom, China, Israel, and others (Gomes and Rodrigues, 2007; Alves et al., 2025; Yan et al., 2018; Fan et al., 2018; Xu et al., 2020; Lu et al., 2021). The field images related to CJBs are presented in Figure 1 (Vasseur and Wadsworth, 2019; Zhou et al., 2024). Currently, China’s large-scale hydropower projects are mainly concentrated in the mountainous and gorge regions in the southwest of the country, where Emeishan basalt is extensively spread. In particular, the tensile strength (TS) of rock is less than its compressive strength (CS), and the presence of columnar joints tends to weaken the TS of the rock mass, potentially leading to situations such as rock mass fracture and collapse. Under tensile conditions, CJBs typically undergo brittle failure, and their fracture patterns and deformation characteristics differ from those under other conditions. Therefore, conducting in-depth research on the mechanical traits, rupture patterns, and energy features of CJBs under tensile conditions can help better understand the laws governing their mechanical behaviors. This kind of research will enhance the design level, construction quality, and operational monitoring quality of rock mass engineering, which is of substantial importance for the development of the rock mass engineering field.

Figure 1

Figure 1. On-site images of CJBs: (a) the CJBs at Tsumekizaki Izu, Japan (Vasseur and Wadsworth, 2019); (b) the CJBs at Changle, China (Zhou et al., 2024).

Currently, experimental tests in the laboratory and computational modeling studies regarding the mechanical traits of CJBs predominantly focus on their compressive mechanical features (Lin et al., 2017; Zhu et al., 2020; Que et al., 2020; 2024; Niu et al., 2020), while there is scant research on the tensile mechanical traits of CJBs (Xu et al., 2020; Zhu et al., 2023). Concerning indoor physical experiments, Lin et al. (2018) carried out a series of uniaxial compression tests to examine the strength and deformation modulus of CJBs, taking into account different column inclination angles and specimen heights. Lu et al. (2021) implemented uniaxial compression experiments to ascertain the anisotropic properties and failure mechanisms of CJBs. Que et al. (2021) executed uniaxial compression experiments on samples of CJBs with quadrilateral, pentagonal, and hexagonal column cross-sections to analyze their mechanical behaviors. Subsequently, a comparative study was carried out on the strength and deformation anisotropies among these samples. Regarding numerical simulation, Yan et al. (2018) utilized the FLAC3D numerical software application to mimic the mechanical behaviors of CJBs under various column dip angles and stress conditions. They suggested that as the confining pressure increases, the mechanical anisotropy of the CJBs decreases. Zhou et al. (2024) used MATLAB to generate stochastic models of irregular CJBs and then employed 3DEC software application to perform numerical simulations analyzing the size effects of irregular CJBs under compression. Hu et al. (2017) conducted borehole core sampling at the construction site and obtained basalt rock samples containing primary hidden cracks. They carried out uniaxial compression tests in the laboratory and simultaneously collected acoustic emission (AE) information during the deformation and failure process of the basalt rock samples. Wang et al. (2022b), Wang et al. (2022c), and Wang et al. (2023a) employed the rock failure process analysis (RFPA) numerical technique to scrutinize the influences of multiple variables on the mechanical size effect, anisotropy, and fracture mechanisms of CJBs under compressive conditions. The abovementioned research studies mainly examined the mechanical features of CJBs under compressive scenarios, such as their bearing capacity, stress distribution, and failure modes. However, due to the unique structural characteristics of CJBs, mere compressive mechanics research is inadequate to fully elucidate their mechanical properties. In comparison, the study on tensile mechanical properties can further emphasize the vulnerability of CJBs under tensile conditions.

At the engineering site involving CJBs, as excavation operations progress, the stress state within the rock mass gradually changes, particularly with notable unloading effects occurring in rock masses that were originally at higher stress levels. Unloading results in rapid stress discharge within the rock mass, gradual opening of joints, and the formation of localized tensile stress zones. In these zones, the tensile strength of the rock mass cannot withstand the tensile stresses, leading to relaxation, crack extension, and even localized breakdown of the rock mass. Researchers (Jiang et al., 2013; Fan et al., 2018; Xiang et al., 2021; Zhang J. C. et al., 2021) have conducted field investigations, field monitoring, or real-time monitoring for engineering projects involving CJBs. Jiang et al. (2013) performed field investigations and test research on the anisotropic characteristics of CJBs, revealing the anisotropic behavior in strength and deformation of the CJBs in the directions perpendicular and parallel to the column axis. Through field investigations and in situ testing, Fan et al. (2018) found that the relaxation depth of CJBs is related to geo-stress, rock mass quality, and shear zones and that the time impact of unloading loosening in CJBs is evident. Xiang et al. (2021) utilized the AE method to detect in situ blasting signals in CJB tunnels. They proposed that the rock mass can be categorized into three zones, namely, a strongly relaxed zone characterized by numerous AE occurrences and rapid rock distortion, a weakly relaxed zone with moderate rock deformation response, and an undisturbed zone with virtually no AE events. In the test cave at the dam site of Baihetan Hydropower Station, Shi et al. (2020) successfully obtained six in situ basalt rock samples sized 50 cm × 50 cm × 100 cm and carried out in situ true triaxial tests. Zhang Q. L. et al. (2021) conducted ultrasonic P-wave assessments to examine the excavation damage zone in CJBs on a dam foundation. They believed that the unloading loosening of CJBs is chiefly triggered by the time-dependent tensile cracking of joints subjected to tensile stress during the excavation process. The tensile mechanical properties of CJBs hold significant research value as localized tensile stress concentrations often serve as critical triggers for rock mass structural instability, directly impacting the overall stability and safety of engineering endeavors.

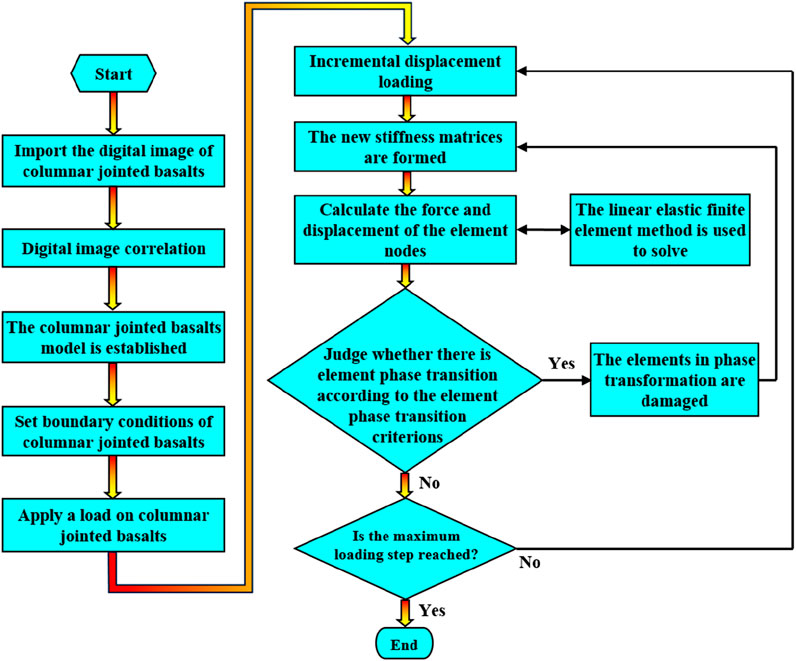
Therefore, based on mesoscopic damage mechanics, probabilistic strength theory, and continuum mechanics, the digital visual treatment is utilized via the digital image correlation (DIC)-enhanced RFPA to convert visual representations of CJBs into inhomogeneous numerical calculation models. Numerical tests on CJBs under the direct tensile condition (DTC) and Brazilian splitting condition (BSC) are then carried out. The strength–deformation traits and fracture features of CJBs are displayed, and the energy progression laws are examined. The cumulative AE energy that matches the sample peak stress is determined as the micro-crack energy index (MCEI), and then the impacts of multiple variables (including the direction perpendicular to the column axis, the column tilt angle, joint constitutive behavior, joint strength, rock homogeneity, meso-rock strength, and the secondary joint sets) on the MCEI are explored. A sensitivity analysis of factors is carried out.

2 Methodology

2.1 Reasoning behind the upgraded RFPA featuring DIC

Simulating fracture propagation evolution without assuming when and where additional fissures will arise and how they will expand and interconnect with each other is where the RFPA approach truly excels (Liang et al., 2019a; Liang et al., 2019b; Tang and Kou, 1998; Gong et al., 2019; Gong et al., 2022). Several common numerical tests (Tang et al., 2001; Xu et al., 2013) have also been used to evaluate the effectiveness and credibility of the RFPA code. Additionally, jointed rock mass security evaluation (Li et al., 2009; Liu et al., 2017; Gong et al., 2025a) and studies on scale effects (Wang et al., 2023a; 2023b; Wang et al., 2024) and anisotropy (Wang et al., 2022b; 2022d; Yang et al., 2015; Feng et al., 2022; Gong et al., 2024a) have all extensively utilized the RFPA technique. Integrating the RFPA method with DIC augments its capacity for modeling. It is evident that RFPA is improved by incorporating features such as picture input, gray threshold segmentation, and pixel analysis. By turning the information in the visualization into vectorized details requisite for modeling, a digital representation can be rendered as a non-uniform finite element mesh system. Precisely, a digital representation is composed of square pixels. Before being introduced into the DIC-enhanced RFPA, the grayscale value scale for every pixel in the digital image (original image) is from 0 to 255 (where the grayscale value of black is 0, that of white is 255, and that of other colors lies within these two). Afterward, being loaded into the DIC-enhanced RFPA, pixels in the digital representation are grouped as joint material or rock material via threshold division of their grayscale values, thereby assigning corresponding material parameters. Upon the original image being inputted into the DIC-enhanced RFPA, this digital visualization has a specific thickness, allowing every pixel to be regarded as a finite element mesh in three-dimensional space. By converting the vertex positions of each pixel into associated vector space points, each pixel is endowed with its respective side length and thickness.

Lattice element modeling has been widely applied in numerical simulations of cemented geomaterials to capture discontinuous fracture mechanics (Rizvi et al., 2020). According to the aforementioned methodology, the converted heterogeneous finite element mesh models are shown in Figure 2. In these non-uniform numerical models, the elastic moduli (or strengths) among contiguous meso-elements (MEs) are not identical, commonly adhering to a stated statistical spread such as the Weibull spread, consequently taking account of heterogeneity inherent in joints and rocks. The Weibull spread was described by Tang and Kou (1998), Tang et al. (2015), and Tang et al. (2020) in the form of Equation 1.

$f\left(u\right)=\frac{m}{u_0}{\left(\frac{u}{u_0}\right)}^{m-1}\mathit{exp}{\left(-\frac{u}{u_0}\right)}^m,(1)$

Figure 2

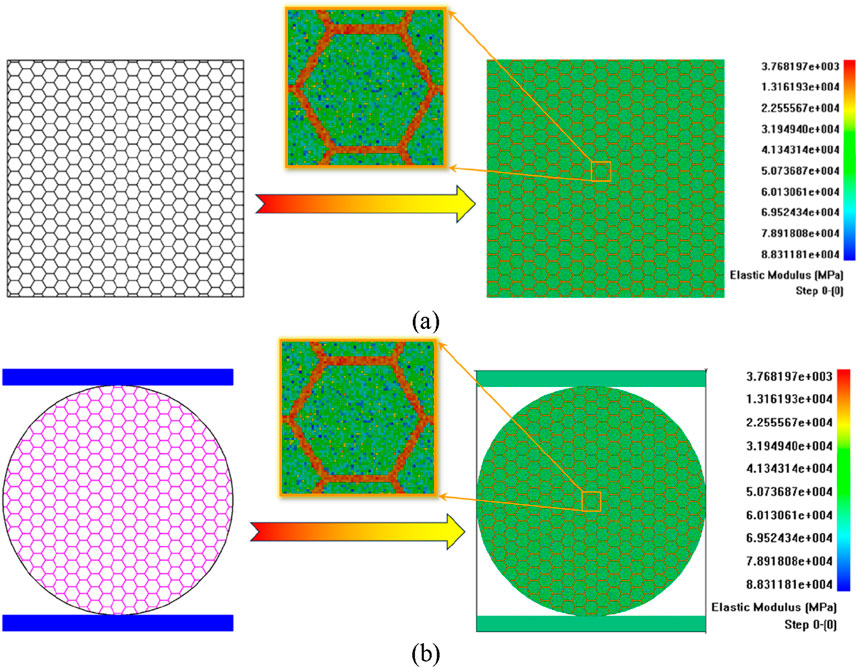
Figure 2. Illustrative diagram showing the conversion of digital visuals into an inhomogeneous finite element mesh model: (a) the square specimen of CJBs under the direct tensile condition; (b) the Brazilian disc specimen of CJBs under the indirect tension condition (Brazilian splitting).

where u embodies the varied mechanical attributes of individual elements, comprising Poisson’s ratio, compressive strength, or elastic modulus; u₀ is the matching average result of the elements for the sample; and m, recognized as the homogeneity indicator, governs the shape of f(u) and reflects the extent of homogeneity. Usually, an elevated m signifies a larger homogeneity.

The number of AEs and their associated energy in the DIC-enhanced RFPA code are proportional to the amount of damaged elements. Figure 3 illustrates the computation scheme of the DIC-enhanced RFPA technique. For a more detailed explanation of the DIC-enhanced RFPA approach, please refer to Gong et al. (2025b); Gong et al. (2024b); Liu et al. (2022); and Lang et al. (2022).

Figure 3

Figure 3. Computation scheme plot of the DIC-enhanced RFPA approach.

2.2 Numerical modeling validation

In this section, the computational modeling approach used in this study is validated through the direct tensile physical test conducted by Liu Z. L. et al. (2021) and the indirect tensile (Brazilian splitting) physical test performed by Liu E. et al. (2021).

Liu Z. L. et al. (2021) carried out direct tensile experiments using red–brown sandstone samples with pre-existing fractures. The samples were cylindrical, with a diameter of 50 mm and a height of 100 mm. A small circular hole with a diameter of 2 mm was drilled at the geometric core of each sample, and a crack measuring 1 mm in width and 24 mm in length was cut symmetrically from the edge of the hole. The tilt angles of the crack are 0°, 15°, 30°, 45°, 60°, 75°, and 90°. The specimen and metal cap were embedded into a tensile–compression conversion device, and they were rotated to a specific extent to prevent eccentric tensile forces throughout the experiment. Direct tensile experiments were performed utilizing the MTS815 hydraulic servo testing apparatus. In this setup, the actuator moved upward to exert compressive stress on the tensile–compression conversion device, which then transferred the compressive stress to the upper end of the sample to impose tensile stress. Before the experiment commenced, a contact load of 0.2 kN was first imposed on the sample, and then loading was carried out at a displacement rate of 0.002 mm/s.

Liu E. et al. (2021) conducted Brazilian splitting experiments using red sandstone samples possessing pre-existing fissures. The geometric dimensions of the specimens were a disk diameter of 50 mm and a thickness of 25 mm. The pre-existing fracture at the center of the specimen was created using water jet cutting. The length of the fracture was 15 mm, the width was 1 mm, and the tilt angles were 0°, 30°, 45°, 60°, and 90°, respectively. For comparison, they also conducted a Brazilian splitting test on the specimen without pre-existing fractures. The experimental equipment used was the RMT-150 testing machine.

The specimen dimensions used for direct tensile numerical verification in this section are 50 mm in width and 100 mm in height. The size parameters of the pre-existing fractures within the specimens are consistent with the physical experiments conducted by Liu Z. L. et al. (2021). Using the DIC-enhanced RFPA, the digital visuals are converted into non-uniform numerical models. The material parameters for these models are taken from Table 1, which references relevant literature on rock specimens (Liu Z. L. et al., 2021). The boundary situation of the entities is plane strain (with displacement constraints implemented on both surfaces in the thickness direction of the sample). Displacement-controlled loading is employed in the computational tests, involving a loading augmentation of 0.0025 mm per step, and the displacement load is gradually imposed until failure occurs in the sample.

Table 1

Table 1. Rock mechanical parameter values for specimens used in the verification of computational modeling under the direct tension condition.

The Brazilian disc specimens used for numerical validation in this section have a diameter of 50 mm. The size parameters of the pre-formed fissures within the specimens are consistent with those used in the physical experiments performed by Liu E. et al. (2021); specifically, the pre-formed fissure length is 15 mm and the width is 1 mm. Employing the DIC-enhanced RFPA, the digital visuals are converted into non-uniform numerical models, with material parameters matching those listed in Table 2, which references relevant literature on rock specimens (Liu E. et al., 2021). The blank area inside the numerical model is composed of meso-scale air elements with extremely low elastic modulus. Under the conditions of small deformation or small displacement, these meso-scale air elements have little impact on the results of the numerical tests (Liang et al., 2019a; 2019b; Tang and Tou, 1998; Liu et al., 2022; Lang et al., 2022). The model’s boundary condition remains as plane strain. Displacement-controlled loading is utilized, with a loading increment of 0.00085 mm per step. The displacement load is implemented step by step till the sample breaks.

Table 2

Table 2. Rock mechanical parameter values for specimens used in the verification of computational modeling under the Brazilian splitting condition.

A contrast of the sample strengths and rupture features between computational tests and laboratory-based physical experiments is illustrated in Figure 4. As shown in Figure 4a, with increasing joint dip angle, the strengths of both the physical and numerical specimens generally display a trend of initially decreasing sharply, followed by a more gradual decline. The root-mean-square error (RMSE) is 0.096, indicating that the difference in strength between the physical and numerical specimens is very small. Figure 4b reveals that the strengths of both the physical and numerical specimens show a trend of decreasing sharply, then gradually, and finally increasing. The RMSE is 0.159, which implies that the difference in strength between the physical and numerical specimens is small. The main reason for the strength difference between the physical and numerical specimens is that there are certain discrepancies between the mineral distribution of the physical specimens and the heterogeneous distribution of the meso-rock grid of the numerical specimens. The numerical test outcomes are in fairly satisfactory conformity with the laboratory physical experiment outcomes in Figures 4c, d, proving the rather high validity of the computational simulation method used in this study.

Figure 4

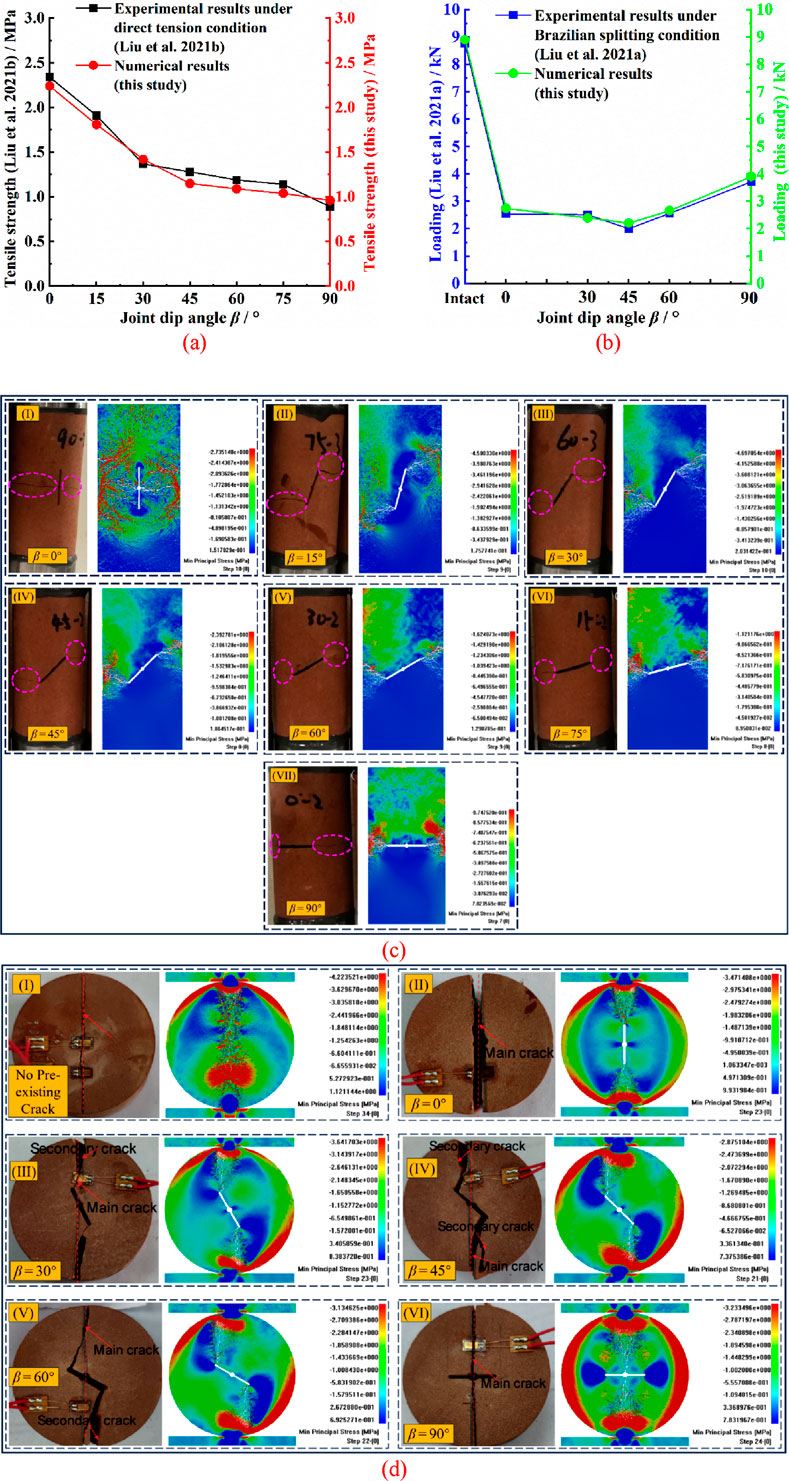
Figure 4. Comparison between the laboratory-based physical experimental outcomes and computational test findings under tension conditions: (a, c) the sample strengths and failure modes from Liu Z. L. et al. (2021) and this study under the direct tension condition; (b, d) the sample strengths and failure manifestations in Liu (E) et al. (2021) and this study under the indirect tension condition (Brazilian splitting).

2.3 Numerical configuration

In actual engineering, the mechanical traits and energy responses of CJBs located in different geological zones or at different engineering stages (for instance, design, construction, and long-term operation) under tensile conditions may be affected by many factors. By conducting research on the tensile strength and deformation features, stress–strain curves, fracture modes, and energy evolution principles of CJBs, the MCEIs and their contributing factors can be additionally investigated. With regard to the emerging order and extent of micro-cracks, a calculation formula for energy trait sensitivity in the tensile state of CJBs can be constructed, and the sensitivity of factors influencing MCEIs can be analyzed using this formula. This body of research provides valuable insights into the energy responses of CJBs, thus offering a scientific foundation for project monitoring related to CJBs. This holds considerable scientific significance and practical importance. Hence, the corresponding model settings and parameters for CJBs are established in this section.

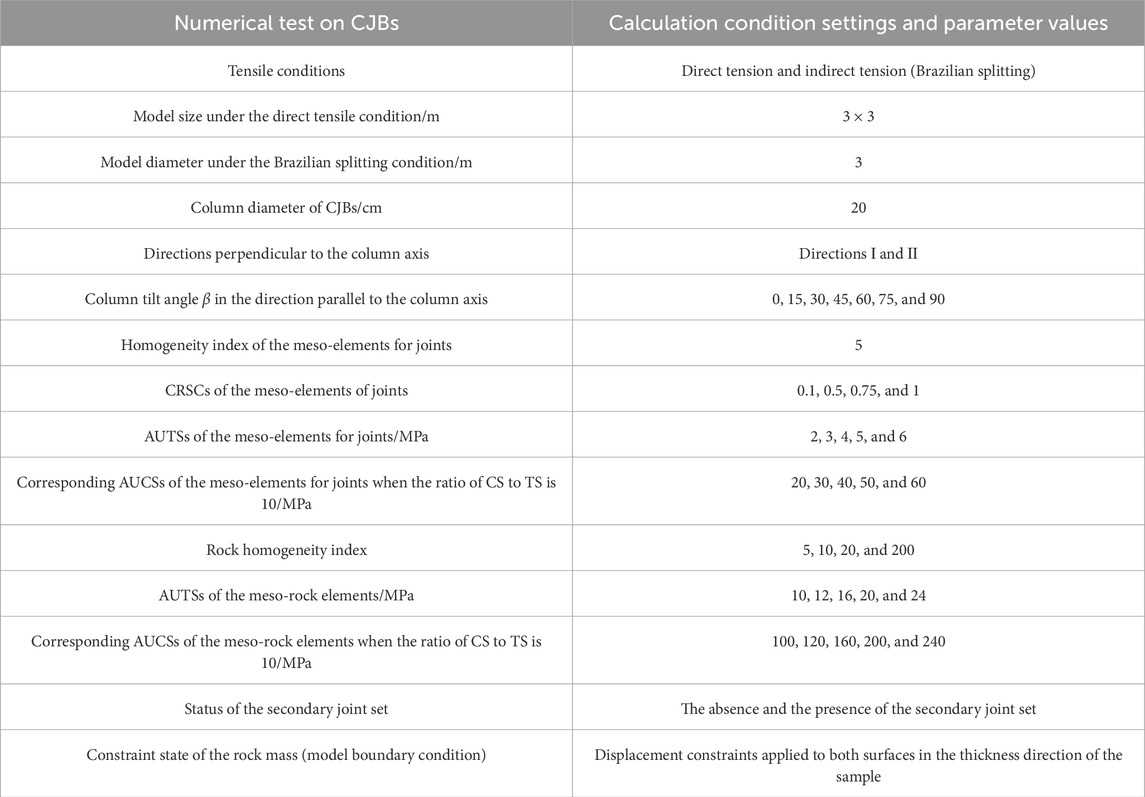
The model setups and parameter specifications for CJBs are presented in Table 3. Tensile conditions are divided into direct tension and indirect tension (Brazilian splitting). Regarding the directions orthogonal to the column axis, two typical cross-sectional cases, namely, I and II, are considered. Concerning the direction parallel to the column axis, the column angles β are considered to be 0°, 15°, 30°, 45°, 60°, 75°, and 90°. Figure 5a presents the illustrative diagram of the mechanical constitutive behaviors of joints with diverse compressive remnant strength coefficients (CRSCs). The CRSCs of the MEs of joints are regarded as 0.1, 0.5, 0.75, and 1, which demonstrate the shift in the MEs’ constitutive traits of the joints from brittle to ductile under compression. Figure 5b displays the illustrative diagram of the mechanical characteristics of joints with different strengths. The average uniaxial tensile strengths (AUTSs) of the MEs for joints are taken as 2 MPa, 3 MPa, 4 MPa, 5 MPa, and 6 MPa. When the ratio of CS to TS is 10, the corresponding average uniaxial compressive strengths (AUCSs) of the MEs for joints are 20 MPa, 30 MPa, 40 MPa, 50 MPa, and 60 MPa, respectively. Cyclic heating effects have been observed to impact subsurface material stability (Ahmad et al., 2021; 2025), which is one of the reasons for the changes in the strength of joints and meso-rocks. Figure 5c depicts the illustrative diagram of the mechanical characteristics of meso-rock elements with various strengths. The AUTSs of the meso-rock elements are taken as 10 MPa, 12 MPa, 16 MPa, 20 MPa, and 24 MPa. When the ratio of CS to TS is 10, the corresponding AUCSs of the meso-rock elements are 100 MPa, 120 MPa, 160 MPa, 200 MPa, and 240 MPa, respectively. The illustrative diagrams of the model boundary conditions, loading settings, and joint settings for the numerical samples of CJBs are shown in Figures 6a–d. The boundary condition of the rock mass (model boundary condition) is set as a plane strain condition, where displacement restrictions are applied to both surfaces in the thickness direction of the sample. The homogeneity index of the MEs for joints is set to 5. According to some studies (Lin et al., 2018; Xu et al., 2020; Wang et al., 2022b; 2022c; 2023a), there are differences in rock heterogeneity among CJBs in various regions. Therefore, four scenarios of rock homogeneity indexes (RHIs) are considered in this study: 5, 10, 20, and 200. The distribution of mechanical traits of meso-rocks within numerical specimens owning diverse rock homogeneity indexes (taking the elastic modulus of meso-rocks as an example) is displayed in Figure 7.

Table 3

Table 3. Calculation configurations and parameter values for CJBs.

Figure 5

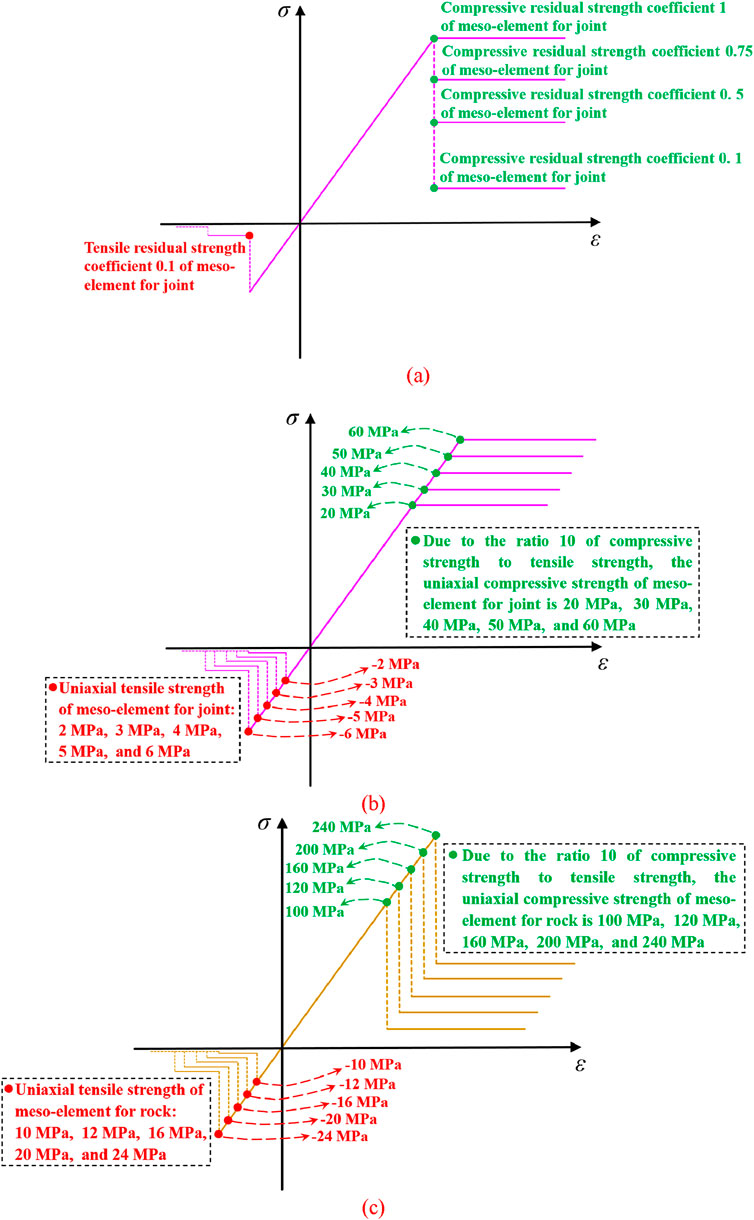
Figure 5. (a) Mechanical constitutive behaviors of meso-elements for joints with different compressive residual strength coefficients (CRSCs); (b) mechanical characteristics of MEs for joints with different strengths; (c) mechanical characteristics of meso-rocks with various strengths.

Figure 6

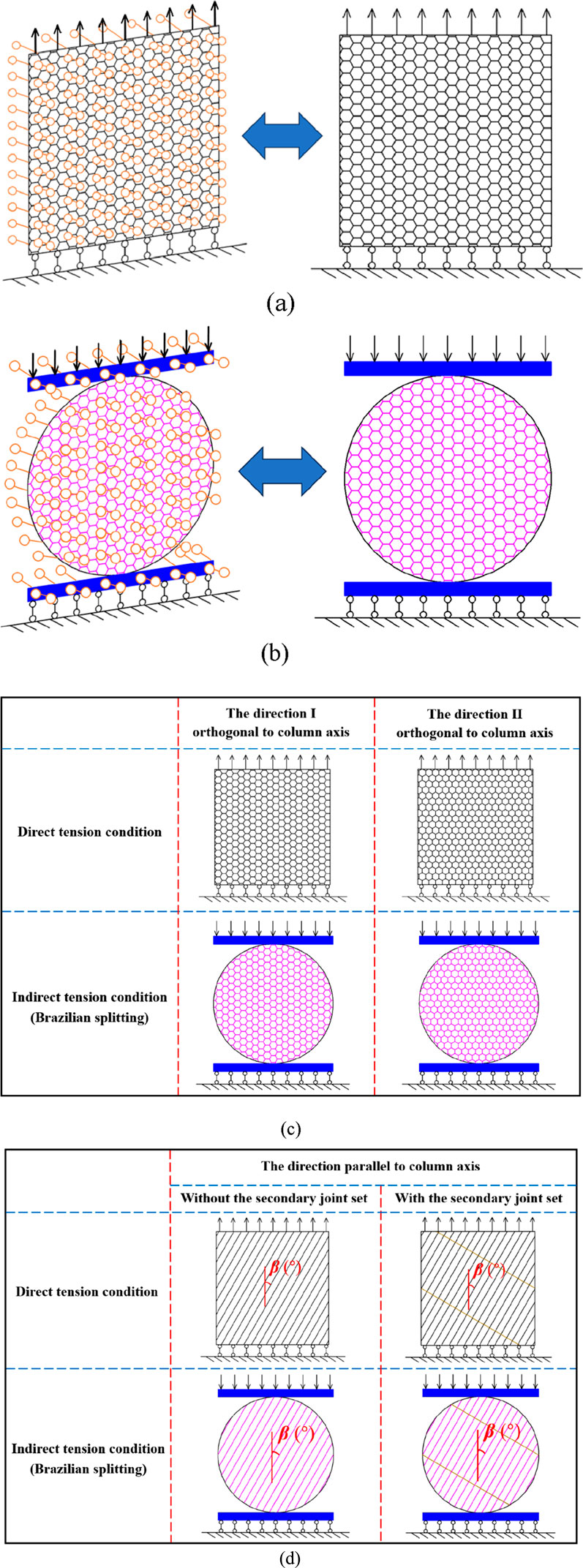
Figure 6. Schematic diagrams of model boundary conditions, loading setups, and joint settings for numerical specimens of CJBs: (a) the direct tensile condition; (b) the Brazilian splitting condition; (c) directions I and II perpendicular to the column axis; (d) specimens without and with the secondary joint set in the direction parallel to the column axis.

Figure 7

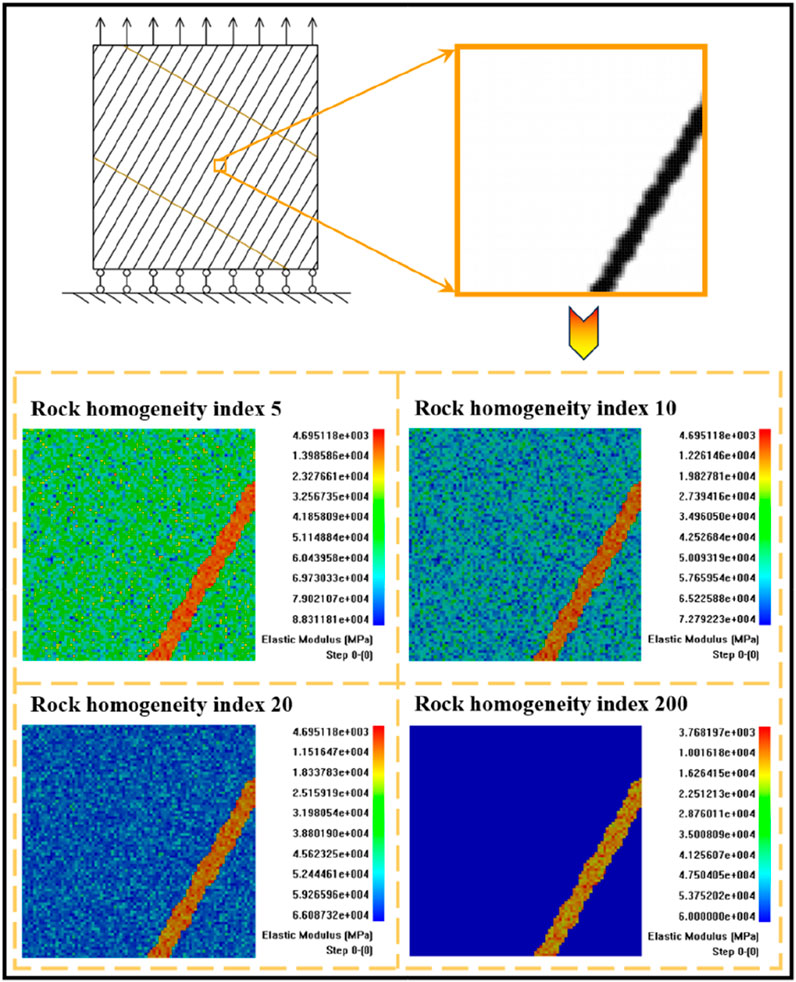
Figure 7. Distribution of mechanical traits of meso-rocks within numerical specimens having diverse rock homogeneity indexes (taking the elastic modulus of meso-rocks as an example).

Using the digital image analysis technology based on the DIC-enhanced RFPA, the digital visuals of the CJBs are converted into heterogeneous numerical models, showing their local characteristics as shown in Figure 2 and Figure 7. If the resolution of the digital visuals contains 780 × 780 pixels, the number of elements in the converted computational model equals 608,400. The material properties for the meso-rocks and joints in the computational model are sourced from appropriate studies (Jiang et al., 2013; Hu et al., 2017; Fan et al., 2018; Zhang J. C. et al., 2021; Wang et al., 2023b; 2024), with the precise specifications described in Table 4. In the direct tensile computational tests, a vertical displacement load is applied to the top of each model. The proportion of the displacement exerted in each step to the original lateral side length of the model equals 0.000017. The displacement load is progressively imparted until failure occurs in the sample. During the Brazilian splitting numerical test, a vertical displacement load is applied to the top of each model, with the ratio of the displacement imparted in each step to the original diameter of the Brazilian disc being 0.000017. The displacement load is applied incrementally until the sample fails.

Table 4

Table 4. Mechanical property values of the joint and rock of CJBs in computational tests.

3 Results and analysis

3.1 Effect of diverse variables on the mechanical traits of CJBs under direct and indirect tensile conditions

For the CJBs along the direction orthogonal to the column axis, Figures 8a, b present the comparisons of the strength and deformation characteristics of the samples under the conditions of direct tension and Brazilian splitting. As illustrated in Figure 8a, under the direct tensile condition, the TSs of the specimens in directions I and II perpendicular to the column axis are both greater than those under the Brazilian splitting condition, with ratios of 1.15 and 1.01, respectively. The abovementioned results are because, under the direct tensile condition, the sample strength is controlled by the TS of multiple joints within the specimen, whereas under the Brazilian splitting condition, the sample strength is primarily influenced by the TS of localized joints within the specimen. Referring to Figure 8b, it can be observed that the equivalent deformation moduli (EDMs) of the specimens in directions I and II perpendicular to the column axis subjected to the direct tensile condition are both greater than those under the Brazilian splitting condition, with ratios of 3.46 and 2.88, respectively. The above circumstances are due to the relatively rapid increase in stress within the specimens during direct tensile testing compared to the slower increase in stress during Brazilian splitting testing (Li et al., 2009; Huang et al., 2021).

Figure 8

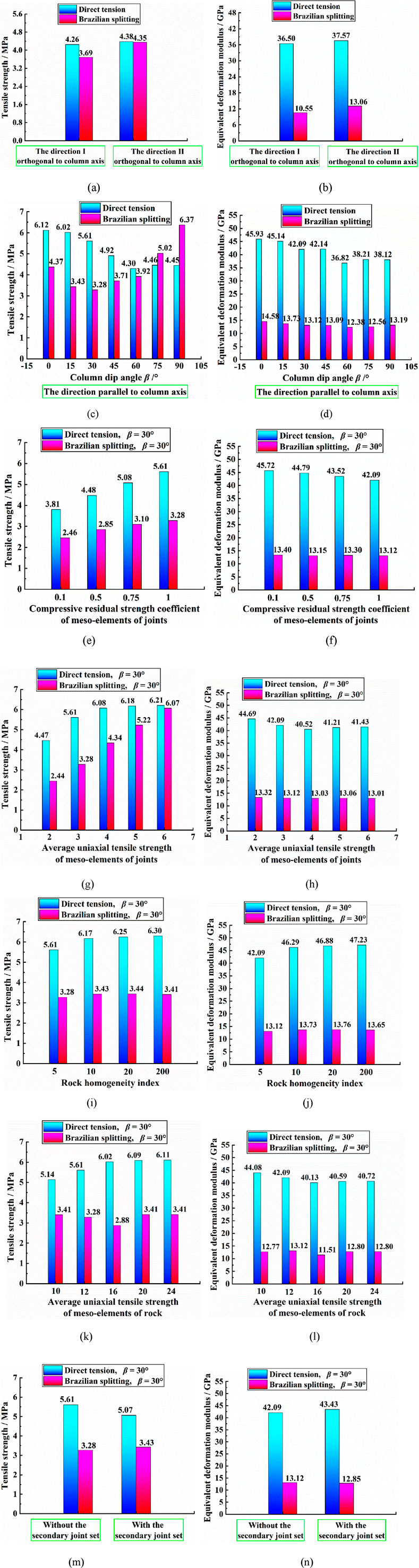
Figure 8. Influence of various factors on the TSs and equivalent deformation moduli (EDMs) of CJBs under direct and indirect tensile situations: (a, b) specimens for the direction perpendicular to the column axis; (c, d) samples with varied column tilt angles for the direction parallel to the column axis; (e, f) samples with various mechanical constitutive behaviors of joints; (g, h) specimens possessing diverse joint strengths; (i, j) specimens having varied rock homogeneity indexes; (k, l) specimens with different meso-rock strengths; ((m, n) samples without and with the secondary joint set.

Regarding the CJBs in the direction parallel to the column axis, Figures 8c, d display the comparisons of strength and deformation traits of the specimens in direct tension and Brazilian splitting conditions, respectively. From Figure 8c, the following phenomena can be noticed: ① under the direct tensile condition, the TS of the specimen first decreases and then exhibits a gradual variation as the column tilt angle augments. In contrast, under the Brazilian splitting condition, the TS of the specimen initially decreases and then increases. ② Under the direct tensile condition, the minimum and maximum TSs of the samples occur at β = 60° and β = 0°, respectively, whereas under the Brazilian splitting condition, the minimum and maximum TSs of the specimens occur at β = 30° and β = 90°, respectively. ③ At the positions of β = 0°, β = 15°, β = 30°, β = 45°, β = 60°, β = 75°, and β = 90°, the ratios of TSs under the direct tensile condition to those under the Brazilian splitting condition are 1.40, 1.76, 1.71, 1.33, 1.10, 0.89, and 0.70, respectively. The abovementioned results indicate that there are notable differences in the TS variation pattern as the column dip angle increases and in the locations of the minimum and maximum values between the direct tensile and Brazilian splitting conditions. Furthermore, there is a certain level of discrepancy in the magnitude of sample strength under these two loading conditions, which depends on the column angle (Figure 11 displays the failure modes and stress distributions of the samples with different column dip angles under direct tensile and Brazilian splitting conditions). From Figure 8d, it can be noticed that ① under the direct tensile condition, the EDM of the sample usually shows a trend of initially decreasing and then gradually stabilizing as the column tilt angle increases, whereas under the Brazilian splitting condition, the EDM of the specimen exhibits a pattern of first decreasing and then gradually increasing. ② For both the direct tensile and Brazilian splitting conditions, the minimum and maximum EDMs of the samples occur at β = 60° and β = 0°, respectively. ③ At the positions of β = 0°, β = 15°, β = 30°, β = 45°, β = 60°, β = 75°, and β = 90°, the ratios of tensile EDMs under the direct tensile condition to those under the Brazilian splitting condition are 3.15, 3.29, 3.21, 3.22, 2.97, 3.04, and 2.89, respectively. The abovementioned observations suggest that for both the direct tensile and Brazilian splitting conditions, the trends in specimen EDMs with increasing column dip angle are relatively similar. The minimum and maximum EDM values occur at the same dip angles for both loading conditions, but there is a notable difference in the magnitude of EDMs between the specimens.

Figures 8e, f display the comparisons of the strength and deformation traits of samples with β = 30° and varied joint constitutive models under direct tensile and Brazilian splitting conditions. According to Figure 8e, under the direct tensile condition, the TSs of specimens with different joint constitutive models are all greater than those under the Brazilian splitting condition. The ratios of the TSs under the direct tensile condition to those under the Brazilian splitting condition are 1.55 (for the CRSC 0.1 of the MEs of joints), 1.57 (for the CRSC 0.5), 1.64 (for the CRSC 0.75), and 1.71 (for the CRSC 1), respectively. As presented in Figure 8f, the EDMs of samples with diverse joint constitutive models under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of the EDMs under the direct tensile condition to those under the Brazilian splitting condition are 3.41 (for the CRSC 0.1 of the MEs of joints), 3.41 (for the CRSC 0.5), 3.27 (for the CRSC 0.75), and 3.21 (for the CRSC 1), respectively. The abovementioned results demonstrate that for specimens with different joint constitutive models, both TSs and EDMs under the direct tensile condition are greater than those under the Brazilian splitting condition. Under the direct tensile condition, the specimen with β = 30° is subjected to overall loading. If the compressive constitutive behavior of the MEs for joints tends to be plastic, the cooperative bearing capacity of both the joints and the meso-rocks is higher. Consequently, the TSs of the specimens are higher, and the stress increases significantly more rapidly. Under the Brazilian splitting condition, the specimen with β = 30° is primarily subjected to localized forces (within a partial area around the vertical centerline of the specimen). The influence of the compressive constitutive behavior of the MEs for joints on the mechanical properties of the specimen is relatively limited.

Figures 8g, h illustrate the comparisons of the strength and deformation traits of specimens possessing various ME strengths of joints under the direct tensile and Brazilian splitting conditions. As observed in Figure 8g, under the direct tensile condition, the TSs of specimens with diverse ME strengths of joints are all greater than those under the Brazilian splitting condition. The ratios of the TSs in the direct tensile to Brazilian splitting conditions are 1.83 (AUTS 2 MPa of MEs of joints), 1.71 (AUTS 3 MPa), 1.40 (AUTS 4 MPa), 1.18 (AUTS 5 MPa), and 1.02 (AUTS 6 MPa), respectively. Figure 8h shows that the EDMs of specimens with varied joint strengths under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of the EDMs under the direct tensile to Brazilian splitting conditions are 3.36 (AUTS 2 MPa of MEs of joints), 3.21 (AUTS 3 MPa), 3.11 (AUTS 4 MPa), 3.16 (AUTS 5 MPa), and 3.18 (AUTS 6 MPa), respectively. These findings imply that in the process of joint strength augmentation, the proportion of sample TSs under the direct tensile to Brazilian splitting conditions decreases, while the ratio of specimen EDMs may increase. This is because the increase in joint strength significantly raises the difficulty of specimen failure along the joints under the Brazilian splitting condition but makes it slightly more prone to meso-rock damage near the joints (Hao et al., 2020; Cen et al., 2020).

Figures 8i, j show the comparisons of the strength and deformation traits of samples featuring diverse degrees of rock homogeneity under the direct tensile and Brazilian splitting conditions. Figure 8i shows that the TSs of specimens with different degrees of rock homogeneity under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of the TSs under the direct tensile to Brazilian splitting conditions are 1.71 (RHI 5), 1.80 (RHI 10), 1.82 (RHI 20), and 1.85 (RHI 200), respectively. Figure 8j reveals that the EDMs of specimens with varying degrees of rock homogeneity under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of the EDMs under the direct tensile to Brazilian splitting conditions are 3.21 (RHI 5), 3.37 (RHI 10), 3.41 (RHI 20), and 3.46 (RHI 200), respectively. The abovementioned observations suggest that as the degree of rock homogeneity increases, the differences in mechanical properties of specimens between direct tensile and Brazilian splitting conditions tend to enlarge. Compared to the locally loaded Brazilian splitting test, the overall stress distribution in specimens under direct tensile conditions is more pronounced. An increase in rock homogeneity can improve the TS and deformation resistance of each column within the specimen to a certain extent.

Figures 8k, l present the comparisons of the strength and deformation traits of samples with different meso-rock strengths under the direct tensile and Brazilian splitting conditions. As displayed in Figure 8k, the TSs of specimens with diverse meso-rock strengths under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of TSs under direct tensile to Brazilian splitting conditions are 1.51 (AUTS 10 MPa of MEs of rock), 1.71 (AUTS 12 MPa), 2.09 (AUTS 16 MPa), 1.79 (AUTS 20 MPa), and 1.79 (AUTS 24 MPa), respectively. As depicted in Figure 8l, the EDMs of specimens with various meso-rock strengths under the direct tensile condition are all greater than those under the Brazilian splitting condition. The ratios of EDMs under the direct tensile to Brazilian splitting conditions are 3.45 (AUTS 10 MPa of MEs of rock), 3.21 (AUTS 12 MPa), 3.49 (AUTS 16 MPa), 3.17 (AUTS 20 MPa), and 3.18 (AUTS 24 MPa), respectively. The abovementioned phenomena indicate that as the meso-rock strength increases, the TS and EDM ratios for specimens under direct tensile and Brazilian splitting conditions do not monotonously increase or decrease. This is because the growth in meso-rock strength can enhance the TS of each column within the specimen under the direct tensile condition, thereby increasing the TS of the specimen. However, the coordinated deformation resistance between the columns and joints within the specimen may be weakened. The elevation of meso-rock strength under Brazilian splitting condition may lead to further stress transfer to the joint locations within the localized areas along the vertical centerline of the specimen, promoting joint damage (Zhang et al., 2022; Li et al., 2009). Consequently, the TS and EDM of the specimen may decrease.

Figures 8m, n illustrate the comparisons of strength and deformation traits of samples with the varied statuses of the secondary joint set in the direct tension and Brazilian splitting conditions. According to Figure 8m, under the direct tension condition, the TSs of specimens with diverse statuses of the secondary joint set are greater than those under the Brazilian splitting condition. The ratios of the TSs under direct tension to Brazilian splitting conditions are 1.71 (without the secondary joint set) and 1.48 (with the secondary joint set). Referring to Figure 8n, it can be noticed that the EDMs of specimens with various statuses of the secondary joint set in the direct tension condition are greater than those in the Brazilian splitting condition. The ratios of the EDMs under direct tension to Brazilian splitting conditions are 3.21 (without the secondary joint set) and 3.38 (with the secondary joint set). The abovementioned findings suggest that the presence of the secondary joint set results in a reduction in the TS ratio between direct tension and Brazilian splitting conditions while increasing the EDM ratio between these two conditions. This is because the presence of the secondary joint set can lead to easier damage and cracking along the secondary joint set within the β = 30° sample under the direct tension condition, thereby weakening the sample TS. Under the Brazilian splitting condition, the presence of the secondary joint set causes the columnar joints and the secondary joint set within the sample to share the load, leading to synergistic slip and cracking. This alters the stress distribution within the specimen, resulting in a slight increase in TS rather than a decrease. The secondary joint set participates in damage and deformation, resulting in a slight weakening of the coordinated deformation resistance between the columns and joints within the sample.

3.2 Failure modes and AE responses of CJBs under direct and indirect tensile conditions

3.2.1 Direction perpendicular to the column axis

For direction I perpendicular to the column axis, Figure 9 presents the diagrams of the specimen models, stress–strain curves, AE quantity features, stress field evolutions, displacement field characteristics, and AE spatial distribution characteristics under the conditions of direct tension and Brazilian splitting. Figures 9a, c show that for the specimen under the direct tensile condition, as the stress reaches point A on the stress–strain graph, the stress concentration inside the sample becomes evident, particularly with significant tensile stress exhibited in the columns between vertical joints. When the stress reaches point B on the curve, sporadic tensile failures occur at the horizontal joints inside the sample. As the stress reaches peak point C on the curve, the tensile failures in the horizontal joints further increase. Upon the stress decreasing to point D, tensile failures in the horizontal joints become more pronounced. When the stress keeps decreasing to point E, tensile failures also begin to appear in some oblique joints. As the stress continues to decrease to point F, the number of oblique joints with tensile failures within the specimen continues to increase, meaning that at this point, tensile cracking occurs in both the horizontal and oblique joints surrounding some of the columns. From the maximum principal stress diagram of the specimen shown in Figure 9e, it can be recognized that at the eighth calculation step, tensile stress concentration and damage cracking occur in the horizontal joints within the specimen. From the x- and z-direction displacement illustrations of the specimen in Figure 9e, it can be noticed that the left and right wings of the specimen undergo horizontal displacement toward the interior of the sample, while the upper portion of the sample experiences vertical upward displacement. Combining the AE spatial distribution diagrams of the specimen under the direct tensile condition in Figure 9g, it is found that tensile damage (represented by blue AEs) occurs around each column within the specimen. Furthermore, Figure 9a depicts that the AE count of the sample showcases a single-peaked profile, with the peak occurring before the point of maximum stress. This AE peak is predominantly due to the combined tensile damage of horizontal and oblique joints within the specimen.

Figure 9

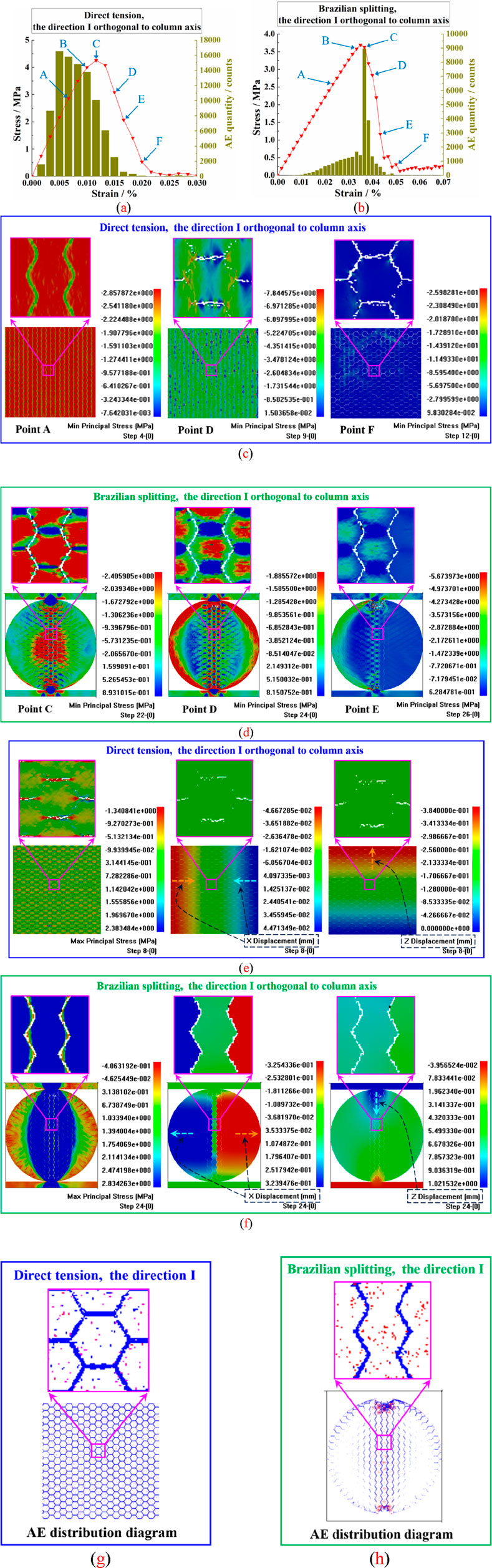
Figure 9. Fracture mechanisms and AE characteristics of the CJBs in direction Ⅰ perpendicular to the column axis under the direct and indirect tensile conditions: (a, b) stress–strain graphs and AE amounts under the direct tensile and Brazilian splitting conditions; (c, d) evolutions of the minimum principal stress fields in the models; (e, f) maximum principal stress diagrams, x-direction displacement diagrams, and z-direction displacement diagrams under the direct tensile and Brazilian splitting conditions; (g, h) AE spatial distribution diagrams.

As shown in Figures 9b, d, for the specimen under the Brazilian splitting condition, when the stress attains point A on the stress–strain graph, there is a significant accumulation of compressive stress at the top and bottom extremities of the disk, while a notable concentration of tensile stress appears between these two ends. When the stress reaches point B on the curve, the region of tensile stress concentration within the disk expands, and the tensile damage of the vertical joints between the top and bottom ends of the disk increases. At point C, near the peak of the curve, vertical joint cracking occurs between the upper and lower extremities of the disk, and the concentration area of tensile stress within the disk narrows toward the center of the disk. When the stress descends to point D, there is mixed compression–tension damage near the upper and lower ends, with tensile stress concentration at the center of each column section between the upper and lower ends. There are also appreciable tensile stress localizations at the contour edge of the disk. When the stress continues to decrease to point E, the damage near the upper and lower ends continues to develop with sporadic stress concentrations, and the tensile stress concentration within the disk and at its contour edge significantly decreases. When the stress further decreases to point F, fragmentation near the upper and lower extremities of the sample intensifies. From the maximum principal stress diagram of the sample in Figure 9f, it can be found that at the 24th calculation step (point D), there exists an elliptical region of compressive stress localization between the upper and lower extremities of the disk; meanwhile, the tensile stress is pronounced at the contour edges on the left and right wings of the disk. From the x- and z-direction displacement illustrations of the specimen in Figure 9f, it can be observed that there is a relatively significant horizontal displacement that occurs outward on the left and right wings of the disk, accompanied by a notable settlement near the upper end of the disk. According to the AE spatial dispersion features of the specimen in Figure 9h, tensile damage (indicated by blue AEs) occurs at the vertical joints between the upper and lower ends of the disk and near the contour edges. Additionally, there is some extent of compressive damage (manifested by pink AEs) in the columns between the upper and lower ends. Near these two ends, there is significant coexisting compressive–tensile damage. Furthermore, Figure 9b demonstrates that the AE amount of the sample displays a unimodal profile, illustrating that the AE amount peak tends to occur after the stress peak point. This AE quantity peak is mainly triggered by the combined effects of tensile damage in the joints between these two extremities of the disk, and compressive damage within the columns.

Moreover, by comparing Figures 9a, b, it can be observed that under the direct tensile condition, both the peak strength and the maximum AE amount of the sample in direction I perpendicular to the column axis are higher than those under the Brazilian splitting condition. This is because under the direct tensile condition, all the joints within the specimen in direction I perpendicular to the column axis contribute to the bearing capacity, collectively resisting the tensile load and, thus, demonstrating a greater peak-bearing ability. Nevertheless, under the Brazilian splitting condition, it is primarily the joints within a localized area along the vertical centerline of the specimen that contribute to the bearing capacity, resulting in a lower bearing capacity and a lower peak AE quantity (Zhao et al., 2022; Zhang Q. L. et al., 2021).

Figure 10 depicts the failure modes and stress distributions of the specimens in direction Ⅱ under the DTC and BSC. When subjected to the DTC, tensile stress exists in the oblique joint of the sample at the eighth calculation step, leading to micro-cracks. Under the BSC, that joint cracking occurs near the center of the disk, with two bands of compressive stress concentration appearing on both sides of the center. Additionally, tensile stress exists near the contours on the left and right sides of the disk.

Figure 10

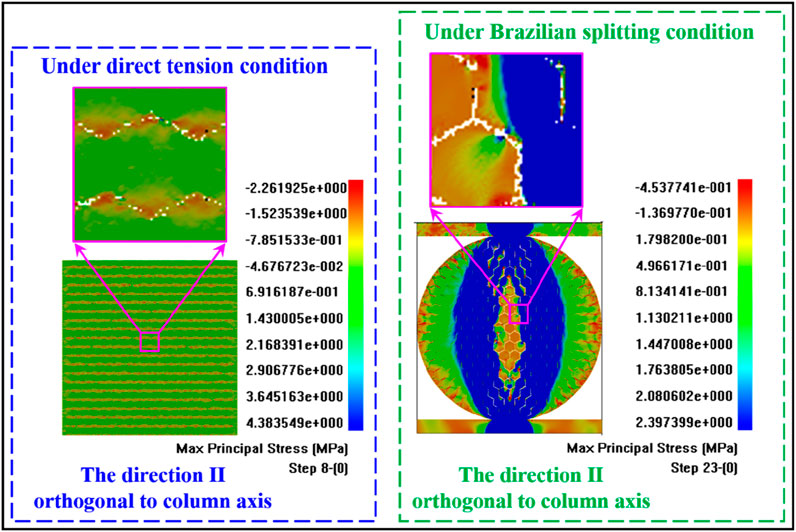
Figure 10. Failure modes and stress distribution of the CJBs in direction Ⅱ perpendicular to the column axis under the direct and indirect tensile conditions.

3.2.2 The direction parallel to the column axis

Figure 11 shows the failure modes (crack propagation features) and stress distributions of the specimens with different column dip angles under direct tensile and Brazilian splitting conditions. As shown in Figure 11a, for the specimen with β = 0° under the DTC, there are dispersed micro-cracks, and the compressive and tensile stresses are unevenly distributed; for the specimen with β = 45°, the micro-cracks mainly occur at the joint positions, and these joints are in a certain degree of compressive sliding state; and for the specimen with β = 90°, there is a significant tensile stress concentration at the joint positions, accompanied by the occurrence of micro-cracks. It can be found from Figure 11b that for the specimen with β = 0° under the BSC, the joints are tensile-cracked, and there may be compressive stress or tensile stress concentration in the local areas of the columns; for the specimen with β = 45°, the joints get slipped and cracked. There are tensile micro-cracks near the edges of the columns, and the tensile stress at the crack tips is obvious. For the specimen with β = 90°, there are significant compressive stress and tensile micro-cracks, indicating the state of compression-induced tensile cracking.

Figure 11

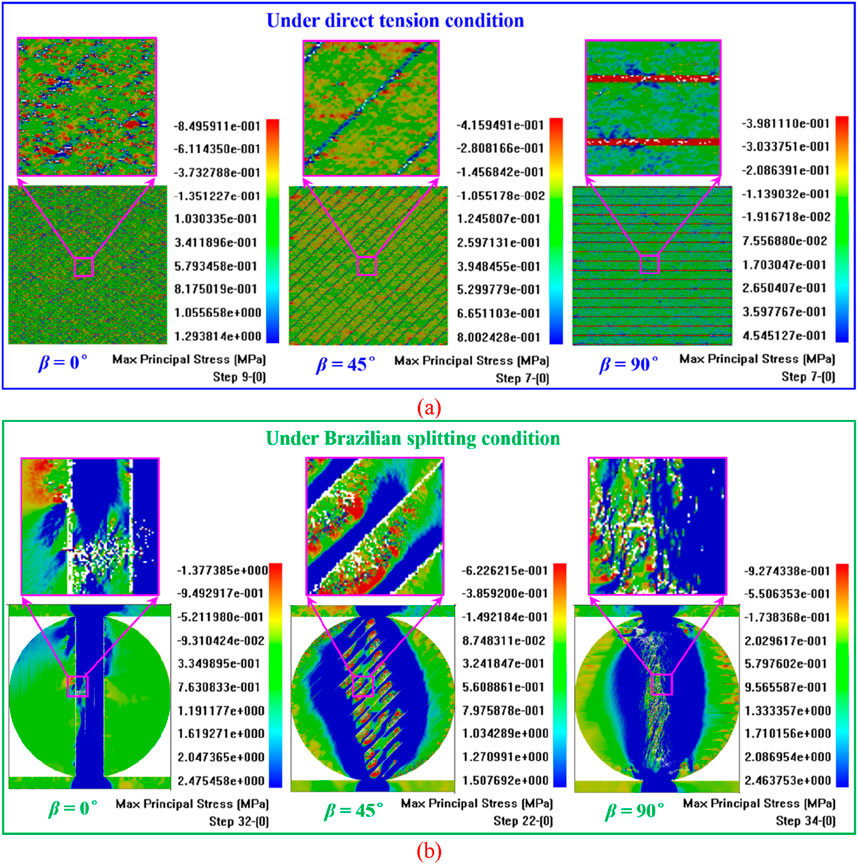
Figure 11. Failure modes and stress distribution of the specimens with different column dip angles: (a) under the DTC; (b) under the BSC.

Figure 12 presents the diagrams of the β = 30° specimen models, stress–strain curves, AE quantity features, stress field evolutions, displacement field characteristics, and AE spatial distribution characteristics under the direct tension and Brazilian splitting conditions. According to Figures 12a, c, for the sample under the direct tensile condition, when the stress reaches point A of the stress–strain graph, there is considerable stress localization within the specimen. As the stress attains point B of the curve, tensile damage forms at the columnar joints, accompanied by sporadic tensile cracks. When the stress reaches the peak point C of the curve, the number of mesoscopic tensile cracks at the columnar joint locations increases. Upon the stress decreasing to point D, signs of cracking emerge at the columnar joints, accompanied by sporadic micro-cracks inside the columns. Once the stress subsequently decreases to point E, the cracking at the columnar joints progresses, and localized crack initiation occurs inside the columns. Upon the stress decreasing to point F, the columnar joints further crack and the localized cracks in the columns develop slightly. As noticed from the maximum principal stress diagram of the specimen in Figure 12e, at the eighth calculation step (point C), the columnar joints within the sample exhibit a certain degree of compressive sliding, with tensile stresses distributed throughout each column. From the x- and z-direction displacement diagrams of the specimen shown in Figure 12e, it can be detected that there are apparent horizontal displacements toward the interior of the sample at the lower left and upper right sides of the sample. There is a vertical upward displacement at the upper portion of the sample. Additionally, Figure 11a reveals that the AE amount of the sample demonstrates a unimodal spread, with the AE amount peak emerging before the stress peak point. This AE quantity peak predominantly stems from tensile damage in the columnar joints (as depicted by Figure 12i).

Figure 12

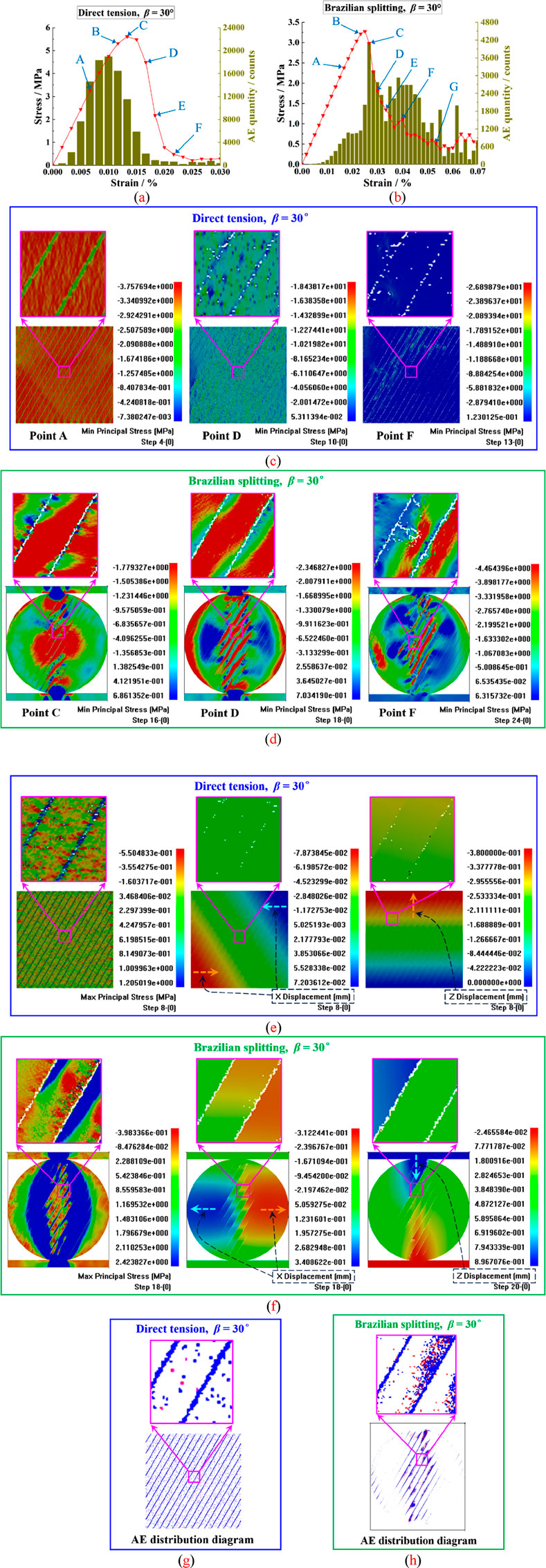
Figure 12. Fracture mechanisms and AE characteristics of the CJBs with β = 30° under the direct and indirect tensile conditions: (a, b) stress–strain graphs and AE amounts under the direct tensile and Brazilian splitting conditions; (c, d) evolutions of the minimum principal stress fields in the models; (e, f) maximum principal stress diagrams, x-direction displacement diagrams, and z-direction displacement diagrams under the direct tensile and Brazilian splitting conditions; (g, h) AE spatial distribution diagrams.

According to Figures 12b, d, for the specimen under the Brazilian splitting condition, once the stress reaches point A of the stress–strain graph, there are noticeable concentrations of compressive stress at the upper and lower extremities of the disk, while pronounced concentrations of tensile stress appear between these two ends. As the stress approaches point B close to the peak of the curve, tensile damage develops and gradually leads to cracking in the columnar joints between the upper and lower extremities of the disk. As the stress attains point C, cracking in the columnar joints subsequently progresses, resulting in the narrowing of the stress localization area between the upper and lower extremities of the disk. As the stress decreases to point D, apparent stress concentrations appear near the margins of the columns, between the upper and lower terminals, and along the contour of the disk. When the stress further decreases to point E, crack emergence occurs at the margins of several columns between the upper and lower terminals of the disk, and the stress concentration at the contour edge on the right side of the disk reduces significantly. As the stress reaches point F, crack propagation appears at the edges of several columns between the upper and lower extremities of the disk. Several joints at the edge of the left contour turn cracked, and stress aggregations develop near the crack apices. As the stress continues to decrease to point G, the cracks in several columns between the upper and lower ends further propagate. From the maximum principal stress diagram of the sample in Figure 12f, it can be found that at the 18th calculation step (point D), the columnar joints near the center of the disk become cracked, with compression stress accumulation bands forming on the left and right wings of these cracked columnar joints. Additionally, tensile stresses exist near the contour edges on both the left and right wings of the disk. From the x- and z-direction displacement illustrations of the sample in Figure 12f, it can be recognized that there are apparent horizontal displacements occurring toward the outside of the sample on both the left and right edges of the disk. In addition, there is a noticeable settlement near the left upper end of the disk, which is distributed along the columnar joint. From the AE spatial spread features of the specimen in Figure 12h, it can be detected that tensile damage occurs at the columnar joints and margins of several columns between the upper and lower ends of the disk, while tensile–compressive damage happens in the vicinity of both ends. Furthermore, Figure 12b shows that the AE amount of the sample demonstrates a multi-peak profile, with the first AE amount peak tending to occur after the stress peak point. This AE quantity peak is chiefly triggered by the fracturing of columnar joints between the upper and lower extremities of the disk.

In addition, by comparing Figures 12a, b, it can be observed that under the direct tensile conditions, the peak strength and the peak AE amount for the β = 30° specimen are both greater than those under the Brazilian splitting condition. This is because, under the direct tensile condition, not only are all the columnar joints damaged, but micro-damages are also diffusely distributed among the columns within the specimen, indicating that the specimen fully exerts its bearing capacity. Under the Brazilian splitting condition, the joints and columns within a localized area along the vertical centerline of the specimen primarily bear the applied load.

For the specimen with the secondary joint sets and β = 30°, Figure 13 presents the diagrams of the specimen models, stress–strain curves, AE quantity features, stress field evolutions, displacement field characteristics, and AE spatial distribution characteristics under the direct tension and Brazilian splitting conditions. As shown in Figures 13a, c, for the specimen under the direct tensile condition, when the stress approaches point A of the stress–strain graph, there is significant stress localization within the specimen. When the stress reaches point B of the curve, tensile damage arises at columnar joints, and sporadic tensile cracks appear at the secondary joint sets. As the stress arrives at the peak point C of the curve, sporadic tensile cracks also emerge at the columnar joints, and the number of tensile cracks at the secondary joint sets increases. When the stress decreases to point D, the number of tensile cracks at the columnar joints increases, and cracking at the secondary joint sets becomes evident. As the stress further descends to point E, tensile stress aggregation is observed on the top left portion of the sample, with increased cracking in the columnar joints, and tensile stress accumulation appears on the bottom right side of the sample. From the maximum principal stress diagram of the sample in Figure 13e, it can be observed that at the tenth calculation step (point E), cracking occurs in the secondary joint sets inside the sample, and localized areas near the upper and lower ends of the sample encounter small-scale tensile stress concentration and compressive stress concentration. From the x- and z-direction displacement plots of the specimen in Figure 13e, it can be noticed that there are noticeable horizontal displacements toward the interior of the sample at the lower left and upper right sides of the sample. Additionally, there is a significant vertical upward displacement in the area above the secondary joint set at the upper portion of the specimen. A clear vertical upward displacement also occurs on the left side of the area between the upper and lower secondary joint sets. Furthermore, Figure 13a shows that the AE amount of the sample exhibits a single-peaked distribution, with the AE amount peak arising before the stress peak point. This AE quantity peak is chiefly triggered by the conjoint effects of the tensile damage in the columnar joints and the tensile damage and cracking in the secondary joint sets (as depicted in Figure 13g).

Figure 13

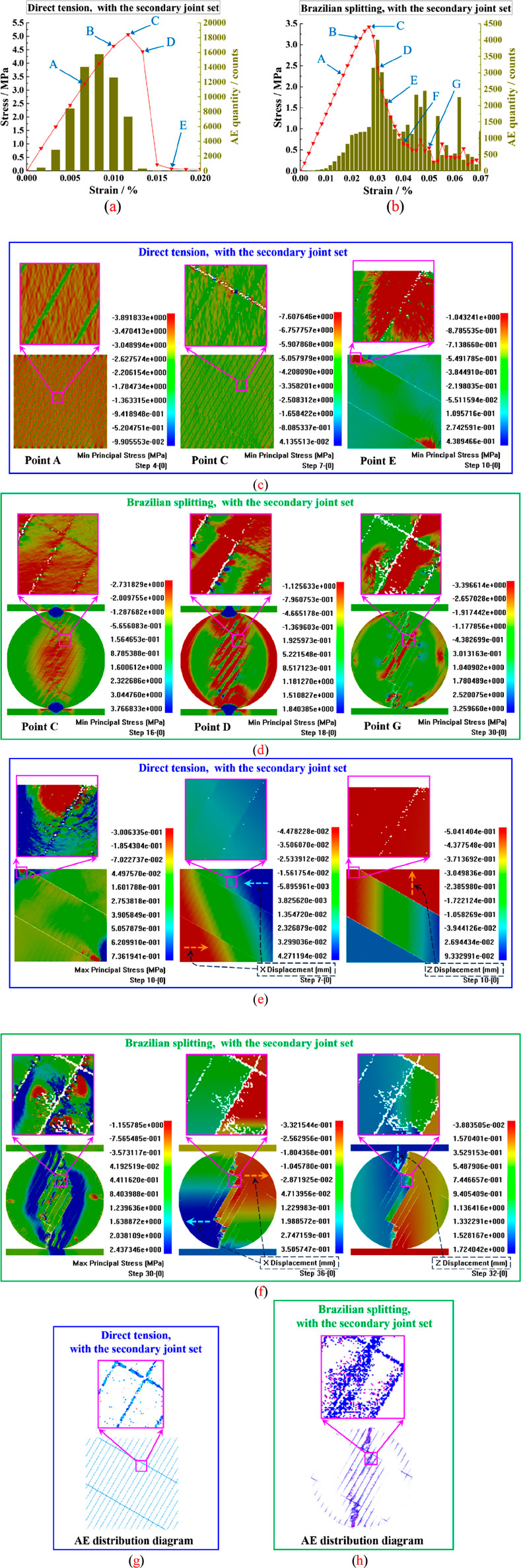
Figure 13. Fracture mechanisms and AE characteristics of the CJBs with the secondary joint sets under the direct and indirect tensile conditions: (a, b) stress–strain graphs and AE amounts under the direct tensile and Brazilian splitting conditions; (c, d) evolutions of the minimum principal stress fields in the models; (e, f) maximum principal stress diagrams, x-direction displacement diagrams, and z-direction displacement diagrams under the direct tensile and Brazilian splitting conditions; (g, h) AE spatial distribution diagrams (taking β = 30° as an example).

According to Figures 13b, d, for the specimen under the Brazilian splitting condition, when the stress reaches point A of the stress–strain graph, there are apparent compressive stress aggregations at the upper and lower extremities of the disk, while there is prominent tensile stress concentration between the upper and lower ends. As the stress attains point B close to the peak of the curve, tensile damage in the columnar joints between the upper and lower ends of the disk develops and gradually leads to cracking. Once the stress reaches the peak point C of the curve, cracking at the columnar joints further progresses, and the region of the stress concentration between the upper and lower extremities of the disk narrows. As the stress descends to point D, cracking at the columnar joints becomes pronounced, and significant stress concentration is observed both in the columns between the upper and lower extremities of the disk and on the left and right sides of the disk’s contour edge. When the stress further descends to point E, crack initiation takes place at the margins of several columns and secondary joint sets between the upper and lower extremities of the disk. The stress concentrations in the columns between these two ends and at the edges of the disk contour are significantly reduced. As the stress reaches point F, cracking at the secondary joint sets subsequently progresses, and the cracks at the margins of several columns between the upper and lower extremities of the disk also expand. Stress localization reappears in the columns between these two ends of the disk and at the left and right wings of the disk contour edge. As the stress continues to decrease to point G, localized cracking at the secondary joint sets within the disk becomes interconnected, and the cracks in several columns between the upper and lower ends further develop, with significant stress concentration observed in these columns. Additionally, the secondary joint set slip-induced cracking arises on the right side of the disk contour edge. From the maximum principal stress diagram of the specimen in Figure 13f, it can be detected that at the 30th calculation step (point G), the columnar joints and secondary joint sets between the upper and lower extremities of the disk encounter cracking. The compressive stress localization bands appear on the left and right wings of the zone of these cracked joints. Tensile stress exists at the ends of the cracked secondary joint sets on the left and right edges of the disk contour. From the x- and z-direction displacement illustrations of the specimen in Figure 13f, it can be observed that the lower left side of the disk undergoes displacement to the left direction, while the right upper side of the disk experiences displacement to the right direction. Additionally, there is a noticeable settlement close to the upper left side of the disk, which distributes along the columnar joints and secondary joint sets. According to the AE spatial distribution characteristics of the sample in Figure 13h, tensile damage occurs in the columnar joints and secondary joint sets and at the margins of several columns between the upper and lower ends of the disk. Additionally, tensile–compressive damage occurs near these two ends. In addition, Figure 13b shows that the AE amount of the sample showcases a multi-peaked pattern. The first AE amount peak tends to occur after the stress peak point, which is mainly caused by the combined effects of the damage and cracking in the columnar joints and secondary joint sets and the initiation and propagation of cracks at the edges of several columns.

In addition, by comparing Figures 13a, b, it can be found that under the direct tensile condition, the sample with the secondary joint sets exhibits a higher strength peak and a higher AE quantity peak, with the AE quantity showing a unimodal distribution. In contrast, under the Brazilian splitting condition, the specimen displays a lower strength peak and a lower AE quantity peak, with the AE quantity presenting a multi-peaked distribution. This is because, under the direct tensile condition, the columnar joints, secondary joint sets, and individual columns within the specimen synergistically contribute to the specimen-bearing capacity, resulting in a relatively concentrated sequence of micro-cracks. Under the Brazilian splitting condition, within a localized area along the vertical centerline of the specimen, the columnar joint slippage occurs first, followed by cracking in the secondary joint sets. Subsequently, the cracked secondary joint sets connect with newly cracked columnar joints, thereby forming a localized, multi-stage bearing process.

3.3 Impact of diverse variables on the MCEIs of CJBs under direct and indirect tensile conditions

Current research studies on CJBs mainly focus on their compressive mechanical properties (Lin et al., 2018; Que et al., 2021; Yan et al., 2018; Wang et al., 2023a), with limited studies addressing their tensile mechanical behavior. Moreover, there is a lack of exploration into the MCEI (which corresponds to the AE energy accumulation at the sample’s strength peak). Therefore, this study aims to examine the MCEI and its influencing variables in CJBs under direct and indirect tensile conditions. By examining the energy accumulations released by damage and micro-cracks as CJBs reach their tensile strengths, this study highlights the differences in energy behavior across tensile conditions and other factors, thereby providing theoretical support for understanding the energy aspects of CJBs.

As shown in Figure 14a, in terms of the appearing sequence of MCEIs along the strain axis, the order is as follows: direction I perpendicular to the column axis (under the DTC) [direction II (under the DTC)], direction II (under the BSC), and direction I (under the BSC). The magnitudes of MCEIs in ascending order are as follows: direction I perpendicular to the column axis (under the BSC), direction II (under the DTC), direction I (under the DTC), and direction II (under the BSC). The abovementioned results indicate that for the specimens in directions I and II—perpendicular to the column axis—compared to the direct tensile condition, MCEIs occur at a later stage and may have a larger magnitude under the Brazilian splitting condition. This is because Brazilian splitting is a process of compression-induced tensile fracture. During this process, the meso-rocks and joints within the specimen gradually exhibit their load-bearing capacity. A considerable number of meso-rock elements inside the specimen in direction II suffer compression damage.

Figure 14

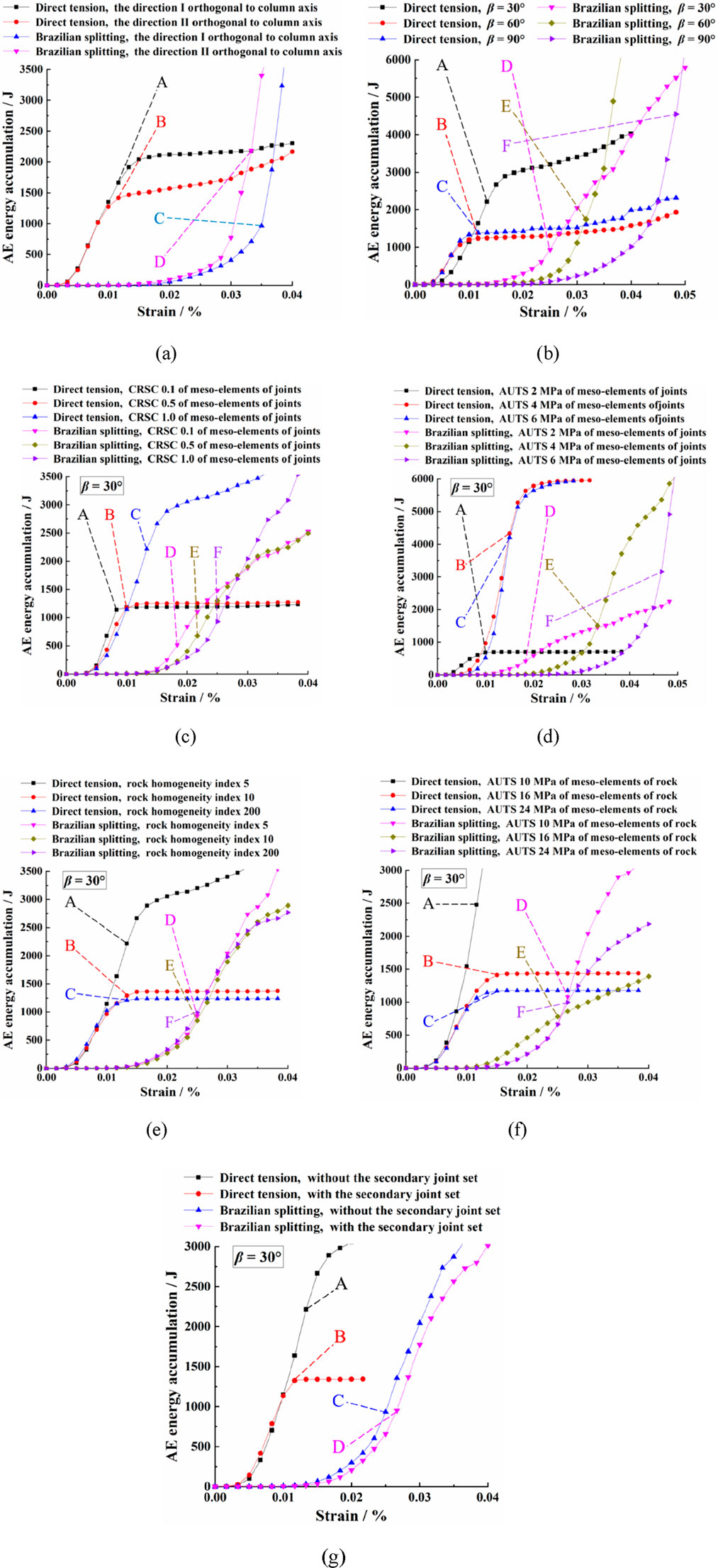
Figure 14. Influence of various factors on the MCEIs of CJBs under direct and indirect tensile situations: (a) specimens in the direction perpendicular to the column axis; (b) samples with varied column tilt angles in the direction parallel to the column axis; (c) specimens with various mechanical constitutive behaviors of joints; (d) specimens possessing diverse joint strengths; (e) samples with varied rock homogeneity indexes; (f) samples with different meso-rock strengths; (g) specimens without and with the secondary joint set (the MCEIs refer to the AE energy accumulations corresponding to the apex stresses of the specimens).

As shown in Figure 14b, from the perspective of the occurrence sequence of the MCEIs upon the strain axis, the order is as follows: β = 60° (under the DTC) [β = 90° (under the DTC)], β = 30° (under the DTC), β = 30° (under the BSC), β = 60° (under the BSC), and β = 90° (under the BSC). The magnitudes of the MCEIs in ascending order are as follows: β = 30° (under the BSC), β = 60° (under the DTC), β = 90° (under the DTC), β = 60° (under the BSC), β = 30° (under the DTC), and β = 90° (under the BSC). The abovementioned findings suggest that for the specimens with varied column tilt angles in the direction parallel to the column axis, compared to the Brazilian splitting condition, the MCEIs occur at an earlier stage and may have smaller magnitudes under the direct tensile condition, which hinges on the specific column dip angle. This means that in practical engineering monitoring, when CJBs are subject to direct tensile stress, monitoring personnel should focus on crack propagation at an earlier stage. When evaluating the state of CJBs, the monitoring personnel need to combine the inclination angle of the columns relative to the principal stress direction to predict the characteristics of energy release during crack propagation and assess the safety of the structure in advance.

Figure 14c reveals that, in terms of sequence of MCEI occurrences along the strain axis, the order is as follows: the CRSC 0.1 of MEs of joints (under the DTC), the CRSC 0.5 of MEs of joints (under the DTC), the CRSC 1.0 of MEs of joints (under the DTC), the CRSC 0.1 of MEs of joints (under the BSC), the CRSC 0.5 of MEs of joints (under the BSC), and the CRSC 1.0 of MEs of joints (under the BSC). The magnitudes of the MCEIs in increasing order are as follows: the CRSC 0.1 of MEs of joints (under the BSC), the CRSC 0.5 of MEs of joints (under the BSC), the CRSC 1.0 of MEs of joints (under the BSC), the CRSC 0.1 of MEs of joints (under the DTC), the CRSC 0.5 of MEs of joints (under the DTC), and the CRSC 1.0 of MEs of joints (under the DTC). The abovementioned situations imply that for various joint compression mechanical constitutive behaviors, in contrast to the direct tensile condition, the MCEIs of the specimens under the Brazilian splitting condition appear at a later stage, and the magnitudes of these MCEIs are lower. It is difficult to consider the influence of different joint constitutive models in physical experiments of direct tension and Brazilian splitting (Zhang Q. L. et al., 2021; Zhao et al., 2022). However, the numerical simulation in this study considers the influence of joint constitutive models, which helps predict the occurrence sequence and magnitude of the MCEI of CJBs with different joint constitutive models.

From Figure 14d, it can be noticed that the sequence of MCEI manifestations along the strain axis is as follows: the AUTS 2 MPa of MEs of joints (under the DTC), the AUTS 4 MPa of MEs of joints (under the DTC) [the AUTS 6 MPa of MEs of joints (under the DTC)], the AUTS 2 MPa of MEs of joints (under the BSC), the AUTS 4 MPa of MEs of joints (under the BSC), and the AUTS 6 MPa of MEs of joints (under the BSC). The magnitudes of the MCEIs in increasing order are as follows: the AUTS 2 MPa of MEs of joints (under the BSC), the AUTS 2 MPa of MEs of joints (under the DTC), the AUTS 4 MPa of MEs of joints (under the BSC), the AUTS 6 MPa of MEs of joints (under the BSC), the AUTS 6 MPa of MEs of joints (under the DTC), and the AUTS 4 MPa of MEs of joints (under the DTC). The abovementioned observations demonstrate that for diverse joint strengths, compared to the Brazilian splitting condition, the MCEIs of the specimens under the direct tensile condition occur at an earlier stage, and the magnitudes of these MCEIs are higher. Previous theoretical studies may not have investigated the influence of joint strength on the occurrence sequence and magnitude of the MCEI of CJBs under the DTC and BSC (Liu E. et al., 2021; Cen et al., 2020). The findings obtained in this study in this regard can deepen the understanding of the development laws of damage and micro-cracks of CJBs under different loading scenarios and joint strength conditions.

According to Figure 14e, in terms of the appearing sequence of the MCEIs along the strain axis, the order is as follows: the RHI 5 (under the DTC) [the RHI 10 (under the DTC), the RHI 200 (under the DTC)], and the RHI 5 (under the BSC) [the RHI 10 (under the BSC) and the RHI 200 (under the BSC)]. The magnitudes of the MCEIs in ascending order are as follows: the RHI 10 (under the BSC), the RHI 5 (under the BSC), the RHI 200 (under the BSC), the RHI 200 (under the DTC), the RHI 10 (under the DTC), and the RHI 5 (under the DTC). The abovementioned results indicate that for varied degrees of rock homogeneity when juxtaposed with the direct tensile condition, the MCEIs of the specimens under the Brazilian splitting condition emerge at a later stage, and the magnitudes of these MCEIs are smaller. Studies (Lin et al., 2018; Xu et al., 2020; Wang et al., 2022b; 2022c; 2023a) indicate that there are differences in rock heterogeneity among CJBs in various regions. The numerical simulation results of this study provide a basis for engineering monitoring. Differentiated monitoring schemes can be formulated according to the rock homogeneity degree and the crack propagation characteristics under different loading conditions. For example, in locations subjected to direct tensile stress and characterized by poor rock homogeneity, monitoring points should be more densely arranged and the monitoring frequency should be increased to enable timely detection of early crack formation. As for the locations under the stress state similar to Brazilian splitting, the monitoring strategy can be appropriately adjusted, and the long-term development of cracks needs to be paid attention to.

From Figure 14f, it can be found that from the perspective of the occurrence sequence of the MCEIs upon the strain axis, the order is as follows: the AUTS 10 MPa of MEs of rock (under the DTC), the AUTS 16 MPa of MEs of rock (under the DTC) [the AUTS 24 MPa of MEs of rock (under the DTC)], the AUTS 16 MPa of MEs of rock (under the BSC), and the AUTS 10 MPa of MEs of rock (under the BSC) [the AUTS 24 MPa of MEs of rock (under the BSC)]. The magnitudes of the MCEIs in ascending order are as follows: the AUTS 16 MPa of MEs of rock (under the BSC), the AUTS 24 MPa of MEs of rock (under the BSC), the AUTS 10 MPa of MEs of rock (under the BSC), the AUTS 24 MPa of MEs of rock (under the DTC), the AUTS 16 MPa of MEs of rock (under the DTC), and the AUTS 10 MPa of MEs of rock (under the DTC). The abovementioned findings suggest that for various meso-rock strengths, compared to the Brazilian splitting condition, the MCEIs of specimens arise at an earlier stage and have larger magnitudes under the direct tensile condition. In practical engineering, the presence of water or changes in humidity can change the strength of meso-rocks. For the locations that are in a state similar to direct tension and are significantly affected by water or humidity, key monitoring points should be set up.

As illustrated in Figure 14g, regarding the appearance series of the MCEIs on the strain axis, the order is as follows: the sample with the secondary joint set (in the DTC), the specimen without the secondary joint set (in the DTC), the sample without the secondary joint set (in the BSC), and the specimen with the secondary joint set (in the BSC). The magnitudes of the MCEIs, in increasing order, are as follows: the sample without the secondary joint set (in the BSC), the specimen with the secondary joint set (in the BSC), the sample with the secondary joint set (in the DTC), and the specimen without the secondary joint set (in the DTC). The abovementioned observations imply that for varied states of the secondary joint set, in contrast to the direct tensile condition, the MCEIs of the specimens appear at a later stage and have lower magnitudes under the Brazilian splitting condition. If the stress state of the CJBs is similar to the DTC and CJBs possess the secondary joint set, the MCEI appears relatively early. Therefore, in practical engineering, it is necessary to adopt a combination of multiple monitoring methods in order to obtain the status information of the CJBs more comprehensively, accurately, and promptly.

3.4 Sensitivity analysis of factors influencing the MCEIs of CJBs under direct and indirect tensile conditions

With reference to pertinent research studies (Dinmohammadpour et al., 2022; Wang H. P. et al., 2022; Xue et al., 2020; Wang et al., 2020) and taking into account both the sequence of appearance (strain) and the magnitude of the MCEI, a calculation formula is developed in this section for the sensitivity indicator $A_{Di}$ or $A_{Br}$ of the MCEI to a specific affecting variable under DTC or BSC for CJBs, as shown below:

$A_{Di}\text{or}{A}_{Br}=\left(B_{Di}\text{or}{B}_{Br}\right)\times C+\left(D_{Di}\text{or}{D}_{Br}\right)\times E,(2)$

where $B_{Di}$ or $B_{Br}$ denotes the sensitivity parameter of the appearing sequence of the MCEI to a specific affecting variable under the DTC or BSC, respectively. The calculation method for this coefficient is provided in Equation 3. $C$ signifies the corresponding weighting parameter, which generally falls within the range 0.5–0.7 (Wang H. P. et al., 2022; Wang et al., 2020; Yang H. Q. et al., 2022; Deng et al., 2021), and it is assigned a value of 0.5 in this instance. $D_{Di}$ or $D_{Br}$ denotes the sensitivity parameter of the magnitude of the MCEI to a specific affecting variable under the DTC or BSC, respectively. The calculation method for this coefficient is outlined in Equation 4. $E$ is the corresponding weighting parameter, typically ranging from 0.3 to 0.5 (Xue et al., 2020; Yang et al., 2021; Song et al., 2022), and it is assigned a value of 0.5 in this instance.

$B_{Di}\text{or}{B}_{Br}=\frac{\Delta F_{Di}\text{or}\Delta F_{Br}}{\Delta G},(3)$

$D_{Di}\text{or}{D}_{Br}=\frac{\Delta H_{Di}\text{or}\Delta H_{Br}}{\Delta G},(4)$

where $\Delta F_{Di}$ or $\Delta F_{Br}$ represents the percentage variation in the appearing sequence of the MCEI under the DTC or BSC. $\Delta H_{Di}$ or $\Delta H_{Br}$ signifies the percentage variation in the magnitude of the MCEI under the direct tensile or Brazilian splitting condition. $\Delta G$ denotes the percentage alteration of a specific affecting variable.

The sensitivity indicators of the MCEIs of CJBs to a specific affecting variable under direct tension and Brazilian splitting conditions are derived from Equation 2, and the results are presented in Table 5. Under the direct tensile condition and when β = 30°, the sensitivity level of the MCEI to diverse variables, graded from the highest to the lowest, is as follows: joint strength, the secondary joint set, joint constitutive behavior, meso-rock strength, and rock homogeneity degree. However, under the Brazilian splitting conditions and when β = 30°, the sensitivity level of the MCEI to diverse variables, ranked from the highest to the lowest, is as follows: joint strength, joint constitutive behavior, the secondary joint set, meso-rock strength, and rock homogeneity degree.

Table 5

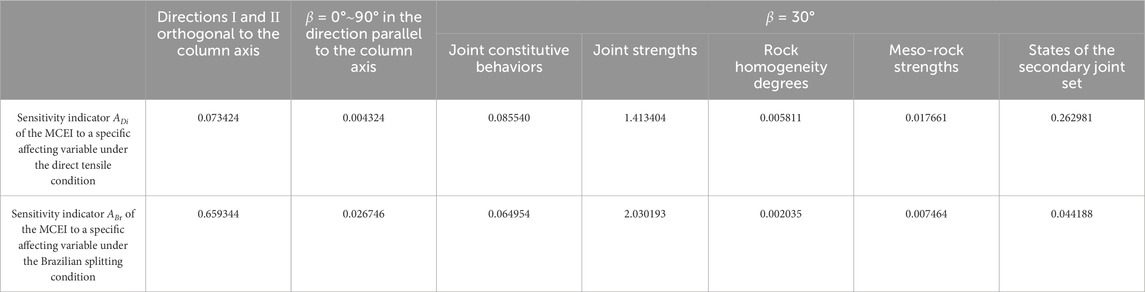
Table 5. Sensitivity analysis of factors influencing the MCEIs of CJBs under direct and indirect tensile conditions.

4 Discussion

4.1 Energy features of jointed rock mass under direct and indirect tensile conditions

Direct tensile loading is more likely to induce crack propagation, leading to an earlier release of energy. In contrast, the Brazilian splitting test involves a compression-induced tensile fracture process, where the vicinities of the upper and lower extremities of the sample are under biaxial stress conditions. The process of energy absorption and release in the specimen under the Brazilian splitting condition may be more complex (Zhang Q. L. et al., 2021; Liu Z. L. et al., 2021). Figure 14b in this study reveals that regarding the manifestation series of the MCEIs along the strain axis, the order is as follows: β = 60° (under the direct tensile condition) [β = 90° (under the direct tensile condition)], β = 30° (under the direct tensile condition), β = 30° (under the Brazilian splitting condition), β = 60° (under the Brazilian splitting condition), and β = 90° (under the Brazilian splitting condition). The magnitudes of the MCEIs in ascending order are as follows: β = 30° (under the Brazilian splitting condition), β = 60° (under the direct tensile condition), β = 90° (under the direct tensile condition), β = 60° (under the Brazilian splitting condition), β = 30° (under the direct tensile condition), and β = 90° (under the Brazilian splitting condition). The abovementioned results indicate that under the Brazilian splitting condition, the specimen releases energy at a later stage, but the magnitude of the energy may be higher, depending on the column dip angle.

The mechanical properties of joints influence the energy characteristics of jointed rock masses when subjected to tensile forces, and the specific manifestations of this influence under direct and indirect tensile conditions require further investigation (Zhao et al., 2022; Cen et al., 2020; Yang Z. et al., 2022). Figure 14d in this study displays that, for different joint strengths, concerning the manifestation series of the MCEIs on the strain axis, the order is as follows: the AUTS 2 MPa of MEs of joints (under the direct tensile condition), the AUTS 4 MPa of MEs of joints (under the direct tensile condition) [the AUTS 6 MPa of MEs of joints (under the direct tensile condition)], the AUTS 2 MPa of MEs of joints (under the Brazilian splitting condition), the AUTS 4 MPa of MEs of joints (under the Brazilian splitting condition), and the AUTS 6 MPa of MEs of joints (under the Brazilian splitting condition). The magnitudes of the MCEIs in increasing order are as follows: the AUTS 2 MPa of MEs of joints (under the Brazilian splitting condition), the AUTS 2 MPa of MEs of joints (under the direct tensile condition), the AUTS 4 MPa of MEs of joints (under the Brazilian splitting condition), the AUTS 6 MPa of MEs of joints (under the Brazilian splitting condition), the AUTS 6 MPa of MEs of joints (under the direct tensile condition), and the AUTS 4 MPa of MEs of joints (under the direct tensile condition). These observations suggest that for varied joint strengths, the specimens under the Brazilian splitting condition release energy at a later stage than those under the direct tension condition, and the magnitudes of energy released under the Brazilian splitting condition are smaller than those under the direct tension condition.

Typically, when jointed rock masses composed of minerals with higher hardness are subjected to tensile forces, due to their stronger resistance to deformation, they may release energy at a later stage (Hao et al., 2020; Liu et al., 2021a). Figure 14f in this study demonstrates that for diverse meso-rock strengths, regarding the manifestation series of the MCEIs along the strain axis, the order is as follows: the AUTS 10 MPa of MEs of rock (under the direct tensile condition), the AUTS 16 MPa of MEs of rock (under the direct tensile condition) [the AUTS 24 MPa of MEs of rock (under the direct tensile condition)], the AUTS 16 MPa of MEs of rock (under the Brazilian splitting condition), and the AUTS 10 MPa of MEs of rock (under the Brazilian splitting condition) [the AUTS 24 MPa of MEs of rock (under the Brazilian splitting condition)]. The magnitudes of the MCEIs in ascending order are as follows: the AUTS 16 MPa of MEs of rock (under the Brazilian splitting condition), the AUTS 24 MPa of MEs of rock (under the Brazilian splitting condition), the AUTS 10 MPa of MEs of rock (under the Brazilian splitting condition), the AUTS 24 MPa of MEs of rock (under the direct tensile condition), the AUTS 16 MPa of MEs of rock (under the direct tensile condition), and the AUTS 10 MPa of MEs of rock (under the direct tensile condition). The abovementioned situation implies that for different meso-rock strengths, the specimens under the Brazilian splitting condition release energy later than those under the direct tension condition, and the energy magnitudes under the Brazilian splitting condition are lower than those under the direct tension condition.

5 Conclusion

(1) Under the DTC, both the TSs and EDMs of samples in directions I and II orthogonal to the column axis are greater than those under the BSC. For the direction parallel to the column axis, compared to the DTC, the TS of specimens under the BSC is smaller at the column lean angle β = 0°–60° and larger at β = 75°–90°. For different joint constitutive behaviors, the TSs and EDMs of the β = 30° specimens under the DTC are both greater than those under the BSC. The higher the joint strength, the smaller the ratio of the specimen TSs under direct tensile to Brazilian splitting conditions, while the ratio of the specimen EDMs may be higher. As the rock homogeneity index increases, the difference in mechanical properties between the specimens under the DTC and BSC tends to increase. When the meso-rock strength increases, the TS and EDM ratios for specimens under the DTC and BSC do not monotonously increase or decrease. The presence of the secondary joint set results in a reduction in the TS ratio between the DTC and BSC, while it increases the EDM ratio between these two conditions.

(2) Regarding the case involving the secondary joint set, under the DTC, the columnar joints, secondary joint sets, and individual columns within the specimen synergistically contribute to the specimen-bearing capacity, and there is a relatively concentrated sequence of appearance of micro-cracks. Under the BSC, within a localized area along the vertical centerline of the specimen, the columnar joint slippage occurs first, followed by cracking in the secondary joint sets. Subsequently, the cracked secondary joint sets connect with newly cracked columnar joints, thereby forming a localized, multi-stage bearing process.

(3) Regarding the specimens in directions I and II perpendicular to the column axis, compared to the DTC, the MCEIs occur at a later stage and may have a larger magnitude under the BSC. For the specimens with diverse column tilt angles in the direction parallel to the column axis, compared to the BSC, the MCEIs occur at an earlier stage and may have smaller magnitudes under the direct tensile condition, which depends on the specific column dip angle. For various joint mechanical constitutive behaviors/joint strengths/rock homogeneity indexes/meso-rock strengths/secondary joint set conditions, compared to the DTC, the MCEI for the β = 30° specimens arises at a later stage and possesses a lower magnitude under the BSC.

(4) When subjected to the DTC, the sensitivity of the MCEI to diverse factors ranks from the highest to lowest as follows: joint strength, the secondary joint set, joint constitutive behavior, meso-rock strength, and the rock homogeneity index. However, when undergoing the BSC, the sensitivity of the MCEI to various factors ranks in decreasing order as follows: joint strength, joint constitutive behavior, the secondary joint set, meso-rock strength, and the rock homogeneity index. These discoveries can serve as an academic basis for understanding the arising sequence and magnitude differences of the MCEIs in CJBs under tensile conditions, thus providing scientific support for rock mass project monitoring, reinforcement, and operational maintenance.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

DL: conceptualization, methodology, resources, writing – original draft, and writing – review and editing. HY: conceptualization, funding acquisition, investigation, methodology, supervision, writing – original draft, and writing – review and editing. ZP: conceptualization, investigation, methodology, writing – original draft, and writing – review and editing. YW: conceptualization, data curation, investigation, resources, software, supervision, writing – original draft, and writing – review and editing. KS: data curation, methodology, and writing – review and editing. CC: data curation, methodology, and writing – review and editing. HL: methodology, software, and writing – review and editing. XL: data curation, methodology, and writing – review and editing. LP: methodology, software, and writing – review and editing. AJ: data curation, methodology, and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The financial support from the Chongqing Talent Program Young Top Talents (No. cstc2024ycjh-bgzxm0047) is greatly appreciated.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, S., Rizvi, Z. H., Arp, J. C. C., Wuttke, F., Tirth, V., and Islam, S. (2021). Evolution of temperature field around underground power cable for static and cyclic heating. Energies 14 (23), 8191. doi:10.3390/en14238191

CrossRef Full Text | Google Scholar

Ahmad, S., Rizvi, Z. H., and Wuttke, F. (2025). Unveiling soil thermal behavior under ultra-high voltage power cable operations. Sci. Rep. 15, 7315. doi:10.1038/s41598-025-91831-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, D. T., Ribeiro, R. P., Xavier, G. D., Monteiro, S. N., and de Azevedo, A. R. G. (2025). Technological evaluation of stones from the eastern region of the state of São Paulo, Brazil, for railway ballast. Sci. Rep. 15, 1444.

PubMed Abstract | CrossRef Full Text | Google Scholar

Cen, D. F., Huang, D., Song, Y. X., and Jiang, Q. H. (2020). Direct tensile behavior of limestone and sandstone with bedding planes at different strain rates. Rock Mech. Rock Eng. 53 (6), 2643–2651. doi:10.1007/s00603-020-02070-x

CrossRef Full Text | Google Scholar

Deng, P. H., Liu, Q. S., Huang, X., Bo, Y., Liu, Q., and Li, W. W. (2021). Sensitivity analysis of fracture energies for the combined finite-discrete element method (FDEM). Eng. Fract. Mech. 251, 107793. doi:10.1016/j.engfracmech.2021.107793

CrossRef Full Text | Google Scholar

Dinmohammadpour, M., Nikkhah, M., Goshtasbi, K., and Ahangari, K. (2022). Application of wavelet transform in evaluating the Kaiser effect of rocks in acoustic emission test. Measurement 192, 110887. doi:10.1016/j.measurement.2022.110887

CrossRef Full Text | Google Scholar

Fan, Q. X., Wang, Z. L., Xu, J. R., Zhou, M. X., Jiang, Q., and Li, G. (2018). Study on deformation and control measures of columnar jointed basalt for Baihetan super-high arch dam foundation. Rock Mech. Rock Eng. 51 (8), 2569–2595. doi:10.1007/s00603-017-1378-9

CrossRef Full Text | Google Scholar

Feng, X. H., Gong, B., Cheng, X. F., Zhang, H. H., and Tang, C. A. (2022). Anisotropy and microcrack-induced failure precursor of shales under dynamic splitting. Geomatics, Nat. Hazards Risk 13 (1), 2864–2889. doi:10.1080/19475705.2022.2137440

CrossRef Full Text | Google Scholar

Gomes, R. L., and Rodrigues, J. E. (2007). Quality ranking of twelve colunmar basalt occurrences in the northern portion of the Parana Basin-Brazil. Eng. Geol. 91, 265–278.

CrossRef Full Text | Google Scholar

Gong, B., Tang, C. A., Wang, S. Y., Bai, H. M., and Li, Y. C. (2019). Simulation of the nonlinear mechanical behaviors of jointed rock masses based on the improved discontinuous deformation and displacement method. Int. J. Rock Mech. Min. Sci. 122, 104076. doi:10.1016/j.ijrmms.2019.104076

CrossRef Full Text | Google Scholar

Gong, B., Wang, Y. Y., Chen, X., Song, W. C., Wang, K. K., and Yu, J. (2025a). Analysis of sensitivity factors on CJB mechanical behavior from specimen scale to engineering scale. Eng. Fract. Mech. 314, 110673. doi:10.1016/j.engfracmech.2024.110673

CrossRef Full Text | Google Scholar

Gong, B., Wang, Y. Y., Zhao, T., Tang, C. A., Yang, X. Y., and Chen, T. T. (2022). AE energy evolution during CJB fracture affected by rock heterogeneity and column irregularity under lateral pressure. Geomatics, Nat. Hazards Risk 13 (1), 877–907. doi:10.1080/19475705.2022.2047114

CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., and Tang, C. A. (2024a). Modelling rock fracturing by a novel implicit continuous to discontinuous method. Comput. Geotechnics 166, 106035. doi:10.1016/j.compgeo.2023.106035

CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., Tang, C. A., and Zhou, G. G. D. (2024b). Integrating RFPA and DEM in Adaptive RDFA modeling of rock fracturing process. Rock Mech. Rock Eng. 58, 2569–2587. doi:10.1007/s00603-024-04239-0

CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., Tang, C. A., and Zhou, G. G. D. (2025b). The random RFPA method for modelling rock failure. Rock Mech. Rock Eng. doi:10.1007/s00603-025-04400-3

CrossRef Full Text | Google Scholar

Hao, X. J., Du, W. S., Zhao, Y. X., Sun, Z. W., Zhang, Q., Wang, S. H., et al. (2020). Dynamic tensile behaviour and crack propagation of coal under coupled static-dynamic loading. Int. J. Min. Sci. Technol. 30 (5), 659–668. doi:10.1016/j.ijmst.2020.06.007

CrossRef Full Text | Google Scholar

Hu, W., Wu, A. Q., Chen, S. H., Huang, S. L., and Zhang, L. J. (2017). Mechanical properties of columnar jointed basalt rock with hidden fissures under uniaxial loading. Chin. J. Rock Mech. Eng. 36 (08), 1880–1888. doi:10.13722/j.cnki.jrme.2017.0149

CrossRef Full Text | Google Scholar

Huang, Z. J., Zhang, Y., Li, Y., Zhang, D., Yang, T., and Sui, Z. L. (2021). Determining tensile strength of rock by the direct tensile, brazilian splitting, and three-point bending methods: a comparative study. Adv. Civ. Eng., 5519230.

Google Scholar

Jiang, Q., Feng, X. T., Fan, Y. L., Zhu, X. D., Hu, L. X., Li, S. J., et al. (2013). Survey and laboratory study of anisotropic properties for columnar jointed basaltic rock mass. Chin. J. Rock Mech. Eng. 32 (12), 2527–2535.

Google Scholar

Lang, Y. X., Liang, Z. Z., Dong, Z., and Wu, N. (2022). Mechanical behavior of porous rock based on the 3D digital image reconstruction and parallel computation. Environ. Earth Sci. 81 (18), 438. doi:10.1007/s12665-022-10566-8

CrossRef Full Text | Google Scholar

Li, L. C., Tang, C. A., Zhu, W. C., and Liang, Z. Z. (2009). Numerical analysis of slope stability based on the gravity increase method. Comput. Geotech. 36, 1246–1258. doi:10.1016/j.compgeo.2009.06.004

CrossRef Full Text | Google Scholar

Liang, Z. Z., Gong, B., and Li, W. R. (2019a). Instability analysis of a deep tunnel under triaxial loads using a three-dimensional numerical method with strength reduction method. Tunn. Undergr. Space Technol. 86, 51–62. doi:10.1016/j.tust.2018.11.015

CrossRef Full Text | Google Scholar

Liang, Z. Z., Wu, N., Li, Y. C., Li, H., and Li, W. R. (2019b). Numerical study on anisotropy of the representative elementary volume of strength and deformability of jointed rock masses. Rock Mech. Rock Eng. 52 (11), 4387–4402. doi:10.1007/s00603-019-01859-9

CrossRef Full Text | Google Scholar

Lin, Z. A., Xu, W. Y., Wang, W., Wang, H. L., Wang, R. B., Ji, H., et al. (2018). Determination of strength and deformation properties of columnar jointed rock mass using physical model tests. Ksce J. Civ. Eng. 22 (9), 3302–3311. doi:10.1007/s12205-018-0257-6

CrossRef Full Text | Google Scholar

Lin, Z. N., Xu, W. Y., Wang, H. L., Zhang, J. C., Wei, W., Wang, R. B., et al. (2017). Anisotropic characteristic of irregular columnar-jointed rock mass based on physical model test. Ksce J. Civ. Eng. 21 (5), 1728–1734. doi:10.1007/s12205-016-1796-3

CrossRef Full Text | Google Scholar

Liu, E., Liu, F., Xiong, Y., Lei, X., and Wang, S. (2021a). Study on the effect of precrack on specimen failure characteristics under static and dynamic loads by Brazilian split test. Math. Problems Eng. 2021, 1–8. doi:10.1155/2021/5747768

CrossRef Full Text | Google Scholar

Liu, X., Liang, Z. Z., Meng, S. W., Tang, C. A., and Tao, J. P. (2022). Numerical simulation study of brittle rock materials from micro to macro scales using digital image processing and parallel computing. Appl. Sciences-Basel 12 (8), 3864. doi:10.3390/app12083864

CrossRef Full Text | Google Scholar

Liu, X. Z., Tang, C. A., Li, L. C., Lv, P. F., and Liu, H. Y. (2017). Microseismic monitoring and 3D finite element analysis of the right bank slope, Dagangshan hydropower station, during reservoir impounding. Rock Mech. Rock Eng. 50 (7), 1901–1917. doi:10.1007/s00603-017-1191-5

CrossRef Full Text | Google Scholar

Liu, Z. L., Ma, C. D., Wei, X. A., and Xie, W. B. (2021b). Experimental study on mechanical properties and failure modes of pre-existing cracks in sandstone during uniaxial tension/compression testing. Eng. Fract. Mech. 255, 107966. doi:10.1016/j.engfracmech.2021.107966

CrossRef Full Text | Google Scholar

Lu, W. B., Zhu, Z. D., He, Y. X., and Que, X. C. (2021). Strength characteristics and failure mechanism of a columnar jointed rock mass under uniaxial, triaxial, and true triaxial confinement. Rock Mech. Rock Eng. 54 (5), 2425–2439. doi:10.1007/s00603-021-02400-7

CrossRef Full Text | Google Scholar

Niu, Z. H., Zhu, Z. D., and Que, X. C. (2020). Constitutive model of stress-dependent seepage in columnar jointed rock mass. Symmetry-Basel 12 (1), 160. doi:10.3390/sym12010160

CrossRef Full Text | Google Scholar

Que, X. C., Zhu, S., Zhu, Z. D., Zhang, J., Xie, X. H., and Niu, Z. H. (2024). Anisotropic characteristic strength and energy evolution of irregular columnar jointed rock masses before and after excavation. Rock Mech. Rock Eng. 2024. doi:10.1007/s00603-024-03925-3

CrossRef Full Text | Google Scholar

Que, X. C., Zhu, Z. D., and Lu, W. B. (2020). Anisotropic constitutive model of pentagonal prism columnar jointed rock mass. Bull. Eng. Geol. Environ. 79 (1), 269–286. doi:10.1007/s10064-019-01521-2

CrossRef Full Text | Google Scholar

Que, X. C., Zhu, Z. D., Niu, Z. H., and Lu, W. N. (2021). Estimating the strength and deformation of columnar jointed rock mass based on physical model test. Bull. Eng. Geol. Environ. 80 (2), 1557–1570. doi:10.1007/s10064-020-01974-w

CrossRef Full Text | Google Scholar

Rizvi, Z. H., Mustafa, S. H., Sattari, A. S., Ahmad, S., Furtner, P., and Wuttke, F. (2020). “Dynamic lattice element modelling of cemented geomaterials,”. Advances in computer methods and Geomechanics. Lecture Notes in Civil engineering. Editors A. Prashant, A. Sachan, and C. Desai (Singapore: Springer), 55, 655–665. doi:10.1007/978-981-15-0886-8_53

CrossRef Full Text | Google Scholar

Shi, A. C., Wei, Y. F., Zhang, Y. H., and Tang, M. F. (2020). Study on the strength characteristics of columnar jointed basalt with a true triaxial Apparatus at the Baihetan hydropower station. Rock Mech. Rock Eng. 53, 4947–4965. doi:10.1007/s00603-020-02195-z

CrossRef Full Text | Google Scholar

Song, K. L., Yang, H. Q., Xie, J. N., and Karekal, S. (2022). An optimization methodology of cutter-spacing for efficient mechanical breaking of jointed rock mass. Rock Mech. Rock Eng. 55 (6), 3301–3316. doi:10.1007/s00603-022-02806-x

CrossRef Full Text | Google Scholar

Tang, C. A., and Kou, S. Q. (1998). Crack propagation and coalescence in brittle materials under compression. Eng. Fract. Mech. 61, 311–324. doi:10.1016/s0013-7944(98)00067-8

CrossRef Full Text | Google Scholar

Tang, C. A., Lin, P., Wong, R. H. C., and Chau, K. T. (2001). Analysis of crack coalescence in rock-like materials containing three flaws - Part II: numerical approach. Int. J. Rock Mech. Min. Sci. 38 (7), 925–939. doi:10.1016/s1365-1609(01)00065-x

CrossRef Full Text | Google Scholar

Tang, C. A., Tang, S. B., Gong, B., and Bai, H. M. (2015). Discontinuous deformation and displacement analysis: from continuous to discontinuous. Sci. China-Technol Sci. 58 (9), 1567–1574. doi:10.1007/s11431-015-5899-8

CrossRef Full Text | Google Scholar

Tang, C. A., Webb, A. A. G., Moore, W. B., Wang, Y. Y., Ma, T. H., and Chen, T. T. (2020). Breaking Earth's shell into a global plate network. Nat. Commun. 11 (1), 3621. doi:10.1038/s41467-020-17480-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Vasseur, J., and Wadsworth, F. B. (2019). The permeability of columnar jointed lava. J. Geophys. Research-Solid Earth 124 (11), 11305–11315. doi:10.1029/2019jb018118

CrossRef Full Text | Google Scholar

Wang, H. P., Zhang, B., Yuan, L., Wang, S., Yu, G. F., and Liu, Z. Z. (2022a). Analysis of precursor information for coal and gas outbursts induced by roadway tunneling: a simulation test study for the whole process. Tunn. Undergr. Space Technol. 122, 104349. doi:10.1016/j.tust.2021.104349

CrossRef Full Text | Google Scholar

Wang, P., Jia, H. J., and Zheng, P. Q. (2020). Sensitivity analysis of bursting liability for different coal-rock combinations based on their inhomogeneous characteristics. Geomatics, Nat. Hazards Risk 11 (1), 149–159. doi:10.1080/19475705.2020.1714754

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., and Tang, C. A. (2022b). Numerical investigation on anisotropy and shape effect of mechanical properties of columnar jointed basalts containing transverse joints. Rock Mech. Rock Eng. 55 (11), 7191–7222. doi:10.1007/s00603-022-03018-z

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Tang, C. A., and Yang, X. Y. (2023a). Size effect and lateral pressure effect on the mechanical resistance of columnar jointed basalt. Int. J. Rock Mech. Min. Sci. 171, 105571. doi:10.1016/j.ijrmms.2023.105571

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Tang, C. A., and Zhao, T. (2022c). Numerical study on size effect and anisotropy of columnar jointed basalts under uniaxial compression. Bull. Eng. Geol. Environ. 81, 41. doi:10.1007/s10064-021-02499-6

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Yang, X. Y., and Tang, C. A. (2023b). Investigation into the Multistage mechanical damage behavior of columnar jointed basalts with different meso-constitutive Relations and model sizes. Lithosphere 2023 (1), 8711959. doi:10.2113/2023/8711959

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Zhang, Y. J., Yang, X. Y., and Tang, C. A. (2022d). Progressive fracture behavior and acoustic emission release of CJBs affected by joint distance ratio. Mathematics 10 (21), 4149. doi:10.3390/math10214149

CrossRef Full Text | Google Scholar

Wang, Y. Y., Yang, H. Q., Song, K. L., Chen, C. W., Li, H., and Li, X. Y. (2024). The energy characteristics of columnar jointed basalt size effect considering the occurrence sequence and magnitude of micro-cracks. Rock Mech. Rock Eng. 57 (12), 11139–11175. doi:10.1007/s00603-024-04142-8

CrossRef Full Text | Google Scholar

Xiao, W. M., Han, J. C., Tian, M. T., and Wu, Z. Y. (2023). Experimental study on mechanical anisotropy of irregular columnar jointed rock mass under conventional triaxial compression condition. Chin. J. Rock Mech. Eng. 42 (S1), 3131–3140. doi:10.13722/j.cnki.jrme.2022.0272

CrossRef Full Text | Google Scholar

Xiang, X., Fan, L., Sun, Z. Y., Zhang, G. C., Zhang, S., and Zhang, Y. H. (2021). Blasting relaxation characteristics of columnar jointed rock mass with AE technology. Arab. J. Geosci. 14, 2827.

Google Scholar

Xu, J. R., Li, H., Meng, Q. X., Xu, W. Y., He, M. J., and Yang, J. H. (2020). A study on triaxial unloading test of columnar-jointed-rock-mass-like material with AW velocity analysis. Adv. Civ. Eng. 2020, 6693544. doi:10.1155/2020/6693544

CrossRef Full Text | Google Scholar

Xu, T., Ranjith, P. G., Wasantha, P. L. P., Zhao, J., Tang, C. A., and Zhu, W. C. (2013). Influence of the geometry of partially-spanning joints on mechanical properties of rock in uniaxial compression. Eng. Geol. 167, 134–147. doi:10.1016/j.enggeo.2013.10.011

CrossRef Full Text | Google Scholar

Xue, D. J., Gao, L., Lu, L., Zhou, J., Zhou, H. W., Wu, Z. D., et al. (2020). An acoustic emission-based cluster damage model for simulating triaxial compression behaviors of granite. Rock Mech. Rock Eng. 53 (9), 4201–4220. doi:10.1007/s00603-020-02169-1

CrossRef Full Text | Google Scholar

Yan, L., Xu, W. Y., Wang, R. B., and Meng, Q. X. (2018). Numerical simulation of the anisotropic properties of a columnar jointed rock mass under triaxial compression. Eng. Comput. 35 (4), 1788–1804. doi:10.1108/ec-07-2017-0240

CrossRef Full Text | Google Scholar

Yang, H. Q., Liu, B. L., and Karekal, S. (2021). Experimental investigation on infrared radiation features of fracturing process in jointed rock under concentrated load. Int. J. Rock Mech. Min. Sci. 139, 104619. doi:10.1016/j.ijrmms.2021.104619

CrossRef Full Text | Google Scholar

Yang, H. Q., Song, K. L., and Zhou, J. Y. (2022a). Automated recognition model of geomechanical information based on operational data of tunneling boring machines. Rock Mech. Rock Eng. 55, 1499–1516. doi:10.1007/s00603-021-02723-5

CrossRef Full Text | Google Scholar

Yang, T. H., Wang, P. T., Xu, T., Yu, Q. L., Zhang, P. H., Shi, W. H., et al. (2015). Anisotropic characteristics of jointed rock mass: a case study at Shirengou iron ore mine in China. Tunn. Undergr. Space Technol. 48, 129–139. doi:10.1016/j.tust.2015.03.005

CrossRef Full Text | Google Scholar

Yang, Z., Zhu, W. C., Guan, K., Yan, B. X., and Jia, H. W. (2022b). Influence of dynamic disturbance on rock creep from time, space and energy aspects. Geomatics, Nat. Hazards Risk 13 (1), 1065–1086. doi:10.1080/19475705.2022.2064775

CrossRef Full Text | Google Scholar

Zhang, J. C., Pei, S. F., Xu, X., and Li, H. R. (2021a). Insights into unloading relaxation mechanism of columnar jointed basalt at the Baihetan left dam foundation. Adv. Mater. Sci. Eng. 2021, 9953768. doi:10.1155/2021/9953768

CrossRef Full Text | Google Scholar

Zhang, Q. L., Zhi, Z. H., Feng, C., Li, R. X., Yue, J. C., and Cong, J. Y. (2021b). Using continuum-discontinuum element method to model the foliation-affected fracturing in rock Brazilian test. Adv. Civ. Eng. 2021, 1404568. doi:10.1155/2021/1404568

CrossRef Full Text | Google Scholar

Zhang, Z. H., Ma, K., Li, H., and He, Z. L. (2022). Microscopic investigation of rock direct tensile failure based on statistical analysis of acoustic emission waveforms. Rock Mech. Rock Eng. 55, 2445–2458.

CrossRef Full Text | Google Scholar

Zhao, T. B., Zhang, W., Xing, M. L., Qiu, Y., and Yao, J. P. (2022). Study on determination method of rock tensile modulus of Brazilian disc splitting test based on digital speckle correlation method (DSCM). Arabian J. Sci. Eng. 47, 4287–4300. doi:10.1007/s13369-021-06038-z

CrossRef Full Text | Google Scholar

Zhou, H. Y., Li, S. C., Wang, M. L., Wang, X. W., Yuan, C., Xiong, B., et al. (2024). Stochastic modeling method and elastic parameter analysis of the irregular columnar jointed rock masses considering the joint characteristics within the cross section. Environ. Earth Sci. 83 (6), 157. doi:10.1007/s12665-023-11364-6

CrossRef Full Text | Google Scholar

Zhu, S., Que, X. C., Zhu, Z. D., and Han, B. (2023). Improved polygonal constitutive model for columnar jointed basalt and its application in tunnel stability analysis. Tunn. Undergr. Space Technol. 142, 105449. doi:10.1016/j.tust.2023.105449

CrossRef Full Text | Google Scholar

Zhu, S. Y., He, C. D., Peng, F., Shi, A. C., Yuan, D. Y., and Zhang, W. K. (2020). Experimental and numerical studies on the mechanical properties of columnar jointed basalt. Adv. Civ. Eng. 2020, 6659718. doi:10.1155/2020/6659718

CrossRef Full Text | Google Scholar

Nomenclature

u Mechanical parameter of meso-elements

u₀ Average value of u for all the elements

m Homogeneity index

β Column inclination angle

CJBs Columnar jointed basalts

CJRMs Columnar jointed rock masses

TS Tensile strength

CS Compressive strength

EDM Equivalent deformation modulus

RFPA Rock failure process analysis

AE Acoustic emission

DIC Digital image correlation

CRSCs Compressive residual strength coefficients

MEs Meso-elements

AUTSs Average uniaxial tensile strengths

AUCSs Average uniaxial compressive strengths

BSC Brazilian splitting condition

DTC Direct tensile condition

RHIs Rock homogeneity indexes

RMSE Root-mean-square error

MCEI Micro-crack energy index, i.e., the cumulative AE energy matching the sample peak stress

A_Di Sensitivity parameter of the MCEI to a specific affecting variable under direct tension

A_Br Sensitivity parameter of the MCEI to a specific affecting variable under Brazilian splitting

B_Di Sensitivity parameter of the appearing sequence of the MCEI to a specific affecting variable under direct tension

B_Br Sensitivity parameter of the appearing sequence of the MCEI to a specific affecting variable under Brazilian splitting

C Weighting parameter corresponding to B_Di or B_Br

D_Di Sensitivity parameter of the magnitude of the MCEI to a specific affecting variable under direct tension

D_Br Sensitivity parameter of the magnitude of the MCEI to a specific affecting variable under Brazilian splitting

E Weighting parameter corresponding to D_Di or D_Br

△F_Di Percentage variation in the appearing sequence of the MCEI under direct tension

△F_Br Percentage alteration in the appearing sequence of the MCEI under Brazilian splitting

G Percentage alteration of a specific affecting variable

△H_Di Percentage variation in the magnitude of the MCEI under direct tension

△H_Br Percentage variation in the magnitude of the MCEI under Brazilian splitting