Study on strength prediction of grouting filling body in karst areas considering pressure filter effect

The slurry within the grouting pressure and karst boundary constraints produces a pressure filtration effect, resulting in the initial consolidation strength of the embankment curtain stone body in karst areas being significantly higher than the natural consolidation strength of the slurry. Consequently, using the natural consolidation strength of the slurry as the initial condition for constructing the curtain life prediction model often leads to substantial deviations from engineering practice. To address this issue, this paper first derives a theoretical formula for calculating the initial consolidation strength of the grouted curtain body, taking into account the erosive effects of karst water ions and the pressure-filtering effect. Secondly, a life prediction model for grouting curtains in karst areas, which incorporates the pressure-filtering effect, is developed, and its feasibility is demonstrated through indoor accelerated testing. Finally, the research findings were successfully applied to guide the curtain de-reinforcement project at the Yingpan Reservoir in Yunnan Province. The results indicate that the theoretical formula for the initial consolidation strength of the grouted curtain body, which considers the pressure-filtering effect, more accurately characterizes the initial conditions of the curtain. Additionally, the theoretical values derived from the curtain life prediction model closely align with the accelerated experimental test values, with an error margin of less than 15%. This demonstrates that the theoretical prediction model can effectively forecast the service life of the curtain body under conditions of karst water erosion. The successful engineering application further confirms the feasibility and practicality of the theoretical prediction model. Given the increasing number of similar cases, the research findings hold significant application potential and practical value.

1 Introduction

In the 1950s–1970s, many dam projects were constructed in China. Due to the design standards, construction conditions, and level of mechanization at that time, numerous dams experienced varying degrees of seepage, either during the initial stages of operation or after several years. This seepage significantly affected the operational safety of the dams (Ge et al., 2024; Jian et al., 2024; Xiang et al., 2022). Consequently, over the past decade, large-scale danger removal and reinforcement work has been conducted on dams in China. Grouting has played a crucial role in these projects due to its advantages, including simple construction, low environmental impact, and high construction efficiency (Fazeli, 2007; ZHANG et al., 2021; Dou et al., 2020). However, after a period of operation, some dams that underwent danger removal and reinforcement experienced seepage again, primarily in the areas of the grouting anti-seepage body. This issue is particularly pronounced in karst dams. Numerous studies have shown (Mozafari et al., 2021; Romanov et al., 2003) that the grouting anti-seepage body is susceptible to erosion and damage under the combined effects of high water pressure and karst water ions, leading to a significant reduction in its service life. Given the large number of dams in China and the widespread distribution of karst areas, researching the service life prediction of grouting curtains for dams in karst regions is of great practical significance and engineering value. This research can guide subsequent dam danger removal and reinforcement projects, as well as the design and construction of new dams.

At this stage, scholars have conducted extensive research on the life prediction of grouting curtains in karst areas through numerical simulation, model testing, and theoretical analysis, yielding significant results. In numerical simulations, Nagihara (1996), Wang et al. (2020), and others explored the deterioration of slurry crenellations in erosive environments by establishing a multivariate grey prediction model, a mechanical damage model for grouting plus solids under seepage, and a service life-cycle prediction model. Meanwhile, Dafny et al. (2015), Chen et al. (2022), and Huo et al. (2019) employed multi-coupled physical field software to investigate the decay processes and characteristics of service performance and impermeability in embankment curtains within karst areas. Although the numerical simulation results provide valuable insights for predicting the lifespan of grouted curtains in karst environments, these studies often simplify the karst water erosion process, leading to discrepancies between predicted lifespans and actual project outcomes. In terms of model testing, researchers have employed dry-and-wet cyclic deterioration tests (Muntaha, 2017; Zhou et al., 2022), accelerated erosion experiments (Paglia et al., 2003; Wang et al., 2021), drenching tests, and uniaxial compression tests (He et al., 2021; Ran et al., 2021) to investigate the performance deterioration of karst fillers, producing supportive findings for life prediction studies. However, due to limitations of model tests, it is challenging to conduct large-sample and long-cycle tests that comprehensively represent the entire service life of grouting curtains in karst areas. The theoretical analysis method, which can circumvent many shortcomings of model testing through specific assumptions and straightforward derivation processes, is increasingly being adopted by scholars for life prediction research on grouting curtains in karst areas. For instance, Dong et al. (2022) enhanced the initial weights and thresholds of a BP neural network using genetic algorithms to create a GA-BP model for predicting compressive strength; Peng (2012) developed a GA-BP model based on acid-base test methods to assess the service life of slurry-cemented bodies; and Hou et al. (2020) established a life-cycle prediction model for slurry-cemented body specimens based on deformation modulus measurements from indoor tests. Literature reviews indicate that these studies advance theoretical research on life prediction for grouted curtains in embankment dams situated in karst areas. However, existing research often neglects the impact of the pressure-filtering effect on the performance of grouted curtains during formation, resulting in significant discrepancies between the initial conditions of life prediction models and engineering realities. Specifically, the slurry subjected to grouting pressure and constrained by karst boundaries produces a pressure-filtering effect (Chen et al., 2021), which precipitates free water and solidified water in the slurry. This results in the initial consolidation strength of the curtain stone body being significantly higher than that of the natural-state slurry consolidation strength (Axelsson et al., 2009; Eklund and Stille, 2008; Bouchelaghem et al., 2007). Therefore, using the natural consolidation strength of the slurry as the initial condition in life prediction models for curtains is unlikely to effectively guide engineering practice.

This paper first derives the theoretical formula for the initial consolidation strength of the grouting curtain body under karst water ion erosion, considering the filtering effect. Based on this theoretical formula, a life prediction model for the grouting curtain in karst areas is constructed. Next, the feasibility and practicality of the life prediction model are validated through indoor accelerated erosion tests of the cemented stone body, conducted using a self-developed filter-pressing grouting device. Finally, the grouting curtain life prediction model, which accounts for the pressure-filtering effect, is applied to the Zhumashao Reservoir in Kaiyuan City to determine the optimal grouting pressure during the design and construction stages of the reservoir. The results of this study aim to provide a reference for real-world projects.

2 Grouted curtain body life prediction model under pressure-filtration effect

2.1 Basic assumptions of the model

(1) The slurry is an incompressible fluid, and its properties remain consistent throughout the diffusion process, adhering to Darcy’s law.

(2) The slurry undergoes cylindrical diffusion, resulting in a grout curtain body structure that is uniform, isotropic, and composed of incompressible homogeneous material.

(3) During the filtration process, the structure and number of capillary pores within the grout curtain remain unchanged, allowing water in the slurry to precipitate freely.

(4) The pressure-filtering effect is present throughout the entire grouting process; however, its influence varies along the horizontal direction of the grouting curtain.

(5) The primary component of the cement slurry forming the curtain is calcium silicate, with hydrated calcium silicate gel playing a crucial role in determining the curtain’s properties.

(6) The hydration of cement in the grouting curtain is complete, and there is no air present in the pore spaces of the curtain.

2.2 Model construction and solution

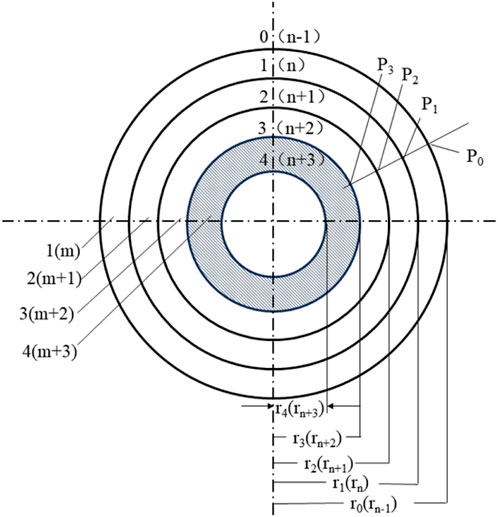
Based on the above assumptions and references (Chen et al., 2021), it is evident that during the formation stage of the grout curtain, the cement slurry in the grouting process is influenced by a pressure-filtering effect. This effect causes the free and combined water in the slurry to continuously precipitate, resulting in the initial consolidation strength of the curtain body being significantly higher than the natural consolidation strength of the slurry. In the operational stage, the grout curtain body interacts with erosive ions present in the karst water. The calcium oxide within the grout curtain is gradually dissolved, which diminishes its seepage control and reinforcement capabilities until the grout curtain ultimately fails, marking the end of its service life. Therefore, during the formation stage of the grout curtain, and in accordance with assumptions (Equations 2–4), this paper performs a force analysis on a unit body within the curtain. The radial load calculation sketch is illustrated in Figure 1.

Figure 1

Figure 1. Radial load calculation diagram.

As shown in Figure 1, a cylindrical model of the curtain body is cut into rings of varying heights using a circular cross-section. Here, $m$ denotes the number of rings, $n$ denotes the number of demarcation surfaces, and r_n represents the radius of the rings. The radial pressure acting on the demarcation surface is $P$, the modulus of elasticity of the circular body is $E$, and the Poisson’s ratio is $\mu$. The equilibrium condition at the interface between the rings (Equation 1) is given by He (1990).

$\left\{\begin{array}{l}{U}_{m,n}=U_{\left(m+1\right),n}\left(\text{Equilibrium\hspace{0.17em}equation\hspace{0.17em}of\hspace{0.17em}radial\hspace{0.17em}displacement\hspace{0.17em}}\mathrm{U}\right)\\ P_{m,n}=P_{\left(m+1\right),n}\left(\text{Equilibrium\hspace{0.17em}equation\hspace{0.17em}of\hspace{0.17em}radial\hspace{0.17em}force\hspace{0.17em}}\mathrm{P}\right)\end{array}\right.(1)$

If the height of the curtain is assumed to be $h$, the radial ${\sigma }_r$ and tangential stresses ${\sigma }_{\tau }$ are related to the same radius by the equation.

${\sigma }_r=\frac{\frac{1-\mu }{Eh}\times \frac{r_1}{2}\left(r_2-r_1\right)E}{1-\mu }+\frac{\frac{1-\mu }{Eh}\times \frac{r_2}{2}\left(r_3-r_2\right)E}{\left(1+\mu \right)r^2}(2)$

${\sigma }_{\tau }=\frac{\frac{1-\mu }{Eh}\times \frac{r_1}{2}\left(r_2-r_1\right)E}{1-\mu }+\frac{\frac{1-\mu }{Eh}\times \frac{r_2}{2}\left(r_3-r_2\right)E}{\left(1+\mu \right)r^2}(3)$

The equilibrium differential equation for a planar circular ring under uniform external radial pressure is simplified as follows:

$U={\sigma }_{1}r+\frac{{\sigma }_2}{r}(4)$

Two adjacent rings of circular cross-section, the m-th and the (m+1)-th, are selected for analysis. The m-th ring is bounded by the radii $r_{n-1}$ and $r_n$, and the (m+1)-th ring is bounded by $r_n$ and $r_{n+1}$. Then, the equilibrium differential equations of the planar circular rings under radial pressure for the m-th rings (Equations 5, 6) and (m+1)-th rings (Equations 7, 8) are obtained from Equation 4 as:

$\left\{\begin{array}{l}{U}_{m,\left(n+1\right)}=\frac{1-\mu }{Eh}\times \frac{r_{1,m}}{2}\left(r_{2,m}-r_{1,m}\right)r_{n+1}+\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m}}{2}\left(r_{3,m}-r_{2,m}\right)}{r_{n+1}}\\ U_{m,n}=\frac{1-\mu }{Eh}\times \frac{r_{1,m}}{2}\left(r_{2,m}-r_{1,m}\right)r_n+\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m}}{2}\left(r_{3,m}-r_{2,m}\right)}{r_n}\end{array}\right.(5)$

$\left\{\begin{array}{l}{\sigma }_{r,m,\left(n+1\right)}=\frac{\frac{1-\mu }{Eh}\times \frac{r_{1,m}}{2}\left(r_{2,m}-r_{1,m}\right)E}{1-\mu }-\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m}}{2}\left(r_{3,m}-r_{2,m}\right)E}{\left(1+\mu \right)r_{n+1}^2}\\ {\sigma }_{r,m,n}=\frac{\frac{1-\mu }{Eh}\times \frac{r_{1,m}}{2}\left(r_{2,m}-r_{1,m}\right)E}{1-\mu }-\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m}}{2}\left(r_{3,m}-r_{2,m}\right)E}{\left(1+\mu \right)r_n^2}\end{array}\right.(6)$

$\left\{\begin{array}{l}{U}_{\left(m+1\right),n}=\frac{1-\mu }{Eh}\times \frac{r_{1,m+1}}{2}\left(r_{2,m+1}-r_{1,m+1}\right)r_n\\ +\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m+1}}{2}\left(r_{3,m}-r_{2,m+1}\right)}{r_n}\\ U_{\left(m+1\right),\left(n+1\right)}=\frac{1-\mu }{Eh}\times \frac{r_{1,m+1}}{2}\left(r_{2,m+1}-r_{1,m+1}\right)r_{n+1}\\ +\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m+1}}{2}\left(r_{3,m}-r_{2,m+1}\right)}{r_{n+1}}\end{array}\right.(7)$

$\left\{\begin{array}{l}{\sigma }_{\tau ,\left(m+1\right),n}=\frac{\frac{1-\mu }{Eh}\times \frac{r_{1,m+1}}{2}\left(r_{2,m+1}-r_{1,m+1}\right)E}{1-\mu }\\ -\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m+1}}{2}\left(r_{3,m}-r_{2,m+1}\right)E}{\left(1+\mu \right){r_n}^2}\\ {\sigma }_{\tau ,\left(m+1\right),\left(n+1\right)}=\frac{\frac{1-\mu }{Eh}\times \frac{r_{1,m+1}}{2}\left(r_{2,m+1}-r_{1,m+1}\right)E}{1-\mu }\\ -\frac{\frac{1-\mu }{Eh}\times \frac{r_{2,m+1}}{2}\left(r_{3,m}-r_{2,m+1}\right)E}{\left(1+\mu \right){r_{n+1}}^2}\end{array}\right.(8)$

When $U_{m,n}=U_{\left(m+1\right),n}$,then there were:

$r_n\left({\sigma }_{1,m}-{\sigma }_{1,m+1}\right)+\frac{1}{r_n}\left({\sigma }_{2,m}-{\sigma }_{2,m+1}\right)=0(9)$

According to the system of Equation 6, the stress balance equations for m and m+1 neighboring rings can be obtained as Equations 10, 11.

$\left\{\begin{array}{l}{\sigma }_{1,m}=\frac{1-\mu }{E\left(r_{n-1}^2-r_n^2\right)}\times \left(\frac{r_{n-1}^2{P}_{n-1}-r_n^2{P}_n}{h}\right)\\ {\sigma }_{2,m}=\frac{\left(1+\mu \right)r_{n-1}^2{r}_n^2}{E\left(r_{n-1}^2-r_n^2\right)}\times \frac{P_{n-1}-P_n}{h}\end{array}\right.(10)$

$\left\{\begin{array}{l}{\sigma }_{1,\left(m+1\right)}=\frac{1-\mu }{E\left(r_n^2-r_{n+1}^2\right)}\times \left(\frac{r_n^2{P}_n-r_{n+1}^2}{h}\right)\\ {\sigma }_{2,\left(m+1\right)}=\frac{\left(1+\mu \right)r_n^2{r}_{n+1}^2}{E\left(r_n^2-r_{n+1}^2\right)}\times \left(\frac{P_n-P_{n+1}}{h}\right)\end{array}\right.(11)$

Bringing ${\sigma }_{1,m}$, ${\sigma }_{2,m}$, ${\sigma }_{1,\left(m+1\right)}$, ${\sigma }_{2,\left(m+1\right)}$ into Equation 9. The stress balance equations at the m and m+1 contact surfaces are shown in Equation 12.

$l_m{P}_{n-1}-\left(l_m+l_m+1+b_n\right)P_{\mathrm{n}}+l_m·P_{n+1}=0(12)$

where $P_{n-1}$, $P_n$ and $P_{n+1}$ are the radial pressures acting on the ring at the separating interface ($P_0$ is the hydrostatic pressure, $P_0=\rho gh$).

According to Reference He (1990), the expressions for the coefficients $l_m$, $l_{m+1}$ and $b_n$ are as follows:

$l_m=\frac{r_{n-1}^2{r}_n^2}{Eh\left(r_{n-1}^2-r_n^2\right)}(13)$

$l_{m+1}=\frac{r_n^2{r}_{n+1}^2}{Eh\left(r_n^2-r_{n+1}^2\right)}(14)$

$b_n=\frac{r_n^2}{2}\times \frac{1-\mu }{Eh}(15)$

Expression of coefficients in Equations 13–15, where $r_{n-1}$, $r$ and $r_{n+1}$ are the radii of the interfaces when the number of interfaces is $n$.

According to the assumption condition (Equation 2), the trinomial system of equations is obtained as follows:

$\left\{\begin{array}{l}\begin{array}{l}{P}_0-\left(l_1+l_2+{\sigma }_1\right)P_1+l_2{P}_2=0\\ P_1-\left(l_2+l_3+{\sigma }_2\right)P_2+l_3{P}_3=0\\ l_3{P}_2-\left(l_3+l_4+{\sigma }_2\right)P_3=0\end{array}\\ l_{\mathrm{n}}=\frac{r_{n-1}^2{r}_n^2}{Eh\left(r_{n-1}^2-r_n^2\right)}\end{array}\right.(16)$

Substitute $l_1,l_2,l_3,l_4,{\sigma }_1,{\sigma }_2,{\sigma }_3$ into Equation 16 to find the pressure P at the contact surface of the ring as follows:

$\left\{\begin{array}{c}{P}_1=\frac{\left(a_2{a}_3-l_3^2\right)l_1}{a_1{a}_2{a}_3-\left(a_1{l}_3^2+l_2^2{a}_3\right)}·P_0\\ P_2=\frac{l_1{l}_2{a}_3}{a_1{a}_2{a}_3-\left(a_1{l}_3^2+l_2^2{a}_3\right)}·P_0\\ P_3=\frac{l_1{l}_2{l}_3}{a_1{a}_2{a}_3-\left(a_1{l}_3^2+l_2^2{a}_3\right)}·P_0\\ a_1=l_1+l_2+O_1\\ a_2=l_2+l_3+O_2\\ a_3=l_3+l_4+O_3\end{array}\right.(17)$

Take the average value of $P_1$, $P_2$, and $P_3$ as the natural consolidation strength $f_0$ of the grouted curtain body. Then,

$f_0=\frac{P_1+P_2+P_3}{3}(18)$

According to the assumption condition (Equation 5) and in combination with the research findings of POWERS (1960), Equation relationship between the initial consolidation strength $f$ of the grouted curtain body considering the pressure-filtering effect and the gel-void ratio $X$ of the curtain body:

$f=f_0·X^{\mathrm{n}}(19)$

where $X$ is the gel-void ratio; $n$ is an experimental constant ranging from 2.6 to 3.0, which is related to the type of cement and experimental conditions.

According to Reference (Chen et al., 2021), the calculation formula for the gel-void ratio is as follows:

$X=\frac{V_{\mathrm{p}}}{V_{\mathrm{s}}}(20)$

$V_p=V_s+V_d+V_h(21)$

where $V_p$ represents the pore volume of the curtain body filling the fractures after drainage and hydration under the grouting pressure (m³); $V_s$ is the volume of the grout curtain body, which is also the volume of the grout filling the fractures (m³); $V_d$ is the volume of the drained water from the grout filling the fractures during the grouting project (m³); $V_h$ is the volume of the hydration water in the grout (m³).

The volume $V_s$ of the grout curtain body can be calculated by Equation 22:

$V_{\mathrm{s}}=\pi r^{2}h(22)$

During a variable time interval $dt$ in the grouting process, the reduction in the pore volume within the unit body should be equal to the amount of water seeped out, that is Equation 23:

$\frac{\mathrm{\partial }{V}_{\mathrm{s}}}{\mathrm{\partial }t}dt=\frac{\mathrm{\partial }q}{\mathrm{\partial }h}dhdt(23)$

where $t$ is the time (s); $q$ is the amount of water seeped out from the pores (m³). Generally, the pore diameter of the cement curtain body ranges from 10^–5 to 10⁻¹⁰ m. Based on the assumption condition (Equation 3), it can be deduced that:

$q=\frac{p{r}^4}{gh}J(24)$

where $r$ is the radius of the pore (m), which gradually decreases as the pore water is discharged; $J$ is the hydraulic gradient in the pore (MPa·m^–1); $\eta$ is the viscosity coefficient of water (Pa·s).

After the grouting time $t$, the total amount of water seeped out from the pores is:

$V_d=\int \frac{\pi r^4}{g\eta }J\mathrm{t}Ndt(25)$

where $N$ is the number of pores on the calculation cross-section.

According to Reference Chen et al. (2021), the amount of water required for the hydration reaction with cement particles during complete hydration is 0.227 times the mass of the cement particles. Therefore, the formula for calculating the volume $V_h$ of hydration water in the Equation 26:

$V_h=0.227\times \frac{V_s{\rho }_s{m}_c}{1+\left(m_w/m_c\right){\rho }_w}(26)$

where ${\rho }_s$ is the density of the grout (kg·cm^–3); ${\rho }_w$ is the density of water (kg·cm^–3); m_c and m_w are the masses of cement particles and water in a unit volume of the grout (kg), respectively.

Therefore, according to the different durations of pressure application during the grouting process, the initial consolidation strength $f$ of the curtain body considering the pressure-filtration effect can be obtained as follows:

$f=f_0\times {\left[\frac{\pi r^{2}h+\int \frac{\pi r^4}{gJ\eta }tNdt+0.227\times \frac{\pi r^{2}h{\rho }_s{m}_c}{1+\left(m_w/m_c\right){\rho }_w}}{\pi r^{2}h}\right]}^{\mathrm{n}}(27)$

During the operational stage of the grouted curtain body, ion erosion from karst water causes continuous dissolution of calcium oxide within the grouting material. As calcium oxide dissolves, solid-phase calcium hydroxide begins to dissolve as well. Subsequently, high-alkaline hydrated silicates and hydrated aluminates decompose into low-alkaline hydrates, ultimately transforming into substances such as gaseous silicon dioxide, which lacks cementing ability (Gao et al., 2024). Additionally, the consumption rate of calcium oxide is closely related to the pH of the environment (Peng, 2012). Consequently, the degree of strength attenuation in the curtain body varies with different pH levels.

The standard curve of the strength-pH of the calcified body is fitted using the plotting software SPSS (Version 19.0), and the Equation 28 of the standard curve is obtained.

$F=f+\frac{A}{w\sqrt{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{e}^{-2\frac{{\left(pH-p{H}_0\right)}^2}{{w_1}^2}}(28)$

where $F$ is the residual strength of the curtain body after being eroded by karst water; $f$ is the initial consolidation strength; $p{H}_0$ is the initial $pH$ of the solution; $A$ and $w_1$ are constants obtained from the curve fitting.

Based on the unconfined compressive strength of the calcified body obtained from the experimental tests, a relationship curve between the strength and the service life of the calcified body is plotted. Then, the plotting software is used to fit the standard curve of the strength-service life of the calcified body, and the calculation formula of the standard curve is obtained as follows:

$F=f+B{e}^{\frac{{\left(T-T_c\right)}^2}{2w_2^2}}(29)$

where $T_c$ is the initial time constant of the solution; $B$ and $w_2$ are constants obtained from the curve fitting.

According to Reference Peng (2012), the strength of the grouting curtain body and the pH of the karst water satisfy the following relationship:

$pH=p{H}_0+\zeta \left(R\right)(30)$

where R is the attenuation rate of the compressive strength.

Combining Equations 18, 27, 30, we can obtain the residual strength of the curtain body’s initial consolidation strength after erosion by karst water:

$F=\frac{P_1+P_2+P_3}{3}·{\left(\frac{\pi r^{2}h-\int \frac{\pi r^4}{gJ\eta }tNdt-0.227\times \frac{\pi r^2{h}_s{\rho }_s{m}_c}{1+\left(m_w/m_c\right){\rho }_w}}{\pi r^{2}h}\right)}^n·R(31)$

Taking the reaction between hydrochloric acid and cement stone as an example, $m$ moles of Ca(OH)₂ will consume $2m$ moles of hydrochloric acid. When the volume of the corrosive solution is n liters and the initial $pH$ is $p{H}_0$, the consumption of Ca(OH)₂ and the $pH$ of the solution satisfy the following relationship:

$pH=\lg \left(\frac{n}{n{10}^{-p{H}_0}-2m}\right)(32)$

where $n$ is the volume of the corrosive solution; $m$ is the cumulative consumption of CaO; $p{H}_0$ is the initial $pH$ of the corrosive solution.

Combining Equation 30 and Equation 31 and substituting the critical $p{H}_T$ calculated from Equation 32 into the combined formulas, the service life T of the grouted calcified body can be calculated.

Numerous studies have shown (Huo et al., 2019; Peng, 2012) that the consumption rate of calcium oxide in the grouted curtain body (i.e., the ratio of the consumed amount to the original internal total amount) is closely related to the strength of the grouted curtain body. Especially when the cumulative consumption rate of calcium oxide exceeds 25%, the strength of the curtain body will decline sharply, indicating that the grouted curtain has failed. Therefore, the failure of the curtain body, defined as reaching the critical value of its service life, occurs when its initial consolidation strength diminishes to 50% in a karst water environment.

There is the following relationship between the compressive strength of the curtain body and its service life:

$R=\eta \left(t\right)(33)$

where $R$ is the attenuation rate of the compressive strength decay rate versus erosion time equation.

Therefore, by combining Equations 28–31, the service-life prediction model for the grouted curtain in karst areas considering the pressure-filtration effect can be obtained as follows:

$\left\{\begin{array}{l}f=\frac{P_1+P_2+P_3}{3}·{\left(\frac{V_{\mathrm{p}}}{V_s}\right)}^n·R\\ pH-p{H}_0=\zeta \left(R\right)、pH=\lg \left(\frac{n}{n{10}^{-p{H}_0}-2m}\right)\\ R=\eta \left(t\right)、T=t\left|\text{CaO}=25\%\right.\end{array}\right.(34)$

2.3 Determination of model formula parameters

(1) In the formula, the elastic modulus $E$ and Poisson’s ratio $\mu$ of the grouting curtain body can be obtained through tests using a triaxial stress testing machine. Specifically, the specifications in the Standard for Geotechnical Test Methods (Ministry of Water Resources of the People’s Republic of China, 2019) should be referred to.

(2) The hydraulic gradient (MPa·m^-1) in the pores is equal to the ratio of the water head difference $p$ to the drainage length $h$. The calculation can be seen in Equation 35:

$J=\frac{p}{h}(35)$

(3) The $\eta$ is defined as the viscosity coefficient of water at 20°C, which is generally taken as 1.0087.

(4) The density of the grout ${\rho }_s$ is equal to the ratio of the average saturated mass in the initial state to the volume of the specimen. The density of water ${\rho }_w$ is generally taken as 1 × 10³ kg·m^-3.

(5) The $N$-values of grouts with different water-cement ratios can be calculated by referring to the test method in Reference You (2010).

3 Verification of the service - life prediction model

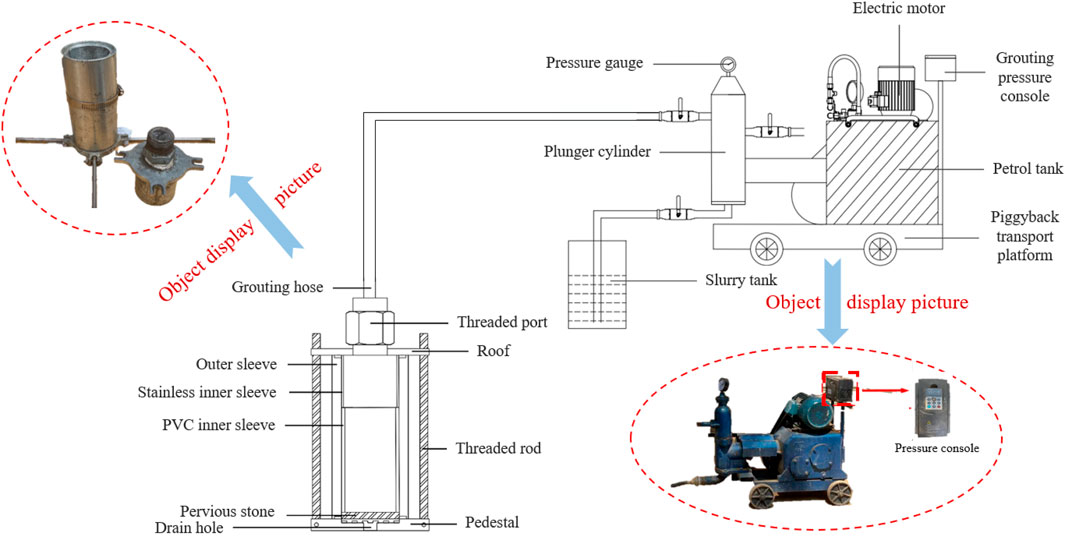
3.1 Pressure-filtration sample preparation system

To verify the feasibility of the derived service-life prediction model for the grouting curtain under the pressure filtration effect, a set of sample preparation equipment was developed for creating grouting test blocks of calcified bodies in karst areas, as shown in Figure 2. This equipment comprises two main components: a constant-pressure grouting machine and a sample preparation mold. By utilizing the properties of filter paper and permeable stones, which permit water to pass through while preventing grout from doing so, specimens of grouting-reinforced bodies can be created using different grouting materials and construction parameters under the pressure-filtration effect.

Figure 2

Figure 2. Sample preparation device for grouting stone test blocks in karst areas.

3.2 Specimen preparation and curing

3.2.1 Specimen preparation

In this test, pure cement grout was selected to create specimens of the grouting calcified body. The grout was prepared according to the commonly used mix proportions for grouting curtains in karst areas. Specifically, the water-to-cement ratio of the pure cement grout was 1:2, the grouting pressure was set at 1 MPa, and the grouting time was 6 s.

3.2.2 Specimen curing

Curing was conducted in accordance with the standard requirements outlined in the Standard for Test Methods of Mechanical Properties of Ordinary Concrete (Ministry of Construction of the People’s Republic of China, 2019). These standards specify a temperature of 20°C ± 1°C and a humidity level of at least 95%.

3.3 Design of accelerated deterioration of specimens

To determine the service life of the grouting curtain body in a karst water environment within a short time frame, this paper accelerates the deterioration process of the grouting calcified body by adjusting the concentration of corrosive ions in the karst water and the curing temperature. The accelerated deterioration curing of the specimens is illustrated in Figure 3.

Figure 3

Figure 3. Accelerated curing of grouting stone body.

3.3.1 Acceleration by ion concentration

When the influence of the binding capacity of aggressive ions within the grouted stone body and the time-dependent structural defects on the diffusion coefficient is not considered, the diffusion theoretical model of aggressive ions (Equation 36) can be obtained based on Fick’s second law (Zuo et al., 2012):

$c=c_s\left(1-\mathit{erf}\frac{x}{2\sqrt{Dt}}\right)(36)$

where $c_s$ is the concentration of aggressive ions on the exposed surface of the grouted stone body (mol·L^-1); $\mathit{erf}$ is the error function, ${\mathit{erf}}_u=\frac{2}{\pi }{\int }_0^u{e}^{-t^2}dt$.

If the concentration $c_s$ of aggressive ions on the exposed surface of the grouted stone body is increased by 20 times, then the test acceleration factor $s_1$ = 20.

3.3.2 Temperature acceleration

In the test, the grouting reinforced body test blocks are cured at a constant temperature of 30°C. Then, according to the influence of the environmental temperature on the diffusion of aggressive ions in the calcified body in the Arrhenius equation, the acceleration coefficient $s_2$ can be calculated as shown in Equation 37:

$s_2=\frac{D_T\left(303\right)}{D_T\left(290.9\right)}=\frac{D_0{e}^{\frac{E}{R}\left(\frac{1}{293}-\frac{1}{303}\right)}}{D_0{e}^{\frac{E}{R}\left(\frac{1}{291}-\frac{1}{293}\right)}}=6.95(37)$

where $D_0$ is the diffusion coefficient of aggressive ions at temperature $T_0$ (m²·s^–1); $D_T$ is the diffusion coefficient of aggressive ions at temperature $T$ (m²·s^–1); $T_1$ is the reference temperature, generally taken as 293K; E/R is the activation energy, which is taken as 14,242 according to the test values in Atkinson.

Therefore, the total acceleration factor $S$ of this deterioration test is equal to the product of the acceleration factor of the external aggressive ion concentration and that of the temperature, that is, $S$ = 138.94.

3.4 Test results and comparative analysis

In the laboratory test, the values of the model parameters are as follows: the elastic modulus $E$ = 20 GPa; Poisson’s ratio $\mu$ = 0.2; the test constant $n$ is taken as 3.0; the hydraulic gradient $J$ = 12.5 MPa; the viscosity coefficient $\eta$ = 1.0087; the number of pores on the cross-section $N$ = 2; the density of the grout $\rho$ = 1.745 × 10³ kg·m^–3. Given that the water-cement ratio of the pure cement grout is 1:2, the volume of cement particles $V_c$ = 0.33 m³ and the volume of water $V_w$ = 0.67 m³ in a unit volume of the grout can be obtained. The volume of the corrosion solution $n$ = 0.1 m³, and the initial $pH$ value of the corrosion solution $p{H}_0$ = 5.5. The grouted stone specimens cured in the karst water environment for different durations were subjected to unconfined compression tests, and the results were compared with those of the theoretical model. The test results and the theoretical calculation results are presented in Table 1.

Table 1

Table 1. Calculated compressive strength values of grouting stone body.

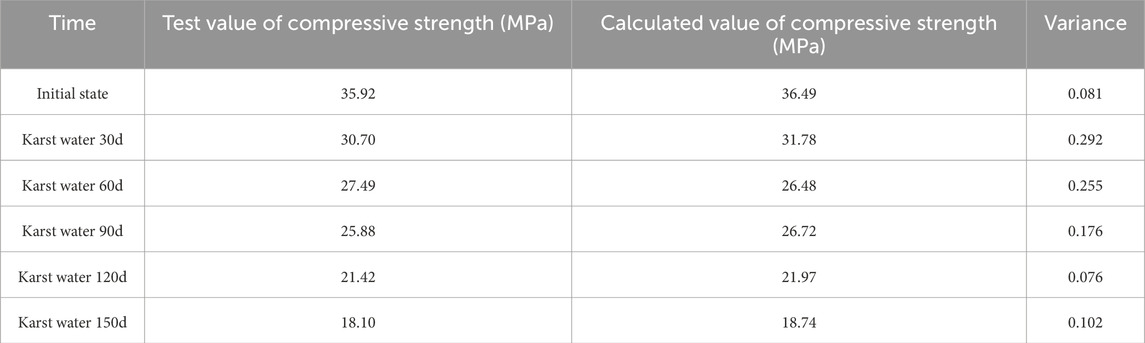
As shown in Table 1, the predicted values from the theoretical model are relatively close to the actual values obtained from experimental tests, with variances all less than 0.35. This indicates that the prediction model has good accuracy. During the accelerated erosion test, the calcified body reaches its service life after approximately 150 days of exposure to karst water curing. Using the acceleration factor of 138.94 applied in the accelerated test, we estimate its service life in a karst environment to be about 57 years. The theoretical predicted value is 63 years, with an error margin of less than 15%. This suggests that the prediction model can effectively guide engineering practice.

4 Application in a typical engineering project

4.1 Project background

The Zhumashao Reservoir is a small-sized (Type II) water conservancy project primarily intended for agricultural irrigation. It features a homogeneous earth dam with a maximum height of 9.0 m, a crest length of 110.3 m, a crest width of 3.6 m, and a crest elevation of 1359.00 m. The total storage capacity is 185,600 m³. This dam site is situated in a karst depression, where the main unfavorable geological phenomenon is karst formation. Karst caves and fissures are well-developed in the area, with cave cavities often filled with clay. The dam was initially constructed in February 1970 and completed for water storage in July 1971. Due to the dam-building technology and economic conditions at that time, certain potential safety hazards were present in the project. As a result, multiple rounds of hazard removal and reinforcement work were carried out subsequently. However, after several years of operation, issues such as seepage in the dam body and at the contact zone between the dam body and the foundation, as well as seepage in the reservoir area caused by the karst-developed zone near the reservoir bank, persisted.

4.2 Construction scheme and effect evaluation

Curtain grouting was implemented to eliminate potential hazards and reinforce the dam. The bottom boundary of the anti-seepage curtain grouting treatment was controlled based on a permeability rate of q ≤ 10 Lu. The axis of the curtain grouting aligned with that of the dam, and the depth of the curtain extended 5 m below the bottom boundary of the dam body. The grouting curtain consisted of single-row holes spaced 1.5 m apart, with hole depths ranging from 3.5 m to 13.97 m. The grouting material used for the dam body was a cement-clay slurry, employing conventional grouting techniques, while the dam foundation was grouted with pure cement slurry. The anti-seepage standards for curtain grouting stipulated that the permeability coefficient of the dam body should be k ≤ 10^⁻⁵ cm/s, and the permeability rate of the bedrock should be q ≤ 10 Lu. The total length of the anti-seepage line for the curtain grouting was 118.26 m. A total of 77 production holes were drilled, resulting in a total drilling footage of 890.33 m and a total grouting section length of 752.35 m. Given that the expected service life of a small-sized water conservancy dam is approximately 100 years (t = 100 a), substituting this value into Equation 34 yields a final grouting pressure of 0.3 MPa necessary to meet the service-life requirement. The on-site construction process is depicted in Figure 4.

Figure 4

Figure 4. Construction photos of the site.

During the construction process, the treatment measures implemented were both reasonable and effective. Following the completion of the anti-seepage project, the anti-seepage effect was remarkable, as confirmed by the water pressure test conducted on the inspection holes. The trial water storage of the reservoir showed normal water balance analysis, indicating that the project’s anti-seepage measures met the expected goals.

5 Conclusion

(1) Based on the deterioration law of the initial consolidation strength of the curtain body under karst erosion conditions, a service-life prediction model for the grouting curtain of dams in karst areas considering the filter-pressing effect has been established. This model is simple to calculate, and its parameters are easy to obtain. It can efficiently and accurately predict the service life of grouting curtains in karst areas, demonstrating good practicality and applicability. Furthermore, this model can not only guide the design and construction of grouting curtains for dams in karst areas, but it can also be applied to similar projects in these regions, providing a new approach for predicting the service life of grouting curtains in karst areas.

(2) An accelerated erosion test of the grouting curtain calcified body in a karst environment, under the filter-pressing effect, was conducted. This study explored the strength deterioration of the grouting curtain calcified body and verified the feasibility of a theoretical model for predicting its service life. With a water-cement ratio of 1:2 for the pure cement grout, a grouting pressure of 1 MPa, and a grouting time of 6 s, the measured service life of the calcified body was 57 years, while the theoretical predicted value was 63 years, resulting in an error of less than 15%. This indicates that the prediction model can effectively guide engineering practice.

(3) A sample-making device for dams in karst areas, which considers the filter-pressing effect, has been independently designed and developed. This device can produce standard calcified body specimens under various grouting parameters for compressive strength testing. It is easy to operate and boasts high sample-making efficiency, providing new equipment for testing the performance of grouting materials in karst environments. Additionally, by adjusting the mesh numbers of the filter paper and the permeable stone, calcified body specimens with different filter-pressing coefficients can be obtained for performance testing.

(4) The research results have been successfully applied to guide the curtain danger removal and reinforcement project of the Yingpan Reservoir in Yunnan Province, further demonstrating the feasibility and practicality of the theoretical prediction model. Based on the on-site investigation data from Yingpan Reservoir and aligned with the service life requirements stipulated in the design, the construction parameter for the curtain danger removal and reinforcement were determined using the research findings from this paper. The subsequent evaluation of the grouting effect achieved the expected goals. Given the practicality and applicability of the curtain body service life prediction model developed in this paper, this method can be further promoted and applied in the design and construction of grouting curtains in the fields of transportation, mining, and industrial and civil construction in karst areas.

(5) A sample-making device for dams in karst areas considering the filter-pressing effect was independently designed and developed. It can obtain standard calcified body specimens under different grouting parameters for compressive strength testing. This device is easy to operate and has high sample - making efficiency, providing a new piece of equipment for testing the performance of grouting materials in a karst environment. In addition, by adjusting the mesh numbers of the filter paper and the permeable stone, grouting calcified body specimens with different filter-pressing coefficients can be obtained for performance testing.

(6) The research results have been successfully applied to guide the curtain danger - removal and reinforcement project of Yingpan Reservoir in Yunnan Province, further demonstrating the feasibility and practicality of the theoretical prediction model. Based on the on-site investigation data of Yingpan Reservoir and combined with the service-life requirements stipulated in the design, the construction parameter control conditions such as the grouting material mix ratio and the designed grouting pressure value (> 0.3 MPa) for the curtain danger-removal and reinforcement were determined using the research results of this paper, and the subsequent evaluation of the grouting effect achieved the expected goals. Considering the practicality and applicability of the curtain body service-life prediction model derived in this paper, this method can be further popularized and applied in the design and construction of grouting curtains in the fields of transportation, mining, industrial and civil construction in karst areas.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZY: Writing – original draft, Data curation, Validation, Writing – review and editing. DJ: Methodology, Writing – review and editing, Conceptualization. LY: Conceptualization, Writing – review and editing. XM: Writing – original draft, Methodology. LW: Data curation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Major water conservancy science and technology project of Hunan Province (XSKJ2023059-02) and the water conservancy science and technology project of Yunnan Province (Project Name: Research on Key Technologies of Intelligent Grouting in Soft Strata and System Integration). The corresponding author gratefully acknowledges this financial support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Axelsson, M., Gustafson, G., and Fransson, Å. (2009). Stop mechanism for cementitious grouts at different water-to-cement ratios. Tunn. Undergr. Space Technol. 24 (4), 390–397. doi:10.1016/j.tust.2008.11.001

CrossRef Full Text | Google Scholar

Bouchelaghem, F., Benhamida, A., and Dumontet, H. (2007). Mechanical damage behaviour of an injected sand by periodic homogenization method. Comput. Mater. Sci. 38 (3), 473–481. doi:10.1016/j.commatsci.2005.12.044

CrossRef Full Text | Google Scholar

Chen, Y., Yuan, J., Wang, G., Xu, J., Hu, R., and Yang, Z. (2022). Evaluation of groundwater flow through a high rockfill dam foundation in karst area in response to reservoir impoundment. Int. J. Rock Mech. Min. Sci. 160, 105268. doi:10.1016/j.ijrmms.2022.105268

CrossRef Full Text | Google Scholar

Chen, W., Xing, Z., Wang, K., Fu, P., Luo, G., and Pei, X. (2021). A study on the effect of pressure filtration on the strength of cement slurry stones. Water Resour. Hydropower Eng. 52 (05), 196–202. doi:10.13928/j.cnki.wrahe.2021.05.021

CrossRef Full Text | Google Scholar

Dafny, E., Tawfeeq, K. J., and Ghabraie, K. (2015). Evaluating temporal changes in hydraulic conductivities near karst-terrain dams: dokan Dam (Kurdistan-Iraq). J. Hydrology 529, 265–275. doi:10.1016/j.jhydrol.2015.07.048

CrossRef Full Text | Google Scholar

Dong, J., Xie, H., Dai, Y., Zhai, J., and Dai, Y. (2022). “Compressive strength prediction of blast furnace slag-fly ash concrete based on GA-BP algorithm,” in International Conference on Computational Modeling, Simulation, and Data Analysis (CMSDA 2021). SPIE, 12160, 398–407. doi:10.1117/12.2627604

CrossRef Full Text | Google Scholar

Dou, J., Zhang, G., Chen, A., Yang, B., Xin, R., Duan, J., et al. (2020). Grouting experiment in a completely weathered granite dam abutment: case study on grouting technique and test analysis. Environ. Earth Sci. 79, 1–15. doi:10.1007/s12665-020-9140-x

CrossRef Full Text | Google Scholar

Eklund, D., and Stille, H. (2008). Penetrability due to filtration tendency of cement-based grouts. Tunn. Undergr. Space Technol. 23 (4), 389–398. doi:10.1016/j.tust.2007.06.011

CrossRef Full Text | Google Scholar

Fazeli, M. A. (2007). Construction of grout curtain in karstic environment case study: salman Farsi Dam. Environ. Geol. 51 (5), 791–796. doi:10.1007/s00254-006-0397-8

CrossRef Full Text | Google Scholar

Gao, X., Zhaofeng, L., Zhihao, Z., Wu, F., Huang, H., and Chen, J. (2024). Long-term erosion resistance of grouting curtain in coastal karst fracture area. J. Build. Eng. 85, 108721. doi:10.1016/j.jobe.2024.108721

CrossRef Full Text | Google Scholar

Ge, W., Sun, H., Jing, L., Li, Z., Li, Y., Cao, B., et al. (2024). Economic life evaluation of reservoir dams based on comprehensive costs and benefits analysis considering potential dam breach: a case study of the Luhun reservoir in China. J. Hydrology 639, 131613. doi:10.1016/j.jhydrol.2024.131613

CrossRef Full Text | Google Scholar

He, Z., Zhao, K., Yan, Y., Ning, F., Zhou, Y., and Song, Y. (2021). Mechanical response and acoustic emission characteristics of cement paste backfill and rock combination. Constr. Build. Mater., 288. doi:10.1016/j.conbuildmat.2021.123119

CrossRef Full Text | Google Scholar

He, X. (1990). Strength calculation of grouting curtain in porous rock formations. Metal. Mines (05), 25–27. (in Chinese).

Google Scholar

Hou, J., Guo, Z., Liu, W., and Zhang, Y. (2020). Mechanical properties and meso-structure response of cemented gangue-fly ash backfill with cracks under seepage-stress coupling. Constr. Build. Mater. 250, 118863–211874. doi:10.1016/j.conbuildmat.2020.118863

CrossRef Full Text | Google Scholar

Huo, J., Ma, F., and Xiaolei, J. I. (2019). Porosity and permeability variations of a dam curtain during dissolution. Water Sci. Eng. 12 (02), 155–161. doi:10.1016/j.wse.2019.05.007

CrossRef Full Text | Google Scholar

Jian, J., Lu, J., Guo, Q., Wang, J., Sun, L., Mao, D., et al. (2024). Characterization and quantification of dam seepage based on resistivity and geological information. Water 16 (17), 2410. doi:10.3390/w16172410

CrossRef Full Text | Google Scholar

Ministry of Construction of the People's Republic of China (2019). GB/T50081-2019 standard for test methods for physical and mechanical properties of concrete. Beijing: China Construction Industry Press. (in Chinese).

Google Scholar

Ministry of Water Resources of the People's Republic of China (2019). GB/T50123-2019. standard for geotechnical test methods. Beijing: China Plan Publishing House, organized by the Institute of Standard and Quotas of the Ministry of Housing and Urban-Rural Development. (in Chinese).

Google Scholar

Mozafari, M., Milanović, P., and Jamei, J. (2021). Water leakage problems at the Tangab Dam Reservoir (SW Iran), case study of the complexities of dams on karst. Bull. Eng. Geol. Environ. 80 (10), 7989–8007. doi:10.1007/s10064-021-02387-z

CrossRef Full Text | Google Scholar

Muntaha, M. (2017). The effect of drying-wetting cycle’s repetition to the characteristic of natural and stabilization residual soils Jawa Timur-Indonesia. IOP Publ. 267 (1), 012030. doi:10.1088/1757-899x/267/1/012030

CrossRef Full Text | Google Scholar

Nagihara, S. (1996). Seepage-induced erosion of submarine carbonate escarpments: a numerical simulation. Earth Planet. Sci. Lett. 144 (1-2), 263–271. doi:10.1016/0012-821x(96)00162-8

CrossRef Full Text | Google Scholar

Paglia, C., Wombacher, F., and Böhni, H. (2003). The influence of alkali-free and alkaline shotcrete accelerators within cement systems: influence of the temperature on the sulfate attack mechanisms and damage. Cem. Concr. Res. 33 (3), 387–395. doi:10.1016/S0008-8846(02)00967-5

CrossRef Full Text | Google Scholar

Peng, T. U. (2012). Theoretical study on durability test and evaluation of grouting stone body. Central South University. (in Chinese).

Google Scholar

Powers, T. C. (1960). Physical properties of cement paste. Washington: Fourth International Symposium on the Chemistry of Cement, 577–609.

Google Scholar

Ran, H., Guo, Y., Feng, G., Qi, T., and Du, X. (2021). Creep properties and resistivity ultrasonic-AE response of cemented gangue backfill column under high-stress area. Int. J. Min. Sci. Technol. 31 (3), 401–412. doi:10.3969/j.issn.2095-2686.2021.03.006

CrossRef Full Text | Google Scholar

Romanov, D., Gabrovek, F., and Dreybrodt, W. (2003). Dam sites in soluble rocks: a model of increasing leakage by dissolutional widening of fractures beneath a dam. Eng. Geol. 70 (1-2), 17–35. doi:10.1016/s0013-7952(03)00073-5

CrossRef Full Text | Google Scholar

Wang, H., Liu, Q., Sun, S., Zhang, Q., Li, Z., and Zhang, P. (2020). Damage model and experimental study of a sand grouting-reinforced body in a seawater environment. Water 12 (9), 2495–2507. doi:10.3390/w12092495

CrossRef Full Text | Google Scholar

Wang, H., Zhipeng, L. I., Wang, X., Zhang, Q., and Zhang, L. (2021). Study on grouted body deterioration mechanism of sand layer in seawater environment. Adv. Mater. Sci. Eng. 2021 (1), 1–8. doi:10.1155/2021/6329257

CrossRef Full Text | Google Scholar

Xiang, Y., Sheng, J. B., Wang, L., Cai, Y., Meng, Y., and Cai, W. (2022). Research progresses on equipment technologies used in safety inspection, repair, and reinforcement for deepwater dams. Sci. China Technol. Sci. 65 (5), 1059–1071. doi:10.1007/s11431-021-1958-y

CrossRef Full Text | Google Scholar

You, W. (2010). Performance test and application of special clay curing slurry. J. Nanchang Eng. Coll. 29 (03), 42–46. doi:10.3969/j.issn.1006-4869.2010.03.009

CrossRef Full Text | Google Scholar

Zhang, W., Shen, Z., Chen, G., Zhang, W., Xu, L., Ren, J., et al. (2021). Optimization design and assessment of the effect of seepage control at reservoir sites under karst conditions: a case study in Anhui Province, China. Hydrogeology J. 29 (5), 1831–1855. doi:10.1007/s10040-021-02357-5

CrossRef Full Text | Google Scholar

Zhou, R., Xiaochuan, Q. I. N., Jianfan, S. H. A., Guo, F., and Qi, W. (2022). Influence of wet or dry conditions on the fatigue life of grout cementitious materials under cyclic loading. Geofluids 2022 (1), 1–7. doi:10.1155/2022/3615221

CrossRef Full Text | Google Scholar

Zuo, X. B., Sun, W., Li, H., and Zhao, Y. K. (2012). Modeling of diffusion-reaction behavior of sulfate ion in concrete under sulfate environments. Comput. Concr. An Int. J. 10 (1), 79–93. doi:10.12989/cac.2012.10.1.079

CrossRef Full Text | Google Scholar