A combined approach to lithology identification using reinforcement learning and transformer algorithms

Lithology identification plays a pivotal role in logging interpretation during drilling operations, directly influencing drilling decisions and efficiency. Conventional lithology identification methods predominantly depend on manual interpretation of formation physical property data, which is inherently subjective and susceptible to inconsistency. To overcome these limitations, this study proposes a novel lithology identification framework that synergistically combines reinforcement learning (RL) for automated hyperparameter optimization and feature selection with a Transformer-based model capable of capturing complex temporal dependencies within large-scale well logging data. The RL agent systematically explores the hyperparameter and feature space to enhance model performance, while the Transformer encoder extracts meaningful sequential patterns essential for accurate lithology classification. Empirical evaluation on a dataset exceeding two million samples demonstrates that the proposed method achieves a prediction accuracy of 94.89%, evidencing its effectiveness and robustness. The results indicate that this approach can provide rapid, objective, and reliable lithology recognition in drilling environments, thereby facilitating improved operational efficiency and reduced costs.

1 Introduction

Lithology identification plays a vital role in logging interpretation during drilling (Shi et al., 2023; Xie et al., 2018). Traditionally, lithology identification relies on manual analysis and empirical judgment, and is usually combined with measured formation physical property data, such as gam-ma rays, density, resistivity, etc. For lithology classification (Xu et al., 2021). However, this process is limited by reliance on human expertise and is easily affected by subjective factors, and cannot ensure the accuracy and consistency of lithology identification. In practical applications, the accuracy of lithology identification is crucial for decision-making during drilling, which directly affects drilling efficiency and safety (Ren et al., 2019).

In recent years, with the rapid development of big data and deep learning technology, lithology identification methods have gradually developed in the direction of automation and intelligence (Ren et al., 2023). Deep learning models, especially reinforcement learning and Transformer (Cao et al., 2024), provide new ideas for solving this problem with their powerful data processing and model optimization capabilities (Qingfeng et al., 2023). Reinforcement learning automatically optimizes the model’s hyperparameters and feature selection by exploring different strategies, thereby improving the model’s generalization ability and training efficiency; and the Transformer algorithm’s advantage (Wang et al., 2022) in processing time series data enables it to effectively capture long-term dependencies in formation physical property data, providing a more accurate solution for lithology identification.

Ren et al. (2022) combined fuzzy theory, decision tree and K-means++ algorithm to pro-pose a new hybrid lithology identification technology, which can better overcome the ambiguity and uncertainty of logging data. In the actual data test, six logging parameters were selected: density (RHOB), neutron porosity (NPHI), natural gamma (GR), compressional wave velocity (VP), shallow formation resistivity (LLS), and deep formation resistivity (LLD). Then, the K-means++ clustering algorithm was used to cluster the logging data. Finally, the triangular membership function was selected according to the obtained cluster center point to fuzzify the logging data and construct a fuzzy decision tree lithology identification model. The model prediction accuracy reached 93.92%. Li et al. (2022) pro-posed a lithology identification characterization enhancement method for logging data based on feature decomposition, selection and transformation, which converted the original logging curve into an improved high-dimensional representation with more effective information and less noise. The local mean decomposition was used to extract the change information of multiple depth scale logging curves and superimposed it on the features of adjacent samples. Considering the different contributions of features to lithology identification, an optimized feature selection method based on Shapley additive interpretation is designed to reduce the redundant and noisy information in logging data. In order to mine the complementary information between sequence features, a representation learning model integrating feature transformation and lithology classification is established by using multi-granularity scanning and cascade extreme learning machine. The effective-ness and generalization ability of the proposed method are verified on baseline and shale oil field datasets. The results show that the proposed method can enable logging data to obtain more effective information through representation enhancement, thereby achieving high-precision lithology identification. Hou et al. (2023) first improved the target detection algorithm of the single multi-box detector by adding residual network and adaptive moment estimation, and constructed a lithology identification model. Secondly, based on the above improved algorithm, combined with database technology and geographic information system technology, a comprehensive recognition method is proposed. Then the proposed method is applied to 12 lithologies in Xingcheng area, China to test its effective-ness and feasibility in field geological surveys. Finally, the influence of learning rate and batch size on the recognition effect with the increase of epoch number is discussed. The results show that the average recognition rates of the improved single multi-frame detection method and the integrated method are 89.4% and 98.4%, respectively, and the highest recognition rate can reach 100%. The recognition results are evaluated by accuracy, precision, recall, F1 score and average precision. The results show that compared with other neural network methods, the integrated method has stronger recognition ability. Yan et al. (2024) aimed at the problems of difficulty in feature information extraction, low accuracy of thin layer recognition and limited model applicability in intelligent lithology recognition, and tried to improve the comprehensive performance of the lithology recognition model from three aspects: data feature extraction, class balance and model design. A real-time intelligent lithology recognition model based on dynamic felling strategy weighted random forest algorithm (DFW-RF) was proposed. According to the feature selection results, gamma ray and 2 MHz phase resistivity are the logging while drilling (LWD) parameters that have a significant impact on lithology recognition. The comprehensive performance of the DFW-RF lithology recognition model was verified in the application of 3 wells in different regions. By comparing the prediction results of five typical lithology identification algorithms, the DFW-RF model has higher lithology identification accuracy and F1 score.

This study proposes a lithology intelligent identification method that combines reinforcement learning and Transformer algorithm, aiming to improve the accuracy and efficiency of lithology identification and further reduce construction costs by optimizing hyperparameters and feature selection processes. This method optimizes the hyperparameters and features of the model through reinforcement learning, and combines the Trans-former model’s ability to process time series data to ensure high accuracy of lithology identification.

2 Methodology

In this study, we combined the Actor-Critic algorithm and the Transformer algorithm in reinforcement learning to solve the two major problems of the difficulty in optimizing a large amount of field data and the lack of consideration of time series in the lithology identification process.

2.1 Reinforcement learning optimization process

In lithology identification, feature selection and hyperparameter optimization are key factors affecting model performance. We use reinforcement learning (RL) to automate this optimization process (Zhang et al., 2024). Specifically, the RL agent dynamically adjusts the hyperparameters (such as learning rate, batch size, regularization coefficient, etc.) and feature selection strategies of the lithology identification model by interacting with the training environment (Perrusquía and Yu, 2021). The agent’s reward mechanism is based on the performance of the model on the validation set, and the agent gradually optimizes the strategy to achieve the best performance of the lithology identification task. One of the key issues in reinforcement learning is how to efficiently learn a strategy so that the agent can maximize long-term rewards in a given environment. In traditional reinforcement learning methods, the two common methods are value-based methods, which find the optimal strategy by learning an action-value function. And policy-based methods, which directly optimize the policy function and improve the reward through gradient ascent (Martinsen, Lekkas, and Gros, 2020).

The Actor-Critic algorithm (Oh et al., 2021) used in this study combines the advantages of these two methods, using the value function (Critic) to estimate the performance of the current strategy, and optimizing the strategy through the policy gradient (Actor), so as to achieve the purpose of dimensionality reduction and optimization of the feature data before the lithology identification model and improve the prediction efficiency. In the Actor-Critic algorithm, Actor and Critic are two different components. Among them, Actor is responsible for generating strategies and determining the actions to be taken in a given state. It is usually a policy function ${\pi }_{\theta }\left(a|s\right)$ based on a parameterized model, and optimizes the strategy through gradient ascent. Critic: Responsible for evaluating the quality of the current strategy, giving a value function $V_{\theta }\left(s\right)$ or a state-action value function $Q_{\theta }\left(s,a\right)$, and using this value to guide the update of the Actor. Critic provides feedback to the Actor by calculating the value of each state or state-action pair, and the Actor adjusts the strategy based on these feedbacks.

Suppose we have a Markov decision process (MDP) (Wari et al., 2023) containing a state space S, an action space A, a state transition probability $P\left(s^{\prime }\left|s,a\right.\right)$, a reward function $r\left(s,a\right)$, and a policy function $\pi \left(a|s\right)$. Our goal is to maximize the total reward $J\left(\pi \right)$. In the AC algorithm, we train by optimizing the following objectives (Equation 1):

$J\left(\pi \right)=E\left[{\displaystyle \sum _{t=0}^{T-1}}{\gamma }^t{r}_t\right](1)$

Among them, $E$ represents the mathematical expectation, $T$ represents the current time step, $r_t$ is the reward obtained at time $t$, and ${\gamma }^t$ is the discount factor at time $t$.

The task of the Critic is to evaluate the value of the current strategy, which is usually represented by the state value function $V\left(s\right)$ or the state-action value function $Q\left(s|a\right)$. Generally speaking, the time difference (TD) method is used to update the value function (Equation 2):

${\delta }_t=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)(2)$

Among them, ${\delta }_t$ is the time difference error, which represents the difference between the current estimate and the actual return. The update rule of Critic is (Equation 3):

$V\left(s_{\mathrm{t}}\right)\leftarrow V\left(s_{\mathrm{t}}\right)+{\mathrm{\alpha }}_{\mathrm{v}}{\mathrm{\delta }}_{\mathrm{t}}(3)$

Where ${\alpha }_{\mathrm{v}}$ is the learning rate of the value function.

The goal of an actor is to maximize the expected reward by gradient ascent. We want to update the parameters by policy gradient. The calculation of policy gradient is implemented by the advantage function (Yao et al., 2025), which measures how much better an action $a_{\mathrm{t}}$ is than other actions in state $s_{\mathrm{t}}$. The advantage function is defined as (Equation 4):

$\left(s_t,a_{\mathrm{t}}\right)=Q\left(s_t,a_{\mathrm{t}}\right)-V\left(s_t\right)(4)$

Among them, $Q\left(s_t,a_{\mathrm{t}}\right)$ is the state-action value function, and $V\left(s_t\right)$ is the state value function.

Using the above formula, Actor optimizes the policy parameter θ through gradient ascent (Equation 5):

$\theta \leftarrow \theta +{\alpha }_{\mathrm{a}}{\nabla }_{\mathrm{\theta }}J\left(\mathrm{\pi }\right)(5)$

Where ${\alpha }_{\mathrm{a}}$ is the policy learning rate.

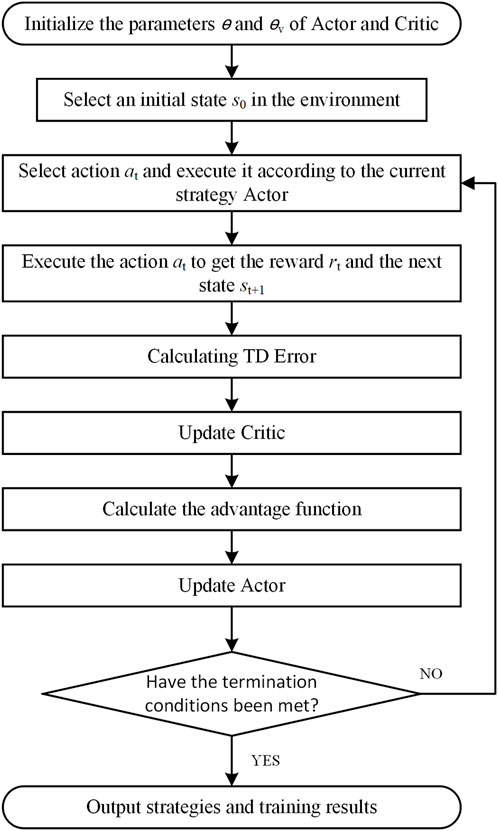
Since the Critic provides feedback by estimating the value function, the Actor-Critic algorithm is usually more stable than the pure policy gradient method. At the same time, compared with value-based Q-learning, Actor-Critic is usually able to use samples more efficiently, especially in high-dimensional space. However, although Actor-Critic has high sample efficiency, it may lead to slow convergence due to the large calculation variance of the policy gradient. The need to adjust multiple hyperparameters (such as learning rate, discount factor, etc.) may lead to instability in the learning process. The Actor-Critic algorithm flow is shown in Figure 1.

Figure 1

Figure 1. Actor-critic algorithm process.

Although our optimization task does not involve dynamic state transitions or sequential decision-making in the traditional sense of reinforcement learning, it can still be modeled as an episodic Markov Decision Process (MDP) with deterministic transitions. In this setting, each episode represents a complete evaluation cycle of a proposed configuration (i.e., feature subset and hyperparameters), where the agent takes an action (selects a configuration), evaluates the model on a validation set, and receives a scalar reward based on the performance (e.g., accuracy, F1-score).

This episodic and static environment formulation is similar to recent RL-based approaches in AutoML and Neural Architecture Search (NAS), where the reinforcement learning agent interacts with a meta-optimization problem rather than a dynamic environment. The Actor network proposes new configurations (policies), while the Critic provides feedback on their performance to guide policy updates. This design allows our method to adaptively explore the high-dimensional search space of configurations in a sample-efficient manner, leveraging the strengths of the Actor-Critic framework for black-box optimization tasks.

To clarify this design, we emphasize that the role of reinforcement learning in our study is not for time-series prediction but to optimize the combination of features and hyperparameters through episodic reward-driven learning.

2.2 Clarification of RL formulation

In our approach, the reinforcement learning (RL) agent does not interact with a dynamic, sequential environment in the traditional sense. Instead, the feature selection and hyperparameter optimization process is formulated as an episodic Markov Decision Process (MDP) with deterministic transitions. Each episode corresponds to a complete evaluation of a candidate feature subset and hyperparameter configuration. The agent selects a configuration (action), trains the model, and receives a scalar reward based on validation performance (e.g., accuracy, F1-score). This static, episodic RL formulation is consistent with recent RL-based AutoML and Neural Architecture Search (NAS) frameworks, where the agent optimizes over a meta-learning landscape rather than a temporally evolving environment.

We acknowledge that this differs from standard RL settings involving sequential decision-making and environment transitions. However, the Actor-Critic framework remains effective for black-box optimization tasks, as it enables efficient exploration of high-dimensional configuration spaces. The agent’s policy is updated based on the reward signal from model evaluation, allowing adaptive search for optimal feature and hyperparameter combinations.

2.3 Transformer model application

Lithology identification tasks usually involve a large amount of time series data, especially logging data collected during drilling. These logging data include but are not limited to sequence data of physical properties such as gamma rays, density, porosity, and natural gamma. Each type of logging data carries important geological information and can be used to distinguish different lithology types. In addition, other formation physical property data such as formation pressure, temperature, and fluid properties can also provide strong support for lithology identification.

In order for the model to better understand the inherent relationship of these data, we need to preprocess the input data and select features. By standardizing different types of logging data, or extracting features that help distinguish lithology through feature engineering. On this basis, the Transformer model can automatically identify important features and establish relationships between these features.

The core advantage of the Transformer model lies in its self-attention mechanism, which can efficiently capture the dependencies between elements in sequence data, especially long-distance dependencies. Compared with traditional recurrent neural networks (RNNs) (Zhang et al., 2023) and long short-term memory networks (LSTMs) (Huang et al., 2022), Transformers have higher parallel processing capabilities, so the training speed is greatly improved when processing large-scale time series data.

The basic structure of Transformer consists of two main parts: encoder and decoder. In the lithology recognition task, we mainly use the encoder part of Transformer to extract the contextual information of the input features. The encoder consists of multiple self-attention layers and a feed-forward network (FFN) (Hu et al., 2022). Each self-attention layer aggregates the information of all elements in the sequence by calculating the attention weights between each element in the input sequence. Multiple self-attention heads enable the model to focus on different subspaces in the sequence, thereby learning richer feature representations. By adding a multi-head attention mechanism, the model can automatically focus on the most important part of the input data by calculating the correlation between different positions. The calculation formula for self-attention is as follows (Equation 6).

$\text{Attention}\left(Q,K,V\right)=\text{softmax}\left(\frac{\mathrm{Q}{\mathrm{K}}^{\mathrm{T}}}{\sqrt{d_k}}\right)V(6)$

$Q$ is query matrix, which represents the query value we want to find relevance.

$K$ is key matrix, which represents the content related to the query.

$V$ is value matrix, which represents the final weighted information.

$d_k$ is the dimension of query and key, which is used to scale the calculation results to avoid too large values.

In the lithology identification task, this means that the model can automatically identify which well logging data or formation physical property data have an important impact on the prediction of lithology type and ignore irrelevant information. At the same time, since the Transformer does not rely on the temporal structure, it is necessary to capture the order information of the data in the sequence through position encoding. This is achieved by adding the position encoding to the feature vector of the input data to ensure that the model can understand the order relationship of the input data. There is a feed-forward neural network after each encoder layer to further learn the nonlinear characteristics of the data. This process enhances the model’s expressiveness in complex tasks.

Based on the representation of the output of the encoder part of the Transformer, the model can predict lithology types or other related geological features. In the lithology recognition task, the output of Transformer is usually a vector of fixed dimension, which represents the semantic understanding of the input logging data in context. Based on this vector, we can use a fully connected layer to map it to different lithology categories. In some more complex tasks, the output may also need to be post-processed. For example, the output can be converted into a probability distribution through a SoftMax layer, and finally the predicted probability of each lithology is obtained. In addition, for multi-classification problems, the cross-entropy loss function can also be used to train the model.

In our implementation, the input to the Transformer encoder consists of sequential logging measurements (e.g., GR, Density, RT, Depth) sampled at regular depth intervals. Each input sequence corresponds to a window of consecutive depth samples, preserving the spatial (depth-wise) order of the data.

To enable the model to capture positional information, we add sinusoidal positional encoding to the input feature vectors, following the original Transformer design. This allows the model to distinguish between measurements at different depths and learn depth-dependent patterns.

The Transformer encoder is trained from scratch on our lithology dataset, as no suitable pre-trained models exist for this domain. The model consists of 4 encoder layers, each with 8 attention heads and a hidden size of 128. The output of the encoder is aggregated via global average pooling and passed to a fully connected classification head.

This architecture enables the model to capture both local and long-range dependencies in the logging data, which is critical for accurate lithology identification in complex geological settings.

3 Results and discussion

In this section, we present and discuss the experimental results of our lithology identification method based on Actor-Critic and Transformer algorithms. We first quantitatively analyze the performance of our model, then compare it with other existing methods, and finally discuss the advantages, limitations, and future improvements of our model.

3.1 Model parameters

In this study, in order to verify the effectiveness of the lithology identification method based on reinforcement learning and Transformer algorithm, we used a real well logging data set collected during the drilling process. This data set contains lithology characteristics of multiple different formations and covers measurements at multiple depths and different geological conditions.

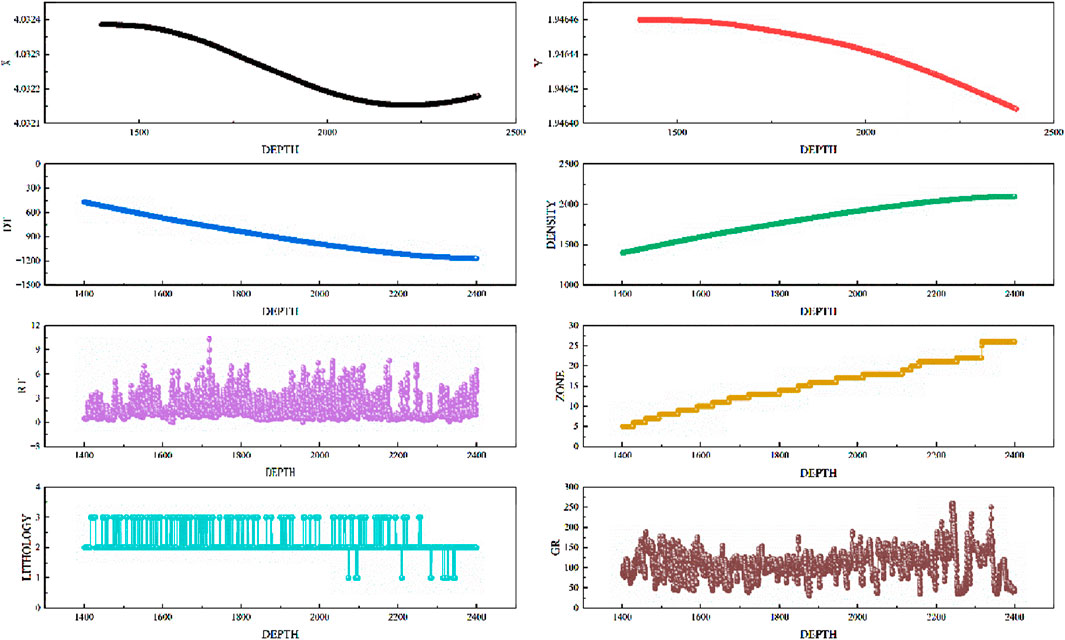
The original data set for this study collected data including basic static parameters of wells, logging, and manual interpretation results. Among them, static data includes well location coordinates. Logging data includes gamma rays, porosity, rock density, resistivity, etc. Measured while drilling. Manual interpretation data includes formation data of drilled wells. The changes in these parameters can not only reflect the characteristics of different lithological layers, but also reveal the laws of lithological distribution under formation depth and geological conditions. Therefore, it is very appropriate to use these parameters for lithology identification. Our data set contains measurement data obtained from multiple wells, covers lithology information at different depths, and covers a variety of different geological environments. The diversity and complexity of the data provide sufficient challenges for the model.

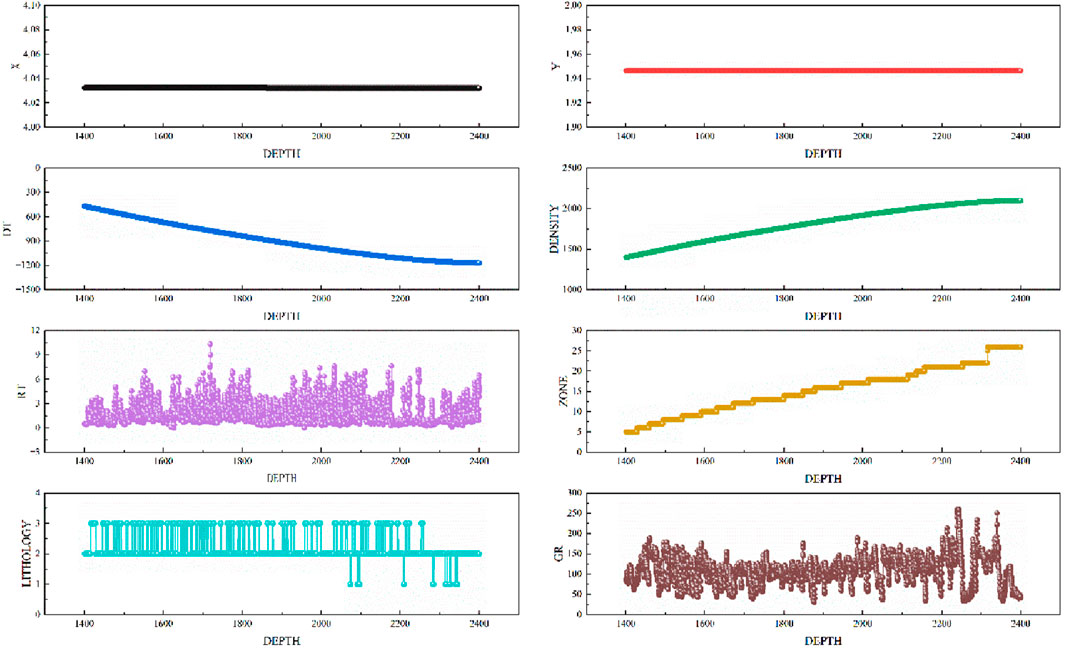
In order to use the dataset for model training and evaluation, we first performed data preprocessing (Çetin and Yıldız, 2022), including the following steps: Missing value processing: In some logging data, there may be missing values due to instrument failure or other reasons. We used interpolation to fill these missing values to ensure the integrity of the data. Data standardization: In order to avoid the unbalanced impact of measurements of different dimensions on model training, we standardized all input features so that the mean of each feature is zero and the standard deviation is one (Li et al., 2025). This can help the model converge better and avoid affecting the model performance due to the large numerical range of a certain feature. The comparison of data before and after processing is shown in Figures 2, 3 respectively.

Figure 2

Figure 2. Data distribution before processing.

Figure 3

Figure 3. Data distribution after processing.

From the comparison results before and after data processing, we can see that the data distribution is messy and contains many outliers before data processing. However, after data processing, the data values remain in a relatively stable range and there are no outliers.

Data partitioning: In order to verify the generalization ability of the model, we divided the entire dataset into a training set and a test set in a ratio of 7:3. The training set is used for model training, and the test set is used to evaluate the performance of the model in practical applications.

In the lithology identification task, feature selection is a key step that affects the model performance. Well logging datasets usually contain a large number of features, some of which contribute more to lithology classification, while others may be redundant or noisy. In order to improve the efficiency and accuracy of the model, we introduced the Actor-Critic algorithm to automatically optimize the feature parameters that affect lithology identification. The Actor-Critic algorithm performs intelligent search in the feature space through a reinforcement learning framework to automatically select the optimal feature subset. This process not only helps us reduce the dimension of the features, but also im-proves the generalization ability of the model.

The specific process of applying the Actor-Critic algorithm for feature selection in lithology identification is as follows: First, define the state space.

In the Actor-Critic algorithm, the state space represents the feature set selected by the current model (Cheng et al., 2022). Each state is a configuration of feature selection, indicating which features are currently selected into the model and which features are excluded. For the lithology identification task, the state space is defined as follows: The state space contains the features in all logging data sets, such as gamma rays (GR), porosity (Porosity), density (Density), etc. Each state can be regarded as a binary vector, where each position corresponds to a feature. If the position is 1, it means that the feature is selected; if it is 0, it means that the feature is not selected.

Then define the action space. In the Actor-Critic algorithm, the action space represents possible feature selection behaviors. At each time step, the Actor selects an action based on the current state, that is, decides whether to add or remove a feature from the current feature set. For example, if the current state is to select gamma rays and porosity, then the action space selection is to add density features or remove gamma ray features.

Finally, the reward function needs to be designed. The reward function is a key part of the Actor-Critic algorithm, which is used to measure the quality of the feature selection strategy. In the lithology recognition task, the reward function we designed is based on the classification performance of the model on the validation set. The reward function can be defined as the accuracy, F1-score, or the combined score of precision and recall of the model. Specifically, the reward function can be expressed as (Equation 7):

$R=ACC+\alpha \times F1+\beta \times S\mathrm{p}(7)$

Where ACC is accuracy, Sp is specificity, α and β are weight factors that can be adjusted according to the specific requirements of the task. The reward function is designed to enable the Actor to not only consider accuracy when selecting features, but also balance the precision and recall of the model, thereby improving the overall performance of lithology recognition.

Finally, the Actor-Critic algorithm updates the feature selection strategy through the following steps: First, randomly initialize the Actor’s strategy and the Critic’s value function. Second, in each round of training, the Actor selects a feature selection strategy (i.e., a feature set) based on the current state, and then trains the lithology recognition model. Then the Critic calculates the value of the current strategy based on the performance of the lithology recognition model under the current feature set (such as accuracy, F1-score, etc.), and feeds it back to the Actor as a reward signal.

Finally, the Actor updates its strategy based on the Critic’s feedback, and uses optimization algorithms such as gradient descent to adjust the feature selection strategy, gradually improving the quality of feature selection.

Repeating the above process, the Actor and Critic continuously optimize alternately until they converge to an optimal feature selection strategy.

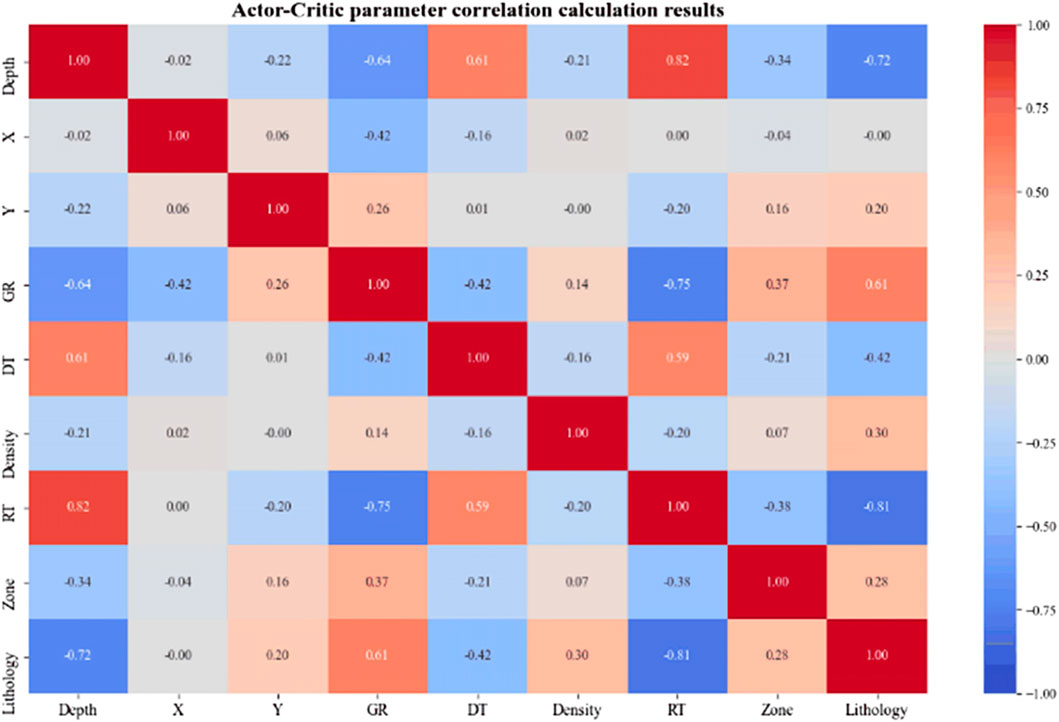
The Actor-Critic algorithm was used to optimize the 9 parameters collected previously, and the correlation coefficients between the parameters were calculated (Figure 4).

Figure 4

Figure 4. Heat map of pearson correlation coefficients between model parameters.

As shown in Figure 4, the horizontal and vertical axes represent model parameters, and the numbers in the matrix indicate the correlation coefficients between them. A higher absolute value denotes a stronger correlation. Based on this analysis, formation interpretation results (RT), depth (Depth), gamma ray (GR), and density were selected as the model input features. Gamma radiation, porosity, and density logs provide complementary information that is critical for lithology identification. Specifically, GR logs measure the natural radioactivity of formations, primarily reflecting the presence of clay minerals and potassium-bearing feldspars (Bhuyan and Passey, 1994). High GR values usually indicate shale-rich or clay-rich intervals, whereas low GR values are characteristic of cleaner sandstones, carbonates, or other non-shaly formations. Porosity logs, derived from density, neutron, or acoustic measurements, quantify pore volume and offer insights into reservoir quality (Hook, 2003). Sandstones generally show higher porosity compared with compacted shales or dense carbonates, and porosity variations also reflect depositional facies and diagenetic processes. Bulk density logs (Pickell and Heacock, 1960) measure electron density and are closely related to mineral composition and compaction degree: shales typically display lower density due to clay minerals and water content, while carbonates and well-compacted sandstones exhibit higher values. When integrated, these parameters enable more reliable lithology discrimination. For example, low GR, high porosity, and moderate density often indicate clean sandstones; high GR combined with low porosity suggests shale; and low GR with high density commonly points to carbonate rocks. In practice, density–porosity or GR–porosity crossplots are widely applied to reduce ambiguity and enhance lithological interpretation. Overall, the number of input parameters was reduced by 55.6%, significantly decreasing computational cost and model training time.

3.2 Model training and evaluation

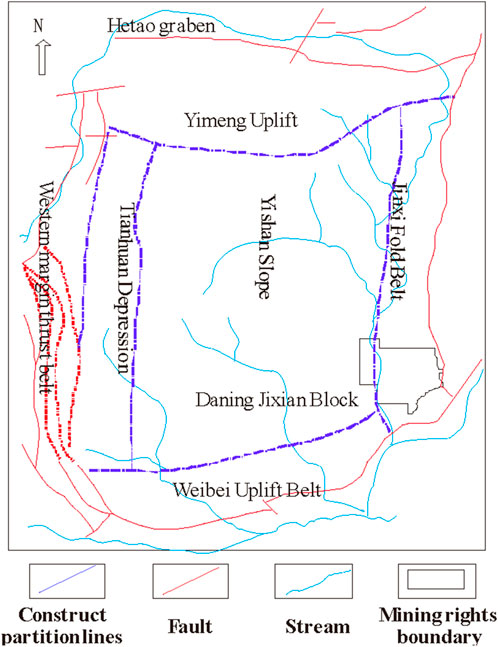
The DJ block (Figure 5) of the CQ Oilfield in the Ordos Basin (Gong et al., 2023) has typical geological characteristics, including a variety of lithology types, such as sandstone, mudstone, carbonate rock, etc. These lithologies show obvious physical property differences in logging data and are ideal data sources for lithology identification research. This study uses drilling data from this block to verify the performance of the lithology identification model constructed based on reinforcement learning and the Transformer algorithm.

Figure 5

Figure 5. Location of the DJ block.

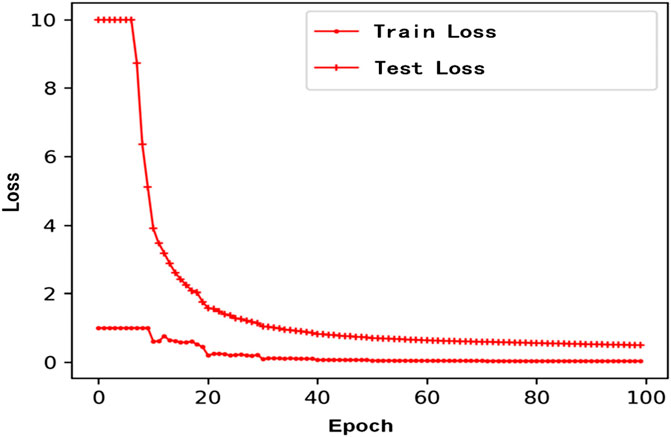
Through the Actor-Critic algorithm in the reinforcement learning framework, the four parameter combinations that have the greatest impact on lithology identification are selected from the original features. The goal is to maximize the reward to ensure the balanced performance of the model on multiple indicators. Based on the Transformer encoder structure, a multi-head self-attention mechanism is used to capture long-distance dependencies. During training, the initial value of the learning rate is set to 0.001, and it is dynamically adjusted in combination with reinforcement learning. The optimizer selects the AdamW optimizer to take into account both training stability and convergence speed (Ma et al., 2025). The loss function is set to cross entropy loss to solve multi-classification problems such as lithology identification. The loss function change curve of the training process is shown in Figure 6.

Figure 6

Figure 6. Loss function change.

From the curve changes in Figure 5, it can be seen that the values of all loss functions drop rapidly in the first 20 epochs of training and tend to stabilize after about 60 epochs, which indicates that there is no overfitting phenomenon during the model training process.

We used the four optimal characteristic parameters and the Transformer algorithm to train the lithology recognition model, and then projected the actual prediction effect of the test set onto the specific well section (Figure 7) to intuitively judge the prediction accuracy.

Figure 7

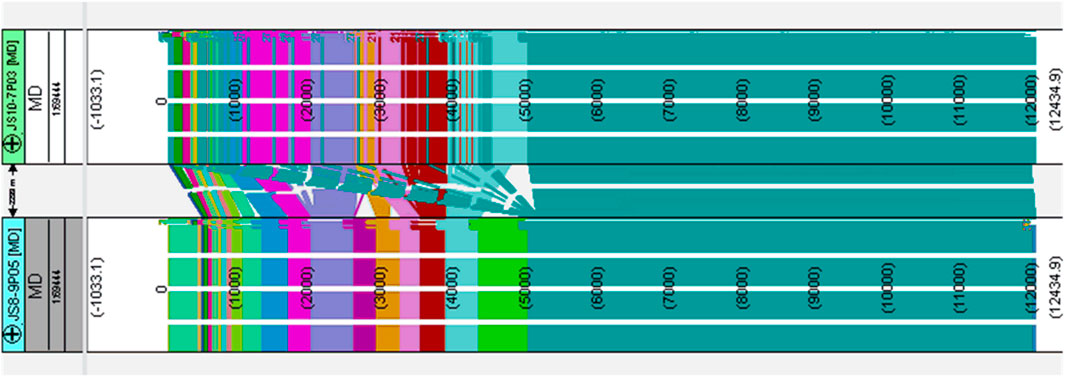
Figure 7. Comparison between the predicted value and the actual value of the lithology identification model.

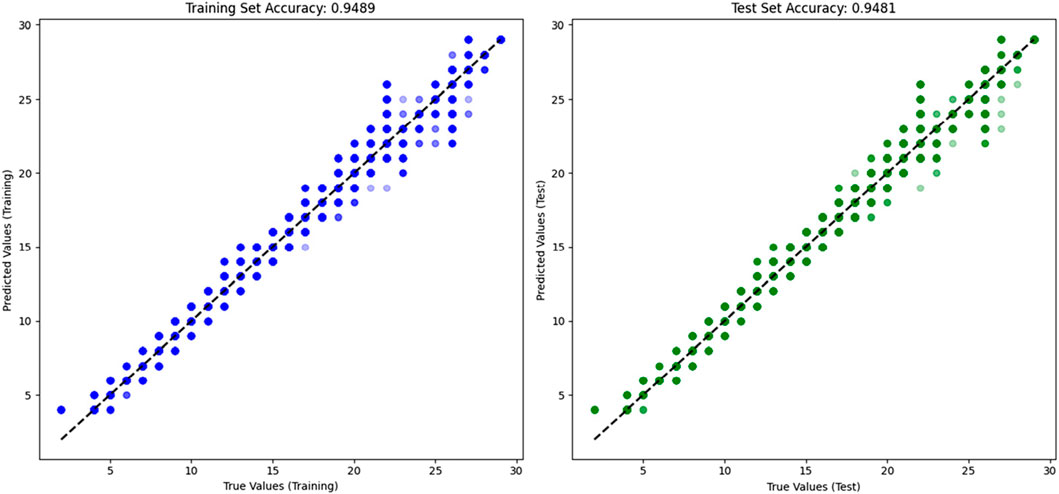
In Figure 7, we projected the predicted lithology values and true values onto two wells to evaluate the prediction accuracy. In the figure, from left to right, the depth of the well is represented, the lower color band represents the predicted lithology value, and the upper color band represents the true lithology value. It can be seen that the two-color bands are consistent in most areas, especially in the deep formations, where the lithology recognition accuracy is high. Finally, the specific prediction accuracy of the constructed lithology identification model was statistically analyzed. The accuracy calculation formula is shown in Equation 8, and the accuracy of the training set and the test set is shown in Figure 8.

Figure 8

Figure 8. Model training set and test set prediction accuracy.

Figure 7 shows the projected results of predicted and actual lithology values along the well trajectory. It can be observed that the predicted lithology matches the true lithology in most intervals, with particularly strong agreement in the deeper sections. This indicates that the proposed model is capable of accurately and effectively identifying the target formation lithology in new wells (Equation 8).

$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}(8)$

In this context, Accuracy represents the model’s prediction accuracy and is used to evaluate the model’s ability to make precise predictions. TP (True Positive) refers to the correctly predicted positive cases, TN (True Negative) refers to the correctly predicted negative cases, FP (False Positive) refers to the incorrectly predicted positive cases, and FN (False Negative) refers to the incorrectly predicted negative cases.

Figure 8 shows the prediction accuracy of the model training set and test set. As shown in Figure 8, the horizontal axis represents the true value of the lithology, and the vertical axis represents the predicted value of the lithology. The prediction accuracy of the model can be explained by the distribution of data points on the 45° line. It can be seen that the lithology identification model constructed in this study has accurate prediction performance, and most of the data points are distributed on and near the 45° line. At the same time, the prediction accuracy values of the training set and the test set reached 94.89% and 94.81% respectively, which can meet the needs of on-site lithology identification.

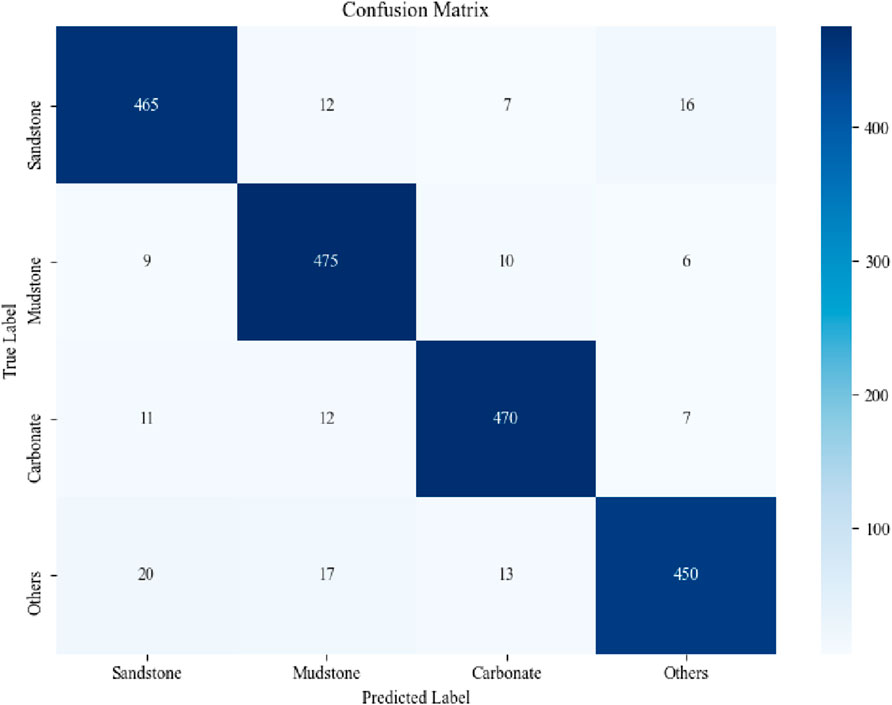
Figure 8 presents the confusion matrix for the test set, illustrating the distribution of true and predicted labels. The model demonstrates strong discrimination between major lithology types, with most misclassifications occurring between lithologies with similar physical properties. These results confirm that our method achieves not only high overall accuracy but also balanced performance across classes, addressing the challenge of class imbalance in lithology prediction.

3.3 Comprehensive performance metrics

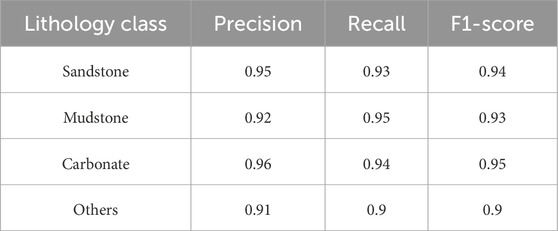
To provide a more complete evaluation of our model, we report additional classification metrics, including per-class precision, recall, and F1-score, as well as the confusion matrix (Figure 9) for the test set. Table 1 summarizes the precision, recall, and F1-score for each lithology class.

Figure 9

Figure 9. Confusion matrix for the test set.

Table 1

Table 1. Comprehensive performance of lithology prediction.

The overall macro-averaged F1-score is 0.93, indicating robust performance across all classes, including minority lithologies.

In addition to visual comparison, we provide quantitative performance analysis using standard classification metrics as described above. The inclusion of per-class metrics and the confusion matrix enables detailed error analysis and interpretation of model strengths and weaknesses. For example, the model achieves the highest F1-score on carbonate rocks, while most misclassifications occur between sandstone and mudstone, likely due to overlapping logging signatures. This quantitative breakdown complements the visual results and provides a more rigorous assessment of model performance.

4 Conclusion

This paper proposes an intelligent lithology identification method based on reinforcement learning and Transformer algorithm, which successfully solves the problems of traditional lithology identification that relies on manual experience, is highly subjective, and has limited identification accuracy. By optimizing the hyperparameters and feature selection of the model through reinforcement learning, the efficiency of lithology identification and the generalization ability of the model are significantly improved; the powerful self-attention mechanism of the Transformer algorithm is used to fully capture the temporal relationship of the well logging data and ensure the recognition accuracy. During the construction process, the model achieved a prediction accuracy of 94.89% on millions of drilling data samples, proving its efficiency and robustness under massive data. Com-pared with traditional methods, the model in this paper can not only quickly determine the lithology category, significantly improve the decision-making efficiency at the drilling site, but also effectively reduce the construction cost, and has high engineering application value. In the future, this method can be further extended to drilling operations with more complex geological conditions, providing important support for intelligent drilling technology.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XL: Writing – original draft, Conceptualization, Investigation. PL: Conceptualization, Data curation, Investigation, Writing – review and editing. HQ: Data curation, Methodology, Writing – review and editing. YW: Formal Analysis, Project administration, Validation, Writing – review and editing. TZ: Formal Analysis, Resources, Visualization, Writing – review and editing. QL: Conceptualization, Data curation, Methodology, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

We sincerely appreciate the technical support and guidance provided by China National Logging Corporation, Changqing Oilfield, and Henan Polytechnic University.

Conflict of interest

Authors XL, PL, YW, and TZ were employed by China National Logging Corporation. Author HQ was employed by No. 3 Oil Production Plant, Changqing Oil Field, CNPC.

The remaining author declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1595574/full#supplementary-material

References

Bhuyan, K., and Passey, Q. (1994). Clay estimation from GR and neutron-density porosity logs. In: Paper presented at the SPWLA annual logging symposium; 1994 June 19–22; Tulsa, Oklahoma.

Google Scholar

Cao, Z., Ma, C., Tang, W., Zhou, Y., Zhong, H., Ye, S., et al. (2024). CoreViT: a new vision transformer model for lithofacies identification in cores. Geoenergy Sci. Eng. 240, 213012. doi:10.1016/j.geoen.2024.213012

CrossRef Full Text | Google Scholar

Çetin, V., and Yıldız, O. (2022). A comprehensive review on data preprocessing techniques in data analysis. Pamukkale Üniversitesi Mühendislik Bilim. Derg. 28 (2), 299–312. doi:10.5505/pajes.2021.62687

CrossRef Full Text | Google Scholar

Cheng, C.-A., Xie, T., Jiang, N., and Agarwal, A. (2022). Adversarially trained actor critic for offline reinforcement learning. In: International Conference on Machine Learning; 2025 July 13–19; Vancouver, Canada.

Google Scholar

Gong, B., Wang, H., Wang, H., Song, W., Sun, X., and Yang, J. (2023). Integrated intelligent decision-making technology for deep coalbed methane geology and engineering based on big data analysis algorithms. Acta Pet. Sin. 44 (11), 1949.

Google Scholar

Hook, J. R. (2003). An introduction to porosity. Petrophysics 44.

Google Scholar

Hou, Z., Jikang, W., Shen, J., Liu, X., and Wentian, Z. (2023). Intelligent lithology identification methods for rock images based on object detection. Nat. Resour. Res. 32 (6), 2965–2980. doi:10.1007/s11053-023-10271-8

CrossRef Full Text | Google Scholar

Hu, M., Gao, R., Suganthan, P. N., and Tanveer, M. (2022). Automated layer-wise solution for ensemble deep randomized feed-forward neural network. Neurocomputing 514, 137–147. doi:10.1016/j.neucom.2022.09.148

CrossRef Full Text | Google Scholar

Huang, R., Wei, C., Wang, B., Yang, J., Xu, X., Wu, S., et al. (2022). Well performance prediction based on long short-term memory (LSTM) neural network. J. Petroleum Sci. Eng. 208, 109686. doi:10.1016/j.petrol.2021.109686

CrossRef Full Text | Google Scholar

Li, S., Zhou, K., Zhao, L., Qi, X., and Liu, J. (2022). An improved lithology identification approach based on representation enhancement by logging feature decomposition, selection and transformation. J. Petroleum Sci. Eng. 209, 109842. doi:10.1016/j.petrol.2021.109842

CrossRef Full Text | Google Scholar

Li, J.-Yu, Tang, J.-Z., Zhao, X.-Z., Fan, B., Jiang, W.-Y., Song, S.-Y., et al. (2025). A large-scale, high-quality dataset for lithology identification: construction and applications. Petroleum Sci. 22, 3207–3228. doi:10.1016/j.petsci.2025.04.013

CrossRef Full Text | Google Scholar

Ma, T., Xiao, H., and Yang, Y. (2025). Deep transfer learning with bayesian optimization for evolutionary stage prediction of step-like landslides. Front. Earth Sci. 13, 1634728. doi:10.3389/feart.2025.1634728

CrossRef Full Text | Google Scholar

Martinsen, A. B., Lekkas, A. M., and Gros, S. (2020). Combining system identification with reinforcement learning-based MPC. IFAC-PapersOnLine 53 (2), 8130–8135. doi:10.1016/j.ifacol.2020.12.2294

CrossRef Full Text | Google Scholar

Oh, D.-H., Adams, D., Vo, N. D., Gbadago, D. Q., Lee, C.-H., and Oh, M. (2021). Actor-critic reinforcement learning to estimate the optimal operating conditions of the hydrocracking process. Comput. Chem. Eng. 149, 107280. doi:10.1016/j.compchemeng.2021.107280

CrossRef Full Text | Google Scholar

Perrusquía, A., and Yu, W. (2021). Identification and optimal control of nonlinear systems using recurrent neural networks and reinforcement learning: an overview. Neurocomputing 438, 145–154. doi:10.1016/j.neucom.2021.01.096

CrossRef Full Text | Google Scholar

Pickell, J. J., and Heacock, J. G. (1960). Density logging. Geophysics 25 (4), 891–904. doi:10.1190/1.1438769

CrossRef Full Text | Google Scholar

Qingfeng, L., Peng, C., Fu, J., Zhang, X., Su, Y., Zhong, C., et al. (2023). A comprehensive machine learning model for lithology identification while drilling. Geoenergy Sci. Eng. 231, 212333. doi:10.1016/j.geoen.2023.212333

CrossRef Full Text | Google Scholar

Ren, X., Hou, J., Song, S., Liu, Y., Chen, D., Wang, X., et al. (2019). Lithology identification using well logs: a method by integrating artificial neural networks and sedimentary patterns. J. Petroleum Sci. Eng. 182, 106336. doi:10.1016/j.petrol.2019.106336

CrossRef Full Text | Google Scholar

Ren, Q., Zhang, D., Xiang, Z., Yan, L., Rui, J., and Rui, J. (2022). A novel hybrid method of lithology identification based on k-means++ algorithm and fuzzy decision tree. J. Petroleum Sci. Eng. 208, 109681. doi:10.1016/j.petrol.2021.109681

CrossRef Full Text | Google Scholar

Ren, Q., Zhang, H., Zhang, D., and Xiang, Z. (2023). Lithology identification using principal component analysis and particle swarm optimization fuzzy decision tree. J. Petroleum Sci. Eng. 220, 111233. doi:10.1016/j.petrol.2022.111233

CrossRef Full Text | Google Scholar

Shi, H., Xu, Z. H., Lin, P., and Wen, M. (2023). Refined lithology identification: methodology, challenges and prospects. Geoenergy Sci. Eng. 231, 212382. doi:10.1016/j.geoen.2023.212382

CrossRef Full Text | Google Scholar

Wang, J., Zhang, X., Zhang, F., Wan, J., Lei, K., and Ke, W. (2022). Review on evolution of intelligent algorithms for transformer condition assessment. Front. Energy Res. 10, 904109. doi:10.3389/fenrg.2022.904109

CrossRef Full Text | Google Scholar

Wari, E., Zhu, W., and Lim, G. (2023). A discrete partially observable markov decision process model for the maintenance optimization of oil and gas pipelines. Algorithms 16 (1), 54. doi:10.3390/a16010054

CrossRef Full Text | Google Scholar

Xie, Y., Zhu, C., Wen, Z., Li, Z., Liu, X., and Tu, M. (2018). Evaluation of machine learning methods for formation lithology identification: a comparison of tuning processes and model performances. J. Petroleum Sci. Eng. 160, 182–193. doi:10.1016/j.petrol.2017.10.028

CrossRef Full Text | Google Scholar

Xu, Z., Wen, M., Lin, P., Shi, H., Pan, D., and Liu, T. (2021). Deep learning of rock images for intelligent lithology identification. Comput. & Geosciences 154, 104799. doi:10.1016/j.cageo.2021.104799

CrossRef Full Text | Google Scholar

Yan, T., Xu, R., Sun, S.-H., Hou, Z.-K., and Feng, J.-Y. (2024). A real-time intelligent lithology identification method based on a dynamic felling strategy weighted random forest algorithm. Petroleum Sci. 21 (2), 1135–1148. doi:10.1016/j.petsci.2023.09.011

CrossRef Full Text | Google Scholar

Yao, Z., Xu, K., Wang, Z., Sun, H., and Cui, P. (2025). Estimating shear strength of dredged soils for marine engineering: experimental investigation and machine learning modeling. Front. Earth Sci. 13, 1645393. doi:10.3389/feart.2025.1645393

CrossRef Full Text | Google Scholar

Zhang, S., Luo, J., Wang, S., and Liu, F. (2023). Oil price forecasting: a hybrid GRU neural network based on decomposition–reconstruction methods. Expert Syst. Appl. 218, 119617. doi:10.1016/j.eswa.2023.119617

CrossRef Full Text | Google Scholar

Zhang, P., Gao, T., Li, R., and Fu, J. (2024). Advanced machine learning framework for enhanced lithology classification and identification. In: International Petroleum Technology Conference; 2024 February 12; Dhahran, Saudi Arabia: OnePetro.

Google Scholar