Assessing low free gas saturation via acoustic velocity in porous media

This study proposes a novel quantitative evaluation method for acoustic logging velocities in sedimentary porous media with free gas saturation below 2$\%$. This issue is of critical importance for gas migration analysis, geological hazard prediction, and environmental safety monitoring; however, conventional rock physics models suffer from significantly diminished accuracy in scenarios with ultra-low gas saturation and are unable to capture the pronounced nonlinear changes in acoustic velocity. To address these challenges, a dynamic coupling factor $J$ is introduced within a revised Biot theoretical framework, and, in conjunction with core experimental data, the associated dynamic and elastic parameters are systematically optimized with respect to gas saturation. The new model accurately reflects the rapid decline of P-wave velocity with increasing gas content in the 0–2$\%$ saturation range, reducing velocity prediction error from 55.7$\%$ (typical of traditional approaches) to just 5.27$\%$. Application to well-logging data from the LS-361 site in the South China Sea demonstrates that the model is capable of effectively resolving gas-bearing layers with extremely low saturations (0–0.12$\%$), thereby verifying its practical utility. This method significantly enhances the quantitative interpretability of subtle free gas indicators in subseafloor sediments and advances the theoretical understanding of multiphase poroelastic mechanisms, contributing to improved accuracy in gas reservoir identification and environmental risk assessment.

1 Introduction

In marine or lacustrine sediments, the decomposition of organic matter generates gases such as methane. When the amount of gas produced exceeds its solubility in water, the excess gas accumulates within the pore spaces of the sediments in the form of free gas. Free gas saturation is a key parameter that describes the proportion of free gas occupying the pore volume in sediments, and it directly affects the pore fluid flow characteristics, gas migration behavior, and the safety of gas storage in sediments (Agnew and Halihan, 2018; Gurevich and Carcione, 2022). Evaluating the free gas saturation holds significant importance across a wide range of disciplines, spanning hydrocarbon exploration (Zhou et al., 2022; Liu et al., 2024; Mu et al., 2024), geological hazard mitigation (Malakhova et al., 2024; Ge et al., 2022), and environmental infrastructure security (Deng et al., 2023; Zhou et al., 2024).

Free gas saturation, even at ultra-low levels, is a critical parameter that governs the reservoir’s flow dynamics, acoustic response, mechanical stability, and overall performance in both natural and engineered systems (Tóth et al., 2014; Tŕehu and Flueh, 2001; Cheng, 2017). Experimental observations have revealed that, compared to water-saturated sediments, the presence of free gas in sediment pores significantly affects acoustic wave propagation (Wang et al., 2018; Guangying and Xiumei, 2018; Wang et al., 2019). As the free gas content increases from zero, the P-wave velocity experiences a significant decrease, while the reduction in S-wave velocity is comparatively smaller (Zhu et al., 2015; Hongxing et al., 2015; Fei et al., 2017; Leighton et al., 2021; Zhan et al., 2022; Chen et al., 2023). Zhan et al. (2022) found that the acoustic attenuation in free gas-bearing sediments is significantly greater than that in water-saturated sediments.

To evaluate free gas saturation, scientists have conducted extensive acoustic experiments and tested various velocity models (Anderson and Hampton, 1980; Gei and Carcione, 2003; Lei and Xue, 2009). Based on bubble resonance theory, Anderson and Hampton (1980) developed a bubble resonance frequency model, a P-wave velocity model, and an attenuation model for free gas-bearing sediments. Due to the irregular geometry of bubbles within the pores and discrepancies in the bubble resonance frequency, the gas saturation calculated using the Anderson-Hampton method may be underestimated compared to the measured values (Gardner and Sills, 2001; Best et al., 2004; Tóth et al., 2014; Cheng, 2017; Wang et al., 2018). Lebedev et al. (2009) injected water into dry synthetic sandstone to achieve near-complete pore water saturation. During this process, due to capillary retention and pore connectivity, a minor proportion of free gas persisted in the form of isolated patches. From the test results, it can be calculated that when the gas saturation is close to 10$\%$, the velocity reduction rate reaches 7$\%$. Wang et al. (2019) evaluated the P-wave velocity of water-saturated sandstone by combining the Hashin-Shtrikman bounds interpolation method and the Gassmann equation, with gas saturation calculated using the Wood equation. Chen et al. (2023) used a low gas injection method to slowly inject methane gas from the bottom of the sand sample. When the gas saturation was close to 10$\%$, the velocity reduction rate was approximately 20$\%$. The study improved the accuracy of gas saturation prediction in the Biot-Gassmann Theory with Losses (BGTL) model by modifying the effective fluid modulus. Traditional gas saturation evaluation models mainly focus on high saturation regions and simplify the impact of free gas on velocity, thus having certain limitations when assessing low saturation levels. By depressurization and using a ${\text{CO}}_2$-saturated aqueous solution to maintain effective pressure in the sand body, Cheng (2017) and Wang et al. (2018) generated nearly uniformly distributed free microbubbles. From the experimental data, it can be calculated that when the free gas saturation is close to 0.5$\%$, the velocity reduction rate is approximately 40$\%$, which is greater than the results of Lebedev and Chen. Additionally, the experimental data show that as gas saturation increases from zero, the velocity significantly decreases (Lei and Xue, 2009; Zhu et al., 2015; Hongxing et al., 2015; Fei et al., 2017; Wang et al., 2018). These experimental results reveal the important role of gas saturation in the reduction of P-wave velocity. The Anderson-Hampton method is constrained by its high-frequency bubble resonance theory assumption, which mismatches the low-frequency conditions of acoustic logging, leading to significant velocity prediction deviations. Traditional models based on linear superposition assumptions neglect the nonlinear velocity reduction characteristics dominated by microbubble interfacial tension under low saturation conditions. Therefore, developing new velocity models is essential for accurately evaluating low-saturation free gas.

In fact, sediments containing low-level free gas can be considered as a three-phase porous medium, consisting of a solid grain framework, pore fluid, and free gas bubbles (Santos et al., 1990; Santos et al., 2004; Lo et al., 2005). Acoustic wave propagation in this type sediments is fundamentally governed by Biot poroelastic theory (Biot, 1956a; Biot, 1956b; Biot, 1962). The Biot theory does not require assumptions about the detailed geometrical features of microscopic pores or the solid skeleton; it is only necessary that, at the macroscopic scale, the medium exhibits spatial uniformity and satisfies reasonable thermodynamic and static conditions. A significant advantage of this theory is that it employs physical parameters with clear physical interpretations, making it broadly applicable to the elastic and inelastic dynamic modeling of rocks, soils, and a wide range of engineering and natural porous materials. Biot theory was validated (Plona and Johnson, 1980; Berryman, 1980), and successfully extended to more complex situations (Leclaire et al., 1994; Gei and Carcione, 2003; Guangying and Xiumei, 2018; Gei et al., 2022; Liu et al., 2021; Shi et al., 2024).

Although the Biot theory has become a fundamental framework for describing solid-fluid interactions, elastic wave propagation, and their attenuation and dispersion in porous media, its direct application to low-saturation free gas reservoirs remains challenging. Natural formations exhibit highly heterogeneous physical property distributions, and under partial saturation or in the presence of gas bubbles, the influence of free gas on elastic wave characteristics shows strong frequency dependence. The velocity and attenuation of elastic waves are controlled by the complex coupling among pore structure, fluid distribution, capillary forces, as well as the size, shape, and spatial distribution of fluid patches (Kong et al., 2022; Gurevich and Carcione, 2022). These multi-scale physical mechanisms in heterogeneous media are difficult to be fully captured by the conventional Biot theory. In particular, the Biot framework has limitations in accounting for patchy flow, local gas bubble effects, slow waves induced by capillary forces, and the resulting frequency-dependent acoustic responses observed in real formations. Therefore, achieving accurate modeling of wave response and quantitative assessment of gas saturation based solely on the Biot theory remains a considerable challenge in low-saturation free gas reservoirs.

To address these issues, a novel methodological framework is developed by systematically introducing a dynamic coupling factor $J$ into the classical Biot theory, thereby refining the modeling of fluid density, viscosity, and effective bulk modulus-parameters that are critically sensitive to low gas saturation. This innovative approach substantially enhances the ability to characterize the nonlinear variations in acoustic velocity within sediments exhibiting extremely low gas saturation (0–2$\%$), reducing the velocity estimation error from 55.7$\%$ (as observed in conventional models) to only 5.27$\%$. The proposed model demonstrates excellent agreement with laboratory measurements and enables accurate identification of sub-percent free gas layers in field well-logging applications. This significantly improves the quantitative interpretation of weak free gas signatures in subseafloor sediments and provides both a robust theoretical foundation and a technical advance for investigating multiphase poroelastic mechanisms.

2 Methods

In order to accurately assess low free-gas saturation, this chapter first selects a robust and reliable modeling approach. The formulation of model parameters associated with free-gas saturation is then systematically refined, and the impact of these improvements is evaluated through comprehensive analysis.

2.1 Velocity model

According to extensions of the classical Biot theory, if the distributions of free gas and pore water in a porous medium are sufficiently uniform, and the spatial scale of the representative volume element (RVE) is much larger than that of capillary pressure fluctuations or fluid patch sizes, then the fine-scale pressure differences between the gas and water phases average out across the RVE. Under these conditions, the two fluids can be regarded as a uniformly distributed ‘mixture’ characterized by a common, macroscopic pore pressure, facilitating the use of equivalent medium theory for large-scale analyses. Under this assumption, the effective elastic and dynamic parameters of the medium can be accurately described by using volume-fraction-weighted averages of the fluid bulk moduli and densities. Therefore, at low free gas saturation (i.e., when the gas content is extremely low), the pressure difference between gas and water is negligible, and the overall wave response of the medium resembles that of a ‘single fluid’ system. The motion equations for these sediments, under the Biot theory framework, can be written as follows:

$\rho \left(\begin{array}{c}\hfill \ddot{u^s}\hfill \\ \hfill \ddot{u^l}\hfill \end{array}\right)+B\left(\begin{array}{c}\hfill \dot{u^s}\hfill \\ \hfill \dot{u^l}\hfill \end{array}\right)=K\nabla \nabla \cdot \left(\begin{array}{c}\hfill u^s\hfill \\ \hfill u^l\hfill \end{array}\right)+\mu {\nabla }^2\left(\begin{array}{c}\hfill u^s\hfill \\ \hfill u^l\hfill \end{array}\right)(1)$

where $u^s$ and $u^l$ represent the displacement vectors of the solid framework and the pore fluid, respectively. The pore fluid consists of water and free gas, and the subscripts $s$, $l$, $w$, and $g$ represent solid particles, liquid, water, and gas, respectively. The coefficient matrix presented in Equation 1 is given by:

$\rho =\left(\begin{array}{cc}\hfill {\rho }_{11}\hfill & \hfill {\rho }_{12}\hfill \\ \hfill {\rho }_{21}\hfill & \hfill {\rho }_{22}\hfill \end{array}\right),B=\left(\begin{array}{cc}\hfill b\hfill & \hfill -b\hfill \\ \hfill -b\hfill & \hfill b\hfill \end{array}\right)(2)$

$K=\left(\begin{array}{cc}\hfill A+N\hfill & \hfill Q\hfill \\ \hfill Q\hfill & \hfill R\hfill \end{array}\right),\mu =\left(\begin{array}{cc}\hfill N\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)(3)$

Here, $\rho$, $B$, $K$, and $\mu$ represent the mass density matrix, friction coefficient matrix, bulk modulus matrix, and shear modulus matrix, respectively. Gei et al. (2022) discovered that gas saturation-related parameters are influenced by the surrounding environment. Accordingly, this paper refine the motion equations by incorporating a dynamic coupling factor $J$ to adjust the gas saturation-dependent parameters. Parameters associated with free gas saturation, namely, $\rho$, $B$, and $K$, are introduced below. We elaborate on the physical significance of each parameter and present enhanced methodologies for the assessment of free gas saturation. The components of the mass density matrix ${\rho }_{ij}$ are:

${\alpha }_{\infty }=1+r\left(\frac{1}{\varphi }-1\right),{\rho }_{12}=-\left({\alpha }_{\infty }-1\right)\varphi {\rho }_l(4)$

${\rho }_{11}=\left(1-\varphi \right){\rho }_s-{\rho }_{12},{\rho }_{22}=\varphi {\rho }_l-{\rho }_{12}(5)$

${\rho }_l=S_g^J{\rho }_g+\left(1-S_g^J\right){\rho }_w,S_g={\varphi }_g/\varphi ,S_w={\varphi }_w/\varphi (6)$

Here, the apparent liquid density ${\rho }_l$ with free gas is improved by introducing the factor $J$. ${\alpha }_{\infty }$ represents the tortuosity of the pore space. In practice, the solid particles are not perfectly spherical (Juntao et al., 2015); however, for the purposes of analytical tractability, we approximate them as spheres and set $r=0.5$. ${\varphi }_g$ and ${\varphi }_w$ are the volume fractions of gas and water in the pores, respectively, ${\varphi }_g+{\varphi }_w=1$. In the expression for the friction coefficient, $b={\eta }_l{\varphi }^2/\kappa$, the effective permeability of the solid skeleton is $\kappa ={10}^{-5}\left(m^2\right)$, which is independent of pore fluid properties and only characterizes the intrinsic property of the solid skeleton. The apparent liquid viscosity coefficient with free gas is adjusted to:

${\eta }_l={\eta }_g{\left(\frac{{\eta }_w}{{\eta }_g}\right)}^{\left(1-S_g^J\right)}.(7)$

The bulk modulus and shear modulus of the sediment are expressed as:

$A={\left(\left(1-c\right){\varphi }_s\right)}^2{K}_{av}+K_m-2{\mu }_m/3,{\varphi }_s=1-\varphi (8)$

$Q=\left(1-c\right){\varphi }_s\varphi K_{av},R={\varphi }^2{K}_{av},c=\frac{K_m}{{\varphi }_s{K}_s},N={\mu }_m(9)$

$K_m=\frac{K_s\left(1-\varphi \right)}{1+\alpha \varphi },{\mu }_m=\frac{{\mu }_s\left(1-\varphi \right)}{1+\alpha \gamma \varphi },\gamma =\frac{1+2\alpha }{1+\alpha }(10)$

Here, $K_s$, $K_w$, and $K_g$ represent the bulk moduli of solid particles, water, and free gas, respectively. $K_m$ and ${\mu }_m$ are the bulk modulus and shear modulus of the dry skeleton, respectively. $\alpha$ is the formation Biot consolidation parameter.In this context, the apparent average bulk modulus of the sediment, accounting for gas saturation, is defined as:

$K_{av}={\left[\frac{\left(1-c\right){\varphi }_s}{K_s}+\frac{\left(1-S_g^J\right)\varphi }{K_w}+\frac{S_g^J\varphi }{K_g}\right]}^{-1}.(11)$

In the aforementioned formulations for the sediment parameters ${\rho }_l$, ${\eta }_l$, and $K_{av}$, the influence of gas saturation is more accurately accounted for through the introduction of the factor $J$. An examination of these three formulas reveals that when the parameter $J=1$, they reduce to the traditional expressions for the parameters in the Biot equations of motion. For $J>1$, the physical parameters ${\rho }_l$, ${\eta }_l$, and $K_{av}$ all exceed the values obtained from the conventional formulas. Additionally, when $S_g=0$, it indicates the absence of free gas within the sediment.

Substituting the plane harmonic wave into Equation 1 (Liu et al., 2021) together with parameters (Equations 2–11), the characteristic equation can be obtained:

$det\left({\omega }^2\rho +i\omega B-k_p^{2}K\right)=0(12)$

Here, the operator $\mathrm{d}\mathrm{e}\mathrm{t}\left(\cdot \right)$, in Equation 12, represents the calculation of the determinant of a matrix. According to the characteristic equation, the calculation formula for the P-wave velocity can be expressed as:

$v_p=\frac{w}{\mathrm{R}\mathrm{e}\left(\sqrt{k_p^2}\right)}(13)$

Here, $\mathrm{R}\mathrm{e}$ denotes the real part. The P-wave velocity comprises two components: the first P-wave velocity $(v_{p1})$, which characterizes the propagation of compressional waves through the sediment matrix, and the second P-wave velocity $(v_{p2})$, which corresponds to the propagation of compressional waves within the pore fluid. There is a substantial difference between these two velocities; notably, the second P-wave $(v_{p2})$ undergoes rapid attenuation and is typically difficult to observe experimentally. In practical applications, the first P-wave velocity is used. Accordingly, the velocity model presented in this study is formulated based on the first P-wave velocity, as given by Equation 13. Hereafter, this formulation is referred to as the ‘velocity model’ (see Equation 13).

2.2 Key parameters

From the calculation process of the velocity model (Equation 13), it can be seen that several parameters affect the P-wave velocity, and the degree of influence varies. Studying which parameters have the greatest impact on velocity as gas saturation changes and identifying the key parameters is of great significance for constructing a gas saturation evaluation model. Based on differentiation and dimensional analysis, sensitivity analysis quantifies the impact of variable changes on the output results. Sensitivity analysis can be used to identify the key parameters for estimating gas saturation, and the sensitivity function can be expressed as:

$S{A}_p\left(v\right)=\frac{p}{v}\frac{\partial v}{\partial p}(14)$

Here, $v$ denotes velocity, and $p$ represents the parameters in the formula, such as $\varphi ,J,w,r,K_s,{\mu }_s$, and $\eta$, etc. $S{A}_p\left(v\right)$ represents the application of sensitivity analysis to velocity $v$ with respect to the variable $p$. $S{A}_p$ is still a function of these parameters and is dimensionless (unitless). If the sensitivity function $S{A}_p$ is positive, it indicates that velocity $v$ increases as the variable $p$ increases. Conversely, it indicates that velocity decreases as the variable increases. Unless otherwise specified, the parameter values used in this paper are shown in Table 1. Parameter values in this table are mainly representative of typical subsea sediments and rocks, and are compiled from Cheng (2017) and Wang et al. (2019). Notably, the porosity value (52$\%$) reflects direct measurements from unconsolidated coastal sediment cores in our study area (Cheng, 2017; Wang et al., 2019), which is significantly higher than that of consolidated rocks due to minimal compaction and abundant intergranular pore space.

Table 1

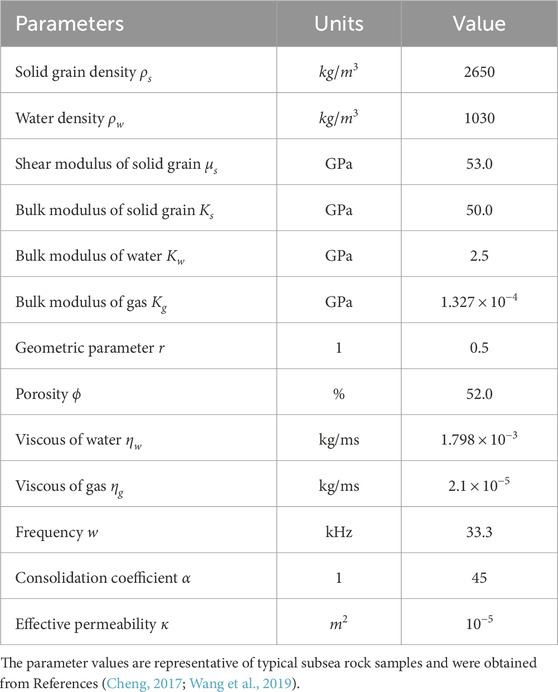
Table 1. The values of the parameters in Equation 1.

To identify the key parameters for evaluating gas saturation, it is necessary to study the variation of the sensitivity function with gas saturation for all parameters, as shown in Figure 1. The curves with relatively large sensitivity function values are marked for clarification. Figure 1 shows the variation of the sensitivity function (Equation 14) of the P-wave velocity $v_p$ with gas saturation. The figure indicates that the parameters having the greatest impact on the P-wave velocity as gas saturation changes are $J$, $\varphi$, $S_g$, and $K_s$.

Figure 1

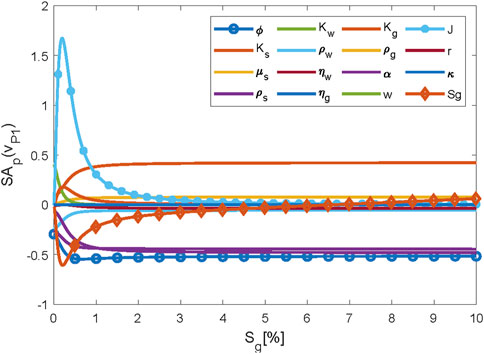
Figure 1. Variation of P-wave velocity sensitivity function with varying free gas saturation. Each curve denotes a sensitivity function with respect to a specific parameter. Except for the target parameter being analyzed, all other parameters are held constant at their default or representative values as provided in Table 1 (e.g., $\varphi$ = 52, $K_s$ = 50 [GPa]). All parameter values are based on experimental measurements or standard recommendations.

The sensitivity function with respect to $\varphi$ is negative, indicating that the primary P-wave velocity decreases as $\varphi$ increases. In contrast, the sensitivity function with respect to $K_s$ is positive, which is consistent with the actual situation. As gas saturation $S_g$ increases from zero, the sensitivity function with respect to $S_g$ initially decreases rapidly. Then, as gas saturation continues to increase, the rate of decrease becomes smaller.

For the factor $J$, its sensitivity function value is positive. When gas saturation is low, such as $S_g\le 2\%$, the sensitivity function first increases rapidly and then decreases quickly. As gas saturation continues to increase, the sensitivity function value gradually decreases. This indicates that the factor $J$ is most sensitive to free gas saturation at low levels, making it particularly suited for capturing the behavior of P-wave velocity, which initially decreases rapidly and then tapers off as gas saturation increases from zero. In the following section, we explore the utilization of the velocity model to quantitatively evaluate gas saturation.

3 Results and discussion

3.1 Optimizing factor $J$

The Biot motion equation is the ideal model for describing wave propagation in porous media containing free gas (Biot, 1956a; Lo et al., 2005). This model assumes that free gas is uniformly distributed throughout the sediment’s pore space; however, most experimental tests indicate that this assumption is difficult to satisfy. Cheng (2017) generated nearly uniform free gas in the pore space of sediments by depressurizing ${\text{CO}}_2$-saturated pore fluid while maintaining the effective stress. During this process, the P-wave velocity was continuously measured, and the gas fraction was calculated. The maximum gas saturation achieved was around 2$\%$. The experiments found that during the stage of gas saturation increasing from 0 to 0.5$\%$, the P-wave velocity decreased rapidly. After that, the rate of velocity decrease slowed down, until the velocity remained almost unchanged. This experiment clearly demonstrates the significant impact of free gas on P-wave velocity at low gas saturation levels. The parameter $J$ is determined by fitting to experimental data (Cheng, 2017; Wang et al., 2018). With the data at zero gas saturation, the Biot consolidation parameter is calculated to be $\alpha$ = 45.

The surface in Figure 2 illustrates model velocity derived from Equation 13, with varying values of $J$ and $S_g$. The surface shows that the model velocity decreases as $S_g$ increases from zero, and the rate of velocity decrease rapidly increases as $J$ decreases. The blue dots in Figure 2 are obtained by Gei modle (Gei et al., 2022). Due to the strong dependence of the Gei model on accurate pore pressure estimation-which is itself constrained by the quality of well logging data, formation complexity, and interpretation models-precise determination of pore pressure is often challenging. As a result, the applicability of the Gei model in real geological settings is substantially limited, and its prediction uncertainty is notably increased. In Figure 1, the velocities calculated using the Gei model are based on the non-effective stress version described in the original publication. Furthermore, it is difficult for the model-predicted velocities to be lower than 1635 [m/s] with the parameters in Table 1, even when the empirical parameter $A\ge 10$.

Figure 2

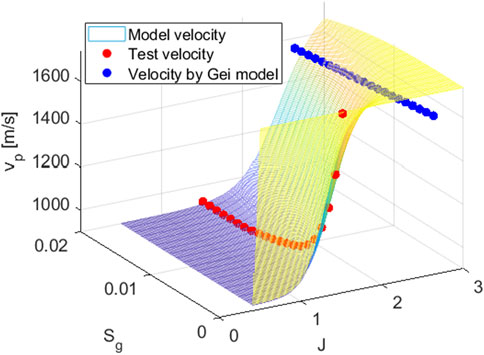
Figure 2. Comparison of model-predicted and measured velocities as functions of $J$ and $S_g$. The surface represents predictions from Equation 13; blue markers correspond to velocities given by Gei’s model (Gei et al., 2022); and red markers represent experimental data from Cheng (2017); Wang et al. (2018).

The red dots in Figure 2 is laboratory test velocity (Cheng, 2017; Wang et al., 2018). The observed decline characteristics of test velocities are predetermined, while the velocity decay pattern in our model can be modulated through factor $J$. This enables us to determine an optimal $J$ parameter through experimental data calibration, thereby accurately simulating the velocity decline characteristics observed in experiments. The optimal parameter is determined by minimizing the error Formula 15.

$Error\left(J\right)=\sqrt{\sum \frac{{\left(v_p^{\mathit{ref}}-v_p\right)}^2}{{\left(v_p^{\mathit{ref}}\right)}^2}}(15)$

Here, $v_p^{\mathit{ref}}$ denotes the measured (test) velocity, and $v_p$ is the predicted (model) velocity. The optimal parameter is determined to be $J=1.51$, as shown in Figure 3, resulting in a minimum error of 5.27$\%$. In contrast, setting $J=1$ increases the error sharply to 55.7$\%$. For reference, the minimum relative error achieved by the Gei model is no less than 24.65$\%$. These results underscore the significantly improved accuracy of the proposed velocity model, with prediction errors reduced to about one-tenth of the conventional approach and substantially lower than those obtained with the Gei model.

Figure 3

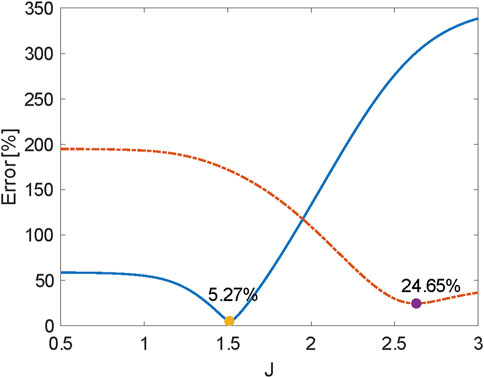
Figure 3. The blue solid line indicates the relative error between model-predicted and measured velocities, while the red dashed line shows the relative error between model-predicted and Gei model velocities. Errors are computed using Equation 15 at eleven $S_g$ values (0–2$\%$) with corresponding $J$ variations.

3.2 Well logging application

This section employs the velocity model (Equation 13) to evaluate free gas saturation in the gas-bearing water layer of well LS-361 at a depth of 1790–1800 m, where the gas saturation can be considered negligible. Well LS-361 is located in the central South China Sea, where the underlying rock is incompletely cemented, similar to the experimental samples. The optimal parameters presented in this paper can be used to perform inversion assessments of free gas saturation.

The calculation process for the velocity model (Equation 13) requires parameters such as the skeleton modulus, consolidation parameter, and the physical properties of the pore fluid, all of which can be obtained from well logging data. In all calculations, the empirical parameter $J$ is set to 1.51 for consistency. The following steps outline the procedure for determining free gas saturation:

• Step 1. Extract the measured velocity, rock modulus, density, and other physical parameters from the well logging data in the pure water layer.

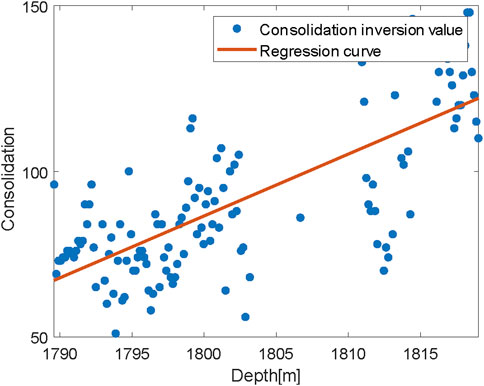
• Step 2. Calculate the model velocity of the pure water layer using the velocity model (Equation 13). Solve for the formation Biot consolidation parameters by minimizing the relative error between the measured velocity and the model velocity.

• Step 3. Use the formation depth as the independent variable and the consolidation parameters obtained in step (2) as the dependent variable to perform regression analysis and calculate the maximum likelihood estimate of the consolidation parameters.

• Step 4. Incorporate the consolidation parameters derived in step (3) into the velocity model (Equation 13), then solve for the free gas saturation by minimizing the relative error between the measured velocity and the model velocity.

The Biot consolidation parameter values for pure water formations are shown in Figure 4, along with the regression line derived from these values. From this regression line, it is evident that as formation depth increases, the Biot consolidation parameter values also increase, a trend that aligns with common sense. The inversion results for the empirical parameter $A$ in the Gei model, based on well log data, indicate that $A$ shows no correlation with formation depth, and its average value is 0.87.

Figure 4

Figure 4. Inversion parameters and regression lines for pure water formations at different depths.

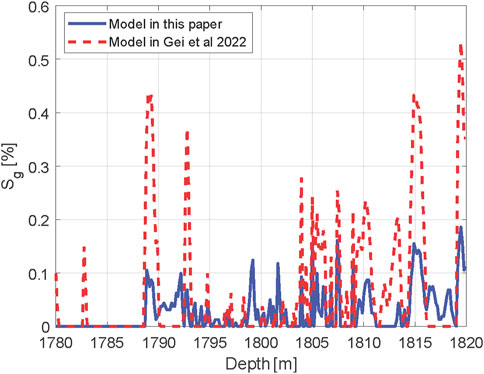
Figure 5 presents a comparison of gas saturation $(S_g)$ profiles predicted by the model proposed in this paper (blue solid line) and the Gei et al. (2022) model (red dashed line) as a function of depth. The Gei model produces substantially higher and more scattered $S_g$ values throughout the interval, characterized by numerous sharp spikes-several exceeding 0.4$\%$-that are largely absent in the results of the present model. This pronounced scatter and overestimation indicate instability and excessive sensitivity to uncertain input parameters in the Gei model. The resulting erratic variations are geologically implausible and stand in stark contrast to the smoother and more consistent $S_g$ distribution obtained with our approach. These findings highlight the limitations of the Gei model for reliable formation evaluation and underscore the improved robustness of the method proposed in this work.

Figure 5

Figure 5. The curve of saturation inversion values varying with formation depth.

3.3 Dissusion

The findings of this study represent a significant advancement in the quantitative evaluation of ultralow free gas saturation in porous marine sediments through acoustic velocity measurements. By embedding a dynamically optimized coupling factor $J$ into the classical Biot framework, the proposed velocity model effectively addresses the pronounced nonlinear attenuation of P-wave velocity observed at extremely low gas saturations $(S_g\le 2\%)$ - a phenomenon that conventional models consistently fail to capture. Experimental validation using laboratory core samples reveals that the reduction in acoustic velocity exhibits a rapid and nonlinear decline as free gas saturation increases, particularly within the critical 0–0.5$\%S_g$ interval. This behavior underscores the dominant influence of microbubble interfacial tension and multiphase coupling mechanisms under ultralow gas saturation conditions.

Sensitivity analyses further highlight the critical role of the optimized parameter $J$, whose sensitivity function exhibits a pronounced peak at ultralow saturations before diminishing-mirroring the abrupt P-wave velocity drop documented in controlled laboratory experiments. This distinct bimodal response substantiates the interpretation that $J$ encapsulates the microscale bubble-fluid-solid interaction mechanisms governing acoustic behavior in dilute gas environments. Calibration of $J$ to an optimal value of 1.51-derived from laboratory measurements-ensures that the proposed model not only provides superior theoretical fidelity but also achieves a remarkable reduction in root mean square velocity prediction error, from 55.7$\%$ to just 5.27$\%$, within the pivotal 0–2$\%S_g$ range.

Field application in the LS-361 well of the South China Sea further affirms the model’s robustness under natural, heterogeneous sediment conditions. The model facilitates high-resolution inversion of free gas saturation down to 0–0.12$\%$, with results exhibiting excellent agreement with well-log observations. Moreover, the observed trend of increasing Biot consolidation parameter $\alpha$ with formation depth reveals the model’s inherent capacity to capture compaction effects-an environmental factor critical in modulating in situ acoustic properties.

Collectively, this work constitutes a methodological breakthrough, providing a rigorous, physics-based framework that quantitatively links acoustic velocity to sub-percent levels of gas saturation, thereby surmounting key limitations of traditional approaches such as linear superposition and static phase assumptions. By enriching the theoretical depiction of nonlinear poroelastic phenomena-particularly those driven by microbubble interfacial effects-the proposed model significantly enhances the ability to detect and quantify subtle geophysical gas signatures and deepens insights into the fundamental multiphase dynamics of marine sediments.

Nonetheless, these results also highlight the need to generalize and validate the approach across a broader spectrum of sedimentary environments. While current parameter calibration relies on laboratory-derived data, future research should pursue multiscale validation by integrating advanced imaging modalities (e.g., CT, MRI) to directly correlate microbubble distributions with acoustic responses, and test the model’s applicability to fine-grained, carbonate-rich, or clay-rich geological settings. Ultimately, the proposed methodology offers a robust platform for improved risk assessment in marine geohazard early warning, gas hydrate exploration, and environmental monitoring of ${\text{CO}}_2$ geological storage.

4 Conclusion

This study provides a systematic solution to the quantitative evaluation of acoustic logging velocities in sedimentary porous media under conditions of ultra-low free gas saturation $(S_g\le 2\%)$, through comprehensive theoretical modeling, parameter sensitivity analysis, and field validation. To address the significant limitations of conventional models-including substantial prediction errors and the inability to accurately capture pronounced nonlinear variations in this saturation regime-a dynamic coupling factor $J$ is introduced within the classical Biot framework. This development enables the derivation of optimized physical parameter expressions, such as apparent fluid density, viscosity, and effective bulk modulus with free gas, all as explicit functions of gas saturation.

Both numerical simulations and laboratory data fitting demonstrate that the proposed model effectively captures the sharp decline in P-wave velocity associated with increasing gas saturation in the 0–2$\%$ range, reducing the prediction error from 55.7$\%$ (typical of conventional methods) to as low as 5.27$\%$. Sensitivity analysis further reveals that the $J$ factor plays a critical role in driving the nonlinear decrease in P-wave velocity, emphasizing the influence of complex mechanisms such as microbubble interfacial tension at ultra-low saturations.

Field application to well LS-361 in the South China Sea further corroborates the practical feasibility of the model, enabling high-resolution inversion of free gas saturation down to 0–0.15$\%$, which shows excellent agreement with calibrated logging data. Altogether, this approach overcomes longstanding challenges in the quantitative identification of acoustic responses in low-gas-saturation sediments and offers a robust foundation for the precise detection of gas layers with sub-percent saturations.

These research findings not only advance the theoretical understanding of multiphase poroelastic mechanisms but also bear substantial scientific and practical significance for the interpretation of weak free gas signals in marine sediments, early warning of gas-related geohazards, and the implementation of environmental safety monitoring.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RS: Conceptualization, Investigation, Funding acquisition, Software, Formal Analysis, Methodology, Writing – original draft, Writing – review and editing. JW: Data curation, Formal Analysis, Validation, Writing – review and editing, Resources, Methodology. ZW: Methodology, Conceptualization, Supervision, Software, Writing – review and editing. XG: Visualization, Project administration, Supervision, Writing – review and editing. LX: Investigation, Visualization, Funding acquisition, Writing – review and editing. JZ: Validation, Data curation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the Key Support Project of Regional Innovation and Development Joint Fund (Grant No. U24A20608), the Major Scientific and Technological Projects of CNPC under Grant (ZD2019-184-001), the National Science Foundation of China (Grant No. 42374152, 41404091), and the Shandong Province Natural Science Foundation (Grant No. ZR2020MD050). The authors declare that this study received funding from CNPC. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

JW is an employee of the Fourth Oil Production Plant, PetroChina Qinghai Oilfield Company, and JZ is an employee of the Processing and Interpretation Center, Sinopec Matrix Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agnew, R. J., and Halihan, T. (2018). Why springs bubble: a framework for gas discharge in groundwater. Groundwater 56 (6), 859–870. doi:10.1111/gwat.12789

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, A. L., and Hampton, L. D. (1980). Acoustics of gas-bearing sediments. ii. measurements and models. J. Acoust. Soc. Am. 67, 1890–1903. doi:10.1121/1.384454

CrossRef Full Text | Google Scholar

Berryman, J. G. (1980). Confirmation of Biot’s theory. Appl. Phys. Lett. 37, 382–384. doi:10.1063/1.91951

CrossRef Full Text | Google Scholar

Best, A. I., Tuffin, M. D. J., Dix, J., and Bull, J. M. (2004). Tidal height and frequency dependence of acoustic velocity and attenuation in shallow gassy marine sediments. J. Geophys. Res. 109, 1–17. doi:10.1029/2003jb002748

CrossRef Full Text | Google Scholar

Biot, M. A. (1956a). Theory of propagation of elastic waves in a fluid-saturated porous solid. i. low frequency range. J. Acoust. Soc. Am. 28, 168–178. doi:10.1121/1.1908239

CrossRef Full Text | Google Scholar

Biot, M. A. (1956b). Theory of propagation of elastic waves in a fluid-saturated porous solid. ii. higher frequency range. J. Acoust. Soc. Am. 28, 179–191. doi:10.1121/1.1908241

CrossRef Full Text | Google Scholar

Biot, M. A. (1962). Generalized theory of acoustic propagation in porous dissipative media. J. Acoust. Soc. Am. 34, 1254–1264. doi:10.1121/1.1918315

CrossRef Full Text | Google Scholar

Chen, J., Hu, G., Bu, Q., Wu, N., Liu, C., Chen, Q., et al. (2023). Elastic wave velocity of marine sediments with free gas: insights from CT-acoustic observation and theoretical analysis. Mar. Petroleum Geol. 150, 106169. doi:10.1016/j.marpetgeo.2023.106169

CrossRef Full Text | Google Scholar

Cheng, P. (2017). Experimental study on acoustic properties of seabed gas charged sand sediments (PhD thesis). University of Science and Technology, AnHui, China.

Google Scholar

Deng, Y., Wang, Y., Zhao, Y., Gu, P., Xiao, J., Zhou, J., et al. (2023). Carbon dioxide storagein China: current status, main challenges, and future outlooks. Earth Sci. Front. 30 (4), 429–439.

Google Scholar

Fei, W., Yi-Wang, H., and Qi-Hang, S. (2017). Effect of gas bubble volume fraction on low-frequency acoustic characteristic of sandy sediment. Acta Phys. Sin. 66 (19), 194302. doi:10.7498/aps.66.194302

CrossRef Full Text | Google Scholar

Gardner, T. N., and Sills, G. C. (2001). An examination of the parameters that govern the acoustic behavior of sea bed sediments containing gas bubbles. J. Acoust. Soc. Am. 110 (4), 1878–1889. doi:10.1121/1.1388005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, Y., Cao, C., Chen, J., Wang, H., Zhang, P., He, J., et al. (2022). Monitoring and research on submarine hydrate mound: review and future perspective. Mar. Technol. Soc. J. 56 (4), 140–162. doi:10.4031/mtsj.56.4.14

CrossRef Full Text | Google Scholar

Gei, D., and Carcione, J. M. (2003). Acoustic properties of sediments saturated with gas hydrate, free gas and water. Geophys. Prospect. 51, 141–158. doi:10.1046/j.1365-2478.2003.00359.x

CrossRef Full Text | Google Scholar

Gei, D., Carcione, J. M., and Picotti, S. (2022). “’Seismic rock physics of gas-hydrate bearing sediments,” in World atlas of submarine gas hydrates in continental margins. Editors M. Jürgen, and B. Christian (Cham: Springer), 55–63.

CrossRef Full Text | Google Scholar

Guangying, Z., and Xiumei, H. (2018). “’The acoustic properties of gassy sediments due to gas-content fluctuations,” in Proceedings of the 10th international conference on wireless communications and signal processing (Hangzhou, China), 1–7. 18–20 October 2018.

Google Scholar

Gurevich, B., and Carcione, J. M. (2022). Attenuation and dispersion of elastic waves in porous rocks: mechanisms and models. Houston: Society of Exploration Geophysicists, 189–234.

Google Scholar

Hongxing, L., Chunhui, T., Fulin, L., and Jianping, Z. (2015). Effect of gas bubble on acoustic characteristic of sediment: taking sediment from east China sea for example. Acta Phys. Sin. 64, 109101. doi:10.7498/aps.64.109101

CrossRef Full Text | Google Scholar

Juntao, M., Liang, L., Al-Hamad, M. F., Van Steene, M., Ma, S. M., and Abdallah, W. (2024). “Aspect-ratio-dependent pore-size distribution from micp measurement,” in International petroleum technology conference (IPTC, 2024), D021S050R007.

Google Scholar

Kong, L., Ma, Y., and Gurevich, B. (2022). Modelling elastic properties of partially saturated porous rocks with aligned fractures. Geophys. J. Int. 230, 2003–2018. doi:10.1093/gji/ggac146

CrossRef Full Text | Google Scholar

Lebedev, M., Toms-Stewart, J., Clennell, B., Pervukhina, M., Shulakova, V., Paterson, L., et al. (2009). Direct laboratory observation of patchy saturation and its effects on ultrasonic velocities. Geophysics 28, 24–27. doi:10.1190/1.3064142

CrossRef Full Text | Google Scholar

Leclaire, Ph., Cohen-Tenoudji, F., and Aguirre-puente, J. (1994). Extension of Biot theory of wave propagation to frozen porous media. J. Acoust. Soc. Am. 67, 1711–1719.

Google Scholar

Lei, X., and Xue, Z. (2009). Ultrasonic velocity and attenuation during co2 injection into water-saturated porous sandstone: measurements using difference seismic to mography. Phys. Earth Planet. Interiors 176, 224–234. doi:10.1016/j.pepi.2009.06.001

CrossRef Full Text | Google Scholar

Leighton, T. G., Dogan, H., Fox, P. D., Mantouka, A., Best, A. I., Robb, G., et al. (2021). Acoustic propagation in gassy intertidal marine sediments: an experimental study. J. Acoust. Soc. Am. 150 (4), 2705–2716. doi:10.1121/10.0006530

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., Wang, X., Su, P., Li, Q., Wan, X., Li, J., et al. (2024). Identification of interbedded gas hydrate and free gas using amplitude versus offset forward modelling. Geophys. Prospect. 72 (4), 1536–1552. doi:10.1111/1365-2478.13402

CrossRef Full Text | Google Scholar

Liu, L. Y., Xie, G., Ding, J., Liu, B., Xing, D., Ren, N., et al. (2021). Microbial methane emissions from the non-methanogenesis processes: a critical review. Sci. total Environ. 806 (4), 151362. doi:10.1016/j.scitotenv.2021.151362

PubMed Abstract | CrossRef Full Text | Google Scholar

Lo, W.-C., Sposito, G., and Majer, E. (2005). Wave propagation through elastic porous media containing two immiscible fluids. Water Resour. Res. 41, 1–20. doi:10.1029/2004wr003162

CrossRef Full Text | Google Scholar

Malakhova, T. V., Budnikov, A. A., Ivanova, I. N., Khurchak, A. I., Khurchak, A. P., and Krasnova, E. A. (2024). Passive acoustic monitoring for seabed bubble flows: case of shallow methane seeps at Laspi Bay (Black Sea). J. Acoust. Soc. Am. 156 (6), 4202–4216. doi:10.1121/10.0034605

PubMed Abstract | CrossRef Full Text | Google Scholar

Mu, Y., Hu, Z., Guo, Q., Duan, X., and Chang, J. (2024). Impacts of water saturation on gas-bearing property and recovery ratio of marine shale. Energy & Fuels 38 (4), 3089–3104. doi:10.1021/acs.energyfuels.3c04620

CrossRef Full Text | Google Scholar

Plona, T. J., and Johnson, D. L. (1980). “Experimental study of the two bulk compressional modes in water-saturated porous structures,” in Proceedings of the 1980 ultrasonics symposium, 868–872. Boston MA, United States, 05-07 November 1980.

Google Scholar

Santos, J. E., Douglas, J., Corberó, J. M., and Lovera, O. M. (1990). A model for wave propagation in a porous medium saturated by a two-phase fluid. J. Acoust. Soc. Am. 87 (4), 1439–1448.

CrossRef Full Text | Google Scholar

Santos, J. E., Ravazzoli, C. L., Gauzellino, R. M., Carcione, J. M., and Cavallini, F. (2004). Simulation of waves in poro-viscoelastic rocks saturated by immiscible fluids: numerical evidence of a second slow wave. J. Comput. Acoust. 12 (1), 1–21. doi:10.1142/s0218396x04002195

CrossRef Full Text | Google Scholar

Shi, R., Wei, Z., Ge, X., Qi, L., and Yao, Z. (2024). Numerical simulation of hydrate reservoir based on three-phase Biot velocity-stress wave equaiton. J. China Univ. Petroleum Ed. Nat. Sci. 48 (3), 57–64.

Google Scholar

Tóth, Z., Spiess, V., Mógollon, J. M., and Jensen, J. B. (2014). Estimating the free gas content in baltic sea sediments using compressional wave velocity from marine seismic data. J. Geophys. Res. Solid Earth 119, 8577–8593. doi:10.1002/2014jb010989

CrossRef Full Text | Google Scholar

Tŕehu, A. M., and Flueh, E. R. (2001). Estimating the thickness of the free gas zone beneath hydrate ridge, Oregon continental margin, from seismic velocities and attenuation. J. Geophys. Res. 106, 2035–2045. doi:10.1029/2000jb900390

CrossRef Full Text | Google Scholar

Wang, J., Wu, S., Zhao, L., Wang, W., Wei, J., and Sun, J. (2019). An effective method for shear-wave velocity prediction in sandstones. Mar. Geophys. Res. 10, 655–664. doi:10.1007/s11001-019-09396-4

CrossRef Full Text | Google Scholar

Wang, Y., Huang, L., Wang, Y. L., and Cheng, P. G. (2018). “Improved Anderson Hampton acoustic velocity model for marine sandy gas-bearing sediments,” in Proceedings of the IOP conference series: materials science and engineering (Nanchang, China), 423. 25–27 May 2018.

Google Scholar

Zhan, L., Kang, D., Lu, H., and Lu, J. (2022). Characterization of coexistence of gas hydrate and free gas using sonic logging data in the shenhu area, south China sea. J. Nat. Gas Sci. Eng. 101, 104540. doi:10.1016/j.jngse.2022.104540

CrossRef Full Text | Google Scholar

Zhou, J., Wang, X., Zhu, Z., Jin, J., Song, H., Su, P., et al. (2022). The influence of submarine landslides on the distribution and enrichment of gas hydrate and free gas. Chin. J. Geophys. (in Chinese) 65 (9), 3674–3689.

Google Scholar

Zhou, S., Li, Q., Zhu, J., Zhou, Y., Zhao, C., and He, Y. (2024). Consideration on co2 marine storage and exploration of new paths. Natural Gas Industry 44 (4), 1–10.

Google Scholar

Zhu, H., Tan, Y., Chen, Q., Wang, L., Guanghua, Y., and Cao, H. (2015). The effects of gas saturation on the acoustic velocity of carbonate rock. Journal of Natural Gas Science and Engineering 26, 149–155. doi:10.1016/j.jngse.2015.06.013

CrossRef Full Text | Google Scholar