Coal-bed methane migration analysis and numerical model construction of fractured coal body based on multi-field coupling conditions

As an associated resource of coal, coal-bed methane (CBM) has the advantages of high quality and cleanliness, and its development and utilization are of great significance for sustainable development. Deep CBM mining is a multi-field coupling process affected by multiple factors. Therefore, a theoretical and numerical model of fractured coal was established in this paper, and the interaction relationship among the stress of coal, seepage, and diffusion field of gas was explored. Then, the migration laws of coal-bed methane under different circumferential pressure conditions were investigated. The results showed that the stress field of coal affected the diffusion and seepage of CBM by changing the porosity and permeability, and the migration of CBM changed the effective stress and adsorption expansion stress, thus affecting the stress field of coal. Under axial loading, the distribution of Darcy velocity in fractured coal was divided into three regions: fast decrease (in the depth of 0–0.022 m), slow decrease (in the depth of 0.022–0.06 m), and stable stage (more than 0.06 m) from the top boundary to the bottom boundary of the model. With the change of time, the pressure in the three stages decreased from 200 Pa to 0 Pa, and the Darcy velocity decreased from 4.5 × 10⁻² m/s to 0 m/s. Along the vertical direction of the model, the Darcy velocity in the fissure and matrix decreased, and the decrease rate of the fissure is faster than that of the matrix. Under a three-dimensional load, the Darcy velocity of the same position shows an approximate linear change with the pressure increase. Finally, based on the difference between the fissure Darcy velocity in uniaxial and three-dimensional conditions, the dominant extraction area of model CBM was determined. The research results can further enrich the theory of gas migration law in coal and improve gas extraction efficiency. Clarifying the principle of gas–solid coupling and increasing the extraction rate will help supplement the supply of clean energy, reduce greenhouse gas emissions, achieve safe coal mine production, and promote environmental protection and sustainable development.

1 Introduction

With the impact of the imbalance between supply and demand of conventional oil and gas resources, people are increasingly focusing on the development of green and efficient unconventional energy (Chai et al., 2021; Zhao et al., 2025; Li et al., 2024). As a new type of energy, coal-bed methane (CBM), characterized by large reserves, wide range, and cleanliness, has received extensive attention from scholars and has become an important research topic (Yuan et al., 2024; Xu et al., 2023). The main carrier of CBM is the deep coal seam. As a dual medium system, it mainly includes matrix pores and fissures, in which the gas is mainly stored in matrix pores, and the fissures are the main channel for gas transportation (Chu et al., 2024; Wang et al., 2024). The study of the gas transport characteristics of a fissure coal body is of great theoretical and practical significance for the efficient extraction of coal-bed methane.

The gas flow in the coal body results from multiple fields, such as the stress field, the gas diffusion field, and the gas seepage field. (Hu et al., 2022; Ji et al., 2024). The establishment of a multi-field coupling model of coal is helpful in evaluating coal deformation and CBM exploitation and promoting the efficient utilization of coal seam gas (Cao et al., 2016; Tian et al., 2022). In the process of research, some scholars have established a multi-field coupling model of the stress field, damage field, gas diffusion field, and seepage field of the coal body and analyzed the influence of stress changes on the pressure relief damage of the coal seam and gas extraction (Liu et al., 2017; Lu et al., 2019). Lin et al. (2016) established a solid–gas coupling model based on single-component gas transport considering the coal deformation, fissure gas flow, and permeability dynamics and studied the relationship between the adsorption constants, permeability, and gas pressure. Kong et al. (2017) considered the fracture and pore gas pressure, established the two-pore seepage model, and analyzed the coupling effect of stress and gas pressure in coal mining and coal-bed methane mining. Zhang T. et al. (2024) analyzed the oil and gas migration law of pore fractures and monitored and analyzed the interaction between stress, pore, and gas migration affected by mining activities. Xue et al. (2021) established a hydraulic coupling model based on the damage characteristics of coal seam and the interaction between coal deformation and gas seepage during gas fracturing.

In the process of coal-bed methane storage, the fluid channel fracture-pore undergoes a complex coupling process, and in the fractured coal body, the single fracture, as the basic unit of the fracture network, is the basis for exploring its seepage law (Yu et al., 2022; Hou et al., 2022). Nemoto et al. (2009) carried out rough fracture seepage experiments and found a relationship between confining pressure and fracture permeability. Guo et al. (2022) used 3D scanning techniques and COMSOL software to create fracture models with different contact rates. Zhang et al. (2022) established a numerical simulation method for the stress seepage coupling test of rough single cracks. Arianfar et al. (2021) carried out a numerical study of the nonlinear fluid flow behavior in natural fractures in the vicinity of porous media.

Because the change of permeability under changing stress is much larger than that of the matrix, the influences of matrix gas migration and seepage on fractures are ignored in most studies. Gas transport in the matrix is a diffusion process, which satisfies Fick’s law of diffusion, but some scholars believe that gas transport in the coal matrix is a seepage process (Qin et al., 2023; Mostafa et al., 2023). Based on the previous research results, this paper considers that gas transport in the matrix is a process dominated by diffusion and supplemented by seepage and, therefore, establishes a coupling mechanism that considers the matrix–fracture interaction and the influence of coal deformation. Using COMSOL numerical simulation software, we establish a gas flow model for a single-fracture coal body and further study the fluid flow law and pressure distribution in the fissure of the fractured rock body and the matrix under different peripheral rock pressures. The research results can further enrich the theory of gas transportation law in a coal body.

2 Multiphysics coupling theory of CBM extraction

2.1 Model simplification

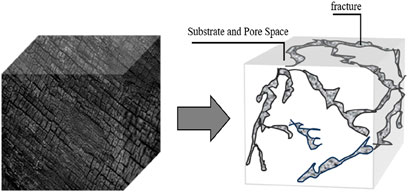
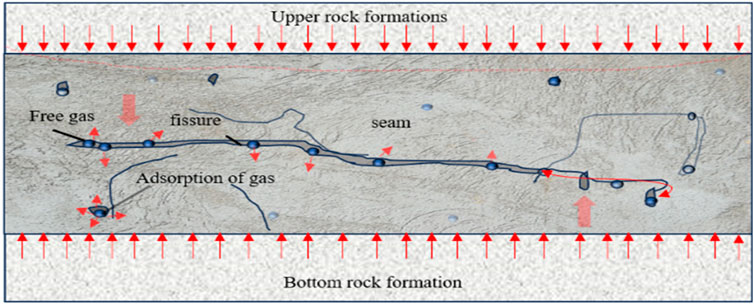
The complexity of the structure of the coal body itself and the variability of the storage conditions lead to the complexity of the gas in the extraction process. It is difficult to accurately describe gas flow in a coal body under large-scale conditions, and it is even more difficult to describe the gas flow in the microscopic pore fissures. Therefore, scholars use a simplification process to examine gas diffusion and seepage according to their importance in the discussion (Zhang K. et al., 2024). The coal body structure is simplified into pure diffusion of a uniform pore model, pure seepage of a uniform fissure model, and diffusion and seepage at the same time in a dual-media model. At present, the pore–fissure dual-media model is recognized by a large number of scholars, as shown in Figure 1.

Figure 1

Figure 1. Pore–fracture dual medium model.

The gas in the coal body is endowed with an adsorption state and free state in the pores and fissures of the matrix of the coal body. Before the original stress is changed and the coal body is destroyed, the free state gas and adsorption state gas in the fissures and matrix are in a dynamic equilibrium state, and there is a mass exchange from the microscopic point of view, but it does not appear on the macroscopic point of view. Influenced by mining or other factors, this original state is destroyed, and the stress is redistributed. The free gas in the coal body fissure system starts to flow under the effect of the stress difference between coal seams; the adsorbed gas in the matrix pores desorbs and diffuses under the effect of the difference in the concentration of gas content in coal seams. The seepage rate of free gas in the fissure is much larger than the diffusion rate of adsorbed gas in the pore. The matrix gas pressure is larger than the fissure gas pressure, and the adsorbed gas in the matrix pore must be desorbed and diffused into the fissure so there is a mass exchange between the matrix pore and the fissure (Liu et al., 2024).

The gas desorption, diffusion, and seepage processes in the coal body are not affected by a single factor, but the coupling between the stress field, gas seepage field, and gas diffusion field causes a series of reactions. Therefore, based on the dual-media model of coal body and isotropy and ignoring the influence of temperature on gas transport, the dynamic change model of gas transport under multi-field coupling is established, as shown in Figure 2.

Figure 2

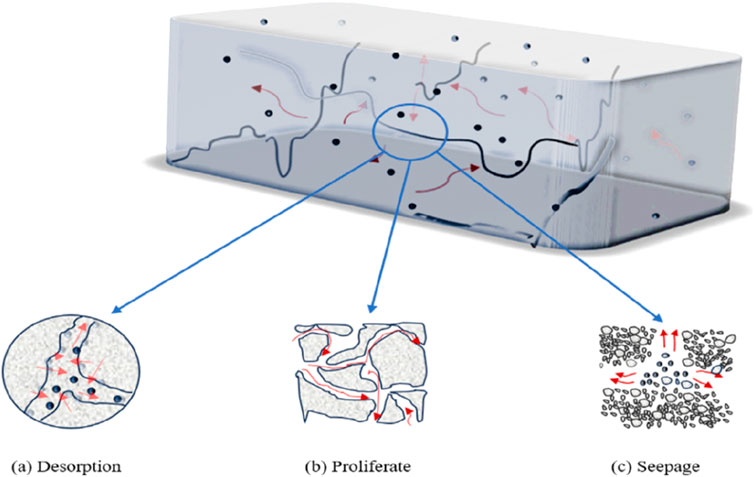
Figure 2. Simplified model of gas flow in fissured coal body. (a) Desorption. (b) Proliferation. (c) Seepage.

2.2 Analysis of the coupled action of deformation and diffusion fields

The inner surface of pores and fissures is the storage location of adsorbed gas, and adsorbed gas, accounting for more than 90% of the total gas content, does not transfer pore pressure. The transportation of adsorbed gas obeys Fick’s law of diffusion. The free gas mainly exists in the fissures and can transfer pore pressure, and the seepage process of free gas obeys Darcy’s law. After the adsorption of gas, the surface tension of coal particles decreases, and the volume of coal particles expands, which in turn leads to the volume expansion of the coal skeleton (Kong et al., 2016).

Coal body adsorption of gas transfers pore pressure, surface tension decreases, and volume expansion occurs. Based on the assumption of isotropy, the coal body adsorption expansion strain can be (Hao et al., 2022) described by Equation 1:

${\epsilon }_{P\hspace{0.5em}=\hspace{0.5em}\frac{2a{p}_{s}RT{K}_Y}{3V_m}\mathit{ln}\left(1+bp\right)},(1)$

where $p_s$ is the density of coal, kg/m³; $V_m$ is the molar volume of gas, $m^3/mol$; $a$ is the adsorption constant; b is the adsorption equilibrium constant of coal.

When the coal body gas pressure decreases and the effective stress increases, the coal body skeleton is compressed, the matrix shrinks, the matrix permeability decreases, and the gas diffusion process is affected by the influence of the diffusion process. The gas pressure in the coal body produces changes, which affect the coal body stress balance and coal body deformation.

The effect of the diffusion field on the deformation field of the coal body is mainly manifested in the decrease of surface energy and compressive strength of the coal body after coal adsorption of gas, and the larger the gas pressure is, the more the deformation strength of coal decreases with the decrease of surface free energy. The experiments show that the peak strength, modulus of elasticity, and residual strength of gas-containing coal decrease linearly with the increase in gas pressure (Yang et al., 2019). On the one hand, the gas reduces the surface energy of the pore cleavage, and on the other hand, it generates an air wedge effect in the coal body, which reduces the effective stress, decreases the cohesion between matrices, and then weakens the mechanical strength of the gas-containing coal.

2.3 Analysis of the coupled action of diffusion and seepage fields

The driving force for the diffusion of gas in the coal body is the difference in gas-phase gas concentration between the matrix of the coal body and the fissure system, and the matrix-adsorbed gas continuously desorbs and diffuses during gas flow to ensure the continuity of the seepage movement as a source of internal mass for the fissure seepage (Su et al., 2018).

The mass exchange between the coal matrix and the fracture system can be expressed as Equation 2:

${\mathit{Q}}_{\mathit{s}}=\mathit{D}{\mathit{\sigma }}_{\mathit{c}}\left({\mathit{C}}_{\mathit{m}}-{\mathit{C}}_{\mathit{f}}\right),(2)$

where $Q_S$ is the mass exchange rate per unit volume of coal matrix and fissure system, kg/(m³∙s); D is the gas diffusion coefficient, m²/s; ${\sigma }_C$ is the matrix shape factor, m⁻²; $C_m$ is the gas-phase gas concentration in the matrix, kg/m³; $C_f$ is the gas-phase gas concentration in the fissure, kg/m³.

The matrix system and the fissure system are their respective positive and negative mass sources, and according to the law of conservation of mass, the rate of mass exchange between the matrix system and the fissure system is equal to the amount of change in the mass of the matrix with time, as shown by Equation 3 (Liu J. et al., 2015):

$\frac{\partial m_m}{{\partial }_t}=-\frac{M}{\tau RT}\left(P_m-P_f\right)(3)$

2.4 Analysis of the coupled action of seepage and deformation fields

Gas seepage movement in a coal seam is a complex process. The interaction between coal body structure, coal body deformation, adsorption deformation, etc., will affect the seepage process, and the effect of stress on gas seepage mainly lies in the fact that the compression deformation of the skeleton will change the parameters of the coal body, such as porosity, permeability, and gas pressure.

2.4.1 The role of stress on gas seepage

Gas seepage in the coal body mainly exists in the fracture system, while adsorbed gas is mainly endowed in the microporosity. Stress changes lead to changes in the porosity and permeability of the coal body, which in turn affects the gas seepage rate. Based on the previous research results, the porosity of the coal body can be expressed as Equation 4 (Pan and Connell, 2012).

$d\varnothing =\frac{1}{K}\left(\alpha -\varnothing \right)\left(d\overline{\sigma }+dp\right),(4)$

where K is the bulk modulus; $\overline{\sigma }$ is the average value of the total stress; α is the effective stress coefficient or Biot coefficient, 0 ≤ α ≤ 1, p is the gas pressure, MPa; and ∅ represents the porosity, defined as the ratio of pore volume to total volume.

Assuming that porosity and permeability satisfy the cubic law, the permeability equation is expressed by Equation 5:

$k=k_0{\left(\varphi /{\varphi }_0\right)}^3,(5)$

where $k$ is the permeability at porosity $\varphi$ and $k_0$ is the initial permeability; $\varphi$ and ${\varphi }_0$ are the porosity and initial porosity of the coal, respectively.

The process of gas seepage in a coal seam can be described by Equation 6, Darcy’s law:

$q_g=\frac{k}{\mu }\nabla p,(6)$

where $q_g$ is the Darcy seepage velocity, m/s; $\mu$ is the dynamic viscosity coefficient of the gas, $Pa·s$; $p$ is the gas pressure, $MPa$.

2.4.2 The role of gas seepage on stresses

The stresses acting in the coal seam are mainly two kinds: the total stress acting on the porous medium and the pore pressure of the gas on the pore wall of the coal seam. Similarly, the deformation of a coal body includes two basic deformation mechanisms. One is the deformation of the coal body caused by the deformation of solid skeleton particles, that is, the deformation of the body, which is generally regarded as the recoverable elastic deformation; the other is the deformation generated by the relative displacement between the skeleton particles, that is, the deformation of the structure, which is generally regarded as the permanent plastic deformation.

In a fluid-filled porous media pore space, the fluid pressure is distributed in the pore surrounding according to the basic theory of fluid mechanics. When external force is applied, the saturated–unsaturated porous media skeleton will be deformed, and the fluid in the pore and fissure system will flow (Ahamed et al., 2021). The deformation of the coal body is produced by the joint action of external force and pore pressure, which establishes the coupling relationship between the seepage field and the stress field of single-phase fluid flow.

The concept of effective stress was first proposed by Terzaghi and later demonstrated by Skempton to be accurate in engineering. Terzaghi’s effective stress principle can be expressed as Equation 7 (Liu Q. et al., 2015).

$\dot{{\sigma }_{ij}}={\sigma }_{ij}-p{\delta }_{ij},(7)$

where ${\sigma }_{ij}^{\prime }$ is the effective stress, MPa; ${\sigma }_{ij}$ is the total stress, $MPa$; ${\delta }_{ij}$ is the Kronecker function.

When the fluid flows through the pore space, the pore pressure is uniformly distributed around the pore space, and the increase in pore pressure produces compressive strain on the coal particles. Based on the assumption of isotropy, the line compressive strain produced by the gas pressure is expressed as Equation 8:

${\epsilon }_p=-\frac{K_Y}{3}\left(p-p_0\right),(8)$

where $K_Y$ is the volume compression factor, MPa⁻¹; $p_0$ is the initial gas pressure, MPa.

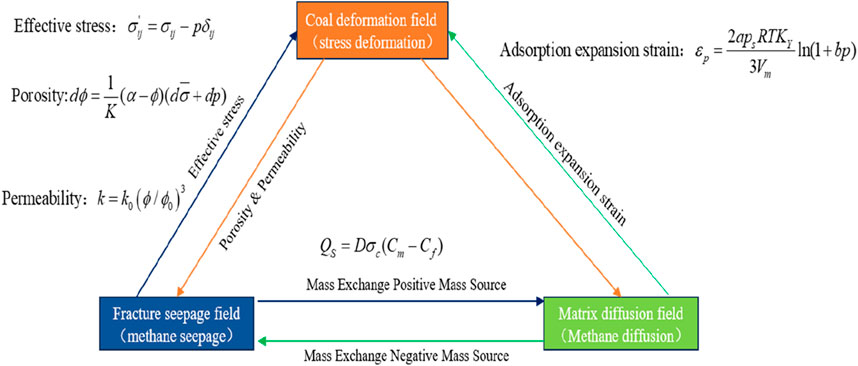
The cross-coupling relationships between the gas seepage field, diffusion field, and deformation field are shown in Figure 3.

Figure 3

Figure 3. Cross-coupling relationships.

Coal body stress changes act on the skeleton, matrix, and fissure permeability changes, affecting methane seepage and diffusion processes; methane acts on the fissure and pore walls during the flow process, generating pore pressures and peripheral rock stress phases, and at the same time, mass exchange between matrix pores and fissures, and methane adsorption/desorption will change the mechanical strength of the coal body.

In summary, the transportation characteristics of gas in the coal body must consider the coupling effect between multiple fields and establish the coupling effect relationship between the deformation field–seepage field–diffusion field of the coal body, as shown in Figure 4.

Figure 4

Figure 4. Flow–solid coupling interaction mode between coal and gas.

The theoretical framework developed in this section provides the foundation for the numerical model presented in Section 3. By discretizing and solving the governing equations, we can simulate the complex interactions among the deformation, diffusion, and seepage fields under realistic conditions.

3 Numerical analysis of CBM extraction

Gas transport in the coal body is a complex multi-phase coupling process, assuming that the flow of gas in the coal body is an incompressible and isothermal process. We use COMSOL Multiphysics software based on the fissure–porosity dual–media model to establish a fissure gas seepage model and add the solid mechanics and Darcy seepage of the two physical fields to study the change of pressure and Darcy seepage velocity in the fissure and matrix under different pressures.

The numerical model presented in this section is based on the theoretical framework described in Sections 2.2 and 2.3. The governing equations for gas adsorption, diffusion, and seepage, as well as the stress-deformation relationships, are discretized and solved using the finite element method in COMSOL Multiphysics. This approach allows us to simulate the coupled multiphysics processes under realistic boundary and initial conditions, providing insights into the behavior of fractured coal under different pressure regimes.

3.1 Geometric modeling and boundary conditions

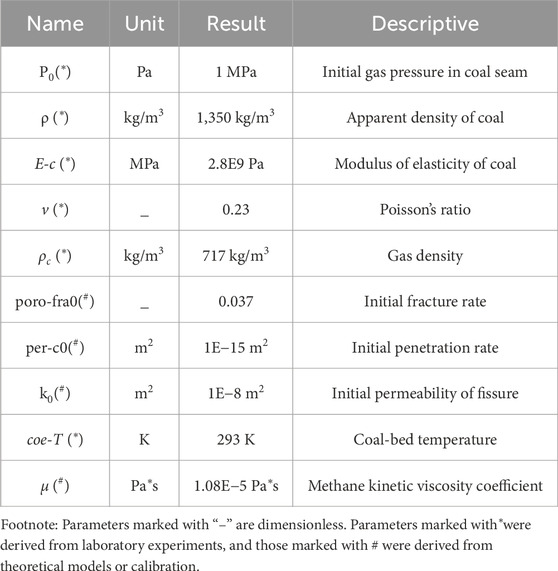
The influencing factors of gas seepage in a fissured coal body are complex and affected by surrounding rock pressure, ground stress, temperature, geological conditions, and the structural characteristics of the fissure. The fissure itself does not have regular geometric characteristics, but to simplify the fissure for the convenience of research, ignoring the influence of fissure opening and fissure roughness on gas seepage, a rectangular (0.1 m × 0.05 m) area is used to simulate the coal matrix. The intermediate area formed by dividing the rectangle with two line segments is used to simulate the fissure. The two form a joint to simulate the gas transport law of a fissured coal body, as shown in Figure 5. The initial gas pressure p₀ of the coal seam is 1 MPa, the apparent density of coal is 1,350 kg/m³, and the gas density is 717 kg/m³. The specific parameters are shown in Table 1.

Figure 5

Figure 5. Geometric model boundary condition setting.

Table 1

Table 1. Numerical model parameters and their sources.

In the Darcy seepage field, the choice of adding fissure flow, the model on the left and right sides of the no-flow boundary, the top of the pressure inlet boundary, the bottom of the outlet boundary, in the physical field of solid mechanics. The bottom of the fixed constraints is set on the top of the boundary load, the left and right sides of the free boundary, and the top and the left and right sides of the different boundary loads, respectively, to study the law of the transport of the gas under different stress cases, as shown in Figure 5.

The distribution and size of fissures in the coal body are not uniform, and the flow patterns of fluids in large fissures and microfissures are different. According to the experiments and the study of the gas movement law, the flow of gas in the fissures can be regarded as a linear flow, which follows Darcy’s seepage law as expressed by Equation 9 (Kong et al., 2017):

$\frac{\partial }{{\partial }_t}\left({\epsilon }_p\right)+\nabla ·\left(\rho u\right)=Q_{m.}(9)$

Fluid flow in a fissure follows the most basic conservation laws, that is, conservation of mass, conservation of momentum, and conservation of energy, and can be described by the Navier–Stokes equations (Kong et al., 2021) as expressed by Equation 10:

$\frac{\partial u}{\partial t}+\left(u·\nabla \right)u=F-\frac{1}{\rho }\nabla p+\frac{\mu }{\rho }{\nabla }^{2}u,(10)$

where u-flow rate fitness; t-time; F-volume force; fluid density; fluid viscosity; pressure gradient.

The transient governing equations for the physical field of solid mechanics are expressed by Equation 11:

$0=\nabla ·s+F_V(11)$

The equation used in this study is implemented in the COMSOL Multiphysics software and is based on the theoretical framework of Darcy’s law for fluid flow.

The mechanical model is solved in two stages. In the first stage, the coal deformation due to applied stresses is calculated and removed to establish the equilibrium state of the coal matrix. In the second stage, the methane flow simulation is initialized, and the coupled mechanical and flow processes are solved iteratively. This approach ensures a realistic approximation of the coal seam behavior under stress and gas flow conditions.

3.2 Mesh division and solution setup

Based on the geometrical model constructed, the mesh dissection criteria, and realistic requirements of physics, the choice was made to apply the sequence type model of user-controlled networks and to mesh the model with a free triangle network using the division tool module in COMSOL Multiphysics. In the cell size, due to the simplicity of the structural model, the choice was made to be more refined, and the model was constructed using a free triangular network, resulting in 2,166 mesh domains. The transient study was chosen to be added to study the transient change rules of gas transport and pressure in the fractured coal body under the action of multi-field coupling.

3.3 Results

3.3.1 Gas transportation laws of split coal bodies under uniaxial loads.

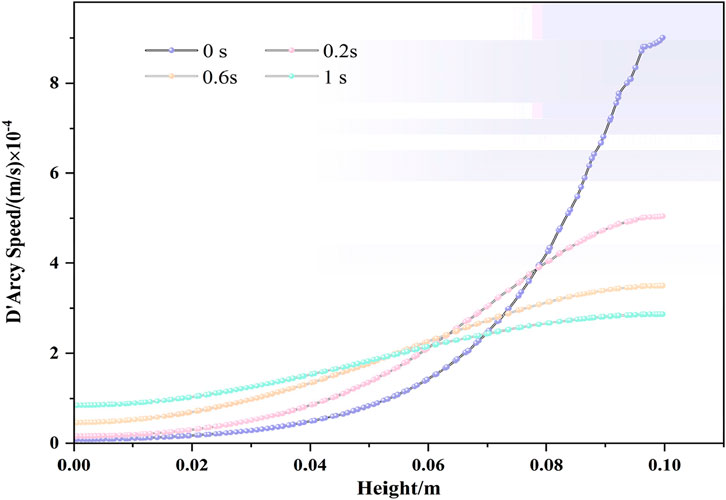
The results of the gas transport solution for the coal body of the rift under uniaxial loading are shown in Figure 6. Under the initial conditions, that is, t = 0 s, the gas in the matrix on both sides of the fissure flows from the matrix to the fissure, the maximum Darcy velocity appears at the top of the fissure, the gas flow rate distribution is more uniform, and there is no obvious difference in the flow rate of the various regions. At t = 0.2 s, the gas in the matrix on both sides of the fissure flows to the fissure, the gas flow rate regional distribution is obvious, and the fissure will be divided into three changing regions from the top to the bottom of the fissure in turn. It will be divided into a fast-changing region and a slow-changing region according to the change of the Darcy velocity. The maximum Darcy velocity occurs in the fast change region, and the streamline distribution has obvious changes compared with the initial moment. When t = 0.6 s, the gas in the matrix on both sides of the fissure flows to the fissure, the distribution of the gas flow rate region is obvious, and the first region and the second region expand along the fissure to the bottom of the coal body. The streamline is more dense. When t = 1 s, the gas in the matrix flows to the fissure, and the gas flow rate zoning is obvious.

Figure 6

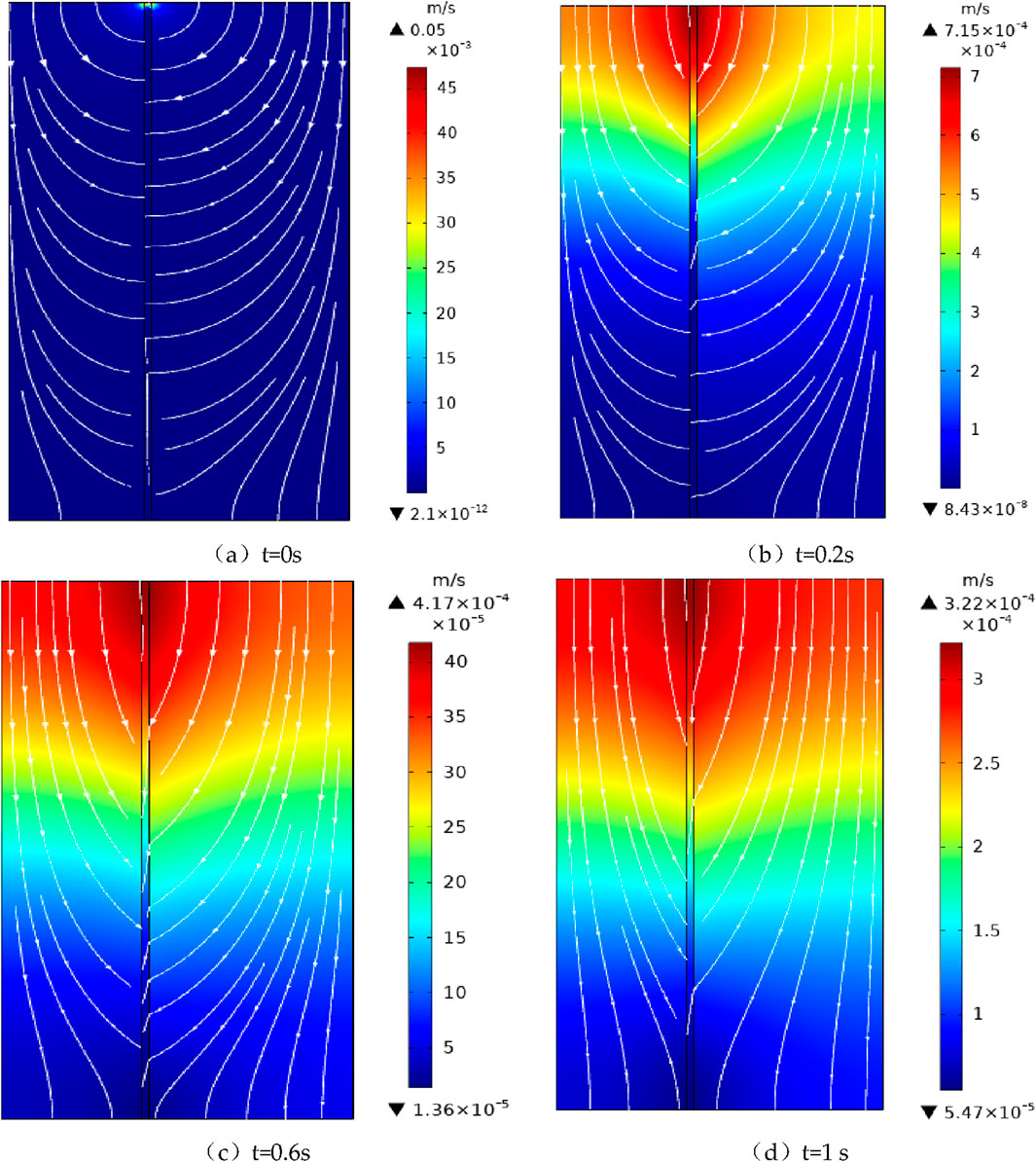
Figure 6. Darcy velocity field and streamline distribution. (a) t = 0 s. (b) t = 0.2 s. (c) t = 0.6 s. (d) t = 1 s.

At the initial moment, the coal body stress is in equilibrium, and the top of the fissure is the starting point of seepage. With the seepage movement of free gas in the fissure, the concentration difference between the gas in the matrix pores and the fissure is generated, and the adsorbed gas in the matrix is desorbed and diffused to the fissure through the matrix pores. When the top load is suddenly added to the coal body, the original stress balance is broken, and with the flow of time, the coal body is compressed along the bottom, the skeleton is deformed, and the matrix and fissure permeability changes, affecting the seepage flow of the coal body, which is manifested in the change of the fluid flow density. The pressure difference of the fissure gas increases, and the fissure seepage velocity increases, which is specifically expressed in the change of the three regions of the Darcy velocity. The increase in the seepage velocity changes the concentration of the matrix and the fissure gas. The increase of seepage velocity changes the difference between matrix and fissure gas concentrations, the matrix gas desorption and diffusion, and constantly replenishes the gas consumed by fissure seepage, which is specifically shown in the three regions of Darcy velocity change over time along the fissure from the top to the bottom of the expansion.

To study the variation of gas seepage velocity and pressure in the fissure with time, we choose to add a one-dimensional truncation line in the model, and the results are shown in Figure 7. In Figure 7, the pressure change and Darcy velocity change have the same trend at different moments, and the model surface pressure and Darcy velocity reach the maximum at the moment of t = 0. With the increase of fissure depth, the pressure and Darcy velocity decreased sharply to a certain value and then stabilized, and then changed linearly with the increase of fissure depth. At t = 0.2 s, the pressure in the fissure decreased sharply at first, then decreased slowly, and then stabilized, and the Darcy velocity decreased slowly until stabilized. At t = 0.6 s and t = 1 s, the fissure pressure changed from linear to nonlinear with the increase of fissure depth. The Darcy velocity changed to nonlinear, and the pressure changed to nonlinear. Finally, the Darcy velocity decreased slowly.

Figure 7

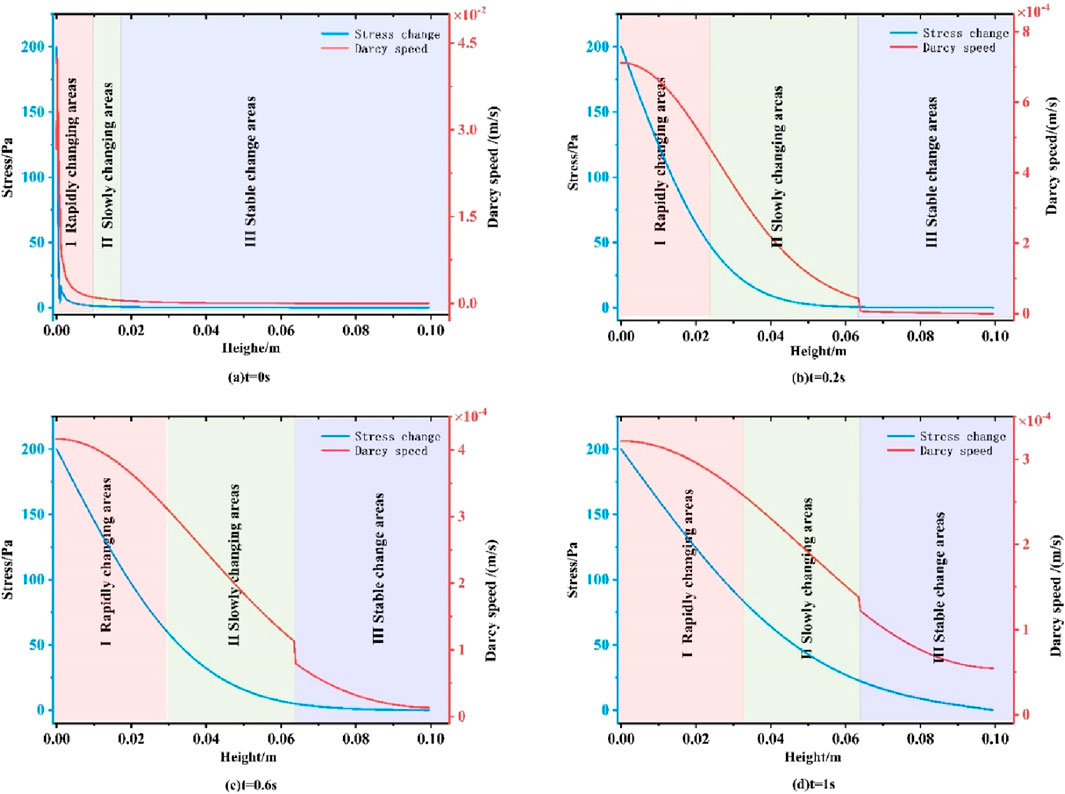
Figure 7. Variation of pressure and Darcy’s velocity in the fissure at different moments. (a) t = 0 s. (b) t = 0.2 s. (c) t = 0.6 s. (d) t = 1 s

At different moments, the gas pressure inside the fissure decreases with the increase of depth, and the decreasing trend of pressure gradually becomes slower with the increase of time. The load is applied to the top of the model, the bottom is fixed, the matrix is deformed, and the gas pressure inside the coal body changes from equilibrium to regular change at the initial moment, which is the reaction and action time of the coal body being compressed and deformed and the pressure change. With the increase of time and depth, the load action decays with the interaction of the gas pressure, the surrounding rock, and the fluid flow.

The variation of the Darcy velocity of gas flow in the matrix is shown in Figure 8. At different moments, the Darcy velocity of gas flow in the matrix decreases with the increase of depth. Among the three regions of Darcy velocity variation, the Darcy velocity of region Ⅰ varies rapidly with the increase of depth, the Darcy velocity of region Ⅱ decreases slowly with the increase of depth, and the Darcy velocity of region Ⅲ stabilizes in the region of the variation with depth and time.

Figure 8

Figure 8. Variation of Darcy’s velocity in the substrate at different moments.

We chose to add the transverse intercept line in the model, and the results are shown in Figure 9. The gas pressure in the matrix decreases along the direction of the fissure. The gas pressure in the fissure is lower than that of the matrix on both sides and increases simultaneously in the fissure and the matrix with the increase of time. The gas in the matrix is continuously desorbed, the free gas increases, and the intermolecular collision increases. With the top loading, the skeleton is deformed, and the internal pressure must be released. The pressure in the fissure is obviously different from the top to the bottom, but at the same level, the pressure in the fissure is almost the same, so there is a gas pressure difference between the matrix and the fissure. As a result, the gas flows continuously from the matrix to the fissure until it reaches an equilibrium.

Figure 9

Figure 9. Variation of pressure in the model at different moments.

3.3.2 Gas transportation laws of split coal bodies under three-dimensional loads

The uniaxial load makes it difficult to simulate the stress of the fractured coal body in a real situation, so the fracture model is chosen to add a three-dimensional load. The results indicate that the fracture seepage starts from the top of the fracture, and the gas flow rate in the fracture shows three obvious change areas. With the change of time, the three change areas change along the fracture to the bottom of the fracture, and the substrate on the two sides of the fracture has the same change trend but at the same horizontal position. However, at the same horizontal position, the gas flow rate in the fissure is larger than the gas flow rate in the matrix. The gas in the matrix flows toward the rift, the streamline density increases, and the range of variation of Darcy’s velocity increases compared with the uniaxial load. The gas pressure in the fissure is smaller than that in the matrix, the gas flow rate in the fissure decreases with depth, and the change time is shorter than that of uniaxial loading.

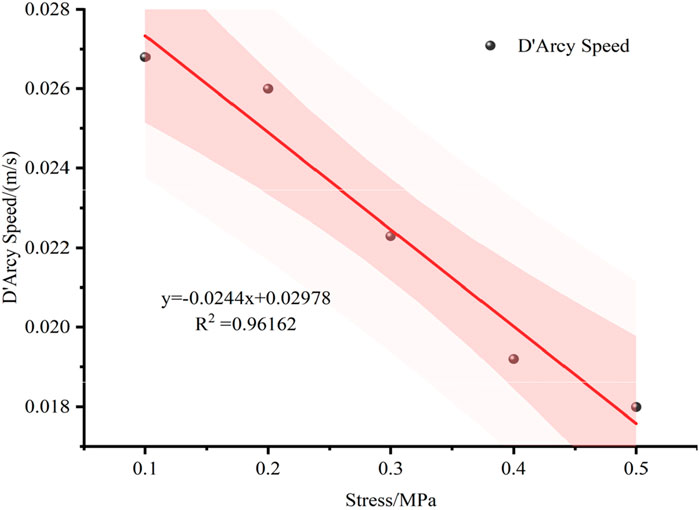
In the model fissure, we choose to add a one-dimensional intercept line, as shown in Figure 10 for the three-dimensional load and uniaxial load Darcy velocity difference. In the initial moment, the uniaxial load under the action of the fissure gas seepage Darcy velocity is greater than the three-dimensional load under the action of the fissure gas Darcy seepage velocity. As the depth increases, the three-dimensional load under the action of the fissure Darcy velocity increases, and the difference between its and the uniaxial load under the action of the Darcy velocity is constantly growing. With the change of time, at t = 0.2 s and t = 0.6 s, the difference between the Darcy seepage velocity in the fissure under a three-axis load and a uniaxial load increases, reaches the peak value, and then decreases until the region stabilizes. The difference between the Darcy velocity at t = 1 s decreases and reaches the minimum value and increases until it tends to stabilize. Figure 11 shows the Darcy velocity change at the same location under the option of changing the top pressure by keeping the surrounding rock pressure unchanged. With the increase of pressure, the Darcy velocity at the same location shows an approximate linear change.

Figure 10

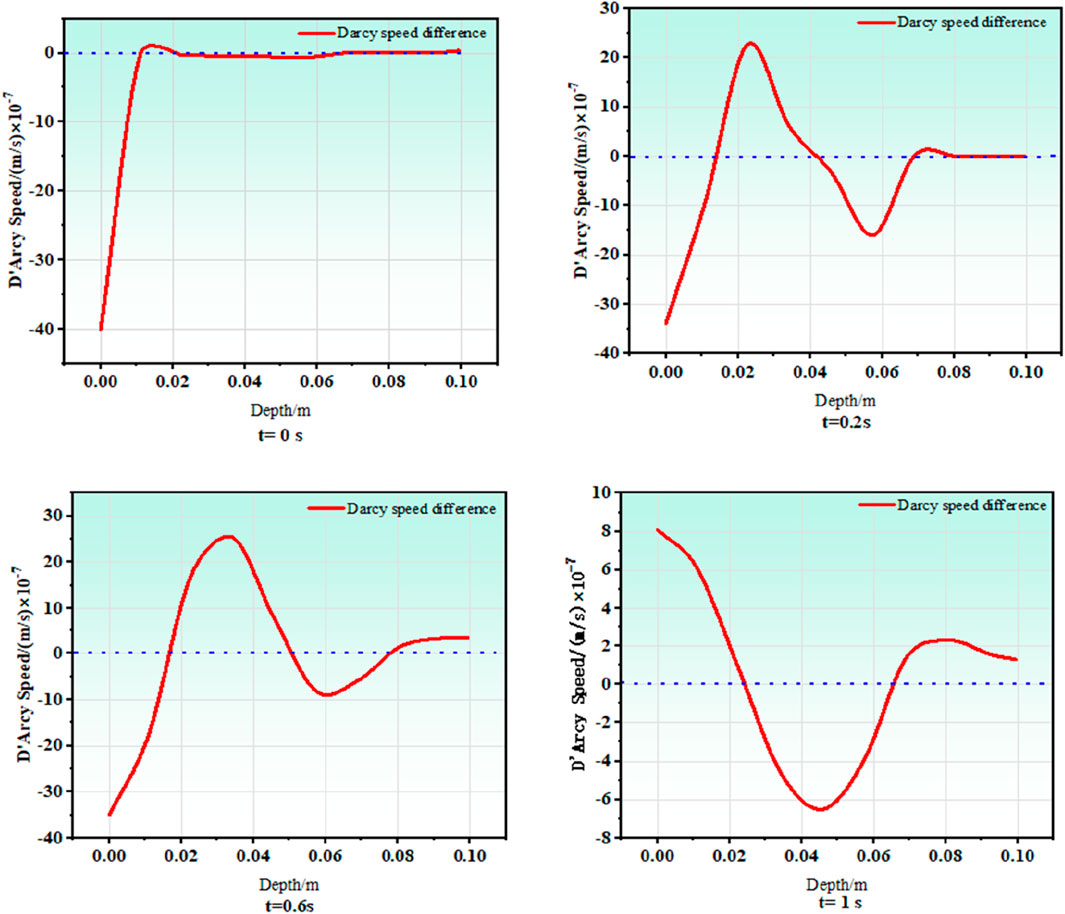
Figure 10. Difference in Darcy velocity of gas seepage in the fissure under three-dimensional loading and uniaxial loading.

Figure 11

Figure 11. Variation of Darcy’s velocity at different pressures at the same position.

When the three-dimensional load is applied to the cleft coal body, the matrix effective stress increases, and the gas pressure decreases. Therefore, at the initial time, the gas flow rate is larger than that of the uniaxial loading when the three-dimensional load is applied. With the stress action, the matrix compression, fissure deformation, and fissure top opening along the fissure to the bottom all increase, so in region Ⅰ, which is the Darcy velocity rapid change region of three-dimensional load and uniaxial load action, the Darcy velocity difference is increasing. In region Ⅱ, which is the Darcy velocity slow change region, the fissure openness and Darcy velocity have reached the maximum. In region Ⅲ, which is the Darcy velocity stable change region, the stress action attenuates, the impact on the fissure is small, and the Darcy velocity change tends to stabilize.

The numerical results presented in this section reveal the gas transport behavior in fractured coal under different loading conditions. In Section 4, we discuss the implications of these findings for CBM extraction and compare them with existing studies.

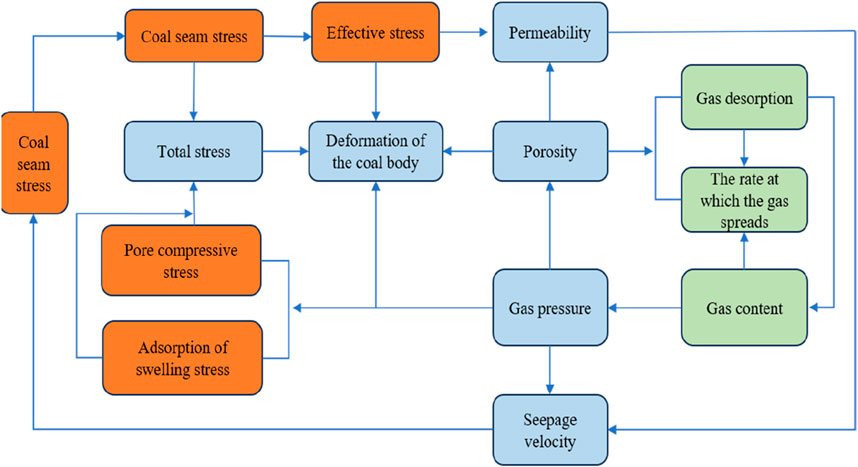
4 Discussion

The multi-field coupling action of coal-bed methane mining in deep coal beds is essentially the interaction between rock seams and coal seams, as shown in Figure 12. The upper rock layer of the coal body and the bottom rock layer are affected by the outside world, changing the form of the role of the surrounding rock force from a static load to a static and dynamic load, which causes the coal seam structure to change. Coal body structure changes affect the storage space of coal-bed methane. As a result, the surrounding space changes, and the gas state changes and, in turn, acts with the coal rock body. Therefore, the change of coal rock body stress affects the adsorption/desorption of CBM, which influences the seepage and diffusion of CBM in the fissure and matrix. The force generated in the process of gas transportation, in turn, acts on the coal rock body, which is a dynamic process of change from the causative factor to the medium and then to the resultant feedback until the stress reaches equilibrium again.

Figure 12

Figure 12. Forms of rock–seam–coal seam interaction.

CBM adsorption/desorption under the influence of stress change is of great significance to the unpressurized extraction efficiency of coal-bed methane, but CBM desorption produces a thermal effect, and the constant temperature condition is difficult to maintain. A coupled thermal–fluid–solid model of CBM mining of a fissured coal body under the influence of stress change should be established to further reveal the characteristics of CBM adsorption/desorption under the influence of stress.

5 Conclusion

This article uses theoretical analysis and numerical simulation methods to explore multi-field coupling in the coal mining process and the gas migration model of fractured coal under different pressure conditions. The main conclusions are as follows:

(1) The deformation processes of coal body gas desorption, diffusion, seepage under the action of pressure are dynamic change processes that influence and interact with each other. The influence of stress on gas seepage and diffusion mainly lies in the fact that the skeleton compression deformation will change the parameters of porosity, permeability, and gas pressure of the coal body. The influence of gas seepage and diffusion lies in the parameters of pore pressure, pore compression strain, and adsorption upward stress. The influence of gas seepage and diffusion lies in the mass exchange between each other.

(2) Under uniaxial loading, the Darcy velocity of gas flow in the coal body of the fissure shows three obvious regions of change and expands along the fissure to the bottom of the fissure with the change of time. The Darcy velocity in the fissure and matrix decreases with the increase of the depth. When t = 1 s, the Darcy velocity of the fracture decreases from 3.5 × 10⁻⁴ m/s to 0.5 × 10⁻⁴ m/s, a decrease of 86%, and the Darcy velocity of the matrix decreases from 3 × 10⁻⁴ m/s to 0.9 × 10⁻⁴ m/s, a decrease of 72%. The rate of the Darcy velocity decline is greater than that of the matrix. The pressure of gas in the matrix is larger than that in the fissure, and the gas in the matrix flows to the fissure.

(3) Under triaxial loading, the Darcy velocity in the fissure and matrix decreases with the increase of depth, and the Darcy velocity at the same location in the matrix changes approximately linearly with the increase of pressure. In the model, the Darcy velocity at the model optimal coal-bed methane extraction location changes steadily in the region.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

ZG: methodology and writing – original draft. HZ: writing – original draft. RY: methodology and writing – review and editing. JY: writing – review and editing and formal analysis. GC: writing – review and editing. YoM: writing – review and editing. YaM: writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by National Natural Science Foundation of China (Grant No. 52474251).

Conflict of interest

Authors ZG, RY, JY, GC, and YoM were employed by Shandong Energy Group Xibei Mining Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahamed, M. A. A., Perera, M. S. A., Elsworth, D., Ranjith, P. G., Matthai, S. K. M., and Li, D. Y. (2021). Effective application of proppants during the hydraulic fracturing of coal seam gas reservoirs: implications from laboratory testings of propped and unpropped coal fractures. Fuel 304 (2), 121394. doi:10.1016/j.fuel.2021.121394

CrossRef Full Text | Google Scholar

Arianfar, A., Ramezanzadeh, A., and Khalili, M. (2021). Numerical study of nonlinear fluid flow behavior in natural fractures adjacent to porous medium. J. Petroleum Sci. Eng. 204, 108710. doi:10.1016/j.petrol.2021.108710

CrossRef Full Text | Google Scholar

Cao, P., Liu, J. S., and Leong, Y. K. (2016). A fully coupled multiscale shale deformation-gas transport model for the evaluation of shale gas extraction. Fuel 178, 103–117. doi:10.1016/j.fuel.2016.03.055

CrossRef Full Text | Google Scholar

Chai, J., Zhang, X. K., Lu, Q. Y., Zhnag, X. J., and Wang, Y. B. (2021). Research on imbalance between supply and demand in China's natural gas market under the double-track price system. Energy Policy 155, 112380. doi:10.1016/j.enpol.2021.112380

CrossRef Full Text | Google Scholar

Chu, P., Xie, H. P., Gao, M. Z., Li, C. B., Shang, D. L., Liu, Q. Q., et al. (2024). Influence of desorption hysteresis effects on coalbed methane migration and production based on dual-porosity medium model incorporating hysteresis pressure. Comput. Geotechnics 165, 105893. doi:10.1016/j.compgeo.2023.105893

CrossRef Full Text | Google Scholar

Guo, P. Y., Gao, K., Wang, M., Wang, Y. W., and He, M. C. (2022). Numerical investigation on the influence of contact characteristics on nonlinear flow in 3D fracture. Comput. Geotechnics 149, 104863. doi:10.1016/j.compgeo.2022.104863

CrossRef Full Text | Google Scholar

Hao, J. F., Liang, B., Sun, W. J., Shi, Z. S., Shi, Y. W., and Zhao, H. (2022). State-of-the-art review and prospect of thermo-hydro-mechanical coupling relation between coal and gas. J. Min. and Saf. Eng. 39, 1051–1060. doi:10.13545/j.cnki.jmse.2021.0186

CrossRef Full Text | Google Scholar

Hou, C. L., Jiang, B., Li, M., Song, Y., and Cheng, G. X. (2022). Micro-deformation and fracture evolution of in-situ coal affected by temperature, confining pressure, and differential stress. J. Nat. Gas Sci. Eng. 100, 104455. doi:10.1016/j.jngse.2022.104455

CrossRef Full Text | Google Scholar

Hu, Y. H., Liu, G. N., Luo, N., Gao, F., Yue, F. T., and Gao, T. (2022). Multi-field coupling deformation of rock and multi-scale flow of gas in shale gas extraction. Energy 238, 121666. doi:10.1016/j.energy.2021.121666

CrossRef Full Text | Google Scholar

Ji, P. F., Lin, H. F., Kong, X. G., and Li, S. G. (2024). Coal deformation characteristics during methane displacement by pulsed nitrogen injection: new method of using pulsed energy to improve coal permeability. Energy 308, 132779. doi:10.1016/j.energy.2024.132779

CrossRef Full Text | Google Scholar

Kong, X. G., Li, S. G., Wang, E. Y., Wang, X., Zhou, Y. X., Ji, P. F., et al. (2021). Experimental and numerical investigations on dynamic mechanical responses and failure process of gas-bearing coal under impact load. Soil Dyn. Earthq. Eng. 142, 106579. doi:10.1016/j.soildyn.2021.106579

CrossRef Full Text | Google Scholar

Kong, X. G., Wang, E. Y., Hu, S. B., Shen, R. X., Li, X. L., and Zhan, T. Q. (2016). Fractal characteristics and acoustic emission of coal containing methane in triaxial compression failure. J. Appl. Geophys. 124, 139–147. doi:10.1016/j.jappgeo.2015.11.018

CrossRef Full Text | Google Scholar

Kong, X. G., Wang, E. Y., Liu, Q. L., Li, Z. H., Li, D. X., Cao, Z. Y., et al. (2017). Dynamic permeability and porosity evolution of coal seam rich in CBM based on the flow-solid coupling theory. J. Nat. Gas Sci. and Eng. 40, 61–71. doi:10.1016/j.jngse.2017.02.011

CrossRef Full Text | Google Scholar

Li, S. G., He, D., Kong, X. G., Lin, H. F., Ma, Y. K., Li, X. L., et al. (2024). Relationship between micro-pores fractal characteristics about NMR T2 spectra and macro cracks fractal laws based on box dimension method of coal under impact load from energy dissipation theory. Chaos, Solit. and Fractals 189, 115685. doi:10.1016/j.chaos.2024.115685

CrossRef Full Text | Google Scholar

Lin, H. F., Huang, M., Li, S. G., Zhang, C., and Chen, L. H. (2016). Numerical simulation of influence of Langmuir adsorption constant on gas drainage radius of drilling in coal seam. Int. J. Min. Sci. Technol. 26 (3), 377–382. doi:10.1016/j.ijmst.2016.02.002

CrossRef Full Text | Google Scholar

Liu, T., Lin, B. Q., Yang, W., Liu, T., Kong, J., Huang, Z. B., et al. (2017). Dynamic diffusion-based multifield coupling model for gas drainage. J. Nat. Gas Sci. Eng. 44, 233–249. doi:10.1016/j.jngse.2017.04.026

CrossRef Full Text | Google Scholar

Liu, Z., Han, J., Yang, H., Lv, J. L., and Dong, S. (2024). A new model for coal gas seepage based on fracture-pore fractal structure characteristics. Int. J. Rock Mech. Min. Sci. 173, 105626. doi:10.1016/j.ijrmms.2023.105626

CrossRef Full Text | Google Scholar

Liu, J., Wang, E. Y., Song, D. Z., Wang, S. H., and Niu, Y. (2015). Effect of rock strength on failure mode and mechanical behavior of composite samples. Arab. J. Geosci. 8, 4527–4539. doi:10.1007/s12517-014-1574-9

CrossRef Full Text | Google Scholar

Liu, Q. Q., Cheng, Y. P., Wang, H. F., Zhou, H. X., Liang, W., Wei, L., et al. (2015). Numerical assessment of the effect of equilibration time on coal permeability evolution characteristics. Fuel 140, 81–89. doi:10.1016/j.fuel.2014.09.099

CrossRef Full Text | Google Scholar

Lu, S. Q., Zhang, Y. L., Sa, Z. Y., Si, S. F., Shu, L. Y., Shu, L. Y., et al. (2019). Damage-induced permeability model of coal and its application to gas predrainage in combination of soft coal and hard coal. Energy Sci. and Eng. 7 (4), 1352–1367. doi:10.1002/ese3.355

CrossRef Full Text | Google Scholar

Mostafa, A., Scholtès, L., and Golfier, F. (2023). Pore-scale hydro-mechanical modeling of gas transport in coal matrix. Fuel 345, 128165. doi:10.1016/j.fuel.2023.128165

CrossRef Full Text | Google Scholar

Nemoto, K., Watanabe, N., Hirano, N., and Tsuchiya, N. (2009). Direct measurement of contact area and stress dependence of anisotropic flow through rock fracture with heterogeneous aperture distribution. Earth Planet. Sci. Lett. 281, 81–87. doi:10.1016/j.epsl.2009.02.005

CrossRef Full Text | Google Scholar

Pan, Z., and Connell, L. D. (2012). Modelling permeability for coal reservoirs: a review of analytical models and testing data. Int. J. Coal Geol. 92, 1–44. doi:10.1016/j.coal.2011.12.009

CrossRef Full Text | Google Scholar

Qin, X. J., Cai, J. C., and Wang, G. (2023). Pore-scale modeling of pore structure properties and wettability effect on permeability of low-rank coal. Int. J. Min. Sci. Technol. 33, 573–584. doi:10.1016/j.ijmst.2023.02.005

CrossRef Full Text | Google Scholar

Su, Y. L., Wang, H., Shen, G. L., Wang, w. D., Zhang, Q., and Zhan, S. Y. (2018). A model for gas transport in organic matter with isolated pores in shale gas reservoirs. J. Nat. gas Sci. Eng. 57, 177–188. doi:10.1016/j.jngse.2018.06.042

CrossRef Full Text | Google Scholar

Tian, J. W., Liu, J. S., Elsworth, D., Leong, Y. K., Li, W., and Zeng, J. (2022). Shale gas production from reservoirs with hierarchical multiscale structural heterogeneities. J. Petroleum Sci. Eng. 208, 109380. doi:10.1016/j.petrol.2021.109380

CrossRef Full Text | Google Scholar

Wang, K., Guo, L., Xu, C., Wang, W. J., Yang, T., Lin, S. S., et al. (2024). Multiscale characteristics of pore-fracture structures in coal reservoirs and their influence on coalbed methane (CBM) transport: a review. Geoenergy Sci. Eng. 242, 213181. doi:10.1016/j.geoen.2024.213181

CrossRef Full Text | Google Scholar

Xu, A. X., Yang, L. X., Huang, W., Zhang, y. C., Long, H. W., Liu, Z. Q., et al. (2023). Exergy, economic, exergoeconomic and environmental (4E) analyses and multi-objective optimization of a PEMFC system for coalbed methane recovery. Energy Convers. Manag. 297, 117734. doi:10.1016/j.enconman.2023.117734

CrossRef Full Text | Google Scholar

Xue, Y., Liu, J., Ranjith, P. G., Liang, X., and Wang, S. H. (2021). Investigation of the influence of gas fracturing on fracturing characteristics of coal mass and gas extraction efficiency based on a multi-physical field model. J. Petroleum Sci. Eng. 206, 109018. doi:10.1016/j.petrol.2021.109018

CrossRef Full Text | Google Scholar

Yang, R., Ma, T. R., Xu, H., Liu, W. Q., Hu, Y., and Sang, S. (2019). A model of fully coupled two-phase flow and coal deformation under dynamic diffusion for coalbed methane extraction. J. Nat. Gas Sci. Eng. 72, 103010. doi:10.1016/j.jngse.2019.103010

CrossRef Full Text | Google Scholar

Yu, B. C., Liu, C., Chen, W. X., Lu, J., and Liu, Y. B. (2022). Experimental study on deformation and fracture characteristics of coal under different true triaxial hydraulic fracture schemes. J. Petroleum Sci. Eng. 216, 110839. doi:10.1016/j.petrol.2022.110839

CrossRef Full Text | Google Scholar

Yuan, Y. Q., Rong, T., Yu, H. F., Zuo, H. B., Guo, H., Gao, Y., et al. (2024). Application of coalbed methane assisted iron ore sintering: injection effect, pollutant abatement and economic evaluation. J. Clean. Prod. 470, 143360. doi:10.1016/j.jclepro.2024.143360

CrossRef Full Text | Google Scholar

Zhang, A. A., Yang, J., Cheng, L., and Ma, C. H. (2022). A simulation study on stress-seepage characteristics of 3D rough single fracture based on fluid-structure interaction. J. Petroleum Sci. Eng. 211, 110215. doi:10.1016/j.petrol.2022.110215

CrossRef Full Text | Google Scholar

Zhang, K., Jin, Y., Meng, Z. P., Wang, X. M., and Li, M. (2024). Experimental investigation on pore characteristics of heterogenous coal structures reservoir and coalbed methane diffusion/seepage behaviors. Phys. Fluids 36 (7), 076612. doi:10.1063/5.0211848

CrossRef Full Text | Google Scholar

Zhang, T., Yuan, L., Tang, M., Zheng, K. G., Xie, Z. Z., Wang, M. C., et al. (2024). Investigation on the coupling response of stress-fracture-seepage field during oil-bearing coal mining. Int. J. Rock Mech. Min. Sci. 174, 105648. doi:10.1016/j.ijrmms.2024.105648

CrossRef Full Text | Google Scholar

Zhao, P. X., Chang, Z. C., Li, S. G., Zhuo, R. S., Jia, Y. Y., Shao, Q. D., et al. (2025). Study and application of the influence of inclination angle on the cross-fusion mechanism of high gas thick coal seam. Int. J. Min. Sci. Technol. 35 (01), 69–85. doi:10.1016/j.ijmst.2024.12.003

CrossRef Full Text | Google Scholar