Numerical evaluation of design factors for effective debris flow mitigation of closed-type check dams

Debris flows are one of the major natural disasters originating from mountainous areas, causing severe casualties and property damage when occurring near populated areas. Consequently, establishing structural and non-structural countermeasures against debris flows is essential in hazard-prone regions. This study aims to identify the critical factors for determining optimal locations of check dams, which are highly effective structures for mitigating debris flow damage. Numerical simulations were conducted using debris flow incidents from Raemian Apartments on 2011 Mt. Umyeon in Seoul and 2019 Gallam-ri in Gangwon-do, Republic of Korea. The simulation outcomes were quantitatively analyzed using Spearman’s rank correlation analysis. The results revealed that topographic features had a more significant impact on optimal check dam placement than flow characteristics. Specifically, check dams located at sites capable of storing large volumes of debris were the most effective in reducing debris flow damage.

1 Introduction

Debris flows are one of the most hazardous types of mass movements, capable of causing severe damage to infrastructure and posing significant threats to human life. Debris flows are rapid mass movements of saturated soil and rock that can be triggered by various mechanisms, including landslides and surface runoff (Coe et al., 2008; Simoni et al., 2020). Their sudden occurrence and high velocity make them particularly difficult to predict and respond to effectively (Lai et al., 2018). To respond effectively to such events, it is essential to investigate the flow mechanisms of debris flows through field observations and physical experiments (Takahashi, 2007). Building upon these findings, numerical modeling provides a valuable tool for predicting potential debris flow behavior in susceptible areas. Numerical modeling of debris flows not only enhances understanding of their complex flow mechanisms—thereby supporting the development of effective mitigation strategies—but also plays a crucial role in identifying threatened regions and evaluating the performance of control structures (Barbini et al., 2024).

The debris flow numerical modeling has been upgraded over the past 20 years (Denlinger and Iverson, 2001; Pitman et al., 2003; Rickenmann et al., 2006; Wang et al., 2016; An et al., 2019; Liu and He, 2020). In addition, various studies have analyzed erosion, entrainment, and deposition processes, which are influential factors in the flowing phenomenon of debris flow (Takahashi, 2007; Medina et al., 2008; Frank et al., 2015; Pudasaini and Krautblatter, 2021; Lee et al., 2022b). Numerical models have been widely used to evaluate the performance of check dams (Remaitre et al., 2008; Osti and Egashira, 2008; Liu et al., 2013; Bernard et al., 2019), as well as other debris-flow control structures (Boreggio et al., 2024), and even to assess dam failure scenarios (Baggio and D’Agostino, 2022). As such, numerical modeling serves as a cost-effective approach to pre-evaluate the effectiveness of check dams by simulating their performance under potential debris flow events. This allows for informed decision-making in designing appropriate structures before actual events.

Therefore, to mitigate debris flow damage, it is crucial to plan and design mitigation structures—such as check dams—using numerical simulations. Among various design parameters, the placement of the check dam plays a critical role in maximizing its effectiveness. To investigate the function and performance of check dams, several studies have employed laboratory experiments (Satofuka and Mizuyama, 2005; Shrestha et al., 2012; Zhou et al., 2019; Chen et al., 2020) and numerical modeling techniques (Chen et al., 2019; Lee et al., 2019; Shen et al., 2019; Shen et al., 2020; Choi et al., 2021; Zhang et al., 2022).

Chen et al. (2019), Shen et al. (2019), Choi et al. (2021), and Barbini et al. (2024) studied the effect of the location of the check dam to determine the best position for mitigating debris flow. In particular, Chen et al. (2019) analyzed debris flows that occurred in a long catchment extending 4.2 km. They investigated potential check dam failure scenarios using smoothed particle hydrodynamics and the finite element method. Their results demonstrated that placing a check dam in the lower part of the catchment effectively blocked the debris flow. However, they did not account for erosion and entrainment processes—key phenomena that can significantly increase debris flow volume as it travels downstream (Remaître et al., 2005; Reid et al., 2016; Simoni et al., 2020; Pudasaini and Krautblatter, 2021). Therefore, incorporating these processes into check dam analyses is essential to more accurately evaluate their performance and effectiveness. Remaitre et al. (2008), Osti and Egashira (2008), Shen et al. (2019), Shen et al. (2020) and Choi et al. (2021) considered erosion and entrainment processes in mitigation effect analysis by the check dam. According to studies that account for debris flow erosion and entrainment processes, check dams are most effective when they are designed near the debris flow initiation zone. Choi et al. (2021) analyzed the relationship between the mitigation effect and the volume of soil stored by the check dam, depending on the location of the check dam. Barbini et al. (2024) evaluated not only the effectiveness of check dam placement in reducing debris flow damage but also addressed constructability and long-term performance aspects, providing a comprehensive framework for planning, sizing, and verifying control works through numerical modeling. In the studies above, each scenario assumed the installation of a single check dam, and fewer than ten such scenarios were simulated to identify the most efficient dam placement within the basin. And the factors determined to be important in each study were different as follows: 1) distance from the initiation zone, 2) the erosion-entrainment process, and 3) the storage capacity of the check dam. For effective check dam construction in various areas, it is essential to analyze the mitigation effect of check dams and the factors that affect them. However, the aforementioned studies considered only a limited number of check dam placement scenarios and provided limited quantitative analysis on which factors most influence the effective placement of check dams for debris flow mitigation. Therefore, this study aims to expand upon previous work by incorporating a broader range of check dam placement scenarios and quantitatively analyzing the key factors that influence the effectiveness of check dam design. In this study, the topographical characteristics of the catchment and the flow dynamics of debris flows—both of which are known to influence check dam construction—were defined with reference to previous research. A correlation analysis was then performed to quantitatively assess the degree to which these factors affect the optimal placement and design of check dams.

In this study, both morphological and flow-related factors were considered to evaluate their influence on the effectiveness of closed-type check dam placement. The morphological factors considered included (1) the distance from the initiation zone, (2) the slope of the basin, and (3) the storage capacity of the check dam. The flow-related factors identified were (1) the maximum flow depth, (2) the maximum flow velocity, and (3) the volume increase due to erosion and entrainment processes. The Deb2D numerical model (developed in An et al., 2019), which incorporates the Voellmy rheological model to simulate basal shear stress, was employed in this study to reproduce debris flow events and evaluate the optimal locations for check dam installation. The model also simulates the erosion–entrainment–deposition processes to capture the volumetric evolution of debris flows. Two historical landslide-induced debris flow events were numerically reproduced: the 2011 event at the Raemian apartment complex in Seoul and the 2019 event in Gallam-ri, Gangwon-do, Republic of Korea. To quantitatively evaluate the mitigation effectiveness of the check dam placements, Spearman’s rank correlation coefficient was used to assess the relationship between various flow characteristics and the reduction in debris flow volume downstream of the dam.

2 Materials and methods

2.1 Governing equation

In this study, the Deb2D numerical model developed by An et al. (2019) was employed to simulate debris flow events. This model was previously validated by Lee et al. (2023) using laboratory experiment results from Sun et al. (2021), which included both open- and closed-type check dam scenarios. Deb2D solves two-dimensional shallow-water equations on a rectangular grid, incorporating an adaptive mesh refinement technique to improve computational efficiency and resolution. The shallow-water equations are formulated in compact hyperbolic conservation form as follows:

$\frac{\mathrm{\partial }\mathbf{q}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }\mathbf{f}}{\mathrm{\partial }x}+\frac{\mathrm{\partial }\mathbf{g}}{\mathrm{\partial }y}=\mathbf{s},(1)$

where $t$ denotes time; $x$ and $y$ are Cartesian coordinates; and $\mathbf{q}$, $\mathbf{f}$, $\mathbf{g}$, and $\mathbf{s}$ are vectors representing conserved variables, fluxes in the $x$ and $y$ directions, and source terms, respectively. The vectors can be written as

$\mathbf{q}=\left(\begin{array}{c}h\\ hu\\ hv\end{array}\right),\mathbf{f}=\left(\begin{array}{c}hu\\ h{u}^2+g{h}^2/2\\ huv\end{array}\right),\mathbf{g}=\left(\begin{array}{c}hv\\ huv\\ h{v}^2+g{h}^2/2\end{array}\right),\mathbf{s}=\left(\begin{array}{c}ED\\ S_{gx}-S_{fx}\\ S_{gy}-S_{fy}\end{array}\right),(2)$

where $h$ is the depth of the debris-flow mixture; $u$ and $v$ are the depth-averaged velocity components in the $x$ and $y$ directions, respectively; $g$ is the acceleration of gravity; $ED$ is the entrainment ($ED>0$) or deposition rate ($ED<0$); $S_{gx}$ and $S_{gy}$ represent the gravitational acceleration in the $x$ and $y$ directions, respectively; $S_{fx}$ and $S_{fy}$ represent the driving friction in the $x$ and $y$ directions, respectively.

Recently, Pudasaini and Mergili (2019) developed a multiphase, multilayer physical mechanism to simulate debris flow. Although recent studies have investigated the effects of cyclic loading on geomaterials in thermal domains (Ahmad et al., 2019; Ahmad et al., 2021; Ahmad et al., 2025), these effects are not considered in this study due to the complexity and number of physical parameters required to represent such mechanisms. In this study, debris flow was simulated using the Voellmy rheological model, which is widely used due to its simplicity and proven accuracy. The model requires only two parameters, making it relatively easy to calibrate while still providing reliable results for debris flow analysis (Lee et al., 2022a). Voellmy friction is expressed as follows:

$S_{fx}=\mu gh+\frac{g{\left|u\right|}^2}{\xi },S_{fy}=\mu gh+\frac{g{\left|v\right|}^2}{\xi },(3)$

where $\mu$, the Coulomb friction coefficient, dominates the deceleration behavior when the flow is slow, and $\xi$, the turbulent friction coefficient, dominates when the flow is fast (Bartelt et al., 2013; Frank et al., 2015).

The erosion, entrainment, and deposition that occur in the flow process must be considered in numerical modeling to accurately analyze the damage scale caused by debris flow. These three phenomena significantly influence the flow and damage scale (Takahashi, 2007; An et al., 2019; Lee et al., 2022a; 2022b). Therefore, based on recent studies (Medina et al., 2008; Frank et al., 2015; Lee et al., 2022a), erosion, entrainment, and deposition processes were simulated using the algorithm developed by Lee et al. (2022b). The algorithm proposed by Lee et al. (2022b) is as follows:

$ED\left(x,y,t\right)=\left\{\begin{array}{ll}\frac{dz}{{dt}_{eros}}& {if)\tau >\tau }_{eros}\\ -\frac{dz}{{dt}_{depos}}& {elseif)\tau <\tau }_{depos}\end{array}\right.(4)$

$h_{\max }\left(x,y,0\right)=\left\{\begin{array}{ll}\frac{dz}{d\tau }\left(\tau -{\tau }_{eros.}\right)=\frac{dz}{d\tau }\left(\rho ghs-{\tau }_{eros.}\right)& \text{if})\tau >{\tau }_{eros}\\ 0& \text{else}\end{array}\right.(5)$

where $dz/d{t}_{eros.}$ is a constant erosion-entrainment rate, $dz/d{t}_{depos.}$ is a constant deposition rate, $h_{\max }\left(x,y,0\right)$ is the maximum potential erosion depth, $\tau$ is the shear stress, ${\tau }_{eros.}$ and ${\tau }_{depos.}$ are the critical shear stress of erosion and deposition, $dz/d\tau$ is the average potential erosion depth, $\rho$ is the mass density, and $s$ is the channel slope. Although it is difficult to simulate definite physical phenomena using this algorithm, which is a physics-based empirical/conceptual equation, it is suitable for implementing the overall phenomenon.

2.2 Numerical evaluation of effective check dam location

The check dam is classified as open-or closed-type (Hübl et al., 2005; Piton and Recking, 2016; Piton et al., 2017). However, this study focuses exclusively on a closed-type check dam. The dam height was set to 10 m and the thickness was fixed at 4 m, while the installation location was varied to evaluate its influence on the mitigation effect. The mitigation effect/ratio by the check dam was calculated based on the volume of debris flow that damaged the residential area. The mitigation ratio quantifies the effectiveness of a check dam placed at each location, and is defined as:

$\text{Mitigation\hspace{0.17em}ratio}=\left[1-\frac{Damagescalewithcheckdam}{Damagescalewithoutcheckdam}\right]\times 100\left(\%\right)(6)$

Here, the damage scale with a check dam refers to the volume of debris deposited in the residential area under each check dam placement scenario, while the damage scale without a check dam refers to the deposited debris volume in the residential area when no check dam is present. In general, while damage scale is typically assessed based on debris flow deposition height and velocity (Santi et al., 2011; Jakob et al., 2012), this study interprets the volume of debris deposited in the residential area—represented as a spatial distribution of deposition height over a two-dimensional plane—as a direct measure of actual damage (Kim and Jun, 2018; Yoon et al., 2018). Based on this interpretation, the effective location of a closed-type check dam was identified by determining the scenario in which the volume of debris reaching and depositing within the residential area was minimized.

In addition, we estimated the best check dam location using the most influential factor for the mitigation effect. The factors in the preamble were analyzed as follows: 1) the distance from the initiation zone, 2) the slope of the basin, 3) the capacity of the check dam, 4) the maximum flow depth, 5) the maximum flow velocity, and 6) volume increase. The first factor is measured by the length of the check dam along the basin, not the straight line. The second factor was measured at the basal along the debris flow direction. The third factor is the storage it has when the structure is constructed. The fourth and fifth factors are the values measured at the point where the check dam locate. The last factor is the volume increase due to the erosion-entrainment process as the debris flows.

In this study, a correlation analysis was performed to estimate the most influential of the factors on the mitigation effect. Correlation analysis is a method used to determine the presence/absence of a linear relationship between two variables, and it indicates the degree of correlation between two variables. The correlation analysis was separated into parametric (Pearson correlation method) and non-parametric (Spearman’s rank correlation method) methods. Since it is challenging that assume the factors defined above for analysis follow a normal distribution, we cannot use parametric correlation analysis. Therefore, the Spearman’s rank correlation method was used to quantitatively assess the influence of each factor on the mitigation effect. This correlation coefficient is distributed between −1 and 1, and the evaluation index is summarized in Table 1 (Schober et al., 2018).

Table 1

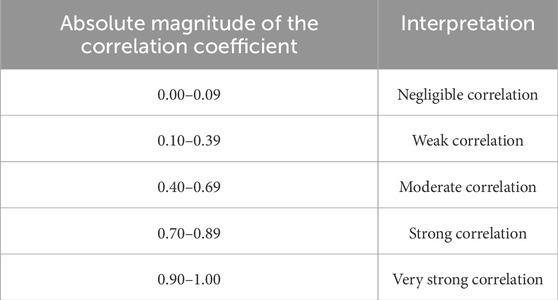
Table 1. Interpretation of the Spearman’s rank correlation coefficients (Schober et al., 2018).

3 Study area and events

Two debris flow events that occurred in different regions of South Korea were analyzed in this study (Figure 1). The first event was the landslide and debris flow that occurred at Mt. Umyeon in Seoul in July 2011, which attracted significant academic attention and prompted extensive field investigations and research efforts (An et al., 2019; Lee et al., 2020; Lee et al., 2022a; Lee et al., 2022b). The second event took place in Gallam-ri, Gangwon Province, in October 2019. In both cases, debris flows originating from the upper slopes propagated downslope, inundating residential areas, temporarily blocking roads, and damaging buildings and infrastructure, thereby causing substantial property losses. Moreover, these events resulted in a considerable number of casualties and displaced residents.

Figure 1

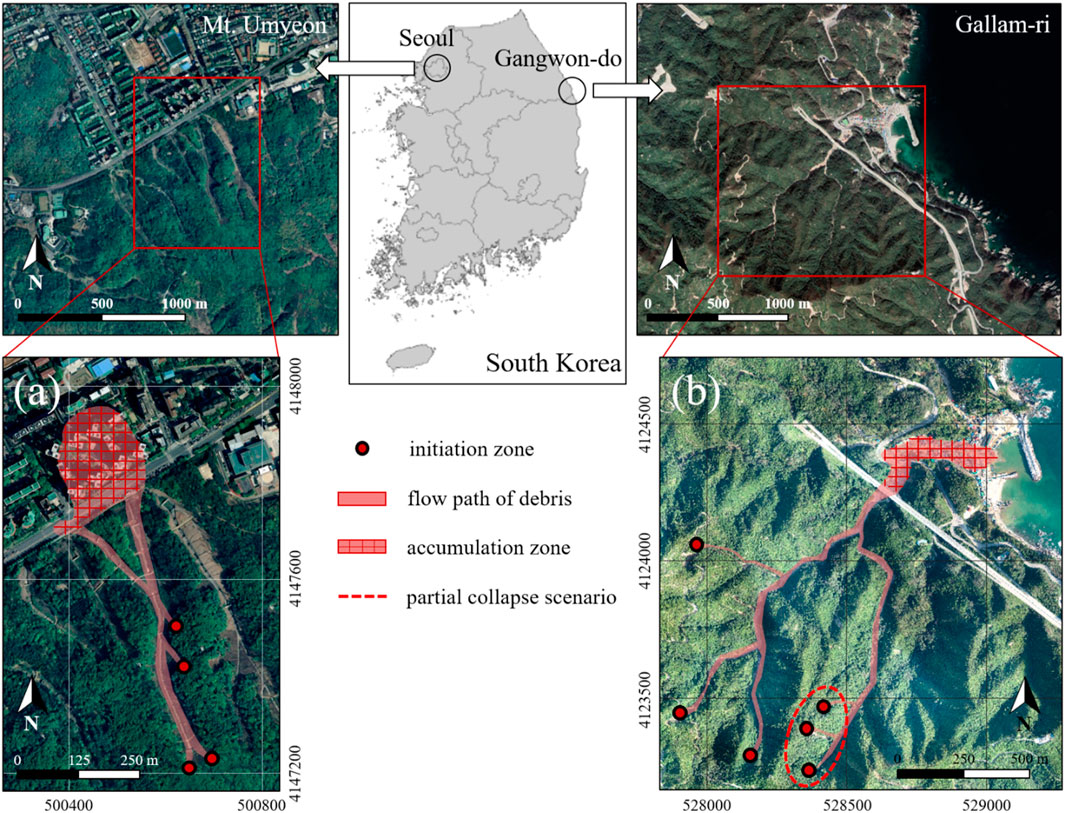
Figure 1. Study area and events: (a) the 2011 landslide at Mt. Umyeon, Raemian apartment basin, and (b) the 2019 landslide at Gangwon-do, Gallam-ri basin. Base image: © Google Earth. Image used for illustrative academic purposes only.

Despite the inherent limitations in acquiring real-time field measurements due to the sudden and hazardous nature of debris flows, both sites were found to possess post-event observational data that enabled the reconstruction of flow characteristics. Accordingly, debris flow simulations were conducted for both the Raemian and Gallam-ri basins using a numerical model. Based on the simulation results, hypothetical check dams were introduced within the catchments. The effectiveness of the check dam installations was then analyzed to determine the characteristics of locations that yielded the most significant mitigation outcomes under various influencing factors.

3.1 Raemian apartment basin

In the Umyeon Mountain area, located in Seoul City, 150 shallow landslides and 33 debris flows occurred in July 2011. According to a report (Seoul, 2014), approximately 340 mm of rainfall occurred in the area from 09:00 on July 24, before landslides and debris flows. Approximately 590 mm of heavy rainfall occurred for 72 h (July 26–28), and it was reported that a landslide and debris flow occurred at 09:00 on July 27th. As such, rainfall continued even during the landslide and debris flow. As a result, the maximum flow velocity of the debris flow was analyzed by CCTV and dashboard cameras in a car near Raemian and Shindonga apartments and was extremely high at 28 m/s and 18 m/s, respectively. Because of this rapid velocity, approximately 3,700 houses and commercial buildings were inundated (Seoul, 2014). In particular, the Raemian apartment basin caused damage reaching up to the third floor of the building (approximately 10 m) and resulted in three casualties.

The bedrock in this area is primarily composed of Precambrian banded biotite gneiss and granitic gneiss, and the debris flow area had an average 34° slope. The length of the Raemian Basin was approximately 650 m. The soil depth within the hillslopes in the Raemian apartment basin ranges between 1 m and 4 m (average 2 m), and the soil profile could be divided into three main layers: (i) a colluvium soil layer (one to two m from ground level); (ii) a transition zone composed mainly of a clay layer (0.2–0.5 m below the colluvium soil layer); and (iii) weathered bedrock (Seoul, 2014; Kim et al., 2019). In addition, the eroded sediment volume, which was evaluated by comparing the DEMs using light detection and ranging (LiDAR DEMs) before and after debris flow events, was calculated as 25,940 m³.

In this study, a LiDAR DEM (1 m $\times$ 1 m), collected by the aircraft at an average altitude of 1 500 m above ground level in late January and February 2009, was used as input data for the topography. The scale of the collapse spots was determined based on the differences in the LiDAR DEMs before and after the landslide. Therefore, the initially measured landslide volume was 350 m³. This debris flow event was simulated based on a report (Seoul, 2014) and on-site investigation data such as the maximum flow velocity at a specific point, directly damaged height, eroded sediment volume in the basin, and damaged range.

3.2 Gallam-ri basin

On October 2–3, 2019, a landslide accompanied by a debris flow occurred in Gallam-ri, Gangwon-do. According to a field survey conducted by the Korea Meteorological Administration, Typhoon Mitak, accompanied by torrential rain, landed in Korea on 2 October 2019, resulting in approximately 420 mm (maximum rainfall intensity, 65.5 mm/h) of rainfall (October 2–3). Therefore, landslides and debris flows occurred at 23:00. Similar to the landslides at Mt. Umyeon that experienced 590 mm of rainfall for just 3 days, the Gallam-ri debris flow event also occurred due to heavy rainfall. However, unlike the Raemian apartment basin, the Gallam-ri, which was composed of low-rise houses surrounded by mountains, is vulnerable to debris flows (Figure 1b). Because of these characteristics, it has been reported that approximately 62 houses were inundated, with one causality.

The bedrock in the areas where landslides occurred is composed of granitic banded gneiss. The average slope was over 35°, and the soil depth on the bedrock was approximately 2–5 m in the landslide scars, based on the field survey. Colluvial red-brown soil covers the hillslopes, except for narrow ridges or steep slip scars with exposed bedrock. Joints in the exposed bedrock within the debris flow path were observed to run in the downslope direction, parallel to the landslide path. The landslide was initiated on the upper slopes, which were covered with pine trees and then moved swiftly down the slope as a debris flow. The path of the debris flow generally coincided with a first-order stream where the bedrock was exposed.

The topography of the Gallam-ri was constructed using a digital elevation map (1:5,000 scale) by the National Geographic Information Institute (https://www.ngii.go.kr), and the length of the Gallam-ri basin was analyzed to be approximately 1 200 m. However, compared to the Raemian apartment basin, in the Gallam-ri basin, there were no specific postmortem or field investigations. Therefore, the soil depth and collapsed volume (initial volume) were determined based on a field survey of the input data. The initial volume was analyzed at 12,600 m³. Although field data for this site were more limited compared to the Raemian apartment basin, post-event aerial imagery was available and utilized to estimate the extent of the damage, which served as a basis for the debris flow simulation.

4 Results and discussion

4.1 Raemian apartment basin

In this study, the mitigation effect of different check dam locations was analyzed using numerical modeling results. Therefore, the debris flow event that occurred in Raemian apartment was simulated first without a check dam. The parameters used in the Raemian apartment basin are listed in Table 2, and the simulation results are shown in Figure 2.

Table 2

Table 2. Calibrated parameters for the Deb2D debris-flow model (Voellmy rheological model with erosion-entrainment-deposition model) at the Mt. Umyeon and Gallam-ri debris flow events.

Figure 2

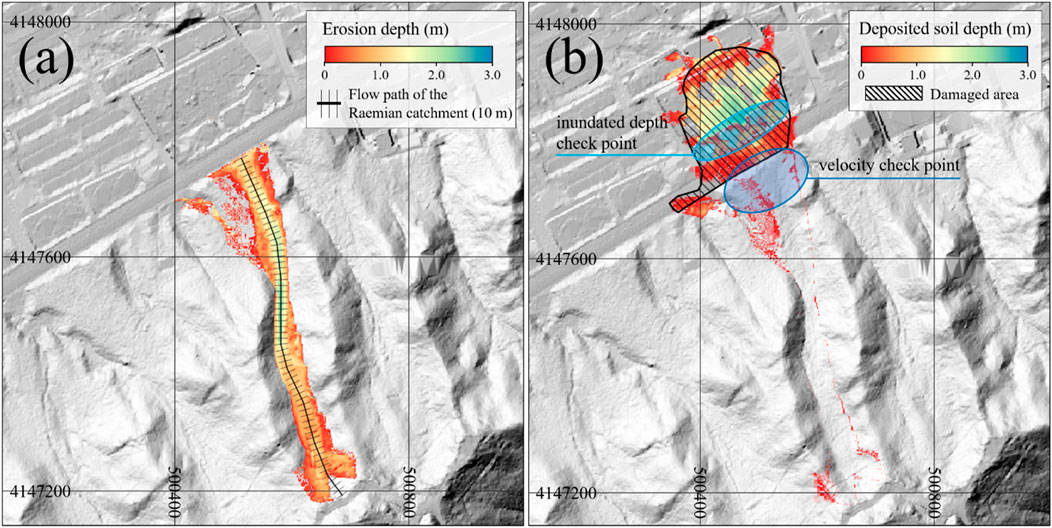
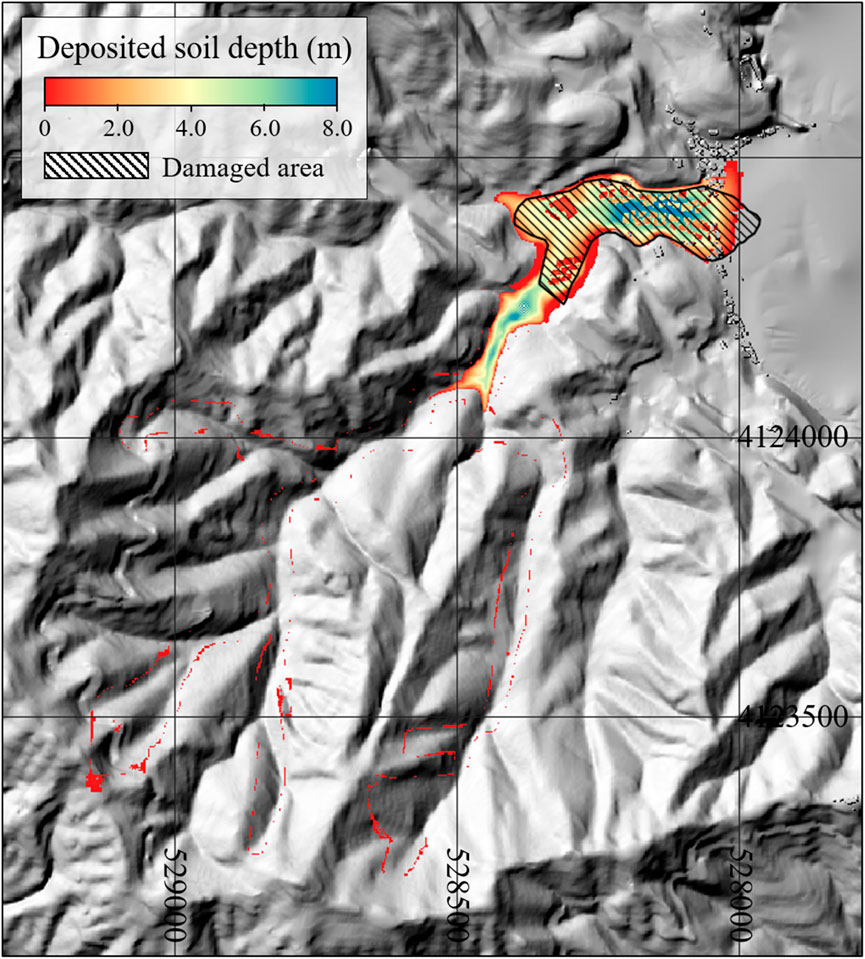
Figure 2. Numerical simulation results for the debris flow event at the Raemian apartment basin: (a) simulated erosion depth and (b) simulated deposit thickness.

Figure 2a shows the simulated erosion depth, whereas Figure 2b presents the simulation results for the deposited height after the debris flow stopped. The area marked by black lines in Figure 2b corresponds to the reported damaged area based on a field survey. The maximum flow velocity of the debris flow was confirmed in the area marked in blue, and the maximum flow height was analyzed in the light-blue area. Table 3 summarizes the simulation results corresponding to Figure 2. The estimated eroded sediment volume was 25,260 m³, which is comparable to the observed volume of 25,940 m³. In addition, debris flows were simulated up to 10 m, which was consistent with the reported inundation height in the field survey. However, the simulated maximum flow velocity was 10 m/s lower than the data analyzed using the CCTV and dashboard camera in a car near the road. This phenomenon resulted in a dramatic increase in the flow velocity as extreme rainfall continued, even at the time of debris flow occurrence (Park et al., 2013). However, it was determined that there was no difficulty in analyzing the mitigation effect of the check dam.

Table 3

Table 3. Simulation results and observation data of the 2011 landslide at the Raemian apartment catchment.

To evaluate the mitigation effect of check dam placement, 65 hypothetical locations were defined at 10 m intervals along the 650 m flow path, as shown in Figure 2b. However, some sections of the valley were shallower than the predefined check dam height (10 m), making it infeasible to implement a check dam. Therefore, the mitigation effect was analyzed only within the range of 90–390 m from the initiation zone.

As shown in Figure 3, the black lines represent the spatial distribution of each of the six comparison factors along the debris flow path, while the red lines indicate the corresponding mitigation ratios calculated through numerical modeling. The figure enables direct comparison between physical or hydraulic conditions and the potential effectiveness of check dam placement. In Figure 3, the x-axis represents the distance from the initiation zone, which also corresponds to the hypothetical check dam placement scenarios along the flow path. The left y-axis indicates the values of the influencing factors, while the right y-axis shows the corresponding mitigation ratio for each scenario. Figure 3a shows the relationship between the distance from the initiation zone and the mitigation ratio. The distance was inversely proportional to the mitigation ratio, and it was confirmed that the opposite aspect to the analysis by Chen et al. (2019). Figure 3b shows the relationship between the slope of the basin and the mitigation ratio, demonstrating an inverse relationship between the two. This means that the check dam was constructed in an area where the gentle slope had a high mitigation effect. The mitigation effect was analyzed based on the capacity of the check dam, as shown in Figure 3c, and the damage scale decreased as the check dam trapped numerous debris flows. The maximum flow depth of the debris flow was inversely proportional to the mitigation effect (Figure 3D). It was found to be effective when the check dam was located in the 100–250 m where the flow depth was low, and the mitigation effect plummeted in 250–350 m where the flow height increased rapidly. The maximum flow velocity of the debris flow was similar to that in Figure 3a (Figure 3e). Accordingly, the mitigation effect showed an inverse relationship with the flow velocity. Figure 3f shows the results of the analysis of the relationship with the erosion-entrainment process derived from Shen et al. (2019), Shen et al. (2020) and Choi et al. (2021). They found that the volume increases in the flow path due to erosion-entrainment was inversely proportional to the mitigation effect. In addition, the efficient location of the check dam was found to be present in the 150–200 m section where the volume increase was the lowest (that is, the erosion-entrainment acted slowly).

Figure 3

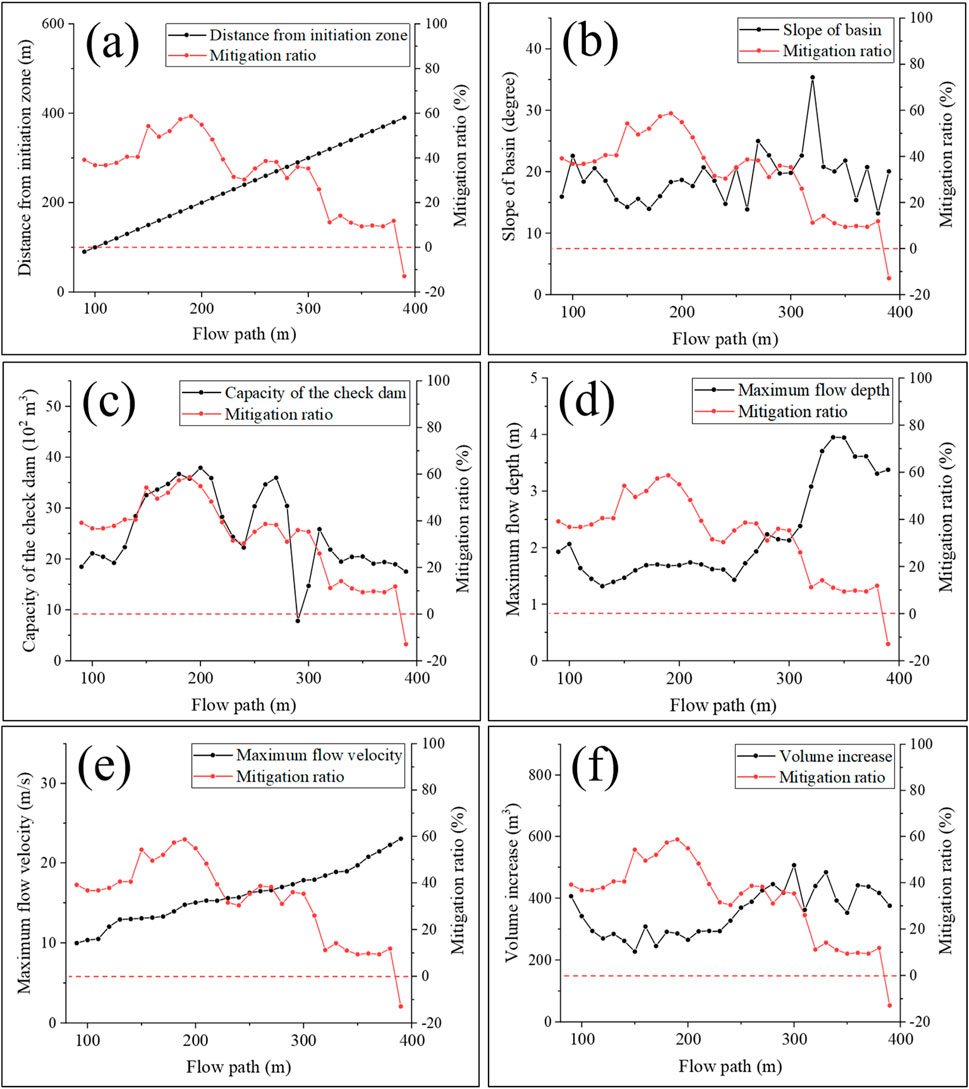
Figure 3. Analysis of the mitigation effects and influencing factors according to check dam location in the Raemian apartment basin: (a) distance from the initiation zone, (b) slope of the basin, (c) capacity of the check dam, (d) maximum flow depth, (e) maximum flow velocity, and (f) volume increase due to erosion and entrainment.

The results of the quantitative correlation analysis (Spearman’s rank correlation coefficient) with the mitigation ratio for these factors are summarized in Figure 4. In the case of the Raemian apartment basin, when the check dam was constructed, there were five factors: the distance from the initiation zone (−0.779), the slope of the basin (−0.417), the maximum flow depth (−0.709), the maximum flow velocity (−0.778), and the volume increase (−0.695), which showed an inverse correlation with the mitigation ratio, and the only one factor capacity of the check dam (0.677), which demonstrated a proportional relationship. The flow characteristic factors showed superior correlations compared to the topographical components factors, and flow characteristic factors showed a “strong correlation” in general. In particular, the maximum flow velocity was evaluated as the most influential factor. And topographical components factors showed a wide deviation from 0.417 to 0.779 in the correlation analysis results. Among them, the distance from the initiation zone factor was assessed as the most influential factor.

Figure 4

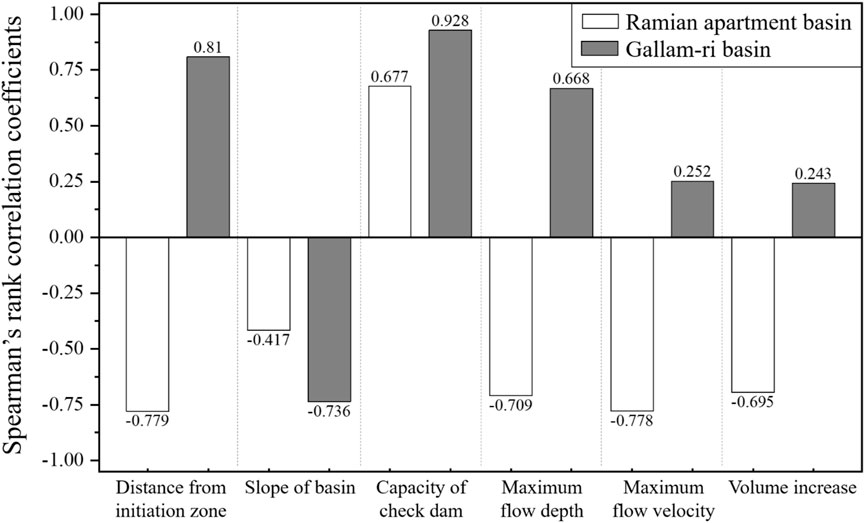
Figure 4. Spearman’s rank correlation analysis results of the mitigation ratio by check dam with factors in Raemian apartment and Gallam-ri basins.

Figure 5a shows the final deposited height of debris flow for the scenario in which the smallest debris volume was deposited in the residential area. In this case, the check dam placed 190 m from the initiation zone achieved the highest mitigation effect, with a mitigation ratio of 58.7%. In contrast, Figure 5b presents a case where the check dam placement resulted in increased damage. Although mitigation was observed in the lower-right area, new damage occurred in the previously unaffected lower-left area due to check dam overflow-driven diversion of debris into adjacent basins. These findings highlight the potential for suboptimal dam placement to exacerbate damage, underscoring the need for careful numerical analysis before implementation.

Figure 5

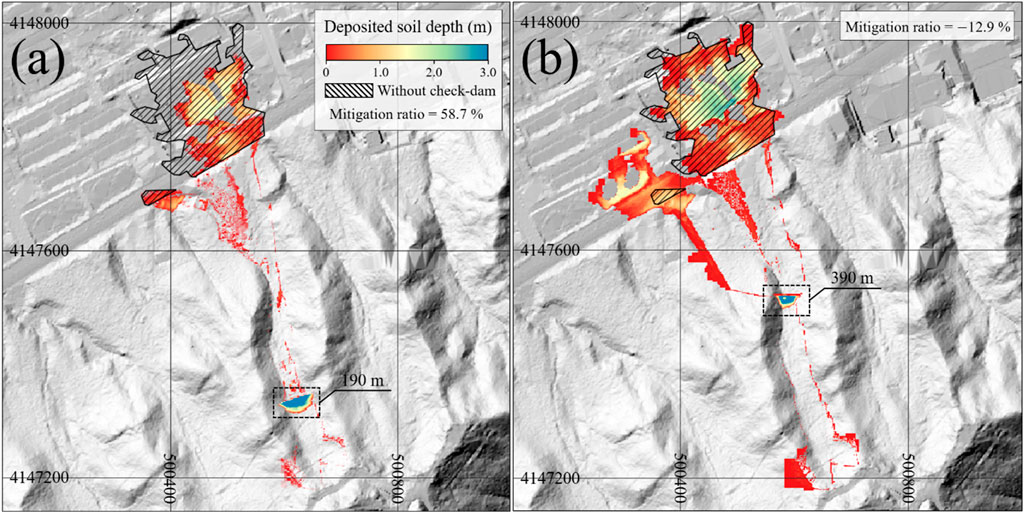
Figure 5. Debris flow mitigation scenario on Raemian apartment basin by a check dam: the (a) best and (b) worst case.

4.2 Gallam-ri basin

The Gallam-ri basin was simulated, as shown in Figure 6. It depicts the simulated final deposition height when the debris flow stopped, and the shaded areas in black are the damaged areas reported through on-site investigations. In this basin, the damage range data from the field survey were the only data to be compared; therefore, the parameters were calibrated based on the damaged area. The Gallam-ri debris flow was simulated using the parameters listed in Table 2. However, as shown in Figures 1b,6, the Gallam-ri basin has two debris flows merging in the lower part of the basin; therefore, the simulation analysis according to the location of the check dam was somewhat limited. Therefore, debris flow on the right side was simulated, as shown in Figure 7. Figure 7a shows the simulation results of erosion depth, and Figure 7b depicts the deposition height after the debris flow stopped. The Gallam-ri basin was approximately twice as long as the Raemian apartment basin. As shown in Figure 7a, the channel was divided into 59 sections at 20-meter intervals to simulate check dam scenarios and evaluate their mitigation effects.

Figure 6

Figure 6. Simulation result of Gallam-ri basin’s debris flow event showing deposited soil depth.

Figure 7

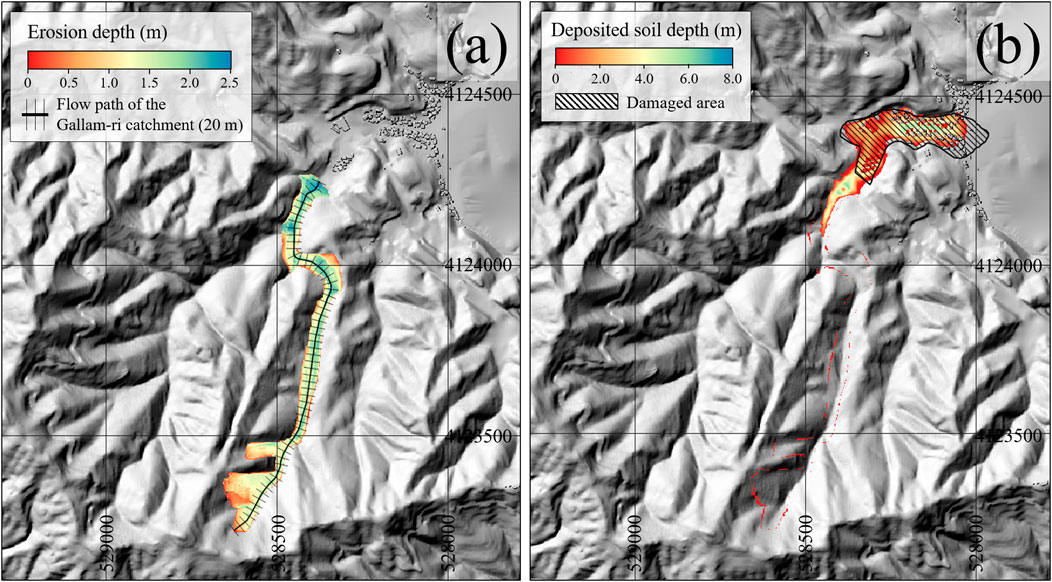
Figure 7. Numerical simulation results for the debris flow event at the Gallam-ri basin: (a) simulated erosion depth and (b) simulated deposit thickness.

The simulation analysis of the check dam for the Gallam-ri basin is depicted in Figure 8. Figure 8a shows the correlation between the distance from the initiation zone and the mitigation ratio. Similar to that observed by Chen et al. (2019), a proportional relationship was determined, in which the mitigation effect increased as the check dam was located farther from the initiation zone. Figure 8b shows a comparison of the mitigation ratio and increase in volume owing to the erosion-entrainment process, and it was analyzed in a proportional relationship similar to that shown in Figure 8a. Therefore, the check dam had a high mitigation ratio when it was located in the 850–900 m area where the erosion-entrainment process occurred actively. This is in contrast to the results of Shen et al. (2019), Shen et al. (2020), and Choi et al. (2021). In the case of the slope of the basin, the mitigation effect was inversely proportional, as shown in Figure 8C. As shown in Figure 8d, the maximum flow depth showed a similar pattern to the mitigation effect. The mitigation effect was decent when the check dam was located at points where the flow depth was high. The maximum flow velocity was analyzed in a proportional relationship with the mitigation effect, which is interpreted as the superior performance of the check dam when constructed in a place with a high flow velocity (Figure 8e). Figure 8f shows the correlation between the capacity of the check dam and the mitigation ratio. They have a proportional relationship; furthermore, they fluctuate similarly. Therefore, the check dam had a high mitigation effect when constructed in an area with a large capacity of soil trapped by the check dam.

Figure 8

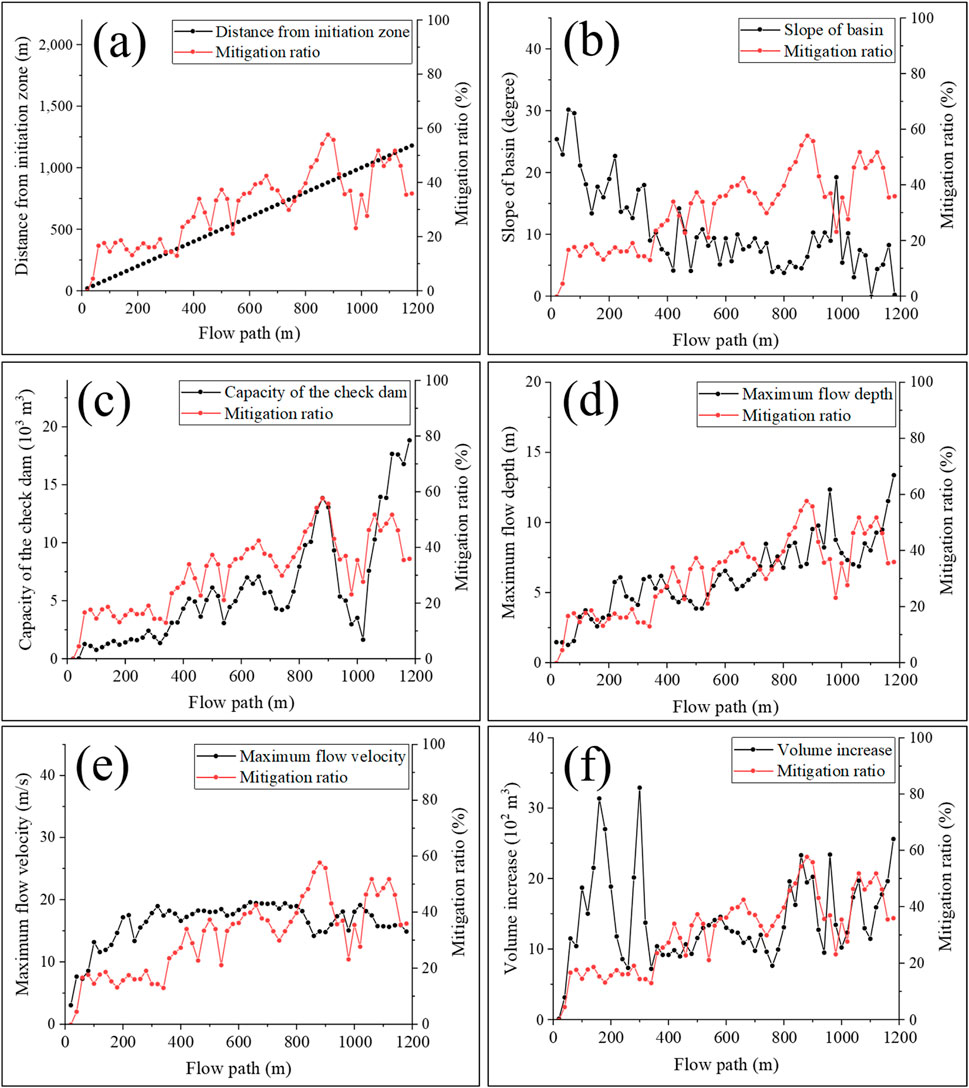
Figure 8. Analysis of the mitigation effects and influencing factors according to check dam location in the Gallam-ri basin: (a) distance from the initiation zone, (b) slope of the basin, (c) capacity of the check dam, (d) maximum flow depth, (e) maximum flow velocity, and (f) volume increase due to erosion and entrainment.

The results of the Spearman’s rank correlation analysis are summarized in Figure 4. In the Gallam-ri basin, five factors: the distance from the initiation zone (0.810), capacity of the check dam (0.928), maximum flow depth (0.668), maximum flow velocity (0.252), and volume increase (0.243) were proportionally correlated with the mitigation effect. In contrast, the slope of the basin (−0.736) was inversely proportional to the mitigation effect. In the Gallam-ri basin, topographical factors have a higher correlation than flow characteristic factors, and topographical factors showed a “strong correlation” and “very strong correlation” with mitigation effects. In particular, the capacity of the check dam factor reveals the most influence on the check dam construction with a 0.928 correlation analysis result. And the flow characteristics factors all showed a correlation coefficient of less than 0.7. The maximum flow depth showed a “moderate correlation”, and the others revealed a “weak correlation”.

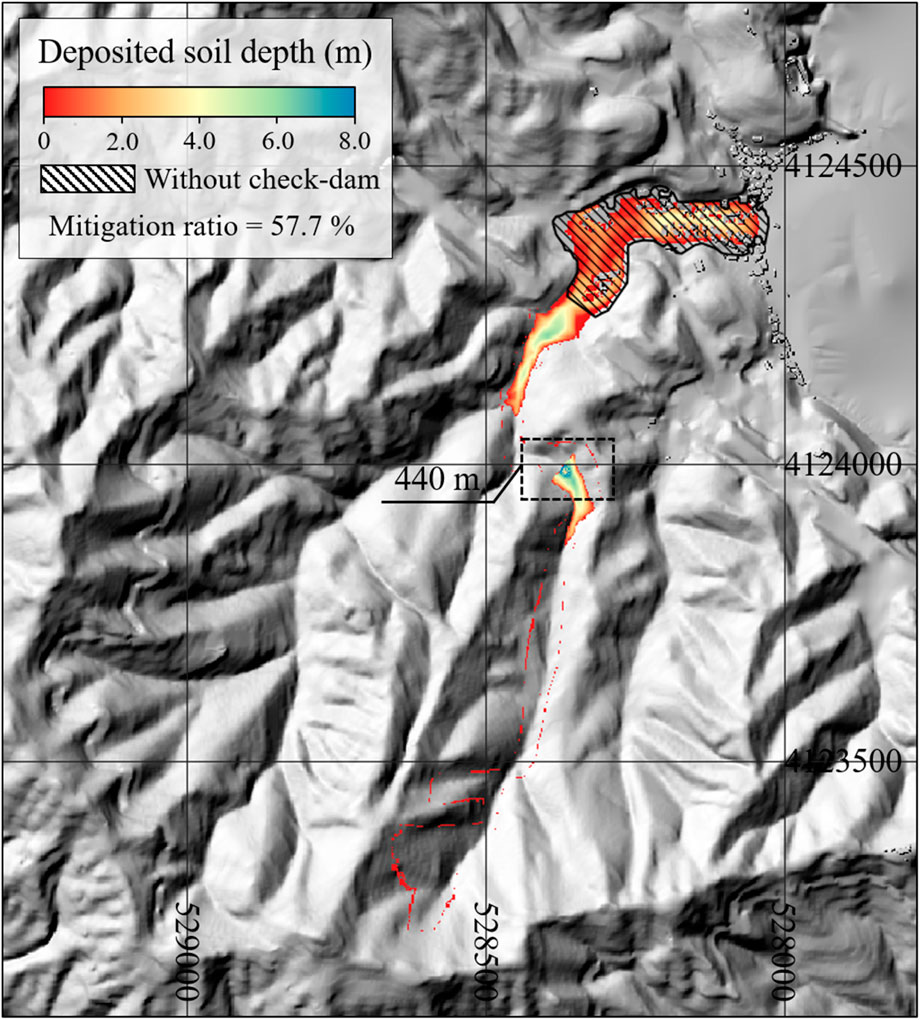
As shown in Figure 9, when the check dam was located at 440 m away from the initiation zone, the check dam performance was maximized with a 57.7% mitigation ratio compared to that without a check dam.

Figure 9

Figure 9. The best debris flow mitigation scenario on Gallam-ri basin by a check dam.

4.3 Discussion

In the Raemian apartment basin, considering should focus more on topographical component factors than flow characteristics to construct an effective check dam. However, in the Gallam-ri basin, it was overwhelmingly advantageous to consider topographical components. First of all, among the three topographical component factors, the slope of the basin and capacity of the check dam demonstrated the same correlation direction for both, which means that these factors can use universally in the construction of a check dam in the future. In particular, the capacity of the check dam showed a correlation coefficient of 0.677 or higher in the two basins, indicating not only versatility but also high correlation. Therefore, we can effectively use it for the check dam construction in the future. However, the slope component showed a low correlation of 0.417. Although we can use it universally, it is hard to identify precise locations. The distance from the initiation zone can be evaluated as an influential factor as it shows a “strong correlation” between basins. However, since the correlation direction was opposite in the two event areas, it could be a factor that could confuse the construction of the check dam.

A correlation analysis was performed between the three topographical factors for each basin to identify the reason for these results (Figure 10). In the Raemian apartment basin, the correlation between the three factors is low, but based on this, we estimated the overall topography. The slope became steeper (0.284), and the width of the basin narrowed (−0.362) as the distance from the initiation zone increased. These characteristics work organically with the results of Figures 3, 4, and can reasonably explain the results of this study. The slope became gentler (−0.708), and the width of the basin widened (0.839) as the distance from the initiation zone increased in the Gallam-ri basin. This topographical analysis is able to clarify the method and reason for constructing an effective check dam in the Gallam-ri basin. It might be seen as a natural result that the check dam capacity was determined to be the most influential factor. However, we performed the result through physics-based numerical analyses. In addition, this study can rationally explain the reason for the conflicting results of previous studies. Therefore, it can help the check dam construction as a general and influential factor.

Figure 10

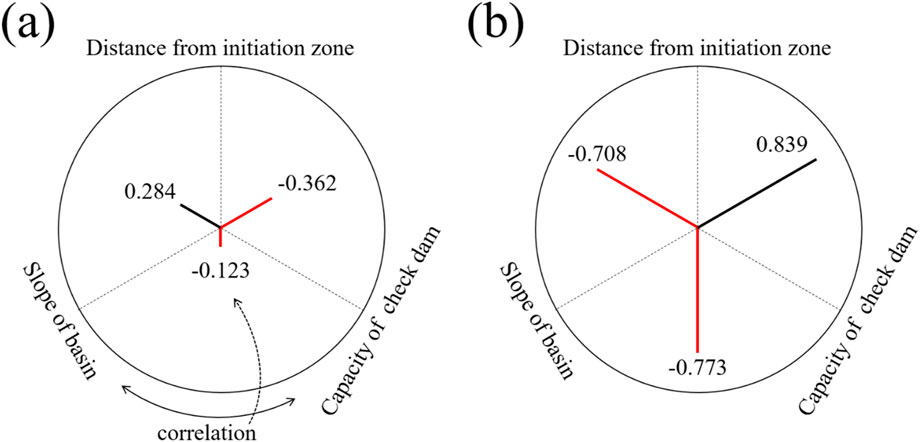
Figure 10. Spearman’s rank correlation analysis results between topographic components factors in (a) the Raemian apartment basin, and (b) Gallam-ri basin.

For the three flow characteristics, all factors exhibited contrasting patterns between the two basins. In the Raemian apartment basin, all flow characteristics showed strong correlations with the effectiveness of check dam installation and were therefore identified as significant influencing factors. In contrast, for the Gallam-ri basin, only the maximum flow depth appeared to serve as a reasonable indicator for check dam design. Even so, the direction of its correlation was opposite to that observed in the Raemian basin, suggesting that its applicability as a universal design indicator is limited. Although the increase in debris flow volume through erosion and entrainment—reflecting both flow dynamics and topographical features—has been recognized in previous studies as a key factor in determining check dam effectiveness, the present study found that its influence varied substantially depending on the study area. Therefore, to identify optimal closed-type check dam installation sites, it is recommended to prioritize universally accepted indicators such as slope gradient and potential check dam capacity. Nonetheless, it is essential to conduct preliminary analyses using numerical modeling that account for the specific triggering scenarios of debris flows in the region under investigation.

5 Limitation and further study

In this study, to demonstrate the most influential factor in check dam construction, we assumed that only one closed-type check dam was located in a catchment. However, in general, two or more check dams can be constructed in catchments against debris flows. Therefore, additional research is needed to design multi-check dams effectively. In this study, to identify the most influential factor in check dam construction, we assumed the presence of only a single closed-type check dam within each catchment. However, in practice, two or more check dams are often installed in series to mitigate debris flows more effectively. Therefore, further research is required to develop optimal strategies for multi-check dam design. Although this study considered the mechanical interaction between a rigid closed-type check dam and the debris flow, it did not account for the material properties of the dam and the complex interactions that may arise as a result. Since such interactions can directly affect the structural stability of the check dam, future research should address not only the spatial placement of check dams but also their material-dependent stability under both short-term and long-term perspectives (Rizvi et al., 2020).

6 Conclusion

This study analyzed the factors that affect the construction of effective check dams and determined the factors that have the greatest influence. Therefore, analysis of the check dam was performed on two debris flow events that occurred in the Raemian apartment basin, the Mt. Umyeon landslide in Seoul in July 2011, and the Gallam-ri debris flow at Gangwon-do in October 2019. The factors affecting the check dam design were selected as the topographical component factors: 1) the distance from the initiation zone, 2) the slope of the basin, and 3) the capacity of the check dam; and the flow characteristic factors: 4) the maximum flow depth, 5) the maximum flow velocity, and 6) volume increase due to the erosion-entrainment process, referring to previous studies. The Spearman’s rank correlation method was used to evaluate the correlation rate as a quantitative indicator.

According to the simulation results, the topographical component factors were the more influential factor in the construction of the check dam than the flow characteristic factors. In particular, we determined that a superior mitigation effect was revealed when the check dam was constructed at the point where it could store more debris. Although this result might be expected qualitatively, it would have scientific value if we figured out this result quantitatively through numerical analysis. The erosion-entrainment process, which was evaluated as the most influential factor in previous studies, was addressed as an extensive deviation depending on the study area; therefore, it is hard to consider erosion-entrainment process as an influencing factor for a general scenario. A quantitative analysis of such an effective check dam design can help in the construction of check dams in the future.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SL: Writing – original draft, Software, Visualization, Conceptualization, Methodology, Validation, Formal Analysis. HA: Formal Analysis, Conceptualization, Writing – review and editing, Methodology, Software, Supervision. MK: Writing – review and editing, Methodology, Investigation. JL: Investigation, Resources, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Basic Research Project of the Korea Institute of Geoscience and Mineral Resources (Project code: 25-3412) and the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2021R1A2C200553012).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. During the preparation of this work, the authors used ChatGPT in order to enhance grammatical accuracy and clarity. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, S., Rizvi, Z., Khan, M. A., Ahmad, J., and Wuttke, F. (2019). Experimental study of thermal performance of the backfill material around underground power cable under steady and cyclic thermal loading. Mater. Today Proc. 17, 85–95. doi:10.1016/j.matpr.2019.06.404

CrossRef Full Text | Google Scholar

Ahmad, S., Rizvi, Z. H., Arp, J. C. C., Wuttke, F., Tirth, V., and Islam, S. (2021). Evolution of temperature field around underground power cable for static and cyclic heating. Energ 14, 8191. doi:10.3390/en14238191

CrossRef Full Text | Google Scholar

Ahmad, S., Rizvi, Z. H., and Wuttke, F. (2025). Unveiling soil thermal behavior under ultra-high voltage power cable operations. Sci. Rep. 15, 7315. doi:10.1038/s41598-025-91831-1

PubMed Abstract | CrossRef Full Text | Google Scholar

An, H., Kim, M., Lee, G., Kim, Y., and Lim, H. (2019). Estimation of the area of sediment deposition by debris flow using a physical-based modeling approach. Quat. Int. 503, 59–69. doi:10.1016/j.quaint.2018.09.049

CrossRef Full Text | Google Scholar

Baggio, T., and D’Agostino, V. (2022). Simulating the effect of check dam collapse in a debris-flow channel. Sci. Total Environ. 816, 151660. doi:10.1016/j.scitotenv.2021.151660

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbini, M., Bernard, M., Boreggio, M., Schiavo, M., D’Agostino, V., and Gregoretti, C. (2024). An alternative approach for the sediment control of in-channel stony debris flows with an application to the case study of Ru Secco Creek (Venetian Dolomites, Northeast Italy). Front. Earth Sci. 12, 1340561. doi:10.3389/feart.2024.1340561

CrossRef Full Text | Google Scholar

Bartelt, P., Buehler, Y., Christen, M., Deubelbeiss, Y., Graf, C., and McArdell, B. W. (2013). RAMMS–rapid mass movement simulation, A modeling system for debris flows in research and practice, user manual v1.5, Debris flow, manuscript update: 31 January 2013. WSL Institute for Snow and Avalanche Research SLF, Available online at: http://ramms.slf.ch/ramms/downloads/RAMMS_DBF_Manual.pdf (Accessed 27 February 2015)

Google Scholar

Bernard, M., Boreggio, M., Degetto, M., and Gregoretti, C. (2019). Model-based approach for design and performance evaluation of works controlling stony debris flows with an application to a case study at Rovina di Cancia (Venetian Dolomites, Northeast Italy). Sci. Total Environ. 688, 1373–1388. doi:10.1016/j.scitotenv.2019.05.468

PubMed Abstract | CrossRef Full Text | Google Scholar

Boreggio, M., Barbini, M., Bernard, M., Degetto, M., and Gregoretti, C. (2024). Proposed solution for stony debris-flow control works in two headwater basins with morphological changes. GeoHazards 5, 1346–1369. doi:10.3390/geohazards5040064

CrossRef Full Text | Google Scholar

Chen, H.-X., Li, J., Feng, S.-J., Gao, H.-Y., and Zhang, D.-M. (2019). Simulation of interactions between debris flow and check dams on three-dimensional terrain. Eng. Geol. 251, 48–62. doi:10.1016/j.enggeo.2019.02.001

CrossRef Full Text | Google Scholar

Chen, J., Wang, D., Zhao, W., Chen, H., Wang, T., Nepal, N., et al. (2020). Laboratory study on the characteristics of large wood and debris flow processes at slit-check dams. Landslides 17, 1703–1711. doi:10.1007/s10346-020-01409-3

CrossRef Full Text | Google Scholar

Choi, S.-K., Park, J.-Y., Lee, D.-H., Lee, S.-R., Kim, Y.-T., and Kwon, T.-H. (2021). Assessment of barrier location effect on debris flow based on smoothed particle hydrodynamics (SPH) simulation on 3D terrains. Landslides 18, 217–234. doi:10.1007/s10346-020-01477-5

CrossRef Full Text | Google Scholar

Coe, J. A., Kinner, D. A., and Godt, J. W. (2008). Initiation conditions for debris flows generated by runoff at Chalk Cliffs, central Colorado. Geomorphol 96 (3–4), 270–297. doi:10.1016/j.geomorph.2007.03.017

CrossRef Full Text | Google Scholar

Denlinger, R. P., and Iverson, R. M. (2001). Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res. Solid Earth 106, 553–566. doi:10.1029/2000JB900330

CrossRef Full Text | Google Scholar

Frank, F., McArdell, B. W., Huggel, C., and Vieli, A. (2015). The importance of entrainment and bulking on debris flow runout modeling: examples from the Swiss Alps. Nat. Hazards Earth Syst. Sci. 15, 2569–2583. doi:10.5194/nhess-15-2569-2015

CrossRef Full Text | Google Scholar

Hübl, J., Holub, M., Strauss, A., and Suda, J. (2005). “Structural mitigation measures,” in 3rd probabilistic workshop: technical Systems+ natural hazards. Universität für Bodenkultur, Department für Bautechnik und Naturgefahren. Editors K. Bergmeister, D. Rickenmann, A. Strauss, S. Wieshofer, M. Curbach, and D. Proske, 115–126.

Google Scholar

Jakob, M., Stein, D., and Ulmi, M. (2012). Vulnerability of buildings to debris flow impact. Nat. Hazards 60, 241–261. doi:10.1007/s11069-011-0007-2

CrossRef Full Text | Google Scholar

Kim, S., Kim, M., An, H., Chun, K., Oh, H.-J., and Onda, Y. (2019). Influence of subsurface flow by Lidar DEMs and physical soil strength considering a simple hydrologic concept for shallow landslide instability mapping. Catena 182, 104137. doi:10.1016/j.catena.2019.104137

CrossRef Full Text | Google Scholar

Kim, Y. H., and Jun, K. W. (2018). Analysis of debris flow disaster area according to location change of check dam using kanako-2d. J. Korean Soc. Saf. 33, 128–134. doi:10.14346/JKOSOS.2018.33.1.128

CrossRef Full Text | Google Scholar

Lai, J., Wang, G., Wang, Z., Chen, J., Pang, X., Wang, S., et al. (2018). A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 177, 436–457. doi:10.1016/j.earscirev.2017.12.003

CrossRef Full Text | Google Scholar

Lee, K., Kim, Y., Ko, J., and Jeong, S. (2019). A study on the debris flow-induced impact force on check dam with- and without-entrainment. Comput. Geotech. 113, 103104. doi:10.1016/j.compgeo.2019.103104

CrossRef Full Text | Google Scholar

Lee, S., An, H., and Kim, M. (2023). Analysis of mitigation effect of the open-and closed-type check dam. E3S Web Conf. EDP Sci. 415, 06011. doi:10.1051/e3sconf/202341506011

CrossRef Full Text | Google Scholar

Lee, S., An, H., Kim, M., Lee, G., and Shin, H. (2022a). Evaluation of different erosion–entrainment models in debris-flow simulation. Landslides 19, 2075–2090. doi:10.1007/s10346-022-01901-y

CrossRef Full Text | Google Scholar

Lee, S., An, H., Kim, M., and Lim, H. (2020). Analysis of debris flow simulation parameters with entrainment effect: a case study in the Mt. Umyeon. J. Korea Water Resour. Assoc. 53, 637–646. doi:10.3741/JKWRA.2020.53.9.637

CrossRef Full Text | Google Scholar

Lee, S., An, H., Kim, M., Lim, H., and Kim, Y. (2022b). A simple deposition model for debris flow simulation considering the erosion–entrainment–deposition process. Remote Sens. 14, 1904. doi:10.3390/rs14081904

CrossRef Full Text | Google Scholar

Liu, J., Nakatani, K., and Mizuyama, T. (2013). Effect assessment of debris flow mitigation works based on numerical simulation by using Kanako 2D. Landslide 10, 161–173. doi:10.1007/s10346-012-0316-x

CrossRef Full Text | Google Scholar

Liu, W., and He, S. (2020). Comprehensive modelling of runoff-generated debris flow from formation to propagation in a catchment. Landslides 17, 1529–1544. doi:10.1007/s10346-020-01383-w

CrossRef Full Text | Google Scholar

Medina, V., Hürlimann, M., and Bateman, A. (2008). Application of FLATModel, a 2D finite volume code, to debris flows in the northeastern part of the Iberian Peninsula. Landslides 5, 127–142. doi:10.1007/s10346-007-0102-3

CrossRef Full Text | Google Scholar

Osti, R., and Egashira, S. (2008). Method to improve the mitigative effectiveness of a series of check dams against debris flows. Hydrol. Process. 22, 4986–4996. doi:10.1002/hyp.7118

CrossRef Full Text | Google Scholar

Park, D., Lee, S., Nikhil, N., Kang, S., and Park, J. (2013). Debris flow hazard zonation by probabilistic analysis (Mt. Woomyeon, Seoul, Korea). Int. J. Innov. Res. Sci. Eng. Technol. 2, 2381–2390.

Google Scholar

Pitman, E. B., Nichita, C. C., Patra, A., Bauer, A., Sheridan, M., and Bursik, M. (2003). Computing granular avalanches and landslides. Phys. Fluids 15, 3638–3646. doi:10.1063/1.1614253

CrossRef Full Text | Google Scholar

Piton, G., Carladous, S., Recking, A., Tacnet, J. M., Li´ebault, F., Kuss, D., et al. (2017). Why do we build check dams in Alpine streams? An historical perspective from the French. Earth Surf. Proces. Landf. 42, 91–108. doi:10.1002/esp.3967

CrossRef Full Text | Google Scholar

Piton, G., and Recking, A. (2016). Design of sediment traps with open check dams. I: hydraulic and deposition processes. J. Hydraul. Eng. 142, 04015045. doi:10.1061/(ASCE)HY.1943-7900.0001048

CrossRef Full Text | Google Scholar

Pudasaini, S. P., and Krautblatter, M. (2021). The mechanics of landslide mobility with erosion. Nat. Commun. 12, 6793. doi:10.1038/s41467-021-26959-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Pudasaini, S. P., and Mergili, M. (2019). A multi-phase mass flow model. J. Geophys. Res. Earth Surf. 124, 2920–2942. doi:10.1029/2019JF005204

CrossRef Full Text | Google Scholar

Reid, M. E., Coe, J. A., and Dianne, L. B. (2016). Forecasting inundation from debris flows that grows volumetrically during travel, with application to the Oregon Coast Range, USA. Geomorphol 273, 396–411. doi:10.1016/j.geomorph.2016.07.039

CrossRef Full Text | Google Scholar

Remaître, A., Malet, J.-P., and Maquaire, O. (2005). Morphology and sedimentology of a complex debris flow in a clay-shale basin. Earth Surf. Proces. Landf. 30, 339–348. doi:10.1002/esp.1161

CrossRef Full Text | Google Scholar

Remaitre, A., van Asch, H., Malet, G., and Maquaire, O. I. (2008). Influence of check dams on debris flow run-out intensity. Nat. Hazards Earth Syst. Sci. 8, 1403–1416. doi:10.5194/nhess-8-1403-2008

CrossRef Full Text | Google Scholar

Rickenmann, D., Laigle, D., McArdell, B. W., and Hübl, J. (2006). Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 10, 241–264. doi:10.1007/s10596-005-9021-3

CrossRef Full Text | Google Scholar

Rizvi, Z. H., Mustafa, S. H., Sattari, A. S., Ahmad, S., Furtner, P., and Wuttke, F. (2020). “Dynamic lattice element modelling of cemented geomaterials. Adv. Comput. Methods Geomechanics IACMAG Symposium 1, 655–665. doi:10.1007/978-981-15-0886-8_53

CrossRef Full Text | Google Scholar

Santi, P. M., Hewitt, K., VanDine, D. F., and Barillas Cruz, E. (2011). Debris-flow impact, vulnerability, and response. Nat. Hazards 56, 371–402. doi:10.1007/s11069-010-9576-8

CrossRef Full Text | Google Scholar

Satofuka, Y., and Mizuyama, T. (2005). Numerical simulation on debris flow control by a grid dam. J. Jpn. Soc. Eros. Control. Eng. 57, 21–27. doi:10.11475/sabo1973.57.6_21

CrossRef Full Text | Google Scholar

Schober, P., Boer, C., and Schwarte, L. A. (2018). Correlation coefficients: appropriate use and interpretation. Anesth. Analg. 126, 1763–1768. doi:10.1213/ane.0000000000002864

PubMed Abstract | CrossRef Full Text | Google Scholar

Seoul (2014). Research contract report: addition and complement causes survey of Mt Woomyeon landslide, Seoul.

Google Scholar

Shen, W., Li, T., Li, P., and Lei, Y. (2020). Numerical assessment for the efficiencies of check dams in debris flow gullies: a case study. Comput. Geotech. 122, 103541. doi:10.1016/j.compgeo.2020.103541

CrossRef Full Text | Google Scholar

Shen, W., Wang, D., Qu, H., and Li, T. (2019). The effect of check dams on the dynamic and bed entrainment processes of debris flows. Landslides 16, 2201–2217. doi:10.1007/s10346-019-01230-7

CrossRef Full Text | Google Scholar

Shrestha, B. B., Nakagawa, H., Kawaike, K., Baba, Y., and Zhang, H. (2012). Driftwood deposition from debris flows at slit-check dams and fans. Nat. Hazards 61, 577–602. doi:10.1007/s11069-011-9939-9

CrossRef Full Text | Google Scholar

Simoni, A., Bernard, M., Berti, M., Boreggio, M., Lanzoni, S., Stancanelli, L., et al. (2020). Runoff-generated debris flows: observation of initiation conditions and erosion-deposition dynamics along the channel at Cancia (eastern Italian Alps). Earth Surf. Proces. Landf. 45, 3556–3571. doi:10.1002/esp.4981

CrossRef Full Text | Google Scholar

Sun, H., You, Y., Liu, J., Zhang, G., Feng, T., and Wang, D. (2021). Experimental study on discharge process regulation to debris flow with open-type check dams. Landslides 18, 967–978. doi:10.1007/s10346-020-01535-y

CrossRef Full Text | Google Scholar

Takahashi, T. (2007). Debris flow: mechanics, prediction and countermeasures. 1st Edn. London: Taylor and Francis. doi:10.1201/9780203946282

CrossRef Full Text | Google Scholar

Wang, W., Chen, G., Han, Z., Zhou, S., Zhang, H., and Jing, P. (2016). 3D numerical simulation of debris-flow motion using SPH method incorporating non-Newtonian fluid behavior. Nat. Hazards 81, 1981–1998. doi:10.1007/s11069-016-2171-x

CrossRef Full Text | Google Scholar

Yoon, B., Jun, K., Jun, B., and Jung, W. (2018). A analysis on the debris flow reduction effect of debris barrier through Simulation. J. Korean Soc. Hazard Mitig. 18, 167–173. doi:10.9798/KOSHAM.2018.18.2.167

CrossRef Full Text | Google Scholar

Zhang, Z., Chai, J., Li, Z., Xu, Z., and Yuan, S. (2022). Reconstruction and effects of a failure of a typical check dam system under an extreme rainstorm on the Loess Plateau, China. Nat. Hazards 111, 1401–1419. doi:10.1007/s11069-021-05101-0

CrossRef Full Text | Google Scholar

Zhou, G. G. D., Hu, H. S., Song, D., Zhao, T., and Chen, X. Q. (2019). Experimental study on the regulation function of slit dam against debris flows. Landslides 16, 75–90. doi:10.1007/s10346-018-1065-2

CrossRef Full Text | Google Scholar