Stability control of open stopes in high-stress deep mining: a structural parameter design methodology based on the improved mathews stability graph method

Introduction: With the depletion of shallow mineral resources and surging demand for deep mining, metal mines in China have generally entered the kilometer-depth mining stage, confronting challenges in stope stability caused by high ground stress, elevated rock temperatures, high seepage pressure, and intense mining disturbances (“three highs and one disturbance”).

Methods: Taking the Dahongshan Copper Mine (800–1000 m depth) as a case study, this paper proposes an enhanced design methodology for structural parameters of deep open stopes to address the limitations of the traditional Mathews stability graph method in 3D mechanical characterization, dynamic evolution analysis, and model generalization.

Results: First, an improved stability graph model was developed by refining hydraulic radius calculations through cross-sectional collaborative analysis and establishing quantifiable zoning thresholds for span and exposure area based on geological variations between eastern and western ore sections. Second, time-series cavity scanning revealed dynamic evolution patterns of stope stability, demonstrating that hydraulic radius and collapse height peak post-blasting. This finding highlights the pre-final blasting state as the critical node for stability evaluation. An ensemble model integrating Stacking, Bagging, Boosting, and Voting strategies demonstrated significant improvements in prediction accuracy and classification performance over traditional logistic regression.

Discussion: Finally, validation in high-stress stopes at 600–1000 m depths confirmed the model’s generalization capability, offering a data-mechanism dual-driven decision framework for structural parameter design in deep open stopes.

1 Introduction

With the surging global demand for mineral resources and the gradual depletion of shallow deposits, deep mining has become an inevitable choice to ensure sustainable development in the mining industry (Fairhurst, 2017; Ranjith et al., 2017). Leading mining nations such as South Africa have reached depths of 4,000 m, while Australia and Canada operate at 1,900 m and 3,000 m, respectively (Li X. et al., 2017). In China, nearly 50 metal mines have exceeded 1,000 m in depth, though none have yet surpassed 2,000 m. Over the next decade, one-third of China’s mines are projected to operate at depths exceeding 1,000 m, with some extending to 2,000–3,000 m (Cai et al., 2019), marking a full transition into the “second-depth space” (1,000–2,000 m) for metal resource extraction (Li X. et al., 2017; Wang et al., 2023). The “three highs and one disturbance” environment (high in situ stress, high rock temperature, high pore pressure, and intense mining-induced disturbances) in deep mining significantly exacerbates stope stability risks (Wang et al., 2025). For instance, at China’s Dahongshan Copper Mine—a representative deep mining operation exceeding 800 m in depth—the rational design of stope structural parameters is critical to safety, productivity, and economic viability. However, conventional design methods exhibit inadequate adaptability under complex deep geological conditions, underscoring the urgent need for more precise stability assessment models.

The determination of stope structural parameters currently relies primarily on empirical analogy, numerical simulation, and theoretical analysis (Ju et al., 2019; Zhou et al., 2023). The Mathews stability graph method has been widely adopted due to its simplicity and engineering applicability (Mathews et al., 1980). This method delineates stability zones in stopes through the critical relationship between hydraulic radius (HR) and stability number (N). Its core parameters include the rock mass quality index (Q), stress ratio (Factor A), joint orientation adjustment coefficient (Factor B), and gravitational adjustment coefficient (Factor C). Subsequent studies by Potvin et al., Stewart, Forsyth, and Trueman et al. have updated the zoning criteria of the stability graph and refined the computational methods for certain factors; however, these modifications have not significantly improved the predictive performance of the technique (Brown and Block, 2002). Nickson (1992) and Hadjigeorgiou et al. (1995) further enhanced the modified stability graph method proposed by Potvin et al., introducing distinct zones for supported and unsupported conditions within the stability graph. The original Mathews stability graph classified zones into three categories: stable zone, unstable zone, and caving zone. Stewart and Forsyth (1995) redefined the chart into four regions using three transitional boundaries: potentially stable zone, potentially unstable zone, potentially severe failure zone, and potential collapse zone. While their approach incorporated the concept of stability probability, it lacked quantitative data to represent the likelihood of stability. Trueman et al. (2000) expanded the stability graph database by integrating numerous large-scale stope case studies, culminating in a dataset of approximately 500 entries. Building on this database, Mawdesley et al. (2001) extended the Mathews stability graph for open stoping using log-log axes and logistic regression, establishing a probability density function model and plotting multiple iso-probability contour lines. Subsequent research has widely adopted this model to derive stability-failure boundary equations with 95% probability for stope structural parameter design. In recent years, scholars have extended classical methods through the integration of machine learning (Santos et al., 2020; Huang and Zhou, 2024; Putra et al., 2024), theoretical analysis (Zhao et al., 2019; Li et al., 2023; Li et al., 2025) and 3D numerical simulations (Jia et al., 2022; Zhang et al., 2024); however, their limitations in deep mining scenarios remain unresolved.

Despite significant advancements in the Mathews stability graph method, its application remains constrained by the following limitations: (1) Restricted applicability: Existing models predominantly rely on hard rock shallow mining datasets (depth <500 m), exhibiting insufficient adaptability to high-stress soft rock formations in deep mining environments; (2) Dimensional oversimplification: Most studies employ two-dimensional analyses of single cross-sections, neglecting the influence of three-dimensional geometric characteristics of stopes on stability; (3) Data representativeness deficiencies: Case databases are limited in scale (n < 200), with deep mining scenarios constituting less than 40% of the dataset; (4) Algorithmic homogeneity: Decision boundaries predominantly depend on logistic regression, which demonstrates limited capability in capturing nonlinear relationships; (5) Parameter uncertainty: Induced stresses are approximated through parameter estimations or simplified as vertical stresses, while hydraulic radius calculations disregard the projected area of inclined roof surfaces, leading to cumulative errors.

This study develops an integrated data-mechanism approach to address three critical limitations of the Mathews stability graph method in deep mining: inadequate 3D mechanical characterization, unclear dynamic evolution patterns, and poor model generalization. Key innovations include: (1) A 3D parametric model overcoming traditional 2D geometric oversimplification through cross-sectional synergy analysis and reconstructed hydraulic radius calculation, establishing zone-specific stability thresholds for distinct geological conditions; (2) First identification of critical stability assessment timing through void sequence scanning, revealing pre-final-blasting conditions as the decisive evaluation node; (3) A multi-algorithm ensemble (Stacking/Bagging/Boosting) achieving 5%–10% accuracy improvement over conventional logistic regression, validated in 600–1000 m deep high-stress stopes. The proposed “threshold-dynamics-warning” framework offers an engineering-theoretical integrated solution for deep stope optimization in metal mines.

2 Materials and methods

2.1 Mathews stability graph method

Mathews et al. (1980) established a two-dimensional stability graph based on 55 stope case studies from Canadian mines, incorporating the stability number N and shape factor S (HR). This graph classified open stopes into three distinct stability zones based on roof stability criteria: the stable zone, unstable zone, and caving zone.

2.1.1 Stability number N

The stability number N, representing the rock mass’s capacity to maintain stability under prescribed stress conditions, is analogous to the Mining Rock Mass Rating (MRMR) in conventional evaluation methodologies. The relationship between N and its governing factors is defined as:

$N=Q^{\prime }·A·B·C(1)$

where Q’ denotes the modified Q-value, reflecting adjusted rock mass quality; A represents the rock stress coefficient, quantifying in situ stress effects; B corresponds to the joint orientation adjustment coefficient, accounting for discontinuity alignments; C signifies the gravitational adjustment coefficient, addressing depth-induced stress variations.

2.1.1.1 Q’ value

Q’ is determined through geological survey maps or borehole core log analysis and shares conceptual similarities with the rock mass quality Q-index (Equation 2). Specifically, Q’ is calculated by assuming both the joint water reduction coefficient (J_w) and stress reduction factor (SRF) equal to 1 (i.e., J_w/SRF = 1), resulting in:

$Q=\frac{RQD}{J_n}·\frac{J_r}{J_a}·\frac{J_w}{SRF}(2)$

Parameter Definitions:

•RQD: Rock Quality Designation, quantifying intact rock integrity;

•J_n: Joint set number, reflecting the density of discontinuities;

•J_r: Joint roughness coefficient, characterizing surface asperities;

•J_a: Joint alteration coefficient, describing infilling material properties;

•J_w: Joint water reduction coefficient, assessing groundwater effects;

•SRF: Stress reduction factor, addressing in situ stress magnitudes.

Interpretation of Parameter Groups:

1. RQD/J_n evaluates the intactness of the rock mass;

2. J_r/J_a represents the morphological characteristics of discontinuities, including surface roughness and alteration degree;

3. J_w/SRF accounts for environmental influences, such as groundwater pressure and tectonic stresses.

2.1.1.2 Factor A

Factor A, the rock stress coefficient, is determined by the ratio of the intact rock uniaxial compressive strength (Rc) to the induced stress (σ_I) generated by mining activities at the stope centerline, as illustrated in Figure 1. Rc is obtained through field sampling and laboratory rock mechanics testing. The induced stress σ_I, defined as the stress parallel to the exposed stope walls or roof in the analysis, is estimated using parameters such as the height-to-span ratio and lateral pressure coefficient. Consequently, the mean stress parallel to the cross-section is utilized in subsequent parameter calculations to replace estimated values.

Figure 1

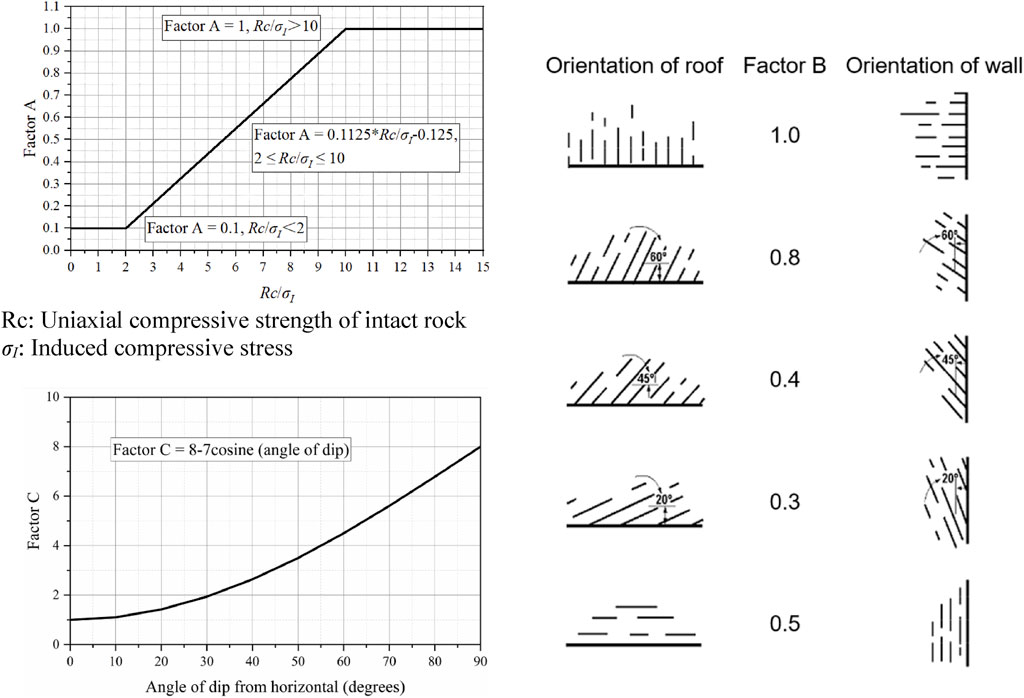
Figure 1. Evaluation of adjustment factors in the Mathews stability graph method (Mathews et al., 1980). Rc: Uniaxial compressive strength of intact rock, σ_I: Induced compressive stress.

2.1.1.3 Factor B

Factor B, the joint orientation adjustment coefficient, is quantified by the angular difference between the dip angle of the stope face and the dominant joint set orientation, as depicted in Figure 1. The calculation process involves first identifying the dip angle of the dominant joint set within the stope, followed by determining the corresponding value of coefficient B.

2.1.1.4 Factor C

Factor C, the gravitational adjustment coefficient, quantifies the influence of stope face orientation on the stability of mine rock masses. Its value is determined by failure mechanisms including caving of exposed roof surfaces, sliding along inclined planes, and sidewall sloughing. As depicted in Figure 1, which illustrates the dip angle (α) of the stope relative to the horizontal plane.

2.1.2 Hydraulic radius

The hydraulic radius (HR), which reflects the stope’s dimensions and geometry, is determined by the following equation:

$HR=\text{xy}/\left(2x+2y\right)(3)$

where HR represents the permissible hydraulic radius of the excavation surface, expressed in meters (m); x denotes the stope length along the dip direction, in meters (m); y signifies the stope length along the strike direction, in meters (m).

2.1.3 Cooperative analysis

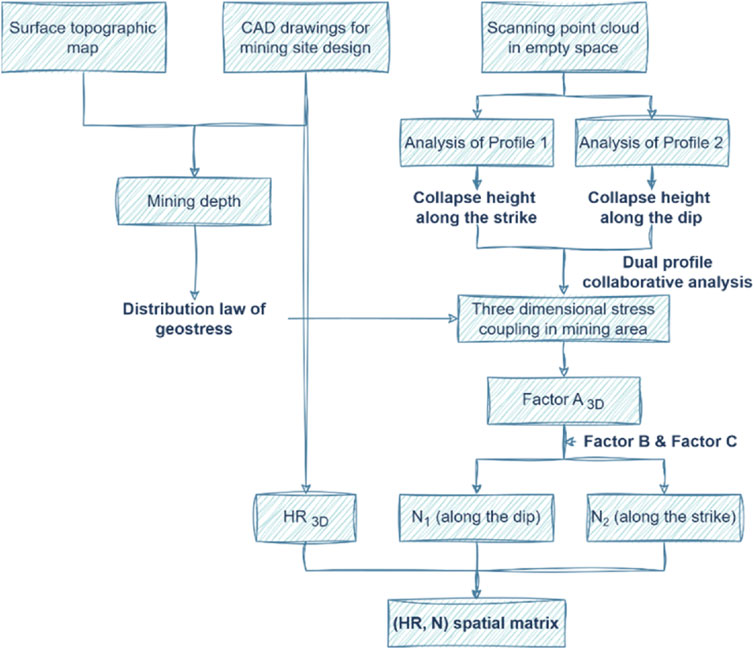
In response to the limitations of traditional Mathews methods in characterizing three-dimensional mechanical states, this study proposes a three-dimensional parameterized improved Mathews stability diagram model. Through collaborative analysis of transverse and longitudinal profiles and correction of hydraulic radius calculation, a (HR, N) spatial matrix is constructed to achieve 3D mechanical characterization of the mining site, as shown in Figure 2.

Figure 2

Figure 2. Multi profile collaborative analysis construction (HR, N) matrix.

2.2 Ensemble learning

Stacking, also known as stacked generalization, was first proposed by Wolpert (1992). This method aims to minimize prediction errors by combining outputs from diverse base learners (referred to as primary learners) through a meta-machine learning (ML) algorithm (termed the meta-model). As illustrated in Figure 3a, the predictions of primary learners are aggregated as new input features for the meta-model to generate final predictions.

Figure 3

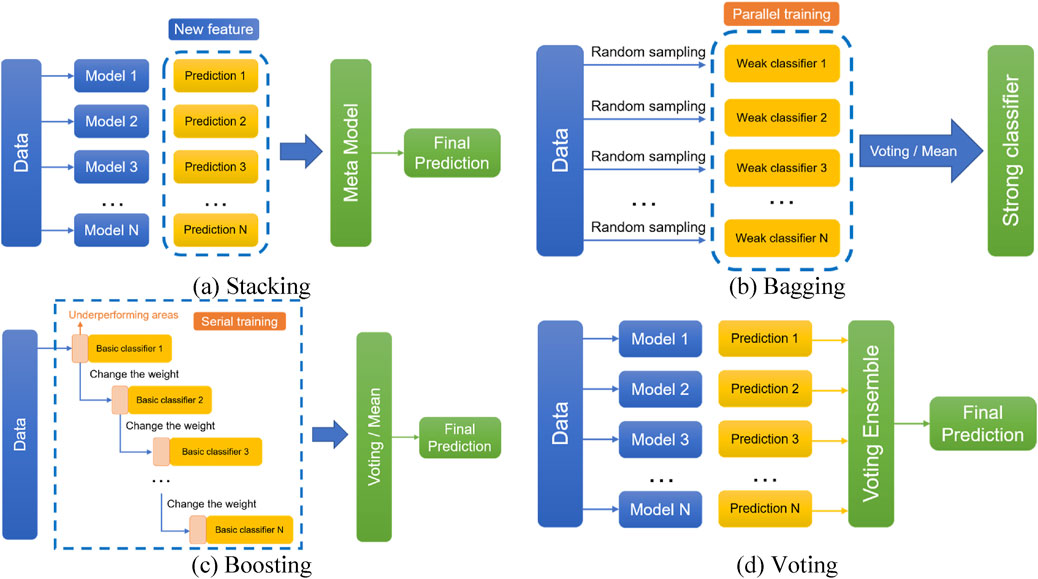
Figure 3. Principles of ensemble learning algorithms. (a) Stacking, (b) bagging, (c) boosting, (d) voting.

Bagging (Bootstrap Aggregating) offers a straightforward approach to enhance model performance by training multiple instances of a base algorithm on bootstrapped subsets of the original dataset (Breiman, 1996). Shown in Figure 3b, weak classifiers trained on randomly sampled data (with replacement) are combined via voting (for classification) or averaging (for regression) to form a robust ensemble classifier. The independence among classifiers arises from parallel training on distinct subsets.

Boosting adopts a sequential strategy to iteratively link base learners, where each subsequent learner prioritizes samples misclassified by previous ones (Li Q. et al., 2017). As depicted in Figure 3c, misclassified instances receive higher weights in successive training iterations. The final prediction is a weighted sum of all learners, with higher weights assigned to more accurate models.

Voting synthesizes predictions from multiple ML models to derive consensus results (Dong et al., 2020). In Figure 3d, base models trained on the full dataset contribute individual “votes,” and the majority prediction (for classification) or averaged value (for regression) is selected as the final output.

2.3 Mine overview

The Dahongshan Copper Mine, located in Yuxi City, Yunnan Province, China (as shown in Figure 4), has an annual ore production of 4.29 million tonnes. Mining operations are divided into the Eastern and Western Sections. In the Eastern Section, the primary production is currently conducted at the 285 mining level with a depth exceeding 800 m. Future operations at the planned 185 mining level and deeper zones will extend beyond 800 m. In the Western Section, active mining is focused on sub-level 80 of the 180 mining level at depths of 900–1,000 m. Post-2025, operations will transition to the −20 mining level, reaching depths of 800–1,100 m.

Figure 4

Figure 4. The location of Dahongshan copper mine.

The Dahongshan Copper Mine features stratified orebodies with thicknesses of 1–21 m and dip angles ranging from 17° to 43° (average 27°), classified as gently dipping thin to medium-thick deposits with interburden layers of 2–10 m and an average copper grade of 0.38%. The mine operates with Class II rock mass quality and predominantly employs open stoping with subsequent backfill. In the Eastern Section, downward parallel long-hole drilling is utilized, with stope spans typically exceeding 25 m (maximum 30 m) and ultimate lengths of 50–100 m. In the Western Section, upward fan drilling is adopted at the −20 mining level, where designed panel dimensions reach 45–51 m in strike length (maximum 74 m) and 18–29.2 m in dip span (maximum 39 m), collectively indicating oversized stope geometries with elevated roof caving risks.

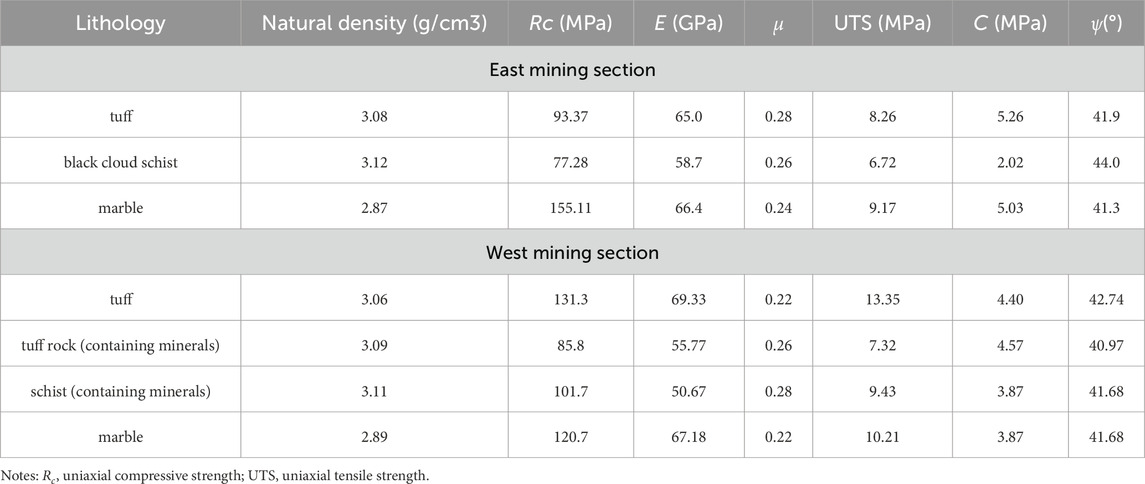
Rock mechanics test samples were collected from the following locations: the Eastern Section focused on the B12–B64 zones at the 285–385 m elevation of the 285 mining level, and the Western Section concentrated on the B88–B120 zones at sub-level 140 of the −20 mining level. Data in Table 1 demonstrate significant differences in rock mass parameters between the two sections.

Table 1

Table 1. Indoor rock mechanics test results of Dahongshan copper mine.

2.4 Stope investigation

Based on the void scanning data obtained from the mining operations and comparative analysis against the stope design CAD drawings, we conducted a comprehensive investigation on roof collapse mechanisms in open stope subsequent backfill mining systems. The study encompasses 108 stopes distributed across four mining levels: Level 285 and Level 385 in the eastern mining section, as well as Level −20 and Level 180 in the western mining section. Critical parameters including stope geometry (length/width), roof exposure characteristics (projected area, overburden depth, and inclination angle), and collapse development metrics (average collapse height) were systematically analyzed. The spatial distribution patterns of investigation outcomes across different mining levels are visually presented in Figure 5.

Figure 5

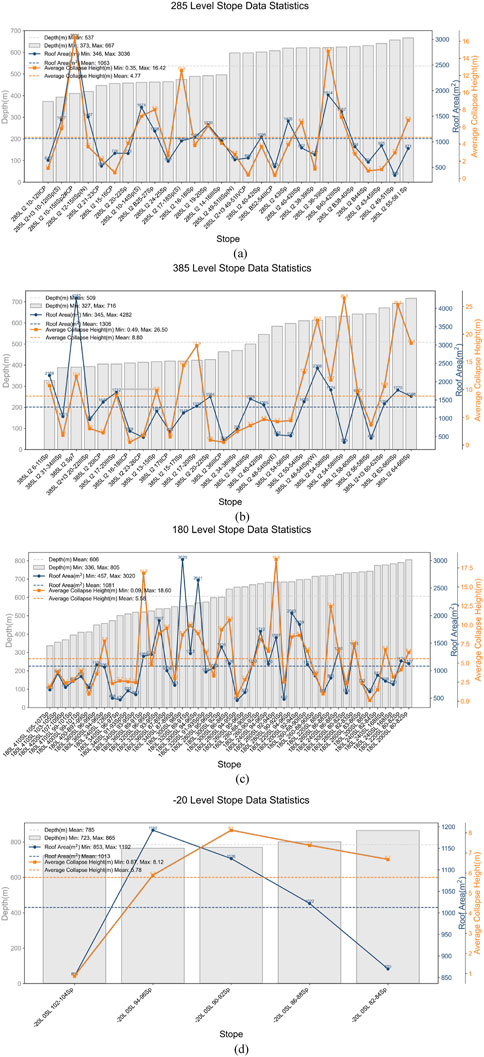
Figure 5. Results of stope investigation: (a) 285 level, (b) 385 level, (c) 180 level and (d) −20 level.

2.5 Parameter calculations

2.5.1 Determination of Q’ value

Rock mass quality evaluation was conducted using the Q-system, with both the joint water reduction factor (J_w) and stress reduction factor (SRF) set to 1, resulting in the simplified Q’-value. The engineering geological investigation included 12 tunnels in the eastern mining section and 8 tunnels in the western mining section. Accordingly, the mean Q’-value of 161.72 from the eastern section was applied to the 285 and 385 levels, while the mean Q’-value of 167.08 from the western section was used for the 180 and -20 levels.

2.5.2 Determination of A value

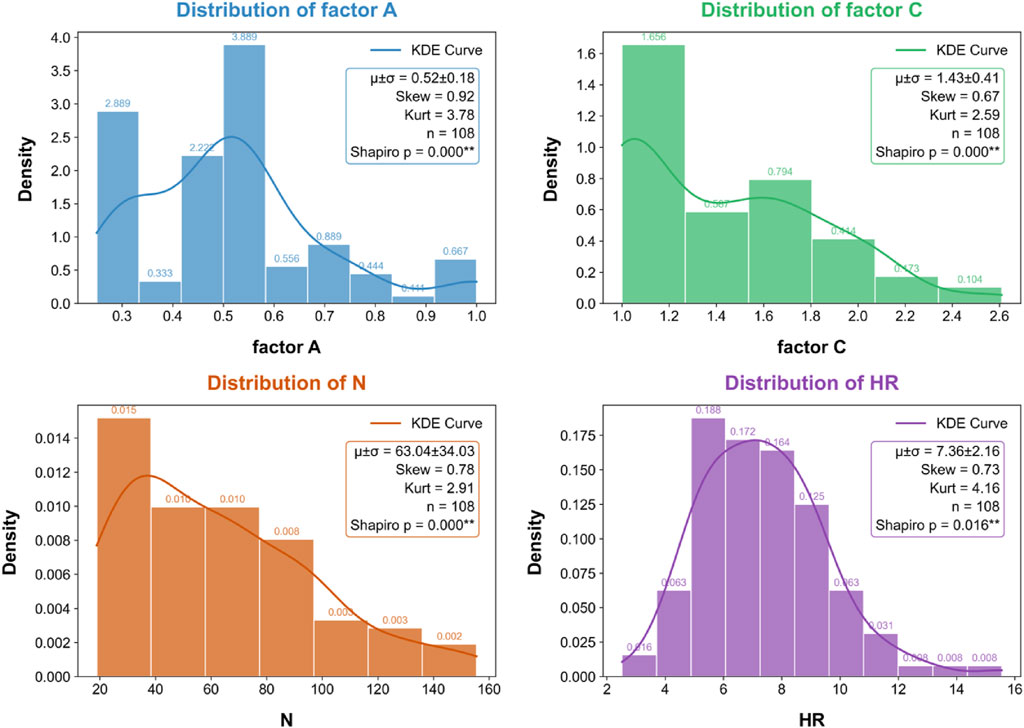
Factor A for each stope was determined based on laboratory rock mechanics tests and induced stress calculations. As shown in Figure 6, Factor A exhibits a right-skewed distribution (skewness = 0.92) with a mean of 0.52 and standard deviation of 0.18. The positive skewness indicates data concentration in lower-value ranges and a long tail toward higher values. The leptokurtic distribution (kurtosis = 3.78) demonstrates steeper peaks and heavier tails compared to a normal distribution, suggesting significant clustering around the mean with outliers at higher values. The Shapiro-Wilk test ($p<0.01$) strongly rejected the normality assumption, necessitating non-parametric methods for subsequent analysis. A moderate coefficient of variation (CV, Coefficient of Variation = 34.6%) reflects balanced data dispersion.

Figure 6

Figure 6. Data distribution: factor A, factor C, N and HR.

2.5.3 Determination of B value

Engineering geological investigations at the Dahongshan Copper Mine revealed that the dip angles of structural discontinuities in the rock mass are predominantly distributed between 40° and 90°, classifying them as steeply dipping structural discontinuities. In accordance with the B-value evaluation criteria, Factor B was determined to be 0.8 for subsequent geomechanical analyses.

2.5.4 Determination of C value

Based on the dip angles of roofs in stop cross-sectional profiles (Figure 1), Factor C was calculated for each stope. As shown in Figure 6, Factor C exhibits a mildly right-skewed distribution (skewness = 0.67) with a mean of 1.43 and standard deviation of 0.41. The platykurtic distribution (kurtosis = 2.59) indicates flatter peak and lighter tails compared to the normal distribution, suggesting relatively uniform data dispersion around the central region. Despite proximity to the normal distribution benchmark (kurtosis = 3), the Shapiro-Wilk test ($p<0.01$) confirmed significant deviation from normality. The low coefficient of variation (CV = 28.7%) demonstrates limited data dispersion.

2.5.5 Determination of N value

Based on the aforementioned parameters and Equation 1, Parameter N was calculated for each stope. As illustrated in Figure 6, Parameter N exhibits a pronounced right-skewed distribution (skewness = 0.78) with a mean value of 63.04 and standard deviation of 34.03. The platykurtic distribution (kurtosis = 2.91) approximates the normal distribution benchmark but demonstrates flattened morphology, reflecting weakened central clustering and extended tail dispersion. The Shapiro-Wilk test ($p<0.01$) conclusively rejected normality, while the exceptionally high coefficient of variation (CV = 54.0%) highlights substantial dataset heterogeneity. This variability likely originates from multi-factorial contributions (e.g., multiplicative interactions) to Parameter N, resulting in an extensive numerical range.

2.5.6 Calculation of HR

Hydraulic radius (HR) was calculated using stope lengths along dip and strike directions as parameters (Equation 3), where the inclined dip length replaced traditional span measurements to better characterize actual stope area and perimeter. As shown in Figure 6, HR exhibits a right-skewed distribution (skewness = 0.73) with a mean of 7.36 and standard deviation of 2.16. The leptokurtic distribution (kurtosis = 4.16) demonstrates steep central clustering and heavy tails, where rare high-value outliers significantly influence the distribution despite most data being tightly grouped around the mean. The Shapiro-Wilk test ($p=0.016$) marginally rejected normality at α = 0.05, indicating subtle deviation from Gaussian assumptions. While the low coefficient of variation (CV = 29.3%) suggests moderate dispersion, the interplay between skewness and kurtosis implies potential subpopulation existence.

3 Results

Stability charts and classification criteria were developed separately for the eastern and western mining sections, as significant differences exist in rock compressive strength, stope structural parameters, and drilling techniques between these two zones.

3.1 Scatter plots and data processing

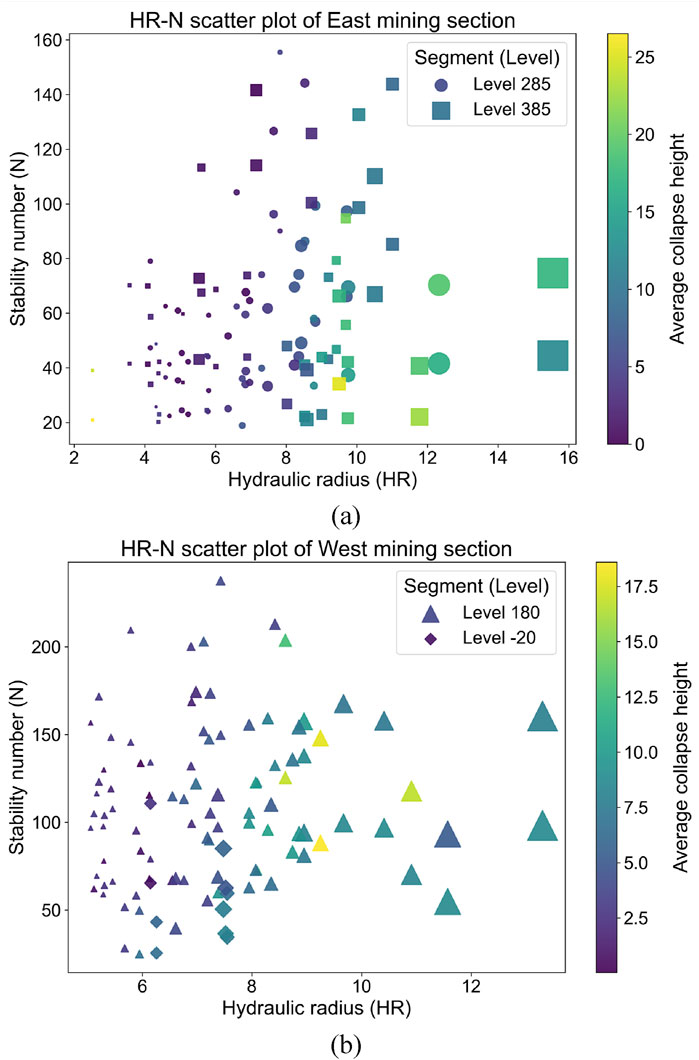
The eastern mining section documented a total of 56 stopes, with 28 located at the 285 level and 28 at the 385 level, while the western section comprised 52 stopes, including 47 at the 180 level and 5 at the −20 level. HR values, calculated uniformly from roof dip angles across transverse and longitudinal axial profiles of each stope, yielded 216 paired datasets (HR, N), subsequently partitioned into training and testing sets at a 7:3 ratio. Scatterplots of HR-N relationships (Figure 7) were generated separately for both mining sections, employing distinct geometric markers: circular markers for the 285 level, square markers for the 385 level, triangular markers for the 180 level, and diamond markers for the −20 level. Color gradients from yellow (indicating poor stability) to purple (denoting high stability) visually encoded stope stability, while marker sizes proportionally represented exposed areas. Annotations within the plots provided quantitative metrics including mean collapse height (m) and exposed area (m²) for individual stopes.

Figure 7

Figure 7. Scatter plot of HR-N data: (a) East mining section and (b) West mining section.

3.2 Model development

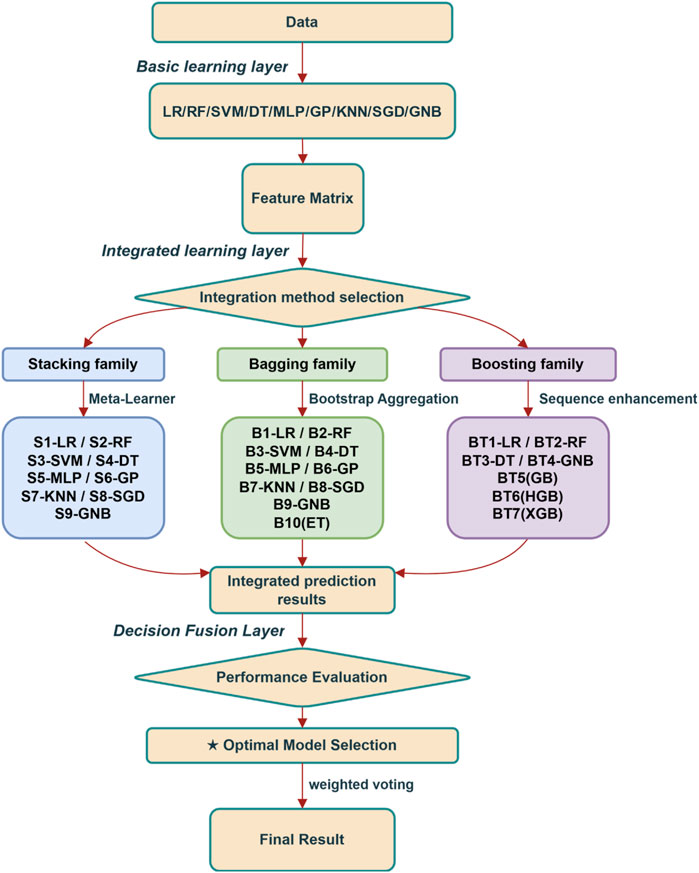
Nine machine learning algorithms—Logistic Regression (LR), Random Forest (RF), Support Vector Machine (SVM), Decision Tree (DT), Multilayer Perceptron (MLP), Gaussian Process (GP), K-Nearest Neighbors (KNN), Stochastic Gradient Descent (SGD), and Gaussian Naive Bayes (GNB)—were applied to the training dataset. The predictive outputs of these base learners served as input features for ensemble learning architectures, generating 9 stacking meta-learners (S1–S9), 10 bagging ensembles (B1–B10), and 7 boosting ensembles (BT1–BT7). Specifically, the Extra Trees (ET) algorithm was derived from bagging with extreme randomized trees, while Gradient Boosting (GB), Histogram-based Gradient Boosting (HGB), and Extreme Gradient Boosting (XGB) were implemented under the boosting framework. High-performing ensemble classifiers participated in majority voting to construct the stability classification model for deep open stoping, ultimately deriving decision boundaries and categorical outcomes. The model development process is illustrated in Figure 8.

Figure 8

Figure 8. Modeling flowchart.

The stope stability classification models adopted distinct ensemble learning strategies for the eastern (V-east) and western (V-west) mining sections based on test set accuracy and decision boundary performance. For the V-east model, LR, RF, SVM, MLP, and GNB were selected as base learners for the stacking meta-algorithm, while ensemble classifiers S1, S5, B1, B3, and BT2 participated in the final voting mechanism. Conversely, the V-west model utilized LR, RF, and SVM as stacking base learners, with ensemble classifiers S1, S5, S6, S9, and B1 incorporated into the voting system, reflecting section-specific geomechanical heterogeneity in optimal classifier combinations.

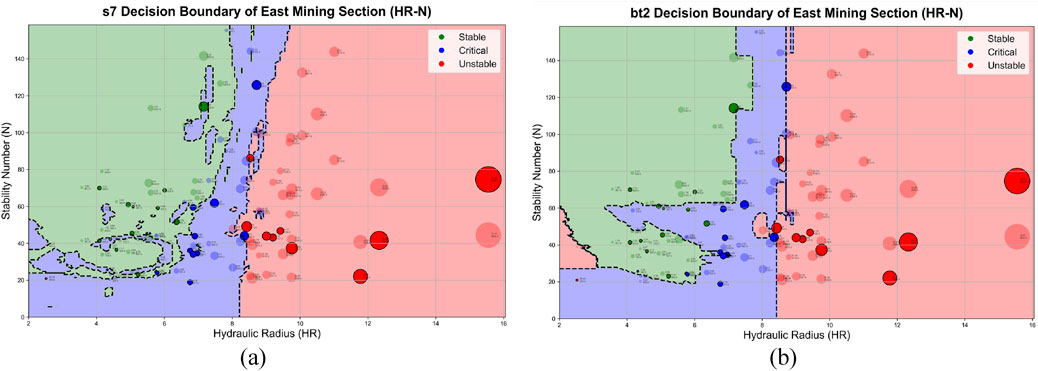
3.3 Decision boundaries and classification criteria

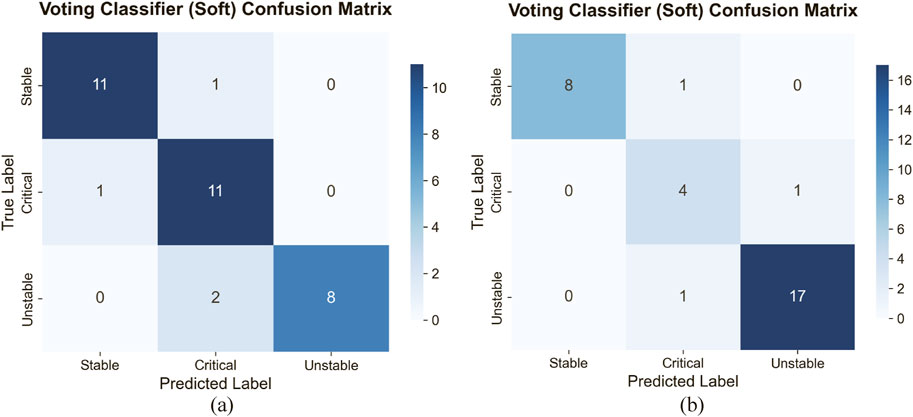
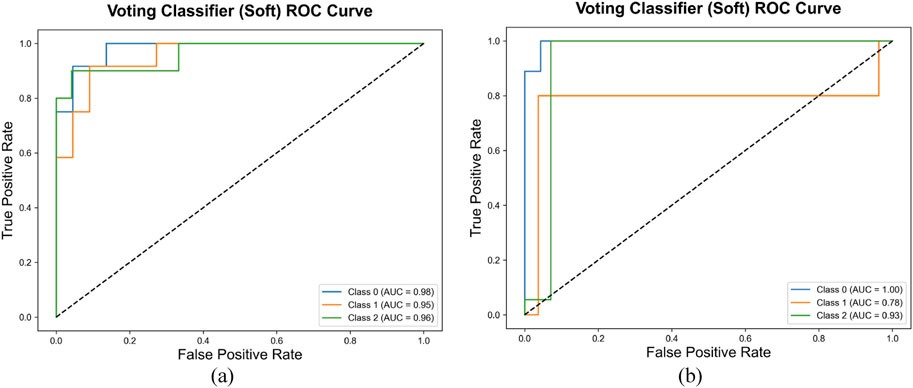
The models were trained on the training set to delineate decision boundaries, as illustrated in the accompanying Figure 9. Two critical boundaries were derived: Boundary 1 (boundary 3) separates stable zones from critical zones, while Boundary 2 (boundary 4) distinguishes critical zones from unstable zones. Translucent markers represent training data, whereas opaque markers denote test data. The experimental results demonstrate divergent classification performance between the decision boundary models of the eastern and western mining sections. Specifically, the eastern section model achieved an accuracy of 88.24% and an F1-score of 88.36% on the test set, while the western section model exhibited superior discriminative capacity with accuracy and F1-score values reaching 90.63% and 90.96%, respectively. As revealed by the confusion matrix in Figure 10, the eastern model demonstrated relatively balanced classification performance across all three target categories. Although the western model displayed outstanding overall performance, as evidenced by its Receiver Operating Characteristic (ROC) curve in Figure 11, its classification efficacy for critical-class samples (AUC = 0.78) slightly underperformed the model’s average benchmark.

Figure 9

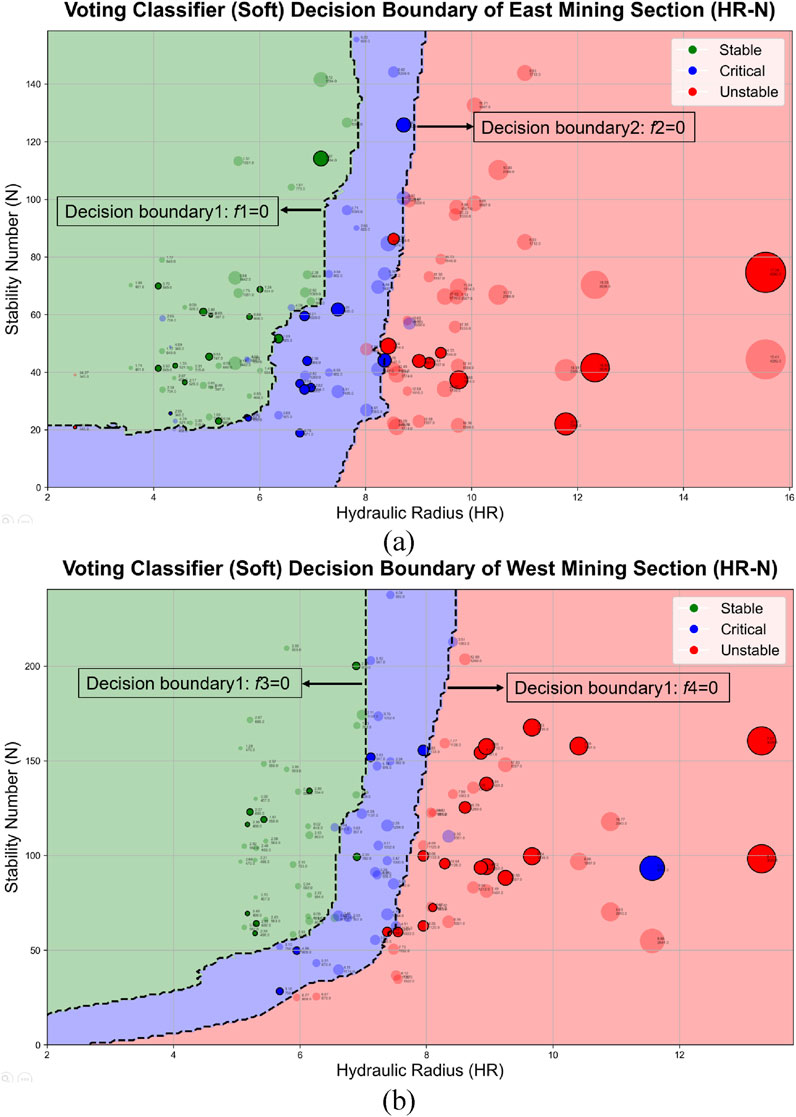
Figure 9. Classification decision boundary for mining stability: (a) East mining section and (b) West mining section.

Figure 10

Figure 10. Confusion matrix: (a) East mining section and (b) West mining section.

Figure 11

Figure 11. ROC curve: (a) East mining section and (b) West mining section.

The decision boundaries of ensemble models typically represent complex combinations of multiple constituent models, making direct derivation of simplified analytical expressions impractical. However, approximate interpretations can be achieved by analyzing boundaries from base classifiers exhibiting high accuracy and geometric congruence with ensemble decision patterns. Consequently, we extracted linear decision boundary approximations (Equations 4–7) from Logistic Regression (LR). These formulations preserve the critical separation between stable, critical, and unstable zones while maintaining engineering applicability through their interpretable parametric form. N is a dimensionless quantity, and the HR unit is m.

$\mathrm{f}10.049+0.591HR-0.170N-0.010H{R}^2+0.013HR·N=0(4)$

$\mathrm{f}2-0.124-1.293HR-0.090N+0.205H{R}^2+0.005HR·N=0(5)$

$\mathrm{f}30.096+0.647HR-0.458N+0.051H{R}^2+0.055HR·N=0(6)$

$\mathrm{f}4-0.052-0.497HR-0.391N+0.170H{R}^2+0.043HR·N=0(7)$

To enhance the operational utility of decision boundaries, stability classification criteria for roof stability in deep open stoping at the Dahongshan Copper Mine were formulated by synthesizing decision boundary expressions Equations 8–13 with projection areas of proximal data points along boundary regions.

(1) Eastern Section:

$\text{Stable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p\le 863{\mathrm{m}}^2\\ \mathrm{f}1\le 0\end{array}\right.(8)$

$\text{Critical\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}863{\mathrm{m}}^2<A_p\le 1623{\mathrm{m}}^2\\ \mathrm{f}1>0,\mathrm{f}2\le 0\end{array}\right.(9)$

$\text{Unstable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p>1623{\mathrm{m}}^2\\ \mathrm{f}2>0\end{array}\right.(10)$

(2) Western Section:

$\text{Stable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p\le 811{\mathrm{m}}^2\\ \mathrm{f}3\le 0\end{array}\right.(11)$

$\text{Critical\hspace{0.17em}zone}\left\{\begin{array}{l}811{\mathrm{m}}^2<A_p\le 1067{\mathrm{m}}^2\\ \mathrm{f}3>0,\mathrm{f}4\le 0\end{array}\right.(12)$

$\text{Unstable\hspace{0.17em}zone}\left\{\begin{array}{l}{A}_p>1067{\mathrm{m}}^2\\ \mathrm{f}4>0\end{array}\right.(13)$

4 Discussion

4.1 Temporal effects

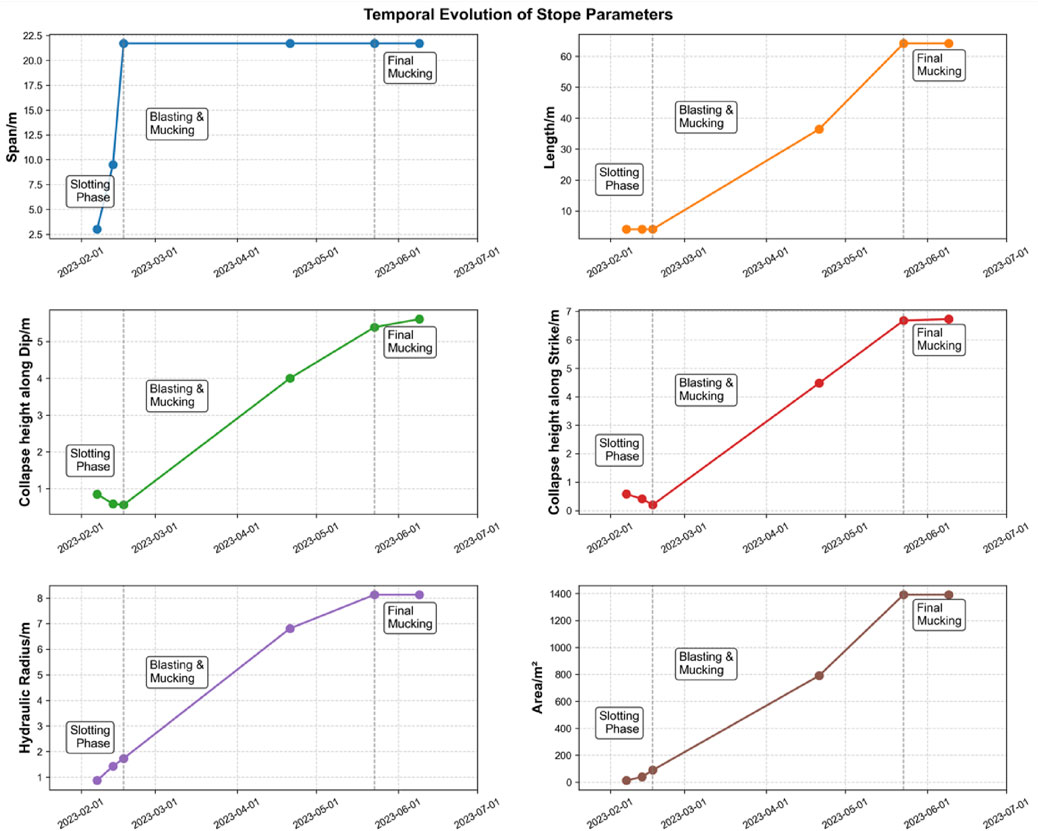
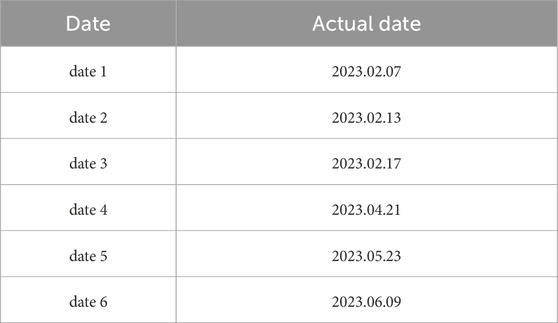
The stope extraction process encompasses sequential phases including development, slot slashing, blasting, mucking, and backfilling, as illustrated in Figure 12. Through void scanning analysis, key geometric parameters—dip and strike collapse heights, exposed surface span, length, hydraulic radius (HR), and area—were quantified across operational phases to investigate temporal effects on roof stability post-exposure. Temporal trends of stability-related parameters reveal distinct phase-dependent behaviors: the exposed surface span exhibited significant growth during date1–date3 before stabilizing, while the exposed length continued increasing through date3–date5 until achieving equilibrium by date6. This progression indicates slot slashing completion by date3 and blasting cessation by date5, defining date3–date5 as the blasting-mucking phase and date5–date6 as the post-mucking stabilization period. The correspondence between Date1∼date6 and specific periods is shown in Table 2.

Figure 12

Figure 12. Status of stope at different periods.

Table 2

Table 2. Date correspondence table.

The analysis of graphical data reveals distinct temporal patterns in geomechanical parameters across mining phases. During slot slashing (date1–date3), the mean collapse height demonstrated gradual reduction, while it exhibited significant time-dependent escalation throughout blasting operations (date3–date5) before stabilizing post-blasting. The mucking phase (date5–date6) showed marginal variation in collapse height. Hydraulic radius and exposed area followed similar trends, with accelerated growth during blasting followed by stabilization after full roof exposure. These observations confirm that post-blasting roof conditions provide critical safety benchmarks for operational planning.

4.2 Zoning criteria and definitions

The Mathews stability graph originally classified open stopes into three zones: stable zone, unstable zone, and caving zone (Mathews et al., 1980). Subsequently, Stewart and Forsyth refined the Mathews stability graph by proposing four zones demarcated by three transitional boundaries: potentially stable zone, potentially unstable zone (failure zone), potentially major failure zone, and potential caving zone. Caving is defined as occurring when rock mass failure and collapse progress until all available void space becomes filled with fragmented rock, continuing as fragmented material is removed from stope boundaries. Major failure is identified when over 30% dilution occurs or caving extends into stopes with wall penetration depths exceeding 50% of the opening’s smaller dimension. However, the distinction between failure and major failure remains ambiguous compared to the clearer differentiation between stability and caving, resulting in significant misclassification risks (Brown and Block caving geomechanics, 2002). To address this limitation, our study redefines the stability graph into three zones based on the mean collapse height (h) and its ratio to stope height (H): stable zone (h < 0.1H, h < 2.5–3 m), critical zone (0.1H < h < 0.4H), and unstable zone (h > 0.4H). This tripartite classification system enhances operational predictability while maintaining compatibility with field monitoring thresholds.

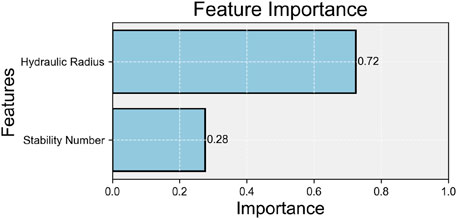
4.3 Analysis of stope stability factors

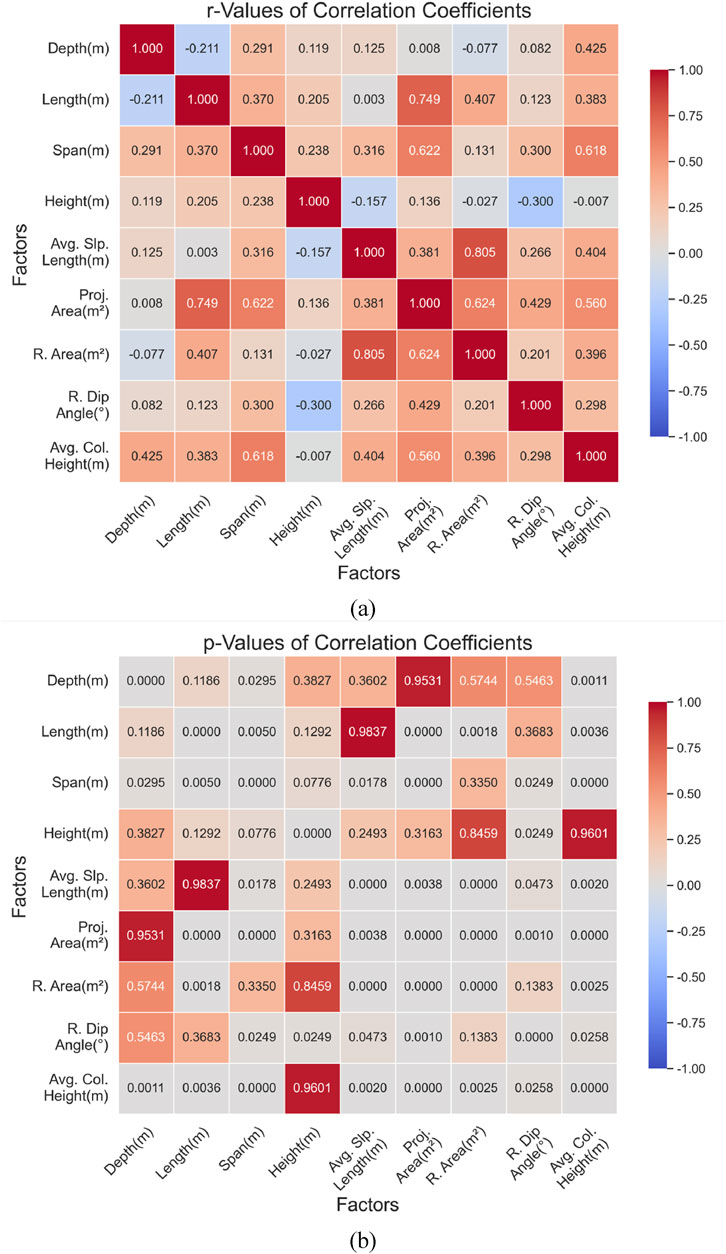
To optimize engineering decision-making in stope stability analysis, it is imperative to quantify the interrelationships among critical geological and geometric parameters (including burial depth, length, span, and roof dip angle). This study calculated Pearson correlation coefficients for these variables to evaluate their association strength. As demonstrated in the heatmap (Figure 13), significant correlations (∣r∣>0.5, $p<0.001$) were observed between span, projected roof area, and average caving height, indicating these parameters’ substantial influence on stope stability. Based on these findings, this research establishes engineering application guidelines for stope stability classification criteria. The core Equations 14–19 integrates two critical parameters - span (S) and projected area (Ap) - providing a theoretical foundation for designing structural parameters in deep open stope mining operations at the Dahongshan Copper Mine.

(1) Critical Control Parameters for Stopes in the Eastern Mine Section

$\text{Stable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p\le 863{\mathrm{m}}^2\\ S\le 25\mathrm{m}\end{array}\right.(14)$

$\text{Critical\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}863{\mathrm{m}}^2<A_P\le 1623{\mathrm{m}}^2\\ 25\mathrm{m}<S\le 31\mathrm{m}\end{array}\right.(15)$

$\text{Unstable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p>1623{\mathrm{m}}^2\\ S>31\mathrm{m}\end{array}\right.(16)$

(2) Critical Control Parameters for Stopes in the Western Mine Section

$\text{Stable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_p\le 811{\mathrm{m}}^2\\ S\le 20\mathrm{m}\end{array}\right.(17)$

$\text{Critical\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}811{\mathrm{m}}^2<A_P\le 1067{\mathrm{m}}^2\\ 20\mathrm{m}<S\le 25\mathrm{m}\end{array}\right.(18)$

$\text{Unstable\hspace{0.17em}zone\hspace{0.17em}}\left\{\begin{array}{l}{A}_P>1067{\mathrm{m}}^2\\ S>25\mathrm{m}\end{array}\right.(19)$

Furthermore, analytical results demonstrated a statistically significant positive correlation ($p<0.001$) between burial depth and average caving height in both the −20 and 385 mining levels. Notably, the magnitude of this influence was notably amplified compared to other mining levels. This phenomenon suggests that increased mining depth, coupled with high-stress environments, may impose greater destabilizing effects on stope stability as extraction progresses to deeper horizons. Furthermore, the random forest feature importance analysis (Figure 14) demonstrates that the hydraulic radius (HR) exhibits significantly higher predictive dominance (72%) in stope stability classification compared to the stability number (N, 28%).

Figure 13

Figure 13. Correlation of stability factors in the mining area: (a) r-value and (b) p-value.

Figure 14

Figure 14. Feature importance.

4.4 Model comparison

Conventional methodologies for stope stability classification in the literature have predominantly employed single-algorithm models such as Logistic Regression (LR). Nevertheless, these models exhibit inherent limitations in processing noisy data and outliers, as demonstrated by their suboptimal performance in Figure 15. In comparison, ensemble models integrating multiple base learners and diverse ensemble strategies demonstrate superior efficacy in reducing model bias and variance, thereby significantly enhancing classification performance. Additionally, the ensemble framework proposed in this study achieves an optimized equilibrium between model complexity and generalization capability by aggregating predictions from heterogeneous base learners. This approach reduces sensitivity to classification errors inherent in single-model paradigms, effectively mitigating overfitting risks while concurrently improving model robustness. Consequently, the proposed framework exhibits enhanced stability and reliability in practical engineering applications.

Figure 15

Figure 15. Classification results of a single ensemble model: (a)S7 and (b) BT2.

5 Conclusion

(1) A three-dimensionally parameterized Mathews stability graph model was developed to classify open stope mining stopes into three zones: stable, critical, and unstable. Cross-sectional and longitudinal profiles were integrated to characterize 3D stope behavior, while the hydraulic radius (HR) calculation was refined by incorporating dip length and actual roof exposure area, addressing the limitations of conventional 2D methods in representing deep stope mechanics. Stability thresholds based on span (S) and exposed area (Ap) were quantified for the Dahongshan Copper Mine’s eastern (stable: 25 m/863 m²; critical: 31 m/1,623 m²) and western sections (stable: 20 m/811 m²; critical: 25 m/1,067 m²), establishing a data-mechanism dual-driven framework for structural parameter design in deep open stope mining.

(2) The dynamic evolution of stope stability was investigated through temporal cavity scanning analysis, revealing that hydraulic radius (HR), exposed area (Ap), and average caving height (Hc) peak post-blasting and stabilize during ore-drawing. The pre-blasting phase was identified as the critical stability assessment window, providing a theoretical basis for dynamic risk intervention in open stope mining.

(3) By integrating multi-algorithm strategies, model engineering applicability was significantly enhanced, achieving prediction accuracies of 88.23% (eastern), 91.07% (western) and f1 scores of 88.36% (eastern), 90.96% (western),outperforming single-model approaches. Robust generalization capabilities were demonstrated in deep, high-stress environments (600–1,000 m depth) with complex structural configurations, yielding an interpretable and adaptive framework for stability analysis in deep metal mine engineering.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Z-BL: Writing – original draft. D-PQ: Writing – review and editing. T-YY: Funding acquisition, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the Basic Research Project of the Yunnan Provincial Department of Science and Technology (No. 202301AU070185).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1610234/full#supplementary-material

References

Breiman, L. (1996). Bagging predictors. Mach. Learn. 24 (2), 123–140. doi:10.1007/bf00058655

CrossRef Full Text | Google Scholar

Brown, E. T.Block caving geomechanics (2002). 2nd ed. Queensland, Australia: Julius Kruttschnitt Mineral Research Centre, University of Queensland.

Google Scholar

Cai, M., Xue, D., and Ren, F. (2019). Current status and development strategy of metal mines. Chin. J. Eng. 41 (4), 417–426. doi:10.13374/j.issn2095-9389.2019.04.001

CrossRef Full Text | Google Scholar

Dong, X., Yu, Z., Cao, W., Shi, Y., and Ma, Q. (2020). A survey on ensemble learning. Front. Comput. Sci. 14 (2), 241–258. doi:10.1007/s11704-019-8208-z

CrossRef Full Text | Google Scholar

Fairhurst, C. (2017). Some challenges of deep mining. ENGINEERING 3 (4), 527–537. doi:10.1016/j.eng.2017.04.017

CrossRef Full Text | Google Scholar

Hadjigeorgiou, J., Leclair, J., and Potvin, Y. (1995). An update of the stability graph method for open stope design. CIM Rock Mech. Strata Control Sess. Halifax, N. S. 14, 18.

Google Scholar

Huang, S., and Zhou, J. (2024). Refined approaches for open stope stability analysis in mining environments: hybrid SVM model with multi-optimization strategies and GP technique. Rock Mech. Rock Eng. 57 (11), 9781–9804. doi:10.1007/s00603-024-04055-6

CrossRef Full Text | Google Scholar

Jia, H., Yan, B., Guan, K., Liu, H., Wu, Q., Yin, Y., et al. (2022). Stability analysis of shallow goaf based on field monitoring and numerical simulation: a case study at an open-pit iron mine, China. Front. Earth Sci. 10, 897779. doi:10.3389/feart.2022.897779

CrossRef Full Text | Google Scholar

Ju, Y., Wang, Y., Su, C., Zhang, D., and Ren, Z. (2019). Numerical analysis of the dynamic evolution of mining-induced stresses and fractures in multilayered rock strata using continuum-based discrete element methods. Int. J. Rock Mech. Min. Sci. 113, 191–210. doi:10.1016/j.ijrmms.2018.11.014

CrossRef Full Text | Google Scholar

Li, J., Gao, Y., Yang, T., Zhang, P., Zhao, Y., Deng, W., et al. (2023). Integrated simulation and monitoring to analyze failure mechanism of the anti-dip layered slope with soft and hard rock interbedding. Int. J. Min. Sci. Technol. 33 (9), 1147–1164. doi:10.1016/j.ijmst.2023.06.006

CrossRef Full Text | Google Scholar

Li, J., Yang, T., Deng, W., Du, S., Zhang, Z., Ma, H., et al. (2025). Evaluating failure mechanisms of excavation-induced large-scale landslides in xinjing open-pit coal mine through integrated UAV imagery and 3D simulation. Landslides 22, 2021–2036. doi:10.1007/s10346-025-02460-8

CrossRef Full Text | Google Scholar

Li, Q., Li, G., Niu, W., Cao, Y., Chang, L., Tan, J., et al. (2017a). Boosting imbalanced data learning with Wiener process oversampling. Front. Comput. Sci. 11 (5), 836–851. doi:10.1007/s11704-016-5250-y

CrossRef Full Text | Google Scholar

Li, X., Zhou, J., Wang, S., and Liu, B. (2017b). Review and practice of deep mining for solid mineral resources. J. Nonferrous Met. 27 (6), 1236–1262. doi:10.19476/j.ysxb.1004.0609.2017.06.021

CrossRef Full Text | Google Scholar

Mathews, K., Hoek, E., Wyllie, D. C., and Stewart, S. B. V. (1980). Prediction of stable excavation spans for mining at depths below 1,000 meters in hard rock. Vancouver, British Columbia, Canada: Canada Department of Energy Mines and Resources.

Google Scholar

Mawdesley, C., Trueman, R., and Whiten, W. (2001). Extending the Mathews stability graph for open stoke design. Min. Technol., 110. doi:10.1179/mnt.2001.110.1.27

CrossRef Full Text | Google Scholar

Nickson, S. D. (1992). Cable support guidelines for underground hard rock mine operations. Montreal, Canada: University of British Columbia.

Google Scholar

Putra, D., Karian, T., Sulistianto, B., and Heriawan, M. N. (2024). Integrating mathews stability chart into the stope layout determination algorithm. Min. Metallurgy & Explor. 41 (3), 1351–1364. doi:10.1007/s42461-024-00993-5

CrossRef Full Text | Google Scholar

Ranjith, P. G., Zhao, J., Ju, M., De Silva, R. V., Rathnaweera, T. D., and Bandara, A. K. (2017). Opportunities and challenges in deep mining: a brief review. Engineering 3 (4), 546–551. doi:10.1016/j.eng.2017.04.024

CrossRef Full Text | Google Scholar

Santos, A. E. M., Amaral, T. K. M., Mendonça, G. A., and Silva, D. d. F. S. d. (2020). Open stope stability assessment through artificial intelligence. REM - Int. Eng. J. 73 (3), 395–401. doi:10.1590/0370-44672020730012

CrossRef Full Text | Google Scholar

Stewart, S. B. V., and Forsyth, W. W. (1995). The Mathew’s method for open stope design. Mathew’s method open stope Des. 88 (992), 45–53.

Google Scholar

Trueman, R., Mikula, P., Mawdesley, C., and Harries, N. (2000). Experience in Australia with the application of the Mathews’ method for open stope design. 93.

Google Scholar

Wang, L., Shao, A., Qu, F., Yue, X., Wang, H., Zhang, X., et al. (2025). Current status and prospects of mining technology in metal mines. Chin. J. Eng., 1–13. doi:10.13374/j.issn2095-9389.2024.08.20.001

CrossRef Full Text | Google Scholar

Wang, Y., Wu, A., Yang, J., Yang, G., Wang, Z., and Li, J. (2023). Progress and prospective of the mining key technology for deep metal mines. Chin. J. Eng. 45 (8), 1281–1292. doi:10.13374/j.issn2095-9389.2022.11.12.004

CrossRef Full Text | Google Scholar

Wolpert, D. H. (1992). Stacked generalization. Neural Netw. 5 (2), 241–259. doi:10.1016/s0893-6080(05)80023-1

CrossRef Full Text | Google Scholar

Zhang, M., Liu, H., Yang, Y., Wei, J., and Zha, W. (2024). Modified rock stress factor for the mathews stability graph method and its application. Geomatics, Nat. Hazards And Risk 15 (1), 2344792. doi:10.1080/19475705.2024.2344792

CrossRef Full Text | Google Scholar

Zhao, X., Li, H., Zhang, S., and Yang, X. (2019). Stability analyses and cable bolt support design for a deep large-span stope at the Hongtoushan Mine, China. Sustainability 11 (21), 6134. doi:10.3390/su11216134

CrossRef Full Text | Google Scholar

Zhou, X., Zhao, X., Qu, Q., and Shi, J. (2023). Stope structural parameters design towards green and deep mining: a review. PROCESSES 11 (11), 3125. doi:10.3390/pr11113125

CrossRef Full Text | Google Scholar