Modeling seismic wave propagation in partially saturated porous media: a comparative study

Seismic wave propagation in partially saturated porous media involves multiscale wave-induced fluid flow (WIFF) mechanisms, which significantly impact distinct wave dispersion and attenuation across different frequency bands. It is well known that WIFF at different scales leads to distinct characteristics of wave dispersion and attenuation. Therefore, accurately modeling multiscale WIFF over a wide frequency range is crucial for reservoir characterization and geophysical interpretation based on multiscale measurements. In this study, we integrate the stable effective fluid (SEF) model with squirt flow (SQ) mechanism dominated by microscopic compressibility, developing and validating two multiscale wave propagation models, SEF-SQ and Biot-SQ, by integrating the stable effective fluid and squirt flow mechanisms into existing theoretical frameworks. This model is capable of describing the wave propagation in the porous medium containing two immiscible fluids over a broadband frequency range. Moreover, we incorporate the microscopic WIFF mechanism into the classical macroscopic Biot’s theory through certain characteristic parameters, formulating the Biot-SQ model, which couples global and local wave propagation mechanisms. Numerical simulations demonstrate that both SEF-SQ and Biot-SQ models successfully capture wave dispersion and attenuation characteristics across different frequency bands, confirming their capability to describe the wave propagation over a broadband frequency range. Furthermore, we implement a GPU-based numerical method to efficiently solve the two developed integrated multiscale wave equation systems, and compare the simulated seismic wavefields under different physical parameters, verifying the applicability of this multiscale framework for seismic wavefield modeling. The results emphasize the influence of fluid saturation on WIFF mechanisms in complex porous media, providing valuable insights for reservoir characterization and hydrocarbon exploration.

1 Introduction

Research on seismic wave propagation in porous media saturated with fluid/fluids has attracted significant interests over the years, particularly in the fields of reservoir characterization and hydrocarbon production (e.g., Biot, 1956; Biot, 1962; Brutsaert, 1964; Müller et al., 2010; Ba et al., 2011; Behseresht and Bryant, 2017; Ben-Noah et al., 2023). The pressure gradient caused by seismic wave propagation in porous media leads to fluid flow. Such phenomena are also known as wave-induced fluid flows (WIFFs), which is considered the main cause of seismic wave dispersion and attenuation, manifested as the variation of wave velocity with frequency or wavelength. According to the length-scale of pressure gradient due to the intricate and diverse pore structures within the porous medium, WIFFs can be classified into global, mesoscopic, and microscopic scales.

At the macroscopic scale, where fluid diffusion lengths are much larger than the average fluid patch, Biot’s theory (1956, 1962) proposed a basic framework for wave propagation in homogeneous and isotropic porous media containing a single viscous fluid. Wave equations were derived based on the principles of analytical mechanics and the predicted slow wave was confirmed experimentally by Plona (1980), which further promoted its application for quantitatively modeling the macroscopic wave propagation in porous media (Berryman, 1980; Bourbié et al., 1992; Pride, 2005). However, it has been noted in some previous studies that fluid flow at mesoscopic scale (larger than the pore size but much smaller than the wavelength), resulting from spatial variations in fluid saturation and pore-scale flow, are generally believed to cause significant attenuation at higher frequencies, such as those in seismic or ultrasonic bands (Chapman et al., 2016; Solazzi et al., 2017). The discrepancy between the predictions by Biot’s theory and the real measurements, sometimes underestimating attenuation by up to five orders of magnitude (Dvorkin and Nur, 1993; Pride et al., 2004; Müller et al., 2010), had prompted to the extension of Biot’s theory. The relevant studies primarily focus on two aspects: the porous medium saturated with two immiscible fluids, and multiscale fluid flow mechanisms for more complicated multiphase systems across a wide frequency range such as orders of magnitude, from Hz to MHz. It was pointed out that the dispersion and attenuation of seismic wave are strongly dependent on the fluid saturation (Solazzi et al., 2017; Li et al., 2020) and controlled by the porous structure such as the pore aspect ratio (Wang and Tang, 2021). Chapman et al. (2021) utilized the medical X-ray computed tomography (CT) to experimentally visualize the spatial distribution of fluids in rocks, providing experimental approaches to better understand its influences on dispersion and attenuation. Additionally, the so-called patchy-saturation models (White, 1975; Qi et al., 2014; Zhao et al., 2017) are also developed to characterize the wave loss at mesoscopic scale, which accounts for the influence of the interaction between different fluid patches on wave propagation.

A simple and straightforward approach of modeling the effect of different fluids on wave propagation is to approximate multiple fluids into one equivalent fluid (Papageorgious and Chapman, 2017; Zhang et al., 2022). Wave propagation model can be established based on similar approach of dealing with porous media saturated with single fluid as long as the physical property parameters of the equivalent fluid are suitably determined such as the Reuss average or arithmetic average (Johnson, 1986; Pride et al., 1992; Müller and Gurevich, 2004). Some studies focus more on the calculation of equivalent bulk modulus which can combine the microscopic periodic porous medium with its effective properties on the macroscale (Norris, 1985; Wang and Tang, 2021; Gurevich and Carcione, 2022; Ba et al., 2023). Leonardo et al. (2020) first derived an exact expression for the bulk modulus as a weighted average of the arithmetic and harmonic averages of the individual parameters of the two fluids. Then, it was integrated into the framework of wave equations, and the effectiveness of this approach was verified by comparing the predicted velocity with laboratory data. Rozhko (2020) extended the Gassmann equation to the case of porous media with multiple fluids and the analytical expression of the effective fluid modulus was derived. The predicted results fall between the Voigt and Reuss averages. It is noted that the volume averaging method could be employed to derive the motion equations and constitutive relations (e.g., Tuncay and Corpcioglu, 1997). Based on this, Xiong et al. (2021) and Xiong and Yong (2022) developed a stable equivalent fluid (SEF) model, and the mathematical stability of the established wave equations was considered. The importance of stability was demonstrated through numerical examples on shale oil reservoirs (Xiong et al., 2021) and verified using real data inversion tests (Xiong and Yong, 2022).

On the other hand, based on extensive studies that investigated the microscopic fluid flow mechanisms, it is widely accepted that squirt flow predominantly arising from microscopic compressibility is a major mechanism for seismic wave dispersion and attenuation (Mavko and Nur, 1975; Pride et al., 2004; Gurevich et al., 2010; Song et al., 2016; Solazzi et al., 2021). Dvorkin and Nur (1993) proposed the so-called Biot/squirt (BISQ) model, which accounts for multiscale WIFFs occurring in both the parallel direction for global flow and perpendicular direction for squirt flow relative to the wave propagation. Recent research aims to integrate various WIFF mechanisms into unified multiscale models to capture the relationship between these flows. Following the BISQ model, Sun (2021) and Li et al. (2022) developed a dual-scale model by incorporating the squirt flow. Shi et al. (2024) developed a unified multiscale wave propagation model by integrating global, mesoscopic and squirt flows into the poroelasticity theory, where Rayleigh’s spherical bubble oscillation and Gurevich’s porous grain mechanisms are respectively served as the mesoscopic and microscopic attenuation factors. The predicted results match well with experimental data. Furthermore, Zhao et al. (2021) proved that there would be two peaks in the attenuation curve in their experiment on Fontainebleau sandstone with partially oil-saturated, which provides evidence of WIFFs existing simultaneously at two scales.

This paper is organized as follows. In Section 2, we present the derivation of wave equations from the stable effective fluid (SEF) model for porous media saturated with two immiscible fluids, along with the approach for incorporating the squirt mechanism into these two macroscopic models using frequency-dependent modulus parameters. Section 3 presents numerical examples comparing the dispersion and attenuation predicted by the original macroscopic models with the multiscale models after incorporating the squirt flow mechanism for partially saturated porous medium. Additionally, numerical modeling of seismic wavefields plays a crucial role in validating theoretical models and exploring the effects of multiscale WIFF mechanisms under realistic scenarios (Carcione, 2014; Alkhimenkov et al., 2021). Therefore, Section 3 also demonstrates the application of the developed integrated dynamic equations for seismic wavefield simulations in porous media, implemented using a GPU-based numerical scheme that adapts and extends the finite-volume staggered-grid method of Alkhimenkov et al. (2021) to the SEF-SQ and Biot-SQ models.

2 Methodology

To describe the wave propagation in porous media saturated with two immiscible fluids, we briefly introduce the constructions of two models: the SEF model and the Biot’s model featuring an effective fluid for two fluids. The incorporation of the squirt mechanism into the two models will also be introduced, along with the corresponding numerical solution scheme.

2.1 The SEF model

The modeling of elastic wave equations considered for porous media saturated with two immiscible fluids is derived using volume averaging theory by Tuncay and Corpcioglu (1997). They combined the macroscopic momentum balance equation with the constitutive relation and incorporated the capillary effects into the bulk modulus. Based on this framework and the corresponding mathematical stability analysis, Xiong et al. (2021) simplified the system by transforming the two saturated fluids into an equivalent fluid, considering the case in which one fluid phase is entirely wrapped by the other. Consequently, the wrapped fluid is assumed to have no contact with the boundary of the representative elementary volume (REV) selected by the volume averaging theory. In this way, only one fluid phase, which affects the whole unit, needs to be considered.

By averaging the microscopic relations over the REV, the macroscopic momentum balance equations for a porous medium with an effective fluid can be represented as follows:

$\left\{\begin{array}{l}〈{\rho }_s〉{\ddot{\overline{\mathbf{u}}}}^s=\nabla ·〈\mathbf{\sigma }〉+\frac{\eta {\varphi }^2}{\kappa }\left({\dot{\overline{\mathbf{u}}}}^f-{\dot{\overline{\mathbf{u}}}}^s\right)\\ 〈{\rho }_f〉{\ddot{\overline{\mathbf{u}}}}^f=\nabla ·〈\mathbf{s}〉+\frac{\eta {\varphi }^2}{\kappa }\left({\dot{\overline{\mathbf{u}}}}^f-{\dot{\overline{\mathbf{u}}}}^s\right)\end{array}\right.(1)$

where the angle brackets and overbar denote operators of taking the volume average and intrinsic average of the corresponding microscopic quantity, respectively; the subscripts s and f respectively represent the solid phase and equivalent fluid; u and U are the average displacements of solid and fluid, respectively. The dot above the quantity indicates the time derivative of the quantity. ϕ is the total porosity which can be divided into ϕ₁ = S₁ϕ and ϕ₂ = S₂ϕ, where S₁ and S₂ are the saturations of the two fluids, with the relation of S₁ + S₂ = 1; η and κ are the viscosity and intrinsic permeability of the effective fluid, respectively. σ and s respectively represent the stress components of solid and fluid, which need to be determined by the constitutive relation of the solid and the effective fluid phases further.

Based on the relations of the disturbances δ(1-ϕ) and δϕ, the pressures of solid (p_s) and fluid (p_f) in terms of $\nabla ·{\overline{u}}_s$ and $\nabla ·{\overline{u}}_f$, the macroscopic constitutive equations of the effective fluid model can be expressed as follows:

$\left\{\begin{array}{l}〈\mathbf{\sigma }〉=\left({\stackrel{\sim }{a}}_{11}\nabla ·{\overline{\mathbf{u}}}^s+{\stackrel{\sim }{a}}_{12}\nabla ·{\overline{\mathbf{u}}}^f\right)\mathbf{I}+G\left(\nabla \overline{\mathbf{u}}+{\left(\nabla \overline{\mathbf{u}}\right)}^{\mathrm{T}}-\frac{2}{3}\left(\nabla ·\overline{\mathbf{u}}\right)\mathbf{I}\right)\\ 〈\mathbf{s}〉=\left({\stackrel{\sim }{a}}_{21}\nabla ·{\overline{\mathbf{u}}}^s+{\stackrel{\sim }{a}}_{22}\nabla ·{\overline{\mathbf{u}}}^f\right)\mathbf{I}\end{array}\right.(2)$

where the elastic coefficients a_ij (i, j = 1, 2) are determined with the following Equation 3:

$\begin{array}{l}{\stackrel{\sim }{a}}_{11}{E}_3=K_s\left[E_1\left(1-\varphi \right)\left(K_1{E}_2{S}_1+K_1{K}_2+K_2{A}_2{S}_2\right)+K_s{K}_b\varphi \left(K_1{S}_2+K_2{S}_1+E_2\right)\right],\\ {\stackrel{\sim }{a}}_{12}{E}_3=K_s{K}_1{E}_1{S}_1\varphi \left(E_2+K_2\right),\\ {\stackrel{\sim }{a}}_{21}={\stackrel{\sim }{a}}_{12},\\ {\stackrel{\sim }{a}}_{22}{E}_3=K_1{S}_1\varphi \left[\varphi K_s^2\left(K_2{S}_1+E_2\right)+K_2{E}_1{E}_2{S}_2\right].\end{array}(3)$

where $E_1=\left(1-\varphi \right)K_s-K_b$ and $E_2=\frac{\alpha }{100}{\left[{\left(1-S_1\right)}^{-n/\left(n-1\right)}-1\right]}^{\left(1-n\right)/n}$${\left(1-S_1\right)}^{-\left(2n-1\right)/\left(n-1\right)}$, α and n are the fitting parameters needed to calculate the capillary force (Van Genuchten, 1980). $E_3=E_1\left(K_1{E}_2{S}_1+K_1{K}_2+K_2{E}_2{S}_2\right)+K_s^2\varphi \left(K_1{S}_2+E_2+K_2{S}_1\right)$.

By substituting the macroscopic constitutive Equation 2 into the macroscopic momentum balance Equation 1, we obtain the system of poro-elastic wave equations for an isotropic porous medium saturated with two fluids. This equation system can be expressed in terms of displacements of solid and fluid phases as follows:

$\left\{\begin{array}{l}〈{\rho }_s〉\frac{{\mathrm{\partial }}^2\mathbf{u}}{\mathrm{\partial }{t}^2}=\nabla \left[{\stackrel{\sim }{a^{\prime }}}_{11}\nabla ·\mathbf{u}+{\stackrel{\sim }{a}}_{12}\nabla ·\mathbf{U}\right]+\nabla ·\left(G\nabla \mathbf{u}\right)+b\left(\frac{\mathrm{\partial }\mathbf{U}}{\mathrm{\partial }t}-\frac{\mathrm{\partial }\mathbf{u}}{\mathrm{\partial }t}\right),\\ 〈{\rho }_f〉\frac{{\mathrm{\partial }}^2\mathbf{U}}{\mathrm{\partial }{t}^2}=\nabla \left({\stackrel{\sim }{a}}_{21}\nabla ·\mathbf{u}+{\stackrel{\sim }{a}}_{22}\nabla ·\mathbf{U}\right)-b\left(\frac{\mathrm{\partial }\mathbf{U}}{\mathrm{\partial }t}-\frac{\mathrm{\partial }\mathbf{u}}{\mathrm{\partial }t}\right),\end{array}\right.(4)$

The governing equations for P and S waves can be derived by taking the divergence and curl to both sides of Equation 4, respectively.

2.2 Biot’s equations for porous media with two immiscible fluids

Here we introduce another wave propagation model for porous media containing two fluids. To ensure the simplicity of the equations form, we adopt the framework of Biot’s theory and then introduce the effects of two fluids on wave propagation. The wave equations established by Biot (1956) can be expressed as follows:

$\begin{array}{l}N{\nabla }^2{u}_i+\left(A+N\right)\nabla e+Q\nabla \xi ={\rho }_{11}{\ddot{u}}_i+{\rho }_{12}{\ddot{U}}_i+b\left({\dot{u}}_i-{\dot{U}}_i\right),\\ Q\nabla e+R\nabla \xi ={\rho }_{12}{\ddot{u}}_i+{\rho }_{22}{\ddot{U}}_i-b\left({\dot{u}}_i-{\dot{U}}_i\right),\end{array}(5)$

where ${\dot{u}}_i=\mathrm{\partial }{u}_i/\mathrm{\partial }t$, ${\dot{U}}_i=\mathrm{\partial }{U}_i/\mathrm{\partial }t$, and i = 1, 2, 3 represents the three directions in space, respectively. Based on Gedanken experiments conducted under specific conditions, the elastic responses of the fluid phase are characterized by elastic coefficients expressed as follows (Biot and Willis, 1957; Johnson, 1986; Williams, 1992):

$\begin{array}{l}A=\frac{\left(1-\varphi \right)\left(1-\varphi -K_b/K_s\right)K_s+\varphi \left(K_s/K_f\right)K_b}{1-\varphi -K_b/K_s+\varphi K_s/K_f}-\frac{2{\mu }_b}{3},\\ N=G={\mu }_b,\\ Q=\frac{\left(1-\varphi -K_b/K_s\right)\varphi K_s}{1-\varphi -K_b/K_s+\varphi K_s/K_f},\\ R=\frac{{\varphi }^2{K}_s}{1-\varphi -K_b/K_s+\varphi K_s/K_f}.\end{array}(6)$

Here K_f denotes the bulk modulus of the fluid phase. With the help of Gassmann’s fluid substitution theory (Gassmann, 1951), Biot’s theory is capable of describing complex fluid flow patterns resulting from the existence of two fluids by considering the equivalent bulk modulus of their effective fluid. This can be expressed through the arithmetic mean and harmonic mean as follows (Wollner and Dvorkin, 2018):

${\overline{K}}_f=X·K_{f,\text{AR}}+\left(1-X\right)·K_{f,\text{HR}}(7)$

with Equation 8

$\left\{\begin{array}{l}{K}_{f,\text{AR}}=S_1{K}_{f1}+S_2{K}_{f2},\\ K_{f,\text{HR}}={\left(\frac{S_1}{K_{f1}}+\frac{S_2}{K_{f2}}\right)}^{-1},\end{array}\right.(8)$

where X can be determined by Zong et al. (2022) Equation 9:

$X=\frac{\varphi M_{\text{dry}}}{\varphi M_{\text{dry}}+\left[1-\left(1+\varphi \right)K_{\text{dry}}/K_s+G\left(1-\varphi -K_{\text{dry}}/K_s\right)·4/3\right]·\left(S_1{K}_{f1}+S_2{K}_{f2}\right)},(9)$

Here, $M_{\text{dry}}=K_{\text{dry}}+G·4/3$ denotes the wave modulus of the dry rock skeleton. This implies that by substituting Equation 7 into Equations 5 and 6, Biot’s equations can effectively describe the wave propagation through porous rock saturated with two fluids.

2.3 Incorporating squirt flow mechanism

We have introduced two sets of wave propagation models above, which did not consider the influence of relatively complex fluid flow mechanisms, i.e., fluid flow occurred below the macroscopic scale, on wave propagation. To accurately depict the intricate dispersions and attenuations of seismic wave over a wide frequency range, we are motivated to incorporate the squirt flow on a microscopic scale, which simultaneously exists and interacts with the global flow described by the above-mentioned SEF and Biot’s models. Following the approach outlined by Shi et al. (2024), based on the model proposed by Gurevich et al. (2010) for evaluating the stiffening effect of the combined squirt flow, the frequency-dependent elastic modulus corresponding to multiscale fluid flow patterns can be expressed as follows:

$\begin{array}{l}\frac{1}{K_{mf}\left(P,\omega \right)}=\frac{1}{K_h}+\frac{1}{\frac{1}{\frac{1}{K_m\left(P\right)}-\frac{1}{K_h}}+\frac{1}{\frac{1}{K_f^{*}\left(P,\omega \right)}-\frac{1}{K_s}}{\varphi }_c\left(P\right)},\\ \frac{1}{N_{mf}\left(P,\omega \right)}=\frac{1}{N_m\left(P\right)}-\frac{4}{15}\left[\frac{1}{K_m\left(P\right)}-\frac{1}{K_{mf}\left(P,\omega \right)}\right],\end{array}(10)$

where $K_f^{*}\left(P,\omega \right)=\left[1-\frac{2J_1\left(ka\right)}{ka{J}_0\left(ka\right)}\right]K_{ef}\begin{array}{cc},& ka=\frac{1}{\alpha }{\left(-\frac{3\mathrm{i}\omega \eta }{K_{ef}}\right)}^{1/2}\end{array}$, and ω is the angular frequency, K_h denotes the original dry bulk modulus of the rock skeleton, J₀ and J₁ are respectively the zero-order and first-order Bessel functions, and K_ef means the bulk modulus of the effective fluid, which can be calculated using Equation 7. More details on the derivation of Equation 10 and its required parameters can be found in Shi et al. (2024).

Therefore, by substituting K_mf and N_mf in Equation 10 into Equation 4 of SEF model and Equation 5 of Biot’s equations with the equivalent fluid K_f, we can incorporate the squirt flow mechanism into the above macroscopic wave propagation theories.

2.4 Numerical scheme for time-domain seismic wavefields

In addition to the plane wave solutions, the Biot’s model and SEF model can be universally reformulated as a first-order velocity-stress formulation as Equation 11:

$\left[\begin{array}{l}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }t}\\ -\frac{\mathrm{\partial }{\mathbf{q}}^D}{\mathrm{\partial }t}\end{array}\right]=\frac{1}{〈\rho 〉〈{\rho }_a〉-{〈{\rho }_f〉}^2}\left[\begin{array}{cc}〈{\rho }_a〉& 〈{\rho }_f〉\\ 〈{\rho }_f〉& 〈\rho 〉\end{array}\right]\left[\begin{array}{l}{\nabla }_j\left(-p{\delta }_{ij}+{\mathbf{\sigma }}_{ij}\right)\\ \frac{\eta {\varphi }^2}{\kappa }{\mathbf{q}}^D+{\nabla }_i{p}_f\end{array}\right](11)$

where ⟨ρ⟩ represents the total density of porous medium, and ⟨ρ_f⟩ = ϕρ_f corresponds to the fluid density ρ_f scaled by the porosity ϕ, ⟨ρ_a⟩ denotes the coupling coefficient between the solid and fluid phases, which is set to zero for the SEF model. We solved this system by using a conservative staggered space-time grid discretization, which is mathematically equivalent to a finite-volume (FV) method. This approach was developed by Alkhimenkov et al. (2021) for Biot’s equations on multi-graphical processing unit (GPU) architectures, along with a semi-implicit discretization for the Darcy’s flux q^D (Alkhimenkov et al., 2021).

The discretized rectangular time-space grids with sides parallel to the coordinate axes is assumed to be superimposed on the domain {x, y, z ≥ 0} × {t ≥ 0}, with the spatial grid sizes {Δx, Δy, Δz}> 0 and time discretization Δt > 0. The time and spatial coordinates are discretized as $t^m=m\Delta t\begin{array}{cc},& x_i=i\Delta x\end{array}\begin{array}{cc},& y_j=j\Delta y\end{array}\begin{array}{cc},& z_k=k\Delta z\end{array}$.

In this framework, the velocity field variables of both the solid and fluid phases are located at half-integer spatial nodes and inter time nodes, and can be expressed as ${\left[v_x^s\right]}_{i+1/2,j,k}^m$, ${\left[v_y^s\right]}_{i,j+1/2,k}^m$, ${\left[v_z^s\right]}_{i,j,k+1/2}^m$. Moreover, the pressure scalar field variables are allocated to the integer spatial nodes and half-integer time nodes, they are represented as ${\left[p\right]}_{i,j,k}^{m+1/2}$ and ${\left[p_f\right]}_{i,j,k}^{m+1/2}$, respectively.

A similar staggered discretization is employed to the stress deviator tensor fields and Darcy’s flux, constructing a conservative staggered-grid formulation with second-order accuracy in both space and time. The one-dimensional discrete representation of this system can be written as Equation 12:

$\left\{\begin{array}{l}\begin{array}{l}\frac{{\left[\mathbf{v}\right]}_{i+1/2}^{m+1}-{\left[\mathbf{v}\right]}_{i+1/2}^m}{\Delta t}=\frac{〈{\rho }_a〉}{〈\rho 〉〈{\rho }_a〉-{〈{\rho }_f〉}^2}\frac{{\left[-p+{\sigma }_{xx}\right]}_{i+1}^{m+1/2}-{\left[-p+{\sigma }_{xx}\right]}_i^{l+1/2}}{\Delta x}+\frac{〈{\rho }_f〉}{〈\rho 〉〈{\rho }_a〉-{〈{\rho }_f〉}^2}·\\ \left[\frac{\eta {\varphi }^2}{\kappa }\left(\chi {\left[{\mathbf{q}}^D\right]}_{i+1/2}^{m+1}+\left(1-\chi \right){\left[{\mathbf{q}}^D\right]}_{i+1/2}^m\right)+\frac{{\left[p_f\right]}_{i+1}^{m+1/2}-{\left[p_f\right]}_i^{m+1/2}}{\Delta x}\right],\end{array}\\ \begin{array}{l}\frac{-{\left[{\mathbf{q}}^D\right]}_{i+1/2}^{m+1}+{\left[{\mathbf{q}}^D\right]}_{i+1/2}^m}{\Delta t}=\frac{〈{\rho }_f〉}{〈\rho 〉〈{\rho }_a〉-{〈{\rho }_f〉}^2}\frac{{\left[-p+{\sigma }_{xx}\right]}_{i+1}^{m+1/2}-{\left[-p+{\sigma }_{xx}\right]}_i^{m+1/2}}{\Delta x}+\frac{〈\rho 〉}{〈\rho 〉〈{\rho }_a〉-{〈{\rho }_f〉}^2}·\\ \left[\frac{\eta {\varphi }^2}{\kappa }\left(\chi {\left[{\mathbf{q}}^D\right]}_{i+1/2}^{m+1}+\left(1-\chi \right){\left[{\mathbf{q}}^D\right]}_{i+1/2}^m\right)+\frac{{\left[p_f\right]}_{i+1}^{m+1/2}-{\left[p_f\right]}_i^{m+1/2}}{\Delta x}\right].\end{array}\end{array}\right.(12)$

Herein, the weight parameter χ is introduced to control the stability of the equation system and the convergence rate of the numerical scheme, χ = 0 and 1 correspond to a fully explicit scheme and an implicit scheme, respectively.

For numerical experiments, we consider a two-dimensional domain of 9.35 × 9.35 m, discretized into 256 × 256 grid cells. Based on the von-Neumann stability analysis by Alkhimenkov et al. (2021) for linear schemes with constant coefficients, the time step Δt is determined with the given spatial grid sizes {Δx, Δy, Δz}, following the Courant–Friedrichs–Lewy (CFL) condition. In addition, it has been pointed out that this CFL condition can be extended to a fourth-order accurate in space, second-order accurate in time numerical scheme in the case that the fourth-order approximation to the first derivative is applied (Masson et al., 2006). This extension can be further explored in the construction of coefficients.

Furthermore, considering the configurations of SEF model and its discretization, we imposed reflecting boundary conditions and implemented a Ricker wavelet as the source function, which is centered within the spatial domain and can be expressed as Equation 13:

$s\left(t\right)=\left(1-2{\pi }^2{f}_c^2{\left(t-t_0\right)}^2\right)e^{-{\pi }^2{f}_c^2{\left(t-t_0\right)}^2},(13)$

where f_c is the source peak frequency and t₀ is the wavelet delay.

We adapt and extend the GPU-based finite-volume staggered-grid scheme of Alkhimenkov et al. (2021) to solve the SEF-SQ and Biot-SQ models efficiently. The solver adopts second-order spatial and temporal discretization on a staggered grid, with improved stability and significant computational speed-up over CPU-based implementations.

In this section, we present an investigation of the seismic wave propagation characteristics in the porous solid media saturated with two immiscible fluids based on the two models established above, which includes the variation of P-wave velocities, the inverse quality factors with frequency, and the time-domain seismic wavefield. The rock physics parameters of the reservoir considered are enumerated in Table 1 (Tuncay and Corapcioglu, 1996; Santos et al., 2004).

Table 1

Table 1. Rock physics parameters.

3 Results

3.1 Dispersion and attenuation analysis

The dispersion and attenuation analysis of seismic waves play crucial roles in the field of seismic rock physics. Here we examine the relationship between the wave velocity (V_P) and the inverse attenuation quality factor (Q⁻¹) varies with the frequency (ω) and the water saturation (S₁).

To investigate the impact of incorporating the squirt flow mechanism, we compare the original macroscopic models, which include the SEF model and Biot’s equations with effective fluid, with their corresponding multiscale extensions, referred to as the SEF-SQ and Biot-SQ models in the following. Figure 1 illustrates the predicted V_P and Q⁻¹ as functions of frequency for the porous media partially saturated with water.

Figure 1

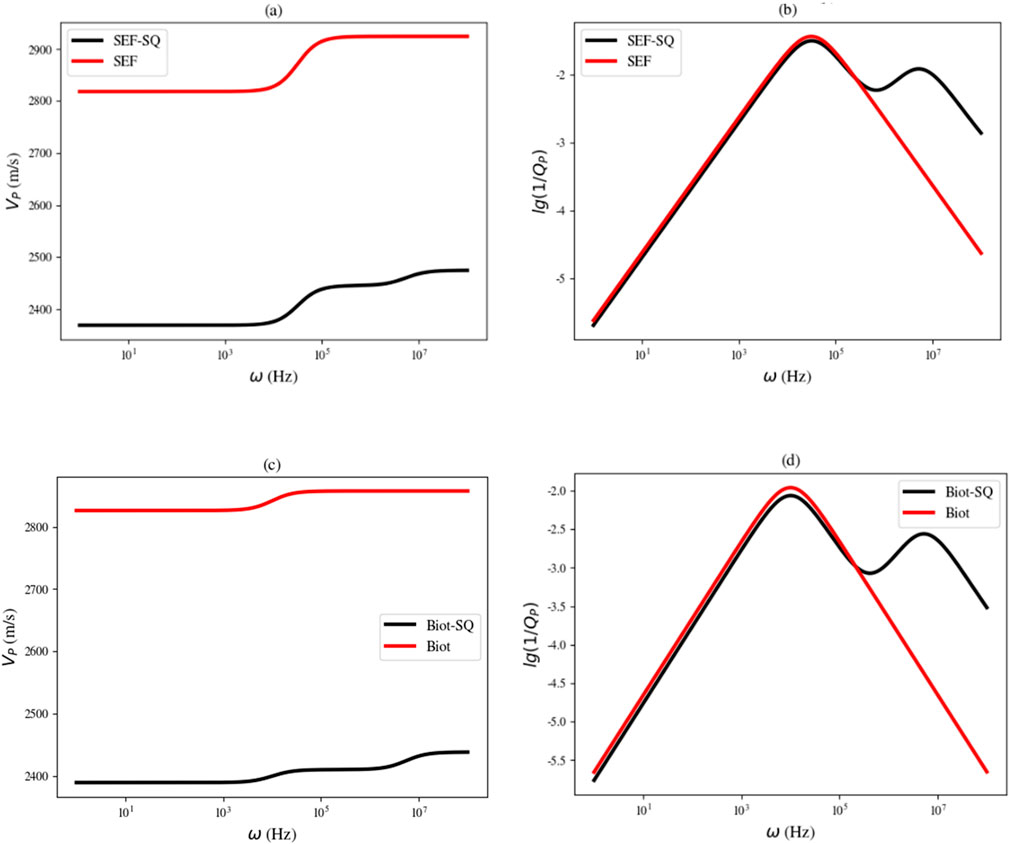
Figure 1. Comparisons of the dispersion and attenuation vary with frequency when water saturation S₁ = 0.9, which are predicted by the SEF model (a,b) and Biot’s equations (c,d) with K_f from the equivalent of two fluids after incorporating the squirt mechanisms.

From the left column of Figure 1, it can be observed that compared with the original (single-scale) models, both the SEF-SQ model and the Biot-SQ model with K_f exhibit an additional increase stage in attenuation. The first peaks, present in the single- and multiscale models, occur in the same frequency region. This observation is consistent with the fact that the attenuation characteristic occurring in the lower frequency range is primarily governed by the global wave-induced fluid flow. Meanwhile, the second peak, which appears at a higher frequency (approximately 10⁷ Hz), is exclusively predicted by the multiscale models. This phenomenon is attributed to the incorporated squirt flow effects, which are introduced into the two macroscopic models through K_mf and N_mf in Equation 10. As illustrated in the right column of Figure 1, a similar pattern can be observed in the dispersion curves. The curves by the single-scale models and their corresponding multiscale models overlapped well within the lower frequency range. As frequency increases, all models predict a general increase, but only the SEF-SQ and Biot-SQ models can capture the wave dispersion characteristics related to the squirt flow at higher frequencies, as evidenced by the presence of the second peaks. From a broad perspective, the multiscale wave propagation theories provide a more comprehensive characterization of P-wave attenuation and dispersion across a wide frequency range. These models not only accurately depict the attenuation and dissipation characteristics captured by the original single-scale models, but also capture additional attenuation peaks and enhance the representation of wave dispersion in the high-frequency band, which benefits the interpretation of seismic wave observations as frequency increases.

In addition to frequency-dependent effects, the multiscale Biot-SQ model includes an additional factor K_f, allowing for considering partially saturated cases. However, it can be revealed from the comparisons between the first and second rows in Figure 2 that, while the Biot’s equations with K_f is applicable for predicting the attenuation and dispersion in the partially saturated porous medium, its predictions are consistently lower than those of the SEF and SEF-SQ models.

Figure 2

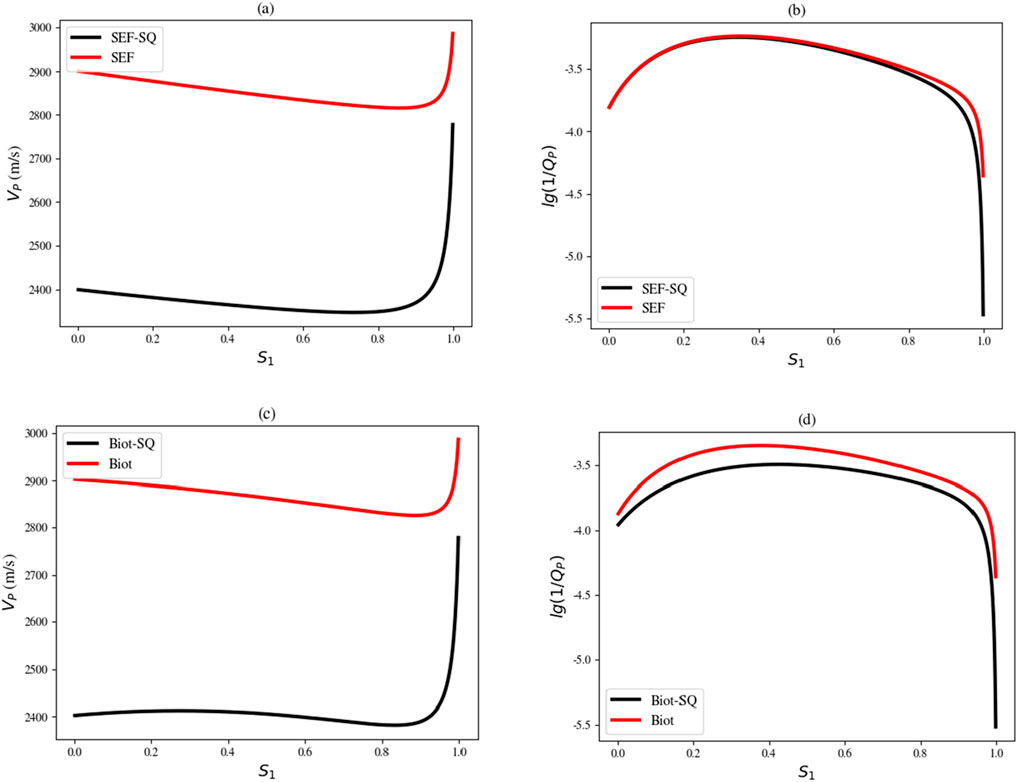
Figure 2. Comparisons of the dispersion and attenuation vary with saturation when frequency ω = 100 Hz, which are predicted by the SEF model (a,b) and Biot’s equations (c,d) with K_f from the equivalent of two fluids after incorporating the squirt mechanisms.

To further validate the combination of the Biot’s equations with K_f and to investigate the influence of saturation on wave dispersion and attenuation, we analyze the variations of V_p and Q⁻¹ as functions of water saturation S₁ predicted by the single-scale and multiscale models in Figure 2. As saturation increases, all models exhibit similar trends in the inverse quality factor curves: their change is smooth but then decreases suddenly as water saturation approaches 1. However, even though both the Biot-SQ and SEF-SQ models are multiscale models, the predictions of the Biot-SQ model consistently appear to be lower than those of the SEF-SQ model at low water saturation. A similar discrepancy can be observed in comparison to P-wave velocity curves. Although V_P curves from these two multiscale models show sudden increases as S_w approaches 1, distinct variations occur when water saturation is approximately less than 0.4. This can be explained by the fact that, in the Biot-SQ model, as water saturation (S1) increases from 0 to approximately 0.5, the effective fluid bulk modulus increases significantly due to the replacement of compressible gas by less compressible water in the pore space, resulting in an increase in the composite P-wave velocity. Beyond this range, capillary and squirt flow effects become more significant, which tend to stabilize or slightly reduce the velocity as saturation approaches unity. This discrepancy can be attributed to the fact that the SEF model accounts for capillary force effects on the bulk modulus of both fluids (as detailed in the above Methodology section). As a result, the SEF-SQ model demonstrates superior predictive capabilities over the Biot-SQ model, providing a more reliable theoretical framework for interpreting seismic responses, particularly in cases of relatively low-saturation conditions.

The developed integrated SEF-SQ and Biot-SQ models complement each other. While both account for multiscale WIFF effects, SEF-SQ explicitly incorporates capillary effects on bulk modulus, providing superior predictions at low saturations. Biot-SQ, on the other hand, extends the Biot framework by including squirt flow, facilitating its application within a familiar theoretical structure.

3.2 Wavefields results analysis

In this section, we investigate the time-domain seismic wavefields to evaluate the two established models. A conservative staggered space-time grid discretization, developed by Alkhimenkov et al. (2021) specifically designed for multi-graphical processing units (GPU) numerical applications, is employed. This numerical scheme, equivalent to a finite volume approach, focuses on effectively solving the first-order velocity-stress formulation of the framework of Biot’s equations using GPU. Since the form of the equations in the SEF model can be considered as a special case of Biot’s equations, the scheme remains applicable to obtaining the wavefields based on the required relationship between the elastic parameters of the two models as Equation 14:

$\begin{array}{l}Q=\frac{{\rho }_{11}{a}_{12}}{〈{\rho }_s〉}+\frac{{\rho }_{12}{a}_{22}}{〈{\rho }_f〉},\\ R=\frac{{\rho }_{12}{a}_{12}}{〈{\rho }_s〉}+\frac{{\rho }_{22}{a}_{22}}{〈{\rho }_f〉},\\ N=\frac{\left({\rho }_{11}{\rho }_{12}-{\rho }_{12}^2\right)Q}{{\rho }_{12}{\rho }_{22}}+\frac{\left({\rho }_{11}{\rho }_{12}-{\rho }_{12}^2\right)a_{21}}{{\rho }_{12}〈{\rho }_f〉}-\frac{\left({\rho }_{11}{\rho }_{12}-{\rho }_{12}^2\right)a_{11}}{{\rho }_{22}〈{\rho }_s〉},\\ A=\frac{\left(2{\rho }_{12}^2-{\rho }_{11}{\rho }_{12}\right)Q}{{\rho }_{12}{\rho }_{22}}+\frac{2\left({\rho }_{11}{\rho }_{12}-{\rho }_{12}^2\right)a_{11}}{{\rho }_{22}〈{\rho }_s〉}+\frac{\left({\rho }_{11}{\rho }_{12}-{\rho }_{12}^2\right)a_{21}}{{\rho }_{12}〈{\rho }_f〉}.\end{array}(14)$

We utilize a rectangular time-space grid with time discretization (Δt) and spatial grid (Δx, Δy, Δz) for the following analysis. The velocity field variables of solid (v) and fluids are situated at half-integer spatial nodes and integer time nodes, while the pressure scalar field variables of solid (σ) and fluids (s) are defined at integer spatial nodes and half-integer time nodes. This configuration establishes a conservative staggered grid formulation with second-order accuracy in spatial and temporal fields. The numerical experiments are conducted on a two-dimensional domain of 9.35 m × 9.35 m with 256 × 256 grid cells. The time step Δt is determined according to the Courant-Friedrichs-Lew (CFL) condition proposed by Alkhimenkov et al. (2021), and 300 time-steps are executed. The reflecting boundary conditions are employed, and the seismic source function is set as a Morlet wavelet centered at the midpoint of the spatial domain.

Figures 3, 4 depict the snapshots of the time-domain seismic wavefield in the x-z spatial domain for fluid-saturated porous medium with different water saturations, as outlined in Table 1. The components {v_x, v_y, σ_xx, σ_xy, s} are plotted for comparison. Differences across the entire numerically computed fields are calculated using the following Equation 15:

$Error=\frac{\left|{\zeta }_{SEF-SQ}-{\zeta }_{Biot-SQ}\right|}{\max \left({\zeta }_{Biot-SQ}\right)}.(15)$

Figure 3

Figure 3. Numerical simulations of wavefields based on the parameters of rock and fluids with a water saturation of 0.9. (a–c) Are the respective predictions from the Biot-SQ model, the SEF-SQ model, and the difference between these two models calculated by Equation 20. From top to bottom: solid velocity fields {v_x, v_y}, and the solid and fluids stress fields {σ_xx, σ_xy, s}.

Figure 4

Figure 4. Numerical simulations of wavefields based on the parameters of rock and fluids with water saturation of 0.1. (a–c) Are the respective predictions from the Biot-SQ model, the SEF-SQ model, and the difference between these two models calculated by Equation 20. From top to bottom: solid velocity fields {v_x, v_y}, and the solid and fluids stress fields {σ_xx, σ_xy, s}.

Here, the symbol ζ denotes the component under consideration for estimation, including the solid velocity fields (v_x, v_y), along with the stress fields of the solid phase (σ_xx, σ_xy) and that of the fluid. The operator max(·) represents taking the maximum value. The subscripts ‘SEF-SQ’ and ‘Biot-SQ’ respectively represent the simulation results from the two models.

Figure 3 illustrates a comparative analysis involving the Biot-SQ model (Figure 3a), the SEF-SQ model (Figure 3b), and their difference (Figure 3c) with water saturation (S₁) of 0.9. It is observed that both models are capable of accurately simulating the wavefields of components {v_x, v_y, σ_xx, σ_xy, s} across the entire spatial domain for the partially saturated porous medium. As depicted in Figure 3c, the relative errors of the solid velocity fields {v_x, v_y} and the solid stress fields {σ_xx, σ_xy} are consistently maintained below 2%, while the error of the fluid stress field {s} is relatively significant. It can be observed that the relative discrepancy related to the fluid stress calculated by the two models can reach up to 40%, which may be attributed to the different effective fluid modeling approaches for the two immiscible fluids applied in the models.

Figure 4 depicts a similar comparative analysis involving the Biot-SQ model (Figure 4a), the SEF-SQ model (Figure 4b), and their difference (Figure 4c) with water saturation (S₁) of 0.1. We can observe the similar wavefields to those in Figure 3, albeit with smaller magnitudes of the calculated fluid stress fields due to the lower water saturation. It is noted that the errors of the fluid stress field {s} between the two models remain almost the same for different water saturations, further confirming that this discrepancy essentially originates from the models rather than the parameters.

4 Discussion

The results demonstrate that multiscale WIFF mechanisms significantly affect dispersion, attenuation, and seismic wavefield behavior. The appearance of dual attenuation peaks (Figure 1) reflects the coexistence of macroscopic and microscopic fluid flow, consistent with theoretical predictions (Gurevich et al., 2010) and experimental results (Zhao et al., 2021). The increase of P-wave velocity with saturation (Figure 2) arises from the replacement of compressible gas by incompressible water, enhancing the effective fluid bulk modulus. At higher saturations, capillary and squirt-flow effects dominate. The SEF-SQ model incorporates capillary effects more explicitly, improving predictions at low saturations (Solazzi et al., 2017; Wang and Tang, 2021).

Wavefield simulations (Figures 3, 4) show that both models provide consistent solid velocity and stress predictions, with discrepancies in the fluid stress field. These differences originate from the treatment of immiscible fluids: SEF-SQ accounts for capillary effects, while Biot-SQ relies on equivalent fluid assumptions. This observation agrees with prior analyses on effective fluid models (Müller and Gurevich, 2004; Rozhko, 2020).

5 Conclusion

This study develops two wave propagation models that integrate the SEF model and Biot’s equations with the squirt-flow mechanism, effectively capturing the characteristics of wave propagation through the porous media containing two immiscible fluids. The derivations of the equation system are provided, along with the incorporation of the frequency-dependent elastic modulus. Numerical results demonstrate that the developed integrated multiscale models can effectively and comprehensively describe the coupling effects of WIFF mechanisms on wave dispersion and attenuation across different frequency bands. Furthermore, the study successfully applies the GPU-based numerical method to efficiently simulate seismic wavefields in the porous media with different physical parameters, reinforcing the practical applicability of the models. In this way, the developed integrated multiscale models are expected to play a significant role in broadband geophysical data inversion and reservoir characterization applications. They offer researchers and practitioners enhanced tools to interpret broadband seismic observations in reservoirs with varying fluid saturations and types (e.g., oil, gas, water), overcoming the limitations of classical Biot’s model, particularly in partially saturated conditions. Future work will focus on extending the developed integrated models to investigate the effects of other key reservoir parameters, such as porosity and permeability, on seismic wave dispersion and attenuation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

WC: Conceptualization, Writing – original draft, Writing – review and editing. XZ: Writing – original draft, Writing – review and editing. TD: Validation, Writing – review and editing. JP: Validation, Writing – review and editing. ZN: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the National Key Research and Development Program of China (Grant No. 2021YFA0719200), and Hunan Provincial Natural Science Foundation of China under Grant 2021JJ40723.

Conflict of interest

Authors WC, XZ, TD, JP, and ZN were employed by Powerchina Chongqing Engineering Corporation Limited.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alkhimenkov, Y., Räss, L., Khakimova, L., Quintal, B., and Podladchikov, Y. (2021). Resolving wave propagation in anisotropic poroelastic media using graphical processing units (GPUs). J. Geophys. Res. Solid Earth 126, e2020JB021175. doi:10.1029/2020jb021175

CrossRef Full Text | Google Scholar

Ba, J., Carcione, J. M., and Nie, J. X. (2011). Biot-Rayleigh theory of wave propagation in double-porosity media. J. Geophys. Res. Solid Earth 116, B06202–B06212. doi:10.1029/2010jb008185

CrossRef Full Text | Google Scholar

Ba, J., Zhu, H., Zhang, L., and Carcione, J. M. (2023). Effect of multiscale cracks on seismic wave propagation in tight sandstones. J. Geophys. Res. Solid Earth 128 (10), e2023JB027474. doi:10.1029/2023jb027474

CrossRef Full Text | Google Scholar

Behseresht, J., and Bryant, S. L. (2017). Physical mechanisms for multiphase flow associated with hydrate formation. J. Geophys. Res. Solid Earth 122 (5), 3585–3623. doi:10.1002/2016jb013503

CrossRef Full Text | Google Scholar

Ben-Noah, I., Friedman, S. P., and Berkowitz, B. (2023). Dynamics of air flow in partially water-saturated porous media. Rev. Geophys. 61 (2), e2022RG000798. doi:10.1029/2022rg000798

CrossRef Full Text | Google Scholar

Berryman, J. G. (1980). Confirmation of Biot’s theory. Appl. Phys. Lett. 37, 382–384. doi:10.1063/1.91951

CrossRef Full Text | Google Scholar

Biot, M. A. (1956). Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 28, 168–178. doi:10.1121/1.1908239

CrossRef Full Text | Google Scholar

Biot, M. A. (1962). Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 33, 1482–1498. doi:10.1063/1.1728759

CrossRef Full Text | Google Scholar

Biot, M. A., and Willis, D. G. (1957). The elastic coefficients of the theory of consolidation. J. Appl. Mech. 24 (4), 594–601. doi:10.1115/1.4011606

CrossRef Full Text | Google Scholar

Bourbié, T., Coussy, O., Zinszner, B., and Junger, M. C. (1992). Acoustics of porous media. Paris: Editions Technip.

Google Scholar

Brutsaert, W. (1964). The propagation of elastic waves in unconsolidated unsaturated granular mediums. J. Geophys. Res. 69, 243–257. doi:10.1029/jz069i002p00243

CrossRef Full Text | Google Scholar

Carcione, J. M. (2014). Wave fields in real media: theory and numerical simulation of wave propagation in anisotropic, anelastic, porous and electromagnetic media. 3rd ed. Amsterdam: Elsevier Science.

Google Scholar

Chapman, S., Tisato, N., Quintal, B., and Holliger, K. (2016). Seismic attenuation in partially saturated Berea sandstone submitted to a range of confining pressures. J. Geophys. Res. Solid Earth 121 (3), 1664–1676. doi:10.1002/2015jb012575

CrossRef Full Text | Google Scholar

Chapman, S., Borgomano, J. V., Quintal, B., Benson, S. M., and Fortin, J. (2021). Seismic wave attenuation and dispersion due to partial fluid saturation: direct measurements and numerical simulations based on x-ray CT. J. Geophys. Res. Solid Earth 126 (4), e2021JB021643. doi:10.1029/2021jb021643

CrossRef Full Text | Google Scholar

Dvorkin, J., and Nur, A. (1993). Dynamic poroelasticity: a unified model with the squirt and the Biot mechanisms. Geophysics 58, 524–533. doi:10.1190/1.1443435

CrossRef Full Text | Google Scholar

Gassmann, F. (1951). Über die Elastizität poröser Medien. Vierteljahrsschrift der Naturforschenden Gesellschaft Zürich 96, 1–23. doi:10.1190/1.1437718

CrossRef Full Text | Google Scholar

Gurevich, B., and Carcione, J. M. (2022). Attenuation and dispersion of elastic waves in porous rocks: mechanisms and models. Tulsa: Society of Exploration Geophysicists.

Google Scholar

Gurevich, B., Makarynska, D., de Paula, O. B., and Pervukhina, M. (2010). A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks. Geophysics 75 (6), N109–N120. doi:10.1190/1.3509782

CrossRef Full Text | Google Scholar

Johnson, D. L. (1986). Recent developments in the acoustic properties of porous media. Front. Phys. Acoustics XCIII.

Google Scholar

Li, H., Wang, D., Gao, J., Zhang, M., Wang, Y., Zhao, L., et al. (2020). Role of saturation on elastic dispersion and attenuation of tight rocks: an experimental study. J. Geophys. Res. Solid Earth 125, e2019JB018513. doi:10.1029/2019jb018513

CrossRef Full Text | Google Scholar

Li, H.-X., Zhang, J.-H., Fan, J.-W., Tao, C.-H., Xiao, K., Huang, G.-N., et al. (2022). Wave propagation theory of multi-scale wave induced flow in unsaturated porous medium. Acta Phys. Sin. 71, 089101. doi:10.7498/aps.71.20211463

CrossRef Full Text | Google Scholar

Masson, Y. J., Pride, S. R., and Nihei, K. (2006). Finite difference modeling of Biot's poroelastic equations at seismic frequencies. J. Geophys. Res. 111 (B10), B10305. doi:10.1029/2006jb004366

CrossRef Full Text | Google Scholar

Mavko, G., and Nur, A. (1975). Melt squirt in the asthenosphere. J. Geophys. Res. 80, 1444–1448. doi:10.1029/jb080i011p01444

CrossRef Full Text | Google Scholar

Monachesi, L. B., Wollner, U., and Dvorkin, J. P. (2020). Effective pore fluid bulk modulus at patchy saturation: an analytic study. J. Geophys. Res. Solid Earth 125, e2019JB018267. doi:10.1029/2019jb018267

CrossRef Full Text | Google Scholar

Müller, T. M., and Gurevich, B. (2004). One-dimensional random patchy saturation model for velocity and attenuation in porous rocks. Geophysics 69 (5), 1166–1172. doi:10.1190/1.1801934

CrossRef Full Text | Google Scholar

Müller, T. M., Gurevich, B., and Lebedev, M. (2010). Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks—a review. Geophysics 75, 75A147–75A164. doi:10.1190/1.3463417

CrossRef Full Text | Google Scholar

Norris, A. N. (1985). A differential scheme for the effective moduli of composites. Mech. Mater. 4 (1), 1–16. doi:10.1016/0167-6636(85)90002-x

CrossRef Full Text | Google Scholar

Papageorgiou, G., and Chapman, M. (2017). Wave-propagation in rocks saturated by two immiscible fluids. Geophys. J. Int. 209 (3), 1761–1767. doi:10.1093/gji/ggx128

CrossRef Full Text | Google Scholar

Plona, T. J. (1980). Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Appl. Phys. Lett. 36, 259–261. doi:10.1063/1.91445

CrossRef Full Text | Google Scholar

Pride, S. R. (2005). “Relationships between seismic and hydrological properties,” in Hydrogeophysics. Editors Y. Rubin, and S. Hubbard (Dordrecht: Springer Netherlands), 253–290.

CrossRef Full Text | Google Scholar

Pride, S. R., Gangi, A. F., and Morgan, F. D. (1992). Deriving the equations of motion for porous isotropic media. J. Acoust. Soc. Am. 92 (6), 3278–3290. doi:10.1121/1.404178

CrossRef Full Text | Google Scholar

Pride, S. R., Berryman, J. G., and Harris, J. M. (2004). Seismic attenuation due to wave-induced flow. J. Geophys. Res. Solid Earth 109, 2003JB002639–19. doi:10.1029/2003jb002639

CrossRef Full Text | Google Scholar

Qi, Q., Müller, T. M., Gurevich, B., Lopes, S., Lebedev, M., and Caspari, E. (2014). Quantifying the effect of capillarity on attenuation and dispersion in patchy-saturated rocks. Geophysics 79, WB35–WB50. doi:10.1190/geo2013-0425.1

CrossRef Full Text | Google Scholar

Rozhko, A. Y. (2020). Effective fluid bulk modulus in the partially saturated rock and the amplitude dispersion effects. J. Geophys. Res. Solid Earth 125 (3), e2019JB018693. doi:10.1029/2019jb018693

CrossRef Full Text | Google Scholar

Santos, J. E., Ravazzoli, C. L., Gauzellino, P. M., Carcione, J. M., and Cavallini, F. (2004). Simulation of waves in poro-viscoelastic rocks saturated by immiscible fluids: numerical evidence of a second slow wave. J. Comput. Acoust. 12 (01), 1–21. doi:10.1142/s0218396x04002195

CrossRef Full Text | Google Scholar

Shi, Z., He, X., Chen, D., and Wang, X. (2024). Seismic wave dispersion and attenuation resulting from multiscale wave-induced fluid flow in partially saturated porous media. Geophys. J. Int. 236 (2), 1172–1182. doi:10.1093/gji/ggad475

CrossRef Full Text | Google Scholar

Solazzi, S. G., Guarracino, L., Rubino, J. G., Müller, T. M., and Holliger, K. (2017). Modeling forced imbibition processes and the associated seismic attenuation in heterogeneous porous rocks. J. Geophys. Res. Solid Earth 122 (11), 9031–9049. doi:10.1002/2017jb014636

CrossRef Full Text | Google Scholar

Solazzi, S. G., Lissa, S., Rubino, J. G., and Holliger, K. (2021). Squirt flow in partially saturated cracks: a simple analytical model. Geophys. J. Int. 227 (1), 680–692. doi:10.1093/gji/ggab249

CrossRef Full Text | Google Scholar

Song, Y., Hu, H., and Rudnicki, J. W. (2016). Dynamic bulk and shear moduli due to grain-scale local fluid flow in fluid-saturated cracked poroelastic rocks: theoretical model. J. Mech. Phys. Solids 92, 28–54. doi:10.1016/j.jmps.2016.03.019

CrossRef Full Text | Google Scholar

Sun, W. (2021). On the theory of biot-patchy-squirt mechanism for wave propagation in partially saturated double-porosity medium. Phys. Fluids 33 (7), 076603. doi:10.1063/5.0057354

CrossRef Full Text | Google Scholar

Tuncay, K., and Corapcioglu, Y. (1996). Body waves in poroelastic media saturated by two immiscible fluids. J. Geophys. Res. 101 (B11), 25149–25159. doi:10.1029/96JB02297

CrossRef Full Text | Google Scholar

Tuncay, K., and Corapcioglu, M. Y. (1997). Wave propagation in fractured porous media. Transp. Porous Media 23 (3), 237–258. doi:10.1007/bf00167098

CrossRef Full Text | Google Scholar

Wang, H. M., and Tang, X. M. (2021). Inversion of dry and saturated P- and S-wave velocities for the pore-aspect-ratio spectrum using a cracked porous medium elastic wave theory. Geophysics 86 (6), A57–A62. doi:10.1190/geo2021-0071.1

CrossRef Full Text | Google Scholar

White, J. E. (1975). Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics 40 (2), 224–232. doi:10.1190/1.1440520

CrossRef Full Text | Google Scholar

Williams, J. L. (1992). Ultrasonic wave propagation in cancellous and cortical bone: prediction of some experimental results by Biot’s theory. J. Acoust. Soc. Am. 91 (2), 1106–1112. doi:10.1121/1.402637

PubMed Abstract | CrossRef Full Text | Google Scholar

Wollner, U., and Dvorkin, J. (2018). Effective bulk modulus of the pore fluid at patchy saturation. Geophys. Prospect. 66 (7), 1372–1383. doi:10.1111/1365-2478.12632

CrossRef Full Text | Google Scholar

Xiong, F., and Yong, W. A. (2022). Learning stable seismic wave equations for porous media from real data. Geophys. J. Int. 230, 349–362. doi:10.1093/gji/ggac082

CrossRef Full Text | Google Scholar

Xiong, F., Ba, J., Gei, D., and Carcione, J. M. (2021). Data-driven design of wave-propagation models for shale-oil reservoirs based on machine learning. J. Geophys. Res. Solid Earth 126, e2021JB022665. doi:10.1029/2021jb022665

CrossRef Full Text | Google Scholar

Zhang, L., Ba, J., Carcione, J. M., and Wu, C. (2022). Seismic wave propagation in partially saturated rocks with a fractal distribution of fluid-patch size. J. Geophys. Res. Solid Earth 127 (2), e2021JB023809. doi:10.1029/2021jb023809

CrossRef Full Text | Google Scholar

Zhao, L., Yuan, H., Yang, J., Han, D. H., Geng, J., Zhou, R., et al. (2017). Mobility effect on poroelastic seismic signatures in partially saturated rocks with applications in time-lapse monitoring of a heavy oil reservoir. J. Geophys. Res. Solid Earth 122 (11), 8872–8891. doi:10.1002/2017jb014303

CrossRef Full Text | Google Scholar

Zhao, L., Tang, G., Sun, C., Zhao, J., and Wang, S. (2021). Dual attenuation peaks revealing mesoscopic and microscopic fluid flow in partially oil-saturated Fontainebleau sandstones. Geophys. J. Int. 224 (3), 1670–1683. doi:10.1093/gji/ggaa551

CrossRef Full Text | Google Scholar

Zong, Z., Song, L., and Yin, X. (2022). Seismic wave velocity attenuation and dispersion in the patchy saturated medium with complex pores and cracks. Chin. J. Geophys. (in Chinese) 65 (10), 4012–4027. doi:10.6038/cjg2022P0322

CrossRef Full Text | Google Scholar