Experimental analysis of rainfall-induced shallow landslides: a case study of a loess slope in Gaolan County, China

Rainfall is a major trigger for loess landslides, and understanding the associated deformation and failure mechanisms is essential for effective hazard mitigation. This study employed physical model experiments to investigate the hydrological response, deformation behavior, and failure evolution of homogeneous loess slopes subjected to intermittent rainfall. Key parameters, including volumetric water content, pore water pressure, wetting front migration, and displacement, were continuously monitored throughout the tests. The results revealed periodic fluctuations in hydrological parameters and spatially heterogeneous responses across the slope. Repeated transitions between saturated and unsaturated conditions, combined with surface runoff erosion and seepage-induced forces, contributed to a progressive reduction in soil shear strength and increased slope instability. The failure process evolved through three distinct stages: toe erosion, fissure expansion, and gully erosion. These findings improve the understanding of rainfall-induced loess slope failures and support the development of stage-specific hazard mitigation strategies.

1 Introduction

Gansu Province, China, is located at the intersection of the Loess Plateau, Inner Mongolia Plateau, and Qinghai-Tibet Plateau, characterized by its complex geology and frequent rainfall-triggered hazards (Wan et al., 2024; Qiu et al., 2025). The Lanzhou area is mainly composed of Quaternary loess deposits formed around 2.5 million years ago under arid and semi-arid conditions (Lyu et al., 2018). This loess is wind-deposited, under-consolidated, and features high porosity, vertical joints, and collapsibility when exposed to moisture (Zhang and Liu, 2009; Liu et al., 2025). These properties make the region highly susceptible to erosion and landslides. While loess slopes can remain steep and stable under dry conditions, rainfall increases soil saturation, weakens its structure, causes internal deformation (Figure 1), and eventually leads to slope failure through progressive erosion and particle washout (Derbyshire et al., 1994; Zhu et al., 2024). Since the last century, rainfall-induced landslides have caused substantial losses of life and property, with several catastrophic events underscoring the destructive potential of intense or intermittent rainfall in loess regions (Zhuang and Peng, 2014; Peng et al., 2015; Xu et al., 2017; Shi et al., 2020; Wang et al., 2020; Li et al., 2024).

Figure 1

Figure 1. Characterization of loess slopes: (a) Vertical position; (b) Inward erosion; (c) Slippage on slopes.

Landslide research is typically approached through field monitoring, physical model experiments, and numerical simulations, providing complementary insights into failure mechanisms, particularly in loess regions (Fang et al., 2023; Xu and Fang, 2025). Field-scale artificial rainfall experiments have revealed progressive failure sequences, such as initial sliding, liquefaction, and mudflow in Ibaraki Prefecture, Japan (Ochiai et al., 2004), and showed that rainfall intensity affects deformation timing but has limited influence on the final failure mode in Jingyang County (Sun et al., 2021). Physical modeling offers controllability, enabling detailed failure mechanism studies. For example, loess slopes with different inclinations exhibited varying failure modes: combined scouring and spalling at 45° and 60°, and pure spalling at 75° (Zhen et al., 2023). Increased pore water pressure, often starting at the slope toe, was a key trigger for failure (Wu et al., 2017; Wang et al., 2019). Numerical simulations, such as finite element modeling for the Zhonglou Mountain landslide (Xie et al., 2021) and SEEP/W and SLOPE/W for simulating loess slope stability (Wang et al., 2021), provide cost-effective insights into complex landslide processes, enhancing understanding and informing prevention strategies. Further studies have identified early-stage strength degradation factors, including erosion-induced soil property deterioration (Zhang B. et al., 2023; Zhang Z. et al., 2023), reduced matrix suction due to rainfall (Sorbino and Nicotera, 2013), and preferential infiltration pathways (Tang et al., 2015). Rainfall-induced damage in loess slopes typically transitions from localized toe failure to multi-stage rotational sliding and gully erosion under sustained rainfall (Guo et al., 2023), with characteristic crack-related damage, such as deep gullies and material retreat (Xiao and Tian, 2024). Ultimately, slope deformation is governed by shallow soil movement driven by progressive erosion (Leng et al., 2024).

However, most existing experiments focus on the overall trends in soil parameter changes induced by continuous rainfall, with limited attention to the dynamic evolution of internal slope changes over time under intermittent rainfall. This study investigates a typical loess slope in the Gansu Loess Plateau, China. Through comprehensive monitoring of volumetric water content, pore water pressure, wetting front migration, and slope displacement, we propose a three-stage instability evolution model. The research evaluates the failure process, mechanisms, and hydrological responses of shallow loess landslides triggered by intermittent rainfall. These findings enhance the understanding of rainfall-induced shallow landslides and provide a theoretical basis for targeted mitigation strategies.

2 Test materials and methods

2.1 Study area and test materials

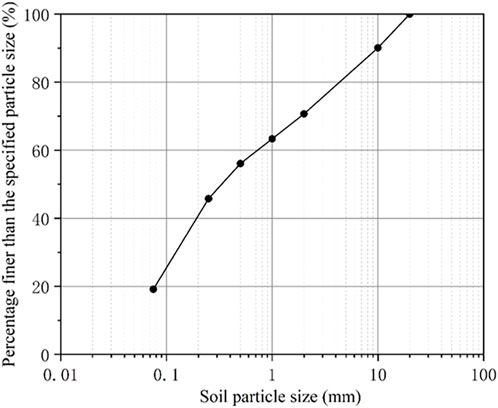
The study area is situated at the leading edge of the tertiary terrace on the left bank of the Yellow River in Gaolan County, Lanzhou City, China. The foot of the slope is a densely populated residential area, while the tertiary terrace is covered with orchards and farmland. Soil landslides and slope failures frequently occur due to rainfall. In this study, a typical unstable loess slope within the study area was selected as the experimental geological prototype (Figure 2). The basic physical properties of the test loess were determined through indoor testing, as presented in Table 1. The particle size distribution of the test loess was determined using a combination of dry sieving methods in accordance with the GB/T 50123-2019 Standard for Soil Test Methods. A standard set of sieves was used to classify soil particles with diameters greater than 0.075 mm. Each test was conducted under controlled laboratory conditions to ensure repeatability and accuracy. The resulting grain-size distribution curve is shown in Figure 3, and corresponding test results are summarized in Table 2.

Figure 2

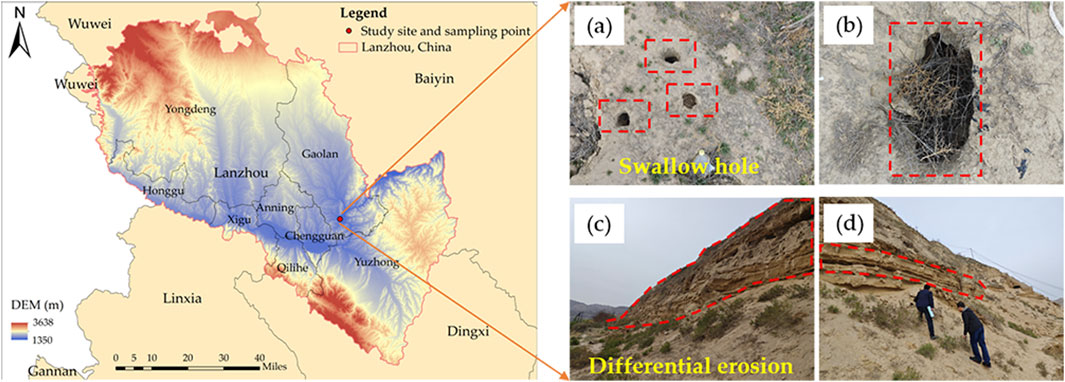
Figure 2. Study area and sampling points: (a) Small swallow holes; (b) Big swallow hole; (c) Differential erosion of the slopes; (d) Slope stability survey.

Table 1

Table 1. Basic physical indicators of the soil tested.

Figure 3

Figure 3. Particle size distribution of experimental loess.

Table 2

Table 2. Percentage of experimental loess grain size.

2.2 Experimental device

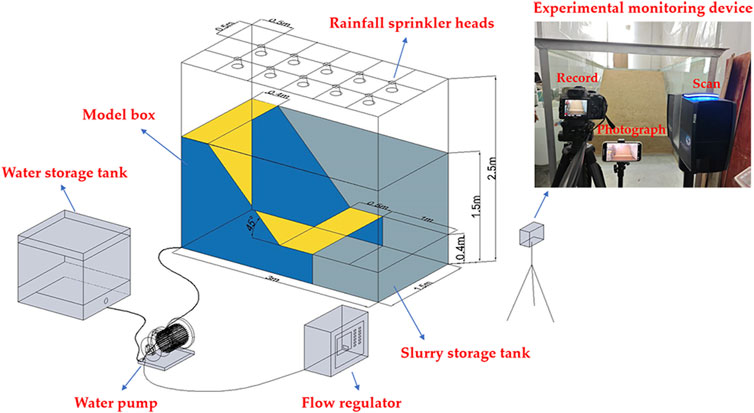
To facilitate the observation of the rainfall infiltration process and slope deformation characteristics, an experimental setup was designed and constructed, as shown in Figure 4, comprising a model box, an artificial rainfall simulation system, and a monitoring system.

(1) The model box is a frame structure, measuring 3.0 m in length, 1.5 m in width, and 1.5 m in height. The front part of the model box is used for soil filling and observation, without any baffle panels, while the remaining sides are composed of 16 mm thick tempered glass panels, facilitating direct visual observation during testing. The bottom is made of a steel plate, with the surrounding area reinforced using angled supports. Additionally, a mud-water mixture collection basin is installed in the anterior section of the model box to collect the slurry discharged during the rainfall process.

(2) The artificial rainfall simulation system consists of a water pump, a water storage tank, a flow regulator, and atomizing nozzles. The nozzles are positioned 1.0 m above the model box with a spacing of 0.5 m, each branch of the pipeline contains five nozzles, totaling 10 in the system. The function of the water pump is to transport water from the storage tank to the pipes and spray it out from the nozzles, with rainfall intensity adjustable via valve control and nozzle rotation. The simulated rainfall achieves fine atomization and uniform distribution, ensuring compliance with precipitation experiment requirements.

(3) The monitoring system is illustrated in Figure 4. It comprises six volumetric water content sensors, measuring 0%–100% with an accuracy of ±3% for 0%–50% and ±5% for 50%–100% (Figure 5a), as well as six pore water manometers with a range of 20 kPa and an accuracy of 0.3% F∙S (Figure 5b). Additionally, it is paired with a 24-channel DH3818Y-type data collector (Figure 5c) and a Nikon D3400 DSLR camera (Figure 5d). During the rainfall process, volumetric water content and pore water pressure readings were automatically recorded at 60-s intervals, which ensured sufficient temporal resolution to capture dynamic infiltration, saturation transitions, and pore pressure buildup.

Figure 4

Figure 4. Experimental model device.

Figure 5

Figure 5. Monitoring system: (a) MDK-05 water content sensor; (b) BMWK pore water manometer; (c) DH3818Y static strain tester; (d) Nikon D3400 DSLR camera.

2.3 Test program

2.3.1 Design of slopes

To provide a rational foundation for scaling in physical modeling, the Buckingham π theorem was applied. According to this theorem (Buckingham, 1914), if a physical problem involves n variables and k fundamental dimensions, it can be reduced to (n–k) independent dimensionless products (π terms). This approach ensures dimensional homogeneity and helps identify key governing parameters that must maintain proportional relationships between the model and the prototype.

In our study, the primary objective was to investigate the failure process of a homogeneous loess fill slope subjected to rainfall infiltration. Given the complexity of on-site slope systems—including heterogeneous stratigraphy, irregular topography, and uncertain boundary effects—achieving complete geometric, kinematic, and dynamic similarity was impractical. Instead, we adopted a semi-empirical strategy that emphasizes replicating the dominant physical mechanisms: rainfall infiltration, pore water pressure evolution, and progressive deformation.

Fifteen relevant physical quantities were initially considered (e.g., slope geometry, time, rainfall intensity, pore water pressure, displacement, stress, permeability, cohesion, elastic modulus, etc.), corresponding to three basic dimensions (mass, length, time), which leads to 12 independent π terms. However, recognizing the practical constraints of model fabrication and material preparation, we selectively enforced similarity in the most critical parameters:

(1) Based on the size relationship between the field slope and the model box, a scale factor ($C_l$) of 20 was set. Accordingly, the landslide body was designed with dimensions of 2 m in length, 1.5 m in width, and 1.4 m in height to maintain consistent geometric scaling. The slope angle was set at 45°, consistent with field observations.

(2) Material similarity was ensured by using natural loess from the prototype site and controlling initial dry density and water content, thus preserving key mechanical and hydraulic properties such as permeability ($C_k=1$), cohesion ($C_c=1$), internal friction angle ($C_{\varphi }=1$), and elastic modulus ($C_E=1$).

(3) Gravitational acceleration remained unchanged ($C_g=1$), as the model was tested under normal gravity conditions.

(4) Poisson’s ratio, and water content are scale-invariant ($C=1$).

Despite not achieving full similitude in all dimensions, the above approach effectively captures the fundamental hydromechanical responses of loess slopes under rainfall, thereby ensuring the physical relevance and interpretability of the model results. Acknowledging these scaling limitations, our design focuses on reproducing key failure mechanisms rather than precise numerical replication of field stress states.

2.3.2 Sensor placement method

Three sensor layers were deployed inside the slope, parallel to the horizontal plane, positioned 30 cm, 80 cm, and 130 cm from the bottom of the model box. The outermost sensors of each layer were placed at the same distance from the slope. Considering the disturbance caused by deployment density, the horizontal spacing between sensors in the same layer was controlled to range from 10 cm to 20 cm. The volumetric water content sensor and the pore water pressure sensor were placed adjacent to each other in each layer, as they are positively correlated and can be cross-verified. The specific placement of each sensor is illustrated in Figure 6.

Figure 6

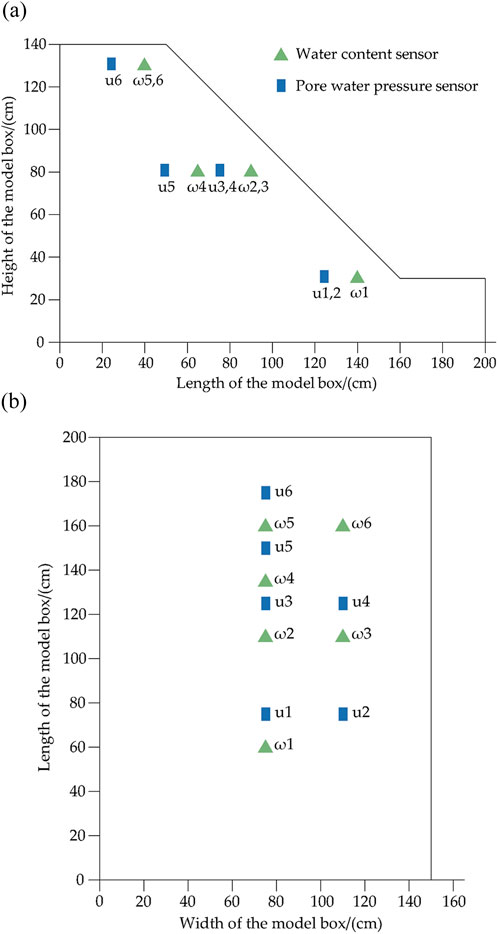
Figure 6. Profile and plan views of sensor arrangement for monitoring in loess slope model experiments: (a) profile view; (b) plan view.

2.3.3 Slope filling process

Prior to soil placement, all articulated joints of the model container were sealed using waterproof epoxy resin to ensure hydraulic integrity. The interior surfaces of the plexiglass sidewalls were coated with a thin layer of petroleum jelly to reduce surface friction and minimize boundary effects. A 10 × 10 cm coordinate grid was inscribed on the tempered glass baseplate to facilitate: (a) precise control of fill height and slope geometry during model construction, and (b) quantitative tracking of slope displacement through digital image correlation analysis.

(1) Stratified filling procedure. During the slope model construction, a systematic and controlled compaction procedure was adopted to ensure uniformity and repeatability. The remolded loess soil was placed in successive horizontal layers, each with a thickness of 30 cm. For each layer, the required mass of soil was calculated according to the target dry density (determined from undisturbed field samples) and accurately weighed using an electronic balance. The weighed soil was then evenly spread across the bottom of the model container and manually compacted using a hand tamper. Compaction was carried out in a standardized manner, with a consistent maximum drop height and number of blows per unit area applied to ensure uniform energy input across the layer. A laser level was employed to verify the flatness and thickness uniformity of each compacted layer. Prior to compaction, the initial moisture content of the test soil was adjusted to match the natural water content of the undisturbed sample. After compaction, ring cutter samples were collected from the four corners of each layer (Figure 7a), and their average dry density and water content were measured to assess compliance with the target values. If significant deviations were observed, the layer was reworked to meet the specifications. This compaction protocol ensured consistent homogeneity throughout the slope model and improved the reliability of the test results. The completed slope model after filling is shown in Figure 7b.

(2) Burial of monitoring sensors in layers. The sensors were buried with loose loess to evenly cover a certain thickness before tamping. The wire was reserved with sufficient tension to prevent displacement from pulling it off. After filling, the sensors were connected to the collection equipment, and computer testing was performed to ensure the instruments were functioning properly. The initial readings of each device were recorded.

(3) Slope cutting. The slope was cut according to the set 45° angle, ensuring that disturbance to the remaining soil was minimized. The slope model is shown in Figure 7c after cutting is complete. Afterward, plastic film was laid on its surface and maintained for 48 h.

Figure 7

Figure 7. Modeled slope filling process: (a) Sampling with a cutting ring; (b) Completion of filling; (c) Slope model.

2.3.4 Determination of rainfall pattern

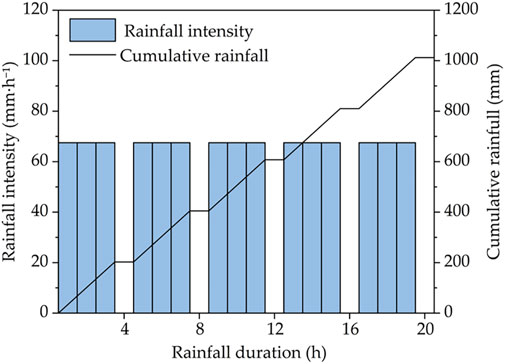
Lanzhou City has a temperate continental climate, with precipitation primarily concentrated from July to September, accounting for over 60% of the annual total. The long-term average annual precipitation is approximately 300–311.7 mm, with historically recorded maximum daily and hourly rainfall of 96.8 mm and 51.9 mm, respectively. However, recent meteorological data show that hourly rainfall intensities in central Gansu can reach 60–80 mm/h during short-duration heavy rainfall events indicating an upward trend in extreme precipitation due to climate variability. For example, official data released in July 2023 showed that the maximum hourly rainfall intensity in Gansu Province reached 73.5 mm. Based on meteorological data and in comparison with previous loess slope model test conditions in the region, the rainfall intensity for this experiment was set at 67.5 mm/h. The simulated rainfall followed an intermittent pattern of 3 h rainfall followed by 1 h pause, starting at 10:00 a.m. and continuing for a total of 20 h. This configuration aims to realistically reproduce short-term, high-intensity rainfall conditions that commonly trigger slope instability. The rainfall curve is shown in Figure 8.

Figure 8

Figure 8. Rainfall curve.

3 Results and analysis

Before the experiment, we conducted repeated calibration tests on the sensors to ensure data consistency and accuracy. Additionally, to improve the interpretability of the sensor data, all time series of volumetric water content and pore water pressure were post-processed using a five-point moving average smoothing technique. This approach reduces random noise while preserving the overall trend in the measurements. Additionally, in cases of non-uniform sampling intervals or minor data gaps due to sensor latency, linear interpolation was applied to align all sensor outputs along a unified time axis. These methods ensured consistent comparison across different monitoring positions and improved the reliability of temporal trend analysis.

3.1 Analysis of the change of volumetric water content of loess slope during rainfall process

The variation in water content at different locations within the slope during the rainfall infiltration process is shown in Figure 9, with two behaviors observed regarding soil volumetric water content.

Figure 9

Figure 9. Changes in volumetric water content of loess slopes during rainfall.

At the initial stage of the experiment, the rainfall infiltration depth was shallow, and the soil volumetric water content remained close to the initial value of 5%. As infiltration progressed, the wetting front gradually advanced to the sensor positions, leading to an increase in volumetric water content, which eventually stabilized after reaching its peak. The response time of each sensor to precipitation varied depending on its location. In the longitudinal section (Figure 9, sensors ω1, ω2, and ω5), ω5, positioned at the shoulder of the slope, exhibited the earliest response, with the wetting front reaching it approximately 1 h after precipitation began. ω1, located at the toe of the slope, has the latest response time, with the wetting front arriving after 2 h of precipitation. Compared with ω5, ω1 and ω2 exhibit a clear lag effect in response to rainfall infiltration. ω3 and ω6 also support this conclusion, with the response of ω3, located farther from the shoulder of the slope, lagging behind that of ω6, located nearer to the shoulder. This can be attributed to the fact that ω5, located at the shoulder of the slope, is closer to the top, allowing precipitation to infiltrate directly at the top of the slope after it accumulates, with the wetting front reaching ω5 first. In contrast, a portion of the precipitation is lost to runoff before reaching ω1 and ω2, reducing the available infiltration. Additionally, coupled with greater energy loss due to the longer infiltration path, this results in a later arrival of the wetting front at ω1 and ω2. In the cross-section, as shown by ω2, ω3, and ω4 in Figure 9, the response times of ω2 and ω3, closer to the slope face, are almost the same, with water content changes beginning after 1 h of precipitation. In contrast, ω4, located in the interior of the slope body, responds significantly later, with data changes appearing after about 4.5 h. This is because ω4 is buried at a deeper depth, and the path required for precipitation to infiltrate, either from the slope or the top of the slope, is longer, causing the wetting front to take longer to arrive at this location. Additionally, although ω2 and ω3 are at the same distance from the slope surface and located at the same height, ω3 responds slightly earlier than ω2 and ultimately achieves a maximum water content about 2% higher than ω2. This is because the soil around the central axis can freely infiltrate water, while the soil near the side is restricted by the side wall, the direction of seepage is relatively single, resulting in a faster accumulation of water in this region, making the moisture content sensor feel the moisture change earlier.

Additionally, regarding the final stabilized maximum water content, ω5 and ω6, located at the slope shoulder, exhibited the highest values, stabilizing at approximately 30%, whereas ω4, positioned within the slope interior, had the lowest value, stabilizing at around 22%. This discrepancy arises from the fact that the soil at the slope crest is more susceptible to saturation during rainfall, as precipitation is directly applied to the surface without being dissipated by runoff. Consequently, the highest stabilized water content is observed at the slope shoulder. In contrast, water infiltrating into the slope interior follows a longer percolation pathway, during which gravitational potential energy dissipates, pore water flow encounters resistance, and a portion of the infiltrated water is redirected laterally. These factors collectively limit the increase in water content within the deeper soil layers.

By analyzing the variation in water content at different locations during the rainfall process, it can be observed that:

(1) As the elevation increases, the soil’s response time to rainfall becomes shorter, while the final stabilized water content exhibited an increasing trend. At the top of the slope, direct exposure to rainfall accelerates infiltration, leading to a rapid rise in water content and a higher stabilization value. In contrast, at the midslope and slope foot, a portion of the precipitation is carried away by runoff, and the extended infiltration pathway further delays the response of water content, resulting in a relatively lower stabilization value.

(2) The moisture levels in deeper soil layers showed a lagged response to precipitation events and fluctuated less significantly compared to upper soil layers, demonstrating greater hydrological reactivity in surface soils to rainfall inputs.

3.2 Analysis of pore water pressure changes in fill slopes during rainfall process

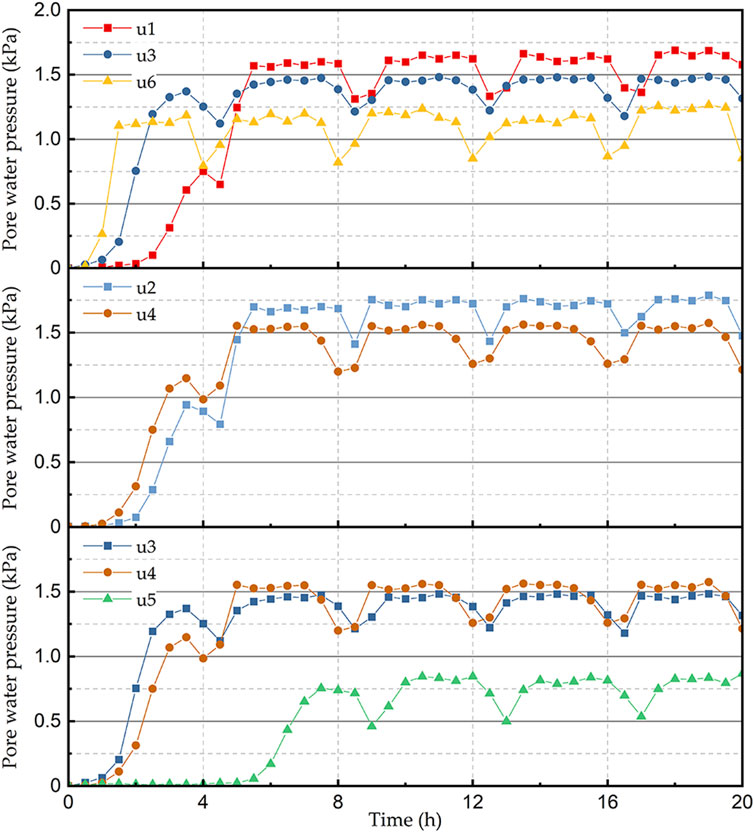
The changes in pore water pressure within loess slopes during rainfall infiltration are illustrated in Figure 10. The overall trend aligns with changes in volumetric water content, exhibiting cyclical fluctuations with rainfall. However, the response of pore water pressure to rainfall infiltration lags behind that of volumetric water content. This delay occurs because volumetric water content increases immediately upon the arrival of the wetting front at the sensor, whereas pore water pressure changes only after water permeates through the sensor’s porous stone.

Figure 10

Figure 10. Changes in pore water pressure of loess slopes during rainfall processes.

As shown in Figure 10, u6, located near the top of the slope, has the fastest response time. The pore pressure begins to increase after 1 h of rainfall and eventually stabilizes at approximately 1.22 kPa u1, located furthest from the top of the slope, exhibits the latest response time. It does not reach the maximum pore pressure within the first precipitation cycle (the maximum pore pressure being 0.75 kPa during the cycle) and only reaches a maximum pore pressure of approximately 1.65 kPa after 4.5 h of testing. u3, located in the central part of the slope, the response time and maximum pore pressure value fall between those of u1 and u6. Similarly, the same conclusion can be drawn from the pore pressure-time graphs of u2 and u4 in Figure 10. The more downwardly located u2 exhibits a later response time but a larger maximum pore pressure value, approximately 0.15 kPa greater than u4. Notably, the pore pressure at u5 in Figure 10 takes longer to reach its maximum value and is lower than the maximum pore pressure measured by the other sensors. Under rainfall conditions, the shallow soil layer initially absorbs water, generating higher pore pressure, while gravity and matric forces drive water infiltration downward. However, as the infiltration depth increases, capillary forces between soil particles become more pronounced, impeding water migration and reducing the accumulation rate of moisture in deeper soil layers. Additionally, the deep soil is in a relatively enclosed environment with limited drainage capacity, resulting in a delayed increase in pore pressure. Furthermore, a portion of the precipitation is discharged as surface runoff along the slope, decreasing the effective infiltration into the deeper layers, thereby leading to lower pore pressure levels in the deep soil compared to the shallow layer.

The data results of pore water pressure changes in loess slopes show that:

(1) At different heights along the same profile, pore water pressure generally decreases as height increases, while the response speed accelerates with height. During the initial rainfall stage, the surface soil preferentially absorbs rainwater, causing a rapid increase in pore pressure in the shallow layer (particularly along the slope surface), whereas the deeplayer pore pressure responds with a delay. During the intermittent rainfall stage, as infiltration progresses, the deeper part of the slope gradually becomes saturated. The pore pressure increases and reaches its peak near the foot of the slope. Water continues to infiltrate toward the foot of the slope between rainfall intervals. The pore pressure near the top of the slope decreases rapidly as rainfall ceases, whereas the lower part experiences a slower decline due to the hysteresis effect.

(2) The pore water pressure inside the loess slope is lower than that near the slope surface. Due to the low permeability of loess, the wetting front advances downward slowly during rainfall, consequently, rainwater cannot rapidly penetrate the slope’s interior at the onset of rainfall, and the deep soil remains insufficiently saturated, resulting in relatively low pore water pressure. Moreover, loess exhibits strong capillary action, and the matrix suction in the unsaturated soil layer is high, which hinders rapid water penetration into deeper layers, causing water to preferentially accumulate in the surface layer and increase pore pressure along the slope surface, and the outward infiltration force generated by the slope further influences this process.

The reduction in slope stability during rainfall infiltration is governed by changes in the effective stress of the unsaturated loess. According to Bishop’s effective stress principle (Bishop, 1959), the effective stress ${\sigma }^{\prime }$ for unsaturated soils can be expressed as:

${\sigma }^{\prime }=\left(\sigma -u_a\right)+\chi \left(u_a-u_w\right)(1)$

where $\sigma$ is the total stress, $u_a$ is the pore air pressure, $u_w$ is the pore water pressure, $\left(u_a-u_w\right)$ is the matric suction, and $\chi$ is the effective stress parameter (ranging from 0 to 1 depending on the degree of saturation). As rainfall infiltration progresses, the pore water pressure $u_w$ increases, leading to a decrease in matric suction and thus a lower contribution to effective stress. Meanwhile, the reduction in effective stress directly results in a decrease in the shear strength of the soil, which can be expressed using the extended Mohr–Coulomb failure criterion for unsaturated soils:

$\tau =c^{\prime }+\left(\sigma -u_a\right)\tan {\varphi }^{\prime }+\chi \left(u_a-u_w\right)\tan {\varphi }^{\prime }(2)$

where $\tau$ is the shear strength, $c^{\prime }$ is the effective cohesion, and ${\varphi }^{\prime }$ is the effective internal friction angle. Under continuous or intermittent rainfall, the reduction of $\left(u_a-u_w\right)$ and the corresponding change in $\chi$ significantly weaken the mechanical resistance of the slope material, especially in the shallow zone. This theoretical framework, as described in Equations 1, 2, supports the experimental observations of increased displacement and failure progression during the wetting process.

3.3 Analysis of the migration process of wetting fronts on slope faces during rainfall process

The wetting front is defined as the dynamic boundary between the wetted zone and the underlying dry soil during infiltration. It marks the transition where the volumetric water content shows a sharp increase due to moisture advancement. The position and timing of the wetting front serve as key indicators of infiltration behavior. In this study, the wetting front transport was analyzed by tracking the wetting front infiltration positions over time using grid lines on the glass panel on the model box’s left side. Figure 11 characterizes the four-stage wetting front migration process: (1) rapid infiltration (0–40 min), (2) dominant infiltration (40 min–5 h 25 min), (3) equilibrium infiltration (5 h 25 min–7 h 9 min), and (4) closure (7 h 9 min–20 h). The corresponding schematic representation is presented in Figure 12.

Figure 11

Figure 11. Photographic observation of wetting front migration: (a) T = 40 min; (b) T = 5 h 25 min; (c) T = 7 h 9 min; (d) T = 20 h.

Figure 12

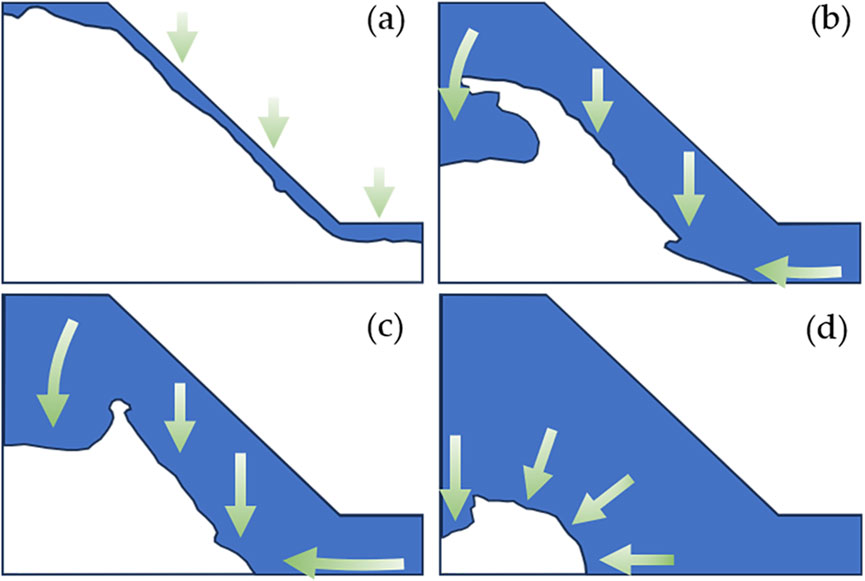
Figure 12. Schematic of wetting front migration stages: (a) T = 40 min; (b) T = 5 h 25 min; (c) T = 7 h 9 min; (d) T = 20 h.

During the rapid infiltration stage (0–40 min), moisture initially accumulates on the soil surface as rainfall begins, wetting front form rapidly, and precipitation gradually infiltrates the soil (Figures 11a, 12a). During the dominant infiltration stage (40 min–5 h 25 min), wetting fronts rapidly migrate along preferential flow paths created by fissures. The significant moisture accumulation at the slope’s back edge and foot accelerates wetting front transport, progressively surrounding the central slope from both downward and inward directions (Figures 11b, 12b). During the equilibrium infiltration stage (5 h 25 min–7 h 9 min), the wetting front gradually stabilizes as rainfall continues. Its downward movement slows, leading to a more uniform moisture distribution inside the soil (Figures 11c, 12c). During the closure stage (7 h 9 min–20 h), the wetting front continues advancing downward until moisture fully saturates the soil (Figures 11d, 12d).

The closure of the wetting front largely depends on when rainfall ceases. If rainfall stops earlier, the wetting front may not fully close but instead stabilizes over time as moisture dissipates through evaporation and lateral seepage.

The primary factors influencing wetting front migration during rainfall include rainfall intensity and duration, soil hydraulic properties, soil type and particle size distribution, initial moisture state, slope gradient, and soil structure heterogeneity. Rainfall intensity and duration directly influence infiltration rate and wetting front formation, intense rainfall accelerates wetting front penetration into deeper soil layers, whereas prolonged rainfall causes water accumulation, expanding wetting front both downward and laterally.

In this experiment, under rainfall infiltration, the wetting front within the slope exhibits a progressive migration from the shallow to deeper layers and from the upslope to the downslope regions. Initially, rainfall infiltration increases the volumetric water content in the shallow soil, forming an early-stage wetting front near the surface. As infiltration continues, gravitational forces drive water downward, while matric suction facilitates lateral and vertical moisture redistribution, leading to the gradual downward migration of the wetting front. Surface runoff influences this process by reducing effective infiltration, causing the wetting front to form earlier at the slope shoulder while appearing later at the slope toe due to the accumulation of percolating water. Moreover, the heterogeneity of the soil and the presence of microcracks on the slope surface result in spatial variations in infiltration rates. In particular, transverse cracks at the rear edge of the slope create preferential flow paths, facilitating localized rapid infiltration. As a result, the overall infiltration rate at the slope crest is higher than that on the slope surface, leading to differential moisture distribution and influencing the wetting front migration dynamics.

3.4 Analysis of fill slope displacement changes during rainfall process

Displacement is the most direct and visible indicator of slope instability evolution and the landslide body displacement is illustrated in Figure 13. By tracking the coordinates of the slope’s top edge within the square grid during the test, the wet subsidence of loess can be directly measured.

Figure 13

Figure 13. Changes in loess slope displacement during rainfall infiltration: (a) T = 10 min; (b) T = 6 h 11 min; (c) T = 10 h 23 min; (d) T = 20 h.

At T = 10 min, the slope surface exhibits no noticeable displacement, the slope structure remains intact, and no cracks or deformation are observed, indicating a stable state (Figure 13a). By T = 6 h 11 min, slight displacements begin to emerge at the slope crest, while deformation becomes more pronounced at the slope edges, particularly at the toe, where the maximum displacement reaches approximately 20 cm (Figure 13b). At T = 10 h 23 min, displacement intensifies significantly, the deformation zone expands, and the internal soil structure deteriorates further. Both displacement magnitude and deformation rate increase markedly, with the deformation at the slope toe propagating upslope toward the shoulder, eventually leading to flowtype failure. At this stage, the maximum vertical settlement at the crest reaches approximately 3 cm (Figure 13c). By T = 20 h, after rainfall ceases, displacement continues to develop, and the entire slope exhibits creeping deformation, indicating a high risk of overall failure. The maximum vertical settlement at the crest reaches approximately 10 cm (Figure 13d).

Under continuous rainfall infiltration, the progressive deformation of the slope is primarily controlled by the reduction in matric suction, the increase in pore water pressure, and the deterioration of soil strength. In the initial stage, infiltration is limited to the shallow layer, and the slope remains stable. As rainfall continues, water percolates deeper, leading to the softening of the soil and the initiation of localized displacement, particularly at the slope toe where stress concentration occurs. With prolonged infiltration, the wetting front propagates downward, increasing the degree of saturation and reducing effective stress, thereby accelerating deformation. The gradual expansion of the deformation zone weakens the internal structure of the slope, ultimately triggering a flow-type failure. After rainfall ceases, residual pore water pressure dissipation and creep deformation further contribute to the potential for large-scale slope instability.

To quantitatively illustrate the temporal evolution of slope deformation and support the classification of failure stages, displacement–time curves were plotted for two key locations: vertical settlement at the slope crest and horizontal displacement at the slope toe (Figure 14).

Figure 14

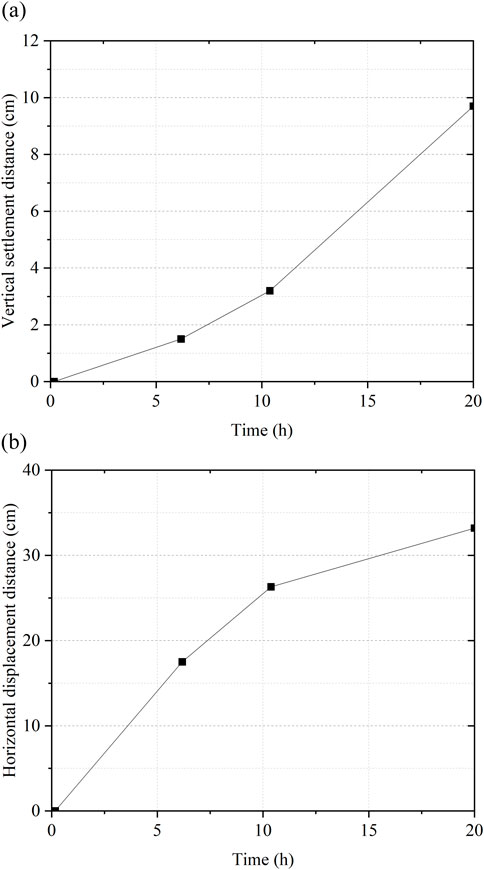
Figure 14. Displacement changes with time: (a) Vertical displacement at the top of the slope; (b) Horizontal displacement at the toe of the slope.

Under rainfall conditions, slope deformation and failure are characterized by the coordinated growth of vertical settlement at the slope top and horizontal displacement at the slope toe over time, primarily driven by the degradation of soil mechanical properties due to water infiltration. The curve at the crest captures cumulative subsidence associated with the gradual loss of shear strength and structural weakening, as shown in Figure 14a, progresses in three stages: initially (0–6 h), the deformation is slow, reflecting the gradual infiltration of water; in the middle stage (6–10.5 h), the deformation accelerates as increased pore water pressure leads to reduced effective stress and shear strength; in the later stage (10.5–20 h), the deformation increases further, indicating that the slope saturation continues to rise, and the overall subsidence of the slope top occurs, with the loss of matric suction and the formation of a slip surface jointly causing slope instability. For the horizontal displacement at the slope toe, as shown in Figure 14b, the deformation is initially significant but gradually decreases with continuous rainfall. This is because the slope toe is damaged early, leading to a rapid increase in displacement. This process reveals the chain failure mechanism of rainfall-induced landslides, where the increase in pore water pressure weakens shear strength, causing shear failure at the slope toe, which ultimately leads to the settlement of the slope top. These trajectories clearly reflect the phase-wise failure process, providing visual evidence of the transitions between the toe erosion, fissure expansion, and gully erosion stages.

4 Analysis of rainfall-induced damage patterns on loess slopes

The rainfall-induced loess slope damage process exhibits a clear transformation in damage patterns, as illustrated in Figure 15. The classification of the three-stage failure process—namely toe erosion, fissure expansion, and gully erosion—was based on integrated observations of hydrological responses, deformation patterns, and surface failure characteristics during the physical model tests. In the initial toe erosion stage, a localized increase in pore water pressure near the slope foot and minor displacement (<5 cm) indicated incipient instability. This was followed by the fissure expansion stage, characterized by tensile cracking at the slope crest and shoulder, accompanied by accelerated settlement and horizontal displacement. In the final gully erosion stage, concentrated runoff and deep infiltration through fissures led to the formation of erosion gullies and collapse features, with maximum crest settlement exceeding 10 cm. These features reflect the progressive destabilization of the slope from localized erosion to overall failure. The specific characteristics of each stage are described as follows:

Figure 15

Figure 15. Slope damage process during rainfall infiltration: (a) T = 6 h 10 min; (b) T = 12 h 35 min; (c) T = 20 h; (d) T = 6 h 5 min; (e) T = 12 h 30 min; (f) T = 19 h 55 min.

Toe Erosion Stage (0–6 h 10 min): At the onset of rainfall, the infiltration rate exceeds the rainfall intensity, resulting in minimal surface runoff. At this stage, the slope remains nearly intact (Figure 15d). As rainfall continues, the hydraulic gradient decreases, leading to surface runoff and ponding at the slope toe. This process forms a transient saturated zone where strain generates excess pore water pressure, reducing effective stress and shear strength. Once the driving forces surpass the soil’s shear resistance, failure initiates at the slope foot (Figure 15a). The erosion at the toe weakens the overall slope stability, while raindrop impact and runoff degrade the loess structure, washing away fine-grained particles and forming initial surface gullies.

Fissure expansion stage (6 h 10 min–12 h 35 min): The instability at the slope foot induces downward movement of the upper slope under gravitational forces. Rainwater infiltration increases pore water pressure, reducing effective stress and further weakening shear strength. This facilitates fissure formation at the slope’s trailing edge (Figure 15e), while longitudinal fissures develop along the surface (Figure 15b). Over time, continued infiltration and deformation enlarge these fissures, eventually forming through-cracks that compromise slope integrity.

Gully erosion stage (12 h 35 min–20 h): At this stage, gullies serve as primary runoff channels, concentrating rainfall and intensifying erosive forces (Figure 15c). Runoff undercuts the gully bed, deepening it and forming an unstable free surface. The gully walls collapse under gravitational stress, further exacerbating trailing-edge erosion (Figure 15f). Enlarged fissures promote deeper infiltration, accelerating fine-grained loess loss and forming surface depressions or holes at the slope top.

The rainfall-induced loess slope failure exhibits a distinct stage-by-stage evolution, governed by mechanical and hydrological interactions that dictate slope stability trends.

In the early stage of rainfall, rapid surface water infiltration and accumulation at the slope foot lead to localized saturation and elevated pore water pressure, which reduces effective stress, triggering localized shear failure and erosion at the slope toe, weakening the overall load-bearing capacity and setting the stage for subsequent instability. As rainfall continues, progressive toe erosion undermines slope support, causing the upper slope to deform under self-weight. This induces the expansion of tensile cracks at the trailing edge. Concurrently, infiltration and seepage forces further degrade soil strength and reduce the slope’s overall stability. In the final stage, increased surface runoff scours and shears the slope surface, deepening gullies and progressively destabilizing the upper slope. As the integrity of the surface layer deteriorates, soil mass gradually displaces toward the slope foot, expanding the damage zone. This progressive failure may ultimately evolve into a large-scale landslide.

To further investigate the effect of saturation increase due to rainfall infiltration on shear strength, remolded loess samples with water contents of 5%, 15%, 25%, 35%, and 45% were prepared according to the “Standard for Geotechnical Testing Methods” (GB/T 50123-2019) for a series of direct shear tests. During sample preparation, the density was controlled at 1.49 g/cm³. After preparation, shear tests were conducted using a Model ZJ Strain Controlled Direct Shear Apparatus and the shear rate was set to 0.8 mm/min. The variation curves of loess cohesion and internal friction angle with shear strength at different water contents were plotted based on the test results, as presented in Figure 16.

Figure 16

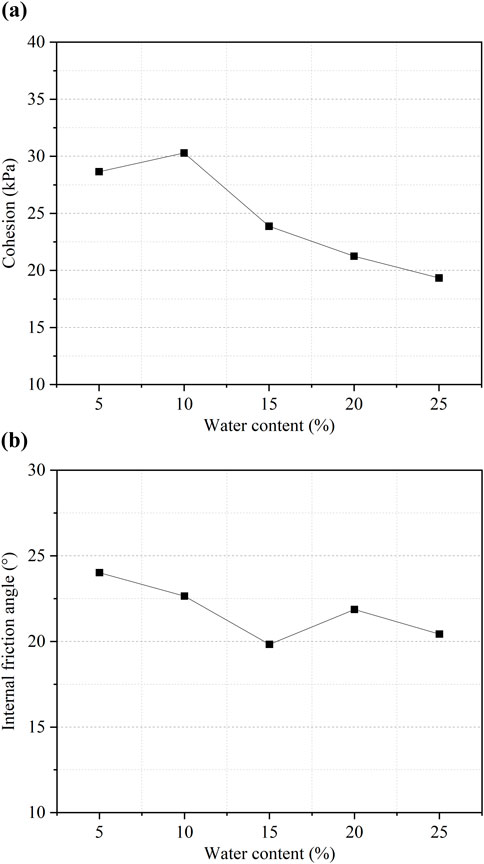
Figure 16. Relationships between loess shear strength parameters and water content: (a) Cohesion; (b) Internal friction angle.

The experimental results show a significant non-linear relationship between cohesion and internal friction angle of loess with respect to water content. As shown in Figure 16a, cohesion slightly increases between 5% and 10% water content, reaching a peak of 30.29 kPa, but then sharply decreases due to water activation of clay minerals in loess, enhancing particle cementation. However, excess water dissolves soluble salts and disrupts structural bonds, leading to a decrease in cohesion. As shown in Figure 16b, The internal friction angle decreases when the water content is below 15%, and increases and then decreases when the water content exceeds 15%. Overall, the internal friction angle changes from 24.02° at 5% water content to 20.43° at 25% water content, showing a slight decreasing trend. The mechanism explanation is as follows: at low water content, the contact friction between particles is high, resulting in a higher friction angle; as water content increases (5%–15%), the water film thickens, reducing direct particle contact and lowering friction, which leads to a reduction in the friction angle. Near the plastic limit, the soil is in a transitional state, with water not enough to liquefy the soil but also not reducing friction, causing the strength to depend more on cementation, which leads to the smallest friction angle. When the water content increases further (15%–20%), water facilitates the reorganization of particles, and the frictional resistance increases in a way that is favorable for shear strength, causing the internal friction angle to increase. Once the water content exceeds 20%, the pores become almost fully saturated, reducing the effective contact area between particles, leading to a decrease in both friction and interlocking forces, and the friction angle decreases again. This phenomenon explains the mechanical nature of loess slope failure induced by rainfall: water infiltration causes cementation softening and friction weakening, which sharply reduces shear strength and leads to sliding. This study provides a significant theoretical basis for landslide early warning and prevention in loess regions.

5 Discussion

5.1 Boundary effects and experimental constraints

The boundary conditions of the physical model inevitably differ from those of natural slopes. In this study, the model was constructed within a rectangular container with tempered glass sidewalls and a steel base. These rigid boundaries allowed for visual observation and structural stability but may have introduced constraints on lateral deformation and vertical water migration. To minimize such effects, petroleum jelly was applied to reduce friction along the glass walls, and the container width was sufficiently large to ensure that the central failure zone was minimally affected by sidewall confinement.

Nonetheless, limitations remain. The steel base, though impermeable and supportive, may not reflect natural drainage conditions. Future improvements may include the use of transparent porous bases to simulate vertical seepage, or flexible sidewalls to better replicate in-situ stress conditions. Expanding the model size could further reduce boundary interference and improve the representativeness of failure patterns.

5.2 Experimental limitations and directions for future research

While the study offers valuable insights into the progressive failure behavior of loess slopes under intermittent rainfall, several limitations should be acknowledged. First, as with all physical models, scaling effects may distort the replication of natural stress conditions, and remolded loess cannot perfectly reproduce the microstructure and bonding strength of intact field soils. Second, laboratory conditions necessarily simplify environmental variables such as temperature, evaporation, and antecedent moisture content, all of which can strongly influence infiltration patterns and failure onset.

Moreover, although the study focused on macro-scale hydrological and mechanical responses, these are inherently linked to the microstructural characteristics of loess—such as interparticle bonding, porosity, and vertical jointing. Without microscopic analysis, key mechanisms of strength degradation and crack initiation at the particle level remain inferred. Future work could incorporate SEM, CT scanning, or other imaging techniques to directly observe microstructural changes. In addition, introducing controlled environmental variations such as temperature fluctuations or antecedent moisture conditions would better approximate field realities.

To enhance generalizability, future studies may also benefit from integrating physical models with numerical simulations or field monitoring data, thereby bridging laboratory observations with real-world applications.

5.3 Engineering implications and practical applications

The experimental identification of a three-stage failure sequence—comprising toe erosion, fissure expansion, and gully development—offers a conceptual model for interpreting loess slope behavior under intermittent rainfall. This staged progression provides a foundation for early warning indicators, whereby initial signs such as surface cracking or sudden displacement acceleration may signal transitions to more severe instability.

For practical slope management in loess regions, the study supports the development of real-time monitoring systems that track volumetric water content, pore water pressure, and surface movement. The threshold responses observed here, such as sharp pore pressure rises preceding gully formation, could be used to refine rainfall-triggered landslide warning systems. Furthermore, the experimental data serve as a robust calibration basis for numerical simulations, which can support scenario-based hazard analysis, design optimization, and the definition of rainfall intensity-duration thresholds for engineering decision-making.

6 Conclusion

This study investigated the hydrological response, deformation behavior, and failure mechanism of a loess slope under intermittent rainfall through physical modeling. Based on the experimental results and observations, the following key conclusions can be drawn:

(1) Hydrological and mechanical responses of the loess slope under intermittent rainfall exhibit spatial and temporal variability. The cyclic infiltration process leads to fluctuations in volumetric water content and pore water pressure across different locations and depths. Sensors positioned closer to the slope surface respond earlier, while deeper sensors show delayed and attenuated responses. These repeated saturation–desaturation cycles reduce matric suction and accelerate the degradation of shear strength, especially in shallow soil layers.

(2) Crack development and fine particle migration significantly affect slope instability. Transverse and longitudinal fissures initiated in the mid- and upper slope zones as a result of rainfall infiltration and internal deformation. Meanwhile, seepage and surface runoff promoted the downward transport of fine particles toward the slope toe, reducing soil permeability and inducing excess pore water pressure. These factors jointly weaken the slope structure and increase the potential for localized failure.

(3) The failure process follows a distinct three-stage mechanism.

i. Toe erosion stage: This stage is primarily caused by super pore water pressure from rainfall infiltration, leading to reduced effective stress and weakened shear strength. The surface runoff exacerbates the migration of fine materials, further destabilizing the slope;

ii. Fissure expansion stage: Continuous rainfall causes the upper part of the slope to deform under its self-weight, leading to the expansion of transverse cracks at the rear edge. Meanwhile, vertical shear and tensile fissures along the slope surface extend both upward and downward, eventually forming a through-going failure surface.

iii. Gully erosion stage: Concentrated runoff scours and destabilizes the slope surface, enlarging gullies and fissures. This forms a positive feedback loop that accelerates mass loss and slope collapse.

The three-stage failure pattern identified in this study—comprising toe erosion, fissure expansion, and gully erosion—offers practical value for rainfall-induced landslide mitigation. At the toe erosion stage, drainage ditches or horizontal drains can be installed near the slope foot to reduce water accumulation and delay failure onset. In the fissure expansion stage, surface and trailing-edge cracks can be monitored using sensors or image-based systems for early warning. During gully erosion, surface protection measures such as geotextiles, combined with upslope flow diversion structures, can effectively reduce runoff concentration and surface scouring.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

JL: Resources, Investigation, Visualization, Funding acquisition, Validation, Conceptualization, Writing – review and editing. ZS: Writing – original draft, Data curation, Methodology. BH: Software, Writing – review and editing. YZ: Validation, Writing – review and editing. XO: Writing – review and editing, Investigation. KC: Validation, Writing – review and editing. YB: Validation, Writing – review and editing. YL: Software, Writing – review and editing. BD: Formal Analysis, Writing – review and editing. PL: Project administration, Supervision, Conceptualization, Writing – review and editing, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by The 2023 Innovation Fund Project of Gansu Provincial Bureau of Geology and Mineral Exploration and Development (Grant no. 2023CX18); Central Government’s Science and Technology Development Guidance Fund for Local Areas Project (Grant no. 23ZYQA0326); Science and Technology Innovation Project of Department of Natural Resources of Gansu Province (Grant no. 202406); Special Fund for Basic Scientific Research Business of Central Universities (Grant no. lzujbky-2024-ou03); and National College Students’ Innovation and Entrepreneurship Training Program (Grant no. 202410730127).

Acknowledgments

The authors thank all those who contributed to the study with support and valuable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1613118/full#supplementary-material

References

Bishop, A. W. (1959). The principle of effective stress. Tek. Ukebl. 39, 859–863.

Google Scholar

Buckingham, E. (1914). On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 4 (4), 345–376. doi:10.1103/PhysRev.4.345

CrossRef Full Text | Google Scholar

Derbyshire, E., Dijkstra, T. A., Smalley, I. J., and Li, Y. (1994). Failure mechanisms in loess and the effects of moisture content changes on remoulded strength. Quat. Int. 24 (24), 5–15. doi:10.1016/1040-6182(94)90032-9

CrossRef Full Text | Google Scholar

Fang, K., Tang, H., Li, C., Su, X., An, P., and Sun, S. (2023). Centrifuge modelling of landslides and landslide hazard mitigation: a review. Geosci. Front. 14 (1), 101493. doi:10.1016/j.gsf.2022.101493

CrossRef Full Text | Google Scholar

Guo, Z., Huang, Q., Liu, Y., Wang, Q., and Chen, Y. (2023). Model experimental study on the failure mechanisms of a loess-bedrock fill slope induced by rainfall. Eng. Geol. 313, 106979. doi:10.1016/j.enggeo.2022.106979

CrossRef Full Text | Google Scholar

Leng, X., Dong, Y., Cui, L., Zhou, L., and Luo, S. (2024). An integrated investigation of the failure mechanism of loess landslide induced by raining: from field to laboratory. Bull. Eng. Geol. Environ. 83 (11), 442. doi:10.1007/s10064-024-03937-x

CrossRef Full Text | Google Scholar

Li, R., Sun, P., Sang, K., Ke, C., and Zhang, S. (2024). Characteristics and initiation mechanism of the large mudstone Dongping landslide induced by heavy rainfall in Gansu Province, NW China. Geoenvironmental Disasters 11 (1), 39. doi:10.1186/s40677-024-00302-8

CrossRef Full Text | Google Scholar

Liu, Z., Qiu, H., Yang, S., Zhou, C., Zhang, L., Zhou, C., et al. (2025). Two-decadal evolution of irreversible surface deformation in a coal mining area revealed by improved InSAR observations. CATENA 254, 108996. doi:10.1016/j.catena.2025.108996

CrossRef Full Text | Google Scholar

Lyu, H.-M., Shen, J., and Arulrajah, A. (2018). Assessment of geohazards and preventative countermeasures using AHP incorporated with GIS in Lanzhou, China. Sustainability 10 (2), 304. doi:10.3390/su10020304

CrossRef Full Text | Google Scholar

Ochiai, H., Okada, Y., Furuya, G., Okura, Y., Matsui, T., Sammori, T., et al. (2004). A fluidized landslide on a natural slope by artificial rainfall. Landslides 1 (3), 211–219. doi:10.1007/s10346-004-0030-4

CrossRef Full Text | Google Scholar

Peng, J., Fan, Z., Wu, D., Zhuang, J., Dai, F., Chen, W., et al. (2015). Heavy rainfall triggered loess–mudstone landslide and subsequent debris flow in Tianshui, China. Eng. Geol. 186, 79–90. doi:10.1016/j.enggeo.2014.08.015

CrossRef Full Text | Google Scholar

Qiu, H., Li, Y., Zhu, Y., Ye, B., Yang, D., Liu, Y., et al. (2025). Do post-failure landslides become stable? Catena 249, 108699. doi:10.1016/j.catena.2025.108699

CrossRef Full Text | Google Scholar

Shi, W., Li, Y., Zhang, W., Liu, J., He, S., Mo, P., et al. (2020). The loess landslide on 15 march 2019 in Shanxi Province, China. Landslides 17 (3), 677–686. doi:10.1007/s10346-019-01342-0

CrossRef Full Text | Google Scholar

Sorbino, G., and Nicotera, M. V. (2013). Unsaturated soil mechanics in rainfall-induced flow landslides. Eng. Geol. 165, 105–132. doi:10.1016/j.enggeo.2012.10.008

CrossRef Full Text | Google Scholar

Sun, P., Wang, H., Wang, G., Li, R., Zhang, Z., and Huo, X. (2021). Field model experiments and numerical analysis of rainfall-induced shallow loess landslides. Eng. Geol. 295, 106411. doi:10.1016/j.enggeo.2021.106411

CrossRef Full Text | Google Scholar

Tang, Y. M., Xue, Q., Li, Z. G., and Feng, W. (2015). Three modes of rainfall infiltration inducing loess landslide. Nat. Hazards 79 (1), 137–150. doi:10.1007/s11069-015-1833-4

CrossRef Full Text | Google Scholar

Wan, B., An, N., and Bai, G. (2024). Monitoring and evaluation of debris flow disaster in the Loess Plateau area of China: a case study. Water 16 (17), 2539. doi:10.3390/w16172539

CrossRef Full Text | Google Scholar

Wang, H., Sun, P., Wang, G., and Wu, L. (2021). Experimental and numerical study of shallow loess slope failure induced by irrigation. Catena 206, 105548. doi:10.1016/j.catena.2021.105548

CrossRef Full Text | Google Scholar

Wang, H., Sun, P., Zhang, S., Han, S., Li, X., Wang, T., et al. (2020). Rainfall-induced landslide in loess area, Northwest China: a case study of the Changhe landslide on September 14, 2019, in Gansu Province. Landslides 17 (9), 2145–2160. doi:10.1007/s10346-020-01460-0

CrossRef Full Text | Google Scholar

Wang, J., Zhang, D., Wang, N., and Gu, T. (2019). Mechanisms of wetting-induced loess slope failures. Landslides 16 (5), 937–953. doi:10.1007/s10346-019-01144-4

CrossRef Full Text | Google Scholar

Wu, L. Z., Zhou, Y., Sun, P., Shi, J. S., Liu, G. G., and Bai, L. Y. (2017). Laboratory characterization of rainfall-induced loess slope failure. Catena 150, 1–8. doi:10.1016/j.catena.2016.11.002

CrossRef Full Text | Google Scholar

Xiao, W., and Tian, W. (2024). Experimental study on the failure process and modes of loess spoil slope induced by rainfall and engineering disturbance. PLoS One 19 (7), e0305871. doi:10.1371/journal.pone.0305871

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, W. L., Guo, Q., Wu, J. Y., Li, P., Yang, H., and Zhang, M. (2021). Analysis of loess landslide mechanism and numerical simulation stabilization on the Loess Plateau in Central China. Nat. Hazards 106, 805–827. doi:10.1007/s11069-020-04492-w

CrossRef Full Text | Google Scholar

Xu, J., and Fang, K. (2025). Deformation characteristics of unsaturated slope during post-rainfall earthquake: insights from centrifuge and numerical modeling. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2025.03.004

CrossRef Full Text | Google Scholar

Xu, X.-Z., Guo, W.-Z., Liu, Y.-K., Ma, J.-Z., Wang, W.-L., Zhang, H.-W., et al. (2017). Landslides on the Loess Plateau of China: a latest statistics together with a close look. Nat. Hazards 86 (3), 1393–1403. doi:10.1007/s11069-016-2738-6

CrossRef Full Text | Google Scholar

Zhang, B., Fang, K., Tang, H., Sumi, S., and Ding, B. (2023a). Block-flexure toppling in an anaclinal rock slope based on multi-field monitoring. Eng. Geol. 327, 107340. doi:10.1016/j.enggeo.2023.107340

CrossRef Full Text | Google Scholar

Zhang, M., and Liu, J. (2009). Controlling factors of loess landslides in western China. Environ. Earth Sci. 59 (8), 1671–1680. doi:10.1007/s12665-009-0149-7

CrossRef Full Text | Google Scholar

Zhang, Z., Zeng, R., Meng, X., Zhao, S., Wang, S., Ma, J., et al. (2023b). Effects of changes in soil properties caused by progressive infiltration of rainwater on rainfall-induced landslides. Catena 233, 107475. doi:10.1016/j.catena.2023.107475

CrossRef Full Text | Google Scholar

Zhen, J., Yang, X., Wang, B., Fan, H., and Meng, M. (2023). Study on the destruction of backfilled loess slopes by short-term extreme rainfall erosion. Bull. Eng. Geol. Environ. 82 (11), 406. doi:10.1007/s10064-023-03426-7

CrossRef Full Text | Google Scholar

Zhu, Y., Qiu, H., Liu, Z., Ye, B., Tang, B., Li, Y., et al. (2024). Rainfall and water level fluctuations dominated the landslide deformation at Baihetan Reservoir, China. J. Hydrology 642, 131871. doi:10.1016/j.jhydrol.2024.131871

CrossRef Full Text | Google Scholar

Zhuang, J.-q., and Peng, J.-b. (2014). A coupled slope cutting—a prolonged rainfall-induced loess landslide: a 17 October 2011 case study. Bull. Eng. Geol. Environ. 73 (4), 997–1011. doi:10.1007/s10064-014-0645-1

CrossRef Full Text | Google Scholar