A sustainable approach to deep geothermal energy exploitation: feasibility of clustered U-shaped multi-branch wells

To overcome the limitations of unstable heat extraction power and low efficiency in current deep geothermal energy exploitation technologies, we propose a novel and sustainable approach using clustered U-shaped multi-branch wells (UMW). This method enables efficient heat exchange by circulating working fluid through U-shaped wells, where thermal energy is transferred between the working fluid and the reservoir via the wellbore wall, avoiding any material exchange. For the validation of UMW method, based on the high-temperature and high-pressure thermal conductivity tests using hot dry rock samples from the Gonghe Basin, we developed a UMW field-scale reservoir-wellbore coupling model to assess the efficient heat extraction processes and the potential generating power of Organic Rankine Cycle (ORC). The results highlight that high injection rates lead to rapid thermal breakthrough and a sharp decline in early-stage heat extraction power, indicating the need for careful optimization of operational parameters. The average heat recovery power of a single set of six branch wells over a 50-year operating cycle is ∼4.32 MW. The ORC power generation capacity was conservatively estimated at ∼284.4 kW over the first 21.5 years, and ∼144.6 kW over the 50-year period. Sensitivity analysis of injection rates and the number of branch wells further suggests that balancing short-term power and long-term thermal stability requires adjusting injection rates, the number of branch wells, well spacing, and branch well operational schematic. We also provide a partial quantitative relationship between ORC power and operational parameters (injection rate and the number of branch wells) for optimization. This study demonstrates the promising potential of the UMW method for sustainable deep geothermal energy development. Future research will focus on refining quantitative optimization strategies for injection rates and operational cycles to ensure efficient and long-term heat extraction while maintaining system stability.

1 Introduction

Geothermal energy, a widely distributed, high-potential, renewable, stable, and reliable non-carbon-based energy source, is crucial for energy structure transformation and achieving low-carbon development goals (Martín-Gamboa et al., 2015; Kumari and Ranjith, 2019). It can be categorized into three types based on its formation and production conditions: shallow geothermal (Xu et al., 2020), hydrothermal (Kong et al., 2014), and hot dry rock. Deep geothermal energy is considered a future altering cleaning energy source due to the carbon peaking and carbon neutrality goals (Wang et al., 2020). However, its exploitation poses significant challenges (Tomac and Sauter, 2018; Hu et al., 2022) including the complexity of deep drilling, high operational costs, uncertain reservoir properties, and risks related to induced seismicity and long-term sustainability of heat extraction (Yuan et al., 2025).

The reservoir lithology of deep geothermal resources varies based on local geology; however, granitic rocks are the most extensively studied. Granite, characterized by its dense and low-permeability nature, cannot directly utilize the reservoir heat through conventional hydrothermal extraction techniques (Yang et al., 2020). The efficient extraction of geothermal energy from deep high-temperature reservoirs often requires the enhancement of reservoir permeability through artificial stimulation, commonly referred to as Enhanced Geothermal Systems (EGS) (Olasolo et al., 2016; Lu, 2018; Lin et al., 2023). In addition to EGS, several other technologies have been developed for mid-to-deep geothermal energy exploitation, including fault zone fluid circulation (Brogi, 2008; Zucchi, 2020; Brogi et al., 2021), coaxial casing systems (Yekoladio et al., 2013; Yin et al., 2021; Du et al., 2023; Chappidi et al., 2024; Li M. et al., 2024), and Annular Ground Source (AGS) systems (Javadi et al., 2019; Violante et al., 2021; Beckers et al., 2022; Liang et al., 2022; Anand et al., 2024). Each of these methods has unique mechanisms and applications, offering potential solutions to the challenges associated with geothermal energy extraction. Current technologies for deep geothermal energy extraction can be categorized into two main types based on the mechanism of interaction with the geothermal reservoir: first type involving material exchange with the reservoir, such as Enhanced Geothermal Systems (EGS), and second type focused solely on heat extraction without material exchange, often referred to as “heat extraction without water withdrawal” approaches.

EGS represents the primary technology for geothermal energy extraction involving material exchange. This approach enhances the permeability of low-porosity, low-permeability reservoirs through hydraulic fracturing (Sun et al., 2017), chemical stimulation (Portier et al., 2009), or thermal stimulation (Bradford et al., 2014) to create artificial reservoirs. By injecting low-temperature working fluid into the reservoir through an injection well and recovering heated working fluid from a production well, EGS enables the utilization of geothermal energy from hot dry rocks. EGS has gained significant attention and is regarded as a mainstream method for hot dry rock utilization (Olasolo et al., 2016). However, the efficiency of EGS remains limited, as evidenced by the commercially operational Soultz project in France, which achieves only 1.5 MW of power generation (Schill et al., 2015). Additionally, EGS operations carry a high risk of induced seismicity due to the fluid injection required for reservoir stimulation (Baisch et al., 2006; 2010; Kim et al., 2018). These challenges, combined with the high cost of reservoir stimulation and the difficulty in maintaining long-term stability, limit the widespread application of EGS. The fault zone fluid circulation method, is another method with material exchange, relies on natural fracture systems within high-temperature rock formations. Cold working fluid is injected into shallow fault zones, flowing through deep, high-temperature fractures before being recovered as heated working fluid from production wells in deeper fault zones. This method effectively utilizes the heat stored in deep fault systems but requires precise localization of fault zones (Duwiquet et al., 2021). The fault zone fluid circulation method faces scalability limitations due to the difficulty of identifying and accessing deep fault zones, along with the risk of induced seismicity (Gan et al., 2021). Both EGS and fault zone fluid circulation methods involve not only energy exchange with the geothermal reservoir but also material exchange. Prolonged material exchange during extraction can lead to mineral alterations, structural changes, and variations in in-situ stress within deep geothermal reservoirs. Mineral alterations primarily manifest as transformations of elemental minerals due to water-rock interactions. Structural changes in hydraulic fractures and fault zones are reflected in permeability reduction caused by scaling in reservoir fractures and conduits. Changes in far-field reservoir and fault stress, induced by hydraulic fracturing and fluid circulation, can destabilize faults and trigger seismic events.

In contrast, non-material-exchange methods extract heat without interacting directly with the reservoir fluids. Technologies such as coaxial casing systems and Annular Ground Source (AGS) systems are typical examples of this approach. The coaxial casing method, also known as deep well heat exchange technology, uses a coaxial pipe system to extract heat without material exchange. The coaxial casing method utilizes a double-layer pipe system, where cold working fluid flows down the outer pipe, absorbs heat from the surrounding rocks, and rises as heated working fluid through the inner pipe (RybachL, 1995). AGS systems increase heat transfer efficiency by employing annular heat exchange pipes around the wellbore, allowing injected cold working fluid to be heated as it circulates back to the surface (Yang et al., 2016). While these methods avoid issues such as induced seismicity and reservoir degradation, they face their own limitations. Coaxial casing systems often suffer from poor thermal insulation between the inner and outer pipes, leading to low heat extraction efficiency less than 150 W/m (Kong et al., 2017). Similarly, AGS systems are challenging to install and operate under deep, high-temperature, and high-pressure conditions, restricting their application to shallow or mid-depth geothermal resources (Violante et al., 2021; Beckers et al., 2022).

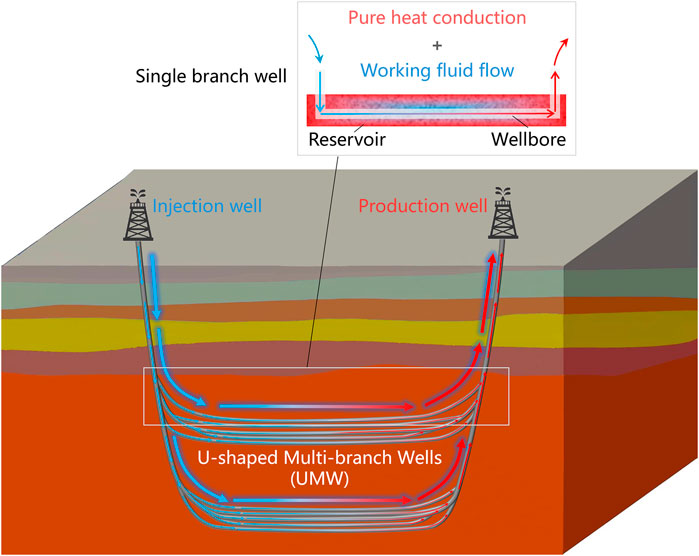
To address these challenges, we propose a novel deep geothermal energy extraction method: clustered U-shaped multi-branch wells (UMW). The UMW method combines the advantages of non-material-exchange approaches. By circulating working fluids within U-shaped wells, the UMW method facilitates heat exchange between the fluid and the reservoir via the wellbore wall, eliminating the need for direct interaction with reservoir fluids. The use of clustered multi-branch wells significantly increases the heat exchange area and enables stratified reservoir exploitation, enhancing heat extraction efficiency and recovery rates. Moreover, the UMW method reduces the risks associated with induced seismicity and avoids issues of reservoir depletion and fluid loss, ensuring a more sustainable and stable heat extraction process. Focusing on the exploitation of low-permeability hot dry rock resources in the Gonghe Basin, Qinghai (Zhu et al., 2022; Zhang et al., 2024a), we established a three-dimensional field-scale UMW model based on reservoir-wellbore thermal-hydraulic coupling algorithm. Then, we study the effective heat extraction processes by wellbore/reservoir temperature, heat extraction power, and sensitive analysis based on this model. Through this research, we aim to explore the theoretical feasibility of the UMW method and evaluate its application potential.

2 Methodology

In alignment with the principle of energy exchange without material exchange and aiming for the large-scale, sustainable, and stable development of deep geothermal energy, this study draws inspiration from the cluster horizontal well technology used in oil and gas development (Gao, 2019) to propose the clustered U-shaped Multi-branch Well (UMW) heat extraction method for deep geothermal energy (Figure 1). This method employs U-shaped multi-branch wells, where the heat extraction fluid is circulated within the branch wells. Heat exchange occurs between the fluid and the wellbore in the reservoir section. Clustered multi-branch wells significantly increase the heat exchange area and enable stratified reservoir exploitation, enhancing both heat extraction power and heat recovery efficiency (Li S.-D. et al., 2024).

Figure 1

Figure 1. Schematic of cluster U-shaped multi-branch wells (UMW) method.

2.1 High-temperature high-pressures thermal conductivity

In geothermal energy development, thermal conductivity is a critical physical parameter that determines the characteristics of subsurface rocks and their geothermal reservoirs. Thermal conductivity measurements provide fundamental data for evaluating the thermal transport properties of geothermal resources. Under high-temperature conditions, the thermal conductivity of rocks typically undergoes changes due to the movement of heat carriers, variations in mineral composition, and structural alterations. Additionally, rocks are often subjected to surrounding pressure and stress, which can modify their pore structure and, consequently, their thermal conductivity. This is particularly relevant during geothermal extraction, where the stress state of the rocks may undergo significant changes (Lin et al., 2025).

We have developed a high-temperature and high-pressure thermal conductivity instrument for hot dry rock. The instrument employs the steady-state heat flow meter method to measure the thermal conductivity of the material. The designed technical specifications for confining pressure and temperature are 150 MPa and 200°C, respectively. Granite samples from the hot dry rock reservoir in the Gonghe Basin, Qinghai, China, were tested using this instrument under both room temperature and high-temperature, high-pressure conditions. The Gonghe Basin hot dry rock (HDR) reservoir targets depths of 3,000–4,000 m, where lithostatic pressure ranges 70–100 MPa. The basin-specific thermal gradient is 45°C/km (Zhang et al., 2020; Song et al., 2021). Experimental conditions including temperature and pressure (80 MPa, 150°C) referred from borehole log information.

The measured thermal conductivities were 1.99 W/(m·°C) at room temperature and 1.69 W/(m·°C) under high-temperature and high-pressure conditions (Li S.-D. et al., 2024). These results indicate that the thermal conductivity of granite decreases by approximately 15% under high-temperature and high-pressure conditions compared to room temperature. The thermal conductivity of samples was utilized in the subsequent sections.

2.2 Numerical model

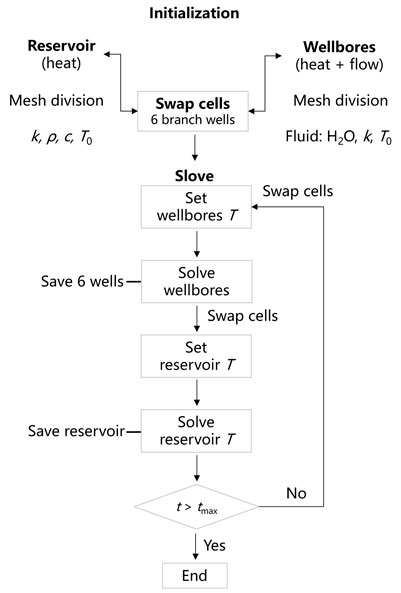
The heat extraction system for deep geothermal energy using cluster multi-branch U-shaped wells (UMW) involves coupled heat conduction between reservoir, wellbore and working fluid, and the design of complex well configurations is a typical three-dimensional problem. Therefore, it is necessary to develop a three-dimensional numerical algorithm for thermal-hydraulic coupling in reservoir-wellbore-working fluid.

We utilized the simulator allowing for three-dimensional numerical simulations of thermal-hydraulic coupling in deep geothermal reservoirs (https://gitee.com/geomech/hydrate) and undergone extensive benchmarking and validation at multiple scales (Xu et al., 2021; Li et al., 2023; Zhang et al., 2023; 2024b; 2024c).

In the numerical simulation of deep geothermal systems, the fundamental governing equations include the heat exchange between the working fluid in the wellbore and the reservoir. The energy conservation equation for the reservoir is expressed as follows (Equation 1):

${\rho }_r{c}_r\frac{\mathrm{\partial }{T}_r}{\mathrm{\partial }t}+{\rho }_r{c}_r\mathbf{u}·\nabla T_r=\nabla ·\left(k_r\nabla T_r\right)+q,(1)$

where ρ_r is the density of the reservoir rock (kg/m³), c_r is the specific heat capacity of the reservoir rock (J/(kg·°C)), T_r is the temperature of the reservoir rock (°C), k_r is the thermal conductivity of the reservoir rock (W/(m·°C)), t is time (s), q is the heat exchange term between the reservoir and the working fluid in the wellbore (W/m³).

For the heat transfer fluid in the wellbore, the energy conservation equation is expressed as (Equation 2):

${\rho }_f{c}_f\frac{\mathrm{\partial }{T}_f}{\mathrm{\partial }t}+{\rho }_f{c}_f\mathbf{u}·\nabla T_f=\nabla ·\left(k_f\nabla T_f\right)+q,(2)$

where ρ_f is the density of the working fluid (kg/m³), c_f is the specific heat capacity of the reservoir rock (J/(kg·°C)), T_f is the temperature of the working fluid (°C), k_f is the thermal conductivity of the working fluid (W/(m·°C)), t is time (s), u is the velocity vector of the working fluid (m/s).

The heat extraction power P can also be calculated based on the change in energy within the reservoir over time. The specific calculation formula is as follows (Equation 3):

$P=\frac{\Delta E}{\Delta t},(3)$

where ΔE is the change in energy within the reservoir (J), Δt is the time interval over which the energy change is measured (s).

The change in energy ΔE within the reservoir can be expressed as (Equation 4):

$\Delta E={\int }_V{\rho }_r{c}_r\Delta T_{r}dV,(4)$

where ρ_r is the density of the reservoir rock (kg/m³), c_r is the specific heat capacity of the reservoir rock (J/(kg·°C)), ΔT_r is the temperature of the reservoir rock (°C), V is the volume of the reservoir (m³).

In this model, heat conduction between the reservoir and the wellbore is prioritized, followed by heat conduction and convection processes of the working fluid within the wellbore. Heat transfer between the reservoir and the wellbore is exclusively governed by conduction, with no convective processes assumed within the reservoir. The temperature distributions of the reservoir and wellbore serve as mutual boundary conditions during the simulation, with data exchange occurring at regular intervals to ensure accurate evaluation of the heat exchange efficiency over long horizontal sections (Figure 2).

Figure 2

Figure 2. Flowchart of reservoir-wellbore thermal-hydraulic coupling algorithm.

To validate the effectiveness and accuracy of the numerical method, we established a one-dimensional unsteady heat transfer model with a domain size of 100 m, discretized into 500 uniform grids. The left boundary was set as a fixed temperature boundary at 100°C, while the initial temperature of the model was 0°C. The thermal conductivity, density, and specific heat capacity of the model were configured based on experimental results from samples of the Gonghe Basin, with values set to 1.69 W/(m·°C), 2,640 kg/m³, and 754.4 J/(kg·°C), respectively. Temperature distribution results were extracted at six time points with intervals of 500 days. The numerical simulation results demonstrated excellent agreement with theoretical solutions, thereby validating the accuracy of the heat transfer simulation program to a certain extent (Figure 3a). The specific error analysis shows that the simulation results are close to analytic calculations. The mean absolute error (MAE) and root mean squared error (RMSE) are lower than 0.13°C and 0.3°C respectively (Figure 3b).

Figure 3

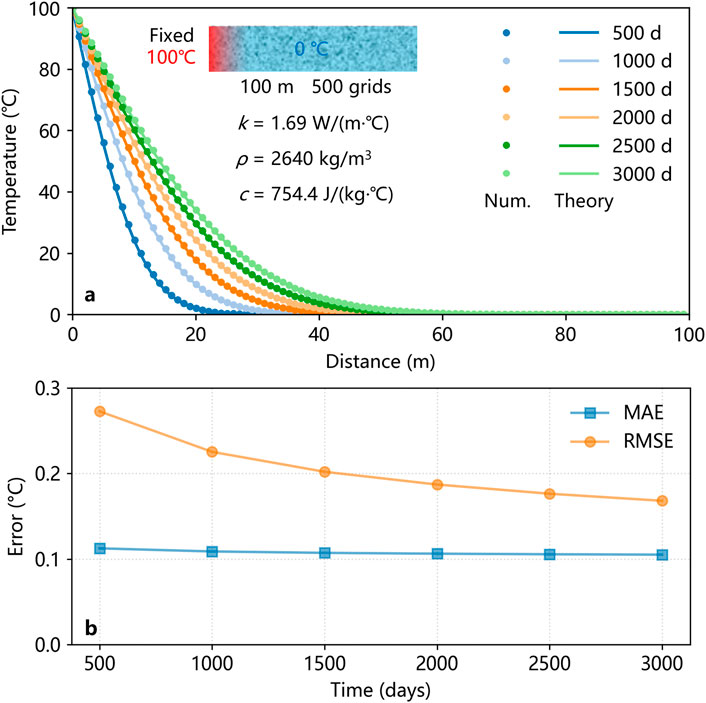
Figure 3. Comparison and validation of numerical simulation results with theoretical calculations. (a) Comparison between the numerical simulation results and theoretical calculations. Subfigure shows the schematic of heat conduction model and the model parameters. Points represent the results of numerical simulations and lines represent the results of theoretical solutions (Zhang et al., 2025); (b) Error analysis between numerical simulation results and theoretical calculations. Metrics include Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE).

2.3 Model setting

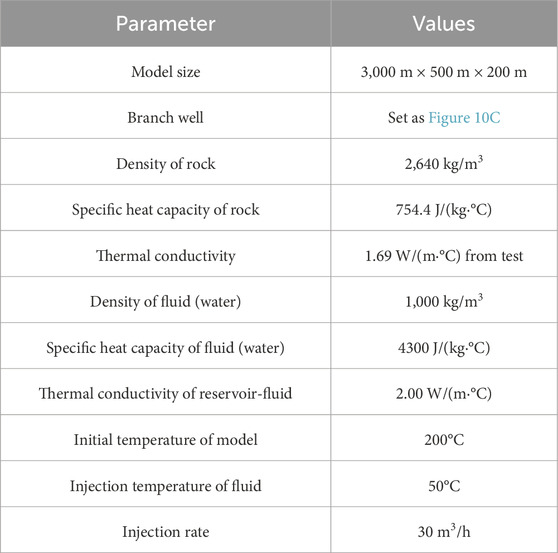
Traditional two-dimensional numerical models for geothermal development often simplify the wellbore direction through linear scaling, which fails to accurately reflect the actual heat exchange efficiency of long-distance horizontal wells. To address this limitation, we established a three-dimensional reservoir-working fluid thermal-hydraulic coupled model at the field scale, based on the geothermal distribution characteristics of the Gonghe Basin in Qinghai Province, China (Figure 4a). This model incorporates a U-shaped multi-lateral well system with six branch wells, enabling a more effective investigation of the influence of wellbore flow dynamics on horizontal well heat exchange efficiency and the calculation of effective power during the heat exchange process. Based on high-temperature and high-pressure thermal conductivity measurements of dry hot rock samples, the thermal conductivity of the reservoir in the numerical simulation is set to 1.69 W/(m·K), with a density of 2,640 kg/m³ and a specific heat capacity of 754.4 J/(kg·K). Additional parameters for the numerical model are provided in Table 1 (Song et al., 2021; Zhang et al., 2021).

Figure 4

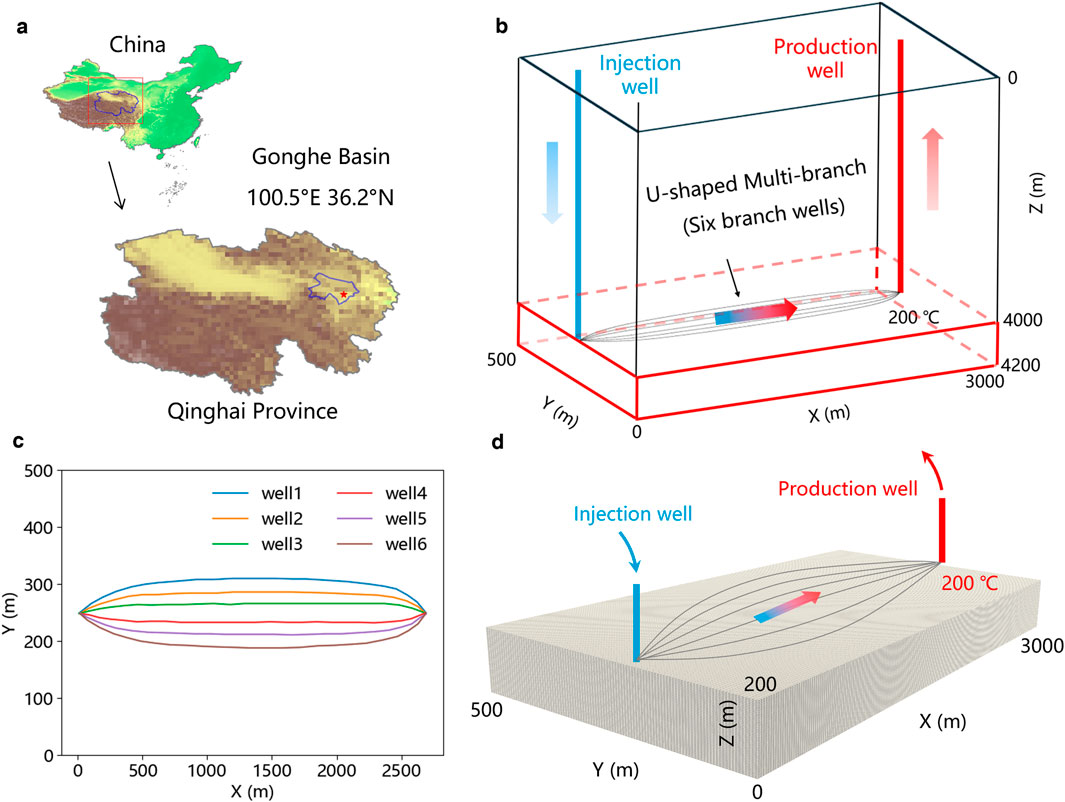
Figure 4. Schematic diagram of UMW method. (a) Geographic location of the Gonghe Basin, Qinghai, China; (b) Schematic diagram of the UMW numerical model (Red block); (c) Geometric distribution of six branch wells; (d) Mesh division of numerical simulation.

Table 1

Table 1. Setting of physical parameters for the model.

2.4 Mesh division

The model employs a three-dimensional reservoir with dimensions of 3,000 m × 500 m × 200 m (Figure 4b). The model includes six horizontal branch wells arranged in an axisymmetric distribution, each with a length of approximately 2,500 m (Figure 4c). The reservoir model is discretized into a uniform grid with cell sizes of 15 m × 5 m × 4 m (Figure 4d).

2.5 Boundary conditions

The boundaries of the model are treated as adiabatic, and the initial reservoir temperature is set to 200°C, with the injected fluid temperature fixed at 50°C. To enhance computational efficiency and facilitate result visualization, only half of the actual geological model is simulated. The simulation period is set to 50 years.

3 Results and discussion

3.1 Reservoir temperature

Figure 5 presents the temporal evolution of the temperature field in a geothermal reservoir over 1 year, 5 years, and 50 years, highlighting the interaction between the injection well (blue rectangle) and the production well (red rectangle). At the 1-year mark, the injection well creates a localized cooling zone, as evidenced by the blue region surrounding it. The thermal front propagates outward along the flow path toward production well, forming distinct temperature gradients. This stage reflects the initial response of the reservoir to fluid injection and heat extraction. By the 5-year mark, the cooling front expands significantly along the flow channel, driven by advective heat transfer. While noticeable cooling occurs near the wells, regions farther from the flow path retain substantial thermal energy, showcasing the anisotropic nature of heat transfer within the reservoir. The combined effects of conduction and advection lead to progressive thermal changes over time.

Figure 5

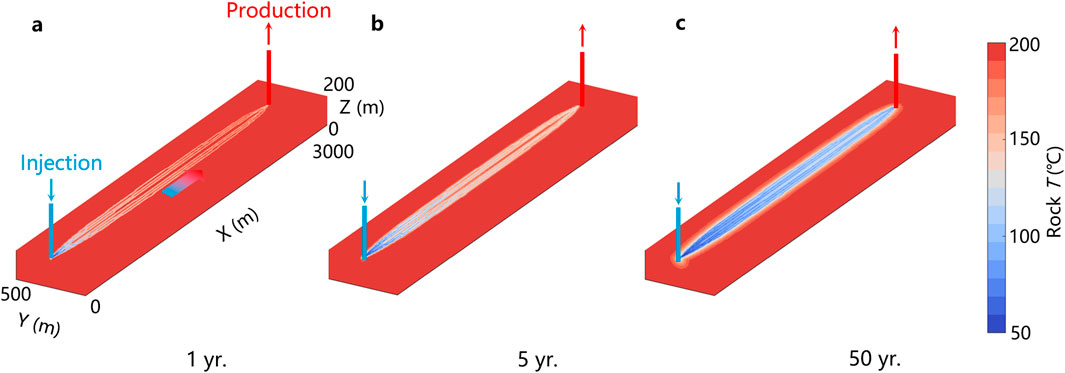
Figure 5. Temperature field of the reservoir rock at different time points. (a) 1 year, (b) 5 years, (c) 50 years. Blue rectangle represents the injection well and red rectangle represents the production well.

Figure 6 provides a quantitative depiction of the reservoir thermal response over a 50-year operational period under a constant injection rate of 30 m³/h, tracking the three key indicators. The average reservoir temperature (blue line, circle markers, left y-axis), initiates at the original reservoir temperature of 200°C and exhibits a consistent, near-linear decrease throughout the simulation, reaching approximately 195.5°C by the 50-year mark. Concomitantly, the average temperature drop (orange line, square markers, right y-axis), which quantifies the deviation from the initial 200°C, shows a corresponding and steady increase from 0°C at the start to approximately 4.5°C after 50 years of operation. Complementing these temperature metrics, the proportion of grid cells experiencing a temperature decrease greater than 0.1°C (green line, diamond markers, far-right y-axis) demonstrates a progressive expansion of the thermal response zone, rising from 0% at the beginning of the simulation to approximately 45% by the end of the 50-year period. Collectively, these trends illustrate the continuous and progressive thermal drawdown and expansion of the thermally affected zone within the reservoir due to sustained heat extraction at the specified injection rate.

Figure 6

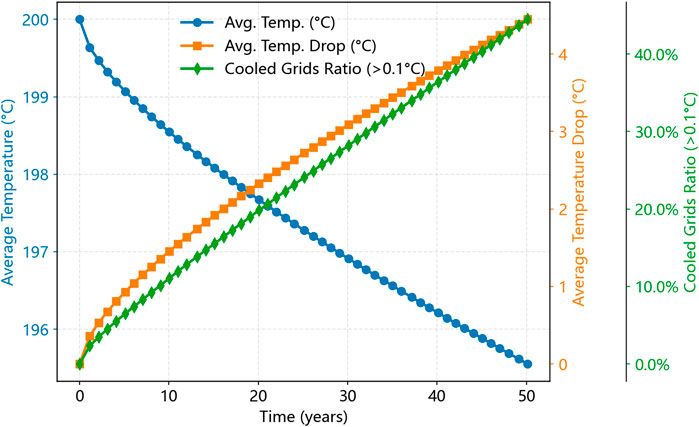
Figure 6. Temporal evolution of reservoir thermal properties under a constant injection rate of 30 m³/h (i) the average reservoir temperature (°C, blue line with circle markers, left y-axis); (ii) the corresponding average temperature drop (°C, orange line with square markers, right y-axis) relative to an initial temperature of 200°C; and (iii) the proportion of grid cells experiencing a temperature decrease greater than 0.1°C (%, green line with diamond markers, far-right y-axis).

At 50 years, the reservoir undergoes pronounced thermal depletion along the primary flow pathway, with the cooling front reaching the production well. The extensive cooling zone near the injection well indicates significant heat extraction from the surrounding rock. The thermal breakthrough of injected cooler fluids at the production well reduces heat extraction efficiency, marking a critical point in the reservoir’s thermal lifespan. This long-term behavior underscores the balance between advective and conductive heat transfer mechanisms, as well as the impact of flow dynamics and reservoir heterogeneity. The analysis highlights the importance of optimizing injection and production strategies to delay thermal breakthrough, mitigate reservoir depletion, and ensure the sustainable utilization of geothermal energy resources over extended operational periods.

3.2 Wellbore temperature

Figure 7 illustrates the spatial and temporal evolution of fluid temperature within six branch wells (a-f) over a 50-year operational period. The temperature distribution ranges from 50°C (blue) to 200°C (red), with yellow contour lines highlighting two critical temperature thresholds: ∼129°C, the normal operating temperature for the organic Rankine cycle (ORC), and ∼100°C, the minimum temperature required for ORC operation (Altun and Kilic, 2020). The analysis demonstrates distinct variations in thermal performance among the six wells due to differences in flow dynamics, heat extraction rates, and reservoir heterogeneity.

Figure 7

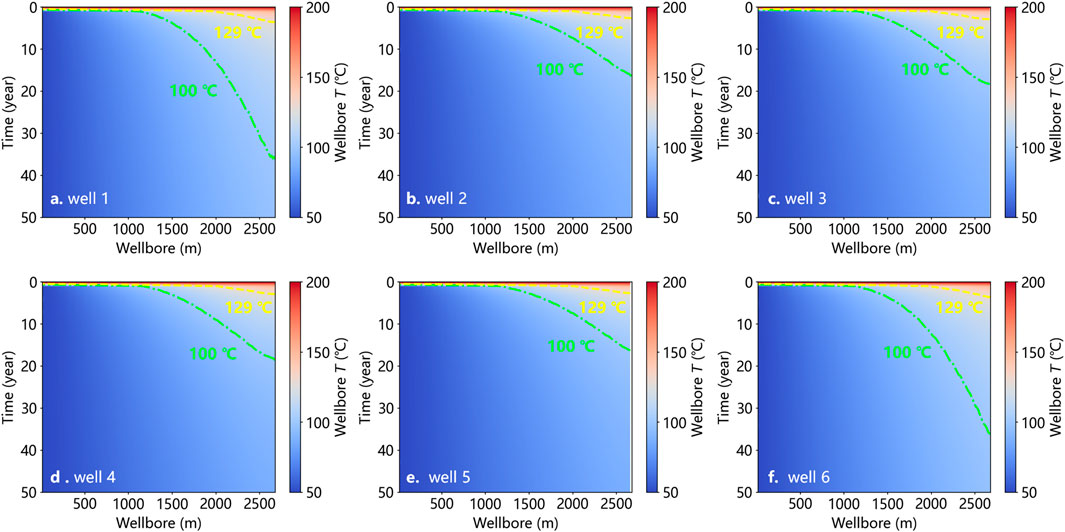
Figure 7. Spatial and temporal evolution of fluid temperature at six different branch wells. (a) well 1; (b) well 2; (c) well 3; (d) well 4; (e) well 5; (f) well 6. Green lines represent the contour line of 100°C and yellow lines represent the contour line of 129°C.

Over time, all six wells exhibit a downward trend in fluid temperature, with the 129°C and 100°C contours progressively moving toward the wellhead. The results for well 1 and well 6, well 2 and well 5, as well as well 3 and well 4, show identical thermal behaviors due to axisymmetric of six branch wells. Wells 1, 2, and 3 experience faster cooling, as the 129°C contour retreats rapidly, indicating earlier thermal breakthrough of cooler fluids. The movement of the 129°C contour is crucial for assessing the long-term efficiency of ORC power generation. As 129°C contour retreats, the area of the reservoir capable of sustaining ORC at its normal operating temperature diminishes, reducing system efficiency. This behavior suggests higher flow rates or more efficient heat extraction in these wells, leading to faster reservoir thermal depletion. The 100°C contour also moves closer to the wellhead over time, particularly in wells 1 and 3, further limiting the usable thermal energy in the reservoir, which suggests that within the cluster of branched wells, the presence of numerous heat-extracted branch wells results in a reduction of the average heat exchange capacity per well for a given total heat exchange area. Consequently, the temperature of the wellbore in the internal branched wells decreases more rapidly compared to that in the external branched wells (well 1 and well 6). The accelerated cooling of internal wells is fundamentally attributed to the overlapping thermal influence zones between closely spaced internal wells. This spatial configuration creates shared thermal depletion regions where cumulative heat extraction exceeds the natural thermal recharge capacity of the localized reservoir volume. According to Fourier’s law of heat conduction, the thermal gradient between adjacent depletion zones becomes attenuated, reducing the effective heat flux toward internal wells. Concurrently, flow dynamics demonstrate that clustered wells create converging flow paths that preferentially channel cooler reinjected fluids toward the internal well network. This establishes a positive feedback loop: localized cooling increases fluid viscosity, enhancing convective heat transfer that further accelerates thermal drawdown. In contrast, external wells benefit from undisturbed peripheral reservoir sections where radial heat conduction from deeper formations maintains steeper thermal gradients.

3.3 ORC power

We also calculated the outlet temperature of well 1-3 horizontal branch wells and the variation of heat extracted power (Figure 8). At the onset of operation, the outlet temperatures of wells 1-3 exceed 129°C, enabling a maximum total average power of 5.95 MW when the outlet temperature excess129°C. According to feedback from on-site construction experience, when the outlet temperature exceeds 129°C, the ORC power generation capacity may be approximately 10% of the heat extraction power (595 kW). This high initial power output is attributed to the optimal thermal gradient and efficient heat exchange conditions within the reservoir. The elevated outlet temperatures indicate a substantial thermal energy reserve, which is effectively harnessed during the early stages of operation. This phase is critical for establishing baseline performance metrics and understanding the initial energy extraction potential of the geothermal system.

Figure 8

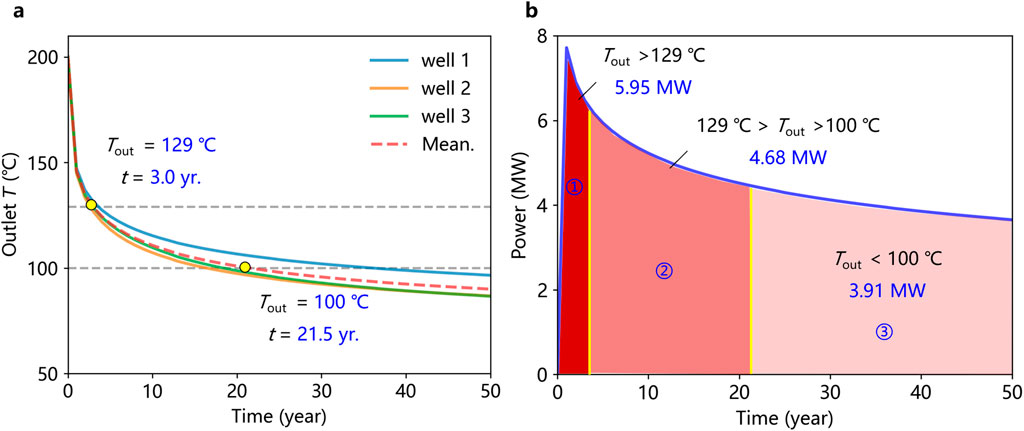
Figure 8. Temporal variation of the wellbore outlet temperature and the evolution of total heat extracted power. (a) Outlet temperature of branch wells (well 1, well 2, well3, due to the symmetrical arrangement of the branch wells, the results for the other three wells are identical). Red dotted line represents the mean temperature of six branch wells. Yellow points marked the critical time points of ORC generation (129°C and 100°C); (b) Evolution of total heat extracted power. We divided the operation into three phases according to outlet temperature considering the ORC (t = 3 yr , 21.5 yr). The mean powers of three phases are marked in blue. The gray dashed line represents 129°C and 100°C.

Over time, the outlet temperatures of wells 1-3 exhibit a gradual decline. This decline is primarily driven by the continuous extraction of thermal energy from the reservoir, leading to a reduction in the available heat flux. The rate of temperature decrease is influenced by the temperature difference between the reservoir rocks and the working fluid. As the outlet temperature drops below 129°C but remains above 100°C, the total average power decreases to 4.68 MW. the ORC power generation capacity may be lower than ∼10% of the heat extraction power. We assume a conversion efficiency of 5% at this phase for ORC power generation (234 kW). This reduction reflects the diminishing thermal driving force available for energy conversion in the Organic Rankine Cycle (ORC) system.

When the outlet temperature falls below 100°C but remains above 80°C, the power output further declines to 3.91 MW. We assume a conversion efficiency of 1% at this phase for ORC power generation (39.1 kW). This phase underscores the importance of temperature management in maintaining efficient power generation. The decline in the outlet temperature below 100°C indicates a shift in the reservoir thermal dynamics, where the heat extraction process becomes less efficient, and alternative strategies, such as altering the number of branch wells in operation, may need to be considered. During the subsequent heat extraction process, the horizontal branch wells located near the central region have already exchanged the majority of the reservoir thermal energy, resulting in the reservoir temperature (200°C) closes to that of the injected working fluid (50°C). Consequently, it is advisable to design an economical operation plan for multi branch wells, such as deactivating the low-efficiency branch wells gradually, to minimize costs associated with inefficient energy extraction.

From the perspective of the average heat extraction power, the average heat extraction power of a single set of six branch wells over a 50-year operating cycle is ∼4.32 MW. As for the ORC generation, the average generating power of the first two decades (21.5 years) is ∼ 284.4 kW. Roughly five similar clusters of branch wells (six branch wells) would be needed to achieve 1.2 MW of generating power. The average generating power of 50 years would be relatively low, ∼ 144.6 kW. Roughly nine similar clusters of branch wells (six branch wells) would be needed to achieve 1.2 MW of generating power.

It can be observed that the results from previous two-dimensional horizontal well calculations, which did not account for flow processes within the wellbore, are less accurate compared to those obtained when incorporating both the flow of working fluid within the wellbore and heat exchange between the reservoir and the wellbore. This is because the heat exchange due to fluid flow within the wellbore is subject to periodic limitations and may also be influenced by convective effects within the wellbore, leading to a relatively lower heat extraction power. Based on the analysis of the wellbore outlet temperature, it is recommended that a staged utilization of geothermal energy be considered during the extraction process. During high-temperature periods, electricity generation should be prioritized, while during subsequent stable periods, the focus can shift to heating and other energy demands.

The analysis of wells 1-3 provides valuable insights into the temporal variation of outlet temperatures and their impact on heat extraction power. The observed trends emphasize the need for proactive reservoir management strategies, such as optimizing well spacing, working strategy for branched wells, or integrating hybrid energy systems, to sustain power output over extended periods. Future research should focus on developing predictive models to simulate long-term thermal behavior and exploring innovative technologies to improve the efficiency and sustainability of UMW method.

3.4 Sensitive analysis

3.4.1 Injection rate

In this section, we explored the performance of the UMW method under varying injection rates (10 m³/h, 30 m³/h, 50 m³/h, 70 m³/h). The injection rate is a critical operational parameter that significantly influences the heat extraction efficiency and overall power output of geothermal systems. By examining the behavior of UMWs under different flow conditions, we aim to identify the optimal injection rate schadule that maximize heat extraction while maintaining the sustainability of the reservoir. Understanding these relationships is essential for optimizing the design and management of geothermal resources, particularly in complex branched well configurations.

The temperature field of 50th year demonstrates that higher injection rates result in a larger thermal impact region and a more pronounced temperature difference between the working fluid and the reservoir, which suggests that, from the perspective of energy extraction, higher injection rates enable the working fluid to extract more heat from the reservoir (Figure 9) but the improved effect is limited, especially when the injection rate exceed 30 m³/h (Figure 10). However, to evaluate whether the heat extraction process is efficient relative to the operational objectives, it is necessary to consider the outlet temperature of the wellbore and the duration of heat extraction. Therefore, we analyzed the spatiotemporal evolution of wellbore temperatures for different branches (well 1 – well 3) and plotted the isothermal contours for two critical temperature thresholds in ORC geothermal power generation, 129°C and 100°C (Figure 11). The results indicate that higher injection rates lead to faster thermal breakthrough and shorter duration during which the wellbore outlet temperature remains above 129°C and 100°C. These findings suggest that higher injection rates deliver more heat transfer energy but may also result in a shorter effective heat extraction period. This trade-off highlights a conflict in evaluating heat extraction efficiency. Consequently, further analysis was conducted by integrating the extracted power and the wellbore outlet temperature to investigate the effective heat transfer process in greater detail.

Figure 9

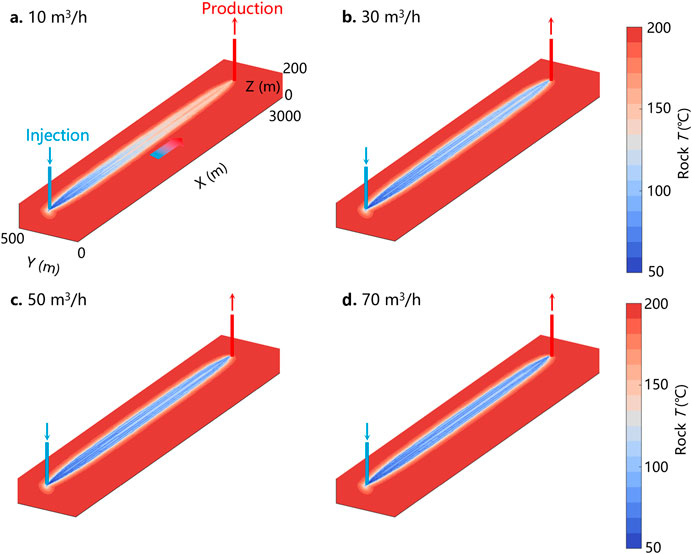
Figure 9. Temperature field of the reservoir at 50th year. (a) 10 m³/h; (b) 30 m³/h; (c) 50 m³/h; (d) 70 m³/h; Blue rectangle represents the injection well and red rectangle represents the production well.

Figure 10

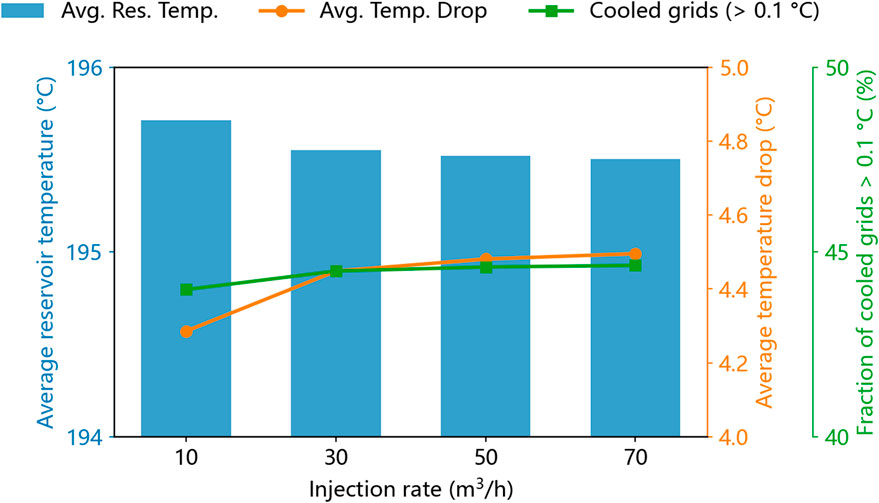
Figure 10. Impact of varying injection rates (m³/h) on reservoir thermal response. The figure presents: (i) average reservoir temperature (°C, blue bars, left y-axis), (ii) average temperature drop from the initial state (°C, orange line, right y-axis), and (iii) the fraction of grid cells experiencing a temperature decrease greater than 1°C (%, green line, far-right y-axis).

Figure 11

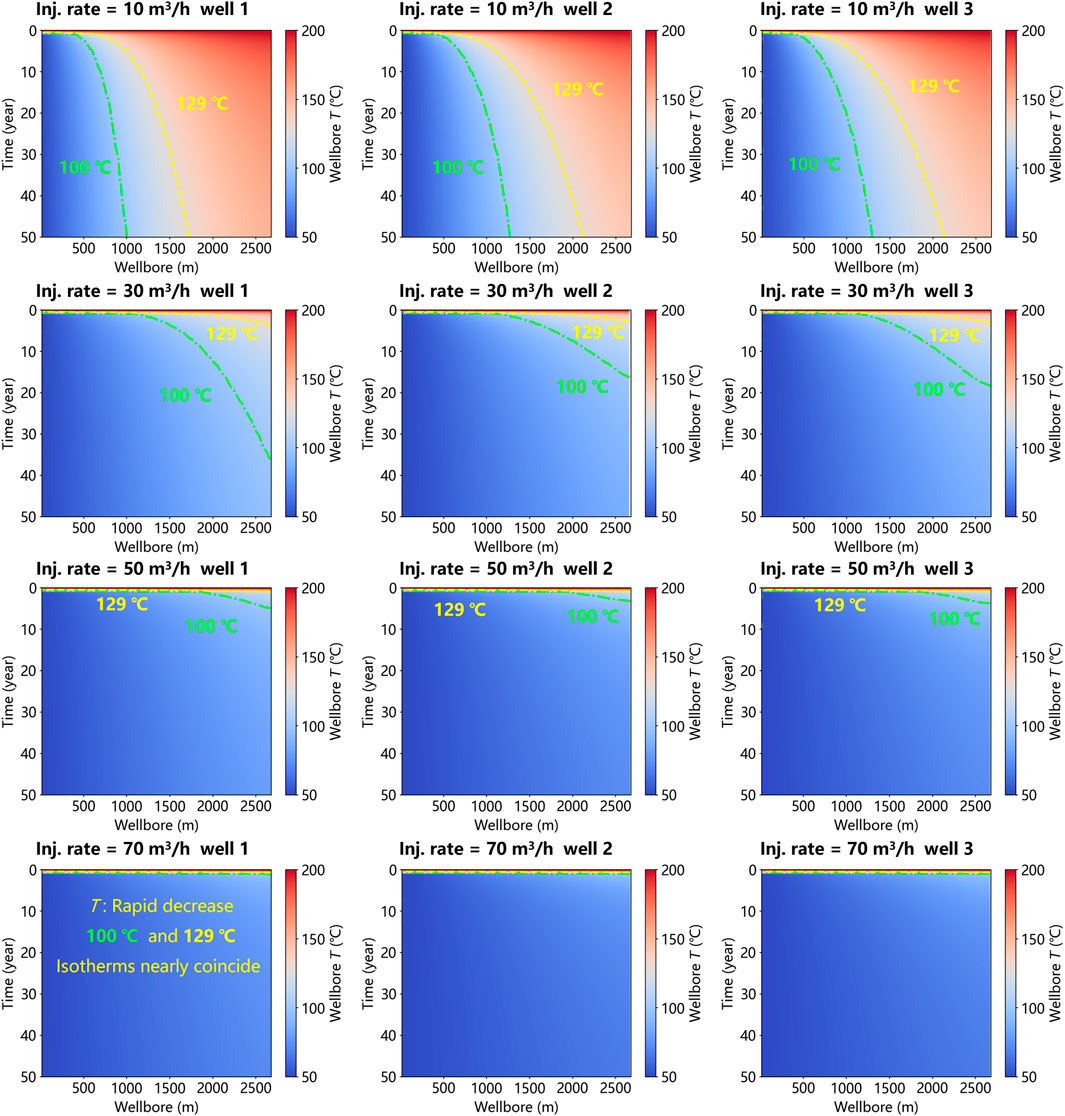
Figure 11. Spatial and temporal evolution of wellbore temperature in branch wells with different injection rate. Each row represents the spatiotemporal evolution of wellbore temperature for branch wells 1-3 under a specific injection rate (from left to right: well 1, well 2, well 3; due to the symmetrical arrangement of the branch wells, the results for the other three wells are identical). Each column illustrates the spatiotemporal evolution of wellbore temperature for the same branch well under different injection rates (from top to bottom: 10 m³/h, 30 m³/h, 50 m³/h, 70 m³/h). Green lines represent the contour line of 100°C and yellow lines represent the contour line of 129°C.

The temporal variation of the wellbore outlet temperature (Figure 12) under different injection rates (10 m³/h, 30 m³/h, 50 m³/h, 70 m³/h) reveals critical insights into the effective heat extraction process. At higher injection rates, the wellbore outlet temperature declines more rapidly, reaching critical operational thresholds (129°C and 100°C) much sooner. For instance, at 70 m³/h, the outlet temperature drops below 129°C within approximately 2 years, while at 10 m³/h, it remains above this threshold for over 50 years. This indicates that higher injection rates lead to faster thermal breakthrough and shorter effective heat extraction periods. The evolution of total heat extracted power demonstrates a similar pattern. Higher injection rates yield greater initial power, with 70 m³/h achieving ∼10.72 MW compared to ∼3.23 MW at 20 m³/h. However, this higher power diminishes rapidly over time, reflecting the faster thermal depletion of the reservoir. In contrast, lower injection rates produce a more stable power over a longer period, suggesting a more sustainable but less intensive heat extraction process (Figure 13a). We further calculated the average heat extraction power under different injection rates, as well as the heat extraction power generated per unit volume injected per hour (Figure 13b). The results indicate that a higher injection rate can achieve a greater average heat extraction power, but the heat extraction power per unit volume injected per hour tends to decrease. Figure 13c illustrates the fitting relationship between injection rate and the duration of outlet temperature above specific thresholds (Data in Figure 12b). Two temperature thresholds are considered: 129°C (blue curve) and 100°C (red curve). Due to the increase in flow rate, the rate of decrease in outlet temperature accelerates. There exists an exponential relationship between the injection rate and the duration (T > 129°C: 201.34e^−0.14x, T > 100°C: 83.22e^−0.05x). We can utilize this exponential relationship to optimize the injection rate and outlet temperature. Based on previous field experience, we calculated the ORC power generation over a 50-year period under different injection rates and performed data fitting. An exponential relationship was identified between the injection rate and ORC power generation (Figure 13d), expressed as y = 383.76e^−0.03x. Excessive injection rates lead to a rapid decline in wellhead outlet temperature, resulting in significantly reduced ORC efficiency. Conversely, lower injection rates can increase the wellhead outlet temperature but may reduce the total heat extraction power, thereby also diminishing ORC efficiency. Therefore, optimizing the injection rate is crucial for achieving balanced and efficient ORC power generation.

Figure 12

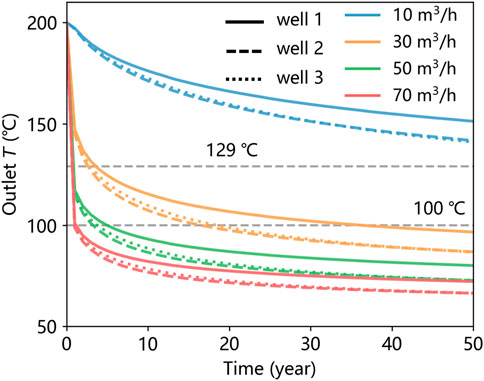
Figure 12. Temporal variation of the wellbore outlet temperature. Outlet temperature of branch wells (well 1, well 2, well 3, due to the symmetrical arrangement of the branch wells, the results for the other three wells are identical) with different injection rates (10 m³/h, 30 m³/h, 50 m³/h, 70 m³/h). Different line styles represent different branch wells and different colors represent different injection rates; The gray dashed line represents 129°C and 100°C.

Figure 13

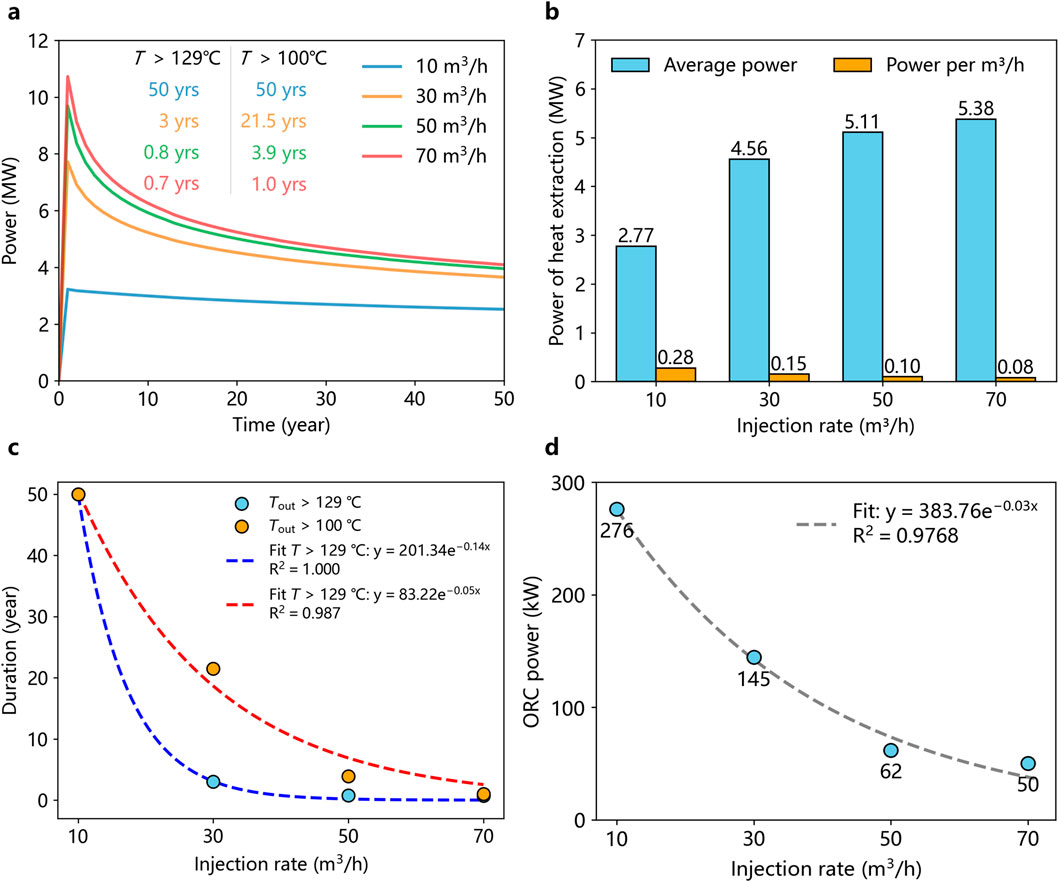
Figure 13. Power analysis of different injection rate in UMW method. (a) Variation of heat extraction power; (b) Average heat extraction power and heat extraction power per m³/h; (c) Duration of outlet temperature which exceeds 129°C and 100°C; (d) Organic Rankine Cycle generation power.

3.4.2 Number of branch wells

The conventional U-shaped well configuration is characterized by a single horizontal heat exchange segment. In contrast, the UMW method distinguishes itself by employing multiple horizontal lateral wells at the same depth level, which share a common set of injection and production wells. Consequently, the number of horizontal laterals within a single cluster emerges as a critical design parameter in this methodology. This section presents a comprehensive comparative analysis of thermal extraction performance across varying numbers of horizontal laterals. We have developed six distinct lateral well configurations, corresponding to 1-6 lateral wells respectively (Figure 14). It is noteworthy that all simulation cases maintain a constant total injection rate of 30 m³/h to ensure comparative consistency.

Figure 14

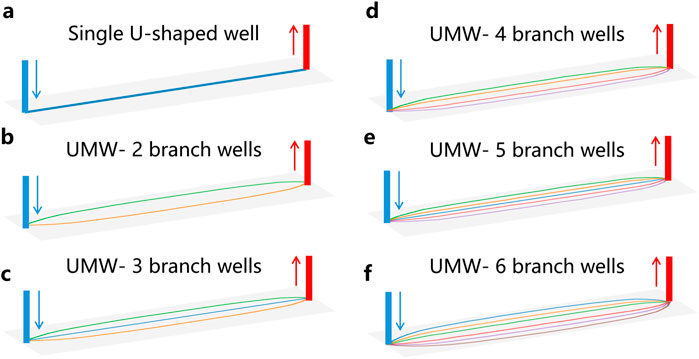
Figure 14. Schematic of different number of branch wells in UMW method. (a) Single U-shaped well; (b) 2 branch wells; (c) 3 branch wells; (d) 4 branch wells; (e) 5 branch wells; (f) 6 branch wells.

By comparing the temperature field results for different numbers of horizontal lateral wells (Figure 15), it is evident that an increased number of lateral well heat exchange segments significantly enhances the volume of thermal disturbance and reduces the reservoir temperature to a lower level. Analysis of the outlet temperatures from different lateral wells reveals that the outlet temperature of a single lateral well decreases more rapidly (Figure 16). Since the total flow rate remains constant, an increase in the number of lateral wells leads to a reduction in the flow rate per well, thereby further slowing the rate of outlet temperature decline.

Figure 15

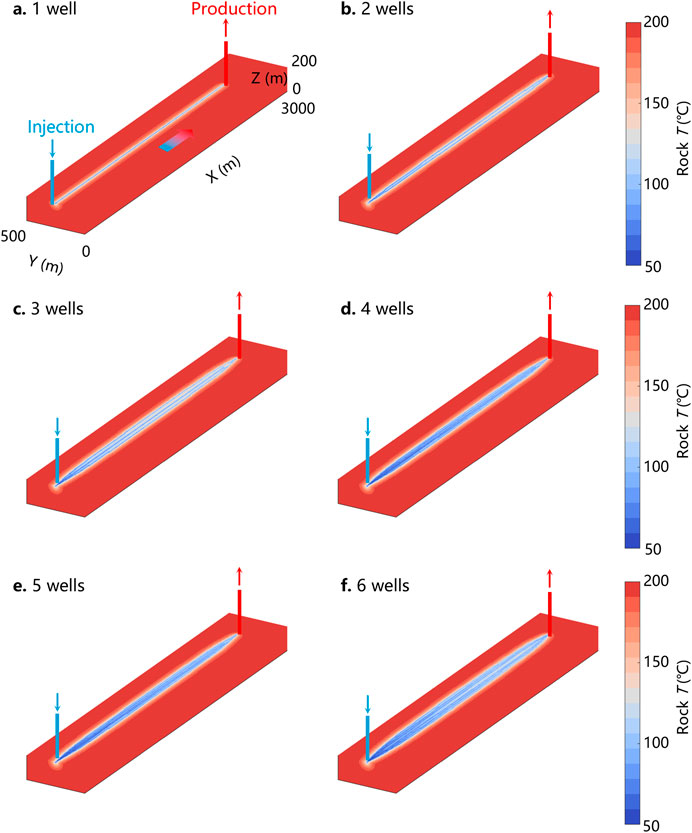
Figure 15. Temperature field of the reservoir at 50th year. (a) Single U-shaped well; (b) 2 branch wells; (c) 3 branch wells; (d) 4 branch wells; (e) 5 branch wells; (f) 6 branch wells.

Figure 16

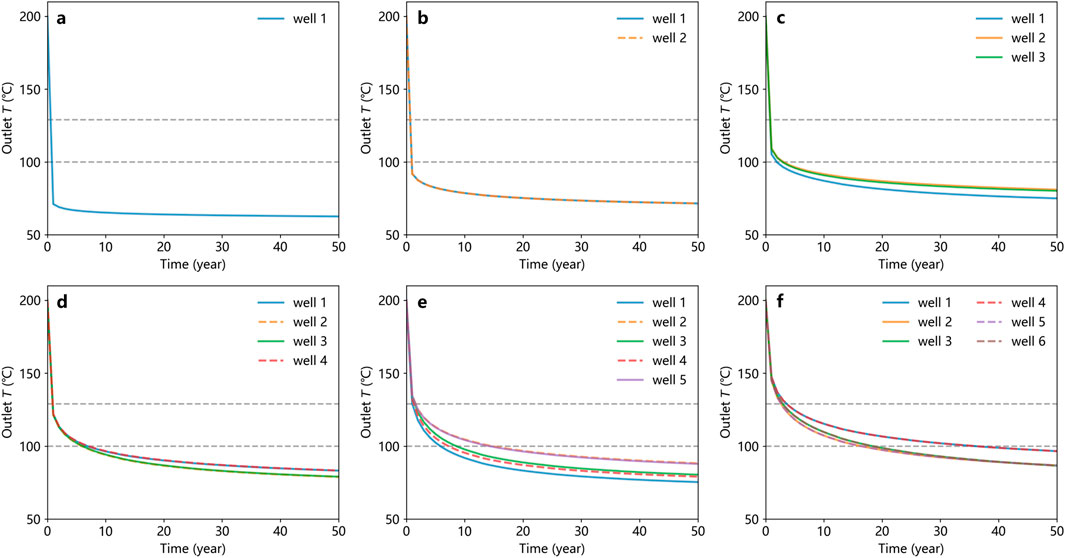
Figure 16. Temporal variation of the wellbore outlet temperature. (a) Single U-shaped well; (b) 2 branch wells; (c) 3 branch wells; (d) 4 branch wells; (e) 5 branch wells; (f) 6 branch wells. The gray dashed line represents 129°C (upper) and 100°C (lower).

Following the analysis of reservoir temperature and wellbore outlet temperature, we further quantified the heat extraction power (Figure 17a). The results demonstrate that a greater number of horizontal lateral wells can achieve higher peak heat extraction power and greater total heat extraction. Under the same total flow rate conditions, more lateral wells provide a larger heat exchange area, resulting in a higher average heat extraction power over a 50-year period (Figure 17b). However, the average heat extraction power per well decreases due to increased overlap in heat extraction zones, which limits the heat exchange efficiency of individual wells.

Figure 17

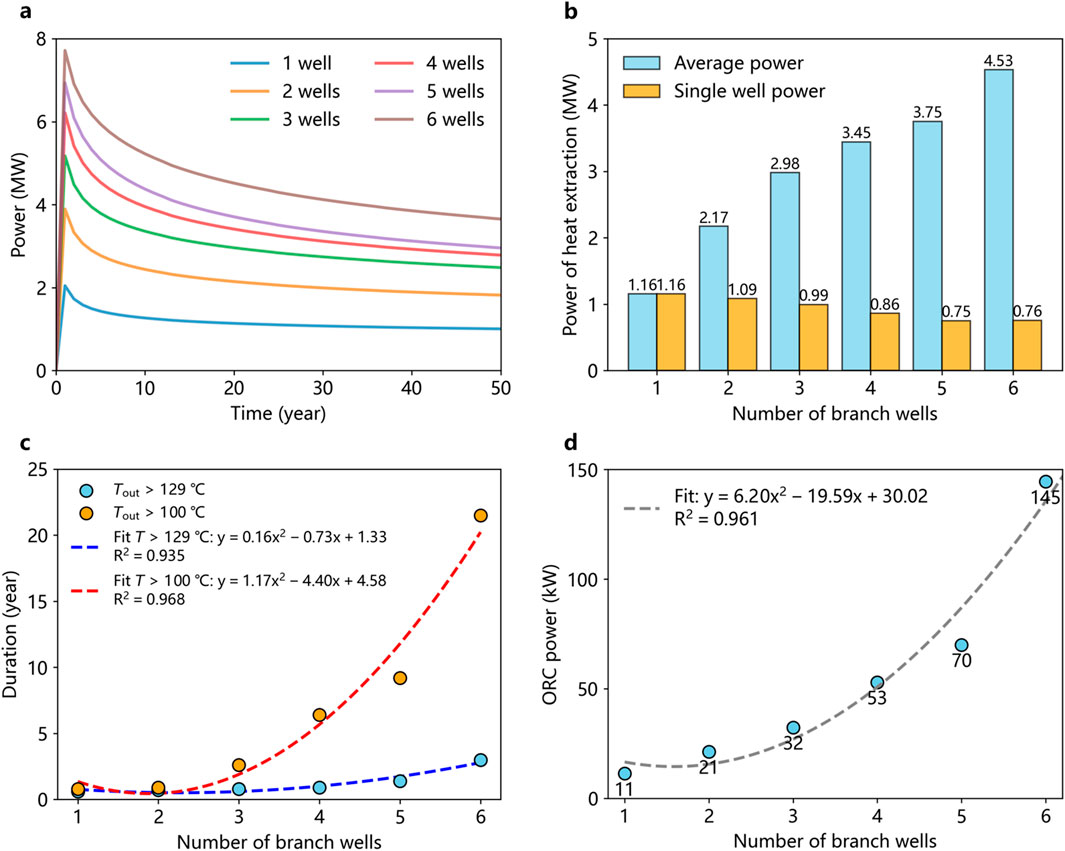
Figure 17. Power analysis of different number of branch wells in UMW method. (a) Variation of heat extraction power; (b) Average heat extraction power and heat extraction power of single branch well; (c) Duration of outlet temperature which exceeds 129°C and 100°C; (d) Organic Rankine Cycle generation power.

To quantitatively evaluate the potential ORC power generation, we first analyzed the duration during which the average outlet temperature exceeded 129°C and 100°C for different lateral well configurations (Figure 17c). A fitting relationship was established between the duration and the number of lateral wells. The results indicate a quadratic relationship under the same total injection flow rate conditions: for temperatures above 129°C, the relationship is y = 0.16x²-0.73x+1.33, and for temperatures above 100°C, it is y = 1.17x²-4.40x+4.58. Within the current data range, a greater number of lateral wells extends the duration of high outlet temperatures, i.e., the time during which the outlet temperature exceeds 129°C and 100°C. Building on the heat extraction power data and incorporating field production experience, we comprehensively calculated the potential ORC power generation (Figure 17d). The quadratic fitting relationship between the number of lateral wells and ORC power generation (y = 6.20x²-19.59x+30.02) aligns with the conclusions drawn from the outlet temperature duration analysis, indicating that more lateral wells can improve ORC generation power. In practical applications, it is also necessary to consider the construction costs of individual lateral wells and the optimization of well spacing. This fitting relationship can serve as a reference for optimizing the number of lateral wells.

4 Limitation and prospect

While this study provides valuable insights into the performance of clustered UMW systems for deep geothermal extraction, several limitations should be acknowledged. First, the current model employs simplified assumptions, particularly neglecting chemo-mechanical coupling effects, which may influence long-term reservoir stability. Second, the parameter ranges (e.g., permeability, thermal conductivity) were calibrated for specific reservoir lithologies, limiting direct applicability to heterogeneous or fractured formations. Third, numerical simulations lack validation against field-scale experiments, which could introduce uncertainties in operational predictions.

To address these constraints, future work should prioritize multi-physics coupling (THMC modeling) to capture interactions between thermal, hydraulic, mechanical, and chemical processes. Field trials are also recommended to verify the scalability of UMW configurations under real-world conditions. Additionally, machine learning-assisted optimization could enhance branch placement strategies while reducing computational costs. These advancements would strengthen the practical viability of UMW systems for sustainable geothermal exploitation.

While this study provides valuable insights into the thermal-hydraulic performance of clustered multi-branch U-shaped geothermal systems, certain practical engineering and economic aspects warrant further investigation. A significant limitation of the current work is the exclusion of a detailed techno-economic analysis, particularly concerning drilling and completion costs. The economic viability of multi-branch systems is intrinsically linked to the substantial investment in drilling numerous deviated wellbores. Future research should therefore focus on developing integrated models that couple reservoir performance simulations with comprehensive cost analyses, considering factors such as drilling depth, number of branches, trajectory complexity, and local drilling market conditions to optimize the system from both a thermal extraction and economic standpoint.

Furthermore, a more explicit sensitivity analysis of inter-branch well spacing and its impact on long-term thermal interference and overall system efficiency represents an important avenue for future work. Although the current design, constrained by practical directional drilling considerations for a gentle build-up trajectory, resulted in a relatively consistent inter-branch spacing of approximately 20 m, a dedicated study exploring a wider range of spacings–perhaps by varying the cluster’s lateral extent or considering different build-up rates where feasible–would be beneficial. Such an analysis would allow for a more granular understanding of thermal drawdown profiles between branches and help define optimal spacing strategies to maximize sustainable heat extraction while minimizing detrimental thermal interaction over the project lifecycle. Addressing these limitations will be crucial for translating the theoretical potential of these advanced geothermal systems into practical and economically feasible field-scale deployments.

5 Conclusion

To address the issues of unstable heat extraction power, and low heat extraction efficiency associated with current deep geothermal energy exploitation technologies, we proposed a sustainable deep geothermal energy extraction method using clustered U-shaped multi-branch wells (UMW). Based on a three-dimensional field-scale reservoir-wellbore thermal-hydraulic coupling model, we preliminary verified the feasibility of UMW method for deep geothermal energy exploration. The average heat extraction power of a single set of six branch wells over a 50-year operating cycle is ∼4.32 MW (30 m³/h, six branch wells). The ORC power generating power was conservatively estimated at ∼284.4 kW over the first 21.5 years, and approximately ∼144.6 kW over the 50-year period. The rapid decline in early-stage heat extraction power and the thermal breakthrough phenomenon under different injection rates and different number of branch wells suggest the need for optimization of construction and operational parameters to balance short-term power output with long-term system stability.

Sensitive analysis reveals that designing reasonable parameters in terms of injection rate, the number of branch wells, well spacing, and the operational cycle of branch wells is necessary to ensure efficient and long-term operation. We also provide a partial quantitative relationship between ORC power and operational parameters (injection rate and the number of branch wells) for optimization.

In field applications, the clustered U-shaped multi-branch well (UMW) heat extraction technology faces significant challenges, including the high cost and complexity of drilling multiple parallel horizontal wells. Therefore, the next step will focus on developing a more effective quantitative optimization methodology for the UMW approach, aiming to provide robust support for its efficient implementation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TX: Visualization, Formal Analysis, Writing – original draft, Methodology, Conceptualization, Investigation. SL: Conceptualization, Supervision, Project administration, Writing – review and editing, Funding acquisition. ZZ: Data curation, Methodology, Conceptualization, Formal Analysis, Writing – review and editing. YK: Resources, Investigation, Validation, Writing – review and editing. BZ: Formal Analysis, Methodology, Software, Visualization, Writing – review and editing. SM: Writing – review and editing, Investigation, Data curation, Validation. SZ: Data curation, Visualization, Writing – review and editing, Investigation, Resources. JH: Writing – review and editing, Investigation, Validation, Resources. XL: Writing – review and editing, Methodology, Data curation, Formal Analysis.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research is supported by the National Key R&D Program of China (No. 2024YFB4206700).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altun, A. F., and Kilic, M. (2020). Thermodynamic performance evaluation of a geothermal ORC power plant. Renew. Energy 148, 261–274. doi:10.1016/j.renene.2019.12.034

CrossRef Full Text | Google Scholar

Anand, R. S., Li, A., Huang, W., Chen, J., Li, Z., Ma, Q., et al. (2024). Super-long gravity heat pipe for geothermal energy exploitation - a comprehensive review. Renew. Sustain. Energy Rev. 193, 114286. doi:10.1016/j.rser.2024.114286

CrossRef Full Text | Google Scholar

Baisch, S., Vörös, R., Rothert, E., Stang, H., Jung, R., and Schellschmidt, R. (2010). A numerical model for fluid injection induced seismicity at soultz-sous-forêts. Int. J. Rock Mech. Min. Sci. 47, 405–413. doi:10.1016/j.ijrmms.2009.10.001

CrossRef Full Text | Google Scholar

Baisch, S., Weidler, R., Voros, R., Wyborn, D., and De Graaf, L. (2006). Induced seismicity during the stimulation of a geothermal HFR reservoir in the cooper basin, Australia. Bull. Seismol. Soc. Am. 96, 2242–2256. doi:10.1785/0120050255

CrossRef Full Text | Google Scholar

Beckers, K. F., Rangel-Jurado, N., Chandrasekar, H., Hawkins, A. J., Fulton, P. M., and Tester, J. W. (2022). Techno-economic performance of closed-loop geothermal systems for heat production and electricity generation. Geothermics 100, 102318. doi:10.1016/j.geothermics.2021.102318

CrossRef Full Text | Google Scholar

Bradford, J., Ohren, M., Osborn, W. L., Mclennan, J., Moore, J., and Podgorney, R. (2014). “Thermal stimulation and injectivity testing at raft river, ID EGS site,” in Proceedings of 39th Workshop on geothermal reservoir engineering, (CA, USA).

Google Scholar

Brogi, A. (2008). Fault zone architecture and permeability features in siliceous sedimentary rocks: insights from the rapolano geothermal area (northern apennines, Italy). J. Struct. Geol. 30, 237–256. doi:10.1016/j.jsg.2007.10.004

CrossRef Full Text | Google Scholar

Brogi, A., Alçiçek, M. C., Liotta, D., Capezzuoli, E., Zucchi, M., and Matera, P. F. (2021). Step-over fault zones controlling geothermal fluid-flow and travertine formation (denizli basin, Turkey). Geothermics 89, 101941. doi:10.1016/j.geothermics.2020.101941

CrossRef Full Text | Google Scholar

Chappidi, S., Kumar, A., and Singh, J. (2024). Geothermal energy extraction using a novel combined coaxial and U-shaped closed-loop system. Geothermics 119, 102968. doi:10.1016/j.geothermics.2024.102968

CrossRef Full Text | Google Scholar

Du, D., Li, Y., Wang, K., Zhao, Y., Hu, Z., Zhang, W., et al. (2023). Experimental and numerical simulation research on heat transfer performance of coaxial casing heat exchanger in 3500m-deep geothermal well in weihe basin. Geothermics 109, 102658. doi:10.1016/j.geothermics.2023.102658

CrossRef Full Text | Google Scholar

Duwiquet, H., Guillou-Frottier, L., Arbaret, L., Bellanger, M., Guillon, T., and Heap, M. J. (2021). Crustal fault zones (CFZ) as geothermal power systems: a preliminary 3D THM model constrained by a multidisciplinary approach. Geofluids 2021, 1–24. doi:10.1155/2021/8855632

CrossRef Full Text | Google Scholar

Gan, Q., Feng, Z., Zhou, L., Li, H., Liu, J., and Elsworth, D. (2021). Down-dip circulation at the united downs deep geothermal power project maximizes heat recovery and minimizes seismicity. Geothermics 96, 102204. doi:10.1016/j.geothermics.2021.102204

CrossRef Full Text | Google Scholar

Gao, D. (2019). A high-efficiency development mode of shale gas reservoirs in mountainous areas based on large cluster horizontal well engineering. Nat. Gas. Ind. B 6, 122–128. doi:10.1016/j.ngib.2018.08.001

CrossRef Full Text | Google Scholar

Hu, Y., Cheng, H., and Tao, S. (2022). Opportunity and challenges in large-scale geothermal energy exploitation in China. Crit. Rev. Env. Sci. Tec. 52, 3813–3834. doi:10.1080/10643389.2021.1971004

CrossRef Full Text | Google Scholar

Javadi, H., Mousavi Ajarostaghi, S. S., Rosen, M. A., and Pourfallah, M. (2019). Performance of ground heat exchangers: a comprehensive review of recent advances. Energy 178, 207–233. doi:10.1016/j.energy.2019.04.094

CrossRef Full Text | Google Scholar

Kim, K.-H., Ree, J.-H., Kim, Y., Kim, S., Kang, S. Y., and Seo, W. (2018). Assessing whether the 2017 m_w 5.4 pohang earthquake in South Korea was an induced event. Science 360, 1007–1009. doi:10.1126/science.aat6081

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, Y., Pang, Z., Shao, H., Hu, S., and Kolditz, O. (2014). Recent studies on hydrothermal systems in China: a review. Geotherm. Energy 2, 19. doi:10.1186/s40517-014-0019-8

CrossRef Full Text | Google Scholar

Kong, Y.-L., Chen, C.-F., Shao, H.-B., Pang, Z.-H., Xiong, L.-P., and Wang, J.-Y. (2017). Principle of deep borehole heat exchanger technology and its heat exchange assessment. Chin. J. Geophys. 60, 4741–4752. doi:10.6038/cjg20171216

CrossRef Full Text | Google Scholar

Kumari, W. G. P., and Ranjith, P. G. (2019). Sustainable development of enhanced geothermal systems based on geotechnical research – a review. Earth Sci. Rev. 199, 102955. doi:10.1016/j.earscirev.2019.102955

CrossRef Full Text | Google Scholar

Li, M., Shi, Y., Chen, H., Liu, C., and Li, H. (2024). Study on the heat transfer performance of coaxial casing heat exchanger for medium and deep geothermal energy in cold regions. Renew. Energy 237, 121666. doi:10.1016/j.renene.2024.121666

CrossRef Full Text | Google Scholar

Li, S.-D., Zhang, S.-P., Xu, T., Zhang, Z.-B., Zheng, B., Ma, S.-W., et al. (2024). Heat extraction technology and heat transfer algorithm for deep geothermal energy clustered multi-branch U-tube wells. J. Eng. Geol. 32, 1397–1411. doi:10.13544/j.cnki.jeg.2024-0399

CrossRef Full Text | Google Scholar

Li, Y., Zhang, Z., Li, S., Li, X., and Lu, C. (2023). Numerical investigation of the depressurization exploitation scheme of offshore natural gas hydrate: enlightenments for the depressurization amplitude and horizontal well location. Energy fuels. 37, 10706–10720. doi:10.1021/acs.energyfuels.3c01223

CrossRef Full Text | Google Scholar

Liang, B., Chen, M., and Orooji, Y. (2022). Effective parameters on the performance of ground heat exchangers: a review of latest advances. Geothermics 98, 102283. doi:10.1016/j.geothermics.2021.102283

CrossRef Full Text | Google Scholar

Lin, H., Liu, W., Zhang, D., Chen, B., and Zhang, X. (2025). Study on the degradation mechanism of mechanical properties of red sandstone under static and dynamic loading after different high temperatures. Sci. Rep. 15, 11611. doi:10.1038/s41598-025-93969-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, W., Wang, G., Gan, H., Zhang, S., Zhao, Z., Yue, G., et al. (2023). Heat source model for enhanced geothermal systems (EGS) under different geological conditions in China. Gondwana Res. 122, 243–259. doi:10.1016/j.gr.2022.08.007

CrossRef Full Text | Google Scholar

Lu, S.-M. (2018). A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 81, 2902–2921. doi:10.1016/j.rser.2017.06.097

CrossRef Full Text | Google Scholar

Martín-Gamboa, M., Iribarren, D., and Dufour, J. (2015). On the environmental suitability of high- and low-enthalpy geothermal systems. Geothermics 53, 27–37. doi:10.1016/j.geothermics.2014.03.012

CrossRef Full Text | Google Scholar

Olasolo, P., Juárez, M. C., Morales, M. P., D´Amico, S., and Liarte, I. A. (2016). Enhanced geothermal systems (EGS): a review. Renew. Sustain. Energy Rev. 56, 133–144. doi:10.1016/j.rser.2015.11.031

CrossRef Full Text | Google Scholar

Portier, S., Vuataz, F.-D., Nami, P., Sanjuan, B., and Gérard, A. (2009). Chemical stimulation techniques for geothermal wells: experiments on the three-well EGS system at Soultz-sous-Forêts, France. Geothermics 38, 349–359. doi:10.1016/j.geothermics.2009.07.001

CrossRef Full Text | Google Scholar

Rybach, L., and Hopkirk, R. (1995). Shallow and deep borehole heat exchangers achievements and prospects. Pro. World Geothermal Congress 2133–2139.

Google Scholar

Schill, E., Cuenot, N., Genter, A., and Kohl, T. (2015). “Review of the hydraulic development in the multi-reservoir/multi-well EGS project of soultz-sous-forets,” in Proceedings world geothermal congress, 19–25.

Google Scholar

Song, G., Song, X., Li, G., Xu, R., Cao, W., and Zhao, C. (2021). Multi-objective optimization of geothermal extraction from the enhanced geothermal system in qiabuqia geothermal field, gonghe basin. Acta Geol. sin-engl. 95, 1844–1856. doi:10.1111/1755-6724.14875

CrossRef Full Text | Google Scholar

Sun, Z., Zhang, X., Xu, Y., Yao, J., Wang, H., Lv, S., et al. (2017). Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 120, 20–33. doi:10.1016/j.energy.2016.10.046

CrossRef Full Text | Google Scholar

Tomac, I., and Sauter, M. (2018). A review on challenges in the assessment of geomechanical rock performance for deep geothermal reservoir development. Renew. Sustain. Energy Rev. 82, 3972–3980. doi:10.1016/j.rser.2017.10.076

CrossRef Full Text | Google Scholar

Violante, A. C., Proposito, M., Donato, F., Guidi, G., and Falconi, L. M. (2021). Preliminary study of a closed loop vertical ground source heat pump system for an experimental pilot plant (rome, Italy). Renew. Energy 176, 415–422. doi:10.1016/j.renene.2021.05.083

CrossRef Full Text | Google Scholar

Wang, Y., Liu, Y., Dou, J., Li, M., and Zeng, M. (2020). Geothermal energy in China: status, challenges, and policy recommendations. Util. Policy 64, 101020. doi:10.1016/j.jup.2020.101020

CrossRef Full Text | Google Scholar

Xu, T., Zhang, Z., Li, S., Li, X., and Lu, C. (2021). Numerical evaluation of gas hydrate production performance of the depressurization and backfilling with an in situ supplemental heat method. ACS Omega 6, 12274–12286. doi:10.1021/acsomega.1c01143

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y.-S., Wang, X.-W., Shen, S.-L., and Zhou, A. (2020). Distribution characteristics and utilization of shallow geothermal energy in China. Energy Build. 229, 110479. doi:10.1016/j.enbuild.2020.110479

CrossRef Full Text | Google Scholar

Yang, S.-Q., Tian, W.-L., Elsworth, D., Wang, J.-G., and Fan, L.-F. (2020). An experimental study of effect of high temperature on the permeability evolution and failure response of granite under triaxial compression. Rock Mech. Rock Eng. 53, 4403–4427. doi:10.1007/s00603-019-01982-7

CrossRef Full Text | Google Scholar

Yang, W., Lu, P., and Chen, Y. (2016). Laboratory investigations of the thermal performance of an energy pile with spiral coil ground heat exchanger. Energy Build. 128, 491–502. doi:10.1016/j.enbuild.2016.07.012

CrossRef Full Text | Google Scholar

Yekoladio, P. J., Bello-Ochende, T., and Meyer, J. P. (2013). Design and optimization of a downhole coaxial heat exchanger for an enhanced geothermal system (EGS). Renew. Energy 55, 128–137. doi:10.1016/j.renene.2012.11.035

CrossRef Full Text | Google Scholar

Yin, H., Song, C., Ma, L., Gao, L., Yang, X., Li, W., et al. (2021). Analysis of flow and thermal breakthrough in leaky downhole coaxial open loop geothermal system. Appl. Therm. Eng. 194, 117098. doi:10.1016/j.applthermaleng.2021.117098

CrossRef Full Text | Google Scholar

Yuan, Y., Zhang, X., Yu, H., Zhong, C., Wang, Y., Wen, D., et al. (2025). Research progress and technical challenges of geothermal energy development from hot dry rock: a review. Energies 18, 1742. doi:10.3390/en18071742

CrossRef Full Text | Google Scholar

Zhang, C., Hu, S., Zhang, S., Li, S., Zhang, L., Kong, Y., et al. (2020). Radiogenic heat production variations in the gonghe basin, northeastern Tibetan plateau: implications for the origin of high-temperature geothermal resources. Renew. Energy 148, 284–297. doi:10.1016/j.renene.2019.11.156

CrossRef Full Text | Google Scholar

Zhang, C., Huang, R., Qin, S., Hu, S., Zhang, S., Li, S., et al. (2021). The high-temperature geothermal resources in the gonghe-guide area, northeast Tibetan Plateau: a comprehensive review. Geothermics 97, 102264. doi:10.1016/j.geothermics.2021.102264

CrossRef Full Text | Google Scholar

Zhang, S., Li, S., Zhang, L., Li, X., Jin, X., Kong, Y., et al. (2024a). Characterization for 3D pore-fracture systems in hot-dry-rock samples from Gonghe Basin, China. Geothermics 117, 102886. doi:10.1016/j.geothermics.2023.102886

CrossRef Full Text | Google Scholar

Zhang, Z., Li, Y., Li, S., He, J., Li, X., Xu, T., et al. (2024b). Optimization of the natural gas hydrate hot water injection production method: insights from numerical and phase equilibrium analysis. Appl. Energy 361, 122963. doi:10.1016/j.apenergy.2024.122963

CrossRef Full Text | Google Scholar

Zhang, Z., Xie, Z., Montilla, M. J. B., Li, Y., Xu, T., Li, S., et al. (2024c). Feasibility and recovery efficiency of in-situ shale oil conversion in fractured reservoirs via steam heating: based on a coupled thermo-flow-chemical model. J. Anal. Appl. Pyrolysis 183, 106787. doi:10.1016/j.jaap.2024.106787

CrossRef Full Text | Google Scholar

Zhang, Z., Xu, T., Li, S., Guo, P., Li, X., Lu, C., et al. (2025). Comparative analysis of three heating methods for natural gas hydrate production: electric heating, steam injection, and hot water injection. Appl. Therm. Eng. 269, 126131. doi:10.1016/j.applthermaleng.2025.126131

CrossRef Full Text | Google Scholar

Zhang, Z., Xu, T., Li, S., Li, X., Briceño Montilla, M. J., and Lu, C. (2023). Comprehensive effects of heat and flow on the methane hydrate dissociation in porous media. Energy 265, 126425. doi:10.1016/j.energy.2022.126425

CrossRef Full Text | Google Scholar

Zhu, Y.-Q., Li, D.-Q., Zhang, Q.-X., Zhang, X., Liu, Z.-J., and Wang, J.-H. (2022). Characteristics of geothermal resource in qiabuqia, gonghe basin: evidence from high precision resistivity data. Ore Geol. Rev. 148, 105053. doi:10.1016/j.oregeorev.2022.105053

CrossRef Full Text | Google Scholar

Zucchi, M. (2020). Faults controlling geothermal fluid flow in low permeability rock volumes: an example from the exhumed geothermal system of eastern elba island (northern tyrrhenian sea, Italy). Geothermics 85, 101765. doi:10.1016/j.geothermics.2019.101765

CrossRef Full Text | Google Scholar