- 1Jiangxi Transportation Engineering Group Co., Ltd, Nanchang, Jiangxi, China
- 2Jiangxi Intelligent Maintenance Engineering Technology Research Center of Bridge, Nanchang, Jiangxi, China
- 3Jiangxi Hengtong Traffic Engineering Inspection Co., Ltd, Nanchang, Jiangxi, China
- 4Institute of Geotechnical Engineering, School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, Jiangxi, China
Introduction: Soft clay foundations exhibit complex nonlinear consolidation characteristics under cyclic loading, which significantly affects long-term stability.
Methods: This study proposes an innovative one-dimensional nonlinear consolidation analysis framework by comprehensively considering continuous drainage boundary conditions and cyclic dynamic loads, more realistically simulating the behavior of soft clay under complex loads and actual drainage boundary conditions in engineering practice. Additionally, under the assumptions of proportional reduction in permeability and compression coefficients and uniform initial effective stress distribution, the analytical solutions for effective stress and settlement during the consolidation process under cyclic loading are derived through variable substitution and separation methods.
Results: The consistency of the solution with that of Terzaghi’s permeable boundary case verifies the correctness and convergence of the proposed solution. Moreover, it is found that in the hyperbolic consolidation model, the variation of the initial void ratio has a negligible effect on the consolidation and settlement characteristics of the soil.
Discussion: An increase in the initial compression modulus and the slope n of the compression curve will reduce the fluctuation amplitude of the soil consolidation settlement curve and slow down the development of soil consolidation settlement. This study enhances the predictive capability for evaluating the behavior of soft clay foundations under complex loading and drainage conditions.
1 Introduction
Due to the nonlinear characteristics of soft clay, the traditional linear elastic model must be revised using a nonlinear stress-strain relationship to accurately predict the deformation response of soft clay foundations under load. Davis and Raymond (Davis and Raymond, 1965) proposed an empirical semi-logarithmic equation to characterize the stress-strain relationship during soil consolidation and stated that the clay consolidation is controlled by indicators such as the critical pressure ratio, load increment ratio, and total compression amplitude. Subsequently, it was modified by Mesri and Rokhsar (1974) by introducing the relationships of
Additionally, the boundary permeability of soft soil layers is a critical factor governing consolidation behavior in practical engineering applications. Based on the 1D consolidation theory, Zheng et al. (2010) and Mei et al. (2011) proposed an asymmetric boundary condition in which one side is permeable, and the other side is impermeable, and then provided analytical solutions for 1D consolidation under such conditions. It is important to note that the fully permeable and impermeable conditions described in Terzaghi consolidation theory represent only two special cases. Based on the continuous drainage boundary conditions, Zong et al., 2018; (Zong et al., 2022; Zong et al., 2021) employed a finite difference method to derive a 1D analytical solution under instantaneous loading. Feng et al. (Feng et al., 2023) further obtained an approximate solution to this problem and explored the effects of boundary drainage duration on the consolidation of foundation soils. Jiang et al. (2022) investigated the effect of temperature variation on the consolidation characteristics of soils during the single-stage linear loading under semi-permeable boundary conditions. The results revealed that the consolidation rate of the soil increases with increasing temperature gradient. To address time-dependent drainage effects at boundaries, Mei et al. (2021) proposed a continuous drainage boundary model governed by pore pressure. Zhou et al. (2023) demonstrated that the installation of horizontal drainage layer accelerates the consolidation process and further identified the optimal depth for such a drainage layer. Despite these advancements, the studies did not address the effects of cyclic loading. Based on Davis’s assumption, Chen et al. (2018) examined the 1D consolidation of the soil under low-frequency cyclic loading using the finite volume solution. Li et al. (2019) derived consolidation equations considering arbitrary loading and then performed a parametric analysis based on the 1D consolidation theory. The new intermittent load algorithm (Chai et al., 2022) streamlines computation through load equivalence and demonstrates high reliability. Yu et al. (2021) studied consolidation of two-layer saturated foundations under sinusoidal loading, finding that increased boundary drainage accelerated pre-consolidation settlement and expedited stabilization.
However, the results from numerous triaxial tests indicate that hyperbolic curves can better describe the vertical stress-strain relationship of the soil under loading (Wang et al., 2004; Gu et al., 2020; Mao et al., 2019). Arab et al. (2025) confirms the hyperbolic model better captures soft clay’s compressive characteristics than the semi-logarithmic model (Fan and Xia, 2025; Yachin Islam and Hossain, 2025; Tuc et al., 2025; Li et al., 2025). Chivukula et al. (Sairam Satwik and Chakraborty, 2022) further identify a critical rest period effect in non-Darcy consolidation under cyclic loading. Nevertheless, coupled modifications of one-dimensional consolidation theory—integrating hyperbolic nonlinearity with continuous drainage boundaries under cyclic loading—remain scarcely documented. However, coupled modifications of 1D consolidation theory—integrating hyperbolic nonlinearity, cyclic loading, and continuous drainage boundaries—remain scarcely documented. In this study, the analytical solutions for the effective stress and settlement of a 1D hyperbolic consolidation model under continuous drainage boundary conditions and cyclic loading were derived by employing the variable separation method. The key factors affecting consolidation settlement were analyzed. Loads caused by earthquakes, changes in groundwater levels and ocean waves can all be regarded as cyclic loads. Incorporating such nonlinear loading conditions with continuous drainage boundaries enhances model applicability to real-world scenarios and improves agreement with field measurements (Wang, 2020), thereby offering more actionable guidance for engineering practice.
2 Soil consolidation modeling and solution
2.1 Establishment of soil consolidation model
The schematic diagram illustrating the calculation of soil consolidation under continuous drainage boundary conditions and cyclic loading is presented in Figure 1, where represents the cyclic load, which varies over time; H denotes the thickness of the soil layer; and z indicates the depth of the soil layer.
(1) The stress-strain relationship of the soil is assumed to be hyperbolic as shown in Equation 1 (Zhang and Sun, 2007):
where
where
(2) In the process of soil consolidation, the compression coefficient is proportional to the permeability coefficient as shown in Equation 4 (Zong et al., 2022):
where
(3) Assuming a uniform distribution of the initial effective stress
where
Based on these basic assumptions, the governing equation for the consolidation of the hyperbolic model can be derived as shown in Equation 6:
It follows from the equality of the total stresses (Shi et al., 2001):
Continuous drainage boundary conditions are introduced into Equation 7 to obtain the initial and boundary conditions as follows:
Initial condition as shown in Equation 8:
Top surface boundary conditions as shown in Equation 9:
Bottom boundary conditions:
where b and c in Equation 10 are boundary permeability parameters which can be obtained through test fitting or engineering measurement. When the boundary condition is set to a completely permeable state, b and c approach infinity; conversely, when the boundary condition is impermeable, b and c equal zero.
2.2 Equation solving
Equation 7 is solved via variable substitution:
Substituting
where
The initial and boundary conditions for Equation 12 are expressed as:
Initial condition as shown in Equation 13:
Top surface boundary condition:
Bottom boundary condition:
The non-homogeneous boundary is homogenized as follows:
Substituting Equations 14, 15 into Equation 16 yields:
Next, we calculate the first-order derivative of with respect to t and the second-order derivative with respect to z in the above equation and substitute these results to Equation 12 to obtain:
where
At this point, the homogeneous boundary conditions are shown in Equation 19:
The variable separation method is utilized to solve Equation 18, and the solution is expressed as:
Substituting Equation 20 into Equation 18 and simplifying gives in Equation 21:
To solve the first-order nonhomogeneous differential equation of the above formula, we obtain:
In accordance with the description in Chen (Chen, 2002), the method of separation of variables is employed. Substituting Equation 20 in Equation 22 yields the solution of Equation 18 as:
Substituting Equation 23 into Equation 17 yields:
The analytical solution for the effective stress which is shown in Equation 25 is obtained by combining Equation 24 with Equation 11:
The increment of the foundation relative to the initial effective stress is expressed as Equation 26:
The analytical solution for the consolidation settlement is given in Equation 27:
3 Solution verification
The parameters for a 4-m thick soft clay foundation were referenced from (Wu et al., 2022), including the effective weight
For comparison and verification purposes, the scenario where the calculated effective stress in this study degenerated to the Terzaghi consolidation boundary
4 Parametric analysis
4.1 Parametric analysis of boundary permeability
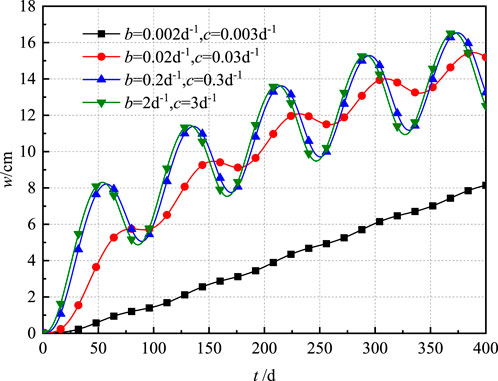
To gain deeper insight into the consolidation settlement behavior of the soil within this specific model, a comprehensive parametric analysis was meticulously conducted. The purpose of this investigation was to elucidate the intricate relationships between soil properties and the resultant settlement patterns, thereby enhancing the understanding of soil behaviors under varying conditions of stress and compaction. By systematically varying key soil parameters such as permeability, compressibility, and shear strength, we aimed to uncover the underlying mechanisms governing soil consolidation and settlement. Dynamic loads, which may vary over time due to factors such as traffic, wind, or seismic activity, impose additional stresses that can lead to increased soil deformation and potential failure. Figure 4 provides a detailed depiction of consolidation settlement variations over time under diverse boundary conditions, characterized by the parameters b and c. These parameters represent the boundary permeability quality of the soil and can be used to simulate the permeability behaviors of the corresponding consolidated soil in engineering practice. Specifically, larger b and c values corresponded to enhanced boundary permeability, facilitating the efficient drainage of pore water and thus accelerating the consolidation process. Conversely, smaller values denoted reduced permeability, which hindered drainage and subsequently slows down settlement. The figure clearly illustrated that, under sinusoidal loading, the amplitude of oscillation in the consolidation settlement curve is positively correlated with the model parameters b and c. This correlation highlighted the influence of boundary permeability on the soil’s dynamic response to cyclic loading. As permeability increased, the soil’s capacity to dissipate pore water pressure under load also increased, leading to a more pronounced oscillation in settlement. Furthermore, the settlement variation curve over time, similar to the effective stress, exhibited a trend of oscillatory incrementation. This oscillatory behavior was a manifestation of the soil’s viscoelastic behavior and its capacity to adapt to the applied loads over time. The cyclic nature of the load induced a corresponding cyclic response in settlement, which was superimposed on the overall trend of consolidation settlement. Moreover, as the permeability of the soil boundary increased, evidenced by larger values of parameters b and c, there was a corresponding escalation in the growth rate of settlement curve. Conversely, when the permeability of the boundary decreased, represented by smaller values of b and c, the settlement hysteresis effect became more pronounced. This effect arose from the restricted drainage conditions that led to a slower consolidation process and a more significant lag in settlement response to load changes, as observed in the soil behavior under cyclic loading. In addition, the similarity between the two consolidation settlement curves,
When parameters b and c were assigned varying values, Figure 5 illustrates the resultant changes in the effective stress along the depth of the soil. As depicted in Figure 5, influenced by the permeability of the side boundaries, variation curve of the effective stress initially decreased and then increased with increasing soil depth. This behavior was a direct consequence of the interplay between fluid flow and stress distribution within the soil matrix. The fluid flow within the soil is influenced by its permeability, which is a measure of its ability to transmit fluids. The permeability is a key factor in determining how quickly water can drain from the soil, thereby affecting the rate at which effective stress is established. As water drains from the soil pores, the effective stress increases, leading to soil consolidation and settlement. When the permeability is high, indicated by larger values of b and c, the soil readily expelled pore water, resulting in a swift decrease in pore water pressure and a corresponding increase in effective stress near the surface. This initial decrease in the effective stress curve reflected the rapid dissipation of excess pore water pressure due to the high permeability conditions, which facilitated a more rapid consolidation process. As depth increased, the effective stress subsequently increased due to the overburden pressure exerted by the overlying soil layers. This resulted in a characteristic S-shaped curve, where the inflection point corresponded to the depth at which the influence of boundary permeability on stress distribution became less pronounced. In contrast, when the permeability was low, represented by smaller values of b and c, the pore water drainage was impeded, leading to a more gradual decrease in pore water pressure and a delayed increase in effective stress. The reduced permeability resulted in a more pronounced hysteresis effect in the subsidence response to load changes, as the soil’s ability to consolidate was constrained by the limited capacity to expel water from the soil matrix. This delayed consolidation was particularly evident in the shallower portions of the soil profile, where the effective stress curve exhibited a less steep initial decrease, followed by a more gradual increase with depth. As depicted in Figure 5, when b and c took different values, the distribution of effective stress with soil depth exhibited a non-monotonic pattern, which was in contrast to the scenario under constant loading conditions.
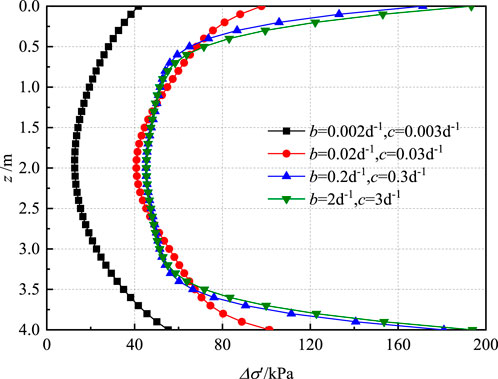
Figure 5. Distribution curve of effective stress along soil layer under different boundary permeability parameters (
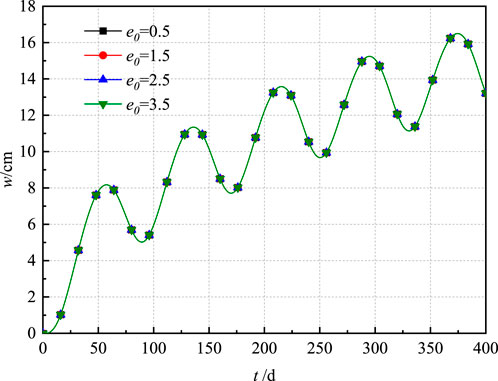
4.2 Impact of initial void ratio and compression modulus
Figure 6 visually represents the impact of the initial void ratio
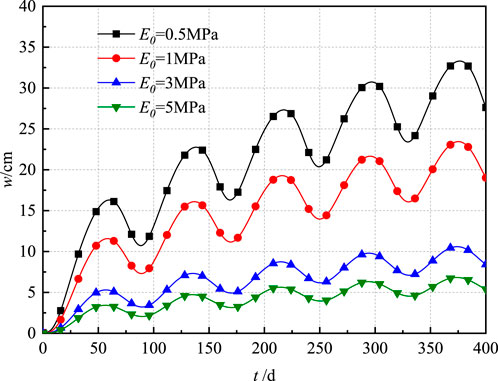
Figure 7 illustrates the impact of varying initial compression modulus on the consolidation settlement within the hyperbolic model. As the initial compression modulus gradually increased from 0.5 MPa to 5 MPa, there was a significant decrease in the rate of consolidation settlement of the soil. This trend was evident because the initial compression modulus that reflects the soil’s inherent stiffness was directly related to its resistance to compression under initial loading conditions. A higher initial compression modulus indicated a stiffer soil, which resulted in a lower settlement rate. The cumulative decrease in settlement became more pronounced in the later stages of consolidation. This observation was attributed to the increased stiffness of the soil at higher compression module, which limited further compression as consolidation progressed. Additionally, the oscillation caused by cyclic load was smaller. Conversely, a lower modulus suggested a softer, more compressible soil that settled more rapidly under the same load.
4.3 Influence of compression curve slope
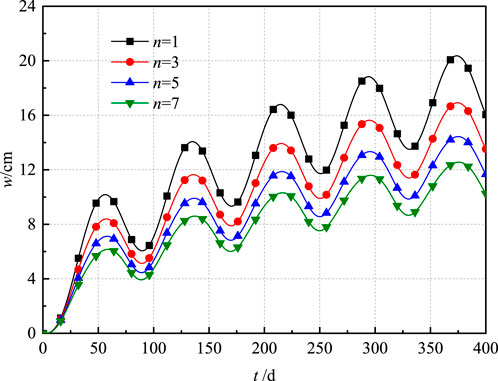
As depicted in Figure 8, the variation in the slope n of the compression curve corresponded to distinct changes in soil subsidence behavior. Here, n represents the rate of modulus growth during the loading process. A smaller value of n indicates a lower rate of modulus growth, while a larger value of n signifies a higher rate of modulus growth, which indicates that the soil’s stiffness increases rapidly under load. This rapid increase could lead to a more abrupt response to loading and a larger settlement rate during the early stages of loading. Therefore, as n increased, the rate of soil consolidation slowed down and the fluctuation of the curve became less pronounced.
5 Conclusion
This study investigated the nonlinear consolidation characteristics of a foundation with a continuous drainage boundary under cyclic loading, based on a hyperbolic model. The analytical solutions for effective stress and settlement during soil consolidation were derived using variable substitution and variable separation methods. The effective stress calculated in this study was then reduced to the Terzaghi consolidation boundary condition for validation purpose. The comparison results confirmed the correctness and convergence of the derivations presented in this study, providing a more accurate prediction of the settlement behavior of soft clay under realistic conditions. The conclusions can be summarized as follows:
(1) The boundary permeability conditions of the soil significantly influenced the calculation results of the model. The better the permeability of the soil boundary, the higher the oscillation value of the consolidation settlement curve of the hyperbolic model, and the less obvious the settlement hysteresis effect caused by the load changes.
(2) The initial void ratio of the soil exhibits a negligible influence on the consolidation settlement, demonstrating that the hyperbolic model inherently minimizes the dependency on this parameter and thereby simplifies the process of parameterization.
(3) Changes in the initial compression modulus
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
ZH: Methodology, Formal Analysis, Writing – original draft. XW: Methodology, Formal Analysis, Writing – original draft. LT: Writing – review and editing, Project administration, Conceptualization. JW: Writing – review and editing, Project administration. PZ: Data curation, Writing – review and editing. ZX: Writing – original draft, Formal Analysis, Conceptualization, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Science and Technology Project of Jiangxi Transportation Department of Jiangxi Province (No. 2021H0004), Jiangxi Provincial Science and Technology Cooperation Special Project (No. 20212BDH81034), and Subject of the Jiangxi Provincial Department of Education (No. GJJ210618). Additionally, the grant recipient of the above three funds is Lihong Tong.
Conflict of interest
Authors ZH and ZX were employed by Jiangxi Transportation Engineering Group Co., Ltd.
Author XW was employed by Jiangxi Hengtong Traffic Engineering Inspection Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arab, M., Benessalah, I., Hage Chehade, F., and Arab, A. (2025). One-dimensional consolidation and stress–strain behaviour of chlef or standard granular sand mixed with bentonite. Arabian J. Sci. Eng. doi:10.1007/s13369-025-09961-7
Chai, J.-C., Shen, S.-L., Wang, J., and Liu, M. D. (2022). Intermittent cyclic load induced 1D consolidation settlement. Transp. Geotech. 36, 100814. doi:10.1016/j.trgeo.2022.100814
Chen, C. (2002). Partial differential equations in mathematicalphysics. Nanjing: Southeast University Press, 59–105. (in Chinese).
Chen, X., Guo, G., and Guo, H. (2018). The solution for one-dimensional non-linear consolidation equantion under low-frequency cyclic loading by using finite volume method. China Sci. 13 (01), 27–30+36.
Davis, E. H., and Raymond, G. P. (1965). A non-linear theory of consolidation. Geotechnique 15 (2), 161–173. doi:10.1680/geot.1965.15.2.161
Fan, X., and Xia, T. (2025). One-dimensional consolidation analysis of normally consolidated soft clays under vibratory loads. Soil Dyn. Earthq. Eng. 191, 109241. doi:10.1016/j.soildyn.2025.109241
Feng, X., Zong, M., Tian, Y., Mei, G., and Wu, W. (2023). Approximate solution for one-dimensional nonlinear consolidation theory of soil considering the time effect of boundary drainage. Eng. Mech. 40 (01), 100–110. doi:10.6052/j.issn.1000-4750.2021.07.0575
Gu, J., Fan, L., Lu, H., and Chen, Y. (2020). Simulation of the stress-strain curves of red clay based on modified Duncan-Chang model. J. Guilin Univ. Technol. 40 (02), 351–357.
Hu, J., Bian, X., and Chen, Y. (2019). Nonlinear consolidation of multilayer soil under cyclic loadings. Eur. J. Environ. Civ. Eng. 25, 1042–1064. doi:10.1080/19648189.2019.1566096
Hu, M., Cao, W., Cui, P., Xu, Z., Li, H., and Li, Z. (2024). One-dimensional nonlinear consolidation analysis of soft soil considering variable load and non-Darcy seepage. J. Changjiang River Sci. Res. Inst. 41 (2), 151–158. doi:10.11988/ckyyb.20220973
Jiang, W., Li, J., Huang, X., Cheng, X., and Wan, Y. (2022). Analytical solution for one-dimensional consolidation of saturated clay considering partial drainage boundary under nonisothermal distribution condition. Rock Soil Mech. 43 (10), 2744–2756. doi:10.16285/j.rsm.2021.2040
Li, Y., Feng, J., and Mei, G. (2019). One-dimensional consolidation analysis of the trapezoidal cyclic loading under continuous drainage boundary. Eng. Mech. 36 (02), 137–143. doi:10.6052/j.issn.1000-4750.2017.12.0928
Li, H., Wu, J., Guo, C., Yang, H., Wu, Z., and Qin, S. (2025). Microstructural characteristics and prediction of hydraulic properties of geotextile envelopes via image analysis and pore network modeling. Geotext. Geomembranes 53 (1), 106–120. doi:10.1016/j.geotexmem.2024.09.007
Mao, G., Chen, X., Wang, X., and Li, Y. (2019). Modified Duncan-Chang E-ν constitutive model using non-linear Poisson's ratio and its application analysis. J. Railw. Sci. Eng. 16 (01), 71–78.
Mei, G., Xia, J., and Mei, L. (2011). Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary. Chin. J. Geotechnical Eng. (01), 34–37.
Mei, G., Feng, J., Xu, M., and Ni, P. (2021). Estimation of interface parameter for one-dimensional consolidation with continuous drainage boundary conditions. Int. J. Geomechanics 22 (3), 04021292. doi:10.1061/(asce)gm.1943-5622.0002300
Mesri, G., and Rokhsar, A. (1974). Theory of consolidation for clays. J. Geotechnical Geoenvironmental Eng., 100. doi:10.1061/AJGEB6.0000075
Sairam Satwik, C., and Chakraborty, M. (2022). Numerical analysis of one-dimensional consolidation of soft clays subjected to cyclic loading and non-Darcian flow. Comput. Geotechnics 146, 104742. doi:10.1016/j.compgeo.2022.104742
Shi, J., Yang, L., and Zhao, W. (2001). Research of one-dimensional consolidation theory considering nonlinear characteristics of soil. J. Hohai Univ. 29 (1).
Tuc, E., Akbas, S., and Babagiray, G. (2025). Reliability and validity analysis of correlations on strength and consolidation parameters for ankara clay and proposal for a new correlation. Arabian J. Sci. Eng. 50, 8107–8126. doi:10.1007/s13369-024-09181-5
Wang, J. (2020). One-dimensional consolidation of saturated soil with continuous drainage boundary under cyclic loadings. Nanchang: East China Jiaotong University.
Wang, L., Zhao, Z., and Li, L. (2004). Non-linear elastic model considering soil structural damage. J. Hydraulic Eng. (01), 83–89.
Wu, S., Luo, W., Li, Y., Cui, W., and Wang, S. (2022). Analysis of one-dimensional nonlinear consolidation of soft soil considering time-dependent loading with continuous drainage boundary. Rock Soil Mech. 43 (06), 1503–1512. doi:10.16285/j.rsm.2021.6603
Xie, K., Xie, X., and Jiang, W. (2002). A study on one-dimensional nonlinear consolidation of double-layered soil. Comput. Geotechnics 29 (2), 151–168. doi:10.1016/s0266-352x(01)00017-9
Xie, K., Zhou, J., and Dong, Y. (2006). Analytical solution for one-dimensional nonlinear consolidation of soil under cyclic loadings. Chin. J. Rock Mech. Eng. 25 (1), 21.
Yachin Islam, Md, and Hossain, Z. (2025). Investigating the one-dimensional consolidation properties of river sludge enhanced by sustainable additive synergy for eco-friendly stabilization. J. Build. Eng. 101, 111851. doi:10.1016/j.jobe.2025.111851
Yang, X., Zong, M., Wu, W., Mei, G., and Jiang, G. (2021). Analytical solution for one-dimensional nonlinear consolidation of double-layered soil based on continuous drainage boundary. J. Hunan Univ. Sci. 48 (03), 136–143.
Yu, Z., Zhai, G., Mei, G., and Wu, W. (2021). One-dimensional consolidation of double layered soft soils with continuous drainage boundaries under cyclic loading. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 49 (01), 99–105.
Zhang, L., and Sun, S. (2007). One-dimensional consolidation theory based on hyperbola model under time-dependent loading for saturated soil. Chin. J. Rock Mech. Eng. 26 (S2), 4306–4310.
Zhang, L., Sun, S., Gong, X., and Zhang, J. (2010). Solution for one-dimensional consolidation based on hyperbola model under cyclic loading. Rock Soil Mech. 31 (2), 455–460.
Zheng, Y., Mei, G., and Mei, L. (2010). Generalized continuous drainage boundary applied in one-dimensional consolidation theory. J. Nanjing Univ. Technol. Nat. Sci. Ed. (06), 58–62.
Zhou, T., Wang, L., Li, T., Wen, M., and Zhou, A. (2023). Semi-analytical solutions to the one-dimensional consolidation for double-layered unsaturated ground with a horizontal drainage layer. Transp. Geotech. 38, 100909. doi:10.1016/j.trgeo.2022.100909
Zong, M., Wu, W., Mei, G., Liang, L., and Tian, Y. (2018). An analytical solution for one-dimensional nonlinear consolidation of soils with continuous drainage boundary. Chin. J. Rock Mech. Eng. 37 (12), 193–202.
Zong, M., Ye, C., Liang, R., Mei, G., Liang, X., and Wu, W. (2021). One-dimensional consolidation analysis considering exponential flow and self-weight based on continuous drainage boundary. J. Central South Univ. Sci. Technol. 52 (10), 3613–3622.
Zong, M., Tian, Y., Liang, R., Wu, W., Xu, M., and Mei, G. (2022). One-dimensional nonlinear consolidation analysis of soil with continuous drainage boundary. J. Central South Univ. 29 (01), 270–281. doi:10.1007/s11771-022-4916-x
Keywords: cyclic loading, continuous drainage boundary, hyperbolic model, settlement, consolidation
Citation: Huang Z, Wang X, Tong L, Wang J, Zhong P and Xu Z (2025) One-dimensional nonlinear consolidation of a hyperbolic model with continuous drainage boundary under cyclic dynamic loading. Front. Earth Sci. 13:1653133. doi: 10.3389/feart.2025.1653133
Received: 24 June 2025; Accepted: 30 July 2025;
Published: 02 September 2025.
Edited by:
Binbin Yang, Xuchang University, ChinaReviewed by:
Genbao Zhang, Hunan City University, ChinaAhmad Reshad Noori, Gelisim University, Türkiye
Timuçin Alp Aslan, Cukurova University, Türkiye
Copyright © 2025 Huang, Wang, Tong, Wang, Zhong and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peijia Zhong, MTQ2MjEzMzcxMkBxcS5jb20=
 Zhigang Huang1,2
Zhigang Huang1,2 Peijia Zhong
Peijia Zhong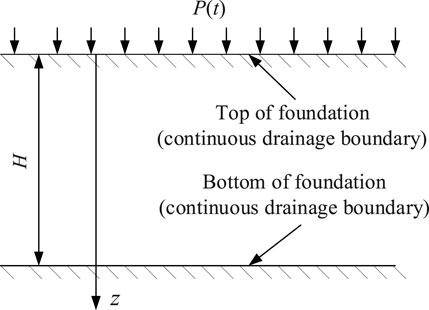
![Line graph showing pressure difference in kilopascals (∆d) versus time (t/d). The x-axis ranges from 0 to 400, and the y-axis from 0 to 50. A black line represents Reference [6], while red dots depict the Text solution (b = c → ∞). The graph shows an overall increasing trend with fluctuating values.](https://www.frontiersin.org/files/Articles/1653133/feart-13-1653133-HTML/image_m/feart-13-1653133-g003.jpg)