Phase field modelling of the hydro-mechanical coupling failure mechanisms of fissured rock masses

Exploring the mechanical response and damage mechanism of fractured rocks under hydro-mechanical coupling is a key approach to address the safety and stability problems of rock engineering under hydro-mechanical coupling conditions. Based on Biot theory and pore elasticity theory, a numerical simulation method of hydro-mechanical coupled phase field is developed, and a staggered time integration scheme is proposed to obtain stable solutions of fluid pressure and solid deformation, in which the obtained control equations adopt the volume strain separation and partial strain separation of the elasticity theory of fully saturated porous media. Two different numerical examples of fluid permeability tests and hydraulic fracturing with natural fracture interaction are used for validation. During the comparison of the numerical model with the analytical solution, the numerical results and the previous data are in better agreement, which verifies the validity and correctness of the model method. In addition, in order to investigate the unloading damage mechanism in the actual engineering excavation process, a hydro-mechanical coupled unloading damage model was established by combining numerical examples of borehole injection tests to simulate the whole process of fracture rock propagation damage under the dual conditions of hydro-mechanical coupling and surrounding pressure unloading. The study shows that fluid infiltration and hydraulic fracture crack expansion are mainly controlled by tensioning action, while mixed tensile-shear crack expansion and connection dominate the final damage mode during coupled hydro-mechanical unloading damage.

1 Introduction

With the rapid development of China’s modern comprehensive three-dimensional transportation system, the scale of metro and tunnel construction projects has gradually expanded, leading to a flourishing geotechnical engineering industry (Chen X. S. et al., 2025; Zhang et al., 2025). At the same time, frequent engineering accidents such as slope instability and sudden water inrush in tunnels have resulted in significant property and safety losses, attracting increasing attention from experts and scholars (Zhao Z. H. et al., 2021; Jiang et al., 2022; Wang et al., 2025). Therefore, investigating the mechanical response and failure mechanisms of fractured rocks under hydro-mechanical coupling is of great significance for ensuring the safety and stability of geotechnical engineering projects.

Regarding the hydro-mechanical coupling failure of fractured rocks, researchers both domestically and internationally have conducted a series of studies using laboratory experiments and numerical simulation methods (Li and Liu, 2021; Zhao C. X. et al., 2021; Gao et al., 2023). Laboratory experiments, through controlled variable approaches, allow for the investigation of the physical and mechanical properties and the evolution of permeability in rocks. Numerical simulation methods, on the other hand, focus on the simulation of crack propagation processes to explore fracture development patterns. Due to the complexity of hydro-mechanical coupling and the anisotropy of rocks, numerical simulation methods offer certain advantages over laboratory experiments. Currently, these numerical approaches are mainly divided into two categories: (i) continuum mechanics-based methods such as the finite element method (FEM), extended finite element method (XFEM) (Dehghan et al., 2017), and phase-field method (PFM) (Zhou et al., 2018; Zhou et al., 2019); and (ii) discontinuum mechanics-based methods such as the discrete element method (DEM) (Ghaderi et al., 2018) and the numerical manifold method (NMM) (Yu et al., 2018).

In recent years, the phase-field method has attracted increasing attention from researchers, especially in the field of hydro-mechanical coupling (Cheng et al., 2022; Xing and Zhao, 2023; Liu et al., 2024). The phase-field method describes crack propagation based on the principle of energy minimization, whereby cracks always extend along the most easily fractured direction. This approach does not require explicit crack tracking, and the mesh does not need to be updated before or after interface failure, greatly optimizing the workload involved in modeling fracture processes. Moreover, the phase-field method, with its inherent capability for multiphysics coupling, can incorporate hydraulic theories such as porous media theory and Biot poroelasticity theory (Heider, 2021; Li et al., 2022; Liu et al., 2025). By establishing fluid continuity partial differential equations, the phase-field method enables the modeling of crack propagation under hydro-mechanical coupling.

Currently, notable progress has been made in applying the phase-field method to hydro-mechanical coupling problems. Ehlers and Luo. (2017); Ehlers and Luo. (2018) conducted numerical studies of hydraulic fracturing via finite element analysis, integrating porous media theory with fracture mechanics elements and embedding the phase-field method within the porous media framework, thereby providing new perspectives for the study and computation of dynamic hydraulic fracturing. Heider and Markert, (2017), Heider et al. (2018) developed a numerical simulation framework for hydraulic fracturing in tight, low-permeability, brittle rocks. Based on the continuum mechanics theory of porous media and extended by the phase-field modeling approach, this framework considers two-phase materials composed of solid and liquid phases, employing macroscopic TPM to describe solid deformation and pore fluid flow behaviors. Yi et al. (2020) developed a nonlinear system of equations for hydraulic fracture propagation in porous media by integrating seepage mechanics, Biot poroelasticity theory, and the phase-field method, and solved these equations using FEM discretization.

Although previous studies have explored coupled thermal-mechanical behavior of soil backfill materials under cyclic loading (Ahmad et al., 2021; Ahmad et al., 2025b), hydro-mechanical interactions in fractured rock masses demand a distinct modeling approach. It is important to note that hydro-mechanical coupling problems are not simply a combination of mechanical relations; the physical and mechanical properties of rocks are also affected by water (Chen G. B. et al., 2025; Özdemír et al., 2025). For example, porosity and the Biot coefficient tend to increase as damage intensifies (Hu et al., 2010). Therefore, developing an accurate numerical model capable of predicting crack propagation and failure under hydro-mechanical coupling is critical. The phase-field method has demonstrated its effectiveness in addressing such problems in recent years. Recent advances in AI-driven assessment of material degradation (Ahmad et al., 2025a) suggest potential avenues for integrating data-driven models with phase-field approaches to enhance computational efficiency and predictive capability. This paper establishes a strain decomposition method that can simultaneously consider both tensile and shear failure by incorporating parameters such as porosity and Biot coefficient, which vary with the phase-field value. Compared to methods that only account for tensile failure, this approach can more accurately capture the results of hydro-mechanically coupled crack propagation and fracture. Building upon this, the author intends to develop a porous media hydro-mechanical coupling fracture model based on the phase-field approach, with the aim of systematically investigating the hydro-mechanical coupling failure mechanisms of fractured rocks.

2 Hydro-mechanical coupled phase-field model

2.1 Crack topology characterization

Within the computational domain $\mathrm{\Omega }=\mathrm{\Gamma }\times L$, where $\mathrm{L}=\left[-\infty ,+\infty \right]$ represents an infinitely long region, a crack is assumed to occur at the axial position $x=0$, with the cross-section $\mathrm{\Gamma }$ representing the fully fractured crack surface. Based on the principle of computational homogenization and accounting for the effects of microcracks and micropores, the phase-field variable $d\left(x\right)\in \left[0,1\right]$ in the numerical model allows the “sharp” crack topology to be described as a “diffuse” crack topology. The diffuse crack topology enables a smooth transition of geomaterials from intact to fully fractured states. In the phase-field numerical model, $d=0$ indicates that the material is intact (i.e., undamaged), whereas $d=1$ corresponds to a fully damaged state.

Under Dirichlet boundary conditions, the one-dimensional phase field can be characterized by the solution of a homogeneous differential equation, as shown in Equation 1:

$d=e^{-\frac{\left|x\right|}{{\mathcal{l}}_0}}(1)$

where ${\mathcal{l}}_0$ denotes the characteristic length of the geomaterial, which is used to describe the width of the “diffuse” crack within the phase-field model.

According to Miehe et al. (2010), the regularized crack topology can be described by defining the crack surface density function in its classical form, as given by Equation 2:

$\gamma \left(d,\nabla d\right)=\frac{1}{2{\mathcal{l}}_0}{d}^2+\frac{{\mathcal{l}}_0}{2}{\left|\nabla d\right|}^2(2)$

where $\nabla d$ represents the spatial gradient of the phase-field variable.

Through regularization, the crack topology in the phase-field model can be defined as Equation 3:

$\mathrm{\Gamma }\left(d\right)=\int \gamma \left(d,\nabla d\right)dV(3)$

Furthermore, the fracture energy ${\mathrm{\Psi }}_{\text{frac}}$ can be expressed by Equation 4:

${\mathrm{\Psi }}_{frac}={\int }_{\mathrm{\Omega }}{\mathcal{G}}_c\gamma \left(d,\nabla d\right)dV(4)$

where ${\mathcal{G}}_c$ denotes the critical energy release rate of the geomaterial.

2.2 Elastic strain energy

In the study by Miehe et al. (2010), it is assumed that damage in rocks leads only to the degradation of tensile stresses. Accordingly, the strain tensor is decomposed into tensile and compressive components, as shown in Equation 5:

${\mathit{\epsilon }}_{\pm }=\sum _{i=1}^3{〈{\epsilon }_i〉}_{\pm }+n_i\otimes n_i(5)$

In this equation, ${\epsilon }_i$ denotes the principal strains and $n_i$ represents the directions of the principal strains. The bracket operator is defined as ${〈x〉}_{\pm }=\left(x\pm \left|x\right|\right)/2$.

However, this approach is not effective for simulating Mode II cracks induced by shear strains. To address this limitation, discrete methods such as lattice element modeling have also been successfully applied to simulate crack evolution in cemented geomaterials (Rizvi et al., 2020). Given that current methods are capable of modeling Mode II cracks, this study adopts an alternative approach in which the strain tensor is decomposed into volumetric and deviatoric components (Liu et al., 2022), as shown in Equations 6a, b:

$\mathit{\epsilon }={\mathit{\epsilon }}_{sph}^{\pm }+{\mathit{\epsilon }}_{dev}(\mathrm{6a})$

${\mathit{\epsilon }}_{dev}=\mathit{\epsilon }-\frac{1}{3}tr\left(\mathit{\epsilon }\right)\mathit{I}(\mathrm{6b})$

In this equation, $\mathit{\epsilon }$ is the strain tensor, ${\mathit{\epsilon }}_{\text{sph}}^{\pm }$ denotes the volumetric strain tensor, ${\mathit{\epsilon }}_{\text{dev}}$ is the deviatoric strain tensor, and $\mathit{I}$ is the second-order identity tensor.

Similarly, the strain energy density of geomaterials can be decomposed as shown in Equations 7a–c:

${\psi }_s\left(\mathit{\epsilon }\right)={\psi }_n^{\pm }\left(\mathit{\epsilon }\right)+{\psi }_t\left(\mathit{\epsilon }\right)(\mathrm{7a})$

${\psi }_n^{\pm }\left(\mathit{\epsilon }\right)=\frac{1}{2}{\mathit{\epsilon }}_{sph}^{\pm }:\mathbb{C}:{\mathit{\epsilon }}_{sph}^{\pm }(\mathrm{7b})$

${\psi }_t\left(\mathit{\epsilon }\right)=\frac{1}{2}{\mathit{\epsilon }}_{dev}:\mathbb{C}:{\mathit{\epsilon }}_{dev}(\mathrm{7c})$

where $\mathbb{C}$ is the fourth-order elastic stiffness tensor; ${\psi }_n^{+}$ and ${\psi }_n^{-}$ denote the strain energy densities associated with tensile and compressive deformations, respectively; and ${\psi }_t$ represents the strain energy density due to deviatoric deformation.

During the phase-field evolution process, the present model accounts for the degradation of strain energy resulting from both tensile-shear and compressive-shear deformations:

${\psi }_s\left(\mathit{\epsilon },d\right)=g\left(d\right)\left[{\psi }_n^{+}\left(\mathit{\epsilon }\right)+{\psi }_t\left(\mathit{\epsilon }\right)\right]+{\psi }_n^{-}\left(\mathit{\epsilon }\right)(8)$

where $\mathrm{g}\left(d\right)={\left(1-d\right)}^2$ is the strain energy degradation function.

2.3 Hydro-mechanical phase-field model

The free energy density within the solid computational domain primarily consists of two components, as shown in Equation 9:

$\psi \left(\mathit{\epsilon },d\right)={\psi }_s\left(\mathit{\epsilon },d\right)+{\psi }_{frac}\left(d\right)(9)$

where $\psi$ denotes the total free energy density within the computational domain, and ${\psi }_{\text{frac}}$ is the fracture energy density.

Based on the theory of porous media mechanics, it is assumed that the porous geomaterial domain is fully saturated. During the simulation of hydraulic fracturing, the contribution of fluid potential energy must be considered. That is, the deformation energy density of the pore fluid, ${\psi }_{\mathrm{f}\text{luid}}$, should be included, and the free energy density of the saturated porous geomaterial can thus be expressed as Equation 10:

$\psi ={\psi }_s+{\psi }_{\text{frac}}+{\psi }_{\mathrm{f}\text{luid}}(10)$

The deformation energy density of the pore fluid, ${\psi }_{\mathrm{f}\text{luid}}$, is given by Mikelic et al. (2015):

${\psi }_{fluid}=\frac{M\left(d\right)}{2}{\left[\zeta -\alpha \left(d\right){\epsilon }_{ii}\right]}^2=\frac{p^2}{2M\left(d\right)}(11)$

where $p$ denotes the fluid pressure and $\zeta$ is the fluid volumetric content.

Experimental studies have shown that the Biot coefficient $\alpha$, Biot modulus $M\left(d\right)$, and porosity $\phi$ vary with the damage and failure evolution of rock materials, i.e., they can be regarded as functions of the damage evolution. Therefore, in this model, the phase-field variable is used to describe the Biot coefficient $\alpha$ and Biot modulus $M\left(d\right)$, as shown in Equations 12–14:

$\alpha \left(d\right)=1-\frac{\mathrm{g}\left(d\right)K}{K_s}(12)$

where $K$ is the bulk modulus of the porous rock, and $K_s$ is the bulk modulus of the solid grains in the porous medium.

$\frac{1}{M}=\frac{\phi \left(d\right)}{K_f}+\frac{\alpha \left(d\right)-\phi \left(d\right)}{K_s}(13)$

where, $K_s$ is the bulk modulus of the solid grains in the porous medium, and $K_f$ is the bulk modulus of the fluid.

$\phi \left(d\right)={\phi }_0+\left(1-{\phi }_0\right)\left[1-{\left(1-d\right)}^2\right](14)$

where ${\phi }_0$ denotes the initial porosity.

Additionally, the bulk modulus of the porous geomaterial can be expressed as shown in Equations 15a, b:

$K=\frac{1-\phi }{1-m\phi }{K}_m(\mathrm{15a})$

$m=\frac{1+\upsilon }{2\left(1-2\upsilon \right)}(\mathrm{15b})$

Based on Darcy’s law and Equation 11, the fluid continuity equation for a poroelastic medium can be derived as follows:

$\frac{\partial }{\partial t}\left[\frac{p}{M\left(d\right)}+\alpha \left(d\right){\epsilon }_{ii}\right]-\nabla ·\left(\frac{k\left({\epsilon }_{ii}\right)}{\mu }\nabla p\right)=0(16)$

where $\mu$ is the fluid viscosity, and $k\left({\epsilon }_{ii}\right)$ is the permeability of the porous geomaterial. In this study, the permeability is assumed to be a function of the maximum principal strain, given by $k\left({\epsilon }_{ii}\right)=\left(1+b{〈{\epsilon }_1〉}_{+}\right)k_0$, where b is an amplification factor.

Under hydro-mechanical coupling conditions, the effective stress in the porous geomaterial can be expressed as Equation 17:

$\mathit{\sigma }=\frac{\partial {\psi }_s\left(\mathit{\epsilon },d\right)}{\partial \mathit{\epsilon }}+\frac{\partial {\psi }_{fluid}\left(\mathit{\epsilon },d\right)}{\partial \mathit{\epsilon }}(17)$

By manipulating Equation 8 and Equation 11, we obtain Equation 18:

$\mathit{\sigma }=g\left(d\right)\mathbb{C}:\left({\mathit{\epsilon }}_{sph}^{+}+{\mathit{\epsilon }}_{dev}\right)+\mathbb{C}:{\mathit{\epsilon }}_{sph}^{-}-\alpha \left(d\right)p\mathit{I}(18)$

Therefore, the stress equilibrium equation for the porous geomaterial can be written as:

$\nabla ·\left[g\left(d\right)\mathbb{C}:\left({\mathit{\epsilon }}_{sph}^{+}+{\mathit{\epsilon }}_{dev}\right)+\mathbb{C}:{\mathit{\epsilon }}_{sph}^{-}-\alpha \left(d\right)p\mathit{I}\right]=0(19)$

Since fracture in solids is an irreversible process, to ensure that the numerical model captures this irreversibility during crack propagation, a local history variable $\mathcal{H}\left(\mathit{\epsilon },d\right)$ is introduced to drive the phase-field evolution, as shown in Equations 20a–c:

${\mathcal{H}}_{\mathit{n}}\left(\mathit{\epsilon },\mathit{d}\right)=\mathit{max}\left\{{\mathit{\psi }}_{\mathit{n}}^{+}\left(\mathit{\epsilon },\mathit{d}\right)\right\}\mathit{t}\mathit{r}\left(\mathit{\epsilon }\right)\ge \mathbf{0}(\mathrm{20a})$

${\mathcal{H}}_{\mathit{n}}\left(\mathit{\epsilon },\mathit{d}\right)=\mathbf{0}\mathit{t}\mathit{r}\left(\mathit{\epsilon }\right)<\mathbf{0}(\mathrm{20b})$

${\mathcal{H}}_{\mathit{t}}\left(\mathit{\epsilon },\mathit{d}\right)=\mathit{max}\left\{{\mathit{\psi }}_{\mathit{t}}\left(\mathit{\epsilon },\mathit{d}\right)\right\}(\mathrm{20c})$

Accordingly, the phase-field evolution equation for the porous geomaterial can be formulated as:

$\frac{{\mathcal{G}}_{\mathit{c}}}{{\mathcal{l}}_{\mathbf{0}}}\left[\mathit{d}-{\mathcal{l}}_{\mathbf{0}}{\nabla }^{\mathbf{2}}\mathit{d}\right]=\mathbf{2}\left(\mathbf{1}-\mathit{d}\right)\left[{\mathcal{H}}_{\mathit{n}}\left(\mathit{\epsilon },\mathit{d}\right)+{\mathcal{H}}_{\mathit{t}}\left(\mathit{\epsilon },\mathit{d}\right)\right](21)$

Based on the above governing equations for saturated porous geomaterials, namely, Equations 16, 19, 21, together with the corresponding hydro-mechanical coupling boundary conditions, the mechanical response of the hydro-mechanical coupling failure process in saturated porous geomaterials can be comprehensively described. The expressions for the relevant boundary conditions are as shown in Equations 22a–c:

$\left\{\begin{array}{l}\mathit{d}=\mathbf{1},\mathit{\Gamma }\\ \nabla \mathit{d}·\mathit{n},\mathit{\partial }\mathit{\Omega }\end{array}\right.(\mathrm{22a})$

$\left\{\begin{array}{l}\mathit{\sigma }·\mathit{n}=\overline{\mathit{t}},\mathit{\partial }{\mathit{\Omega }}^{\mathit{t}}\\ \mathit{u}=\overline{\mathit{u}},\mathit{\partial }{\mathit{\Omega }}^{\mathit{u}}\end{array}\right.(\mathrm{22b})$

$\left\{\begin{array}{l}\mathit{p}=\overline{\mathit{p}},\mathit{\partial }{\mathit{\Omega }}^{\mathit{p}}\\ \left(-\frac{\mathit{k}}{\mathit{\mu }}\nabla \mathit{p}\right)·\mathit{n}=\overline{\mathit{q}},\mathit{\partial }{\mathit{\Omega }}^{\mathit{q}}\end{array}\right.(\mathrm{22c})$

where $\partial {\mathrm{\Omega }}^{\mathit{u}}$ and $\partial {\mathrm{\Omega }}^p$ represent Dirichlet boundary conditions, while $\partial {\mathrm{\Omega }}^{\mathit{t}}$ and $\partial {\mathrm{\Omega }}^q$ correspond to Neumann boundary conditions, as illustrated in Figure 1. The Dirichlet and Neumann boundaries are related as shown in Equations 23a, b:

$\left\{\begin{array}{l}\mathit{\partial }\mathit{\Omega }=\mathit{\partial }{\mathit{\Omega }}^{\mathit{u}}\cup \mathit{\partial }{\mathit{\Omega }}^{\mathit{t}}\\ \mathit{\partial }{\mathit{\Omega }}^{\mathit{u}}\cap \mathit{\partial }{\mathit{\Omega }}^{\mathit{t}}=\varnothing \end{array}\right.(\mathrm{23a})$

$\left\{\begin{array}{l}\mathit{\partial }\mathit{\Omega }=\mathit{\partial }{\mathit{\Omega }}^{\mathit{p}}\cup \mathit{\partial }{\mathit{\Omega }}^{\mathit{q}}\\ \mathit{\partial }{\mathit{\Omega }}^{\mathit{p}}\cap \mathit{\partial }{\mathit{\Omega }}^{\mathit{q}}=\varnothing \end{array}\right.(\mathrm{23b})$

Figure 1

Figure 1. Hydro-mechanical coupling phase-field model for saturated porous geological media.

3 Numerical validation

To verify the accuracy and reliability of the hydro-mechanical phase-field numerical model proposed in this study, a series of numerical examples are presented. These examples investigate the interaction between hydraulically induced fractures and natural pre-existing cracks, with detailed model descriptions provided below.

3.1 Material parameters and boundary conditions

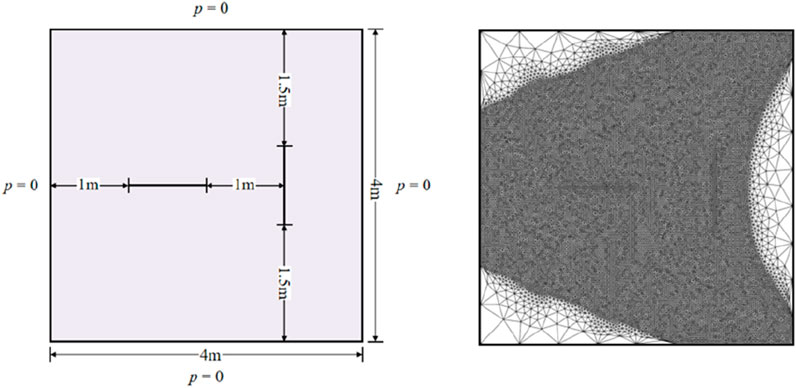
Based on the plane strain assumption, the computational domain is defined as a square region with a side length of $L=4.0$ m. Two pre-existing cracks, each with a length of $a=1.0$ m, are symmetrically placed about the x-axis and are orthogonal to each other within the domain. The boundaries of the computational domain are set as fixed and drained, while the effect of in-situ stress is neglected. Hydraulic fracturing is simulated by injecting water at a rate of $q=0.01$ m²/s within the two pre-existing cracks. The material parameters for the porous geomaterial used in the numerical model are listed in Table 1, with the characteristic length in the phase-field model set to ${\mathcal{l}}_0=0.06$ m and the time step set to $\Delta t=1.0\times {10}^{-7}$ s. Based on the finite element method, the computational domain is discretized into 45,846 triangular elements, with a minimum element size of $h_{\min }=0.024$ m, as illustrated in Figure 2.

Table 1

Table 1. Simulate parameters required for the calculation process.

Figure 2

Figure 2. Geometric and boundary conditions, and FE mesh discretization.

3.2 Fracture evolution process

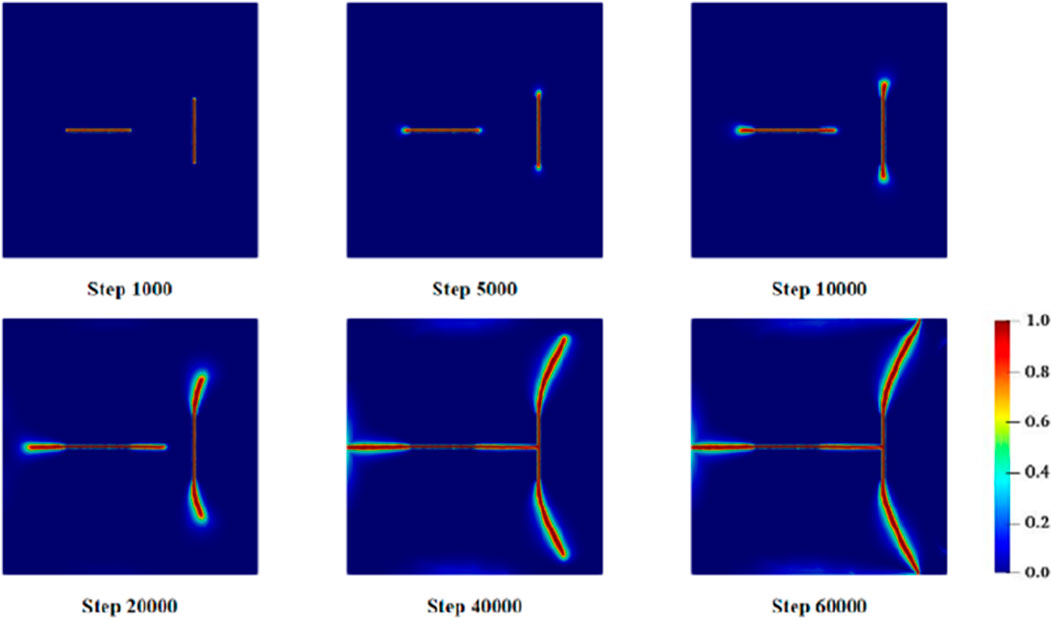
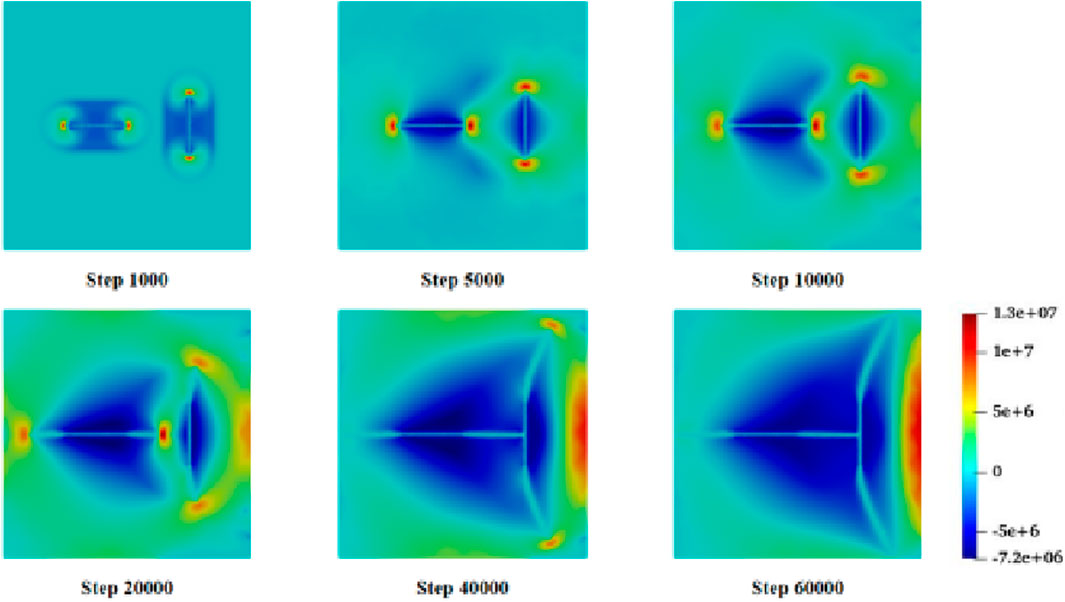
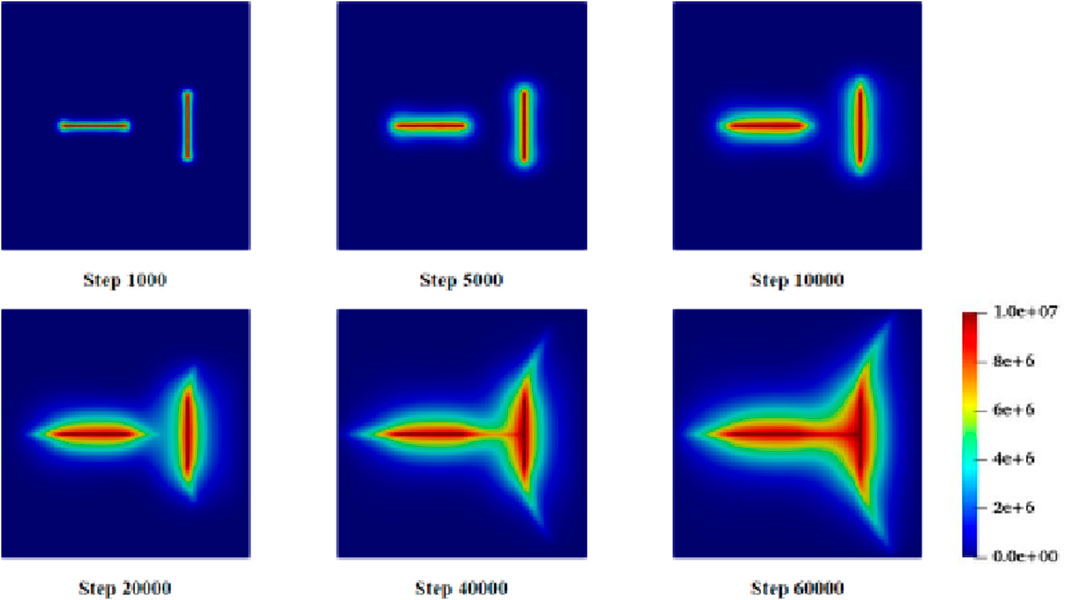
Figures 3–5 illustrate the evolution of crack propagation, maximum principal stress, and pore water pressure during the deformation and failure process of fractured porous geomaterials under hydro-mechanical coupling conditions.

Figure 3

Figure 3. Crack evolution process under the hydro-mechanical coupling process.

Figure 4

Figure 4. The evolution of maximum principal stress during hydraulic fracturing process.

Figure 5

Figure 5. The evolution of pore water pressure.

In the early stage of hydraulic fracturing (i.e., steps 1,000 to 5,000), the injection fluid pressure initiates crack propagation from the tips of both pre-existing cracks, with cracks extending along their initial orientations. In the intermediate stage of hydraulic fracturing (i.e., steps 10,000 to 20,000), hydraulic fractures continue to extend, but the maximum principal stress at the crack tips becomes concentrated, and mutual interactions between the cracks are observed. At step 10,000, a tendency for the right crack to deflect toward the right is observed, which is attributed to changes in fluid pressure within the left crack. At step 20,000, as the cracks further extend, the degree of deflection in the crack propagation path becomes more pronounced. Additionally, it is observed that the horizontal crack propagates faster on the left side than on the right, as mutual interactions between the two cracks exert pressure on the central region, thereby hindering crack growth.

In the late stage of hydraulic fracturing (i.e., steps 40,000 to 60,000), the two cracks eventually come into contact and connect, with the main crack extension occurring at the vertical crack. Since the expansion of the horizontal crack is essentially complete by this stage, the rate of increase of interaction forces between the two cracks slows down. The deflection effect on the vertical crack also gradually weakens, and its direction gradually aligns with the tangential direction until it reaches the boundary of the square domain. At this point (Step 60,000), the fracture process of the two perpendicular cracks is essentially complete.

In this example of hydro-mechanical fracturing, the primary failure mode is tensile failure. It can be observed that the maximum principal stress consistently drives the fracture at the crack tips. Due to the inherent lag in the diffusion of water pressure, the process of fracture propagation and fluid migration is cyclical, and failure continues until the cracks coalesce. Similar to the results of Yan et al. (2021), the right tip of the horizontal crack intersects the vertical crack, while the left tip extends to the left boundary of the model. Due to the influence of the horizontal crack, the vertical crack deflects to the right and eventually intersects the boundary. Overall, the numerical simulation results are in good agreement, thereby providing a certain degree of validation for the reliability of the proposed numerical modeling approach.

3.3 Convergence control

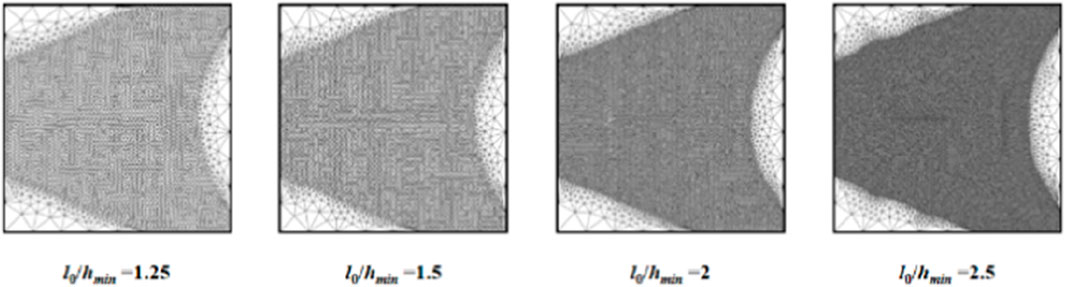
To further investigate the reliability of the phase-field method presented in this study, four different levels of mesh refinement were applied to the vertical crack model. The characteristic length scale was consistently set to 0.06 m, and convergence was evaluated by controlling the nonlocal ratio l₀/h_min. The values of the nonlocal ratio were set to 2.5, 2, 1.5, and 1.25, respectively, as shown in Figure 6.

Figure 6

Figure 6. Numerical model with different discretized meshes.

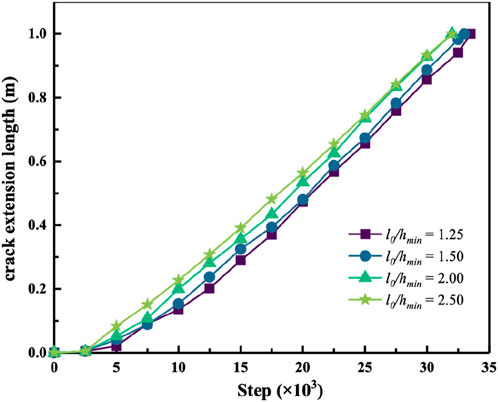
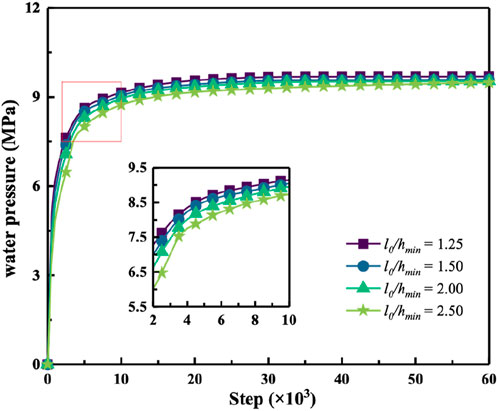
Considering that the vertical crack tends to deflect under loading, making data collection challenging, the left side of the horizontal crack was selected for data extraction in this study. As shown in Figures 7, 8, data were recorded from the left side of the horizontal crack in the vertical crack model, extracting the crack extension length and the water pressure at the crack tip at each time step.

Figure 7

Figure 7. Different meshes refine the left extension length increment of the horizontal crack.

Figure 8

Figure 8. Trend of pore water pressure at left tip of horizontal crack refined by different meshes.

The curves in Figures 7, 8 are closely aligned, with negligible differences in crack extension lengths and overlapping trends in the tip water pressure curves. As the tip water pressure approaches the initial value within the crack, the curves gradually stabilize, demonstrating good convergence. The simulation results are highly consistent across different mesh refinements. Based on these simulations and curve comparisons, it can be concluded that the proposed hydro-mechanical phase-field model exhibits improved accuracy with increasing mesh refinement.

4 Hydro-mechanical coupled unloading example

Current research on hydro-mechanical coupling is primarily focused on simulations of hydraulic fracturing or loading tests under seepage conditions, while studies on hydro-mechanical coupled unloading behavior remain relatively limited. However, there are significant mechanical differences between loading and unloading processes. To investigate the failure mechanisms, variation patterns, and permeability behavior associated with hydro-mechanical coupled unloading, this section presents a study on the failure mechanisms under unloading conditions.

Taking as an example a model with an initial confining pressure of 8 MPa, an initial unloading stress at 80% of the confining pressure, and a water pressure of 2 MPa, the entire simulation process is carried out as follows: First, both the confining pressure and axial pressure are simultaneously increased to 8 MPa. Subsequently, water is injected by maintaining a constant water pressure of 2 MPa at the lower boundary and zero at the upper boundary. The confining pressure is then held constant while the axial pressure is increased to the initial unloading stress level. Finally, the confining pressure is reduced until failure occurs. The other parameters required for the simulation, including those related to rock material properties and hydro-mechanical coupling, are listed in Table 2.

Table 2

Table 2. Simulate parameters required for the calculation process.

4.1 Fracture evolution process

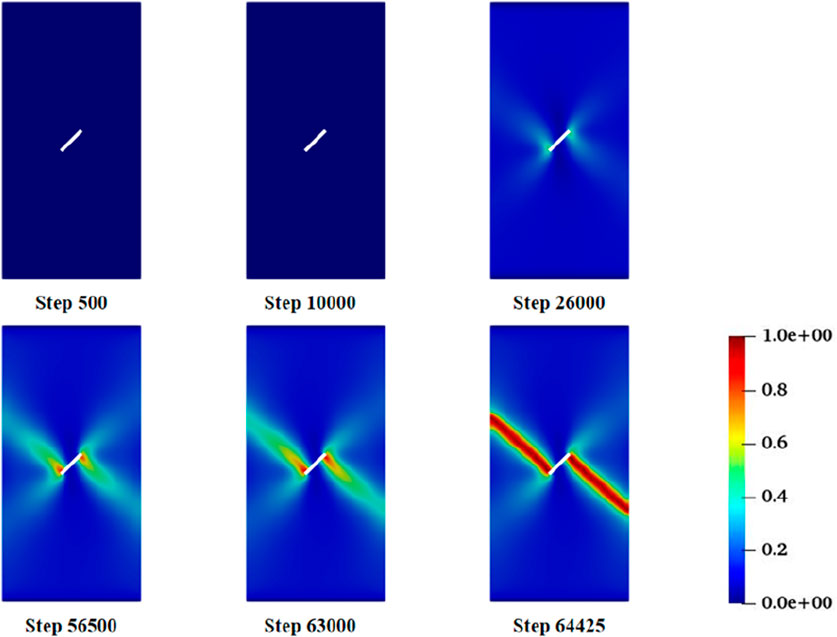
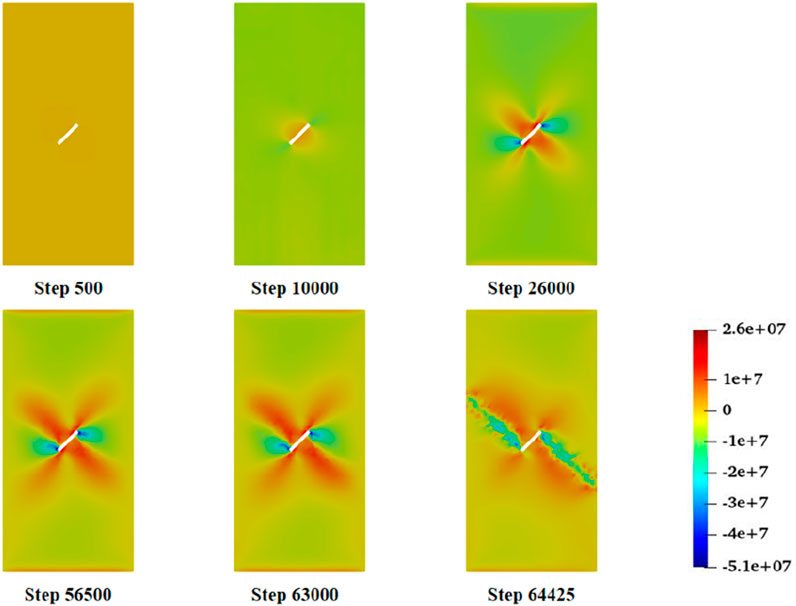
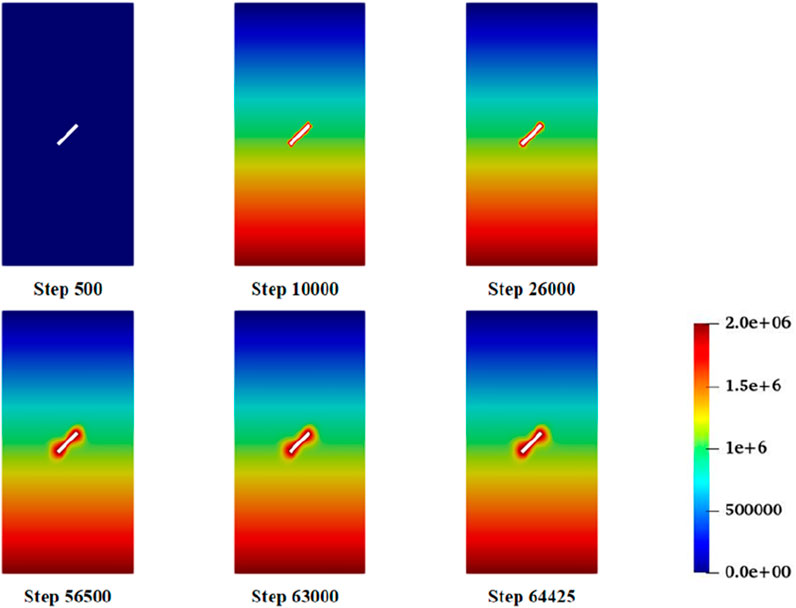
Figures 9–11 illustrate the evolution of the phase-field variable, shear stress, and pore water pressure during the hydro-mechanical coupled failure process of two orthogonal cracks. It can be observed that the development of cracks in the hydro-mechanical unloading model generally follows the loading and unloading sequence imposed at the boundaries.

Figure 9

Figure 9. The evolution of crack growth paths in the rocks.

Figure 10

Figure 10. The evolution of principal stress.

Figure 11

Figure 11. The evolution of pore water pressure.

During the confining pressure loading stage (Step 0 ∼ Step 10,000), the axial and confining pressures are equal, resulting in a near-zero deviatoric stress. At this stage, the shear stress is relatively low, and the resulting strain energy is insufficient to initiate fractures, so the model remains in a compressed state. Subsequently (Step 10,000 ∼ Step 26,000), the model is subjected to injected pore water pressure, and the initial unloading stress has been applied to 80% of the confining pressure by Step 10,000. In this phase, the axial stress far exceeds the confining pressure, leading to axial compression, a gradual increase in deviatoric stress, and the appearance of localized bright spots in the pre-existing cracks.

During the confining pressure unloading stage (Step 26,000 ∼ Step 64,425), as unloading progresses, the damage zone at the crack tips deepens continuously. When the deviatoric stress reaches its maximum (Step 56,500), significant damage occurs at the cracks, and four potential crack propagation directions emerge in the model. Unloading causes the axial pressure to exceed the confining pressure, leading to an increase in deviatoric stress. This results in the formation of X-shaped zones of maximum shear stress and principal compressive stress radiating from the crack tips. The direction of the maximum principal compressive stress is oriented at approximately 45° to the two sets of conjugate shear planes. Consequently, each crack tip corresponds to two most favorable directions for mixed-mode tensile-shear propagation. With further damage accumulation and cyclic stress degradation, the damage value continues to rise, and the fracture gradually develops in a Z-shaped pattern until complete failure occurs at Step 64,425. At this point, the entire unloading failure simulation is concluded.

In this example of hydro-mechanical coupled unloading failure, the confining pressure remains higher than the water pressure throughout the simulation, and the permeability of the model is relatively low. As a result, the final failure mode is dominated by the propagation and coalescence of mixed-mode (tensile-shear) cracks, with shear stress providing the primary driving energy for fracture. In the final stage of model failure, as the damage increases significantly, extensive degradation of shear stress occurs.

4.2 Investigation of factors influencing fracture evolution

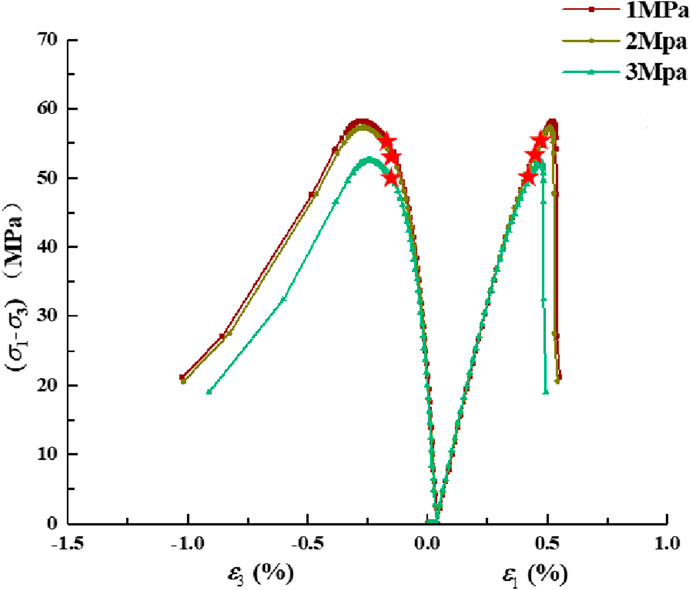
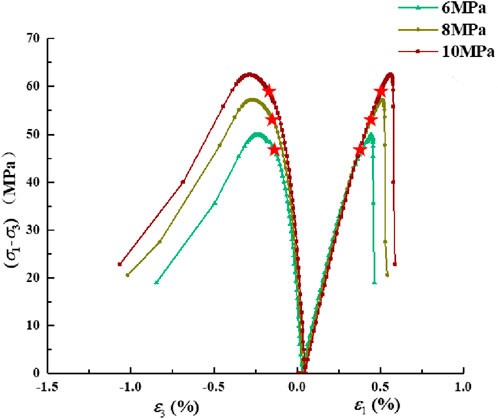
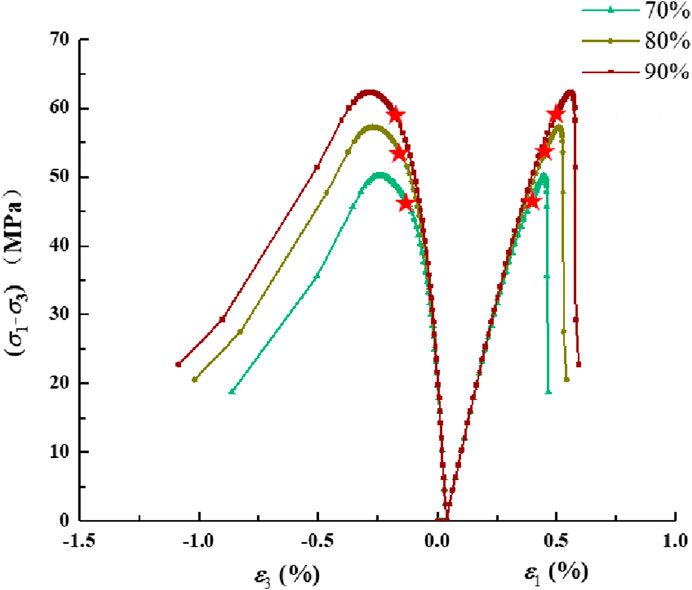
To further explore the hydro-mechanical coupled unloading failure mechanism of fractured rock and investigate the laws governing crack propagation, a series of numerical simulations were conducted using a controlled variable approach. Different levels of water pressure, initial unloading stress, and initial confining pressure were considered, and the deviatoric stress under each condition was recorded using predefined functions. The resulting stress–strain curves are shown below, where the red stars in the figures mark the unloading points.

As illustrated in Figures 12–14, it can be observed that with increasing water pressure, the peak deviatoric stress of the model decreases, indicating that water has a certain deteriorating effect on the rock. As the water pressure increases from 1 MPa to 3 MPa, the peak deviatoric stress decreases from approximately 58.4 MPa–53.9 MPa, and the failure strain also decreases slightly. Higher confining pressure more strongly restrains tensile effects, thereby increasing the proportion of energy provided by shear strain for fracture. When the confining pressure is increased from 6 MPa to 10 MPa, the peak deviatoric stress increases by approximately 26%–63 MPa, and the axial strain simultaneously increases by about 0.05%. In other words, confining pressure promotes the development of shear fractures. The initial unloading stress state also facilitates the development of shear cracks. For every 10% increase in the initial unloading level, the peak strength increases by approximately 5 MPa, and the failure strain also increases slightly. In terms of boundary conditions, a higher initial unloading stress brings the system closer to the deviatoric stress at failure, thus requiring a smaller amount of confining pressure to be unloaded to reach failure.

Figure 12

Figure 12. Stress-strain curve under different water pressure.

Figure 13

Figure 13. Stress-strain curves for different surrounding pressures.

Figure 14

Figure 14. Stress-strain curves at different initial unloading stresses.

5 Discussion and limitations

This paper presents a coupled phase-field numerical framework based on Biot’s theory and poroelasticity theory to simulate the failure evolution of fissured rock masses under hydro-mechanical coupling. Under plane strain conditions, the model is validated with permeability tests and hydraulic fracturing numerical examples, and the entire process of unloading-induced fracturing is numerically reproduced.

This study employs a two-dimensional plane strain assumption, which treats the crack as a through-thickness flaw extending infinitely in the out-of-plane direction, thereby neglecting the crack front curvature, through-thickness stress gradients, and the non-uniform distribution of seepage in the z-direction. This simplification may not only overestimate the energy release rate and underestimate the fracture initiation threshold, but also smooths out local pore pressure peaks and permeability evolution, and is unable to fully capture three-dimensional effects such as fan-shaped crack branching, wing crack twisting, and shear slip. Therefore, while the 2D model offers advantages in mechanistic analysis and computational efficiency, its quantitative conclusions (e.g., critical water pressure, crack propagation resistance, and seepage flux) still require correction through thickness corrections, supplementary three-dimensional numerical analysis, or calibration with physical experiments.

Due to the complex multi-physics synergy involved in the actual unloading-seepage process, which includes high pressure, variable confining pressure, and seepage, the experimental apparatus and measurement techniques are highly complex. The conclusions from the unloading numerical example in this paper are of methodological significance, but they still require experimental corroboration at a quantitative level. In future research, we first plan to employ servo-controlled triaxial unloading paths, coupled with high-precision monitoring of pore pressure/seepage and combined observation using digital image correlation (DIC) and Acoustic emission (AE), to capture the real-time evolution of crack propagation and permeability. Subsequently, the evolution laws of parameters such as damage, permeability, and the Biot coefficient will be systematically determined to calibrate and upgrade the phase-field model, particularly concerning crack-tip energy dissipation, the anisotropy of the permeability tensor, and the fluid-solid coupling coefficient. Finally, preliminary tests will be conducted on standard ϕ50 mm sandstone specimens, and the test results will be compared with the numerical simulation results for comparison and cross-validation.

6 Conclusion

In this study, a hydro-mechanical coupled phase-field numerical simulation method was developed, and a hydro-mechanical coupled unloading model for fractured rock was established. The following conclusions were drawn:

(1) The propagation of hydraulic fractures is mainly governed by tensile mechanisms, whereas in the process of hydro-mechanical coupled unloading failure, the propagation and coalescence of mixed-mode (tensile-shear) cracks dominate the final failure mode.

(2) Water exhibits a deteriorating effect on rock, reducing the peak deviatoric stress required for fracture propagation.

(3) Both the initial confining pressure and the initial unloading stress state have a restraining effect on tensile failure during the specimen failure process. As either parameter increases, the required peak deviatoric stress also increases.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MK: Conceptualization, Writing – review and editing. CL: Writing – original draft. YW: Funding acquisition, Writing – review and editing. FL: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the Open Fund of the State Key Laboratory of Water Resource Protection and Utilization in Coal Mining (Grant No. GJNY-21-41-04) and Shandong Provincial Natural Science Foundation (Grant No. ZR2023QE136).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, S., Rizvi, Z. H., Arp, J. C. C., Wuttke, F., Tirth, V., and Islam, S. (2021). Evolution of temperature field around underground power cable for static and cyclic heating. Energies 14 (23), 8191. doi:10.3390/en14238191

CrossRef Full Text | Google Scholar

Ahmad, S., Ahmad, S., Akhtar, S., Ahmad, F., and Ansari, M. A. (2025a). Data-driven assessment of corrosion in reinforced concrete structures embedded in clay dominated soils. Sci. Rep. 15 (1), 22744. doi:10.1038/s41598-025-08526-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, S., Rizvi, Z. H., and Wuttke, F. (2025b). Unveiling soil thermal behavior under ultra-high voltage power cable operations. Sci. Rep. 15 (1), 7315. doi:10.1038/s41598-025-91831-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G. B., Tang, W., Chen, S. J., Wang, E. R. Y., Wang, C. Y., Li, T., et al. (2025a). Damage effect and deterioration mechanism of mechanical properties of fractured coal-rock combined body under water-rock interaction. Rock Mech. Rock Eng. 58 (1), 513–537. doi:10.1007/s00603-024-04163-3

CrossRef Full Text | Google Scholar

Chen, X. S., He, Q. F., Qiu, J. S., Wang, L., Su, D., Liu, M. L., et al. (2025b). Simultaneous construction of subways and utility tunnels: a case project in Shenzhen, China. Tunn. Undergr. Space Technol. 158, 106421. doi:10.1016/j.tust.2025.106421

CrossRef Full Text | Google Scholar

Cheng, P. P., Zhu, H. H., Zhang, Y. M., Jiao, Y., and Fish, J. (2022). Coupled thermo-hydro-mechanical-phase field modeling for fire-induced in concrete. Comput. Methods Appl. Mech. Eng. 389, 37. doi:10.1016/j.cma.2021.114327

CrossRef Full Text | Google Scholar

Dehghan, A. N., Goshtasbi, K., Ahangari, K., Jin, Y., and Bahmani, A. (2017). 3D numerical modeling of the propagation of hydraulic fracture at its intersection with natural (Pre-existing) fracture. Rock Mech. Rock Eng. 50 (2), 367–386. doi:10.1007/s00603-016-1097-7

CrossRef Full Text | Google Scholar

Ehlers, W., and Luo, C. Y. (2017). A phase-field approach embedded in the Theory of Porous Media for the description of dynamic hydraulic fracturing. Comput. Methods Appl. Mech. Eng. 315, 348–368. doi:10.1016/j.cma.2016.10.045

CrossRef Full Text | Google Scholar

Ehlers, W., and Luo, C. Y. (2018). A phase-field approach embedded in the Theory of Porous Media for the description of dynamic hydraulic fracturing, Part II: the crack-opening indicator. Comput. Methods Appl. Mech. Eng. 341, 429–442. doi:10.1016/j.cma.2018.07.006

CrossRef Full Text | Google Scholar

Gao, J. Y., Peng, S. Y., Chen, G. Q., Mitani, Y., and Fan, H. Y. (2023). Coupled hydro-mechanical analysis for water inrush of fractured rock masses using the discontinuous deformation analysis. Comput. Geotechnics 156, 105247. doi:10.1016/j.compgeo.2023.105247

CrossRef Full Text | Google Scholar

Ghaderi, A., Taheri-Shakib, J., and Nik, M. A. S. (2018). The distinct element method (DEM) and the extended finite element method (XFEM) application for analysis of interaction between hydraulic and natural fractures. J. Petroleum Sci. Eng. 171, 422–430. doi:10.1016/j.petrol.2018.06.083

CrossRef Full Text | Google Scholar

Heider, Y. (2021). A review on phase-field modeling of hydraulic fracturing. Eng. Fract. Mech. 253, 107881. doi:10.1016/j.engfracmech.2021.107881

CrossRef Full Text | Google Scholar

Heider, Y., and Markert, B. (2017). A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech. Res. Commun. 80, 38–46. doi:10.1016/j.mechrescom.2016.07.002

CrossRef Full Text | Google Scholar

Heider, Y., Reiche, S., Siebert, P., and Markert, B. (2018). Modeling of hydraulic fracturing using a porous-media phase-field approach with reference to experimental data. Eng. Fract. Mech. 202, 116–134. doi:10.1016/j.engfracmech.2018.09.010

CrossRef Full Text | Google Scholar

Hu, D. W., Zhou, H., Zhang, F., and Shao, J. F. (2010). Evolution of poroelastic properties and permeability in damaged sandstone. Int. J. Rock Mech. Min. Sci. 47 (6), 962–973. doi:10.1016/j.ijrmms.2010.06.007

CrossRef Full Text | Google Scholar

Jiang, M. J., Niu, M. Y., Zhang, F. G., Wang, H. N., and Liao, Z. W. (2022). Instability analysis of jointed rock slope subject to rainfall using DEM strength reduction technique. Eur. J. Environ. Civ. Eng. 26 (10), 4664–4686. doi:10.1080/19648189.2020.1864477

CrossRef Full Text | Google Scholar

Li, M., and Liu, X. S. (2021). Experimental and numerical investigation of the failure mechanism and permeability evolution of sandstone based on hydro-mechanical coupling. J. Nat. Gas Sci. Eng. 95, 104240. doi:10.1016/j.jngse.2021.104240

CrossRef Full Text | Google Scholar

Li, H., Lei, H. W., Yang, Z. J., Wu, J. Y., Zhang, X. X., and Li, S. D. (2022). A hydro-mechanical-damage fully coupled cohesive phase field model for complicated fracking simulations in poroelastic media. Comput. Methods Appl. Mech. Eng. 399, 115451. doi:10.1016/j.cma.2022.115451

CrossRef Full Text | Google Scholar

Liu, S. J., Wang, Z. Q., Zhang, Y. J., Kou, M. M., and Bi, J. (2022). The phase-field simulations of blasting failure in granites. Int. J. Impact Eng. 167, 104274. doi:10.1016/j.ijimpeng.2022.104274

CrossRef Full Text | Google Scholar

Liu, S. F., Wang, W., Jia, Y., Bian, H. B., and Shen, W. Q. (2024). Modeling of hydro-mechanical coupled fracture propagation in quasi-brittle rocks using a variational phase-field method. Rock Mech. Rock Eng. 57 (9), 7079–7101. doi:10.1007/s00603-024-03896-5

CrossRef Full Text | Google Scholar

Liu, J. P., Yang, Z. Z., Yi, L. P., Yi, D., and Li, X. G. (2025). Coupled thermo-hydro-mechanical cohesive phase-field model for hydraulic fracturing in deep coal seams. Appl. Math. Mechanics-English Ed. 46 (4), 663–682. doi:10.1007/s10483-025-3236-7

CrossRef Full Text | Google Scholar

Miehe, C., Hofacker, M., and Welschinger, F. (2010). A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 199 (45-48), 2765–2778. doi:10.1016/j.cma.2010.04.011

CrossRef Full Text | Google Scholar

Mikelic, A., Wheeler, M. F., and Wick, T. (2015). Phase-field modeling of a fluid-driven fracture in a poroelastic medium. Comput. Geosci. 19 (6), 1171–1195. doi:10.1007/s10596-015-9532-5

CrossRef Full Text | Google Scholar

Özdemír, M., Beyhan, S., and Özgür, A. (2025). Evalution of the relationship between capillary water absorption and physical-mechanical properties of some sedimentary rocks. Acta Geodyn. Geomaterialia 22 (1), 27–40. doi:10.13168/agg.2025.0003

CrossRef Full Text | Google Scholar

Rizvi, Z. H., Mustafa, S. H., Sattari, A. S., Ahmad, S., Furtner, P., and Wuttke, F. (2020). “Dynamic lattice element modelling of cemented geomaterials,” in Advances in computer methods and geomechanics. Editors A. Prashant, A. Sachan, and C. S. Desai (Singapore: Springer Singapore), 655–665.

CrossRef Full Text | Google Scholar

Wang, J. C., Dong, L. J., and Ji, S. Y. (2025). Rock mass instability early warning model: a case study of a high and steep annular slope mining areas using Sen's slope trend analysis. Tunn. Undergr. Space Technol. 159, 106514. doi:10.1016/j.tust.2025.106514

CrossRef Full Text | Google Scholar

Xing, J. Q., and Zhao, C. (2023). A hydro-mechanical phase field model for hydraulically induced fractures in poroelastic media. Comput. Geotechnics 159, 105418. doi:10.1016/j.compgeo.2023.105418

CrossRef Full Text | Google Scholar

Yan, C. Z., Fan, H. W., Huang, D. R., and Wang, G. (2021). A 2D mixed fracture-pore seepage model and hydromechanical coupling for fractured porous media. Acta Geotech. 16 (10), 3061–3086. doi:10.1007/s11440-021-01183-z

CrossRef Full Text | Google Scholar

Yi, L. P., Waisman, H., Yang, Z. Z., and Li, X. G. (2020). A consistent phase field model for hydraulic fracture propagation in poroelastic media. Comput. Methods Appl. Mech. Eng. 372, 113396. doi:10.1016/j.cma.2020.113396

CrossRef Full Text | Google Scholar

Yu, X. Y., Xu, T., Heap, M., Zhou, G. L., and Baud, P. (2018). Numerical approach to creep of rock based on the numerical manifold method. Int. J. Geomechanics 18 (11), 04018153. doi:10.1061/(asce)gm.1943-5622.0001286

CrossRef Full Text | Google Scholar

Zhang, J. R., Huang, Y. H., Yan, Z. J., Liu, J. B., and Sun, W. H. (2025). Influence of shallow-buried bias tunnel unloading on the longitudinal displacement of the underlying tunnel. Transp. Res. Rec. 2679 (5), 522–535. doi:10.1177/03611981241312217

CrossRef Full Text | Google Scholar

Zhao, C. X., Zhang, Z. X., and Lei, Q. H. (2021a). Role of hydro-mechanical coupling in excavation-induced damage propagation, fracture deformation and microseismicity evolution in naturally fractured rocks. Eng. Geol. 289, 106169. doi:10.1016/j.enggeo.2021.106169

CrossRef Full Text | Google Scholar

Zhao, Z. H., Xu, J. Y., Yuan, J. H., Chang, W. Y., and Guo, G. H. (2021b). Investigation of cusp catastrophe model of rock slope instability with general constitutive equations. Bull. Eng. Geol. Environ. 80 (1), 303–315. doi:10.1007/s10064-020-01946-0

CrossRef Full Text | Google Scholar

Zhou, S. W., Zhuang, X. Y., and Rabczuk, T. (2018). A phase-field modeling approach of fracture propagation in poroelastic media. Eng. Geol. 240, 189–203. doi:10.1016/j.enggeo.2018.04.008

CrossRef Full Text | Google Scholar

Zhou, S. W., Zhuang, X. Y., and Rabczuk, T. (2019). Phase-field modeling of fluid-driven dynamic cracking in porous media. Comput. Methods Appl. Mech. Eng. 350, 169–198. doi:10.1016/j.cma.2019.03.001

CrossRef Full Text | Google Scholar