Enhancing snow depth estimation with snow cover geometrical descriptors

Snow depth (SD) estimations are very valuable in particular for snow-hydrological modelling, water resource management, ecological studies, and natural hazard assessment such as avalanche forecasting. In statistical SD models, snow-covered area is often used as a source of information. This study explores whether including additional snow cover geometrical descriptors, i.e., the second and third Minkowski functionals: total perimeter (MF2) and Euler-Poincaré characteristic (MF3), improves SD estimation. We performed two different SD simulation setups employing a Random Forest regression framework in the Tuolumne River Basin, California, U.S., at a 500 m resolution. We used the high-resolution remote sensing-derived SD maps of the multi-year Airborne Snow Observatory (ASO) dataset (2013–2016) at a 3 m spatial resolution for model development regarding the geometrical descriptors and evaluation regarding SD. In the baseline setup (BL-MF1), we trained the model with fractional snow-covered area, being the first Minkowski functional (MF1), topographic, and geographic variables. In the enhanced setup (EN-MF123), we also applied MF2 and MF3. Model performance, assessed by using R², RMSE, MAE and MBE was compared between the enhanced model run including MF2 and MF3 and the baseline simulation. Results show that adding MF2 and MF3 (R² = 0.87, RMSE = 0.17 cm, MAE = 0.10, MBE = 0.00) consistently improves model accuracy across diverse snow conditions and topographies compared to the baseline (R² = 0.85, RMSE = 0.19 cm, MAE = 0.11, MBE = 0.00), however, with both variants performing in general well. The inclusion of the additional descriptors was beneficial in late-season melt conditions and fragmented snow cover areas, as the spatial structure captured by the geometrical descriptors improved prediction accuracy and reducing overestimation errors. However, the largest improvements were observed in deep, homogeneous snow cover areas where traditional predictors showed less variability. The methodology shows potential for enhancing snow-hydrological and avalanche risk models, with future work exploring its scalability across different mountain environments and spatial resolutions including different remote sensing products, and applicability to snow water equivalent estimation.

1 Introduction

Seasonal snow can cover up to approximately one-third of the Earth’s land surface, making it one of the most temporary yet crucial natural water reservoirs (Dayal et al., 2023). It is an established fact that the meltwater from this region plays a vital role in sustaining forelands and large river systems (Castellazzi et al., 2019; Nienow et al., 2017; Flett et al., 2017). This, in turn, provides support for the livelihoods of billions of people worldwide (Viviroli et al., 2007). Snow-covered area (SCA), snow depth (SD), and snow water equivalent (SWE) are considered essential climate variables and serve as key indicators for climatology, hydrology, and ecology. The use of long-term records is essential for the identification of trends, particularly important within mountainous regions (Safavi et al., 2017). It is evident that alterations in snow cover properties and shifts in precipitation seasonality significantly affect runoff timing, ecosystem dynamics, and avalanche risk (Lebiedzinski and Fürst, 2018; Callaghan et al., 2011). In recent decades, both the extent and the duration of snow cover in mountain regions have been subject to a general decline, with significant regional variations (Hock et al., 2019; Thackeray et al., 2019; Notarnicola, 2020). Combined with ongoing glacier retreat, these changes are expected to substantially impact mountain hydrology and water security in the coming decades (Kuttippurath et al., 2024; Deng et al., 2019; Huss et al., 2017).

In response to these challenges, consistent and spatially extensive snow monitoring has become necessary (Gascoin et al., 2024; Tsai et al., 2019). The field of operational satellite remote sensing has witnessed considerable advancements in this respect, offering a range of products with high temporal resolution and global coverage. These products, including binary and fractional SCA, have been available for over 2 decades, largely facilitated by the MODIS (Hall et al., 2002) and the subsequent VIIRS. More recently, high-resolution datasets from the Landsat and Sentinel-2 missions have become freely accessible (Gascoin et al., 2019), albeit with lower temporal frequency than MODIS. The use of satellite-based observations in the context of large-scale snow monitoring has been demonstrated to be of considerable importance (Helbig et al., 2021; Dong, 2018).

However, in contrast to SCA, freely available satellite-derived SD and SWE products remain scarce, particularly in mountainous regions and at high spatial and temporal resolutions (Gascoin et al., 2024). Consequently, there is an increasing demand for precise SD data (Deschamps-Berger et al., 2020; Lievens et al., 2019; Painter et al., 2016), particularly to support hydrological modelling and water resource management, but also for other purposes, e.g., to support avalanche forecasting (Richter et al., 2021) and ecosystem monitoring (Pauli et al., 2013; Revuelto et al., 2022). Numerous studies have sought to estimate SD and SWE indirectly through a combination of terrestrial and remote observations, such as those obtained from drones, satellites, and aircraft (McGrath et al., 2022; Jenssen and Jacobsen et al., 2021). These observations have been integrated through photogrammetry, radar, or LiDAR methods, and those datasets are frequently utilized in conjunction with physically based or empirical snowpack models and data assimilation techniques (Alonso-Gonzàlez et al., 2022; Girotto et al., 2024).

In light of the persistent lack of spatially distributed SD data with fine temporal and spatial resolution in many mountainous areas, especially during snowmelt, statistical and machine learning approaches have emerged as practical alternatives to physically-based models, which require high-quality meteorological input that is often unavailable. Earth Observation data combined with machine learning techniques has shown great potential in supporting large-scale and continuous SD and SWE monitoring (Persello et al., 2022). Deep learning models (e.g., convolutional and recurrent neural networks) have proven to be useful in complex image-based hydrological data, although their accuracy remains constrained by the spatial resolution of input data in topographically heterogeneous alpine environments (Elyoussfi et al., 2025; Anderson and Radić, 2022; Lu et al., 2022). A significant advancement was proposed by Daudt et al. (2023), who developed a recurrent convolutional neural network that integrates multispectral optical, SAR, and elevation data for high-resolution SD estimation across Switzerland. Other approaches, such as those by Wang et al. (2022) using deep belief networks and Xing et al. (2022) combining CNNs with residual blocks for the Qinghai-Tibet Plateau, further demonstrate the potential of these methods. Among the various input variables explored, SCA is the most commonly used predictor for estimating SD and SWE, and although challenges remain, current research increasingly aims to develop robust models based on SCA and other satellite observations.

Despite these methodological advances, one important aspect remains largely unexplored in current SD and SWE estimation models: the geometric structure of snow cover patterns. While several studies have highlighted the influence of topographic variables such as slope, elevation, and SD in hydrological processes (Grünewald et al., 2013), few have focused specifically on the geometric structure of snow cover distribution. Early work by Blöschl et al. (1991) demonstrated that snow cover patterns are shaped by both topography and meteorological conditions, and that hydrological processes, such as snowmelt, directly reflect these influences. Their findings indicated that, despite spatial complexity, the fundamental structure of snow cover patterns tend to persist throughout the melt season due to topographic controls. Snow accumulation and melt processes are highly variable across both spatial and temporal scales and are influenced by wind redistribution, gravitational effects, and inter-annual climate variability (Winstral et al., 2013; Clark et al., 2011). In this context, the final spatial distribution of snow at the end of the accumulation season plays a critical role in determining hydrological responses in alpine basins (Freudiger et al., 2017; Liston, 2004), as heterogeneity in SD, combined with meteorological forcings, drives asynchronous melt patterns, faster runoff from shallow areas, and prolonged melt in deeper zones (Brauchli et al., 2017). Ferrarin et al. (2023) introduced the use of geometrical descriptors, i.e., Minkowski Functionals (MF) and average chord length distributions, to characterize snow cover patterns in the Zugspitze catchment (Germany), linking geometric features of snow cover to topography and seasonal dynamics. Their results suggest that incorporating such geometrical descriptors alongside in situ observations or modelling frameworks could improve spatial SWE estimation in high-alpine environments. These findings suggest that adding geometrical descriptors to the existing set of predictors (with SCA being the most widely used) could enhance current semi-empirical and machine learning models, which frequently rely predominantly on fractional snow-covered area as an input.

To address this gap, in this study we investigate the impact of incorporating two specific snow cover geometrical descriptors (describing features of the topological structure of snow cover patterns) into predictive, statistically-based models for estimating SD in mountainous terrain. Specifically, we examine whether including the second and third MF, respectively the total perimeter of snow cover boundaries (MF2) and the Euler-Poincaré characteristic (MF3), improves model accuracy. The research utilizes high-resolution remote sensing-derived SD and thereof derived snow cover maps. A predictive model setup for SD based solely on fractional snow-covered area (i.e., MF1), topographic conditions, and seasonal information is compared as a baseline with a model setup that also integrates geometrical descriptors MF2 and MF3. The study aims to determine whether these additional descriptors enhance SD estimation accuracy and to identify the conditions under which their inclusion is most beneficial. Furthermore, we explore the key drivers of these conditions, such as seasonality, snow accumulation, and topographic influences, to better understand the role of snow cover geometric features in SD predictive modelling and give an outlook of potential future next steps.

2 Methods and data

2.1 Study area

The Tuolumne River Basin (Figure 1), located in California’s Sierra Nevada within Yosemite National Park, is a crucial water source for the San Francisco Bay Area in the U.S. (Painter et al., 2016). Covering ca. 1,180 km² with elevations ranging from 1,150 to 3,999 m (Hedrick et al., 2018), it lies upstream of the Hetch Hetchy Reservoir, which supplies drinking water and hydropower to nearly three million residents (Lundquist et al., 2016). The region experiences a Mediterranean climate, with most precipitation falling between November and March. Snow serves as a seasonal reservoir, releasing meltwater in summer when demand is highest. However, large interannual variability results in runoff ranging from below 50% to over 200% of climatological averages, requiring adaptive water management (Lundquist et al., 2003). More than half of the annual precipitation falls as snow, though this varies due to droughts and atmospheric river events (Li et al., 2017; Lahmers et al., 2022; Hedrick et al., 2020; Pflug et al., 2022). Precipitation type varies with elevation: 60% of precipitation falls as rain below 1,600 m; the 1,600–2,000 m range marks the rain-snow transition zone; and above 2,000 m, covering 90% of the basin, snowfall dominates, although summer rain can occur even at high elevations (Lundquist et al., 2016). Vegetation varies with elevation, from deciduous and coniferous forests in lower areas to subalpine and alpine zones above the 2,900 m treeline. The upper 35% of the basin (2,900–3,999 m) consists of sparsely vegetated alpine terrain, where snow distribution is shaped by wind and exposed granodiorite. The basin’s role as a “water tower” has made it a key site for snow-hydrology research (Viviroli et al., 2007; Henn et al., 2018a; Raleigh and Small, 2017; Rice et al., 2011).

Figure 1

Figure 1. Location and relief map of the Tuolumne River Basin within the U.S. State of California.

2.2 Minkowsky functionals as snow pattern predictors

We computed Minkowski Functionals (MF) for each date with snow cover to characterize the spatial structure of snow distribution. MF are mathematical tools used to describe the geometry and connectivity of spatial patterns and have been applied across various disciplines, including soil structure (Vogel et al., 2005) and snow microstructure analysis (Schleef et al., 2014). Recently, they have also been employed to assess snow cover dynamics (Ferrarin et al., 2023). In two-dimensional space, three MF can be defined (Parker et al., 2013):

i. Total Area Density (MF1), which quantifies the proportion of the extent covered by snow in a selected area, and is equivalent to the fractional Snow Covered Area (fSCA);

ii. Total Perimeter Density (MF2), which measures the total length of the boundary between snow-covered and snow-free regions, normalized by the total area. It represents a measure of the complexity of the boundary between snow-covered and snow-free regions: a higher perimeter density indicates a more intricate or irregular snow cover boundary, while a lower value suggests a smoother, more continuous snow cover. This metric helps capture the variability in snow distribution and is useful for assessing the heterogeneity and connectivity of snow-covered areas.

iii. Euler–Poincaré Characteristic Density (MF3), which captures the connectivity of the snow cover. A positive MF3 indicates that the snow cover is fragmented, with isolated snow patches scattered across the area. Conversely, a negative MF3 suggests a more connected snow network, with the absolute value representing the number of internal gaps or holes within the snow cover. This metric is particularly useful for assessing the degree of fragmentation or continuity of snow-covered regions, helping to understand the spatial configuration of snow distribution (Vogel and Babel, 2006). MF3 is given in Equation 1:

$MF3\left(X\right)=\frac{1}{2\pi }{\int }_X\left[\frac{1}{R}\right]dc(1)$

where X is the snow cover pattern, R is the radius of curvature of the circumference of a single snow cover object in the pattern and dc is an infinitesimal element of the circumference (Vogel et al., 2005).

All MF are affected by a saturation effect: they provide meaningful information only when the analysed area includes both snow-covered and snow-free regions. Once snow depth becomes sufficient to completely cover the area, MF1 simply reflects the total extent of the area, while MF2 and MF3 drop to zero.

Figure 2 illustrates examples of MF calculated over four distinct snow cover patterns, each covering an area of 500 m: MF1 (i.e., fractional snow-covered area) increases as the extent of snow cover increases. MF2 (i.e., perimeter of the snow-covered regions) increases when the snow pattern is more fragmented and irregular (i.e., more complex and heterogeneous, Figures 2B,C), and decreases in cases where the snow cover consists of either small, isolated patches (Figure 2A) or forms a large, continuous, and homogeneous area (Figure 2D). MF3 (i.e., Euler-Poincaré characteristic) shows low positive values when there are only a few small and isolated snow patches (Figure 2A), higher positive values appear when there are many disconnected patches (Figure 2B), high negative values when the snow cover is highly heterogeneous but forms a well-connected structure with multiple internal interruptions (Figure 2C), and low negative values in cases of extended, mostly homogeneous snow cover with few discontinuities (Figure 2D).

Figure 2

Figure 2. Examples of different snow cover patterns (500 m extent) and corresponding geometrical descriptors MF1, MF2, and MF3 (A–D).

In this study, MF were calculated using the imMinkowski MATLAB toolbox (Legland, 2025), applied to binary snow cover maps for each available date. All metrics were computed relative to the total extent of the study area and aggregated across the full dataset. Further methodological details and examples of MF application to snow cover can be found in Ferrarin et al. (2023).

2.3 The airborne snow observatory dataset

We used freely available data from the Airborne Snow Observatory (ASO), which combines scanning LiDAR and imaging spectrometry in the study area (Painter, 2018). ASO provided high-resolution maps of SD, SWE, and snow albedo across mountain watersheds from April 2013 to October 2019, supporting both research and operational water management (Painter et al., 2016). For this study, we used the 3 m resolution ASO-derived snow-free digital elevation model (DEM) and SD datasets. SD was calculated by differencing snow-on and snow-off DEMs in non-forested areas, with bias correction applied using snow-free zones set to zero (Painter et al., 2016). ASO performed annual flights from peak SWE through the melt season; we used data from five flights in 2013, eleven in 2014, nine in 2015, and two in 2016. Comparison with 80 in situ manual measurements showed no significant bias, and a RMSE of 0.08 m per 3 m pixel and <0.02 m per 50 m pixel (Painter et al., 2016). Snow cover maps were derived from the SD maps. Further details on ASO instrumentation and processing methodology are provided in Painter et al. (2016).

Overall, the applied ASO dataset is often used to develop and validate modelling and remote sensing products due to their high temporal and spatial availability of SD data over a quite large area over several years. Recently, numerous studies have used the ASO dataset to analyse snow cover dynamics and improve water resources management. Deschamps-Berger et al. (2020) used it for example, to validate stereo-satellite derived and Sourp et al. (2025) to evaluate it against high-resolution snowpack simulations from global datasets and a comparison with Sentinel-1 SD retrievals. Pinder et al. (2024) employed neural network-based forecasting models using ASO data to predict snow water equivalent by considering SD and density. Several studies reconstructed continuous space-time estimates for SWE based on the dataset applying different techniques such as physically-based modelling, data assimilation and machine learning techniques (e.g., Margulis et al., 2019; Oaida et al., 2019; Painter et al., 2016; Premier et al., 2023; Smyth et al., 2020). Henn et al. (2018b) combined ASO LiDAR-derived snow data with streamflow observations to estimate basin-scale water balance and assess processes such as snowmelt, infiltration, and evapotranspiration during drought conditions.

We employ the ASO dataset to derive two distinct types of variables for the construction of the predictive models:

i. SD distribution resampled to a 500-m resolution and utilized as the dependent variable for model calibration and validation. The resampling is necessary because the MF are area-based metrics therefore they relate to the cell-mean SD of the grid used for their computation (further details on the selected resolution are provided in the next section). Two examples are shown in Figure 3A for peak snow cover conditions (left, 29/4/2013) and for minimum snow cover conditions (right, 8/6/2013).

ii. Binary snow cover maps, derived from the native 3-m resolution snow height data, from which the MF were computed on the 500-m grid as predictor variables. Figure 3B shows two examples of snow cover maps for peak (left) and minimum (right) snow cover conditions (same dates as Figure 3A), and Figure 3C shows examples of 500 m extents used for the computation of MF in three separate locations (P1, P2, P3).

Figure 3

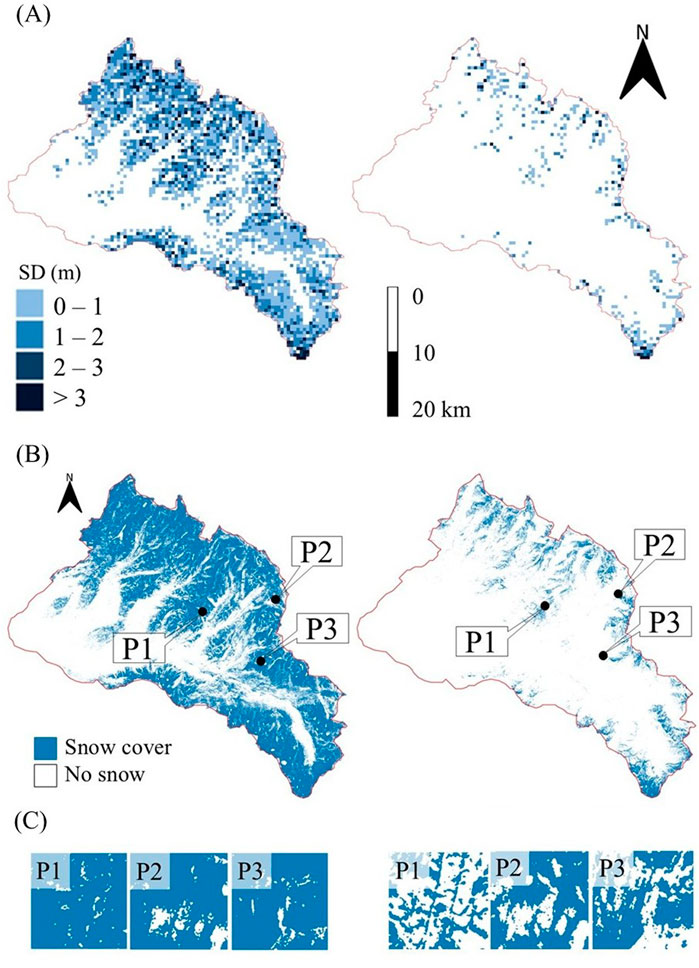
Figure 3. (A) 500 m resolution snow depth map examples of left: peak snow-cover conditions, acquired on 29/04/2013, and right: low snow cover conditions, acquired on 08/06/2013. (B) 3 m resolution snow cover map examples of left: peak snow cover conditions, acquired on 29/04/2013, 50.8% of total snow coverage, and right: low snow cover conditions, acquired on 08/06/2013, 8.0% of total snow coverage. (C) Examples of snow cover patterns of 500 m × 500 m extents used to compute the MF in different locations (P1, P2, P3). White areas represent no snow cover in all plots.

2.4 Snow depth model setup using a random forest approach

For SD modelling, we adopted the Random Forest (RF) algorithm (Breiman, 2001), an ensemble learning method that aggregates the predictions of multiple regression trees to reduce variance and improve generalization (Guo et al., 2011). Each tree is trained on a bootstrap sample, i.e., a subset of the original data generated by sampling with replacement (bagging), which contains two-thirds of the original observations. The remaining one-third, known as out-of-bag (OOB) samples, are not used in training and serve as an internal validation set to estimate an unbiased generalization error (Breiman, 2001; Peters et al., 2007). At each node, RF does not evaluate all available predictors but instead selects a random subset of size m_try. The best split is chosen only among this subset, which reduces correlation among trees while maintaining predictive strength.

Splits are chosen by maximizing the reduction in impurity, given by the ratio between the weighted variance and the Mean Squared Error (MSE). For a parent node $t$ split into children $t_L$ and $t_R$ on predictor $x_j$, the reduction in impurity can be calculated as:

$\Delta \left(t,x_j\right)=p\left(t\right)*MSE\left(t\right)-\left[\right(\left.p\left(t_L\right)*MSE\left(t_L\right)+p\left(t_R\right)*MSE\left(t_R\right)\right](2)$

Where $p\left(·\right)$ is the empirical node probability (Louppe et al., 2013). The reduction Δ is the basis for the importance scores (Section 3.2).

The ensemble prediction is then obtained by averaging the outputs of all trees in the forest. Random Forest was selected because it has been applied effectively to related cryospheric and snow-mapping problems (e.g., Revuelto et al., 2020; Yang et al., 2020; Meloche et al., 2022) and is well suited to capture non-linear relationships and interactions among multi-source predictors while remaining robust to noise and collinearity. More detailed on the RF method are given in the supplementary. For further details on the mathematical procedure used see Breiman (2001).

Two user-defined parameters are central to the algorithm: the number of trees (n_tree) and the number of variables considered at each split (m_try) (Rodriguez-Galiano et al., 2012). As the number of trees increases, the generalization error converges to a limiting value, preventing overfitting. In practice, a sufficiently large n_tree ensures stability, while m_try controls the trade-off between tree correlation and individual tree strength. Reducing m_try tends to decrease correlation between trees but may also weaken their predictive power; hence, an optimal balance must be sought (Breiman, 1996). For the RF algorithm in this study, n_tree was set to 500: this value was selected based on preliminary tests in which increasingly higher numbers of trees, typically used in literature for similar analysis, were evaluated, and performance gains from increasing the number of trees became negligible above this threshold. The parameter m_try was set to 4, consistent with the default setting of p/3, where p is the total number of predictors, 13 in this study.

Model robustness was evaluated using a simple cross-validation approach. Specifically, models were trained on 100 randomly selected subsets (according to Filzmoser et al., 2009), each comprising 70%–80% of the dataset while ensuring high spatial and temporal variability. The calibration-to-validation ratio was chosen based on values commonly adopted in similar applications, as reported in recent literature (e.g., Khosravi et al., 2023; Blandini et al., 2023), where 70/30 or 80/20 partitions are frequently used to balance training representativeness and validation reliability. The subsets were drawn by randomly sampling individual grid cells rather than entire geographic sub-regions, thereby minimising potential biases associated with distinctive local topographic or climatic conditions; this strategy, well established in literature (e.g., Ma et al., 2023; Blandini et al., 2023), ensures the model is calibrated and validated across a wide spectrum of conditions, avoiding cluster-specific over- or under-representation. With this configuration, every cell of the grid was included at least once in the validation group. To test the sensitivity of model performance to training set variability, additional experiments were conducted using up to 200 randomly selected subsets. The results obtained with this expanded sampling scheme did not significantly differ from those of the initial configuration, confirming the robustness of the model performance observed in the previous analysis; Given that an increase in the number of subsets results in a proportional increase in computational time, it was decided to limit the analysis to 100 subsets.

RF provides a measure of feature importance, which is particularly useful in studies involving heterogeneous data sources (Pal, 2005). This is quantified by permuting the values of each predictor and evaluating the resulting increase in OOB error (Breiman, 2001; Gislason et al., 2006). Features that cause a larger drop in accuracy are considered more relevant to the model. This property is of particular interest in environmental modelling, where multiple interacting predictors are often available and their relative contributions are not known a priori.

To evaluate the influence of the MF 2 and MF3, two RF models were developed for this study:

i. A baseline model (BL-MF1) incorporating fractional snow cover (MF1), topographic predictors, i.e., elevation (mean and standard deviation), slope (mean and standard deviation), curvature (profile, plan, and tangential), North/South and East/West exposition (mean values), Topographic Position Index (TPI, Wilson and Gallant, 2000), Terrain Roughness Index (TRI, Amatulli et al., 2018), Wind Shelter index (WSI, Winstral et al., 2002), latitude, longitude, distance from the coast, and month.

ii. An enhanced model (EN-MF123) that also includes two snow-cover geometrical descriptors, MF2 (total perimeter) and MF3 (connectivity and fragmentation), to assess the impact of snow cover geometric structure on SD estimation and evaluate whether their inclusion improves predictive performance. Predictors included in the two setups are shown in Table 1.

Table 1

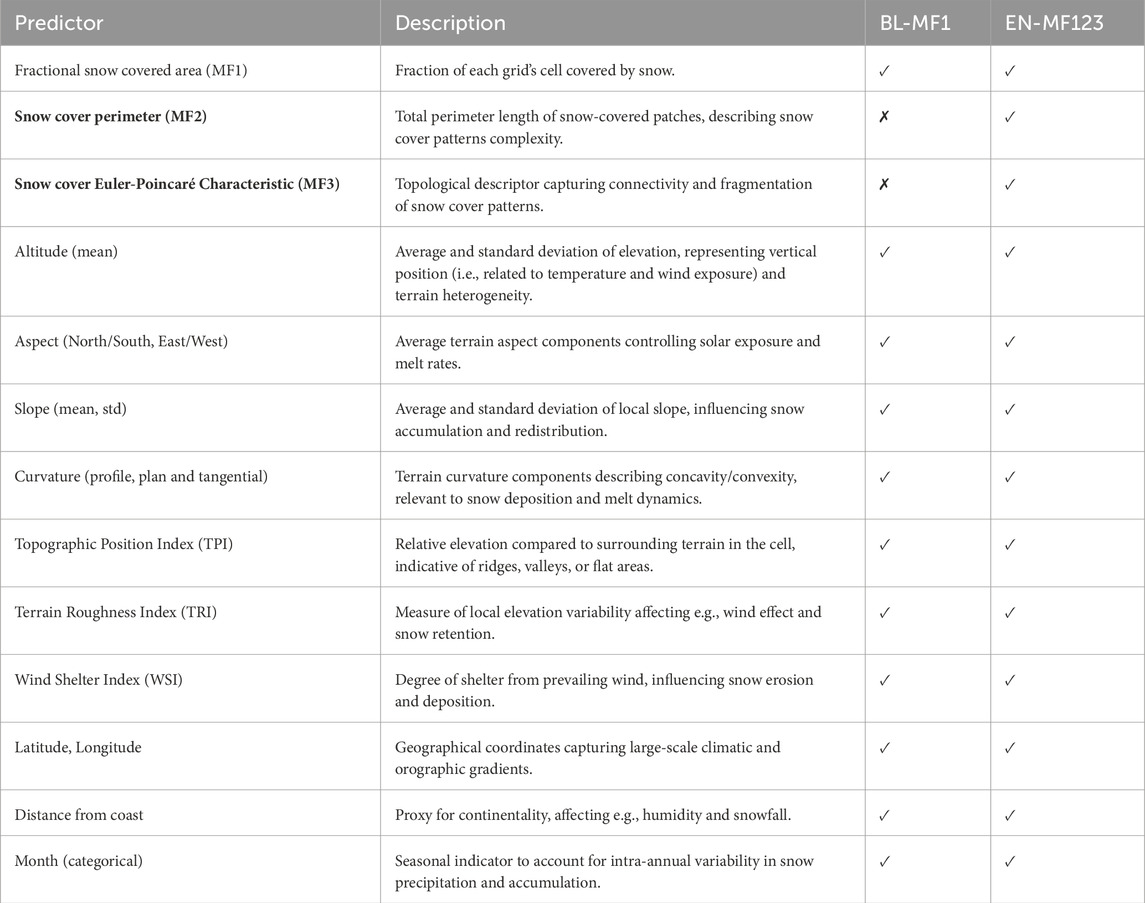
Table 1. Overview of predictor variables included in the baseline (BL-MF1) and enhanced (EN-MF123, including MF2 and MF3 as predictors) random forest models. All predictors were computed on a 500 m grid resolution over the study domain.

All predictors were computed on a 500 m resolution grid covering the entire study area.

The model specification was identical for both cases. SD was aggregated to a 500 m grid, and all topographic predictors were resampled to the same resolution. The MF, being area-based metrics, were computed on the 3 m snow cover maps, over the same 500 m cells. This ensures a one-to-one correspondence between the geometric descriptors of the snow-cover pattern, the cell-average SD, and the underlying topographic attributes, all defined on the same spatial support.

A spatial resolution of 500 m was adopted in this study due to its frequent application in snow cover research (Yang et al., 2022; Zhu et al., 2021; Schneider et al., 2020), thereby ensuring methodological consistency with previous literature and interoperability with satellite-derived products (e.g., Ferrarin et al., 2023). This resolution provides a balanced trade-off between computational efficiency and the capacity to resolve physiographic and snowpack heterogeneity. Moreover, it enables the integration of multiple geospatial datasets while retaining sufficient granularity for the characterization of snow cover geometric structure and the estimation of SD. To validate this choice, a sensitivity analysis was conducted during the preliminary phase of the study, evaluating three spatial resolutions: 250 m, 500 m, and 1 km. Stepwise linear regression revealed that R² and relative contribution of the geometrical descriptors MF2 and MF3 in the predictive model, increased with decreasing spatial resolution (e.g., coarser grids). Consequently, the 500 m resolution was selected as an optimal compromise, offering adequate spatial fidelity for SD representation while maximizing the effectiveness of MF. Ferrarin et al. (2023) also employed a 500 m spatial scale in their correlation analysis between MF indices and SWE.

2.5 Model evaluation

To evaluate the impact of including MF2 and MF3 in SD estimation models, we analysed the following standard performance metrics: the coefficient of determination (R²), which quantifies the proportion of the observed variance explained by the model; the Root Mean Square Error (RMSE), which measures the typical magnitude of prediction errors and is sensitive to large deviations; the Mean Bias Error (MBE), which indicates the average tendency of the model to overestimate or underestimate observations; and the Mean Absolute Error (MAE), which represents the average absolute difference between simulated and observed values, providing a robust measure of overall accuracy.

To obtain a robust estimate of the influence of MF2 and MF3, we examined the distributions of R, RMSE, MBE and MAE across the two models, trained on the 100 different random subsets of the dataset. To assess the statistical significance of performance differences, we applied the Wilcoxon paired test (Wilcoxon, 1945) to compare the results from EN-MF123 and BL-MF1 models. As a non-parametric test, it does not require assumptions of normality and evaluates differences based on ranked pairs. This approach allowed us to determine whether the inclusion of MF2 and MF3 leads to significant improvements in SD prediction performance.

Secondly, we restricted the analysis to R² and RMSE, and we investigated how these metrics change over time and across different snow-cover pattern conditions as well as different topographic conditions. The focus was placed on these two metrics, because together they capture the most relevant aspects of model performance for snow depth estimation in a hydrological modelling context (variance explained and magnitude of errors). MBE was not further considered, as both models exhibit negligible systematic bias, rendering this metric of limited interpretative value. Similarly, MAE was not reported because it exhibited very similar patterns to RMSE. Since no strong outlier effects were observed in the data, the additional information provided by MAE would have been limited, and RMSE alone was considered sufficient for interpretation.

3 Results and discussion

In this chapter we present the evaluation of the two SD model setups: BL-F1 and EN-MF123, focusing on the impact of including MF2 and MF3, the predictor importance, and SD error distributions. Additionally, we examine the temporal dynamics of R² and RMSE, variations in model performance across different snow cover patterns and topographic conditions and addresses the potential limitations of the derived SD models.

3.1 Effect of including MF2 and MF3 on modelling SD

Table 2 reports the average, maximum, and minimum values of each performance metric, computed across all runs of the models over the 100 subsets. Overall, the EN-MF123 model outperforms the BL-MF1 model for all metrics, except for MBE, where no meaningful improvement is observed (average value remains below 10⁻² m for both models). On average, R² increases by 0.02 (2%), while RMSE and MAS decrease by 0.02 m (11%) and 0.01 m (9%), respectively. To assess the statistical significance of these differences, a non-parametric Wilcoxon signed-rank test was applied. The results confirm that the distributions differ significantly at the 95% confidence level, with p-values below 4∙10⁻¹⁸ for both metrics.

Table 2

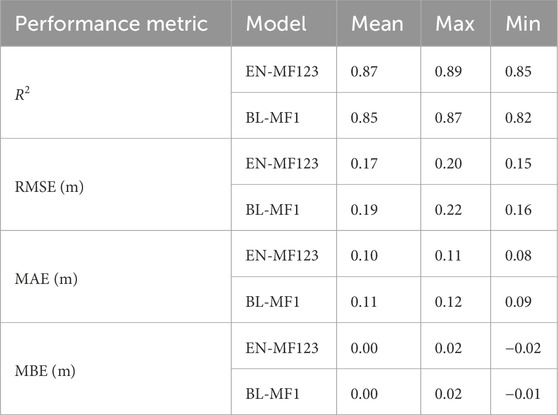
Table 2. Summary statistics of model performance metrics, R², RMSE (m), MAE (m) and MBE (m), computed over 100 random subsets of the dataset. The table reports the mean, maximum, and minimum values for models trained with (EN-MF123) and without MF2 and MF3 (BL-MF1).

The reduction in average RMSE, corresponds to approximately 5% of the mean snow depth across the entire basin. Quantifying the impact of this reduction in terms of SWE would be useful, but it is not straightforward. However, a simple assessment indicates that, assuming an average snow density of 400 kg m⁻³, this reduction corresponds to approximately 6% of the basin-average SWE provided by ASO for the same dates considered in this study (Yang et al., 2025). Moreover, since the absolute reduction in RMSE is 0.02 m, and the RMSE of the ASO snow depth data at 50 m resolution is reported as <0.02 m (Painter et al., 2016), the decrease observed in this study is larger than the intrinsic uncertainty of the reference dataset, which, given the coarser 500 m resolution applied here, is expected to be even smaller, further supporting the significance of the result.

Figure 4 presents the histograms of the performance metrics across the 100 subsets. The inclusion of MF2 and MF3 produces a marked shift in the distributions, with R² moving towards higher values (Figure 4A) and RMSE and MAE shifting towards lower values (Figures 4B,D). MAE shows a stronger decrease compared to RMSE, suggesting that EN-MF123 decreases the overall magnitude of errors more effectively and provides more consistent accuracy across the majority of predictions compared to BL-MF1, while few relatively large errors persist. Histogram of MBE (Figure 4C) shows no differences, indicating that both models exhibit no tendency toward estimation/underestimation and that MF2 and MF3 do not substantially affect this aspect.

Figure 4

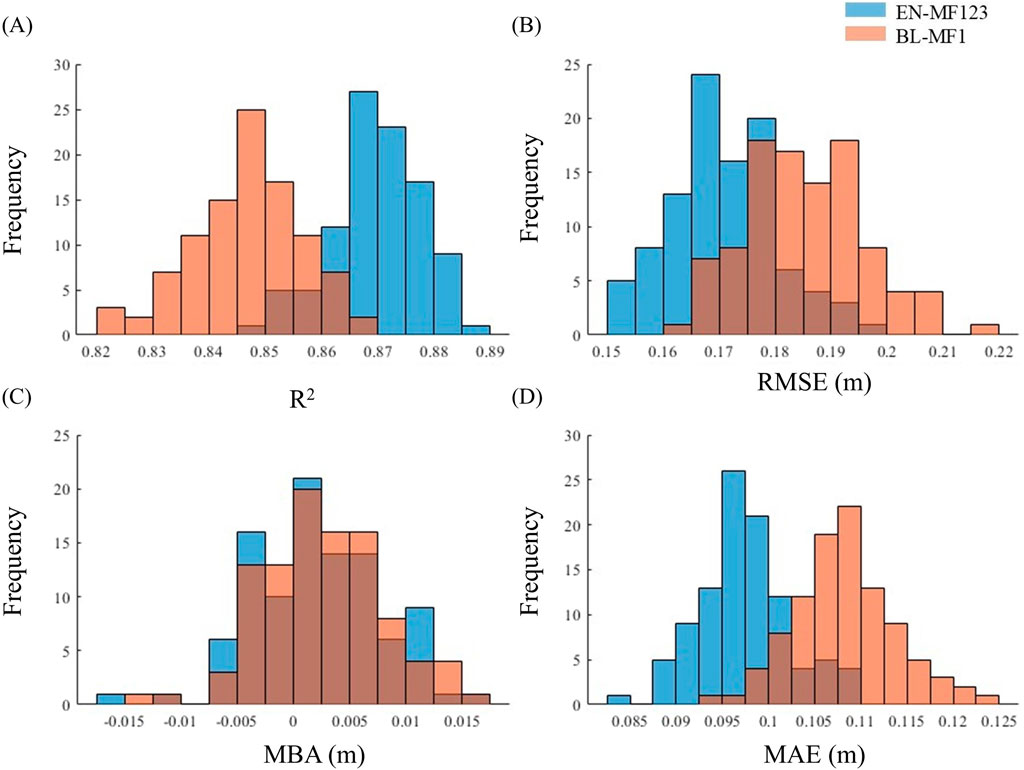
Figure 4. Frequency distributions of (A) R², (B) RMSE (m), (C) MBA (m) and (D) MAE (m) of snow depth estimation models, computed over 100 random subsets of the dataset. Results are shown for models excluding (BL-MF1) and including (EN-MF123) snow cover geometrical descriptors of perimeter (MF2) and Euler-Poincaré Characteristic (MF3).

3.2 Predictors’ importance of the SD model

To further investigate the role of MF in SD prediction, we analysed the relative importance of each predictor used in the models. Predictor importance was computed by evaluating reductions in node risk at each split in the decision trees, where node risk is defined as the node error weighted by node probability (Equation 2). The importance of each predictor was then estimated by summing the reductions in mean squared error due to its splits and normalizing by the total number of branch nodes across the ensemble (Louppe et al., 2013).

Figure 5 shows predictor importance scores for BL-MF1 and EN-MF123. The scores were normalized by dividing each predictor’s score by the sum of all predictor scores for the specific model, so that their total equals 100%, thereby expressing the relative percentage contribution of each predictor. When MF2 and MF3 are excluded, MF1 (fractional snow cover) dominates the model (importance score above 70%), reflecting the strong relationship between snow extent and SD variability. Other predictors contribute only marginally (all below 10%). When MF2 (perimeter density of the snow cover, i.e., heterogeneity of the pattern) and MF3 (Euler–Poincaré characteristic of snow cover, i.e., connectivity or fragmentation of the pattern) are included, they emerge as highly relevant predictors (with an importance score of, in order, 11% and 23%), second only to MF1. Importantly, the importance of MF1 decreases in this case (reaching 50%), suggesting that MF2 and MF3 provide new, non-redundant information that complements the contribution of fractional snow cover. This implies that MF2 and MF3 capture aspects of snow cover spatial structure not represented by MF1, improving model generalization under varying snow conditions. Interestingly, MF3 shows an importance factor which is double the one of MF2; this result suggest the Euler-Poincaré characteristic is more relevant in capturing additional information on snow cover geometric characteristics, compared to the extent of the snow cover boundaries. This may reflect the intrinsic ambiguity of low MF2 values: they can correspond either to nearly homogeneous snow cover with few or small gaps, or to patterns with only a few small snow patches (e.g., Figures 2A,D). By contrast, MF3, because it can take negative as well as positive values, better discriminates between these very different snow-cover condition, providing more predictive information for SD.

Figure 5

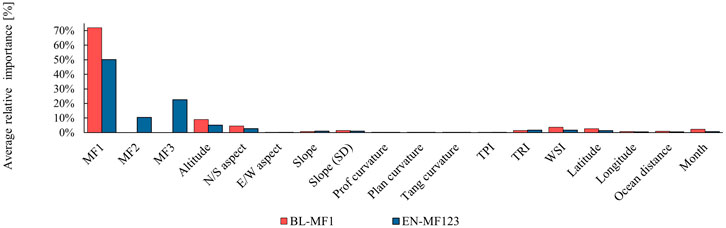
Figure 5. Predictor importance for the SD estimation, for EN-MF123 (blue), and BL-MF1 model (red). Scores are normalized so that their total equals 100%, representing the relative percentage contribution of each predictor to the overall prediction.

Beyond MF predictors, elevation and north-south aspect are the most influential topographic variables and keep their rank whether or not MF2 and MF3 are included. Elevation reflects temperature and precipitation gradients, while aspect controls incoming solar radiation. Next in importance are TRI and WSI, with overall stable rankings, followed by latitude, whose influence on SD is mainly mediated by synoptic and local weather conditions and, to a lesser extent, by its impact on solar radiation. Slope gains importance once MF2 and MF3 are included, suggesting that slope effects are better resolved when the geometric structure of the snow cover is explicitly captured by these descriptors. On the other hand, the temporal predictor “month” drops markedly in importance with MF2 and MF3, implying that these metrics encode richer seasonal signals. East-west aspect, curvature indices, TPI, longitude, and distance to the ocean remain of very low importance in both models, indicating a marginal role for these factors in SD prediction at the scales considered.

3.3 Error distributions of SD estimates

A comparative analysis of the error distributions derived from BL-MF1 model and the enhanced EN-MF123 model was conducted to delineate the SD ranges where MF2 and MF3 most effectively enhance estimation accuracy. Errors were quantified as the difference between observed and predicted SD values. Figure 6 presents histograms showing the frequency distributions of these errors for EN-MF123 model (blue) versus BL-MF1 (red). To facilitate interpretation and emphasize differences around zero, we applied a logarithmic transform of the shifted errors, with the shift being equal to the absolute value of the minimum observed error to ensure positivity. Letting $e_i$ denote the signed error, the corresponding transformed value z_i is:

$z_i=\log \left(e_i\left.+\right|\min \left.\left(e\right)\right|\right)(3)$

This strictly increasing transformation compresses the tails and enhances resolution near zero while preserving the relative ordering of errors and their sign. The results demonstrate that the error distribution for EN-MF123 model is more tightly centred around zero, indicating improved predictive accuracy. Notably, the most significant divergence is observed in the negative error range (i.e., overestimation) where EN-MF123 model exhibits a marked reduction in error frequency compared to models without these descriptors. This reduction in overestimation suggests that the incorporation of snow cover geometric structure via MF2 and MF3 substantively mitigates bias in SD estimation.

Figure 6

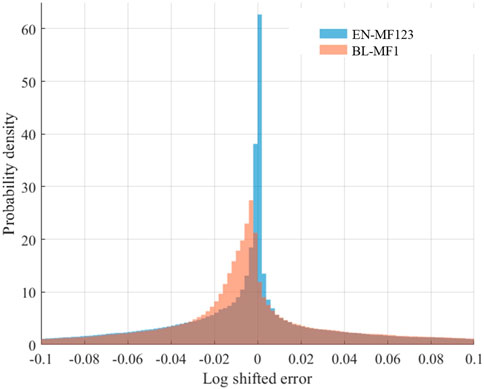
Figure 6. Frequency distribution of SD estimation errors (log-shifted, see Equation 3 for mathematical transformation) for EN-MF123 model (blue) and BL-MF1 (red).

3.4 Temporal dynamics of R2 and RMSE of SD model estimates

In this section we analyse the temporal evolution of the average R² and RMSE of SD estimation models, comparing EN-MF123 model (blue line in Figure 7) with BL-MF1 (red line), during the study period (February-June). Each panel in the figure represents 1 year from 2013 to 2016, and each point corresponds to a prediction date. Overall, model EN-MF123 outperform BL-MF1 in most cases (26 out of 27 dates), as attested by higher R² values and lower RMSE. The time series of both R² and RMSE exhibit a similar temporal pattern. On average, the daily mean R² increases by 0.036, while daily RMSE improves by 0.015 m; the maximum improvement of R2, equal to +0.125, is observed on the 9/4/2015, while maximum improvement of RMSE, equal to −0.038 cm, is observed on the 29/4/2013. The slight decrease in model performance on 23/3/2014, with a reduction of −0.013 in R² and an increase of +0.006 cm in RMSE, can be attributed to the model calibration approach and the specific snow cover conditions on that day. The models were calibrated using subsets spanning the entire study period, ensuring no single day was exclusively used for calibration or validation. This method prevents biases tied to specific days, as the models are optimized for the overall period. Consequently, the performance deterioration on 23/3/2014 is likely due to unique snow cover patterns on that day, which resulted in low correlations between MF2 and MF3 descriptors and SD. The model, calibrated for the entire range of conditions happening between middle-winter to late melting season, does not adapt well to these particular conditions. No significant temporal dependency in R² and RMSE improvements was observed.

Figure 7

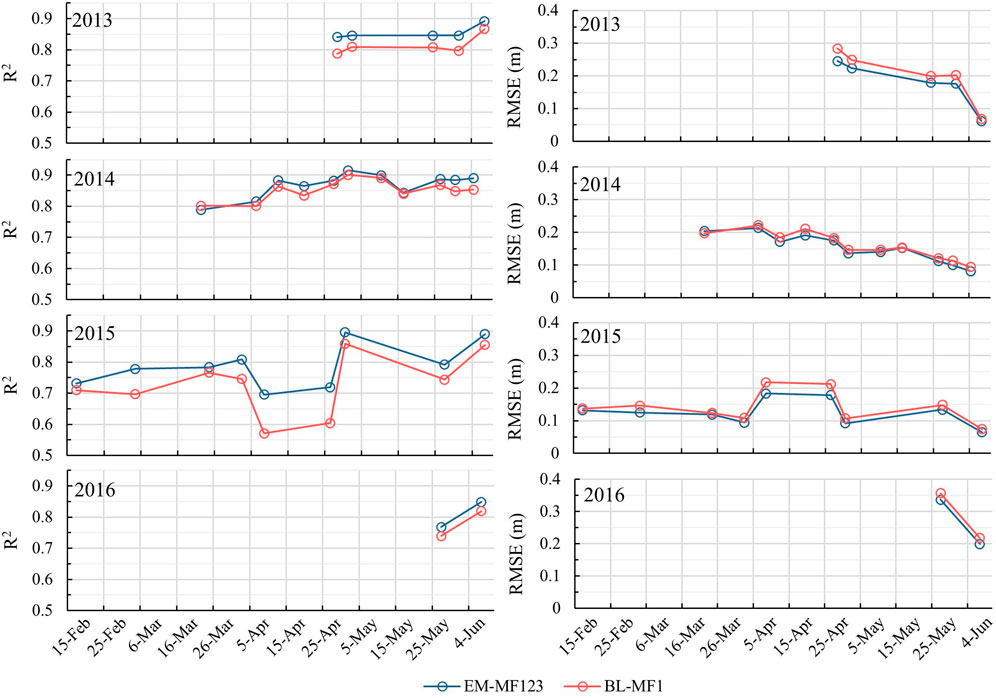
Figure 7. Temporal evolution of R² (left) and RMSE (right) for snow depth estimation models with (blue, EN-MF123) and without (red, BL-MF1) geometrical descriptors MF2 and MF3 across 4 years (2013–2016). Each point represents model performance for a single date.

To better understand the snow cover pattern conditions affecting model performance, Figure 8 illustrates the temporal evolution of mean SD (left) and the three geometrical descriptors (MF1, MF2, MF3, right), for each year from 2013 to 2016 (SD spatial distribution at every recorded date is shown in Figure 1 of the Supplementary). In general, SD and MF show a strong time dependence, which can be observed in 2013, 2014 and, in the few dates where data is available, 2016; for these years SD and MF show also the same range of values. On the other hand, 2015 shows lower values of SD, alongside lower values of MF1 and MF2, and higher values of MF3. These values suggest a particularly dry year, with smaller amount of snow cover in terms of depth and extension, and a higher level of fragmentation (with the exception of April). In particular, MF2 and MF3 exhibit evident seasonal cycles, albeit with interannual phase shifts. This recurrence of melt-season snow-cover patterns under persistent topographic controls supports their utility as SD predictors, consistent with the high predictor-importance scores reported earlier. In addition, we also examined the temporal evolution of the standard deviation of SD (both absolute and relative), but this metric did not reveal clear temporal trends and therefore did not provide additional explanatory value. For this reason, it is not shown among the main results.

Figure 8

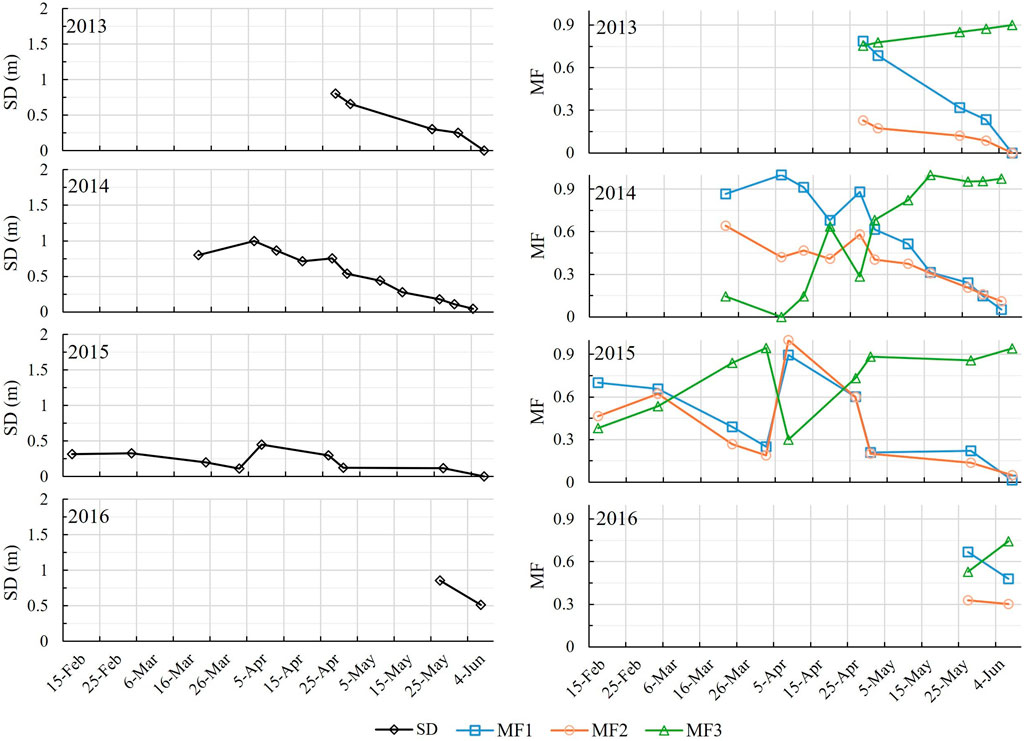
Figure 8. Temporal evolution of the average SD (left) and the three geometrical descriptors (MF1, MF2, MF3, right) for each year from 2013 to 2016.

As expected, the mean SD tends to decrease throughout the study period, from late winter into spring. As the season progresses and melt processes begin, particularly at mid and lower elevations, SD progressively decreases throughout the entire study area, and the terrain becomes increasingly exposed. This exposure gives rise to increasingly fragmented and topographically influenced snow cover patterns. This shift in snow cover complexity is reflected in the model performance: R² values tend to increase, while RMSE values tend to decrease, as the season progresses. This suggests that more complex and heterogeneous snow patterns provide richer spatial cues that can be effectively captured by MF2 and MF3, leading to improved model accuracy. A notable exception to this general trend occurs in 2015 (Figure 8), when two dates in April (9/4 and 27/4) exhibit a sharp decline in model accuracy, reaching the lowest R² values observed across the 4-year period and the highest RMSE vales of the year. These drops coincide with a spike in average SD, indicating a late-season snow event that temporarily reset the snowpack to a more homogeneous state. Snow cover maps from those dates (Figures 9B,C), along with those from days before and after (Figure 9A acquired on 03/04; Figure 9D, acquired on 01/05), reveal the drastic change in the conditions of the snow cover, characterized by a lower fragmentation, typically associated with decreased model accuracy. Despite the challenging conditions, the difference in R² and RMSE between EN-MF123 and BL-MF1 on those dates is the largest observed across the entire study period. This underscores the significant contribution of MF2 and MF3 even under conditions of relatively uniform snow cover, demonstrating their ability to enhance SD estimation performance even and especially when snow pattern complexity is reduced.

Figure 9

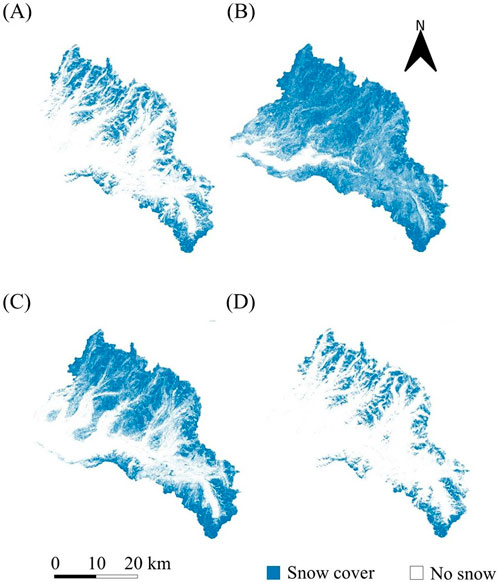
Figure 9. Snow cover maps acquired on (A) 03/04/2015, (B) 09/04/2015, (C) 27/04/2015 and (D) 01/05/2015, displaying a late-season snow event.

Regarding MF1, plots in Figure 8 reveal a strong similarity with the mean SD, confirming the role of MF1 as the dominant predictor in all models (as previously shown in Figure 5). This is expected, as greater SD generally corresponds to more extensive snow coverage. MF2, shows a similar, but not identical, trend to MF1. In fact, while higher SD often corresponds to greater boundary extent, this relationship breaks down in cases of highly homogeneous snowpack, with small and sparse empty spots. MF3 exhibits an inverse trend compared to MF1 and SD. As SD and coverage decrease, MF3 tends to increase, indicating the emergence of patchy and discontinuous snow distributions, and the increase of small ad isolated snow-covered areas. Conversely, when snow is more continuous and extensive, MF3 values drop, reflecting fewer isolated snow patches and more internal gaps within the snow cover. These trends support the interpretation that SD estimation models perform best under conditions of high MF2 and low MF3, i.e., when the snowpack is spatially heterogeneous and present multiple diffused non-snow-covered patches. In such configurations, topographic features are more exposed, and spatial structure is more complex, providing more informative cues for SD prediction. This again reinforces the importance of including MF2 and MF3 in the models. Focusing once more on the two anomalous April dates in 2015, we observe low MF3 values combined with unusually high MF2 values. This pattern indicates the presence of large, contiguous snow-covered areas with multiple but small and isolated gaps, confirming an extended and homogeneous snowpack hypothesized earlier. These conditions explain both the drop in model performance and the particularly large difference in R² between EN-MF123 and BL-MF1 models, as discussed with respect to Figure 8.

The similarity in the temporal evolution of MF1 and MF2, and their clear divergence from MF3, partially explains the predictor-importance scores in Figure 5. As discussed above, MF3 ranks as the second most informative predictor, whereas MF2 is less influential for SD because it contributes less novel information beyond MF1, however still more than any other topographical descriptor, which show lower predictor-importance scores.

3.5 Variation of R² and RMSE of SD model estimates across different snow pattern conditions

To further investigate the influence of snow cover conditions on the accuracy of SD estimation, boxplots of R² and RMSE were generated (Figure 10), comparing EN-MF123 model with BL-MF1 model, across different snow cover patterns conditions, identified by different MF classes. Figure 11 shows the distribution of observed SD values in the same MF classes, providing contextual insight for interpreting model performance.

Figure 10

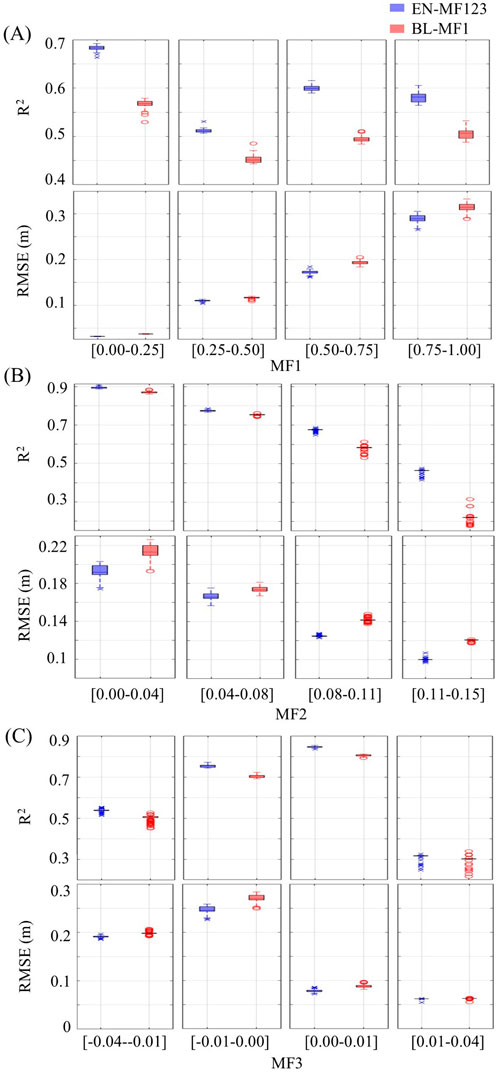
Figure 10. Boxplots of R² and RMSE (m) for snow depth estimation models EN-MF123 (blue) and BL-MF1 (red). The analysis is divided into different snow cover classes based on (A) MF1 (fractional snow cover): 0%–25%, 25%–50%, 50%–75%, and 75%–100%. (B) MF2 (total perimeter length of snow-covered areas): 0–0.0375, 0.0375–0.0750, 0.0750–0.1125 and 0.1125–0.1500. High positive MF2 values represent complex and discontinuous snow cover (typical of late melt season), while low values represent either an extended and homogenous snow cover (typical of peak accumulation conditions) or small and few snow cover patches (typical of very early or very late snow season). (C) MF3 (Euler-Poincaré Characteristic): −0.04 to −0.01, −0.01 to 0.00, 0.00 to 0.01, and 0.01 to 0.04. High positive MF3 values represent numerous disconnected snow patches, while high negative values indicate many internal gaps within a discontinuous but connected snow cover.

Figure 11

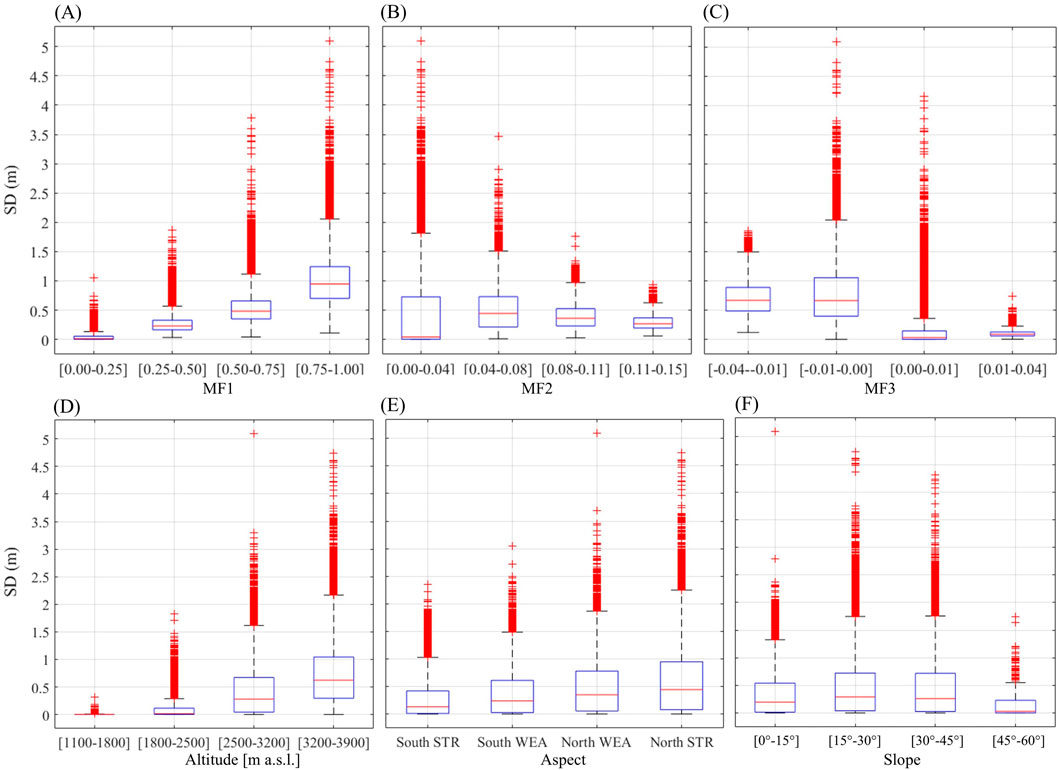
Figure 11. Boxplots of observed SD categorized by the same geometrical descriptor and topographic classes used in the model performance analysis: (A) fractional snow-covered area (MF1), (B) snow cover perimeter (MF2), (C) snow cover connectivity and fragmentation (MF3), (D) elevation, (E) exposure, and (F) slope.

In Figure 10A data is categorized according to four MF1(snow covered area) classes: 0%–25%, 25%–50%, 50%–75%, and 75%–100%. EN-MF123 model consistently show higher R² and lower RMSE across all MF1 classes. Although no consistent trend in accuracy with MF1 is observed, the highest model performance is found in the 0%–25% class, likely corresponding to late-season snow conditions when snow is patchy and topographically influenced. These settings are associated with the lowest SD values of the season, as shown in Figure 11A. Conversely, the lowest model accuracy is found in the 25%–50% MF1 class, representing a transitional snow cover phase. Meanwhile, RMSE increases with MF1, reflecting the expected relationship between greater snow cover and larger absolute SD values. However, RMSE remains consistently lower in EN-MF123 model, confirming the added value of geometrical information in improving prediction.

In Figure 10B, the analysis is repeated using MF2 classes (perimeter density of the snow-covered area, which quantifies the heterogeneity of the snow pattern): 0–0.0375, 0.0375–0.0750, 0.0750–0.1125, and 0.1125–0.1500. Across all classes, the EN-MF123 model outperforms the BL-MF1 model. The best performance is observed in the lowest MF2 class. Low MF2 values can correspond to two contrasting situations: (i) nearly continuous snow cover with very few and small gaps, typical of peak accumulation periods (e.g., Figure 2D), or (ii) very sparse snow remaining in isolated patches, typical of late melt season (e.g., Figure 2A. These conditions are usually associated with either very high (case i) or very low (case ii) snow depth values, as shown by the SD distribution in Figure 11B. In both cases, model accuracy is high for EN-MF123 and BL-MF1, and the benefit of including MF2 and MF3 is limited.

As MF2 increases, the snow cover pattern becomes more complex and heterogeneous: the number and size of snow patches or gaps within the snowpack grows (e.g., Figures 2B,C), reflecting a more fragmented distribution. These intermediate MF2 values are typically observed in transitional phases, just before or after peak accumulation. Under such conditions, snow depth values cluster around a narrower low-to-medium range (∼0.25 m), making accurate prediction more difficult. Both models show reduced accuracy in these scenarios; however, the inclusion of MF2 and MF3 substantially improves the EN-MF123 model, as the additional geometrical descriptors help capture the spatial variability of the snowpack that is not represented by MF1 alone.

Finally, Figure 10C groups the data according to MF3 values (Euler–Poincaré characteristic of snow cover, which describes the degree of connectivity or fragmentation of snow-covered areas), using four classes: -0.04 to −0.01, −0.01 to 0.00, 0.00 to 0.01, and 0.01 to 0.04. Negative MF3 values indicate a more connected snowpack, where snow cover is extensive but includes internal gaps (e.g., Figure 2C). While positive MF3 values reflect fragmented patterns with numerous disconnected snow patches (e.g., Figure 2B).

Across all MF3 classes, the EN-MF123 model outperforms the BL-MF1 model, achieving higher R² and lower RMSE across all MF3 classes. The best performance is observed in the central classes (−0.01 to 0.00 and 0.00–0.01), which correspond to intermediate connectivity states: (i) conditions with only a few isolated snow patches (e.g., Figure 2A), or (ii) a continuous snow cover layer with scattered gaps (e.g., Figure 2D). These scenarios are generally associated with either low SD values with exceptions at high-altitude sites where snow accumulation remains deep outside peak season (case i) or high SD values with exceptions at low-altitude sites that maintain shallow snow even during peak accumulation (case ii). The differences in RMSE between these classes can be explained by the distinct SD distributions shown in Figure 11C.

The lowest R² values occur in the highest MF3 class (0.01–0.04), which reflects highly fragmented snow patterns with many small, disconnected patches (e.g., Figure 2B). These conditions are typically associated with low-to-medium SD values, consistent with the findings from the MF1 and MF2 analyses. Importantly, even in this fragmented regime, including MF2 and MF3 substantially improves prediction accuracy, highlighting the added value of geometrical descriptors in representing the spatial variability of the snowpack.

Some additional considerations in regards of the importance MF as predictors can be done:

i. MF2 is the least important among the 3 MFs. It produces a marked performance increase only in the highest MF2 class (1.72% of the data) and a smaller increase in the second-highest class (49.52%). Hence, MF2 improves SD prediction for just over half of the dataset; for the remaining half, its contribution is negligible.

ii. For MF3, the magnitude of the performance gain decreases across its classes, but the sample size in each class also decreases. Overall, the benefit of including MF3 is evident for the majority of the dataset, 53.68%, 32.49%, and 11.70% in the first three classes, respectively, whereas only 2.13% falls into the last class, where the improvement is negligible. These observations are consistent with, and help explain, the predictor-importance distribution discussed earlier and shown in Figure 5.

3.6 Variation of R² and RMSE of SD model estimates across different topographic conditions

To assess how terrain characteristics influence SD model performance, we analysed R² and RMSE across classes of elevation, aspect, and slope (Figure 12). The distribution of observed SD values within the same categories (Figures 11D–F) provides the necessary context for interpreting model behaviour. We selected these variables because elevation and aspect emerge as particularly relevant descriptors for both models, consistently influencing snow distribution and model accuracy; slope although it does not exhibit a high relative importance score in the predictor analysis, remains a fundamental topographic variable, affecting snow redistribution and stability, with implications for various applications, including avalanche hazard assessment, hydrological modelling, ecosystem processes, and the planning and maintenance of infrastructure in mountain regions.

Figure 12

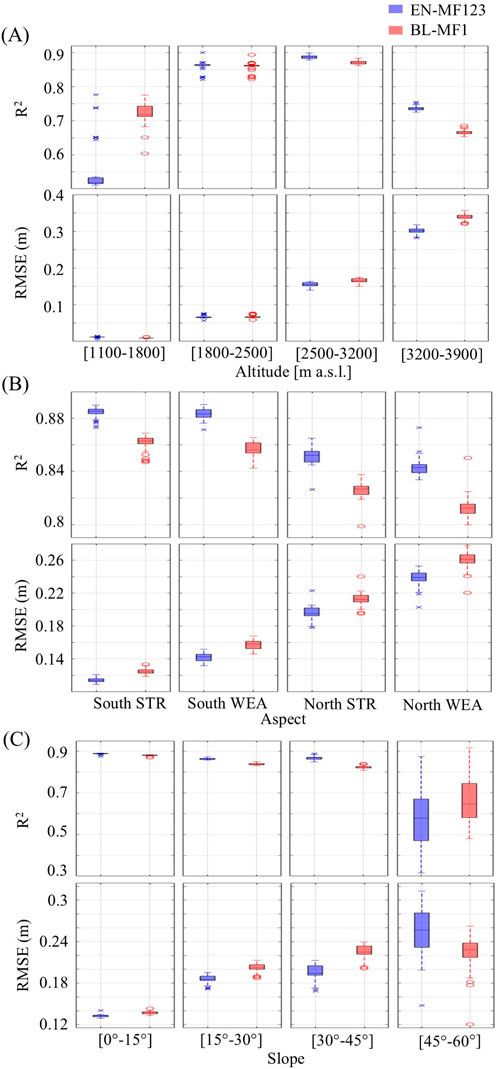
Figure 12. Boxplots of R² and RMSE (m) for snow depth estimation model EN-MF1 (blue) and BL-MF1 (red), grouped by: (A) Elevation (1,100–1,800 m, 1,800–2,500 m, 2,500–3,200 m, 3,200–3,900 m), (B) Exposure, computed as the sine of the angle in respect to the North direction (South STR, −1 to −0.3, South WEA, −0.3 to 0, North WEA, 0 to 0.3, North STR, 0.3–1) and (C) Slope (0°–15°, 15°–30°, 30°–45°, 45°–60°).

In terms of model performance, both EN-MF123 and BL-MF1 achieved the highest accuracy under these conditions: intermediate elevations (1,800–3,200 m, Figure 12A) and gentle slopes (0°–15°, Figure 12C), where SD is moderate to high, and south-facing aspects, associated with moderate to low SD. These results suggest that estimation is most reliable when snowpacks are thick enough to reflect terrain controls, but not so deep as to mask them.

The inclusion of geometrical descriptors MF2 and MF3 proved particularly beneficial under conditions of generally high SD. At high elevations (3200–3900 m, Figure 12A), the mean R² increased by 0.07 and RMSE decreased by 0.04 m; on strongly north-facing aspects (Figure 12B, R² increased by 0.03 and RMSE decreased by 0.03 m; and on steep slopes (30°–45°; Figure 12C), R² improved by 0.04 and RMSE decreased by 0.03 m. In these cases, the additional spatial information provided by MF2 and MF3 enhanced the models’ ability to capture snowpack variability that is less apparent when snow cover is consistently deep.

By contrast, the inclusion of MF2 and MF3 reduced model accuracy under conditions associated with low SD, namely, low elevations (<1800 m, Figure 12A) and very steep slopes (>45°, Figure 12C). In these settings, mean R² decreased by 0.2 and 0.1 respectively, while changes in RMSE were negligible at low elevations and slightly adverse on steep slopes (+0.029 m). Besides the limited representation of these settings in the training data (1.05% and 0.28% of the study area, respectively), several factors likely contribute. First, when snow depth is low, the geometric structure of the snowpack is weak or short-lived, so MF2 and MF3 might provide ambiguous/low-signal information relative to MF1, increasing model variance. Second, MF areal descriptors at 500 m may be mismatched to the fine-scale heterogeneity typical of steep or low-elevation areas. Third, because predictor-SD relationships vary across topographic classes (non-stationarity, e.g., differing accumulation/ablation controls) and MF2 and MF3 can be collinear with existing variables, the ensemble may, especially with few samples, choose splits that are optimal globally but mis-specified locally, yielding sub-optimal partitions and degraded predictive accuracy within those subsets under these conditions.

3.7 Potential limitations of the derived SD models

First, one potential limitation of this study is that the spatial distribution of the SD estimation was set to a resolution of 500 m, however, results might be different for other resolutions. This goes along with the fact that, to include MF in a predictive model, it is necessary to average topographic indices over entire grid cells and relate them to mean SD, which may limit the applicability of the results in contexts where finer spatial detail is required. This would be particularly important for applications such as avalanche forecasting, habitat modelling, or very localized hydrological assessments, which rely on high-resolution SD maps to capture small-scale variability, especially in complex and heterogeneous alpine terrain. It is acknowledged that using MF as predictors entails an intrinsic change-of-support. Because MF are area-based geometric indices, they refer to cell-averaged conditions; linking them to SD therefore requires aggregating SD to the MF support. Consequently, either SD estimates must be produced at a coarser resolution, or, if the target resolution is preserved, the MF must be computed from higher-resolution inputs. However, the question remains as to whether it would be possible to obtain higher-resolution SD maps, compared to a coarser resolution of 500 m applied in this study, by applying a finer grid resolution during the computation of the MF. Also scaling issues for finer or coarser resolutions, e.g., continental or global scale applications, could occur due to non-linarites whilst averaging SD and topographic indices.

Second, the snow cover maps used to compute the geometrical descriptors were derived from an exceptionally high-resolution SD dataset (3 m). While this allowed for a detailed characterization of snow cover patterns, such high-resolution input data (see e.g., Cimoli et al., 2017; Wulf et al., 2020; Bühler et al., 2015) are rarely available across broader regions or other climate zones and for different time steps within a year and over multiple years. As a result, the testing of our method in other regions, as derived in this study, may be limited in areas where no or only coarser resolution datasets are available.

Third, our analysis is restricted to the late accumulation and ablation phases of the snow season (from late February to June). This period is hydrologically relevant, as it includes peak SWE and the melt season, but excludes early-winter and mid-winter accumulation and redistribution processes. The lack of data for the full snow season limits our ability to assess whether the added value of MF2 and MF3 persists under early-winter conditions, when snow distribution is strongly influenced by storm sequences, wind redistribution, and shallow snowpacks. Applying the method across the entire season, including accumulation onset, would be useful to evaluate its robustness in different snow regimes.

Fourth, in a limited number of specific cases, such as low-elevation zones, areas with very steep slopes, or on isolated dates (e.g., 23/03/2014), the inclusion of MF2 and MF3 resulted in a slight reduction in model accuracy. Under these particular conditions, (caused by e.g., exceptional meteorological events, such as intense snowfall, strong wind episodes, or sudden warming or specific topographic features), the geometric signal of the snow cover patterns is weak or ambiguous (e.g., low MF2 can reflect either thin continuous cover or scattered patches, and MF3 may be noisy where patch connectivity is poorly resolved) and can introduce additional uncertainty into the estimation of SD. Moreover, because MF areal descriptors are computed at 500 m, areas with strong sub-cell heterogeneity can suffer change-of-support mismatch. In small, imbalanced subsets (e.g., low represented topographic areas, rare snow cover conditions) these weak or collinear signals can steer the ensemble toward globally good but locally sub-optimal splits, increasing variance/bias. The model, trained on data from the entire 4-year period, lacks the adaptability to account for such specific conditions. Therefore, the slight underperformance of the EN-MF123 model compared to the BL-MF1 model under certain specific conditions (whether temporal or topographical) can be attributed to the high spatial and temporal variability of the SD distribution in the study area, which makes it challenging for the models to adapt to all observed conditions. Accordingly, the inclusion of MF2 and MF3 must be best evaluated case by case, balancing the anticipated accuracy gains against the additional computational cost, with particular attention to low-SD or highly heterogeneous settings where the benefits are more context-dependent.

Finally, as the analysis was conducted in one specific study area, the influence of local topographic and/or climatic conditions at other regions on model performance remains uncertain. We cannot conclude if the enhanced RF SD model with MF2 and MF3 also exceeds the baseline simulation at other resolutions and in other locations, which will be subject of further investigations.

4 Conclusion and outlook

This study evaluates the added value of two geometric descriptors of snow cover, MF2 (perimeter density) and MF3 (Euler–Poincaré characteristic, i.e., connectivity/fragmentation), alongside fractional snow-covered area (MF1) and standard topographic/geographic predictors, for snow-depth (SD) estimation with a Random Forest. The analysis was conducted in the Tuolumne River Basin (California, United States) using multi-year ASO SD maps (2013–2016). Using cross-validation, we calibrated two RF models: an enhanced model, EN-MF123 (including MF2 and MF3), and a baseline model, BL-MF1 (excluding them). Both models were trained on 100 random subsets to obtain robust performance estimates.

By analysing model performance across a range of spatial, temporal, topographic and geographic conditions, the results consistently show that adding these geometrical descriptors improves both the accuracy and robustness of SD predictions. Overall, both model realizations perform well. The EN-MF123 setup (incorporating MF2 and MF3) generally outperforms the BL-MF1 model, as indicated by higher R² and lower RMSE in the vast majority of test scenarios. Improvements are not uniform: they are visible under complex snow-cover patterns, such as during late melt seasons, in areas with fragmented snow distribution, and at higher elevations and steeper slopes, where the two additional descriptors capture spatial characteristics not adequately represented by traditional baseline predictors. However, the most substantial contribution of MF2 and MF3 emerges under deep, homogeneous snow cover, where terrain-induced variability is less apparent in areal extent and conventional predictors often struggle to provide accurate estimates. In these cases, the spatial information conveyed by MF2 and MF3 becomes especially valuable, allowing the model to account for subtle patterns in snow distribution and to improve prediction reliability. MF2 and MF3 predictors’ importance scores exceed those of all other predictors (except MF1), indicating that they provide strong, non-redundant information on snowpack geometry that enhances SD predictability; overall, the EN-MF123 model outperforms the BL-MF1 model, as shown by the general increase in R² and the decrease in RMSE and MAE. This study underscores the value of including snow-cover geometrical descriptors for improved spatially distributed SD estimation using remote sensing, with applications in water management, ecology, and avalanche forecasting.

Future work could go in the direction of extending this analysis by investigating how the spatial resolution of input data influences the performance of SD estimation. Specifically, the methodology could be applied using different grid sizes to test snow cover products of varying spatial resolutions, such as MODIS, VIIRS, Sentinel-3, Landsat and Sentinel-2, which are globally available and commonly used in large-scale snow monitoring, but also fine-scale webcam- and drone-derived snow cover maps. The goal would be to assess how the spatial structure of snow cover patterns, as captured by MF2 and MF3, changes across spatial resolutions, and whether these geometrical descriptors retain its predictive value when derived from coarser or finer input data. Particular attention should be given to analysing the relationship between the spatial resolution of the input data and the resolution of the grid used to compute MF, as this affects the resolution of the output (e.g., SD, SWE). Specifically, when the objective is to enhance the resolution of the output, it would be valuable to investigate the minimum grid resolution that can be used, given the spatial resolution of the input data (e.g., in this study, the input data had a spatial resolution of 3 m, while a grid resolution of 500 m was chosen). Therefore, a key aspect to investigate would be the minimum grid resolution at which the snow cover pattern within each cell remains sufficient to generate informative MF, which, of course, depends also on the spatial resolution of the input data. Understanding this sensitivity is crucial for extending the applicability of the method to broader spatial and temporal scales, especially in regions where high-resolution SD datasets are not available. More broadly, further validation of the SD estimation approach including MF2 and MF3 in other mountain regions with differing climate, terrain, and snow regimes will be important to assess its generalizability and robustness across diverse environmental settings. In parallel, a multidimensional exploration jointly considering all combinations of MF would help characterize interactions among these descriptors and inform future refinements of the SD modelling framework. A further outlook in this regard, would be the possibility of deriving SD directly from optical stereo-imagery from satellites or drones for more local applications (e.g., Bühler et al., 2015; Deschamps-Berger et al., 2020) compared to the more regional airborne laserscanning flights as used here. In addition, for dry snow also SAR-derived SD estimates such as from Sentinel-1 (Lievens et al., 2019) could come into play for training the models developed here. With the ongoing improvement of satellite spatial resolution, such an approach could progressively achieve, or even surpass, the accuracy and resolution of airborne-based methods.

An important future step regarding monitoring of water resources and snow-hydrology could be to extend this analysis also to SWE estimation models, integrating MF2 and MF3 as predictors, although spatially distributed SWE information in complex, high-alpine terrain is absolutely scarce and lacks therefore a solid validation basis. However, in contrast to SD, SWE is even more rarely available for validation. For this at current stage, SWE simulations based on rather complex physically-based models with adequate meteorological input and applying precipitation undercatch correction methods (Pulka et al., 2024) could be used often applying assimilated SD data as input. Also, as demonstrated in Koch et al. (2024), signals of a superconducting gravimeter can provide for the first time directly measured information of SWE over a kilometre scale range in a complex mountain environment for evaluation of SWE modelling.

In addition, we believe future research could also go in the direction of exploring the use of MF2 and MF3 as indicators in climate-related studies. Since these geometrical descriptors capture the connectivity, fragmentation, and spatial complexity of snow cover, they may serve as valuable metrics to detect and quantify changes in snow distribution patterns over time in response to climate variability and long-term change.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LF: Writing – original draft. KS: Writing – review and editing. DB: Writing – review and editing. FK: Writing – review and editing, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the Austrian Science Fund (FWF) (grant DOI: 10.55776/I6489, FWF-DFG Weave project G-MONARCH, project start in 2023).

Acknowledgments

This research was funded in part by the Austrian Science Fund (FWF) (grant DOI: 10.55776/I6489). For open access purposes, the author has applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1672558/full#supplementary-material

References

Alonso-González, E., Aalstad, K., Baba, M. W., Revuelto, J., López-Moreno, J. I., Fiddes, J., et al. (2022). The multiple snow data assimilation system (MuSA v1. 0). Geosci. Model Dev. 15 (24), 9127–9155. doi:10.5194/gmd-15-9127-2022

CrossRef Full Text | Google Scholar

Amatulli, G., Domisch, S., Tuanmu, M. N., Parmentier, B., Ranipeta, A., Malczyk, J., et al. (2018). A suite of global, cross-scale topographic variables for environmental and biodiversity modeling. Scientific Data. 5 (01), 1–15. doi:10.1038/sdata.2018.40

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, S., and Radić, V. (2022). Evaluation and interpretation of convolutional long short-term memory networks for regional hydrological modelling. Hydrology Earth Syst. Sci. 26 (3), 795–825. doi:10.5194/hess-26-795-2022

CrossRef Full Text | Google Scholar

Blandini, G., Avanzi, F., Gabellani, S., Ponziani, D., Stevenin, H., Ratto, S., et al. (2023). A random forest approach to quality-checking automatic snow-depth sensor measurements. Cryosphere 17 (12), 5317–5333. doi:10.5194/tc-17-5317-2023

CrossRef Full Text | Google Scholar

Blöschl, G., Kirnbauer, R., and Gutknecht, D. (1991). Distributed snowmelt simulations in an alpine catchment : 1. Model evaluation on the basis of snow cover patterns. Water Resour. Res. 12 (27), 3171–3179. doi:10.1029/91WR02250

CrossRef Full Text | Google Scholar

Brauchli, T., Trujillo, E., Huwald, H., and Lehning, M. (2017). Influence of slope-scale snowmelt on catchment response simulated with the Alpine3D model. Water Resour. Res. 53 (12), 10723–10739. doi:10.1002/2017WR021278

CrossRef Full Text | Google Scholar

Breiman, L. (1996). Bagging predictors. Mach. Learn. 24, 123–140. doi:10.1007/BF00058655

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi:10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Bühler, Y., Marty, M., Egli, L., Veitinger, J., Jonas, T., Thee, P., et al. (2015). Snow depth mapping in high-alpine catchments using digital photogrammetry. Cryosphere 9 (1), 229–243. doi:10.5194/tc-9-229-2015

CrossRef Full Text | Google Scholar

Callaghan, T. V., Johansson, M., Brown, R. D., Groisman, P. Y., Labba, N., Radionov, V., et al. (2011). Multiple effects of changes in Arctic snow cover. Ambio 40, 32–45. doi:10.1007/s13280-011-0213-x

CrossRef Full Text | Google Scholar

Castellazzi, P., Burgess, D., Rivera, A., Huang, J., Longuevergne, L., and Demuth, M. N. (2019). Glacial melt and potential impacts on water resources in the Canadian Rocky Mountains. Water Resour. Res. 55 (12), 10191–10217. doi:10.1029/2018WR024295

CrossRef Full Text | Google Scholar

Cimoli, E., Marcer, M., Vandecrux, B., Bøggild, C. E., Williams, G., and Simonsen, S. B. (2017). Application of low-cost UASs and digital photogrammetry for high-resolution snow depth mapping in the Arctic. Remote Sens. 9 (11), 1144. doi:10.3390/rs9111144

CrossRef Full Text | Google Scholar

Clark, M. P., Hendrikx, J., Slater, A. G., Kavetski, D., Anderson, B., Cullen, N. J., et al. (2011). Representing spatial variability of snow water equivalent in hydrologic and land-surface models: a review. Water Resour. Res. 47 (7). doi:10.1029/2011WR010745

CrossRef Full Text | Google Scholar

Daudt, R. C., Wulf, H., Hafner, E. D., Bühler, Y., Schindler, K., and Wegner, J. D. (2023). Snow depth estimation at country-scale with high spatial and temporal resolution. ISPRS J. Photogrammetry Remote Sens. 197, 105–121. doi:10.1016/j.isprsjprs.2023.01.017

CrossRef Full Text | Google Scholar

Dayal, A., Hodson, A. J., Šabacká, M., and Smalley, A. L. (2023). Seasonal snowpack microbial ecology and biogeochemistry on a high Arctic ice cap reveals negligible autotrophic activity during spring and summer melt. J. Geophys. Res. Biogeosciences 128 (10), e2022JG007176. doi:10.1029/2022JG007176

CrossRef Full Text | Google Scholar

Deng, H., Chen, Y., and Li, Y. (2019). Glacier and snow variations and their impacts on regional water resources in mountains. J. Geogr. Sci. 29, 84–100. doi:10.1007/s11442-019-1585-2

CrossRef Full Text | Google Scholar

Deschamps-Berger, C., Gascoin, S., Berthier, E., Deems, J., Gutmann, E., Dehecq, A., et al. (2020). Snow depth mapping from stereo satellite imagery in mountainous terrain: evaluation using airborne laser-scanning data. Cryosphere 14 (9), 2925–2940. doi:10.5194/tc-14-2925-2020

CrossRef Full Text | Google Scholar

Dong, C. (2018). Remote sensing, hydrological modeling and in situ observations in snow cover research: a review. J. Hydrol. 561, 573–583. doi:10.1016/j.jhydrol.2018.04.027

CrossRef Full Text | Google Scholar

Elyoussfi, H., Boudhar, A., Belaqziz, S., Bousbaa, M., Nifa, K., Bargam, B., et al. (2025). Leveraging advanced deep learning and machine learning approaches for snow depth prediction using remote sensing and ground data. J. Hydrology Regional Stud. 57, 102085. doi:10.1016/j.ejrh.2024.102085

CrossRef Full Text | Google Scholar

Ferrarin, L., Schulz, K., Bocchiola, D., and Koch, F. (2023). Morphological indexes to describe snow-cover patterns in a high-alpine area. Ann. Glaciol. 65, e7. doi:10.1017/aog.2023.62

CrossRef Full Text | Google Scholar

Filzmoser, P., Liebmann, B., and Varmuza, K. (2009). Repeated double cross validation. J. Chemom. A J. Chemom. Soc. 23 (4), 160–171. doi:10.1002/cem.1225

CrossRef Full Text | Google Scholar

Flett, V., Maurice, L., Finlayson, A., Black, A. R., MacDonald, A. M., Everest, J., et al. (2017). Meltwater flow through a rapidly deglaciating glacier and foreland catchment system: Virkisjökull, SE Iceland. Hydrol. Res. 48 (6), 1666–1681. doi:10.2166/nh.2017.205

CrossRef Full Text | Google Scholar

Freudiger, D., Kohn, I., Seibert, J., Stahl, K., and Weiler, M. (2017). Snow redistribution for the hydrological modeling of alpine catchments. Wiley Interdiscip. Rev. Water 4 (5), e1232. doi:10.1002/wat2.1232

CrossRef Full Text | Google Scholar

Gascoin, S., Grizonnet, M., Bouchet, M., Salgues, G., and Hagolle, O. (2019). Theia Snow collection: high-resolution operational snow cover maps from Sentinel-2 and Landsat-8 data. Earth Syst. Sci. Data 11 (2), 493–514. doi:10.5194/essd-11-493-2019

CrossRef Full Text | Google Scholar

Gascoin, S., Luojus, K., Nagler, T., Lievens, H., Masiokas, M., Jonas, T., et al. (2024). Remote sensing of mountain snow from space: status and recommendations. Front. Earth Sci. 12, 1381323. doi:10.3389/feart.2024.1381323

CrossRef Full Text | Google Scholar

Girotto, M., Formetta, G., Azimi, S., Bachand, C., Cowherd, M., De Lannoy, G., et al. (2024). Identifying snowfall elevation patterns by assimilating satellite-based snow depth retrievals. Sci. Total Environ. 906, 167312. doi:10.1016/j.scitotenv.2023.167312

PubMed Abstract | CrossRef Full Text | Google Scholar

Gislason, P. O., Benediktsson, J. A., and Sveinsson, J. R. (2006). Random forests for land cover classification. Pattern Recognit. Lett. 27 (4), 294–300. doi:10.1016/j.patrec.2005.08.011

CrossRef Full Text | Google Scholar

Grünewald, T., Stötter, J., Pomeroy, J. W., Dadic, R., Moreno Baños, I., Marturià, J., et al. (2013). Statistical modelling of the snow depth distribution in open alpine terrain. Hydrology Earth Syst. Sci. 17 (8), 3005–3021. doi:10.5194/hess-17-3005-2013

CrossRef Full Text | Google Scholar

Guo, L., Chehata, N., Mallet, C., and Boukir, S. (2011). Relevance of airborne lidar and multispectral image data for urban scene classification using random forests. ISPRS J. Photogrammetry Remote Sens. 66 (1), 56–66. doi:10.1016/j.isprsjprs.2010.08.007

CrossRef Full Text | Google Scholar

Hall, D. K., Riggs, G. A., Salomonson, V. V., DiGirolamo, N. E., and Bayr, K. J. (2002). MODIS snow-cover products. Remote Sens. Environ. 83 (1-2), 181–194. doi:10.1016/S0034-4257(02)00095-0

CrossRef Full Text | Google Scholar

Hedrick, A. R., Marks, D., Havens, S., Robertson, M., Johnson, M., Sandusky, M., et al. (2018). Direct insertion of NASA airborne snow observatory-derived snow depth time series into the iSnobal energy balance snow model. Water Resour. Res. 54 (10), 8045–8063. doi:10.1029/2018WR023190

CrossRef Full Text | Google Scholar

Hedrick, A. R., Marks, D., Marshall, H. P., McNamara, J., Havens, S., Trujillo, E., et al. (2020). From drought to flood: a water balance analysis of the Tuolumne river basin during extreme conditions (2015–2017). Hydrol. Process. 34 (11), hyp.13749–2574. doi:10.1002/hyp.13749

CrossRef Full Text | Google Scholar

Helbig, N., Schirmer, M., Magnusson, J., Mäder, F., van Herwijnen, A., Quéno, L., et al. (2021). A seasonal algorithm of the snow-covered area fraction for mountainous terrain. Cryosphere 1 (28), 4607–4624. doi:10.5194/tc-15-4607-2021

CrossRef Full Text | Google Scholar

Henn, B., Newman, A. J., Livneh, B., Daly, C., and Lundquist, J. D. (2018a). An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 556, 1205–1219. doi:10.1016/j.jhydrol.2017.03.008

CrossRef Full Text | Google Scholar

Henn, B., Painter, T. H., Bormann, K. J., McGurk, B., Flint, A. L., Flint, L. E., et al. (2018b). High-elevation evapotranspiration estimates during drought: using streamflow and NASA Airborne Snow Observatory SWE observations to close the Upper Tuolumne River Basin water balance. Water Resour. Res. 54 (2), 746–766. doi:10.1002/2017WR020473

CrossRef Full Text | Google Scholar

Hock, R., Rasul, G., Adler, C., Cáceres, B., Gruber, S., Hirabayashi, Y., et al. (2019). “High Mountain areas,” in IPCC special report on the Ocean and cryosphere in a changing climate. Editors H.-O. Pörtner, D. C. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, and E. Poloczanska (Cambridge, UK and New York, NY: Cambridge University Press), 131–202. doi:10.1017/9781009157964.004

CrossRef Full Text | Google Scholar

Huss, M., Bookhagen, B., Huggel, C., Jacobsen, D., Bradley, R. S., Clague, J. J., et al. (2017). Toward mountains without permanent snow and ice. Earth's Future 5 (5), 418–435. doi:10.1002/2016EF000514

CrossRef Full Text | Google Scholar

Jenssen, R. O. R., and Jacobsen, S. K. (2021). Measurement of snow water equivalent using drone-mounted ultra-wide-band radar. Remote Sens. 13 (13), 2610. doi:10.3390/rs13132610

CrossRef Full Text | Google Scholar

Khosravi, K., Golkarian, A., Omidvar, E., Hatamiafkoueieh, J., and Shirali, M. (2023). Snow water equivalent prediction in a mountainous area using hybrid bagging machine learning approaches. Acta Geophys. 71 (2), 1015–1031. doi:10.1007/s11600-022-00934-0

CrossRef Full Text | Google Scholar

Koch, F., Gascoin, S., Achmüller, K., Schattan, P., Wetzel, K. F., Deschamps-Berger, C., et al. (2024). Superconducting gravimeter observations show that a satellite-derived snow depth image improves the simulation of the snow water equivalent evolution in a high alpine site. Geophys. Res. Lett. 51 (24), e2024GL112483. doi:10.1029/2024GL112483

CrossRef Full Text | Google Scholar

Kuttippurath, J., Patel, V. K., and Sharma, B. R. (2024). Observed changes in the climate and snow dynamics of the Third Pole. Clim. Atmos. Sci. 7, 162. doi:10.1038/s41612-024-00710-5

CrossRef Full Text | Google Scholar

Lahmers, T. M., Kumar, S. V., Rosen, D., Dugger, A., Gochis, D. J., Santanello, J. A., et al. (2022). Assimilation of NASA's airborne snow observatory snow measurements for improved hydrological modeling: a case study enabled by the coupled LIS/WRF-Hydro system. Water Resour. Res. 58 (3), e2021WR029867. doi:10.1029/2021WR029867

CrossRef Full Text | Google Scholar

Lebiedzinski, K., and Fürst, J. (2018). Development of alpine flow regimes in Austria in the period 1961–2010. Österreichische Wasser-und Abfallwirtsch. 70, 474–484. doi:10.1007/s00506-018-0499-z

CrossRef Full Text | Google Scholar

Legland, D. (2025). imMinkowski. MATLAB Central File Exchange. Available online at: https://www.mathworks.com/matlabcentral/fileexchange/33690-imminkowski (Accessed March 19, 2025).

Google Scholar

Li, D., Wrzesien, M. L., Durand, M., Adam, J., and Lettenmaier, D. P. (2017). How much runoff originates as snow in the western United States, and how will that change in the future? Geophys. Res. Lett. 44 (12), 6163–6172. doi:10.1002/2017GL073551

CrossRef Full Text | Google Scholar

Lievens, H., Demuzere, M., Marshall, H. P., Reichle, R. H., Brucker, L., Brangers, I., et al. (2019). Snow depth variability in the Northern Hemisphere mountains observed from space. Nat. Commun. 10 (1), 4629. doi:10.1038/s41467-019-12566-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Liston, G. E. (2004). Representing subgrid snow cover heterogeneities in regional and global models. J. Clim. 17 (6), 1381–1397. doi:10.1175/1520-0442(2004)017<1381:RSSCHI>2.0.CO;2

CrossRef Full Text | Google Scholar

Louppe, G., Wehenkel, L., Sutera, A., and Geurts, P. (2013). “Understanding variable importances in forests of randomized trees,” in Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS'13). Editors C. J. Burges, L. Bottou, M. Welling, and Z. Ghahramani (Red Hook, NY, United States: Curran Associates Inc.), 431–439.

Google Scholar

Lu, Y., James, T., Schillaci, C., and Lipani, A. (2022). Snow detection in alpine regions with convolutional neural networks: discriminating snow from cold clouds and water body. GIScience and Remote Sens. 59 (1), 1321–1343. doi:10.1080/15481603.2022.2112391

CrossRef Full Text | Google Scholar

Lundquist, J. D., Cayan, D. R., and Dettinger, M. D. (2003). “Meteorology and hydrology in Yosemite National Park: a sensor network application,” in Information processing in sensor networks (Berlin, Heidelberg: Springer Berlin Heidelberg), 518–528. doi:10.1007/3-540-36978-3_35

CrossRef Full Text | Google Scholar

Lundquist, J. D., Roche, J. W., Forrester, H., Moore, C., Keenan, E., Perry, G., et al. (2016). Yosemite hydroclimate network: distributed stream and atmospheric data for the Tuolumne River watershed and surroundings. Water Resour. Res. 52 (9), 7478–7489. doi:10.1002/2016WR019261

CrossRef Full Text | Google Scholar

Ma, X., Li, D., Fang, Y., Margulis, S. A., and Lettenmaier, D. P. (2023). Estimating spatiotemporally continuous snow water equivalent from intermittent satellite observations: an evaluation using synthetic data. Hydrology Earth Syst. Sci. 27 (1), 21–38. doi:10.5194/hess-27-21-2023

CrossRef Full Text | Google Scholar

Margulis, S. A., Fang, Y., Li, D., Lettenmaier, D. P., and Andreadis, K. (2019). The utility of infrequent snow depth images for deriving continuous space-time estimates of seasonal snow water equivalent. Geophys. Res. Lett. 46 (10), 5331–5340. doi:10.1029/2019GL082507

CrossRef Full Text | Google Scholar

McGrath, D., Bonnell, R., Zeller, L., Olsen-Mikitowicz, A., Bump, E., Webb, R., et al. (2022). A time series of snow density and snow water equivalent observations derived from the integration of GPR and UAV SfM observations. Front. Remote Sens. 3, 886747. doi:10.3389/frsen.2022.886747

CrossRef Full Text | Google Scholar

Meloche, J., Langlois, A., Rutter, N., McLennan, D., Royer, A., Billecocq, P., et al. (2022). High-resolution snow depth prediction using random forest algorithm with topographic parameters: a case study in the Greiner watershed, Nunavut. Hydrol. Process. 36 (3), e14546. doi:10.1002/hyp.14546

CrossRef Full Text | Google Scholar

Nienow, P. W., Sole, A. J., Slater, D. A., and Cowton, T. R. (2017). Recent advances in our understanding of the role of meltwater in the Greenland Ice Sheet system. Curr. Clim. Change Rep. 3, 330–344. doi:10.1007/s40641-017-0083-9

CrossRef Full Text | Google Scholar

Notarnicola, C. (2020). Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 243, 111781. doi:10.1016/j.rse.2020.111781

CrossRef Full Text | Google Scholar

Oaida, C. M., Reager, J. T., Andreadis, K. M., David, C. H., Levoe, S. R., Painter, T. H., et al. (2019). A high-resolution data assimilation framework for snow water equivalent estimation across the Western United States and validation with the airborne snow observatory. J. Hydrometeorol. 20 (3), 357–378. doi:10.1175/JHM-D-18-0009.1

CrossRef Full Text | Google Scholar

Painter, T. (2018). “ASO L4 Lidar snow depth 3m UTM Grid. (ASO_3M_SD, version 1). [Data Set],”Boulder, Colorado: NASA National Snow and Ice Data Center Distributed Active Archive Center. Spatial Coverage N: 38.2451472 S: 37.53568061 E: -118.9505367 W: -119.9391373. Date accessed 04-16-2025. doi:10.5067/KIE9QNVG7HP0

CrossRef Full Text | Google Scholar

Painter, T., Berisford, D., Boardman, J., Bormann, K., Deems, J., Gehrke, F., et al. (2016). The Airborne Snow Observatory: fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 184, 139–152. doi:10.1016/j.rse.2016.06.018

CrossRef Full Text | Google Scholar

Pal, M. (2005). Random forest classifier for remote sensing classification. Int. J. Remote Sens. 26 (1), 217–222. doi:10.1080/01431160412331269698

CrossRef Full Text | Google Scholar

Parker, J., Sherman, E., van de Raa, M., van der Meer, D., Samelson, L. E., and Losert, W. (2013). Automatic sorting of point pattern sets using Minkowski functionals. Phys. Rev. E—Statistical, Nonlinear, Soft Matter Phys. 88 (2), 022720. doi:10.1103/PhysRevE.88.022720

PubMed Abstract | CrossRef Full Text | Google Scholar

Pauli, J. N., Zuckerberg, B., Whiteman, J. P., and Porter, W. (2013). The subnivium: a deteriorating seasonal refugium. Front. Ecol. Environ. 11 (5), 260–267. doi:10.1890/120222

CrossRef Full Text | Google Scholar

Persello, C., Wegner, J. D., Hänsch, R., Tuia, D., Ghamisi, P., Koeva, M., et al. (2022). Deep learning and earth observation to support the sustainable development goals: current approaches, open challenges, and future opportunities. IEEE Geoscience Remote Sens. Mag. 10 (2), 172–200. doi:10.1109/MGRS.2021.3136100

CrossRef Full Text | Google Scholar

Peters, J., De Baets, B., Verhoest, N. E., Samson, R., Degroeve, S., De Becker, P., et al. (2007). Random forests as a tool for ecohydrological distribution modelling. Ecol. Model. 207 (2-4), 304–318. doi:10.1016/j.ecolmodel.2007.05.011

CrossRef Full Text | Google Scholar

Pflug, J. M., Margulis, S. A., and Lundquist, J. D. (2022). Inferring watershed-scale mean snowfall magnitude and distribution using multidecadal snow reanalysis patterns and snow pillow observations. Hydrol. Process. 36 (6), e14581. doi:10.1002/hyp.14581

CrossRef Full Text | Google Scholar

Pinder, N., Joseph, A., Himmele, G., Ofekeze, E., Jain, A., Espada, K., et al. (2024). “Predicting snow water equivalent in the Tuolumne River Basin, CA through time series forecasting using deep-learning,” in IGARSS 2024-2024 IEEE international geoscience and remote sensing symposium (Athens, Greece: IEEE), 1859–1863. doi:10.1109/IGARSS53475.2024.10640835

CrossRef Full Text | Google Scholar

Premier, V., Marin, C., Bertoldi, G., Barella, R., Notarnicola, C., and Bruzzone, L. (2023). Exploring the use of multi-source high-resolution satellite data for snow water equivalent reconstruction over mountainous catchments. Cryosphere 17 (6), 2387–2407. doi:10.5194/tc-17-2387-2023

CrossRef Full Text | Google Scholar

Pulka, T., Herrnegger, M., Ehrendorfer, C., Lücking, S., Avanzi, F., Formayer, H., et al. (2024). Evaluating precipitation corrections to enhance high-alpine hydrological modeling. J. Hydrol. 645, 132202. doi:10.1016/j.jhydrol.2024.132202

CrossRef Full Text | Google Scholar

Raleigh, M. S., and Small, E. E. (2017). Snowpack density modeling is the primary source of uncertainty when mapping basin-wide SWE with lidar. Geophys. Res. Lett. 44 (8), 3700–3709. doi:10.1002/2016GL071999

CrossRef Full Text | Google Scholar

Revuelto, J., Billecocq, P., Tuzet, F., Cluzet, B., Lamare, M., Larue, F., et al. (2020). Random forests as a tool to understand the snow depth distribution and its evolution in mountain areas. Hydrol. Process. 34 (26), 5384–5401. doi:10.1002/hyp.13951

CrossRef Full Text | Google Scholar

Revuelto, J., Gómez, D., Alonso-González, E., Vidaller, I., Rojas-Heredia, F., Deschamps-Berger, C., et al. (2022). Intermediate snowpack melt-out dates guarantee the highest seasonal grasslands greening in the Pyrenees. Scientific Reports 12 (01), 18328. doi:10.1038/s41598-022-22391-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rice, R., Bales, R. C., Painter, T. H., and Dozier, J. (2011). Snow water equivalent along elevation gradients in the Merced and Tuolumne River basins of the Sierra Nevada. Water Resour. Res. 47 (8). doi:10.1029/2010WR009278

CrossRef Full Text | Google Scholar

Richter, B., Schweizer, J., Rotach, M. W., and van Herwijnen, A. (2021). Modeling spatially distributed snow instability at a regional scale using Alpine3D. J. Glaciol. 67 (266), 1147–1162. doi:10.1017/jog.2021.61

CrossRef Full Text | Google Scholar

Rodriguez-Galiano, V. F., Ghimire, B., Rogan, J., Chica-Olmo, M., and Rigol-Sanchez, J. P. (2012). An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogrammetry Remote Sens. 67, 93–104. doi:10.1016/j.isprsjprs.2011.11.002

CrossRef Full Text | Google Scholar

Safavi, H. R., Sajjadi, S. M., and Raghibi, V. (2017). Assessment of climate change impacts on climate variables using probabilistic ensemble modeling and trend analysis. Theor. Appl. Climatol. 130, 635–653. doi:10.1007/s00704-016-1898-3

CrossRef Full Text | Google Scholar

Schleef, S., Löwe, H., and Schneebeli, M. (2014). Hot-pressure sintering of low-density snow analyzed by X-ray microtomography and in situ microcompression. Acta Mater. 71, 185–194. doi:10.1016/j.actamat.2014.03.004

CrossRef Full Text | Google Scholar

Schneider, D., Molotch, N. P., Deems, J. S., and Painter, T. H. (2020). Analysis of topographic controls on depletion curves derived from airborne lidar snow depth data. Hydrol. Res. 52 (1), 253–265. doi:10.2166/nh.2020.267

CrossRef Full Text | Google Scholar

Smyth, E. J., Raleigh, M. S., and Small, E. E. (2020). Improving SWE estimation with data assimilation: the influence of snow depth observation timing and uncertainty. Water Resour. Res. 56 (5), e2019WR026853. doi:10.1029/2019WR026853

CrossRef Full Text | Google Scholar

Sourp, L., Gascoin, S., Jarlan, L., Pedinotti, V., Bormann, K. J., and Baba, M. W. (2025). Evaluation of high-resolution snowpack simulations from global datasets and comparison with Sentinel-1 snow depth retrievals in the Sierra Nevada, USA. Hydrology Earth Syst. Sci. 29 (3), 597–611. doi:10.5194/hess-29-597-2025

CrossRef Full Text | Google Scholar

Thackeray, C. W., Derksen, C., Fletcher, C. G., and Hall, A. (2019). Snow and climate: Feedbacks, drivers, and indices of change. Curr. Clim. Change Rep. 5, 322–333. doi:10.1007/s40641-019-00143-w

CrossRef Full Text | Google Scholar

Tsai, Y. L. S., Dietz, A., Oppelt, N., and Kuenzer, C. (2019). Remote sensing of snow cover using spaceborne SAR: a review. Remote Sens. 11 (12), 1456. doi:10.3390/rs11121456

CrossRef Full Text | Google Scholar

Viviroli, D., Dürr, H. H., Messerli, B., Meybeck, M., and Weingartner, R. (2007). Mountains of the world, water towers for humanity: typology, mapping, and global significance. Water Resour. Res. 43 (7). doi:10.1029/2006WR005653

CrossRef Full Text | Google Scholar

Vogel, H. J., and Babel, U. (2006). “Soil space diversity and its dynamics: qualitative and quantitative considerations,” in Biodiversity in agricultural production systems. Boca Raton, Florida: Taylor and Francis Group (CRC Press), 41–67. doi:10.1201/b13577

CrossRef Full Text | Google Scholar

Vogel, H. J., Hoffmann, H., and Roth, K. (2005). Studies of crack dynamics in clay soil: I. Experimental methods, results, and morphological quantification. Geoderma 125 (3-4), 203–211. doi:10.1016/j.geoderma.2004.07.009

CrossRef Full Text | Google Scholar

Wang, Y., Su, J., Zhai, X., Meng, F., and Liu, C. (2022). Snow coverage mapping by learning from sentinel-2 satellite multispectral images via machine learning algorithms. Remote Sens. 14 (3), 782. doi:10.3390/rs14030782

CrossRef Full Text | Google Scholar

Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biom. Bull. 1 (6), 80–83. doi:10.2307/3001968

CrossRef Full Text | Google Scholar

J. P. Wilson, and J. C. Gallant (2000). Terrain analysis: principles and applications (John Wiley and Sons).

Google Scholar

Winstral, A., Elder, K., and Davis, R. E. (2002). Spatial snow modeling of wind-redistributed snow using terrain-based parameters. J. Hydrometeorol. 3 (05), 524–538. doi:10.1175/1525-7541(2002)003<0524:SSMOWR>2.0.CO;2

CrossRef Full Text | Google Scholar

Winstral, A., Marks, D., and Gurney, R. (2013). Simulating wind-affected snow accumulations at catchment to basin scales. Adv. Water Resour. 55, 64–79. doi:10.1016/j.advwatres.2012.08.011

CrossRef Full Text | Google Scholar

Wulf, H., Sassik, B., Milani, G., and Leiterer, R. (2020). “High-resolution snow depth monitoring for entire mountain ranges,” in 2020 7th Swiss conference on data science (SDS) (Luzern, Switzerland: IEEE), 1–4. doi:10.1109/SDS49233.2020.00008

CrossRef Full Text | Google Scholar

Xing, D., Hou, J., Huang, C., and Zhang, W. (2022). Estimation of snow depth from AMSR2 and MODIS data based on deep residual learning network. Remote Sens. 14 (20), 5089. doi:10.3390/rs14205089

CrossRef Full Text | Google Scholar

Yang, J., Jiang, L., Luojus, K., Pan, J., Lemmetyinen, J., Takala, M., et al. (2020). Snow depth estimation and historical data reconstruction over China based on a random forest machine learning approach. Cryosphere 14 (6), 1763–1778. doi:10.5194/tc-14-1763-2020

CrossRef Full Text | Google Scholar

Yang, K., Musselman, K. N., Rittger, K., Margulis, S. A., Painter, T. H., and Molotch, N. P. (2022). Combining ground-based and remotely sensed snow data in a linear regression model for real-time estimation of snow water equivalent. Adv. Water Resour. 160, 104075. doi:10.1016/j.advwatres.2021.104075

CrossRef Full Text | Google Scholar

Yang, K., Painter, T. H., Deems, J. S., and Molotch, N. P. (2025). Bias correction for near-real-time estimation of snow water equivalent using machine learning algorithms: a case study in the Tuolumne River basin, California. Remote Sens. Environ. 323, 114693. doi:10.1016/j.rse.2025.114693

CrossRef Full Text | Google Scholar

Zhu, L., Zhang, Y., Wang, J., Tian, W., Liu, Q., Ma, G., et al. (2021). Downscaling snow depth mapping by fusion of microwave and optical remote-sensing data based on deep learning. Remote Sens. 13 (4), 584. doi:10.3390/rs13040584

CrossRef Full Text | Google Scholar