Duncan–Chang damage model of granite residual soil under acidic conditions

To study the mechanical properties of granite residual soil under acid leaching conditions, triaxial consolidated undrained shear tests were conducted on granite residual soil collected from Chenggu County, Hanzhong City. In the experiments, environments with different acidities were simulated, and the shear stress–strain relationship of the soil under different acidities was determined by adjusting the molar concentration of the acid solution. The results indicated that as the molar concentration of acid increased, the shear stress of granite residual soil decreased significantly, especially under high confining pressure conditions, where the attenuation effect of acid on shear stress is more significant. These findings indicated that the acid sensitivity of the soil increased in acidic environments, and the degree of consolidation significantly affected acid sensitivity. Based on experimental data, a Duncan–Chang constitutive model considering acid-induced damage was established, and the applicability of the model was confirmed through parameter analysis. The adjustment of model parameters can reflect the effect of acid damage on the internal friction angle and cohesion of soil. Additionally, this study revealed a quantitative relationship between acid damage and the molar concentration of H⁺. The acid damage coefficient can be determined by fitting the curve, providing a basis for predicting the mechanical behavior of soil under different acidic conditions. This study provided a new perspective for understanding the mechanism of damage to granite residual soil during acidification.

1 Introduction

Granite residual soil is a product of completely weathered igneous rocks formed in the Triassic period. It is characterized by high porosity, low strength, easy water absorption, disintegration, fragmentation, and difficulty in compaction (Zhou et al., 2023; Feng et al., 2024; Yuan et al., 2024). For example, in the Hanzhong region in southern Shaanxi, granite is widely distributed in the central part of Nanzheng District, the southern part of Chenggu County, the southern part of Yang County, and the northwestern part of Xixiang County. These granites formed during the Triassic period, and after more than 200 million years of long-term action (climate change-induced thermal expansion, contraction, hydrolysis, carbonation, etc.), the shallow 10–30 m of the surface was mostly in a fully weathered (grade V) state. The residual soil (grade VI) formed can reach a thickness of more than 20 m. Due to the influence of greenhouse gases (such as CO₂), pyrite, acid rain (Xiao et al., 2025), industrial dust deposition (Petersen, 1986), the return of farmland to forests, the use of nitrate fertilizers (Amiotti et al., 2007; Zhao et al., 2007; Krusche et al., 2003; Matson et al., 1999), leachate from landfills (Xiong and Zheng, 2015), etc., soil acidification in fully weathered granite areas has become quite prominent.

In relatively weakly acidic environments, the basic ions Ca²⁺, Mg²⁺, K⁺, Na⁺, etc., adsorbed on the surface of fully weathered granite particles are exchanged by H⁺, while the leaked water leaches out with basic ions (Xin et al., 2016). If acidity further increases with pollution, it can directly lead to the dissolution of feldspar and calcite inside the particles within a short period, which can further weaken the bonding force between soil particles, causing rearrangement of the particles and significant changes in the microstructure. In acidic environments, residual granite soil undergoes dissolution, leading to a further increase in porosity and the compression coefficient. Previous studies have shown that the shear strength of residual granite soil (Sun et al., 2024) and sandstone (Duan et al., 2025) significantly decreases with an increase in solution acidity and prolonged erosion time, especially with a greater decrease in cohesion. Additionally, the acidic wet–dry cycle greatly affects the deterioration of the cohesion of sandstone (Liu et al., 2016). The same applies to other soil types. Bakhshipour et al. (2016a) and Bakhshipour et al. (2016b) reported that under simulated acid rain, the strength and maximum dry density of kaolin decreased, whereas its compressibility, permeability, and optimal moisture content increased. Gratchev and Towhata (2011) studied the effects of acid pollutants on the compression properties of natural clay and reported that the compression index increased with an increase in acidity. Xu et al. (2018) also found through indoor unconfined compression tests that the unconfined compressive strength gradually decreases with an increase in acid rain concentration, and the pore space expands from small pores to large pores. Xiao et al. (2025) studied the effect of acid rain on the mechanical properties of red clay and found that the dissolution rate of minerals such as Si, Al, Fe, and cement in red clay was high, which destroyed the original structure of the soil and produced a large number of pores. As the pH value of acid rain decreased, the structural gaps of the soil increased, particle aggregation decreased, and the cohesion and internal friction angle of the soil decreased. Fu et al. (2018) obtained Mohr–Coulomb strength criterion parameters and Hoek–Brown strength criterion parameters based on the degradation law of strength under acidic dry‒wet cycles of sandstone. Liang et al. (2023) established a mechanical damage model of sandstone subjected to pH = 1 and 3 HCl solutions by continuous damage mechanics theory. Wang et al. (2016) obtained the strength index under acidic wet‒dry cycling conditions by combining it with the generalized Hoek‒Brown criterion. Based on continuum damage mechanics and elastic–plastic theory, Zhong et al. (2013) assumed that plastic deformation and irreversible damage deformation followed Hyushin’s hypothesis and derived the damage function and loading function, establishing an elastic–plastic damage constitutive model for unsaturated loess. However, according to the research on remolded granite residual soil in the Hanzhong area, even if the strain of the soil is greater than 15%, it is still in the elastic deformation stage, and the strain of plastic yielding is relatively high. Therefore, modeling the residual granite soil in the region based on elastic–plastic theory is not practical.

Therefore, the acid addition condition was considered based on the H⁺ molar concentration of the acid solution, and granite-remolded soil samples were prepared with the optimal moisture content and a compaction degree of 90%. Indoor triaxial consolidation undrained shear tests were conducted to establish a Duncan–Chang constitutive model that can consider acid addition damage and also provide a corresponding theoretical reference for slope and foundation engineering in the residual soil area of Hanzhong granite under acidic conditions.

2 Experimental materials and methods

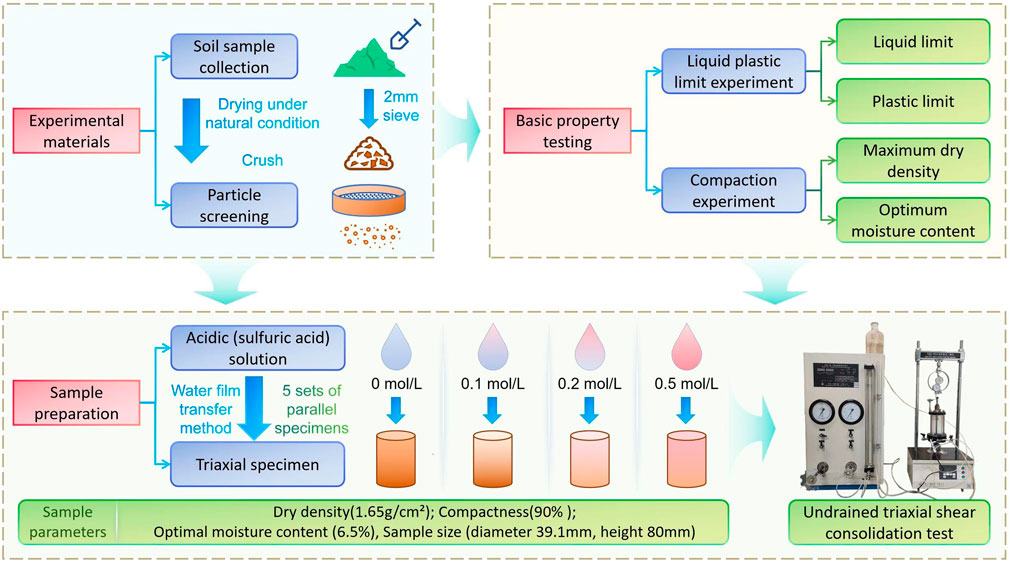
The residual granite soil investigated was collected from a road slope in Tianming Town, Chenggu County, Hanzhong City. The retrieved granite residual soil was air-dried under ambient conditions, crushed, and sieved through a 2 mm sieve, and its physical property indicators were measured (Table 1). The particle size distribution is shown in Figure 1.

Table 1

Table 1. Basic physical indices of granite residual soil and clay.

Figure 1

Figure 1. Particle size distribution diagram of residual granite soil.

To simulate an acidic environment, based on existing methods, a solution simulating an acidic environment was prepared with deionized water. Acidic (sulfuric acid) solutions with acidity levels of 0 mol/L (deionized water), 0.1 mol/L, 0.2 mol/L, and 0.5 mol/L were prepared to simulate an acidic environment. It should be noted that this experiment uses concentrated sulfuric acid with a mass fraction of 98% to prepare the acid solution. The volumes of concentrated sulfuric acid required to prepare the 3 M concentrations of acid solution are 2.7 mL, 5.4 mL, and 6.8 mL, respectively (taking the preparation of 500 mL of acid solution as an example). Cylindrical samples with a dry density of 1.65 g/cm³ (90% compaction degree) (diameter: 39.1 mm, height: 80 mm; five sets of parallel samples) were prepared and loaded with the optimal moisture content (6.5%). The water film transfer method was used to add different concentrations of acidic solution and deionized water so that each set of samples reached the predetermined moisture content (increase in acidity). The experimental method used in this study was the triaxial shear consolidation undrained test, with confining pressures of 100 kPa, 200 kPa, 300 kPa, and 400 kPa and a loading rate of 5 mm/min. The entire experimental process is shown in Figure 2.

Figure 2

Figure 2. Experimental process diagram.

3 Results

3.1 Shear stress–strain

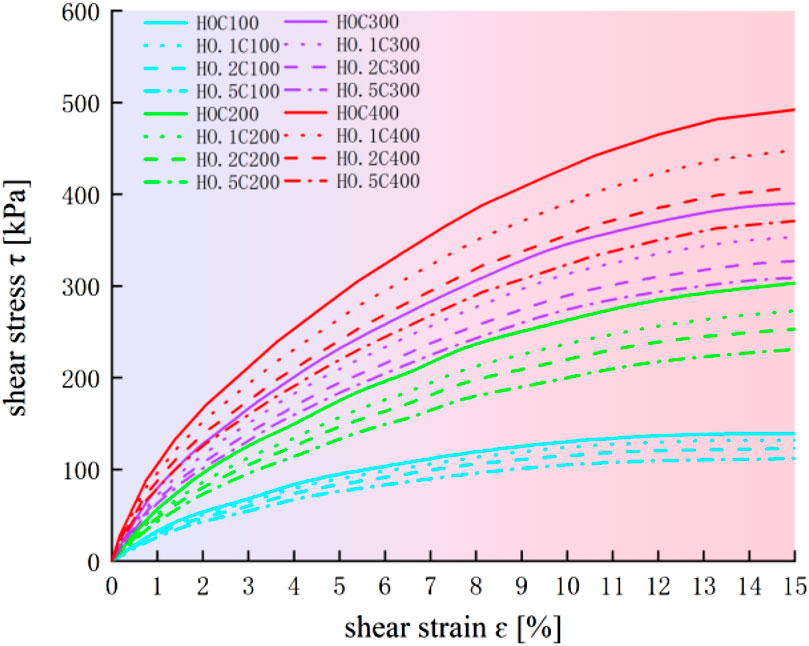
The state of the sample before and after damage is shown in Figure 3. The morphology of the damage diagram shows that the overall failure is bulging, and although the shear band is not very obvious, it can still be observed. In addition, due to the action of the acid solution, some erosion cracks appeared in both the upper and lower parts (above and below the shear band) of the sample during the failure process. It is the presence of these microcracks that caused damage to the entire specimen. The shear stress–strain relationship curves under different acid addition amplitudes and confining pressures are shown in Figure 4, where the number after H in the legend represents the acid concentration in mol/L, and the number after C represents the confining pressure (in kPa).

Figure 3

Figure 3. The state of the sample before and after damage. (a) Initial state and (b) after damage.

Figure 4

Figure 4. Shear stress–strain curves for different acid addition amounts and confining pressures.

The overall curves exhibited shear hardening. Under the same confining pressure conditions, the overall shear stress significantly decreased with an increase in the molar concentration of the acid solution. Particularly, under high confining pressure conditions, the molar concentration of the acid solution had a greater effect on the attenuation of shear stress, whereas under low confining pressure conditions, it had the smallest effect. This occurred because under high confining pressure, the degree of consolidation was sufficient, and the acid solution and granite residual soil particles were in more complete contact, exhibiting stronger acid sensitivity. Overall, under acidic conditions, soluble salts in residual granite soil decompose easily, leading to larger pores (Bai et al., 2024). In addition, particles may break during this process, resulting in a weakened structure (Bai et al., 2025). Both of the above factors can degrade soil strength.

3.2 Duncan–Chang damage model considering the addition of acid

The damage caused by acid addition is denoted as D, which is numerically equal to 1 minus the ratio of the magnitude of the failure shear stress after acid addition to the magnitude of the failure shear stress without acid addition, as expressed by Equation 1:

$D=1-\frac{{\tau }_i^{\max }}{{\tau }_0^{\max }}=1-\frac{{\left({\sigma }_1-{\sigma }_3\right)}_i^{\max }}{{\left({\sigma }_1-{\sigma }_3\right)}_0^{\max }}.(1)$

In the equation, ${\sigma }_1,{\sigma }_3$ are the maximum principal stress and minimum principal stress, respectively.

According to the expression of the Duncan–Chang model and considering the situation of greater acid damage, the Duncan–Chang constitutive model under the influence of an acidic environment is expressed by Equation 2:

$\mathrm{\tau }=\frac{{\sigma }_1-{\sigma }_3}{2}=\frac{\mathrm{\epsilon }}{\mathrm{a}+\mathrm{b}\mathrm{\epsilon }}.(2)$

Here, $\mathrm{\epsilon }$ represents the strain, and a and b represent the coefficients related to the initial deformation modulus and ultimate deviation stress, respectively.

According to the Duncan–Chang model, the coefficient a is the reciprocal of the initial tangent modulus $E_0$ and can be expressed by Equation 3:

$\mathrm{a}=\frac{1}{E_0}.(3)$

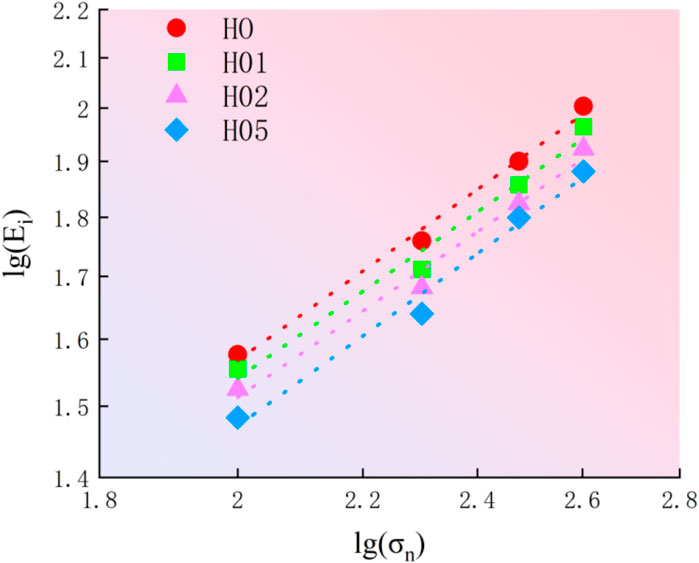
Additionally, based on the relationship between the initial tangent modulus and the confining pressure, the initial tangent modulus of residual granite soil can be expressed by Equation 4:

$E_0=K{\left({\sigma }_n\right)}^n.(4)$

Based on the findings of An et al. (2020), the tangent modulus of residual granite soil during shear can also be expressed by Equation 5:

${\mathrm{E}}_{\mathrm{t}}=\mathrm{K}{\left({\mathrm{\sigma }}_{\mathrm{n}}\right)}^{\mathrm{n}}{\left(1-\frac{\mathrm{\tau }-{\mathrm{R}}_{\mathrm{f}}}{{\mathrm{\tau }}_{\mathrm{f}}}\right)}^2.(5)$

In the equation, ${\mathrm{E}}_{\mathrm{t}}$ represents the tangent modulus, and ${\mathrm{R}}_{\mathrm{f}}$ represents the failure ratio, which can be expressed by Equation 6:

${\mathrm{R}}_{\mathrm{f}}=\frac{{\mathrm{\tau }}_{\mathrm{f}}}{{\mathrm{\tau }}_{\text{ult}}}.(6)$

In the Equation 6, ${\mathrm{\tau }}_{\mathrm{f}}$ represents the failure strength of residual granite soil, and ${\mathrm{\tau }}_{\text{ult}}$ represents the ultimate shear strength of residual granite soil. b in Equation 2 is expressed as Equation 7.

$\mathrm{b}=\frac{1}{{\mathrm{\tau }}_{\text{ult}}}=\frac{2}{{\left({\mathrm{\sigma }}_1-{\mathrm{\sigma }}_3\right)}_{\text{ult}}}.(7)$

Further verification is needed to determine whether the Duncan–Chang model can be applied to the shear deformation of residual granite soil. Therefore, Equation 2 can be expressed as Equation 8:

$\frac{\mathrm{\epsilon }}{\mathrm{\tau }}=\frac{1}{{\mathrm{E}}_0}+\frac{\mathrm{\epsilon }}{{\mathrm{\tau }}_{\text{ult}}}.(8)$

Similarly, Equation 4 can be expressed by Equation 9:

$\lg \left({\mathrm{E}}_{\mathrm{i}}\right)=\text{lgK}+\text{nlg}\left({\mathrm{\sigma }}_{\mathrm{n}}\right).(9)$

Based on the above analysis, the Duncan–Chang model applicable to residual granite soil was transformed to verify the linear relationship between $\frac{\mathrm{\epsilon }}{\mathrm{\tau }}\sim \mathrm{\epsilon }$ and $\lg \left({\mathrm{E}}_{\mathrm{t}}\right)\sim \lg \left({\mathrm{\sigma }}_{\mathrm{n}}\right)$ (An et al., 2020; Wang et al., 2004).

3.3 Applicability condition verification

The relationship curve of $\frac{\mathrm{\epsilon }}{\mathrm{\tau }}\sim \mathrm{\epsilon }$ is as shown in Figure 5. Additionally, $\lg \left({\mathrm{E}}_{\mathrm{t}}\right)\sim \lg \left({\mathrm{\sigma }}_{\mathrm{n}}\right)$ was plotted, as shown in Figure 6. A strong linear relationship was observed between $\frac{\mathrm{\epsilon }}{\mathrm{\tau }}\sim \mathrm{\epsilon }$ and $\lg \left({\mathrm{E}}_{\mathrm{t}}\right)\sim \lg \left({\mathrm{\sigma }}_{\mathrm{n}}\right)$, indicating that the shear stress and strain of residual granite soil followed a hyperbolic relationship. Additionally, determined by the shear test, E_i was found to meet the applicability conditions of the Duncan–Chang model. ${\mathrm{E}}_{\mathrm{i}}$ determined by the shear test also met the applicability conditions of the Duncan–Chang model.

Figure 5

Figure 5. $\frac{{\mathrm{\epsilon }}_1}{{\mathrm{\sigma }}_1-{\mathrm{\sigma }}_3}\sim {\mathrm{\epsilon }}_1$ relationship curve of residual. (a) [H₊] = 0 mol/L, (b) [H₊] = 0.1 mol/L, (c) [H₊] = 0.2 mol/L, and (d) [H₊] = 0.5 mol/L.

Figure 6

Figure 6. Curve of $\lg \left({\mathrm{E}}_{\mathrm{i}}\right)\sim \lg \left({\mathrm{\sigma }}_{\mathrm{n}}\right)$ is shown.

3.4 Model parameter analysis

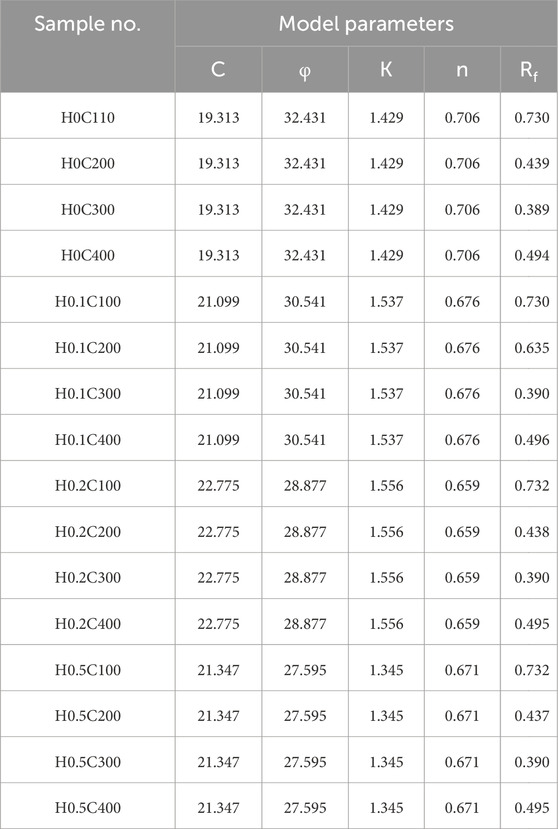
The Duncan–Chang model has five parameters ($\mathrm{c},\mathrm{\phi },\mathrm{K},\mathrm{n},{\mathrm{R}}_{\mathrm{f}}$), among which $\mathrm{c},\mathrm{\phi }$ can be determined from the shear stress–strain data of four confining pressures (100 kPa, 200 kPa, 300 kPa, and 400 kPa); $\mathrm{K},\mathrm{n}$ can be determined by fitting the C data. The five parameters of the Duncan–Chang model for residual granite soil are shown in Table 2, where the first column represents the sample number, and the naming convention is the same as in Figure 4.

Table 2

Table 2. Duncan–Chang model parameters.

To assess the effect of different $\left[{\mathrm{H}}^{+}\right]$ values on the main parameters of the Duncan–Chang model for granite residual soil, $\left[{\mathrm{H}}^{+}\right]$ was used as the independent variable, and $\mathrm{c},\mathrm{\phi },\mathrm{K},\text{and\hspace{0.17em}}\mathrm{n}$ were used as the dependent variables (Figure 7). The effect of $\left[{\mathrm{H}}^{+}\right]$ on various dependent variables had a certain regularity, which can reflect and predict the strain law of granite residual soil under different acid damage conditions. However, because only four different acidification scenarios were studied and a single acidic solution was used, neglecting the effect of anions, this issue will be investigated in another study.

Figure 7

Figure 7. Influence of H⁺ molar concentration on the main parameters of the Duncan–Chang model. (a) Relationship of $\mathrm{c}$ and [H⁺], (b) relationship of $\mathrm{\phi }$ and [H⁺], (c) relationship of K and [H⁺], and (d) relationship of $\mathrm{n}$ and [H⁺].

It can be observed that the H⁺ molar concentration has a significant effect on the internal friction angle and n value because under the action of an acid solution, some rough large particles are broken into smooth small particles. The effect of H⁺ molar concentration on cohesion and K value shows different trends: cohesion and K value first increase and then decrease, reaching their peak at a concentration of 0.2 mol/L. This may be due to acidification causing changes in the distribution of pores and particle size distribution, with the strongest bonding force between soil particles at this molar concentration.

The damage under different confining pressures was normalized, and the relationship curve between $\mathrm{D}$ and $\left[{\mathrm{H}}^{+}\right]$ under different confining pressures is shown in Figure 8a. The damage $\mathrm{D}$ increased with an increase in H+ molar concentration, with the maximum damage amplitude at a confining pressure of 400 kPa and the minimum damage amplitude at a confining pressure of 100 kPa. The relationship between the molar concentrations of H⁺ and $\mathrm{D}$ is expressed in Equation 10, and the relationship between $\frac{\left[{\mathrm{H}}^{+}\right]}{1+\mathrm{D}}$ and $\left[{\mathrm{H}}^{+}\right]$ is represented in Figure 8b.

$1+\mathrm{D}=\frac{\left[{\mathrm{H}}^{+}\right]}{\mathrm{m}+\mathrm{n}\left[{\mathrm{H}}^{+}\right]}.(10)$

Figure 8

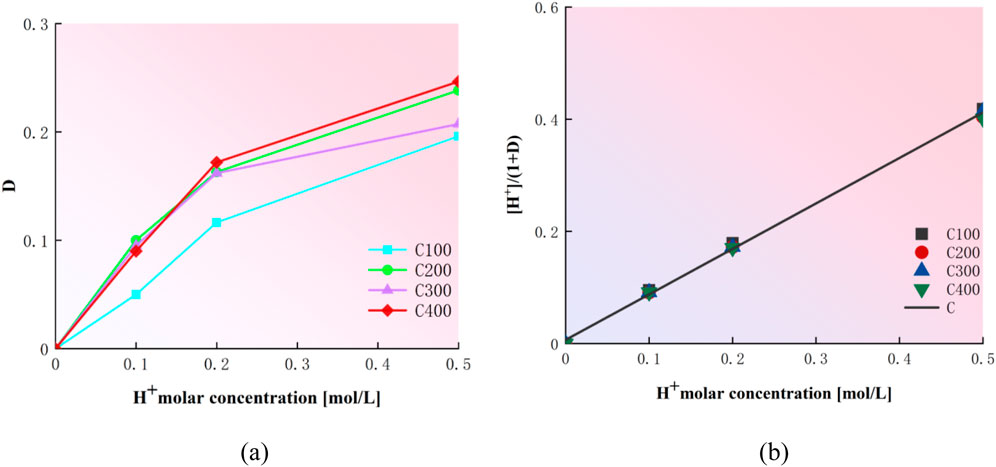
Figure 8. Relationship curve between H⁺ molar concentration and acid damage. (a) Relationship of D and [H⁺] and (b) relationship of [H⁺]/(1 + D) and [H⁺].

The parameters m and n represent the coefficients related to acid damage, independent of the confining pressure, and can be obtained by fitting the intercept and slope of the $\frac{\left[{\mathrm{H}}^{+}\right]}{1+\mathrm{D}}\sim \left[{\mathrm{H}}^{+}\right]$ curve. In this example, from Figure 8B, where m and n are the intercepts and slopes of line C, it was observed that $\mathrm{m}=0.006525$, and $\mathrm{n}=0.811125$. This indicated a quantitative relationship between the H⁺ molar concentration and acid damage D for the same acid solution.

It should be noted that this article confirms that the Duncan–Chang model is applicable not only to the mechanical properties of granite residual soil but also to granite residual soil after acid erosion. The reason for linking the H⁺ molar concentration with damage D is to explore the damage patterns of granite residual soil under different acid concentrations. In the next stage of research, the author will continue to improve the Duncan–Chang constitutive model by incorporating acid concentration as a variable into the model.

4 Conclusion and discussion

This study investigated the mechanical behavior of residual granite soil under acidic conditions through a series of indoor triaxial consolidation undrained shear tests. A modified Duncan–Chang constitutive model that incorporates acid damage effects was subsequently established. The principal findings are summarized as follows:

1. The mechanical properties of residual granite soil are significantly degraded in acidic environments. An increase in the molar concentration of the acid solution leads to a marked reduction in soil shear stress. This attenuation effect is more pronounced under high confining pressures, indicating that the soil’s acid sensitivity is enhanced, particularly under well-consolidated conditions.

2. The Duncan–Chang model effectively describes the shear deformation behavior of the soil under acidic conditions. The applicability was confirmed as the shear stress–strain relationship maintained a hyperbolic form, and the failure ratio was successfully determined from the test data.

3. Parameter analysis of the Duncan–Chang model revealed that acid damage profoundly influences a soil’s key parameters, such as the internal friction angle and cohesion. The degradation of soil strength with increasing acid concentration can be accurately represented by corresponding adjustments to these model parameters.

4. A quantitative relationship between acid damage and H⁺ concentration was established. Through curve fitting, the acid damage coefficients m and n were obtained, enabling the prediction of soil mechanical behavior under varying levels of acidity.

In summary, this research provides a theoretical foundation for the design of slopes and foundations in granite residual soil areas exposed to acidic conditions. By accounting for increased acid damage, the stability and bearing capacity of soils in such environments can be evaluated more accurately. A primary limitation of this study is the use of a single acid type, which did not account for the potential effects of different anions on the soil’s acidification process and mechanical response. Future work should investigate the influence of various acid solutions and explore the practical application of these findings in engineering design.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DL: Conceptualization, Writing – original draft. FD: Conceptualization, Writing – original draft, Writing – review and editing. YW: Data curation, Formal analysis, Writing – original draft, Writing – review and editing. YL: Data curation, Writing – original draft. HG: Conceptualization, Funding acquisition, Methodology, Resources, Writing – original draft, Writing – review and editing.

Funding

The authors declare that financial support was received for the research and/or publication of this article. The research was funded by the Scientific Research Plan Projects of Shaanxi Education Department, grant number 23JC019, the Key Research and Development Projects of Shaanxi Province, grant number 2023-YBSF-324 and the Research Project of China DK Comprehensive Engineering Investigation and Design Research Institute Co., Ltd., grant number 2024-DKY-W02.

Conflict of interest

Authors DL and YL were employed by China DK Comprehensive Engineering Investigation and Design Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from China DK Comprehensive Engineering Investigation and Design Research Institute Co., Ltd. The funder had the following involvement in the study: research on the deformation and strength degradation of soil under acid pollution conditions.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amiotti, N. M., Bravo, O., Zalba, P., and Peinemann, N. (2007). Effect of landscape position on the acidification of loess-derived soils under Pinus radiata. Austral Ecol. 32 (5), 534–540. doi:10.1111/j.1442-9993.2007.01725.x

CrossRef Full Text | Google Scholar

An, R., Kong, L. W., and Zhang, X. W. (2020). Mechanical properties and generalized duncan-chang model for granite residual soils using borehole shear tests. Chin. J. Geotech. Eng. 42 (09), 1723–1732. doi:10.11779/CJGE202009017

CrossRef Full Text | Google Scholar

Bai, B., Chen, J., Bai, F., Nie, Q. K., and Jia, X. X. (2024). Corrosion effect of acid/alkali on cementitious red mud-fly ash materials containing heavy metal residues. Environ. Technol. Innov. 33, 103485. doi:10.1016/j.eti.2023.103485

CrossRef Full Text | Google Scholar

Bai, B., Zhang, B. X., Chen, H. J., and Chen, P. P. (2025). A novel thermodynamic constitutive model of coarse-grained soils considering the particle breakage. Transp. Geotech. 50, 101462. doi:10.1016/j.trgeo.2024.101462

CrossRef Full Text | Google Scholar

Bakhshipour, Z., Asadi, A., Huat, B. B. K., and Sridharan, A. (2016a). Long-term intruding effects of acid rain on engineering properties of primary and secondary kaolinite clays. Int. J. Geosynth. Ground Eng. 2 (3), 21. doi:10.1007/s40891-016-0059-1

CrossRef Full Text | Google Scholar

Bakhshipour, Z., Asadi, A., Huat, B. B. K., Sridharan, A., and Kawasaki, S. (2016b). Effect of acid rain on geotechnical properties of residual soils. Transp. Geotech. 56 (6), 1008–1020. doi:10.1016/j.sandf.2016.11.006

CrossRef Full Text | Google Scholar

Duan, M. T., Jin, C. H., Wang, D., and Xie, H. (2025). Tensile and acid–base properties of sandstone in a Saltwater-CO₂ environment. Geotech. Geol. Eng. 43 (2), 82. doi:10.1007/s10706-024-03055-1

CrossRef Full Text | Google Scholar

Feng, D. L., Wang, Y. X., Chen, D. Y., and Liang, S. H. (2024). Experimental study on the influence mechanism of clay particles on the microbial treatment of granite residual soil. Constr. Build. Mater. 411, 134659. doi:10.1016/j.conbuildmat.2023.134659

CrossRef Full Text | Google Scholar

Fu, Y., Yuan, W., Liu, X. R., Miao, L. L., and Xie, W. B. (2018). Deterioration rules of strength parameters of sandstone under cyclical wetting and drying in acid-based environment. Rock Soil Mech. 39 (09), 3331–3339. doi:10.16285/j.rsm.2016.2711

CrossRef Full Text | Google Scholar

Gratchev, I., and Towhata, I. (2011). Compressibility of natural soils subjected to long-term acidic contamination. Environ. Earth Sci. 64 (1), 193–200. doi:10.1007/s12665-010-0838-2

CrossRef Full Text | Google Scholar

Krusche, A. V., de Camargo, P. B., Cerri, C. E., Ballester, M. V., Lara, L. B. L. S., Victoria, R. L., et al. (2003). Acid rain and nitrogen deposition in a sub-tropical watershed (piracicaba): ecosystem consequences. Environ. Pollut. 121 (3), 389–399. doi:10.1016/s0269-7491(02)00235-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Y. L., Huo, R. K., Mu, Y. H., and Song, Z. Y. (2023). Coupled chemical and mechanical damage model for acid-corroded sandstone. Int. J. Geomech. 23 (3), 04022300–04022311. doi:10.1061/IJGNAI.GMENG-7825

CrossRef Full Text | Google Scholar

Liu, X. R., Li, D. L., Wang, Z., and Zhang, L. (2016). The effect of dry-wet cycles with acidic wetting fluid on strength deterioration of shaly sandstone. Chin. J. Rock Mech. Eng. 35 (08), 1543–1554. doi:10.13722/j.cnki.jrme.2015.1419

CrossRef Full Text | Google Scholar

Matson, P. A., Mcdowell, W. H., Townsend, A. R., Vitousek, P. M., and Townsend, A. R. (1999). The globalization of N deposition: ecosystem consequences in tropical environments. Biogeochemistry 46 (1-3), 67–83. doi:10.1007/978-94-011-4645-6_4

CrossRef Full Text | Google Scholar

Petersen, L.(1986). Effects of acid deposition on soil and sensitivity of the soil to acidification. Experientia. 42 (4), 340–344. doi:10.1007/bf02118613

CrossRef Full Text | Google Scholar

Sun, Y. L., Li, Z. F., Zhang, X. S., Huang, Q., Wu, Y. Q., and Xie, J. B. (2024). Experimental study on tensile strength of granite residual soil during drying and wetting. Geomech. Energy Environ. 37, 100523. doi:10.1016/j.gete.2023.100523

CrossRef Full Text | Google Scholar

Wang, L. Z., Zhao, Z. Y., and Li, L. L. (2004). Non-linear elastic model considering soil structural damage. J. Hydraul. Eng. (01), 83–89. doi:10.13243/i.cnki.slxb.2004.01.016

CrossRef Full Text | Google Scholar

Wang, Z. J., Liu, X. R., Fu, Y., Zhang, L., and Yuan, W. (2016). Deterioration of mechanical parameters of argillaceous sandstone under wetting-drying cycles in acidic environment. Chin. J. Geotech. Eng. 38 (06), 1152–1159. doi:10.11779/CJGE201606024

CrossRef Full Text | Google Scholar

Xiao, S. B., Xu, Y., Tang, S. T., Cui, H., and Wei, S. Q. (2025). Effects of soil acidification on the distribution and availability of arsenic in aggregates. Environ. Sci. 46 (3), 1762–1773. doi:10.13227/j.hjkx.202402134

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, P., Liang, C. Y., Wu, S. R., Liu, Z., Shi, J. S., and Wang, T. (2016). Kinematic characteristics and dynamic mechanisms of large-scale landslides in a Loess Plateau: a case study for the north bank of the baoji stream segment of the wei river, China. Bull. Eng. Geol. Environ. 75 (2), 659–671. doi:10.1007/s10064-015-0824-8

CrossRef Full Text | Google Scholar

Xiong, J. Y., and Zheng, Z. (2015). Characteristics of the dissolved organic matter in landfill leachate and their removal technology: a review. Environ. Chem. 34 (01), 44–53. doi:10.7524/j.issn.0254-6108.2015.01.2014033001

CrossRef Full Text | Google Scholar

Xu, S. F., Wu, X. H., Cai, Y. Q., Ding, Y. H., and Wang, Z. (2018). Strength and leaching characteristics of magnesium phosphate cement-solidified Zinc- contaminated soil under the effect of acid rain. Soil Sediment. Contam. 27 (2), 161–174. doi:10.1080/15320383.2018.1438364

CrossRef Full Text | Google Scholar

Yuan, B. X., Liang, J. K., Zhang, B. F., Chen, W. J., Huang, X. L., Yun, L., et al. (2024). Optimized reinforcement of granite residual soil using a cement and alkaline solution: a coupling effect. J. Rock Mech. Geotech. Eng. 17 (1), 509–523. doi:10.1016/j.jrmge.2024.01.009

CrossRef Full Text | Google Scholar

Zhao, W., Cai, Z. C., and Xu, Z. H. (2007). Does ammonium-based N addition influence nitrification and acidification in humid subtropical soils of China. Plant and Soil 297 (1-2), 213–221. doi:10.1007/s11104-007-9334-1

CrossRef Full Text | Google Scholar

Zhong, Z. L., Liu, X. R., and Liu, Y. X. (2013). Research on elastoplastic damage constitutive model of intact Q2l loess in northwestern of China. Environ. Earth Sci. 69 (1), 85–92. doi:10.1007/s12665-012-1936-0

CrossRef Full Text | Google Scholar

Zhou, Y., Chen, D. X., Yu, J. J., and Li, Q. (2023). Test and micro-mechanism of disintegration of granite residual soil under dry-wet cycles. J. Yangtze River Sci. Res. Inst. 40 (01), 153–160. doi:10.11988/ckyyb.20210902

CrossRef Full Text | Google Scholar