Fast simulation of array laterlog utilizing optimized computational model and neural networks

A new method has been developed to rapidly simulate array laterolog (ALL) responses in invaded formations drilled by deviated wells. This method is characterized by two key aspects: simplification of the computational model and acceleration using neural networks. Initially, a five-layered model in combination with an equivalent resistivity scheme is chosen to describe the formations with arbitrary vertical layers. Additionally, three radially invaded layers among the five vertical layers are identified, with the remaining two invaded layers assumed to an uninvaded bed using the radial geometrical factor. These simplifications result in a computational model with only comprises 17 parameters, ensuring both accuracy and generalization. The ALL database for the simplified model is then established using the three-dimensional finite element method (FEM). The Convolutional Neural Network (CNN) algorithm is employed to train the nonlinear mapping between formation parameters and ALL responses. Subsequently, this new ALL simulation method is applied to classical Oklahoma formations with varying well deviations. Numerical results demonstrate the simplified model’s excellent generalization ability for accommodating formations with arbitrary layers while maintaining a relative computation error within 2%. Compared to the traditional simulation method, the CNN-predicted ALL responses improves the computational speed by over two orders of magnitude, establishing a robust foundation for expeditious ALL data processing.

1 Introduction

Precise resistivity measurements of underground rocks are crucial for both qualitative identification and quantitative evaluation of oil and gas reservoirs (Chen, 2021; Ren et al., 2020; Deng et al., 2018; Yang et al., 2025). The array laterolog (ALL), known for its high vertical resolution, multiple lateral detection depths, and wide operating resistivity range, has been widely employed in this field (Maurer et al., 2009; Xiao et al., 2016). In vertical wells, ALL curve separation serves as a reliable indicator for the invasion status, allowing for straightforward visual or eye-ball interpretation (Tan et al., 2012; Si et al., 2020). However, in deviated wells, the combined effects of well deviation, mud filtrate invasion, and layer thickness distort ALL responses, rendering qualitative interpretation ineffective ((Deng et al., 2010; Deng et al., 2010; Nan et al., 2002; Ni et al., 2018). To accurately recover the formation electrical parameters, parametric inversion is typically employed. Unfortunately, ALL inversion demands extensive forward simulations, and rapid ALL modeling remains challenging (Zhu et al., 2019).

Due to the formation inhomogeneity, complicated tool structures, and arbitrary well deviation, the 3D FEM has become the preferred approach for current ALL modeling (Pan et al., 2013; Feng et al., 2013). Theoretically, the computational efficiency of 3D ALL modeling depends on the size of the sparse matrix and the solver used. By leveraging the symmetry of the formation model and electric current fields, the matrix size can be reduced by half (Xing et al., 2008; Pan et al., 2016; Hu et al., 2019). Additionally, front solvers and domain decomposition methods have been developed to accelerate matrix solutions by optimizing the electrode installation sequence (Wang et al., 2009; Wang et al., 2023; Wang et al., 2024; Wang et al., 2025a). Despite these advancements, the computational complexity of 3D modeling still limits processing speed, making it unable to meet real-time ALL data processing requirements.

To enhance the computational speed of ALL, numerous data-driven approaches have been explored (Zhang and Zhou, 2002; Wu et al., 2025; Hagiwara, T., 2023). These approaches primarily focus on two key aspects: the computational model construction and the selection of deep learning (DL) algorithms. The model is typically established in two ways: a fixed computational domain approach and a fixed number of layers approach. The former, defined by a pixel-based representation, accommodates formations with arbitrary beds but faces challenges in database generation due to high computational demands from excessive pixel counts. In contrast, the fixed-layer model relies on a limited set of control parameters, enabling efficient database construction since the required data size decreases exponentially with fewer parameters (Liu et al., 2024; Zhao et al., 2024). However, since the number of layers within the tool’s detection range is uncertain, this approach may oversimplify the problem, leading to significant computational errors. Thus, balancing the tradeoff between generalization capability for complex formations and simulation accuracy remains a key challenge.

Another key factor influencing the accuracy and efficiency of data-driven ALL simulation is the optimal selection of DL algorithms. For models with parametric descriptions, either deep neural networks (DNNs) or convolutional neural networks (CNNs) can be employed (Zhu et al., 2020; Wu and Fan, 2021). However, due to the high dimensionality of pixel-based models, CNNs are generally more suitable. Although CNNs handle large inputs more effectively, their prediction accuracy tends to be slightly lower than that of DNNs. Thus, further research is needed to determine the best integration of computational models and DL algorithm selection.

2 Optimization of computation model

2.1 Simplification of vertical layers

The response of ALL is susceptible to the coupled effects of multiple factors such as mud invasion, formation dip, and layer thickness, resulting in complex logging response characteristics. Therefore, constructing a computational model that aligns with actual formation conditions is of great significance for improving the efficiency and accuracy of ALL forward modeling (Yan et al., 2022). This study adopts the high-resolution array laterologging tool (HRLA) developed by Schlumberger as the research vehicle. This tool achieves a vertical resolution of up to 0.3 m in vertical wells. During logging, the logging response of the target layer is significantly affected by the surrounding rocks of the upper and lower 1 to 2 layers, while the influence of surrounding rocks at a farther distance can be ignored.

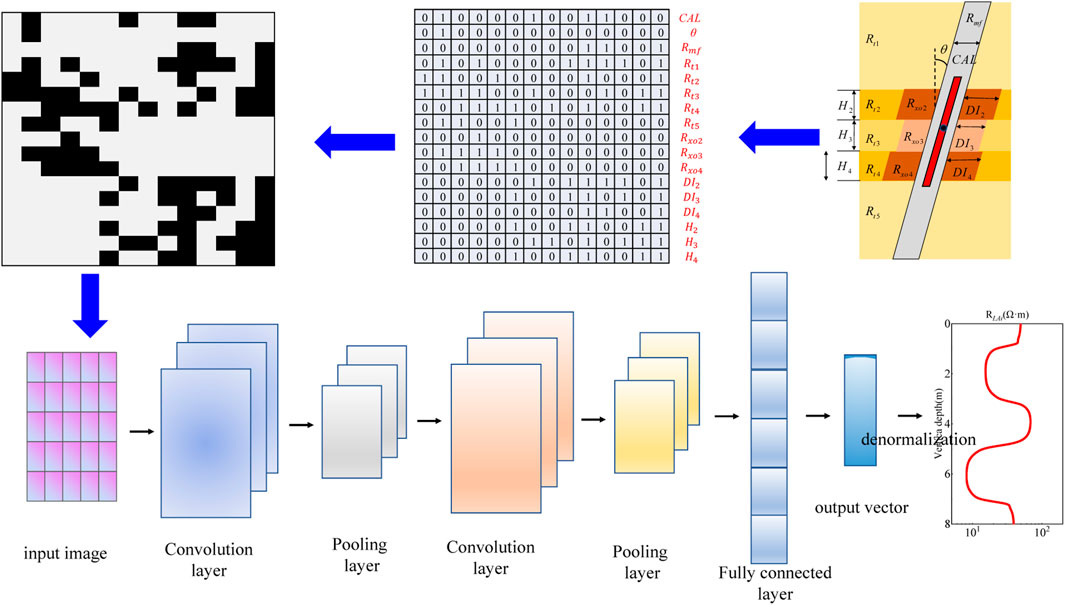
To establish an optimal computational model for ALL, this study conducted parameter optimization from both radial and longitudinal dimensions. The longitudinal dimension focused on optimizing the formation layering structure, specifically constructing an arbitrary-layer formation model and three simplified layered models: Model Vertical 3 (Model V_3), Model Vertical 5 (Model V_5) and Model Vertical 7 (Model V_7), as shown in Figures 1a–d. The core difference among the three simplified models lies in the number of layers: Model V_3 is a three-layer structure, Model V_5 is a five-layer structure, and Model V_7 is a seven-layer structure. To standardize parameter representation, the well deviation angle is defined as θ, the target layer resistivity as R_t, the resistivity of the upper (lower) jth layer of surrounding rock as $R_{sj}^u$ ($R_{sj}^d$), and the equivalent surrounding rock resistivity as $R_{s2}^{ue}$ ($R_{s2}^{de}$).

Figure 1

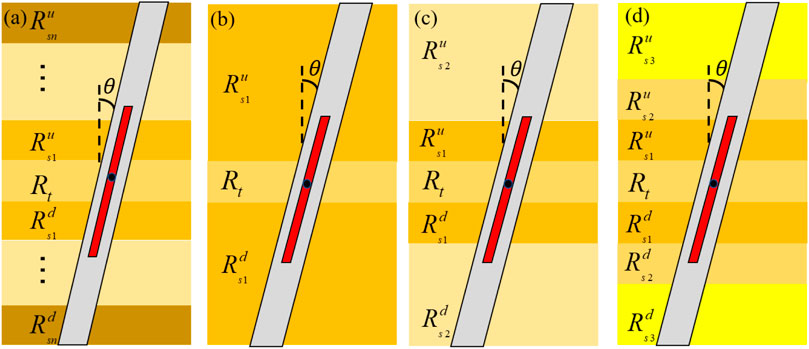
Figure 1. Selection of the Number of Layers of the Calculation Model: (a) multi-layer model; (b) Model V_3; (c) Model V_5; (d) Model V_7.

Figures 2a–c compare the relative errors between the logging responses of Model V_3, Model V_5 and Model V_7, and the original formation model under three detection modes: RLA1, RLA3, and RLA5. Table 1 shows the relative errors of the computational results for the three vertical models. Error analysis indicates that Model_V3 exhibits relatively large relative errors compared to FEM results across all three detection modes. Under the RLA1 mode, both Model_V5 and Model_V7 maintain relative errors within 2%, meeting the accuracy requirements. However, it should be noted that in actual drilling operations, if borehole enlargement occurs, the reliability of apparent resistivity data acquired in shallow detection modes (RLA1) significantly decreases, necessitating comprehensive analysis combined with caliper correction data. Under the RLA3 and RLA5 modes, Model V_7 (the seven-layer model) demonstrates better agreement with the response of the original formation, whereas Model V_5 (the five-layer model) exhibits a relative error of approximately 5% only in areas where the surrounding rock is thin. Balancing computational accuracy and model complexity, Model V_5 maintains an error level comparable to Model V_7 while reducing the number of model parameters and computational cost, offering greater value for engineering applications and advantages in computational efficiency.

Figure 2

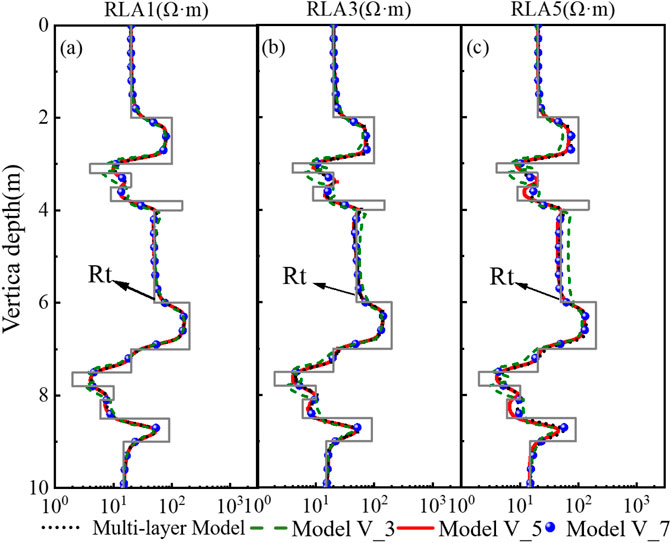
Figure 2. Array lateral log responses of two calculation models in layered medium under different detection modes: (a) RLA1, (b) RLA3, (c) RLA5, where the well deviations are 60°.

Table 1

Table 1. Comparison of calculation accuracy among three vertical models.

It is noteworthy that in high-angle or horizontal well environments, the formation resolution of array laterologging (ALL) significantly decreases, and the logging response of the target layer is subject to enhanced interference from more distant surrounding rock, directly leading to reduced computational accuracy of Model V_5. To address this issue, this study proposes that when the thickness of the surrounding rock above and below the target layer is small, equivalent processing methods should be employed to integrate the electrical properties of the surrounding rock, thereby mitigating interference from distal layers and enhancing the adaptability of Model V_5. Specific equivalent processing methods will be elaborated in the following section.

2.2 Resistivity equivalence for outmost surrounding beds

In highly deviated/horizontal wells, due to the reduced resolution of the tool, the resistivity contrast between distant surrounding rocks and the target layer is significant. When the thickness of the target layer is small, the influence of distant surrounding rocks on the target layer cannot be ignored. For one-dimensional cylindrical and planar layered formations, an equivalence transformation into a single layer can be achieved by leveraging numerical geometric factors (Wang et al., 2025b). Equation 1 presents the definition of the numerical geometric factor.

${\mathit{G}}_{\mathit{i}}=\left\{\begin{array}{c}\frac{{\mathit{R}}_{\mathit{L}\mathit{A}\mathit{i}}-{\mathit{R}}_{\mathit{t}\mathit{e}}}{{\mathit{R}}_{\mathit{s}}^{\mathit{u}}-{\mathit{R}}_{\mathit{t}\mathit{e}}},\mathit{z}<{\mathit{z}}_0\\ \frac{{\mathit{R}}_{\mathit{L}\mathit{A}\mathit{i}}-{\mathit{R}}_{\mathit{t}\mathit{e}}}{{\mathit{R}}_{\mathit{s}}^{\mathit{d}}-{\mathit{R}}_{\mathit{t}\mathit{e}}},\mathit{z}\ge {\mathit{z}}_0\end{array}\right.(1)$

where z and z₀ denote the vertical depths of the laterolog tool and the target layer midpoint, respectively; R_te and R_LAi represent the equivalent resistivity of the target zone and the apparent resistivity from the ith array laterolog electrode, respectively.

Building upon the theory of numerical geometric factors, this study proposes an equivalent method for the surrounding rocks in the five-layer model. Figure 3 illustrates the detailed process of the equivalent method for surrounding rocks, whose core lies in replacing multiple formations beyond the five layers with two formations of semi-infinite thickness. The resistivity of the equivalent formations is shown in Equation 2.

${{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}}^{\prime }=\frac{{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}+{\displaystyle {\sum }_{\mathit{i}=3}^{\mathit{N}}}\left\{\begin{array}{c}\left({\mathit{G}}_{\mathit{i}}^{\mathit{u}}-{\mathit{G}}_{\mathit{i}-1}^{\mathit{u}}\right)\sqrt{{\mathit{R}}_{\mathit{s}\mathit{i}-1}^{\mathit{u}}-{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}},\left({\mathit{R}}_{\mathit{s}2}^{\mathit{u},\mathit{i}-1}>{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}\right)\\ -\left({\mathit{G}}_{\mathit{i}}^{\mathit{u}}-{\mathit{G}}_{\mathit{i}-1}^{\mathit{u}}\right)\sqrt{{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}-{\mathit{R}}_{\mathit{s}\mathit{i}-1}^{\mathit{u}}},\left({\mathit{R}}_{\mathit{s}2}^{\mathit{u},\mathit{i}-1}>{\mathit{R}}_{\mathit{s}2}^{\mathit{u}}\right)\end{array}\right.}{\left(1-{\mathit{G}}_2^{\mathit{u}}\right)}(2)$

where ${R_{s2}^u}^{\prime }$ is the equivalent outermost layer resistivity, $R_{si}^u$ is the resistivity of the ith overlying surrounding rock, and $G_i^u$ is the vertical numerical geometric factor at the ith upper interface.

Figure 3

Figure 3. Surrounding rock equivalent method: (a) Original multi-layer model; (b) Equivalent five-layer model.

Among the six detection modes of the HRLA tool, the RLA5 mode possesses the deepest depth of investigation, which also leads to the greatest degree of interference from surrounding rock on the target zone’s logging response. Figure 4 illustrates the logging response characteristics of a thin interbedded formation model under the RLA5 detection mode at well inclination angles of 30°, 60°, and 80°, and compares the results from different computational models. The detailed analysis is as follows: In low-inclination wells (30°), the RLA5 logging response curves obtained by the three computational methods largely coincide. This indicates that under such well conditions, the structural distribution of the formation has limited influence on the logging signal, and the impact of distal surrounding rock on the tool response is negligible. Thus, a simplified model is sufficient to meet computational requirements. In contrast, in high-angle (60°) and horizontal (80°) wells, the RLA5 response calculated by Model V_5 (the five-layer model) without equivalent treatment shows significant deviation from the true formation response, and this deviation increases markedly with higher well inclination angles. This occurs because, as the well inclination increases, the spatial relationship between the tool’s detection range and the formation interfaces changes, amplifying the electrical influence of distal surrounding rock. The Model Vertical five equal (Model V_5e) struggle to accurately represent actual formation conditions under these circumstances. In stark contrast, the results from the equivalent surrounding rock model align almost perfectly with those from the high-accuracy finite element method, fully validating the accuracy and engineering feasibility of the equivalent processing approach in complex well conditions. In terms of model applicability: for low-inclination wells, both Model V_5 and Model V_5e can meet the accuracy requirements for simulating array laterologging responses, and the choice between them can be based on computational efficiency needs. However, for rapid and accurate modeling of array laterologging responses in high-angle and horizontal wells, the equivalent surrounding rock model demonstrates clearly superior performance over Model V_5, owing to its effective correction for interference from distal surrounding rock. In summary, the equivalent surrounding rock method offers flexible adaptation to logging response computation under arbitrary well inclination angles, effectively balancing computational accuracy and efficiency. It exhibits strong generalization capability and provides reliable model support for the interpretation of array laterologging data in complex well conditions.

Figure 4

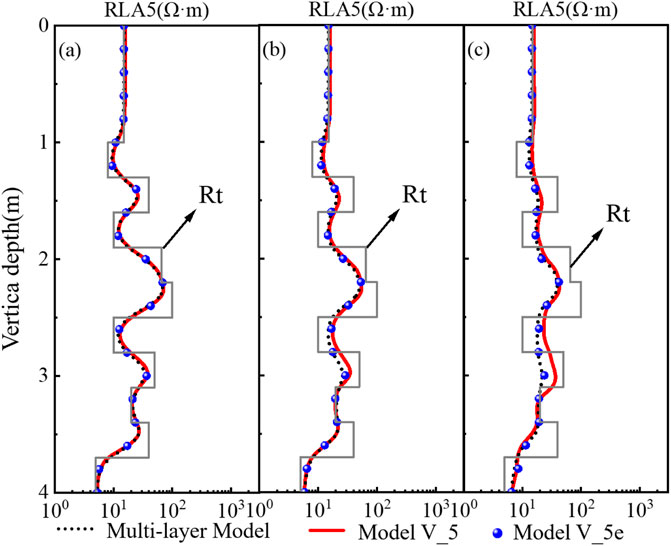
Figure 4. Comparison of ALL responses simulated by the surrounding rock equivalent method of the Model V_5, where the well deviations are (a) 30°, (b) 60° and (c) 80°.

2.3 Optimization of radial layers

To address the optimization of formation layering parameters in the radial dimension, Figure 5 presents three computational models for comparative analysis: Model Radial 1 (Model R_1): invasion only in the target zone, Model Radial 3 (Model R_3): invasion in both the target zone and adjacent layers, and Model Radial 5 (Model R_5): invasion across all formation layers. The parameters associated with each model are as follows: The dipping angle, resistivity of the jth formation, flushed zone resistivity, and equivalent resistivity are denoted by θ, R_tj, R_xoj, and R_tje, respectively. The core of this method is to equivalent the undisturbed formation and flushed zone into one layer. The resistivity of the equivalent formations is shown in Equation 3.

${{\mathit{R}\mathit{L}\mathit{A}}_{\mathit{i}}}^{\prime }={\mathit{G}}_{\mathit{i}}{\mathit{R}}_{\mathit{x}\mathit{o}}+\left(1-{\mathit{G}}_{\mathit{i}}\right){\mathit{R}}_{\mathit{t}}(3)$

Figure 5

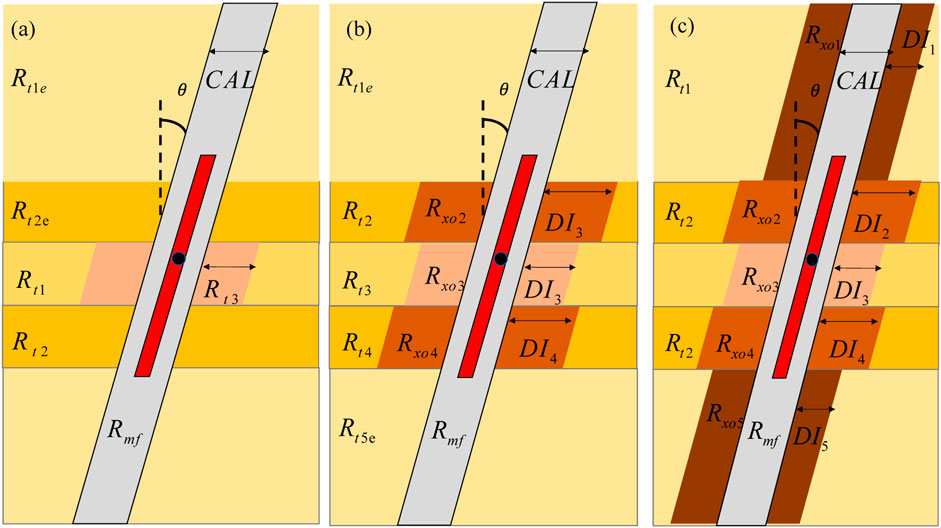
Figure 5. Optimization of invaded formations in the five-layer model: (a) Model R_1, (b) Model R_3, (c) Model R_5.

Where R_LAi’ is the equivalent resistivity under the ith detection mode, R_t and R_xo are the resistivities of the uninvaded formation and the flushed zoneand G_i is the radial numerical geometric factor, the definition of Gi is shown in Equation 4.

${\mathit{G}}_{\mathit{i}}=\frac{{\mathit{R}}_{\mathit{L}\mathit{A}\mathit{i}}-{\mathit{R}}_{\mathit{t}}}{{\mathit{R}}_{\mathit{x}\mathit{o}}-{\mathit{R}}_{\mathit{t}}}(4)$

Figures 6a–c compare the array resistivity responses of three invaded formation models (Model R_1, Model R_3, and Model R_5) with the computational results from the FEM. Table 2 shows the relative errors of the computational results for the three radial models. It can be observed that as the depth of investigation increases, the apparent resistivity is increasingly influenced by surrounding rocks and invaded zones, leading to notable differences in simulation accuracy among the models:

Figure 6

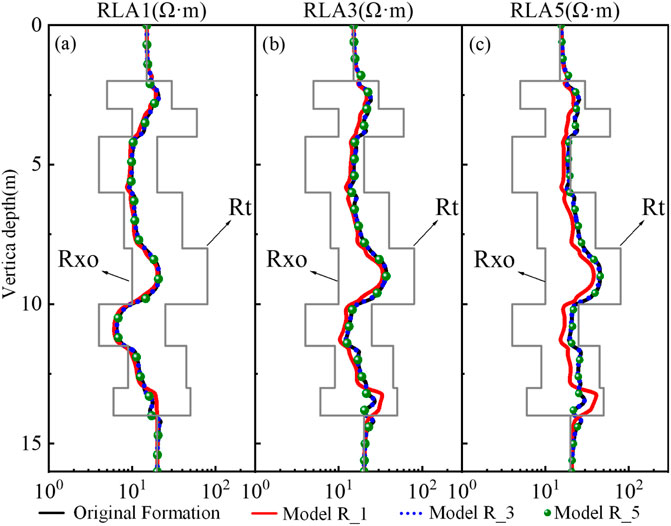
Figure 6. Simulated Array Lateralog Responses of Invaded-Layered Formations Under Different Detection Modes (a) RLA1; (b) RLA3; (c) RLA5, where the well deviations are 60°.

Table 2

Table 2. Comparison of calculation accuracy among three radial models.

For operating modes with shallow investigation depths (RLA1), all three models accurately reproduce the formation logging responses. The deviations between the simulation results and FEM references remain minimal, meeting the accuracy requirements for shallow detection scenarios. As the investigation depth increases (RLA3 and RLA5), the simulation accuracy of Model R_1 declines significantly. This model fails to effectively represent the apparent resistivity characteristics of the original formation, and the simulation error increases progressively with depth. In contrast, the results from Model R_3 and Model R_5 remain in close agreement with the FEM solutions throughout, maintaining high simulation accuracy even under deep investigation conditions. Considering both computational accuracy and model complexity from an engineering practicality perspective, Model R_3 achieves computational error levels comparable to those of Model R_5 while incorporating a more parameter-efficient design. This reduction in the number of required parameters enhances its suitability for efficient computation and parameter inversion in subsequent engineering applications.

3 Neural networks basedall modelling

3.1 Database construction and training scheme

To achieve real-time calculation of ALL responses, a neural network algorithm is adopted. The primary step of this algorithm is to generate a high-precision and fully annotated database. Based on the optimized number of longitudinal formations and radial invaded formations in the previous section, the calculation model shown in Figure 7 is constructed. This model includes 17 parameters: dipping angle θ, borehole diameter CAL, mud resistivity Rmf, resistivity of the jth formation Rt_j, flushed zone resistivity Rxo_j, formation thickness H_j, and invasion depth DI_j.

Figure 7

Figure 7. The training process of a Convolutional Neural Network (CNN).

The parameter ranges and generation strategy of the model samples are as follows: The well deviation angle θ is 0–89°, divided into 10 groups with an interval of 10°. The caliper CAL is 6–15 in, divided into 11 groups with an interval of 0.9 in. The mud resistivity R_mf is 0.01–10 Ω m, which is divided into 11 groups in logarithmic form with a logarithmic interval of 0.3. The invasion depth DI is 0–1.5 m, divided into 16 groups with an interval of 0.1 m. The formation resistivity R_t of the five layers and the flushed zone resistivity R_xo of the middle three layers all range from 0.1 to 1,000 Ω m, each of which is divided into 21 groups in logarithmic form with a logarithmic interval of 0.2. The thickness H of the middle three layers is 0–4 m, divided into 15 groups with an interval of 0.26 m. There are 10 measuring points in the middle layer, with a sampling interval of H₃/10.

More than 10 million sets of models have been generated through the above strategy, and the corresponding array laterologging responses have been simulated and calculated. To improve the training accuracy, the data can be normalized. The min-max normalization method is adopted in this study, with Equation 5 illustrating the uniform normalization of the output data Y to [0,1].

${\mathit{Y}}_{\mathit{L}\mathit{A}\mathit{i}}=\frac{{\mathit{log}}_{10}{\mathit{Y}}_{\mathit{L}\mathit{A}\mathit{i}}-\mathit{min}\left({\mathit{log}}_{10}{\mathit{Y}}_{\mathit{L}\mathit{A}\mathit{i}}\right)}{\mathit{max}\left({\mathit{log}}_{10}{\mathit{Y}}_{\mathit{L}\mathit{A}\mathit{i}}\right)-\mathit{min}\left({\mathit{log}}_{10}{\mathit{Y}}_{\mathit{L}\mathit{A}\mathit{i}}\right)}(5)$

It is imperative to emphasize that the predictive outputs generated by the neural network model must undergo a denormalization process to revert them to their original physical scales.

Convolutional Neural Network (CNN) have emerged as a cornerstone in the realm of machine learning, particularly excelling in intricate pattern recognition tasks such as image classification, speech processing, and object detection. Their superiority stems from two defining architectural innovations: local receptive fields and parameter sharing. These mechanisms not only mitigate the computational burden associated with traditional fully connected networks but also confer enhanced generalization capabilities by implicitly encoding spatial invariance properties. Consequently, CNN exhibit remarkable efficiency in capturing hierarchical feature representations while drastically reducing the number of trainable parameters, thereby accelerating convergence and minimizing the risk of overfitting. The CNN consists of an input layer, an output layer, and n convolutional layers and pooling layers. Assume the input feature map is X∈R^H×W×C (with height H, width W, and C channels), and the convolution kernel is K∈R^k×k×C×N (kernel size k × k, producing N output channels). The output feature map can be expressed as: Z∈R^{H′×W′×N}, the height H′ and width W′ of the output feature map Z are shown in Equation 6.

${\mathit{H}}^{\prime }=\frac{\mathit{H}+2\mathit{p}-\mathit{k}}{\mathit{s}}+1,{\mathit{W}}^{\prime }=\frac{\mathit{W}+2\mathit{p}-\mathit{k}}{\mathit{s}}+1(6)$

where s denotes the stride of the convolution kernel and p denotes the padding size. Equation 7 shows the feature value at position (i,j) in the n-th channel of the output feature map, Z∈R^{H′×W′×N}.

${\mathit{Y}}_{\mathit{i},\mathit{j},\mathit{n}}=\mathit{f}\left({\displaystyle \sum _{\mathit{c}=0}^{\mathit{C}}}\sum _{\mathit{m}=0}^{\mathit{k}-1}\sum _{\mathit{n}=0}^{\mathit{k}-1}{\mathit{X}}_{\mathit{n}}\left(\mathit{i}\times \mathit{s}+\mathit{m},\mathit{j}\times \mathit{s}+\mathit{m}\right)\times {\mathit{K}}_{\mathit{n}}\left(\mathit{m},\mathit{n}\right)+{\mathit{b}}_{\mathit{n}}\right)(7)$

where b_n is the bias term, K_n(m,n) represents the weight of the nth convolution kernel at position (m,n) for input channel, and f denotes the activation function applied afterward.

In CNN, the input layer is generally a 2D image, while the calculation model is essentially a 1D discrete parameter vector. To meet the network requirements, binary conversion is used to transform a series of 1D model arrays into 2D strings, and then synthesize a series of binary images (as shown in Figure 7. Figure 7 shows the basic architecture of the CNN. In this training process, a 9-layer neural network model is adopted to train the dataset. Specifically, the Adam algorithm is selected as the training algorithm, the learning rate is set to 0.001, and the ReLU function is chosen as the activation function.

3.2 Prediction performance of ALL responses

Figure 8 further compares the array resistivity responses calculated by the FEM and CNN methods in highly deviated wells. The solid lines and scatter points represent the calculation results of the FEM and CNN methods, respectively. Table 3 presents the relative errors between the computational results of the FEM and CNN methods for the three formation models. The formation model considers the influences of surrounding rocks and invasion. The array resistivity curves calculated by the two methods completely overlap, verifying the robustness of the CNN calculation method.

Figure 8

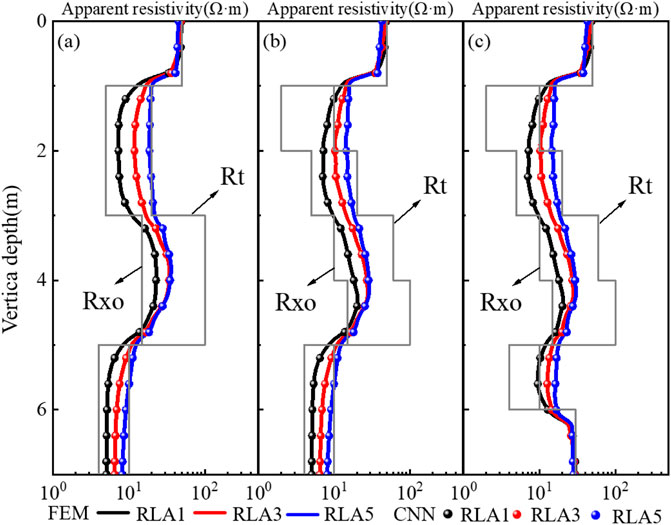
Figure 8. Comparison of Calculation Results between FEM and CNN, where the well deviations are (a) 30°, (b) 60° and (c) 80°.

Table 3

Table 3. Comparison of calculation accuracy among formation with different layer counts.

4 Numerical examples

To verify the applicability of the CNN method under complex geological conditions, multiple groups of numerical experiments were designed. The physics-driven model uses the FEM to solve Maxwell’s equations, with the mesh division precision controlled within 1/10 of the target feature size to ensure that the error of the benchmark solution is less than 0.1%.

Figure 9 compares the array resistivity responses calculated by FEM and CNN methods in the Oklahoma model, where the solid lines and scatter points represent the calculation results of the FEM and CNN methods, respectively. Table 4 shows the calculation accuracy and calculation speed of the two methods. The formation model covers combined scenarios of different resistivity contrasts (0.5–20), invasion zone thicknesses (0.5m–5 m), and formation dips (30°–80°). Numerical examples show that the CNN algorithm outperforms traditional physics-driven methods in terms of accuracy, efficiency, and robustness, providing a feasible solution for real-time high-precision processing of logging data. In addition, in the thin interbedded zone, the equivalent method of surrounding rocks is used to further improve the generalization ability of the model.

Figure 9

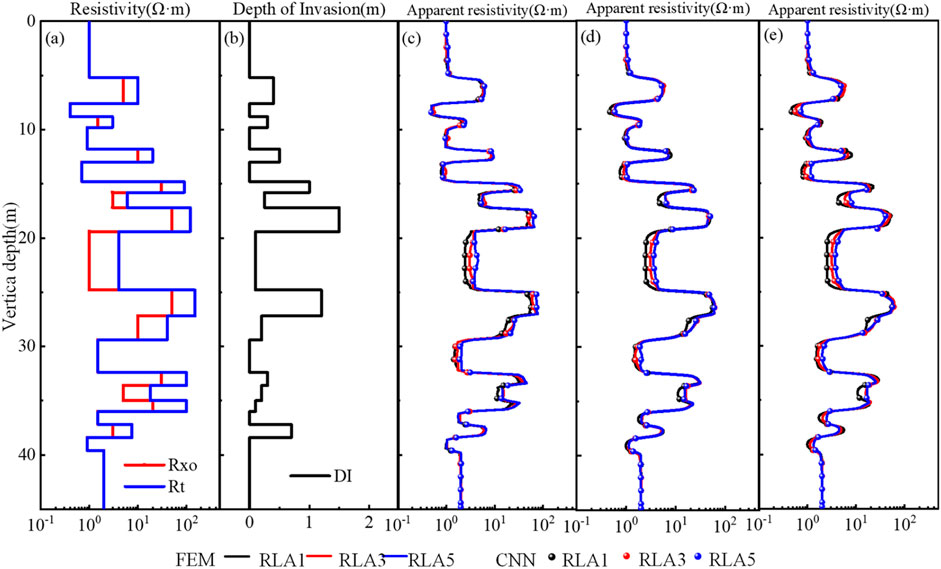
Figure 9. Simulated ALL Responses by FEM and CNN in Oklahoma Formation: (a) Resistivity; (b) Depth of invasion, where the well deviations are (c) 30°, (d) 60° and (e) 80°.

Table 4

Table 4. Comparison of computational accuracy and speed between FEM and CNN.

5 Conclusion

In this study, a novel rapid forward-modeling method for ALL is introduced to fulfill the requirement for real-time processing of ALL data in complex formations. Unlike previous approximate forward-modeling approaches, this method approximates the multi-layer formation model as a model in which the middle three layers of a five-layer formation are invaded. It addresses the issue of the fixed number of layers in traditional forward-approximation methods and exhibits strong generalization capabilities. Through the introduction of the convolutional neural network algorithm, while ensuring calculation accuracy, the forward-modeling speed is enhanced by over two orders of magnitude. This algorithm was applied to the Oklahoma model, demonstrating its effectiveness and applicability.

It should be noted that under more complex three-dimensional formation conditions, such as those encountered in carbonate formations characterized by fracture development, vuggy porosity, and formation anisotropy, the database and network architecture presented in this study are no longer applicable. Therefore, future research should focus on further enriching and refining both the neural network architecture and forward modeling methods, with the aim of providing more efficient and reliable processing solutions for oil and gas field development.

Data availability statement

The datasets presented in this article are not readily available because The data in this paper is only applicable to the rapid forward modeling of array laterolog (ALL) in deviated well 3D formations (considering layer thickness and invasion). Under more complex 3D formation conditions (e.g., formations with developed fractures, vuggy porosity, and significant formation anisotropy), the database proposed in this study will no longer be applicable. Requests to access the datasets should be directed to Donghan Hao, MjAwMUAxNjMuY29t">haodonghanMjAwMUAxNjMuY29t.

Author contributions

LW: Writing – original draft, Writing – review and editing. DH: Writing – review and editing, Writing – original draft. XY: Writing – review and editing, Writing – original draft. JL: Writing – review and editing, Writing – original draft. CL: Writing – original draft, Writing – review and editing. ZC: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the National Natural Science Foundation of China (Grant Nos 42474152, U23B2086), Shandong Provincial Natural Science Foundation (Grant No. ZR2023MD053), the National Science and Technology Major Project of China (No. 2025ZD1402102-05).

Conflict of interest

Author XY was employed by SINOPEC Matrix Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, H. (2021). Geophysical study of oil and gas reservoirs in oil and gas filed development. Prog. Geophys. 36 (02), 565–575. doi:10.6038/pg2021EE0154

CrossRef Full Text | Google Scholar

Deng, S., Li, Z., Fan, Y., and Chen, H. (2010). Numerical simulation of mud invasion and its array laterolog response in deviated Wells. Chin. J. Geophys. 53 (04), 994–1000. doi:10.3969/j.issn.0001-5733.2010.04.024

CrossRef Full Text | Google Scholar

Deng, S., Yuan, X., Wang, Z., Liang, S., and Zhang, P. (2018). Numerical simulation of azimuthal laterolog response in fractured formation. Chin. J. Geophysics-Chinese Ed. 61 (08), 3457–3467. doi:10.6038/cjg2018L0241

CrossRef Full Text | Google Scholar

Feng, L., Wang, D., He, F., Zhang, H., Wang, P., Guan, Z., et al. (2013). On response characteristics analysis of HAL tool in thin inter-beds and deviated hole formation. Well Logging Technol. 37 (01), 80–84.

Google Scholar

Hagiwara, T. (2023). Machine-Learning-Based convolution method for fast forward modeling of induction log. Petrophysics 64 (02), 312–322. doi:10.30632/PJV64N2-2023a11

CrossRef Full Text | Google Scholar

Hu, S., Chen, L., and Wang, J. (2019). Fast inversion of array laterolog measurements in an axisymmetric medium. Appl. Geophys. 16 (04), 539–548. doi:10.1007/s11770-019-0767-0

CrossRef Full Text | Google Scholar

Liu, L., Li, T., and Ma, C. (2024). Research on 3D geological modeling method based on deep neural networks for drilling data. Appl. Sciences-Basel 14 (01), 423. doi:10.3390/app14010423

CrossRef Full Text | Google Scholar

Maurer, H., Antonov, Y., Corley, B., Khokhar, R., Rabinovich, M., and Zhou, Z. (2009). “Advanced processing for a new array laterolog tool,” in Proc. SPWLA 50th annu. Logging symp. (Woodlands, TX, USA).

Google Scholar

Nan, Z., Tan, M., Li, J., and Fan, X. (2002). Numerical simulation, response analysis, and physical experiment of induction logging in an inclined fractured formation. IEEE Trans. Geoscience Remote Sens. 60, 1–11. doi:10.1109/TGRS.2021.3056133

CrossRef Full Text | Google Scholar

Ni, X., Xu, G., Bei, K., Feng, J., Xu, S., and Liu, D. (2018). Array laterolog response and rapid correction of the surrounding rock/layer thickness influence for highly deviated/horizontal wells. Petroleum Geol. and Oilfield Dev. Daqing 37 (02), 144–151. doi:10.19597/J.ISSN.1000-3754.201705058

CrossRef Full Text | Google Scholar

Pan, K., Wang, W., Tang, J., and Tan, Y. (2013). Mathematical model and fast finite element modeling of high resolution array laterologging. Chin. J. Geophys. 56 (09), 3197–3211. doi:10.6038/cjg20130932

CrossRef Full Text | Google Scholar

Pan, K., Tang, J., Du, H., and Cai, Z. (2016). Trust region inversion algorithm of high resolution array laterologging in axisymmetric formation. Chin. J. Geophys. 59 (08), 3110–3120. doi:10.6038/cjg20160833

CrossRef Full Text | Google Scholar

Ren, Y., Gong, R., Feng, Z., and Li, M. (2020). Valuable data extraction for resistivity imaging logging interpretation. Tsinghua Sci. Technol. 25 (02), 281–293. doi:10.26599/TST.2019.9010020

CrossRef Full Text | Google Scholar

Si, Z., Deng, S., Lin, F., Yuan, X., Li, H., and Tian, C. (2020). Numerical simulation of array laterolog responses in anisotropic formation with mud invasion. Oil Geophys. Prospect. 55 (01), 187–196.

Google Scholar

Tan, M., Gao, J., Zou, Y., Xie, G., and Qiao, Y. (2012). Environment correction method of dual laterolog in directional well. Chin. J. Geophysics-Chinese Ed. 55 (04), 1422–1432. doi:10.6038/j.issn.0001-5733.2012.04.038

CrossRef Full Text | Google Scholar

Wang, G., Torres-Verdin, C., Salazar, J., and Voss, B. (2009). Fast 2D inversion of large borehole EM induction data sets with an efficient Frechet-Derivative approximation. Geophysics 74 (01), E75–E91. doi:10.1190/1.3033213

CrossRef Full Text | Google Scholar

Wang, L., Qiao, P., Zhao, W., Cao, F., and Fan, Y. (2023). A new propagator matrix algorithm to compute electromagnetic fields in multilayered formations with full anisotropy. IEEE Trans. Geoscience Remote Sens. 61, 1–11. doi:10.1109/TGRS.2023.3302513

CrossRef Full Text | Google Scholar

Wang, L., Cao, F., Li, Z., Yuan, X., and Fan, Y. (2024). A novel propagator coefficient algorithm for modeling induction-type logging responses in cylindrically layered media. IEEE Geoscience Remote Sens. Lett. 21, 1–5. doi:10.1109/LGRS.2024.3401126

CrossRef Full Text | Google Scholar

Wang, L., Wu, K., Liu, Y., Xu, X., and Qiao, P. (2025a). Focusing mechanism and anisotropy correction of array induction logging responses for shale reservoirs in horizontal wells. Petroleum Sci. doi:10.1016/j.petsci.2025.08.009

CrossRef Full Text | Google Scholar

Wang, L., Han, Y., Li, Z., Hao, D., and Deng, S. (2025b). The joint physics and data-driven geometrical factor of array laterolog in layered formations. Geophysics 90 (01), D11–D25. doi:10.1190/GEO2024-0112.1

CrossRef Full Text | Google Scholar

Wu, Y., and Fan, Y. (2021). Fast hierarchical inversion for borehole resistivity measurements in high-angle and horizontal wells using ADNN-AMLM. J. Petroleum Sci. Eng. 203, 108662. doi:10.1016/j.petrol.2021.108662

CrossRef Full Text | Google Scholar

Wu, K., Wang, L., Deng, S., and Kou, X. (2025). A novel logging method for detecting highly resistive formations in oil-based mud using high-frequency electrodes. Petroleum Sci. 22 (05), 1946–1958. doi:10.1016/j.petsci.2025.03.010

CrossRef Full Text | Google Scholar

Xiao, D., Mao, B., Ma, H., Zhang, Q., and Zhang, Z. (2016). EALT array laterologging well site processing software algorithm. Well Logging Technol. 40 (04), 432–438. doi:10.16489/j.issn.1004-1338.2013.01.016

CrossRef Full Text | Google Scholar

Xing, G., Wang, H., and Yang, S. (2008). The response functions of electromagnetic wave logs in the 2-D axis-symmetric formation. Chin. J. Geophysics-Chinese Ed. 03, 924–932.

Google Scholar

Yan, L., Jin, Y., Qi, C., Yuan, P., Wang, S., Wu, X., et al. (2022). Deep learning-assisted real-time forward modeling of electromagnetic logging in complex formations. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2022.3171122

CrossRef Full Text | Google Scholar

Yang, K., Wang, L., Fang, H., Ai, W., Wang, N., and Zeng, Z. (2025). A new logging-while-drilling azimuthal electromagnetic measurement for highly resistive coal mines. J. Geophys. Eng. 22 (04), 1017–1025. doi:10.1093/jge/gxaf056

CrossRef Full Text | Google Scholar

Zhang, Z., and Zhou, Z. (2002). Real-time quasi-2-D inversion of array resistivity logging data using neural network. Geophysics 67 (02), 517–524. doi:10.1190/1.1468612

CrossRef Full Text | Google Scholar

Zhao, N., Shen, S., Li, N., Hu, H., Qi, C., and Qin, Ce. (2024). Physics-driven deep learning inversion for Azimuthal LWD electromagnetic wave measurement. Oil Geophys. Prospect. 59 (05), 1069–1079. doi:10.13810/j.cnki.issn.1000-7210.2024.05.014

CrossRef Full Text | Google Scholar

Zhu, P., Li, Z., Chen, M., and Dong, Y. (2019). Study on forward and inversion modeling of array laterolog logging in a horizontal/highly deviated well. Acta Geophys. 67 (05), 1307–1318. doi:10.1007/s11600-019-00321-2

CrossRef Full Text | Google Scholar

Zhu, G., Gao, M., Kong, F., and Li, K. (2020). A fast inversion of induction logging data in anisotropic formation based on deep learning. IEEE Geoscience Remote Sens. Lett. 17 (12), 2050–2054. doi:10.1109/LGRS.2019.2961374

CrossRef Full Text | Google Scholar