- 1Department of Mathematics, LMU Munich, Munich, Germany
- 2Department of Psychology, LMU Munich, Munich, Germany
Assessment and intervention in the early years should ideally be based on evidence-based models describing the structure and development of students’ skills. Mathematical word problems have been identified as a challenge for mathematics learners for a long time and in many countries. We investigate flexibility in dealing with additive situations as a construct that develops during grades 1 through 3 and contributes to the development of students’ word problem solving skills. We introduce the construct based on prior research on the difficulty of different situation structures entailed in word problems. We use data from three prior empirical studies with N = 383 German grade 2 and 3 students to develop a model of discrete levels of students’ flexibility in dealing with additive situations. We use this model to investigate how the learners in our sample distribute across the different levels. Moreover, we apply it to describe students’ development over several weeks in one study comprising three measurements. We derive conclusions about the construct in terms of determinants of task complexity, and about students’ development and then provide an outlook on potential uses of the model in research and practice.
1 Introduction
Mathematics instruction at school not only aims at conveying mathematical concepts and procedures, but also at students’ skills in mathematical modelling, which means to apply these concepts and procedures in more or less realistic real-life situations (Cevikbas et al., 2022). Word problems are mathematical tasks, which are presented in verbal form and embedded in a short narrative, e.g., “Chris has 4 marbles. Chris has 3 marbles less than Alex. How many marbles does Alex have? “They constitute a standard part of school curricula world-wide (e.g., Verschaffel et al., 2020; Krawitz et al., 2022), where they serve two main purposes: They can be seen as very basic exercises in mathematical modelling, but more importantly they allow to engage students with relationships between mathematical concepts and real-world phenomena they can describe (Freudenthal, 1983; Verschaffel et al., 2020). In grade 1 and early grade 2, most of the encountered word problems require addition or subtraction since other operations are often not introduced before mid-grade 2. We focus on additive one-step word problems in this contribution, since they are frequent in mathematics text books (Gabler et al., 2023) and research (Verschaffel et al., 2020). These word problems can be solved with a single additive arithmetic operation (addition or subtraction) and contain no irrelevant information. They are part of primary school curricula from grade 1 onwards.
It is a long-standing result that solving word problems poses a substantial challenge for mathematics learners in primary school and beyond (Greeno, 1980; Verschaffel et al., 1992; Daroczy et al., 2015, 2020). Further, it is also well-established that these problems are modulated by a range of individual characteristics such as general cognitive abilities, language skills, and arithmetic (symbolic) calculations skills as well as by linguistic or mathematical task characteristics (Daroczy et al., 2015). In addition, strategies to solve word problems have received substantial attention in prior research. Based on traditional models of word problem solving (e.g., Kintsch and Greeno, 1985; Blum and Leiß, 2007), some authors have proposed that, after initially reading a difficult word problem, learners may be able to reinterpret the presented situation in a way, that results in an easier word problem type (Greeno, 1980; Stern, 1993). Recent research has found that primary school students differ systematically in their ability to reinterpret situations presented in additive one-step word problems in the proposed way (Gabler and Ufer, 2021, 2022). The skill to engage in such re-interpretations has been studied as flexibility in dealing with additive situations (Gabler and Ufer, 2021, 2022). To provide a conceptual basis for assessments and interventions in the early school years, we propose a level model of this skill construct, that is based on a re-analysis involving an IRT-scaling of data from three empirical studies. Such level models structure a one-dimensional skill construct into a sequence of discrete levels, that describe increasing demands and item complexity associated with the skill construct. They may also allow a criterial interpretation of students’ individual skills in terms of the demands they can or cannot master (Koeppen et al., 2008; Ufer and Neumann, 2018). Further, they may provide an important link from assessing the skill towards interventions building on the students’ current skill levels and targeting more complex, but still within-reach demands.
To introduce the flexibility skill construct and our study, we will first discuss models of the word problem solving process and task characteristics influencing students’ performance on additive one-step word problems. Based on this, we will introduce the flexibility skill construct and present methodological backgrounds on level models of mathematical skill constructs based on item response theory.
1.1 Word problem solving
Many established models of the word problem solving process are transformative in nature (Czocher, 2018): They assume that learners transform an initial situation model of the presented real-world situation into a mathematical model, and after solving the problem entailed in this mathematical model, they transform their solution back to their initial situation model (cf. Kintsch and Greeno, 1985; Verschaffel et al., 2020). The situation model comprises the learner’s mental representation of the textual presentation of the situation in the word problem, the text base (Figure 1). For additive one-step word problems, a situation model should at least contain the two quantities given in the word problem (number of Chris’ marbles, and the difference between the number of Chris’ and Alex’s marbles), the related numbers (4 and 3), an unknown quantity (number of Alex’s marbles), and a relation between the three quantities as described in the problem text (direction of the difference: Chris has 3 less than Alex). According to models of reading comprehension (e.g., Kintsch, 1998), (re-)constructing this situation model from the text base is not limited to decoding and representing the presented verbal information, but may also comprise making further inferences about the situation based on students’ knowledge about the context presented in the situation itself (e.g., exchanging marbles, or shopping), or about typical situation structures that can be described mathematically by addition or subtraction. The reinterpretation strategies mentioned above (Greeno, 1980; Stern, 1993) are examples of such further inferences.
The mathematical model contains the numbers from the situation model, and the relation between them in terms of a mathematical operation (addition or subtraction). It may have the form of an operation that directly provides the number related to the unknown quantity (7–3 = ___), or of an implicit characterization of this number (e.g., ___ + 3 = 7) like a mathematical equation. Based on knowledge about arithmetic operations, learners may transform a mathematical model into an equivalent one in the further solution process, e.g., by solving the subtraction problem 7–3 = ___ by the indirect addition 3 + ___ = 7 (Torbeyns et al., 2009).
Even though more extensive models, for example the modelling cycle (Blum and Leiß, 2007), comprise further phases such as interpreting and validating the results, these phases may not be necessary and can be omitted in simple situations such as one-step word problems (Kaiser, 2017). It is well-known that learners do not necessarily follow the model of the word problem solving process. Hegarty et al. (1992, 1995) provide evidence of a direct translation strategy (also keyword strategy), in which students focus primarily on the numbers and specific terms in the text base, e.g., relational terms such as “more” or “less,” or actions such as “getting” or “losing” to directly infer the necessary mathematical operation. They offer convergent evidence from behavioral, eye-tracking and problem-recall studies, that less successful word problem solvers frequently apply this strategy, resulting in difficulties extracting and representing relational information from the text. In the literature, the importance of rich situation models, “in which all key elements and relations in the problem situation that are relevant to the solution of the mathematical problem posed are represented” is highlighted repeatedly (e. g., Mellone et al., 2017, p. 3). Accordingly, many authors call to “provide instruction in a method that emphasizes understanding the situation described in the problem” (Hegarty et al., 1995, p. 29), for example by conveying strategies to build up and make use of rich situation models. They also point out, that applying this strategy is not a stable person characteristic but may depend on person and task characteristics.
1.2 Task characteristics
Several task characteristics have been found to influence word problem solution rates. In their review, Daroczy et al. (2015) distinguish between mathematical factors such as the complexity of the entailed numerical calculation, and linguistic factors, such as the structure of the presented situation or the way it is presented verbally. In a sample of grade 2 students, and in a restricted number range up to 20, Gabler and Ufer (2020, p. 77, 79) could not find systematic differences in word problem difficulty related to the specific numbers (or contexts) used. Consequently, we will focus on three linguistic factors that describe the situation structure presented in the word problem: the semantic structure, which describes the structure of the presented situation, the unknown set, that needs to be determined in the word problem, and the additive vs. subtractive wording of the word problem, which relates to additive (“more,” “getting”) vs. subtractive (“less,” “loosing”) terms used to describe the situation.
1.2.1 Semantic structure
A range of different real-world phenomena can be described by the same mathematical model (e.g., an additive operation such as 4 + 3 = 7, Figure 1). Up to four different types of so-called semantic structures in additive one-step word problems have been differentiated (Riley et al., 1983; Figure 1). While word problems can also refer to other quantities, these problem types are usually exemplified with word problems relating to the numbers of objects in different sets. Change structures refer to an increase or decrease of a set of objects. Combine structures relate to part-whole structures between a set, and two subsets that together make up the whole set. Compare structures comprise two disjoint quantities, and a relational statement about their difference. Equalize structures have been studied less frequently. Like compare structures, they contain two disjoint sets (Chris’s and Alex’s marbles), but the relation between the two sets is presented by an action—as in change structures—that would (hypothetically) equalize the two sets (someone giving Chris 3 more marbles). Change and equalize structures are called dynamic, because they entail an action, while compare and combine structures are called static (Riley et al., 1983).
Word problems with different semantic structures have been found to be of systematically different difficulty. Numerous studies (e.g., Riley and Greeno, 1988) show that compare problems are more difficult than change and combine problems. Few studies have investigated equalize problems. However, Stern (1994) reported high solution rates (96%) for equalize problems, similar to those for change and combination problems, in a sample of first graders. Several reasons for this specific difficulty of compare problems have been discussed. Stern (1993) points out that in combine and change problems, all sets exist as concrete sets, that are observable separate quantities or in terms of an observable action. The difference in compare problems, in contrast does not describe a concrete set, but a relation between two concrete sets (a difference set), that is only observable when considering both concrete sets. This can be done by setting up a one-to-one correspondence between one concrete set and a subset of the other concrete set, and then counting the excess objects (Stern, 1998). Representing relational statements as difference sets may pose a substantial problem for learners. Here, it makes a substantial difference, if quantitative (i.e., described by numbers, e.g., three more than) differences are describe, or if only qualitative differences (more than, less than) are considered. For example, some learners understand quantitative relational statements such as “Chris has 3 marbles more than Alex” as being equivalent to “Chris has 3 marbles, and Chris has more marbles than Alex” – interpreting the quantitative relation as a qualitative relation (more than) and a statement about a concrete set (Mekhmandarov et al., 1996; Gabler and Ufer, 2021). In line with these difficulties, understanding numbers as quantitative comparisons between sets is allocated to later phases in models of the development of the number concept (under the term “relationality”; for an overview see Hartmann and Fritz, 2021).
1.2.2 Unknown set
Three different sets are involved in one-step word problems. In change, compare and equalize problems, one set provides a reference: This can be the start of a change of equalize action, or the set to which another set is compared (e.g., “Chris has 4 marbles. Chris has 3 marbles less than Alex. How many marbles does Alex have?”). One set serves as a result, which can be the result of the change or equalize action, or the set that is compared to another one (e.g., “Alex has 7 marbles. Chris has 3 marbles less than Alex. How many marbles does Chris have?”). The third set describes the relation between the other two sets as a concrete set in the change or equalize actions, or as a difference set in compare statements (e.g., “Alex has 7 marbles. Chris has 4 marbles. How many marbles does Chris have less than Alex?”). The situation is different for combine problems, where two parts, which play similar but complementary roles in the situation, and the whole set need to be distinguished.
There is evidence that, at least for young learners, word problems with unknown reference or relation set are more difficult than those with unknown result set (Gabler and Ufer, 2020; Van Lieshout and Xenidou-Dervou, 2020). One reason may be that the learners’ standard mathematical model related to the situation structures is of the form <reference > <operation (+/−) > <relation > = < result>. This would imply, that the unknown result set situations directly provide all numerical information to perform the arithmetic operation entailed in the model. For unknown reference and relation sets, this standard model would result in an implicit characterization of the required numerical solution (e.g., <unkown reference > + < known relation > = < known result>). In the second case, either the implicit problem needs to be solved directly (e.g., by fact retrieval or trial and error) or it needs to be transferred into an equivalent, directly solvable mathematical model (e.g., <unkown reference > = < known result > − < known relation>). Yet, the exact reasons for the observed difficulty pattern are still to be clarified.
1.2.3 Additive vs. subtractive wording and consistency
In change, equalize, and compare word problems, the change and relations can be expressed additively (“more,” “getting”: additive wording) or subtractively (“less,” “loosing”: subtractive wording) in the problem text. If students apply the direct translation strategy (Hegarty et al., 1995), they will use addition of the two given numbers as mathematical model in case of additive wording and subtraction of the two numbers in case of subtractive wording. For some word problems (e.g., those with unknown result set) this results in a correct mathematical model, for others (e.g., those with unknown reference set) it leads to a wrong model. For problems with unknown relation set, a correct mathematical model results only for subtractive wording. Word problems are called consistent, if the direct translation strategy results in a (addition/subtraction), that correct mathematical model, i.e., if the wording of the word problem (additive/subtractive) reflects the operation (addition/subtraction) that can be applied to the given numbers directly, to obtain a valid mathematical model. Consistent word problems have been found to be easier than inconsistent ones (Lewis and Mayer, 1987, “consistency hypothesis”) for primary school students (Verschaffel, 1994; Gabler and Ufer, 2020) and adults (Daroczy et al., 2020). This means, for example, that the inconsistent word problem “Chris has 4 marbles. Chris has 3 marbles less than Alex. How many marbles does Alex have?” can be expected to be more difficult than the very similar, but consistent word problem “Chris has 4 marbles. Alex has 3 marbles more than Chris. How many marbles does Alex have?.” One explanation of this effect could be that, while consistent word problems can be directly solved using the direct translation strategy, inconsistent word problems require a deeper conceptual analysis of either the situation model or the mathematical model, to arrive at a correct solution (Scheibling-Sève et al., 2020).
1.3 Flexibility in dealing with additive situations
Already slight changes to the way a word problem is presented can substantially affect their difficulty. Several researchers have argued that this could provide a starting point to help students solve more difficult word problems.
For example, Stern (1993) and other researchers (Verschaffel, 1994; Fuson et al., 1996) stress the importance of understanding the meaning of relational statements and being able to deal with them. The symmetry of relational statements poses substantial challenges to students. Only 30% of the first-graders in Stern (1993) interview study could identify statements such as “Chris has 3 marbles less than Alex.” as equivalent to the symmetric statement “Alex has 3 marbles more than Chris.” Being able to do so, however, could allow students to convert the inconsistent word problem “Chris has 4 marbles. Chris has 3 marbles less than Alex. How many marbles does Alex have?” with unknown reference set into the easier, consistent problem “Chris has 4 marbles. Alex has 3 marbles more than Chris. How many marbles does Alex have?” with unknown result set.
Similarly, Greeno (1980) argued that learners might find it easier to solve change problems with unknown relation set (change) such as “Jill had 3 apples. Betty gave her some more apples. Now Jill has 8 apples. How many did Betty give her?,” if they reinterpret the situation as a combine situation with the result set as a whole (8 apples afterwards), the reference set (3 apples initially) as one part, and the relation set (change) as the other part. Considering that compare problems have been found to be harder than equalize problems speaks for a similar idea for solving compare problems (Nesher et al., 1982; Fuson et al., 1996). Both structures contain two disjoint sets offering the opportunity to reinterpret static compare statements such as “Alex has 3 marbles more than Chris” in terms of a (dynamic) equalization action “If Chris gets 3 more marbles (from someone else), Chris has as many as Alex.”
One idea is common to both arguments: Re-interpreting word problems in terms of a different situation structure may allow students to turn difficult word problems into easier ones. Providing students with a range of different perspectives—connected to different situation structures—on the same situation may support word problem solving. This resonates with works stressing the importance of deep processing of situation models in word problem solving or mathematical modelling in general (e.g., Stern and Lehrndorfer, 1992; Thevenot et al., 2007; Leiss et al., 2010). Having perspectives available that correspond to easier word problem types may increase the chance to find a mathematical model and to solve the word problem. This re-interpretation can be seen as a part of the reading process in terms of Kintsch (1998) model of reading comprehension: Based on a mental representation of the text base in an initial situation model, the learner adds new perspectives on the situation by making further inferences based on his or her knowledge about connections between different situation structures. This idea, however, strongly depends on students’ knowledge about these connections, their ability to identify similarities and differences between different perspectives on the same situation, and their ability to infer new perspectives that are fruitful for solving the problem.
Based on these considerations, Gabler and Ufer (2020, 2021) hypothesize that being able to perform these re-interpretations for additive one-step word problems might be a person characteristic, that shows systematic inter-individual variation between primary school students. Flexibility in dealing with additive situations can be defined as the skill to compare or restructure situation models of additive one-step word problems by inferring alternative perspectives on the situation that relate to different situation structures (e.g., different wording, semantic structures, or unknown sets). Flexibility is understood here similar as in cognitive flexibility theory, which “includes the ability to represent knowledge from different conceptual and case perspectives and then, when the knowledge must later be used, the ability to construct from those different conceptual and case representations a knowledge ensemble tailored to the needs of the understanding or problem-solving situation at hand” (Spiro et al., 1991, p. 24). It can be seen as a special case of conceptual knowledge of addition and subtraction in the sense of “implicit or explicit understanding of the principles that govern a domain and of the interrelations between units of knowledge in a domain” (Rittle-Johnson et al., 2001, p. 346). We note that the conceptualization of flexibility applied in this manuscript differs from other views that relate flexibility to humans’ ability to shift between different tasks (Ionescu, 2012). Instead, flexibility in this manuscript refers to students’ knowledge how to solve a specific (word) problem in different ways (Heinze et al., 2009; Ionescu, 2012).
Starting from this idea, a test instrument for flexibility in dealing with additive situations was investigated in Gabler and Ufer (2022). Here, students are asked to compare two verbal descriptions of the same situation and decide whether they believe these are description about the same situation, or not. Note that this is very different from the work by Zorrilla et al. (2024, p. 6, Figure 3) where students were provided with a number of related complete word problems, among which one problem contained the solution to another one—potentially leading to the high frequency of superficial strategies found there. The analyses of our skill construct assumed a one-dimensional scale, and results showed good reliability (α = 0.80) with second graders rating 20 dichotomous items. This finding supports the assumption of a flexibility in dealing with additive situations as a one-dimensional personal characteristic. Moreover, Gabler and Ufer (2022) report that the construct predicts students’ word problem solving skills above general cognitive abilities, language skills, and symbolic arithmetic calculation skills. They conclude, that language skills and symbolic arithmetic calculation skills, but not general cognitive abilities significantly explain inter-individual differences in students’ flexibility. Gabler and Ufer (2024) provide evidence from an experimental intervention study, in which training second graders flexibility in dealing with additive situations increased not only their flexibility, but also their word problem solving performance. The qualitative analysis in Gabler and Ufer (2021) showed that students varied substantially in their progress during the intervention, depending on their flexibility at the start of the intervention. To conceptualize adaptive support in future studies, models are needed that allow a criterial interpretation of students’ current performance in terms of concrete demands the students can (and cannot yet) master systematically. Moreover, little is known about how students’ flexibility develops over time, for example, if certain transitions between levels are less frequent than others or take more time or if certain demands take longer to cope with than others.
1.4 Level models for assessment and intervention
Prior studies have unveiled substantial inter-individual differences in students’ number-related knowledge and skills at the start of primary school (Schmidt and Weiser, 1982; Fuson, 1988), which persist during the first years of schooling and beyond (Krajewski and Schneider, 2009; Niklas and Schneider, 2017; Balt et al., 2020). Current models of numerical development often propose a sequence of levels, which describe demands of increasing complexity and are assumed to also reflect students’ temporal development (Hartmann and Fritz, 2021). Each level in these models is characterized by specific content-related insights, e.g., grasping the idea of cardinality of a set. Often knowledge and skills related to previous levels are considered necessary to acquire the next one. This underpins the necessity to align instruction to students’ current knowledge and skill level, optimally targeting the next level that is within students’ reach. Indeed, Wildgans-Lang et al. (2020) argue that level models provide useful information that support teachers’ diagnosis of students’ current level of understanding.
Level models are usually generated based on analytic approaches towards test performance based on item response theory (IRT) models. They are one special case of models for cognitive knowledge or skill constructs, which differentiate skills along one coherent dimension of individual scores and define discrete levels of observable performance by defining the demands, that usually can be mastered on each level (Koeppen et al., 2008; Ufer and Neumann, 2018). Level models can be created for one-dimensional skill constructs, or for single dimensions of multi-dimensional skill constructs. This has a long tradition in large scale assessments (Heine et al., 2013), but level models also exist for different mathematical knowledge areas such as broad arithmetic skills in primary school (Reiss and Obersteiner, 2019), proportional reasoning skills or fraction knowledge (Schadl and Ufer, 2023), and mathematical knowledge required for undergraduate mathematics learning at university (Rach and Ufer, 2020; Pustelnik et al., 2023). Often level models are seen as a preliminary step towards models that describe development such as learning trajectories (Simon, 1995) or learning progressions (Jin et al., 2019). In this sense, level models may not only support diagnosis, but also provide useful (though often in the first place heuristic) hints towards reasonable learning goals and possible learning opportunities that would be most promising for a student on a specific level. If a student can be assigned to a level in a level model, providing learning opportunities and—if necessary—scaffolding on the next more complex level might be a plausible heuristic to support this student’s progress. In this sense, level models provide a heuristic to identify what Lave and Wenger (1991) call a “scaffolding interpretation” of the concept of “zone of proximal development” (Vygotsky et al., 1978). It can be assumed that level models are the more useful to this end, the more they focus on a coherent, well-defined, and well-delineated skill or conceptual knowledge construct.
Level models are usually generated by analyzing the difficulties of a set of test items based on a scaling study. Two main approaches can be distinguished: Some researchers use statistical clustering methods (e.g., Marcoulides and Drezner, 2000) based on the empirical item difficulties, to obtain item subsets with coherent difficulty within each set and large difficulty gaps between the item subsets (e.g., Jiang et al., 2021). The main advantage of this approach is, that it results in clearly distinguishable item subsets. Its disadvantages are that it does not consider the sampling error of item difficulties and that it may result in item subsets that are hard to interpret in terms of common item demands. Variants of the so-called bookmark method are an alternative (Mitzel et al., 2013; Dimitrov, 2022). Items are sorted in an item booklet by increasing difficulty. This booklet is then analyzed for subsets of consecutive items, that share common item demands. This is an interpretative process, that results in subsets of items that cluster along the difficulty scale alongside with verbal descriptions of the common item demands. Depending on the implementation of the method, one expert or a group of experts are involved in this interpretation (e.g., Reiss and Obersteiner, 2019; Rach and Ufer, 2020; Pustelnik et al., 2023; Schadl and Ufer, 2023). The item subsets from these analyses are interpreted as levels of demands regarding the skill construct. If the item difficulties stem from a one-dimensional item response theory (IRT) model, that can align test participants’ performance scores and item difficulties on the same scale, test participants can be allocated to one of the levels, indicating which levels of demand the participant usually can already master, and which levels the participant probably will struggle with. In this sense, the levels can also be interpreted as levels of participants’ knowledge or skill.
2 The current study
Assuming a relevance of flexibility in dealing with additive situations, central steps for targeted assessment and intervention in early primary school have been achieved in prior research. An applicable test instrument is available, that is based on a clear skill construct definition, and there is evidence speaking for its validity in terms of the importance for learning word problem solving. However, a level model that can guide teachers’ diagnosis and adaptive instruction is still missing. The main goal of this study was to develop a level model for flexibility in dealing with additive situations, and to describe students’ current flexibility and its development using this model. We analyzed data of students’ flexibility in dealing with additive situations from prior studies with an IRT approach aiming at the construction of a level model for this skill construct.
To clarify whether constructing a level model is reasonable, at all, we first investigated if a one-dimensional model is suited to describe participants’ flexibility in dealing with additive situations in our data (Q1).
Since models allowing to describe students’ current performance in terms of concrete demands, they can master are rare, we the aimed to construct a level model for the flexibility construct, focusing on question Q2: Can we distinguish levels of coherent difficulty and item demands in primary school students’ flexibility in dealing with additive situations? Which task features differentiate consecutive levels in terms of item demands?
Based on the generated level model, we aimed to characterize students’ performance on the flexibility construct in more detail and investigated how students from our sample distributed across these levels (Q3).
Finally, we were interested whether such a model would be of added value to describe how students’ flexibility develops over the span of few weeks. We investigated to which extent the model can be used to descriptively characterize students’ progress in flexibility across a span of several weeks (Q4).
3 Materials and methods
3.1 Design and sample
We reanalyzed data from three studies which measured students’ flexibility in dealing with additive situations. Study 1 was an unpublished, cross-sectional scaling study and comprised N = 130 grade 3 students (62 female, 68 male, Mage = 8.5 years) who worked only on the flexibility test instrument and provided some demographic data. In study 2, N = 119 grade 2 students (56 female, 63 male, Mage = 7.6 years) worked on this and other instruments in a cross-sectional experimental study. Some data from this study were reported in Gabler and Ufer (2021), but not including data on flexibility. Study 3 was an intervention study with N = 134 grade 2 students (66 female, 73 male, Mage = 7.6 years), in which the instrument was applied together with other measures in a pre-test, five weeks later in a post-test and four more weeks later in a follow-up test. Here, data from all three measurements were included in the analysis, including students who participated in only one (N = 5) or two (N = 17) of the measurements. Results of the intervention study are reported in (Gabler and Ufer, 2024). Overall, data from N = 624 test participations by N = 383 students were included in our analyses.
3.2 Flexibility instrument
The flexibility instrument was slightly adapted between the three studies. In study 1, an initial instrument with 18 items was used. Two items were removed due to their psychometric properties after initial scaling and replaced by four new items in study 2. After study 2, again five items were removed, because they turned out to be of very similar difficulty as other items, and five additional items were introduced to better cover areas of higher difficulty. Consequently, 27 different items in total were included in our initial analyses. The Marginal Maximum Likelihood Approach was used, so that the missing data for some items in small groups of participants could be accommodated when estimating the IRT models, by only including those items into the Likelihood Function for a specific person, which the person had worked on.
The test was framed as a story about a birthday party of two twins, Alma and Ben. In each item, two statements from participants of the party were given, and the students were asked, whether the two participants tell the same thing about the party. All presented statements were similar to the sentences that present changes or relations in usual word problems, e.g., “There were four chairs less than children on the party.” and “There were four more children than chairs on the party.” Most statements comprised change actions, equalize actions, and quantitative or qualitative comparisons. Integrating combine situations into the item format proved difficult, thus only few items contained two combine statements. Since combine situations are considered quite easy anyway, we did not see this as an issue. All statements contained exactly one numerical information, except for qualitative comparisons, which contained no numerical information. If an item contained a numerical information, the same number was provided in both statements. The two statements within each item differed in terms of different additive vs. subtractive wording, different semantic structures, or both. Note that calculations were neither possible nor useful, as at most one numeric information was given in each item. The answer options were “yes” (the two participants tell the same thing), “no” (they do not tell the same thing) or “I do not know.” The last answer option was used very rarely, so that a probability of 50% for choosing the correct solution just by guessing must be assumed for all items.
3.3 Analyses
The generation of a level model (Q2) usually requires modelling the response data with an appropriate IRT model (Q1). Different IRT models were estimated using the R package tam (Robitzsch et al., 2020) and compared using Chi-Square-Likelihood-Ratio tests (investigating differences in model-data-fit), and the Akaike (AIC) and Bayes Information Criterion (BIC, lower values reflect better model fit) as information indices. First, we explored different one-dimensional models, that reflect different assumptions about how to model the item answer process: A three-parameter model, that assumes varying difficulty, guessing, and discrimination parameters over all items (model 1), a model that assumes constant item discriminations, but varying difficulty and guessing parameters (model 2), a model that assumed constant item discriminations, constant guessing parameters of 50%, and varying item difficulty parameters (model 3), and a one-parameter Rasch model with constant item discriminations and no (zero) guessing parameter (model 4). When testing these models, we balanced model parsimony with fit to the data and interpretability. For example, model 4 with varying item discriminations has the disadvantage of crossing item characteristic curves, which implies “substantive illogic in attempting to define a construct with item characteristic curves (ICC) that cross, because their slopes differ due to differing discriminations, or their asymptotes differ due to differing guessing parameters. Crossing curves cause the hierarchy of relative item difficulty to change at every ability level. This destroys the variable’s criterion definition” (Wright, 1999, p. 74). We primarily used Warm’s unbiased maximum likelihood estimator (WLE) for person parameters (Warm, 1989). Expected-A-Posteriori (EAP) (Bock and Aitkin, 1981) estimators were used to calculate a second measure of person reliability, but not for person parameter estimation, since these typically have a “larger inward bias toward the prior mean but smaller variance” (Wang, 2015, p. 445) than WLE estimates.
For example, the one-dimensional, restricted three-parameter model 3 would mean, that a difficulty parameter for each item and a single ability estimate for each person are estimated, assuming equal discrimination indices for all items, as well as a constant guessing parameter of 50%. The probability that a student i with performance parameter solves an item j with difficulty parameter in this model can be calculated as
with guessing parameter and discrimination parameter for all items j.
Given the decision for specific assumptions on the item answering process, we furthermore explored whether a two-dimensional model (model 5) would be superior for our purpose compared to the corresponding one-dimensional model. To this end, we investigated the two-dimensional model that was most plausible from our perspective, separating the ability to identify equivalent statements as equivalent from the ability to identify non-equivalent statements as non-equivalent into separate dimensions.
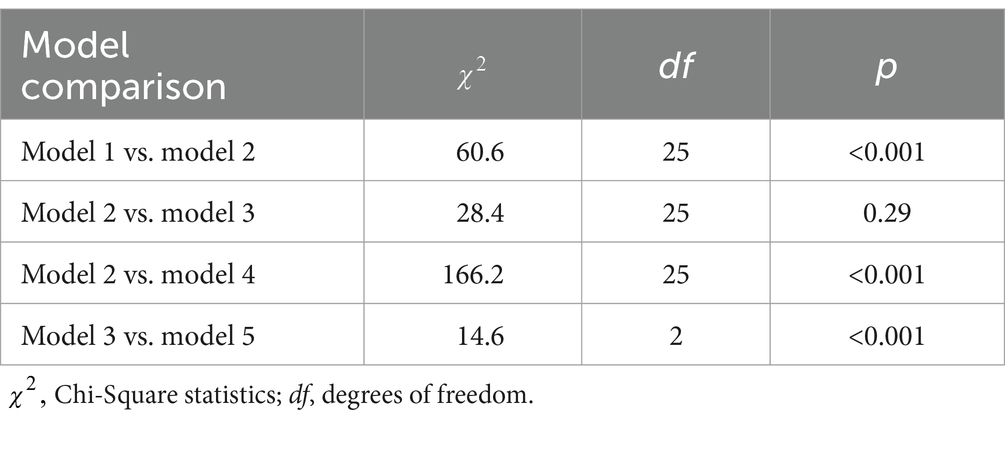
When deciding for a final model we used information criteria (AIC, BIC) and Chi-Square-Difference tests to compare models. Infit (weighted) and outfit (unweighted) Root Mean Square Deviation (RMSD) item fit measures (Adams and Wu, 2007) were used to evaluate model fit, with values above 1.5 considered unproductive for measurement (Linacre, 2002). Additionally, we inspected the Q3 statistics, interpreting values above 0.25 as indication of a violation of the local independence assumption in IRT models (Christensen et al., 2017). Consideration of these model comparison and model fit measures was balanced against model parsimony (preferring models with fewer parameters, that were equally plausible) and usefulness of the model for measurement (e.g., acceptable reliabilities).
To generate a level model (Q2), items were first ordered by their difficulty in an item booklet as in the bookmark method (cf. Mitzel et al., 2013 for a similar approach). Then, each item was characterized in its specific demands (e.g., involved statement types, necessity to deal with qualitative or quantitative comparisons, direction of the wording, equivalence of the two statements), to identify similarities between consecutive items as well as differences between neighboring groups of items with similar demands (cf. Rach and Ufer, 2020). In this way, groups of items with similar difficulty and similar item demands were identified. This mostly focused on the similarities and differences between the two statements in each item, but also considered reasonable comparison strategies and possible errors from the literature. This resulted in verbal descriptions of the common demands of the items in each level. Later, the differences in the demands between adjacent levels were analyzed based on these texts to make the model more accessible. Moreover, thresholds between the levels were established by calculating the average difficulty of the easiest item of one level and the most difficult item of the next lower level. Furthermore, the difficulty of the easiest and the most difficult items in the test were used as lower threshold of the lowest and upper threshold of the highest level.
To allocate student performance on the item difficulty scale for Q3, we assigned a student to that point on the scale, where she or he would have a 75% probability of solving the item, which is exactly the position of the students’ performance parameter . In large scale studies that do not apply guessing parameters, values from 62.5 to 70% have been used. The exact cut-off value has been found to make little difference in some analyses (Rolfes and Heinze, 2022). We decided to use a substantially higher cut-off due to the high assumed guessing probability of 50%.
Assigning students to levels is usually done by assigning a student to the level, in which his or her performance parameter is located (i.e., between the lower and the upper threshold of this level). Consequently, being on a level means that a student can solve all items of the easier levels with more than 75% probability and all items of the more difficult levels with less than 75% probability. The assigned level comprises items, which the students has not (yet) mastered, but which are closest to being mastered. A far-reaching interpretation would be, that this level is the students’ “zone of proximal development” (Vygotsky et al., 1978). Since person parameters often carry substantial measurement error, this assignment procedure with strict cut-offs can be debated: A student that has an estimated performance parameter close to a level threshold has a high probability of being assigned to the wrong level, since the (unknown) real performance parameter might be on the other side of the threshold. Therefore, we applied an alternative approach: For each student with estimated person parameter θ, corresponding standard error seθ and each level i, we calculated a statistics S(θ, i) as the percentage of a normal distribution around θ with variance seθ, that falls within the respective level. This results in one value per level and student, and the sum of the values across all levels for a single student is one. S(θ, i) can be interpreted as the probability density of obtaining a measured person parameter around θ, if one repeatedly would test students, whose real person parameter was surely at the respective level. Thus, summing S(θ, i) over all levels i yields a sum of one (since each real person parameter is one of the summed levels) for each (measured) person parameter value. We interpret the sum of S(θ, i) over all participants as a measure of the number of participants that can be allocated to level i, weighting each student by its distance to the respective level. We will refer to individual values of S as level sampling probability and to sample sums of S as number of persons allocated to this level.
Students’ average development (Q4) was investigated using analysis of variance. A deeper, more qualitative description using the generated level model was based on bivariate density plots and local regression models.
4 Results
4.1 Item selection and model comparison (Q1)
Initial scaling analyses revealed that one item asking for a comparison of two combine statements showed a very high solution rate (90%) and problematic item fit values. Consequently, this item was excluded from further analyses. During the further analysis, another item that required to match equivalent compare and equalize statements was removed from the analysis due to substantial residual correlations with two other items (Q3 = 0.35 and Q3 = 0.36).
Table 1 shows the fit information and Table 2 shows Chi-Square-Likelihood-Ratio tests for the models reflecting different assumptions about the item answer process. Model 3 shows the lowest AIC and BIC indices, making it preferable over the other three models. Model 2 with freely estimated guessing parameters did not fit significantly better than model 3 with constant guessing parameters of 50%. It did, however, fit better than model 4 without guessing parameters. Guessing parameters in model 2 ranged between 34 and 50%. Model 1 showed significantly better fit than model 3. However, we decided to use the more restrictive model 3 for several reasons: (i) It contained less parameters but was preferable in terms of information indices. (ii) We considered the number of parameters in model 1 as high in relation to our restricted sample size. (iii) Varying item discriminations make it hard to describe students’ performance in terms of item demands as item characteristic curves may intersect (“This destroys the variable’s criterion definition,” Wright, 1999, p. 74).
For model 3 the person reliabilities were acceptable (WLE: 0.67, EAP: 0.75). Also, item RMSD infit (0.98–1.03) and outfit (0.64–1.68) indices were mostly within the acceptable range (Linacre, 2002), except for one item with a high outfit (1.68) indicating some underfit. An analysis of the item showed that it contained statements about the height of block towers, while all other items dealt with numbers of objects. Since it was one of the few items containing qualitative comparisons, and since it was not of extremely low or high difficulty, we decided to keep the item in the analysis. The other items showed outfit values of 1.30 and below. Residual correlations between items (Q3) provided no indications of substantially violating the local independence assumption of the applied IRT model. The average person performance parameter was M = 1.49 (SD = 1.54).
Moreover, we investigated a two-dimensional model separating items with pairs of equivalent statements and items with pairs of non-equivalent statements into different dimensions (model 5). Indeed, this two-dimensional model fit the data significantly better than model 3 (Table 2). However, the WLE reliabilities of the two dimensions were unacceptably low (equivalent statements: WLE: 0.37, EAP: 0.67; non-equivalent statements: WLE: 0.34, EAP: 0.73; correlation between the two dimensions latent: 0.86, manifest WLE: 0.39). Since this indicates that the model is not well suited to derive individual person parameter estimates, the two-dimensional model was disregarded.
4.2 Level model (Q2)
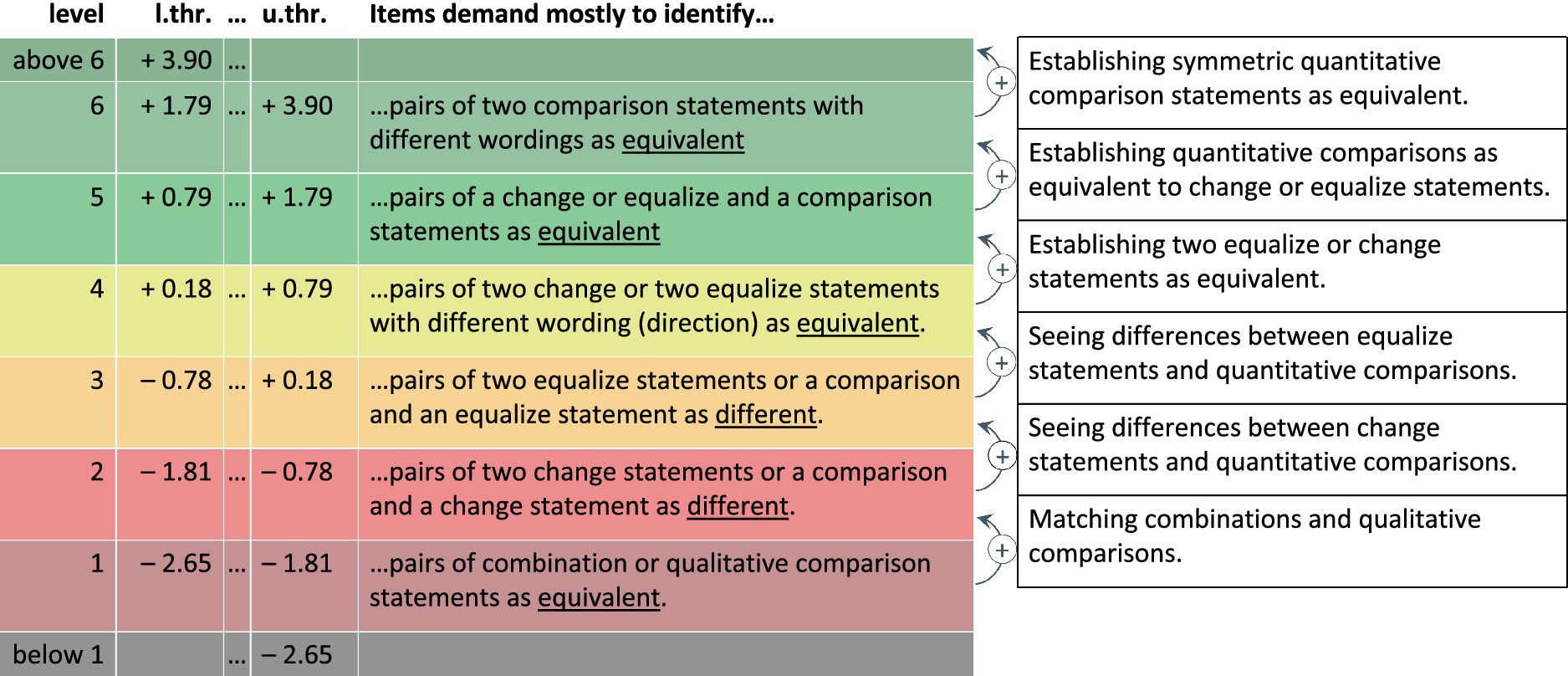
Analyzing the item booklet sorted by empirical difficulty revealed, that investigating two qualitative compare statements or two combine statements constituted the easiest demands (level 1, ). For example, one item required to match the (equivalent) qualitative comparison statements “Alma’s tower is smaller than Ben’s tower.” and “Ben’s tower is higher than Alma’s tower.”
All of the remaining items involving two equivalent statements (two statements referring to the same situation) turned out to be harder than items requiring to find differences between the descriptions in the two statements. Within those items asking the students to identify two statements as describing different situations, one set of eight items contained either two change statements in different directions (additive vs. subtractive), or a statement describing a temporal change of one of two initially equal sets and a compare statement about the two sets after the change (e.g., item 10: “Before the party, Alma and Ben had equally many wristbands. Ben got 3 bands more on the party” vs. “Alma has 3 bands more than Ben now”). Also, two items containing two compare statements each can be found on this level (level 2, , e.g., item 11: “Ben got 2 presents more than Alma” vs. “Alma got 2 presents more than Ben”). Different from the items on level 1, these items contained a quantitative relation information, but the two situations could be identified as different by a qualitative comparison – even if the quantitative relation was misunderstood as a concrete set. Similarly, one item with an additively worded equalize statement and a non-equivalent subtractively worded compare statement was in this interval, as well. Level 2 primarily requires establishing a change statement as being different from another change or a compare statement.
The next set of six items (level 3, ) comprised items that involved either two equalize statements (e.g., item 18. “If Ben takes 3 cards more, he has as many cards as Alma.” vs. “If Ben puts 3 cards away, he has as many cards as Alma.”) or an equalize statement and a compare statement with the same (additive vs. subtractive) wording (e.g., item 21: “Currently, Alma has 4 postcards more than Ben.” vs. “Alma needs to get 4 more postcards, so that she has as many postcards as Ben”). Regarding the matching of equalize and compare statements, statement pairs with different wording (level 2) were assigned to lower levels than statement pairs with the same wording (both additive or both subtractive). Level 3 requires establishing an equalize statement as being different from another equalize statement or a compare statement with the same wording.
Within those items asking to identify two statements as being equivalent (describing the same situation), three items contained either two change statements or two equalize statements (level 4, , e.g., item 23: “Alma sold 3 lemonades to Ben” vs. “Ben bought 3 lemonades from Alma.”). Thus, level 4 requires establishing two dynamic (change or equalize) statements as equivalent.
The next set of four items contained either a change and a compare statement or an equalize and a compare statement (similar to level 2 resp. 3, but with two statements matching the same situation; level 5, , e.g., item 19: “If Ben gives 3 cookies to another child, he has as many cookies as Alma.” vs. “Ben currently has 3 cookies more than Alma.”). Level 5 requires establishing quantitative comparisons as being equivalent to change or equalize statements.
Each of the two items from the last set (level 6, ) contained two symmetric compare statements, one with additive and one with subtractive wording (e.g., “On the party, there were 4 chairs less than children.” vs. “On the party, there were 4 children more than chairs.”). Thus, level 6 is characterized by identifying symmetric quantitative compare statements as equivalent.
Figure 2 shows the level descriptions and the differences between consecutive levels.
4.3 Student distribution across the levels (Q3)
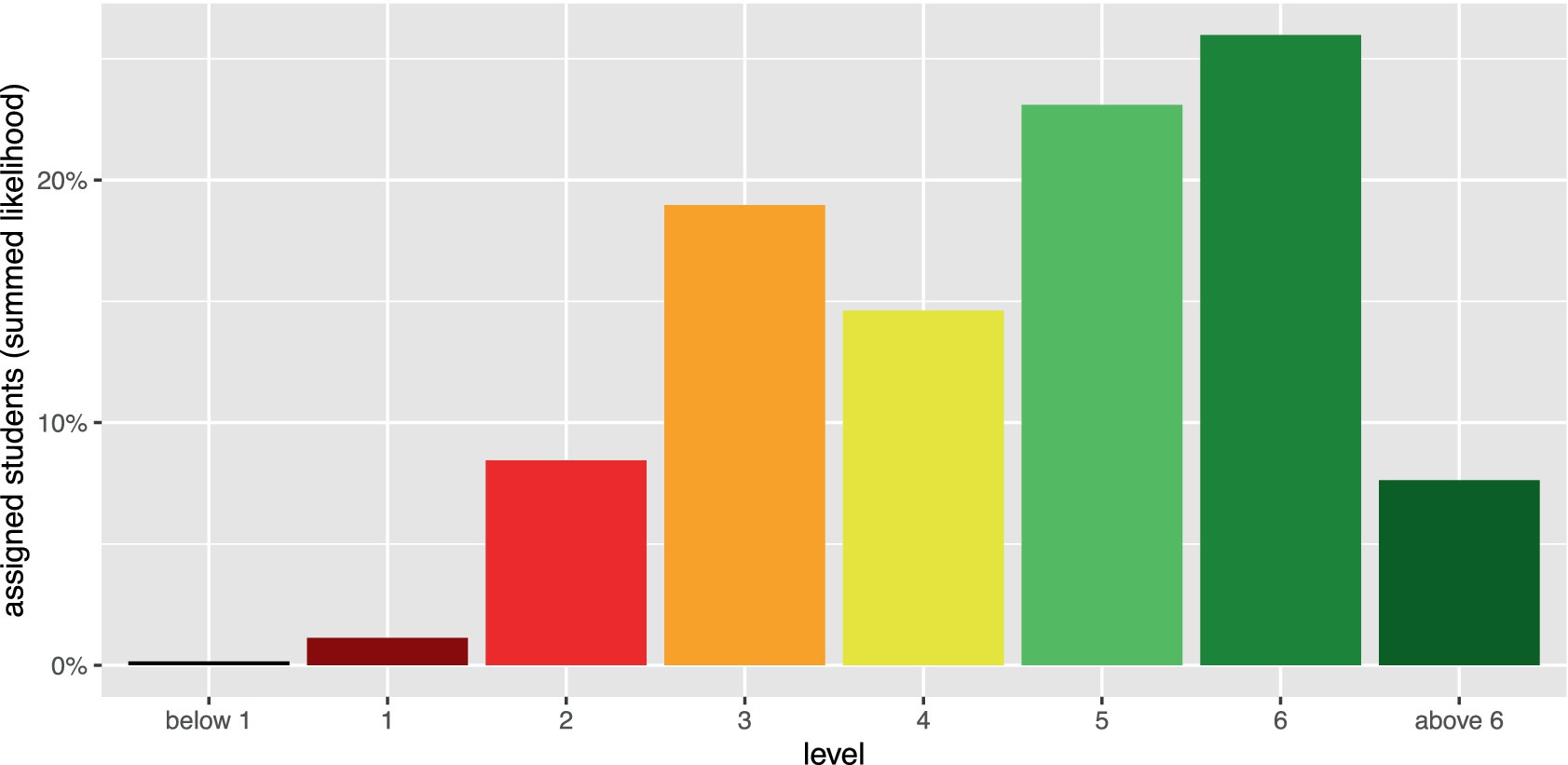
Figure 3 displays the smoothed level sampling probability of a participant being allocated to each level, depending on the participant’s performance parameter . As expected, there is substantial overlap around the level thresholds. Note that participants have the highest level sampling probability for the narrow level 4 only in a very small interval of performance parameters. Moreover, for participants with very low performance parameters, level 1 assignment is hard to differentiate from assignment below level 1. On the other hand, for example, a high-level sampling probability of belonging to level 3 can be determined for performance parameters around zero.
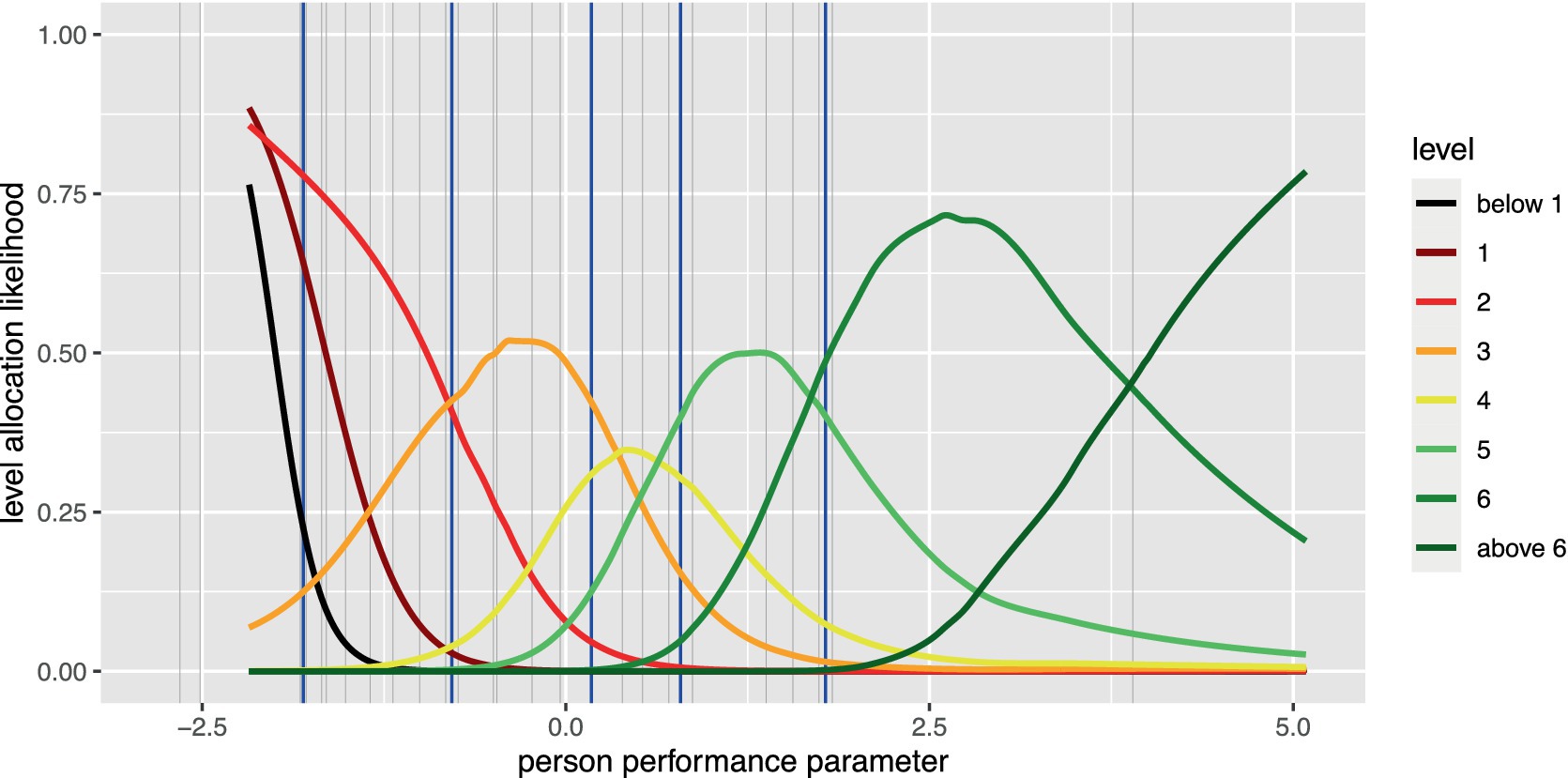
Figure 3. Level sampling probability by level and person performance parameter. Blue lines indicate level thresholds, light grey lines indicate item difficulties.
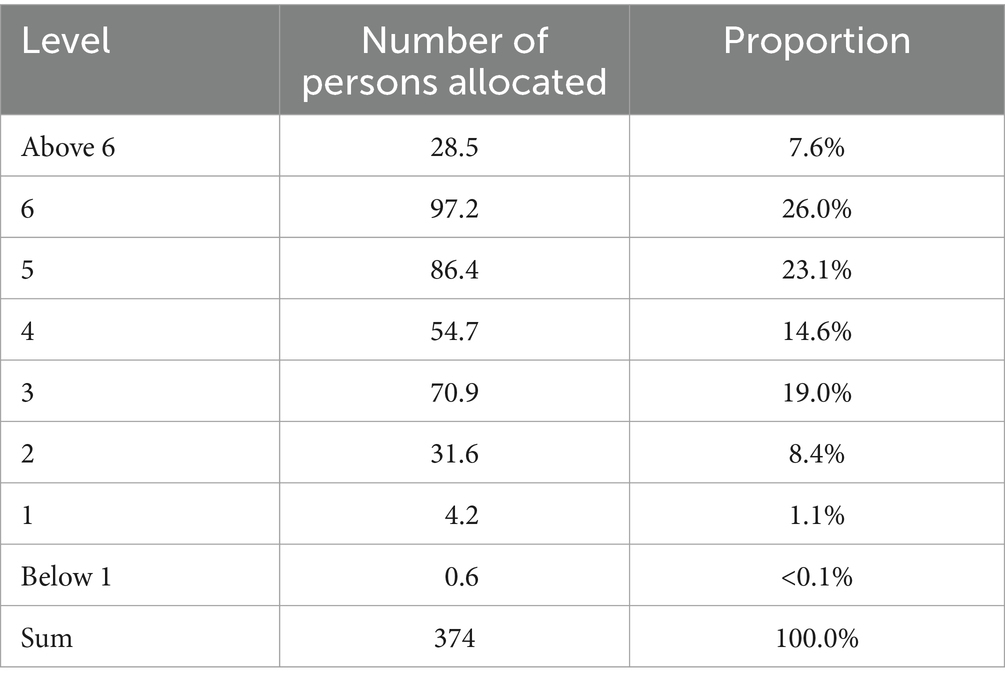
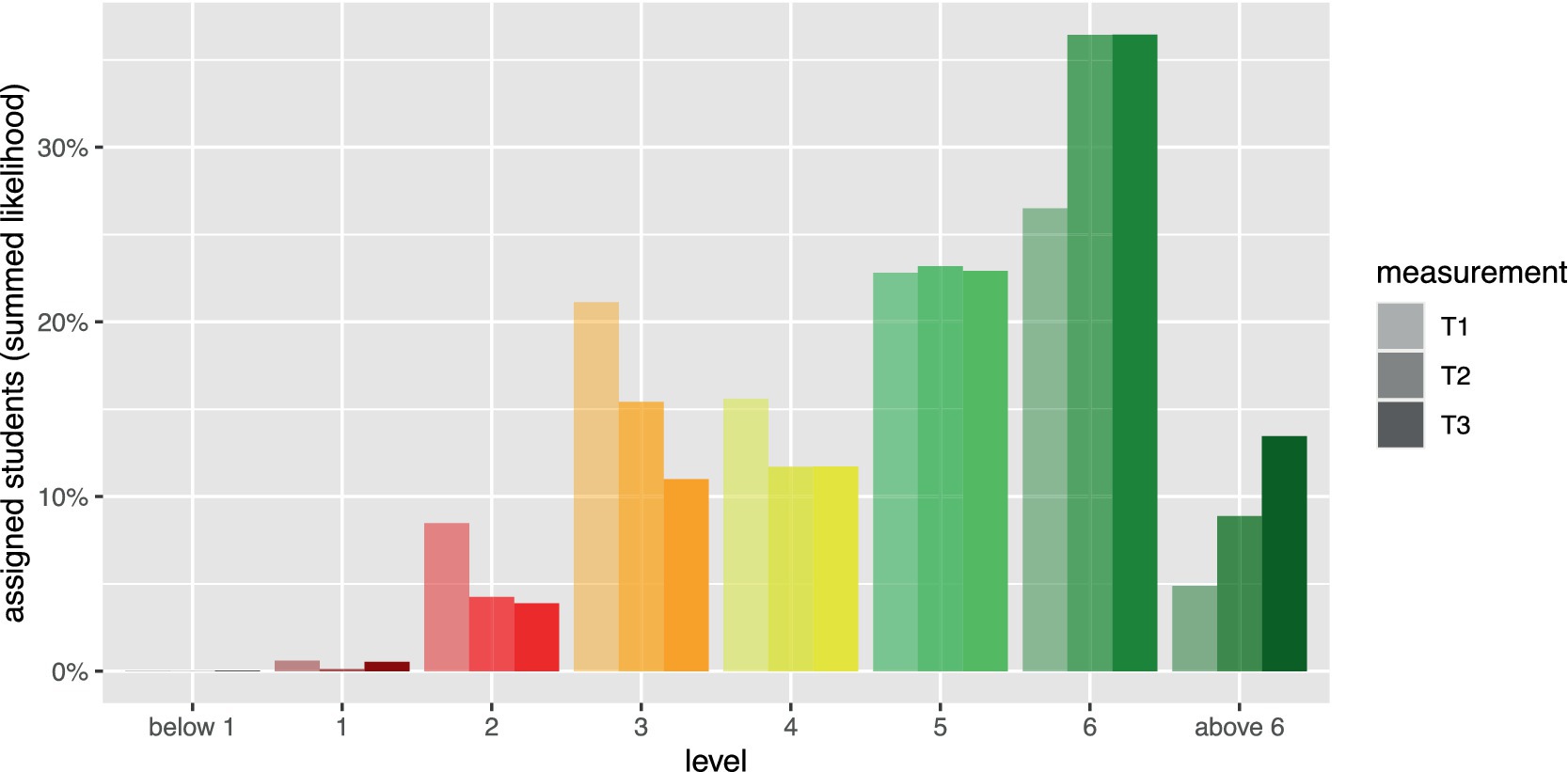
To investigate students’ distribution over the levels, we considered data from study 1, study 2, and the first measurement of study 3 (N = 374). Figure 4 and Table 3 display participants’ distribution across the levels. Note that Figure 4 and the second column of Table 3 show the expected number of persons per level. In this sense, every participant counts into all levels, with higher shares on levels near to the participant’s performance parameter and lower shares on more distal levels, as described by their level sampling probabilities. The findings indicate that while few participants can be found at level 1 or below, about one quarter of all participants was allocated to level 2 or 3. This indicates that these students still struggle with establishing two situation descriptions as being different. On the other hand, 26.0% of the participants can be assumed to be at level 6, indicating that they are able to identify change or equalize statements and quantitative compare statements as equivalent, but still struggle with symmetric quantitative comparisons. The finding, that only 7.6% of the participants seem to be able to identify symmetric quantitative compare statements as equivalent must be interpreted with care, since only two items of very different difficulty constitute this highest level.
4.4 Describing development using the level model (Q4)
To analyze the development in students’ levels, we considered data from N = 112 grade 2 students only, who participated in all measurements of study 3. A repeated measures ANOVA with flexibility as dependent variable showed a significant effect for measurement [ ] and pairwise contrasts between each of the two measurements were significant (p’s < 0.05, Tukey correction). Figure 5 shows the distribution of participants (counted by their level sampling probability) across the levels by measurement. A decrease can be observed for the levels 4 and below, primarily between T1 and T2. Level 5 assignment remained stable, most likely due to students from lower levels progressing to level 5 and students from level 5 progressing to higher levels. An increase can be observed for level 6 between T1 and T2, and above level 6 between each pair of measurements.
Even though Figure 5 may indicate that level population decreases for lower levels and increases for higher levels, it allows only restricted insight into students’ development. To obtain a clearer picture, we plotted students’ performance parameter in T2 (resp. T3) against their performance in T1 (resp. T2) using two-dimensional density plots (Figures 6A,B). Lighter colors indicate more students in the respective areas. The number of students allocated to each combination of levels from pre-and post-test (resp. pre-and follow-up-test), calculated from the sum of level sampling percentages, is provided in Supplementary Tables S1, S2. Moreover, we used bivariate non-linear regression methods to estimate the average local T3 performance score for each T1 performance score.
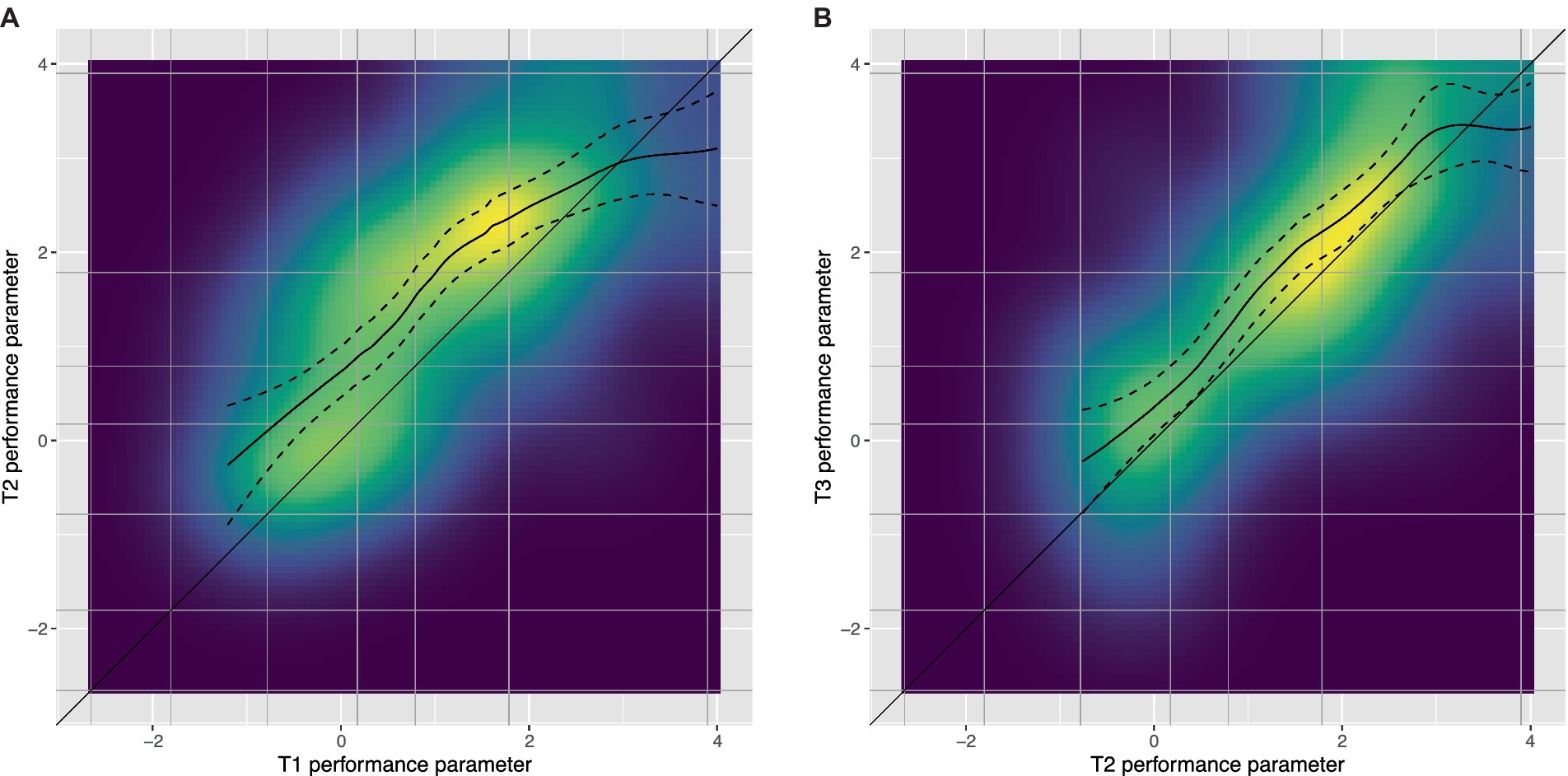
Figure 6. Density plots for person performance parameter at T2 (A) resp. T3 (B) by person performance parameter at T1 (A) resp. T2 (B) with bivariate non-linear regression line and 95% confidence interval. Grey lines indicate level thresholds.
Figure 6A indicates that, on average, participants throughout the whole range of initial (T1) performance, except those with very high values (above 2.5), show significant progress until T2 (the non-linear regression line and its confidence interval lie below the diagonal line indicating no progress from T1 to T2 for these students). This may be due to a ceiling effect, meaning that the flexibility test was very easy at T2 for participants with initially high scores. The regression line is a bit steeper at the upper end of level 4, indicating that being able to identify change (or equalize) and compare statements as equivalent already initially may substantially benefit students’ progress from T1 to T2.
Analyzing the two-dimensional distribution in Figure 6A indicates that few students outperform level 6 even at T2 (dark colors at the upper end of the figure). Out of those students who were on level 5 at T1, quite some—but not all—were allocated to level 6 at T2, showing that these students could benefit and learn how to match equalize and compare statements. Students who were on the (narrow) level 4 at T1 spread out across levels 3–5 and—less frequently—level 6 at T2. Some students remain on level 4 or even show lower scores at T2—possibly due to measurement error variation. Others show scores on level 5 and the lower end of level 6. This indicates that students at the transition to being able to identify statements as equivalent benefited very differently from learning opportunities between T1 and T2. Moreover, many of those students who were on level 3 at T1, who were still struggling to identify compare and equalize statements as different, remained at this level and showed little progress.
Figure 6B indicates significant progress also from T2 to T3 over almost the whole range of T2 performance, again except for T2 scores above 2.5. Now, some of the students who were at level 3 at T2 progress to level 4 at T3. The pattern is less clear for level 4 at T2, which is less populated than at T1 (cf. Figure 5). Similarly, there is some progress for students from level 5 at T2 to level 6 at T3.
5 Discussion
In this study, we report the development of a level model of primary school students’ flexibility in dealing with additive situations. We were able to distinguish six different levels of coherent difficulty and coherent item demands. Further, students were assigned to the most likely levels according to their person performance parameters which were estimated from their ability to rate whether two mathematical statements referred to the same or a different situation. The data from three different studies with a total of 383 primary school children in Grades 2 and 3 were used in the development of the model and children were assigned mostly to levels 5 and above with only few children in level 2 and below. However, a substantial number of students remained below level 6, which describes beginning mastery of symmetric comparison statements. In addition, we were able to analyze children’s progression across about 2 months. Children on level 4 and 5 at the beginning of the assessments often progressed to the next level, whereas children on level 3 often did not progress to higher levels. This may indicate a qualitative step between levels 3 (and below) and levels 4 (and above). This kind of information will be valuable for teachers in their support of children’s flexibility and their mathematical word problem solving skills.
5.1 A level model for flexibility in dealing with additive situations
To generate a level model, we applied an exploratory approach using data from an existing test instrument. With our IRT approach, we were able to identify a fairly clear level structure for children’s flexibility in dealing with additive situations. The most pronounced differentiation was visible for identifying statements as non-equivalent (on lower levels) and as equivalent (on higher levels). It remains to be explored, if this reflects a general tendency of students to mark statements as different in the case of doubt. Taking a closer look, it is sufficient to identify even a small difference in the described situations to establish two statements as non-equivalent. Contrary, to establish two statements as equivalent, the existence of such two differences must be ruled out, for example by explicitly transforming perspective described by one statement into the one described by the other (e.g., by seeing that an equalization action described in one statement would balance the quantitative relation described in the other one). Apart from these two broad areas, the easiest level 1 comprised dealing with combine statements and qualitative comparisons.
A bit different patterns occurred within each of the two areas (identifying statements as non-equivalent resp. equivalent). For identifying statements as equivalent, matching with two dynamic statements was easiest (level 4) followed by matching a dynamic statement and a compare statement (level 5) and two compare statements (level 6). This speaks for a learning trajectory from dynamic situations to static situations, as it was also conjectured in (Gabler and Ufer, 2021). For identifying two statements as different, matching two quantitative compare statements was part of the lower level 2, together with dealing with two change statement or one change and one compare statement. This low difficulty of identifying two quantitative compare statements as different should not be overestimated, as it can be solved by just considering the entailed qualitative comparisons (“Chris has 3 marbles more than Alex” vs. “Alex has 3 marbles more than Chris”), and it can be even solved correctly if statements such as “Chris has 3 marbles more than Alex” are interpreted as “Chris has 3 marbles, and Chris has more marbles than Alex” (Mekhmandarov et al., 1996). Apart from this, dealing with equalize statements (possibly along with one compare statement, level 3) turned out more difficult than dealing with change statements (possibly along with one compare statement, level 2). Since equalize statements comprise a (imagined) change action together with a statement about the effect of this action, this can be explained by the different complexity the two dynamic statement types.
It should be noted that these differences in item difficulty can not necessarily be interpreted as a naturally occurring, individual learning trajectory in the psychological sense. As a didactic model, progressing from identifying statements as non-equivalent to identifying statements as equivalent would not make sense. Our results still may serve to generate hypothetical learning trajectories, which are not purely descriptive psychological models, but are strongly engendered within a specific instructional context (Simon, 1995; Clements and Sarama, 2012). They also carry a normative component, making proposals on how to (more effectively) treat a certain content in instruction. Progressing from the analysis of qualitative comparison and dynamic statements to matching dynamic statements with quantitative compare statements and finally pairs of compare statements would be reasonable based on our findings. When informally reviewing first grade mathematics textbooks in Germany, we did not find activities related to the interpretation of quantitative comparison statements and Gabler et al. (2023) found few compare word problems in German first and second grade textbooks. Even though it does not follow from our findings, discussing the meaning of quantitative compare statements, for example by considering two concrete sets, establishing a one-to-one-correspondence between the smaller set and a subset of the larger one, and highlighting the remaining items as the difference set, seems to be a reasonable learning opportunity before matching compare statements to other statements.
The most striking difference in difficulty was between qualitative comparison statements, which belonged to the lowest levels, and quantitative comparison statements, which made up the upper end of the difficulty continuum. This reflects the specific difficulty of representing (Mekhmandarov et al., 1996; Gabler and Ufer, 2021) and flexibly interpreting (Stern, 1993) quantitative comparison statements.
5.2 Students’ flexibility in dealing with additive situations
Even though the average student performance parameter was in the range of level 5, the substantial standard deviation raises the question about a qualitative interpretation of inter-individual differences in students’ performance. Our model allows to allocate students to the levels, offering ways to provide teachers with more specific information than a rough overall performance measure (in terms of, for example, percent tasks solved correctly). Each level comes with a criterial interpretation (Ufer and Neumann, 2018) of the demands students can systematically master (below the assigned level), which they master partially (assigned level) and which demands they will typically fail currently (above the assigned level). This may allow teachers to identify individual learning needs of each student. However, we also note that level assignment underlies measurement error. Determining the level sampling probability of a student “being” on this level allows to make this natural uncertainty transparent to teachers by reporting the two or three most likely levels for a student—at the cost of providing a quite conservative (i.e., too much spread out) picture of the assignment uncertainty. It might be of interest how teachers deal with this kind of uncertainty when evaluating this information as diagnostic evidence and deriving didactical conclusions (Heitzmann et al., 2019). This uncertainty is part of teachers’ everyday practice and should also be acknowledged in teacher education—instead of, for example, asking (active or pre-service) teachers to make definite decisions between levels in simulations (Wildgans-Lang et al., 2020).
We found that around 60% of the students are systematically able to identify non-equivalent statements as non-equivalent. However, this also means that about 40% of the students in our sample are not able to do so. Thus, comparing and contrasting (Hattikudur and Alibali, 2011) different verbal statements about mathematical structures in real-world situations may be promising for all students—either learning about differences between non-equivalent pairs of statements, or learning to correctly match equivalent statements.
It must be noted that almost all students in our study mastered level 1, comprising combine and qualitative compare statements, and few still struggled with differentiating descriptions of different change situations (level 2). This indicates, that change situations might be a good didactical starting point for the learning trajectory proposed above. Dealing with equalize statements posed problems to at least 40% of the students, indicating that understanding them may not be taken for granted and should also be addressed in instruction. Since equalize statements may provide a didactical bridge to reinterpreting and understanding compare statements, more than the currently still restricted evidence (one example is Stern, 1994) on students’ understanding of and performance on equalize word problems might be desirable. Finally, less than 10% or our sample systematically mastered to identify symmetric quantitative compare statements as equivalent. This is in line with findings by Stern (1993) and underpins the importance of dealing with compare statements in more depth in first years mathematics instruction.
5.3 Development of flexibility in dealing with additive situations
The longitudinal analyses provide insights into students’ development of flexibility in dealing with additive situations. As may be expected when a skill develops positively over time in a population, lower levels decrease in frequency, while higher levels increase, and middle levels remain rather stable over the short period of several weeks in our study. Thus, in terms of an interpretation of students’ development, level frequencies contain little more information than analyses of average development. At least we can say, that an increasing number of students master symmetric quantitative compare statements after several weeks.
Deeper, qualitative analyses of the bivariate distributions based on performance from two consecutive measurements allows to derive more elaborate conjectures. Firstly, some progress seems to be observable for students all over the whole range of prior performance range. Students with high initial flexibility form an exception, most likely due to a ceiling effect of the instrument. This indicates that flexibility is a skill that can be learned and developed.
However, there are first indications that this progress is not equally strong for all students. Until T2, there was little progress of students who were initially on level 3, and from T2 to T3 only few students progress towards level 4. The levels 3 and 4 differentiate between finding differences between statements (level 2 and 3) and identifying statements as equivalent (levels 4 and above). It seems that students, who were on level 3 initially, cannot really benefit from eventual opportunities in the investigated time span between T1 and T3. It seems that the challenge to identify different descriptions of the same situation as equivalent requires specific instructional support, for example by establishing strategies such as the dynamization or the inversion strategies described above. On the other hand, the acquisition of these strategies might still require a basic understanding of the corresponding situation structures. It remains an open question if what constitutes level 3 in our model provides sufficient prior knowledge and skills for this purpose.
Indeed, students who were on level 4 initially, showed varying progress from T1 to T2. This may indicate that other factors, not explicitly investigated in our analyses, influence students’ progress here. Given that flexibility comprises verbal descriptions of mathematical structures in everyday situations, students language skills (Purpura and Reid, 2016; Peng et al., 2020; Ufer and Bochnik, 2020) may be an important factor here, but also their mathematical prior knowledge. Future research should clarify not only which student characteristics explain students’ performance in word problem solving or flexibility, but also the development of this performance (e.g., Paetsch et al., 2016).
Moreover, almost exclusively those students progressed to level 6, who were on level 5 at the preceding measurement. This indicates that being able to match compare statements to equivalent dynamic statements might be an important prerequisite for (at least partially) mastering symmetric compare statements. Future research considering students’ development with a better temporal resolution or applying deeper analysis of their learning and reasoning processes when dealing with symmetric quantitative compare statements should investigate this hypothesis in more detail.
One option to put the developmental hypotheses from this study to a test would be to provide students adaptively with instruction targeting the assigned next level and compare this to offering instruction targeting different higher levels. This may provide useful insights into whether students’ prior flexibility plays a role, at all, for further learning, and if yes, which level of instruction requires which prior skills. Furthermore, such evidence may support the conceptualization of adaptive instruction (Plass and Pawar, 2020) that teachers (or other actors in the educational system) may provide based on a diagnosis of students’ flexibility. Finally, the results are also of practical significance, as they may be used in the development of textbooks which may even contain activities to train flexibility, and for specific diagnostic processes, in which the current student’s approach towards additive situations and their current level of flexibility are assessed and considered in a subsequent training.
5.4 Limitations
This study is marked by several limitations. We used an interpretational method based on item contents and item difficulties to arrive at our levels and their characterizations. It would be helpful to replicate the model with an independent sample if persons and, optimally, with a new set of items that was constructed based on the model. This would also allow to extend the test beyond the few items, that were used to build the level model. It would also be helpful to improve the level model and to contribute to a better differentiation between different learners. Future extensions of the instrument should cover typical errors, such as the misinterpretation of quantitative compare statements as statements about a concrete set and a qualitative comparison. Moreover, demands on higher levels of flexibility still need to be conceptualized. One idea would be to have students actively produce alternative, equivalent descriptions of the same situation (using, for example, provided words) instead of judging given statements. This would, however, also come with stronger demands in terms of language skills (Gabler and Ufer, 2022). Finally, other kinds of situations could be included, covering not only statements about the cardinality of sets, but also about other measures such as lengths, weights, etc.
When doing so, dimensionality of the construct should be considered further. The observed reliability of the whole scale was satisfactory, but not optimal. Including more items per dimension by varying the existing situation description statements could potentially remedy the very low reliabilities of the whole scale or the two assumed subscales. However, an eventual two-dimensional model would differentiate matching vs. unmatching statement pairs, which are also separated into the upper and the lower end of the one-dimensional current difficulty scale. For many participants one the two dimensions would end up being either very easy or very hard. Furthermore, the two dimensions showed a very high latent correlation in our analysis, also pointing to little added explanatory value above a one-dimensional model. If multi-dimensional models are considered, level models would need to be established for each dimension separately. For the two-dimensional model considered in this manuscript, it would be plausible that levels 1 to 3 would arise for one scale and levels 4 to 6 for the other one. Alternative multi-dimensional could be explored, e.g., differentiating the type of statements entailed each item.
Our study applied mostly descriptive methods to either characterize observed student performance or to derive hypotheses about developmental questions. Formal statistical inference methods could be applied to investigate the average development in the study 3 sample—which is not the main contribution of the study. Other methods such as think aloud methods, more intensive tracking of student performance over a longer time span, or intervention studies are necessary to further investigate our exploratory findings. Developmental conclusions are also limited by the ceiling effect of the test instrument, speaking again for an extension of the test with more complex demands. Relatedly, we assumed sufficient longitudinal measurement invariance in this manuscript, but this assumption needs to be tested. Such analyses might also provide deeper insights into the development of students’ flexibility. Finally, note that our approach to allocate participants to the levels is still quite pragmatic and not based on a systematic estimation of participants’ probability to belong to the profiles. Future works might explore more advanced allocation techniques, such as calculating this probability by using the overall score distribution, or even a-priori-distributions for each participant based on prior measurements as a reference.
Finally, our results are limited by the fact that they are solely based on an observation of students’ final performance on the flexibility test items. A closer consideration of students’ solution strategies, in particular for items containing equivalent vs. non-equivalent findings could extend prior results that primarily address the interpretation of quantitative compare statements (Mekhmandarov et al., 1996).
6 Conclusion and outlook
The contribution proposes a model of different levels of complexity for students’ flexibility in dealing with additive situations. Even though longitudinal interpretations should be taken with care, the model itself may support informal observation and formative assessment of students’ flexibility in the first 2 years of primary school. To this end, it should be investigated to which extent teachers can make use of this model to either observe students or interpret students’ solutions on statement matching tasks or word problems, or to make use of findings from an externally applied assessment of students’ skills with a flexibility test like the one analyzed here. Regarding the latter use of the instrument, the uncertainty entailed in the level assignment from such tests is a matter that should be addressed explicitly when informing teachers about their students’ performance, but also when investigating teachers’ use of such information.
A further step would be to conceptualize and investigate adaptive instruction based on the model. This could provide useful and more reliable insights into the contingencies between different subskills in the development of students’ flexibility, but also evidence about effective strategies to support this development. Specific focus could be put on the difference between levels 1–3 and levels 4–6, which turned out to be particularly challenging in our longitudinal analysis.
Summarizing, we highlight a skill in this manuscript that plays an important role in students’ development of word problem solving skills. The proposed level model requires further validation, extension, and investigation, but may develop into a useful tool for assessment and intervention in mathematics instruction in the early school years.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical approval was not required for the study involving humans in accordance with the local legislation and institutional requirements. The study was approved by the local school authorities under the Bavarian Ministry of Education. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.
Author contributions
SU: Conceptualization, Formal analysis, Funding acquisition, Methodology, Resources, Supervision, Visualization, Writing – original draft, Writing – review & editing. AK: Validation, Writing – review & editing. LG: Conceptualization, Data curation, Investigation, Methodology, Project administration, Writing – review & editing. FN: Validation, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1340322/full#supplementary-material
References
Adams, R. J., and Wu, M. L. (2007). The mixed-coefficients multinomial logit model: a generalized form of the Rasch model. In: Multivariate and mixture distribution Rasch models: extensions and applications, Eds. van Davier M and C. H. Carstensen (New York, US: Springer). 57–75.
Balt, M., Fritz, A., and Ehlert, A. (2020). Insights into first grade Students' development of conceptual numerical understanding as drawn from progression-based assessments. Front. Educ. 5:80. doi: 10.3389/feduc.2020.00080
Blum, W., and Leiß, D. (2007). “How students and teachers deal with modelling problems.” In: Mathematical Modelling: Education, Engineering and Economics - ICTMA12. Eds. C. Haines, P. Galbraith, W. Blum, and S. Khan (Chichester, UK: Horwood Publishing). 222–231.
Bock, R. D., and Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: application of an EM algorithm. Psychometrika 46, 443–459. doi: 10.1007/BF02293801
Cevikbas, M., Kaiser, G., and Schukajlow, S. (2022). A systematic literature review of the current discussion on mathematical modelling competencies: state-of-the-art developments in conceptualizing, measuring, and fostering. Educ. Stud. Math. 109, 205–236. doi: 10.1007/s10649-021-10104-6
Christensen, K. B., Makransky, G., and Horton, M. (2017). Critical values for Yen’s Q 3: identification of local dependence in the Rasch model using residual correlations. Appl. Psychol. Meas. 41, 178–194. doi: 10.1177/0146621616677520
Clements, D. H., and Sarama, J. (2012). “Learning trajectories in mathematics education.” In: Hypothetical learning trajectories. Eds. D. H. Clements and J. Sarama (New York, US: Springer), 81–90.
Czocher, J. A. (2018). How does validating activity contribute to the modeling process? Educ. Stud. Math. 99, 137–159. doi: 10.1007/s10649-018-9833-4
Daroczy, G., Meurers, D., Heller, J., Wolska, M., and Nürk, H.-C. (2020). The interaction of linguistic and arithmetic factors affects adult performance on arithmetic word problems. Cogn. Process. 21, 105–125. doi: 10.1007/s10339-019-00948-5
Daroczy, G., Wolska, M., Meurers, W. D., and Nuerk, H.-C. (2015). Word problems: a review of linguistic and numerical factors contributing to their difficulty. Front. Psychol. 6:348. doi: 10.3389/fpsyg.2015.00348
Dimitrov, D. M. (2022). The response vector for mastery method of standard setting. Educ. Psychol. Meas. 82, 719–746. doi: 10.1177/00131644211032388
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, NL: D. Reidel.
Fuson, K. C., Carroll, W. M., and Landis, J. (1996). Levels in conceptualizing and solving addition and subtraction compare word problems. Cogn. Instr. 14, 345–371. doi: 10.1207/s1532690xci1403_3
Gabler, L., and Ufer, S. (2020). Flexibilität im Umgang mit mathematischen Situationsstrukturen: Eine Vorstudie zu einem Förderkonzept zum Lösen von Textaufgaben zu Addition und Subtraktion [Flexibility when dealing with situational structures in mathematical contexts—a preliminary study investigating a learning framework on solving additive word problems]. J. Math.-Didakt. 42, 61–96. doi: 10.1007/s13138-020-00170-3
Gabler, L., and Ufer, S. (2021). Gaining flexibility in dealing with arithmetic situations: a qualitative analysis of second graders’ development during an intervention. ZDM 53, 375–392. doi: 10.1007/s11858-021-01257-y
Gabler, L., and Ufer, S. (2022). Contribution of flexibility in dealing with mathematical situations to word-problem solving beyond established predictors. In: Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education, Eds.
Gabler, L., and Ufer, S. (2024). Training flexibility in dealing with additive word problems. Learn. Instr. 92:101902. doi: 10.1016/j.learninstruc.2024.101902
Gabler, L., von Damnitz, F., and Ufer, S. (2023). “Additive word problems in German 1st and 2nd grade textbooks.” In: Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education. Eds. M. Ayalon, B. Koichu, R. Leikin, M. Rubel, and M. Tabach (Haifa, Israel: PME), 2, 355–362.
Greeno, J. G. (1980). “Some examples of cognitive task analysis with instructional implications.” In: Aptitude, learning, and instruction: volume 2: cognitive process analysis of learning and problem solving. Eds. E. Snow, P.-A. Frederico, and W. E. Montague (Hillsdale, US: Lawrence Erlbaum Associates), 1–21.
Hartmann, J., and Fritz, A. (2021). “Language and mathematics: how children learn arithmetic through specifying their lexical concepts of natural numbers.” In: Diversity dimensions in mathematics and language learning. Eds. A. Fritz, E. Gürsoy, and M. Herzog (Boston, US: De Gruyter), 21–39.
Hattikudur, S., and Alibali, M. (2011). The role of comparison in mathematics learning. Proc. Annu. Meet. the Cogn. Sci. Soc. 33, 306–311.
Hegarty, M., Mayer, R. E., and Green, C. E. (1992). Comprehension of arithmetic word problems: evidence from students' eye fixations. J. Educ. Psychol. 84, 76–84. doi: 10.1037/0022-0663.84.1.76
Hegarty, M., Mayer, R. E., and Monk, C. A. (1995). Comprehension of arithmetic word problems: a comparison of successful and unsuccessful problem solvers. J. Educ. Psychol. 87, 18–32. doi: 10.1037/0022-0663.87.1.18
Heine, J.-H., Sälzer, C., Borchert, L., Sibberns, H., and Mang, J. (2013). “Technische Grundlagen des fünften internationalen Vergleichs.” In: PISA 2012- Fortschritte und Herausforderungen in Deutschland. Eds. M. Prenzel, C. Sälzer, E. Klieme, and O. Köller (Münster, DE: Waxmann), 309–346.
Heinze, A., Star, J. R., and Verschaffel, L. (2009). Flexible and adaptive use of strategies and representations in mathematics education. ZDM Münster, DE 41, 535–540. doi: 10.1007/s11858-009-0214-4
Heitzmann, N., Seidel, T., Opitz, A., Hetmanek, A., Wecker, C., Fischer, M., et al. (2019). Facilitating diagnostic competences in simulations: a conceptual framework and a research agenda for medical and teacher education. Frontline Learn. Res. 7, 1–24. doi: 10.14786/flr.v7i4.384
Ionescu, T. (2012). Exploring the nature of cognitive flexibility. New Ideas Psychol. 30, 190–200. doi: 10.1016/j.newideapsych.2011.11.001
Jiang, Z., Mok, I. A. C., and Li, J. (2021). Chinese students’ hierarchical understanding of part-whole and measure subconstructs. Int. J. Sci. Math. Educ. 19, 1441–1461. doi: 10.1007/s10763-020-10118-1
Jin, H., Mikeska, J. N., Hokayem, H., and Mavronikolas, E. (2019). Toward coherence in curriculum, instruction, and assessment: a review of learning progression literature. Sci. Educ. 103, 1206–1234. doi: 10.1002/sce.21525
Kaiser, G. (2017). The teaching and learning of mathematical modeling. In: Compendium for research in mathematics education. Ed. J. Cai (Reston, US: NCTM), 267–291.
Kintsch, W. (1998). Comprehension: a paradigm for cognition Cambridge, UK: Cambridge University Press.
Kintsch, W., and Greeno, J. G. (1985). Understanding and solving word arithmetic problems. Psychol. Rev. 92, 109–129. doi: 10.1037/0033-295X.92.1.109
Koeppen, K., Hartig, J., Klieme, E., and Leutner, D. (2008). Current issues in competence modeling and assessment. J. Psychol. 216, 61–73. doi: 10.1027/0044-3409.216.2.61
Krajewski, K., and Schneider, W. (2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: findings from a four-year longitudinal study. Learn. Instr. 19, 513–526. doi: 10.1016/j.learninstruc.2008.10.002
Krawitz, J., Chang, Y.-P., Yang, K.-L., and Schukajlow, S. (2022). The role of reading comprehension in mathematical modelling: improving the construction of a real-world model and interest in Germany and Taiwan. Educ. Stud. Math. 109, 337–359. doi: 10.1007/s10649-021-10058-9
Lave, J., and Wenger, E. (1991). Situated learning: legitimate peripheral participation. Cambridge, UK: Cambridge University Press.
Leiss, D., Schukajlow, S., Blum, W., Messner, R., and Pekrun, R. (2010). The role of the situation model in mathematical modelling: task analyses, student competencies, and teacher interventions. J. Math.-Didakt. 31, 119–141. doi: 10.1007/s13138-010-0006-y
Lewis, A. B., and Mayer, R. E. (1987). Students' miscomprehension of relational statements in arithmetic word problems. J. Educ. Psychol. 79, 363–371. doi: 10.1037/0022-0663.79.4.363
Linacre, J. M. (2002). What do infit and outfit, mean-square and standardized mean. Rasch Meas. Trans. 16:878.
Marcoulides, G. A., and Drezner, Z. (2000). “A procedure for detecting pattern clustering in measurement designs.” In: Objective measurement: theory into practice. Eds. M. R. Wilson and G. Engehlhard (Norwood, US: Ablex Publishing Corporation), 287–302.
Mekhmandarov, I., Meron, R., and Peled, I. (1996). Performance and understanding: a closer look at comparison word problems. In: Proceedings of the 20th Conference of the International Group for the Psychology of Mathematics Education, Eds. L. Puig and A. Gutiérrez, Lisbon, Portugal: PME, 3, 385–390.
Mellone, M., Verschaffel, L., and Van Dooren, W. (2017). The effect of rewording and dyadic interaction on realistic reasoning in solving word problems. J. Math. Behav. 46, 1–12. doi: 10.1016/j.jmathb.2017.02.002
Mitzel, H. C., Lewis, D. M., Patz, R. J., and Green, D. R. (2013). “The bookmark procedure: psychological perspectives.” In: Setting performance standards. Ed. G. J. Cizek (New York, US: Routledge), 263–296.
Nesher, P., Greeno, J. G., and Riley, M. S. (1982). The development of semantic categories for addition and subtraction. Educ. Stud. Math. 13, 373–394. doi: 10.1007/BF00366618
Niklas, F., and Schneider, W. (2017). Home learning environment and development of child competencies from kindergarten until the end of elementary school. Contemp. Educ. Psychol. 49, 263–274. doi: 10.1016/j.cedpsych.2017.03.006
Paetsch, J., Radmann, S., Felbrich, A., Lehmann, R., and Stanat, P. (2016). Sprachkompetenz als Prädiktor mathematischer Kompetenzentwicklung von Kindern deutscher und nicht-deutscher Familiensprache. Z. Entwicklungspsychol. Pädagog. Psychol. 48, 27–41. doi: 10.1026/0049-8637/a000142
Peng, P., Lin, X., Ünal, Z. E., Lee, K., Namkung, J., Chow, J., et al. (2020). Examining the mutual relations between language and mathematics: a meta-analysis. Psychol. Bull. 146, 595–634. doi: 10.1037/bul0000231
Plass, J. L., and Pawar, S. (2020). Toward a taxonomy of adaptivity for learning. J. Res. Technol. Educ. 52, 275–300. doi: 10.1080/15391523.2020.1719943
Purpura, D. J., and Reid, E. E. (2016). Mathematics and language: individual and group differences in mathematical language skills in young children. Early Child. Res. Q. 36, 259–268. doi: 10.1016/j.ecresq.2015.12.020
Pustelnik, K., Rach, S., Ufer, S., and Sommerhoff, D. (2023). Levels of mathematical knowledge in linear algebra for entering university. In: Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education, Eds. M. Ayalon, B. Koichu, R. Leikin, M. Rubel, and M. Tabach Haifa, Israel: PME, 4, 75–82.
Rach, S., and Ufer, S. (2020). Which prior mathematical knowledge is necessary for study success in the university study entrance phase? Results on a new model of knowledge levels based on a reanalysis of data from existing studies. Int. J. Res. Undergrad. Math. Educ. 6, 375–403. doi: 10.1007/s40753-020-00112-x
Reiss, K., and Obersteiner, A. (2019). “Competence models as a basis for defining, understanding, and diagnosing students’ mathematical competences.” In: International handbook of mathematical learning difficulties: from the laboratory to the classroom. Eds. A. Fritz, V. G. Haase, and P. Räsänen, (Cham, DE: Springer), 43–56.
Riley, M. S., and Greeno, J. G. (1988). Developmental analysis of understanding language about quantities and of solving problems. Cogn. Instr. 5, 49–101. doi: 10.1207/s1532690xci0501_2
Riley, M. S., Greeno, J. G., and Heller, J. I. (1983). “Development of children's problem-solving ability in arithmetic.” In: The development of mathematical thinking. Ed. H. P. Ginsburg (New York, US: Academic Press), 153–196.
Rittle-Johnson, B., Siegler, R. S., and Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: an iterative process. J. Educ. Psychol. 93, 346–362. doi: 10.1037/0022-0663.93.2.346
Robitzsch, A., Kiefer, T., and Wu, M. (2020). TAM: Test analysis modules. R package version, 3. Online source: https://cran.r-project.org/web/packages/TAM/index.htm
Rolfes, T., and Heinze, A. (2022). “Nur 30 Prozent der Abiturientinnen und Abiturienten erreichen Mindeststandards in voruniversitärer Mathematik!?.” In: Das Fach Mathematik in der gymnasialen Oberstufe. Eds. T. Rolfes, S. Rach, S. Ufer, and A. Heinze (Münster, DE: Waxmann), 237–260.
Schadl, C., and Ufer, S. (2023). Beyond linearity: using irt-scaled level models to describe the relation between prior proportional reasoning skills and fraction learning outcomes. Child Dev. 94, 1642–1658. doi: 10.1111/cdev.13954
Scheibling-Sève, C., Pasquinelli, E., and Sander, E. (2020). Assessing conceptual knowledge through solving arithmetic word problems. Educ. Stud. Math. 103, 293–311. doi: 10.1007/s10649-020-09938-3
Schmidt, S., and Weiser, W. (1982). Zählen und Zahlverständnis von Schulanfängern. J. Math.-Didakt. 3, 227–263. doi: 10.1007/BF03338666
Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. J. Res. Math. Educ. 26, 114–145. doi: 10.2307/749205
Spiro, R. J., Feltovich, P. J., Jacobson, M. J., and Coulson, R. L. (1991). Cognitive flexibility, constructivism, and hypertext: random access instruction for advanced knowledge in ill-structured domains. Educ. Technol. 31, 24–33.
Stern, E. (1993). What makes certain arithmetic word problems involving the comparison of sets so difficult for children? J. Educ. Psychol. 85, 7–23. doi: 10.1037/0022-0663.85.1.7
Stern, E. (1994). Die Erweiterung des mathematischen Verständnisses mit Hilfe von Textaufgaben. Grundschule 26, 23–25.
Stern, E. (1998). Die Entwicklung des mathematischen Verständnisses im Kindesalter. Lengerich, DE: Pabst Science Publishers.
Stern, E., and Lehrndorfer, A. (1992). The role of situational context in solving word problems. Cogn. Dev. 7, 259–268. doi: 10.1016/0885-2014(92)90014-I
Thevenot, C., Devidal, M., Barrouillet, P., and Fayol, M. (2007). Why does placing the question before an arithmetic word problem improve performance? A situation model account. Q. J. Exp. Psychol. 60, 43–56. doi: 10.1080/17470210600587927
Torbeyns, J., De Smedt, B., Stassens, N., Ghesquière, P., and Verschaffel, L. (2009). Solving subtraction problems by means of indirect addition. Math. Think. Learn. 11, 79–91. doi: 10.1080/10986060802583998
Ufer, S., and Bochnik, K. (2020). The role of general and subject-specific language skills when learning mathematics in elementary school. J. Math.-Didakt. 41, 81–117. doi: 10.1007/s13138-020-00160-5
Ufer, S., and Neumann, K. (2018). “Measuring competencies.” In: International handbook of the learning sciences. Eds. F. Fischer, C. E. Hmelo-Silver, S. R. Goldman, and P. Reimann (New York, US: Routledge), 433–443.
Van Lieshout, E. C., and Xenidou-Dervou, I. (2020). Simple pictorial mathematics problems for children: locating sources of cognitive load and how to reduce it. ZDM 52, 73–85. doi: 10.1007/s11858-019-01091-3
Verschaffel, L. (1994). Using retelling data to study elementary school children's representations and solutions of compare problems. J. Res. Math. Educ. 25, 141–165. doi: 10.5951/jresematheduc.25.2.0141
Verschaffel, L., De Corte, E., and Pauwels, A. (1992). Solving compare problems: an eye movement test of Lewis and Mayer's consistency hypothesis. J. Educ. Psychol. 84, 85–94. doi: 10.1037/0022-0663.84.1.85
Verschaffel, L., Schukajlow, S., Star, J., and Van Dooren, W. (2020). Word problems in mathematics education: a survey. ZDM 52, 1–16. doi: 10.1007/s11858-020-01130-4
Vygotsky, L. S., Cole, M., John-Steiner, V., Scribner, S., and Souberman, E. (1978). Mind in society: the development of higher psychological processes. Havard, US: Harvard University Press.
Wang, C. (2015). On latent trait estimation in multidimensional compensatory item response models. Psychometrika 80, 428–449. doi: 10.1007/s11336-013-9399-0
Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika 54, 427–450. doi: 10.1007/BF02294627
Wildgans-Lang, A., Scheuerer, S., Obersteiner, A., Fischer, F., and Reiss, K. (2020). Analyzing prospective mathematics teachers’ diagnostic processes in a simulated environment. ZDM 52, 241–254. doi: 10.1007/s11858-020-01139-9
Wright, B. D. (1999). “Fundamental measurement for psychology” in The new rules of measurement: what every psychologist and educator should know. eds. S. E. Embretson and S. L. Hershberger (New York, US: Erlbaum), 65–104.
Keywords: flexibility in dealing with additive situations, level model, mathematics, word problem solving, primary school, assessment, assessment-based intervention
Citation: Ufer S, Kaiser A, Niklas F and Gabler L (2024) I have three more than you, you have three less than me? Levels of flexibility in dealing with additive situations. Front. Educ. 9:1340322. doi: 10.3389/feduc.2024.1340322
Edited by:
Natalie Förster, University of Wuppertal, GermanyReviewed by:
Boris Forthmann, University of Münster, GermanyLukas Baumanns, Technical University Dortmund, Germany
Copyright © 2024 Ufer, Kaiser, Niklas and Gabler. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Ufer, dWZlckBtYXRoLmxtdS5kZQ==
 Stefan Ufer
Stefan Ufer Anna Kaiser
Anna Kaiser Frank Niklas
Frank Niklas Laura Gabler1
Laura Gabler1