Unpacking constructs used to describe teachers’ mathematics knowledge for teaching: insights into MKT and MMT

Rocha, Abby

doi:10.3389/feduc.2025.1575771

REVIEW article

Front. Educ., 08 July 2025

Sec. Teacher Education

Volume 10 - 2025 | https://doi.org/10.3389/feduc.2025.1575771

This article is part of the Research TopicMathematics teachers' construction and enactment of disciplinary knowledgeView all articles

Unpacking constructs used to describe teachers’ mathematics knowledge for teaching: insights into MKT and MMT

Abby Rocha^*

Central College, Pella, IA, United States

Over the past 30 years, researchers in the United States have investigated teachers’ mathematical knowledge and its interaction with their instructional practices. This research has produced a significant body of literature related to teachers’ Mathematical Knowledge for Teaching (MKT). A review of this body of literature revealed diversity in the ontological perspectives and research priorities, highlighting constructs such as MKT, Mathematical Meanings for Teaching (MMT), and Key Pedagogical Understandings (KPUs). This analysis provides a comprehensive overview of these constructs, detailing their definitions, applications, and interrelationships. By clarifying these concepts, the report aims to consolidate understanding and inform future research and practice in mathematics education.

Introduction

Evolving conceptions of what mathematics teachers need to know have fundamentally reshaped the field of mathematics education. These shifts reflect not only theoretical developments but also changing priorities in educational policy and research. For well over a century, mathematics educators have wrestled with the question, “What do teachers need to know to teach effectively?” In the late 1800s, discussions focused primarily on teachers’ subject matter expertise (Shulman, 1986). However, by the mid-20th century, attention to content knowledge waned as standardized testing and pedagogical technique became central to policy-driven evaluations of teacher effectiveness. During the 1960s and 1970s, research agendas increasingly emphasized general teaching methods, often at the expense of content understanding. Shulman (1986) identified this imbalance as the “missing paradigm problem” and responded by proposing a framework that reintegrated content knowledge with pedagogy. His introduction of pedagogical content knowledge (PCK)—a form of professional knowledge that combines deep subject matter understanding with effective, context-sensitive instructional strategies—marked a turning point in conceptualizing what teachers need to know.

Building upon Shulman’s foundational ideas, mathematics education researchers began extensively exploring teachers’ knowledge within instructional contexts, an area now widely recognized as Mathematical Knowledge for Teaching (MKT; Thompson and Thompson, 1996). Since its introduction, the construct of MKT, most notably advanced by Ball et al. (2005) (e.g., Ball, 1990; Ball and Bass, 2003), has profoundly shaped the landscape of teacher education and professional development. Their work provided insights into the specialized mathematical knowledge necessary for effective teaching, highlighting different dimensions such as common content knowledge (CCK) and specialized content knowledge (SCK).

Despite its considerable influence, some scholars have critiqued the static, competency-based conception of MKT promoted by Ball et al. (2005) Researchers such as Silverman and Thompson (2008) argued for viewing MKT as a dynamic and evolving cognitive construct rather than a fixed set of competencies. Thompson (2016) introduced Mathematical Meanings for Teaching (MMT) to underscore how teachers’ cognitive schemes and reflective practices give rise to personal, evolving mathematical understandings that shape their instructional decisions. This paper aims to explore the distinctions between these two constructs—MKT and MMT—and how they have been utilized in the research literature. By examining the work of various scholars, this paper seeks to clarify the conceptual boundaries between MKT as a static body of knowledge and MMT as a dynamic, personalized construct that evolves through teachers’ engagement with practice. While both constructs offer valuable insights into teachers’ mathematical knowledge, they represent fundamentally different conceptualizations of how this knowledge develops and how it impacts teaching. Understanding these distinctions is essential for advancing the conversation around teacher knowledge and practice, particularly when researchers from different theoretical perspectives engage in dialogue.

To support this goal, the paper is organized as follows. It begins by outlining Ball et al.’s (2005) domain-based model of MKT, followed by cognitive-developmental perspectives from Silverman and Thompson and Tallman (Although Silverman, Thompson, and Tallman refer to this knowledge as MKT, their meaning-oriented conceptualization is more closely aligned with the construct later articulated as MMT). A comparative analysis then clarifies distinctions between these frameworks, culminating in the introduction of MMT, a construct that better captures the evolving and reflective nature of teachers’ knowledge as conceptualized in this study. Subsequent sections explore how both constructs—MKT and MMT—have been used in the literature and examine the implications of these perspectives for teacher education, particularly through the lenses of tasks, reflection, and decentering.

One of the key challenges in the field is ensuring that researchers from diverse perspectives—whether focused on the competency-based aspects of MKT or the cognitive, reflective nature of MMT—can communicate clearly with one another. Without shared conceptual frameworks and a mutual understanding of each construct’s aims and limitations, cross-perspective discussions risk becoming fragmented, limiting the field’s ability to develop comprehensive strategies for teacher development. This paper advocates for a more nuanced understanding of MKT and MMT to bridge the gap between different perspectives, fostering richer, more productive conversations about the future of teacher education. Ultimately, this exploration will not only clarify these distinctions but also contribute to a deeper, more cohesive understanding of the complex, evolving nature of teachers’ mathematical knowledge and its role in fostering student learning.

Mathematical knowledge for teaching

Over the past three decades, research on teachers’ MKT has become a key focus in efforts to improve the quality of mathematics instruction in the United States. While the body of literature on MKT is extensive, different research groups have concentrated on diverse aspects of the topic. Ball et al. (2005) have primarily explored the complex, multi-dimensional nature of the knowledge teachers rely on in their teaching, classifying MKT into several specialized categories (Ball, 1990; Ball and Bass, 2003; Ball et al., 2005). Their research has also demonstrated positive correlations between teachers’ knowledge and student achievement (Ball et al., 2008; Hill and Ball, 2004; Hill et al., 2008a; Hill et al., 2004; Hill et al., 2008b). In contrast, researchers like Silverman and Thompson (2008) and Tallman (2015; 2021) have examined how MKT develops over time and the factors that influence teachers’ pedagogical decisions.

Ball et al.’s framework: a practice-based view of MKT

Ball et al. (2005) (e.g., Ball, 1990; Ball and Bass, 2003) sought to answer the question, “what do teachers do in teaching mathematics, and in what ways does what they do demand mathematical reasoning, insight, understanding, and skill?” (Ball et al., 2005, p. 17). This line of inquiry began with Ball’s (1990) study of 252 pre-service teachers’ understanding of division with fractions. While most teacher candidates could carry out the procedures for dividing fractions, few could provide a meaningful contextual representation for students. This finding underscored the inadequacy of procedural proficiency alone and pointed to a broader conception of the knowledge needed for teaching.

In response, Ball and Bass (2003) proposed focusing on the specific mathematical work of teaching. Their empirical analyses revealed that the mathematical knowledge teachers need differs from that of mathematicians and other professionals, emphasizing the unique demands of teaching. They identified that mathematics teaching requires (1) engaging in problem solving, (2) unpacking one’s own understandings of mathematical ideas for others, and (3) helping students connect concepts across mathematical domains.

Building on this foundation, Hill et al. (2004) introduced a more refined, multidimensional model of MKT. They proposed subdividing Shulman’s (1986) original category of subject matter knowledge into CCK and SCK. CCK refers to general mathematical knowledge that is not unique to teaching, while SCK involves knowledge specific to teaching—such as explaining procedures or diagnosing and addressing common student misconceptions. For example, teachers must not only recognize that 307−168 = 261 is incorrect but also understand the mathematical reasoning behind the error (Ball et al., 2008).

Later refinements introduced additional components of MKT. Hill et al. (2008a) described Knowledge of Content and Students (KCS), which combines knowledge of mathematics with insights into how students typically understand or misunderstand that mathematics. Distinct from KCS, Ball et al. (2008) also identified Knowledge of Content and Teaching (KCT), referring to teachers’ strategic decision-making in instructional contexts—such as selecting representations or building on student ideas in real-time. These distinctions were incorporated into their widely cited multidimensional framework for MKT.

Beyond defining components of MKT, Ball et al. (2008) also sought to measure it and link it to student outcomes. In a seminal study, Hill et al. (2005) developed instruments to assess teachers’ MKT and analyzed its relationship to student achievement. Teachers completed self-report logs detailing instructional activities and annual questionnaires designed to evaluate their content knowledge. Meanwhile, student performance was measured using the Terra Nova standardized assessment. Results revealed a positive correlation between teachers’ MKT and student achievement in early grades, with students gaining over two points on average for every standard deviation increase in their teacher’s MKT score. However, the study also acknowledged limitations, including the difficulty of disentangling content-specific knowledge from general teaching aptitude.

Ball et al.’s (2005) MKT framework has influenced teacher education programs significantly, extending its impact beyond empirical studies. Their conceptualization of MKT has informed the design of teacher preparation curricula and professional development initiatives, providing a structured approach to assessing and enhancing teacher readiness (Hill et al., 2008a).

In sum, Ball et al. (2005) made foundational contributions to understanding MKT. They identified critical domains of teacher knowledge, developed tools to measure it, and empirically linked it to student learning outcomes. However, their work stops short of examining how MKT develops over time or the cognitive mechanisms that underlie its enactment. For example, while they stress that teachers must be able to represent multiplication meaningfully (e.g., 35 × 25), they do not explore the mental operations that enable such representations. This omission leaves room for complementary frameworks—such as those of Silverman and Thompson—to elaborate on how MKT is formed, transformed, and refined through practice.

Silverman and Thompson: a developmental perspective

While Ball and Colleagues (e.g., Ball, 1990; Ball and Bass, 2003; Hill et al., 2005) conducted empirical studies that identified distinct domains of teacher knowledge, Silverman and Thompson (2008) developed theories on the nature and development of MKT. They posited that teachers’ MKT is rooted in personally powerful understandings of mathematical concepts and evolves as these understandings are transformed from having pedagogical potential into possessing pedagogical power. Although Silverman and Thompson refer to this knowledge as MKT, their emphasis on personal mathematical meanings and conceptual transformations anticipates the construct Thompson would later name MMT.

A mathematical understanding is personally powerful if it endures through an instructional sequence, forms the basis for learning other concepts, and integrates within a network of ideas that shape students’ reasoning (Thompson, 2008). Silverman and Thompson (2008) highlighted Simon’s (2006) construct of Key Developmental Understandings (KDUs) as examples of such understandings. A KDU is an individual’s understanding of a concept that is crucial for learning related ideas. It develops when a person has a conceptual breakthrough- a shift in how they perceive a mathematical relationship (Simon, 2006, p. 362)- and actively constructs that understanding through reflection. They further proposed that developing MKT involves transforming these KDUs into insights about (1) how they can enhance students’ learning of related ideas and (2) the instructional actions that foster this learning (p. 502). In this process, KDUs evolve into Key Pedagogical Understandings (KPUs)—mini-theories that teachers develop to guide students toward the intended mathematical meanings (Byerley and Thompson, 2017).

An illustrative example reported by Silverman and Thompson (2008) comes from Simon’s (1995) work on area measurement which illustrates how teachers develop an understanding of area as a multiplicatively defined quantity. This KDU involves conceptualizing area as a multiplicatively defined quantity rather than merely the product of length and width. Simon designed instructional tasks to help prospective teachers develop a deeper understanding of the multiplicative relationships inherent in area measurement, moving beyond procedural applications. Through activities such as the “Double Counting” and “Turned Rectangles” problems, he challenged prospective teachers to examine why multiplication is used in area calculations and to recognize the role of unit structure in defining area. Silverman and Thompson (2008) highlighted this work as an illustration of how teachers can develop MKT by constructing deeper understandings of key mathematical ideas. By shifting prospective teachers’ thinking from viewing area as a formulaic result to understanding it as a relationship between two linear measurements that generate a two-dimensional quantity, this KDU provides a foundation for reasoning about other multiplicatively related quantities, such as volume and distance.

Overall, Silverman and Thompson’s (2008) framework reorients teacher education from simply developing MKT to fostering practices that enable teachers to continually refine their MKT throughout their careers by developing KDUs, cultivating reflective awareness, and situating these understandings within models of student learning (Silverman and Thompson, 2008, p. 509). Although theoretical rather than empirically derived, their framework offers a robust conceptual basis for reimagining teacher education.

Tallman’s contributions: cognitive coherence in MKT

In his 2015 dissertation, Tallman¹ provided evidence supporting Silverman and Thompson’s claim that MKT extends beyond powerful mathematical understandings. Tallman’s analysis revealed that a teacher’s understanding, as demonstrated in a clinical interview, often differed from—and at times contradicted—the meanings conveyed during instruction. He attributed these inconsistencies to the teacher’s MKT being composed of “disorganized and disconnected cognitive schemes” (p. 592). Consequently, Tallman (2015) argued that effective MKT involves an awareness of the mental actions and operations that form productive ways of understanding mathematical ideas. He elaborated,

A teacher’s awareness of the mental actions and operations that constitute powerful ways of understanding mathematical ideas supports him or her in: (1) defining instructional goals and objectives in cognitive rather than behavioristic terms, (2) designing and/or selecting curriculum materials that promote intended mental activity, (3) employing pedagogical actions that help students engage in—and internalize—productive mathematical meanings, (4) developing a disposition to attend to students’ thinking, and (5) constructing models of students’ epistemic ways of understanding (p. 598).

Tallman (2015) proposed a framework suggesting that teachers’ awareness of these mental actions is a crucial component of MKT, helping them reorganize their mathematical knowledge to engage in effective teaching practices.

Further expanding on these ideas, Tallman’s subsequent research provided additional empirical and theoretical insights. In his 2021 study, Tallman empirically investigated the cognitive processes involved in a secondary teacher’s transformation of personal mathematical knowledge, particularly focusing on trigonometric functions, into effective instructional practices. His findings emphasized the critical role teachers’ conscious awareness of their cognitive schemes plays in effectively translating mathematical understandings into classroom practices.

In his theoretical work (Tallman, 2023), he critiqued existing frameworks for PCK as implicitly behaviorist and neglectful of cognitive complexity. Integrating philosophical perspectives from Dewey and Piaget, Tallman proposed a radical constructivist reorientation of PCK, advocating for its recognition as inherently cognitive and developmental. This approach emphasizes that MKT should be viewed as dynamic, continuously evolving through teachers’ reflective practices and engagement with student thinking. Tallman’s combined empirical and theoretical contributions thus deepen our understanding of the intricate cognitive processes underlying effective mathematics teaching.

Research on MKT has emerged from distinct theoretical commitments and focal points. Ball et al. (2005) concentrated on identifying and categorizing the types of professional knowledge teachers use in practice, while Silverman, Thompson, and Tallman have emphasized the cognitive and developmental nature of teacher knowledge. These differences reflect contrasting ontological stances: Ball et al. (2005) treat MKT as objective knowledge external to the knower, whereas Silverman, Thompson, and Tallman adopt a constructivist view that frames knowledge as individually constructed and continually evolving. The following section offers a detailed comparison of these perspectives, highlighting how each contributes to a broader understanding of MKT and laying the groundwork for the introduction of MMT.

Epistemological distinctions among MKT frameworks

Over the past two decades, multiple frameworks have emerged to conceptualize MKT, each rooted in distinct theoretical commitments and research priorities. A key point of contrast among these frameworks lies in their epistemological commitments, which shape how teacher knowledge is conceptualized and studied. Ball et al.’s (2005) framework, for instance, is grounded in a domain-specific orientation, viewing MKT as a set of knowledge types that can be delineated, categorized, and measured. This reflects a more positivist or analytic stance, where knowledge is treated as something relatively stable and external to the knower. In contrast, Silverman and Thompson (2008) draw from a constructivist perspective that foregrounds cognition, viewing knowledge as dynamic, situated, and deeply personal. Their work emphasizes teachers’ mental structures and the meanings they construct through activity and reflection. Thompson’s later work on MMT builds explicitly on Piagetian genetic epistemology, which holds that knowledge and meaning are inseparable and evolve through a person’s interactions with their environment. This epistemological shift—from treating knowledge as an object to viewing meaning as a construction—marks a significant theoretical divergence and has implications for both research and practice. It orients studies toward understanding how teachers’ mental schemes develop over time and how those evolving schemes guide instructional decision-making, rather than focusing solely on the identification or assessment of discrete knowledge types.

Ball et al. (2008) conceptualize MKT as a structured set of professional knowledge domains that support effective mathematics teaching. Their framework identifies CCK, SCK, and KCS as key components. These categories help researchers and teacher educators define the types of mathematical knowledge linked to instructional quality and student learning. Empirical studies have shown that higher levels of MKT, as measured through targeted assessments, correlate positively with student achievement (Hill et al., 2005).

In contrast, Silverman and Thompson (2008) offer a developmental perspective grounded in cognitive theory. They define MKT as a dynamic construct shaped by teachers’ evolving mathematical meanings and their reflective engagement with student thinking. Their framework introduces KDUs and KPUs to describe how conceptual breakthroughs and pedagogical insight guide instructional decisions. Rather than focusing on what teachers know, they explore how teachers construct and refine mathematical meanings through practice.

The epistemological foundation of Silverman and Thompson’s approach draws from Piaget’s genetic epistemology and radical constructivism, which conceptualize knowledge as actively constructed through interaction rather than passively received. In this view, knowledge and meaning are synonymous, grounded in the schemes individuals develop and reorganize through experience (Montangero and Maurice-Naville, 1997; Thompson, 2016). Teachers construct meanings for mathematical ideas through assimilation to existing cognitive schemes and accommodate those schemes in response to perturbations—moments when existing understandings are insufficient to make sense of a situation. This process aligns with Glasersfeld’s (1995) radical constructivism, which holds that knowledge is viable when it proves functional within a context, not when it reflects an objective reality. Such commitments contrast sharply with frameworks like Ball et al.’s (2008), which approach teacher knowledge as discrete and assessable domains. In contrast, the meaning-oriented view espoused by Silverman and Thompson (2008), Tallman (2021), and Thompson (2016) emphasizes that teacher knowledge is not merely possessed but constructed and enacted through ongoing interaction, reflection, and cognitive adaptation. These commitments position MMT as a framework for understanding not just what teachers know, but how that knowing evolves through instructional activity.

This distinction highlights a key affordance of Silverman and Thompson’s approach: it theorizes how MKT develops, a dimension largely absent in Ball et al.’s (2008) work. For example, while Ball et al. (2008) emphasize the need for SCK to diagnose student errors, Silverman and Thompson focus on how a teacher’s evolving understanding of a concept—such as fractions—informs their pedagogical choices. Their developmental model complements Ball et al.’s (2008) categorical framework by addressing the processes through which knowledge is constructed.

Tallman’s contributions build on this developmental orientation while adding empirical and theoretical depth. Drawing from classroom observations and constructivist theory, Tallman (2015, 2021, 2023) emphasizes the role of teachers’ cognitive schemes in shaping instruction. He argues that MKT must account not only for what teachers know but also for how they consciously reorganize mental actions in response to instructional goals and student reasoning. His research shows that a teacher’s enacted meanings in the classroom may differ from those expressed in interviews, pointing to the context-dependent nature of teacher knowledge. Like Silverman and Thompson, Tallman frames MKT as evolving through reflection and interaction, but his work further highlights the importance of coherence between teachers’ cognitive schemes and their instructional practice.

Although Thompson and Tallman used the term MKT in earlier work, their meaning-oriented descriptions—grounded in evolving cognitive schemes—align more closely with the construct Thompson later articulated as MMT. This paper adopts the term MMT to reflect their conception and to distinguish it from Ball et al.’s (2008) domain-based framing.

Taken together, these three frameworks offer complementary insights into the nature and development of MKT. Ball et al. (2005) provide a structured categorization of knowledge and demonstrate its links to student achievement. Silverman and Thompson theorize how knowledge develops through meaning-making, while Tallman contributes empirical evidence showing how teachers reorganize cognitive schemes to achieve instructional coherence. These later two perspectives converge on the view that MKT is not static but dynamically constructed and enacted in context. This broader understanding informs the introduction of MMT, a construct that captures the evolving, personalized, and cognitive nature of teacher knowledge as it takes shape in practice. These varying epistemological commitments underscore the need for a construct that more precisely captures the evolving, meaning-based nature of teacher knowledge—an aim that underpins the development of MMT.

From MKT to MMT: theoretical motivations for a new construct

Building on the epistemological distinctions described in the previous section, this section introduces MMT as a construct that captures the evolving, situated, and personally constructed nature of teacher knowledge. While the construct of MKT has played a central role in shaping research and practice, a growing body of work has proposed MMT as an alternative that better aligns with constructivist and developmental perspectives. This section traces the theoretical motivations for developing MMT, outlines its conceptual underpinnings, and demonstrates how this shift refocuses research toward teachers’ evolving cognitive schemes and instructional reasoning.

Rather than offering a general literature review, the subsections that follow use specific strands of research—including studies on quantitative reasoning, task design and reflection, and decentering—as examples of what adopting an MMT perspective affords researchers. Each subsection illustrates how MMT foregrounds the processes by which teachers construct personal meanings for mathematical ideas and how these meanings shape instruction. By organizing the section this way, I aim to show that MMT is not only a theoretical refinement of MKT but also a productive lens for designing studies, interpreting teacher learning, and supporting instructional improvement.

While Thompson and Tallman initially referred to this evolving cognitive knowledge as MKT, Thompson (2016) later introduced the term MMT to more precisely capture its orientation toward cognitive development. In this paper, references to their work are interpreted through the lens of MMT to highlight the evolving, personal, and meaning-oriented nature of teacher knowledge described in their research. The term MMT is used consistently to distinguish this construct from more domain-based models of MKT. MMT emphasizes how teacher knowledge is constructed through reflection, interaction, and instructional practice, and serves as a bridge between the cognitive development of individual teachers and their enacted understandings in classrooms.

Thompson’s preference for the term “meaning” over “knowledge” stems from its more personal and dynamic connotation, which contrasts with the potentially external or static framing that “knowledge” can evoke. This shift allows researchers to attend more closely to the cognitive processes that underlie teaching practices and to explore how teachers’ personal understandings of mathematical concepts shape their pedagogy. While the theoretical foundations of this view are grounded in Piagetian genetic epistemology, which holds that knowledge and meaning are inseparable and evolve through an individual’s interactions with their environment, MMT offers a concrete way to operationalize this view in empirical research.

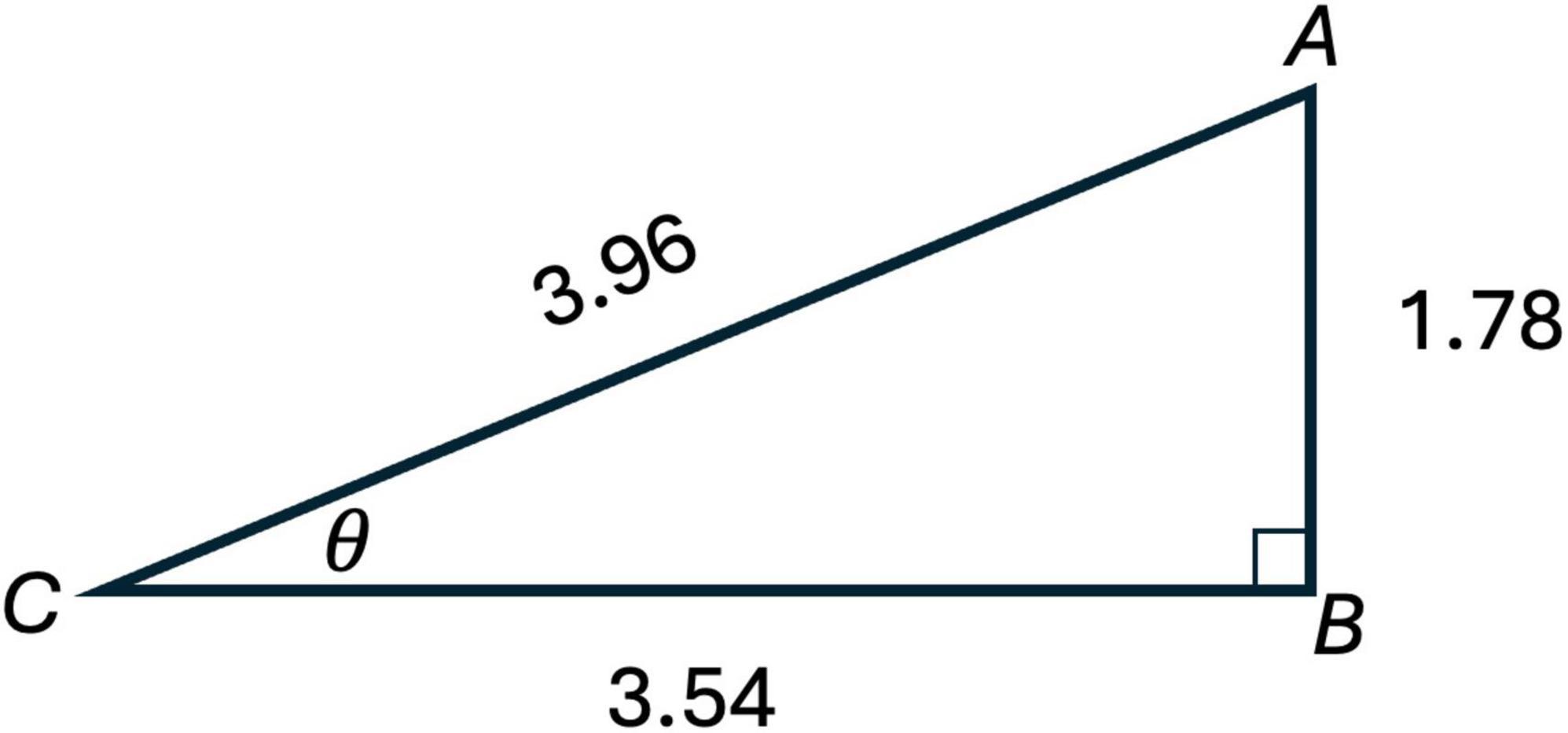
For example, consider two teachers, Teacher A and Teacher B, who are asked to determine the value of sin(θ) in a given right triangle (see Figure 1 below). Both correctly compute $s i n (θ) = \frac{1.78}{3.96} = 0.45$ , demonstrating procedural knowledge of trigonometric ratios. However, this correct answer alone provides little insight into the meanings a teacher holds for sine or the instructional approach a teacher uses when teaching this idea to students.

FIGURE 1

Figure 1. The value of the output of the sine function.

Teacher A, relying on a procedural understanding, may explain sine as a rule that dictates dividing the length of the opposite side by the hypotenuse (SOHCAHTOA), presenting it as a fixed operation with little conceptual depth. In contrast, Teacher B interprets sine as a function that describes how a length varies with an angle’s measure. Viewing sine as a dynamic relationship, Teacher B understands $s i n (θ) = \frac{1.78}{3.96} = 0.45$ as indicating that the vertical distance of a point on the terminal ray of θ is approximately 0.45 times as large as the circle’s radius when measured from the 3 o’clock position. Because Teacher B has constructed a richer meaning for sine, they are more likely to guide students toward a conceptual understanding, emphasizing its role in describing variation rather than just applying a formula.

This contrast highlights the importance of attending to a teacher’s meanings for an idea rather than solely their knowledge. Just as Thompson (2013) found that a teacher’s understanding of slope influenced their ability to determine a line’s equation, a teacher’s meaning for sine shapes their ability to convey the concept to students in meaningful ways. Recognizing these differences is essential for understanding the instructional choices teachers make and the opportunities students have to construct robust mathematical meanings.

Research on the development of teachers’ MMT

This subsection introduces empirical work that demonstrates the value of studying teacher learning through the lens of MMT. Rather than treating knowledge acquisition as additive, these studies investigate how teachers’ conceptual schemes are reorganized through reflective and sense-making activity.

Research has demonstrated that merely requiring teachers to take additional advanced mathematics courses does not necessarily improve their mathematical understanding or teaching practices (O’Bryan and Carlson, 2016; Speer, 2008; Speer et al., 2015; Musgrave and Carlson, 2017). O’Bryan and Carlson (2016) suggest that this might be because mathematics coursework often does not address how students learn specific mathematical concepts, nor does it help teachers navigate the challenges of selecting and implementing curricula for particular courses (p. 1192). While Silverman and Thompson’s (2008) framework provides some direction for the development of teachers’ mathematical meanings, there is still limited research on the mechanisms that can help advance these meanings effectively.

One promising avenue identified by researchers is quantitative reasoning, which is considered a crucial way of thinking that supports the development of coherent mathematical meanings and improves teachers’ ability to notice and respond to student thinking during instruction (O’Bryan and Carlson, 2016; Musgrave and Carlson, 2017; Tallman and Frank, 2018; Carlson et al., 2023). For example, Musgrave and Carlson (2017) examined graduate teaching instructors’ understanding of average rate of change (AROC) both before and after an intervention designed to support advances in their understanding of precalculus ideas, including their conceiving of AROC as a constant rate of change on an interval of a function that results in the same change in the dependent quantity, as was achieved by the function on that interval. Prior to the intervention, only one of seven teachers expressed a meaning for AROC as a constant rate of change on a function’s interval. After participating in a summer workshop and weekly seminar designed to foster more conceptually rich teaching practices, most instructors were able to express more productive and conceptually focused meanings for AROC. However, many still struggled to articulate these meanings coherently, suggesting that improving teachers’ mathematical meanings is an ongoing challenge (Musgrave and Carlson, 2017).

Building on these insights, O’Bryan and Carlson (2016) also found that teachers who engaged in quantitative reasoning were able to reinterpret their own meanings for mathematical concepts and design activities that promoted similar reasoning in their students. They observed that engaging with quantitative reasoning helped teachers think more deeply about the relationships between quantities and the meaning behind algebraic expressions. As a result, teachers were better able to interpret and respond to student thinking in the classroom. These findings suggest that fostering teachers’ engagement in quantitative reasoning can play a key role in refining their mathematical meanings and improving their teaching practices.

Pathways conventions for supporting quantitative reasoning

One mechanism that has emerged from MMT-informed research is quantitative reasoning, which supports teachers in constructing coherent meanings for mathematical ideas. The work summarized here illustrates how promoting reasoning about quantities can facilitate deeper cognitive reorganization in line with MMT goals.

In a related study, Carlson et al. (2023) proposed a set of conventions known as the “Pathways Conventions” to support teachers in reasoning quantitatively and representing quantitative relationships. These conventions are designed to promote specific patterns for discussing quantities and their relationships, such as “speaking with meaning” (using language that connects quantities to real-world contexts), “quantity tracking” (viewing graphs as records of how quantities change together), and “emergent symbolization” (creating and using algebraic expressions and equations in ways that align with students’ reasoning). The Pathways Conventions are intended to help teachers develop a deeper understanding of key precalculus concepts and promote a consistent approach to teaching these concepts.

Carlson et al. (2023) argue that consistently using these conventions can help teachers reorganize their cognitive schemes toward their conceptualizing functions as a way of expressing and representing how two quantities values are related and change together. They claim that a teacher who views teaching through this lens has developed a KDU for the class of functions introduced in an algebra or precalculus course. Teachers who regularly use these conventions have reported recognizing the positive impact of their quantitative reasoning on students’ thinking and learning. This approach suggests that by establishing consistent teaching practices that emphasize quantitative reasoning, teachers can not only improve their own understanding of key mathematical concepts but also enhance their students’ learning experiences.

Tasks and reflection as tools for developing teachers’ MMT

This strand of research demonstrates how reflective engagement with well-designed tasks can support the refinement of MMT. These studies exemplify how targeted instructional activities and sustained inquiry into one’s teaching support the evolution of mathematical meanings.

Another approach to developing teachers’ mathematical meanings is through engaging them in tasks that encourage reflection and coordination of their understandings. Thompson et al. (2007) found that teachers’ mathematical meanings became more refined when they reflected on the meanings they applied to tasks at a micro level—specifically, when they considered how their reasoning influenced student learning. However, the researchers also identified several factors that limited teachers’ ability to coordinate and refine their mathematical meanings, such as prior meanings, curricular commitments, and a lack of attention to meaning-making during instruction. These factors hindered teachers’ ability to align their own meanings for concepts, thus limiting the development of more robust mathematical meanings for teaching (Thompson et al., 2007). This highlights the importance of creating spaces for teachers to reflect on their practice and providing the necessary support to help them make sense of and improve their own mathematical understandings.

Decentering and mathematical meanings for teaching an idea

Finally, this line of research illustrates how adopting an MMT lens helps illuminate the cognitive demands of teaching specific concepts. The construct of decentering offers a theoretical tool for understanding how teachers shift perspectives in ways that support the development of their MMT.

The construct of decentering, as explored in prior research (e.g., Baş-Ader and Carlson, 2021; Carlson et al., 2007; Carlson et al., 2023; Steffe and Thompson, 2000; Thompson, 2013), offers a valuable lens through which to examine the cognitive processes underpinning a teacher’s MMT for teaching an idea. Piaget (1995) introduced the construct of decentering to describe the cognitive and social processes occurring during a child’s transition from pre-operational to concrete operational stages of development. He defined decentering as the child’s shift away from egocentric thought toward the capability to adopt another person’s perspective and simultaneously coordinate multiple aspects of an object or situation.

Extending Piaget’s foundational work, contemporary researchers have adopted and refined the term “decentering” to specifically characterize individuals’ attempts to understand another’s actions from the other’s perspective (Baş-Ader and Carlson, 2021; Carlson et al., 2007; Carlson et al., 2024; Carlson et al., 2023; Rocha and Carlson, 2020; Teuscher et al., 2016). From this viewpoint, an individual acts in a decentered manner when they deliberately attempt to understand another’s actions by modeling the cognitive processes the other person might have employed. Conversely, an individual acts in a non-decentered manner when they impose their own reasoning, goals, or understandings onto another’s actions to interpret or explain them (Carlson et al., 2024).

Decentering, thus, involves an individual’s ability to construct cognitive models of another’s thinking. In educational contexts, a teacher’s first-order model refers to the meanings and knowledge a student constructs to comprehend and organize their experiences (Steffe et al., 1983). While forming first-order models, teachers rely primarily on their personal meanings and interpretations to make sense of students’ behaviors, actions, and utterances, making these inherently subjective. In contrast, a second-order model emerges when teachers intentionally position themselves from the student’s perspective, cognitively examining and reconstructing the mental operations and constraints the student might employ to logically behave in the observed manner (Thompson, 1982). Through creating these second-order models—effectively decentering—teachers develop deeper insights into students’ mathematical understandings, enabling them to better align their instructional actions with students’ conceptual needs (Baş-Ader and Carlson, 2021). This Piagetian-inspired conceptualization of decentering provides a robust theoretical foundation for examining how teachers’ cognitive and reflective practices evolve through their interactions with student thinking.

Researchers (e.g., Carlson et al., 2024; Rocha, 2023) have provided examples of how a teacher’s decentering actions can support student learning. It is through acts of decentering that teachers expand their image of the conceptions and misconceptions that students have about an idea. As their repertoire of images of students’ thinking related to understanding or learning an idea expands, teachers are better equipped to anticipate student misconceptions and recognize diverse cognitive pathways for learning the idea. These images of students’ conceptions support teachers in constructing more accessible and meaningful learning experiences for students. It is through these deliberate acts of decentering that a teacher’s MMT can advance, resulting in the ongoing refinement of both a teacher’s meanings and pedagogical practices. In this way, teaching is not just about possessing mathematical content knowledge, but about continuously reshaping one’s understanding of ideas, how they are connected, and how they are learned through interaction and reflection.

Rocha’s (2023) dissertation offers an illustrative example of decentering in action, examining how teachers refine their MMT through interactions with student reasoning. In this study, Enzo, a graduate instructor, sought to introduce radian angle measure—a concept defined by the multiplicative comparison of an angle’s subtended arc length to the radius. When a student struggled to understand why an angle’s measure remained unchanged despite variations in the size of the circle used to measure it, Enzo recognized that the student was conceptualizing angle measure in terms of absolute distances rather than as a ratio (multiplicative comparison of two quantities’ values). This realization led Enzo to adjust his instruction, by prompting students to consider how a single measure for an angle could be determined despite the length of the arc subtended by the angle’s rays varying. One student proposed dividing arc length by the circle’s circumference, an idea Enzo used to guide a class-wide discussion on proportional reasoning. Rather than redirecting immediately, he helped students recognize that because a circle’s circumference is always 2π times its radius, multiplicatively comparing the length of the subtended arc to either (1) the circle’s circumference or (2) radius provides a measure for the angle’s openness that is independent of the circle’s size. This led students to see why dividing arc length by the radius provides an invariant measure across different circle sizes—thus arriving at the definition of radian measure.

Reflecting on the lesson, Enzo realized he had previously overlooked how students’ understanding of the proportional relationship between circumference and radius could serve as an entry point for grasping radian measure. Through decentering, he refined his instructional goals, recognizing the importance of explicitly supporting students in developing proportional reasoning within a circle. This example illustrates how decentering fosters the development of MMT by creating an iterative process in which teachers refine their instructional strategies through engagement with student reasoning. Research has shown that teachers skilled in decentering are more effective at anticipating misconceptions, recognizing diverse cognitive pathways, and designing meaningful learning experiences (Baş-Ader and Carlson, 2021; Carlson et al., 2024). Integrating decentering into discussions of MMT underscores the dynamic nature of teacher knowledge, emphasizing that teaching is not just about possessing mathematical content knowledge but about continuously reshaping one’s understanding through interaction and reflection.

Carlson et al. (2024) have provided more concrete examples of how a teacher’s mathematical meaning for teaching an idea influences a teacher’s pedagogical actions, and how acts of decentering can advance a teacher’s MMT and future explanations. They illustrate how repeated cycles of preparing to teach an idea, teaching the idea, and reflecting on the effectiveness of one’s instructional approaches can lead to the ongoing refinement of both the teacher’s MMT and the many fine-grained decisions a teacher makes when preparing to teach an idea and interacting with students. They and Rocha (2023) argue that advances in a teacher’s MMT and images of future pedagogical actions for supporting student learning, can be fostered by the teacher reflecting on the effectiveness of their instructional choices soon after teaching a lesson. Carlson et al. (2024) emphasize that a teacher’s MMT for teaching an idea emerges through reflections on what is entailed in understanding, learning, and teaching specific ideas and that a teacher’s conceptual connections, insights about productive pedagogical moves, etc., also emerge in the context of teaching a specific idea. Rocha (in preparation) illustrates mechanisms for supporting teachers in engaging in reflections that she documented to be effective for refining a teacher’s MMT and instructional practices.

Discussion

This paper has explored the development and distinction between two key constructs in mathematics education: MKT and MMT. While both constructs address the knowledge and cognitive processes involved in teaching mathematics, they do so from different perspectives, each highlighting distinct aspects of teaching and learning.

Mathematical Knowledge for Teaching, as initially conceptualized by Ball et al. (2005) (e.g., Ball, 1990; Ball and Bass, 2003), describes the specialized mathematical knowledge teachers need to effectively teach. This includes CCK, which is the general mathematical knowledge used in teaching, and SCK, which pertains to the unique knowledge required for teaching specific mathematical tasks. MKT emphasizes that teaching mathematics requires a specialized kind of expertise that goes beyond the general knowledge needed by mathematicians or other professionals. It encompasses the skills, strategies, and knowledge that enable teachers to explain concepts, anticipate student difficulties, and respond effectively to students’ reasoning.

However, early formulations of MKT framed it as a relatively static body of knowledge—something teachers possess and apply in their practice, leading to observable behaviors in the classroom. This perspective has been critiqued by some scholars, who argue that it overlooks the complex, evolving nature of how teachers develop and use knowledge over time. In contrast, Silverman and Thompson (2008) offer a dynamic interpretation, viewing MKT as a fluid, individualized framework shaped by teachers’ cognitive schemes, reflective practices, and interactions with students. This understanding challenges the static view of MKT, highlighting its evolving nature and emphasizing the personal, reflective process through which teachers’ mathematical understanding develops. The distinction between MKT as a set of skills (Ball et al., 2005) and as an evolving framework (Silverman and Thompson) has significant implications for how MKT is applied in teacher education and professional development.

Moving beyond MKT, we also examine MMT, a construct introduced by Thompson (2016), that is focused on how teachers come to understand and make sense of the mathematical concepts they teach. MMT emphasizes that teaching involves developing personal meanings for mathematical ideas, which inform teachers’ instructional decisions. Unlike MKT, which focuses on the knowledge teachers need to teach effectively, MMT emphasizes the cognitive processes behind teaching, viewing mathematical meaning as something constructed by teachers through interactions with both content and students. This approach aligns with a Piagetian view of knowledge, where meaning and understanding arise from individual cognitive schemes and mental operations.

The distinction between MKT and MMT underscores the difference between knowledge as something teachers possess (MKT) and knowledge as something teachers create (MMT). While MKT emphasizes acquiring competencies to perform specific teaching tasks, MMT highlights the development of internalized, personalized meanings that guide teachers’ decisions and behaviors. This shift from a focus on knowledge to a focus on meaning reflects broader trends in educational theory, where emphasis has moved from content mastery to understanding how individuals make sense of and engage with content.

The shift to MMT also stresses the importance of teachers’ cognitive schemes—the mental frameworks that shape their actions and responses in the classroom. By focusing on the meanings teachers develop, researchers can better understand how these meanings influence not only instructional practices but also decision-making processes and interactions with students. This focus on meaning encourages teachers to reflect on the cognitive roots of their actions and how their understanding of mathematics evolves through ongoing professional development and reflection.

The connection between decentering and MMT highlights the role of perspective-taking in refining both instructional strategies and teachers’ mathematical understandings. As shown in Rocha’s (2023) dissertation study, engaging with student reasoning allows teachers to adjust their explanations and deepen their own mathematical meanings. Carlson et al. (2023) and Rocha’s (2023) findings further demonstrate that decentering is not just an instructional tool but a mechanism for teachers’ evolving a teacher’s MMT an idea. As such, the choice to use the term MMT, rather than MKT, is therefore not just a semantic one. It reflects a decision to focus on the mental processes and cognitive schemes that underpin teachers’ practice, framing teaching as a dynamic process of meaning-making. This shift moves beyond viewing MKT as a set of competencies to be assessed and instead positions teaching as an evolving process shaped by teachers’ reflective engagement with content and student thinking. By adopting the term MMT to describe Thompson and Tallman’s meaning-oriented conception of teacher knowledge, this paper helps clarify theoretical boundaries and reduce ambiguity in the use of the term MKT across frameworks.

Both MKT and MMT are essential for understanding teacher development. While MKT offers a framework for identifying the knowledge teachers need to teach mathematics effectively, MMT provides insight into how teachers’ understanding evolves and influences their practice. Researchers such as O’Bryan and Carlson (2016), Musgrave and Carlson (2017), and Carlson et al. (2023) have emphasized that engaging teachers in quantitative reasoning and conceptually focused teaching is crucial for fostering both MKT and MMT. Through strategies like the Pathways Conventions, teachers can develop more coherent and meaningful understandings of mathematical concepts and enhance their ability to respond to students’ reasoning in ways that promote deeper learning.

Implications

The distinction between MKT and MMT has several important implications for research, teacher development, and curriculum design. For teacher education, if MKT is viewed as a set of competencies, teacher preparation may emphasize the acquisition of specific mathematical knowledge and instructional strategies. However, the dynamic view of MKT proposed by Silverman and Thompson, along with research on teachers’ MMT, suggests that teacher development might focus not only on knowledge acquisition but also on fostering reflective practices and developing personal, meaningful understandings of the concepts being taught.

Professional development programs could benefit from encouraging teachers to reflect on how their mathematical understanding evolves and shapes their teaching. Instead of just mastering facts, teachers might engage in reflective learning that explores the cognitive processes behind their mathematical understandings. Workshops, seminars, and professional learning communities (PLCs) might provide opportunities for teachers to construct robust meanings for the concepts they teach and consider how these meanings influence their practice. This approach may support more meaningful professional growth, fostering a deeper engagement with both content and pedagogy.

The distinction between MKT and MMT also invites a reconceptualization of how teacher knowledge is assessed. Traditional assessments focus on factual and procedural knowledge but fail to capture the complexity of teaching. More comprehensive assessments could explore how teachers make meaning of their knowledge, including how they develop understanding over time and adapt their practices based on student thinking. Formative assessments—such as observations, self-reflections, and student feedback—could help track teachers’ evolving knowledge and practices.

The shift from a static view of MKT to the evolving nature of MMT has significant implications for curriculum design. Teaching might be seen not as merely delivering content but as developing deep, personally meaningful understandings and engaging students in constructing their own meanings. Curriculum designers and instructional leaders might consider supporting teachers in developing both content knowledge and the ability to reflect on how they make meaning of that content. Opportunities for real-world connections, inquiry-based learning, and collaborative teacher learning could help foster more meaningful, conceptual understanding in the classroom.

Finally, the distinction between MKT and MMT offers a perspective on teachers’ professional growth. Professional development could focus not only on mastering competencies but also on fostering the development of evolving, personal mathematical understandings. Mentorship and coaching models might support teachers in refining both their instructional strategies and their reflective practices, helping them navigate the complexities of professional growth.

For future research, further exploration could investigate how teachers develop and refine their mathematical meanings over time and how these evolving understandings influence their teaching. Longitudinal studies might offer valuable insights into how changes in teachers’ mathematical understandings affect their practices and students’ learning. Research could also explore how teachers’ cognitive processes shape their responses to students’ thinking, providing a more nuanced understanding of effective teaching practices.

Author contributions

AR: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Publication of this article was supported by individual professional development funds awarded to faculty members by Central College.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that Gen AI was used in the creation of this manuscript. This manuscript was prepared with the assistance of generative AI tools, which were used to help refine writing, improve clarity, and suggest structural improvements. However, the content, analysis, and interpretations presented in the manuscript are solely the work of the author(s) and reflect original research. The AI tools were not used for data collection, analysis, or to generate core ideas in the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^While Tallman refers to this construct as MKT, his emphasis on teachers’ cognitive schemes and instructional coherence reflects a meaning-oriented perspective, which this paper refers to as MMT, following Thompson (2016).

References

Ball, D. L. (1990). The mathematical understandings that prospective teachers bring to teacher education. Elementary School J. 90, 449–466. doi: 10.1086/461626