The influence of flow experience on mathematical creativity among primary school students in China

Introduction: Mathematical creativity refers to personal ability to propose novel and original solutions or ideas in the process of solving mathematical problems. Many studies have confirmed that flow experiences can affect personal creativity, but few have focused on the influence of flow experiences in mathematics learning on mathematical creativity. This study explores the influence of Chinese primary school students’ flow experience in mathematics class on their mathematical creativity.

Methods: This study adopted a convergent method in mixed research, participants were 273 sixth grade students from a public primary school in central China. For quantitative research, this study collected data by using the Mathematics Flow State Scale and the Mathematical Creativity Scale, and then conducted descriptive statistics, independent sample t-test, and linear regression analysis. For qualitative research, this study selected six students to solve two open-ended mathematical problems and conducted a comparative analysis for their performance.

Results and discussion: The results of quantitative research showed that flow experience could positively predict mathematical creativity of primary school students. The qualitative research results showed that students with higher levels of flow experience in mathematics class exhibited better creativity in solving open-ended mathematical problems. Finally, the research results were discussed, and suggestions were made on how to effectively utilize flow experience theory in mathematics class to cultivate students’ mathematical creativity.

1 Introduction

The cultivation of innovative consciousness is one of the important goals of modern mathematics education. Cultivating mathematical creativity of students is a common concern in mathematics education all over the world (Hidajat et al., 2023). Mathematical creativity can enhance students’ problem-solving abilities. When solving open-ended and real-life mathematical problems, students with high mathematical creativity can discover new connections between mathematical knowledge and design unique solutions (Shaw et al., 2022). By creatively solving mathematical problems, students will have a deeper understanding of mathematical concepts. This understanding enables students to apply mathematical knowledge in different environments and helps them tackle complex challenges in the future (Newton et al., 2022). However, in China, many mathematics teachers often focus on students’ mastery of knowledge and neglect the cultivation of mathematical creativity (Zhong, 2024). Therefore, in the Chinese educational environment, how to cultivate and enhance students’ mathematical creativity in mathematics class is still an area that needs further exploration.

Flow experience is an important concept in positive psychology, it is an important human subjective emotional experience (Hart, 2020). The investigation of students’ flow experience in mathematics class can help educators understand students’ mathematics learning process and results from students’ emotions, so as to improve students’ flow experience in mathematics class and promote students’ mathematical performance through teaching adjustment (Abduljabbar, 2023). However, there is still lack of systematic research on mathematical flow experience and its influence on mathematical learning among Chinese students (Zhang, 2020).

Although flow experience has been widely studied in the field of psychology, research on its influence on creativity is currently mostly focused on fields such as music and art (Gray et al., 2019; Harmat et al., 2021; Tan and Sin, 2021; Łucznik et al., 2021). There is insufficient research on the influence of flow experience on mathematical creativity. Especially among Chinese primary school students, there is no research on the relationship between flow experiences and mathematical creativity. Therefore, a study on the influence of Chinese primary school students’ flow experience in mathematics class on their mathematical creativity is conducted, aiming to answer the following questions:

1. What is the level of flow experience in mathematics class among primary school students in China?

2. What is the level of mathematical creativity in mathematics class among primary school students in China?

3. Does flow experience influence mathematical creativity among primary school students?

2 Literature review

2.1 Flow experience

Flow experience refers to the psychological state in which an individual is fully engaged during the process of participating in an activity, in which participants will experience satisfaction and pleasure (Van Der Linden et al., 2021). Through flow experience, students will have a deeper understanding of the learning content and gain a sense of achievement in their studies (Özhan and Kocadere, 2020). In mathematics learning, students’ complete immersion in learning tasks, or students’ complete involvement in solving mathematical problems, usually means that students have a flow experience in learning (Barthelmäs and Keller, 2021).

Flow experience is an important aspect that students especially need in the learning process. Through flow experience, students will have a deeper understanding of the learning content and achieve a sense of achievement in learning (Özhan and Kocadere, 2020). As an emotional factor, flow experience has an effect on students’ anxiety and achievement in learning, and is related to learning motivation and self-efficacy (Tian and Ou, 2023). Golnabi (2017) pointed out that the flow experience in mathematics learning has an important impact on the development of students’ mathematical ability, and the tendency of flow experience is related to students’ own personality. This means that students who have a flow experience in mathematics learning will actively participate in mathematics activities, and they will ignore their learning place and time, which greatly reduces the occurrence of students’ lazy behavior (Yuwanto, 2018). Ljubin-Golub et al. (2018) stated that students who experience flow will have more engagement in classroom learning, resulting in excellent learning performance. Herawati et al. (2020) pointed out that factors such as students’ flow experience, learning interest, and learning ability in mathematics learning can affect their mathematical performance. Nurita et al. (2022) pointed out that students’ flow experience in the mathematics classroom will give them greater motivation for mathematics learning. It can be seen that flow experience has an important influence on students’ math learning, and can help students perform better in mathematics learning.

2.2 Mathematical creativity

Regarding creativity, some researchers pointed out that creativity is a universally applicable ability in various fields, as the creative process in different fields is similar. However, some researchers stated that creativity is always related to specific fields (such as mathematics, science, etc.), and therefore requires a certain degree of knowledge or professional knowledge within specific content areas (Kaufman et al., 2017). Kounios and Beeman (2015) pointed out that creativity is the ability of people to break things down and recombine them in new ways to achieve certain goals and reinterpret things. Creativity can help people generate new ideas that are presented in a fluent, flexible, and innovative manner, ultimately leading to the generation of new products (Paulus, 2000; Adams, 2005). Mathematical creativity is the creativity within the category of mathematics. Mathematics learning requires students to discover problems, prove and summarize conclusions. In this process, students will generate new ideas, new processes, and original solutions (Sriraman, 2009). Sriraman et al. (2013) stated that mathematical creativity as the process of proposing new solutions or ideas to mathematical or new problems. Karwowski et al. (2016) pointed out that mathematical creativity as the characteristics of creativity, openness, and independence exhibited by students when solving problems, which is related to general creativity. In short, mathematical creativity is a special field of creativity, and the connotation of mathematical creativity include creativity and mathematical characteristics. Therefore, the fluency, flexibility, and originality of students in solving mathematical problems can be used as indicators to evaluate their mathematical creativity.

2.3 The theoretical framework

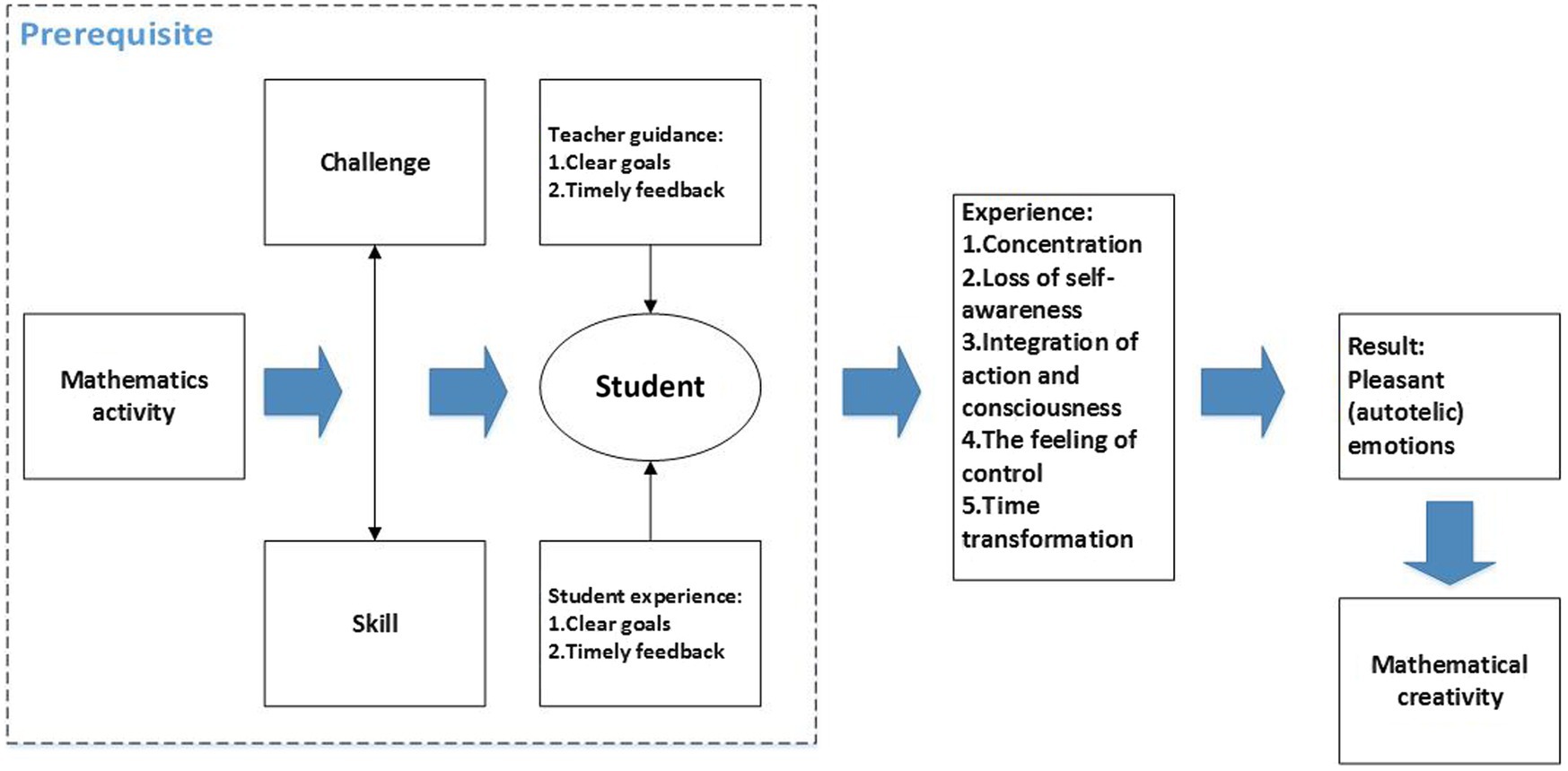
Csikszentmihalyi (2020) pointed out that the flow experience can be divided into nine components, namely: balance between challenge and skill, merging of action and awareness, clear goals, unambiguous feedback, centering of attention, sense of control, loss of self-awareness, time transformation and autotelic nature. These nine components of flow experience can be divided into three types. The first type of components is the prerequisites for flow, including balance between challenge and skill, clear goals, and unambiguous feedback (Conradty et al., 2020). The second type of components is the characteristics of the occurrence of flow experiences, which can only be achieved when individuals focus on what they are doing to generate flow experiences (Subaşı, 2020). Centering of attention is necessary to maintain flow experience. In addition, due to Concentrated attention, action and consciousness need to be combined. At this time, individuals may lose self-awareness or develop a sense of control over their behavior, and their concept of time may also be distorted (Csikszentmihalyi, 2020). The third type of flow experience component refers to the results brought about by flow experience, and individuals who have experienced flow experience may experience autotelic nature. This indicates that ongoing activities can generate a sense of satisfaction for individuals, which can have a reinforcing effect on their behavior (Conradty et al., 2020).

Therefore, based on the flow theory, the theoretical framework of this study was shown in Figure 1. When the challenge of activity and students’ own skills reach a balance, under the guidance of teachers’ clear goals and timely feedback, students will get clear goals and timely feedback of this mathematics activity. After meeting the conditions for the occurrence of flow experience, students enter the process of flow experience, experience the concentration, loss of self-awareness, integration of action and consciousness, the feeling of control and time transformation. Finally, students will have the pleasant (autotelic) emotions, which will affect students’ mathematical creativity.

Figure 1

Figure 1. Theoretical framework.

3 Methods

3.1 Sample

Based on the research questions, this study used the mixed-method. By collecting qualitative and quantitative data, this could better understand the influence of flow experience on mathematical creativity of primary school students. This study adopted a convergent research method in mixed research. The convergent research is a single-stage design that collects both quantitative and qualitative data at the same stage, then merge the two results for in-depth comparison and analysis (Chali et al., 2022).

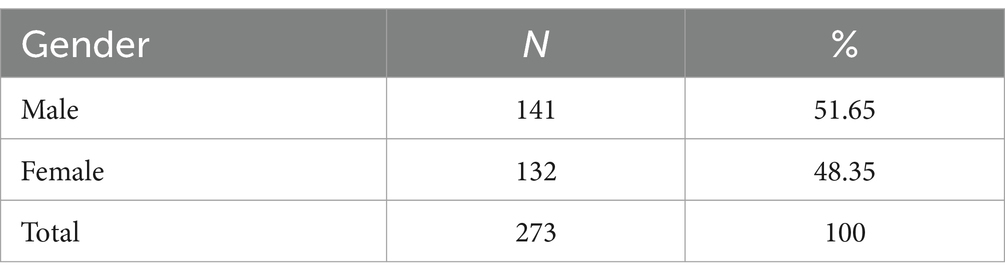
Considering cognitive level, reading ability, and comprehension ability of primary school students, this study was conducted among sixth grade students. A total of 285 students from six classes in sixth grade were invited to participate in a quantitative survey. As shown in Table 1, 273 valid scales were ultimately collected in this study, including 141 male students (51.65%) and 132 female students (48.35%).

Table 1

Table 1. Sample distribution by gender.

In order to compare the performance of students with different levels of flow experience in solving open-ended mathematical problems, the qualitative survey adopted stratified sampling (Lohr, 2021). This study categorizes sixth grade students into three categories based on their self-reported of flow experience in mathematics class: high flow experience, moderate flow experience, and low flow experience. Selected one male and one female student from each category, and a total of six students participated in the qualitative survey.

3.2 Instrument

3.2.1 Mathematics flow state scale

The flow experience in mathematics class was measured using the Mathematics Flow State Scale developed by Zhang (2020) for Chinese primary school students. This scale measured the level of flow experience of students in mathematics learning, including 8 dimensions: balance between skills and challenges (Such as: 6. My math abilities matched the high challenge of the situation in math activity.); clear goals (Such as: 8. When in math task I knew clearly what I wanted to do during math classroom.); unambiguous feedback (Such as: 2. It was really clear to me that I was doing well in math classroom.); merging of action and awareness (Such as: 1. I usually made the correct movements without thinking about trying to do so in math classroom.); centering of attention (Such as: 3. My attention usually was focused entirely on the math activities that I was doing.); sense of control (Such as: 10. I felt like I could control what I was doing in math activities during math class.); loss of self-awareness (Such as: 4. I was not concerned with what others may have been thinking of me in math activities.); and autotelic nature (Such as: 5. I really enjoyed the experience from math class.). Rating ranged from 1 (strongly disagree) to 5 (strongly agree). The higher the score, the higher the level of student’s flow experience. Internal consistency reliability (Cronbach’s alpha) of the Mathematics Flow State Scale was reasonably high at 0.898.

3.2.2 Mathematical creativity scale

This study used the Mathematical Creativity Scale developed by Wei (2023) for Chinese students. This scale includes four dimensions, namely: consciousness of problem exploration (Such as: 1. I enjoy discovering and posing mathematical problems); ability of problem exploration (Such as: 7. I can summarize the mathematical concepts to be discussed in the textbook from mathematical problems/activities); ability of open-ended problems solution (Such as: 14. I often understand mathematical problems from different perspectives.); and formation of mathematical thinking (Such as: 22. I often think about whether the teacher’s teaching methods are suitable for myself). The ratings range from 1 (strongly disagree) to 5 (strongly agree). The higher the score, the higher the level of student’s mathematical creativity. Internal consistency reliability of the Mathematical Creativity Scale was reasonably high at 0.932.

3.2.3 Open-ended mathematical problems

This study designed two open-ended mathematical problems, namely: number classification and problem generation (As shown in Figures 2, 3). This study invited two sixth grade math teachers with ten years of teaching experience to evaluate these two mathematical problems. Both teachers considered that the content of the problems was consistent with the research objective and that sixth grade students were able to complete them independently. This study evaluated the answers given by students in terms of fluency, flexibility, and originality. The evaluation of creativity fluency was determined based on the number of correct answers given by the students. For example, one correct answer counted as 1 point. Flexibility was determined by the number of methods or types of correct answers given by students. For example, if a student’s answer could be divided into 7 types, then the flexibility score was 7 points. Originality was measured by the degree to which the participant’s correct answer was repeated with that of other participants. If the participant’s answer did not repeat anyone’s answer, it indicated originality and could earn 1 point.

Figure 2

Figure 2. Number classification.

Figure 3

Figure 3. Problem generation.

3.2.4 Semi-structured interview

After answering the questions, this study conducted semi-structured interviews with six participants, asking them to report their feelings during the process of answering the questions. Interview questions include: “Did you experience the following feeling when solving the mathematical problems just now? For example, your attention was highly focused; Not caring about others’ evaluations of your performance; Being able to adjust your behavior to better complete the task; You did not need to think too much to give the answer; Your perception of the passage of time did not match the actual situation.” and “If you did not experience the above, please describe how you felt when completing the problems.” The interview questions were evaluated by two sixth grade math teachers, and both teachers stated that the interview questions were consistent with the research objective and could be used for subsequent research.

3.3 Procedure

This study was approved by the Ethics Committee of SEGi University. All students participating in the study were voluntary and provided informed consent forms to their parents. In quantitative research, students filled out survey questionnaires on a class by class basis and submitted anonymously. In qualitative study, six students were asked to complete two open-ended mathematical problems within 30 min. Subsequently, interviews were conducted with each student for approximately 10 min. Finally, by comparing and synthesizing quantitative and qualitative results, the influence of primary school students’ flow experience on their mathematical creativity can be deeply understood.

3.4 Data analysis

This study used SPSS 26.0 software for quantitative analysis, including descriptive analysis, independent sample t-test, and linear regression analysis. Descriptive statistics can provide analysis results such as mean and standard deviation, thereby obtaining the overall and dimensional objective situation of variables (Mishra et al., 2019). Independent sample t-test can compare the means of two independent groups (such as different genders) to determine whether there is a statistically significant difference between them (Manfei et al., 2017). Linear regression models and quantifies the relationship between the dependent variable and the independent variable by fitting a linear equation to observed data. It is used to predict the value of the dependent variable based on the value of the independent variable and explain how changes in the independent variable are related to changes in the dependent variable (James et al., 2023).

This study used comparative analysis method for qualitative analysis. The role of comparative analysis method in qualitative research is to provide a structured, systematic, and rigorous approach to compare different cases, revealing complex causal patterns and generating explanatory insights that combine the depth of qualitative data with the clarity of comparative logic (Cragun et al., 2016). This study encoded boy and girl with high flow experience as SHB and SHG; Encoded boy and girl with moderate flow experience as SMB and SMG; Encoded boy and girl with low flow experiences as SLB and SLG. For the answers given by students, the researcher and two experienced math teachers jointly evaluated them to prevent any bias in the evaluation. This study recorded and transcribed the interview content of students into text, and provided feedback on the text to students for review, ensuring that it matched the meaning they want to express.

4 Results

4.1 Quantitative results analysis

The Cronbach’s alpha of Mathematics Flow State Scale was 0.964 and the Cronbach’s alpha of Mathematical Creativity Scale was 0.965. This indicated that both scales had good internal consistency in the formal research sample. The absolute skewness of all items was between 0.07–0.538, and the absolute kurtosis was between 0.291–0.962, indicating that the sample data conformed to a normal distribution (Kline, 2023).

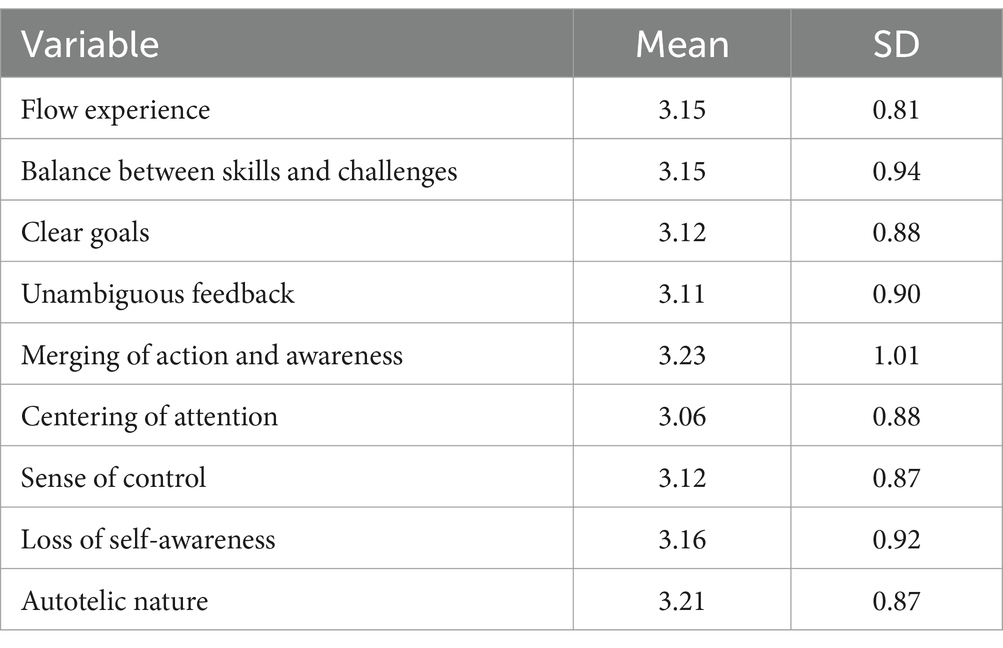
Table 2 showed the flow experience level of primary school students in mathematics class. The mean of flow experience among primary school students in mathematics class was slightly higher than 3 points, which was at a moderate level. Among the 8 dimensions of flow experience, merging of action and awareness had the highest mean value, while unambiguous feedback had the lowest mean value.

Table 2

Table 2. Descriptive statistics for flow experience and dimensions (n = 273).

The differences in flow experience between genders in primary school students were illustrated in Table 3. The results showed that the mean of flow experience in males was higher than that in females, and there was a significant difference between the two (p < 0.05).

Table 3

Table 3. Independent t-test between different genders.

As can be seen in Table 4, the mean of mathematical creativity among primary school students in mathematics class was 3.19, also at a moderate level. Among the 4 dimensions of mathematical creativity, consciousness of problem exploration had the highest mean value, while ability of problem exploration had the lowest mean value.

Table 4

Table 4. Descriptive statistics for mathematical creativity and dimensions (n = 273).

As shown in the results in Table 5, the mean of mathematical creativity in boys was higher than that in girls, and there was also a significant difference between the two (p < 0.05).

Table 5

Table 5. Independent t-test between different genders.

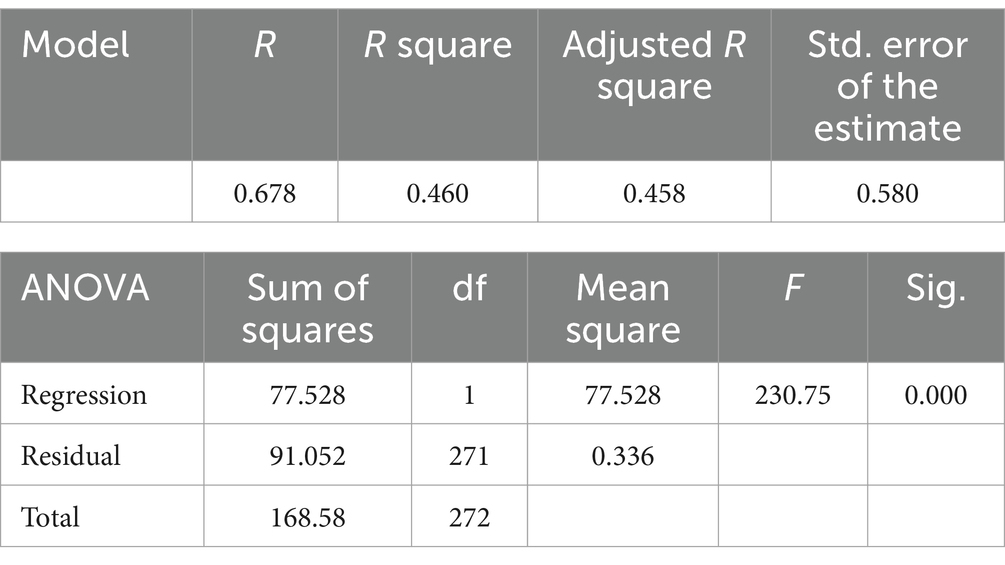
Table 6 manifested the influence of flow experience on mathematical creativity among primary school students. The results showed that F = 230.75, p < 0.05. The linear regression coefficients R = 0.678, R2 = 0.460, and the adjusted R2 = 0.458 this indicated that the flow experience could significantly positively predict mathematical creativity among primary school students.

Table 6

Table 6. Linear regression on mathematical creativity.

4.2 Qualitative results analysis

The answers given by SHB to the open-ended mathematical problems were shown in Figure 4. For numerical classification problem, the fluency score of SHB was 16 points (Such as: 1. 3, 5, 9, 13, 25, 39 and 49 are all odd numbers), flexibility score was 10 points (Such as: Classify numbers from the perspective of prime numbers was: 2. 2, 3, 5 and 13 are all prime numbers), and originality score was 8 points (Such as: 10. The reciprocals of 2, 5, 10 and 25 are all finite decimals). For problem generation problem, the fluency score of SHB was 20 points (Such as: 1. What is the profit for each lily flower?), flexibility score was 9 points (Such as: The math problem proposed from the perspective of adding or subtracting between different unit prices was: 10. How much is the selling price of each lily more expensive than each rose?), and originality score was 8 points (Such as: 3. What is the interest rate for each lily?).

Figure 4

Figure 4. The answers of SHB to open-ended mathematical problems.

Figure 5 illustrated the answers given by SHG to the open-ended mathematical problems were shown in. For numerical classification problem, the fluency score of SHG was 14 points (Such as: 3. 9, 10, 12, 25, 39 and 49 are all composite numbers), flexibility score was 6 points (Such as: Classify numbers from the perspective of odd numbers was: 1. 3, 5, 9, 13, 25, 39 and 49 are all odd numbers), and originality score was 6 points (Such as: 4. The rightmost digit on both 2 and 12 is 2). For problem generation problem, the fluency score of SHG was 12 points (Such as: 1. How much is the selling price of each lily more expensive than each rose?), flexibility score was 5 points (Such as: math problems proposed from the perspective of unit price were: 7. What is the purchase price of each lily? 9. What is the purchase price of each rose?), and originality score was 0 points.

Figure 5

Figure 5. The answers of SHG to open-ended mathematical problems.

As can be seen in Figure 6, for numerical classification problem, the fluency score of SMB was 7 points (Such as: 4. 3, 9, 12 and 39 are all multiples of 3), flexibility score was 5 points (Such as: Classify numbers from the perspective of prime numbers was: 2. 2, 3, 5 and 13 are all prime numbers), and originality score was 1 points (7. 2, 3, 5, 9, 10, 12, 13, 25, 39 and 49 are all natural numbers). For problem generation problem, the fluency score of SMB was 8 points (Such as: 1. What is the selling price of a bouquet of lilies?), flexibility score was 3 points (Such as: Math problems proposed from the perspective of total price were: 1. What is the selling price of a bouquet of lilies? 5. What is the selling price of a bouquet of roses?), and originality score was 0 points.

Figure 6

Figure 6. The answers of SMB to open-ended mathematical problems.

As shown in the results in Figure 7, for numerical classification problem, the fluency score of SMG was 6 points (Such as: 1. 2, 3, 5 and 13 are all prime numbers), flexibility score was 4 points (Such as: Classify numbers from the perspective of multiples were: 3. 2, 10 and 12 are all multiples of 2; 4. 3, 9, 12 and 39 are all multiples of 3; 6. 5, 10 and 25 are all multiples of 5), and originality score was 0 points. For problem generation problem, the fluency score of SMG was 1 points (How many more roses do each bouquet have than each bouquet of lilies?), flexibility score was 1 points (the math problem proposed from the perspective of adding and subtracting the number of flowers was: How many more roses do each bouquet have than each bouquet of lilies?), and originality score was 0 points.

Figure 7

Figure 7. The answers of SMG to open-ended mathematical problems.

The answers given by SLB to the open-ended mathematical problems were manifested in Figure 8. For numerical classification problem, the fluency score of SLB was 0 points, flexibility score was 0 points, and originality score was 0 points. For problem generation problem, the fluency score of SLB was 2 points (1. What is the selling price of each bouquet of lilies as a percentage of the purchase price? 2. How much is the selling price of each bouquet of roses higher than the purchase price?), flexibility score was 2 points (the math problem proposed from the perspective of price percentages was: 1. What is the selling price of each bouquet of lilies as a percentage of the purchase price? The math problem proposed from the perspective of adding or subtracting between different total prices was: 2. How much is the selling price of each bouquet of roses higher than the purchase price?), and originality score was 2 points (1. What is the selling price of each bouquet of lilies as a percentage of the purchase price? 2. How much is the selling price of each bouquet of roses higher than the purchase price?).

Figure 8

Figure 8. The answers of SLB to open-ended mathematical problems.

As illustrated in Figure 9, for numerical classification problem, the fluency score of SLG was 1 points (3, 9, 12 and 39 are all multiples of 3), flexibility score was 1 points (Classify numbers from the perspective of multiples was: 3, 9, 12 and 39 are all multiples of 3), and originality score was 0 points. For problem generation problem, the fluency score of SHB was 2 points (1. How much is the purchase price of each lily more expensive than each rose? 2. How much is the selling price of a bouquet of roses cheaper than a bouquet of lilies?), flexibility score was 2 points (the math problem proposed from the perspective of adding or subtracting between different unit prices was: 1. How much is the purchase price of each lily more expensive than each rose? The math problem proposed from the perspective of adding or subtracting between different total prices was: 2. How much is the selling price of a bouquet of roses cheaper than a bouquet of lilies?), and originality score was 0 points.

Figure 9

Figure 9. The answers of SLG to open-ended mathematical problems.

The results indicated that students with higher levels of flow experience in mathematics class performed better in solving open-ended mathematical problems than students with moderate and low levels. The performance of SHB was the best among all students.

After the event, six students described their experiences in problem-solving. SHB stated that he experienced flow during the problem-solving process:

Yes, I tend to be more focused when doing math problems; And I also like to do questions with multiple answers, so when I do them, I feel more at ease and my thinking is clearer. Moreover, I don't care about how others evaluate my answers because I believe in my own abilities. When I was doing math problems, I felt like only a few minutes had passed, but the teacher told me that half an hour was up (Thursday, September 26th, 2024, 1:05 PM).

SMB and SLG felt that the open-ended mathematical problems were difficult for themselves, so they did not experience flow during the problem-solving process:

SMB: I have seen relatively few of these types of questions, so each question still requires some thinking to determine if my answer is correct (Thursday, September 26th, 2024, 1:45 PM).

SLG: I don't have the feelings you mentioned. I feel like I don't know how to solve these problems anyway. Just write and submit them, I don't want to think too much (Thursday, September 26th, 2024, 2:41 PM).

SHG, SMG and SLB reports experience anxiety during the problem-solving process due to the unfamiliarity or difficulty of open-ended mathematical problems:

SHG: I haven't seen this type of problem much before, so I need to think about how to solve these problems. I feel that my attention is relatively focused, but I am a bit nervous when solving problems (Thursday, September 26th, 2024, 1:23 PM).

SMG: I don't have the above experience. I feel a little scared when solving problems because I find these questions a bit difficult for me. I try my best to figure out how to solve these problems, but some of them are just too difficult (Thursday, September 26th, 2024, 2:02 PM).

SLB: I don't have the feeling you described. Solving problems in the past half hour has been a lot of pressure for me. I have never seen this type of problem before, and I am afraid that I cannot solve these problems on my own, nor do I have any ideas (Thursday, September 26th, 2024, 2:23 PM).

5 Discussion

Mathematical creativity not only helps students achieve excellent performance in mathematics learning, but also provides them with basic skills needed for their future careers. Therefore, the cultivation of students’ mathematical creativity has always been a concern of mathematics educators. This study extends the application scope of flow theory to primary school mathematics education, providing a new perspective for cultivating mathematical creativity among primary school students.

This study investigated the flow experience level of primary school students in mathematics class in China. It was found that students’ flow experience was at a moderate level, and the flow experience level of males was higher than that of females, with a significant difference between the two. Lee (2021) argued that compared to boys, girls tend to underestimate their ability to learn mathematics and have less positive attitudes toward mathematics. Boys usually consider math tasks to be appropriately challenging and have confidence in their mathematical abilities, so they are more likely to enter a flow state. In contrast, girls often lack confidence in their mathematical abilities and find math tasks too difficult for them, making it difficult for them to enter a flow state (Kiili et al., 2021). In addition, the traditional belief among mathematics teachers is that boys have stronger mathematical abilities, so they will provide more positive feedback and assistance to boys in mathematics classes (Radišić et al., 2024). This enhances boys’ confidence and participation, further promoting their flow experience in mathematics class.

This study found that mathematical creativity among primary school students in China was at a moderate level, with males had a higher level of mathematical creativity than females, and there was a significant difference between the two. Shaw et al. (2022) pointed out that boys typically exhibit higher self-efficacy in mathematics, believing that they are more capable of achieving success in this field. High self-efficacy can enable boys to engage more deeply in mathematical tasks and explore creative solutions. In contrast, girls have lower self-efficacy in mathematics, which may hinder the development of their creativity. In addition, boys develop certain cognitive skills earlier than girls, especially those related to spatial reasoning (Alkouri, 2022). These skills are often related to mathematical creativity and can help boys think flexibly about mathematical problems.

Positive emotions play an important role in influencing creativity. Thomson and Jaque (2025) argued that positive emotions such as satisfaction and pleasure can broaden the individual’s attention and enhance cognitive flexibility, which is helpful for creative tasks that require divergent thinking. In addition, positive emotions can increase motivation and engagement, leading to more innovative ideas and solutions (He, 2023). This study found that as a positive emotion, flow experience significantly positively predict mathematical creativity of primary school students. Flow is a psychological state in which students are fully engaged and highly focused in their studies. This high level of focus enables students to delve deeper into mathematical problems, which is crucial for exploring complex mathematical problems and developing creative solutions (d’Entremont and Voillot, 2021). In the state of flow, students will lose self-awareness, thereby reducing their anxiety and fear of failure. In this state, students are able to actively explore new problem-solving solutions and demonstrate better mathematical creativity (Hidajat, 2024). In addition, flow can bring positive experiences to students, such as enjoyment and satisfaction. This will strengthen students’ intrinsic motivation for learning mathematics, stimulate them to think more actively about solving problems with different solutions, and thus generate more innovative ideas (Qablan et al., 2024).

Qualitative research also confirmed the conclusion of quantitative research, that students with high flow experience in mathematics class performed better than other students in solving open-ended mathematical problems. High level of engagement in mathematics class can help students encode the knowledge they have learned into their long-term memory, making it easier for them to retrieve and apply mathematical knowledge in different environments in the future (Orbach and Fritz, 2022). In addition, students who experience flow will generate positive emotions such as happiness, excitement, and satisfaction after learning activities. These emotions not only enhance the immediate learning performance, but also contribute to long-term academic motivation and engagement (Maniriho, 2024). Therefore, students who have a higher flow experience in mathematics class can more actively and flexibly apply their learned knowledge and find more solutions when solving open-ended mathematical problems.

According to flow theory, the balance between challenge and skill is an important prerequisite for the generation of flow experience. The balance between challenge and skill is crucial for flow experience of students, as it directly affects their engagement, motivation, and overall learning performance (Peifer et al., 2022). In order for students to experience flow, the challenges presented in the task must be closely aligned with their skill levels. When tasks are too simple, students may feel bored and lazy. On the contrary, if the task is too difficult, they may feel anxious and at a loss (Zhao and Khan, 2022). In this study, the difficulty of two open-ended mathematical problems reached a dynamic balance with mathematical ability of SHB. Therefore, SHB experienced flow in solving open-ended mathematical problems and performed better than other students.

6 Implications

The findings of this study have important implications for mathematics teachers to cultivate mathematical creativity of primary school students in mathematics class. Mathematics teachers can design corresponding learning content and try different teaching methods based on flow theory to stimulate students’ creativity in solving mathematical problems. Teachers should also consider the differences in students’ abilities as much as possible and provide corresponding challenge activities to enable students in the classroom to experience a balance between challenge and skill. In addition, in primary school mathematics teaching, teachers should pay more attention to the learning experience and creativity development of girls. Teachers can encourage girls to solve problems in various ways, thereby enhancing their participation in mathematics class and stimulating their mathematical creativity.

7 Limitations and prospects

Although this study comprehensively analyzed the influence of primary school students’ flow experience in mathematics class on their mathematical creativity, there were also some limitations. Firstly, the participants of this study were Chinese sixth grade students, whether the results are applicable to primary school students in other grades and countries still needs to be studied and validated through larger quantitative and qualitative samples. Secondly, the level of flow experience among students in this study mainly came from their self-reports, future research can also allow teachers or peers to observe and evaluate flow experiences of primary school students as a supplement to students’ self-report, thereby obtaining more objective measurement results.

8 Conclusion

This study investigated the flow experience and mathematical creativity level of primary school students in mathematics class in China. It was found that the flow experience and mathematical creativity among primary school students were at a moderate level, with boys having higher flow experience and mathematical creativity than girls. This study confirmed from both quantitative and qualitative perspectives that the flow experience among primary school students in mathematics class could positively predict their mathematical creativity. The balance between challenge and skill was crucial for students to experience flow in mathematics learning. The findings of this study have important implications for mathematics teachers to cultivate mathematical creativity of primary school students in mathematics class.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the SEGi Research Ethics Committee. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

XW: Formal analysis, Methodology, Writing – original draft, Writing – review & editing. PS: Supervision, Writing – review & editing. JZ: Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abduljabbar, S. (2023). The relationships between flow, mathematics self-efficacy, and mathematics anxiety among international undergraduate students in the United States : Andrews University. Available at: https://www.proquest.com/openview/91b6b1306b73f2951e4b348392b7935b/1?pq-origsite=gscholar&cbl=18750&diss=y

Google Scholar

Adams, K. (2005). The sources of innovation and creativity. National Center Educ. Econom.

Google Scholar

Alkouri, Z. (2022). Developing spatial abilities in young children: implications for early childhood education. Cogent Educ. 9:2083471. doi: 10.1080/2331186x.2022.2083471

Crossref Full Text | Google Scholar

Barthelmäs, M., and Keller, J. (eds). (2021). “Antecedents, boundary conditions and consequences of flow” in Advances in flow research (Cham: Springer International Publishing), 71–107. doi: 10.1007/978-3-030-53468-4_3

Crossref Full Text | Google Scholar

Chali, M. T., Eshete, S. K., and Debela, K. L. (2022). Learning how research design methods work: a review of Creswell's research design: qualitative, quantitative and mixed methods approaches. Qual. Rep. 27, 2956–2960. doi: 10.46743/2160-3715/2022.5901

Crossref Full Text | Google Scholar

Conradty, C., Sotiriou, S. A., and Bogner, F. X. (2020). How creativity in STEAM modules intervenes with self-efficacy and motivation. Educ. Sci. 10:70. doi: 10.3390/educsci10030070

Crossref Full Text | Google Scholar

Cragun, D., Pal, T., Vadaparampil, S. T., Baldwin, J., Hampel, H., and DeBate, R. D. (2016). Qualitative comparative analysis: a hybrid method for identifying factors associated with program effectiveness. J. Mixed Methods Res. 10, 251–272. doi: 10.1177/1558689815572023

PubMed Abstract | Crossref Full Text | Google Scholar

Csikszentmihalyi, M. (ed). (2020). “Positive psychology and a positive worldview: new hope for the future of humankind” in Positive psychological science (Routledge), 256–265. Available at:

Google Scholar

d’Entremont, Y., and Voillot, M. (2021). The psychology of flow, mathematics pedagogy, and culture. Int. J. Cross Discip. Subj. Educ. 12, 4404–4410. doi: 10.20533/ijcdse.2042.6364.2021.0539

Crossref Full Text | Google Scholar

Golnabi, L. (ed). (2017). Mathematics self-efficacy and flow in developmental mathematics students : Columbia University. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Mathematics+self-efficacy+and+flow+in+developmental+mathematics+students&btnG=

Google Scholar

Gray, K., Anderson, S., Chen, E. E., Kelly, J. M., Christian, M. S., Patrick, J., et al. (2019). “Forward flow”: a new measure to quantify free thought and predict creativity. Am. Psychol. 74, 539–554. doi: 10.1037/amp0000391

PubMed Abstract | Crossref Full Text | Google Scholar

Harmat, L., de Manzano, Ö., and Ullén, F. (eds). (2021). “Flow in music and arts” in Advances in flow research (Cham: Springer International Publishing), 377–391. doi: 10.1007/978-3-030-53468-4_14

Crossref Full Text | Google Scholar

Hart, R. (ed). (2020). Positive psychology: The basics : Routledge. Available at: https://www.taylorfrancis.com/books/mono/10.4324/9781315147857/positive-psychology-rona-hart

Google Scholar

He, W. J. (2023). Positive and negative affect facilitate creativity motivation: findings on the effects of habitual mood and experimentally induced emotion. Front. Psychol. 14:1014612. doi: 10.3389/fpsyg.2023.1014612

PubMed Abstract | Crossref Full Text | Google Scholar

Herawati, M., Muhid, A., and Hamdani, A. S. (2020). Self-efficacy, social support, academic flow, and math anxiety among Islamic senior high school students. Psympathic 7, 315–326. doi: 10.15575/psy.v7i2.8474

Crossref Full Text | Google Scholar

Hidajat, F. A. (2024). Effectiveness of virtual reality application technology for mathematical creativity. Computers Human Behavior Reports 16:100528. doi: 10.2139/ssrn.4811283

Crossref Full Text | Google Scholar

Hidajat, F. A., Haeruman, L. D., Wiraningsih, E. D., and Pambudi, D. S. (2023). The effect of digital technology learning based on guided discovery and self-regulated learning strategy on mathematical creativity. Int. J. Inform. Educ. Technol. 13, 535–543. doi: 10.18178/ijiet.2023.13.3.1836

Crossref Full Text | Google Scholar

James, G., Witten, D., Hastie, T., Tibshirani, R., and Taylor, J. (eds). (2023). “Linear regression” in An introduction to statistical learning: With applications in python (Cham: Springer international publishing), 69–134.

Google Scholar

Karwowski, M., Jankowska, D. M., and Szwajkowski, W. (eds). (2016). “Creativity, imagination, and early mathematics education” in Creativity and giftedness: Interdisciplinary perspectives from mathematics and beyond (Cham: Springer International Publishing), 7–22. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Creativity%2C+imagination%2C+and+early+mathematics+education&btnG=

Google Scholar

Kaufman, J. C., Glăveanu, V. P., and Baer, J. (2017). The Cambridge handbook of creativity across domains : Cambridge University Press. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=The+Cambridge+handbook+of+creativity+across+domains&btnG=

Google Scholar

Kiili, K. J. M., Lindstedt, A., Koskinen, A., Halme, H., Ninaus, M., and McMullen, J. (2021). Flow experience and situational interest in game-based learning: cousins or identical twins. Int. J. Serious Games 8, 93–114. doi: 10.17083/ijsg.v8i3.462

Crossref Full Text | Google Scholar

Kline, R. B. (ed). (2023). Principles and practice of structural equation modeling : Guilford Publications. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Principles+and+practice+of+structural+equation+modeling&btnG=

Google Scholar

Kounios, J., and Beeman, M. (eds). (2015). The Eureka factor: Creative insights and the brain : Random House. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=The+Eureka+factor%3A+Creative+insights+and+the+brain&btnG=

Google Scholar

Lee, E. J. (2021). Biased self-estimation of maths competence and subsequent motivation and achievement: differential effects for high-and low-achieving students. Educ. Psychol. 41, 446–466. doi: 10.1080/01443410.2020.1821869

Crossref Full Text | Google Scholar

Ljubin-Golub, T., Rijavec, M., and Jurčec, L. (2018). Flow in the academic domain: the role of perfectionism and engagement. Asia Pac. Educ. Res. 27, 99–107. doi: 10.1007/s40299-018-0369-2

Crossref Full Text | Google Scholar

Lohr, S. L. (2021). Sampling: design and analysis. Chapman and Hall/CRC. doi: 10.1201/9780429298899-3

PubMed Abstract | Crossref Full Text | Google Scholar

Łucznik, K., May, J., and Redding, E. (2021). A qualitative investigation of flow experience in group creativity. Res. Dance Educ. 22, 190–209. doi: 10.1080/14647893.2020.1746259

Crossref Full Text | Google Scholar

Manfei, X. U., Fralick, D., Zheng, J. Z., Wang, B., Xin, M. T., and Changyong, F. E. N. G. (2017). The differences and similarities between two-sample t-test and paired t-test. Shanghai Arch. Psychiatry 29:184.

Google Scholar

Maniriho, A. (2024). Satisfaction and academic performance of undergraduate economics students. Cogent Educ. 11:2326707. doi: 10.1080/2331186x.2024.2326707

Crossref Full Text | Google Scholar

Mishra, P., Pandey, C. M., Singh, U., Gupta, A., Sahu, C., and Keshri, A. (2019). Descriptive statistics and normality tests for statistical data. Ann. Card. Anaesth. 22, 67–72. doi: 10.4103/aca.aca_157_18

PubMed Abstract | Crossref Full Text | Google Scholar

Newton, D., Wang, Y., and Newton, L. (2022). ‘Allowing them to dream’: fostering creativity in mathematics undergraduates. J. Furth. High. Educ. 46, 1334–1346. doi: 10.1080/0309877x.2022.2075719

Crossref Full Text | Google Scholar

Nurita, L., Riyadi, R., and Komarudin, K. (2022). The influence self efficacy, flow, through achievement motivation on mathematics learning outcomes of class VIII students in DKI Jakarta region. Budapest Int. Res. Critics Institute J. 5. Avaialble at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=The+influence+self+efficacy%2C+flow%2C+through+achievement+motivation+on+mathematics+learning+outcomes+of+Class+VIII+students+in+DKI+Jakarta+region&btnG=

Google Scholar

Orbach, L., and Fritz, A. (2022). Patterns of attention and anxiety in predicting arithmetic fluency among school-aged children. Brain Sci. 12:376. doi: 10.3390/brainsci12030376

PubMed Abstract | Crossref Full Text | Google Scholar

Özhan, Ş. Ç., and Kocadere, S. A. (2020). The effects of flow, emotional engagement, and motivation on success in a gamified online learning environment. J. Educ. Comput. Res. 57, 2006–2031. doi: 10.1177/0735633118823159

Crossref Full Text | Google Scholar

Paulus, P. (2000). Groups, teams, and creativity: the creative potential of idea-generating groups. Appl. Psychol. 49, 237–262. doi: 10.1111/1464-0597.00013

Crossref Full Text | Google Scholar

Peifer, C., Wolters, G., Harmat, L., Heutte, J., Tan, J., Freire, T., et al. (2022). A scoping review of flow research. Front. Psychol. 13:815665. doi: 10.3389/fpsyg.2022.815665

PubMed Abstract | Crossref Full Text | Google Scholar

Qablan, A., Alkaabi, A. M., Aljanahi, M. H., and Almaamari, S. A. (eds). (2024). “Inquiry-based learning: encouraging exploration and curiosity in the classroom” in Cutting-edge innovations in teaching, leadership, technology, and assessment (IGI Global), 1–12. doi: 10.4018/979-8-3693-0880-6.ch001. Available at: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Inquiry-based+learning%3A+Encouraging+exploration+and+curiosity+in+the+classroom&btnG=

Crossref Full Text | Google Scholar

Radišić, J., Buchholtz, N., Yang-Hansen, K., Liu, X., and Kaarstein, H. (2024). Do teachers’ beliefs about the nature and learning of mathematics affect students’ motivation and enjoyment of mathematics? Examining differences between boys and girls across six countries. Eur. J. Psychol. Educ. 39, 1587–1613. doi: 10.1007/s10212-024-00809-6

Crossref Full Text | Google Scholar

Shaw, S. T., Luna, M. L., Rodriguez, B., Yeh, J., Villalta, N., and Ramirez, G. (eds). (2022). Mathematical creativity in elementary school children: general patterns and effects of an incubation break. Front. Educ. 7:835911. doi: 10.3389/feduc.2022.835911

Crossref Full Text | Google Scholar

Sriraman, B. (2009). The characteristics of mathematical creativity. ZDM 41, 13–27. doi: 10.1007/s11858-008-0114-z

Crossref Full Text | Google Scholar

Sriraman, B., Haavold, P., and Lee, K. (2013). Mathematical creativity and giftedness: a commentary on and review of theory, new operational views, and ways forward. ZDM 45, 215–225. doi: 10.1007/s11858-013-0494-6

Crossref Full Text | Google Scholar

Subaşı, M. (2020). Modeling the relationships among mastery goal orientations, positive coping strategy, and motivational beliefs in science. Sci. Educ. Int. 31, 328–333. doi: 10.33828/sei.v31.i4.1

Crossref Full Text | Google Scholar

Tan, L., and Sin, H. X. (2021). Flow research in music contexts: a systematic literature review. Music. Sci. 25, 399–428. doi: 10.1177/1029864919877564

Crossref Full Text | Google Scholar

Thomson, P., and Jaque, S. V. (2025). Creativity, emotion regulation, and maladaptive daydreaming. Creat. Res. J. 37, 94–103. doi: 10.1080/10400419.2023.2230022

Crossref Full Text | Google Scholar

Tian, Y., and Ou, L. (2023). How do personality traits of college students affect their learning flow experience? Learn. Motiv. 83:101917. doi: 10.1016/j.lmot.2023.101917

Crossref Full Text | Google Scholar

Van Der Linden, D., Tops, M., and Bakker, A. B. (2021). Go with the flow: a neuroscientific view on being fully engaged. Eur. J. Neurosci. 53, 947–963. doi: 10.1111/ejn.15014

PubMed Abstract | Crossref Full Text | Google Scholar

Wei, S. N. (ed). (2023). The relationship among mathematics anxiety, mathematics self-efficacy and mathematics creativity in junior high school students : Hubei University. Available at: https://link.cnki.net/doi/10.27130/d.cnki.ghubu.2023.000709doi:10.27130/d.cnki.ghubu.2023.000709.

Google Scholar

Yuwanto, L. (2018). Academic flow and cyberloafing. Psychol. Res. 8, 173–177. doi: 10.17265/2159-5542/2018.04.006

Crossref Full Text | Google Scholar

Zhang, J. (ed). (2020). Students' flow experience in primary math class and its influence on math performance : East China Normal University. Avilable at: https://link.cnki.net/doi/10.27149/d.cnki.ghdsu.2020.002243doi:10.27149/d.cnki.ghdsu.2020.002243

Google Scholar

Zhao, H., and Khan, A. (2022). The students’ flow experience with the continuous intention of using online English platforms. Front. Psychol. 12:807084. doi: 10.3389/fpsyg.2021.807084

PubMed Abstract | Crossref Full Text | Google Scholar

Zhong, F. (2024). Research on the mathematics teaching reform and the cultivation of students’ innovation ability in colleges and universities. Educ. Review USA 8, 863–867. doi: 10.26855/er.2024.06.014

Crossref Full Text | Google Scholar