- School of Mathematics, University of Birmingham, Birmingham, United Kingdom
In recent years, the impact of teaching technology on students’ mathematical intelligence has received essential academic attention. Students’ mathematical intelligence is a crucial criterion to measure their mathematical understanding and problem-solving ability. Geometry Sketchpad (GSP) is a dynamic geometry software which effectively promotes mathematical cognitive development through its interactive visualization features. Given that the exact function of GSP remains inadequately investigated. This study aims to analyze the impact of GSP on mathematical intelligence in two key dimensions: geometric imagination and functional cognition. By following the PRISMA guidelines, 26 articles from Google Scholar, Web of Science and Scopus were screened for data analysis. A major finding is that GSP has an impact on the development of students’ mathematical intelligence. For example, the dynamic visualization feature of GSP can enhance students’ geometric imagination skills and spatial reasoning. Also, using GSP is conducive to improving students’ problem-solving skills and deepening their understanding of geometric concepts. In addition to demonstrating the functions of GSP, I constructed four types of conic curves. By reading this article, readers can easily understand the applications of GSP. Mathematics teachers can understand the functions of GSP and use it in teaching process. Peer researchers can comprehend limitations of the literature in this field.
1 Introduction
“The principle goal of education is to create men who are capable of doing new things, not simply of repeating what other generations have done—men who are creative, inventive, and discoverers.” (Duckworth, 1964, p. 175).
One of the objectives of secondary education is to enhance students’ mathematical intelligence. Mathematical intelligence is understood as a crucial criterion of students’ ability to solve mathematical problems. It includes the following six dimensions: causality, pattern recognition, the existence and uniqueness of solutions, geometric imagination, functional thinking and abstract thinking.
Causality represents students’ ability to interpret the relationship between variables in mathematical situations (Emmert-Streib and Dehmer, 2010). Pattern recognition involves students applying new perspectives to discover critical questions and suggest a suitable mathematical solution (Neimark and Teklina, 2012). The existence and uniqueness of solutions refer to the ability to identify the existence conditions and number of solutions about mathematical problem (Delarue, 2002). Geometric imagination defines the ability to comprehend spatial relationships by manipulating geometric figures such as transformations, rotations, and projections (Host’ovecký et al., 2019). Functional thinking describes the ability to understand and manipulate the concept of infinity, including infinite processes and gradations (Chytrý et al., 2020). Abstract thinking describes the ability to generalize mathematical concepts and recognize underlying structures (Nurhasanah et al., 2017).
In my experience, some secondary school teachers currently continue to use traditional teaching methods. Traditional teaching methods emphasize rote memorization and repetitive mechanical tasks, aiming to enhance students’ ability to retain and reproduce knowledge (Badr and Abu-Ayyash, 2019; Wang, 2022). However, this practice may bring difficulties in supporting students’ understanding of abstract mathematical concepts, development of independent thinking, and formulation of innovative questions (Nilimaa, 2023). Therefore, it is necessary to explore innovative teaching instruments.
In my opinion, GSP can serve as an essential tool to enhance students independent thinking in the mathematics classroom. For instance, GSP can promote comprehension of key concepts for lower-achieving students (Lee et al., 2023). GSP can also cultivate the creative abilities of high achieving students (Dhayanti et al., 2018). However, there is insufficient research related to the impact of GSP on different dimensions of mathematical intelligence in secondary school students. Most researchers focused on geometric imagination (Chvátal et al., 2024; Ganesan and Eu, 2020; Tursynkulova and Madiyarov, 2023). Researchers rarely focused on other aspects of mathematical intelligence, such as abstract functional thinking (Leong, 2013) and innovative cognition (Tyagi, 2017). In addition, the studies about GSP lacked sufficient research regarding individual student differences (Ismail et al., 2020).
With the above brief review, it is necessary to fill in the gaps by answering questions related to GSP. The main objective of this paper is to clarify the operationalization of GSP in teaching. To achieve this goal, this study is guided by the following questions: (1) What are the basic definition and functions of GSP? (2) What is the impact of GSP on students’ mathematical intelligence?
This study has three primary contributions. By reading this article, teachers can optimize teaching strategies and integrate GSP into classroom design (Meng and Sam, 2011). Secondly, researchers can identify the limitations of studies relating to GSP and build theoretical models associated with mathematical intelligence (Hartono, 2020). Finally, educational administrators provide systematic training for teachers to improve their understanding and applications of GSP.
The remainder of this paper is divided into five sections. The first section of this article is a literature review, this article examines the role of GSP regarding mathematical intelligence in secondary schools. This is followed by some background information on ongoing research within which the present study was carried out and a statement of the specific research questions. The third section describes the methodology and procedures for the collection of data on three keywords, including GSP, mathematical intelligence and secondary school students. This paper mainly analyzes the effects of GSP on students’ geometric imagination and functional cognition. Finally, conclusions are presented suggestions and made for further research.
2 Method
2.1 Search strategy
The process of article selection followed the Preferred Reporting of Items for Systematic Reviews and Meta-Analyses (PRISMA) Statement (Page et al., 2021). I searched Scopus and Web of Science on September 30, 2024, for peer-reviewed articles on geometric sketchpad and mathematical intelligence. I operationalized different permutations of each term based on previously validated searches. For the geometric sketchpad, I referenced prior studies, including Roble (2016) and Hartono (2020), which discuss the application of dynamic geometry software in mathematics education. For mathematical intelligence, I referenced previous studies, such as Chytrý et al. (2020). For secondary school students, I used classification from Gyedu et al. (2020) and Ganesan and Eu (2020), which target education research focusing on students aged 12–18 years. In short, using validated search terms from prestigious journals ensured the capture of appropriate citations in my searches.
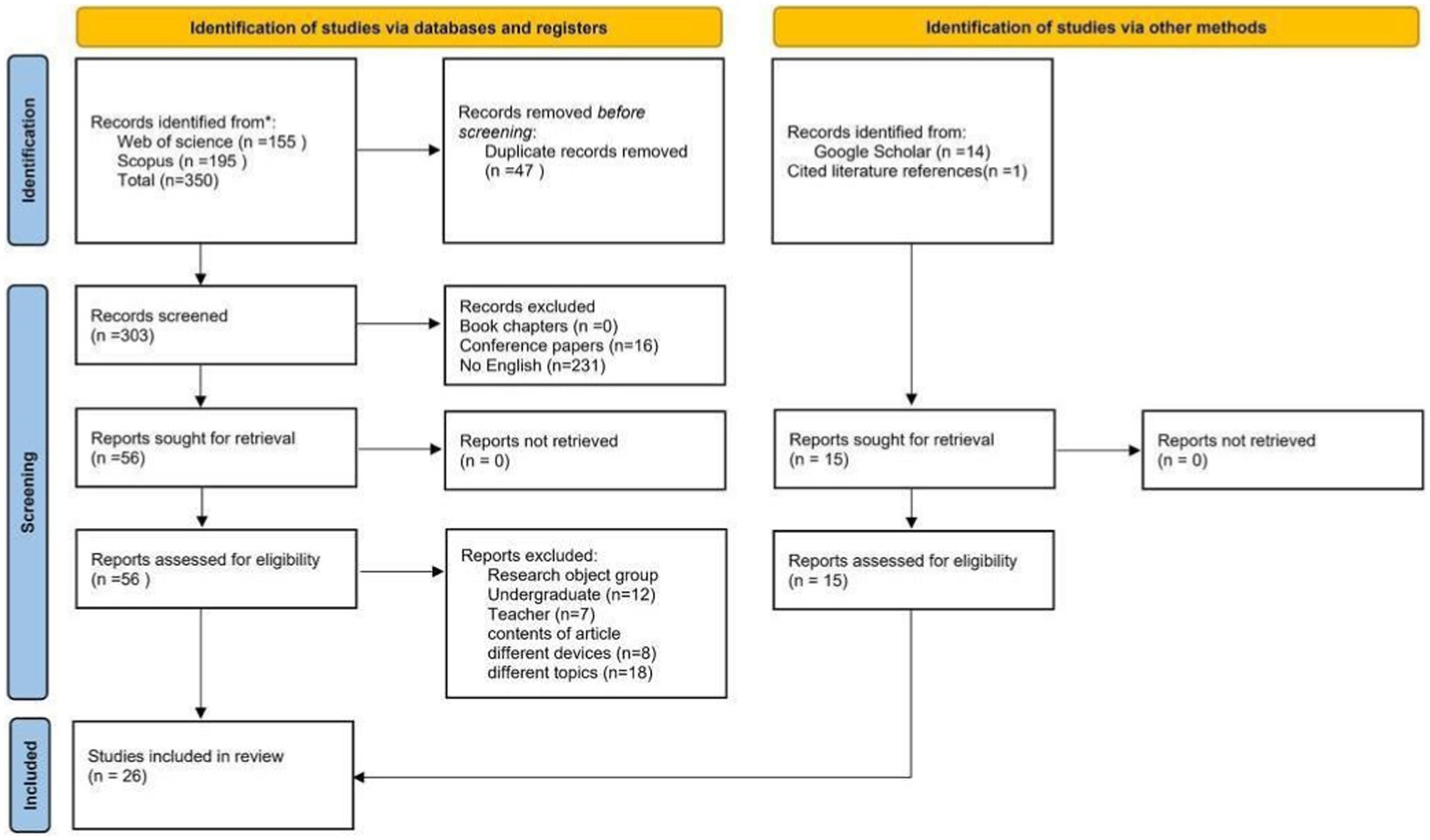
This study applied the fields title/abstract in the search. The full details are available in Appendix 1. My initial search identified a total of 155 articles in Web of Science and 195 in Scopus, which were imported into Zotero reference management software. Of these 350 articles, 47 were identified as duplicates, leaving a total of 303 for screening and eligibility stages.
2.2 Inclusion and exclusion
I applied a series of inclusion and exclusion criteria. Articles were included if they were: (i) written in English; (ii) published in a peer-reviewed journal; (iii) research participants included middle school student; (iv) mathematical intelligence research topics. They are excluded if the articles come from a book or a conference paper and research participants are college students or teachers. Of the 303 records screened, I excluded 16 because they were conference papers, and 231were not in English, leaving a total of 56 articles for retrieval. I was able to find the full text of all articles, resulting in 56 articles for eligibility. At eligibility, upon reviewing the full text, I excluded another 26 articles that did not relate to geometric sketchpad and mathematical intelligence. I also further excluded 19 articles because the populations in these studies did not include middle school student. I also identified additional 1 article by scanning the reference list and then using Google Scholar to find 15 articles. This left the final 26 articles in the final review sample for data analysis. Figure 1 further describes the process of inclusion /exclusion.
3 Findings
3.1 What are the basic definition and functions of GSP?
GSP is an interactive geometry software program for exploring Euclidian (Srinivasan, 2012), analytic (Li, 2017), coordinate geometries (Chan and Leung, 2014), and other mathematics areas. In addition, GSP has different functions in actual teaching process. It also enables dynamic drawing, manipulation, measurement, and visualization of angle relationships (Roble, 2016).
Firstly, for graphing function, students can use many tools on the toolbar to construct complex geometric shapes (Roble, 2016). For example, students can use given conditions and Pythagorean theorem, then drag the auxiliary line and observe transformations of shapes to construct right triangles and rotations (Jiang, 2007).
Secondly, for parametric control function, students can set variables to modify parameters associated with the graph. Students can create a slider and associate it with attributes of a geometric object (e.g., length, angle, coordinates, etc.) (Poon and Wong, 2017). Additionally, GSP may allow synchronized adjustments to several parameters. For instance, students demonstrate the dynamics of the opening direction and vertex position of a quadratic function by manipulating parameters using the slider (Gyedu et al., 2020). These functions might be manipulated, analyzed, and processed into engaging learning experiences (Hartono, 2020). Through using GSP, students are likely to deepen their intuitive learning experiences, promote 3D visualization, and achieve a conceptual understanding of geometric content (Gyedu et al., 2020).
Then GSP might perform geometric transformation functions, including translation, reflection, and deflation. These dynamic operations visually enable students to observe the transformation of shapes. It is possible that students can choose objects in GSP and utilize buttons to modify and rotate entities (Poon and Wong, 2017). Consequently, students could observe distinct spatial relationships between lines and planes, analyzing the angle between two planes through different perspectives (Ganesan and Eu, 2020).
Finally, for data analysis and measurement functions, GSP supports the measurement of geometric properties, including angle size, area, and perimeter (Ganesan and Eu, 2020). For instance, when students learn complex functions like trigonometry, GSP can record dynamic data and display the pattern of function images (Leong, 2013). GSP can support the recording of real-time data and help students to complete mathematical measurements (Roble, 2016), and the data can be directly transformed into a grid view (Tat and Fook, 2005).
In conclusion, these functions synergistically complement each other, converting abstract mathematical concepts into intuitive operational experiences and improving students’ learning efficiency.
3.2 What the impact of GSP on students’ mathematical intelligence?
This section focuses on answering the impact of GSP on the six dimensions of mathematical intelligence of secondary school students. In this section, I will focus on two aspects, including geometric imagination and functional cognition.
3.2.1 Geometric imagination
In the existing literature, geometric imagination represents a unique cognitive ability to mentally modify geometric entities (Chvátal et al., 2024). It comprises the visual examination of spatial structures (Chvátal et al., 2024). In traditional teaching methods, teachers must invest a lot of effort in creating complex graphics on the blackboard, the shapes lack dynamism and accuracy (Li, 2017).
In addition, many students cannot appropriately describe fundamental shapes in three-dimensional space, resulting in challenges in comprehending the entirety of the curriculum (Tursynkulova and Madiyarov, 2023). In spatial geometry programs, students’ comprehension of geometric forms is confined to static two-dimensional plane figures, and they come up with inaccurate answers (Fujita et al., 2020). This constraint complicates the correlation of geometric questions with real-world situations (Ismail et al., 2020). GSP visualizes intricate spatial shapes (e.g., prisms and prismatic columns) using the dynamic modelling function. Students can better understand the structural features of geometric forms by flexibly rotating and modifying the viewing angle (Hartono, 2020). GSP presents geometry not merely as a collection of memorable axioms and theorems, but as an active domain of mathematics (Guerrero and Crites, 2013).
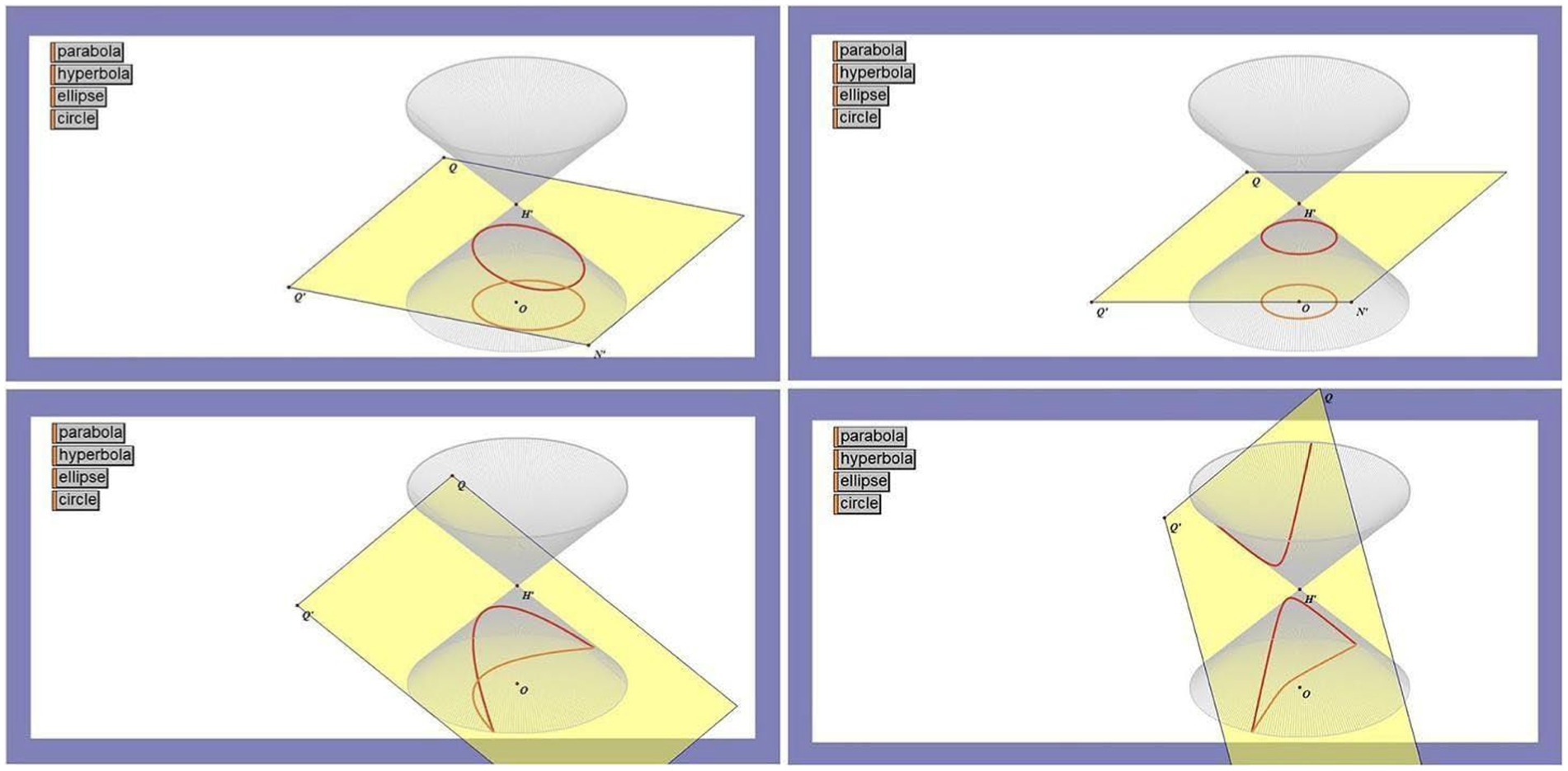
GSP’s dynamic characterization and parametric control features enhance the teaching and learning process. Students can observe translating, reflecting, and rotating geometric shapes (Li, 2017). For instance, students can utilize GSP to produce hyperbolic parabolic surfaces (see Figure 2).
When a plane of rotation intersects a hyperbolic plane, the intersecting lines of a section comprise four standard geometric figures. The resulting crossing lines are elliptical when a plane crosses a hyperbolic surface at a particular angle of inclination. In contrast, the intersecting lines of a hyperbolic surface become parabolic when a plane is parallel to the opening direction of one of it sleaves. Moreover, the intersection creates a circular line when a plane is parallel to the ground. On the other hand, it creates a hyperbolic line when a plane is parallel to the high line. Using GSP to construct geometric shapes, students can observe the intersecting lines produced by a three-dimensional figure and a cross-section (Fujita et al., 2020).
Teachers use GSP to promote students’ innovative thinking in addressing of intricate mathematical questions (Dhayanti et al., 2018). Students construct geometric forms, modify parameters, and observe dynamic transformations in geometric models (Poon and Wong, 2017). For example, when studying plane geometry problems, GSP replicates the trajectory of moving points and helps students transition from tangible to abstract relationships during observation (Tursynkulova and Madiyarov, 2023). Students are encouraged to progress through the first three van Hiele levels, moving from holistic visual thinking to property-based description and analysis. This developmental journey culminates in abstract relational thought, which enables students to utilize logical relationships between properties and classes of shapes (Battista, 2001).
Furthermore, the visualization feature of GSP displays geometric shapes and characteristics, improving the precision of drawing in teaching. Students use GSP to explore geometric relationships, construct, and apply mathematical content (Guerrero and Crites, 2013). Students become enthusiastic when learning patterns differ from traditional methods (Roble, 2016). Simultaneously, this teaching method can also cultivate their positive learning attitudes and beliefs (Ganesan and Eu, 2020). This visualization feature decreases the time students allocate to comprehend the question, while enhancing geometric orientation. Students can enhance comprehension of the questions, leading to a refined assessment of the needed time and effort (Fung and Poon, 2021). In this case, students swiftly understand the pattern of area transformations.
In conclusion, using GSP helps students develop logical reasoning and creativity. This teaching technique offers case studies for geometry education and serves as a reference for teachers seeking educational tactics.
3.2.2 Functional thinking
Functional thinking denotes the capacity to comprehend interrelationships between variables and procedures, coupled with the proficiency to articulate and examine complex mathematical problems through a functional analytical framework (Blanton and Kaput, 2011). This study promotes the study of functions via problem-solving, enabling students to investigate functional dependencies in non-algebraic domains and identify the characteristics of these dependencies (Tursynkulova and Madiyarov, 2023).
In traditional education, teachers used methods such as direct narration or writing on the blackboard and relied on static sketches that were disproportionate or distorted (Tat and Fook, 2005). Students may not conceptualize the graphs’ forms and lack a profound comprehension of their structures. In this case, GSP helps solve these problems. According to the dynamical features of GSP, students can explore variable fluctuations and function transformations, understand fundamental principles and develop models for problem-solving (Leong, 2013). This teaching method enhances students’ comprehension of the relationship between function variables while also cultivating their observational and logical reasoning abilities (Hoffkamp, 2011). By altering the parameters of the power function, students could summarize the shared attributes of the power function across various conditions.
For instance, when studying power functions where α < 0 in the first quadrant, the only function with α = −1, y = . This function alone cannot fully represent the characteristics of power functions with (α < 0) graphs of these functions. In the teaching process, students can study a variety of situations α= , y= ; α= 2, y= Students graph these three functions inside the same coordinate system on the GSP and analyze their shared characteristics in the first quadrant.
Furthermore, using GSP can promote students’ understanding of the complex relationships between mathematical functions (Kotu and Weldeyesus, 2022). For instance, while studying translation transformations of a quadratic function’s graph, students manipulate the slider to observe positional alterations of the function’s vertices (Gyedu et al., 2020). Through this interactive process, they simultaneously witness how these geometric changes correlate with modifications in the function’s analytical expression (Lagrange and Gelis, 2008). Moreover, teachers can help students to make connections between geometry and algebra by using GSP (Lagrange and Gelis, 2008). This dynamic manipulation renders abstract knowledge accessible and helps students in developing methodologies (Tursynkulova and Madiyarov, 2023). The latest version of GSP adds several features (e.g., built-in web integration) and improves example exploration and function manipulation (Leong, 2013). Consequently, GSP fosters a more efficient educational atmosphere for courses (Leong, 2013).
In addition, GSP enhances mathematical reasoning in students’ functional cognition. Using GSP helps students develop learning strategies, facilitates lesson organization, and communicates explicit information about learning objectives (Lagrange, 2005). Moreover, teachers had to contemplate both the potential for technological transformation and the facilitation of student cognition (Hoffkamp, 2011). For instance, dynamic transformations of parametric equations, the properties of composite functions and implicit functions.
The simplicity and visualization feature of GSP can help students understand concepts, develop problem-solving skills and increase motivation (Kotu and Weldeyesus, 2022). GSP is used to simulate real-world situations. Students abstract the relevant elements from the problem and set up different mathematical models of the function (Jones, 2000). Students can use GSP to create statistical modelling (Ganesan and Eu, 2020) and solve practical mathematical problems through functional relationships (Hoffkamp, 2011). Students will have the opportunity to learn mathematical formulas and calculations in the classroom and then apply the principles in real-life scenarios. In conclusion, the application of GSP enhances students’ functional cognition and promotes the transition of their thinking skills from concrete to abstract.
4 Conclusion
This paper defined mathematical intelligence and geometer sketchpad through a literature review, and to explore the specific implications for secondary school students around geometric imagery and functional cognition. This choice was based on the potential value of GSP in the field of education. In addition, this study analyzed two facets of mathematical intelligence, including geometric imagination and functional cognition. By following the PRISMA guidelines, I selected 26 articles based on three different keywords. The analysis revealed few studies focusing on the common areas of GSP and mathematical intelligence, but their research value is significant and has analytical potential. Studies had found that integrating GSP into mathematics education classrooms can enhance the learning efficiency and problem-solving skills of secondary school students.
In addition, I used GSP to draw four conic curves showing the intersection of planar and hyperbolic surfaces at different angles. Students could also graph and analyze the shared characteristics of various power functions. The first limitation of this paper was that the data comes from two databases, including Web of Science and Scopus. This led to the omission of important findings from the other databases. Future research should extend the database, such as Education Resources Information Center and China National Knowledge Infrastructure. This could provide a more diverse perspective on the research topic, reduce potential bias and improve the generalizability of the findings. Another limitation was that this study is mainly derived from analyses of existing literature and lacks primary data regarding the application of GSP for secondary school students. This limitation leads to a restricted scope of application and does not adequately verify the applicability of conclusions. In the future, researchers can choose different methods to collect data, including questionnaires, interviews, and classroom observations. Researchers were able to collect results based on students’ feedback and analyze subjective evaluations. Researchers could also use these methods to ensure the findings with the actual teaching and address deficiencies in current research.
Author contributions
YM: Conceptualization, Investigation, Methodology, Data curation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
The author would like to express sincere gratitude to Zhi Yang from Griggith University for his invaluable guidance and critical feedback throughout this research. Finally, I thank the reviewers and editors for their constructive comments and my families for their support during the study.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1593901/full#supplementary-material
References
Badr, H. M., and Abu-Ayyash, E. A. (2019). Semantic mapping or rote memorization: which strategy is more effective for students’ acquisition and memorization of L2 vocabulary? J. Educ. Learn. 8, 158–174. doi: 10.5539/jel.v8n3p158
Battista, M. T. (2001). Shape makers: a computer environment that engenders students' construction of geometric ideas and reasoning. Comput. Sch. 17, 105–120. doi: 10.1300/J025v17n01_09
Blanton, M. L., and Kaput, J. J. (2011). Functional thinking as a route into algebra in the elementary grades. Early Algebraiz. 37, 5–21. doi: 10.1007/BF02655895
Chan, K. K., and Leung, S. W. (2014). Dynamic geometry software improves mathematical achievement: systematic review and meta-analysis. J. Educ. Comput. Res. 51, 311–325. doi: 10.2190/EC.51.3.c
Chvátal, R., Slezáková, J., and Popelka, S. (2024). Analysis of problem-solving strategies for the development of geometric imagination using eye-tracking. Educ. Inf. Technol. 29, 12969–12987. doi: 10.1007/s10639-023-12395-z
Chytrý, V., Říčan, J., Eisenmann, P., and Medová, J. (2020). Metacognitive knowledge and mathematical intelligence—two significant factors influencing school performance. Mathematics 8, 1–18. doi: 10.3390/math8060969
Delarue, F. (2002). On the existence and uniqueness of solutions to FBSDEs in a non-degenerate case. Stoch. Process. Their Appl. 99, 209–286. doi: 10.1016/S0304-4149(02)00085-6
Dhayanti, D., Johar, R., and Zubainur, C. M. (2018). Improving students’ critical and creative thinking through realistic mathematics education using geometer’s sketchpad. Res. Adv. Math. Educ. 3, 25–35. doi: 10.23917/jramathedu.v3i1.5618
Duckworth, E. (1964). Piaget rediscovered. The Arithmetic Teacher 11, 172–175. doi: 10.5951/AT.11.7.0496
Emmert-Streib, F., and Dehmer, M. (2010). Causality: using math to understand the science of cause and effect. Front. Young Minds 8, 1–6. doi: 10.3389/frym.2023.1155100
Fujita, T., Kondo, Y., Kumakura, H., Kunimune, S., and Jones, K. (2020). Spatial reasoning skills about 2D representations of 3D geometrical shapes in grades 4 to 9. Math. Educ. Res. J. 32, 235–255. doi: 10.1007/s13394-020-00335-w
Fung, C. H., and Poon, K. K. (2021). Can dynamic activities boost mathematics understanding and metacognition? A case study on the limit of rational functions. Int. J. Math. Educ. Sci. Technol. 52, 1225–1239. doi: 10.1080/0020739X.2020.1749905
Ganesan, N., and Eu, L. K. (2020). The effect of dynamic geometry software geometer’s sketchpad on students’ achievement in topic circle among form two students. Malays. Online J. Educ. Technol. 8, 58–68. doi: 10.17220/mojet.2020.02.005
Guerrero, S., and Crites, T. (2013). Technology in an online graduate mathematics education program. Comput. Sch. 30, 191–206. doi: 10.1016/j.stueduc.2016.10.002
Gyedu, A. A., Owusu-Darko, I., and Ofosu, E. K. (2020). Effect of geometer’s sketchpad on senior high school students’ performance in quadratic graphing. Eur. J. Educ. Pedagog. 1, 105–120. doi: 10.24018/ejedu.2020.1.1.4
Hartono, S. (2020). Effectiveness of geometer’s sketchpad learning in two-dimensional shapes. Math. Teach. Res. J. 12, 84–93.
Hoffkamp, A. (2011). The use of interactive visualizations to foster the understanding of concepts of calculus: design principles and empirical results. ZDM Int. J. Math. Educ. 43, 359–372. doi: 10.1007/s11858-011-0322-9
Host’ovecký, M., Huraj, L., and Pribilova, K.. (2019). Virtual reality in mathematics: design of the serious game improves spatial imagination performance. 2019 17th International Conference on Emerging Learning Technologies and Applications (ICETA).
Ismail, H., Abdullah, A. H., Syuhada, N., and Noh, N. (2020). Investigating student’s learning difficulties in shape and space topic: a case study. Int. J. Psychosoc. Rehabil. 24, 5315–5321. doi: 10.37200/IJPR/V24I5/PR2020238
Jiang, Z. (2007). The dynamic geometry software as an effective learning and teaching tool. Electr. J. Math. Technol. 1, 245–257. doi: 10.7870/ejmt.v1i3.4
Jones, K. (2000). Providing a foundation for deductive reasoning: students’ interpretations when using dynamic geometry software and their evolving mathematical explanations. Educ. Stud. Math. 44, 55–85. doi: 10.1023/A:1012789201736
Kotu, A., and Weldeyesus, K. M. (2022). Instructional use of geometer’s sketchpad and students geometry learning motivation and problem-solving ability. J. Math. Educ. 15, 45–62. doi: 10.29333/ejmste/12710
Lagrange, J.-B. (2005). Curriculum, classroom practices, and tool design in the learning of functions through technology-aided experimental approaches. Int. J. Comput. Math. Learn. 10, 143–189. doi: 10.1007/s10758-005-4850-7
Lagrange, J.-B., and Gelis, J.-M. (2008). The casyopee project: a computer algebra systems environment for students’ better access to algebra. Int. J. Contin. Eng. Educ. Life Long Learn. 18, 575–584. doi: 10.1504/IJCEELL.2008.022164
Lee, C.-Y., Lei, K. H., Chen, M.-J., Lee, C.-R., and Chen, C.-C. (2023). Helping low-achieving students to comprehend the area of basic geometric shapes using an enclosing-rectangle scaffold via computer-assisted instruction. Cogent Educ. 10, 1–14. doi: 10.1080/2331186X.2023.2277576
Leong, K. E. (2013). Impact of geometer’s sketchpad on students’ achievement in graph functions. Malays. Online J. Educ. Technol. 1, 19–33. doi: 10.46300/9103.2022.3.10
Li, X. Let high school math teaching plug in the wings--the practice and research of the geometer’s sketchpad in high school mathematics teaching. 2017 3rd International Conference on Economics, Social Science, Arts, Education and Management Engineering (ESSAEME 2017), (2017), 1–3.
Meng, C. C., and Sam, L. C. (2011). Encouraging the innovative use of geometer’s sketchpad through lesson study. Creat. Educ. 2, 236–243. doi: 10.4236/ce.2011.23032
Neimark, Y. I., and Teklina, L. (2012). On possibilities of using pattern recognition methods to study mathematical models. Comput. Math. Math. Phys. 52, 1–10. doi: 10.1134/S1054661812010282
Nilimaa, J. (2023). New examination approach for real-world creativity and problem-solving skills in mathematics. Trends High. Educ. 2, 477–495. doi: 10.3390/higheredu2030028
Nurhasanah, F., Kusumah, Y., Sabandar, J., and Suryadi, D. (2017). Mathematical abstraction: constructing concept of parallel coordinates. J. Phys. Conf. Ser. 895, 1–6. doi: 10.1088/1742-6596/895/1/012076
Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., et al. (2021). The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. BMJ 372:n71. doi: 10.1136/bmj.n71
Poon, K. K., and Wong, K. L. (2017). Pre-constructed dynamic geometry materials in the classroom –how do they facilitate the learning of ‘similar triangles’? Int. J. Math. Educ. Sci. Technol. 48, 735–755. doi: 10.1080/0020739X.2016.1264636
Roble, D. B. (2016). The geometer’s sketchpad: a technological tool enhancing junior high school students’ mathematics achievement, attitude towards mathematics and technology. Am. J. Educ. Res. 4, 1116–1119. doi: 10.12691/education-4-15-10
Srinivasan, V. (2012). The characterizations of triangles using the nine-point circles. Int. J. Math. Educ. Sci. Technol. 43, 972–982. doi: 10.1080/0020739X.2011.644334
Tat, T. B., and Fook, F. S. (2005). The effects of geometer’s sketchpad and graphic calculator in the Malaysian mathematics classroom. Malaysian Online J. Instr. Technol. 2, 82–96. doi: 10.13140/RG.2.1.3580.8880
Tursynkulova, E., and Madiyarov, N. (2023). Applying dynamic geometry environment software as a visualization tool for teaching planimetry construction tasks. Int. J. Inf. Educ. Technol. 13, 1950–1958. doi: 10.18178/ijiet.2023.13.12.2009
Tyagi, T. K. (2017). Mathematical intelligence and mathematical creativity: a causal relationship. Creat. Res. J. 29, 212–217. doi: 10.1080/10400419.2017.1303317
Keywords: geometry sketchpad, mathematical intelligence, secondary school students, geometric imagination, functional cognition
Citation: Ma YF (2025) The effect of geometer sketchpad on secondary school students’ mathematical intelligence. Front. Educ. 10:1593901. doi: 10.3389/feduc.2025.1593901
Edited by:
Amna Mirza, University of Delhi, IndiaReviewed by:
Ralf J. Braun, Danube Private University, AustriaCopyright © 2025 Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yu Fei Ma, WVhNNDQxQHN0dWRlbnQuYmhhbS5hYy51aw==
 Yu Fei Ma
Yu Fei Ma