Ways of thinking about teaching an idea in mathematics: how teachers’ mathematical meanings for teaching ideas impact their instructional practices

Despite decades of reform efforts, many mathematics teachers continue to struggle with implementing instruction that supports deep mathematical understanding and meaningful student engagement. This case study demonstrates how professional development targeting teachers’ mathematical meanings for teaching can transform instructional practice in K-12 algebra. Tracy, an Algebra II teacher, participated in professional development focused on quantitative reasoning while implementing research-based curriculum materials. Through classroom observations, interviews, and artifact analysis, the study shows how quantitative reasoning functioned as (1) a productive framework for analyzing teachers’ mathematical meanings for teaching algebraic concepts, (2) an effective target for professional development that supports teachers in constructing pedagogically powerful mathematical understandings, (3) a vehicle enabling teacher decentering, and (4) a foundation for classroom instruction emphasizing meaningful quantitative relationships. Data were analyzed through the frameworks of mathematical meanings for teaching and ways of thinking about teaching an idea. Findings suggest that professional development addressing teachers’ mathematical meanings, combined with curriculum supporting student reasoning and ongoing classroom support, can produce significant changes in instructional practice that create high-quality learning opportunities for students.

1 Introduction

Over the last few decades, mathematical organizations have prioritized publishing new content and teaching standards documents to provide guidance for improving the quality of students’ mathematical experiences [e.g., Mathematical Association of America (2018), National Council of Teachers of Mathematics (2000), and National Governors Association Center for Best Practices, Council of Chief State School Officers (2010)]. These documents call for inquiry-based teaching featuring deep engagement with mathematics, a focus on coherence across lessons and modules, and creating a positive classroom environment that supports developing students’ mathematical curiosity, confidence, enjoyment, and persistence. Despite these calls, many students still experience math classes that fall short of these goals at all grade levels. Studies continue to show U. S. teachers struggling to move away from direct instruction and teacher-demonstrated algorithms (e.g., Boston (2012), Litke (2020), Schoenfeld (2022), and Stockero et al. (2020a)], highlight the deficiencies of mathematics curricula in developing powerful mathematical ideas [e.g., Frank and Thompson (2021)], and call into question the learning goals instructors choose to assess and value [e.g., Tallman et al. (2016, 2021)]. These findings coincide with both the Programme for International Student Assessment (PISA) and the National Assessment of Educational Progress (NAEP) showing declining student mathematical performance and a widening achievement gap among American students (The National Center for Education Statistics, 2025; Organization for Economic Co-operation and Development, 2023). This persistent gap between reform intentions and classroom realities highlights the critical role professional development must play to support the kinds of instructional changes needed to improve the quality of students’ mathematical learning opportunities.

This paper addresses these persistent challenges by examining how professional development can transform mathematics teaching when it focuses on supporting teachers in developing pedagogically powerful mathematical meanings for teaching. Specifically, this case study explores how professional development targeting teachers’ understanding of quantitative and covariational reasoning (see Section 3.3) can serve as a vehicle for developing the kinds of mathematical meanings for teaching that support high-quality instruction. While this study focuses on quantitative reasoning as the specific set of targeted mathematical ideas, the broader principle being investigated is how professional development that systematically addresses teachers’ mathematical meanings, combined with a coherent curriculum and ongoing support, can produce fundamental changes in instructional practice. The quantitative reasoning focus provides a concrete lens through which to examine the mechanisms by which teachers’ mathematical understandings become pedagogically powerful and influence the quality of learning opportunities they create for students.

This study was guided by the following research questions. Note that key terms in these questions (such as quantitative reasoning and mathematical meanings for teaching) will be unpacked within this paper.

1. How does professional development focused on quantitative reasoning influence a secondary mathematics teacher’s instructional practice?

2. What role does decentering play in a teacher’s development of pedagogically powerful mathematical meanings?

3. How do a teacher’s mathematical meanings for teaching manifest in the quality of learning opportunities provided to students?

2 Literature review and research frameworks

The following literature review establishes the theoretical foundation for this case study by examining four interconnected areas: (1) research on professional development effectiveness and its persistent challenges, (2) frameworks for understanding teachers’ specialized mathematical knowledge, (3) theoretical constructs that explain how teachers’ mathematical meanings influence instruction, and (4) the specific role of quantitative reasoning in mathematics education. This review demonstrates that while researchers have identified characteristics of effective professional development and teaching practices, fewer studies have examined the mechanisms by which teachers’ mathematical understandings become pedagogically powerful. The frameworks presented here provide the theoretical lens for understanding how professional development focused on mathematical meanings can transform teaching practice.

2.1 Professional development

Research on mathematics teacher professional development has revealed both promising practices and persistent challenges. Large-scale studies consistently identify key characteristics of effective professional development, such as a focus on content, active learning, coherence with other reform efforts, sufficient duration, and collective participation (Darling-Hammond and Sykes, 1999; Darling-Hammond et al., 2017; Desimone, 2009). Other researchers have reinforced these findings while adding nuanced understanding of implementation factors. Lee and Vongkulluksn (2022) emphasized that effective professional development must be embedded in teachers’ daily practice and connected to their specific contexts, while Kennedy (2016) highlighted the importance of inquiry-based approaches, teacher agency, and teacher motivation in professional development.

However, Yoon et al.’s (2007) meta-analysis revealed that many professional development programs show minimal impact on teaching practice or student learning, a pattern later research supported. Kraft et al. (2018) conducted a comprehensive meta-analysis of teacher coaching interventions and found that while coaching can be effective, the average effect sizes are modest and highly variable across contexts. Similarly, a randomized controlled trial of a widely used mathematics professional development program found no significant effects on student achievement despite substantial investment in teacher training (Jacob et al., 2017). Several factors contribute to these disappointing outcomes, including insufficient attention to teachers’ existing beliefs and knowledge (Opfer and Pedder, 2011), lack of alignment between professional development goals and school accountability pressures (Coburn and Russell, 2008), and the challenge of scaling effective models while maintaining quality (Domitrovich et al., 2008).

Studies specifically focused on mathematics professional development have revealed additional complexities. Sztajn et al. (2017) found that teachers’ mathematical knowledge for teaching improved following professional development, but these gains did not consistently translate into changes in classroom practice or student learning. Work by Hill and Charalambous (2012) and Carlson et al. (2024a) suggests that the relationship between teacher knowledge and practice is mediated by factors such as curriculum materials, school culture, and administrative support, highlighting the need for systemic approaches to professional development. These perspectives suggest that effective professional development requires attention not only to what teachers learn, but to how that learning is supported within the broader educational system.

One reason for the limited success of many professional development programs may be that they are not strongly grounded in theories of teacher learning (how teachers construct, modify, and apply professional knowledge in classroom contexts). As Kennedy (2016) noted, “Education research is at a stage in which we have strong theories of student learning, but we do not have well-developed ideas about teacher learning, nor about how to help teachers incorporate new ideas into their ongoing systems of practice” (p. 29). This gap highlights the need for professional development approaches that are explicitly grounded in understanding how teachers learn and change their practice.

2.2 Mathematical knowledge for teaching and professional noticing

Mathematical knowledge for teaching (MKT) and professional noticing of students’ mathematical thinking are research areas that can inform professional development efforts. MKT is an extension of Shulman (1986, 1987) work on pedagogical content knowledge (PCK) applied to mathematics education (Ball et al., 2001, 2008; Kahan et al., 2003; Hill et al., 2005, 2008; Silverman and Thompson, 2008; Tallman, 2023). Researchers examining MKT have helped emphasize issues in teacher preparation programs and professional development training by highlighting the disconnect between the kinds of specialized mathematical knowledge teachers need compared to the kinds of mathematical knowledge emphasized in their university courses and professional training. They have also produced categories of both subject matter knowledge and PCK that make up a teacher’s MKT and have developed assessments for measuring aspects of teachers’ MKT. Research studies [e.g., Hill et al. (2005)] have also demonstrated a positive correlation between a teacher’s MKT (as assessed by their instruments) and students’ mathematical achievement.

A teacher’s professional noticing of students’ mathematical thinking refers to their attention to students’ thinking and attempts to make sense of and respond to products students generate. These products include their verbal responses, explanations, and written work [e.g., Jacobs et al. (2010, 2024), Sherin et al. (2010), Stockero et al. (2017, 2020a, 2020b), Stockero and Stenzelbarton (2017), and Van Es and Sherin (2002, 2006, 2008)]. Professional noticing studies claim that “professional noticing of children’s mathematical thinking is challenging and not something that adults routinely know how to do” (Jacobs et al., 2010, p. 191), but also that increased noticing of students’ mathematical thinking can improve the quality of students’ mathematical experiences and learning.

Both MKT and professional noticing studies can provide guidance for mathematics teacher professional development. Professional noticing is a teaching practice intended to foreground students’ contributions to mathematics lessons and discussions. Professional noticing researchers have designed tools to assess a teacher’s skills in various aspects of noticing and to provide guidance for improving teachers’ practice to positively impact student learning. Similarly, researchers studying MKT have examined how effective teachers interact with students during lessons and know how they respond productively to students’ contributions.

2.3 Frameworks relevant to this study

As mentioned earlier, while researchers have identified elements of professional development that lead to higher success in impacting teacher success, many professional development programs fail to produce positive results. One reason may be that many professional development programs and research areas such as MKT and professional noticing are not strongly grounded in theories of learning. As Kennedy (2016) noted, “Education research is at a stage in which we have strong theories of student learning, but we do not have well-developed ideas about teacher learning, nor about how to help teachers incorporate new ideas into their ongoing systems of practice” (p. 29) In this section, I discuss the complexities of shifting teachers’ meanings and practices and describe frameworks that characterize mechanisms for supporting teachers’ learning and teaching practices.

2.3.1 The didactic triad

To understand why professional development interventions may not significantly impact student learning outcomes, we can consider the complexity of teaching via Thompson’s (2009) didactic triad. The didactic triad is a framework that attempts to capture the interconnected nature of teachers’ mathematical meanings, models of students’ mathematical meanings, student learning goals, and their instructional tools and practices (Figure 1). The triad highlights the interdependency of these elements and why shifting teachers’ effectiveness is challenging. Professional development approaches that address only a subset of these elements (such as training teachers on active learning strategies without addressing learning goals or classroom tasks or providing training on new curriculum materials without addressing a teacher’s underlying mathematical meanings) can fail to produce substantive, lasting change (Stigler and Hiebert, 2009). This observation aligns with broader research on teacher change, which emphasizes that sustainable reform requires coherent approaches that address teachers’ knowledge, fundamental beliefs about mathematics and learning, and practices simultaneously [e.g., Clark and Hollingsworth (2002) and Guskey (2002)].

Figure 1

Figure 1. The didactic triad. Note that this was first formally presented by Thompson (2009) but emerged through discussion and collaboration with Carlson, Oehrtman, Moore, Ström, O’Bryan, and their colleagues working in the Pathways research project [see Carlson et al. (2024b)].

2.3.2 Mathematical meanings for teaching and decentering

Silverman and Thompson (2008) and others building on their work [e.g., Carlson et al. (2024a), Rocha (2023), Tallman (2021, 2023), and Thompson (2013, 2016)] have argued that MKT frameworks have not yet addressed at least three important topics critical to shifting teachers’ practice in ways that positively impact student learning. (i) They do not explain how a teacher might develop the special knowledge structures they identify grounded in a theory of how teachers learn. (ii) They do not describe mathematical meanings they conjecture to be necessary for shifting teachers’ instruction to focus on students’ thinking and advancing students’ understandings. (iii) Related to point (ii) and to limitations in research on professional noticing, MKT studies do not typically collect data on and analyze the mathematical meanings participating teachers possess with the goal of linking those meanings with teachers’ pedagogical actions. Further investigation is needed into how a teacher’s mathematical meanings influence such things as their learning goals, choice of curriculum, and the nature of their questions and explanations. It is these decisions and choices that determine potential learning opportunities for students.

Following calls from Silverman and Thompson (2008), researchers such as Thompson (2013, 2016), Baş-Ader and Carlson (2022), Carlson et al. (2024a), and Rocha (2023) have leveraged the construct of mathematical meanings for teaching (MMT) (Thompson, 2013, 2016) to investigate the meanings teachers hold relative to specific ideas and how these meanings influence their instructional decisions. Researchers following this line of inquiry have argued for the need to ground mathematics education research such as MKT and professional noticing in a robust theory of how individuals construct knowledge with an increased focus on “the system of meanings by which the teacher [operates]” (Thompson, 2013, p. 79–80). This is a critical focus if the goal is to help students construct coherent and useful mathematical meanings themselves (Rocha, 2023; Silverman and Thompson, 2008; Tallman, 2023; Thompson, 2013, 2016). A focus on modeling the meanings teachers hold for specific ideas and studying their influences on a teacher’s pedagogical actions allows researchers to make conjectures about links between a teacher’s meanings and their instructional decisions, both when planning for and when delivering instruction (refer back to Figure 1). It is then possible to identify meanings that might lead to more productive learning experiences for students, to design professional development aimed at supporting teachers in developing those meanings and leveraging those meanings to drive pedagogical actions.

Thompson (2013, 2016) clarified MMT as the construct that refers to the meanings a teacher possesses (which could be potentially productive or potentially unproductive, coherent or incoherent, valid or inconsistent with the field’s norms, and so on) and used MKT to refer to the MMT that have been transformed into meanings with pedagogical power. This transformation of personal mathematical knowledge into pedagogically powerful knowledge occurs primarily through decentering (Baş-Ader and Carlson, 2022; Carlson and Baş-Ader, 2019; Carlson et al., 2007, 2024a; Rocha, 2021, 2022; Rocha and Carlson, 2020; Silverman and Thompson, 2008; Teuscher et al., 2016), a process by which teachers inquire about and attempt to understand a student’s thinking. A teacher’s decentering actions typically begin when a teacher demonstrates an interest in how a student is thinking (Baş-Ader and Carlson, 2022). As teachers repeatedly inquire about how their students are thinking they become better at designing learning experiences that are effective in advancing students’ learning. Note that decentering can be thought of as a type of noticing, but differs in that decentering involves actively engaging in describing the mental actions of another.

2.3.3 Ways of thinking about teaching an idea

The concept of MMT emerged over several years and through several works by various researchers. Carlson et al. (2024a) summarized and extended this work in their framework for ways of thinking about teaching an idea, which describes how teachers who have developed pedagogically powerful MMT plan and deliver instruction on specific mathematical concepts. This framework suggests that effective mathematics teaching requires instructors to develop conscious awareness of their own mathematical meanings, construct models of various ways students might understand mathematical ideas, and use these insights to design and adapt instruction in real time. A teacher’s way of thinking about teaching an idea can evolve over time, particularly when the teacher regularly reflects on the impact of their teaching and attempts to decenter relative to students’ thinking. See Figure 2. I will briefly describe the various elements in this framework, but for a more detailed explanation see Carlson et al. (2024a).

Figure 2

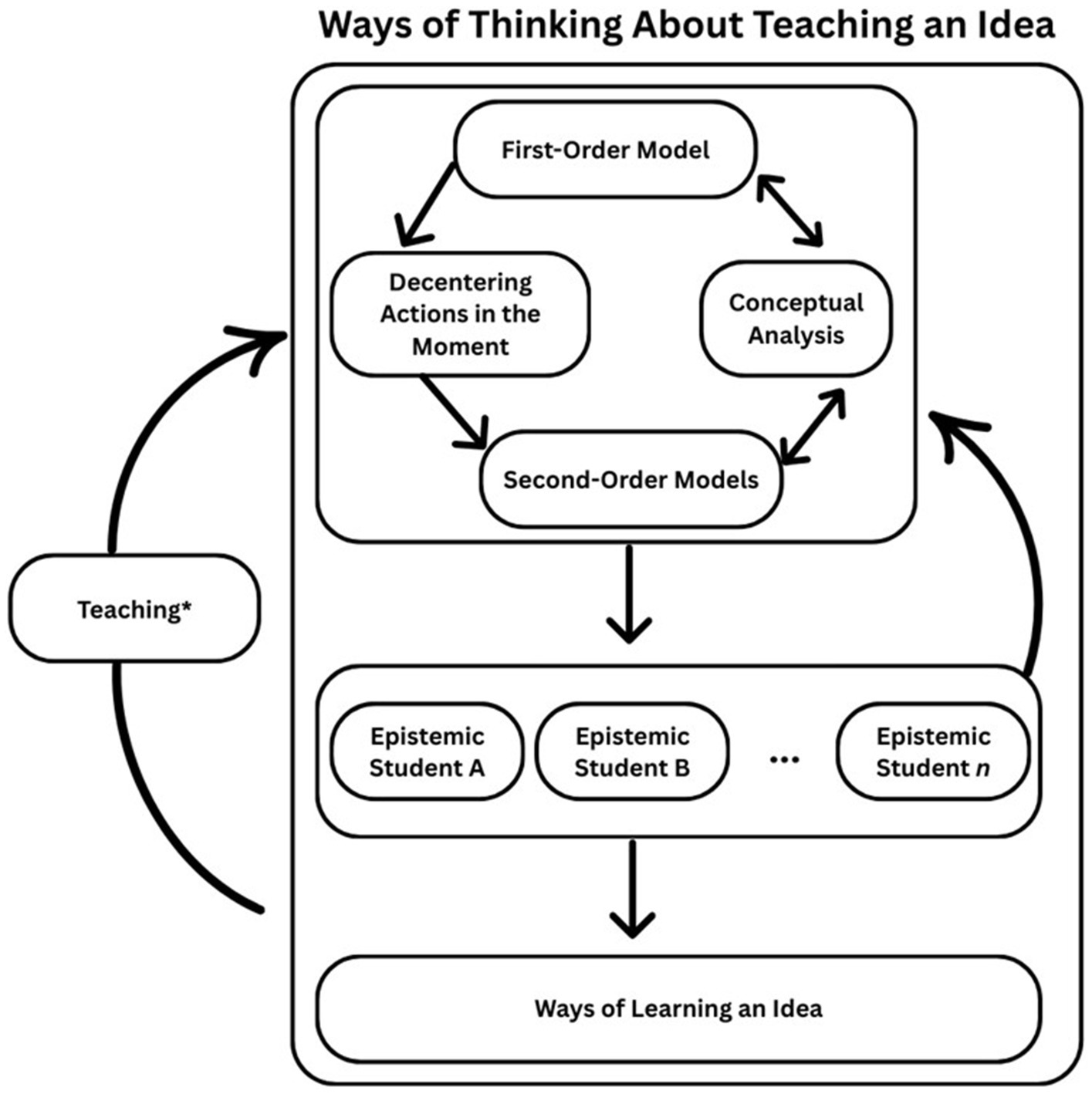
Figure 2. Carlson et al. (2024a) framework for a way of thinking about teaching an idea in mathematics (p. 316).

According to this framework, teachers develop productive ways of thinking about teaching an idea through an iterative process of decentering and reflection. A first-order model (Steffe, 1995; Steffe et al., 1983; Steffe and Thompson, 2000; Thompson, 2000) describes the teacher’s personal mathematical meanings for the idea being taught. Importantly, teachers must have conscious awareness of these meanings to leverage them pedagogically (Tallman, 2021; Tallman and Frank, 2020; Tallman et al., 2024). This requirement for conscious awareness discounts that teachers can effectively teach concepts they understand only tacitly or procedurally. Second-order models (Steffe, 1995; Steffe et al., 1983; Steffe and Thompson, 2000; Thompson, 1982, 2000) describe the teacher’s hypotheses about students’ mathematical meanings, constructed through experience and decentering. The quality of these models depends heavily on teachers’ ability to recognize and distinguish mathematical thinking different from their own and on their conceptual analysis (Thompson, 2008). Conceptual analysis involves the teacher’s systematic reflection on the mathematical idea itself, considering issues such as what mental operations are required to understand it, how it connects to other ideas, and what makes it difficult or accessible for learners.

When teachers have developed conscious awareness of their own meanings and mental models of a variety of ways students understand the concept (and related concepts), they are positioned to construct generalized models of common meanings students possess for the idea (both productive and unproductive). These models are called epistemic students (Thompson, 2002), or epistemic ways of understanding. By considering epistemic students as well as the results of their conceptual analysis of the idea at hand, teachers can conceptualize ways of learning an idea, which includes how to construct learning activities that address, build on, or attempt to modify these meanings. The act of teaching, with interactions informed by their learning goals and images of epistemic students, then provides new data for additional iterations of reflection, decentering, and conceptual analysis that feeds into the iterative process of further developing the teacher’s ways of thinking about teaching the idea.

2.4 Summary

If teachers’ mathematical meanings are central to the quality of instruction they provide, then effective professional development must address these meanings directly. For example, Carpenter et al. (1989) demonstrated that interventions targeting teachers’ understanding of mathematical concepts and student thinking patterns produced measurable improvements in both teaching quality and student achievement. Programs that focus primarily on curriculum implementation, general pedagogical strategies, or even advanced mathematical content may fail to help teachers develop the specific kinds of mathematical meanings that support high-quality instruction.

The MMT and ways of thinking about teaching an idea frameworks have significant implications for professional development. The frameworks suggest that professional development should support teachers in transforming their personal mathematical meanings into pedagogically powerful ones through sustained practice in decentering and reflection on their own and their students’ mathematical meanings. This might involve analyzing student work, reflecting on classroom interactions, and explicitly considering the implications of different mathematical meanings on future learning. As is illustrated in the didactic triad (Figure 1), it is useful to emphasize that what teachers notice about students’ mathematical meanings depend not just on their own mathematical meanings (what they are primed to notice), but also on the nature of their learning goals, pedagogical actions, and classroom tasks that comprise their lessons. For example, a teacher who approaches teaching operations with fractions by demonstrating examples, giving students practice problems similar to the worked examples, and prioritizing accurate calculations is not creating opportunities to gather information about students’ meanings for fractions outside of calculational performance. The images of epistemic students they construct will be shallow and focused on classes of procedural behaviors, and their opportunities will be limited for updating their first-order models to be more robust and coherent relative to other mathematical ideas. It is when teachers intentionally begin to foreground students’ mathematical reasoning that opportunities arise for teachers to deepen their MMT and transform their MMT into meanings with real pedagogical power. Supporting teachers in making this shift requires attention to the teacher’s personal mathematical meanings, their student learning goals, the mathematical tasks they utilize, and their teaching practices. Otherwise, as Stigler and Hiebert (2009) noted, “[t]he system assimilates individual changes and swallows them up” (p. 98).

3 The study

3.1 Study overview

This paper reports on a case study of Tracy, a secondary mathematics teacher who participated in professional development based on the ways of thinking about teaching an idea framework with a focus on developing Tracy’s quantitative, covariational, and algebraic reasoning skills (see Section 3.3) and preparing her to teach with the Pathways Algebra II materials (Carlson and O’Bryan, 2014) that have similar learning goals for students. Tracy participated in one year of training through bimonthly professional learning community meetings. The following fall semester she taught using research-based curriculum materials while receiving ongoing professional development support, classroom observations, and targeted feedback. The study examined Tracy’s evolving understanding of key mathematical ideas, her developing ability to notice and respond to student thinking, and the impact on her instructional practices as evidenced through classroom observations and interview data. The analysis is framed by the theoretical constructs of mathematical meanings for teaching, decentering, and ways of thinking about teaching an idea.

3.2 Methods

The goal of this research was to provide an in-depth examination of how professional development focused on mathematical meanings for teaching can influence instructional practice, using quantitative reasoning as a specific content focus to understand these mechanisms (see Section 3.3). While not necessarily providing findings that automatically generalize to all professional development contexts, this case study provides documentation of the processes by which teacher change occurs when professional development systematically addresses the mathematical meanings teachers hold and use in instruction., this case study aimed to (i) provide detailed documentation of one teacher’s instructional practices after training focused on quantitative reasoning while implementing research-based curriculum materials, (ii) examine the role of decentering in transforming teachers’ personal mathematical knowledge into pedagogically powerful knowledge, and (iii) investigate how teachers’ mathematical meanings impact the quality of learning opportunities provided to students. The analysis is grounded in Carlson et al.’s (2024a) framework of ways of thinking about teaching an idea, offering concrete examples of how this theoretical framework can illuminate the mechanisms of effective professional development.

3.2.1 Research design, participant, and setting

This study employed a longitudinal case study design (Yin, 2018) to examine how professional development focused on mathematical meanings for teaching influenced one secondary mathematics teacher’s instructional practice. Case study methodology was appropriate for this investigation because it enabled deep examination of the complex processes involved in teacher change within the authentic context of classroom practice (Tisdell et al., 2025). The study was conducted as part of the larger Pathways Project, an NSF-funded research program examining approaches to improving secondary STEM teaching through professional development and curriculum innovation (see Carlson et al., 2024b). This paper reports specifically on data collected during one semester of intensive work with Tracy (pseudonym), an Algebra II teacher at a large suburban secondary school in the Southwestern United States.

Tracy was selected based on her willingness to participate in extended professional development, use research-based curriculum materials in her Algebra II class (of 28 students), and allow regular classroom observations. At the time of the study, Tracy had been teaching mathematics for eight years and held a bachelor’s degree in secondary mathematics teaching. Tracy’s school had a population of about 1,200 students with 38% minority enrollment and a school-wide math proficiency of 43%. Tracy provided informed consent for all data collection activities. Student consent was obtained for classroom observations, with seating arrangements modified to ensure that the one non-consenting student did not appear in video recordings. Their participation was redacted from video recordings, transcripts, and data analysis. All participants’ names were replaced with pseudonyms or numbers.

3.2.2 The professional development intervention

During the previous school year, Tracy participated in a year-long intervention consisting of monthly two-hour professional learning community meetings. These meetings focused on helping teachers see mathematical ways of thinking that united various topics in their courses and could be used as key focal points to bring greater coherence to their instruction. Teachers were also supported in working together in a lesson design study (Stigler and Hiebert, 2009). Prior to the subsequent fall semester when data was collected, Tracy participated in an intensive two-day summer workshop with activities designed to support her in constructing productive personal meanings related to quantitative reasoning, covariational reasoning, and representational equivalence in an Algebra II course (see Section 3.3). The workshop was explicitly aligned with features of the Pathways Algebra II research-based curriculum materials (Carlson and O’Bryan, 2014), designed to engage students in quantitative reasoning while providing teachers with opportunities to observe and respond to student thinking. Throughout the semester, Tracy participated in five individual professional development sessions that combined clinical interviews about Tracy’s mathematical meanings and her observations of her students’ thinking along with professional development targeting upcoming ideas in the course and how they built on ideas Tracy had already taught. These sessions were scheduled approximately every three weeks and lasted about 90 min each.¹

The curriculum served multiple functions beyond providing activities for students. For example, it provided models for the kinds of mathematical discussions the professional development promoted and generated artifacts of student reasoning for Tracy to analyze. Without this coherent system, Tracy’s developing mathematical meanings might not have translated into productive changes in her classroom practice.

3.2.3 Data collection and analysis

Data collection occurred over one full semester (August–December) and included multiple sources. Five complete class lessons were video recorded throughout the semester, with observations strategically scheduled to capture Tracy’s teaching at different points in the semester. Each observation lasted the full 65-min class period. All five individual interview/training sessions with Tracy were also video recorded with the camera focused on the table to capture anything Tracy wrote or showed. Transcripts were also created for each classroom observation and interview/training session. Student work samples, lesson plans, and Tracy’s written reflections were collected throughout the semester for analysis. Finally, brief conversations with Tracy before and after observed lessons were documented through field notes.

Data analysis followed an iterative process of open coding (Corbin and Strauss, 1990) with particular attention to evidence of Tracy’s evolving mathematical meanings and teaching practices. Video recordings, transcripts, and reflections were coded to capture instances of (i) Tracy explicitly expressing her mathematical meanings and learning goals, (ii) observable behaviors implying Tracy’s mathematical meanings and learning goals, (iii) observable behaviors in line with elements of reasoning quantitatively related to algebraic expressions (see Table 1 in Section 3.3), (iv) evidence of decentering behaviors, and (v) characteristics of her responses to students’ contributions and work. Codes were analyzed across time to identify patterns in Tracy’s development particularly moments that suggested shifts in her mathematical meanings, learning goals, or instructional practices. Summaries of each lesson and interview/training session were produced to characterize the quality of mathematics in the lesson, the character of the mathematical discussions, and Tracy’s responsiveness to student contributions. The coded lessons and summaries were then analyzed through the lens of the ways of thinking about teaching an idea framework to understand the mechanisms underlying Tracy’s growth. Whenever possible, key interpretations were shared with Tracy during later professional development sessions. The goal was to verify the accuracy of interpretations and gather additional insights about her thinking. For example, in Section 4.2 details are shared of a lesson Tracy designed for the exponential functions module. During this lesson Tracy deviated from the printed curriculum materials and designed her own lesson tasks that created a lesson that unfolded similarly to one of the training sessions. This move was particularly noteworthy, leading to follow-up questions and activities designed to better understand her learning goals and what she learned about her students’ thinking during this lesson.

Table 1

Table 1. Elements of reasoning quantitatively related to creating and interpreting algebraic representations.

3.3 Quantitative and covariational reasoning and their role as learning goals

Quantitative and covariational reasoning are foundational ways of thinking about mathematical relationships in ways that are productive particularly for the algebra to calculus pipeline. It is important to elaborate on this way of thinking because developing Tracy’s quantitative and covariational reasoning skills was a key goal of the professional development intervention, developing students’ quantitative and covariational reasoning skills is a key goal and unifying theme in the curriculum materials Tracy used, and observations of Tracy’s teaching show strong evidence that Tracy conceptualized her lesson goals and engaged in decentering actions grounded in this reasoning.

Quantitative reasoning, as described by Thompson (1990, 2011), involves conceptualizing situations in terms of quantities (measurable attributes of objects) and the relationships among quantities, rather than focusing primarily on numerical calculations and symbol manipulation. When an individual has distinguished between conceptualized quantities in a situation with measurements that can change and those with fixed measurements, then they can begin to coordinate changes in pairs of quantities’ magnitudes or values, identify patterns in those coordinated changes, and reason about the implications of those patterns. This is covariational reasoning (Carlson et al., 2002; Castillo-Garsow et al., 2013; Moore and Thompson, 2015; Saldanha and Thompson, 1998; Thompson and Carlson, 2017) and is foundational to a robust understanding of algebra, functions, and rate of change and accumulation in calculus. The relationships identified can be represented and communicated through a variety of equivalent representations that may highlight different features of these relationships.

Thompson’s work on quantitative reasoning emerged from his analysis of students’ difficulties with algebra and calculus. He observed that many students approached mathematical problems by immediately applying numerical procedures without first conceptualizing the underlying quantitative structure. This tendency often led to procedural errors and limited students’ ability to reason about novel situations. On the other hand, students can accomplish impressive mathematical reasoning when instruction focuses on supporting students in conceptualizing a problem’s quantities, how they are related and vary together as a foundation for representing these relationships with formulas and graphs [e.g., see Castillo-Garsow et al. (2013), Ellis et al. (2012, 2015), Moore (2014), and Thompson (1993, 2011)].

Individuals inclined to engage in quantitative reasoning when encountering mathematical contexts, especially when done with conscious intention, will exhibit certain observable behaviors dependent on the context and the mathematical representation methods given to them or that they choose to use to present their reasoning. For purposes of this paper, I will focus on individuals interpreting and using algebraic statements. If they are reasoning quantitatively, their behaviors will be driven by expectations inherent to such reasoning (O’Bryan, 2020).

1. An expectation that performing calculations or generating expressions should reflect a quantification process for quantities that the individual conceptualizes.

2. An expectation that demonstrating calculations and producing expressions are attempts to communicate an individual’s meanings. Thus, when given a set of calculations or expression/formula, we can hypothesize how the individual conceptualized a situation based on analyzing the products of their reasoning.

3. An expectation that the order of operations used to perform calculations, evaluate expressions, and solve equations “reflects the hierarchy of quantities within a conceptualized quantitative structure” (O'Bryan, 2018, p. 234). (p. 450).

When an individual is operating from expectations such as these, we would expect to see behaviors in which the individual is constructing an image of the quantitative structure of an applied problem and using that image to build meaningful algebraic representations of these quantitative relationships. O'Bryan (2018) and O’Bryan (2020) described individuals doing so as engaging in emergent symbolization (with emergent symbol meaning describing the general conceptualization of algebraic statements in line with these expectations). When teachers hold these meanings and can consciously leverage them in instruction, they become positioned to support students in developing similarly powerful ways of reasoning about algebraic situations.

During the professional development sessions with Tracy she was presented tasks and contexts highlighting the utility of thinking carefully about quantities’ values represented by mathematical expressions. The major points of emphasis related to reasoning about algebraic representations for these sessions are listed in Table 1. It is worth noting that students need to be supported in taking the time to conceptualize situations and construct a mental model of how the quantities are related before attempting to produce algebraic models to represent these relationships and this process is more challenging and more time consuming than teachers usually assume [See Carlson et al. (2022)].

As previously argued, a teacher’s instructional goals, the classroom tasks they select to achieve these goals, and their beliefs about what it means to learn and understand mathematics influence their pedagogical actions [also see Simon et al. (2000), Thompson (2016), and Thompson et al. (1994)]. Therefore, the professional development sessions were focused on supporting Tracy in: (i) constructing the targeted meanings, (ii) seeing the pedagogical power of those meanings, (iii) conceptualizing student learning goals relative to the ideas highlighted in the professional development sessions, and (iv) prompting her to consider the thinking her students were expressing in their verbal contributions, written homework, and assessments. Furthermore, the intervention structure reflected research-based principles of effective professional development. Following Darling-Hammond et al. (2017), the program was content-focused, sustained over time, included opportunities for active learning, and provided ongoing support for implementation.

4 Results

In this section I share data from Tracy’s comments and classroom teaching and analyze it using constructs of MMT and ways of thinking about teaching an idea. As the semester progressed, Tracy (a) often tried to replicate her experiences in the professional development sessions with her students, (b) increasingly discussed her learning goals with me in terms of students’ understandings of the ideas, rather than their performance on specific tasks, (c) increasingly focused on the meanings of the expressions she wrote, the expressions students wrote, and how mathematical formulas reflected quantitative structures someone had conceptualized, (d) began to notice when students were not thinking about particular mathematical expressions and formulas in the ways she intended, and (e) increasingly discussed her reflections on what kinds of activities would support students in thinking about the mathematical ideas in the ways she intended and why.

4.1 Early evidence of attending to students’ quantitative reasoning and decentering

In the examples in this section, we see evidence of Tracy modifying her instruction based on her observations and reflections on her students’ thinking. Rather than simply correcting students’ errors, Tracy created experiences designed to help students construct more productive meanings and advance their quantitative reasoning skills.

Early in the semester, Tracy began noticing that students were not conceptualizing the quantities in a problem statement, nor were they conceptualizing the starting point for variables or constructing formulas that accurately represented the quantitative relationships described in the problem statement. Based on our work in the professional development sessions, she described recognizing the potential issues this would cause for students later in the course. Excerpt 1 is part of Tracy’s reflection on student work from a quiz she gave on linear relationships early in the course.

4.1.1 Excerpt 1

Tracy: On number three (see Figure 3) […] [T]he first one was writing a formula telling them how to define the variables, and then the second two questions were, so how far is your house from the school and how long did it take you to get there? What was interesting is almost everybody got (b) and (c) correct [but] a lot of people missed (a). Because they were like, I know you told me that the distance should be distance from my house, but what I would really like to do is distance from school. […]

Figure 3

Figure 3. A question Tracy wrote for a class quiz during the first module.

So, we really have done several problems like this after that. I’ve had them walk across the room. […] I have problems where I had them model, okay, so now back up. What’s happening? And go forward, what’s happening to the distance? And I also did several problems after this where I made them write both formulas. […] One thing that I realized they were doing is your reference point has to match your variables, so like they would be using a reference point where the d in the reference point was distance from [school], but then they are trying to write a formula [representing the] distance from [their house]. […] That got back to a discussion of how important is it that we define our variables accurately.

Tracy’s main concern was that students were not carefully attending to what quantities she asked them to track as revealed in the students’ variable definitions and expressed that this would become a significant problem for them in future lessons. In particular, she conveyed that it was important that the reference points students chose (the starting point for a quantity’s measurement) align with their variable definitions. Based on her observations, Tracy planned her future instruction to help students improve their attention to detail in terms of conceptualizing quantities they were being asked to consider.

Later in the semester, Tracy described her students’ work to interpret the parts of the general explicit formula for geometric sequences (see Excerpt 2). Over one and a half class sessions, students worked to make sense of situations represented by geometric sequences, including their noticing similarities in how those sequences are constructed, and writing a general formula to express the value of the n^th term based on its position. According to Tracy, students had little difficulty coming up with the general formula a_n = a₁∙r^n–1. However, when she assigned a task from the Pathways Algebra II workbook that asked students to describe the quantities’ values represented by each part of the formula (see Figure 4), she expressed surprise that many students had an inaccurate interpretation of the role the expression n – 1 played in relating the term’s value with its position.

Figure 4

Figure 4. A task from Pathways Algebra II (Carlson and O’Bryan, 2014, p. 94) to explore students’ meanings for expressions in the explicit formula representing the term value in a geometric sequence, a_n, in terms of the term position, n.

4.1.2 Excerpt 2

Tracy: The one that was most concerning to me actually out of these five […] [points to part (b. v.) in Figure 4], they said this is the first term multiplied by the ratio n minus one times. And I said, well, what does that find? Well, the n^th term. Okay, so this represents the n^th term. Then they said this- when I asked them what this was [points to part (b. iii.) in Figure 4] they said that’s the position before the n^th position. They did not see it as that’s how far you need to change, that’s how far your position is changing away from one. So that led to a discussion. And so, and then it had to be linked to this is multiplying by the ratio this many times but why? Because you are changing away that many positions.

Tracy’s ability to interpret and assess the correctness of students’ meaning for the expression n – 1 relied on her understanding a difference as representing an amount of change in a quantity’s value, and in particular conceptualizing the expression as “the change in the term position from the first term to the n^th term.” Understanding that her students’ interpretation differed from her own, Tracy had to recognize the utility of this meaning in helping her students conceptualize what the expression n – 1 represents. Her intentional actions relied on her believing that this meaning would also be valuable for students. This led to her targeting these meanings during her instruction.

Once Tracy recognized that students’ meanings differed from her own, and that the meanings students expressed might not generalize productively to other topics in the course, Tracy modified her interactions with students in subsequent tasks to help them build the meanings she intended (see Excerpt 3 based on the exercises in Figure 5).

Figure 5

Figure 5. Exercises from Pathways Algebra II (Carlson and O’Bryan, 2014, p. 94–95).

4.1.3 Excerpt 3

Tracy: But that kind of continued here [points to Figure 5] […] In problem number six and number seven when, uh, when they had this problem [copies down Exercise 6a part (ii) on a piece of scratch paper] or this one [copies down Exercise 7a part (ii) next to it] they knew that it was about multiplication so they kind of thought of it as two times what equals 250? [She writes the first line of Figure 6, leaving the box empty]. And they said, well 125 [adds 125 to the empty box in Figure 6]. So, then I-I tried to push them to think about, well, what does the 125 represent? And so, they kind of talked about that and came up with, well, that represents r cubed [adds r³ to Figure 6]. Why does it represent r cubed? Because it’s the fourth term, which is three positions over from the first term.

Figure 6

Figure 6. Tracy’s diagram used in a class discussion about the meaning of the exponent in the explicit formula for a geometric sequence.

Excerpt 3 suggests that Tracy’s goal was not for students to simply generate and use the explicit formula for a geometric sequence. She also wanted to make sure that students thought about the exponent as representing a change in term position from the first term to the n^th term. To emphasize this goal, Tracy modified her lesson in the moment of teaching to further support students’ development of this way of understanding. See Excerpt 4.

4.1.4 Excerpt 4

Tracy: So then I made something up where I tried to push them fur- I tried to create a need to actually know what the r [represents without needing to calculate its value]². Something like [writes first line of Figure 7] that wasn’t gonna [trails off].

Figure 7

Figure 7. A problem Tracy created in the moment of teaching to emphasize her learning goals based on her model of how students understood geometric sequences.

Alan: Be nice? [Alan conjectures what words she intended to use to finish her sentence.]

Tracy: At all. [laughs] It was gonna be like a whatever root of something is your r. Good luck with that. [laughs] So then I said, okay, well what about this, um, and so then they had to really think about three times, like, what does this mean? [Writes second line of Figure 7.] Um. So, then they started thinking about that and trying to relate that back.³ What I think I’d like to emphasize even further, and, i-is just, just making sure to always relate that back to how your input, how that position is changing away from one, and just kind of relating, like that applies even though it’s no longer linear, it’s how many times you are multiplying, so to bring it back to that concept […] That is another way that, that the first module can be leveraged, but their instinct wasn’t to say change away from one, their instinct was to say, well, […] it’s the position before the n^th position […] it’s not a valuable way to [trails off].

My understanding of Tracy’s comments is that Tracy had conceptualized differences as directed changes away from a reference point and that she believed it was important for her students to construct the same meaning for themselves. This represents her developing an appreciation for the usefulness of certain mathematical meanings. Excerpts 3 and 4 demonstrate how Tracy modified and focused her instruction on supporting her students in developing these meanings based on her emerging models of how students were thinking about those ideas.

4.2 A detailed look at Tracy’s teaching: the exponential function lesson

To illustrate Tracy’s instruction near the end of the fall teaching semester, this section presents a detailed analysis of one lesson from late in the semester.

4.2.1 Key elements of Tracy’s lesson

Tracy began the lesson by displaying the prompt shown in Figure 8. This task differed from previous problems she had assigned because it provided a growth factor for a three-hour interval rather than a one-hour interval, something the class had not yet discussed how to handle. Tracy stated during our post-lesson debriefing conversation that she wanted to see how students would apply their understanding of the ideas in the module to this novel situation.

Figure 8

Figure 8. The prompt Tracy created to begin a lesson in the exponential functions module.

After giving her students about five minutes to work on the task in small groups, Tracy asked students from various groups to first share with the class approaches they tried that did not work. Groups shared solutions such as $f\left(t\right)=\left(2\right)\left(\frac{t}{3}\right)\left(2500\right)$ and $f\left(t\right)=2500{\left(\frac{1}{3}\right)}^t$ , and for each Tracy led a discussion about the thinking that produced the answer and how they knew it was incorrect. A portion of one such conversation is given in Excerpt 5. Tracy devoted about 25 min to these discussions (out of 65 total minutes in the class), indicating that she valued them as integral to her students’ learning experience.

4.2.2 Excerpt 5

Tracy: Okay, so, um what did you guys try that did not work? Uh, S1.

S1: So, at first, we thought it, the growth factor, would be one third. And you would do it to the t.

Tracy: So you did like one third to the t?

S1: Yeah and the zeroth term would be the twenty-five hundred.

Tracy: So what did you do with the two thousand five hundred again?

S1: I multiplied it by that term.

Tracy: So you had something that maybe looked like this? [Tracy writes Figure 9 during this exchange.] And what did t represent for you?

Figure 9

Figure 9. A student’s work when asked to provide an approach they tried that did not produce a correct answer.

S1: The number of hours that had passed since eight a.m. and we thought that, oh wait it was, yeah, we thought that since every three hours the population of the bacteria doubled, um, you multiply by one-third to the t.

After these discussions, and once the class had collectively decided that $f\left(t\right)=2500{\left(2\right)}^{t/3}$ was an accurate model of the bacteria population in terms of the number of hours since 8 a.m., Tracy asked students to work in their groups to explain what quantities’ values were represented by various parts of the formula. Excerpt 6 shows part of the conversation once groups had discussed their thinking for about one minute.

4.2.3 Excerpt 6

Tracy: Okay, so the twenty-five hundred, what does that represent?

S2: [student abstained from this study].

Tracy: The initial, th-the initial value and um it’s what we are, it’s our reference point, it’s also the initial value because it happens at time equals zero. That’s one thing we are going to talk about in your homework, it talks about the initial value that’s at zero, which is a little bit different than what we were treating it with sequences, right? We’ll talk about that. Okay, so what does two represent? S3.

S3: It’s the growth factor you are multiplying the reference value by to get farther down the line.

Tracy: Now, what do you guys think, do you agree? Growth factor? Can you, like, describe the growth factor though? Like, what kind of, a growth factor for what? A growth factor, like can you be more specific because we can im-, we can imagine the same scenario and talk about different types of growth factors within that scenario, like, corresponding to different times, so what specific, S4?

S4: It’s the growth factor after three hours have passed.

Tracy: Okay, so would you agree it’s the three-hour growth factor? Okay. So then what does my t divided by three represent? S5.

S5: Like, um, how many groups of three there are in that amount of time, like how many groups of three hours there are.

Tracy: So like how many three-hour chunks?

S5: Yeah, intervals of three.

Tracy: Okay, why-why do we need to do that? S6.

S6: Um, because, uh, it’s increased by every three hours.

Tracy: Okay, so it’s every three hours that you have to double.

After this discussion, Tracy presented another prepared task to the class (see Figure 10). This task explicitly raised the issue that, when equivalent formulas are written differently (for example, with different groupings of terms or a different order of operations), it can reflect a different way of conceptualizing the quantities and their relationship to each other (refer back to Table 1).

Figure 10

Figure 10. An example Tracy had ready to present to the class for analysis at an appropriate time.

Tracy allowed groups to work on this task for about three minutes and then reconvened for a whole class discussion. See Excerpt 7.

4.2.4 Excerpt 7

Tracy: Did anyone think that they kind of figured out what might be the difference between the two ways of thinking? [long pause, some students nod while others raise their hands] Cool, some. S7.

S7: Um, I thi- I think the first equation they are trying to find the growth factor for every hour.

Tracy: So where in the equation would you see that?

S7: Uh, because the- the exponent is t and not t divided by three.

Tracy: So then your hypothesis was that this number [Tracy puts a bracket above 2^1/3 in Figure 10] represents what?

S7: Um, the growth factor for an hour. [Tracy writes “1-h growth factor” above the bracket.]

Tracy: Okay did you, whereas in the bottom equation when we discussed, what did two represent?

S7: Um, the growth factor for every three hours.

Tracy: Three hours. [Draws a bracket under “2” in the second formula in Figure 10 and writes “3-h growth factor”].

Tracy concluded the lesson with a final prepared task. Tracy presented a hypothetical alternative answer to the original lesson task (see Excerpt 8 and Figure 11). This task provided Tracy an opportunity to emphasize the importance of clear variable definitions as well as provide another opportunity for students to reason about alternative ways of conceptualizing the situation and formulas that result from those conceptualizations.

Figure 11

Figure 11. A hypothetical student solution Tracy presents to the class.

4.2.5 Excerpt 8

Tracy: Now, one thing we’ll end on before we move on, and we’ll continue to do problems like these, suppose a student writes this [Tracy writes Figure 11 on a piece of paper and displays it under the document camera].

Tracy: Take a second and try and consider what might they have been, I mean is it okay? Is it completely wrong? What might they have been thinking?

[Class] [Class discusses in groups for about one minute.]

Tracy: Okay. What do you guys think? S8.

S8: It seems like this is basically a person that’s thinking they-they, um, they aren’t thinking, uh, basically in terms of hours. It seems more like in hours in pairs of three. So, um, you could not just find the first hour with a whole number. You have to use something like one third kind of thing. So, it seems like they think that it doubles every one hour.

Tracy: So you are thinking maybe they are thinking it doubles every hour? What else? S9.

S9: Well they could, they have to define their variable as, um, that one x is actually three hours. It’s not, not growing by one hour.

Tracy: Okay, so you are saying perhaps their thinking is correct, but they defined their variables differently. Like x does not represent number of hours since eight, what does x represent?

S9: Like the [pause] [some classmates say something not picked up on the microphone].

[Class] [several members of the class speak simultaneously and it is impossible to make out on the recording exactly what they said].

Tracy: Yeah [laughing]. The number of three-hour chunks since eight a.m.

It is worth reiterating that Tracy clearly stated to me that her students had not yet worked with tasks in which they were given n-unit growth factors (n ≠ 1) and expected to reason about the corresponding 1-unit growth factors [although they had worked with contexts where, given the 1-unit growth factor, they reasoned about n-unit growth factors (n ≠ 1)]. Thus, students’ reasoning in this lesson are not examples of students performing rote memorized algorithms on sets of tasks identical to provided examples. Instead, students’ work demonstrated their ability to apply their thinking and build on prior understandings without explicit instruction on specific techniques. This example underscores the impacts of Tracy’s (and the curriculum’s) focus on quantitative reasoning as a foundation for their construction of algebraic statements meaningful to the student.

4.2.6 Commentary on Tracy’s lesson

Tracy’s choice of initial task for this lesson and how she leveraged the task reflect several sophisticated aspects of effective teaching. First, the novelty of the task required students to adapt their understanding to a new situation. This choice, coupled with Tracy’s approach of not over-emphasizing a single solution algorithm and the follow-up activities she designed created opportunities for rich mathematical discussions.

Second, the tasks within the lesson required careful attention to quantities, the relationship between quantities, and the meanings of variables. They illustrate why quantitative reasoning is a cross-cutting and essential way of thinking for learning and using ideas. Tracy’s questions and comments created a lesson focused on connecting symbolic representations with quantitative meaning (such as what the expression t/3 represented in the context), including exploring issues of representational equivalence and the interaction between a variable’s definition and the corresponding algebraic model based on that definition. Rather than treating algebraic expressions as isolated symbolic objects, she consistently connected them to the quantitative relationships they represented.

Third, Tracy’s initial exploration of incorrect solution attempts and the follow-up activities she designed provided her with ample opportunities to gain insights into students’ mathematical meanings and reasoning, thus supporting their engagement in productive decentering. Rather than treating incorrect responses as errors to be corrected, her actions suggested that she recognized student contributions as reflecting specific mathematical meanings that she could leverage in future interactions and discussions with students. She also modeled how different representations of quantitative relationships might emerge from different ways of thinking about a context and conveyed to her students that these differences were mathematically meaningful.

4.3 Evidence of student learning

While this study focuses primarily on Tracy’s development, evidence suggests her evolving teaching practices created high-quality learning opportunities for students. Throughout the observed lesson, students engaged in practices consistent with national calls for improvements in mathematics instruction. These practices included (i) having students analyze their incorrect approaches to understand why they were insufficient, (ii) making connections between current problems and previously studied concepts, (iii) explaining their reasoning using quantitative language, (iv) recognizing structural relationships in algebraic expressions, and (v) engaging in mathematical discussions about alternative solutions.

Students’ facility with these practices suggests they were developing mathematical meanings aligned with Tracy’s instructional goals. Their ability to discuss mathematical ideas in terms of quantities and relationships, rather than just procedures and answers, indicates that Tracy’s emphasis on quantitative reasoning was influencing their mathematical thinking and understandings. The quality of mathematical discourse in Tracy’s classroom also reflected her development as a teacher. Students regularly offered explanations, questioned each other’s reasoning, and built on each other’s ideas. These practices emerged by Tracy consistently modeling and supporting mathematical sense-making rather than answer-seeking.

4.4 Tracy’s reflection on her development

Tracy’s final reflection on her professional development experience provides insight into her perception of the factors that contributed to her growth as a teacher, directly addressing the first research question about how professional development focused on quantitative reasoning influenced her practice. In the final interview, Tracy reflected on the role of professional development in her growth. See Excerpt 9.

4.4.1 Excerpt 9

Tracy: You’ve given me some very helpful feedback when you have come to observe in the classroom. […] Some of it was verbal, like while you were here. But just, um, mathematical feedback [gets hand-written notes I had given her] that I could pull out as discussion points, or, um, things I can work on with the kids. For example, I mean, how to emphasize that it’s not just, um, like the constant rate of change, say it’s three halves. Okay, ways not to emphasize that it’s up three over two, up three over two every time. So just the content feedback on ways to pull thinking out of the students. That was helpful. Or, when you were here and we were talking about whether something was […] a function or not, [like] imagining the Ferris wheel, all the kids totally got that, hey, on the Ferris wheel, if I know the time, I know the position, but if I know the position, I do not necessarily know the time. So, they immediately got that and I think that helped them understand how to transfer that to other scenarios […] I’ve never had observations that were content based. It’s always been more like classroom management.

Tracy’s comments reveal several important aspects of her development. First, she identified the mathematical focus of her professional development as uniquely valuable, contrasting it with typical administrative observations focused on generic teaching behaviors rather than mathematical content and student thinking. This distinction highlights the importance of the kind of content-specific support for teacher development described in other research [e.g., Darling-Hammond et al. (2017)].

Second, Tracy’s specific examples demonstrate her growing ability to think pedagogically about mathematical content. Her mention of “ways to pull thinking out of the students” reflects her developing focus on understanding and advancing student thinking rather than simply delivering content. Her reference to the Ferris wheel example shows how concrete mathematical reasoning tools discussed in professional development interactions became resources she could use to help students understand abstract concepts.

Third, Tracy’s reflection reveals her recognition that teaching is fundamentally about supporting students’ mathematical thinking. This pedagogical awareness was present in her classroom teaching alongside evidence of her mathematical meanings related to quantitative reasoning. Her effectiveness in creating high-quality learning opportunities for her students supports the argument that these are key characteristics of a successful mathematics teacher and useful targets for professional development.

Finally, her ability to articulate specific ways the professional development influenced her instruction suggests that she had developed conscious awareness of her own learning and growth, a metacognitive capacity that likely supports continued development beyond the formal intervention period.

4.5 Results summary

Over the course of the intervention, evidence from classroom observations and interviews suggested that Tracy developed significantly in several areas. Tracy’s lesson design and interactions reflect that she had internalized quantitative reasoning as a lens for interpreting algebraic expressions and mathematical situations, moving beyond procedural approaches to focus on quantitative relationships. This shift enabled her to see connections between different mathematical topics and to help students develop similar connections. As the semester progressed, it appeared that Tracy became increasingly intentional about collecting evidence of her students’ thinking. In the exponential lesson, for example, Tracy asked students to share initial attempts that failed. Her subsequent instructional interactions built on those contributions as well as students’ reasoning for accurate solutions.

The design of her follow-up tasks in this lesson were noteworthy for at least two reasons. First, these activities appeared to be efforts to reproduce discussions and points of emphasis from our professional development and interview/training sessions for her students (see Table 1). This led to interactions with a focus on constructing images and representations of meaningful relationships rather than asking students to reproduce memorized algorithms. Second, the activities and her focus during discussion seemed to reflect an awareness of the existence of multiple ways of understanding the situation and emerging models of the relationship between the bacteria population and the hours elapsed since eight a.m. This suggests progress in Tracy’s developing images of epistemic students and constructing ways of thinking about teaching exponential functions informed by these models.

As the semester progressed, Tracy’s questioning, task selection, and use of student contributions became more sophisticated as her lesson learning goals increasingly appeared to target elements of quantitative reasoning (see Table 1). This is in line with Silverman and Thompson’s (2008) description of a teacher constructing personally powerful mathematical meanings and those meanings coming to have pedagogical power. As this happened, her teaching increasingly reflected the kind of responsive, meaning-centered instruction called for by mathematics education reform.

5 Discussion

This case study examined one teacher’s instruction using a research-based curriculum after participating in professional development focused on developing her quantitative reasoning skills. The findings illuminate three interconnected aspects of teacher development: the influence of content-focused professional development on practice, the role of decentering in developing pedagogical knowledge, and the manifestation of teachers’ mathematical meanings in classroom learning opportunities. Research on professional development has demonstrated that many interventions fail to make an impact on teachers’ practice in ways that improve student learning (Jacob et al., 2017; Kraft et al., 2018; Yoon et al., 2007). The didactic triad framework (Figure 1) provides insight into the source of these challenges, suggesting that effective professional development must address the interconnected elements of teachers’ mathematical meanings, learning goals, pedagogical actions, lesson resources, and models of student thinking. This study documents evidence that professional development that systematically addresses these elements through sustained, content-focused support can support teachers in providing high-quality learning opportunities for students.

Each of the following three sections address one of the research questions outlined at the beginning of this paper.

5.1 How professional development focused on quantitative reasoning influenced teaching practice

Early in the semester, Tracy’s concerns about student variable definitions (Excerpt 1) reflected her developing awareness that students’ mathematical meanings differed from her own and that these differences had pedagogical implications. By the exponential function lesson (Section 4.2), Tracy was systematically designing instruction to reveal and build on student thinking, using tasks that required careful attention to quantitative relationships and creating opportunities for rich mathematical discourse.

This transformation reflects what Silverman and Thompson (2008) described as the result of a teacher transforming personal mathematical meanings into meanings with pedagogical power. Tracy’s growing facility with quantitative reasoning provided her with a coherent lens for interpreting algebraic situations, student work, and instructional decisions. More importantly, her conscious awareness of these meanings enabled her to use them pedagogically, as evidenced by her ability to recognize when students were not thinking about expressions and formulas in quantitatively meaningful ways and her capacity to design instruction to address these gaps.

The specific focus on quantitative reasoning proved particularly productive because it provided a unifying instructional goal that connected different algebraic topics and enabled Tracy to see coherence across the curriculum. As demonstrated in the exponential lesson, Tracy used quantitative reasoning to help students understand why different representations of the same relationship might emerge from different ways of thinking about a context. This represents sophisticated mathematical teaching that goes well beyond procedural instruction or even conceptual explanation to focus on the development of powerful mathematical reasoning.

5.2 The role of decentering in developing pedagogically powerful mathematical meanings

Tracy’s ability to notice and respond to student thinking (her decentering) developed in tandem with her mathematical meanings and proved central to transforming her personal knowledge into pedagogically powerful knowledge. The geometric sequence example (Excerpts 2–4) illustrates this process clearly. Tracy first recognized that students’ interpretation of the expression n – 1 differed from her own. She then considered the implications of her intended meaning and the meanings students expressed and designed instruction to support students in constructing more productive meanings.

This finding supports and extends previous research on teacher noticing [e.g., Jacobs et al. (2010) and Sherin et al. (2010)] and decentering [e.g., Baş-Ader and Carlson (2022) and Teuscher et al. (2016)] by demonstrating that what teachers notice and how they interpret student contributions is fundamentally shaped by their own mathematical meanings. Tracy’s ability to recognize the pedagogical significance of students’ interpretation of n – 1 as “the position before the n^th position” rather than “the change in position from the first term” in the context of the explicit formulas for geometric sequences required both mathematical understanding and awareness of how different meanings might influence future learning.

The development of decentering skills appeared to follow an iterative process consistent with Carlson et al.’s (2024a) framework. Tracy’s first-order models (her personal mathematical meanings) became more conscious and articulated through the professional development activities. Her interactions with students then provided opportunities to construct second-order models of student thinking, which informed her instructional decisions and provided data for further refinement of both her mathematical meanings and her models of student understanding.

Importantly, Tracy’s decentering was not simply about attending to student contributions but about actively seeking to understand the mathematical meanings underlying those contributions and their implications for future learning. This represents a sophisticated form of professional noticing that requires both strong mathematical knowledge and pedagogical insight.

5.3 How mathematical meanings for teaching manifest in learning opportunities

The quality of learning opportunities in Tracy’s classroom reflected her evolving mathematical meanings in multiple ways. Most notably, her lessons increasingly featured tasks that required students to engage in quantitative reasoning, opportunities for mathematical discourse centered on meaning-making rather than answer-getting, and systematic attention to connecting different representations and solution approaches.

The exponential function lesson provides clear evidence of how Tracy’s mathematical meanings shaped the learning opportunities she created. Her choice to begin with a novel task requiring students to adapt their understanding, her systematic exploration of incorrect approaches, and her focus on connecting different ways of thinking about the same relationship all reflect sophisticated pedagogical reasoning grounded in quantitative reasoning. These instructional moves created opportunities for students to develop the kinds of mathematical meanings the professional development targeted.

However, this study’s evidence for the quality of learning opportunities is primarily observational rather than measured through student learning outcomes. While students demonstrated facility with mathematical discourse and reasoning consistent with the instructional goals, claiming direct evidence of improved learning would require additional data. What can be claimed is that Tracy’s instruction increasingly reflected the characteristics of high-quality mathematics teaching identified by research [e.g., National Governors Association Center for Best Practices, Council of Chief State School Officers (2010)] and created opportunities for the kinds of mathematical engagement that support learning.

5.4 Implications for professional development design

This case study provides empirical support for professional development approaches that target teachers’ mathematical meanings for teaching and that simultaneously address multiple aspects of the didactic triad. The findings suggest that effective professional development must address teachers’ personal mathematical meanings, support their development of models of student thinking, and provide ongoing opportunities to apply these insights in classroom practice with targeted feedback.

The specific focus on quantitative reasoning proved effective not only as mathematical content but as a lens for pedagogical reasoning. Quantitative reasoning provided Tracy with tools for analyzing student work, designing tasks, and making in-the-moment instructional decisions. This suggests that professional development content should be selected not only for its mathematical importance but for its potential to serve as a framework for pedagogical thinking.

The sustained nature of the intervention, including preparation during the prior year, intensive workshops, and ongoing support throughout implementation, appears to have been crucial to Tracy’s development. This aligns with research on effective professional development [e.g., Darling-Hammond et al. (2017)] while providing concrete evidence of how sustained support enables the kind of fundamental change in practice that mathematics education reform requires.

5.5 Limitations and future research

The author served dual roles as both the professional developer and the researcher in this study. This positioning provided unique access to Tracy’s mathematical thinking and development but also created potential for bias in data interpretation. Several measures were taken to address this limitation including the following. (i) All professional development and classroom observation sessions were recorded to enable systematic analysis. (ii) Interpretations about Tracy’s thinking were grounded in her explicit statements, observable behaviors, and the activities she designed to achieve stated learning goals. Hypotheses about Tracy’s motivations and goals developed through analysis were confirmed with Tracy during subsequent meetings whenever possible. (iii) The analysis focused on documenting change over time using multiple data points rather than making broad generalizations from single incidents. This single case study of one teacher engaging in professional development and implementing a research-based curriculum is not intended to generate fully generalizable results for all teachers and in all settings. However, the results provide insights into how professional development that supported advances in a teacher’s decentering abilities through a consistent focus on supporting her students’ quantitative reasoning impacted her teaching.

This study raises several questions that warrant further investigation:

1. Scalability: How do these approaches perform when implemented with larger groups of teachers across diverse contexts? What adaptations are needed for different school settings and teacher populations? [See Carlson et al. (2024b)] for some initial work on answering this question.

2. Content Generalizability: While quantitative reasoning proved effective as a focus for this intervention, would similar approaches work with other mathematical content areas? What characteristics make mathematical ideas suitable for this kind of professional development?

3. Student Learning Outcomes: Future research should examine student learning gains associated with teaching practices developed through mathematical meanings for teaching approaches. What evidence can demonstrate that changes in teaching practice translate to improved student learning?

4. Sustainability: How do changes in teaching practice persist over time? What ongoing support is needed to maintain reform-oriented instruction, and how do teachers continue developing their mathematical meanings for teaching beyond formal professional development?

5. Measurement and Assessment: How can the development of teachers’ mathematical meanings for teaching be measured reliably? What tools are needed to assess both the mathematical and pedagogical dimensions of teacher knowledge in this framework? [See Thompson (2016)] for the foundations of one possible approach to addressing this question.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the Arizona State University Institutional Research Board. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

AO’B: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Science Foundation under Grant No. DUE-1323753 and EHR-0412537. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

AO’B was employed by the Rational Reasoning, LLC.

Generative AI statement

The author declares that Gen AI was used in the creation of this manuscript. Generative AI was used to assist in condensing the article's length after it was written (from about 19,000 words to less than 12,000 words) by suggesting content to cut and ways to reword paragraphs to reduce their length.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^To summarize the timeline of this research, during year one, Tracy participated in monthly professional learning community meetings. In the summer between year one and year two, she attended an intensive two-day workshop. During the fall of year two, she taught using the curriculum materials while receiving ongoing support through five individual sessions, and all data collection for this study occurred during the fall semester of year two.

2. ^I reworded the end of this sentence in the transcript. Tracy was referencing back to something she had said in part of the transcript I omitted which made clear she was talking about the meaning of r without knowing its precise value.

3. ^In this passage she is referencing how linear functions was designed in the curriculum with an emphasis in coordinating changes in the values of two quantities, with “Change away from what value?” being a key question to consider.

References

Ball, D. L., Lubienski, S., and Mewborn, D. (2001). Research on teaching mathematics: The unsolved problem of teachers’ mathematical knowledge. In Handbook of Research on Teaching. ed. V. Richardson (4th ed.) (New York: Macmillan).

Google Scholar

Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: what makes it special? J. Teach. Educ. 59, 389–407. doi: 10.1177/0022487108324554

Crossref Full Text | Google Scholar

Baş-Ader, S., and Carlson, M. P. (2022). Decentering framework: a characterization graduate student instructors’ actions to understand and act on student thinking. Math. Think. Learn. 24, 99–122. doi: 10.1080/10986065.2020.1844608

Crossref Full Text | Google Scholar

Boston, M. (2012). Assessing instructional quality in mathematics. Elem. Sch. J. 113, 76–104. doi: 10.1086/666387

Crossref Full Text | Google Scholar

Carlson, M. P., and Baş-Ader, S. (2019). “The Interaction Between a Teacher’s Mathematical Conceptions and Instructional Practices” in Proceedings of the 22nd Annual Conference on Research in Undergraduate Mathematics Ed. eds. A. Weinberg, D. Moore-Russo, H. Soto, and M. Wawro (Oklahoma City, Oklahoma: Mathematical Association of America), 101–110.

Google Scholar

Carlson, M. P., Baş-Ader, S., O’Bryan, A. E., and Rocha, A. (2024a). “The Construct of Decentering in Research on Student Learning and Teaching” in Piaget’s Genetic Epistemology for Mathematics Education Research. eds. P. Dawkins, A. Hackenburg, and A. Norton (Cham: Springer International Publishing), 289–338. doi: 10.1007/978-3-031-47386-9_9

Crossref Full Text | Google Scholar

Carlson, M. P., Bowling, S., Moore, K., and Ortiz, A. (2007). “The emergence of decentering in facilitators of professional learning communities of secondary mathematics and science teachers” in Proceedings of the 29th annual meeting of the north American chapter of the International Group for the Psychology of mathematics education. eds. T. Lamberg and L. R. Wiest (Reno: University of Nevada), 841–848.

Google Scholar

Carlson, M. P., Jacobs, S., Coe, E., Larsen, S., and Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: a framework and a study. J. Res. Math. Educ. 33, 352–378. doi: 10.2307/4149958

Crossref Full Text | Google Scholar

Carlson, M. P., and O’Bryan, A. E. (2014). Pathways algebra II: Implementing the common Core standards. 3rd Edn. Phoenix, AZ: Rational Reasoning.

Google Scholar

Carlson, M. P., O’Bryan, A. E., and Rocha, A. (2022). “Instructional conventions for conceptualizing, graphing and symbolizing quantitative relationships” in Quantitative reasoning in mathematics and science education. Mathematics education in the digital era, 21. eds. G. Karagöz Akar, İ. Ö. Zembat, S. Arslan, and P. W. Thompson (Cham: Springer), 221–259. Doi:10.1007/978-3-031-14553-7_9

Google Scholar

Carlson, M. P., O’Bryan, A. E., Strayer, J. F., McNicholl, T. H., and Hagman, J. E. (2024b). Considering, piloting, scaling and sustaining a research-based precalculus curriculum and professional development innovation. J. Math. Behav. 73, 289–338. doi: 10.1016/j.jmathb.2024.101126

PubMed Abstract | Crossref Full Text | Google Scholar

Carpenter, T. P., Fennema, E., Peterson, P. L., Chiang, C. P., and Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. Am. Educ. Res. J. 26, 499–531. doi: 10.3102/00028312026004499

Crossref Full Text | Google Scholar

Castillo-Garsow, C., Johnson, H. L., and Moore, K. C. (2013). Chunky and smooth images of change. For Learn. Math. 33, 31–37. Available at: https://www.jstor.org/stable/43894859

Google Scholar

Clark, D., and Hollingsworth, H. (2002). Elaborating a model of teacher professional growth. Teach. Teach. Educ. 18, 947–967. doi: 10.1016/S0742-051X(02)00053-7

Crossref Full Text | Google Scholar

Coburn, C. E., and Russell, J. L. (2008). District policy and teachers’ social networks. Educ. Eval. Policy Anal. 30, 203–235. doi: 10.3102/0162373708321829

Crossref Full Text | Google Scholar

Corbin, J. M., and Strauss, A. (1990). Grounded theory research: procedures, canons, and evaluative criteria. Qual. Sociol. 13, 3–21. doi: 10.1007/BF00988593

Crossref Full Text | Google Scholar

Darling-Hammond, L., Hyler, M. E., and Gardner, M. (2017). Effective teacher professional development. Learning Policy Institute. doi: 10.54300/122.311

Crossref Full Text | Google Scholar

Darling-Hammond, L., and Sykes, G. (Eds.) (1999). Teaching as the learning profession: Handbook of policy and practice. San Francisco: Jossey-Bass.

Google Scholar

Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educ. Res. 38, 181–199. doi: 10.3102/0013189x08331140

Crossref Full Text | Google Scholar

Domitrovich, C. E., Bradshaw, C. P., Poduska, J. M., Hoagwood, K., Buckley, J. A., Olin, S., et al. (2008). Maximizing the implementation quality of evidence-based preventive interventions in schools: A conceptual framework. Adv. Sch. Ment. Health Promot. 1, 6–28. doi: 10.1080/1754730x.2008.9715730

Crossref Full Text | Google Scholar

Ellis, A. B., Ozgur, Z., Kulow, T., Williams, C., and Amidon, J. (2012). Quantifying exponential growth: the case of the Jactus. WISDOMe monographs 2, 93–112.

Google Scholar

Ellis, A. B., Özgür, Z., Kulow, T., Williams, C. C., and Amidon, J. (2015). Quantifying exponential growth: three conceptual shifts in coordinating multiplicative and additive growth. J. Math. Behav. 39, 135–155. doi: 10.1016/j.jmathb.2015.06.004

Crossref Full Text | Google Scholar

Frank, K., and Thompson, P. W. (2021). School students’ preparation for calculus in the United States. ZDM Mathematics Education 53, 549–562. doi: 10.1007/s11858-021-01231-8

Crossref Full Text | Google Scholar

Guskey, T. R. (2002). Professional development and teacher change. Teach. Teach 8, 381–391. doi: 10.1080/135406002100000512

Crossref Full Text | Google Scholar

Hill, H. C., Ball, D. L., and Schilling, S. G. (2008). Unpacking pedagogical content knowledge: conceptualizing and measuring teachers' topic-specific knowledge of students. J. Res. Math. Educ. 39, 372–400. doi: 10.5951/jresematheduc.39.4.0372

Crossref Full Text | Google Scholar

Hill, H. C., and Charalambous, C. Y. (2012). Teacher knowledge, curriculum materials, and quality of instruction: Lessons learned and open issues. Journal of Curriculum Studies 44, 559–576. doi: 10.1080/00220272.2012.716978

Crossref Full Text | Google Scholar

Hill, H. C., Rowan, B., and Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. Am. Educ. Res. J. 42, 371–406. doi: 10.3102/00028312042002371

Crossref Full Text | Google Scholar

Jacob, R., Hill, H., and Corey, D. (2017). The impact of a professional development program on teachers’ mathematical knowledge for teaching, instruction, and student achievement. J. Res. Educ. Eff. 10, 379–407. doi: 10.1080/19345747.2016.1273411

Crossref Full Text | Google Scholar

Jacobs, V. R., Empson, S. B., Jessup, N. A., Dunning, A., Pynes, D. A., Krause, G., et al. (2024). Profiles of teachers’ expertise in professional noticing of children’s mathematical thinking. J. Math. Teach. Educ. 27, 295–324. doi: 10.1007/s10857-022-09558-z

Crossref Full Text | Google Scholar

Jacobs, V. R., Lamb, L. L., and Philipp, R. A. (2010). Professional noticing of children's mathematical thinking. J. Res. Math. Educ. 41, 169–202. doi: 10.5951/jresematheduc.41.2.0169

Crossref Full Text | Google Scholar

Kahan, J. A., Cooper, D. A., and Bethea, K. A. (2003). The role of mathematics teachers' content knowledge in their teaching: a framework for research applied to a study of student teachers. J. Math. Teach. Educ. 6, 223–252. doi: 10.1023/A:1025175812582

Crossref Full Text | Google Scholar

Kennedy, M. M. (2016). How does professional development improve teaching? Rev. Educ. Res. 86, 945–980. doi: 10.3102/0034654315626800

Crossref Full Text | Google Scholar

Kraft, M. A., Blazar, D., and Hogan, D. (2018). The effect of teacher coaching on instruction and achievement: A meta-analysis of the causal evidence. Rev. Educ. Res. 88, 547–588. doi: 10.3102/0034654318759268

Crossref Full Text | Google Scholar

Lee, H. J., and Vongkulluksn, V. W. (2022). Enhancing mathematics teacher professional learning through a contextualized professional development program. Teach. Dev. 27, 92–115. doi: 10.1080/13664530.2022.2134195

Crossref Full Text | Google Scholar

Litke, E. (2020). Instructional practice in algebra: building from existing practices to inform an incremental improvement approach. Teach. Teach. Educ. 91:103030. doi: 10.1016/j.tate.2020.10330

Crossref Full Text | Google Scholar

Mathematical Association of America (2018). MAA instructional practices guide. Washington, DC: Mathematical Association of America Retrieved March 28, 2025 from https://www.maa.org/programs-and-communities/curriculum%20resources/instructional-practices-guide

Google Scholar

Moore, K. C. (2014). Quantitative reasoning and the sine function: the case of Zac. J. Res. Math. Educ. JRME 45, 102–138. doi: 10.5951/jresematheduc.45.1.0102

Crossref Full Text | Google Scholar

Moore, K. C., and Thompson, P. W. (2015). “Shape thinking and students’ graphing activity” in Proceedings of the 18th meeting of the MAA special interest group on research in undergraduate mathematics education (Pittsburgh, PA: RUME), 782–789.

Google Scholar

National Council of Teachers of Mathematics (2000). Principles and standards for school mathematics. Reston, VA: NCTM.

Google Scholar

National Governors Association Center for Best Practices, Council of Chief State School Officers (2010). “Common Core State Standards for Mathematics” in National Governors Association Center for best practices. Washington, DC: Council of Chief State School Officers.

Google Scholar

O’Bryan, A. E. (2020). “Quantitative reasoning and symbolization activity: Do individuals expect calculations and expressions to have quantitative significance?” in Proceedings of the twenty-third annual special interest group of the Mathematical Association of America Conference on Research in Undergraduate Mathematics Education. (Boston, MA), 449–457.

Google Scholar

O'Bryan, A. E. (2018). Exponential growth and online learning environments: Designing for and studying the development of student meanings in online courses. Unpublished Ph.D. dissertation, Tempe, AZ: School of Mathematical and Statistical Sciences, Arizona State University.

Google Scholar

Opfer, V. D., and Pedder, D. (2011). Conceptualizing teacher professional learning. Review of educational research 81, 376–407. doi: 10.3102/0034654311413609

Crossref Full Text | Google Scholar

Organization for Economic Co-operation and Development (2023). PISA 2022 results (Volume I): The state of learning and equity in education. PISA, OECD Publishing, Paris. doi: 10.1787/53f23881-en

Crossref Full Text | Google Scholar

Rocha, A. (2021). “The Effectiveness of a Professional Development Video-Reflection Intervention: Mathematical Meanings for Teaching Angle and Angle Measure” in Proceedings of the Twenty-Fourth Annual Special Interest Group of the Mathematical Association of America Conference on Research in Undergraduate Mathematics Education.

Google Scholar

Rocha, A. (2022). “The Influence of Graduate Student Instructors’ Mathematical Meanings for Teaching Sine Function on their Enacted Teaching Practices” in Proceedings of the Twenty- Fifth Annual Special Interest Group of the Mathematical Association of America Conference on Research in Undergraduate Mathematics Education. Boston, MA.

Google Scholar

Rocha, A. (2023). An investigation into the relationships among teachers’ mathematical meanings for teaching, commitment to quantitative reasoning, and actions. Unpublished Ph.D. dissertation, Tempe, AZ: School of Mathematical and Statistical Sciences, Arizona State University.

Google Scholar

Rocha, A., and Carlson, M. (2020). The role of mathematical meanings for teaching and decentering actions in productive student-teacher interactions. Proceedings of the Twenty-Third Annual Special Interest Group of the Mathematical Association of America Conference on Research in Undergraduate Mathematics Education, Boston, MA 1146–1153.

Google Scholar

Saldanha, L., and Thompson, P. W. (1998). “Re-thinking co-variation from a quantitative perspective: simultaneous continuous variation” in Proceedings of the annual meeting of the psychology of mathematics education - North America. eds. S. B. Berenson and W. N. Coulombe (Raleigh, NC: North Carolina State University).

Google Scholar

Schoenfeld, A. H. (2022). “Why are learning and teaching mathematics so difficult?” in Handbook of cognitive mathematics (Cham: Springer International Publishing), 1–35. doi: 10.1007/978-3-030-44982-7_10-1

Crossref Full Text | Google Scholar

Sherin, B. L., Sherin, M. G., Colestock, A. A., Russ, R. S., Luna, M. J., Mulligan, M., et al. (2010). “Using digital video to investigate teachers' in-the-moment noticing” in Proceedings of the international conference of the learning sciences 2010: Learning in the disciplines, Chicago, IL 2, 179–186.

Google Scholar

Shulman, L. S. (1986). Those who understand: knowledge growth in teaching. Educ. Res. 15, 4–14. doi: 10.3102/0013189X015002004

Crossref Full Text | Google Scholar

Shulman, L. (1987). Knowledge and teaching: foundations of the new reform. Harv. Educ. Rev. 57, 1–23. doi: 10.17763/haer.57.1.j463w79r56455411

Crossref Full Text | Google Scholar

Silverman, J., and Thompson, P. W. (2008). Toward a framework for the development of mathematical knowledge for teaching. J. Math. Teach. Educ. 11, 499–511. doi: 10.1007/s10857-008-9089-5

Crossref Full Text | Google Scholar

Simon, M. A., Tzur, R., Heinz, K., Kinzel, M., and Smith, M. S. (2000). Characterizing a perspective underlying the practice of mathematics teachers in transition. J. Res. Math. Educ. 31, 579–601. doi: 10.2307/749888

Crossref Full Text | Google Scholar

Steffe, L. P. (1995). “Alternative epistemologies: an educator’s perspective” in Constructivism in education. eds. L. P. Steffe and J. Gale (Hillsdale, NJ: Erlbaum), 489–523.

Google Scholar

Steffe, L. P., Glasersfeld, E. V., Richards, J., and Cobb, P. (1983). Children’s counting types: Philosophy, theory, and application. New York: Praeger Scientific.

Google Scholar

Steffe, L. P., and Thompson, P. W. (2000). “Teaching experiment methodology: underlying principles and essential elements” in Handbook of research design in mathematics and science education. eds. R. Lesh and A. E. Kelly (Dordrecht, The Netherlands: Kluwer), 267–306.

Google Scholar

Stigler, J. W., and Hiebert, J. (2009). The teaching gap: Best ideas from the world's teachers for improving education in the classroom. New York, NY: Free Press.

Google Scholar

Stockero, S. L., Leatham, K. R., Ochieng, M. A., Van Zoest, L. R., and Peterson, B. E. (2020a). Teachers’ orientations toward using student mathematical thinking as a resource during whole-class discussion. J. Math. Teach. Educ. 23, 237–267. doi: 10.1007/s10857-018-09421-0

Crossref Full Text | Google Scholar

Stockero, S. L., Rupnow, R. L., and Pascoe, A. E. (2017). Learning to notice important student mathematical thinking in complex classroom interactions. Teach. Teach. Educ. 63, 384–395. doi: 10.1016/j.tate.2017.01.006

Crossref Full Text | Google Scholar

Stockero, S. L., and Stenzelbarton, A. D. (2017). An exploration of how aspects of a noticing intervention supported prospective mathematics teacher noticing. Proceedings for the North American Chapter of the International Group for the Psychology of Mathematics Education, 781–788.

Google Scholar

Stockero, S. L., Van Zoest, L. R., Freeburn, B., Peterson, B. E., and Leatham, K. R. (2020b). Teachers’ responses to instances of student mathematical thinking with varied potential to support student learning. Math. Educ. Res. J. 34, 165–187. doi: 10.1007/s13394-020-00334-x

Crossref Full Text | Google Scholar

Sztajn, P., Borko, H., and Smith, T. (2017). Research on mathematics professional development. Compendium for Research in Mathematics Education. 793–823.

Google Scholar

Tallman, M. A. (2021). Investigating the transformation of a secondary teacher’s knowledge of trigonometric functions. J. Math. Behav. 62:100869. doi: 10.1016/j.jmathb.2021.100869

Crossref Full Text | Google Scholar

Tallman, M. A. (2023). What makes pedagogical content knowledge “pedagogical”? Reconnecting PCK to its Deweyan foundations. Math. Educ. 31, 100–128. doi: 10.63301/tme.v31i1.2852

Crossref Full Text | Google Scholar

Tallman, M. A., Carlson, M. P., Bressoud, D. M., and Pearson, M. (2016). A characterization of calculus I final exams in US colleges and universities. Int. J. Res. Undergrad. Math. Educ. 2, 105–133. doi: 10.1007/s40753-015-0023-9

Crossref Full Text | Google Scholar

Tallman, M. A., and Frank, K. M. (2020). Angle measure, quantitative reasoning, and instructional coherence: an examination of the role of mathematical ways of thinking as a component of teachers’ knowledge base. J. Math. Teacher Educ. 23, 69–95. doi: 10.1007/s10857-018-9409-3

Crossref Full Text | Google Scholar

Tallman, M. A., Reed, Z., Oehrtman, M., and Carlson, M. P. (2021). What meanings are assessed in collegiate calculus in the United States? ZDM–Mathematics Education 53, 577–589. doi: 10.1007/s11858-020-01212-3

Crossref Full Text | Google Scholar

Tallman, M. A., Weaver, J., and Johnson, T. (2024). Developing (pedagogical) content knowledge of constant rate of change: the case of Samantha. J. Math. Behav. 76:101179. doi: 10.1016/j.jmathb.2024.101179

Crossref Full Text | Google Scholar

Teuscher, D., Moore, K. C., and Carlson, M. P. (2016). Decentering: a construct to analyze and explain teacher actions as they relate to student thinking. J. Math. Teacher Educ. 19, 433–456. doi: 10.1007/s10857-015-9304-0

Crossref Full Text | Google Scholar

The National Center for Education Statistics. (2025). The nation’s report card reveals declining scores for students entering and exiting high school. https://www.nationsreportcard.gov/

Google Scholar

Thompson, P. W. (1982). Were lions to speak, we wouldn't understand. J. Math. Behav. 3, 147–165.

Google Scholar

Thompson, P. W. (1990). A theoretical model of quantity-based reasoning in arithmetic and algebraic. Center for Research in Mathematics & Science Education: San Diego State University Retrieved March 28, 2025, from https://pat-thompson.net/PDFversions/1990TheoryQuant.pdf.

Google Scholar

Thompson, P. W. (1993). Quantitative reasoning, complexity, and additive structures. Educ. Stud. Math. 25, 165–208. doi: 10.1007/BF01273861

Crossref Full Text | Google Scholar

Thompson, P. W. (2000). “Radical constructivism: reflections and directions” in Radical constructivism in action: Building on the pioneering work of Ernst von Glasersfeld. eds. L. P. Steffe and P. W. Thompson (London: Falmer Press), 412–448.

Google Scholar

Thompson, P. W. (2002). Didactic objects and didactic models in radical constructivism. In K. Gravemeijer, R. Lehrer, B. Oersvan, and L. Verschaffel (Eds.), Symbolizing and modeling in mathematics education. Dordrecth, The Netherlands: Kluwer. doi: 10.1007/978-94-017-3194-2_12

Crossref Full Text | Google Scholar

Thompson, P. W. (2008). Conceptual analysis of mathematical ideas: some spadework at the foundation of mathematics education. Proceedings of the Annual Meeting of the International Group for the Psychology of Mathematics Education 1, 45–64.

Google Scholar

Thompson, P. W. (2009). “The Didactic Triad In Mathematics Teacher Professional Development” in Paper presented at The Didactic Triad In Mathematics Teacher Professional Development Workshop. Tempe, AZ.

Google Scholar

Thompson, P. W. (2011). “Quantitative reasoning and mathematical modeling” in New perspectives and directions for collaborative research in mathematics education, WISDOMe monographs, 1. eds. L. L. Hatfield, S. Chamberlain, and S. Belbase (Laramie, WY: University of Wyoming Press), 33–57.

Google Scholar

Thompson, P. W. (2013). “In the absence of meaning” in Vital directions for mathematics education research, 57–93. doi: 10.1007/978-1-4614-6977-3-4

Crossref Full Text | Google Scholar

Thompson, P. W. (2016). “Researching mathematical meanings for teaching” in Handbook of international research in mathematics education. eds. L. D. English and D. Kirshner (New York: Taylor & Francis), 435–461.

Google Scholar

Thompson, P. W., and Carlson, M. P. (2017). “Variation, covariation, and functions: foundational ways of thinking mathematically” in Compendium for research in mathematics education. ed. J. Cai (Reston, VA: National Council of Teachers of Mathematics), 421–456.

Google Scholar

Thompson, A. G., Philipp, R. A., Thompson, P. W., and Boyd, B. A. (1994). “Calculational and conceptual orientations in teaching mathematics” in 1994 yearbook of the NCTM. ed. A. Coxford (Reston, VA: NCTM), 79–92.

Google Scholar

Tisdell, E. J., Merriam, S. B., and Stuckey-Peyrot, H. L. (2025). Qualitative research: A guide to design and implementation : John Wiley & Sons.

Google Scholar

Van Es, E. A., and Sherin, M. G. (2002). Learning to notice: scaffolding new teachers’ interpretations of classroom interactions. J. Technol. Teach. Educ. 10, 571–596.

Google Scholar

Van Es, E. A., and Sherin, M. G. (2006). How different video club designs support teachers in “learning to notice”. J. Comput. Teach. Educ. 22, 125–135.

Google Scholar

Van Es, E. A., and Sherin, M. G. (2008). Mathematics teachers’ “learning to notice” in the context of a video club. Teach. Teach. Educ. 24, 244–276. doi: 10.1016/j.tate.2006.11.005

Crossref Full Text | Google Scholar

Yin, R. K. (2018). Case study research and applications, vol. 6. Thousand Oaks, CA: Sage. doi: 10.33524/cjar.v14i1.73

Crossref Full Text | Google Scholar

Yoon, K. S., Duncan, T., Lee, S. W. Y., Scarloss, B., and Shapley, K. L. (2007). Reviewing the evidence on how teacher professional development affects student achievement. issues & answers. rel 2007-no. 033. Regional Educational Laboratory Southwest (NJ1).

Google Scholar