Developing geometric thinking through culturally contextualized mathematical modeling: a yurt-building lesson for middle-school students in Kazakhstan

This mixed-methods study examines the impact of a single culturally contextualized STEAM lesson, constructing a scale model of a Kazakh yurt, on sixth-grade students’ geometry confidence and cultural awareness. Forty-four students (aged 11–12) from a public school in East Kazakhstan participated in the hands-on activity during a 45-min mathematics period. Data sources included (i) a post-lesson perception survey (Likert, multiple-choice, open-ended), (ii) teacher field notes, and (iii) photographs of student artifacts. Reliability of the six-item Likert scale was acceptable (Cronbach’s α = 0.81). Descriptive statistics show that students’ self-rated confidence in measuring polygon sides (M = 3.48, SD = 1.17) and applying perimeter formulas (M = 3.61, SD = 1.26) fell in the moderate range, while appreciation for Kazakh cultural heritage was high (Yes = 52.3%; Partially = 29.5%). Thematic analysis of 176 open-ended responses, with 92% intercoder agreement, revealed three recurring themes: (1) recognizing geometry in everyday artifacts, (2) difficulties visualizing the transition from 2D plans to a 3D dome, and (3) heightened respect for nomadic engineering ingenuity. Although the study relies on post-lesson self-report rather than pre- and post-objective testing, the triangulated evidence suggests that a single culturally grounded project can foster meaningful, if preliminary, gains in geometric thinking and cultural connectedness. Limitations include the brief intervention window and single-site design; future work should incorporate objective assessments and multi-lesson sequences to substantiate learning outcomes.

1 Introduction

Educators in many regions have been exploring methods to merge science, technology, engineering, arts, and mathematics (Perignat and Katz-Buonincontro, 2018; Yumin and Isa, 2024; Abildinova et al., 2024; Karatayeva et al., 2024). This integrated approach is often referred to as STEAM. STEM education integrates science, technology, engineering, and mathematics (Leavy et al., 2023). It aims to show that academic subjects are not isolated. Instead, they share concepts and skills that overlap (Connor et al., 2015; Harris and de Bruin, 2017; Perignat and Katz-Buonincontro, 2019; Belbase et al., 2022). Researchers believe that STEAM lessons can improve problem-solving (Wilson et al., 2021). They also see how these lessons can boost creativity and engagement (Quigley et al., 2017). Teachers who plan STEAM projects often use hands-on challenges (Needles, 2020). These include designing small machines or creating digital artworks. Such projects allow students to see how formulas or principles apply in practical, visible ways (Bybee, 2019). The inclusion of the arts in the STEM framework has driven educational reform by fostering transdisciplinary knowledge while preserving the core principles of each discipline (Rabalais, 2014; Bush and Cook, 2019). This integration promotes equitable and early access to STEM education (Burnard et al., 2021) and helps reduce gender disparities and barriers faced by disadvantaged students in STEM fields (Leavy et al., 2023). Prior research indicates that incorporating the arts enhances student participation across age groups (Papavlasopoulou et al., 2019), increases engagement in learning (Vicente et al., 2021), and facilitates the acquisition of new knowledge and skills (Bertrand and Namukasa, 2020; Lage-Gómez and Ros, 2023).

1.1 The rise of interdisciplinary learning

Interdisciplinary lessons encourage students to draw ideas from multiple domains (Quigley et al., 2017). This can make learning more meaningful. For instance, integrating geometry calculations within engineering tasks allows students to measure lengths and angles, assemble physical models, and test prototypes, thereby demonstrating the practical applications of mathematics (Bertrand and Namukasa, 2020). This approach not only makes classwork more engaging but also fosters critical problem-solving skills and creativity (Becker and Park, 2011). According to Hougaard et al. (2024), scaffolding inquiry-based learning in STEM education encourages student persistence by promoting research-oriented engagement in problem-solving tasks. This approach fosters motivation and endurance in the face of challenges. Bai and Nam (2024) emphasize that in STEAM education, tolerance for mistakes and iterative refinement are essential for fostering student confidence and promoting long-term learning persistence. They argue that errors should be viewed as learning opportunities rather than failures. Mustadi and Junaidi (2024) emphasize that project-based learning in STEAM classrooms enables students to repeatedly refine their ideas, thereby strengthening their problem-solving and collaboration skills. Blanco-García et al. (2025) found that STEAM education integrates mathematical concepts into real-world applications, making learning more engaging and meaningful for students. This approach increases mathematical persistence and understanding.

Interdisciplinary learning enhances students’ ability to communicate their ideas effectively, as integrating multiple disciplines encourages them to articulate their thoughts clearly (Dignam, 2025). This approach requires students to discuss numerical data and design concepts with their peers, improving both their verbal and written communication skills (Golegou and Peppas, 2025). Through activities such as sharing measurements and comparing different shapes, students engage in collaborative problem-solving, fostering teamwork and consensus-building (Matsushima et al., 2025). Additionally, interdisciplinary education prompts learners to explain complex concepts clearly, ensuring mutual understanding within a group and strengthening their ability to convey information effectively (Varghese et al., 2025). These communication skills are essential for professional success, as employers value individuals who can work efficiently in diverse teams (Li and Liu, 2025). By experiencing interdisciplinary learning environments in school, students develop adaptability and are better prepared for future challenges in an evolving workforce (Li et al., 2023).

1.2 Culturally responsive teaching in STEAM

Culturally responsive teaching values the cultures and backgrounds of learners by integrating their lived experiences into the educational process, thereby fostering a sense of inclusion (Gay, 2018; Wang and Bussey, 2025). Instead of treating math and science as disconnected from local traditions, teachers link them to students’ cultural contexts, making learning more meaningful through approaches such as wetland-responsive teaching (Listia et al., 2025). Ladson-Billings (1995) states that when students see their identities reflected in lessons, they feel more supported and develop a stronger sense of belonging, particularly in multicultural settings (Treve, 2025). Connecting academic tasks to students’ experiences boosts interest and engagement, as demonstrated by the incorporation of Indigenous knowledge in STEM education, which validates students’ backgrounds (Melis et al., 2025). Some educators highlight regional architecture or traditional crafts to illustrate mathematical concepts, demonstrating that geometry and physics are embedded in everyday objects and practices (Katz and Katz, 1994; Anderson and Makar, 2024; Castro, 2024; Juliantara et al., 2024; Simanjuntak, 2024). This approach enables students to view mathematics as part of their history rather than a foreign concept, thereby fostering pride in their heritage and promoting academic progress (Baidabekov et al., 2023). Furthermore, culturally responsive teaching encourages discussions on historical and scientific applications, such as traditional agricultural techniques and housing designs, demonstrating how communities have applied reasoning to address specific needs without relying on modern technology (Martorana et al., 2025). These studies collectively highlight the role of culturally responsive education in enhancing student engagement, identity, and learning outcomes.

1.3 Yurt construction as a teaching tool

In Kazakhstan, the yurt symbolizes nomadic life and highlights ingenuity in design. Constructed with a circular base, angled rods, and a wooden ring at the top, yurts embody fundamental geometric concepts, including polygons, circles, and curved forms (Kozhabayev and Kostangeldinova, 2015). They also demonstrate eco-friendly construction methods, utilizing local materials such as wool or felt for insulation, and their ease of assembly suits the needs of nomadic travel (Wallace et al., 2017). These characteristics make the yurt a powerful example of how mathematics serves both cultural and practical needs.

Teachers can utilize the yurt model to help students measure lengths, compute perimeters, and understand how multiple two-dimensional pieces combine to form a three-dimensional structure (Allen, 1991). Students can explore how circle-based designs distribute weight efficiently and why a circular base enhances stability (Peppler et al., 2018). This hands-on approach transforms geometry from abstract definitions into real-world applications while illustrating how earlier communities solved complex design challenges with limited resources. Research supports the integration of yurts into mathematical instruction, demonstrating that physical models enhance spatial reasoning and mathematical problem-solving (Kozhabayev and Kostangeldinova, 2015; Wallace et al., 2017; Peppler et al., 2018).

Further supporting the integration of cultural heritage into STEAM education, studies highlight how traditional Kazakh practices enrich learning experiences. The authors emphasize that structures like yurts provide meaningful contexts for teaching engineering and geometry (Videla et al., 2024). Researchers demonstrate how traditional games and cultural activities enhance student engagement in STEAM subjects by linking learning to local heritage (Kobenova and Kaiymova, 2024). These studies provide a strong foundation for integrating culturally relevant models, such as yurt construction, into STEAM education in Kazakhstan.

1.4 Purpose of the current study

Despite increasing global interest in culturally responsive STEAM instruction, very little empirical work has examined how a single, curriculum-aligned lesson grounded in Central Asian artifacts affects middle-school geometric thinking. Existing studies on yurt-based activities (e.g., Kozhabayev and Kostangeldinova, 2015; Peppler et al., 2018) are descriptive or anecdotal, and none report systematic classroom data from Kazakhstan. This leaves an evidentiary gap concerning (i) measurable learning outcomes, (ii) students’ capacity to translate two-dimensional schema into three-dimensional forms, and (iii) the lesson’s impact on cultural identity within a formal mathematics period.

1.5 Research questions

To address that gap, the present study pursues four specific research questions (RQs):

1. RQ1: To what extent does a yurt-building lesson influence sixth-grade students’ confidence in measuring polygon sides and calculating perimeters?

2. RQ2: How does the lesson affect students’ ability to visualize and construct three-dimensional structures from two-dimensional plans?

3. RQ3: In what ways, if any, does the activity enhance students’ appreciation of Kazakh cultural heritage as embodied in traditional housing?

4. RQ4: What challenges emerge during the lesson, and how do those challenges shape both mathematical engagement and cultural reflection?

By answering these questions, the study aims to supply initial, data-driven evidence for the pedagogical value and practical constraints of embedding culturally significant artifacts in middle-school geometry instruction within the Kazakh context.

2 Methodology

This study used a single STEAM lesson to see how sixth-grade students in East Kazakhstan responded to building a yurt model. The lesson linked geometry instruction with a cultural focus on traditional housing. The teacher collected both quantitative and qualitative data to gain a deeper understanding of the outcomes. This section describes the participants and setting, the design of the lesson and materials, the procedure followed in class, the instruments used to collect data, and the methods of data analysis.

2.1 Participants and setting

Forty-four sixth-grade students participated in this study. They were from the Municipal State Institution “Secondary School No. 7” in Altai, East Kazakhstan. The class was split into two sections, labeled 6A and 6 B. Section 6A had 24 students, and Section 6B had 20 students. They were of similar age, usually around 11 or 12 years old. The lesson took place in a regular math period, which lasted about 45 min. The students were familiar with group work. Their standard classroom had tables that could accommodate small teams. The school followed national curriculum standards. It also supported teachers who wanted to try new approaches, such as STEAM-based lessons.

The teacher leading the project had prior experience with inquiry activities. She was interested in embedding local cultural elements into math. The school administrators approved the plan. They saw it as a way to enrich the geometry unit. The class environment was typical of a local public school. Each student had the essential stationery items, including pencils, rulers, and notebooks. They generally studied perimeter formulas and properties of shapes in earlier lessons. However, many had not applied these formulas in a hands-on project. This context made the yurt-building lesson a new experience for most students.

2.2 Lesson design and materials

The lesson was designed to connect geometry concepts. These mainly included measuring the sides of polygons and calculating their perimeters. The students applied these concepts to the practical task of assembling a yurt model. It also aimed to highlight the connection between yurt structures and Kazakh cultural heritage. Figure 1 shows the key materials, which include:

• Wood sticks: These represent the wooden rods that form the authentic lattice and roof supports of a yurt. Each stick measured 30 cm in length and 5 mm in diameter, providing proportional scaling to the real structure.

• Rubber bands: Students used these to tie sticks together at various angles. 16 natural rubber bands were provided for consistent joint fastening.

• Cardboard and glue: Some groups used cardboard to build a base or reinforce corners. Cardboard bases measured 25 cm in diameter and 4 mm in thickness to support the frame.

• Scissors: Allowed students to cut pieces of cardboard or trim wood sticks if needed.

• Samples of felt, eco-leather, wool, and cotton: These fabrics represented the different coverings that a yurt might have.

• A hairdryer served as a source of airflow, allowing students to test wind resistance. The model used was a Philips ThermoProtect 2,300 W dryer with a 45 mm nozzle.

Figure 1

Figure 1. Materials used in the experiment.

The teacher created a brief plan with four main steps. First, she introduced the concept of a yurt, presenting images and explaining its cultural origins. Second, she explained the geometry concepts, especially perimeter and the transition from two-dimensional shapes to three-dimensional forms. Third, she instructed teams of four to construct a mini yurt using the provided materials. Fourth, she asked them to observe how different fabric coverings influenced wind resistance. This plan aimed to integrate math skills, problem-solving, and cultural appreciation into a single session.

2.3 Procedure

The lesson took place during one 45-min math class period. The teacher began by asking students about nomadic dwellings. She mentioned yurts as an essential part of Kazakh history. Students shared any prior knowledge they had, such as how yurts were portable or used felt as insulation. This opening discussion lasted around 5 min.

Next, the teacher gave a brief talk on perimeter formulas, including those for rectangles and circles. She also reminded them that polygons have multiple sides, which they could measure and sum up. Figure 2 captures glimpses of student activity as they engaged in measuring, constructing, and testing their yurt models during the lesson. She briefly connected these formulas to the wooden rods they would use. She said that if the rods did not match the needed perimeter, the structure would be unstable. She also mentioned that angles were important since a yurt roof is domed.

Figure 2

Figure 2. Glimpses of student activity.

The main activity followed. Students watched a two-minute video showing how yurts are traditionally assembled. They saw images of the wooden lattice and the dome shape at the top. After that, they divided into teams of four. Each team was given wood sticks, rubber bands, glue, cardboard, and several small pieces of fabric. They were told to measure the sticks carefully. They also had to decide how to form a circular or polygonal base. Each group had about 25 min to plan, measure, assemble, and then test wind resistance with the hair dryer. Airflow was produced with a Philips ThermoProtect 2,300 W hair dryer, positioned 30 cm from the model at a 30° downward angle, set to high airflow without heat. The teacher walked around to offer guidance or clarify formulas. She noted whether they were using actual measurements or just estimating.

During the wind test, students covered their frames with different fabrics. They observed how the structure reacted when the air was directed at it. Some groups tried heavier fabrics first and saw the rods flex. Others switched to lighter materials. They noticed if the interior shape changed or if the frame stayed steady. The teacher encouraged them to consider how angles and shapes contribute to stability. In the final few minutes, each team shared one quick insight. For instance, one team suggested that triangular sections helped keep the dome intact. Another commented that they felt blocked airflow was addressed more effectively.

At the end of the class, each student filled out a perception survey. They also answered open-ended questions about the most challenging part of the project, the geometry ideas they found most relevant, and how the activity influenced their perspective on Kazakh culture. The teacher collected these surveys. She also took photos of the completed models and kept notes on each team’s process.

2.4 Data collection instruments

The study employed both quantitative and qualitative methods to gather information on students’ experiences. The main tools were:

2.4.1 Student perception survey

This survey had several sections. Likert scale questions used a 1–5 scale. Students rated how well they understood measuring polygon sides, calculating perimeters, distinguishing between two-dimensional and three-dimensional shapes, identifying geometric forms in real-life objects, and grasping the efficiency of circular designs. Another Likert scale question asked about the enjoyment of the learning experience. Multiple-choice questions provided three options: Yes, Partially, and No. These questions evaluated confidence, appreciation of Kazakh culture, opinion about more hands-on math lessons, and whether the students wished to learn about other traditional Kazakh structures.

There were also several open-ended prompts. These prompts asked which parts of the project were most challenging, what role geometry played in making the yurt stable, what new knowledge they gained about yurts, and how they would compare yurts to modern housing. Students could write brief paragraphs or bullet points. These responses captured more nuanced thoughts and personal reflections. The Student Perception Survey included Likert scale, multiple-choice, and open-ended questions designed to assess mathematical understanding and cultural awareness. Table 1 presents the structure of the survey, including question types and content focus areas.

Table 1

Table 1. Student perception survey on mathematics and cultural understanding in the yurt experiment.

2.4.2 Teacher observations

The teacher kept notes on how students collaborated during the activity. She recorded their measurement strategies, how they addressed perimeter errors, and whether they used specific angles when constructing the dome. She also documented group discussions about fabric choices, wind resistance, and cultural considerations. These observations helped verify whether students’ self-reports aligned with their actual behavior during the lesson. Figure 3 presents examples of teacher observations alongside student-built yurt models, highlighting how measurement accuracy and material selection affected structural outcomes.

Figure 3

Figure 3. Teacher observations of student yurt models.

2.4.3 Artifacts and photos

Each team produced a miniature model of a yurt. Some teams also made sketches showing side lengths or angles. The teacher took pictures of these prototypes to document the final designs. She also collected any worksheets that included perimeter calculations. These artifacts provided concrete examples of how teams implemented geometry. Figure 4 shows the final yurt models built by students, highlighting variations in frame shape and assembly approaches.

Figure 4

Figure 4. Yurt models made by the students.

2.4.4 Data analysis

Data analysis involved a blend of quantitative and qualitative approaches. The teacher entered survey responses into a spreadsheet to compute descriptive statistics. She calculated mean ratings for each of the five geometry-related items. She also calculated standard deviations to determine the extent of variation in students’ self-assessments. She tallied the frequency of answers for confidence in perimeter formulas, cultural appreciation, lesson enjoyment, and interest in more hands-on math.

For the qualitative part, the teacher read each open-ended response and coded them according to themes. Common themes included measurement difficulties, confusion between 2D and 3D, excitement about the hair dryer test, observations on how shapes contribute to stability, and reflections on Kazakh culture. These themes were then aligned with the teacher’s observational notes to check for consistency. For instance, if many students mentioned that heavy fabric caused structural bending, the teacher looked for corresponding notes in her logs. In that way, the study triangulated data sources to produce a clearer understanding of what happened during the lesson. Two independent coders conducted the thematic coding process. Inter-rater reliability was assessed using Cohen’s κ, yielding κ = 0.82, which indicates substantial agreement, alongside a percent agreement of 92%.

The final step was to interpret how these results answered the main research questions. This interpretation considered both numerical trends and narrative details. It also compared the findings to known research on STEAM, culturally responsive teaching, and geometry instruction. The teacher sought to see if a single lesson could bring measurable improvements or if more time and repeated practice would be necessary. She also looked at how students responded to the cultural emphasis on yurt design.

2.5 Ethical considerations

The study complied with the Declaration of Helsinki and national research guidelines. Approval was obtained from the Shokan Ualikhanov Kokshetau State University Ethical Commission Team (Protocol No 24-03-2025). Written informed consent was secured from the principal, the classroom teacher, and all parents or guardians. Students provided written assent on the day of the lesson. Participation was voluntary, and no identifiable data were collected.

2.6 Instrument development and validation

The Student Perception Survey contained six Likert-type items, four categorical items, and five open-ended prompts. Item wording was adapted from two validated sources, namely the Mathematics Self-Efficacy Scale (Cohen et al., 2018) and the Cultural Relevance in Teaching Scale (Martínez and Rivera, 2022). Three content experts in mathematics education reviewed the draft for alignment with sixth-grade curricular goals and cultural appropriateness; suggestions concerned reading level and the balance of positive versus neutral stems. A pilot administration with eight grade-six students from a neighboring school resulted in minor wording revisions. Internal consistency of the six Likert items in the present sample was acceptable, with Cronbach’s alpha equal to 0.81. Supplementary Table S1 in the Appendix lists the final survey items together with their scale anchors.

2.7 Qualitative data analysis

Open-ended responses (n = 176) and teacher field notes were analyzed using the six-phase thematic approach outlined by Braun and Clarke (2006). Two researchers independently read and coded all texts, first generating provisional codes and then clustering them into candidate themes. Coding discrepancies were discussed until consensus was reached. Intercoder agreement, calculated as the number of matching code assignments divided by the total number of assignments, was 0.92. In addition, Cohen’s κ was calculated to provide a more robust measure of inter-rater reliability, resulting in κ = 0.82, which is considered substantial agreement. Trustworthiness was further supported through analyst triangulation: themes derived from student responses were compared with teacher observations and artifact photographs to confirm convergence. Representative quotations are provided in the Results section to illustrate each final theme.

3 Results

To facilitate traceability, the findings are organized in four subsections that map directly onto the research questions (RQ1–RQ4). Table 2 summarizes the six Likert-type items (M, SD, n = 44) and Table 3 presents frequency data for all categorical items.

Table 2

Table 2. Summary of scale-based survey responses (N = 44).

Table 3

Table 3. Summary of frequency-based survey responses (N = 44).

3.1 RQ1 — confidence in measuring polygon sides and calculating perimeters

Students’ self-rated confidence in measuring sides of polygons was moderate (M = 3.48, SD = 1.17), while confidence in applying perimeter formulas was slightly higher (M = 3.61, SD = 1.26), as shown in Table 2. Only 27.3 percent of respondents selected “Yes” when asked if they felt fully confident using perimeter formulas in real situations (Table 3). A further 45.5 percent chose “Partially,” and 27.3 percent selected “No.” These patterns indicate that although the lesson fostered some perceived competence, a substantial minority still felt underprepared (Figure 5).

Figure 5

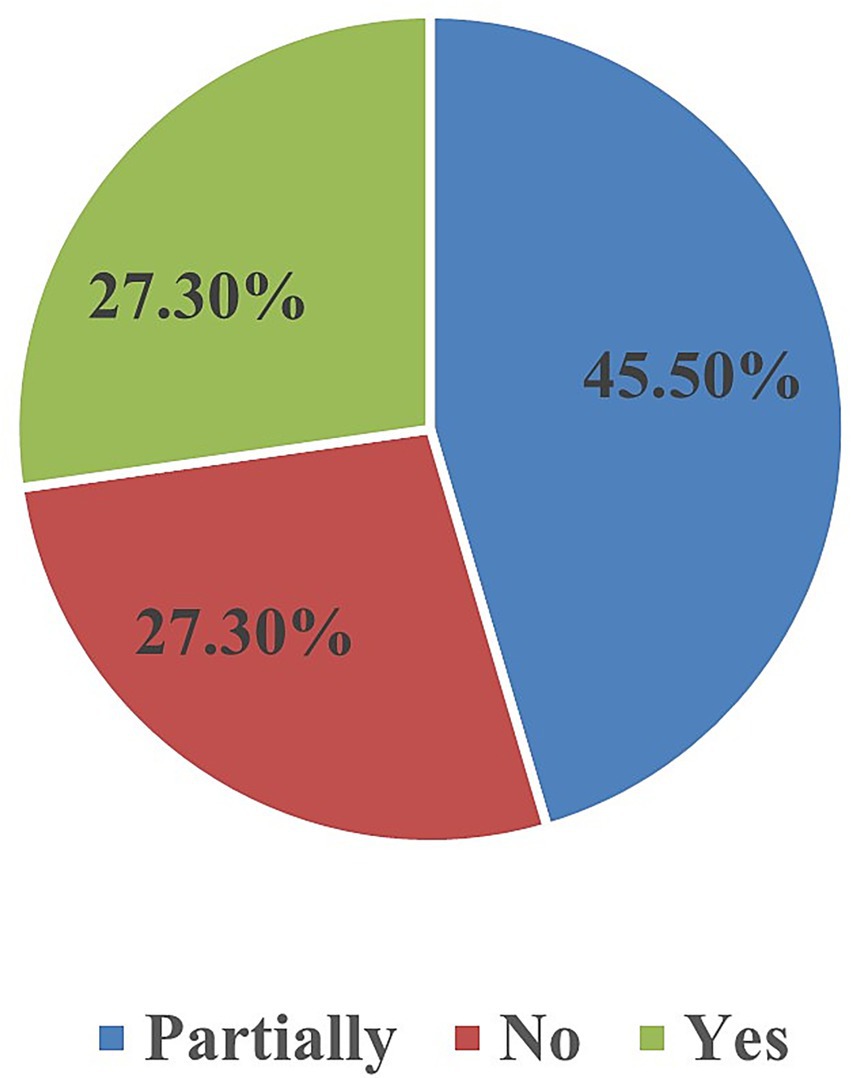
Figure 5. Distribution of student responses on confidence in using perimeter formulas in real situations (Yes, Partially, No).

3.2 RQ2 — visualizing and constructing 3-D structures from 2-D plans

The lowest-rated Likert item concerned understanding the transition from two-dimensional to three-dimensional shapes (M = 3.39, SD = 1.10). Qualitative data help explain this result. One student wrote, “I could not picture how straight sticks would bend into a curve until we tied them,” whereas another reported that “using triangles made the dome stable after many tries.” These comments illustrate persistent, yet partially resolved, difficulties with spatial visualization.

3.3 RQ3 — appreciation of Kazakh cultural heritage

A clear majority of students indicated that the activity enhanced their appreciation of Kazakh culture (Yes = 52.3 percent; Partially = 29.5 percent). Figure 6 shows this distribution visually. Open-ended responses echoed this sentiment:

• “Building the yurt made me proud that our ancestors used maths without calling it maths.”

• “I realised apartments are strong but not movable like yurts; nomads were clever.”

Figure 6

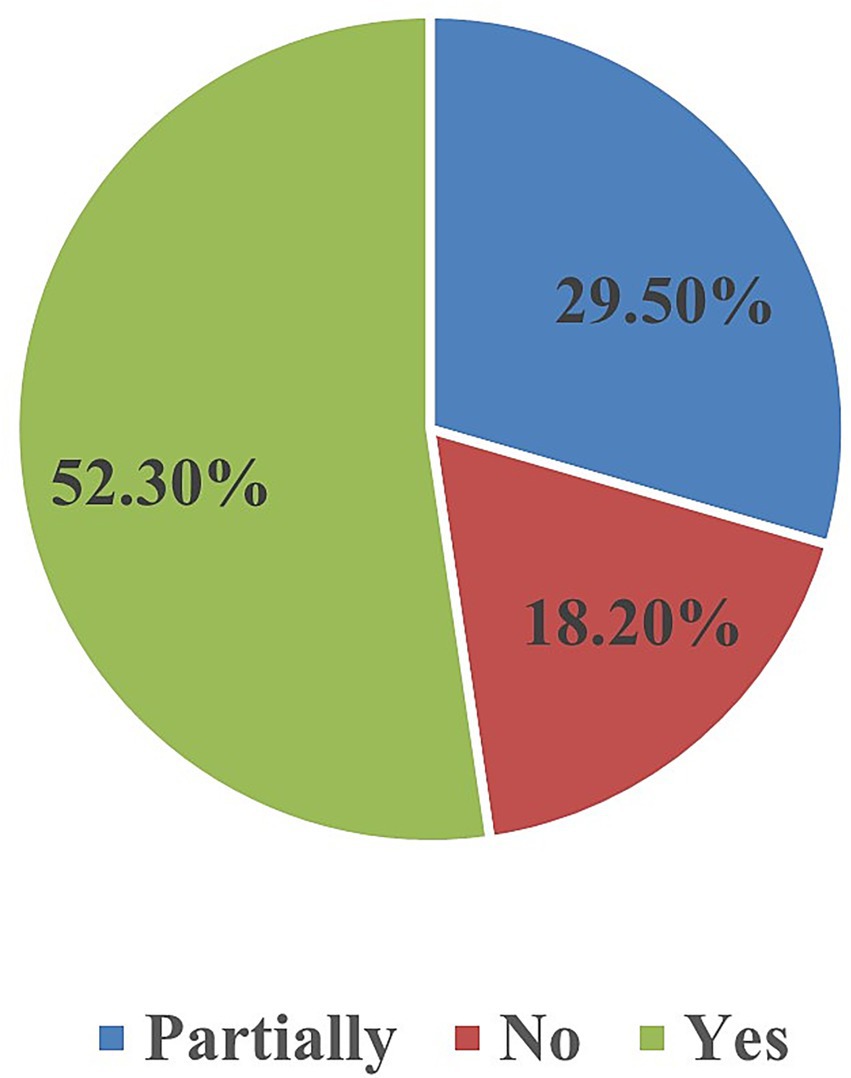
Figure 6. Distribution of student responses on whether the activity enhanced their appreciation of Kazakh culture.

These statements align with the quantitative trend and confirm that cultural connectedness was a salient outcome. Additional quantitative indicators also supported engagement with the activity: 54.5% of students expressed interest in learning about other Kazakh structures (Partially = 34.1%; No = 11.4%; Figure 7), and 63.6% wanted more hands-on mathematics lessons (Partially = 27.3%; No = 9.1%; Figure 8).

Figure 7

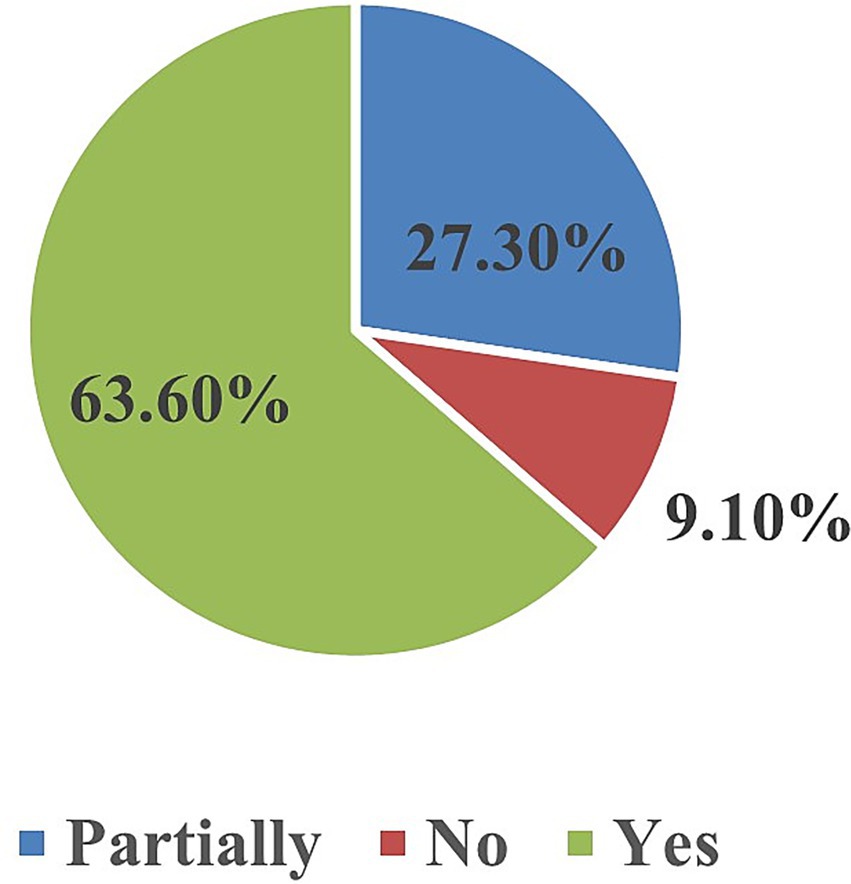
Figure 7. Distribution of student interest in learning about other Kazakh architectural designs after the activity.

Figure 8

Figure 8. Distribution of student responses regarding their desire for more hands-on mathematics lessons.

3.4 RQ4 — challenges shaping mathematical engagement and cultural reflection

Thematic analysis of 176 open-ended responses, with intercoder agreement of 0.92, produced three themes.

1. Measurement uncertainty: Students frequently mentioned “forgetting to re-check lengths,” which sometimes caused misaligned frames.

2. 2-D to 3-D struggle: Several groups “kept changing rod angles” before achieving a dome, underscoring the conceptual leap required.

3. Respect for nomadic engineering: Many learners expressed “new admiration” for how traditional builders solved design problems with limited tools.

Representative quotations are provided in the Supplementary Table S2. These themes triangulate with teacher field notes that documented repeated cutting errors and trial-and-error angle adjustments.

4 Discussion

This section interprets the findings concerning the study’s four research questions. It places the results within broader discussions of STEAM education, geometry instruction, and culturally responsive teaching. The goal is to explain how the yurt-building lesson shaped students’ math skills and cultural awareness and to explore the implications for teaching practices.

4.1 RQ1 — confidence in measuring sides and calculating perimeters

The first research question examined whether the lesson improved students’ skills in measuring polygon sides and applying perimeter formulas. These descriptive gains (Table 2) parallel Bybee’s (2019) argument that visible measurement errors make perimeter concepts salient, yet, as Honey et al. (2014) caution, a single exposure seldom yields full procedural mastery. Survey data revealed moderate self-reported proficiency, with mean ratings of 3.48 for measuring sides and 3.61 for calculating perimeters. These findings indicate that while many students felt somewhat capable, they did not exhibit high confidence in their skills. Notably, 27.3% of students reported a lack of confidence in applying perimeter formulas, while 45.5% expressed only partial confidence. Qualitative responses supported these trends, as some students reported difficulty tracking side lengths, while others were uncertain about selecting the appropriate formula. Teacher observations further corroborated these findings, noting that groups who carefully planned their perimeter calculations constructed more stable structures, whereas others miscalculated or confused measurements, leading to misaligned frames.

These results align with the work of Bybee (2013), who emphasized that hands-on tasks enhance the meaningfulness of mathematical concepts. Students who actively measured rods and observed how errors impacted structural outcomes developed a clearer understanding of numerical relationships. Similarly, Becker and Park (2011) argued that integrative projects facilitate students’ understanding of mathematical applications in real-world contexts. However, 27.3% of students who reported a lack of confidence underscores the necessity for additional practice and reinforcement.

Existing literature highlights the limitations of relying on a single lesson to achieve deep mastery. Honey et al. (2014) cautioned that while hands-on activities may generate interest, they do not necessarily ensure long-term comprehension. Nevertheless, hands-on learning has been demonstrated to enhance mathematical confidence by improving problem-solving abilities and conceptual understanding. Oeltjenbruns et al. (2024) found that interactive tasks strengthen self-efficacy and deepen mathematical comprehension. At the same time, Manuel Jacobo (2024) demonstrated that hands-on activities, particularly those incorporating digital tools, increase students’ confidence in mathematical problem-solving through applied learning approaches.

The integration of engineering design processes into mathematics instruction has also shown efficacy, particularly for students with learning disabilities. It has been reported that hands-on engineering activities support problem-solving skills and bolster confidence in mathematical reasoning (Yilmaz Bilir et al., 2025). Furthermore, Cavallaro et al. (2024) emphasized that a lack of hands-on experiences in schools negatively impacts students’ confidence, whereas interactive learning environments enhance both engagement and understanding. Collectively, these studies highlight the vital role of hands-on, design-based mathematics instruction in fostering student engagement, self-efficacy, and comprehension. They also suggest that sustained practice and iterative learning processes are essential for maximizing the benefits of hands-on educational approaches.

To further solidify perimeter-related skills, repeated practice and additional scaffolding may be required. Teacher observations indicated that some students adapted quickly, recalculating measurements in response to misalignments, demonstrating the efficacy of design-based tasks in promoting real-time learning through feedback. However, other students relied on peers or guesswork, suggesting that short pre-lesson tutorials focused on measuring and verifying dimensions could enhance overall skill development in future lessons.

4.2 RQ2 — transition from 2-D to 3-D visualization

The second research question investigated whether the lesson enhanced students’ ability to visualize and construct three-dimensional structures from flat materials. The struggle students reported (Table 2) is consistent with spatial-reasoning literature showing that hands-on manipulation plus multiple representations, such as those advocated by Azzam et al. (2024), are essential for internalizing 2-D/3-D transformations. Survey results indicated that understanding the transition from 2D to 3D had the lowest mean rating (3.39), suggesting that many students found this concept particularly challenging. Several students reported that constructing a dome proved more difficult than anticipated, as even slight variations in angles resulted in substantial differences in the final structure.

These findings align with the work of Bybee (2013), who emphasized the importance of multiple representations in developing spatial thinking skills. Young learners often require various visual and physical models to fully comprehend how flat shapes bend or fold into three-dimensional structures. Observations revealed that many student groups relied on trial and error, repeatedly adjusting the rods until they achieved a dome-like form. Quigley et al. (2017) argued that providing diagrams or digital models can minimize such guesswork and support structured learning. Teacher notes confirmed that some teams struggled to understand how angles contributed to a curved design, while others realized that a circle must be constructed from many small segments rather than a single curved piece.

The research underscores the significance of spatial reasoning and 2D-to-3D visualization in STEM education, highlighting the effectiveness of hands-on and digital tools in enhancing students’ spatial skills. Azzam et al. (2024) found that interactive technologies, including mixed reality, improve students’ ability to visualize three-dimensional structures from two-dimensional representations, facilitating a deeper understanding of spatial concepts. Similarly, Mouttalib et al. (2024) demonstrated that augmented reality (AR) enhances students’ transition from 2D to 3D thinking by incorporating digital models and interactive activities, leading to measurable improvements in spatial reasoning. Abdo et al. (2024) further confirmed that students who engaged with 3D models while solving problems developed stronger visualization skills and demonstrated a more profound conceptual understanding of scientific content. Subramaniam et al. (2024) reinforced these findings by highlighting the effectiveness of targeted spatial reasoning exercises in enhancing students’ ability to transform shapes between 2D and 3D forms mentally. Collectively, these studies suggest that integrating hands-on modeling, digital tools, and structured spatial reasoning exercises can significantly support students in mastering spatial visualization, a critical skill for success in STEM disciplines.

Despite these challenges, the lesson provided valuable opportunities for experimentation. Students observed firsthand how angled rods contributed to structural stability against wind pressure. Some students reported gaining insights into how triangular and crisscross patterns enhanced support, reinforcing the principle that learning geometry in context allows students to move beyond abstract formulas. To further develop these skills, follow-up lessons could incorporate activities such as drawing cross-sections, constructing cardboard nets, or utilizing 3D modeling software. These additional exercises would provide repeated practice, strengthening students’ spatial reasoning and improving their ability to transition from 2D to 3D thinking.

4.3 RQ3 — appreciation of Kazakh cultural heritage

This study examined whether the lesson increased students’ appreciation for Kazakh cultural housing. This pattern mirrors culturally responsive pedagogy theory, which predicts that situating mathematics in lived culture enhances motivation (Gay, 2018; Ladson-Billings, 1995). The survey results were largely positive, with 52.3% of students reporting a substantial increase in cultural appreciation and another 29.5% indicating a moderate effect. These findings suggest that over 80% of students experienced at least some growth in their respect for Kazakh traditions. Open-ended responses further highlighted how students gained a new understanding of the ingenuity of nomadic life, recognizing that mathematical principles were embedded in yurt construction long before modern tools existed.

Ladson-Billings (1995) argued that culturally relevant teaching integrates academic content with students’ cultural identity, and the findings of this study suggest that the Yurt project aligned with this principle. Students not only practiced measuring and calculating but also discovered that their cultural heritage involved applied mathematics. Gay (2018) describes this connection between culture and curriculum as a powerful motivator, allowing students to view their background as a source of knowledge rather than merely historical information.

The role of culturally responsive teaching in promoting student engagement and fostering an appreciation for cultural heritage in STEM education has been widely documented. Akbar and Cohen (2025) found that integrating cultural relevance into engineering design fosters deeper learning connections and enhances student engagement. Similarly, Wang and Bussey (2025) emphasized that incorporating cultural identity into science education improves student motivation and reinforces inclusive pedagogical approaches. Listia et al. (2025) demonstrated that embedding local culture within scientific learning models strengthens students’ appreciation of their heritage while promoting active participation in the learning process. These findings were supported by highlighting how culturally relevant assessment practices contribute to meaningful engagement and improved learning outcomes in STEM disciplines (Trumbull and Nelson-Barber, 2025). Collectively, these studies suggest that culturally responsive STEM education enhances student engagement while fostering a stronger connection to cultural heritage, ultimately supporting more inclusive and effective learning environments.

Teacher observations further reinforced these findings. Many students expressed curiosity about other Kazakh structures and inquired about how families lived in yurts year-round, demonstrating engagement beyond the lesson’s core focus. Some students also noted the eco-friendly features of the yurt, considering how traditional designs might inspire modern architecture. The teacher remarked that these discussions extended beyond typical math lessons, suggesting that linking geometry to cultural heritage can spark interdisciplinary insights and deepen student engagement.

4.4 RQ4 — challenges that shaped learning and reflection

The fourth research question investigated the challenges students encountered during the lesson and how these difficulties affected their mathematical understanding and cultural engagement. Similar “productive-challenge” dynamics are documented in design-based STEM studies where initial frustration ultimately deepens conceptual understanding (Quigley et al., 2017). The most commonly reported challenges included measurement accuracy, dome formation, and wind resistance. Some students struggled to verify rod lengths due to time constraints, while others found that heavier fabrics placed additional stress on the frame. Groups that carefully planned their measurements and assigned roles generally achieved better structural stability, whereas those who proceeded without a clear strategy encountered repeated errors.

These challenges often became valuable learning experiences. For instance, a group that cut their rods too short had to recalculate the perimeter, reinforcing the practical application of perimeter formulas. Another group experimented with a triangular lattice and observed improved stability, deepening their understanding of how angles contribute to structural strength. Quigley et al. (2017) suggest that real-world obstacles can enhance learning when students are encouraged to solve problems independently. In this study, the teacher provided guiding questions rather than direct answers, fostering student-led problem-solving.

Design-based STEM education has been shown to improve problem-solving skills and mathematical comprehension. Subramaniam et al. (2024) demonstrated that interdisciplinary problem-solving in STEM enhances mathematical reasoning, critical thinking, and the application of knowledge to real-world scenarios. English (2024) further highlighted that mathematical problem-solving strengthens when students apply formulas in practical engineering tasks, reinforcing learning through hands-on experiences. Similarly, Şenel and Şenel (2024) found that design-based learning fosters critical thinking and mathematical skills, mainly when students engage with real-world design challenges. These findings were supported by demonstrating that design-based learning enables students to experiment with mathematical relationships, leading to a deeper conceptual understanding (Parve et al., 2024). Collectively, these studies affirm that engaging students in design-based problem-solving activities enhances both mathematical comprehension and overall engagement in STEM education.

From a cultural perspective, students developed a greater appreciation for traditional yurt construction by building a stable model themselves. Many expressed newfound respect for how nomadic ancestors constructed durable homes without modern tools. This emotional connection, even when formed through moments of frustration, appeared to increase engagement. Becker and Park (2011) emphasize that design-based tasks not only strengthen problem-solving skills but also highlight the real-world relevance of mathematical concepts. In this study, the interplay between mathematical problem-solving and cultural awareness enriched the overall learning experience.

4.5 Linking the findings to STEAM and culturally responsive teaching

The findings suggest that a single STEAM-based activity can lead to moderate improvements in students’ geometry skills, promote cultural appreciation, and identify areas that require further instructional support. The moderate gains observed in measuring sides and calculating perimeters align with Bybee (2013), who asserts that real-world applications encourage students to engage more effectively with mathematical formulas. Additionally, the challenges students faced in transitioning from two-dimensional to three-dimensional thinking corroborate prior research, which suggests that multiple representations and hands-on modeling enhance spatial reasoning (Quigley et al., 2017). The strong cultural engagement observed in this study aligns with the work of Gay (2018) and Ladson-Billings (1995), who emphasize that culturally relevant teaching increases student motivation and curiosity.

STEAM education has been widely recognized for its capacity to enhance both geometry skills and cultural engagement. Pramasdyahsari et al. (2025) found that incorporating cultural elements into geometry education fosters mathematical creativity and engagement, paralleling how the yurt project integrated mathematical concepts with cultural heritage. Similarly, Souza and Ferreira (2025) emphasized that STEAM activities improve spatial reasoning and geometry skills while promoting inclusive engagement, reinforcing the importance of repeated exposure to mathematical concepts. Lavicza et al. (2018) demonstrated that interdisciplinary STEAM approaches deepen students’ understanding of geometric structures, supporting the notion that hands-on lessons strengthen spatial thinking. Additionally, Johnston et al. (2022) highlighted that integrating geometry, measurement, and spatial skills into STEAM curricula enhances student engagement and conceptual mastery. Collectively, these studies confirm that STEAM-based lessons improve both mathematical skills and cultural appreciation, aligning with the findings of this research.

However, the data suggest that a single lesson is insufficient for achieving complete mastery. While many students demonstrated partial confidence in their skills, 27.3% still reported difficulties with perimeter formulas. This aligns with Honey et al. (2014), who argue that meaningful learning requires repeated exposure and reinforcement. To solidify learning outcomes, educators may consider incorporating additional lessons that apply geometric concepts to other local structures. Furthermore, short mini-lessons focusing on perimeter calculations and shape transformations can help students advance from moderate self-assessments to higher proficiency.

The variation in group collaboration effectiveness also highlights the importance of structured roles in collaborative learning. Some groups effectively allocated tasks and demonstrated deeper insights, while others lacked organization, resulting in errors and miscommunication. Quigley et al. (2017) suggest that assigning clear roles such as “measurer,” “assembler,” and “quality checker” can enhance engagement and ensure equitable learning opportunities. Student participation and confidence in mathematical tasks can be maximized if educators consider rotating these roles in future activities, allowing all students to develop proficiency across different aspects of problem-solving and construction.

5 Recommendations for practice

1. Integrating Local Artifacts into Mathematics Lessons: Educators can enhance mathematical instruction by incorporating culturally significant artifacts that illustrate core mathematical concepts. In Kazakhstan, the yurt serves as an example of applied geometry and measurement principles. Similarly, other regions may have traditional structures or crafts that exemplify mathematical concepts such as measurement, geometry, and physics. Research suggests that contextualizing mathematics through culturally relevant artifacts fosters deeper student engagement (Ladson-Billings, 1995; Gay, 2018).

2. Ensuring Repeated Exposure and Scaffolding: While a single lesson can introduce mathematical concepts and enhance motivation, it is insufficient for developing mastery. Repeated exposure and structured scaffolding are necessary for reinforcing perimeter formulas, shape transformations, and spatial reasoning. Honey et al. (2014) emphasized the importance of sustained practice in mathematics education. To support students who lack confidence, educators should implement targeted reviews and incremental practice sessions before engaging in hands-on applications.

3. Supporting 2D-to-3D Visualization: Students often struggle to conceptualize how flat components transform into three-dimensional structures. Providing instructional supports such as paper nets, cardboard cutouts, or digital simulations can facilitate this transition by reinforcing the geometric relationships between 2D and 3D forms. Quigley et al. (2017) highlight the value of multiple representations in supporting spatial reasoning and reducing reliance on trial and error. These instructional aids can systematically enhance students’ understanding of angles, arcs, and structural stability.

4. Structuring Group Collaboration: Collaborative learning can improve mathematical comprehension when group roles are clearly defined. Assigning specific responsibilities, such as measurement, calculation, assembly, and structural testing, ensures that all students actively engage with mathematical concepts. Quigley et al. (2017) emphasize that structured collaboration prevents unequal participation and fosters equitable learning experiences. Additionally, rotating roles across multiple lessons can help students develop confidence in various mathematical tasks.

5. Emphasizing Environmental and Cultural Perspectives: Mathematics lessons incorporating cultural artifacts also provide opportunities for interdisciplinary learning. Discussions on sustainability and local heritage can complement mathematical instruction by illustrating how traditional structures, such as yurts, are adapted to environmental and societal needs. Research by Paris et al. (2017) underscores the significance of integrating cultural identity into STEM education, as it enhances both student motivation and conceptual understanding. By linking mathematical principles to historical and ecological contexts, educators can promote holistic and interdisciplinary learning.

6 Limitations and future research

Several factors constrain the inferences that can be drawn. First, data were collected in a single 45-min lesson at one public school, so external validity is necessarily limited. Second, perceived learning gains rely on post-lesson self-report; although the six-item scale showed acceptable reliability (α = 0.81), objective pre−/post-assessments of geometric knowledge were not administered. Third, the classroom teacher also served as the primary observer, introducing potential researcher bias despite systematic note-taking. Fourth, the novelty of the activity and the researchers’ presence could have generated a Hawthorne effect, inflating engagement ratings. Finally, because the yurt holds strong symbolic meaning in Kazakh culture, results may not translate directly to contexts lacking a comparable artifact.

Future work should address these constraints by implementing multi-session sequences across several schools, incorporating objective outcome measures such as perimeter quizzes or rubric-scored artifacts, and employing independent observers to mitigate bias. Comparative designs that contrast culturally embedded tasks with culturally neutral tasks would help disentangle whether observed benefits arise from the cultural context, the hands-on format, or their interaction. Researchers might also test digital scaffolds, for example, CAD sketches or augmented-reality overlays, to support the 2-D to 3-D transition identified here as a persistent challenge.

7 Conclusion

The yurt-building lesson demonstrated the potential of integrating mathematical instruction with cultural elements through a single STEAM activity. The findings indicate that students developed moderate proficiency in geometry, particularly in measurement and perimeter application, while also increasing their appreciation for Kazakh heritage. Many students expressed a desire to explore local structures further and engage in additional hands-on mathematical learning.

Despite certain limitations, including time constraints and variations in group dynamics, the overwhelmingly positive student responses highlight the effectiveness of culturally responsive STEAM education in fostering engagement. With additional scaffolding and repeated exposure, students could achieve greater mastery of geometry concepts while simultaneously strengthening their connection to regional traditions. This study underscores the importance of integrating academic content with authentic cultural contexts to enhance motivation, foster cultural identity, and support meaningful learning experiences.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by Shokan Ualikhanov Kokshetau State University Ethical Commission Team. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

DK: Formal analysis, Methodology, Writing – original draft, Conceptualization. SS: Supervision, Methodology, Writing – original draft, Data curation, Conceptualization, Project administration, Investigation. AK: Writing – review & editing, Resources, Validation. GT: Visualization, Formal analysis, Writing – review & editing. AS: Supervision, Writing – review & editing, Funding acquisition.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors would like to express their gratitude to the administration and staff at Municipal State Institution “Secondary School No. 7” in Altai, East Kazakhstan. Their support made it possible to conduct this lesson during a regular math class. The authors also thank the students who participated in the project and shared their feedback openly. Their enthusiasm and curiosity were key to the success of this study. In addition, the authors acknowledge colleagues who provided advice on designing a culturally centred lesson. They offered suggestions on how to effectively integrate math content with local heritage.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1622697/full#supplementary-material

References

Abdo, S. N., Hsu, J. L., Kapetanakis, C., Newman, D. L., Wright, L. K., and Bailey, J. (2024). An exploration of spatial visualization skills: investigating students’ use of 3D models in science problems during think-aloud interviews. J. Chem. Educ. 101, 3624–3634. doi: 10.1021/ACS.JCHEMED.3C01355

PubMed Abstract | Crossref Full Text | Google Scholar

Abildinova, G., Abdykerimova, E., Assainova, A., Mukhtarkyzy, K., and Abykenova, D. (2024). Preparing educators for the digital age: teacher perceptions of active teaching methods and digital integration. Front. Educ. 9:1473766. doi: 10.3389/feduc.2024.1473766

Crossref Full Text | Google Scholar

Akbar, S., and Cohen, J. (2025). Inclusive innovation: How culturally relevant engineering design shapes student engagement in K-12 STEM classrooms. Preprint. doi: 10.13140/RG.2.2.17640.79363

Crossref Full Text | Google Scholar

Allen, J. A. (1991). Eureka! A yurt! Integrating mathematics, cooperative learning, and community service. J. Exper. Educ. 14:39.

Google Scholar

Anderson, J., and Makar, K. (2024). The contribution of mathematics to school STEM education. Singapore: Springer.

Google Scholar

Azzam, I., Breidi, F., Aqlan, F., Garcia, J. M., and Asunda, P. (2024). Mixed reality as a teaching Tool for improving spatial visualization in engineering students. Washington, DC: American Society for Engineering Education.

Google Scholar

Baidabekov, A., Kemelbekova, E., and Sadykova, Z. (2023). The study of geometric laws in the patterns of the KHOJA AHMED YASAWI complex. Kazakhstan: VII World Congress of Turkic World Mathematicians, 314–323.

Google Scholar

Bai, Q., and Nam, B. H. (2024). Institutional habitus, cultural capital, and STEAM learner identity in the context of rural Chinese technical vocational education and training: critical participatory action research. Asia Pac. Educ. Rev., 1–16. doi: 10.1007/S12564-024-09979-W

Crossref Full Text | Google Scholar

Becker, K., and Park, K. (2011). Effects of integrative approaches among science, technology, engineering, and mathematics (STEM) subjects on students’ learning: a preliminary meta-analysis. J. STEM Educ. Innov. Res. 12, 23–37.

Google Scholar

Belbase, S., Mainali, B. R., Kasemsukpipat, W., Tairab, H., Gochoo, M., and Jarrah, A. (2022). At the dawn of science, technology, engineering, arts, and mathematics (STEAM) education: prospects, priorities, processes, and problems. Int. J. Math. Educ. Sci. Technol. 53, 2919–2955. doi: 10.1080/0020739X.2021.1922943

Crossref Full Text | Google Scholar

Bertrand, M. G., and Namukasa, I. K. (2020). STEAM education: student learning and transferable skills. J. Res. Innov. Teach. Learn. 13, 43–56. doi: 10.1108/jrit-01-2020-0003

Crossref Full Text | Google Scholar

Blanco-García, Y., Serrano, R. M., and Casanova, O. (2025). Toward a transversal education model: a review of digital and artistic-musical competencies (2014-2024). Arts Educ. Policy Rev. 10:9917. doi: 10.1080/10632913.2025.2459917

Crossref Full Text | Google Scholar

Braun, V., and Clarke, V. (2006). Using thematic analysis in psychology. Qual. Res. Psychol. 3, 77–101. doi: 10.1191/1478088706qp063oa

Crossref Full Text | Google Scholar

Burnard, P., Colucci-Gray, L., and Sinha, P. (2021). Transdisciplinarity: letting arts and science teach together. Curr. Perspect. 41, 113–118. doi: 10.1007/s41297-020-00128-y

Crossref Full Text | Google Scholar

Bush, S. B., and Cook, K. L. (2019). “Structuring STEAM inquiries: lessons learned from practice” in STEAM education: theory and practice. eds. M. S. Khine and S. Areepattamannil (Cham: Springer).

Google Scholar

Bybee, R. (2013). The case for STEM education: challenges and opportunities. California: NSTA Press.

Google Scholar

Bybee, R. W. (2019). Guest editorial: using the BSCS 5E instructional model to introduce STEM disciplines. Sci. Child. 56, 8–12. doi: 10.2505/4/sc19_056_06_8

Crossref Full Text | Google Scholar

Castro, R. S. (2024). Weaving the harmony of cultures into the infinite tapestry of mathematics. ARACÊ 6, 219–230. doi: 10.56238/AREV6N1-013

Crossref Full Text | Google Scholar

Cavallaro, A., Lauri, L., Llorente Lopez, A., and Romano, M. (2024). Designing an AR app for enhancing STEM learning experiences in high schools. ICERI Proc. 1, 8899–8907. doi: 10.21125/ICERI.2024.2238

Crossref Full Text | Google Scholar

Cohen, L., Manion, L., and Morrison, K. (2018). Research methods in education. London: Routledge.

Google Scholar

Connor, A. M., Karmokar, S., and Whittington, C. (2015). From STEM to STEAM: strategies for enhancing engineering & technology education. Int. J. Eng. Pedagogy 5:37. doi: 10.3991/ijep.v5i2.4458

Crossref Full Text | Google Scholar

Dignam, C. (2025). Makerspace and the 5 c’s of learning: constructing, collaborating, communicating, critically-thinking, and creatively-thinking. Int. J. Stud. Educ. Sci. 6, 104–127. doi: 10.46328/IJSES.135

Crossref Full Text | Google Scholar

English, L. (2024). Design-based mathematical modelling within STEM contexts. Singapore: Springer, 181–199.

Google Scholar

Gay, G. (2018). Culturally responsive teaching: theory, research, and practice. Washington, DC: Teachers College Press.

Google Scholar

Golegou, E., and Peppas, K.. (2025). Impact of the COVID-19 pandemic on Stem education and skills: a case study approach. Available online at: https://www.preprints.org/manuscript/202502.0716/v1 (Accessed March 18, 2025).

Google Scholar

Harris, A. M., and de Bruin, L. (2017). Steam education: fostering creativity in and beyond secondary schools. Aust. Art Educ. 38, 54–75. doi: 10.3316/aeipt.221400

Crossref Full Text | Google Scholar

Honey, M. A., Pearson, G., and Schweingruber, H. (2014). STEM integration in K-12 education: Status, prospects, and an agenda for research. Washington, DC: The National Academies Press, 1–165.

Google Scholar

Hougaard, R. F., Andersen, F. D., and Tørring, T.. (2024). Scaffolding scientific inquiry: adapting tiny earth for engaging high school students and their teachers in authentic research. Available online at: https://pure.au.dk/portal/en/publications/scaffolding-scientific-inquiry-adapting-tiny-earth-for-engaging-h (Accessed May 2, 2025).

Google Scholar

Johnston, K., Kervin, L., and Wyeth, P. (2022). STEM, STEAM, and makerspaces in early childhood: a scoping review. Sustainability 14:533. doi: 10.3390/SU142013533

Crossref Full Text | Google Scholar

Juliantara, K. D., Astawa, I. W. P., and Ardana, I. M. (2024). Stem-based learning module oriented towards Balinese ethnomathematics to enhance students’ creative mathematical thinking abilities. J. Pedagogi dan Pembelajaran 7, 262–269. doi: 10.23887/JP2.V7I2.83930

Crossref Full Text | Google Scholar

Karatayeva, Z., Abildinova, G., Karaca, C., and Mukhtarkyzy, K. (2024). Integrated application of digital technologies in interconnected energy sources in renewable energy education. World Trans. Eng. Technol. Educ. 22, 196–204.

Google Scholar

Katz, V. J., and Katz, V. J. (1994). Ethnomathematics in the classroom. Int. J. Math. Educ. 14, 26–30.

Google Scholar

Kobenova, A., and Kaiymova, A. (2024). Making beshbarmak: games for central Asian cultural heritage. Available online at: https://arxiv.org/pdf/2410.09670 (Accessed May 2, 2025).

Google Scholar

Kozhabayev, K. G., and Kostangeldinova, A. A. (2015). Elements of mathematics with Kazakh people’s ethnical colorfulness on an example of yurt. Eur. J. Nat. Hist. 6, 22–24.

Google Scholar

Ladson-Billings, G. (1995). Toward a theory of culturally relevant pedagogy. Am. Educ. Res. J. 32, 465–491. doi: 10.3102/00028312032003465

Crossref Full Text | Google Scholar

Lage-Gómez, C., and Ros, G. (2023). How transdisciplinary integration, creativity, and student motivation interact in three STEAM projects for gifted education? Gift. Educ. Int. 39, 247–262. doi: 10.1177/02614294231167744

Crossref Full Text | Google Scholar

Lavicza, Z., Fenyvesi, K., Hohenwarter, M., Diego-Mantecon, J. M., and Prodromou, T. (2018). Mathematics learning through arts, technology and robotics: Multi-and transdisciplinary STEAM approaches. Taipei, Taiwan: National Taiwan Normal University.

Google Scholar

Leavy, A., Dick, L., Meletiou-Mavrotheris, M., Paparistodemou, E., and Stylianou, E. (2023). The prevalence and use of emerging technologies in STEAM education: a systematic review of the literature. J. Comput. Assist. Learn. 39, 1061–1082. doi: 10.1111/jcal.12806

Crossref Full Text | Google Scholar

Li, K. C., Wong, B. T. M., and Chan, H. T. (2023). Teaching and learning innovations for distance learning in the digital era: a literature review. Front. Educ. 8:8034. doi: 10.3389/feduc.2023.1198034

Crossref Full Text | Google Scholar

Li, M., and Liu, X. (2025). Enhancing humanities and social sciences curriculum in engineering institutions by using interdisciplinary approaches. Cogent Educ. 12:3831. doi: 10.1080/2331186X.2024.2433831

Crossref Full Text | Google Scholar

Listia, A. P., Wijayanti, A., Ernawati, T., and Septiani, D. (2025). Integration of local culture in the search, solve, create, and share (SSCS) learning model to improve scientific literacy: a literature review. Formatif 15, 357–374. doi: 10.30998/FORMATIF.V15I1.27945

Crossref Full Text | Google Scholar

Manuel Jacobo, G. C. (2024). From frustration to understanding: the power of hands-on activities in teaching conic functions. in ICERI2024 Proceedings. IATED. p. 1613–1618. doi: 10.21125/iceri.2024.0478

Crossref Full Text | Google Scholar

Martínez, G., and Rivera, H. (2022). Development and validation of the cultural relevance in teaching scale. J. Educ. Res. 115, 389–403. doi: 10.1080/00220671.2021.1964320

Crossref Full Text | Google Scholar

Martorana, A., Katta, S., Huynh, H., Ulger, E., and Andrion, J. (2025). Critical theory and cultural competency in medical QI projects: lessons from Pacific islander communities. J. Biosoc. Sci. 57, 257–262. doi: 10.1017/S0021932025000100

PubMed Abstract | Crossref Full Text | Google Scholar

Matsushima, M., Nishimura, K., and Ueda, R.. (2025). Citizenship development through value-based consensus building in mathematical sciences education. Available online at: https://www.researchgate.net/publication/389137546 (Accessed May 2, 2025).

Google Scholar

Melis, C., Kvivesen, M., and Munkebye, E. (2025). Perspectives from science teacher educators on the potential contribution of Sámi traditional knowledge to sustainable development. Front. Educ. 10:1563706. doi: 10.3389/FEDUC.2025.1563706/BIBTEX

Crossref Full Text | Google Scholar

Mouttalib, H., Tabaa, M., Youssfi, M., and Bounouader, Y. (2024). Work-in-Progress—Augmented reality in higher education: case of electrical drawings. California: The Immersive Learning Research Network, 238–232.

Google Scholar

Mustadi, A., and Junaidi, A. D. (2024). The implementation of Cambridge curriculum in the international elementary school. Int. J. Elem. Educ. 8, 122–131. doi: 10.23887/IJEE.V8I1.64803

Crossref Full Text | Google Scholar

Needles, T.. (2020). STEAM power: infusing art into your STEM curriculum. Available at: https://books.google.com/books/about/STEAM_Power.html?hl=ru&id=4cefyQEACAAJ (Accessed May 2, 2025).

Google Scholar

Oeltjenbruns, S., Weyers, M., Fogarty, M., and Matera, B.. (2024). Developing problem-solvers: cultivating a scientific way of thinking in early learners. Available online at: https://openriver.winona.edu/eie/vol30/iss2/14 (Accessed May 2, 2025).

Google Scholar

Papavlasopoulou, S., Giannakos, M. N., and Jaccheri, L. (2019). Exploring children’s learning experience in constructionism-based coding activities through design-based research. Comput. Human Behav. 99, 415–427. doi: 10.1016/j.chb.2019.01.008

Crossref Full Text | Google Scholar

Paris, D., Alim, H. S., Kinloch, V., Bucholtz, M., Casillas, D. I., Lee, J.-S., et al. (2017). Culturally sustaining pedagogies: Teaching and learning for justice in a changing world. New York: Teachers College Press.

Google Scholar

Parve, K., Laanpere, M., and Hallika, L.. (2024). Validating a computational thinking assessment tool in the context of steam education. Available online at: https://library.iated.org/authors/Liisa_Hallika (Accessed May 3, 2025).

Google Scholar

Peppler, K. A., Sedas, M., Banks, T., Searcy, J., and Wallace, S. R. (2018). Design math: middle-school youth making math by building yurts. London, UK: International Society of the Learning Sciences, Inc.

Google Scholar

Perignat, E., and Katz-Buonincontro, J. (2018). From STEM to STEAM: using brain-compatible strategies to integrate the arts. Arts Educ. Policy. Rev. 119:970. doi: 10.1080/10632913.2017.1300970

Crossref Full Text | Google Scholar

Perignat, E., and Katz-Buonincontro, J. (2019). Steam in practice and research: an integrative literature review. Think. Skills Creat. 31, 31–43. doi: 10.1016/j.tsc.2018.10.002

Crossref Full Text | Google Scholar

Pramasdyahsari, A. S., Rubowo, M. R., Nindita, V., Astutik, I. D., Pant, B. P., Dahal, N., et al. (2025). Developing engaging STEAM-geometry activities: fostering mathematical creativity through the engineering design process using Indonesian cuisine context. Infin. J. 14, 213–234. doi: 10.22460/INFINITY.V14I1.P213-234

Crossref Full Text | Google Scholar

Quigley, C. F., Herro, D., and Jamil, F. M. (2017). Developing a conceptual model of STEAM teaching practices. Sch. Sci. Math. 117, 1–12. doi: 10.1111/ssm.12201

Crossref Full Text | Google Scholar

Rabalais, M. E. (2014). STEAM: A national study of the integration of the arts into STEM instruction and its impact on student achievement (Ph.D. dissertation, University of Louisiana at Lafayette). ProQuest Dissertations & Theses Global.

Google Scholar

Şenel, H. C., and Şenel, S. (2024). Assessment of computational thinking skills. in Integrating computational thinking through design-based learning: strategies for integration in different disciplines. Chapter 12. eds. M. Saritepeci and H. Yildiz Durak (Singapore: Springer), pp. 209–230. doi: 10.1007/978-981-96-0853-9_12

Crossref Full Text | Google Scholar

Simanjuntak, M. B.. (2024). Integrating Ethnomathematics and design research in STEM education: a case study in maritime institutes. Available online at: https://seminar.ustjogja.ac.id/index.php/edumatnesia/article/view/2058 (Accessed May 2, 2025).

Google Scholar

Souza, D. P., and Ferreira, H. S. (2025). Potentials of the science, technology, engineering, arts and mathematics (STEAM) education for gender inclusion in science: a systematic literature review. Rev. Electrón. Enseñ. Cienc. 24, 186–207.

Google Scholar

Subramaniam, R. C., Morphew, J. W., Rebello, C. M., and Rebello, N. S. (2024). Presenting a STEM ways of thinking framework for engineering design-based physics problems. Available online at: https://arxiv.org/abs/2411.11654 (Accessed March 18, 2025).

Google Scholar

Treve, M. (2025). Pluralism and the culture of education in Thailand: a bibliometric analysis. Policy Fut. Educ. 23, 1086–1101. doi: 10.1177/14782103251323089

Crossref Full Text | Google Scholar

Trumbull, E., and Nelson-Barber, S. (2025). “Reflections on some current approaches to culturally responsive assessment—Commentary on section 3” in Culturally responsive assessment in classrooms and large-scale contexts: theory, research, and practice. ed. M. E. Carla (New York: Routledge), 337–348.

Google Scholar

Varghese, N. N., Jose, B., Bindhumol, T., Cleetus, A., and Nair, S. B. (2025). The power duo: unleashing cognitive potential through human-AI synergy in STEM and non-STEM education. Front. Educ. 10:4582. doi: 10.3389/FEDUC.2025.1534582

PubMed Abstract | Crossref Full Text | Google Scholar

Vicente, F. R., Zapatera Llinares, A., and Montes Sánchez, N. (2021). Curriculum analysis and design, implementation, and validation of a STEAM project through educational robotics in primary education. Comput. Appl. Eng. Educ. 29, 160–174. doi: 10.1002/cae.22373

Crossref Full Text | Google Scholar

Videla, R., Aguayo, C., Aguilera, J., Aros, M., Ibacache, C., Valdivia, P., et al. (2024). Cultivating cultural heritage and fostering belonging in communities through digital and non-digital technologies in generative STEAM education. Knowl. Cult. 12:48. doi: 10.22381/KC12220242

Crossref Full Text | Google Scholar

Wallace, S., Searcy, J., Banks, T., Sedas, M., and Peppler, K.. (2017). Design math: a design and project-based effort to learn geometry in middle school through fabric-based yurts. Available online at: http://hexayurt.com. (Accessed May 2, 2025).

Google Scholar

Wang, S., and Bussey, T. J. (2025). Re-envisioning classroom culture in an introductory general chemistry course: description of a course redesign project. Educ. Sci. 15:307. doi: 10.3390/EDUCSCI15030307

PubMed Abstract | Crossref Full Text | Google Scholar

Wilson, H. E., Song, H. H., Johnson, J., Presley, L., and Olson, K. (2021). Effects of transdisciplinary STEAM lessons on student critical and creative thinking. J. Educ. Res. 114, 445–457. doi: 10.1080/00220671.2021.1975090

PubMed Abstract | Crossref Full Text | Google Scholar

Yilmaz Bilir, E., Bilir, C. K., and Soybas, D.. (2025). Supporting the self-confidence of a student with mathematics learning disabilities through the engineering design process. Available online at: https://docs.lib.purdue.edu/instemed/2025/briefs/1/ (Accessed March 18, 2025).

Google Scholar

Yumin, Z., and Isa, Z. B. M. (2024). Integrating art and engineering in Hebei’s STEAM education. J. Digit. Real. Mast. 3, 49–63. doi: 10.56982/DREAM.V3I05.238

Crossref Full Text | Google Scholar