Towards actionable recommendations for exam preparation using isomorphic problem banks and Explainable Machine Learning

Introduction: Many studies have demonstrated that Machine Learning algorithms can predict students’ exam outcomes based on a variety of student data. Yet it remains a challenge to provide students with actionable learning recommendations based on the predictive model outcome.

Methods: This study examined whether actionable recommendations could be achieved by synchronous innovations in both pedagogy and analysis methods. On the pedagogy side, one exam problem was selected from a large bank of 44 isomorphic problems that was open to students for practice 1 week ahead of the exam. This ensures near-perfect alignment between learning resources and assessment items. On the algorithm side, we compare three Machine Learning models to predict student outcomes on the individual exam problems and a similar transfer problem, and identify important features.

Results: Our results show that 1. The best ML model can predict single exam problem outcomes with >70% accuracy, using learning features from the practice problem bank. 2. Model performance is highly sensitive to the level of alignment between practice and assessment materials. 3. Actionable learning recommendations can be straightforwardly generated from the most important features. 4. The problem bank-based assessment mechanism did not encourage rote learning and exam outcomes are independent of which problems students had practiced on before the exam.

Discussion: The results demonstrated the potential for building a system that could provide data driven recommendations for student learning, and has implications for building future intelligent learning environments.

1 Introduction

Predicting students’ outcomes on future assessments from students’ learning data using Machine Learning (ML) has been one of the major focuses of learning analytics and educational data mining (Arizmendi et al., 2022; Papamitsiou et al., 2020; Tomasevic et al., 2020). While the immediate goal of predictive analysis is to identify students potentially at risk of failing the test, the overall objective has always been to provide students with targeted interventions to improve assessment outcomes and avoid failing. Therefore, an ideal predictive model would not only predict likely outcome, but also make actionable learning recommendation for students to improve the outcome. In particular, most students would benefit from three types of recommendations: Am I ready for the exam? What should I study to get ready for the exam? How should I study to get ready for the exam? Moreover, predictive models could also provide instructors with information on how interventions are contributing to students’ assessment performance, allowing for data driven improvement to interventions.

However, as discussed in detail below, many existing predictive ML models have limited ability in translating prediction outcome into actionable interventions or recommendations (Liu et al., 2023), especially regarding what and how to study for an exam. We believe that overcoming those limitations requires innovations in both pedagogy and analytical methods at the same time. In this paper we present a case where an innovation in assessment method, based on large isomorphic problem banks, combined with Explainable Machine Learning (xML), has the potential to significantly improve the ability of ML models to make actionable recommendations on how students could better prepare for an upcoming exam.

1.1 Existing predictive analysis methods and their limitations

Existing research on using Machine Learning (ML) methods to predict students’ course or assessment outcomes utilizes a variety of data sources including demographic background, academic history, and log data from learning management systems (LMS). Most models could predict a dichotomous pass-fail outcome on an entire course or assessment, with prediction accuracy of 70% or above (Arizmendi et al., 2022). However, we believe that at least three factors limit the ability of the ML models to make recommendations on “what to study” and “how to study.”

First, most existing predictive analysis only predict dichotomous outcome on an entire exam or an entire course. As a result, they are unable to predict students’ level of mastery on individual topics on a multi-topic exam, so they cannot make specific recommendations for the question of “what should I study.” Most models could only make recommendation such as “spend more time on studying will increase your chance of passing the course.”

Second, most predictive analysis research do not account for the level of alignment between learning resources and assessment problems. In other words, most existing predictive models are agonistic to what types problems are being asked on the exam, and whether students had been exposed to similar problems during practice. Research on transfer have shown that similarity between different tasks play a critical role in people’s ability to transfer knowledge to new context (Novick, 1988), and small differences that seems trivial to experts in problem context can lead to larger than expected differences in measured problem difficulty (Fakcharoenphol et al., 2015). Factors that could potentially impact the level of alignment between two problems include the concepts and skills being assessed, the problem type (i.e., multiple-choice, numerical input, open response), the complexity of the problem solving process (for example the level of math skills required), and the similarity of the problem context. Not accounting for the level of similarity between practice problems and assessment problems could significantly reduce the reliability of the model’s performance when the instructor uses a different set of problems on an exam. More importantly, it limits the model’s ability to make good recommendations regarding “what should I study to get ready for the exam,” and to predict when a student is ready for an exam based on the students’ practice history.

Third, conventional ML models are black-box models that lack the ability to provide information on how much and in what direction each factor impact the prediction outcome. ML models generally out-perform conventional regression-based methods in terms of prediction accuracy, since impact of students’ learning behavior on assessment outcome is most likely non-linear (Tomasevic et al., 2020). Unfortunately, their superior performance came at the cost of significantly worse explainability compared to regression-based methods. As a result, they cannot give students meaningful guidance about what or how to study to improve their exam outcome.

Another form of predictive analysis method is Knowledge Tracing (KT) models, which can predict students’ probability of correctly answering a new problem based on students’ performance on prior problems that assess the same concept or skill [(see Abdelrahman et al., 2023) for an overview of the field]. However, many KT models include no or only a small number of data features related to students’ learning or practice behavior, which limits their ability to provide recommendation on “how to study.” For example, should students browse through as many practice problems as possible or focus on studying only a couple of problems? How much time should a student spend on practice problems to have a noticeable impact on exam performance?

In addition, KT is most suitable for cases where most students make multiple problem attempts, and the attempts are mostly authentic, such as intelligent tutoring systems (Mao, 2018) or online courses with large numbers of for credit homework problems (Pardos et al., 2013). They are less suitable in situations where students’ problem attempts are more heterogeneous and less authentic. For example, when students were given a bank of practice problems to prepare for an exam, many of them may submit random answers just to access as many problems as possible. The number of attempted problems could also differ significantly between different students. Therefore, in the current study we will focus on using ML methods instead of KT methods as prediction methods.

1.2 Aligning assessment and practice using isomorphic problem banks

Enabling predictive models to make actionable learning recommendations require more than isolated improvements in analysis algorithm. Rather, it requires simultaneous and complementary innovations in educational technology, pedagogy, and analysis methods. In particular, pedagogical innovation is needed for predictive models to account for the alignment between learning resources, especially practice problems, and assessment problems.

Providing practice problems or practice tests is a common and effective method for preparing students for upcoming exams. Many studies have consistently demonstrated that taking practice tests significantly improves exam performance compared to additional study without testing, especially when the practice comes with detailed feedback (Akbulut, 2024; Lipnevich et al., 2024; Polack and Miller, 2022). A meta-analyses suggests a medium effect size of practice tests around g = 0.50 across over 48,000 students (Yang et al., 2021). Specifically, in college level physics, Zhang et al. (2023) showed that realistic and earlier practice exams in physics courses promoted better self-regulated study behaviors and enhanced metacognitive exam preparation, resulting in improved performance among undergraduates in challenging physics assessments.

However, on conventional exams, students cannot have access to the assessment problems up to the time of the exam. As a result, instructors are constantly faced with a dilemma: if learning and practice resources are too similar to the assessment problem, then students will be motivated to rote memorize problem solution. If learning resources are too different from assessment problems, then the assessment may not accurately reflect students’ mastery of the learning resources. Instructors often have difficulty selecting assessment problems that are “similar but not too similar” to practice problems. As a result, quantify the similarity between learning and practice materials and assessment problems and be very challenging.

The rapid recent development of Large Language Models (LLMs) significantly reduces the time and effort required to write new problems (Bulathwela et al., 2023; Hwang et al., 2023; Wang et al., 2022), which enables the authors to implement a new form of assessment. Assessment problems will be randomly selected from a large bank of isomorphic problems created with the assistance of LLM. Isomorphic problems are problems that test the same set of concepts and share similar solution structures, but contains variation in solution details and problem context. A more detailed definition of isomorphic problems used in the current study is presented in section 2.2.1 The problem bank is open to students for practice prior to the exam, and students are able to receive targeted feedback to the problems. All isomorphic problems share largely overlapping learning objectives. The hypothesis behind this new approach is that when the problem bank is large enough, rote memorization of problem solutions becomes an extremely inefficient, largely infeasible strategy, and students will be more motivated to understand the concepts instead.

Under this new approach, practice problems and assessment problems are nearly perfectly aligned with each other in terms of concepts and skills assessed, format of the problem, and the overall complexity of the solution. Examples of two isomorphic problems used in the current study are shown in Figure 1. As can be seen in the example, the problem context and the details of the solution are similar but contain meaningful differences such as direction of motion of objects to prevent rote memorization. As a result of this alignment, ML models could predict students’ assessment outcome on a single problem on the exam, using data collected from students practicing on the corresponding problem bank. Therefore, this new assessment scheme overcomes the first and second barrier towards making learning recommendations at the same time. Meanwhile, results of the ML model are also needed to validate the hypothesis behind this novel assessment method. In particular, one need to examine would those students who happen to have practiced on the same problem that was selected on the exam have an unfair advantage over other students. The current study employs explainable ML methods to both overcome the third barrier towards making actionable recommendation, and to examine the validity and fairness of the new assessment method, by identifying the most influential factors that impact student performance.

Figure 1

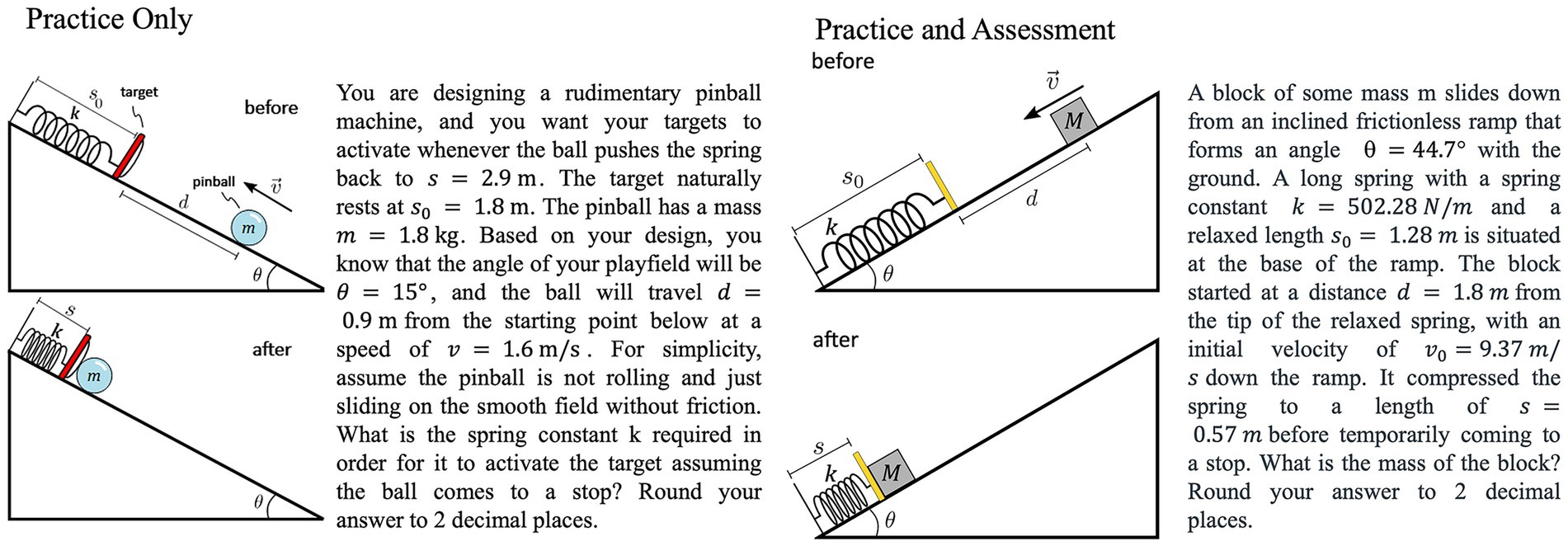
Figure 1. Example of isomorphic problems. The two problems involve identical physics principle, but differ in the detailed problem context (ball vs. block), direction of motion, and the known and unknown variables. Left: a problem used only in the practice. Right: a problem used in both practice and on the assessment.

1.3 Explainable Machine Learning with SHAP value

To overcome the “black-box” nature of traditional ML models, we use Explainable Machine Learning (xML) models, which have several advantages over traditional ML methods. One key advantage is that xML models can effectively identify important features among a large number of potentially relevant features, and reveal relation between feature value and prediction outcome, making the model’s decision-making process more interpretable and actionable.

Specifically, we use the SHAP (SHapley Additive exPlanations) to quantify the feature importance (Lundberg and Lee, 2017). The SHAP framework provides a principal approach for distributing the prediction among all features based on their individual contribution to the outcome (Lundberg et al., 2020). By computing SHAP values, it quantifies the average contribution of each feature across all possible subsets of features, offering a comprehensive view of their influence on the prediction (Lundberg and Lee, 2017). It provides a dimensionless measure of feature importance, where the absolute magnitude of a SHAP value represents the strength of a feature’s relative impact on the prediction, and its sign (positive or negative) corresponds to the direction of the feature’s impact on the predicted outcome. SHAP values are scaled consistently within a model, allowing for easy comparison of relative feature importance. They also help uncover feature interactions by showing how the presence or absence of one feature affects the impact of another. If no specific feature contributed to the prediction, the SHAP value would reflect the expected value of the model, which is the baseline prediction. We used waterfall plots and dependence scatter plots to illustrate the impact of individual features on the predicted outcome, providing insights into how the specific feature contributes to the model prediction (Lundberg et al., 2020).

1.4 Study design and research questions

This study tests a prototype case of the isomorphic problem bank assessment, by providing students in a University introductory level physics course with one isomorphic problem bank as practice material 1 week prior to an upcoming mid-term exam. Providing practice exam problems is a common and effective practice to help students prepare for exam (Fakcharoenphol et al., 2011; Zhang et al., 2020). The exam contains one problem that is directly selected from the problem bank, and a second problem that is not from the bank but similar to the first one. We then built a predictive ML model based on learning features extracted from students’ practice behavior, to answer the following four research questions:

RQ1. Can ML models use predominantly data from students practicing with an isomorphic problem bank to predict students’ outcome on the exam problem selected from the same bank?

Hypothesis 1: The prediction accuracy of ML models relying predominantly on student practice data will be comparable to existing models (>70%). Justification: The high level of alignment between practice problems and assessment items should be sufficient in ensuring a high level of prediction accuracy.

RQ2. How well can the same data predict students’ performance on a similar problem not chosen from the problem bank?

Hypothesis 2: Prediction accuracy for student performance on a similar problem will be slightly lower than on the Original problem bank problems. Justification: The alignment between a similar problem and practice problems is weaker than with the original problem, resulting in reduced prediction accuracy.

RQ3. Which learning features from students’ practice data are most important in predicting students’ exam outcome?

Hypothesis 3: Certain learning features will have much higher contribution to the prediction outcome than others, as indicated by their SHAP values. Justification: Explainable Machine Learning models are capable of identifying features of high importance to the prediction outcome.

RQ4. Does viewing identical or highly similar practice problems significantly increase assessment outcome compared to viewing less similar isomorphic problems?

Hypothesis 4: Viewing identical or highly similar problems will have either a minor or no impact on the assessment outcome. Justification: The size of the isomorphic problem banks and the level of variation between problems should be sufficient to discourage rote memorization of the problem answer or the specific solution. Therefore, whether students had practiced on items that are identical or highly similar to the exam items should not be a key factor predicting their exam performance.

2 Methods

2.1 Instructional condition

The study was implemented in a calculus-based university introductory-level physics class during Spring 2023. The class had 328 registered students, of which 26% were Female, 32% were under-represented minority in STEM, 17% were first generation students, and 21% were transfer students from 2-year institutions. The course was taught in a blended instruction mode: students were instructed to view pre-recorded lecture videos and conduct online homework using the Obojobo online learning platform (Center for Distributed Learning, n.d.).

A total of three mid-term exams were administered throughout the semester. The exams were administered synchronously during class times with an option to take the exam remotely with video camera on per student request. Each exam is conducted as an auto-graded Quiz on the Canvas Learning Management System (Instructure Inc., n.d.). All problems were either multiple-choice or numeric answer problems. All numeric answer problems had randomized variable numbers. Students were allowed 50 min to complete each exam.

2.2 Study design

2.2.1 Creation of isomorphic problem bank

There are multiple different definitions of “isomorphic” problem pairs. For the current study, we define isomorphic problems as problems that are being created from a common “seed” problem by applying a set of isomorphic variations. Each isomorphic variation should: (1) preserve the main concepts and physics principles required to solve the problem, (2) preserve the overall complexity of the solution, such as the number of steps or the type of mathematical operation, and (3) introduce one or more minor changes to the solution that are less likely to affect its difficulty, such as flipping the direction of an applied force that will result in changing a “+” sign to a “−” sign in the solution.

The isomorphic problem bank in the current study is created according to the following four step process:

Step 1: Creating a “seed” problem. A human expert first writes a “seed problem” that would serve as the basis of the isomorphic problem bank, which involves the learning objective(s) that the bank intends to assess.

Step 2: Determine Acceptable Variations. The human expert then determines a number of variations to the seed problem that could be seen as isomorphic. In the current study, the isomorphic variations come in three hierarchical levels:

a. Major variation: change to the problem context, such as replacing a block sliding down a ramp to a human riding a bike up a hill.

b. Minor variation: change of smaller details such as the direction of motion of an object or direction of a force.

c. Rotation of variable: rotate the known and unknown variables for a problem.

A second human expert then reviews the variation, identify ones that could potentially result in a significant shift in solution complexity, and modifies the problem bank in collaboration with the first human expert.

Step 3: Generative AI Assisted Problem Text Writing: Writing of isomorphic problem text is assisted by Generative Pre-trained Transformer 3 (GPT-3) in completion mode (Dale, 2021). To generate the problem text for one isomorphic problem variation, the GPT model is first provided with a simple prompt capturing the essence of the seed problem, followed by the seed problem text itself as an example. A new prompt describing the first isomorphic variation is appended to the input text, creating a “prompt-problem-prompt” structure. When submitted, GPT-3 attempts to generate the first isomorphic variation problem text according to both the seed prompt-problem text pair, and the isomorphic variation prompt. The problem author then reviews the generated problem text and makes edits when necessary and appends a new variation prompt after the previously generated text. The process is repeated 5–7 times for each minor variation.

Step 4: Creation of problem figures and Solution Formula: Problem diagrams are being generated manually in scalar vector graphics (SVG) format, using a free open-source tool named Inkscape. Formulas for calculating the correct answer for each problem are being generated with the assistance of Wolfram Alpha.

The final isomorphic problem bank contains 4 Major variation, each with 2 Minor variations, each with 5–6 Rotation of variables, with a combined total of 44 isomorphic problems. The problem bank assesses students’ ability to solve problems related to the conservation of mechanical energy.

2.2.2 Exam design and implementation

The study was conducted on the second mid-term exam, which contained 9 problems in either multiple choice or numerical input formats. Question 6 was directly selected from the isomorphic problem bank, which we will refer to as the Original problem. Question 6 asks about an object moving up or down an inclined ramp with the presence of a spring. Students were presented with one of two versions of Question 6, Q6_V1 and Q6_V2. V1 involves an object moving up the ramp, and V2 involves the object moving down the ramp. The symbolic solution for both versions is identical. Q6 was a numerical input problem for which students must compute the numeric value of the unknown variable from a set of known variables. The numerical values of the known variables were selected from 20 sets of randomly generated values.

Question 4 was not present in the problem bank, but can be solved with identical process and identical set of concepts as problems in the problem bank. As shown in Figure 2, Question 4 asks about a person doing bungee jumping under a bridge, and the two versions of Q4 refers to the person moving either up or down in direction. The problem context of Q4 can be seen as an isomorph of that of Q6, with the only difference being the absence of a ramp. As a result the symbolic solution of Q4 was very similar but mathematically slightly easier that of Q6. We will refer to Question 4 as the Transfer problem. All other settings of Question 4 are identical to that of Question 6.

Figure 2

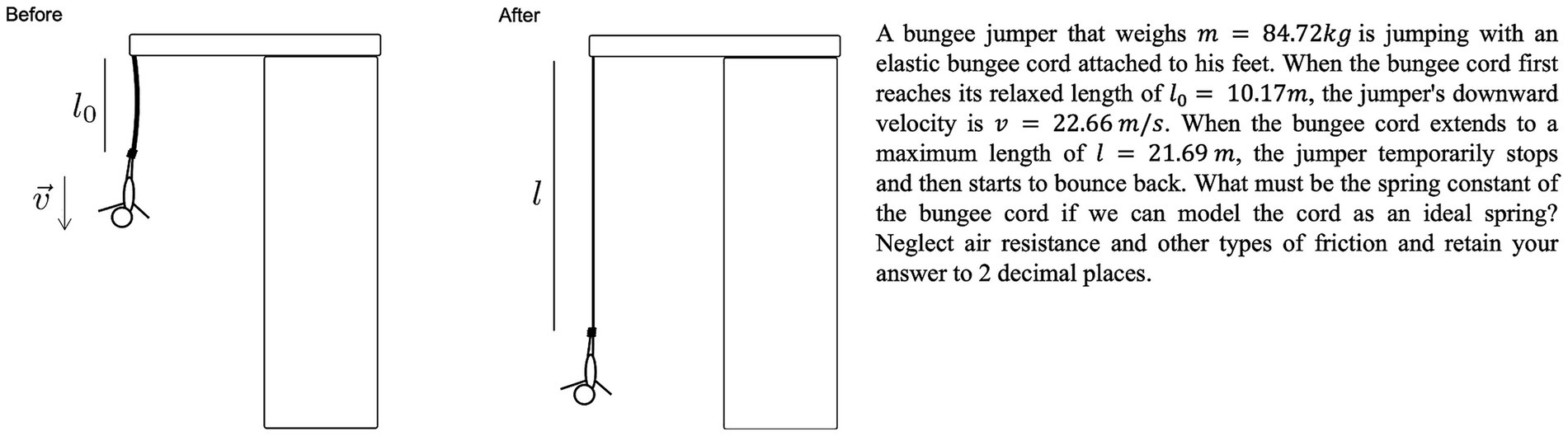
Figure 2. Example of transfer problems (Question 4) used on the assessment, showing a bungee jumper diving down. The jumper and bungee cord system can be seen as isomorphic variation of the block and spring system in the Original problem.

Approximately 1 week prior to the exam, the instructor made an announcement to the class on the topic of each problem to appear on the upcoming exam as a review guide. The announcement explicitly pointed out that one problem would be directly drawn from the practice problem bank that students have access to, and another problem will be similar to the problems in the practice problem bank. The entire problem bank was made available to students together with the announcement. Students can make an infinite number of attempts on the problem bank, and on each attempt students could receive 2 problems randomly selected from 2 different Major variations.

2.3 Extraction of learning features

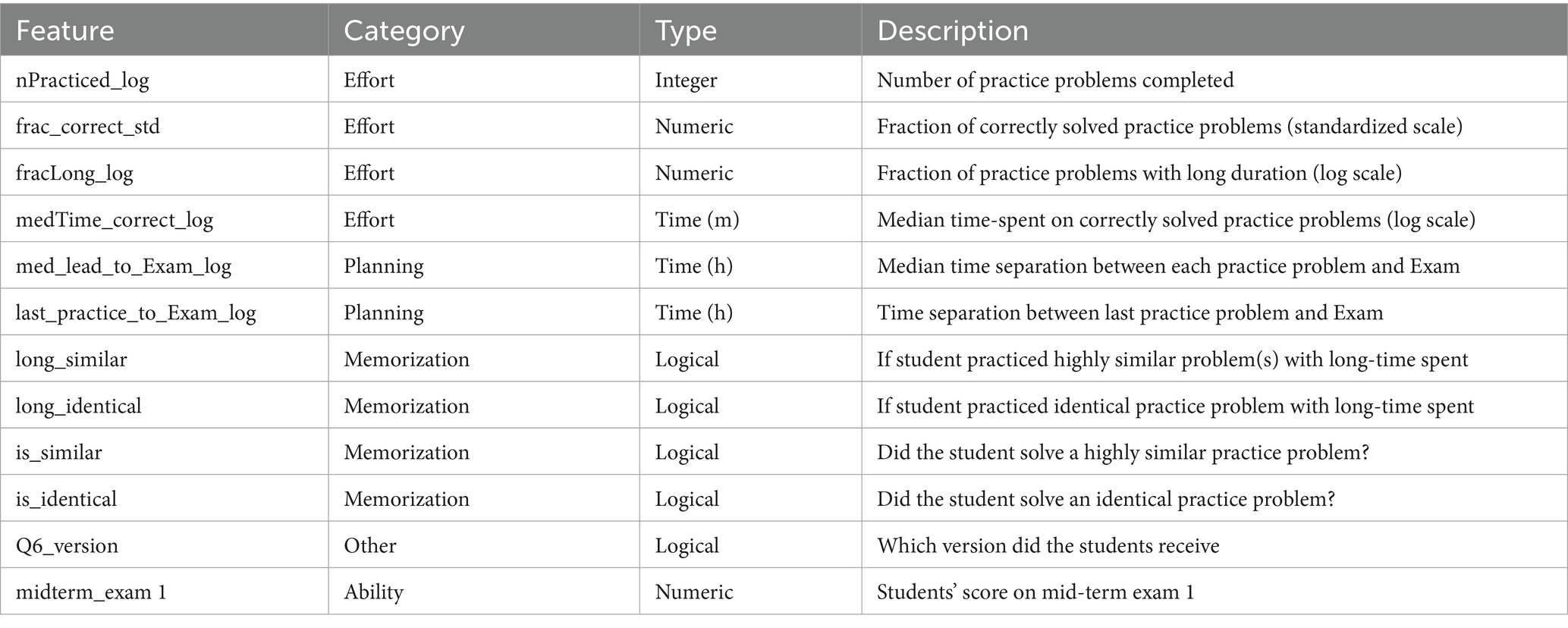
From the log data collected from students’ interaction with practice problem bank, we engineered 10 features related to students’ practice behavior on the isomorphic practice problem bank, most of which can be categorized to the following four categories, and explained in Table 1:

Table 1

Table 1. Features related to students’ practice strategy used for prediction.

Effort: Measure of both quantity and quality of students’ practice process.

Planning: How early did students start their practice effort relative to the exam.

Rote Learning: Whether students had the opportunity to rote learn the solution to the exam problem from identical or similar problems. Those features are included to answer RQ4.

Ability: One academic history feature was included as a proxy for the general subject matter proficiency.

From a self-regulated learning perspective (Winne, 2015), features in “Planning” and “Effort” categories roughly correspond to the “planning” phase and “execution” phase of self-regulation. Many prior research has shown that those features have significant impact on students’ achievement. We did not include the “reflection” phase of self-regulation as it is challenging to find quality proxy measures for reflection in the current dataset.

In addition, we also included students’ score on an earlier mid-term exam (mid-term exam 1) as a proxy for their general ability within the subject matter. Finally, we included the version of the Original question (Q6_Version), to ensure that the two versions created did not accidentally have large differences in difficulty.

Three aspects of features in Table 1 requires additional clarification of their definitions:

Long durations: A significant body of earlier research suggest that abnormally short time-on-task on problem solving process indicates less authentic problem solving behavior, such as guessing or answer copying (Alexandron et al., 2017; Chen, 2022; Chen et al., 2020; Palazzo et al., 2010; Warnakulasooriya et al., 2007). In this study, we classify problem solving duration with more than 70s as “long,” and use long time-spent as a proxy for authentic engagement with problem solving. The cutoff time of 70s between long and short is obtained by applying a mixture model approach over the entire dataset, following the procedure explained in detail in Chen (2022).

Identical and Similar practice problems: “Identical” means that the student submitted an answer to the practice problem that is identical (aside from the actual numbers of the variables) to the Original problem on the exam (Question 6). “Similar” means that the student submitted an answer to a practice problem that is only different from the exam problem by Rotation of variables. In other words, they have the same solution equation. Both “Identical” and “Similar” are defined only with regard to the “Original” problem.

Separation between practice and Exam: This is measured as the time difference between the time of submission to a practice problem, and the start time of the exam. For example, feature last_practice_to_exam is the time separation between the last submission on any practice problem, and the start time of the mid-term exam.

Furthermore, the nPracticed_log and medTime_correct_log are transformed onto log scale in the model, since we believe that the significance of the unit difference in data reduces as the magnitude increases. For example, spending 5 min or 1 min on a problem is a much more significant difference than spending 25 min or 30 min on a problem. Feature fracLong was also log transformed into fracLong_log according to “fracLong_log”=ln(“fracLong”+1), since the distribution of original feature is highly skewed towards 1, and log transformation is necessary to reduce the skewedness. The last_practice_to_Exam_log and med_lead_to_Exam_log are log transformed, because the distributions are highly right skewed and apply to log transformation to reduce skewness. The frac_correct_std is standardized, because the feature has the different scales and standardization was used to prevent the feature from dominating due to its scale.

2.4 Creation of predictive classification models

The primary aim of this study is to provide actionable recommendations for students to better prepare for exams by interpreting the outcomes of predictive models. To achieve this, we employ three tree-based Machine Learning models—Random Forest, eXtreme Gradient Boosting (XGBoost), and Classification and Regression Trees (CART). Each of the three models strikes a balance between predictive accuracy and interpretability, making them well-suited for analyzing complex relationships within the data while offering insights into factors influencing the outcomes. The response variable is a binary indicator of whether a student passed or failed on either the Original problem or the Transfer problem on the exam. The input variables are the 10 learning features plus 2 additional features explained in the previous section.

Random Forest is an ensemble learning technique that integrates multiple decision trees to enhance predictive accuracy and efficiently capture complex, non-linear relationships in the data (Breiman, 2001). It is resistant to overfitting, performs well with high-dimensional data, but can be computationally demanding. XGBoost is another ensemble method based on gradient boosting framework, which enhances predictive accuracy by iteratively improving decision trees to capture complex patterns in the data (Chen and Guestrin, 2016). XGBoost demonstrates exceptional efficiency and accuracy by iteratively constructing a series of decision trees. Its built-in regularization mechanisms effectively mitigate overfitting, ensuring robust generalization. However, achieving optimal performance often necessitates careful tuning of its complex hyperparameters. In contrast, Classification and Regression Trees (CART) is a decision tree algorithm that recursively partitions data into subsets based on the most important features, resulting in a tree-like structure used for classification tasks (Hastie et al., 2009). While CART is straightforward to interpret and visualize with numeric and categorical data, it is prone to overfitting unless appropriate pruning techniques are applied.

We randomly split the data into training and testing sets during the model training process and apply cross-validation to optimize the model’s hyperparameters. The dataset was split with 80% for training and 20% for testing. During training, we employed a 5-fold cross-validation to optimize model hyperparameters and validate model performance. In this approach, the training dataset is divided into five subsets; the model is trained on four subsets and validated on the fifth. This process is repeated five times, with each subset used once for validation, and the results are averaged to ensure the model’s robustness and prevent overfitting.

2.4.1 Explainable Machine Learning (xML) via SHAP value

In this study, we utilized the SHAP package in Python (Version 3.8.10) to compute and visualize SHAP values for the best-performing models for both original and transfer problem outcomes (Lundberg et al., 2018). To visualize the SHAP values of each feature, we used waterfall plots to provide a detailed breakdown of feature importance for each prediction. These plots visually represent how each feature either increases or decreases the predicted log-odds, starting from the expected value of the predicted variable, and adding the contribution of each feature step-by-step according to their SHAP value of each feature in the order of decreasing absolute SHAP value (Lundberg et al., 2018). This approach helps to clearly see the impact of the most influential features on the final prediction. To emphasize the significant factors influencing the model’s predictions, we focused on the top 5 most impactful features. Additionally, to gain deeper insights into the model’s decision-making process, we employed SHAP dependence scatter plot to visualize how the impact of each feature varies across its range of value. The plots illustrated the relationship between the feature actual value and its corresponding SHAP value, which represented the feature’s contribution to the model’s prediction for each data instance (Lundberg, 2023). For most features, the scatter plot shows a general trend in agreement with direction of impact indicated on the waterfall plots. In the Results section, we will focus on only the scatter plots that either shows a different trend as the waterfall plot, or provide additional information for the interpretation of the trends.

3 Results

3.1 Summary statistics of learning features

This study examined the relationship between various student behavior characteristics and two different types of problems: The Original problem outcome and the Transfer problem outcome. Descriptive statistics are provided in Supplementary Table S1, including the mean and standard deviation for continuous variables, as well as frequencies and proportions for categorical variables, stratified by the outcome groups: pass (outcome = 1) and fail (outcome = 0). Statistical comparisons between the pass and fail groups were conducted using t-tests for continuous variables and chi-square tests for categorical variables, applied separately to both the Original and Transfer problem sets.

The analysis of Original problems included 89 students who did not pass and 70 who passed. Seven variables are significantly different between outcome groups. For the Transfer problems, the analysis included 107 students who did not pass and 52 who passed. Six features demonstrated statistically significant differences between outcome groups. These results underscore the potential impact of practice and performance on outcomes. The findings indicated the significant difference in Original outcome and Transfer outcome, prompting us to examine which factors have the greatest impact on student behavior. Given the modest sample size, the stability of SHAP in small subgroups should be viewed with caution.

3.2 ML model performance and selection

In Figure 3, we plot the receiver operating characteristic (ROC) curves of the three models for predicting the performance of the Original problem and the Transfer problem. In Table 2, we report the values of the five performance evaluation metrics.

Figure 3

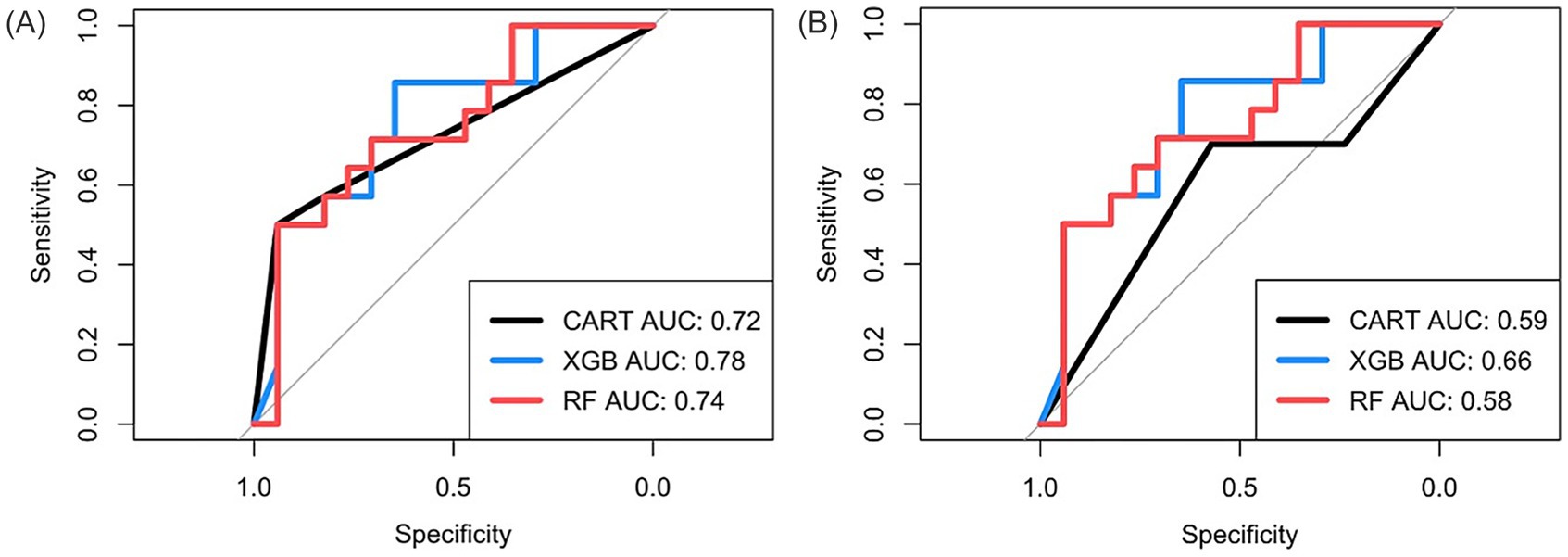
Figure 3. ROC curve plot comparing the performance of three models, CART, XGBoost (XGB), and Random Forest (RF), for the assessment problems. (A): Original problem. (B): Transfer problem.

Table 2

Table 2. Model comparison table for outcomes.

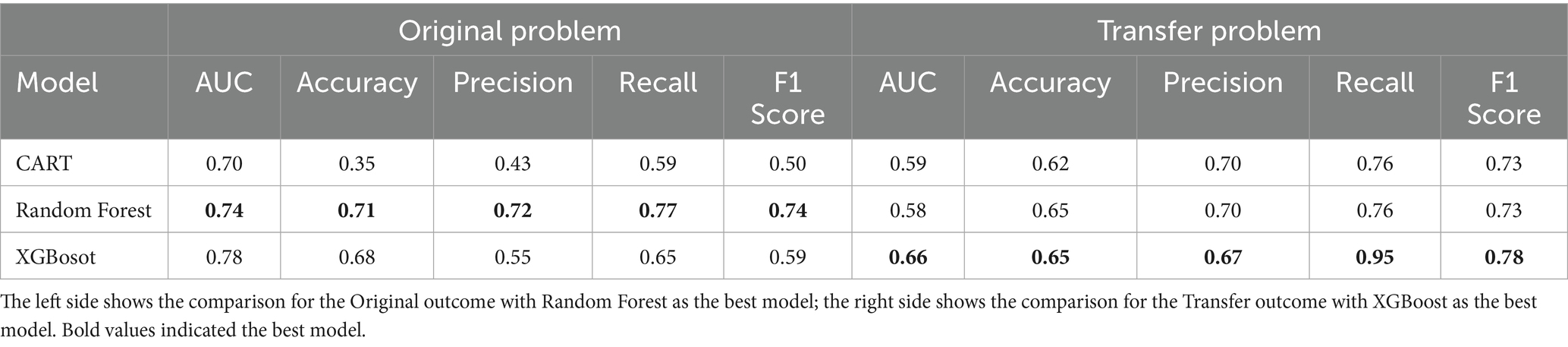
Best model for Original problem: As shown in Figure 3A, the XGBoost model achieved the highest area under the curve (AUC) value of 0.78, indicating best performance in distinguish between classes of original outcome. The Random Forest model followed closely with an AUC of 0.74. However, the Random Forest model showed the best overall performance by outperforming the other two models on the other four performance metrics, with prediction accuracy of 0.71, and F1 score of 0.74, as listed in Table 2. Therefore, we select the Random Forest model as the best performing mode, despite slightly worse AUC value compared to XGBoost.

Best model for Transfer problem: As shown in Figure 3B; Table 2, the XGBoost model outperforms the other two models on all five metrics, achieving the AUC value of 0.66, the accuracy of 0.65 and the F1 score of 0.78. Note that the AUC values of all three models are all lower when predicting Transfer problem outcomes, indicating that all models’ predictive performance is less robust when predicting the performance of Transfer problems compared to predicting the performance on the Original problem.

3.3 Feature importance

Waterfall plots of the SHAP values for the most important features are shown in Figure 4, for the best performing model for both Original problem and Transfer problem. We focus on the top 5 most influential features with the important contributions with SHAP values. The waterfall plot is designed to show how the SHAP value of each feature move the model output from the prior expectation under the background data distribution to the final model prediction given the evidence of the top 5 features. The value of each feature at the left side in Figure 4 represented the mode of the data distribution (Lundberg et al., 2020). Most scatter plots show a general trend that aligns with the waterfall plot. We only display scatter plots that either exhibit a highly non-linear relationship or a trend that differs from the direction in the waterfall plot.

Figure 4

Figure 4. SHAP value waterfall plots for top 5 feature importance assessment problems. (A): Original problem. (B): Transfer problem.

For the RF model predicting the Original problem outcome (Figure 4A), the expected value of log-odds before considering any feature-specific contributions was 0.42, and the final predicted log-odds after accounting for all feature effects was 0.811. Among all features, the number of practiced problems attempted (nPracticed_log) had predominantly the largest impact on the outcome, contributing +0.33 to the log-odds of the positive original outcomes when students practiced approximately 18 questions. From the scatter plot (Figure 5A) we can see that the positive SHAP value is exclusive to students with 10 or more problems practiced. The second most impactful feature was the time separation (in hours) between last practice problem and exam, which added +0.06 to the log-odds when students practiced 22 h before the exam. Surprisingly, midterm exam 1 score had the highest negative contribution of −0.05 to the log-odds for a score of 5 out of 10 points. Examining the scatter plot in Figure 5B revealed that the mid-term 1 score under 6 had negative contribution to the SHAP value, whereas scores >6 had positive SHAP value contribution. When the Q6 question was not version 2, it had an impact of +0.03 on the log-odds. Finally, the fraction of practice problems with long duration (fracLong_log) contributed positively with an addition of +0.02 to the log-odds of the positive original outcomes, when the fraction of the practice problems with long duration was 0.99.

Figure 5

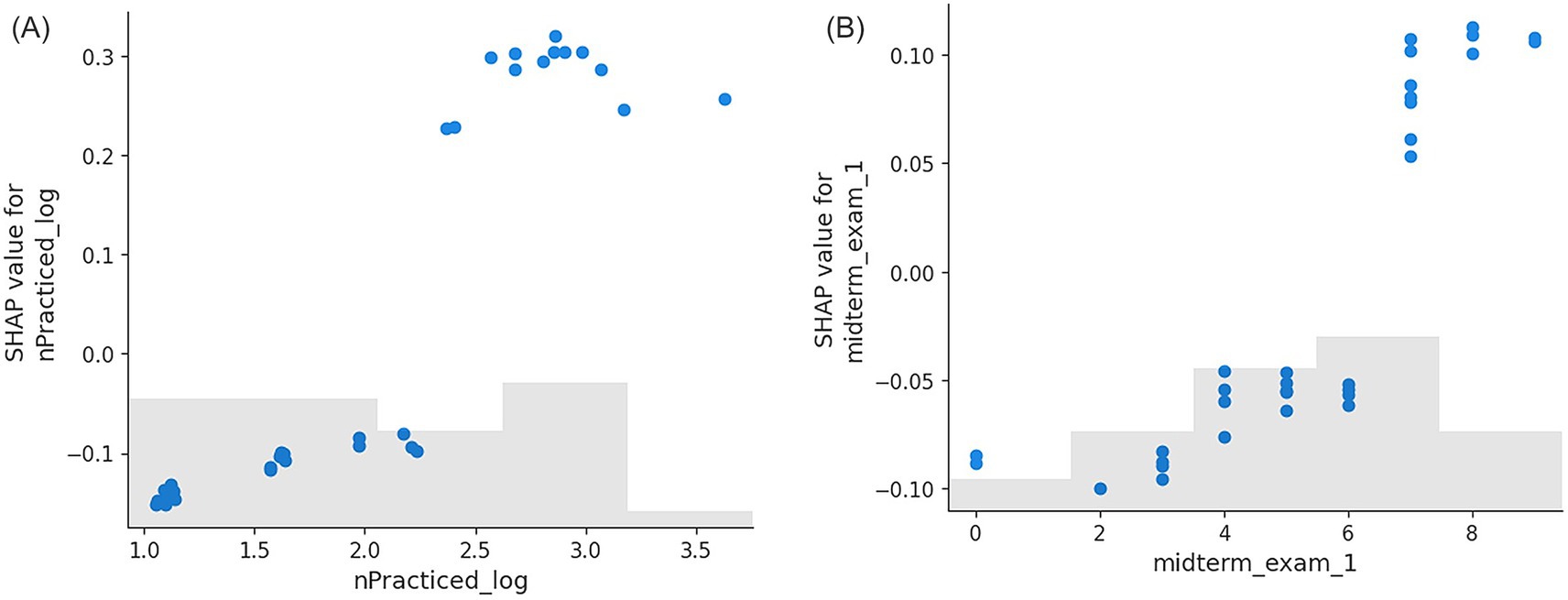
Figure 5. SHAP scatter plot for the impact of individual features on Original problem. (A): the number of practice problems influence the prediction of Original problem. (B): the midterm exam 1 score influences the prediction of Original problem. Takeaways: students who practiced more than 10 problems and spread practice at least 1 day before the exam performed significantly better.

Note that none of the features in the Memorization category had an impact of >0.01 on the log odds of the prediction, despite having statistically significant differences between positive and negative outcomes on the original problem (Supplementary Table S1). Having more correct attempts (frac_correct_std) was also not an important feature influencing the outcome.

For the XGBoost model predicting Transfer problem (Figure 4B), the initial expected value of log-odds was −0.81 before considering feature-specific contributions. After accounting for all feature effects, the final predicted log-odds was adjusted to −1.07. Feature importance was different from that of the Original problem model. As shown in Figure 4B, the most influential feature was median time separation between practice problem and exam (med_lead_to_Exam_log), with a log-odds change of −0.62 when the median time separation was about 47 h, or 1.96 days. The midterm exam 1 of 5 points positively impacted the log-odds by +0.59. Practicing identical problems long time (long_identical) also positively influenced the Transfer problem, contributing a log-odds increase of +0.46. The fraction of practice problems in long duration (fracLong_log) contributed to log-odd of +0.43 when the fraction was 0.99. Conversely, the fraction of correctly solved practice problem (frac_correct_std) negatively contributed the log-odd of −0.41 when the fraction of correctly solved practice problems was 0.05.

Since the direction of impact of med_lead_to_Exam_log and frac_correct_std are counter intuitive, we further examined the SHAP value dependence scatter plots of both features. As shown in Figure 6, it turns out that med_lead_to_Exam has peak positive SHAP value at about 3 (or about 1 day prior to the exam), and the SHAP value is negative when the feature value is greater than 3. For frac_correct_std, a higher correct fraction generally corresponds to a higher and positive SHAP value. Only when the feature value was below zero, which corresponds to roughly no correct attempt, did the SHAP value become negative. However, due to the large number of students with zero correct fraction, a negative SHAP value is reflected on the waterfall plot.

Figure 6

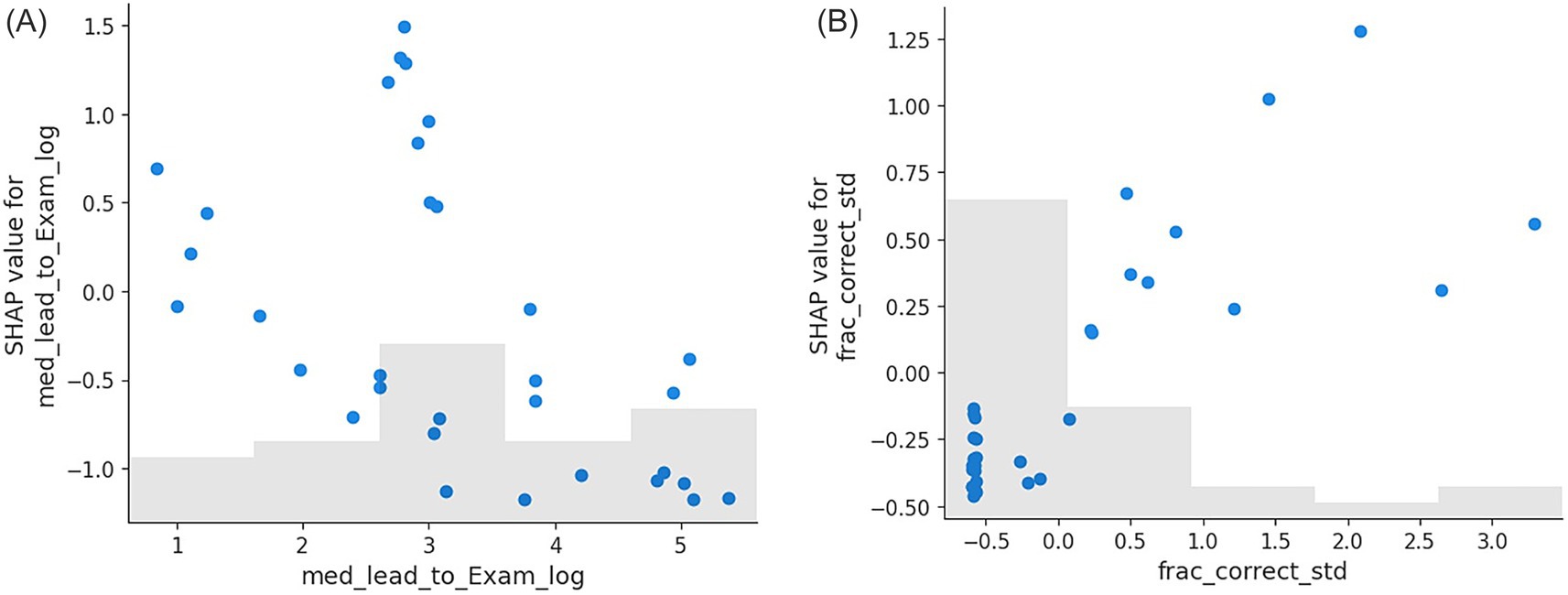
Figure 6. SHAP scatter plot for the impact of individual features on Transfer problem. (A): the impact of median time separation between practice and exam on Transfer problem success. (B): the impact of the fraction of correctly solved practice problems on Transfer problem success.

It is also worth emphasizing that the labels “identical” and “similar” are both defined regarding the similarity between a practice problem and the Original problem on the exam, not the Transfer problem, because the Transfer problem was not drawn from the practice problem bank. In other words, the Transfer problem can be seen as being equally different from all problems in the problem bank. This distinction suggests that features such as long_identical theoretically should have zero impact on the outcome of Transfer problem on the exam. However, out analysis revealed a positive contribution of long_identical to the log-odds in the Transfer problem model, as shown in Figure 4B. This result may be an artifact of the data, potentially arising from the small sample size due to only 6 students having a long_identical = 1 feature.

4 Discussion

4.1 Prediction of individual problem performance (RQ1)

The best performing predictive models are able to reach predictive accuracy of 71% for predicting the outcome of the Original problem, which is similar to the average prediction accuracy of previous Machine Learning modules on entire exam outcome (Arizmendi et al., 2022). Our current method has two key advantages regarding making learning recommendations. First, it is based predominantly on learning data, and uses only one immutable feature (mid-term exam 1 score), which makes the recommendations highly actionable. This also avoids the privacy and ethics concerns associated with collection of students’ demographic data (Arizmendi et al., 2022; Liu et al., 2023). Second, the recommendation can be made with regard to a specific problem since each problem is associated with its corresponding problem bank. Rather than making generic recommendations such as “practice on more problems,” the current system could potentially recommend students to “practice more problems in those problem banks.”

4.2 Impact of alignment on prediction outcome (RQ2)

Performance of ML models on the Transfer problem is clearly worse than that of the Original problem, both in terms of prediction accuracy and interpretability of results. Given that the Transfer problem is designed to be similar to the practice problems, this observation supports our hypothesis that predictive models can be highly sensitive to seemingly small differences between learning material and assessment problems. Therefore, we recommend future predictive models should take-into-account the level of alignment between learning resource and assessment items.

4.3 Recommendations for students (RQ3)

Based on the model outcome, the recommendation for students to improve their performance on the Original Problem is straight-forward: “Practice at least 10 problems and do so at least one day before the exam. It is ok if you make mistakes, but avoid guessing or quickly glancing over the problems.” This recommendation is based on the observation that the feature nPracticed_log is the dominant positive predictor of performance, and both the duration between practice and exam and the fraction of long attempts are major positive contributors to success. On the other hand, having more correct attempts had far less impact on the outcome. This recommendation aligns very well with previous findings regarding the “doer” effect of learning (Koedinger et al., 2015), and is in agreement with deliberate practice (Ericsson et al., 2009) being an effective method to enhance mastery. In addition, mid-term exam 1 score has far less impact on the outcome compared to problems practiced, which might suggest that practicing on isomorphic problem banks could potentially reduce achievement gaps, especially among low performing students. It is worth noting that if all students were to adopt the recommended strategies, the variability in these behavioral variables would decrease, potentially diminishing their predictive power in future models. However, the predictive strength of these variables is not solely dependent on their variability, but rather on their effect size. That is, the magnitude of their relationship with performance outcomes. In our analysis, much of the variation in student performance stems from unmeasured sources of randomness and individual behavioral differences, which are inherently difficult to capture. While the included variables are informative, they account for a relatively small portion of the total variance. Therefore, even if their variability were reduced due to widespread adoption, the directional shift in behavior would likely still exert a meaningful and measurable impact on performance.

It is also worth pointing out that the current predictive models do not directly show evidence for the causality between the predictors and the prediction outcome. As discussed in detail later in the paper, future studies are needed to examine if those recommendations could actually help students improve their exam performance.

The recommendation for preparing for the Transfer problem is less obvious. The most likely recommendation that could be made is to “Spend enough time on each attempt, and study the problem bank about 1 day before the exam.” The fact that mid-term exam 1 score and fraction of correct attempts has much more impact on Transfer problem success may suggest that the ability to transfer depends more on students’ general physics abilities, rather than their learning behavior. In other words, learning from practicing on a problem bank can be very specific to the type of problems in the bank, especially for students who are less proficient with the subject matter.

4.4 Insight on pedagogical validity (RQ4)

The RF model result shows that having seen the identical problem or having seen similar problems during practice had little to no impact on students’ chances of correctly answering the Original problem on the exam. This provides evidence for the hypothesis behind the new assessment approach that having a large enough problem bank could deter rote-memorization of solution, and keep the assessment fair for all students. Even though “long_identical” has high SHAP values for predicting Transfer problem success, we believe this is an artifact of sparce data in the test set, since the feature “identical” is ill defined for Transfer problem.

However, the results also point to potential issues with the current implementation of isomorphic problem banks. For one, different isomorphic versions of the same problem can have a measurable impact on students’ chances of obtaining the correct answer, as Q6_Version_2 has significant contribution for success odds-ratio. Future exams could select multiple problems from the problem bank to increase fairness. Second, it seems that learning from practice problem bank is highly specific to the problem type, and transferring to even a slightly different problem context can be challenging, especially for lower performing students. One possible way of improving transfer ability is to design problem banks that contain more variations between problems to assist with generalization of knowledge (Roelle and Berthold, 2016; Schwartz et al., 2011).

Finally, it is worth noting that had we relied on simple statistical tests of features between student groups with positive and negative outcomes (Supplementary Table S1), both the recommendations for students and insights for instructors would have been drastically different. For example, the feature “is_identical” is significantly different between student groups for the original problem, but determined as unimportant based on its SHAP value. The results from the ML models are more reliable since it could reflect the non-linear and highly inter-dependent nature of student learning data.

4.5 Implications for the development of future learning systems

Results of the current study suggests two possible designs of future learning systems that are based on isomorphic problem banks and Explainable Machine Learning. First, for a learning system with conventional summative assessments with a fixed number of items, multiple practice problem banks aligned with each potential assessment item (or item bank) can be developed using Generative AI. During the learning process, students will be informed whether they have had enough practice to pass the exam based on their practice behavior, and receive suggestions on which problem banks to practice next. This static assessment design is more compatible with existing course structures, and could be implemented relatively easily. The second possible design involves dynamic summative assessments, in which each students’ level of mastery on each topic is estimated by their practice behavior and practice outcome via xML. The summative assessment is then generated dynamically based on students’ estimated level of mastery. In this design, the assessment only need to sample a fraction of the skills that the student should have mastered, and serve the purpose of verifying the validity of the collected learning data. This design has the benefit creating more accurate, flexible and accessible assessments while significantly reducing test anxiety, but requires more drastic reform of the existing course structure.

5 Conclusion and future directions

This paper demonstrates a case of synchronous innovation in both pedagogy and learning analytics. By combining isomorphic problem bank-based assessment with Explainable Machine Learning techniques, the study showed that:

1. ML models can predict the outcome of individual problems on a physics exam with >70% accuracy based predominantly on student learning data collected from aligned isomorphic practice problems.

2. Prediction accuracy and model interpretability of ML models can be very sensitive to the level of similarity between learning resources and assessment problems, which was overlooked in many earlier studies.

3. Explainable Machine Learning (xML) models have clear advantage over traditional ML models in making specific and actionable learning recommendations for students.

4. The hypothesis that large isomorphic problem banks can prevent rote memorization is supported by the current results, but the fairness of the assessment should be improved in the future.

It is also worth mentioning that the potential benefits of the isomorphic problem bank assessments extend well beyond enabling more accurate and informative learning analytics. For example, since the problem banks are openly accessible, students can take the assessment at different times and can have multiple attempts. Test item security is no longer a concern, so the same assessment can be reused over time, and used across many different classes. In short, isomorphic problem banks could lead to completely re-designed assessment mechanism in the future.

As an initial attempt at implementing and studying this new assessment approach, the current study also has multiple limitations and caveats that needs to be addressed in future implementations and follow up studies. We discuss some of the most important future directions below.

First, the current implementation only records binary outcomes of a multi-step problem, without taking into account students’ problem-solving process. From an assessment approach perspective, it only provides very limited amount of information on students’ understanding of the problem-solving process. From a predictive analysis perspective, it is likely one of the reasons for the reduced predictive performance on the transfer problem, since many students could have transferred some partial learning from the practice problem bank, but unable to obtain the correct end-result due to extraneous reasons. With the rapid development of GenAI based automated grading techniques (Kortemeyer, 2024; Pinto et al., 2023; Liu et al., 2024), future implementations could utilize open-ended responses, to achieve more informative assessment and enable more accurate predictive models. It could also provide partial credit to students based on their responses, to improve the fairness of the assessment.

Second, the current study only assessed data from a single problem bank, which prevented us from directly testing the current approaches’ ability to make recommendations regarding “what to study.” Future implementations need to involve multiple problem banks that correspond to multiple assessment problems, and develop Machine Learning models that could estimate different levels of proficiency on different problems. Relatedly, the same pedagogical innovation could be administered to larger and more diverse student populations, which will likely result in more diverse learning behavior. This will likely lead to more robust predictive models, and could potentially lead to different learning recommendation for different student populations.

Third, future studies will need to examine the causality between identified important features and exam performance. This can be achieved solely based on data, using tools such as TETRAD (Scheines et al., 1998). Alternatively, one could conduct randomized or natural experiments (such as in (Felker and Chen, 2023) and (Chen et al., 2024)), that provide one group of students with recommendations based on the previous ML results. Evidence for causality can be obtained by comparing to a second group of students, or the same group of students at an earlier instance, and looking for differences in both practice behavior and assessment outcome.

Forth, the current model only used data from students practicing for the upcoming exam 1 week ahead of time, and do not contain students’ learning behavior data earlier in the process. While practicing shortly before the exam is likely to have the most direct impact on assessment outcome, activities that took place earlier in the learning process likely had more influence on students’ conceptual understanding of the subject matter. Lack of earlier learning data might be part of the reason why the current ML models perform worse on the Transfer problem, as transfer tasks could depend more on conceptual understanding over short-term memory. Future studies with larger student population could include learning data from longer periods of time, which would not only improve model performance, but also allow the model to provide learning recommendations earlier in the learning process. Future studies could also consider combining Machine Learning with Knowledge Tracing methods or further increase prediction accuracy.

Fifth, the method of using Generative AI to develop isomorphic problems reported in the current study did not fully utilize the potential of the latest Generative AI models available. Future studies could further streamline the problem creation process, reducing the steps needed for more efficient creation of isomorphic problem banks. In addition, more student data is needed to verify if the current definition of isomorphic problems is sufficient to ensure an acceptable level of uniformity in difficulty across all problems in the problem bank, which is key to ensuring faireness in problem bank based assessments.

Finally, the current study only explored generating learning recommendations for the entire student population as a whole. The benefit of such recommendations will most likely not be uniform across different student cohorts, especially in large institutions with highly varied student population. It is an important research question to investigate whether those recommendations would mitigate or exacerbate existing achievement gaps between different student population. Furthermore, future ML models could be developed to provide customized learning recommendations for cohorts of student, or even individual students, by incorporating more detailed student learning records.

Data availability statement

The original contributions presented in the study are publicly available. This data can be found here: https://github.com/cl199393/predictive_analysis.

Ethics statement

The studies involving humans were approved by UCF institutional review board. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

CL: Formal analysis, Methodology, Visualization, Writing – original draft. RX: Methodology, Supervision, Validation, Writing – original draft, Writing – review & editing. ZC: Data curation, Conceptualization, Investigation, Supervision, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by National Science Foundation grant number DUE-1845436, and University of Central Florida Digital Learning Course Reform and Innovation Fund.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1632132/full#supplementary-material

References

Abdelrahman, G., Wang, Q., and Nunes, B. (2023). Knowledge tracing: a survey. ACM Comput. Surv. 55, 1–37. doi: 10.1145/3569576

Crossref Full Text | Google Scholar

Akbulut, Y. (2024). Impact of different practice testing methods on learning outcomes. Eur. J. Educ. 59:e12626. doi: 10.1111/ejed.12626

Crossref Full Text | Google Scholar

Alexandron, G., Ruipérez-Valiente, J. A., Chen, Z., Muñoz-Merino, P. J., and Pritchard, D. E. (2017). Copying@scale: using harvesting accounts for collecting correct answers in a MOOC. Comput. Educ. 108, 96–114. doi: 10.1016/j.compedu.2017.01.015

Crossref Full Text | Google Scholar

Arizmendi, C. J., Bernacki, M. L., Raković, M., Plumley, R. D., Urban, C. J., Panter, A. T., et al. (2022). Predicting student outcomes using digital logs of learning behaviors: review, current standards, and suggestions for future work. Behav. Res. Methods 55, 3026–3054. doi: 10.3758/s13428-022-01939-9

Crossref Full Text | Google Scholar

Breiman, L. (2001). Random Forest. Mach. Learn. 45, 5–32. doi: 10.1023/A:1010933404324

Crossref Full Text | Google Scholar

Bulathwela, S., Muse, H., and Yilmaz, E. (2023). Scalable educational question generation with pre-trained language models, In: International Conference on Artificial Intelligence in Education. Cham: Springer Nature Switzerland. 327–339.

Google Scholar

Center for Distributed Learning. (n.d.). Obojobo. Available online at: https://next.obojobo.ucf.edu/ (accessed May 12, 2025)

Google Scholar

Chen, Z. (2022). Measuring the level of homework answer copying during COVID-19 induced remote instruction. Phys. Rev. Phys. Educ. Res. 18:010126. doi: 10.1103/PhysRevPhysEducRes.18.010126

Crossref Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). XGBoost. Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 785–794.

Google Scholar

Chen, Z., Xu, M., Garrido, G., and Guthrie, M. W. (2020). Relationship between students’ online learning behavior and course performance: what contextual information matters? Phys. Rev. Phys. Educ. Res. 16:010138. doi: 10.1103/PhysRevPhysEducRes.16.010138

Crossref Full Text | Google Scholar

Chen, Z., Zhang, T., and Taub, M. (2024). How does a data-informed deliberate change in learning design impact students’ self-regulated learning tactics? J. Learning Anal. 11, 174–196. doi: 10.18608/jla.2024.8083

Crossref Full Text | Google Scholar

Dale, R. (2021). GPT-3: what’s it good for? Nat. Lang. Eng. 27, 113–118. doi: 10.1017/S1351324920000601

Crossref Full Text | Google Scholar

Ericsson, K. A., Nandagopal, K., and Roring, R. W. (2009). Toward a science of exceptional achievement. Ann. N. Y. Acad. Sci. 1172, 199–217. doi: 10.1196/annals.1393.001

Crossref Full Text | Google Scholar

Fakcharoenphol, W., Morphew, J. W., and Mestre, J. P. (2015). Judgments of physics problem difficulty among experts and novices. Phys. Rev. Phys. Educ. Res. 11:020128. doi: 10.1103/PhysRevSTPER.11.020128

Crossref Full Text | Google Scholar

Fakcharoenphol, W., Potter, E., and Stelzer, T. (2011). What students learn when studying physics practice exam problems. Phys. Rev. Phys. Educ. Res. 7:010107. doi: 10.1103/PhysRevSTPER.7.010107

Crossref Full Text | Google Scholar

Felker, Z., and Chen, Z. (2023). Reducing procrastination on introductory physics online homework for college students using a planning prompt intervention. Phys. Rev. Phys. Educ. Res. 19:010123. doi: 10.1103/PhysRevPhysEducRes.19.010123

Crossref Full Text | Google Scholar

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The elements of statistical learning: Data mining, inference, and prediction. New York: Springer.

Google Scholar

Hwang, K., Challagundla, S., Alomair, M., Chen, L. K., and Choa, F. S.. (2023). Towards AI-assisted multiple choice question generation and quality evaluation at scale: aligning with bloom’s taxonomy. NeurIPS’23 workshop on generative AI for education (GAIED).

Google Scholar

Instructure Inc.. (n.d.). Canvas learning management system. Available online at: www.canvaslms.com (accessed May 12, 2025)

Google Scholar

Koedinger, K. R., Kim, J., Jia, J. Z., McLaughlin, E. A., and Bier, N. L. (2015). Learning is not a spectator sport. Proceedings of the second (2015) ACM conference on learning @ Scale, 111–120.

Google Scholar

Kortemeyer, G. (2024). Performance of the pre-trained large language model GPT-4 on automated short answer grading. Discov. Artif. Intell. 4:47. doi: 10.1007/s44163-024-00147-y

Crossref Full Text | Google Scholar

Lipnevich, A. A., Janelli, M., Park, M. J., Calistro, T., and Esser, F. J. (2024). The effects of practice testing and feedback on learners’ performance and persistence in a massive open online course. J. Res. Technol. Educ., 1–20. doi: 10.1080/15391523.2024.2398513

Crossref Full Text | Google Scholar

Liu, T., Chatain, J., Kobel-Keller, L., Kortemeyer, G., Willwacher, T., and Sachan, M. (2024). AI-assisted automated short answer grading of handwritten university level mathematics exams. ArXiv [Preprint] ArXiv.

Google Scholar

Liu, L. T., Wang, S., Britton, T., and Abebe, R. (2023). Reimagining the machine learning life cycle to improve educational outcomes of students. Proc. Natl. Acad. Sci. 120:e2204781120. doi: 10.1073/pnas.2204781120

Crossref Full Text | Google Scholar

Lundberg, S. M.. (2023). SHAP documentation. SHAP. Available online at: https://shap.readthedocs.io/en/latest/ (Accessed August 20, 2024).

Google Scholar

Lundberg, S. M., Erion, G., Chen, H., DeGrave, A., Prutkin, J. M., Nair, B., et al. (2020). From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2, 56–67. doi: 10.1038/s42256-019-0138-9

Crossref Full Text | Google Scholar

Lundberg, S. M., and Lee, S.-I. (2017). A unified approach to interpreting model predictions. Proceedings of the 31st international conference on neural information processing systems, 4768–4777.

Google Scholar

Lundberg, S. M., Nair, B., Vavilala, M. S., Horibe, M., Eisses, M. J., Adams, T., et al. (2018). Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2, 749–760. doi: 10.1038/s41551-018-0304-0

Crossref Full Text | Google Scholar

Mao, Y. (2018). Deep learning vs. Bayesian knowledge tracing: student models for interventions. J. Educ. Data Min. 10, 28–54.

Google Scholar

Novick, L. R. (1988). Analogical transfer, problem similarity, and expertise. J. Exp. Psychol. Learn. Mem. Cogn. 14, 510–520. doi: 10.1037//0278-7393.14.3.510

Crossref Full Text | Google Scholar

Palazzo, D. J., Lee, Y.-J., Warnakulasooriya, R., and Pritchard, D. E. (2010). Patterns, correlates, and reduction of homework copying. Phys. Rev. Phys. Educ. Res. 6:010104. doi: 10.1103/PhysRevSTPER.6.010104

Crossref Full Text | Google Scholar

Papamitsiou, Z., Giannakos, M. N., and Ochoa, X. (2020). From childhood to maturity. Proceedings of the tenth international conference on learning analytics & knowledge, 559–568.

Google Scholar

Pardos, Z., Bergner, Y., Seaton, D., and Pritchard, D. (2013). Adapting Bayesian knowledge tracing to a massive open online course in edX. In Proceedings of the 6th International Conference on Educational Data Mining.

Google Scholar

Pinto, G., Cardoso-Pereira, I., Monteiro, D., Lucena, D., Souza, A., and Gama, K. (2023). Large language models for education: grading open-ended questions using ChatGPT. Proceedings of the XXXVII Brazilian Symposium on Software Engineering, 293–302.

Google Scholar

Polack, C. W., and Miller, R. R. (2022). Testing improves performance as well as assesses learning: a review of the testing effect with implications for models of learning. J. Exp. Psychol. Anim. Learn. Cogn. 48, 222–241. doi: 10.1037/xan0000323

Crossref Full Text | Google Scholar

Roelle, J., and Berthold, K. (2016). Effects of comparing contrasting cases and inventing on learning from subsequent instructional explanations. Instr. Sci. 44, 147–176. doi: 10.1007/s11251-016-9368-y

Crossref Full Text | Google Scholar

Scheines, R., Spirtes, P., Glymour, C., Meek, C., and Richardson, T. (1998). The TETRAD project: constraint based aids to causal model specification. Multivar. Behav. Res. 33, 65–117. doi: 10.1207/s15327906mbr3301_3

Crossref Full Text | Google Scholar

Schwartz, D. L., Chase, C. C., Oppezzo, M. A., and Chin, D. B. (2011). Practicing versus inventing with contrasting cases: the effects of telling first on learning and transfer. J. Educ. Psychol. 103, 759–775. doi: 10.1037/a0025140

Crossref Full Text | Google Scholar

Tomasevic, N., Gvozdenovic, N., and Vranes, S. (2020). An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput. Educ. 143:103676. doi: 10.1016/j.compedu.2019.103676

Crossref Full Text | Google Scholar

Wang, Z., Valdez, J., Basu Mallick, D., and Baraniuk, R. G. (2022). Towards human-like educational question generation with large language models, In: Proceedings of the International Conference on Artificial Intelligence in Education (AIED 2022). Springer Nature Switzerland: Cham. (Conference held in Brazil.) 153–166.

Google Scholar

Warnakulasooriya, R., Palazzo, D. J., and Pritchard, D. E. (2007). Time to completion of web-based physics problems with tutoring. J. Exp. Anal. Behav. 88, 103–113. doi: 10.1901/jeab.2007.70-06

Crossref Full Text | Google Scholar

Winne, P. H. (2015). Self-regulated learning. SFU Educational Review, 9, 1–5. doi: 10.21810/sfuer.v9i.300

Crossref Full Text | Google Scholar

Yang, C., Luo, L., Vadillo, M. A., Yu, R., and Shanks, D. R. (2021). Testing (quizzing) boosts classroom learning: a systematic and meta-analytic review. Psychol. Bull. 147, 399–435. doi: 10.1037/bul0000309

Crossref Full Text | Google Scholar

Zhang, M., Engel, A., Stelzer, T., and Morphew, J. W. (2020). Effect of online practice exams on student performance. In: Proceedings of the Physics Education Research Conference 2019 (PERC 2019). Provo, UT: American Association of Physics Teachers. 672–677.

Google Scholar

Zhang, M., Morphew, J., and Stelzer, T. (2023). Impact of more realistic and earlier practice exams on student metacognition, study behaviors, and exam performance. Phys. Rev. Phys. Educ. Res. 19:010130. doi: 10.1103/PhysRevPhysEducRes.19.010130

Crossref Full Text | Google Scholar