Challenges in using ChatGPT to code student's mistakes

The rapid advancements in artificial intelligence (AI) have sparked interest in its application within mathematics education, particularly in automating the coding and grading of student solutions. This study investigates the potential of ChatGPT, specifically the GPT-4 Turbo model, to assess student solutions to procedural mathematics tasks, focusing on its ability to identify correctness and categorize errors into two domains: “knowledge of the procedure” and “arithmetic/algebraic skills.” The research is motivated by the need to reduce the time-intensive nature of coding and grading and to explore AI's reliability in this context. The study employed a two-phase approach using a dataset of handwritten student solutions of a system of linear equations: first, ChatGPT was trained using student solutions that were rewritten by one of the authors to ensure consistency in handwriting style; its performance was then tested with additional solutions, also in the same handwriting. The findings reveal significant challenges, including frequent errors in handwriting recognition, misinterpretation of mathematical symbols, and inconsistencies in the categorization of mistakes. Despite iterative feedback and prompt adjustments, ChatGPT's performance remained inconsistent, with only partial success in accurately coding solutions. The study concludes that while ChatGPT shows promise as a coding aid, its current limitations—particularly in recognizing handwritten inputs and maintaining consistency—highlight the need for improvement. These findings contribute to the growing discourse on AI's role in education, emphasizing the importance of improving AI tools for practical classroom and research applications.

1 Introduction

The field of artificial intelligence (AI) has seen significant advancements that continue to astonish. The capacity to produce texts, generate images, and conduct image analysis is now attainable through this technological medium. The rapid developments of AI capabilities have given rise to discussions about its use in the field of mathematics education (e.g., Pepin et al., 2025).

Correcting and grading student answers is a time-consuming and labor-intensive undertaking for teachers (Liu et al., 2024). In addition to many other potentials, AI could be a supporting tool in this case. There are already considerations regarding its use in various subject areas, e.g., chemistry (Li et al., 2023), physics (Kortemeyer, 2023) and mathematics (Febrianti et al., 2024). In this sense, AI can also be used for qualitative research in mathematics education. The categorization of student responses is an arduous process that consumes also a significant amount of time. The emphasis of computer-based mathematics assessments was predominantly on standard procedures (Hoogland and Tout, 2018), as these were more straightforward to evaluate prior to the emergence of AI in educational contexts. In the interim, endeavors are underway to utilize AI in the assessment of conceptual knowledge. Though, Hankeln (2024) confirms problems in the evaluation of conceptual knowledge with ChatGPT, this is due to students being unable to formulate ideas unambiguously. Nevertheless, there is evidence that grading by ChatGPT and teacher correlate strongly (Shin et al., 2024). There are two approaches for entering the students' answers: either the answers are typed in or transferred to the AI as a (handwritten) image file. Liu et al. (2024) employed the second method and report some problems with recognizing students' handwriting. However, they conclude ChatGPT 4 represents a reliable and cost-effectiveness tool for initial grading of short answers.

Although the focus in computer-based mathematics examinations is on standard procedures due to their easier feasibility (Hoogland and Tout, 2018), there are hardly any studies investigating the reliability of ChatGPT in grading and categorizing student solutions to procedural tasks.

Since we are focusing on tasks that test procedural knowledge, it is important to clarify what we mean by procedural knowledge. One particularly recent definition is that proposed by Altieri (2016), who based his definition of procedural knowledge on the formulations of Star et al. (2015, p. 45) that “procedural knowledge refers to having knowledge of action sequences for solving a problem” and of Rittle-Johnson and Schneider (2014, p. 5) that “procedural knowledge is the ability to execute action sequences (i.e., procedures) to solve problems.” Altieri (2016) brings these two facets together, defining procedural knowledge as a combination of:

• Knowledge of the procedure: Knowledge of symbols and the formal language of mathematics as well as knowledge of rules and procedures for solving mathematical problems.

• Arithmetic/algebraic skills: Skills required to apply the knowledge of the procedure in a case-specific and targeted manner in a way that leads to a correct result in a reasonable time, especially in the case of procedures (Altieri, 2016, p. 25; translation from Dorner and Ableitinger, 2022, p. 4).

Initial research aim: In light of this, the original objective of our study was to assess the efficacy of ChatGPT in identifying and categorizing mistakes in handwritten student solutions to procedural tasks. It was important to us that this research process takes place within an easy-to-imitate framework. This would allow us to check whether teachers or researchers with limited AI knowledge could use ChatGPT for such purposes.

For our research aim, we needed both a training dataset (the size of one school class) and a test dataset of the same size. The data of the OFF project (Ableitinger and Dorner, 2025), which was collected at Austrian secondary schools in 2021, was ideal for this purpose. In this project, students who were about to take their school-leaving exams had to complete procedural tasks at the secondary level. These tasks were coded according to correctness and type of mistake. As one can have these two above-mentioned sub-facets of procedural knowledge, one can also lack them. According to Dorner et al. (2025), mistakes made by students can be assigned to one of these categories (knowledge of the procedure, arithmetic/algebraic skills) objectively—as the good inter-rater reliability confirms (see Dorner et al., 2025). Having resolved all discrepancies through discussion, the classification of mistakes in this study provides the normative categorization for the present project—on the one hand for training the AI and on the other hand for assessing the quality of the classification to be carried out by the AI afterwards.

2 Method of the initial research project

As a start, we first selected one task—PA07—in the sense of a case study in which mistakes have occurred that are as different as possible, and which therefore provide an interesting database for training or testing an AI as a coding aid:

Task PA07: System of linear equations

Find the solution set of the system of equations

$\begin{array}{c}2x+3y=1\\ -4x+5y=-13\end{array}$

in ℝ² by addition (elimination) method.

2.1 AI training

In a first step, we trained ChatGPT-4 Turbo¹ to evaluate students' solutions to Task PA07 in terms of their correctness and, in the case of incorrect solutions, to classify them according to the type of error. We opted the freely accessible ChatGPT version due to the easy-to-imitate approach. For this purpose, we used 21 students' works on Task PA07, rewritten by one of the authors to ensure consistency in handwriting style and to comply with the General Data Protection Regulation, to train ChatGPT. The 21 training data sets were transferred to ChatGPT in a total of two images.

We have generally formulated role-based prompts that ChatGPT should elevate to an expert role in order to achieve associated positive effects, e.g., output clarity, output depth, professionalism and use of appropriate technical language (Kambhatla et al., 2025; Louatouate and Zeriouh, 2025).

We entered the following two prompts into the chat one after the other:

Prompt 1 (definition): You are an expert in evaluating student work on procedural math tasks. Procedural knowledge is the combination of “Knowledge of the procedure” (Knowledge of symbols and the formal language of mathematics as well as knowledge of rules and procedures for solving mathematical problems) and “Arithmetic/algebraic skills” (Skills required to apply the knowledge of the procedure in a case-specific and targeted manner in a way that leads to a correct result in a reasonable time, especially in the case of procedures.)

Prompt 2 (training): You will now receive a file containing a procedural task (top left) and several student solutions, each marked with a code. We would now like to train you on the following questions: Are the student solutions correct? If not, is the mistake due to a lack of “Knowledge of the procedure” or an error in “arithmetic/algebraic skills”? Please answer these two questions for each of the student solutions. We will then give you feedback.

If the student's solution was coded in the same way as in the double coding by Dorner et al. (2025), ChatGPT was given positive feedback (e.g., “Well done!”). In cases of divergent coding, feedback was provided explaining the difference in coding and how ChatGPT should handle similar mistakes in the future. For example, ChatGPT recognized the student solution 21_S03_A03 (see Figure 1 top left) as incorrect and identified a mistake in the knowledge of the procedure. However, its analysis was not sufficiently differentiated: “Student isolates y and substitutes into the second equation but uses an incorrect and structurally invalid manipulation (e.g., $y=\frac{1}{2x}$). This reflects a misunderstanding of how substitution or elimination works in this context.”

Figure 1

Figure 1. Student solutions to Task PA07 and version digitized by ChatGPT.

Our response was: “Indeed, the solution is incorrect. But: There is a mistake in the knowledge of the procedure, because he chose the wrong equivalent transformation (:2x), that is not target oriented. And there is a mistake in arithmetic/algebraic skills, because he performed this transformation wrongly (he should have also divided the left side of the equation by 2x).

2.2 Testing AI

In a second step, we wanted to test how well the trained ChatGPT could code further student solutions of the same task. To do this, we used another 18 student solutions (again rewritten by the same author) to Task PA07 and prompted the following to test ChatGPT:

Prompt 3 (test): You will now receive a file containing a procedural task (top left) and several student solutions, each marked with a code. (Please ignore fields without a code.) Please answer the following questions: Are the student solutions correct? If not, is the mistake due to a lack of “Knowledge of the procedure” or an error in “arithmetic/algebraic skills”? We don't want a verbal output, but rather only the following: Output a table with three columns: 1st column: code, 2nd column: value 1 if task was solved correctly, value 0 if task was not solved correctly, 3rd column: 00 if there are no mistakes, 10 if there is at least one mistake due to a lack of “knowledge of the procedure” but no mistakes in arithmetic/algebraic skills, 01 vice versa, 11 if there are mistakes in both categories.

3 Rethinking the study focus

3.1 A shift in perspective

When evaluating the initial test data, we made the following observation, which led us to modify the original research project. The first input of test data in ChatGPT, an image file containing 10 student solutions was assessed as correct in all respects, both the identification of correctness and the mistake categorization. Interestingly, the second file, which contained eight student solutions, was not assessed as good as the first. Only four of the solutions were correctly coded.

This drew our attention to the potential issue of font recognition deficiencies. It is conceivable that ChatGPT is not yet capable of identifying handwritten solutions accurately although they were provided with a new and easily legible handwriting. This led us to a new perspective considering the following research question:

How effective is GPT-4 Turbo in the digitization of handwritten procedural task solutions, and what types of errors occur during this process?

3.2 Recognition of handwritten student solutions by ChatGPT

To determine how effectively ChatGPT (specifically the GPT-4 Turbo version) can recognize handwritten solutions to procedural mathematics tasks and convert them into a digital format, we used the following prompt twice. The first time, we provided a file containing 13 student solutions to Task PA07. The second time, we used a different file containing 9 student solutions:

Prompt 4 (digitization): You are a specialist in character recognition. You will now receive written student work on a task. Copy this work exactly as it appears. Copy the following file completely, spelling and punctuation included! Do NOT make any mathematical corrections! Sort according to the code (alphabetically: A01, A02, etc.).

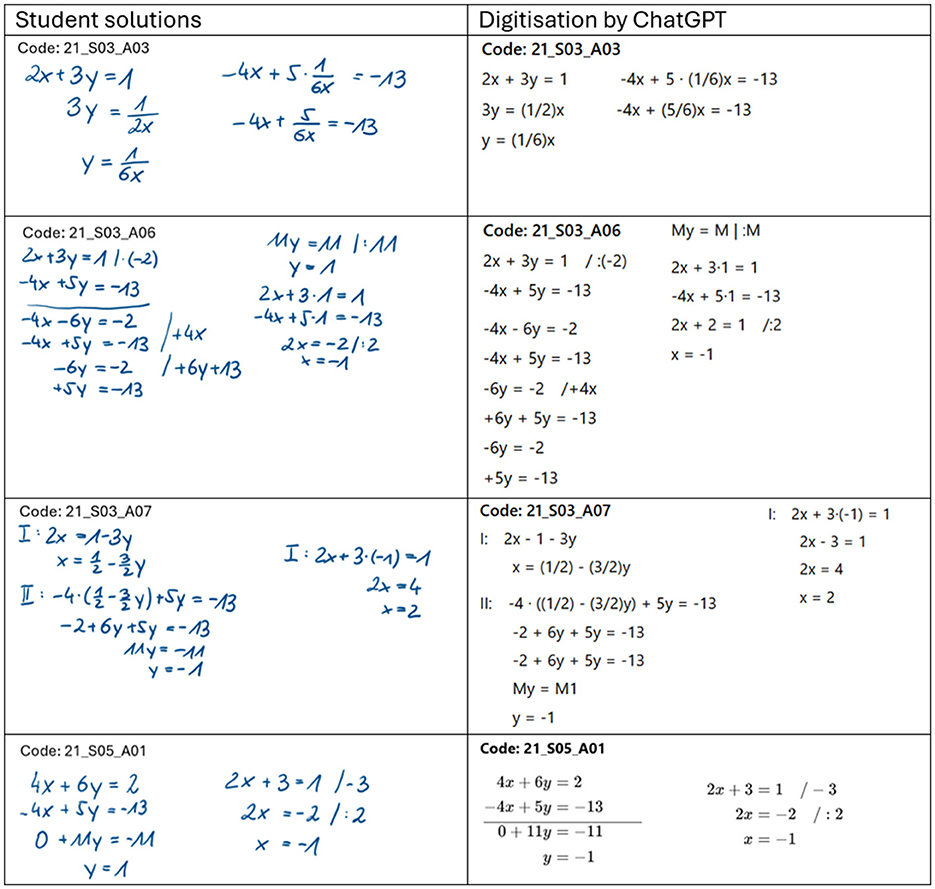
The student solutions in the two files were each labeled with a unique student code. Out of the total of 22 students, 2 did not complete the tasks. Of the remaining 20 solutions, ChatGPT successfully recognized and digitized 4 without any errors, while the other 16 were digitized with inaccuracies. Figure 1 provides a comparison of several student solutions alongside the corresponding outputs generated by ChatGPT.

During the digitization process by ChatGPT, a number of errors occurred, some of which are quite interesting. For instance, in the student solution labeled 21_S03_A03, ChatGPT failed to adhere to the rules of bracket conventions. For example, the expression should read 3y = 1/(2x), but this is not correctly represented in the output.

In the case of 21_S03_A06, multiple translation errors occurred simultaneously. For instance, instead of writing /·(−2), ChatGPT incorrectly used /:(−2) in the first line. This is particularly noteworthy because the student had indeed applied the operation /·(−2) correctly, meaning that ChatGPT introduced a mistake during the digitization process. This operation, as misrepresented by ChatGPT, does not align with the equation written by the student in the subsequent line. Later, we will observe the reverse phenomenon: despite being explicitly instructed in the prompt not to do so, ChatGPT corrects mistakes in the student solutions. Additionally, the horizontal line that should appear between the second and third lines is missing in ChatGPT's output. The operation +4x was inserted at the wrong position. Furthermore, ChatGPT entirely fabricated the line +6y+5y = −13, which seems to have been triggered by the operation + 6y+13. The line −6y=−2 appears twice in ChatGPT's output, even though it should only occur once. Another notable error is that ChatGPT interpreted “11y” as “My” likely due to the specific handwriting style. However, this is an unexpected error in the context of solving this system of equations, as ChatGPT is designed to select the most probable output for a given input. The appearance of “My” in this context is, at least from our perspective, entirely unpredictable and unrelated to the mathematical content. Finally, the line y = 1, which is present in the student solution, was completely omitted in ChatGPT's output.

The incorrect transcription of the equation 2x = 1 − 3y in the first line of 21_S03_A07 as 2x−1 − 3y by ChatGPT can be attributed to the somewhat unclear equal sign in the handwritten solution. This issue could likely be avoided with clearer handwriting. However, the duplication of the equation −2+6y+5y = −13 in ChatGPT's output cannot be explained, nor is there an obvious reason why ChatGPT invented the entirely new line 2x−3 = 1.

In 21_S05_A01, the student incorrectly simplified the equation 11y = −11 to y = 1. As mentioned earlier, ChatGPT corrected this error, producing the correct simplification. However, it then proceeded to work with y = 1, just as the student did, by subsequently writing the equation 2x−3 = 1. This inconsistency highlights how ChatGPT alternates between correcting errors and following the student's flawed reasoning.

In the next step, we provided ChatGPT with feedback on all these errors and included the necessary corrections. ChatGPT incorporated these corrections into a revised output. However, this led to new errors that were not present in the initial output. In one instance, ChatGPT even transferred three lines from solution 21_S03_A07 into solution 21_S03_A06. Additionally, we sought to address the issue of ChatGPT making corrections to the student solutions despite our explicit instructions in the prompt not to do so. To tackle this, we asked ChatGPT how we should formulate our prompt to prevent such behavior and subsequently adjusted the prompt accordingly:

Prompt 5 (accuracy): Please transcribe it exactly as it appears, including all errors, unusual formatting, and incorrect symbols or steps. Do not make any corrections or interpretations, even if something is mathematically or syntactically wrong.

The error rate was reduced to approximately half compared to the initial output during this correction cycle. In total, we conducted four such correction cycles. After the fourth cycle, only the student solution 21_S03_A06 remained erroneous. To address this, we provided ChatGPT with line-by-line instructions for this specific solution.

The transfer of lines from one solution into another suggests that ChatGPT may struggle to handle the digitization of multiple student solutions simultaneously. To investigate this, we attempted to have ChatGPT digitize the student solutions individually (i.e., each in a separate file). However, similar errors occurred as in the case when multiple solutions were processed at once. In one instance, ChatGPT even stopped midway through the digitization process, producing an incomplete output.

4 Discussion

Our initial euphoria has now turned into disappointment with ChatGPT's performance. According to Hoogland and Tout (2018), we thought that student solutions to procedural tasks would be easier for the AI to assess than those to tasks that test conceptual knowledge, as shown by Hankeln (2024).

As previously mentioned, Liu et al. (2024) report issues with the recognition of handwriting by an AI. Kortemeyer (2023) also relates erroneous processing by ChatGPT in the context of student solutions of physics problems. For example, milli-Farad was incorrectly changed to micro-Farad. From this perspective, we were somewhat prepared for the problems with character recognition, but we could not have foreseen the extent to which they would manifest themselves. It is evident that certain errors can be attributed to the quality of the handwriting, e.g., 2x−1 − 3y instead of 2x = 1 − 3y. The fact that students‘ handwriting is often more difficult to recognize than in this case, and that the handwriting of different students can vary greatly (in this instance, only one type of handwriting was worked with) makes the use of ChatGPT in practice even more difficult. Furthermore, it is reasonable to expect that an AI system would be capable of recognizing contextual nuances, from this perspective, mistakes as the inappropriate recognition of the letter M for the number 11 are disappointing. Despite the advance request not to make any mathematical corrections, this happened anyway. Even subsequent prompts did not help satisfactorily. Furthermore, the sequence of the students' solution steps was changed, a phenomenon that could be anticipated from an AI in this developmental stage.

However, it should be noted that problems could have arisen from the intermediate step of character recognition, which possibly would not have occurred if we had only considered the ChatGPT's output of the mistake analysis as planned initially (e.g., due to internal working processes of ChatGPT that are not visible to us). Further research is required in this area.

This also has the following educational implications: As long as AI models cannot reliably recognize students' handwriting, they are not a reliable aid for teachers in grading and diagnosis. We recommend using AI at most for initial analysis, which must in any case be checked and adapted by the teacher (cf. Liu et al., 2024). It remains to be seen whether such an approach actually saves time. Furthermore, the unreflective use of AI would of course also have a direct impact on students, because, for example, errors would be corrected automatically or parts of solutions that are not recognizable by AI would not be taken into account. The use of AI is certainly a promising prospect for qualitative mathematics education research, but in this setting, it is clear that the error rate is currently still too high to allow reliable analyses.

Our conclusion in terms of this research framework and its use in classroom or research for coding or grading student solutions is: not yet.

Data availability statement

The datasets presented in this article are not readily available because the data collected may only be used for scientific purposes and may only be published in anonymised form. Requests to access the datasets should be directed to Christoph Ableitinger, Y2hyaXN0b3BoLmFibGVpdGluZ2VyQHVuaXZpZS5hYy5hdA==.

Author contributions

CA: Methodology, Project administration, Resources, Data curation, Validation, Visualization, Conceptualization, Investigation, Formal analysis, Writing – original draft, Writing – review & editing, Software. CD: Investigation, Resources, Software, Visualization, Data curation, Conceptualization, Formal analysis, Validation, Project administration, Methodology, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Gen AI was used in the creation of this manuscript. Gen AI was used for language improvement of the article and ChatGPT was used as a tool in the study for recognising handwriting and coding solutions provided by students.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ChatGPT-4 Turbo is an optimized variant of GPT-4, designed to deliver comparable performance with significantly improved speed and efficiency.

References

Ableitinger, C., and Dorner, C. (2025). Measuring Austrian students' procedural knowledge at the end of upper secondary level. Int. J. Math. Educ. Sci. Technol. 56, 208–230. doi: 10.1080/0020739X.2023.2209093

Crossref Full Text | Google Scholar

Altieri, M. (2016). Erfolg in Mathematikklausuren Ingenieurwissenschaftlicher Studiengänge unter Besonderer Berücksichtigung Prozeduralen Wissens [Success in Mathematics Exams in Engineering Courses With a Special Focus On Procedural Knowledge] (Ph.D. dissertation). Dortmund: Technical University of Dortmund.

Google Scholar

Dorner, C., Ableitinger, C., and Krammer, G. (2025). Revealing the nature of mathematical procedural knowledge by analysing students' deficiencies and errors. Int. J. Math. Educ. Sci. Technol. 1–22. doi: 10.1080/0020739X.2024.2445666

Crossref Full Text | Google Scholar

Dorner, C., and Ableitinger, C. (2022). Procedural mathematical knowledge and use of technology by senior high school students. Eurasia J. Math. Sci. Technol. Educ. 18:em2202. doi: 10.29333/ejmste/12712

Crossref Full Text | Google Scholar

Febrianti, T. S., Fatimah, S., Fitriyah, Y., and Nurhayati, H. (2024). Leveraging ChatGPT for scoring students' subjective tests. Int. J. Educ. Math. Sci. Technol. 12, 1504–1524. doi: 10.46328/ijemst.4436

Crossref Full Text | Google Scholar

Hankeln, C. (2024). Challenges in using ChatGPT for assessing conceptual understanding in mathematics education. J. Math. Educ. 17, 1–15. doi: 10.26711/007577152790171

Crossref Full Text | Google Scholar

Hoogland, K., and Tout, D. (2018). Computer-based assessment of mathematics into the twenty-first century: pressures and tensions. ZDM Math. Educ. 50, 675–686. doi: 10.1007/s11858-018-0944-2

Crossref Full Text | Google Scholar

Kambhatla, G., Shaib, C., and Govindarajan, V. (2025). Measuring diversity of synthetic prompts and data generated with fine-grained persona prompting. arXiv. 1–10. doi: 10.48550/arXiv.2505.17390

Crossref Full Text | Google Scholar

Kortemeyer, G. (2023). Toward AI grading of student problem solutions in introductory physics: a feasibility study. Phys. Rev. Phys. Educ. Res. 19:020163. doi: 10.1103/PhysRevPhysEducRes.19.020163

Crossref Full Text | Google Scholar

Li, J., Gui, L., Zhou, Y., West, D., Aloisi, C., and He, Y. (2023). Distilling ChatGPT for explainable automated student answer assessment. arXiv. 6007–6026. doi: 10.18653/v1/2023.findings-emnlp.399

Crossref Full Text | Google Scholar

Liu, T., Chatain, J., Kobel-Keller, L., Kortemeyer, G., Willwacher, T., and Sachan, M. (2024). AI-assisted automated short answer grading of handwritten university level mathematics Exams. arXiv. 1-12. doi: 10.48550/arXiv.2408.11728

Crossref Full Text | Google Scholar

Louatouate, H., and Zeriouh, M. (2025). Role-based prompting technique in generative AI-assisted learning: a student-centered quasi-experimental study. J. Comput. Sci. Technol. Stud. 7, 130–145. doi: 10.32996/jcsts.2025.7.2.12

Crossref Full Text | Google Scholar

Pepin, B., Buchholtz, N., and Salinas-Hernández, U. (2025). A scoping survey of ChatGPT in mathematics education. Digit. Exp. Math. Educ. 11, 9–41. doi: 10.1007/s40751-025-00172-1

Crossref Full Text | Google Scholar

Rittle-Johnson, B., and Schneider, M. (2014). “Developing conceptual and procedural knowledge of mathematics,” in The Oxford Handbook of Numerical Cognition, eds. R. C. Kadosh and A. Dowker (Oxford: Oxford University Press), 1118–1134. doi: 10.1093/oxfordhb/9780199642342.013.014

Crossref Full Text | Google Scholar

Shin, B., Lee, J., and Yoo, Y. (2024). Exploring automatic scoring of mathematical descriptive assessment using prompt engineering with the GPT-4 model: focused on permutations and combinations. Math. Educ. 63, 187–207. doi: 10.63311/mathedu.2024.63.2.187

Crossref Full Text | Google Scholar

Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch, K., Newton, K., et al. (2015). Learning from comparison in algebra. Contemp. Educ. Psychol. 40, 41–54. doi: 10.1016/j.cedpsych.2014.05.005

Crossref Full Text | Google Scholar