- 1Department of Mathematics and Science Education, Akrokerri College of Education, Obuasi, Ghana
- 2Department of Mathematics Education, Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development, Kumasi, Ghana
This study examines the increasing relationship between linguistics and mathematics education, highlighting how language influences the comprehension and communication of mathematical concepts. It explores how semantics, syntax, discourse, and metaphor influence comprehension, especially in multilingual classrooms where students face challenges due to language differences. Drawing on global research from 2017 to 2025, it emphasizes the role of classroom discourse, sociocultural theory, and cognitive linguistics, particularly metaphors like “number line” or “function machine,” in supporting mathematical thinking. The paper advocates for linguistically responsive teaching, culturally inclusive pedagogy, and equitable assessment practices to enhance learning and promote inclusion. Ultimately, it argues that language is a fundamental tool, not a barrier, for mathematical understanding. While this study provides valuable insights into the intersection of linguistics and mathematics education, it is limited by its reliance on secondary sources and theoretical perspectives rather than empirical classroom-based data.
1 Introduction
Linguistics and mathematics, though traditionally viewed as distinct disciplines, share deep structural and cognitive connections that influence how meaning is constructed, interpreted, and communicated. The intersection of these fields, especially in educational contexts, has gained growing attention as researchers explore how language shapes mathematical understanding. Mathematical meaning, far from being universally intuitive, is deeply embedded in linguistic structures, syntax, and semantics. Understanding how learners process mathematical statements depends significantly on their linguistic competence, especially in multilingual or second-language settings (Sharma and Sharma, 2023). Consequently, the role of language in mathematics education has evolved from being a supplementary consideration to a central theme in curriculum design and pedagogical strategies.
Research has shown that mathematical language possesses unique syntactic and semantic structures that differ from everyday language, which often creates barriers to comprehension for students. Words such as “difference (-),” “product ( × ),” and “mean ()” possess specialized meanings in mathematics that conflict with their everyday usage, leading to semantic confusion (Song et al., 2024). Furthermore, symbolic representations in mathematics, such as equations and notations, carry inherent meanings that require linguistic scaffolding for effective interpretation. According to (Edelen et al. 2025), the meanings of mathematical expressions are not static but are co-constructed through discourse in the classroom. This aligns with socio-constructivist views that position language as the medium through which mathematical knowledge is developed and internalized.
Another significant area of investigation is the influence of linguistic diversity on mathematical performance. In multilingual classrooms, the language of instruction plays a crucial role in how students access and articulate mathematical ideas. (Smith et al. 2024) argues that learners often face “linguistic dilemmas,” where their home language supports conceptual understanding but the language of instruction poses challenges in formal mathematical expression. These dynamic underscores the importance of code-switching, translanguaging, and culturally responsive pedagogy in mathematics classrooms, especially in post-colonial and linguistically diverse contexts such as sub-Saharan Africa and Latin America. The linguistic framing of mathematical problems influences not only comprehension but also the cognitive strategies that learners employ.
Furthermore, cognitive linguistics offers powerful frameworks for analyzing mathematical meaning-making. The concept of metaphor, central to George Lakoff and Rafael Núñez's earlier work, continues to influence how researchers understand abstraction in mathematics. Recent studies affirm that metaphors like “numbers as points on a line” or “functions as machines” are not merely pedagogical tools but fundamental to how both students and experts conceptualize mathematical structures (Tedre et al., 2021). These cognitive linguistic structures offer insight into the embodied and metaphorical basis of abstract mathematical thought, suggesting that meaning in mathematics is not purely logical but also experiential and grounded in language.
The relationship between linguistics and mathematics is both intricate and indispensable. Contemporary research has underscored the need to integrate linguistic awareness into mathematics instruction to bridge semantic gaps, support multilingual learners, and promote deeper conceptual understanding. The convergence of linguistics and mathematics challenges educators to move beyond numerical proficiency toward fostering meaningful mathematical discourse. As such, advancing equity and excellence in mathematics education will require a holistic view that acknowledges language as a core component of mathematical reasoning and communication (Edelen et al., 2025).
Despite the abstract and universal nature often attributed to mathematics, learners frequently struggle with interpreting mathematical concepts correctly due to language-related barriers. The specialized vocabulary, symbolic syntax, and semantic ambiguity embedded in mathematical discourse often create confusion, especially among students from linguistically diverse backgrounds or those learning in a second language (Povoroznyuk, 2024). Terms such as “difference,” “product,” or “mean” carry distinct meanings in everyday usage and mathematical contexts, leading to semantic conflicts that impair comprehension and problem-solving accuracy (Vallverdu, 2025). Furthermore, complex sentence structures in word problems, coupled with unfamiliar symbolic representations, exacerbate learners' cognitive load, limiting their ability to construct meaningful mathematical interpretations (Hickendorff, 2021). These linguistic challenges are particularly pronounced in multilingual classrooms where the language of instruction does not align with students' home languages, resulting in what (Peyer et al. 2022) describes as “linguistic dilemmas” that hinder equitable access to mathematical learning. Therefore, addressing the language barrier is crucial for improving mathematical understanding and promoting inclusivity in mathematics education.
2 Theoretical framework
Linguistic theories provide a vital lens for understanding how mathematical meaning is constructed, interpreted, and communicated in educational contexts. Central to this framework are semantics, syntax, pragmatics, and discourse analysis. Semantics concerns the meaning of mathematical terms, many of which are polysemous, creating confusion between everyday and technical interpretations (Kontorovich, 2018). Syntax refers to the structure of mathematical statements, which often mirror logical forms that differ from ordinary language, presenting difficulties in comprehension and reasoning. Pragmatics examines how context influences the meaning of mathematical utterances, while discourse analysis explores the flow of classroom communication and how mathematical knowledge is co-constructed through dialogue (Wang and Lin, 2024). Additionally, cognitive linguistics, particularly the metaphor theory proposed by (Francis 2018), emphasizes that abstract mathematical concepts are understood through embodied metaphors such as “numbers as points on a line” or “functions as machines.” These metaphors are not mere teaching aids but cognitive structures that shape the way learners conceptualize mathematics.
The meaning of mathematics emerges through both formal and informal modes of expression. Formal mathematical language involves symbols, definitions, and logical structures governed by strict conventions. In contrast, informal language includes everyday communication, intuitive reasoning, and exploratory talk, which play a key role in meaning-making during the learning process (Coultas and Booth, 2019). A clear distinction between symbolic and natural language is also essential; symbolic language allows for precision and generalization, while natural language supports the explanation and justification of ideas. The sociocultural theory of learning, particularly Vygotsky's concept of mediational tools, posits that language is a primary medium through which learners internalize mathematical concepts. Classroom interaction, therefore, becomes a critical site where language mediates between a learner's everyday experiences and formal mathematical knowledge (Ann and Mellony, 2018).
Viewing mathematics as a language in its own right provides further depth to this framework. Mathematical language possesses its grammar, syntax, and vocabulary, which must be acquired much like a second language. (Edmonds-wathen and Edmonds-wathen 2019) introduced the idea of “mathematics registers,” distinct forms of language used in mathematical contexts that involve specific terminology, sentence structures, and modes of representation. These registers help learners participate meaningfully in mathematical discourse, but can also pose challenges when linguistic proficiency is lacking. Moreover, mathematics is understood as a semiotic system, composed of signs, symbols, and representations that communicate meaning within a shared context (Edward and Masilo, 2023). Mastery of this system requires learners to move fluently between multiple representations, verbal, symbolic, graphical, and numerical, each governed by its conventions. Together, these theoretical insights underscore that understanding mathematics is as much a linguistic endeavor as it is a logical or numerical one.
3 Language as a mediator of mathematical meaning
One of the most persistent linguistic challenges in mathematics education is semantic ambiguity caused by polysemy, when a word has multiple meanings depending on context. Words such as “volume,” “difference,” and “mean” have distinct interpretations in everyday language and in mathematical contexts. For example, “difference” in daily usage may imply disagreement, whereas in mathematics it denotes a specific arithmetic operation (Suryadi, 2019). Similarly, “volume” may refer to sound level in common language, but measures the capacity of a 3D object in mathematics. This overlap of vocabulary leads to confusion, especially for early learners and students who are learning mathematics in a second language. The tension between everyday and academic mathematical language often results in misinterpretation of questions, hindering students' ability to apply correct procedures and develop sound reasoning (Sibanda, 2017). These semantic gaps can distort students' conceptual understanding, particularly when they rely on informal language frameworks to make sense of formal mathematical instructions.
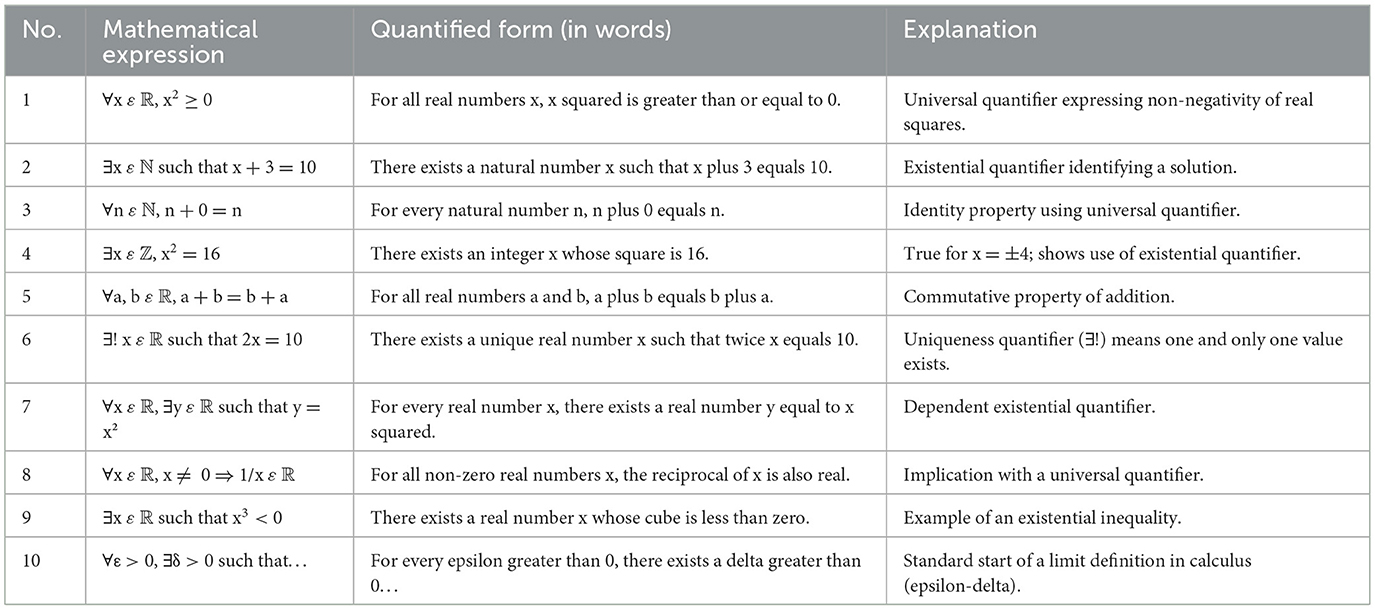
Beyond vocabulary, the syntactic structure of mathematical expressions and problems can significantly affect comprehension. Mathematical syntax often involves conditional statements (e.g., “If x is even, then x2 is even”) and quantified expressions (“For all x in set A, there exists…”) with examples presented in Table 1, which mirror formal logic more than natural language. These constructions can be cognitively demanding, especially when students are unfamiliar with such syntax or when it differs from syntactic norms in their first language. Moreover, complex sentence constructions in word problems, including embedded clauses and passive voice, may obscure the mathematical relationships being described. The directionality of reading mathematical symbols and expressions, left to right in algebraic equations or top to bottom in matrices, also requires specific visual-linguistic skills. Misinterpretation of symbolic representations due to poor syntactic parsing often leads to procedural errors and incorrect answers, underscoring the need for explicit instruction on how to “read” mathematical language (Li et al., 2025). Classroom discourse plays a central role in helping students make sense of mathematical vocabulary, syntax, and representations. Teacher-student and peer interactions create a social context in which mathematical meaning is constructed, negotiated, and refined. Through well-structured dialogue, teachers can model how to use mathematical language precisely, guide learners in making connections between informal ideas and formal terminology, and clarify semantic ambiguities (Wulff, 2024). Discourse analysis in mathematics classrooms reveals that productive conversations often feature frequent use of clarification questions, restatements, and elaborations that support deeper comprehension. Strategies such as teacher questioning, revoicing, and scaffolding help bridge the gap between what students know and what they need to understand conceptually (Wu et al., 2019). Furthermore, encouraging students to explain their reasoning aloud enables teachers to identify linguistic and conceptual misconceptions, fostering a more responsive and inclusive learning environment where language becomes a tool for learning mathematics, not a barrier.
Table 1 illustrates how mathematical syntax, through the precise use of quantifiers and symbolic expressions, mediates the communication and interpretation of mathematical meaning. Each expression reflects how language structures such as universal (∀), existential (∃), and uniqueness (∃!) quantifiers are used to formalize general truths, identify specific instances, or assert uniqueness within mathematical logic. For example, statements like “∀x ε R, x2 ≥ 0” and “∃x ε Z, x2 = 16” translate complex ideas into concise symbolic language that captures universal validity and existence, respectively. These quantified forms demonstrate how formal mathematical language enhances clarity, precision, and abstraction, allowing concepts like identity, commutativity, implication, and limits to be universally understood and communicated. In this way, the syntax of mathematics operates not merely as a tool for calculation but as a linguistic system that shapes and conveys deep mathematical meaning.
4 Multilingualism and linguistic diversity in mathematics education
4.1 Challenges in multilingual classrooms
Multilingual classrooms present unique challenges in mathematics education, particularly when the language of instruction differs from the students' home language. This disconnect can hinder learners' ability to grasp mathematical concepts, articulate reasoning, or engage meaningfully in classroom discourse. In many educational systems, especially in Africa and Asia, mathematics is often taught in an official or colonial language (e.g., English or French), which is not the primary language spoken by students at home (Robertson, 2020). As a result, students may understand the concepts intuitively but struggle to express or apply them due to limited proficiency in the instructional language. Code-switching and translanguaging have emerged as adaptive strategies to navigate these barriers. Teachers and students often shift between languages to clarify meanings, offer explanations, or provide cultural context. However, this practice is not always formally supported, and in some cases, it is discouraged by policy, limiting its effectiveness in promoting inclusive learning.
4.2 Benefits of multilingual resources
Despite the challenges, multilingualism can be a powerful asset in mathematics education when appropriately harnessed. Allowing students to use their first language or indigenous language in mathematical discussions enhances their conceptual understanding by enabling them to draw on familiar linguistic and cognitive frameworks (Ramulumo, 2023). Research shows that bilingual and multilingual learners often demonstrate more flexible thinking, as they can represent and process mathematical ideas across languages. Moreover, the integration of cultural mathematics, also known as ethnomathematics, provides a bridge between students' lived experiences and formal mathematical knowledge. This includes counting systems, spatial reasoning, and problem-solving approaches embedded in indigenous knowledge systems, which can serve as rich sources for mathematical exploration and understanding. When teachers validate and incorporate students' linguistic and cultural resources into the mathematics classroom, it not only supports learning but also affirms students' identities and promotes equity.
4.3 Case studies and global perspectives
Numerous international studies highlight both the complexities and opportunities associated with linguistic diversity in mathematics education. In South Africa, (Mclachlan and Essien 2021) documented how students used a mix of isiZulu and English to navigate mathematical tasks, showing improved engagement when allowed to switch languages. In Latin America, research in bilingual indigenous communities reveals that students learn better when mathematics instruction reflects their native linguistic structures and cultural practices (Robertson, 2020). European studies, particularly in Germany and Sweden, emphasize the need for linguistic scaffolding and visual supports for immigrant students (Morawski and Georgakaki, 2024). Similarly, Asian contexts like Singapore and Malaysia have explored multilingual teaching models to accommodate diverse language backgrounds. Comparative insights from these studies underscore the importance of policy support for multilingual strategies, teacher training in linguistic responsiveness, and the design of culturally and linguistically inclusive curricula. As mathematics becomes increasingly global, addressing linguistic diversity is no longer optional but essential for equitable education. Figure 1 represents multilingualism and linguistic diversity in mathematics education.

Figure 1. Multilingualism and linguistic diversity in mathematics education (source: authors' construct, 2025).
Figure 1 illustrates the key components of Multilingualism and Linguistic Diversity in Mathematics Education, organized into three interconnected areas. At the center is the main theme, which branches into three critical subtopics: Challenges in Multilingual Classrooms, Benefits of Multilingualism Resources, and Case Study and Global Perspectives. This structure emphasizes a comprehensive approach to understanding how linguistic diversity affects the teaching and learning of mathematics. Moreover, it explores the obstacles teachers and students may encounter in multilingual settings, highlights the educational advantages of using multiple languages and culturally relevant materials, and draws on global examples to showcase diverse practices and outcomes.
5 Cognitive linguistics and mathematical thinking
5.1 Role of metaphors in mathematical meaning-making
Cognitive linguistics provides valuable insights into how individuals conceptualize and make sense of abstract mathematical concepts through metaphor (Nathan and Walkington, 2017). According to (Tran et al. 2017), mathematical thought is deeply grounded in metaphorical structures derived from bodily experiences, a concept known as embodied cognition. For example, the “number line” metaphor equates numbers with positions in space, allowing learners to visualize numerical order and distance. Similarly, the “function machine” metaphor frames functions as input-output processes, helping students grasp how variables are transformed. The metaphor of a “balance equation” promotes the idea of equality and preservation, which is essential in algebraic reasoning. These metaphors are not simply instructional conveniences; they are foundational cognitive tools that support abstraction by connecting new mathematical ideas to familiar physical or conceptual experiences. When students use metaphors to reason about unfamiliar content, they rely on prior knowledge, sensory experiences, and intuitive understanding to build meaning in mathematics (Giberti 2023).
5.2 Language-driven misconceptions and concept formation
While metaphors can scaffold understanding, they also carry the risk of generating misconceptions when learners interpret them too literally or transfer inappropriate associations. For instance, interpreting the “balance equation” metaphor may mislead students into thinking that every equation must have equal-looking expressions on both sides, even in cases where transformations temporarily disrupt symmetry. Similarly, viewing graphs purely as “pictures” may cause students to confuse the shape of a graph with the physical appearance of a real-world object it represents (Tenbrink et al., 2019). These language-driven misconceptions arise when metaphorical mappings are either overextended or conflict with formal definitions. Therefore, educators need to make explicit the limitations of metaphors while still using them as stepping stones to deeper understanding. Instructional materials should be designed to guide students from intuitive, metaphor-based reasoning toward formal mathematical abstraction, helping them refine and sometimes “unlearn” the metaphorical models once more precise concepts are developed.
5.3 Implications for instructional design and learning materials
The use of metaphors in mathematics instruction has significant implications for how learning materials, curriculum content, and classroom discourse are structured. Effective instructional design must balance the accessibility of metaphorical representations with the precision of formal mathematical language. Visual models, manipulatives, and analogies should be strategically introduced and explicitly discussed so that students can transition from metaphorical thinking to rigorous mathematical reasoning. Moreover, curriculum developers should include opportunities for learners to critique and evaluate the usefulness and limitations of the metaphors they encounter. Teachers also need professional development to recognize both the pedagogical potential and the cognitive constraints of metaphor use in mathematics classrooms (Daane et al., 2018). By integrating cognitive linguistic insights into instruction, educators can foster a more intuitive and meaningful engagement with mathematical ideas while also building students' capacity for abstract and symbolic reasoning.
6 Pedagogical implications
6.1 Designing linguistically responsive mathematics instruction
Effective mathematics instruction requires more than just procedural fluency; it demands a deliberate focus on language to ensure all students can access and engage with mathematical ideas (Erath et al., 2021). Linguistically responsive teaching integrates strategies that support language development alongside mathematical reasoning. This includes explicit vocabulary instruction, where teachers clarify the meaning of key terms that may have multiple interpretations (e.g., “product,” “table,” “mean”) and provide opportunities for students to use these terms in various contexts. Semantic mapping and concept maps can also help students visualize relationships between words, symbols, and concepts, reinforcing connections and promoting retention. Visual aids such as diagrams, number lines, and symbolic representations serve as powerful scaffolding tools, especially for learners who struggle with verbal explanations. Additionally, teachers can incorporate sentence starters, structured math talk routines, and bilingual resources to help students articulate their mathematical thinking clearly and confidently (Luzano, 2025). These strategies not only enhance comprehension but also foster mathematical discourse and inclusivity.
6.2 Teacher preparation and professional development
To implement linguistically responsive strategies effectively, teachers must receive focused training in language and literacy as part of their mathematics education. Unfortunately, many teacher education programs inadequately prepare teachers to address the linguistic dimensions of mathematical learning, particularly in multilingual or multicultural classrooms (Parkhouse et al., 2019). Developing linguistic awareness involves helping teachers recognize how language shapes mathematical meaning, identify potential sources of confusion, and adapt instruction accordingly. Professional development should also include training in analyzing student errors for language-related causes, such as misinterpreting polysemous terms or symbolic syntax. Teachers need to be equipped with tools to differentiate instruction for English Language Learners (ELLs) and to employ translanguaging strategies when appropriate. Collaborative learning communities and reflective practice are also essential, enabling teachers to share experiences and develop responsive approaches tailored to their specific classroom contexts (Kamali and Javahery, 2025). By cultivating linguistic sensitivity, educators can bridge the gap between students' language skills and their mathematical potential.
6.3 Assessment and equity considerations
Assessments in mathematics often overlook the linguistic demands they place on students, leading to inaccurate judgments about their mathematical ability. Language bias in standardized assessments disproportionately affects ELLs and students from linguistically diverse backgrounds, who may understand the mathematical content but struggle to interpret complex word problems or instructions due to language difficulties (Buono and Jang, 2021). Such assessments may conflate language proficiency with content knowledge, contributing to underperformance and misplacement in intervention programs. To promote equity, assessments must be designed with linguistic accessibility in mind. This includes simplifying language without reducing mathematical rigor, offering alternative formats (e.g., oral responses, visual prompts), and allowing the use of students' first language where possible. Educators and policymakers should also advocate for culturally and linguistically inclusive testing practices that reflect the diversity of learners. Equitable assessment is not just a fairness issue; it is essential for recognizing and nurturing the full range of students' mathematical competencies (Alam and Mohanty, 2023). Figure 2 represents pedagogical implications for linguistics and mathematics.
Figure 2 outlines the Pedagogical Implications of addressing linguistic diversity in mathematics education, divided into three main focus areas. At the core is the overarching theme, from which three essential elements branch out: Designing Linguistically Responsive Mathematics Instruction, Teacher Preparation and Professional Development, and Assessment and Equity Considerations. This framework emphasizes that effectively teaching in multilingual contexts requires intentional instructional design that supports all language learners, equipping teachers through targeted training and ongoing development, and ensuring that assessments are fair, inclusive, and sensitive to students' diverse linguistic backgrounds. Together, these components offer a roadmap for fostering equitable and effective mathematics education in linguistically diverse classrooms.
7 Conclusion
The relationship between linguistics and mathematics is profound, multifaceted, and increasingly critical in understanding how mathematical meaning is constructed, communicated, and internalized. This paper has demonstrated that mathematical learning is not solely a logical or numerical endeavor but a deeply linguistic one, shaped by semantic, syntactic, pragmatic, and sociocultural factors. Language plays a dual role in mathematics education: as a tool for expressing ideas and as a medium through which students interpret, negotiate, and refine those ideas. From the challenges posed by polysemous vocabulary and complex syntactic structures to the affordances of metaphor and discourse in meaning-making, it is evident that linguistic competence is essential for mathematical success.
The issue becomes more pronounced in multilingual settings, where discrepancies between home language and the language of instruction often create “linguistic dilemmas” that hinder equitable access to mathematical knowledge. Yet, as explored in global case studies, linguistic diversity can also be leveraged as a resource when pedagogical approaches are inclusive, culturally responsive, and grounded in students' linguistic realities. Cognitive linguistics, particularly metaphor theory, further underscores that abstract mathematical concepts are often learned through embodied, metaphor-based reasoning, reaffirming that mathematical thought is anchored in both language and experience. Moreover, the effectiveness of mathematics instruction and assessment hinges on teachers' linguistic awareness and their ability to scaffold student understanding through purposeful discourse and multimodal representations.
Finally, the evidence from 2017 to 2025 strongly supports the view that language is not peripheral but central to mathematics education. Educators, curriculum developers, and policymakers must embrace a linguistically informed perspective that recognizes the unique challenges and possibilities that language brings to the mathematics classroom. Doing so is not only a pedagogical necessity but also an ethical imperative, especially in diverse and multilingual societies striving for inclusive and equitable education.
8 Recommendation
Firstly, integrate linguistic awareness into teacher training; that is, pre-service and in-service teacher education programs should include dedicated modules on the role of language in mathematics education. Teachers must be trained to identify linguistic obstacles to comprehension, use precise academic language, and implement strategies such as scaffolding, code-switching, and semantic mapping to support student understanding.
Secondly, promote multilingual pedagogies, that is, schools and educational systems should embrace translanguaging and code-switching as legitimate instructional strategies in mathematics classrooms. Bilingual or multilingual resources, including textbooks and visual aids in students' home languages, should be developed and incorporated to reinforce conceptual understanding and support linguistic inclusivity.
Thirdly, design linguistically accessible curriculum and materials; that is, curriculum designers should pay close attention to the linguistic complexity of mathematical content. Instructional materials must balance formal mathematical language with accessible explanations and provide visual and contextual supports to bridge semantic gaps, particularly for emergent bilinguals and English Language Learners.
Fourthly, develop equitable assessment practices; that is, mathematics assessments must be reviewed for linguistic bias and redesigned to distinguish between language proficiency and mathematical knowledge. This includes simplifying language in word problems, offering alternative formats (e.g., visuals, oral presentations), and allowing students to demonstrate understanding in their strongest language when appropriate.
Finally, support research and policy on language in mathematics education, that is, governments, educational bodies, and research institutions should invest in further studies that explore the interplay between language and mathematics, especially in under-researched multilingual contexts. Educational policy must reflect a commitment to linguistically responsive pedagogy by funding teacher training, resource development, and inclusive curricular reforms.
9 Limitations and suggestions for further studies
While this study provides valuable insights into the intersection of linguistics and mathematics education, it is limited by its reliance on secondary sources and theoretical perspectives rather than empirical classroom-based data. The diversity of multilingual contexts may also lead to varying interpretations of linguistic influence that were not fully explored. Additionally, the study focuses primarily on metaphor and discourse without deeply examining other linguistic features like pragmatics or code-switching. Future research should include in-depth classroom observations and interviews to capture how language use directly affects mathematical reasoning in real-time. Longitudinal studies across diverse linguistic and cultural settings would further enrich our understanding, especially by evaluating the impact of linguistically responsive pedagogies on students' mathematical performance over time.
Author contributions
VM: Writing – review & editing, Writing – original draft, Supervision. BA: Investigation, Resources, Writing – review & editing, Writing – original draft, Visualization.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alam, A., and Mohanty, A. (2023). Cultural beliefs and equity in educational institutions: exploring the social and philosophical notions of ability groupings in teaching and learning of mathematics. Int. J. Adolesc. Youth 28:2270662. doi: 10.1080/02673843.2023.2270662
Ann, S., and Mellony, R. (2018). Using a transdisciplinary framework to examine mathematics classroom talk taking place in and through a second language. ZDM Math. Educ. 50, 1013–1027. doi: 10.1007/s11858-018-0952-2
Buono, S., and Jang, E. E. (2021). The effect of linguistic factors on assessment of english language learners' mathematical ability: a differential item functioning analysis the effect of linguistic factors on assessment of english language learners' mathematical ability: a differential item functioning. Educ. Assess. 26, 125–144. doi: 10.1080/10627197.2020.1858783
Coultas, V., and Booth, P. (2019). Exploratory talk and task-based learning: a case study of a student's learning journey on an MA (education) English language teaching course. Changing English 26, 30–47. doi: 10.1080/1358684X.2018.1545109
Daane, A. R., Close, H. G., Haglund, J., Scherr, R. E., and Robertson, A. D. (2018). The pedagogical value of conceptual metaphor for secondary science teachers. Sci. Teach. Educ. 102, 1051–1076. doi: 10.1002/sce.21451
Edelen, D., Bush, S. B., Karp, K. S., Skukauskaite, A., Sherron, K., Safi, F., et al. (2025). Making visible epistemic authority: a microethnographic examination of children's authority relationships in early elementary mathematics Making visible epistemic authority: a microethnographic examination of children's authority relationships in ea. Res. Math. Educ. 4802, 1–20. doi: 10.1080/14794802.2025.2509025
Edmonds-wathen, C., and Edmonds-wathen, C. (2019). Linguistic methodologies for investigating and representing multiple languages in mathematics education research multiple languages in mathematics education research. Res. Math. Educ. 21, 119–134. doi: 10.1080/14794802.2019.1615981
Edward, M., and Masilo, F. (2023). First year university students use of words, symbols and images to convey mathematical ideas: a case of definitions. Res. Soc. Sci. Technol. 8, 92–105. doi: 10.46303/ressat.2023.16
Erath, K., Ingram, J., Moschkovich, J., and Prediger, S. (2021). Designing and enacting instruction that enhances language for mathematics learning: a review of the state of development and research. ZDM Math. Educ. 53, 245–262. doi: 10.1007/s11858-020-01213-2
Francis, K. (2018). Coding robots as a source of instantiations for arithmetic. Digit. Exp. Math. Educ. 4, 71–86. doi: 10.1007/s40751-018-0042-7
Giberti, C. (2023). The role of metaphors in interpreting students' difficulties in operating with percentages: a mixed method study based on large scale assessment. Eur. J. Sci. Math. Educ. 11, 297–321. doi: 10.30935/scimath/12642
Hickendorff, M. (2021). The demands of simple and complex arithmetic word problems on language and cognitive resources. Front. Psychol. 12:727761. doi: 10.3389/fpsyg.2021.727761
Kamali, J., and Javahery, P. (2025). International and Multidisciplinary Perspectives Collaborative reflection as a means to improve teachers' reflective skills: a community of practice perspective. Reflect. Pract. 26, 246–261. doi: 10.1080/14623943.2024.2426279
Kontorovich, I. (2018). Why Johnny struggles when familiar concepts are taken to a new mathematical domain: towards a polysemous approach. Educ. Studi. Math. 97, 5–20. doi: 10.1007/s10649-017-9778-z
Li, Y., Lin, X., and Cheng, G. (2025). Investigating mathematics writing performance of Chinese middle middle school students. Read. Writ. doi: 10.1007/s11145-025-10649-5
Luzano, J. F. P. (2025). Redefining quality learning practices in mathematics education?: a scoping review of contemporary trends and educational innovations. Int. J. Edu. Mat. Sci. Tech. 13, 744–760. doi: 10.46328/ijemst.4863
Mclachlan, K., and Essien, A. (2021). Language and multilingualism in the teaching and learning of mathematics in South Africa: a review of literature in Pythagoras from 1994 to 2021. Pythagoras 43, 1–11. doi: 10.4102/pythagoras.v43i1.669
Morawski, M., and Georgakaki, P. (2024). Exploring student perspectives and practices with language-aware materials in geography educa- tion: an exploratory case study in a german high school classroom. Eur. J. Geogr. 15, 135–146. doi: 10.48088/ejg.m.mor.15.2.135.146
Nathan, M. J., and Walkington, C. (2017). Grounded and embodied mathematical cognition: promoting mathematical insight and proof using action and language. Nathan Walkington Cogn. Res.: Princ. 2:9. doi: 10.1186/s41235-016-0040-5
Parkhouse, H., Lu, C. Y., Massaro, V. R., Review, S., June, N., Parkhouseo, H., et al. (2019). Multicultural education professional development: a review of the literature published by: American educational research association multicultural education professional development: a review of the literature. Rev. Educ. Res. 89, 416–458. doi: 10.3102/0034654319840359
Peyer, E., Barras, M., Lüthi, G., Barras, M., and Lüthi, G. (2022). Including home languages in the classroom: a videographic study on challenges and possibilities of multilingual pedagogy pedagogy. Int. J. Multiling. 19, 162–177. doi: 10.1080/14790718.2020.1736080
Povoroznyuk, R. (2024). Neuropedagogical guidelines for translation studies: perceiving the markers of the other (foreign) in translation. Rev. Romaneasca Pentru Educ. Multidimens. 16, 185–209. doi: 10.18662/rrem/16.4/912
Ramulumo, M. (2023). Journal of innovative science education science students' attitudes towards the use of indigenous language in understanding visual representations. J. Innova. Sci. Educ. 12, 125–140. doi: 10.15294/jise.v12i2.72094
Robertson, S. (2020). Language as an including or excluding factor in mathematics teaching and learning. Math. Educ. Res. J. 77–101. doi: 10.1007/s13394-019-00302-0
Sharma, S., and Sharma, S. (2023). Successful teaching practices for english language learners in multilingual mathematics classrooms: a meta - analysis. Math. Educ. Res. J. 35, 821–848. doi: 10.1007/s13394-022-00414-0
Sibanda, L. (2017). Grade 4 learners' linguistic difficulties in solving mathematical assessments grade 4 learners' linguistic dif fi culties in solving mathematical assessments. Afr. J. Res. Math. Sci. Technol. Educ. 21, 86–96. doi: 10.1080/18117295.2017.1291476
Smith, M. B., Early, M., Kendrick, M., Bernice, M., Early, M., Kendrick, M., et al. (2024). Teachers' ideological dilemmas: lessons learned from a Language Introduction Program in Sweden Introduction Program in Sweden. J. Multiling. Multicult. Dev. 45, 647–662. doi: 10.1080/01434632.2022.2126485
Song, Y., Xing, W., Li, C., and Tian, X. (2024). Investigating the relationship between math literacy and linguistic synchrony in online mathematical discussions through large- - scale data analytics. Br. J. Educ. Technol. 55, 2226–2256. doi: 10.1111/bjet.13444
Suryadi, D. (2019). Re-interpretation of mathematical literacy based on the teacher's perspective. Int. J. Instruct. 12, 789–806. doi: 10.29333/iji.2019.12450a
Tedre, M., Toivonen, T., Kahila, J., Vartiainen, H., Valtonen, T., Jormanainen, I., et al. (2021). Teaching machine learning in K–12 classroom?: pedagogical and technological trajectories for artificial intelligence education. IEEE 9, 110558–110572. doi: 10.1109/ACCESS.2021.3097962
Tenbrink, T., Conroy Dalton, R., and Williams, A. J. (2019). “The language of architecture diagrams,” in COSIT 2019: 14th Conference on Spatial Information Theory (Wadern: Dagstuhl Publishing), 17:1–17:14.
Tran, C., Smith, B., and Buschkuehl, M. (2017). Support of mathematical thinking through embodied cognition: nondigital and digital approaches. Cogn. Res.: Princ. Implic. 2:16. doi: 10.1186/s41235-017-0053-8
Vallverdu, J. (2025). Disembodied meaning? Generative AI and understanding. Forum Ling. Stud. 7:8060. doi: 10.30564/fls.v7i3.8060
Wang, T., and Lin, F. (2024). Exploring the feasibility of co-construction among mathematics teachers and teacher educators: analysis of discourse in a product-based teacher professional development program. Math. Teach. Educ. Dev. 26, 1–19.
Wu, B., Hu, Y., and Wang, M. (2019). Scaffolding design thinking in online STEM preservice teacher training. Br. J. Educ. Technol. 50, 2271–2287. doi: 10.1111/bjet.12873
Wulff, P. (2024). Physics language and language use in physics — what do we know and how AI might enhance language-related research and Physics language and language use in physics — what do we know and how AI might enhance language-related research and instruction. Eur. J. Phys. 45:023001. doi: 10.1088/1361-6404/ad0f9c
Keywords: linguistics, mathematics, syntactic structure, semantic structures, multilingualism
Citation: Maanu V and Asare B (2025) Linguistics and mathematics meaning. Front. Educ. 10:1657529. doi: 10.3389/feduc.2025.1657529
Received: 10 July 2025; Accepted: 29 August 2025;
Published: 22 September 2025.
Edited by:
Ingrid Gogolin, University of Hamburg, GermanyReviewed by:
Quin Awuor, United State International University, KenyaCopyright © 2025 Maanu and Asare. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bright Asare, YXNhcmVicmlnaHQ2NTkyQGdtYWlsLmNvbQ==
 Vivian Maanu
Vivian Maanu Bright Asare
Bright Asare