Chiller Fault Diagnosis Based on Automatic Machine Learning

Intelligent diagnosis is an important means of ensuring the safe and stable operation of chillers driven by big data. To address the problems of input feature redundancy in intelligent diagnosis and reliance on human intervention in the selection of model parameters, a chiller fault diagnosis method was developed in this study based on automatic machine learning. Firstly, the improved max-relevance and min-redundancy algorithm was used to extract important feature information effectively and automatically from the training data. Then, the long short-term memory (LSTM) model was used to mine the temporal correlation between data, and the genetic algorithm was employed to train and optimize the model to obtain the optimal neural network architecture and hyperparameter configuration. Finally, a transient co-simulation platform for building chillers based on MATLAB as well as the Engineering Equation Solver was built, and the effectiveness of the proposed method was verified using a dynamic simulation dataset. The experimental results showed that, compared with traditional machine learning methods such as the recurrent neural network, back propagation neural network, and support vector machine methods, the proposed automatic machine learning algorithm based on LSTM provides significant performance improvement in cases of low fault severity and complex faults, verifying the effectiveness and superiority of this method.

Introduction

As an industry with high energy consumption, the construction industry has become a key area for energy conservation and emission reduction (Li et al., 2019a; Daneshvar et al., 2020). In particular, the energy waste caused by the aging of heating, ventilation, and air conditioning (HVAC) systems as well as equipment failure accounts for 15–30% of the total energy consumption of buildings (Zhou et al., 2020) and has become a “severe disaster area” in terms of building energy efficiency.

Chiller is the equipment with the largest energy consumption in HVAC system. Relevant research shows that timely troubleshooting of chiller can effectively reduce energy consumption by 20–50% (Zhou et al., 2020). Therefore, rapid and accurate judgment of chiller operation state is an important basis for ensuring safe and stable operation of chiller and saving energy.

In recent years, machine learning methods, as the core of artificial intelligence, have become a research hotspot and have been successfully applied to building energy consumption prediction, system modeling, and industrial process monitoring. In heating, ventilation, and air conditioning system analysis, remarkable progress has also been made in machine learning chiller fault detection and diagnosis (FDD) strategies. Machine learning methods can be divided into two main categories: traditional machine learning methods and deep learning methods.

In traditional machine learning, support vector machines (SVMs) have been widely used in chiller FDD. Liang and Du developed a multi-layer classifier based on an SVM (Zhao et al., 2019a), which could effectively detect chiller faults via residual analysis with high classification accuracy. To improve chiller FDD performance further, Sun et al. (Sun et al., 2016a) utilized signal processing to remove the noise information contained in the original chiller measurements. They proposed a hybrid refrigerant charge adjustment fault diagnosis model based on an SVM and wavelet denoising for the fault of improper refrigerant charge adjustment in chillers. In addition, Han et al. (Han et al., 2011) combined an SVM with other methods to improve the performance and reliability of chiller FDD. They proposed a hybrid SVM model combining an SVM and a genetic algorithm (GA) for chiller FDD. This model performs diagnosis efficiently, but it is not suitable for refrigerant leakage (RL) or refrigerant overcharging failures. To overcome the limitations of this model, Han et al. proposed a least-squares SVM model (Han et al., 2019) and realized the FDD of a centrifugal chiller through cross-validation optimization. Compared with product-based neural networks and SVMs, the proposed method exhibited better FDD performance. In addition, with the improvements in processing unit computing ability and the evolution of machine learning methods, deep learning (LeCun et al., 2015) has attracted extensive research interest. Notably, deep learning has been proven to perform better than traditional machine learning methods and has been widely used in network security (Chen et al., 2020; Dixit and Silakari, 2021), medical image analysis (Grohl et al., 2021; Li et al., 2021; Xie et al., 2021), and computer vision (Hu, 2020; Zhang et al., 2020).

Deep learning architectures are also widely utilized in FDD in industry (Zhao et al., 2019b). For instance, Guo et al. (Yabin et al., 2018) proposed a fault diagnosis method for a variable refrigerant flow system based on a deep belief network. Azamfar et al. (Azamfar et al., 2020) proposed a gearbox fault diagnosis method based on the analysis of motor current characteristics. This method fuses the data collected by multiple current sensors through a novel two-dimensional convolutional neural network architecture and is directly used for classification without manual feature extraction. Further, Liu et al. (Liu et al., 2018) proposed a rotating machinery fault-type recognition method utilizing a recurrent neural network (RNN) based on the ability of an RNN to capture the time correlation of time series data, which showed good robustness and high classification accuracy. Long short-term memory (LSTM) (Shi et al., 2021) is a special type of RNN, which compensates for the shortcomings of RNNs in dealing with nonlinear time problems (Ma et al., 2015). Moreover, owing to the characteristics of the network structure, it is widely used to deal with and predict highly time-related and strongly coupled events. Yuan et al. (Yuan et al., 2016) studied the problem of utilizing standard LSTM to estimate the residual service life of an aeroengine. Similarly, Shahid et al. (Farah et al., 2020) employed LSTM and Gauss, Morelet, Ricker, and Shannon activation kernels to predict the power of various wind farms and compared the results with those of existing mature technologies. An improvement of up to 30% was observed in the mean absolute error, which verified the effectiveness and robustness of the model. LSTM is not only widely used in time series prediction, but also has proven to be effective in various fault diagnosis problems involving time series data. For example, Yin et al. (Yin et al., 2020) proposed a method based on a cosine loss function to optimize an LSTM neural network for fault diagnosis of a wind turbine gearbox. Yang et al. (Yang et al., 2018) used LSTM spatial and temporal correlations to detect faults and to classify the corresponding fault types considering the complexity and uncertainty of rotating machinery. Further, Lei et al. (Lei et al., 2019) employed LSTM for wind turbine fault diagnosis, effectively classifying the original time-series signals collected by a single sensor or multiple sensors. Therefore, the LSTM algorithm can also be applied to the fault diagnosis of chillers in heating, ventilation, and air conditioning systems to solve the problems of complex faults and strong time coupling.

However, when building a chiller fault diagnosis model, the fault feature redundancy cannot always reveal the most important information. With more manual intervention, the LSTM model can easily enter local minima during parameter optimization rather than achieving global optimization. To solve the above problems, we adopted a method based on automatic machine learning (AutoML) for determining the optimal solution of the model automatically. AutoML mainly includes data preparation, feature engineering, model generation, and model evaluation [i.e., neural architecture searching (NAS)] (Yao et al., 2018). Model generation involves model selection and hyperparameter optimization (HPO) (Kanter and Veeramachaneni, 2015; He et al., 2021). With the development of machine learning, increasingly complex network models have been constructed. The popularization of AutoML methods is particularly important (García-Domínguez et al., 2021). Compared with traditional machine learning methods, AutoML simplifies the model generation process by automating some general steps (such as data preprocessing, hyperparameter adjustment, and NAS). As it does not involve manual intervention, AutoML can achieve more effective application of machine learning models. Moreover, AutoML has been widely applied in various fields such as medical science (Tan et al., 2020; Waring et al., 2020), power prediction (Zhao et al., 2021), and signal recognition (Li, 2020). Therefore, AutoML can also be utilized in chiller fault diagnosis to improve the efficiency and level of fault diagnosis and promote the practical application of diagnostic algorithms.

In summary, AutoML has become a research hotspot in artificial intelligence and can automate the entire machine learning process, from construction to application. LSTM networks can be used to mine the time correlations of time series data and map the input to the output to obtain the correct classification results. Based on these advantages, this paper proposes a chiller fault diagnosis method based on AutoML. The main contributions of this report are as follows.

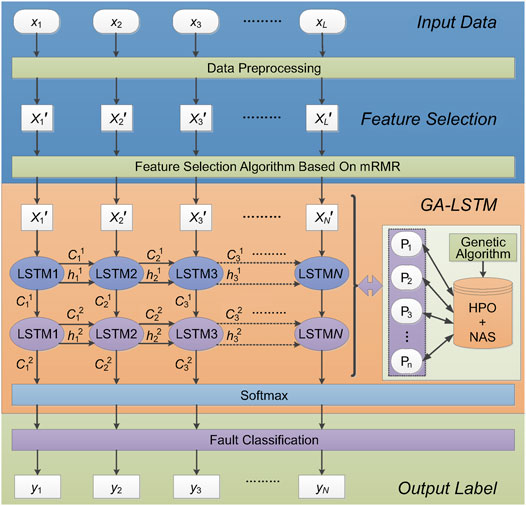
1) A fault diagnosis model utilizing an LSTM network optimized using a GA is proposed. The GA is employed for hyperparameter optimization and the NAS of the LSTM. The advantages of the LSTM mining time correlation and GA spatial search ability are used to achieve efficient and stable chiller fault diagnosis.

2) Based on the GA-optimized LSTM model, a chiller fault diagnosis method based on AutoML is proposed. Unlike the traditional FDD method for chillers, this method has an end-to-end network structure and can directly identify specific fault types in a time series. Firstly, taking the fault data as the input time series, the most important fault feature information is obtained using the improved max-relevance and min-redundancy (mRMR) algorithm, and the fault data label is marked. Then, the GA-optimized LSTM model is constructed, and the diagnosis model training is accelerated based on graphics processing unit parallel technology to construct the optimal fault diagnosis model. Finally, the fault data are sent into the model, and the softmax function outputs the fault label to diagnose the fault of a specific chiller.

3) A transient co-simulation platform for a water chiller based on the engineering equation solver (EES) and MATLAB, thermodynamic model of the unit, and dynamic dataset simulation performed to obtain the required data for the experiment are presented.

4) Detailed experiments considering different degrees and types of faults are presented. An evaluation of the proposed fault diagnosis strategy is provided in terms of both training performance and fault diagnosis performance. To verify the effectiveness and superiority of the proposed method, comparisons with other FDD methods such as RNNs, back-propagation neural networks (BPNNs), and SVMs are presented. The comparison results demonstrate that the performance improvement of the proposed method is significantly greater for low severity faults than for high severity faults. The diagnostic accuracy of this method is much higher than those of the other considered methods in cases of complex fault types and chaotic severity. Therefore, the proposed AutoML method effectively improves the diagnostic level in chiller fault diagnosis and its superiority was verified.

The remainder of this paper is structured as follows. Research Basis introduces the basic theory underlying the methods used in this study. Chiller Fault Diagnosis Strategy Based on Automatic Machine Learning elaborates on the fault diagnosis strategy based on AutoML. Transient Co-Simulation Platform of Water Chiller Based on MATLAB + Engineering Equation Solver describes the joint simulation platform constructed and discusses the specific situation of the simulation dataset, and Experimental Results and Comparison presents the experimental results and compares the proposed method with the existing models. Finally, Conclusion summarizes the findings and provides recommendations for further research.

Research Basis

Long Short-Term Memory

The long short-term memory (LSTM) network was first proposed in (Hochreiter and Schmidhuber, 1997) and is an improved algorithm for RNNs, which compensates for the shortcomings of RNNs in dealing with nonlinear time problems (Ma et al., 2015). The LSTM model can process large-scale parameters and provides the versatility of using nonlinear activation functions in each layer. It can capture nonlinear trends in data and save long-term information (Shi et al., 2021). The LSTM structure is advantageous in that it contains three types of doors: input, forgetting, and output doors, as shown in Figure 1.

FIGURE 1

FIGURE 1. Cell unit diagram of LSTM hidden layer.

Mathematical methods can describe the main information flow of the LSTM hidden layer cell unit (Figure 1) (Barthwal et al., 2020). In Figure 1, x_t, c_t, and h_t are the input unit, cell state, and output unit at time t, respectively; c_t–1 and h_t–1 are the cell state and output unit at time t–1, respectively; σ is the softmax function; $\otimes$ represents multiplication in the model; and the arrow represents the direction of information flow. A tanh-shaped network layer creates a new candidate value vector, c¹_t, which can be added to the cell state. The forgetting gate determines how much of c_t–1 is retained in c_t, which means that one can decide which necessary information to save to the cell state using

$f_t=\sigma \left(W_f\times \left[h_{t-1},x_t\right]+b_f\right),(1)$

where f_t is the forgetting threshold at time t, W_t is the weight, and b_f is the bias.

The input gate determines how much of x_t of the current network is saved to c_t. The specific expressions are as follows:

$i_t=\sigma \left(W_i\times \left[h_{t-1},x_t\right]+b_i\right)(2)$

$c_t^1=\tanh \left(W_c\times \left[h_{t-1},x_t\right]+b_c\right),(3)$

where i_t is the input threshold at time t; W_i, U_i, W_c, and U_c are weights; and b_c is the bias.

The following expression is used to update the cell states at time t:

$c_t=f_t\times c_{t-1}+i_t\times c_t^1.(4)$

As the output information generation unit in the current time step, the output gate controls how much c_t outputs to h_t of the LSTM. The specific expression is as follows:

$o_t=\sigma \left(W_o\times \left[h_{t-1},x_t\right]+b_o\right).(5)$

In this equation, o_t represents the output threshold of time t, W_o and U_o are weights, and b_o is a bias. Then, the cell output can be described as

$h_t=o_t\times tanh\left(c_t\right),(6)$

where tanh represents the activation function. After the data pass through three doors, the effective information is output, and invalid information is forgotten.

Genetic Algorithm

A Genetic Algorithm (GA) (Denkena et al., 2021) is a heuristic random search method that was developed from natural evolution law, which is used to find the near-optimal solutions of optimization problems with large search spaces. This algorithm is easy to parallelize and is not blindly exhausted, but rather is a heuristic search. Simultaneously, this algorithm has an excellent global search ability and superior scalability, utilizing past performance evaluation, and is easy to combine with other algorithms (Ng et al., 2015; Ogunjuyigbe et al., 2021).

TheGA operation principle can be divided into six stages: initialization, termination condition check, fitness calculation, selection, crossover, and mutation (Kim and Shin, 2007). In the initialization phase, a chromosome is randomly selected in the search space to be solved, and the fitness of each selected chromosome is calculated according to the predefined fitness function. In optimization methods, such as GAs, the fitness function is an indicator used to measure chromosome performance (Domingos, 2012). After calculating the fitness, chromosomes are selected, those with excellent performance are retained for the next replication process, and the genetic operators of natural genetics are utilized for combinatorial crossover and mutation to produce new chromosomes. Finally, it is determined whether the termination condition is met until the desired result is output.

Chiller Fault Diagnosis Strategy Based on Automatic Machine Learning

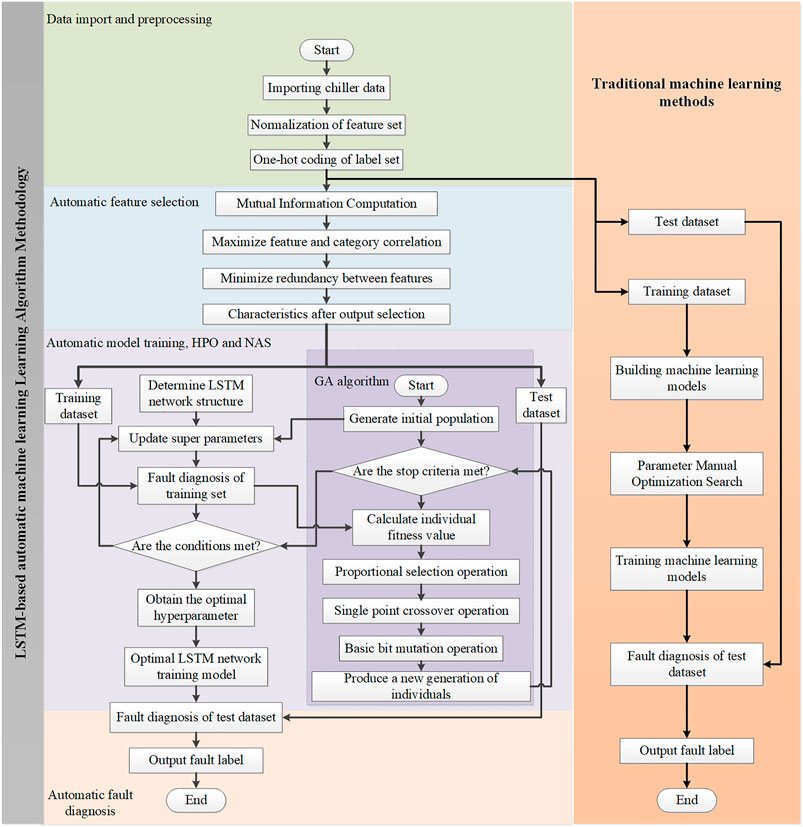
This section describes the principle of the water chiller fault identification method based on AutoML. As shown in Figure 2, this method mainly includes four stages: data preprocessing, feature selection, model training, and fault identification. The model training process involves HPO and NAS. The basic idea of this strategy is as follows. Firstly, the input training dataset for chillers is preprocessed and written into the allowed format for the model input, and the mRMR algorithm selects the key features in the fault data to reduce the model input. Then, the fault diagnosis training model based on the LSTM network is constructed, and the GA is used to optimize the model hyperparameters and neural architecture to obtain relatively optimal parameters and establish the optimal fault diagnosis model. Finally, the test dataset is sent to the best model to obtain the final classification label and complete the fault diagnosis. Data Preprocessing, Feature Selection, Hyperparameter Optimization, Neural Architecture Searching, and Model Training, and Fault Identification Analysis provide analyses of the specifics of each phase. To improve the comprehensibility of the proposed method, we further make a flowchart as shown in Figure 3.

FIGURE 2

FIGURE 2. Principle diagram of AutoML fault diagnosis strategy.

FIGURE 3

FIGURE 3. Flow chart of the proposed method compared with other methods.

Data Preprocessing

A chiller fault dataset containing L features is utilized as the original sample and labeled to form a fault label. The samples are then divided into training samples, verification samples, and test samples in a 6:2:2 ratio. The training samples are used to train the fault diagnosis model, which can be employed to fit the model. The verification samples are the sample sets left alone in the model training process, which can be used to adjust the hyperparameters of the model and evaluate its ability. The test samples are utilized to evaluate the generalization ability and accuracy of the final model. In the training samples, each feature contains M data, and the sample is described as

$x_l=\left(x_1,x_2,x_3,\dots ,x_L\right)\in R^{M\times L},(7)$

where R is the real number set.

Owing to the large differences in the orders of magnitude of the original data, larger value changes will cover smaller value changes. Therefore, it is necessary to require the input data to have similar orders of magnitude to avoid the effects of load forecasting owing to large individual input values. The specific calculation formula for data normalization is as follows:

$X_{normal}=\frac{X-X_{min}}{X_{max}-X_{min}},(8)$

where X and X_normal are the data before and after normalization, respectively, and X_max and X_min are the maximum and minimum values, respectively, among the original sample data.

After normalizing the training samples, the samples are represented as

${X^{\prime }}_{normal}=\left({X^{\prime }}_1,{X^{\prime }}_2,{X^{\prime }}_3,\dots ,{X^{\prime }}_L\right)\in R^{M\times L},(9)$

where X´_normal is the normalized sample data, M is the training sample data quantity, and L is the characteristic quantity.

When using machine learning to solve classification problems, labels as well as discrete independent variables must be encoded. Therefore, it is necessary to expand the dimensions of the fault tags, and one-hot coding is effective for this purpose. It represents classification variables as binary vectors; for instance, the first type of fault is 1 at the corresponding position and 0 at the other positions.

Feature Selection

In supervised machine learning problems, features are explanatory variables used by data scientists to describe certain salient properties of faults, which are key to fault classification. It is worth noting that feature engineering is an important, complex, and time-consuming step in machine learning. On the one hand, the quality of the input features seriously affects the performance of machine learning algorithms. On the other hand, feature creation requires theoretical knowledge in numerous areas, and manual completion by experts is generally necessary.

To reduce the difficulty of feature engineering, the proposed method uses automatic feature engineering to select the most critical data features automatically and to construct a new feature set to improve the performance of the subsequent machine learning tools. Hence, a feature selection method for chiller fault data is utilized, namely, improved max-relevance and min-redundancy (mRMR) algorithm (Sun et al., 2016b).

Peng et al. (HanchuanPeng et al., 2005) proposed a feature selection method based on mutual information (MI) in 2005. The principle is shown in

$MI(x;y)={\displaystyle \int {\displaystyle \int p(x,y)\log \frac{p(x,y)}{p\left(x\right)p\left(y\right)}dxdy}}(10)$

In the formula, x and y are the two given variables, p(x) and p(y) are their respective probability density, and p (x, y) their joint probability.

The mRMR method is realized based on the MI method, and the correlation between features and target classes must be calculated first. Because the Max-Dependency criterion is difficult to achieve, feature selection method based on Max-Relevance criterion is chosen. A feature set S can be obtained using the MI feature selection method, which has m features and is most dependent on the target class c, named x_a. Simultaneously, the average value of all mutual information values between the individual feature x_a and target class c is calculated, as shown in

$\max D(S,c),D=\frac{1}{\left|S\right|}{\displaystyle \sum _{x_a\in S}MI(x_a;c)}(11)$

When the two features are strongly dependent on each other, removing one of them will not affect their class discrimination ability. Therefore, the Min redundancy condition can be added to select mutually exclusive features. The specific mechanism can be expressed as

$\min R\left(s\right),R=\frac{1}{{\left|S\right|}^2}{\displaystyle \sum _{x_a,x_b\in S}MI(x_a;x_b)}(12)$

After data preprocessing, feature selection is required for the sample data. Therefore, the mRMR feature selection algorithm is used to reduce the L feature quantities in the data set to N, extract important fault feature information, and reduce the cost of fault diagnosis. The sample after feature selection can be expressed as

${X^{\prime }}_n=\left({X^{\prime }}_1,{X^{\prime }}_2,{X^{\prime }}_3,\dots ,{X^{\prime }}_N\right)\in R^{M\times N},(13)$

where X´_n is the sample data after feature selection.

Hyperparameter Optimization, Neural Architecture Searching, and Model Training

The LSTM network model has two types of parameters: hyperparameters and conventional parameters. Conventional parameters can be automatically optimized through model training. Hyperparameters are the parameters that the model designer must manually set before training, and the performance of the LSTM method depends heavily on the specific hyperparameter settings. The most basic task of AutoML is to realize the optimal selection of these hyperparameters automatically to optimize the model performance. Therefore, HPO is one of the most critical steps in AutoML-based LSTM model optimization.

In addition, LSTM is a learning process that uses a neural network to solve feature expressions. It contains a neural network structure consisting of multiple hidden layers, learns the input data representation, and maps the input data to the relevant output. To improve the effectiveness of LSTM training, it is necessary to adjust the connection method and activation function of neurons to establish an excellent LSTM neural network architecture. Therefore, NAS is another research focus of AutoML, which can find the best neural network structure for the LSTM method. The efficient spatial search ability of the GA can be employed to search the hyperparameters and neural network architecture parameters, find the most effective parameter combination, and construct the optimal LSTM network model. The specific implementation process is as follows.

Firstly, the LSTM fault identification model is constructed, where the model structure is mainly composed of input, hidden, and output layers. The loss function employs the cross-entropy loss function, and the model training process is optimized utilizing the Nadam algorithm optimizer. The network model was built using the Keras framework.

The specific steps of model training are as follows.

Step 1: Import the sample data into the input layer after data preprocessing and feature selection.

Step 2: The hidden layer contains two LSTM layers. Train the LSTM layer by layer with the data transmitted by the input layer, and send the output of the neurons in the hidden layer of the LSTM network in the upper layer to the next layer for calculation.

Step 3: Send the final result of the output sequence to the softmax classifier as the output layer.

Step 4: Compare the output predicted fault label with the actual label, and continuously optimize the model through loss function calculation. Perform network training based on graphics processing unit parallel computing to realize rapid construction of the LSTM model.

Then, the GA is used for the HPO and neural network architecture search of the LSTM model, and the hyperparameters and neural network architecture parameters can be described as

$P_{s1}=\left(P_1,P_2,P_3,\dots ,P_n\right)\in R^{1\times n},(14)$

where P_s is the model parameter vector set.

In this study, chromosomes were represented by a binary array, and the fitness function of the GA was expressed as

$fitnes{s}_i=\frac{1}{2}\left[\frac{1}{p}{\displaystyle \sum _{p-1}^p\frac{y_p-{y^{\prime }}_p}{y_p}+\frac{1}{Q}{\displaystyle \sum _{q-1}^q\frac{y_q-{y^{\prime }}_q}{y_q}}}\right],(15)$

where P and Q are the numbers of training and validation samples, respectively; y_p and y´_p are the true and predicted values of the training samples, respectively; and y_q and y´_q are the true and predicted values of the validation samples, respectively.

The process of optimizing LSTM parameters by using a GA can be summarized as follows.

1) Establish the basic framework of the LSTM neural network to determine relevant parameters such as the population size and maximum genetic algebra.

2) Initialize the population and set the loss and accuracy function values to 0.

3) Code parameters such as the initial batch processing capacity, learning rate, iteration number, discard rate, and number of neurons in the hidden layer into chromosomes.

4) Randomly generate a complete LSTM neural network from the chromosomes in (Eq. 3), and perform the related model training by employing graphics processing unit parallel technology.

5) Calculate the chromosome fitness value; if it meets the optimization criterion, then enter (Eq. 7).

6) Perform chromosome selection, mutation, and crossover.

7) Check whether the new individuals meet the optimal criteria or reach the maximum evolutionary algebra if they satisfy the next requirement; otherwise return to step (5).

8) Update the LSTM neural network as a new network training model by using the optimal initial batch processing, learning rate, iteration number, discard rate, and number of hidden layer neurons obtained by the GA.

Fault Identification Analysis

Before chiller fault diagnosis, new test samples are input into the trained AutoML model. In the fault diagnosis process, the AutoML model is used to identify the specific fault types in each test time series. In chillers, different types of faults have corresponding fault feature information. Further, in the model training, it is necessary to ensure that the model learns the fault labels corresponding to the fault types as much as possible. The AutoML model outputs fault labels through the softmax function, thus identifying the fault type. The softmax function can be expressed as

$softmax\left(x_i\right)=\frac{\exp \left(x_i\right)}{{\displaystyle {\sum }_{xk}\exp \left(x_k\right)}},(16)$

where x_i is the output value of node i, and k is the number of output nodes, that is, the number of categories classified. Using the softmax function, the output value of multi-classification can be converted into a probability distribution with a range of (0, 1) and a sum of 1.

Transient Co-Simulation Platform of Water Chiller Based on MATLAB + Engineering Equation Solver

Introduction of Joint Simulation Platform

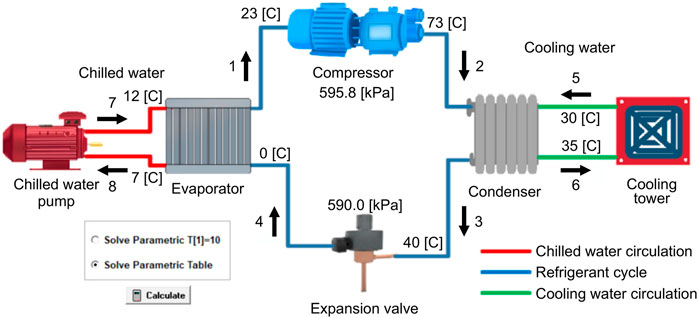
Figure 4 depicts the transient co-simulation platform of the water chiller based on MATLAB + EES. The water chiller system mainly includes four components: the compressor, condenser, expansion valve, and evaporator (Hua, 2012). These four components are interrelated and form three parts: the freezing water, cooling water, and refrigerant circuits. The failure of any component affects the thermodynamic states of the other components.

FIGURE 4

FIGURE 4. Co-simulation platform-thermodynamic model of chiller.

The thermodynamic model of the water chiller was built utilizing the EES, which provides many built-in mathematical and thermophysical functions very useful for engineering calculations. According to any two physical parameters, other physical parameters can be obtained by calling a built-in function. The model can simulate chiller operation in normal mode and various fault modes, and the changes of the physical parameters are used to characterize each fault and the fault severity. Under the premise of setting the fixed parameters of the components, we simulated different fault modes by changing the corresponding physical parameters. To address the problem that the algorithm model cannot be trained in the absence of real data, we established a transient co-fault simulation platform for chillers. First, the steady-state thermodynamic model of the chiller unit is constructed on EES software, and MATLAB is connected with EES through an interface; then, MATLAB is used to control the input parameters to drive the chiller unit model and obtain simulation data from EES for algorithm training and testing; finally, interactive joint simulation and fault diagnosis are realized in the control system software environment. Among them, the interface is the channel for the two software to establish the connection, which is the key to realize the joint simulation and can be realized by programming. The experimental process is an off-line process. Drawing on the idea of segmented linearization, we discretize the dynamic fault process of the chiller plant into multiple steady-state processes according to the customized step length, and use the output of the previous steady-state process as the input of the next steady-state process to simulate the dynamic fault data by simulating the steady-state process. At the same time, the consistent step length of the two software is a key part to ensure the success of the platform co-simulation, which is very important for the accuracy of the simulation data.

Thermodynamic Analysis of Chiller System

The flow path of the refrigerant in the chiller was the same as that in most steam compression equipment. The most important aspect of the chiller simulation model in Figure 4 is the thermodynamic process of the refrigerant cycle. As shown in the figure, the thermodynamic reverse cycle is mainly divided into four processes. Firstly, the low-temperature and low-pressure refrigerant vapor (state point 1) is compressed in the compressor and converted into high-temperature and high-pressure vapor (state point 2). Secondly, the steam enters the condenser and releases heat to the cooling water to become a high-temperature and high-pressure liquid (state point 3). Thirdly, the refrigerant liquid passes through the expansion valve, reducing the pressure and temperature, and becomes a low-temperature and low-pressure vapor-liquid mixture (state point 4). Finally, the refrigerant enters the evaporator, absorbs the heat of the chilled water, becomes low-temperature and low-pressure vapor (state point 1), and is sucked into the compressor to repeat the cycle. During the refrigerant compression process in actual chiller system operation, there is friction between the gas and the cylinder wall, and there is heat exchange between the gas and the outside. Hence, the compression process not isentropic. The refrigerant also experiences pressure loss in the condenser and evaporator, and there is heat exchange with the outside, so condensation heat release and evaporation heat absorption are not equal-pressure processes (Howard and James, 2016). The pressure data in the graph represent the pressure difference between the two sides of the compressor and the pressure difference between the two sides of the expansion valve, respectively.

Dynamic Fault Data Simulation

Firstly, this subsection introduces the types of faults studied and their implementations in the simulation model. In the simulation, the refrigerant was set as R134a, the parameter of the centrifugal chiller was set as 90 tons (316 kW), and the condenser and evaporator were both shell and tube equipment. Considering factors such as fault frequency, severity, and maintenance cost, the platform simulated five faults with four severity levels (SLs), as shown in Table 1. Comstock and Braun (Comstock and Braun, 1999) proved these failures to be the most likely and costly failures associated with centrifugal chillers.

TABLE 1

TABLE 1. Fault types and SLs.

In the centrifugal chiller fault simulation experiment, 13 parameters were selected as the characteristic parameters of the FDD (Table 2). The dynamic fault data simulated by the platform were divided into six datasets according to the fault type, and each dataset was divided into four small datasets according to the SL. Each small dataset consisted of 13 characteristic parameters and had 2000 sampling points.

TABLE 2

TABLE 2. Characteristic parameters.

The following description provides the details of different fault modes considered by the simulation platform and the symbols used to represent these faults.

1) Reduced condenser water flow (FWC)

In an actual unit, the water flow in the condenser can be adjusted by changing the head pressure of the pump through the electronic valve. Corresponding to the simulation model, the FWC fault can be simulated by changing the condenser water flow parameters. The basic water flow was 49.96 m³/h, and each fault level reduced the water flow by 10%. Different severities of FWC faults were considered, as shown in Table 1.

2) Reduced evaporator water flow

Similar to the FWC fault principle, the parameter values can be changed to adjust the water flow in the evaporator. The basic water flow level was 49.05 m³/h, and each fault level reduced the water flow by approximately 10%. Different severities of evaporator water flow faults were considered, as shown in Table 1.

3) Refrigerant leak

The refrigerant flow from the system was reduced to simulate the RL fault. The basic refrigerant weight in the system was 300 pounds (136 kg). Each fault level reduced the refrigerant charge by 10%, and each continuous test reduced the refrigerant mass by 13.6 kg. Four fault SLs were simulated. Different severities of RL faults were considered, as shown in Table 1.

4) Refrigerant overcharging

Similar to the RL fault simulation principle, we simulated refrigerant overcharging by continuously increasing the refrigerant flow in the model system. The basic refrigerant mass in the model was 136 kg. Each failure level increased the refrigerant charge by 10%, and various degrees of failure were considered, as shown in Table 1.

5) Condenser fouling

In the condenser, the fouling layer on the heat transfer surface was uneven and changed with the running time. The thermal resistance of the fouling layer is mainly related to the thickness and composition of the fouling layer, according to the following relationship:

$r=\delta /\lambda ,(17)$

where r is the thermal resistance of the fouling layer in m² h °C/J; $\delta$ is the thickness of the fouling layer in m; and λ is the thermal conductivity of the fouling layer in J/m h∙°C.

The most common finned tube condenser is used in the joint simulation platform:

$K=\frac{1}{K_0+B\left(r-r_0\right)},(18)$

where K is the total heat transfer coefficient of the finned condenser; B is the fouling resistance amplification factor, which is a constant related to the structure of the heat transfer unit; and K₀ is the value of the fouling thermal resistance r₀ corresponding to a certain water quality condition.

In summary, condenser fouling significantly affects the heat transfer coefficient of the condenser. Fouling faults with different severities were simulated by changing the total heat transfer coefficient. Different severities of condenser fouling failures were considered, as listed in Table 1.

Experimental Results and Comparison

Comparison Methods

To verify the superiority of the proposed LSTM-based AutoML model further, it was compared with RNNs, BPNNs, and SVMs, which have been widely studied and applied in fault diagnosis.

Recurrent Neural Network

The RNN method (Liu et al., 2018) considers the correlation between samples and is reflected by the neural network architecture. Its essence is that there is a feedback or feed-forward connection within the unit layer. This structure can effectively retain the information in the data transmission process, that is, the hidden layer node of the RNN retains its state, memory, and other information. Therefore, the RNN can retain the sequence context information in the fault diagnosis process and has good dynamic characteristics and fault diagnosis levels. The forward propagation model of the RNN is

$\begin{array}{l}\{\begin{array}{l}{z}_h^l={\displaystyle \sum _{i=1}^I{w}_{il}{x}_i^t}+{\displaystyle \sum _{l^{\ast }}^L{w}_{l^{\ast }l}{a}_{l^{\ast }}^{t-1}}\\ a_l^t=f_l\left(z_l^t\right)\\ y_k^t={\displaystyle \sum _{l=1}^L{w}_{lk}{a}_h^t}\end{array}i=1,\mathrm{...},I;l=1,\mathrm{...},L;k=1,\mathrm{...},K\\ \end{array}.(19)$

In this formula, x^t_i and a^t−1_l* are the i neurons in the input layer and l neurons in the hidden layer at time t, respectively; z^l_h is the value of the l neurons in the hidden layer before the activation function acts at time t; y^t_k is the k neurons of the output layer at time t; w_ih is the weight between the input and hidden layers; w_l*l is the weight of the hidden and hidden layers; w_lk is the weight of the hidden and output layers; and f_l (▪) is a nonlinear activation function.

Back-Propagation Neural Networks

BPNNs (Li et al., 2019b) are widely used neural network algorithms, especially for fault diagnosis. The entire structure of a BPNN is divided into three layers: input, hidden, and output layers, from top to bottom. This three-layer structure is closely linked and can guarantee the processing ability of BPNN information. The general working principle of this method is as follows.

The input layer sends the external information to the hidden layer through each neuron, and the hidden layer subsequently processes and converts the received information and acts on the next neuron to generate the output signal. When there is an error between the response and the expected value, it is distributed to each unit layer by layer for reverse propagation. Continuous learning and correction of the network is performed until the error of the output layer of the entire network is lower than the previously established value or the set number of iterations is reached.

Support Vector Machines

The SVM approach (Zhao et al., 2019a) is among the most influential fault diagnosis methods. The core idea is to maximize the distance between samples by constructing a mapping Ψ: R→H to obtain a classification hyperplane. Suppose that the sample set is

$G={\left\{\left(c_i,d_i\right)\right\}}_{i=1}^g,i=1,\cdot \cdot \cdot ,g.(20)$

Then, c_i is the input vector, namely, the fault pole data; d_i ∈ {1, –1} is the category label, and g is the number of samples. The necessary and sufficient conditions for the dual quadratic optimization are satisfied through the following transformation:

$\begin{array}{l}\min M\left(\beta \right)=\frac{1}{2}{\displaystyle \sum _{i,j=1}^p{\beta }_i{\beta }_j{d}_i{d}_{j}K(c_i,d_j)-{\displaystyle \sum _{i=1}^p{\beta }_i}}\\ s,t{\displaystyle \sum _i^n{\beta }_i{d}_i=0,i,\cdot \cdot \cdot ,p}\\ 0\le {\beta }_i\le Ci=1,\cdot \cdot \cdot ,p\end{array}(21)$

$h\left(x\right)=\mathrm{sgn}(b+{\displaystyle {\sum }_{i,j=1}^p{\beta }_i{y}_{i}K(c_i,d_i)})(22)$

$K(c_i,d_i)=\varphi \left(c_i\right)\varphi \left(d_i\right),(23)$

where β_i is the introduced Lagrange multiplier, C is the penalty factor in the radial basis function, Eq. 22 is the decision function, and Eq. 23 is the kernel function. Then, the decision function is solved, and finally, the linear separability of the sample is achieved through the nonlinear transformation Φ(•) in the kernel function.

Experimental Configurations

1) Data preprocessing

According to the fault severity, five fault data points and one normal data point in the dynamic fault data of the joint simulation platform were selected for establishing five data sets including SL1, SL2, SL3, SL4 and MSL (Mixed Severity), and each data set was composed of 6,000 groups of data. Faults are represented in the form of 0–5 tags, as shown in Table 3 after one hot coding.

2) Feature selection

TABLE 3

TABLE 3. Fault types and one-hot coding.

As listed in Table 2, the fault dataset included 13 characteristic parameters, which were reduced to six by the mRMR algorithm. These six were the most representative and correlated characteristic quantities in the fault data, which are CP, TCO, TEI, TCI, TEA and Evap Tons.

3) Hyperparameters and neural network architecture

Like other neural network models, LSTM networks have many hyperparameters that must be modified by researchers and neural network structures that need to be searched. However, the time required and computational constraints make it impossible to sweep a parameter space and find the optimal parameter set. Therefore, we used a GA to optimize these model parameters. In this study, nine parameters requiring optimization were finally identified, as shown in Table 4, which respectively present the specific content of the parameters and the optimization search results.

4) Comparison model configuration

TABLE 4

TABLE 4. Hyperparameter optimization results and Neural network search results.

All models in this study were implemented on the configuration of NVIDIA GeForce MX150 using the Keras architecture of the Python platform. Table 5 lists the setting details of the compared fault diagnosis methods, which are the best parameters chosen during the experiment.

TABLE 5

TABLE 5. Method implementation details.

Evaluation Indices

1) Training performance indices

We used the cross-entropy loss function to evaluate the model training performance of the proposed method. The specific principles of this evaluation method can be expressed as follows.

For two probability distributions p and q of the sample set, let p be a real distribution and q be a fitting distribution. The expected encoding length required to identify a sample, i.e., the information entropy, is measured according to p:

$H\left(p\right)=-{\displaystyle \sum _{i=1}^{c}p\left(x_i\right)\log \left(p\left(x_i\right)\right)}.(24)$

If q is used to represent the expected encoding length based on p, that is, the cross-entropy, then

$H\left(p,q\right)=-{\displaystyle \sum _{i=1}^{c}p\left(x_i\right)\log \left(q\left(x_i\right)\right)}.(25)$

The KL divergence, also called the relative entropy, can be used to measure the difference between p and q:

$D\left(p\parallel q\right)=H(p,q)-H\left(p\right)={\displaystyle \sum _{i=1}^{c}p\left(x_i\right)\log \left[\frac{p\left(x_i\right)}{q\left(x_i\right)}\right]}.(26)$

The objective of the classification problem in machine learning is to narrow the gap between the model prediction and label, and the label set remains unchanged, so it is only necessary to pay attention to the cross-entropy in the optimization process. In the multi-classification task in this study, the cross-entropy loss function used to describe the training performance of the fault classification model was calculated as

$Loss=-{\displaystyle \sum _{i=1}^{c-1}{y}_i\log \left(u_i\right)}.(27)$

where u_i = (u₀, …, u_c–1) is a probability distribution, and each element represents the probability that the sample belongs to category i, and y = (y₀, …, y_c–1) is a one-hot representation of the sample label.

2) Diagnostic performance indices

A confusion matrix was used to evaluate the diagnostic performances of the different methods and verify that of the proposed approach. The confusion matrix, also known as the error matrix, is a standard format for precision evaluation, which is expressed in the form of n rows and n columns, as shown in Table 6.

TABLE 6

TABLE 6. Confusion matrix.

Accuracy and precision are the performance indicators derived from the confusion matrix. According to the form of the confusion matrix, accuracy is defined as the ratio of the number of correctly diagnosed samples to the total number of samples, expressed as a percentage, and the calculation formula is as follows:

$Accuracy=\frac{TN+TP}{FP+TN+TP+PN}\times 100\mathrm{\%}.(28)$

In multi-classification problems, the accuracy can represent the overall accuracy of the model. The higher the similarity of the fault label output by the model and the actual fault label, the more accurate the classification, and the higher the diagnostic accuracy.

Precision represents the proportion of correct positive predictions among all positive predictions. The calculation formula is as follows:

$Precision=\frac{TP}{TP+FP}\times 100\mathrm{\%}.(29)$

In certain types of multi-classification problems, the precision can be used to calculate the classification accuracy of the model.

Experimental Results

This section describes the samples from the fault datasets of different SLs that were introduced into the trained model. Figure 5 presents the confusion matrix of the experimental results, where the rows and columns correspond to the predicted and actual labels, respectively. The numbers in the confusion matrix represent the numbers of correct/false predictions for each case. It can be seen that the proposed AutoML method achieves an ideal classification accuracy.

FIGURE 5

FIGURE 5. Diagram of fault diagnosis results.

In addition, LSTM_AML was used to represent the LSTM models based on AutoML. AML is an abbreviation for AutoML. By utilizing the confusion matrix, the fault diagnosis performance of the LSTM_AML method was analyzed for chillers with different types and severities of faults. For this purpose, we converted the numerical values into images.

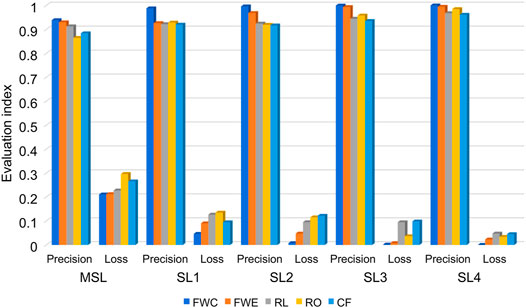
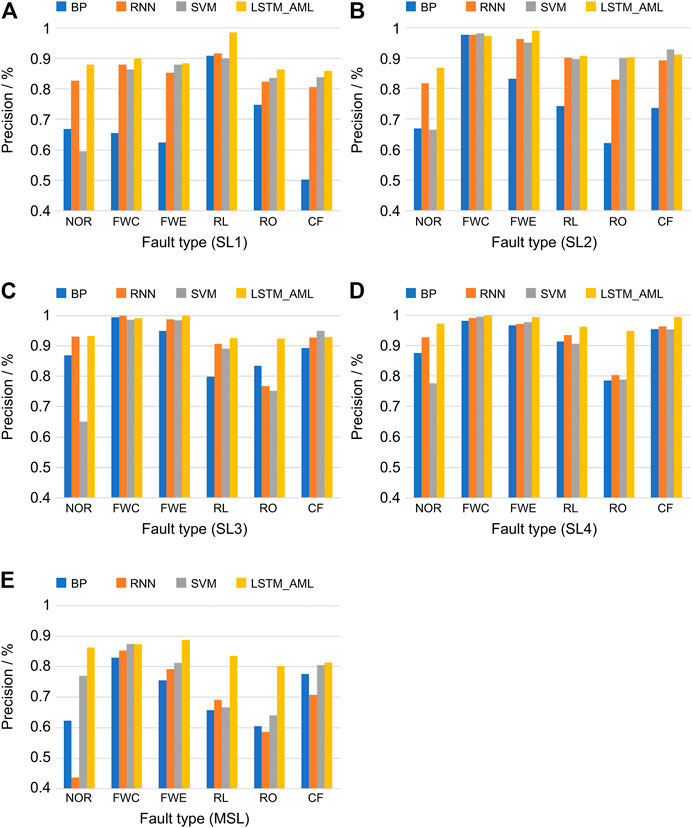
Figure 6 shows the training and diagnostic performances of the LSTM_AML model for different faults and SLs. Among the mixed SL (MSL) fault samples, the FWC fault diagnosis accuracy is the highest at 93.86%, and the diagnosis accuracies for the other fault types are above 86%. The accuracy of MSL diagnosis is generally low, which is due to the intersection of the different fault types and SLs, resulting in very complex changes in the characteristic parameters. In samples SL1, SL2, SL3, and SL4, the FWC and evaporator water flow fault accuracies are higher than those of the other fault types. The results show that in chiller fault diagnosis, the proposed method has the best fault sensitivity and highest accuracy in terms of water flow reduction. Overall, the accuracy for each type of fault is more than 86%, and with increasing fault severity level, the accuracy gradually increases to 100%. The results show that an increase in fault severity will further decrease the system performance, and the LSTM_AML model has excellent diagnostic performance due to the drastic changes of the system parameters. Therefore, the more serious the fault, the higher the diagnostic accuracy.

FIGURE 6

FIGURE 6. Model performance with different fault types.

When we used the loss function to evaluate the training performance of the model, we found that the smaller the loss, the better the training performance of the model. As shown in Figure 6, in samples SL1, SL2, SL3, and SL4, the loss is not more than 10%, and the training effect is good. The MSL fault samples have higher loss function values owing to complex parameter variations, but they are all below 11%. Overall, the loss decreases with increasing fault severity, and the minimum is close to 0. Thus, the proposed method exhibits superior training performance.

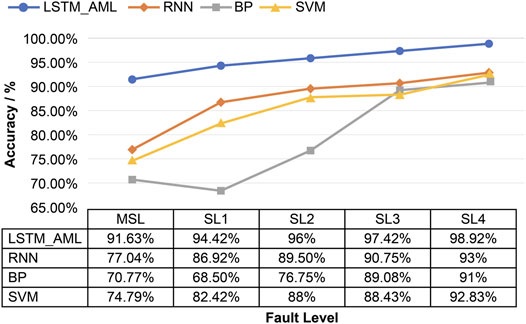
In fault diagnosis, the higher the accuracy, the smaller is the cross-entropy loss, and the better the training performance of the model, the higher is the diagnosis level. Figure 7 presents the recognition accuracy and cross-entropy loss of the proposed method and LSTM network with chiller faults of different SLs. Compared with the traditional LSTM method, the proposed method has a better training effect and higher accuracies in the MSL and SL1 datasets, which are increased by 10.2 and 10.5%, respectively. The recognition accuracies of faults with other SLs increase with increasing fault SL, reaching 98.92%. The loss function also decreases, with the lowest value being 1.24%, showing a good training effect. The proposed method not only collects time-related information and obtains important features in a sufficiently normal time series, but also obtains the optimal fault diagnosis model by HPO. Therefore, compared with LSTM, the proposed method is more sensitive to chiller faults and has better diagnostic performance.

FIGURE 7

FIGURE 7. Model performance with different levels of severity.

Comparison With Other Methods

In this study, the LSTM_AML method was compared with the SVM, RNN, and BPNN methods to verify the effectiveness and superiority of the proposed AutoML method in chiller fault diagnosis. We used five datasets to conduct experiments using these four methods and evaluated them in terms of accuracy and precision. Then, their performances were compared and represented visually.

Figures 8, 9 present the test accuracies of different methods for faults of different SLs in a given dataset. It is worth noting that the higher the fault severity, the higher is the accuracy of the method. Compared with the other methods, the proposed LSTM_AML approach improves the diagnosis of faults with lower SLs more significantly than that of faults with higher SLs. For sample SL1, the proposed method could improve the diagnostic accuracy by up to 25.92%. Thus, the proposed method can accurately diagnose faults in their early stages before they become serious, further reducing the energy consumption and maintenance costs. In addition, the diagnostic performance of the proposed method in the MSL dataset is much higher than those of the other methods, which demonstrates that the proposed method can identify fault types with high accuracy in cases of more fault types and complex severity. The reason for this performance improvement is that the LSTM_AML model can learn and save the temporal correlation information of data from a large number of temporal data. This information facilitates sensitive judgment of the abnormal responses of chillers by the classifier, enabling it to identify different fault types.

FIGURE 8

FIGURE 8. Comparison of methods with different fault types.

FIGURE 9

FIGURE 9. Comparison of methods with different levels of severity.

Therefore, compared with other FDD methods, the AutoML method proposed in this paper not only can diagnose the faults of low-severity chillers with much higher accuracy, but also has a higher diagnostic level in complex fault cases.

Conclusion

This paper presented a chiller fault diagnosis method based on AutoML, which can effectively improve the fault diagnosis performance. The performance of the method was evaluated using experimental data obtained through a simulation platform. The main results of this study can be summarized as follows.

1) The proposed method can effectively extract important feature information from training data. Using the mRMR method, 13 characteristic parameters in the experimental data were reduced to 6, and the most critical data features were automatically selected to reduce the number of redundant features and to improve the fault diagnosis performance effectively.

2) The developed method can mine the time correlations between fault data. The diagnostic accuracy of the proposed method can reach 98.92%, and the diagnostic performance is significantly improved compared with those of the other investigated methods.

3) A GA can automatically optimize and select the hyperparameters and neural network architecture of the LSTM model, obtain the optimal fault diagnosis model, and select model parameters without human intervention.

4) The performance improvement achievable using this method is significantly higher for less severe faults than for more severe faults. Thus, faults can be accurately diagnosed in their early stages before developing into serious faults.

5) In cases of complex fault types and chaotic severity, the diagnostic accuracy of the proposed method is up to 20.86% higher than those of the other methods considered.

In addition, experiments and comparisons showed that the training and fault diagnosis performance of the proposed method are increasing, verifying the effectiveness of feature selection and HPO. Further, the proposed AutoML method can improve the training and fault diagnosis performance. However, this study is limited in that the proposed method cannot effectively improve the speed of fault diagnosis. In future research, we will study other schemes or improved AutoML models to improve the fault diagnosis speed of the model and the diagnostic performance.

Data Availability Statement

The datasets presented in this article are not readily available because the project is still in progress, and it is not convenient to disclose the data due to the restrictions of the confidentiality agreement in the contract. It will be made public only after the project is accepted. Requests for access to the dataset should be directed to the corresponding author.

Author Contributions

CT: Conceptualization, Funding acquisition, Methodology, Software, Writing Original draft preparation. YW: Data Curation, Software, Writing Original draft preparation. XM: Conceptualization, Funding acquisition, Writing- Reviewing and Editing. ZC, HX: Software.

Funding

This work was supported by the Key R&D Program of Shandong Province (Major Science and Technology Innovation Project) (No. 2020CXGC010201), the National Natural Science Foundation of China (No. 62003191), the Youth Fund of Shandong Province (No. ZR202102220769), and the Natural Science Foundation of Shandong Province (No. ZR2020QF072).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azamfar, M., Singh, J., Bravo-Imaz, I., and Lee, J. (2020). Multisensor Data Fusion for Gearbox Fault Diagnosis Using 2-D Convolutional Neural Network and Motor Current Signature Analysis. Mech. Syst. Sig. Process. 144, 106861. doi:10.1016/j.ymssp.2020.106861

CrossRef Full Text | Google Scholar

Barthwal, M., Dhar, A., and Powar, S. (2020). The Techno-Economic and Environmental Analysis of Genetic Algorithm (GA) Optimized Cold thermal Energy Storage (CTES) for Air-Conditioning Applications. Appl. Energ. 283, 116253. doi:10.1016/j.apenergy.2020.116253

CrossRef Full Text | Google Scholar

Chen, D., Wawrzynski, P., and Lv, Z. (2020). Cyber Security in Smart Cities: A Review of Deep Learning-Based Applications and Case Studies. Sustain. Cities Soc. 66, 102655.

Google Scholar

Comstock, M. C., Braun, J. E., and Eckhard, A. G. (2002). A survey of common faults for chillers / discussion. ASHRAE Transactions, 108 (1), p.819-825.

Google Scholar

Daneshvar, Y., Sabzehparvar, M., and Hashemi, S. (2020). Energy efficiency of small buildings with smart cooling system in the summer. Front. Energy., 1–10. doi:10.1007/s11708-020-0699-7

CrossRef Full Text | Google Scholar

Denkena, B., Dittrich, M.-A., Wilmsmeier, S., and Settnik, S. J. (2021). Modular Sequence Optimization with Hybrid Genetic Algorithm. Proced. CIRP 96, 51–56. doi:10.1016/j.procir.2021.01.052

CrossRef Full Text | Google Scholar

Dixit, P., and Silakari, S. (2021). Deep Learning Algorithms for Cybersecurity Applications: A Technological and Status Review. Comp. Sci. Rev. 39, 100317. doi:10.1016/j.cosrev.2020.100317

CrossRef Full Text | Google Scholar

Domingos, P. (2012). A Few Useful Things to Know about Machine Learning. Commun. ACM 55, 78–87. doi:10.1145/2347736.2347755

CrossRef Full Text | Google Scholar

Farah, S., Aneela, Z., and Ammara, M. (2020). A Novel Wavenets Long Short Term Memory Paradigm for Wind Power Prediction. Appl. Energ. 269, 115098. doi:10.1016/j.apenergy.2020.115098

CrossRef Full Text | Google Scholar

García-Domínguez, M., Domínguez, C., Heras, J., Mata, E., and Pascual, V. (2021). UFOD: An AutoML Framework for the Construction, Comparison, and Combination of Object Detection Models. Pattern Recog. Lett. 145, 135–140. doi:10.1016/j.patrec.2021.01.022

CrossRef Full Text | Google Scholar

Grohl, J., Schellenberg, M., Dreher, K., and Maier-Hein, L. (2021). Deep Learning for Biomedical Photoacoustic Imaging: A Review. Photoacoustics 22, 100241. doi:10.1016/j.pacs.2021.100241

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, H., Cui, X., Fan, Y., and Qing, H. (2019). Least Squares Support Vector Machine (LS-SVM)-based Chiller Fault Diagnosis Using Fault Indicative Features. Appl. Therm. Eng. 154, 540–547. doi:10.1016/j.applthermaleng.2019.03.111

CrossRef Full Text | Google Scholar

Han, H., Gu, B., Wang, T., and Li, Z. R. (2011). Important Sensors for Chiller Fault Detection and Diagnosis (FDD) from the Perspective of Feature Selection and Machine Learning. Int. J. Refrigeration 34, 586–599. doi:10.1016/j.ijrefrig.2010.08.011

CrossRef Full Text | Google Scholar

Hanchuan Peng, H., Fuhui Long, F., and Ding, C. (2005). Feature Selection Based on Mutual Information Criteria of max-dependency, max-relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Machine Intell. 27, 1226–1238. doi:10.1109/tpami.2005.159

PubMed Abstract | CrossRef Full Text | Google Scholar

He, X., Zhao, K., and Chu, X. (2021). AutoML: A Survey of the State-Of-The-Art. Knowledge-Based Syst. 212, 106622. doi:10.1016/j.knosys.2020.106622

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Howard, C., and James, E. B. (2016). Empirical Modeling of the Impacts of Faults on Water-Cooled Chiller Power Consumption for Use in Building Simulation Programs. Appl. Therm. Eng. 99, 756–764. doi:10.1016/j.applthermaleng.2016.01.119

CrossRef Full Text | Google Scholar

Hu, C. H. (2020). Face Illumination Recovery for the Deep Learning Feature under Severe Illumination Variations. Pattern Recog 111, 107724. doi:10.1016/j.patcog.2020.107724

CrossRef Full Text | Google Scholar

Hua, H. (2012). Research on Fault Detection and Diagnosis of Refrigeration System Based on Sequential Integration Method. Shanghai Jiaotong University.

Google Scholar

Kanter, J. M., and Veeramachaneni, K. (2015). “Deep Feature Synthesis: Towards Automating Data Science Endeavors,” in Proc. IEEE Int. Conf. Data Sci. Adv. Anal., Paris, France, 19-21 Oct. 2015 (IEEE), 1–10. doi:10.1109/dsaa.2015.7344858

CrossRef Full Text | Google Scholar

Kim, H.-j., and Shin, K.-s. (2007). A Hybrid Approach Based on Neural Networks and Genetic Algorithms for Detecting Temporal Patterns in Stock Markets. Appl. Soft Comput. 7, 569–576. doi:10.1016/j.asoc.2006.03.004

CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, J., Liu, C., and Jiang, D. (2019). Fault Diagnosis of Wind Turbine Based on Long Short-Term Memory Networks. Renew. Energ. 133, 422–432. doi:10.1016/j.renene.2018.10.031

CrossRef Full Text | Google Scholar

Li, D., Li, D., Li, C., Li, L., and Gao, L. (2019). A Novel Data-Temporal Attention Network Based Strategy for Fault Diagnosis of Chiller Sensors. Energy and Buildings 198, 377–394. doi:10.1016/j.enbuild.2019.06.034

CrossRef Full Text | Google Scholar

Li, J., Yao, X., Wang, X., Yu, Q., and Zhang, Y. (2019). Multiscale Local Features Learning Based on BP Neural Network for Rolling Bearing Intelligent Fault Diagnosis. Measurement 153, 107419. doi:10.1016/j.measurement.2019.107419

CrossRef Full Text | Google Scholar

Li, P. (2020). Research on Radar Signal Recognition Based on Automatic Machine Learning. Neural Comput. Appli. 32, 1–11. doi:10.1007/s00521-019-04494-1

CrossRef Full Text | Google Scholar

Li, T., Bo, W., Hu, C., Kang, H., Liu, H., Wang, K., et al. (2021). Applications of Deep Learning in Fundus Images: A Review. Med. Image Anal. 69, 101971. doi:10.1016/j.media.2021.101971

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Zhou, J., Zheng, Y., Jiang, W., and Zhang, Y. (2018). Fault Diagnosis of Rolling Bearings with Recurrent Neural Network-Based Autoencoders. Isa Trans. 77, 167–178. doi:10.1016/j.isatra.2018.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., Tao, Z., Wang, Y., Yu, H., and Wang, Y. (2015). Long Short-Term Memory Neural Network for Traffic Speed Prediction Using Remote Microwave Sensor Data. Transportation Res. C: Emerging Tech. 54, 187–197. doi:10.1016/j.trc.2015.03.014

CrossRef Full Text | Google Scholar

Ng, J. Y. H., Hausknecht, M., Vijayanarasimhan, S., Vinyals, O., Monga, R., and Toderici, G. (2015). “Beyond Short Snippets: Deep Networks for Video Classification,” in Proc. IEEE Conf. Comp. Vision Pattern Recog., Boston, MA, 7-12 June 2015 (IEEE). doi:10.1109/cvpr.2015.7299101

CrossRef Full Text | Google Scholar

Ogunjuyigbe, A. S. O., Ayodele, T. R., and Bamgboje, O. D. (2021). Optimal Placement of Wind Turbines within a Wind Farm Considering Multi-Directional Wind Speed Using Two-Stage Genetic Algorithm. Front. Energ. 15, 240–255. doi:10.1007/s11708-018-0514-x

CrossRef Full Text | Google Scholar

Shi, Y., Song, X., and Song, G. (2021). Productivity Prediction of a Multilateral-Well Geothermal System Based on a Long Short-Term Memory and Multi-Layer Perceptron Combinational Neural Network. Appl. Energ. 282, 116046. doi:10.1016/j.apenergy.2020.116046

CrossRef Full Text | Google Scholar

Sun, K., Li, G., Chen, H., Liu, J., Li, J., and Hu, W. (2016). A Novel Efficient SVM-Based Fault Diagnosis Method for Multi-Split Air Conditioning System's Refrigerant Charge Fault Amount. Appl. Therm. Eng. 108, 989–998. doi:10.1016/j.applthermaleng.2016.07.109

CrossRef Full Text | Google Scholar

Sun, K., Li, G., Chen, H., Liu, J., Li, J., and Hu, W. (2016). A Novel Efficient SVM-Based Fault Diagnosis Method for Multi-Split Air Conditioning System's Refrigerant Charge Fault Amount. Appl. Therm. Eng. 108, 989–998. doi:10.1016/j.applthermaleng.2016.07.109

CrossRef Full Text | Google Scholar

Tan, H.-B., Xiong, F., Jiang, Y.-L., Huang, W.-C., Wang, Y., Li, H.-H., et al. (2020). The Study of Automatic Machine Learning Base on Radiomics of Non-focus Area in the First Chest CT of Different Clinical Types of COVID-19 Pneumonia. Sci. Rep. 10, 18926. doi:10.1038/s41598-020-76141-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Waring, J., Lindvall, C., and Umeton, R. (2020). Automated Machine Learning: Review of the State-Of-The-Art and Opportunities for Healthcare. Artif. Intelligence Med. 104, 101822. doi:10.1016/j.artmed.2020.101822

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, X., Niu, J., Liu, X., Chen, Z., Tang, S., and Yu, S. (2021). A Survey on Incorporating Domain Knowledge into Deep Learning for Medical Image Analysis. Med. Image Anal. 69, 101985. doi:10.1016/j.media.2021.101985

PubMed Abstract | CrossRef Full Text | Google Scholar

Yabin, G., Zehan, T., Huanxin, C., Guannan, L., Jiangyu, W., Ronggeng, H., et al. (2018). Deep Learning-Based Fault Diagnosis of Variable Refrigerant Flow Air-Conditioning System for Building Energy Saving. Appl. Energ. 225, 732–745. doi:10.1016/j.apenergy.2018.05.075

CrossRef Full Text | Google Scholar

Yang, R., Huang, M., Lu, Q., and Zhong, M. (2018). Rotating Machinery Fault Diagnosis Using Long-Short-Term Memory Recurrent Neural Network. IFAC-PapersOnLine 51, 228–232. doi:10.1016/j.ifacol.2018.09.582

CrossRef Full Text | Google Scholar

Yao, Q., Wang, M., Chen, Y., Dai, W., Li, Y.-F., Tu, W.-W., et al. (2018). Taking Human Out of Learning Applications: A Survey on Automated Machine Learning. arXiv preprint arXiv 1810.13306.

Google Scholar

Yin, A., Yan, Y., Zhang, Z., Li, C., and Sánchez, R.-V. (2020). Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss. Sensors 20, 2339–2352. doi:10.3390/s20082339

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, M., Wu, Y., and Lin, L. (2016). “Fault Diagnosis and Remaining Useful Life Estimation of Aero Engine Using LSTM Neural Network,” in Proc. IEEE Int. Conf. Aircraft Utility Syst., Beijing, China, 10-12 Oct. 2016 (IEEE), 135–140. doi:10.1109/aus.2016.7748035

CrossRef Full Text | Google Scholar

Zhang, X., Wang, L., and Su, Y. (2020). Visual Place Recognition: A Survey from Deep Learning Perspective. Pattern Recog 113, 107760. doi:10.1016/j.patcog.2020.107760

CrossRef Full Text | Google Scholar

Zhao, R., Yan, R., Chen, Z., Mao, K., Wang, P., and Gao, R. X. (2019). Deep Learning and its Applications to Machine Health Monitoring. Mech. Syst. Signal Process. 115, 213–237. doi:10.1016/j.ymssp.2018.05.050

CrossRef Full Text | Google Scholar

Zhao, W., Zhang, H., Zheng, J., Dai, Y., Huang, L., Shang, W., et al. (2021). A point Prediction Method Based Automatic Machine Learning for Day-Ahead Power Output of Multi-Region Photovoltaic Plants. Energy 223, 120026. doi:10.1016/j.energy.2021.120026

CrossRef Full Text | Google Scholar

Zhao, Y., Li, T., Zhang, X., and Zhang, C. (2019). Artificial intelligence-based fault detection and diagnosis methods for building energy systems: Advantages, challenges and the future. Renew. Sust. Energ. Rev. 109, 85–101. doi:10.1016/j.rser.2019.04.021

CrossRef Full Text | Google Scholar

Zhou, Z., Li, G., Wang, J., Chen, H., Zhong, H., and Cao, Z. (2020). A Comparison Study of Basic Data-Driven Fault Diagnosis Methods for Variable Refrigerant Flow System. Energy and Buildings 224, 110232. doi:10.1016/j.enbuild.2020.110232

CrossRef Full Text | Google Scholar

Nomenclature

b_c, b_f biases

B fouling resistance amplification factor

β_i Lagrange multiplier

c_t cell state at time t

c_t–1 cell state at time t–1

c¹_t the cell state of the first LSTM layer at t time

C penalty factor in the radial basis function

c the target class

δ thickness of the fouling layer

f_l(▪) nonlinear activation function

f_t forgetting threshold at time t

h_t output unit at time t

h_t–1 output unit at time t–1

i number of neurons in the input layer

k number of output nodes

K total heat transfer coefficient of the fin condenser

K₀ fouling thermal resistance corresponding to a certain water

quality condition

l number of neurons in the hidden layer

L characteristic quantity

λ thermal conductivity of the fouling layer

MI(x; y) mutual information between x and y

m the number of features

M number of data

maxD(S, c),D max-relevance criterion

minR(S),R min-redundancy condition

N number of feature quantities after reduction

o_t output threshold at time t

g number of samples

P number of training samples

p(x) probability density respectively of x

p(y) probability density respectively of y

p(x,y) crossover probability or joint probability of x and y

p_i hyperparametric vector

P_s model parameter vector set

Φ(•) nonlinear transformation in the kernel function

p real distribution

q fitting distribution

Q number of validation samples

r thermal resistance of the fouling layer

R real number set

S the feature set

σ sigmoid function

tanh activation function

U_c, U_i, U_o weights

w_ih weight between the input and hidden layers

w_l*l weight of the hidden and hidden layers

w_lk weight of the hidden and output layers

W_c, W_i, W_o, W_t weights

X data before normalization

x_i output value of node i

X_max maximum value in the original sample data

X_min minimum value in the original sample data

X´_n sample data after feature selection

X_normal, X´_normal data after normalization

x_t input unit at time t

x_a/x_b feature

u_i the probability that the sample belongs to category i

y = (y₀, …, y_c–1] one-hot representation of the sample label

y_i ∈ {1, –1} category label

y_p true values of the training samples

y´_p predicted values of the training samples

y_q true values of the validation samples

y´_q predicted values of the validation samples

c_i input vector

d_i category label

x^t_i i neurons in the input layer at time t

a^t−1_l* l neurons in the hidden layer at time t-1

z^l_h value of the l neurons in the hidden layer before the activation function acts at time t

y^t_k k neurons of the output layer at time t