Distributionally robust chance-constrained operation of distribution grids considering voltage constraints

The distribution grid experiences node voltage fluctuations due to the growing uncertainty of large-scale renewable energy sources A practical solution is establishing a chance-constrained optimal model to deal with the uncertainties. However, using this method needs to know the accurate probability distribution of node power injections, which has limitations in application. Therefore, this paper proposes a distributionally robust chance-constrained optimization method for power grid operation based on the ambiguity set of probability distributions. Firstly, considering voltage security constraints, this paper establishes a chance-constrained model to minimize the cost of active power regulation. Besides, based on the Wasserstein ambiguity set, a linearized method is proposed to convexify the objective function. Moreover, the conditional risk value (CVaR) is applied to convert the uncertain model into a deterministic model. The effectiveness of the proposed method is validated through optimization results obtained for the modified PG&E69-bus distribution grid.

1 Introduction

The global energy crisis and environmental issues have prompted continuous energy-resource structure transformation and upgrading. The gradual proliferation of renewable energy sources (RESs) such as photovoltaic and wind power on a global scale has become an inevitable trend. However, large-scale RESs have intense uncertainty, which brings enormous challenges to the dispatch and operation of active distribution grids (Alismail et al., 2017). For instance, in optimizing real-time operations using active and reactive regulation devices, the traditional dispatch approach overlooks power output uncertainties, leading to scheduling plans based solely on expected node power injections. As a result, there is a risk of violating the secure constraints (Hu et al., 2022). Therefore, considering the uncertainties of various RESs in the power grid and selecting appropriate optimal dispatch strategies have become research hotspots. In other words, it is necessary to propose a new dispatch method to integrate active power regulation devices, deal with the uncertainty of various distributed energy sources, and make the distribution grid operate securely and economically.

Currently, there are three kinds of methods to describe the uncertainty of RESs: stochastic optimization-based method, robust optimization-based method, and distributionally robust chance-constrained (DRCC) optimization-based method. When using the robust optimization-based method, the dispatchers do not need all probability distribution of RES outputs and only consider the worst-case scenario during the optimization process, which often leads to overly conservative results (Chen et al., 2020; Zhai et al., 2020; Chen et al., 2021). Han et al. (2020) considered the security constraints and established a robust optimization model for distribution systems. The constructed probability distribution fuzzy set is complex, resulting in plodding optimization speed. Ding et al. (2015) proposed a robust two-stage operation model. Although the proposed method considers the uncertainties within the power grid, it leads to high economic scheduling costs. Xia et al. (2019) considered the impact of wind power integration into the grid and proposed a robust optimization-based operation model. However, this method sacrifices significant economic costs to ensure secure operation.

According to Zhai et al. (2022), Wang et al. (2012) and Zhao et al. (2014), the stochastic optimization-based method mainly includes the Monte Carlo method, scenario generation method, and chance constraint method. This method needs to assume that the uncertainty of each power injection follows a specific probability distribution. Yang and Yu (2018) used the chance constraint method to convert uncertainty problems into deterministic problems and estimate the probability distribution of node voltages. Guggilam et al. (2016) established a two-stage energy management model for microgrids based on the chance-constrained method. Zhao et al. (2018) applied chance-constrained programming dealing with power flow, voltage, and reserve constraints. Tang et al. (2023) proposed a chance-constrained optimization scheduling method for distribution grids considering photovoltaic carrying capacity. Zhong et al. (2023) proposed a distributed optimization method for integrated transmission and distribution grids with chance constraints. They established a restoration operation model for the transmission and distribution grid to minimize restoration costs. Roald et al. (2013) introduced the fuzzy theory and credibility theory to handle wind power uncertainty, converting deterministic constraints into fuzzy chance constraints. The stochastic reactive power optimization model is established to minimize the entire grid loss and voltage offset, and it is solved by the improved particle swarm optimization algorithm. Lubin et al. (2015) and Dai et al. (2017) proposed the approximate derivation method for chance constraints based on the analytical method and established the two-step optimal scheduling for the power system. Zhao and Jiang, (2017) introduced the chance-constrained programming method to minimize the energy storage configuration in the distribution grid and used the analytical method to establish the deterministic optimal model. Ciftci et al. (2019) proposed a data-driven chance-constrained optimization model for microgrid energy management, constructing confidence sets for uncertainties based on historical data. Since the established optimal model of the stochastic optimization-based method has probability constraints, it is nonlinear and usually solved by intelligent algorithms (Li et al., 2013; Huang, 2017; Xu and Li, 2019). However, the obtained results will likely fall into the local optimum, which means the accuracy is far from the existing engineering requirements.

In contrast to the stochastic optimization-based method, the DRCC optimization-based approach does not necessitate precise probability distribution information for uncertainties; instead, it relies on ambiguity sets, which exhibit enhanced robustness (Cao et al., 2021; Du et al., 2022). Proposed as a hybrid of stochastic and robust optimization, the DRCC optimization-based method addresses uncertain challenges. It operates under the assumption that the probability distribution falls within a predefined ambiguity set and employs the worst-case scenario from this set as the optimization reference. By utilizing the worst-case probability distribution in an ambiguity set, the optimization outcomes can be adjusted, thus mitigating the risk of over-conservatism compared to robust optimization-based methods. He et al. (2019) utilized the moment of uncertainty is to distribute and robustly solve wind power uncertainty and energy optimization problems. Ao et al., 2020 used the DRCC for multiple discrete scenarios to deal with the load uncertainties in distribution grids. However, the above two methods for constructing DRCC ambiguity sets fail to utilize historical data fully and remain highly conservative (Esfahani and Kuhn, 2018). Unlike the above methods, Wasserstein distance is data-driven and uses historical data of distributed power generation outputs to construct an ambiguity set. As the number of samples increases, the ambiguity set gradually converges to the actual situation (Duan et al., 2018). Based on this principle, the ambiguity set based on Wasserstein distance is proposed to depict the degree of difference between actual and empirical distributions (Zhu et al., 2019; Poolla et al., 2020). The conservatism and economic benefits of the flexible control optimization scheme and the established model are easy to solve and have strong applicability. Based on the above, this paper applies DRCC to the optimal operation in the distribution grid.

In addition, the existing nonlinear voltage chance constraints significantly increase the number of variables processed in the operation model. The second-order cone method is used to deal with the voltage chance constraints, but the accuracy of the optimal result is low (Cai et al., 2022). The relaxation variables and interval estimation method were introduced to relax the nonlinear chance constraints (Xiao et al., 2021). However, the approximate model introduces too many variables, resulting in low solving efficiency. For the nonconvex voltage chance-constrained forms, Liu et al. (2020) and Xie W. (2021) used the conditional risk values to transform the nonlinear chance constraints into convex approximation. Chen et al. (2024) applied the risk value and duality theory to transform the chance-constrained form of nonconvex voltages into convex expressions. Although the above-simplified method deals with fewer variables in the operation process than the traditional nonlinear optimization methods, there is still a time-consuming problem. Therefore, it is necessary to propose a fast solution method.

In summary, this paper proposes a distributionally robust chance-constrained dispatch for distribution grids that considers voltage secure constraints. The specific structure is as follows. Section 2 establishes a chance-constrained model considering voltage constraints. In Section 3, based on the Wasserstein ambiguity set, a linearized method is proposed for the objective function. Section 4 uses the conditional risk value to convert the uncertain model into the deterministic model. Simulations validating the effectiveness of the proposed method are conducted in Section 5. Conclusions are shown in Section 6.

2 The chance-constrained model considering voltage constraints

Assume the node set is N (where the dimension is n) and the output of renewable energy sources set is W (where the dimension is w) in the distribution grid. ${\mathit{x}}^0={\left(P_1^0,..,P_n^0,Q_1^0,..,Q_n^0\right)}^T$ is the current operating point. To minimize the regulation cost of distribution grids, the objective function F is as follows:

$F=\min E\left({\displaystyle \sum _{i=1}^n}\left(c_i{P}_i+c_i^U{P}_i^U+c_i^D{P}_i^D\right)\right)(1)$

where $E\left(•\right)$ is the expectation of $•$; $P_i$ and $c_i$ are the active power injection and regulation cost at node $i\in \mathrm{N}$ , respectively; $P_i^U$ and $P_i^D$ are the reserve capacity corresponding to the upper and lower power limits at node $i\in \mathrm{N}$, respectively; $c_i^U$ and $c_i^D$ are the corresponding costs of $P_i^D$ and $P_i^U$, respectively.

Considering the uncertainty of the power injection, we have:

$P_i={\overline{P}}_i-P_i^L+\Delta P_i\left(\xi \right)+{\xi }_i,\forall i\in \mathrm{N}(2)$

where ${\overline{P}}_i$ is the power adjustment of node i; $\Delta P_i\left(\xi \right)$ is the adjustment error caused by the uncertainty of the power injection at node i; $\Delta P\left(\xi \right)={\left[\Delta P_1{\left(\xi \right)}^T,\Delta P_2{\left(\xi \right)}^T,....,\Delta P_n{\left(\xi \right)}^T\right]}^T$; $P_i^L$ is the load of node i. ${\xi }_i$ is the renewable energy output at node i.

According to the linearization method proposed by Ordoudis et al. (2021), $\Delta P\left(\xi \right)$ can be transformed into the following:

$\Delta P_i\left(\xi \right)=Y_i\xi ,Y_i\in {\mathrm{R}}^{1\times n}(3)$

where $Y_i=\left[y_{i,1},y_{i,2},...,y_{i,n}\right]$ is the adjustment coefficient vector to be solved.

Combining (1–3), we have (4):

$F=\underset{{\overline{P}}_i,P_i^U,P_i^D,Y}{\min }{\displaystyle \sum _{i=1}^n}\left(c_i{\overline{P}}_i-c_i{P}_i^L+c_i^U{P}_i^U+c_i^D{P}_i^D\right)+E\left(c^{T}Y\xi \right)(4)$

where $c=\left[c_1,c_2,...,c_n\right]$, $Y={\left[Y_1^T,Y_2^T,...,Y_n^T\right]}^T$.

Additionally, the operational constraints include:

${\overline{P}}_i-P_i^D\ge P_i^m(5)$

${\overline{P}}_i+P_i^U\le P_i^M(6)$

$0\le P_i^U\le \left(P_i^M-P_i^m\right)(7)$

$0\le P_i^D\le \left(P_i^M-P_i^m\right)(8)$

$\psi \left(V_i\le V_i^M\right)\ge 1-{\epsilon }_V(9)$

$\psi \left(V_i\ge V_i^m\right)\ge 1-{\epsilon }_V(10)$

where (5) and (6) are the constraints for the outputs of power regulation devices; (7) and (8) are the constraints for reserve capacities; (9) and (10) are the chance constraints for node voltage magnitudes; $V_i^M$ represents the upper limit, while $V_i^m$ denotes the lower limit of the node voltage magnitude; ${\epsilon }_V$ is the confidence level.

For (9, 10), this paper linearizes the node voltage constraints based on current constraints. According to Yang and Yu. (2018), the voltage security constraints of nodes $k\in \mathrm{N}$ can be written as (11) and (12):

${\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^M{P}_j+{\beta }_{k,j}^M{Q}_j\right)\le 1(11)$

${\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^m{P}_j+{\beta }_{k,j}^m{Q}_j\right)\le 1(12)$

where ${\alpha }_{k,j}^M$, ${\beta }_{k,j}^M$, ${\alpha }_{k,j}^m$, and ${\beta }_{k,j}^m$ can be represented as follows:

$\left\{\begin{array}{l}{\alpha }_{k,j}^M=\frac{1}{V_k^M{H}_k^M}\frac{\partial V_k}{\partial P_j}\\ {\beta }_{k,j}^M=\frac{1}{V_k^M{H}_k^M}\frac{\partial V_k}{\partial Q_j}\\ {\alpha }_{k,j}^m=\frac{1}{V_k^m{H}_k^m}\frac{\partial V_k}{\partial P_j}\\ {\beta }_{k,j}^m=\frac{1}{V_k^m{H}_k^m}\frac{\partial V_k}{\partial Q_j}\end{array}\right.(13)$

where $H_k^M=V_k^M-V_0^0+{\displaystyle \sum _{\forall j\in N}}\left(\frac{\partial V_k}{\partial P_j}{P}_j^0+\frac{\partial V_k}{\partial Q_j}{Q}_j^0\right)$, $H_k^m=V_k^m-V_k^0+{\displaystyle \sum _{\forall j\in N}}\left(\frac{\partial V_k}{\partial P_j}{P}_j^0+\frac{\partial V_k}{\partial Q_j}{Q}_j^0\right)$.

Combining (2, 3), and (12), we can get the explicit expression of the chance constraints for voltage magnitude as (14, 15):

$\psi \left[{\displaystyle \sum _{j=1}^n}{\alpha }_{k,j}^{\mathrm{M}}{Y}_j\xi +{\displaystyle \sum _{j=1}^n}{\alpha }_{k,j}^M{\xi }_j+{\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^M{\overline{P}}_j+{\beta }_{k,j}^M{Q}_j-{\alpha }_{k,j}^M{P}_j^L\right)\le 1\right]\ge 1-{\epsilon }_V(14)$

$\psi \left[{\displaystyle \sum _{j=1}^n}{\alpha }_{k,j}^m{Y}_j\xi +{\displaystyle \sum _{j=1}^n}{\alpha }_{k,j}^m{\xi }_j+{\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^m{\overline{P}}_j+{\beta }_{k,j}^m{Q}_j-{\alpha }_{k,j}^m{P}_j^L\right)\le 1\right]\ge 1-{\epsilon }_V(15)$

3 Linearization of objective based on distributionally robust theory

For the renewable energy sources output $\xi$, its historical statistical data is $\widehat{\xi }$, and the empirical probability distribution is in (16) $\widehat{\mathbb{P}}$:

$\stackrel{⌢}{\mathbb{P}}=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\delta }_i(16)$

where m is the number of historical data vectors used; ${\delta }_i$ is the Dirac measure of the ith historical statistical data ${\widehat{\xi }}_i$.

Considering that the actual probability distribution $\mathbb{P}$ of the distributed power generation vector $\xi$ is unknown, this paper constructs a Wasserstein ambiguity set $\mathbb{D}$ to describe the uncertainty of $\xi$ as (17):

$\mathbb{D}:=\left\{\mathbb{P}\mathbb{\in }M\left(\mathrm{\Xi }\right)\left|\mathbb{W}\left(\mathbb{P},\stackrel{⌢}{\mathbb{P}}\right)\le \rho \right.\right\}(17)$

where $\rho >0$ is the radius of the ambiguity set; $M\left(\mathrm{\Xi }\right)$ is the space set to which the probability distribution $\mathbb{P}$ belongs. $\mathbb{W}\left(\mathbb{P},\widehat{\mathbb{P}}\right)$ is the Wasserstein distance between the actual and empirical probability distribution of the output of renewable energy sources, which can be expressed as (18):

$\mathbb{W}\left(\mathbb{P},\stackrel{⌢}{\mathbb{P}}\right)=\underset{\mathrm{\Pi }}{\inf }\left\{{\int }_{{\mathrm{\Xi }}^2}‖\widehat{\mathit{\xi }}-\mathit{\xi }‖\mathrm{\Pi }\left(\mathrm{d}\widehat{\mathit{\xi }},\mathrm{d}\mathit{\xi }\right)\right\}=\underset{{\mathbb{Q}}_i}{\inf }\left\{\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\right\}(18)$

where $\mathrm{\Pi }$ is the joint distribution set of $\widehat{\xi }$ and $\xi$; ${\mathbb{Q}}_i$ is the conditional probability distribution of $\mathrm{\Pi }$ when $\widehat{\xi }={\widehat{\xi }}_i$. we have (19):

$\mathrm{\Pi }\left(\mathrm{d}{\widehat{\mathit{\xi }}}_i,\mathrm{d}\mathit{\xi }\right)=\frac{1}{m}{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)(19)$

Then, based on the robust optimization theory, the objective function is relaxed as (20, 21):

$\underset{{\overline{P}}_i,P_i^U,P_i^D,Y}{\min }{\displaystyle \sum _{i=1}^n}\left(c_i{\overline{P}}_i-c_i{P}_i^L+c_i^U{P}_i^U+c_i^D{P}_i^D\right)+\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }E\left(c^{T}Y\xi \right)(20)$

Let

$l\left(\xi \right)=\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }E\left(c^{T}Y\xi \right)=\underset{\stackrel{⌢}{\mathbb{P}}}{\sup }{\int }_{\mathrm{\Xi }}{c}^{T}Y\xi \stackrel{⌢}{\mathbb{P}}\left(\mathrm{d}\mathit{\xi }\right)(21)$

Considering the total probability equation:

$\stackrel{⌢}{\mathbb{P}}\left(\mathrm{d}\mathit{\xi }\right)=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)(22)$

Based on the Lagrange function, we have (23):

$\begin{array}{l}\underset{{\mathbb{Q}}_i}{\sup }\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}{c}^{T}Y\xi {\mathbb{Q}}_i\left(\mathrm{d}\xi \right)+\lambda \left(\rho -\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\right)\\ =\lambda \rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}\underset{\xi }{\sup }\left(l\left(\xi \right)-\lambda ‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖\right)\end{array}(23)$

where $\lambda \ge 0$ is the Lagrange multiplier under the condition $\mathbb{W}\left(\mathbb{P},\widehat{\mathbb{P}}\right)\le \rho$.

By introducing the auxiliary variable $s_i$, the dual problem of (22) can be expressed as (24, 25):

$\lambda \rho +\underset{s_i}{\inf }\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_i(24)$

$s.t.\underset{\xi }{\sup }l\left(\mathit{\xi }\right)-\lambda ‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖⩽s_i,\forall i\in \left\{1,2,...,m\right\}(25)$

Besides, by introducing the intermediate variable ${\mathit{z}}_i\left({‖{\mathit{z}}_i‖}_{\infty }⩽\lambda \right)$, (24) can be equivalent as (26):

$\begin{array}{l}\underset{\xi \in \mathrm{\Xi }}{\sup }l\left(\mathit{\xi }\right)-{\mathit{z}}_i^{\mathrm{T}}\left({\widehat{\mathit{\xi }}}_i-\mathit{\xi }\right)=-{z_i}^{\mathrm{T}}{\widehat{\mathit{\xi }}}_i+\underset{{\mathbb{Q}}_i}{\sup }{\int }_{\mathrm{\Xi }}\left(c^{T}Y\xi +{\mathit{z}}_i^{\mathrm{T}}\mathit{\xi }\right){\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\\ =-{z_i}^{\mathrm{T}}{\widehat{\mathit{\xi }}}_i+\underset{{\mathbb{Q}}_i}{\sup }{\int }_{\mathrm{\Xi }}{\left({\mathit{z}}_i+Y^{T}c\right)}^T\xi {\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\le s_i\end{array}(26)$

According to the dual theory, we have (27):

$z_i=-Y^{T}c(27)$

Then, the optimal objective can be expressed as (28, 29):

$\underset{{\overline{P}}_i,P_i^U,P_i^D,Y,\lambda ,s_i,\gamma }{\min }{\displaystyle \sum _{i=1}^n}\left(c_i{\overline{P}}_i-c_i{P}_i^L+c_i^U{P}_i^U+c_i^D{P}_i^D\right)+\lambda \rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_i(28)$

$s.t.\left\{\begin{array}{l}-{z_i}^{\mathrm{T}}{\widehat{\mathit{\xi }}}_i=c^{T}Y{\widehat{\xi }}_i\le s_i\\ ‖z_i{\Vert }_{\infty }=‖-Y^{T}c{\Vert }_{\infty }\le \lambda \end{array}\right.(29)$

4 Convex approximation of chance constrained combining conditional risk value

Given the nonconvex nature of chance constraints, solving the model becomes challenging. To address this issue, the paper proposes utilizing a conditional risk value, as suggested by Ben-Tal et al. (2009), to formulate a convex approximation of these constraints in the worst-case scenario. For the convenience of expression, this paper takes the upper limit of node voltage as an example to deduce, and (13) is recorded as (30):

$\psi \left[a_k^M\xi -b_k^M\le 0\right]\ge 1-{\epsilon }_V(30)$

where $a_k^M={\alpha }_k^M\left(Y+I\right)$; ${\alpha }_k^M=\left[{\alpha }_{k,1}^M,{\alpha }_{k,2}^M,...,{\alpha }_{k,n}^M\right]$; $b_k^M=1-{\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^M{\overline{P}}_j+{\beta }_{k,j}^M{Q}_j-{\alpha }_{k,j}^M{P}_j^L\right)$; $I\in {\mathrm{R}}^{n\times n}$ is the unit diagonal matrix.

This paper uses the conditional risk value to approximate the chance constraint of node voltage upper limit in the worst case, shown as follows:

$\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }\psi \left[a_k^M\xi -b_k^M\le 0\right]\ge 1-{\epsilon }_V(31)$

And the following constraints can be established by conditional risk value (Rockafellar and Uryasev, 2000) in (32):

$\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }\underset{{\tau }_k^M}{\inf }{\tau }_k^M+\frac{1}{{\epsilon }_V}E{\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}=\underset{{\tau }_k^M}{\inf }{\tau }_k^M+\frac{1}{{\epsilon }_V}\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }E{\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}\le 0(32)$

where ${\tau }_k^M$ is the dual variable; $E\left[•\right]$ is the expectations of $•$; ${\left[•\right]}_{+}=\max \left(•,0\right)$. By (31), the original nonconvex chance constraint form can be rewritten as a distributionally robust form

For (31), we have

$\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }E\left({\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}\right)=\underset{{\mathbb{Q}}_i}{\sup }\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}{\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)(33)$

Then, based on the Lagrange function, we have (34):

$\begin{array}{l}\underset{{\mathbb{Q}}_i}{\sup }\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}{\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)+{\lambda }_k^M\left(\rho -\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\int }_{\mathrm{\Xi }}‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖{\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\right)\\ ={\lambda }_k^M\rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}\underset{\xi }{\sup }\left(E\left({\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]}_{+}\right)-{\lambda }_k^M‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖\right)\end{array}(34)$

where ${\lambda }_k^M\ge 0$ is the Lagrange coefficient corresponding to corresponding to the constraint $\mathbb{W}\left(\mathbb{P},\widehat{\mathbb{P}}\right)\le \rho$.

Then, by introducing auxiliary variables $s_{k.i}^M$, the dual problem of (33) can be expressed as (35, 36):

${\lambda }_k^M\rho +\underset{s_{k,i}^M}{\inf }\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_{k,i}^M(35)$

$s.t.\left\{\begin{array}{l}\underset{\xi }{\sup }\left(E\left(\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]\right)-{\lambda }_k^M‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖\right)⩽s_{k,i}^M\\ \underset{\xi }{\sup }\left(0-{\lambda }_k^M‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖\right)⩽s_{k,i}^M\end{array}\right.(36)$

Because $s_{k,i}^M\ge 0$, $-\underset{\xi }{\sup }\left({\lambda }_k^M‖{\widehat{\mathit{\xi }}}_i-\mathit{\xi }‖\right)\le 0\le s_{k,i}^M$ should be established.

Let

$l_k^M\left(\xi \right)=\underset{\mathbb{P}\mathbb{\in }\mathbb{D}}{\sup }E\left(\left[a_k^M\xi -b_k^M-{\tau }_k^M\right]\right)(37)$

Introduce variables ${\mathit{z}}_{k,i}^M,\forall i\in \left\{1,2,...,m\right\}$, where ${‖{\mathit{z}}_{k,i}^M‖}_{\infty }⩽{\lambda }_k^M$, and (35) can be equivalent to (38):

$\begin{array}{l}\underset{\xi \in \mathrm{\Xi }}{\sup }{l}_k^M\left(\mathit{\xi }\right)-\underset{\parallel {\mathit{z}}_{k,i}{\parallel }_{\infty }⩽{\lambda }_k}{\sup }{\left({\mathit{z}}_{k,i}^M\right)}^T\left({\widehat{\mathit{\xi }}}_i-\mathit{\xi }\right)\\ =-{\left({\mathit{z}}_{k,i}^M\right)}^T{\widehat{\mathit{\xi }}}_i-b_k^M-{\tau }_k^M+\underset{{\mathbb{Q}}_i}{\sup }{\int }_{\mathrm{\Xi }}{\left({\mathit{z}}_{k,i}^M+{\left(a_k^M\right)}^T\right)}^T\xi {\mathbb{Q}}_i\left(\mathrm{d}\mathit{\xi }\right)\le s_{k,i}^M\end{array}(38)$

According to the duality theory, we have (39):

${\mathit{z}}_{k,i}^M=-{\left(a_k^M\right)}^T(39)$

The conditional risk value constraints can be depicted as (40):

$\left\{\begin{array}{l}-{\left({\mathit{z}}_{k,i}^M\right)}^T{\widehat{\mathit{\xi }}}_i-b_k^M-{\tau }_k^M=a_k^M{\widehat{\mathit{\xi }}}_i-b_k^M-{\tau }_k^M\le s_{k,i}^M\\ \begin{array}{l}‖{\mathit{z}}_{k,i}^M{\Vert }_{\infty }=‖-a_k^M{\Vert }_{\infty }⩽{\lambda }_k^M\\ {\tau }_k^M+\frac{1}{{\epsilon }_V}\left({\lambda }_k^M\rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_{k,i}^M\right)\le 0\end{array}\end{array}\right.(40)$

In the same way, the node voltage lower limit chance constraint can be expressed as (41):

$\left\{\begin{array}{l}{a}_k^m{\widehat{\mathit{\xi }}}_i-b_k^m-{\tau }_k^m\le s_{k,i}^m\\ \begin{array}{l}{‖-a_k^m‖}_{\infty }⩽{\lambda }_k^m\\ {\tau }_k^m+\frac{1}{{\epsilon }_V}\left({\lambda }_k^m\rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_{k,i}^m\right)\le 0\end{array}\end{array}\right.(41)$

where $a_k^m={\alpha }_k^m\left(Y+I\right)$; ${\alpha }_k^m=\left[{\alpha }_{k,1}^m,{\alpha }_{k,2}^m,...,{\alpha }_{k,n}^m\right]$; $b_k^m=1-{\displaystyle \sum _{j=1}^n}\left({\alpha }_{k,j}^m{\overline{P}}_j+{\beta }_{k,j}^m{Q}_j-{\alpha }_{k,j}^m{P}_j^L\right)$

In summary, the distributionally robust chance-constrained proposed in this paper is as (42, 43):

$\underset{{\overline{P}}_i,r_{+},r_{-},Y,\lambda ,s_i,\gamma }{\min }{\displaystyle \sum _{i=1}^n}\left(c_i{\overline{P}}_i-c_i{P}_i^L+c_i^U{P}_i^U+c_i^D{P}_i^D\right)+\lambda \rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_i(42)$

$s.t.\left\{\begin{array}{l}{c}^{T}Y{\widehat{\xi }}_i\le s_i,{‖-Y^{T}c‖}_{\infty }\le \lambda \\ a_k^M{\widehat{\mathit{\xi }}}_i-b_k^M-{\tau }_k^M\le s_{k,i}^M,{‖-a_k^M‖}_{\infty }⩽{\lambda }_k^M,{\tau }_k^M+\frac{1}{{\epsilon }_V}\left({\lambda }_k^M\rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_{k,i}^M\right)\le 0\\ a_k^m{\widehat{\mathit{\xi }}}_i-b_k^m-{\tau }_k^m\le s_{k,i}^m,{‖-a_k^m‖}_{\infty }⩽{\lambda }_k^m,{\tau }_k^m+\frac{1}{{\epsilon }_V}\left({\lambda }_k^m\rho +\frac{1}{m}{\displaystyle \sum _{i=1}^m}{s}_{k,i}^m\right)\le 0\end{array}\right.(43)$

In summary, it is not difficult to see that the operation model of the distribution grid proposed in this paper is linear and easy to solve. In addition, compared with the traditional method, the model proposed in this paper needs to deal with fewer variables, which can shorten the calculation time.

Let the error rate function as (44):

$\epsilon =\frac{\left|F-F^{MC}\right|}{F^{MC}}(44)$

Where $F^{MC}$ represents the result obtained by the Monte Carlo method, and F represents the result obtained by other methods.

Besides, this paper defines the voltage deviation function as (45):

$\Delta =\max \frac{\left|V_i-V_0\right|}{V_0}\times 100\%,i=1,2,3,\cdots n(45)$

where $\left|•\right|$ is the absolute value of $•$.

5 Simulation results

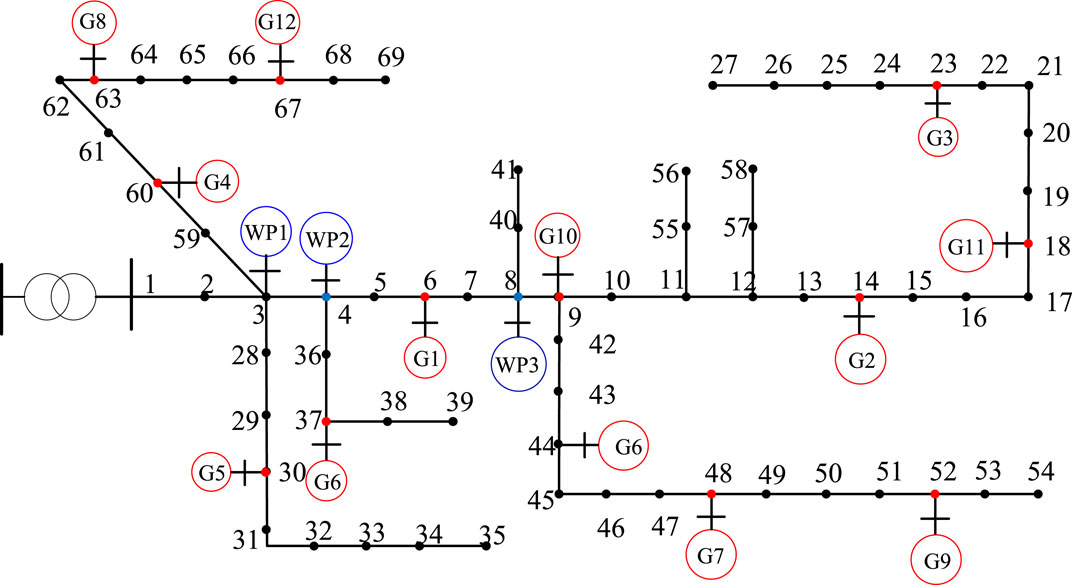
This paper tests the modified PG&E69-bus distribution grids for simulations. The rated output power of the distributed generation device in the example is 150 kW. The power grid in southeastern Australia from 2012 to 2013 was used to construct the Wasserstein ambiguity set and distributed power generation output data. The rated active power of each active power regulating equipment is 333kW, 267kW, 300kW, 300kW, 333kW, 267kW, 300kW, 300kW, 333kW, 267kW, 300kW, 300kW, respectively. The specific grid structure is shown in Figure 1. In addition, the upper and lower limits of the voltage magnitude are 1.03 p.u. and 0.97 p.u. The sample capacity of the Wasserstein ambiguity set is 2000; the Wasserstein radius is $0.5\times {10}^{-3}$.

Figure 1

Figure 1. Improved PG&E69 power distribution system.

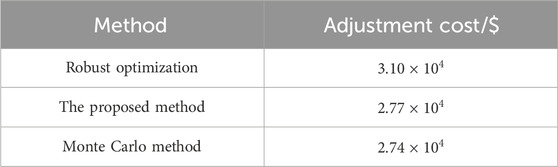
Compared with robust optimization and the Monte Carlo method, the comparison of the optimization results between the method proposed in this paper and the two is shown in Table 1:

Table 1

Table 1. Comparison of optimization results of various methods.

Combined with the optimization results described in Table 1, we can see that the optimization results obtained by the proposed method have an error rate of only 1% compared to the Monte Carlo method, while the error rate of the robust optimization method is 13.1% compared to the Monte Carlo method. Therefore, the method proposed in this paper can fully meet practical engineering requirements in terms of calculation accuracy.

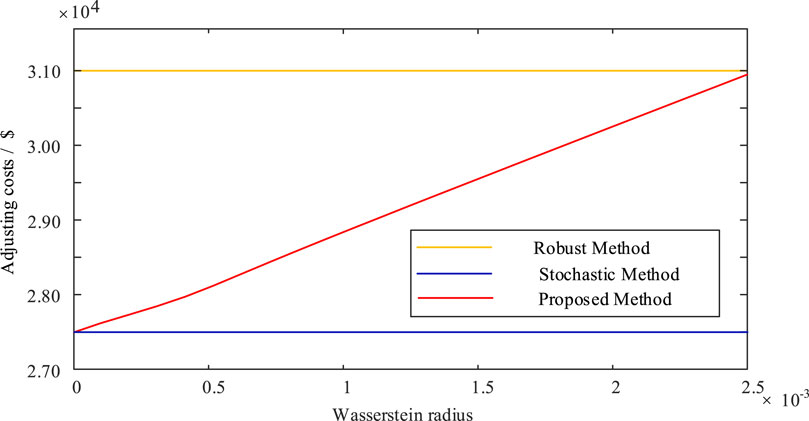
Moreover, compared with the robust and stochastic optimization methods, the adjustment cost of the optimization method proposed in this paper varies with the Wasserstein radius, as shown in Figure 2. It is observable from our analysis that the optimization outcomes yielded by our method gradually diverge from those of risk-neutral stochastic optimization and incline towards robust optimization outcomes as the Wasserstein radius increases. When leaning towards stochastic optimization, it indicates that the decision-maker believes that the probability distribution of uncertain variables in constructing the ambiguity set is accurate enough or there is sufficient historical data to describe the uncertainty of distributed generation, and the decision tends to be economic. Conversely, the shift towards robust optimization indicates the decision-maker’s anticipation of significant future risks, prioritizing decision reliability over economic concerns. In summary, the proposed method can reflect the subjective risk preferences of decision-makers by adjusting the Wasserstein radius parameter, thereby achieving a reasonable choice between scheduling economy and robustness. In other words, this method can realize the flexible choice of optimization decision in economy and robustness, but whether the optimization result tends to be robust or economical is determined by the risk preference of decision makers.

Figure 2

Figure 2. Power generation costs under different Wasserstein radius.

For the optimization case where the sample size is 2000, and the Wasserstein radius is $0.5\times {10}^{-3}$, the impact of different confidence levels on the adjustment cost is shown in Figure 3. We can see that the adjustment cost will also increase as the confidence level increases. This is in line with the general law. When the confidence level is improved, the tolerance of the grid to the voltage limit is reduced, so the output of each active regulation unit will be raised, which will further increase the cost. In general, with the increase of confidence level, it is necessary to sacrifice certain economy to meet the requirements.

Figure 3

Figure 3. Adjustment cost curve with the confidence level.

In addition, when the confidence level is 95%, and the Wasserstein radius is $0.5\times {10}^{-3}$, changes in sample size will also lead to adjustment costs, as shown in Figure 4. We can see that the corresponding optimization cost will decrease as the sample size increases. This is because as the sample size increases, the probability information required by the Wasserstein fuzzy set is more comprehensive. Therefore, the Wasserstein fuzzy set describes the uncertainty of distributed generation output more accurately, reducing the decision-making conservatism. As reflected in the optimization results, the optimization cost will be reduced.

Figure 4

Figure 4. Adjustment cost changes with sample size curve.

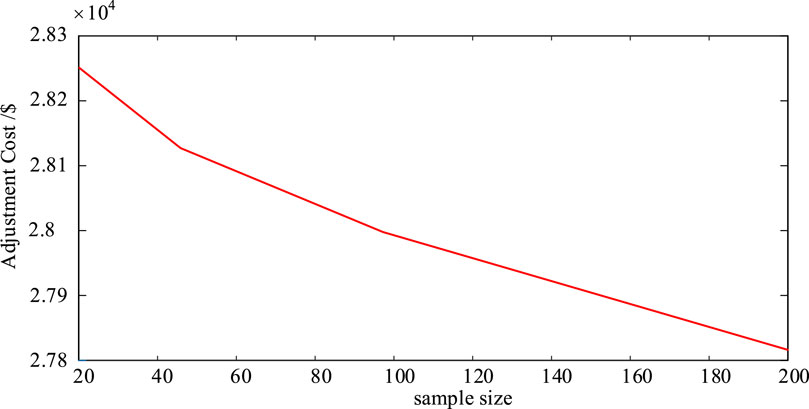
However, it should be noted that the selection of sample size is closely related to the calculation speed. Although the increase in sample size will reduce the optimization cost, the calculation efficiency will also decrease. Therefore, this paper gives the optimization time under different sample methods as shown in Figures 5, 6.

Figure 5

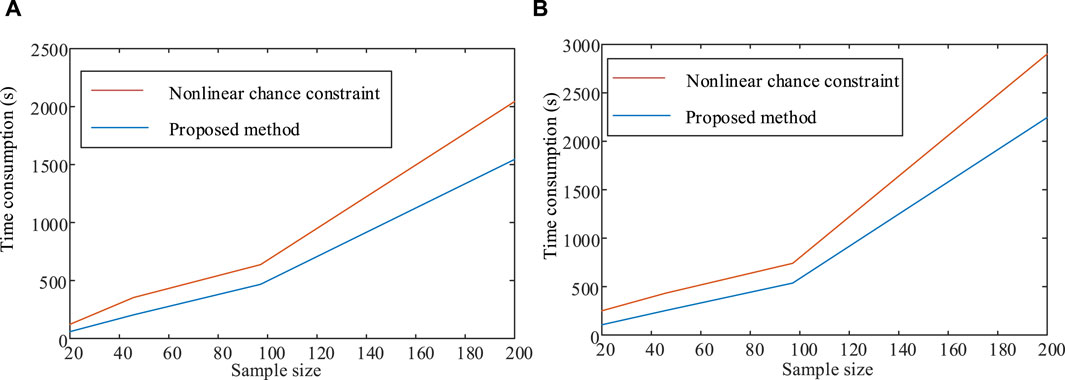
Figure 5. Comparison of computational time with existing nonlinear chance constraint methods in IEEE33 and PG&E69 distribution grids. (A) IEEE33 distribution grids. (B) PG&E69 distribution grids.

Figure 6

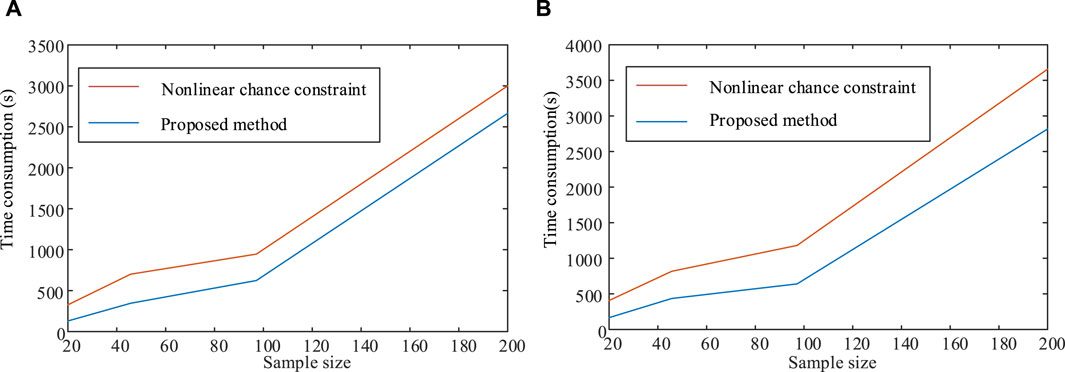
Figure 6. Comparison of computational time with existing nonlinear chance constraint methods in IEEE85 and IEEE 118 distribution grids. (A) IEEE85 distribution grids. (B) IEEE118 distribution grids.

We can see that, compared to the nonlinear chance constraint form, the method proposed in this paper is more time-saving. The calculation time will increase as the number of nodes in the system increases, or the sample size increases. However, the method proposed in this paper takes less time than the existing nonlinear chance-constrained method. Especially when the number of nodes is large and the sample size is enormous, the method proposed in this paper is more time-saving and has more engineering application value.

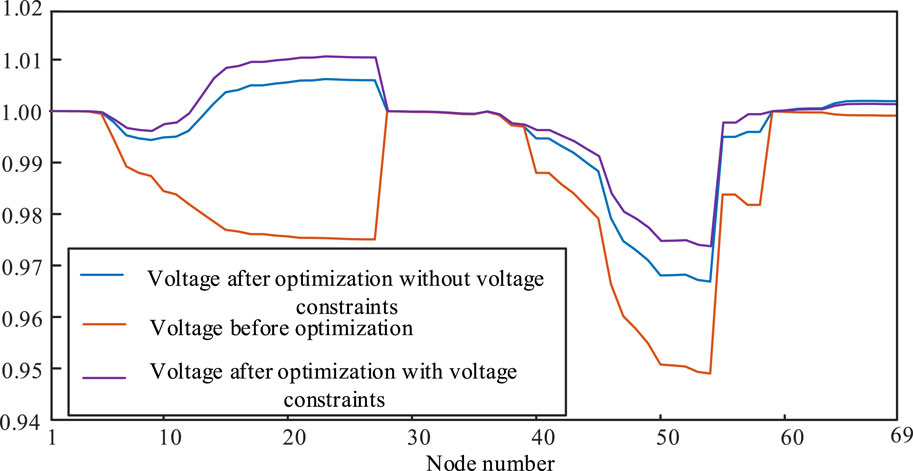
The maximum voltage deviation before and after optimization and its correspondent node are shown in Table 2.

Table 2

Table 2. Voltage deviation comparison.

In addition, the voltage distribution of nodes before and after optimization is shown in Figure 7. Based on Figure 7 and Table 2, it is not difficult to see that the optimized voltage deviation of the proposed method in this paper is significantly smaller than in the other two cases. In addition, there are voltage violation situations before optimization and situations without considering voltage constraints. Still, there is no voltage violation after considering voltage constraints, which is sufficient to demonstrate the effectiveness of the proposed method in ensuring system voltage security.

Figure 7

Figure 7. Comparison of computational time with existing nonlinear chance constraint methods.

6 Conclusion

This paper proposes a distributionally robust chance-constrained optimization dispatch model considering voltage security constraints. First, the comparison between robust optimization and stochastic optimization shows that the method proposed in this paper can reflect the subjective risk preference of distribution grid decision-makers by adjusting the Wasserstein radius parameter, thereby achieving a reasonable choice between dispatch economy and robustness. Second, compared to existing calculation methods, this paper uses the linear power flow method and conditional risk value to convert nonconvex chance constraints into linear constraints, reduce computational complexity, and shorten calculation time, especially for the system with multiple nodes and a high sample size. Finally, as mentioned in the example, the optimized voltage deviation is minor, and no voltage exceeds the limit, indicating the effectiveness of the method proposed in this article in ensuring the security of the distribution grids.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CW: Conceptualization, Investigation, Methodology, Project administration, Writing–review and editing. JS: Conceptualization, Funding acquisition, Resources, Software, Writing–review and editing. XL: Conceptualization, Data curation, Methodology, Writing–review and editing. TY: Conceptualization, Formal Analysis, Visualization, Writing–review and editing. WL: Conceptualization, Supervision, Validation, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the research project of State Grid Liaoning Electric Power Co., Ltd. 2023YF-83).

The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors CW, JS, XL, and WL were employed by Electric Power Research Institute of State Grid Liaoning Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alismail, F., Xiong, P., and Singh, C. (2017). Optimal wind farm allocation in multi-area power systems using distributionally robust optimization approach. IEEE Trans. Power Syst. 33 (1), 536–544. doi:10.1109/TPWRS.2017.2695002

CrossRef Full Text | Google Scholar

Ao, H., Zhang, Y., and Ji, X. (2020). Scenario clustering based distributed robust comprehensive optimization of active distribution grid. Automation Electr. Power Syst. 44 (21), 32–41. doi:10.7500/AEPS20200307001

CrossRef Full Text | Google Scholar

Ben-Tal, A., El Ghaoui, L., and Nemirovski, A. (2009) Robust optimization, 28. Princeton, New Jersey: Princeton university press.

Google Scholar

Cai, H., Dou, F., and Wan, W. (2022). Two-stage voltage optimization of flexible interconnected distribution systems considering source load uncertainty. Power Grid Technol. 46 (04), 1566–1574. doi:10.13335/j.1000-3673.pst.2021.0796

CrossRef Full Text | Google Scholar

Cao, Y., Demin, L., Yihong, Z., Tang, Q., Khodaei, A., Zhang, H., et al. (2021). Optimal energy management for multi-microgrid under a transactive energy framework with distributionally robust optimization. IEEE Trans. Smart Grid 13 (1), 599–612. doi:10.1109/tsg.2021.3113573

CrossRef Full Text | Google Scholar

Chen, C., Guo, S., Dong, Y. D., and Mao, H. (2021). Distributed robust dynamic economic dispatch of integrated transmission and distribution systems. IEEE Trans. Ind. Appl. 57 (5), 4500–4512. doi:10.1109/tia.2021.3091663

CrossRef Full Text | Google Scholar

Chen, Z., Kuhn, D., and Wiesemann, W. (2024). Technical note—data-driven chance constrained programs over Wasserstein balls. Operations Res. 72 (1), 410–424. doi:10.1287/opre.2022.2330

CrossRef Full Text | Google Scholar

Chen, Z., Li, Z., Guo, C., Wang, J., and Ding, Y. (2020). Fully distributed robust reserve scheduling for coupled transmission and distribution systems. IEEE Trans. Power Syst. 36 (1), 169–182. doi:10.1109/tpwrs.2020.3006153

CrossRef Full Text | Google Scholar

Ciftci, O., Mehrtash, M., and Kargarian, A. (2019). Data-driven nonparametric chance-constrained optimization for microgrid energy management. IEEE Trans. Industrial Inf. 16 (4), 2447–2457. doi:10.1109/tii.2019.2932078

CrossRef Full Text | Google Scholar

Dai, Q., Jun, L, Guangyao, H, Bailing, Z., and Jie, L (2017). Calculation of random chance constrained power supply capacity of distribution network considering the randomness of wind power. Hubei Electr. Power 41 (12), 11–17. doi:10.19308/j.hep.2017.12.003

CrossRef Full Text | Google Scholar

Ding, T., Liu, S., Yuan, W., Bie, Z., and Zeng, B. (2015). A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks. IEEE Trans. Sustain. Energy 7 (1), 301–311. doi:10.1109/tste.2015.2494587

CrossRef Full Text | Google Scholar

Du, G., Zhao, D., and Liu, X. (2022). Research review on optimal scheduling considering wind power uncertainty. Proc. CSEE 10, 1–21. doi:10.13334/j.0258-8013.pcsee.212711

CrossRef Full Text | Google Scholar

Duan, C., Fang, W., Jiang, L., Yao, L., and Liu, J. (2018). Distributionally robust chance-constrained approximate AC-OPF with Wasserstein metric. IEEE Trans. Power Syst. 33 (5), 4924–4936. doi:10.1109/tpwrs.2018.2807623

CrossRef Full Text | Google Scholar

Esfahani, P. M., and Kuhn, D. (2018). Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171 (1), 115–166. doi:10.1007/s10107-017-1172-1

CrossRef Full Text | Google Scholar

Guggilam, S. S., Dall’Anese, E., Chen, Y. C., Dhople, S. V., and Giannakis, G. B. (2016). Scalable optimization methods for distribution networks with high PV integration. IEEE Trans. Smart Grid 7 (4), 2061–2070. doi:10.1109/tsg.2016.2543264

CrossRef Full Text | Google Scholar

Han, J., Yang, C., Lim, C. C., Zhou, X., and Shi, P. (2020). Stackelberg–Nash game approach for constrained robust optimization with fuzzy variables. IEEE Trans. Fuzzy Syst. 29 (11), 3519–3531. doi:10.1109/tfuzz.2020.3025697

CrossRef Full Text | Google Scholar

He, C., Zhang, X., Liu, T., and Wu, L. (2019). Distributionally robust scheduling of integrated gas-electricity systems with demand response. IEEE Trans. Power Syst. 34 (5), 3791–3803. doi:10.1109/tpwrs.2019.2907170

CrossRef Full Text | Google Scholar

Hu, R., Wang, W., Wu, X., Chen, Z., Jing, L., Ma, W., et al. (2022). Coordinated active and reactive power control for distribution networks with high penetrations of photovoltaic systems. Sol. Energy 231, 809–827. doi:10.1016/j.solener.2021.12.025

CrossRef Full Text | Google Scholar

Huang, S. (2017). Active/reactive power joint scheduling of distribution network considering reactive power regulation capability of wind turbines. Electr. power Autom. Equip. 37 (02), 44–49. doi:10.16081/j.issn.1006-6047.2017.02.007

CrossRef Full Text | Google Scholar

Li, J., Wen, J., and Cheng, S. (2013). Minimum energy storage power allocation method for power system with large-scale wind power based on p-efficient point theory. Chin. J. Electr. Eng. 33 (13), 45–52. doi:10.1007/s11432-014-5227-0

CrossRef Full Text | Google Scholar

Liu, B., Zhang, Q., Ge, X., and Yuan, Z. (2020). CVaR-based approximations of Wasserstein distributionally robust chance constraints with application to process scheduling. Industrial Eng. Chem. Res. 59 (20), 9562–9574. doi:10.1021/acs.iecr.0c00268

CrossRef Full Text | Google Scholar

Lubin, M., Dvorkin, Y., and Backhaus, S. (2015). A robust approach to chance constrained optimal power flow with renewable generation. IEEE Trans. Power Syst. 31 (5), 3840–3849. doi:10.1109/tpwrs.2015.2499753

CrossRef Full Text | Google Scholar

Ordoudis, C., Nguyen, V. A., Kuhn, D., and Pinson, P. (2021). Energy and reserve dispatch with distributionally robust joint chance constraints. Operations Res. Lett. 49 (3), 291–299. doi:10.1016/j.orl.2021.01.012

CrossRef Full Text | Google Scholar

Poolla, B. K., Hota, A. R., Bolognani, S., Callaway, D. S., and Cherukuri, A. (2020). Wasserstein distributionally robust look-ahead economic dispatch. IEEE Trans. Power Syst. 36 (3), 2010–2022. doi:10.1109/tpwrs.2020.3034488

CrossRef Full Text | Google Scholar

Roald, L., Oldewurtel, F., Krause, T., and Andersson, G. (2013). “Analytical reformulation of security constrained optimal power flow with probabilistic constraints,” in 2013 IEEE grenoble conference (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Rockafellar, R. T., and Uryasev, S. (2000). Optimization of conditional value-at-risk. J. risk 2, 21–41. doi:10.21314/jor.2000.038

CrossRef Full Text | Google Scholar

Tang, Y., Zhang, L., and Zhou, (2023). A fully parallel distributed optimization method for coordinated restoration of transmission and distribution networks considering uncertainty. Grid Technol. 47 (06), 2463–2476. doi:10.13335/j.1000-3673.pst.2022.1870

CrossRef Full Text | Google Scholar

Wang, Q., Guan, Y., and Wang, J. (2012). A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 27 (1), 206–215. doi:10.1109/tpwrs.2011.2159522

CrossRef Full Text | Google Scholar

Xia, P., Deng, C., Chen, Y., and Yao, W. (2019). MILP based robust short-term scheduling for wind-thermal-hydro power system with pumped hydro energy storage. IEEE Access 7, 30261–30275. doi:10.1109/access.2019.2895090

CrossRef Full Text | Google Scholar

Xiao, Y., Bie, C., and Huang, G. (2021). Study on robust optimization of chance constrained distribution based on second order cone optimal power flow. Power Grid Technol. 45 (04), 1505–1518. doi:10.13335/j.1000-3673.pst.2020.1002

CrossRef Full Text | Google Scholar

Xie, W. (2021). On distributionally robust chance constrained programs with Wasserstein distance. Math. Program. 186 (1), 115–155. doi:10.1007/s10107-019-01445-5

CrossRef Full Text | Google Scholar

Xu, , and Li, (2019). Optimized allocation of renewable energy in distribution network considering time series characteristics. Mod. Electr. Power 36 (02), 8–16. doi:10.19725/j.cnki.1007-2322.2019.02.002

CrossRef Full Text | Google Scholar

Yang, T., and Yu, Y. (2018). Steady-state security region-based voltage/var optimization considering power injection uncertainties in distribution grids. IEEE Trans. Smart Grid 10 (3), 2904–2911. doi:10.1109/tsg.2018.2814585

CrossRef Full Text | Google Scholar

Zhai, J., Jiang, Y., Shi, Y., Jones, C. N., and Zhang, X. P. (2022). Distributionally robust joint chance-constrained dispatch for integrated transmission-distribution systems via distributed optimization. IEEE Trans. Smart Grid 13 (3), 2132–2147. doi:10.1109/tsg.2022.3150412

CrossRef Full Text | Google Scholar

Zhai, J., Zhou, M., Li, J., Zhang, X. P., Li, G., Ni, C., et al. (2020). Hierarchical and robust scheduling approach for VSC-MTDC meshed AC/DC grid with high share of wind power. IEEE Trans. Power Syst. 36 (1), 793–805. doi:10.1109/tpwrs.2020.2988297

CrossRef Full Text | Google Scholar

Zhao, C., and Jiang, R. (2017). Distributionally robust contingency-constrained unit commitment. IEEE Trans. Power Syst. 33 (1), 94–102. doi:10.1109/tpwrs.2017.2699121

CrossRef Full Text | Google Scholar

Zhao, C., Wang, Q., Wang, J., and Guan, Y. (2014). Expected value and chance constrained stochastic unit commitment ensuring wind power utilization. IEEE Trans. Power Syst. 29 (6), 2696–2705. doi:10.1109/tpwrs.2014.2319260

CrossRef Full Text | Google Scholar

Zhao, T., Pan, X., Yao, S., Ju, C., and Li, L. (2018). Strategic bidding of hybrid AC/DC microgrid embedded energy hubs: a two-stage chance constrained stochastic programming approach. IEEE Trans. Sustain. Energy 11 (1), 116–125. doi:10.1109/tste.2018.2884997

CrossRef Full Text | Google Scholar

Zhong, C., Liu, X., and Liu, C. (2023). Reactive power optimization strategy for distribution network considering fuzzy chance constraint to deal with uncertainty on both sides of source and load. Electr. Appl. 42 (09), 1–7.

Google Scholar

Zhu, R., Wei, H., and Bai, X. (2019). Wasserstein metric based distributionally robust approximate framework for unit commitment. IEEE Trans. Power Syst. 34 (4), 2991–3001. doi:10.1109/tpwrs.2019.2893296

CrossRef Full Text | Google Scholar