Robust fault detection in electrochemical energy storage systems under label noise: applications to lithium-ion batteries and transformer windings

Reliable fault detection is essential for ensuring the safe and efficient operation of electrochemical energy storage systems, including lithium-ion batteries and transformer. However, the performance of machine learning-based fault diagnosis models is often degraded in practice due to label noise in training data, caused by sensor inaccuracies, ambiguous fault transitions, and imperfect labeling processes. This paper proposes a lightweight and effective kernel-based data rectification framework to improve the robustness of fault detection under noisy label conditions. The method identifies and discards low-density data points that are statistically more likely to be mislabeled, using kernel density estimation and a tunable data discarding strategy. The approach is computationally efficient, classifier-agnostic, and easily applicable to existing fault diagnosis pipelines. We evaluate the proposed method on two datasets: simulated lithium-ion battery voltage data under various fault scenarios, and transformer winding oscillation wave data under multiple winding fault conditions. The results demonstrate that the rectification framework significantly improves classification accuracy across both Support Vector Machine (SVM) and Extreme Learning Machine (ELM) classifiers. Furthermore, the choice of discarding ratio is shown to be critical, with optimal performance achieved when the ratio is tuned close to the underlying noise level. These results highlight the potential of the proposed method to enhance the reliability of fault diagnosis in electrochemical energy storage systems. Future work will explore adaptive strategies to automatically optimize the rectification strength without requiring prior knowledge of the noise rate, and extend the framework to multi-sensor and multi-modal monitoring scenarios.

1 Introduction

Ensuring the safe and reliable operation of electrochemical energy storage systems is of critical importance across a wide range of industrial, transportation, and grid applications. Among these systems, lithium-ion batteries and transformer windings represent two key components with extensive deployments. Lithium-ion batteries are widely used in electric vehicles (Şen et al., 2024), renewable energy storage systems (Wali et al., 2024; Hasan et al., 2025), and portable electronics (Zubi et al., 2018), while power transformers are essential assets for stable and efficient electric power transmission and distribution (??). Faults in lithium-ion batteries, such as short circuits, overcharging, and over-discharging, can cause severe performance degradation, accelerate aging, and in extreme cases, trigger thermal runaway and fire hazards (Wang et al., 2024; Tahir and Tenbohlen, 2023). Likewise, transformer winding faults, including axial displacement, local buckling, inter-disc short circuits, and inter-turn short circuits, can compromise insulation integrity and lead to catastrophic transformer failures (Pei et al., 2023). Therefore, timely and accurate fault detection is a crucial function to ensure the safety, reliability, and longevity of these electrochemical energy storage systems in practical applications.

Recent advances in data-driven fault diagnosis leverage sensor measurements and machine learning techniques to automatically classify the states of electrochemical energy storage systems, including lithium-ion batteries and transformer windings (Kouhestani et al., 2023; Abdolrasol et al., 2024; Wang et al., 2024; Tahir and Tenbohlen, 2023; Pei et al., 2023; Deng et al., 2023; Hong et al., 2021). However, in practical applications, the quality of labeled training data is often compromised. Sensor noise, ambiguous fault transitions, and manual or heuristic labeling processes introduce label noise, where a significant fraction of training labels may be incorrect or inconsistent (Fan et al., 2025). Such label noise severely degrades the performance and reliability of supervised learning models (Goodfellow et al., 2016), posing a major obstacle to deploying robust fault detection frameworks in real-world energy storage systems. In the case of lithium-ion batteries, mislabeling may arise from overlapping voltage patterns during early-stage faults or human annotation errors. Likewise, for transformer windings, data-driven classifiers trained on frequency response analysis (FRA) or vibration signals are also vulnerable to labeling errors, given the subtle and complex nature of winding deformation and short-circuit phenomena. These challenges motivate the development of robust fault detection methods that can tolerate mislabeled data and preserve high diagnostic accuracy.

Although various robust learning techniques have been developed in the machine learning literature to address label noise, many of these approaches suffer from high computational complexity or require prior knowledge of the noise rate (Zhang et al., 2021; Han et al., 2018a; Goldberger and Ben-Reuven, 2017; Yao et al., 2020; Shen et al., 2024), which is typically unknown in practice. Moreover, these methods are often difficult to tune and deploy in resource-constrained hardware for battery or transformer winding fault detection (Wu et al., 2025).

In this paper, we propose a simple and efficient kernel-based data rectification framework for robust battery fault detection under noisy label conditions. Our method leverages kernel density estimation (KDE) to identify and discard data points located in low-density regions of the feature space, where noisy labels are statistically more likely to occur. The approach is computationally lightweight, classifier-agnostic.

We conduct comprehensive experiments on both simulated lithium-ion battery voltage data and transformer winding fault data, covering normal and various fault scenarios, with different synthetic label noise patterns. Our results demonstrate that the proposed rectification method consistently improves classification accuracy across both Support Vector Machine (SVM) and Extreme Learning Machine (ELM) classifiers. Furthermore, we analyze the sensitivity of the method to the rectification strength (controlled by a discarding ratio $\delta$), and provide practical insights on its application to Lithium-Ion Batteries and Transformer Windings. The main contributions of this paper are summarized as follows:

$•$ We propose a lightweight kernel-based data rectification method to enhance the robustness of fault detection under label noise.

$•$ We demonstrate the effectiveness of the method across different classifiers and noise scenarios, without requiring knowledge of the true noise rate.

$•$ We provide practical guidance on tuning the rectification process, and discuss its applicability to real-world fault detection problems in electrochemical energy storage systems.

2 Methods

2.1 Challenging issue of fault diagnosis with noisy labels

Formally, let

${\mathcal{D}}_{\mathsf{norm}}≔{\{({\mathit{x}}_i,y_i)\}}_{i=1}^N(1)$

denote a dataset comprising sensor readings ${\mathit{x}}_i\in \mathcal{X}\subset {\mathbb{R}}^n$ and their corresponding ground-truth labels $y_i\in \mathcal{Y}=\{1,\dots ,c\}\subset \mathbb{N}$, which indicate whether the system is in a normal, minor fault, severe fault, or another state. This dataset ${\mathcal{D}}_{\mathsf{norm}}$ is typically used to train a parameterized classification model $C_{\theta }$¹ by solving the following optimization problem:

$\begin{array}{c}{\min }_{\theta \in \mathrm{\Theta }}{\displaystyle \sum _{i=1}^N}\ell \left(y_i,{\widehat{y}}_i^{\mathsf{est}}\right)\hfill \\ \mathsf{s}.\mathsf{t}.\hspace{0.17em}\hspace{0.17em}{\widehat{y}}_i^{\mathsf{est}}=C_{\theta }({\mathit{x}}_i).\hfill \end{array}(2)$

Here, $\ell (\cdot )$ denotes a loss function, such as the squared error or cross-entropy. Let ${\theta }_{\mathsf{norm}}^{\star }$ be the solution of problem Equation 2. Note that ${\theta }_{\mathsf{norm}}^{\star }$ will vary depending on the dataset used. Therefore, the training process can be viewed as a mapping from a dataset family $\mathcal{F}$ to the optimal parameter ${\theta }_{\mathsf{norm}}^{\star }$, denoted by $\mathcal{T}:\mathcal{F}\to \mathrm{\Theta }$.

However, in practical deployments, the fault labels $y_i$ are often corrupted due to the following reasons:

$•$ Ambiguity in defining fault boundaries (e.g., gradual degradation processes).

$•$ Sensor noise and latency, which can lead to a mismatch between the actual fault occurrence and its recorded label.

$•$ Manual or heuristic-based labeling procedures, which may introduce bias or inconsistencies.

As a result, the dataset may contain noisy labels, i.e., ${\tilde{y}}_i=y_i+\delta y_i\ne y_i$ with non-negligible probability. That is, the available dataset corresponds to a noisy-labeled version, defined as

${\mathcal{D}}_{\mathsf{noisy}}≔{\{({\mathit{x}}_i,{\tilde{y}}_i)\}}_{i=1}^N.(3)$

Using ${\mathcal{D}}_{\mathsf{noisy}}$ for training yields a different model parameter, given by

${\tilde{\theta }}_{\mathsf{noisy}}^{*}=\mathcal{T}({\mathcal{D}}_{\mathsf{noisy}}),(4)$

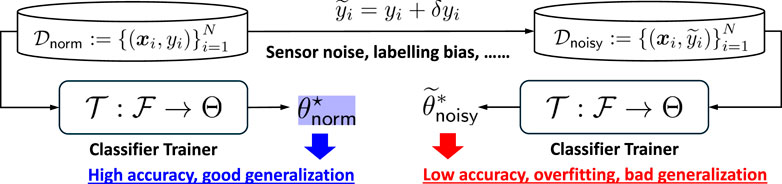
which may result in poor predictive accuracy and weak generalization due to overfitting the noisy labels. Consequently, the resulting classification model is unreliable in safety-critical applications such as system fault detection. The above-described problem and issue are summarized in an intuitive way presented in Figure 1. To address this challenge, it is necessary to propose a robust classification framework that aims to learn accurate decision boundaries despite the presence of label noise.

Figure 1

Figure 1. Intuitive explanation of the challenging issue by the label noises.

2.2 Framework of the proposed robust fault diagnosis

As shown in Figure 2, instead of directly using the noisy-labeled dataset ${\mathcal{D}}_{\mathsf{noisy}}$ for classifier training, this paper introduce a dataset rectification process to filter or clean the data prior to training. This rectification is defined as a mapping $\mathcal{R}:\mathcal{F}\to \mathcal{F}$, which outputs a rectified dataset ${\mathcal{D}}_{\mathsf{rect}}$ consisting of estimated clean data points. Let ${\widehat{N}}_{\mathsf{rect}}$ denote the number of samples in ${\mathcal{D}}_{\mathsf{rect}}$. Importantly, the proposed robust fault diagnosis framework aims not only to optimize the parameter vector $\theta$ but also to design the rectification algorithm $\mathcal{R}$, thereby enhancing the robustness of the diagnostic model. The classification (or regression) problem incorporating the rectification algorithm $\mathcal{R}(\cdot )$ is formulated as follows:

$\begin{array}{c}{\min }_{\theta \in \mathrm{\Theta }}{\displaystyle \sum _{i=1}^{{\widehat{N}}_{\mathsf{rect}}}}\ell \left(y_i,{\widehat{y}}_i^{\mathsf{est}}\right)\hfill \\ \mathsf{s}.\mathsf{t}.{\widehat{y}}_i^{\mathsf{est}}=C_{\theta }({\mathit{x}}_i),\hfill \\ \left({\mathit{x}}_i,y_i\right)\in {\mathcal{D}}_{\mathsf{rect}},\forall i=1,\dots ,{\widehat{N}}_{\mathsf{rect}},\hfill \\ {\mathcal{D}}_{\mathsf{rect}}=\mathcal{R}\left({\mathcal{D}}_{\mathsf{noisy}}\right).\hfill \end{array}(5)$

Figure 2

Figure 2. Framework of the proposed method.

The following subsections provide detailed explanations of the key components of our proposed framework:

$•$ The construction of the rectification algorithm $\mathcal{R}$ using a kernel-based approach, along with a theoretical justification of how this rectification improves the robustness of fault diagnosis;

$•$ A comparative analysis between the proposed kernel-based rectification method and several existing approaches, highlighting the practical advantages of our method for real-world deployment;

$•$ A complete description of the robust fault detection algorithm that integrates the rectification process into the training pipeline.

2.3 Kernel-based rectification

2.3.1 Preliminary assumption

Let $C_{\mathsf{real}}:\mathcal{X}\to \mathcal{Y}$ denote the function that represents the true underlying relationship between a sensor reading $\mathit{x}$ and its corresponding fault-level label $y$ in a system. That is, for every $\mathit{x}\in \mathcal{X}$, $y=C_{\mathsf{real}}(\mathit{x})$ holds. This paper refers to $C_{\mathsf{real}}(\cdot )$ as the real classifier. For $k=1,\dots ,c$, define the input set ${\mathcal{X}}_k$ by

${\mathcal{X}}_k≔\{\mathit{x}\in \mathcal{X}:C_{\mathsf{real}}(\mathit{x})=k\}.(6)$

Note that ${\bigcup }_{k=1}^c{\mathcal{X}}_k=\mathcal{X}$ holds. Following the setup in Shen et al. (2024), this study assumes that noisy labels $\tilde{y}$ are randomly assigned to samples $\mathit{x}$ drawn from an independent and identically distributed (i.i.d.) process, which is a reasonable assumption in practical data collection settings. For any class $k=1,\dots ,c$, let $\tilde{p}(\mathit{x}\mid \tilde{y}=k)$ denote the conditional probability density function of $\mathit{x}$ given the noisy label $\tilde{y}=k$. This study makes the following assumption:

$\tilde{p}(\mathit{x}\mid \tilde{y}(\mathit{x})=k,\mathit{x}\in {\mathcal{X}}_k)>\tilde{p}(\mathit{x}\mid \tilde{y}(\mathit{x})=k,\mathit{x}\notin {\mathcal{X}}_k).(7)$

This assumption states that, within the noisy dataset, the density of inputs $\mathit{x}$ that are correctly labeled is greater than that of inputs incorrectly labeled. Such an assumption is practically reasonable, as label noise in real-world datasets typically arises from measurement inaccuracies or labeling errors, yet correctly labeled data should still form the majority. Moreover, this condition is rather weak, as it merely requires that the correct-label density be marginally greater than the incorrect-label density.

2.3.2 Kernel-based data cleaning

Note that the normal dataset ${\mathcal{D}}_{\mathsf{norm}}$ and the noisy dataset ${\mathcal{D}}_{\mathsf{noisy}}$ share a common component, namely, the set of sensor readings ${\mathcal{X}}_{\mathsf{data}}≔{\left\{{\mathit{x}}_i\right\}}_{i=1}^N$. Furthermore, ${\mathcal{X}}_{\mathsf{data}}$ can be partitioned into $c$ disjoint subsets as follows:

${\tilde{\mathcal{X}}}_{\mathsf{data},k}≔\left\{{\mathit{x}}_i\in {\mathcal{X}}_{\mathsf{data}}\mid {\tilde{y}}_i=k\right\},k=1,\dots ,c.(8)$

Consequently, the dataset ${\mathcal{D}}_{\mathsf{noisy}}$ can also be partitioned into $c$ disjoint subsets as follows:

${\mathcal{D}}_{\mathsf{noisy},k}≔\left\{({\mathit{x}}_i,{\tilde{y}}_i)\in {\mathcal{D}}_{\mathsf{noisy}}\mid {\tilde{y}}_i=k\right\},k=1,\dots ,c.(9)$

Specifically, ${\mathit{x}}_{i,k},i=1,\dots ,{\tilde{N}}_k$ is used to represent a point in ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$ with ${\tilde{N}}_k$ as the data point number of ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$. Each set ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$, for $k=1,\dots ,c$, is assumed to be independently and identically drawn from a probability distribution with an unknown density function ${\tilde{f}}_k(\mathit{x})$. Kernel density estimation (KDE) is employed to estimate this density ${\tilde{f}}_k(\mathit{x})$ based on the dataset ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$. Let ${\widehat{f}}_{\mathsf{kde},k}(\mathit{x})$ denote the kernel density estimator computed from ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$, defined by

${\widehat{f}}_{\mathsf{kde},k}(\mathit{x})=\frac{1}{{\tilde{N}}_{k}h}{\displaystyle \sum _{i=1}^{{\tilde{N}}_k}}\mathsf{K}\mathsf{e}\mathsf{r}\left(\frac{\mathit{x}-{\mathit{x}}_{i,k}}{h}\right),\forall i=1,\dots ,{\tilde{N}}_k,{\mathit{x}}_{i,k}\in {\tilde{\mathcal{X}}}_{\mathsf{data},k}(10)$

where $\mathsf{K}\mathsf{e}\mathsf{r}(\cdot )$ is a kernel function and $h$ is a smoothing parameter known as the bandwidth.

The bandwidth parameter $h$ in the kernel density estimator was selected using Silverman’s rule of thumb, which is a widely adopted, data-driven method for kernel bandwidth selection. Specifically, we used

$h=1.06{\widehat{\sigma }}_k{\tilde{N}}_k^{-1/5},(11)$

where ${\widehat{\sigma }}_k$ is the standard deviation of the observed feature samples. Various kernel functions are commonly used, including uniform, triangular, biweight, triweight, Epanechnikov (parabolic), normal, and others. Owing to its desirable mathematical properties, the normal kernel is frequently adopted, with the kernel function given by the standard normal density:

$\mathsf{K}\mathsf{e}\mathsf{r}\left(\frac{\mathit{x}-{\mathit{x}}_{i,k}}{h}\right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{(\mathit{x}-{\mathit{x}}_{i,k})}^2}{2h^2{\sigma }^2}\right),(12)$

where $\sigma >0$ denotes the standard deviation. In kernel-based data cleaning, the kernel density estimate ${\widehat{f}}_{\mathsf{kde},k}(\cdot )$ is used to determine whether each data point should be retained or discarded from the training set. Let ${\bar{p}}_{\mathsf{th},k}$ denote a density threshold for ${\widehat{f}}_{\mathsf{kde},k}(\cdot )$. Then, the rectified dataset ${\mathcal{D}}_{\mathsf{rect},k}$ is defined as follows:

${\mathcal{D}}_{\mathsf{rect},k}≔\left\{({\mathit{x}}_i,{\tilde{y}}_i)\in {\mathcal{D}}_{\mathsf{noisy}}\mid {\tilde{y}}_i=k,{\widehat{f}}_{\mathsf{kde},k}({\mathit{x}}_i)>{\bar{p}}_{\mathsf{th},k}\right\}.(13)$

For any given density threshold ${\bar{p}}_{\mathsf{th},k}$, the corresponding empirical outlier ratio is defined as

$r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k})≔N_{\mathsf{out}}(f_{\mathsf{ths}})/{\tilde{N}}_k,(14)$

where ${\tilde{N}}_{\mathsf{out},k}({\bar{p}}_{\mathsf{th},k})$ is the number of samples in ${\tilde{\mathcal{X}}}_{\mathsf{data},k}$ whose estimated density is below ${\bar{p}}_{\mathsf{th},k}$. Note that ${\mathcal{D}}_{\mathsf{rect},k}$ satisfies the property ${\mathcal{D}}_{\mathsf{rect},k_1}\cap {\mathcal{D}}_{\mathsf{rect},k_2}=\varnothing$ if $k_1\ne k_2$, since the dataset is partitioned according to ${\tilde{y}}_i=k$. The complete rectified dataset is then defined by

${\mathcal{D}}_{\mathsf{rect}}=\bigcup _{k=1}^c{\mathcal{D}}_{\mathsf{rect},k}.(15)$

This paper adopts the following binary search procedure to determine the density threshold ${\bar{p}}_{\mathsf{th},k}$:

$•$ Set a discarding ratio $\delta \in (\mathrm{0,1})$. Specifically, a proportion of $\delta$ in each ${\mathcal{D}}_{\mathsf{noisy},k}$, for $k=1,\dots ,c$, should be discarded.

$•$ Initialize ${\bar{p}}_{\mathsf{th},k}^{\mathsf{min}}$ and ${\bar{p}}_{\mathsf{th},k}^{\mathsf{max}}$ such that

$r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k}^{\mathsf{min}})<\delta <r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k}^{\mathsf{max}})(16)$

$•$ Iteratively update the midpoint

${\bar{p}}_{\mathsf{th},k}^{\mathsf{mid}}≔({\bar{p}}_{\mathsf{th},k}^{\mathsf{min}}+{\bar{p}}_{\mathsf{th},k}^{\mathsf{max}})/2(17)$

and evaluate $r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k}^{\mathsf{mid}})$;

$•$ If $r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k}^{\mathsf{mid}})>\delta$, update ${\bar{p}}_{\mathsf{th},k}^{\mathsf{max}}≔{\bar{p}}_{\mathsf{th},k}^{\mathsf{mid}}$; otherwise, set ${\bar{p}}_{\mathsf{th},k}^{\mathsf{min}}≔{\bar{p}}_{\mathsf{th},k}^{\mathsf{mid}}$.

After a fixed number of iterations, the binary search converges to a threshold ${\bar{p}}_{\mathsf{th},k}^{\delta }$ such that $r_{\mathsf{out}}({\bar{p}}_{\mathsf{th},k}^{\delta })\approx \delta$. It is worth noting that the above algorithm achieves effective data cleaning performance comparable to the method presented in Shen et al. (2024), while offering significantly greater computational efficiency. The key mechanism by which the proposed method enhances robustness against label noise lies in its use of kernel density estimation to identify and retain data points located in regions of high data density. Intuitively, in high-density regions of the feature space, the probability of encountering incorrectly labeled samples is relatively low, as these regions are well-supported by the true data distribution corresponding to each class. Conversely, mislabeled or noisy samples are more likely to appear in low-density regions, where the overlap between classes or inconsistencies in the labeling process are more prevalent. By explicitly discarding samples whose estimated density falls below a carefully selected threshold, the proposed method effectively filters out a significant proportion of potential label noise, while preserving the core structure of each class in the training data. This selective data retention substantially reduces the risk of overfitting to noisy labels and improves the generalization ability of the resulting classifier—an important property for safety-critical applications such as fault detection.

2.4 Robust fault detection algorithm

We summarize the method in the way of giving the algorithm in this subsection. To mitigate the adverse impact of label noise and enhance the reliability of fault diagnosis, we propose a robust classification framework that incorporates a data rectification step prior to model training. The core idea is to leverage kernel density estimation (KDE) (Botev et al., 2010) to identify and discard samples likely to be mislabeled, based on the observation that true labeled data tends to concentrate in high-density regions of the feature space. The procedure of Robust Fault Detection Algorithm is summarized in Algorithm 1.

Algorithm 1

Algorithm 1. Robust Fault Detection Algorithm.

3 Results

3.1 Validation scenario and data acquisition

3.1.1 Dataset for LIB battery

Voltage data for both healthy and faulty conditions were collected from simulation models developed in the MATLAB/Simulink environment. The simulation utilizes the LIB battery pack system designed for two-wheel electric vehicles, operating under both normal and fault-induced driving conditions. Data were acquired from voltage sensors installed within the battery pack, capturing system behavior under various scenarios. Faulty conditions were simulated by introducing short-circuit, overcharge, and over-discharge faults using the thermal resistive fault block. These faults were triggered at 0.2 s under different resistive load settings. The collected dataset includes multiple parameters such as state of charge (SOC), temperature, voltage, and current. In this study, only voltage data from both normal and faulty conditions were used, with the objective of contributing to the prevention of fire hazards in lithium-ion battery systems.

3.1.2 Fault detections in transformer windings

In addition to the lithium-ion battery dataset, a second dataset was considered for evaluating fault detection in transformer windings. This dataset was acquired via Oscillating Wave Testing (OWT), a non-invasive diagnostic technique that captures high-voltage oscillation signals to characterize winding deformations (Wu et al., 2020). This dataset originates from a 10 kV transformer winding fault simulation platform, where four types of winding faults—axial displacement, local buckling, inter-disc short circuit, and inter-turn short circuit were systematically considered. Each fault scenario was labeled based on the known fault type and its severity, as defined during the experimental setup, and repeated under controlled conditions to ensure labeling consistency. The resulting classification dataset includes labeled oscillation wave measurements for these four fault types as well as healthy conditions, enabling evaluation of the proposed robust classification framework in more applications in energy storage systems.

3.1.3 Methods for label noise

To evaluate the robustness of the proposed method under realistic noise conditions, we consider the following label noise generation strategies:

$•$ (Symm.) Symmetric noise: Label noise is generated according to the symmetric noise model described in Patrini et al. (2017), where each label is flipped uniformly at random to any other class with a specified noise rate.

$•$ (Pair.) Pair flipping noise: Label noise is generated according to the pair flipping model described in Han et al. (2018b), where labels are flipped to a single specific incorrect class (typically the next class) with a given noise probability.

$•$ (Rand.) Random noise: Label noise is generated by sampling from a Dirichlet distribution and combining the resulting label confusion matrix with the identity matrix to achieve a target noise rate. This allows for flexible and realistic noise patterns.

The above three types comprehensively represent a range of practically relevant label noise patterns in electrochemical energy storage systems’ fault diagnosis. In this study, we consider noise rates of $15\%$ and $45\%$ to examine the performance of the proposed method under both moderate and severe label noise scenarios.

3.2 Benchmark algorithms

To evaluate the effectiveness of the proposed robust battery fault detection algorithm, we compare its performance with several baseline and benchmark methods. In particular, we systematically examine how different levels of kernel-based data cleaning affect the performance of two representative classifiers: Support Vector Machine (SVM) and Extreme Learning Machine (ELM).

The following benchmark algorithms are considered:

$•$ ELM-D: Extreme Learning Machine (ELM) classifier trained directly on the noisy dataset ${\mathcal{D}}_{\mathsf{noisy}}$ without data cleaning.

$•$ ELM-C-10%, ELM-C-20%, ELM-C-30%, ELM-C-40%, ELM-C-50%, ELM-C-60%: ELM classifiers trained on the rectified datasets in which 10%, 20%, 30%, 40%, 50%, and 60% of low-density data points are discarded using the proposed kernel-based rectification method.

$•$ SVM-D: Support Vector Machine (SVM) classifier trained directly on the noisy dataset ${\mathcal{D}}_{\mathsf{noisy}}$ without data cleaning.

$•$ SVM-C-10%, SVM-C-20%, SVM-C-30%, SVM-C-40%, SVM-C-50%, SVM-C-60%: SVM classifiers trained on the rectified datasets in which 10%, 20%, 30%, 40%, 50% and 60% of low-density data points are discarded using the proposed kernel-based rectification method.

This experimental design enables a comprehensive analysis of the robustness and accuracy gains provided by the proposed data rectification framework across different classification models and varying levels of data cleaning. By comparing the Direct and Clean variants of both ELM and SVM, we can clearly assess the practical benefits of incorporating the rectification step into the battery fault diagnosis pipeline.

3.3 Performance metric

This section provides an overview of the performance metric used to evaluate the effectiveness of the proposed model. The selected evaluation metric is the classification accuracy, defined as:

$\alpha ≔\left({\displaystyle \sum _{k=1}^c}{N}_{\mathsf{acc},k}\right)/\left({\displaystyle \sum _{k=1}^c}{N}_{\mathsf{all},k}\right),(18)$

where $N_{\mathsf{acc},k}$ denotes the number of correctly classified test samples in class $k$, and $N_{\mathsf{all},k}$ denotes the total number of test samples in class $k$.

3.4 Validation results of LIB battery fault detection

Figures 3, 4 present the classification accuracy results of ELM and SVM models trained either directly on the noisy dataset or on the rectified dataset obtained using different discarding ratios $\delta$. As shown in Figures 3, 4, both ELM and SVM classifiers exhibit significantly degraded accuracy when trained directly on the noisy dataset, highlighting the detrimental impact of label noise on model performance. In contrast, the proposed kernel-based rectification method substantially improves classification accuracy across both models and under various noise scenarios, demonstrating its effectiveness in mitigating the influence of noisy labels. An important observation is that the choice of discarding ratio $\delta$ plays a critical role in achieving optimal performance. In particular, when $\delta$ is set close to the true underlying noise rate (e.g., $15\%$ or $45\%$ in our experiments), the rectification process is able to remove a majority of mislabeled samples while preserving the informative structure of the clean data, thereby leading to superior classification results. It is important to note that in practical applications, the true noise rate is typically unknown. Therefore, developing adaptive strategies to optimize $\delta$ without requiring prior knowledge of the noise level represents an important direction for future research on robust battery fault detection.

Figure 3

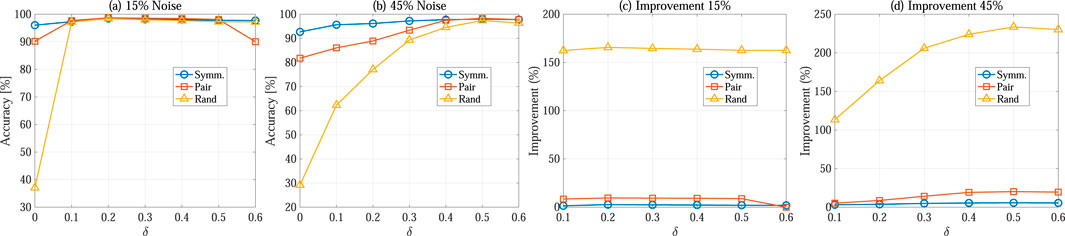
Figure 3. Classification accuracy of ELM. Mean value of 1,000 trials is reported. (A) Accuracy at $15\%$ noise rate; (B) Accuracy at $45\%$ noise rate; (C) Accuracy improvement after data cleaning at $15\%$ noise rate; (D) Accuracy improvement after data cleaning at $45\%$ noise rate.

Figure 4

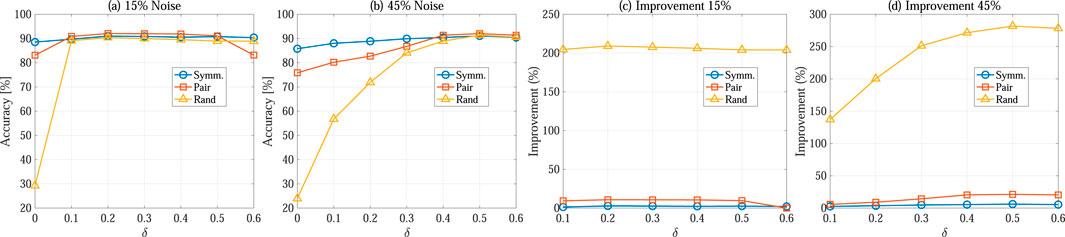
Figure 4. Classification accuracy of SVM. Mean value of 1,000 trials is reported. (A) Accuracy at $15\%$ noise rate; (B) Accuracy at $45\%$ noise rate; (C) Accuracy improvement after data cleaning at $15\%$ noise rate; (D) Accuracy improvement after data cleaning at $45\%$ noise rate.

3.5 Validation results of transformer winding fault detection

In addition to the battery fault detection experiments, the proposed kernel-based rectification method was validated on transformer winding fault detection tasks, with four representative fault types: axial displacement (AD), local buckling (LB), inter-disc short circuit (IDSC), and inter-turn short circuit (ITSC). Figure 5 provides visual evidence of the discriminative oscillating wave signatures used in our fault diagnosis framework. The high-voltage oscillating wave test (OWT) captures these transient responses by applying a damped AC voltage pulse to the transformer winding and recording the resulting oscillation decay profile. These physically interpretable patterns form the basis of the feature vectors processed by our kernel-based rectification framework. The signal preprocessing pipeline, including noise suppression via wavelet thresholding and feature extraction through resonance frequency analysis, follows the methodology established in Wu et al. (2025). Consistent with the battery case study, setting the discarding ratio $\delta$ slightly larger than the true label noise rate led to robust performance improvements, which is practically feasible because conservative estimates of labeling quality are usually available. Here, a severe label noise scenario with a 45% noise rate was evaluated to rigorously test the method. As shown in Figure 6, both ELM and SVM classifiers without rectification (ELM-D, SVM-D) suffered major accuracy drops across all fault types under this high noise condition. In contrast, applying the kernel-based rectification with $\delta =50\%$ (ELM-C-50%, SVM-C-50%) recovered high classification accuracy, exceeding 80% in all cases. These results confirm that the rectification approach effectively filters out noisy samples while preserving the core structure of each class, maintaining reliable classification performance consistent with the battery case study. This demonstrates the framework’s applicability across electrochemical energy storage systems in severe label noise scenarios.

Figure 5

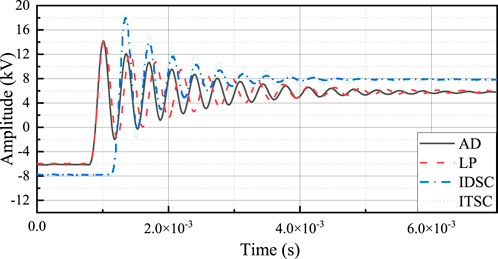
Figure 5. Representative oscillating wave signals under four fault conditions (axial displacement, local buckling, inter-disc short circuit, inter-turn short circuit).

Figure 6

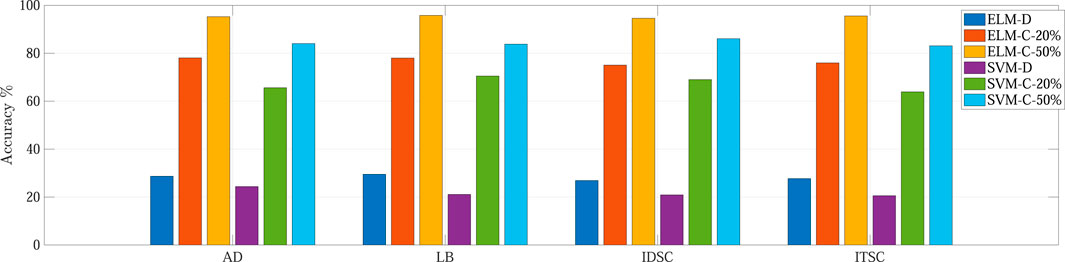
Figure 6. Classification accuracy for transformer winding fault detection. Mean value of 1,000 trials is reported.

3.6 Computational considerations

In terms of computational cost, the proposed kernel-based rectification framework was implemented in MATLAB on a standard laptop (Intel Core i7 processor), where the average runtime of the KDE-based data cleaning step was measured at approximately 15 ms per dataset partition containing 1,000 samples. Although we have not yet ported the algorithm to an embedded hardware platform, this processing time is well within the capabilities of modern embedded processors, especially considering that fault diagnosis generally operates on time scales of seconds to minutes. This supports our description of the method as computationally lightweight, while acknowledging that future work will further validate its runtime characteristics in actual embedded environments.

4 Discussion

This study presents a robust fault detection framework for electrochemical energy storage systems, integrating a kernel-based data rectification process into the standard classifier training pipeline. The motivation stems from the observation that real-world fault diagnosis systems often face label noise due to measurement errors, labeling inconsistencies, and the gradual nature of certain fault phenomena. Our method systematically addresses this challenge by discarding data points located in low-density regions of the feature space, where mislabeled samples are more likely to occur. Through comprehensive experiments on simulated lithium-ion battery voltage data as well as transformer winding fault data with synthetic label noise, we demonstrate that both ELM and SVM classifiers trained directly on noisy data suffer from substantial accuracy degradation. In contrast, applying the proposed kernel-based rectification step prior to training significantly improves classification performance across various noise scenarios and classifier types. Our results further indicate that tuning the discarding ratio $\delta$ to be close to the true underlying noise rate yields the best performance, as it effectively balances noise removal with the preservation of useful information. From an application perspective, this finding is particularly relevant for electrochemical energy storage systems, where ensuring reliable and robust fault diagnosis is critical for operational safety. By improving the generalization capability of classifiers in the presence of label noise, the proposed framework can enhance the reliability of real-time fault monitoring and help mitigate risks such as catastrophic failures or safety hazards. One limitation of the current approach is that selecting an optimal $\delta$ requires knowledge of the noise rate, which is typically unknown in practical settings. Developing adaptive mechanisms to automatically estimate or tune $\delta$ during training is an important direction for future work. Moreover, extending the framework to incorporate additional sensor modalities (e.g., temperature, current, vibration signals) and to support online learning scenarios will further broaden its applicability across advanced energy storage systems. Overall, the proposed method provides a computationally efficient, easy-to-integrate, and practically effective solution for enhancing fault diagnosis in noisy real-world environments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TH: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Writing – original draft, Writing – review and editing. WL: Formal Analysis, Methodology, Validation, Visualization, Writing – original draft, Writing – review and editing. XW: Formal Analysis, Validation, Writing – original draft, Writing – review and editing. YW: Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the State Grid Company Ltd. Science and Technology Program under Grant SGAHMA00YJJS2400635.

Conflict of interest

Authors TH, XW, and YW were employed by State Grid Anhui Electric Power Co., Ltd., Ma’anshan Power Supply Company.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Company Ltd.. The funder had the following involvement in the study: data collection and analysis.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹$C_{\theta }$ may represent a support vector machine, polynomial function, deep neural network, or another model class.

References

Abdolrasol, M. G. M., Ayob, A., Lipu, M. S. H., Ansari, S., Kiong, T. S., Saad, M. H. M., et al. (2024). Advanced data-driven fault diagnosis in lithium-ion battery management systems for electric vehicles: progress, challenges, and future perspectives. eTransportation 22, 100374. doi:10.1016/j.etran.2024.100374

CrossRef Full Text | Google Scholar

Botev, Z. I., Grotowski, J. F., and Kroese, D. P. (2010). Kernel density estimation via diffusion. Ann. Statistics 38, 2916–2957. doi:10.1214/10-AOS799

CrossRef Full Text | Google Scholar

Deng, X., Zhang, Z., Zhu, H., and Yan, K. (2023). Early fault diagnosis of transformer winding based on leakage magnetic field and dsan learning method. Front. Energy Res. 10, 1058378. doi:10.3389/fenrg.2022.1058378

CrossRef Full Text | Google Scholar

Fan, Y., Huang, Z., Li, H., Yuan, W., Yan, L., Liu, Y., et al. (2025). Fault detection for li-ion batteries of electric vehicles with feature-augmented attentional autoencoder. Sci. Rep. 15, 18534. doi:10.1038/s41598-025-03227-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldberger, J., and Ben-Reuven, E. (2017). “Training deep neural networks using a noise adaption layer,” in Proceedings International Conference on Learning Representations.

Google Scholar

Goodfellow, I., Bengio, Y., Courville, A., and Bengio, Y. (2016). Deep learning. Cambridge, Massachusetts: MIT press Cambridge.

Google Scholar

Han, B., Yao, J., Niu, G., Zhou, M., Tsang, I., Zhang, Y., et al. (2018a). “Masking: a new perspective of noisy supervision,” in Advances in neural information processing systems, 5835–5846.

Google Scholar

Han, B., Yao, Q., Yu, X., Niu, G., Xu, M., Hu, W., et al. (2018b). “Co-teaching: robust training of deep neural networks with extremely noisy labels,” in Advances in neural information processing systems, 8527–8537.

Google Scholar

Hasan, M. M., Haque, R., Jahirul, M. I., Rasul, M. G., Fattah, I. M. R., Hassan, N. M. S., et al. (2025). Advancing energy storage: the future trajectory of lithium-ion battery technologies. J. Energy Storage 120, 116511. doi:10.1016/j.est.2025.116511

CrossRef Full Text | Google Scholar

Hong, K., Jin, M., and Huang, H. (2021). Transformer winding fault diagnosis using vibration image and deep learning. IEEE Trans. Power Deliv. 36, 676–685. doi:10.1109/TPWRD.2020.2988820

CrossRef Full Text | Google Scholar

Kouhestani, H. S., Liu, L., Wang, R., and Chandra, A. (2023). Data-driven prognosis of failure detection and prediction of lithium-ion batteries. J. Energy Storage 70, 108045. doi:10.1016/j.est.2023.108045

CrossRef Full Text | Google Scholar

Patrini, G., Rozza, A., Menon, A. K., Nock, R., and Qu, L. (2017). “Making deep neural networks robust to label noise: a loss correction approach,” in Proceedings IEEE Conference on Computer Vision and Pattern Recognition, 1944–1952.

Google Scholar

Pei, X., Han, S., Bao, Y., Chen, W., and Li, H. (2023). Fault diagnosis of transformer winding short circuit based on wkpca-wm and ipoa-cnn. Front. Energy Res. 11, 1151612. doi:10.3389/fenrg.2023.1151612

CrossRef Full Text | Google Scholar

Şen, M., Özcan, M., and Eker, Y. R. (2024). A review on the lithium-ion battery problems used in electric vehicles. Next Sustain. 3, 100036. doi:10.1016/j.nxsust.2024.100036

CrossRef Full Text | Google Scholar

Shen, X., Luo, Z., Li, Y., Ouyang, T., and Wu, Y. (2024). Chance-constrained abnormal data cleaning for robust classification with noisy labels. IEEE Trans. Emerg. Top. Comput. Intell., 1–8. doi:10.1109/tetci.2024.3375518

CrossRef Full Text | Google Scholar

Tahir, M., and Tenbohlen, S. (2023). Transformer winding fault classification and condition assessment based on random forest using fra. Energies 16, 3714. doi:10.3390/en16093714

CrossRef Full Text | Google Scholar

Wali, S. B., Hannan, M. A., Ker, P. J., Rahman, S. A., Le, K. N., Begum, R. A., et al. (2024). Grid-connected lithium-ion battery energy storage system towards sustainable energy: a patent landscape analysis and technology updates. J. Energy Storage 77, 109986. doi:10.1016/j.est.2023.109986

CrossRef Full Text | Google Scholar

Wang, G., Qiu, S., Xie, F., Luo, T., Song, Y., and Wang, S. (2024). Diagnosing fault types and degrees of transformer winding combining fra method with soa-kelm. IEEE Access 12, 50287–50299. doi:10.1109/access.2024.3385229

CrossRef Full Text | Google Scholar

Wu, Z., Zhou, L., Lin, T., Zhou, X., Wang, D., Gao, S., et al. (2020). A new testing method for the diagnosis of winding faults in transformer. IEEE Trans. Instrum. Meas. 69, 9203–9214. doi:10.1109/tim.2020.2998877

CrossRef Full Text | Google Scholar

Wu, Z., Tao, J., Liu, Y., He, T., and Lu, S. (2025). Detection of structure deformation and insulation condition for transformer windings based on high-voltage oscillating wave. IEEE Trans. Instrum. Meas. 74, 1–12. doi:10.1109/tim.2025.3545720

CrossRef Full Text | Google Scholar

Yao, Y., Liu, T., Han, B., Gong, M., Deng, J., Niu, G., et al. (2020). Dual t: reducing estimation error for transition matrix in label-noise learning. in Advances in neural information processing systems.

Google Scholar

Zhang, Y., Niu, G., and Sugiyama, M. (2021). “Learning noise transition matrix from only noisy labels via total variation regularization,” in Proceedings International Conference on Machine Learning.

Google Scholar

Zubi, G., Dufo-López, R., Carvalho, M., and Pasaoglu, G. (2018). The lithium-ion battery: state of the art and future perspectives. Renew. Sustain. Energy Rev. 89, 292–308. doi:10.1016/j.rser.2018.03.002

CrossRef Full Text | Google Scholar