Abstract
Introduction:
This study aims to optimize the location and capacity determination of distributed power flow controllers, in order to enhance the safety and stability of power grid operation and reduce operational costs.
Methods:
Firstly, the concept of weighted power flow entropy is introduced to calculate the weighted power flow entropy values at different installation locations in the power grid. Based on the principle of minimizing this index, the optimal installation location of the distributed power flow controller is determined. Secondly, when considering the economic efficiency of power grid operation, the benefits brought by the improvement of transmission capacity after installing DPFC are quantitatively evaluated along with the cost required for equipment laying. On this basis, a genetic algorithm is used for capacity optimization, where the capacity of the distributed state flow processor chain verification unit is taken as the optimization step size, and the maximization of power grid operation economy is taken as the objective, to search for the optimal configuration capacity of DPFC.
Results:
The proposed location and capacity determination method was validated in the IEEE 30-bus standard test system. Simulation results indicate that the location method based on minimum weighted power flow entropy can effectively identify key vulnerable links in the power grid. Meanwhile, the capacity optimization using genetic algorithms combined with economic analysis can significantly improve the overall economic efficiency of power grid operation while ensuring safety and stability, confirming the effectiveness of the proposed method.
Conclusion:
The method for selecting and sizing distributed power flow controllers proposed in this study, based on weighted power flow entropy and genetic algorithms, can coordinate the safety and economic goals of the power grid, effectively enhance the stability level of power grid operation, and reduce operational costs.
1 Introduction
With the deepening of the global energy transition strategy and the proposal of the “dual carbon” goal, the penetration rate of renewable energy represented by photovoltaics in the power system continues to rise. Among them, Distributed Photovoltaic (DPV) has been widely applied in the distribution network due to its advantages of flexible construction and nearby consumption (Ni et al., 2025). However, the large number, randomness, and intermittent access of DPVs pose unprecedented challenges to the stable and efficient operation of traditional distribution networks. In this context, there is an urgent need to introduce new and flexible trend control technologies. The power flow controller, as an important control device in power systems, has received widespread attention from researchers both domestically and internationally (Gupta et al., 2025; Zhang et al., 2024). In recent years, with the rapid development of smart grids and renewable energy, significant progress has been made in the research and application of power flow controllers. Current research mainly focuses on traditional FACTS devices such as the Unified Power Flow Controller (UPFC) and Static Synchronous Compensator (STATCOM). These control devices play an important role in improving the performance and efficiency of power grids. Literature (Ansho and Nisha, 2023) proposes an optimized distributed power flow controller for enhancing the power quality of grid-connected hybrid systems. Literature (Zhou et al., 2019) presents an optimal UPFC optimization method based on the optimal load shedding model, aiming to improve UPFC performance to enhance the reliability of power generation and transmission systems. Literature (He et al., 2020) proposes a UPFC reactive power optimization strategy based on an optimal UPFC reactive power optimization model, with the goal of reducing active network losses in the power grid. Literature (Altun et al., 2024; Chethan and Kuppan, 2024; Sebi, 2023; Reddy et al., 2025; Jivandas and Pandya, 2022) conducts in-depth studies on the characteristics of multiple FACTS devices, including UPFC, thyristor-controlled series compensators, and STATCOM. The research aims to minimize the investment cost of the power grid and maximize the available transmission capacity. To achieve this, a multi-objective optimization model for these FACTS components has been established, considering multiple factors such as investment cost and transmission capacity to seek the optimal configuration. Literature (Hareesh et al., 2020; Anil et al., 2024) studied the installation location and size of a unified power flow controller for power systems based on hybrid algorithms, and the proposed method can be easily applied to optimize power system objectives. Literature (Canbing et al., 2014) applies economic analysis to the UPFC configuration strategy, aiming to solve transmission congestion issues in the power market environment. Economic analysis allows for a more rational allocation of UPFC resources, improving the economic efficiency of the power grid. Literature (Özdoğan and Bahçeci, 2025) focuses on the power quality issues after the integration of new energy. To verify the effectiveness of intelligent control methods in improving power quality, this study constructs a DSTATCOM control model based on artificial neural networks (ANN) and long short-term memory networks (LSTM), and evaluates its performance. Literature (Ying et al., 2022) combines the node-weight method and the line entropy-weight method to propose a weak index for nodes and lines based on power flow distribution entropy, which effectively reduces errors in the traditional entropy method used for identifying weak links in power systems. This strategy helps reduce power flow entropy in the grid and improves transmission efficiency and stability.
In summary, existing literature has conducted extensive research on traditional FACTS devices such as UPFC and STATCOM, proposing various optimization strategies and methods to improve the performance and efficiency of power grids. These studies provide important theoretical support and practical guidance for the development of smart grids. Although existing methods for determining the location and capacity of FACTS devices have made some progress, most methods still improve from a single perspective or rely on practical engineering experience to determine the optimal location and capacity. As a result, existing methods lack global optimization capabilities to some extent.
For the optimization configuration of DPFC, this paper proposes an optimization strategy based on multi-criteria performance analysis. First, a configuration strategy for a single DPFC system is constructed, and the optimal installation location is determined based on the impact of DPFC on power grid current balance. Then, an economic cost/benefit analysis is applied to optimize its capacity. This strategy is applicable to the optimization configuration of a single DPFC and can be extended to the planning of multiple DPFCs as needed.
2 DPFC site selection strategy
2.1 Power flow entropy
Stability and reliability have always been the primary concerns in power systems. Currently, traditional evaluation methods for the stability and reliability of power systems are no longer sufficient to meet the demands of precise analysis in modern power systems. In recent years, power flow entropy has been introduced into power systems to quantify and reflect the system’s operating state. Entropy originally comes from the thermodynamic concept of “entropy” and, through the development and refinement of modern theory, has now become a powerful indicator for measuring the power flow distribution in power systems.
Power flow entropy quantitatively evaluates the reliability and stability of the power system by describing the disorder of power flow within the system. In the planning and operation of power systems, the concept and application of power flow entropy provide us with a new perspective and method to understand and solve complex problems in power systems.
The calculation of power flow entropy is given by Equation 1:where Pk is the probability of the branch in the load rate interval [ρk-1, ρk]. This formula essentially measures the load distribution of branches in the power system. When the load rates of all lines are within the same interval, the power flow entropy is zero, indicating the most balanced state of the system’s power flow distribution. On the other hand, when no two lines are within the same load rate interval, the power flow entropy reaches its maximum value, indicating the most uneven distribution of power flow in the system.
2.2 Optimal site selection strategy for DPFC
The operation of the power grid is largely determined by the power flow distribution within the grid. Uneven power flow distribution can significantly increase the failure rate of the grid’s operation. However, the deployment of DPFCs (Dynamic Power Flow Controllers) within the grid can significantly improve the power flow conditions of the lines and reduce the failure rate of the grid’s operation.
Based on entropy theory, this paper uses an improved weighted power flow entropy as a quantitative index to determine the optimal installation locations for DPFCs. The goal is to improve the imbalance in the line power flow distribution, which is reflected in the entropy value.
Let the thermal stability limit of line l be pl,max, the actual power flow be pl,0, and the line’s load rate be . Let s = {0, μ, 2μ, … , nμ, (n+1)μ, … , 100%}, so that the load rate is divided into several intervals. Let Ln be the number of lines with a load rate in the interval [nμ, (n+1)μ], then the probability that the line load rate falls within this interval is
To improve the flow entropy using the average load rate of the [nμ, (n+1)μ]-interval as the weight, the modified flow entropy can be expressed as:
From Equation 3, it can be concluded that when the power flow entropy Hpw is minimized, the power flow distribution of the line is the most balanced. Therefore, the lower the power flow entropy, the more stable the line is. Conversely, if the power flow entropy Hpw is higher, the power flow balance of the line is poorer, making the line more susceptible to disturbances during transmission. Thus, when selecting the optimal installation location for DPFC, positions with better power flow balance should be considered. As mentioned above, locations with better flow balance correspond to lower flow entropy. Therefore, the location selection of the Distributed Power Frequency Controller (DPFC) should aim to minimize the improved weighted power flow entropy, as expressed in Equation 4:where D represents the power flow situation with the addition of DPFC at different sections.
2.3 DPFC location selection strategy process
Search for the transmission line to be studied, which typically has k connecting lines at the section.
Select an appropriate engineering experience value as the initial capacity of the DPFC, and connect the DPFC to one of the connecting lines at the section. Assume this connecting line is i, with the initial value i = 1.
Calculate the weighted power flow entropy on this connecting line using Formulas 2, 3.
Increment i sequentially, until the weighted power flow entropy for all k connecting lines at the section is calculated.
Choose the position with the minimum weighted power flow entropy among the k connecting lines at the section as the optimal location for installing the DPFC. The calculation process is shown in Figure 1.
FIGURE 1
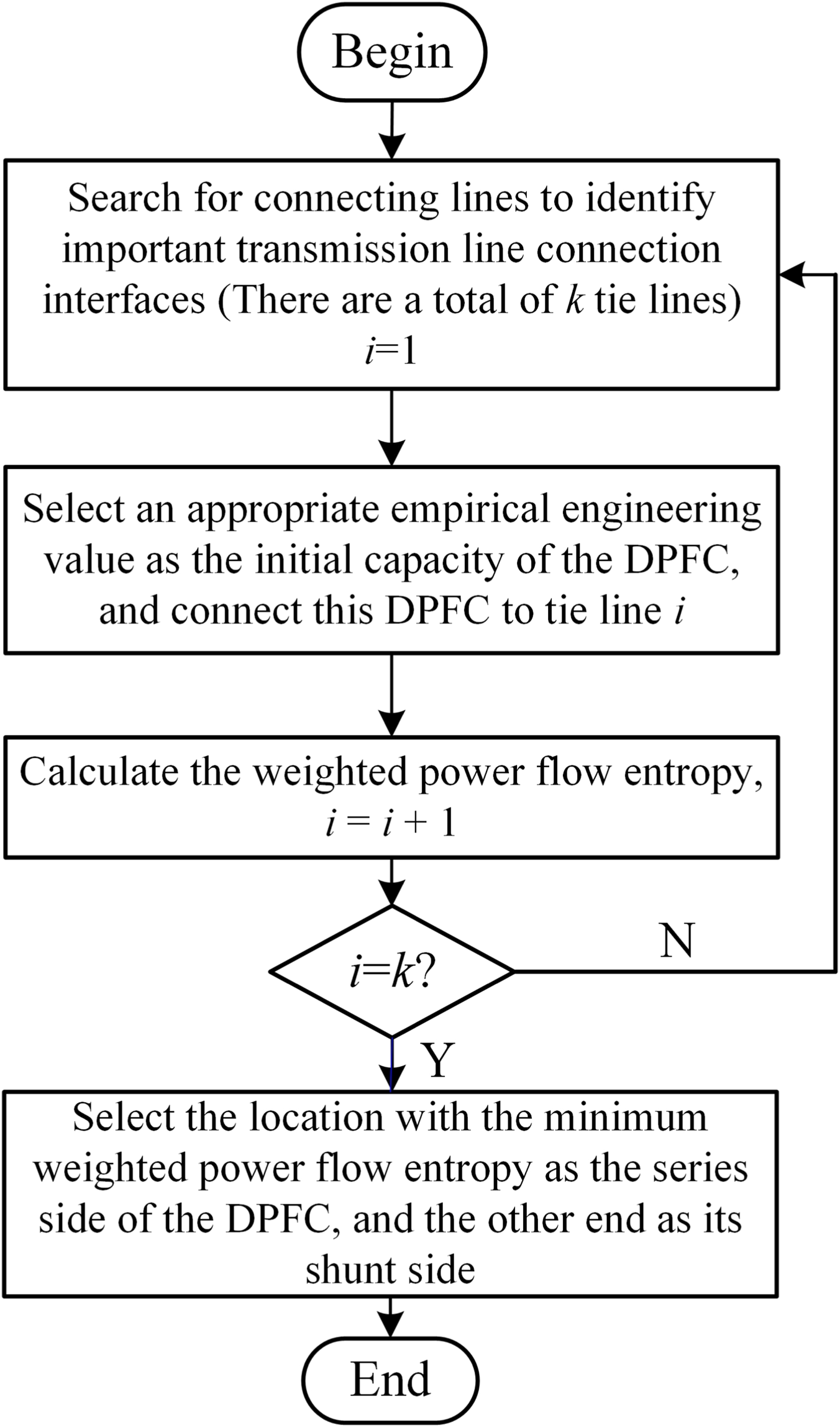
Flowchart of the distributed power flow controller location selection process.
3 Optimal capacity strategy for DPFC
3.1 Economic operation of the power grid
The application of DPFC devices in the power grid significantly enhances its ability to resist disturbances and improves stability. This advantage mainly stems from its enhancement of the power output capability of the electrical system. For modern power systems, the notable advantage of DPFC lies in its ability to provide more flexible and diverse methods for power flow control. When installing a DPFC, the most critical factors are determining the optimal location and appropriate capacity. Due to the vast complexity of power systems, performing point-by-point simulation analysis is not practical. Therefore, careful selection of the installation location and capacity of DPFC is necessary to minimize system losses, maximize power delivery, and reduce economic losses caused by power outages.
For the economic evaluation of DPFC devices, a comprehensive evaluation index system needs to be established. In terms of costs, this includes initial construction investment, operational costs, maintenance costs, and scrap costs. In terms of benefits, both direct and indirect benefits need to be considered. Direct benefits are reflected in the improvement of transmission capacity, reduction of losses, and the conversion of reliability and safety into economic returns.
From an economic perspective, the economic benefits of the DPFC device are influenced by its capacity, the number of series-side distributions, and the installation location. Considering the direct relationship between component costs and power, when the number of series-side distributions is small, the required power of the power electronic components is large, leading to high costs and limited replacement options. However, by increasing the number of series-side distributions, the power shared by each series link decreases, which reduces costs and improves the stability of the electronic components. Moreover, this redundant design significantly reduces the overall impact when facing failures, such as inverter damage, thereby enhancing the system’s reliability and stability, which further improves the overall economic benefits.
3.2 Benefit analysis
3.2.1 Increase in transmission capacity
When DPFC is integrated into the power system, it optimizes the transmission lines, thus increasing its direct benefits. Additionally, since the DPFC reduces the losses in the transmission lines, it brings about indirect benefits. After the installation of DPFC in the transmission line, the transmission capacity of the line is improved, increasing the power margin of the line, reducing the load rate of the line, and generating certain direct benefits. This can be expressed as Equation 5:where t(p) is the electricity price coefficient, and Δp is the increase in transmission redundancy after the enhancement of transmission capacity.
3.2.2 Investment in new transmission lines
In the operation of power networks, various strategies can be employed to enhance the transmission efficiency of the grid. Among these, the most traditional and significant approach is to add more transmission lines or related transmission equipment. However, this strategy not only involves high investment costs but also leads to an increase in resource occupation and consumption as more equipment is added. More critically, even with the addition of more equipment, the overall transmission efficiency may not necessarily improve; instead, it may require more energy due to the increased complexity of the system. In contrast, the DPFC device can optimize the power flow distribution in the grid, achieving a more balanced transmission effect. This strategy not only reduces the need for new transmission lines and related equipment, lowering installation costs, but also improves the utilization of system resources. The benefits can be expressed as Equation 6:where σ is the investment recovery rate of the power industry, and CL is the cost of constructing new transmission lines. By installing a reasonably designed DPFC in the transmission line, it can replace the line, achieving the same effect on improving transmission capacity. Therefore, the investment cost of the new transmission line is given by Equation 7:where ΔL is the estimated length of the new line, a is the unit capacity construction cost of the system, SL is the line capacity, and CH is the cost of the transmission line corridor.
3.2.3 Indirect benefits
When DPFC devices are introduced into the transmission system, they significantly enhance the system’s resistance to external disturbances, effectively reducing the compensation losses caused by power outages. At the same time, because of the reduced need for equipment and the increased efficiency of resource utilization, DPFC devices not only reduce material consumption but also alleviate environmental pollution, bringing significant indirect benefits to the power system. These indirect benefits are related to the direct benefits, so they can be directly calculated and evaluated by setting a reasonable ratio, expressed as Equation 8:where α3 is the set ratio.
3.3 Capacity determination strategy
To meet the economic operation of the power grid, the objective of maximizing economic costs and benefits will be used for selecting the capacity of the DPFC. The cost refers to the manufacturing and installation expenses of the DPFC, while the benefit refers to the supply benefit after the transmission capacity is enhanced and the costs for setting up new transmission lines. The capacity of the DPFC will be reasonably determined with the goal of maximizing the total benefit. When the total benefit of the power grid is maximized, the capacity of the selected DPFC will be considered the optimal capacity. We define the total benefit objective function as Equation 9:where Z is the total benefit value obtained by the power grid, SL is the cost of transmission lines needed by the power grid to achieve the same benefit, SATC is the supply benefit from the increase in transmission capacity after the installation, and (TF) is the equipment installation and related costs. The values of SL and TF are given by Equation 10:where q is the discount rate, L is the maximum service life of the DPFC, and SL,total and TF,total are the net present values of the transmission line costs and the equipment installation costs, respectively.
The calculations of TF,total and SATC are given by Equation 11:where and are the unit costs of STATCOM and DSSC respectively, PIEAR is the electricity price, and VJATC is the increment in transmission capacity after the installation of the DPFC. The calculation method for VJATC is given by Equation 12:where VJATC is the value of the objective function in the optimal power flow state x, representing the difference between the active power Pij(x) in the connected lines of the receiving-end and sending-end grids and the initial active power Pij,0 transmitted through those lines. S and R represent the sets of sending-end and receiving-end lines.
The constraints of the power grid operation are given by Equation 13:where PGi and QGi are the input active and reactive power for the sending-end generators; ηi is the static voltage stability margin; μi is the load factor; Uiand Uk are the voltages at buses i and k, respectively; θik is the phase angle difference between buses i and k.
Using a genetic algorithm, the rated capacity of the DPFC will be increased in steps based on the unit capacity of the DSSC. When the grid’s benefit is maximized, the rated capacity of the DPFC at this point will be considered the optimal rated capacity. Figure 2 shows the overall logic flow diagram.
FIGURE 2
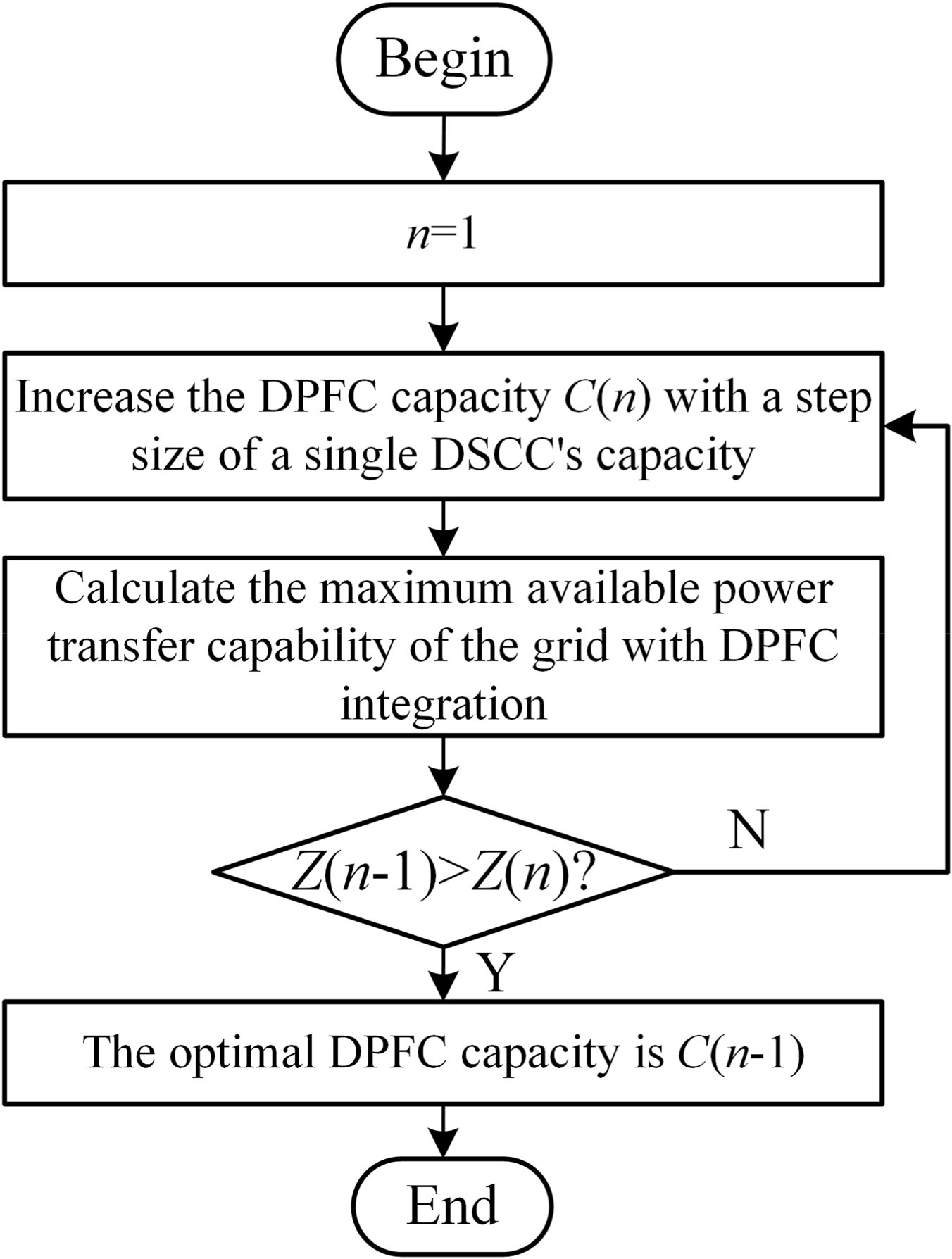
DPFC site selection and capacity determination flowchart.
4 Simulation analysis
4.1 Example system
To verify the feasibility of the site selection and capacity determination method for the DPFC, the IEEE 30-bus system from MATPOWER is selected as an example, as shown in Figure 3. The system is divided into three Areas: A, B, and C. Area A is the transmission end, and Area C is the receiving end. Based on the power grid data analysis, it is found that the generation capacity in Area A is relatively abundant, while Area C has a relatively large load in the entire power system. Therefore, based on these characteristics, Areas A and C are selected as the research subjects. The average electricity price pIEAR is set to 0.6 CNY/(kW·h), the discount rate q is 10%, SL is 50 million, and the DPFC operating time is 20 years.
FIGURE 3
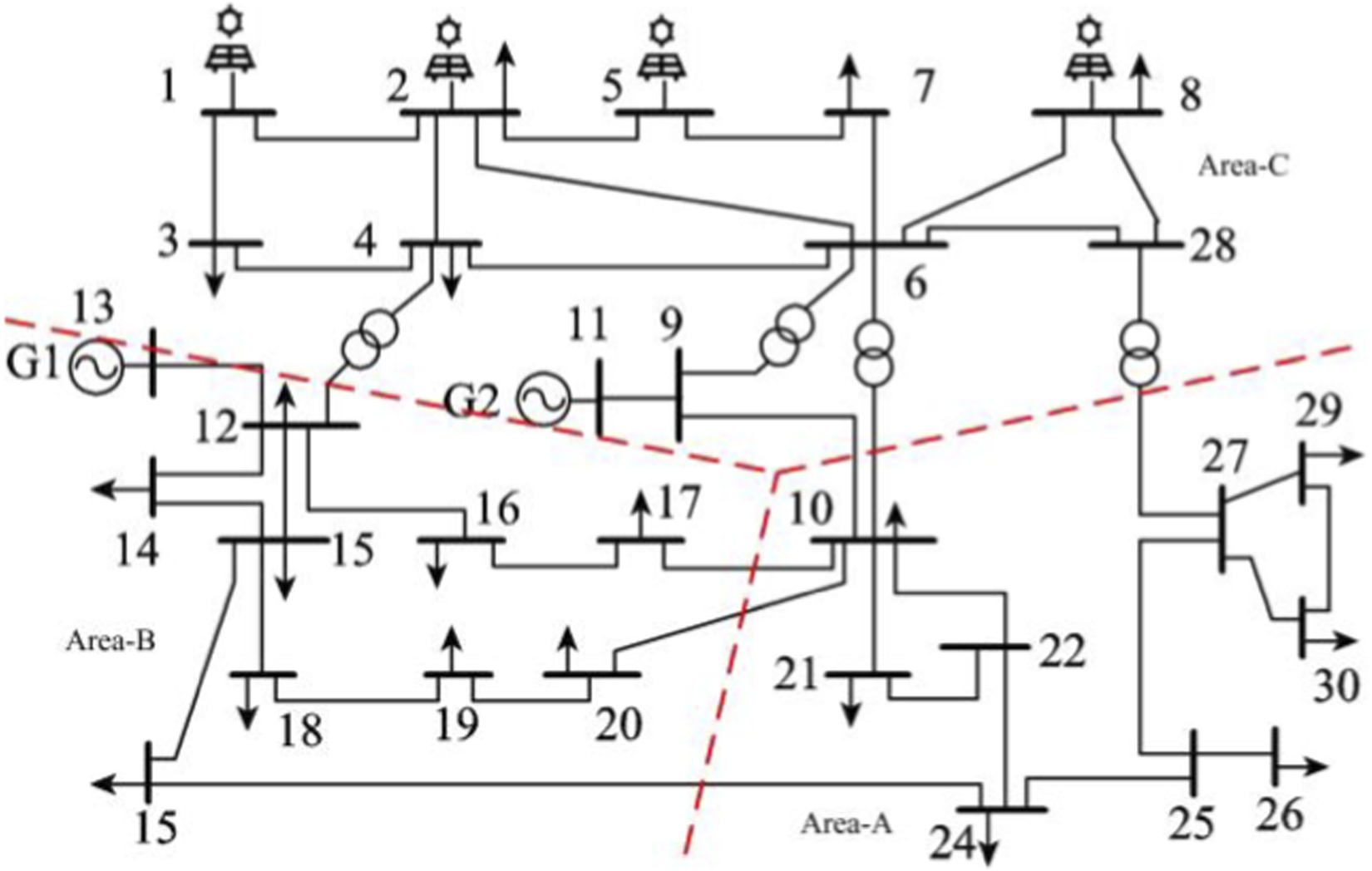
IEEE 30-bus sectional topology diagram.
4.2 DPFC site selection and capacity determination validation
The sections of Region A and Region C, as seen from the topology diagram, are composed of three lines: L6-10, L9-10, and L28-27. Without installing the DPFC on the lines, MATLAB is used to calculate the power flow entropy for these three lines. Without installing the DPFC on the three lines between Regions A and C, the weighted power flow entropy of line L28-27 is the smallest. Therefore, based on the principle of minimizing weighted power flow entropy, L28-27 is selected as the optimal installation location for the DPFC.
Then, a DPFC with a capacity of 10 MVA is installed at L28-27, and the weighted power flow entropy for the three lines is recalculated. It is found that the weighted power flow entropy of L28-27 remains the smallest. The specific flow entropy before and after adding DPFC is shown in Table 1. Next, the capacity of the DPFC is increased in steps, with the capacity of a single DPFC being incremented to calculate the increase in transmission capacity of the lines after adding the DPFC. This is followed by calculating the direct benefits obtained after the transmission capacity improvement and the DPFC installation cost, the total investment budget for line construction, and the final benefits derived from the DPFC installation on the line. Finally, based on the principle of maximizing economic benefits, a genetic algorithm is applied to determine that the total DPFC capacity of 60.1 MVA results in the maximum Z(c).
TABLE 1
| DPFC Capacity/MVA | Weighted power flow entropy | ||
|---|---|---|---|
| L28-27 | L9-10 | L6-10 | |
| 0 | 0.278 | 0.297 | 0.283 |
| 10.00 | 0.313 | 0.336 | 0.312 |
| 60.16 | 0.385 | 0.417 | 0.402 |
| 30.00 | 0.412 | 0.419 | 0.414 |
| 70.00 | 0.392 | 0.420 | 0.406 |
Power flow entropy before and after adding DPFC.
Thus, for the IEEE, 30-bus system, the L28-27 line is the optimal installation location for the DPFC, in Regions A and C. A DPFC, with a capacity of 60.1 MVA, maximizes the benefits for the line and is the optimal capacity choice.
The capacity of the DPFC is determined based on the maximization of economic benefits. According to the benefit function constructed earlier in this paper, the DPFC capacity is incrementally increased in steps of DSCC capacity, and the incremental transmission capacity and installation cost of the DPFC for different capacities are calculated. Based on the genetic algorithm, it is found that when the DPFC capacity is 60.1 MVA, the power flow entropy of the L28-27 line is minimized, meeting the aforementioned site selection requirements. At the same time, when a DPFC with a capacity of 60.1 MVA is installed at L28-27, the total benefits of our power grid are maximized. Table 2 shows the total benefit values when different capacities of DPFC are installed at L28-27.
TABLE 2
| DPFC Capacity/MVA | Total benefits/10,000 CNY | /MW |
|---|---|---|
| 0 | 63.1 | |
| 30.00 | 1701.32 | 92.34 |
| 60.16 | 33058.07 | 125.03 |
| 70.00 | 3018.32 | 127.8 |
Comparison of total benefits after adding DPFC.
5 Conclusion
This paper explores the DPFC (Dynamic Power Flow Controller) site selection and sizing problem based on power flow entropy and economic considerations. By introducing the concept of weighted power flow entropy, a new indicator has been established to evaluate the complexity and unevenness of power flow distribution in the distribution network. Based on this indicator, an effective site selection method has been proposed. At the same time, considering that economic factors are crucial in power grid operations, the sizing problem of DPFC has been analyzed according to economic principles. By calculating the benefits and installation costs associated with changes in transmission capacity after adding DPFC to the line, a genetic algorithm is used to incrementally increase the DPFC capacity with DSCC capacity as the step size. The DPFC with the best capacity is obtained when the objective benefit function reaches its maximum, thus completing the optimization of DPFC sizing.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
BW: Writing – review and editing. LC: Funding acquisition, Formal Analysis, Writing – review and editing, Data curation, Conceptualization. EZ: Resources, Investigation, Writing – review and editing, Methodology, Project administration. XC: Writing – review and editing, Supervision, Software. ZW: Writing – review and editing, Visualization, Validation.
Funding
The author(s) declared that financial support was received for this work and/or its publication. This research was funded by State Grid Corporation of China Science and Technology Project grant number 5400-202313567A-3-2-ZN.
Conflict of interest
Authors BW, LC, EZ, XC, and ZW were employed by State Grid Hebei Electric Power Company Hengshui Power Supply Branch.
This study received funding from the State Grid Corporation of China’s Science and Technology Project Funding, specifically under the grant: “Key Technology Research and Application of Hierarchical Control and Consumption for Low Voltage Distributed Photovoltaics (Project No.: 5400-202313567A3-2-ZN). The funder, the State Grid Corporation of China, was involved in the study through the collection, analysis, and interpretation of data.
Generative AI statement
The author(s) declared that generative AI was not used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Altun E. B. Kaymaz E. Dursun M. Guvenc U. (2024). Hyper-FDB-INFO algorithm for optimal placement and sizing of FACTS devices in wind power-integrated optimal power flow problem. Energies17 (23), 6087. 10.3390/en17236087
2
Anil N. Balaji G. Sireesha G. Vijaya madhavi S. Naresh V. (2024). Optimizing size and location of UPFC for enhanced system dynamic stability using hybrid approach. Comput. Electr. Eng.120 (PB), 109777–109787. 10.1016/j.compeleceng.2024.109777
3
Ansho M. P. Nisha G. M. (2023). Egret swarm optimized distributed power flow controller for power quality enhancement in grid connected hybrid system. J. Electr. Eng. and Technol.19 (4), 2047–2057. 10.1007/s42835-023-01679-6
4
Canbing L. I. Liwu X. Cao Y. Zhu Q. Fang B. Tan Y. et al (2014). Optimal all ocation of multi-type FACTS devices in power systems based on power flow entropy. J. Mod. Power Syst. Clean Energy.2 (2), 173–180. 10.1007/s40565-014-0059-x
5
Chethan M. Kuppan R. (2024). A review of FACTS device implementation in power systems using optimization techniques. J. Eng. Appl. Sci.71 (1), 18. 10.1186/s44147-023-00312-7
6
Gupta K. S. Mallik K. S. Ranjan A. Ranjan M. (2025). An overview of the operation and control of distributed power flow controller. Electr. Eng.107, 1–26. (prepublish). 10.1007/s00202-025-03325-y
7
Hareesh S. Umapathi P. R. R K. (2020). Optimal location and sizing of UPFC for optimal power flow in a deregulated power system using a hybrid algorithm. Int. J. Ambient Energy43 (1), 1–7.
8
He P. Chen J. Geng S. (2020). Analysis of FACTS device on low-frequency oscillation characteristics of a power system with wind farm integration. Power Syst. Prot. Control48 (8), 86–95.
9
Jivandas K. B. Pandya D. J. (2022). Optimal allocation of FACTS devices using kinetic gas molecular optimization and cuckoo search algorithm. J. Institution Eng. (India) Ser. B103 (6), 2057–2072. 10.1007/s40031-022-00784-w
10
Ni J. Zhao Z. Zhu Y. (2025). Unit power rating balancing for differential-power-processing-based distributed photovoltaic systems. Front. Energy Res.13, 131611573. 10.3389/fenrg.2025.1611573
11
Özdoğan N. Bahçeci S. (2025). Control of distribution static synchronous compensator using intelligent methods to improve power quality. Comput. Electr. Eng.126, 110552–110562. 10.1016/j.compeleceng.2025.110552
12
Reddy K. M. K. Rao K. A. Rao S. R. (2025). A multi-objective hybrid meta-heuristic method-based optimal placement of UPFC in power system. Electr. Eng.107 (7), 1–29. 10.1007/s00202-025-02985-0
13
Sebi P. N. (2023). Development of optimal placement and sizing of FACTS devices in power system integrated with wind power using modified krill herd algorithm. COMPEL - International Journal Computation Mathematics Electrical Electronic Engineering42 (6), 1408–1433. 10.1108/compel-12-2021-0502
14
Ying Q. U. Zhang S. Cheng X. (2022). Study on weak link identification method of power system based on power flow distribution entropy. Shanxi Electr. Power (05), 6–9.
15
Zhang N. Qi B. Chen J. (2024). Optimization method for unified power flow controller configuration based on probability sensitivity. Sci. Technol. Innovation (04), 22–26.
16
Zhou W. Chen Q. Shan X. Chen Y. Deng L. Zhang Q. (2019). Multi-objective optimal placement of FACTS devices based on parameter decoupling. Power Syst. Clean Energy35 (7), 1–9.
Summary
Keywords
distributed power flow controller, distribution networks, economy, fixed volume, weighted power flow entropy
Citation
Wang B, Chen L, Zhu E, Cui X and Wang Z (2026) Research on optimization configuration of distributed power flow controllers in distribution networks with distributed photovoltaics. Front. Energy Res. 13:1720521. doi: 10.3389/fenrg.2025.1720521
Received
09 October 2025
Revised
18 December 2025
Accepted
30 December 2025
Published
30 January 2026
Volume
13 - 2025
Edited by
Fateh Krim, University Ferhat Abbas of Setif, Algeria
Reviewed by
Yujia Huang, Northeasten University, China
Omveer Singh, Gautam Buddha University, India
Updates
Copyright
© 2026 Wang, Chen, Zhu, Cui and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bing Wang, 275907421@qq.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.