Challenges in the Evaluation of Observational Data Trustworthiness From a Data Producers Viewpoint (FAIR+)

Recent discussions in many scientific disciplines stress the necessity of “FAIR” data. FAIR data, however, does not necessarily include information on data trustworthiness, where trustworthiness comprises reliability, validity and provenience/provenance. This opens up the risk of misinterpreting scientific data, even though all criteria of “FAIR” are fulfilled. Especially applications such as secondary data processing, data blending, and joint interpretation or visualization efforts are affected. This paper intends to start a discussion in the scientific community about how to evaluate, describe, and implement trustworthiness in a standardized data evaluation approach and in its metadata description following the FAIR principles. It discusses exemplarily different assessment tools regarding soil moisture measurements, data processing and visualization and elaborates on which additional (metadata) information is required to increase the trustworthiness of data for secondary usage. Taking into account the perspectives of data collectors, providers and users, the authors identify three aspects of data trustworthiness that promote efficient data sharing: 1) trustworthiness of the measurement 2) trustworthiness of the data processing and 3) trustworthiness of the data integration and visualization. The paper should be seen as the basis for a community discussion on data trustworthiness for a scientifically correct secondary use of the data. We do not have the intention to replace existing procedures and do not claim completeness of reliable tools and approaches described. Our intention is to discuss several important aspects to assess data trustworthiness based on the data life cycle of soil moisture data as an example.

1 Introduction

Every day, scientists acquire a massive variety and amount of environmental data in real-time or near real-time to understand processes in the earth system better. The exponential growth of data is undisputed and provides answers to various environmental challenges, such as climate change and the rise of extreme events and related hazards. It is essential to consider data processing and analysis as an interdisciplinary, boundary-crossing, data linking step in the data life cycle. Data-driven research investigates available data repositories and links a considerable amount of collected heterogeneous data from various types, such as field sensors, laboratory analyses, remote sensing data, as well as modeling data. The linking usually consists of several data processing steps, which should guarantee the possibility of data quality assessment. Data quality evaluates the condition of data and especially information on data accuracy, data completeness, data consistency, data reliability, and data currency as key attributes of high-quality data. There are already many tools available to evaluate some of these key attributes, such as among others the conformity to the defined data standards [e.g., Infrastructure for Spatial Information in the European Community (INSPIRE)], or quality assurance/quality control tools [e.g., INSPIRE or Integrated Carbon Observation System (ICOS)] to identify inaccurate or incomplete data within a given data set, or the QUACK tool developed by Zahid et al. (2020) in the frame of Copernicus Climate Change Service (C3S) contracts.

High-quality data could help expand the use of joint data visualization (e.g., dashboards) and joint analytical methods (e.g., machine learning) to increase the informative value of data. However, data can be of high quality, but lack of information on reliability and provenience can subsequently lead to misinterpretation and thus to wrong conclusions. In contrast, data of reduced quality could be a source of ambiguity and therefore also inaccurate analysis and weakly derived or wrong conclusions (e.g. Cai and Zhu, 2015; Brown et al., 2018; Bent et al., 2020). Although there are already many tools available to assess the quality and completeness of data, it is not yet a standard practice that the reliability and provenience of the data can be easily checked.

In recent years, there has been a growing awareness that existing research data can be a very valuable base for further research. A prerequisite is the provision of all kinds of scientific data and their detailed descriptions. This should keep in mind the longevity as well as the general purpose of providing other researchers with access to the data for facilitated knowledge discovery and enhanced research transparency. An important approach towards the reuse of research data is the implementation of the FAIR principles. They provide guidance for improving Findability, Accessibility, Interoperability, and Reusability on sharing not only scientific data but all kinds of digital resources (Wilkinson et al., 2016; Mons et al., 2020). These principles aim to enable the maximum benefit from research data by supporting machine-actionable processes in data infrastructures to make the resources findable for machines and humans. FAIR considers the form of providing data sets to the scientific community (Lamprecht et al., 2019). Without appropriate knowledge about the data trustworthiness, the processing of data to a higher level, the associated assumptions and uncertainties as well as data origin, any kind of data can be of limited practical value. However, the FAIR principles do not yet address data or software quality in detail and do not cover content-related trustworthiness aspects (Lamprecht et al., 2019; Jacobsen et al., 2020).

Data quality assessment considers mainly completeness, precision, consistency and timeliness of data (Teh and Kempa-LiehrWang 2020). Two kinds of errors, systematic errors and random errors, cause inaccurate data and lead to a degradation of data quality. Systematic errors are consistent and manifold in nature. For instance, they are related to imperfection of measurement methods and devices, incorrect calibration causing outliers, drifts, bias and noise. In most cases, systematic errors shift data from their true value (bias) all the time and can be predicted and quantified to a certain degree through elaborate experiments, usage of references, and specific mathematical tools. Systematic errors do not affect the data reliability but affect accuracy. In contrast, random errors encompass unknown and unpredictable errors such as statistical fluctuations in environmental conditions, subjective acquisition (e.g., dependency on reaction time) and errors due to the statistical character of the process variable itself. Random errors can be evaluated through statistical analysis of repeated measurements. Reliable random error estimation is possible the more data is collected. Random errors affect the reliability but do not affect the overall accuracy and tend to contribute more to the total error than systematic errors (Bialocerkowski and Bragge, 2008). The term uncertainty is a quantitative specification of all errors and includes both systematic and random errors. Uncertainty in sensor data is the sum of inherent limitations in the accuracy and precision with which the observed data is acquired. It is simply impossible to measure any variable with 100% certainty due to numerous limitations and inadvertent systematic and random errors such as among others non-representative sampling schemes, unspecified effects of environmental conditions on the observed data, effects of specific electrical components of the sensor on the data, or operators bias (Prabhakar and Cheng, 2009). The uncertainty factors need to be detected, quantified, removed if possible, and described in detail to enable data trustworthiness assessment. The key elements of quality assessment in several existing procedures and frameworks are quality flags which are defined codes of numbers assigning the data into different categories and stored along the data.

Another important information regarding trustworthiness are sensor specifications provided by the manufacturer. However, this kind of data refers to the initial test with a brand new sensor and does not take alterations during sensor lifetime and other influencing factors during sensor storage, set up and operation into account. Often, the given manufacturer’s information represents just theoretical accuracy and precision values. It can be summarized that quality flags do not provide information of trustworthiness of single data points, while manufacturer’s information somehow provide ideal information not relevant to sensors in operation.

We propose to record sufficient information on factors that influence the data trustworthiness of sensors during its lifetime and the overall application in second-level datasets and metadata descriptions. A second-level dataset contains more detailed information about data trustworthiness and complements each dataset. Such a collection of extensive data and metadata in separate levels allows data users both to assess the data quality and evaluate the data trustworthiness for the intended application if needed. In addition, such second-level data and the related metadata descriptions ensure that the secondary data users are not overloaded with data and information which he (she) is not interested in. However, data users also have to be made aware of the extent to which the information content of the data is reliable. To guarantee trustworthy data at the highest stage, indicators of trustworthiness such as reliability, validity, and provenience need to be evaluated and described in detail in such second-level datasets and metadata descriptions (see Figure 1). Often, there are no single agreed definitions of these indicators and therefore, the authors will give detailed explanations of the terminology and concepts in this paper.

FIGURE 1

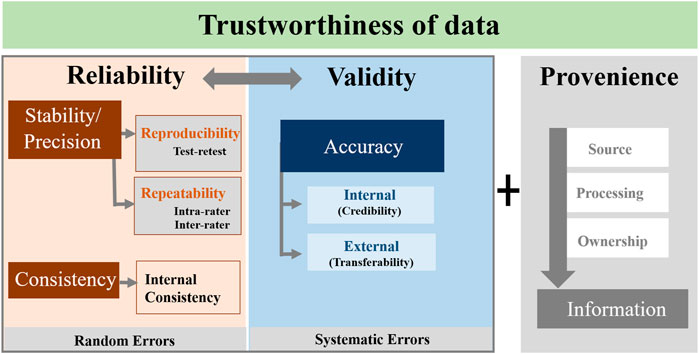
FIGURE 1. Indicators of data trustworthiness, data reliability, data validity and data provenience. (1) Stability/Precision and consistency in data play a major role in reliability assessment. (2) Validity assesses the trueness and accuracy of measured data while considering consistency closeness. (3) Data Provenience supports the confidence or validity of data by providing detailed information (metadata) on data origin and its processing steps in a consistent manner.

For the assessment of the trustworthiness of data, the data reliability and validity in environmental science should be assessed in terms of how precise and stable measurements are and with what uncertainties the measured values reflect the true values.

Regarding the application of FAIR principles in the research process, the evaluation of the data trustworthiness should include (besides the consideration of data reliability and validity) the consideration of data provenience as a term pertaining to the inherent lineage of objects as they evolve over time (Castello et al., 2014). Data provenience represents metadata paired with records providing details about the origin and history of the data, the executed processing steps with the corresponding assumptions and uncertainty evaluations supporting the trustworthiness of data (Diffbot Technologies Corp., 2021). This digital fingerprint can be used to evaluate all relevant aspects of a data object. All processing and transformation steps from the source data to the data object under consideration must be traceable, repeatable, and reproducible to provide more transparency in data analysis. This context shows that provenance description is closely related to reliability and validity assessment. Based on the known data origin and previous processing steps, the quality of the analysis results can be better assessed. This may minimize potential ambiguities.

This statement paper intends to foster a discussion in the scientific community about how to evaluate, describe and implement reliability, validity and provenience issues in a standardized data evaluation approach and a metadata description following the FAIR principles or which additional data should be linked to the data to enable high data trustworthiness. Such a comprehensive data evaluation including data processing assessment and metadata description will improve knowledge generation.

The paper provides data users with insight into the evaluation criteria of data’s trustworthiness and discusses the meaning of data reliability, validity, and provenience. The authors consider relevant issues regarding the significance of data trustworthiness in a comprehensive data analysis. These issues are 1) trustworthiness of the sensor data (reliability issues), 2) data trustworthiness of the data processing (validity), and 3) data trustworthiness of the data integration and visualization (provenience). The paper illustrates these relevancies based on soil moisture data: 1) the reproducibility, repeatability and internal confidence of soil moisture measurements, 2) the credibility and transferability of some processing steps e.g. to derive soil water content from measured permittivity values, 3) need to report point density coverage and describe additional data used to create maps or data products. All examples demonstrate the importance of reliability, validity, and provenience assessment in a second-level metadata description for long-term data provision and could also be transferred to other sensors, methods, and models.

2 Components of Data Trustworthiness

Reliability and validity of data can be seen as the two essential and fundamental features in the evaluation of the quality of research as well as the evaluation of any measurement device or processing step for trustworthy transparent research (Mohajan, 2017). In general, it can be summarized that the uncertainty of a measurement is composed of two parts. 1) Reliability: the effects of random errors on the measurement performance and 2) validity, the effect of one or more influencing quantities on the observed data (systematic errors) represented in the bias.

Reliability relates to the probability that repeating a measurement, method, or procedure would supply consistent results with comparable values by assessing consistency, precision, repeatability, and trustworthiness of research (Bush, 2012; Blumberg et al., 2005; Chakrabartty, 2013). Mohajan (2017) described that observation results are considered reliable if consistent results have been obtained in identical situations but under different circumstances. Often, reliability refers to the consistency of an approach, considering that personal and chosen research method biases may influence the findings (Twycross and Shields, 2004; Noble and Smith, 2015). Therefore, the assessment of data reliability focuses on quantifying the amount of random errors. Reliability is mainly divided into two groups: stability/precision, and internal consistency reliability. The stability/precision is limited mainly by random errors and can be assessed by testing the repeatability (test-retest reliability, see Section 2.1.1) and the reproducibility (intra-rater reliability and inter-rater reliability, see Section 2.1.2). Internal consistency refers to the ability to ensure stable quantification of a variable across different experimental conditions, trials, or sessions (Thigpen et al., 2017). The more reliability exists, the more accurate the results, which increases the chance of making correct assumptions in research (Mohajan, 2017).

Validity is the degree of accuracy of measured data. Predictable systematic errors reduce the accuracy. It is often defined as the extent to which an instrument measures what it asserts or is designed to measure. Furthermore, it involves applying defined procedures to check for the accuracy of the research findings (Blumberg et al., 2005; Thatcher, 2010; Robson and Sussex 2011; Creswell, 2013; Gordon, 2018). For example, a data validation algorithm as a kind of data filtering process evaluates the plausibility of data (EU, 2021). Validity is paramount for avoiding false data analysis conclusions and should be prioritized over precision (Ranstam, 2008). The two essential parts are internal validity (=credibility) and external validity (=transferability). Internal validity indicates whether the study results are legitimate in respect to the manner in which a study was designed, conducted and data analyses were performed (Mohajan, 2017; Andrade, 2018). Internal validity examines the extent to which systematic error (bias) is present (Andrade, 2018). Nowadays, the evaluation of internal data validity is implemented in quality check routines [e.g., checks for completeness, statistical characteristics (e.g., SD), accuracy, and timeliness] and hence in metadata description to some extent. External validity examines whether the research findings can be generalized to other contexts or to what extent the size or direction of a researched relationship remains stable in other contexts and among different samples/measurements (Allen, 2017).

For all secondary data analyses, a detailed assessment of reliability and validity involves an appraisal of applied measurement methods for data collection (Saunders et al., 2009). Reliability is an essential prerequisite for validity and vice versa. It is possible to have reliable data that are not valid; however, valid data must also be reliable (Kimberlin and Winterstein, 2009; Swanson, 2014). The ideal sensor would combine great accuracy with stability and precise measurements in high resolution, but in many cases, increased sensor performance also increases the price (Van Iersel et al., 2013). However, the different understanding of the meaning of terms such as accuracy, precision, consistency, stability describing the quality of measurements proves difficult due to conflicting meaning and misuse (Menditto et al., 2006). Usually, an assessment of sensor performance based on the manufacturer’s initial specifications is impossible mainly due to unclear differentiation between these two terms accuracy and precision and its ideal test setup with a brand new sensor (Van Iersel et al., 2013).

2.1 Sensor Data Reliability

Data reliability analysis evaluates the reliability of research by indicating the observed sensor data’s consistency and stability (repeatability and reproducibility). The reliability assessment relates mainly to measurement data. Therefore, reliability assessment must incorporate an evaluation of relevant uncertainties.

A standardized and consistent workflow for the reliability evaluation is helpful. Here, comprehensive documentation is essential to make the assessment valuable for later access and usage. The procedure of reliability assessment can be appraised in several ways, including test-retest and internal consistency test (Ware and Gandek, 1998). Our suggestion is to use a broader concept adopted from applied psychology and medicine, considering other types of reliability: over time (test-retest reliability), between operation times (intra-rater reliability), different researchers (inter-rater reliability) and across items (internal consistency) (Lo et al., 2017; Chang et al., 2019). Based on these fundamental tests, we obtain information on reliability, especially repeatability and reproducibility, and consistency (see Figure 1). Repeatability and reproducibility can be seen as two extremes of precision, the first describing the minimum and the second the maximum variability in results. Repeatability and reproducibility are expressed quantitatively in terms of the dispersion characteristics of the data (NIST, 1994).

2.1.1 Test-Retest Reliability Test

The test-retest reliability test evaluates the reproducibility of measurements and can be related to the assessments of temporal stability and maximum variability in data (ISO 5725-1). For instance, temporal stability describes the data variability when the same variable is acquired more than one time in terms of a discrete-time series but measured at the same location under the same environmental circumstances. Repeated measurements with appropriate sampling frequency allow the collection of more data and enable an uncertainty assessment and an improvement of accuracy based on statistical methods. These characteristics are especially crucial for reference measurements, sensor drift verifications, incorporation of, for example, low-cost or distributed citizen science sensors into research infrastructures and, to some extent, for intercomparison experiments.

2.1.2 Intra/Inter-Rater Reliability Test

The intra-rater reliability refers to the measurement consistency by one identical operator on two occasions, under the same conditions, using the same standardized protocols and equipment (Domholdt, 2005). In reality, errors occur even when one person undertakes measurements, and assessing the error magnitude is invaluable in interpreting measurement results (Bialocerkowski and Bragge, 2008).

The inter-rater reliability test evaluates the repeatability of measurements and relies on data acquired with the same device/method but different operators and quantifies the equivalence and the agreement within measurement data. It describes the minimum variability in data (ISO 5725-1, 1994). Thus, it establishes the data equivalence obtained with one instrument used by different operators and evaluates the systematic differences among operators (Mohajan, 2017). The operator’s performance, level of skills/expertise, and decisions made by him often have a non-negligible impact on the uncertainty associated with a measurement result (random error). This can concern the measurement itself (e.g., reading errors), but also the subsequent subjective data processing and interpretation. The outcomes of the measurement process depend on the education, training, expertise, and technique of the operators.

Different skill levels and the operator’s ability to identify and minimize potential errors are essential factors for evaluating those errors. However, a description in metadata in a standardized format seems to be difficult due to the lack of standardized tools assessing the skill and competence level of the operators. The subjective description of the skill levels goes beyond the scope of metadata description for many experiments.

2.1.3 Internal Consistency Test

The internal consistency test evaluates the consistency of measurements. In statistics, the internal consistency reliability expresses how closely related a set of items are as a group (UCLA, 2020). (DeVellis 2006) stated that internal consistency reliability examines whether or not the variable within a scale or measuring time is stable across different environmental conditions and tests. The environmental sciences assess the extent of differences within the measured data that investigate the same process variable at the same location and result in comparable data within the same range. Measurements by one or multiple sensors are considered internally consistent if the observed variable remains stable across different environmental conditions.

Furthermore, tests need to be in a pre-defined consistency range and their variations are distributed along the typical bell curve. This type of reliability measure is exemplarily considered in sensor intercomparison experiments – for instance, determining biased sensors in a sensor network. If a calibrated reference sensor is associated, intercomparison experiments examine both precision as well as accuracy (validity) to this reference.

2.2 Data Validity

The concept of validity is akin to the concept of accuracy (Krishnamurty et al., 1995). Therefore, the degree of data validity assesses the data accuracy. Accuracy is an aspect of numerical data quality connected with a standard statistical error between an accepted reference value and the corresponding measured value. As stated before, it is reduced by systematic errors. The accuracy can be described by trueness examining the agreement between the average (mean) value obtained from an extensive data set and an accepted reference value, and precision, a general term for variability or spread between repeated measurements (ISO 5725-1, 1994). Trueness is typically expressed in terms of bias and precision in terms of standard deviations.

The internal validity refers to the bias potential and external validity to the generalizability. The internal and external validity is analyzed and verified through statistical tests and statistical confidence limits, which are often already implemented into automatic quality routines.

A reliable assessment of the validity requires a comparison with an accepted reference standard. It is important to highlight that accuracy is a qualitative concept and should not be assessed quantitatively (NIST, 1994).

Numerous information about data validity and thus about systematic errors (e.g. outliers, missing data, bias, drifts, and noises) can be derived from the validation methods. Internal validity is a prerequisite for external validity and data that deviate from the true value due to systematic error lack the basis for generalizability (Dekkers et al., 2010; Spieth et al., 2016). This means for environmental data that the internal validity must be assessed, corrected and described, and only then can generalizing approaches such as Pedo-Transfer Functions be subsequently applied.

2.3 Data Provenience

Data provenience includes much more information than available in data lineage description. It describes e.g. also the quality of the input data and processes that influence data of interest. Therefore, data provenience is a crucial issue related to secondary data usage. Data made available following the FAIR principle are often not the raw data as original sensor readings. Mostly they are already data products as a result of processed lower-level data deriving parameters of scientific interest. Especially, systems using spatial data rely on spatial provenience properties, such as information about the origin of merged and split objects (Glavic & Dittrich, 2007). Glavic and Dittrich (2007) proposed to divide the provenience evaluation into source provenience and transformation provenience. For example, downloadable soil moisture data in Data Publisher for Earth & Environmental Science (PANGAEA https://www.pangaea.de/) are already processed sensor data providing values in percent (%) derived from measured voltage values. Information about previous data processing such as applied proxy-transfer function is often not given and information about the transformation provenience is often lacking. Indeed, it is also decisive for which primary objective the data is monitored. For example, data can be specially acquired for monitoring purposes, model validation, remote sensing calibration, data assimilation in the model and joint data analysis to study changes. Therefore, a wide variety of different information for each objective is required to evaluate the data correctly. The monitoring objective determines, in many cases, the data evaluation, the extent of the metadata information as well as its auxiliary parameters.

The trustworthiness of the provided data products depends on the trustworthiness of the lower-level data, their spatial and temporal resolution, their uncertainties, their relationships and correlations and the applied processing suitability. The data user should be aware that each selection of the source data and their manipulation within the processing could significantly influence the data value and quality and thus the data trustworthiness. It is evident hereby that provenience description implies reliability and validity assessment of the input data. Hence, sufficient information on data processing is necessary for a reliable evaluation of the provided data’s trustworthiness.

3 The Importance of Data Trustworthiness in Environmental Sciences—Exemplified by Soil Moisture Data

In the following section we want to discuss the challenges in data trustworthiness by using a typical example of measuring environmental in-situ data.

Soil moisture is an essential critical state variable in land surface hydrology and a key component of microclimate. Furthermore, it can be seen as an essential hydrologic variable impacting runoff processes, an essential ecological variable regulating net ecosystem exchange, and an essential agricultural variable regarding water availability to plants and their influence on temperature and humidity conditions near ground (Ochsner et al., 2013; Corradini, 2014). Soil moisture is characterized by high spatial and temporal variability and the complex interactions with pedologic, topographic, vegetative, and meteorological factors influence soil variability. Therefore, this compartment-linking variable is ideally suited to show the importance of assessability of data trustworthiness.

Here we will discuss approaches to assess data reliability, validity and provenience as a basis for selecting appropriate data and evaluation tools for data-driven research and higher-level data assessment.

3.1 Approaches to Assess the Reliability

3.1.1 Test-Retest Reliability

We consider here the temporal variation of measured dielectric permittivity measured by soil moisture probes to discuss the test-retest reliability.

Time-domain reflectometry (TDR) is the most widely used soil water content measurement technique at point scale and is seen as an inexpensive method of measuring the dielectric properties of soil, mainly driven by water in pore space (Schoen, 1996). The measurement of the dielectric permittivity is an accepted technique to monitor and evaluate shallow soil water content, but its accuracy is dependent on the appropriate petro-physical relationship between the measured permittivity and volumetric water content of the soil (Huisman et al., 2003; Steelman and Endres, 2011). Such sensors rely mostly on careful and timely calibration, careful selection of measurement frequency, careful sensor positioning, and the operator’s expertise.

As an example below, we illustrate the evaluation of the TDR dielectric permittivity data reliability based on the readings of standard SMT100 probes (Truebner GmbH, Neustadt, Germany), calibrated under the same conditions and installed at two different locations at a depth of 15 cm below surface. The dielectric permittivity measured every 10 min averaged over 1 h and the standard deviation (n = 6) was calculated. Figure 2 shows that the reproducibility of a measured value is given when environmental conditions do not change. However, when conditions are changing the reproducibility is no longer given. Figure 2 shows low variability among low permittivity readings (dry conditions) and high variability among large permittivity values (wet conditions). For this measurement technique, there is a problem when transitions or rapid changes in environmental conditions occur.

FIGURE 2

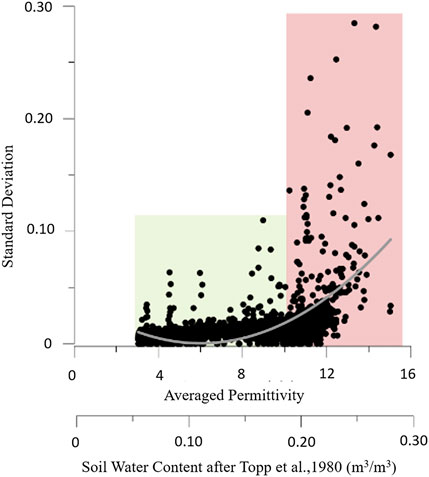
FIGURE 2. Hourly averaged permittivity values of SMT100 probes and its standard deviation (STD, n = 6) over a measuring period of 67 days. Classification according to scattering range possible (green): small STD range indicates nearly stable conditions and slightly changing conditions increase STD scatter range, (red): great STD range due to changing conditions; linear regression for both classified ranges and display of residual sum of squares and residual mean square.

Figure 2 indicates that the standard deviation also increases non-linearly and scatters in a greater range with increasing permittivity values. Therefore, the reproducibility is not comparable under different environmental conditions (dry, wet). This effect is especially relevant during and after rain events when the environmental conditions change and the soil water content increases rapidly. When very dry conditions prevail up to 8 (0.15 m³/m³), the SD is less than 5% in good agreement with the manufacturer’s specifications and varies only slightly. The STD scatter range increases slightly for conditions between 8 and 9 (0.15 and 0.17 m³/m³) and shows a greater variance for measured permittivity values above 9 (0.17 m³/m³). For each classified range a linear regression was carried out to determine the residual sum of squares (RSS) and residual mean square, i.e., mean residual square (MSR). RSS determines the dispersion of data points in considering the difference between data and an estimation fitting model, while MSR is used to provide an unbiased estimate of the variance of the errors. Small RSS values represent easy to define mathematical models. However, the RSS as a single measure cannot answer the question whether one or more data points deviate too much from that model and therefore, the MSR is needed. Figure 2 shows that RSS and MSR for the second range are smaller than the first range.

Therefore, it can be concluded that the permittivity values are consistent and the TDR measurements are accurate and stable when the environmental conditions are not changing significantly. However, when these conditions change, e.g. with increasing soil water content, the STD also increases significantly. Reasons for that increase could be inhomogeneous wetting and heterogeneities in soil properties. It is essential that sufficiently long time series are measured and provided to re-users to assess the temporal stability of this sensor. Also, the standard deviation is an essential statistical parameter in this context. The extent to which other statistical quantities, such as RSS or MRS in our example, are meaningful in terms of temporal variability assessment can be examined on the basis of the respective data. A prerequisite for such analyses is the existence of sufficiently long time series. To describe the trustworthiness of data, the test-retest datasets have to be linked.

3.1.2 Internal Consistency Test

Wireless soil moisture sensor networks provide distributed observations of soil moisture dynamics with high temporal resolution, as they typically involve a high number of TDR-sensors. Low-cost sensors are preferred for this application and unfortunately, they often show a non-negligible sensor-to-sensor variability. However, field measurements with multiple sensors at a nearly identical location and depth over a specific time period do not necessarily provide the same data. The influencing factors can be, among others, installation errors, altering sensors, or the heterogeneity of the soil material. Hence, a sensor-to-sensor consistency needs to be evaluated by assessing the extent to which two identical sensors at almost identical locations measure the same value simultaneously and respond in the same way to changing environmental conditions.

As an example, we evaluate measured data quality acquired with similar SMT100 sensors at two very close locations (10 cm distance) with two sensors at one depth (see Figure 3). The manufacturer provides information on the precision range of a sensor with ±3% for water content. The error range in measured relative permittivity follows a Laplace-Gauss distribution with a maximum range of almost Δϵ = 2.7.

FIGURE 3

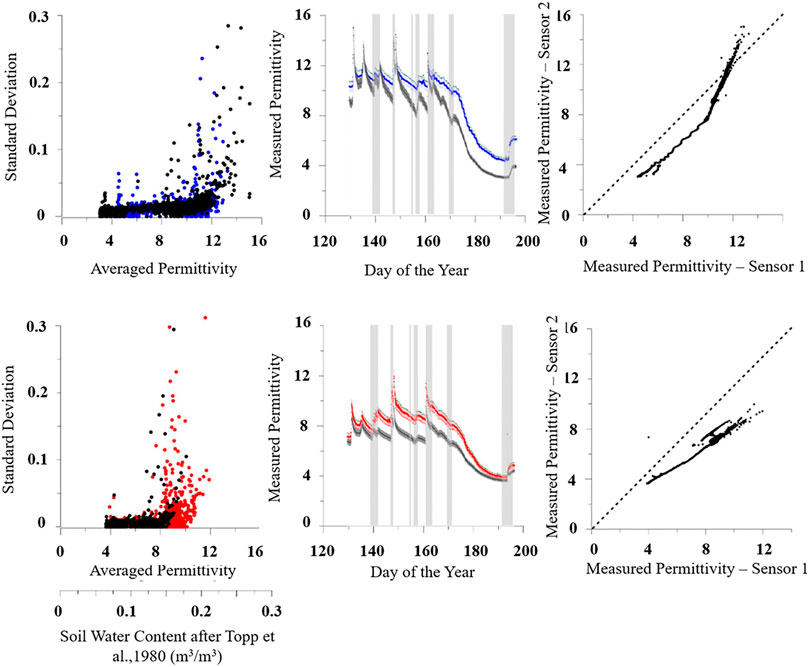
FIGURE 3. shows two examples of measurement behavior of two similar sensors at two almost identical locations at the same time. Above) Two sensors at a depth of 15 cm below the surface. Higher variability in measured permittivity is observed at this depth, and the test-retest reliability is not seen. While the measured permittivity of the two sensors differs only slightly at the beginning of the measurement, the difference rises with time. However, both sensors show the same response characteristics to rain events (displayed as gray bars). The correlation between these two sensors shows no satisfying consistency compared to the ideal consistency (dotted light gray line with uncertainty ranges - below). Two sensors at a depth of 45 cm below the surface. At this depth, a limited permittivity range and test-retest reliability are observed due to only minor changes. The difference in measured permittivity between these sensors is small and it is assumed that these two sensors are consistent because they are very close to the ideal behavior.

Therefore, the percentage error range is the highest for small relative permittivity values and the smallest for high values. In Figure 3 it can be seen that sensors are consistent if the variations in measured relative permittivity values are minimal and the correlation of both sensors correspond with the ideal consistency and is within the specified uncertainty range. The deeper sensors have lower variability and can be evaluated as consistent at least in the permittivity range between 6 and 8. The greater the relative permittivity the greater are the deviations from the ideal correlation line. The lower sensors show more variability and both sensors seem not to be consistent. A possible cause can be an installation error or a sensor malfunctioning.

Figure 4 shows an alternative evaluation method, the Bland-Altman analysis which is based on the quantification of the agreement between two quantitative measurements by determining the bias or mean difference as a measure of accuracy and construct limits of agreement (LOA) as a measure of precision (Altman and Bland, 1983 and; Altman and Bland 1986). It is used to evaluate the agreement among two different instruments or two measurement techniques (Montenij et al., 2017).

FIGURE 4

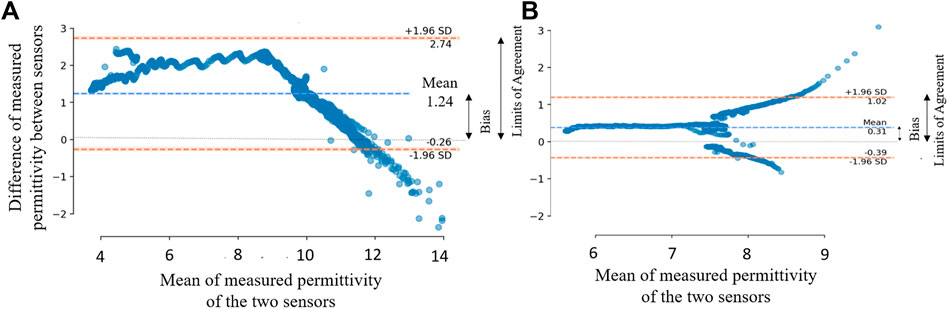
FIGURE 4. Result of a Bland- Altman analysis (Bland and Altman, 1999) for two x two sensors at a depth of 15 cm (A) and 45 cm (B). Panel shows the mean difference between two sensors at one depth (blue dotted line), expressing the bias to the corresponding zero difference. The precision range between the LOA (orange dotted line) is much smaller for the deeper sensors than the shallower sensors. Also, the curve for the deeper sensors indicates a nearly consistent behavior (constant variability until x = 7.8) followed by a constant coefficient of variation that proves an internal consistency. The lower sensors indicate a more significant bias and do not show constant variation coefficients; therefore, they cannot be classified as consistent.

These evaluations are essential for later data integration as well as data blending: whether or not it is possible for two sensors to provide the same measured permittivity data or consistency. For example, such a test may show a considerable variation of soil moisture derived from different sensors installed at almost the same location and the same depth. However, differences in the observed permittivity ranges measured with the sensors reveal biases caused by slightly different sensor characteristics as well as the heterogeneous soil conditions and changing environmental conditions. Hence, the soil moisture data interpretation is complicated without any detailed information on consistency reliability (e.g., based on sensor intercomparison results). Significantly, the lower level uncertainty can be evaluated by sensor intercomparison experiments or long-term data series, and the sensor behavior, especially variability, can also be assessed with the help of this data to some extent.

3.1.3 Inter-Rater Reliability Test

The inter-rater reliability can be caused by different experiences with, or general knowledge of, the behavior and property of relevant materials and instruments. Excellent examples of the operator’s influence on data reliability are 1) the measurement of water depth in a stream with a meter-ruler, 2) deriving data from historic maps or records and, 3) data acquisition/processing based on man-made optical evaluations such as ecological data acquisition (phenology) for ground-truthing of remote sensing campaigns. The expertise of skilled persons is particularly essential when it comes to a subjective assessment of environmental conditions such as choosing the right places for collecting soil samples (e.g., for later laboratory investigations of soil properties), evaluating plant species and the state of vegetation (phenology). It is clear that porosity and bulk density as important soil properties show variability, which is strongly affected by soil sampling quality. For instance, field investigators need to identify and assess all the main uncertainties when estimating field measurement uncertainty. These documented uncertainties also rely on the expertise of the investigator. However, such random errors are difficult to quantify and describe.

Furthermore, the installation, calibration and maintenance of TDR soil moisture sensors, for example, require such expertise. Improper sensor installation can lead to measurement errors that can falsify the overall result. Therefore, standardized operations procedures and standardized tests reported in DIN standards should be performed in the field. To reduce the inter-rater reliability, all measurements should be performed according to these standards and should be documented in this manner.

3.2 Approaches to Assess the Validity

3.2.1 Internal Validity

Internal validity refers to the bias potential: a consistent, repeatable error causing predictable systematic overestimated or underestimated values (Trajković, 2008). Such errors include sensor drifts and outliers, for example. Also, due to the time discretization of the measurements, errors arise when approximating the real conditions between two sampling points by straight-line approaches. However, this error becomes significant when the conditions change rapidly. By increasing the sampling frequency, the error could be reduced.

Many sensors show temporal drifting processes of the measured property, regardless of the manufacturer, the sensor complexity, the sensor acquisition costs, and its application with their lifetime. This temporal sensor drift is caused by physical changes in the sensor, variations caused by the surrounding environment (e.g., temperature or humidity effects, biofouling), or degradation by related sensor-aging. The existence of the drift in the measurement is difficult to detect and distinguish from the fundamental errors and noise in the measurement (Cho, 2012). Implementing sensor redundancy configuration and repeated sensor calibrations can reduce the operational risk from drifting. However, there is still a possibility of out of tolerance drifting before the next calibration. Therefore, it is essential to assess and describe the drift effects caused by various influencing factors through permanent drift evaluation to a defined reference or implemented automatic calibration procedures within a test-retest frame. Accuracy refers to the closeness of the measured value to the true or reference value.

Figure 5 shows an example of the accuracy of measured permittivity values to reference values. These reference values in different depths were gained by gravimetric in-situ determination of soil water content and a recalculation to permittivity values. The accuracy is better for sensors with smaller variability. This can be seen for the deeper sensors.

FIGURE 5

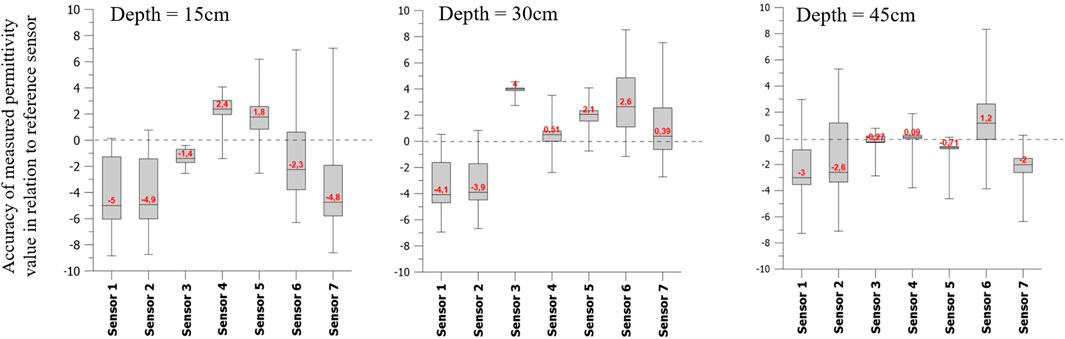
FIGURE 5. Difference to reference sensor for 3 depths (15, 30 and 45 cm), Box-Whisker Plot (Min, Maximum, Median value in red), dotted line median of difference at a certain depth.

3.2.2 External Validity

The external validity refers to the generalizability of the data. In this subsection, we discuss data transferability derived from proxy-transfer functions to obtain water content data.

Many methods of data provisioning are based on indirect measurement of the target variables. Hence, the measured value(s) must be transferred to the required parameters, for instance, by established and reported empirical or sophisticated equations or inversion algorithms. For many geoscientific applications (e.g., for the soil water content), so-called Pedo-Transfer Functions (PTFs) are used. Caused by the fact that pedo indicates the soil, we use the more general term Proxy–Transfer Functions (also PTFs). Examples of such PTFs are manifold and can be found among others in marine science, biogeoscience, hydrology, soil science, remote sensing (e.g., Zhang and Zhou, 2016; Klotz et al., 2017; Van Looy et al., 2017). Well-known soil-related examples include the established transfer from measured relative permittivity to soil water content, the transfer of measured neutron counts of Cosmic Ray measurements to soil water content, the transfer of the measured brightness temperature measured by remote sensing to soil moisture content. The application of such PTFs mainly relies on internal consistency reliability, i.e., with detailed information a specific PTF provides identical results. If the targeted parameter cannot be measured directly and needs to be derived with the help of these PTF, several assumptions are incorporated, and therefore the uncertainties of these assumptions influence the trustworthiness of higher-level data.

Here, we show this with a well-established example relevant to soil science, geophysics, and remote sensing. Mainly, pre-established Pedo-Transfer Functions (PTFs) such as empirical equations based on laboratory data, volumetric mixing formulae using compound electrical properties or model approximations are commonly used (Topp et al., 1980; Ledieu et al., 1986; Roth et al., 1990; Graeves et al., 1996; Wilson et al., 1996).

Out of these, in Table 1 three well-known PTFs are the empirical Topp formula, the empirical relationship established by Roth et al. (1992) or the Complex Refractive Index Method (CRIM) formula describing a three-phase system are discussed (Topp et al., 1980; Graeves et al., 1996; Wilson et al., 1996; Steelman and Endres, 2011).

TABLE 1

TABLE 1. Discussed Pedo-Transfer Functions (PTFs), their relationship of relative permittivity or dielectric constant to volumetric water content in soil (soil water content) and error estimation.

It is difficult to determine the most appropriate PTF without any other geological constraints or additional in situ experimental measurements (Bano, 2004). Figure 6 shows the application of these three PTFs to the data. In general, the soil water content derived through these formulas shows the same trend. However, the Topp and Roth results are generally lower than the CRIM results (Dawreaa et al., 2019; Du et al., 2020). The CRIM formula requires either an estimation based on soil data or a time-consuming laboratory determination of five additional parameters, which also influences the overall uncertainty range. In our case, the porosity was calculated from the particle density and the bulk density and subsequent assumptions for ɛ_solid = 3.4 (Roth et al., 1990), ɛ_air = 1, and the temperature-dependent dielectric permittivity of water, ɛ_water, was assumed to be 78.54 at 25°C (Weast, 1987). However, it is also a frequency-dependent variable.

FIGURE 6

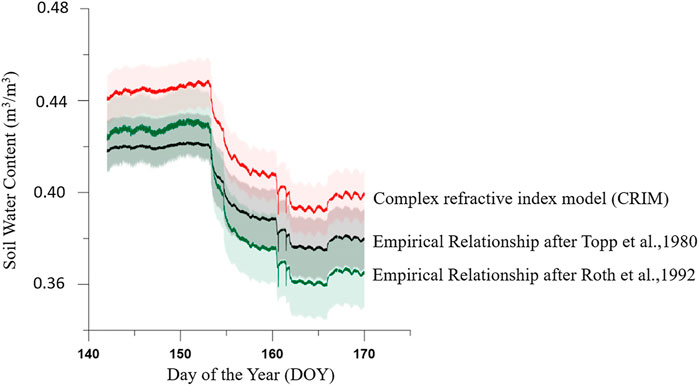
FIGURE 6. Application of different PTFs on measured dielectric permittivity data. The panel shows derived soil water content in cm³/cm³ and the related uncertainty for three different PTFs. Panel shows the changing environmental conditions. Starting at day 153, there are drying processes in the subsurface. The soil water contents derived with different PTF show synchronous course but biased.

Minasny et al. (1999) found that the uncertainty due to the PTFs parameters is usually small compared to the uncertainty inherent in the measured input data. However, Figure 6 indicates that this is not obvious in the exemplary data.

Uncertainty in such Proxy-Transfer Functions can result from the structure, coefficients, bias in the model, uncertainties in the input parameters, and measurement errors (Minasny and Bratney, 2002; Dobarco et al., 2019). The overall uncertainty is difficult to assess, but some approaches result in an uncertainty assessment for some known effects. As one example, Gaussian error propagation can be used to analytically determine the uncertainty by considering that the uncertainties of the individual measured variables can partially compensate for each other. Applied to our data, the uncertainty with the Topp formula is about 5 vol% and 6–7 vol% for the more complex CRIM formula. Studies of Roth et al. (1990) indicate a relative uncertainty of 16 vol%, using the Topp formula for very dry soil, whereas 1.2 vol% are indicated for wet soil. Therefore (Roth et al., 1992), established empirical relationships using TDR for mineral soils, organic soils, and magnetic soils. Especially for dry soils, it is therefore essential to always assess and describe the applied empirical relationship and the related uncertainties in the metadata for interpreting or sharing the data. Another approach to quantify the resulting uncertainty is application of the Monte Carlo method, or machine learning methods such as Latin hypercube sampling, which are tested for their suitability (Minasny and Bratney, 2002).

3.3 Approaches to Describe the Provenience

Data Provenience supports the confidence and validity of data by providing detailed information on data origin and its processing steps in a consistent way. In recent years, the application of blockchain technology to the management of research data and, in particular, to the security of the provenance of research data and its integrity are also being discussed (Stokes, 2016; Ramachandran and Kantacioglu, 2017; Boeker, 2021). There will certainly be outstanding approaches with blockchain technology regarding provenience assessment in the next few years but this technology will not be evaluated in this paper. This subchapter focuses on provenience associated with data visualization and the trustworthiness assessment of maps and Geographical Information Systems (GIS) applications. Nowadays, many maps are used digitally via e.g., Web Map Service (WMS), Web Map Tile Service (WMTS), Web Feature Service (WFS) for further analysis or data blending. The production, distribution and usage of geospatial data is undergoing massive changes in the last years with citizens consuming and producing a huge amount of data. The trustworthiness of maps depends on the trustworthiness of source data and the description of manipulating/processing this source data to gain spatial representative maps. In particular, the density of their input data plays an essential role in describing the source data and is strongly related to the transformation processes.

With the complexity of maps, professional execution and adapted scaling and resolution can give users an unjustified degree of perfection concerning the information displayed. Digital maps generated by applying geostatistical software provided by GIS usually imply a higher coverage than can be attributed to the original observation (source) data. Likewise, different line and dot thicknesses obscure the precise positional accuracy depending on the zoom (displayed scale). This visualization usually gives the impression of being isolated from the acquisition and analyzing process that produced the visual product without closer examination. Besides, visualizing informative maps by combining several independent source data with different reliability characteristics is challenging. Especially if information about source provenience is not given, understanding and assessing this visualization is difficult. Many spatially and temporally varying sources of uncertainties in digital maps reported by Wang et al. (2005) accumulate and are propagated to the maps. These sources of uncertainty include 1) sampling and measurement errors during data acquisition and 2) positioning errors, e.g., due to inaccurate image interpretation and digitizing of boundaries. Besides, sources of uncertainty are also 3) overlapping and scaling errors, 4) errors related to the rectification of images during data processing as well as 5) model errors, e.g., due to misunderstanding of existing relationships during data analysis (Wang et al., 2005).

Standardized geospatial data quality evaluation processes are well described in the ISO 19157 standard, which represents a conceptual model of data quality defining a set of data quality measures for use in evaluating and reporting data quality (completeness, logical consistency, positional consistency, temporal consistency, thematic consistency and usability). This standard is applicable to data producers providing quality information to describe and assess how well a data set conforms to its product specification and to data users attempting to determine whether or not specific geographic data are of sufficient quality for their particular application. ISO 19157 acknowledges that important information on data quality such as % of missing and interpolated data, can exist as standalone quality reports. Even if such standards exist, the implementation and everyday usage is not yet fully established in the scientific community. Besides the data quality as evaluated by this ISO 19157 standard, the description of source and transformation provenience is essential to assess the trustworthiness of the map production.

Interpolation and arithmetic map operations are widespread procedures used in GIS or machine learning procedures. Arithmetic map operations combine raster maps resulting in a new and improved raster map, and the propagation of the associated uncertainty depends on reliable measurements of the local accuracy and local covariance. Spatial interpolations derived from limited measurement data are always associated with uncertainties. The interpolation error should be more significant in areas where small-scale variation is more considerable. Therefore, the resulting map must have some standardized information about assessing these related uncertainties and provide detailed information about the transformation provenience (e.g., Crosetto et al., 2000; Heuvelink and Pebesma, 2002; Atkinson and Foody, 2006).

As an example, we used derived soil water content data over a specific area. Figure 7 shows the kriging result in dependence on the percentage of available source data. A procedure selected a defined percentage (5, 33, 66 and 100%) of the input data and performed kriging. This example shows the strong dependence on the number of data points and the influence of maximum and minimum values on the result and demonstrates the importance of this information for the understanding of the generated maps.

FIGURE 7

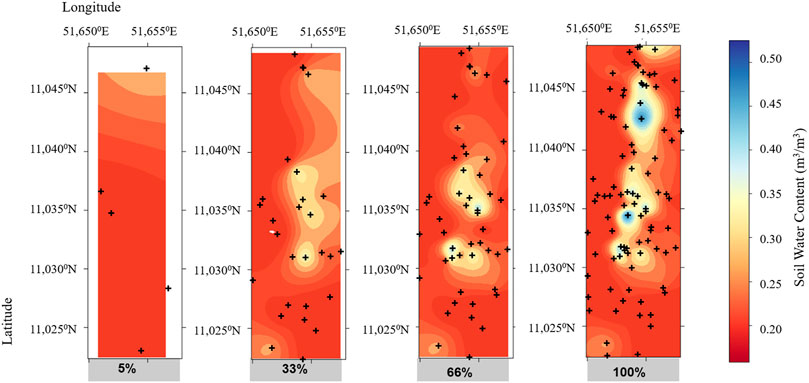
FIGURE 7. Random selection of data points with a defined percentage of source data and kriging (linear slope = 1 and anisotropy = 1.0).

Also, Kriging techniques as a data interpolation method based on pre-defined covariance models predict values at unsampled locations from available measurement data. The different Kriging approaches such as simple Kriging, ordinary Kriging, universal Kriging, external drift Kriging and simple detrended Kriging provide different ways to calculate the weights dependent on the given covariance model and the location of the target point. Therefore, information about the Kriging method used and the covariance model are essential to improve the trustworthiness of maps.

Another important information is the point density coverage describing the distribution of observation points within an interpolated map. Although, the amount of missing and interpolated points is to be mentioned in accordance with ISO 19157, in interpolated maps this kind of information is mostly missing. Therefore, point density analysis seems to be a useful tool for assessing the trustworthiness of maps and has to be included into the provenience description. A simple point density calculation sums up the points within a specific prior defined grid and divides this by the area size. Point density analyses or Kernel density analysis functionalities in GIS such as ArcGIS and QGIS, provide a quantitative value and visual display capability that shows the concentration of points is available. Figure 8 shows the point density coverage in a prior defined regular grid and indicates that no real observation points are present in some grid cells and the given value is based on the used kriging method.

FIGURE 8

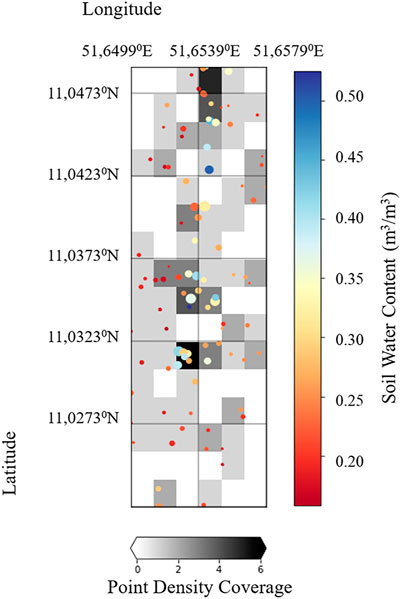
FIGURE 8. Point density coverage (grayscale) and the derived soil water content intensity after Topp formula. The figure shows several grid cells where no measurement points are located and therefore, these map values represent only interpolated values. There are also grid areas where maximum values were measured and where surrounding grid areas have no measured values as a basis. In such cases, the influence of maximum values is particularly noticeable.

Also, some auxiliary data such as remote sensing data or other observation data in a medium or small resolution are used to derive detailed soil moisture patterns and their provenience needs to be described for secondary users. As one example, Schroeter et al. (2015) and (Schroeter et al. 2017) implemented external drivers of soil formation that control processes of water redistribution within fuzzy c-means sampling and estimation (FCM SEA) approach to capture the spatiotemporal variability of soil moisture in an exemplary catchment. The additional integration of several terrain attributes and red-edge based normalized difference vegetation index patterns projected on the Digital Elevation Model (DEM) with a 1.0 m × 1.0 m resolution provides a much more detailed soil moisture map even when the sampling points could not achieve such a high map resolution (see Figure 9). However, without the knowledge and detailed information of the input parameters and their resolution, the assumptions within the fuzzy c-means algorithm and the estimation error to estimate the sampling points for validation, the secondary user of such a map is unable to understand the significance, accuracy and limitations of such a map.

FIGURE 9

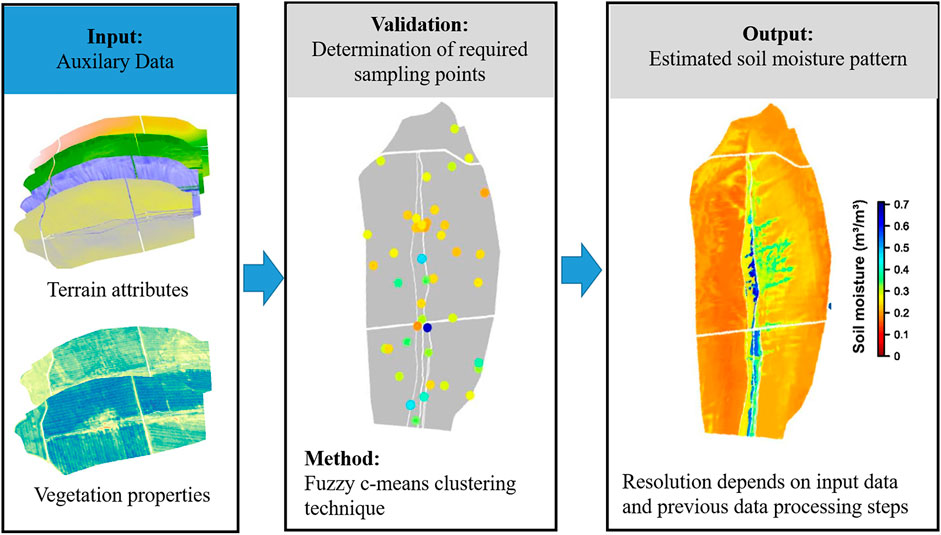
FIGURE 9. Simplified flow chart of the fuzzy c-means sampling and estimation approach (FCM SEA) with combined integration of terrain attributes and red-edge based normalized difference vegetation index patterns (after Schroeter et al., 2017).

Therefore, information on source provenience and their point density coverage and transformation provenience such as the used manipulating methods, the applied interpolation method and their settings used to create the spatial information must be made available to the map user on request to allow a trustworthiness assessment. In consequence, essential information on provenience should include metadata on the data origin (measuring principle, uncertainties, link to corresponding metadata), previous data processing steps (QA/QC steps, defined ranges, manipulating steps such as averaging or smoothing), visualization processing steps and assumptions made (point density coverage and used interpolation method and settings). Here, the two standards ISO 19115 and ISO 19139, dealing with standardizing the metadata of GIS products should be taken into account for metadata description. The plugins for QGIS and ArcGIS allow a rapid implementation and a great acceptance of those tools.

4 Discussion

Data reuse and interoperability for all kinds of data but especially for geospatial data becomes very popular also to minimize the costs and delays and therefore, the roles and responsibilities of producers, distributors and users and services are evolving (Bédard et al., 2015). Extensive data documentation with the help of metadata is essential to provide structured information that describes, explains and locates the data to enable the correct and proper discovery, usage, sharing, as well as management of data resources over a more extended period. The requirements of detailed metadata information depend on the concrete scientific context. Many scientific user communities develop metadata schemes as a precursor of a standard to optimally describe the generated data in accordance with their scientific needs. Also, several different metadata schemes are already available as standards for general purpose (e.g., Dublin Core, Metadata Object Description Schema) or several specific scientific standards such as the Darwin Core, Ecological Metadata Language, or NASA standards (Guenther, 2003; Fegraus et al., 2005; Méndez, 2006; Wieczorek et al., 2012; Hider, 2019). However, scientific communities are often small and highly specialized, establishing extensive and less standardized corresponding metadata. For each standard, e.g. in ICOS variables and parameters, their meaning and unit are specified (ICOS, 2021). However, there is a significant overlap among metadata content schemes/standards.

Nowadays, in addition to the scientists, data engineers and data scientists are involved in the process of generating the appropriate metadata content and deciding on the metadata content necessary for proper data sharing. Often, metadata compilation is perceived as a burden by researchers and, therefore, is incomplete and error-prone (Zilioli et al., 2019a). Nevertheless, curation staff can support scientists by stimulating their willingness to share (meta)data by identifying contextual causes that constrain the practice or simplifying the creation procedures with informatics facilities (e.g., Fugazza et al., 2018; Zilioli et al., 2019b).

Still, many examples show that scientific datasets are often generated with incomplete metadata or do not follow standards to facilitate interoperability and reusability. Metadata are often missing, incomplete, or ambiguous, and sometimes different sources give conflicting information (Kennedy and Kent, 2014). Kent et al. (2007) assessed metadata from International Comprehensive Ocean-Atmosphere Data Set (ICOADS) and World Meteorological Organization (WMO) publications and found disagreement in around 20–40% of cases where metadata was described within both sources. Another difficulty of sharing data is the incompatible representation of data due to, for example, the usage of different schemas and different formats (Wang et al., 2014). (Gordon and Habermann 2018) investigated different conventions and missing metadata in different repositories. They stated that comparing completeness across metadata collections in multiple dialects is a multi-faceted problem. Metadata representations (dialects) are typically specific by the communities and the study determined different grades of completeness in the relevant repositories (Gordon and Habermann, 2018). To avoid this discrepancy within the metadata description, a standardized scheme for data reliability assessment should be discussed and decided within an interdisciplinary scientific community.

In Table 2, the authors summarize the information needed to describe data trustworthiness with its three indicators regarding environmental data elaborated on the basis of the described soil moisture examples. It turns out that it is a big challenge to find statistical quantities or indicators to describe reliability, validity and provenance on soil moisture data sufficiently in a standardized way. However, this list should be seen as a first attempt and a basis for further discussions. It is clear that only some of the points are equally important and can be generalized to other measured data. Other environmental variables often require other reliability and validity assessment approaches and other indicators included in data provenience information. It is obvious, to introduce data trustworthiness issues into metadata description assessment of reliability with reproducibility, repeatability and consistency tests and validity considering the credibility and transferability, as well as provenience issues, need to be taken into account, and a standardized vocabulary within environmental science is the essential precondition to start with. Besides, the meaning of specific terms needs to be clarified and well accepted in an interdisciplinary community.

TABLE 2

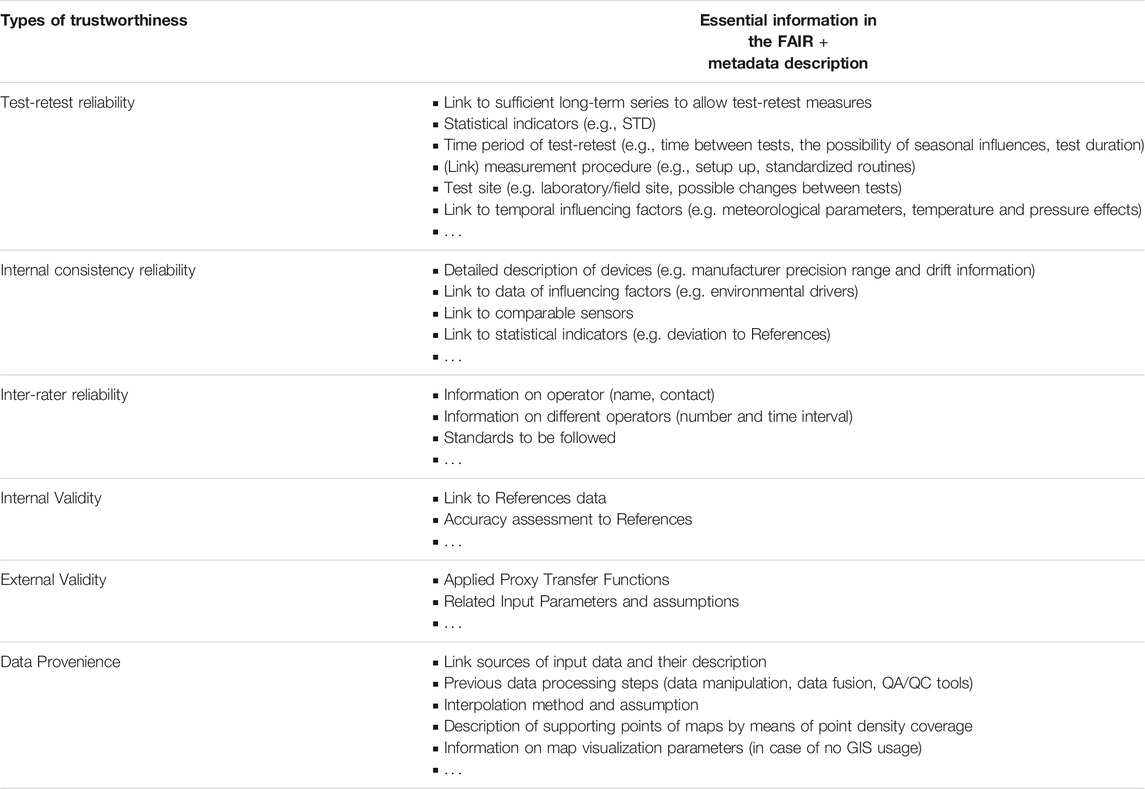
TABLE 2. Summary of essential information in the FAIR + metadata description for the above-discussed data trustworthiness issues. This table should be seen as a first attempt and a basis for further discussions.

An important discussion in the environmental community is to what extent all essential information should be described in the metadata. Too many required metadata generate unmanageability and are then mostly not provided by the observers due to time pressure. Especially for metadata descriptions with a large breadth of varied content, the metadata can be divided into multiple metadata fields. This division can improve the unmanageability but also tend to be not transparent enough for environmental data with its various number of data producers, processors and users.

Perhaps it is more manageable if each dataset is sufficiently linked to secondary datasets with its own metadata description and this linking is described in the metadata. The authors recommend linking the data with descriptive statistical analyses or other data collected with the same instruments and the same task such as the soil moisture measurements from one campaign to data from another campaign using the same devices. Also, automatic tools used for QA/QC and statistical measurement can create records linked to the original dataset and automatically insert information into the metadata.

Many re-users of measurement data assume that manufacturer’s specification, certain calibration routines and the measurement of other auxiliary variables are sufficient to evaluate and describe the data trustworthiness. They are not fully aware of the errors, uncertainties, variability such as drifts with sensor lifetime and non-reproducibility that exist in measurement data and how to assess them.

This paper provides a basis for discussion regarding the requirements to evaluate and describe data trustworthiness. The first possible approaches to assessing reliability, validity and provenience within the data lifecycle are discussed. However, no claim of completeness is made. These requirements in terms of reproducibility, repeatability, consistency, and transferability using TDR soil moisture measurements are discussed and shown in the paper. Soil moisture is a suitable climate variable to point out the whole workflow and the inherent uncertainties starting at the measurement of dielectrical permittivity, the derivation of volumetric soil moisture by using PTFs and subsequently the spatial representation of this derived quantity. Of course, these discussed approaches could be adapted to other variables, sensors or measurement methods, and prediction or models at any time. The authors see the paper as a grounding basis for discussion to evaluate and describe the data trustworthiness in a standardized way and make it available to all further secondary data users.

The paper defined the meaning of data trustworthiness in the context of environmental data. The discussed examples focus only on selected parts within this trustworthiness assessment issue. However, these examples clearly indicate the difficulties and constraints in assessing the data trustworthiness and its related metadata description. FAIR Data protocols, Standard Operating Procedures (SOPs), and information about data trustworthiness assessment should become standard for groups of various sensors. Large observation networks, ICOS for example, have already established standards and follow these standardized routines.

Obviously, there is a crucial requirement to include related data trustworthiness evaluation data and the description in second-level datasets and their metadata to strengthen open data within the scientific community and reuse them. Hence, it is necessary to improve data collectors’ awareness of the established linked datasets or metadata content and to emphasize the advantages of comprehensively archived data and metadata information concerning, for example, secondary data usage, data evaluation and campaign planning, in order to justify the additional expenditure of time.

A guiding principle of all kinds of data research should be that without a detailed data trustworthiness evaluation and corresponding metadata description, data becomes un-FAIR.

Next, the trustworthiness of metadata should be investigated and evaluated. Appropriate approaches should be developed and verified based on existing metadata repositories.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

UK, CS and PD conceived of the presented idea. PS provided associations with assessment approaches in medical sciences. PD supervised the findings of this work. UK took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript.

Funding

This work was supported by from the Initiative and Networking Fund of the Helmholtz Association through project “Digital Earth” (funding code ZT-0025). We also acknowledge funding from the Helmholtz Association in the framework of MOSES (Modular Observation Solutions for Earth Systems).

Conflict of Interest

Author UK was employed by the company Geotomographie GmbH.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The project Digital Earth has been strategically initiated by all eight centers of the Helmholtz research field Earth and Environment (E&E). Digital Earth is funded by the Helmholtz research field Earth and Environment (E&E) and co-financed from eight E&E centers (Alfred Wegener Institute, GEOMAR Helmholtz Centre for Ocean Research Kiel, Forschungszentrum Jülich GmbH, Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences, Helmholtz-Zentrum Hereon, Karlsruhe Institute of Technology (KIT), Helmholtz Centre for Environmental Research - UFZ, Helmholtz-Zentrum München). This work was additionally supported by funding from the Helmholtz Association in the framework of the Helmholtz funded observation system MOSES (Modular Observation Solutions for Earth Systems). The authors also thank the native speaker Paul Ronning for proofreading the manuscript.

References

Allen, M. (2017). External Validity in: The SAGE Encyclopedia of Communication Research Methods. Available at: http://methods.sagepub.com/Reference//the-sage-encyclopedia-of-communication-research-methods/i5084.xml (Accessed February 1, 2021).

Google Scholar

Altman, D. G., and Bland, J. M. (1983). Measurement in Medicine: the Analysis of Method Comparison Studies. The Statistician 32, 307–317. doi:10.2307/2987937

CrossRef Full Text | Google Scholar

Altman, D. G., and Bland, J. M. (1986). Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. The Lancet 327, 307–310.

Google Scholar

Andrade, C. (2018). Internal, External, and Ecological Validity in Research Design, Conduct, and Evaluation. Indian J. Psychol. Med. 40 (5), 498–499. doi:10.4103/IJPSYM.IJPSYM_334_18

PubMed Abstract | CrossRef Full Text | Google Scholar

Atkinson, P. M., and Foody, G. M. (2006). Uncertainty in Remote Sensing and GIS, 1–18. doi:10.1002/0470035269.ch1

CrossRef Full Text | Google Scholar

Bano, M. (2004). Modelling of GPR Waves for Lossy media Obeying a Complex Power Law of Frequency for Dielectric Permittivity. Geophys. Prospecting 52, 11–26. doi:10.1046/j.1365-2478.2004.00397.x

CrossRef Full Text | Google Scholar

National Institute for Standards and Technology (NIST) (1994). in Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. Editors Barry. N. Taylor, and Chris. E. Kuyatt (Gaithersburg, MD: NIST Technical Note 12971994 Edition). Available at: http://physics.nist.gov/Pubs/guidelines/contents.html (Accessed July 7, 2020).

Google Scholar

Bédard, Y., Wright, E., and Rivest, S. (2015). A Guide to Geospatial Data Quality. Conference: Natural Resources Canada (Geoconnexion) Series of Webinars Quebec City, Ottawa, Intelli3, Natural Resources Canada (Geoconnexion). doi:10.13140/RG.2.1.2819.1763

CrossRef Full Text | Google Scholar

Bent, B., Goldstein, B. A., Kibbe, W. A., and Dunn, J. P. (2020). Investigating Sources of Inaccuracy in Wearable Optical Heart Rate Sensors. Npj Digit. Med. 3, 18. doi:10.1038/s41746-020-0226-6

CrossRef Full Text | Google Scholar

Bialocerkowski, A. E., and Bragge, P. (2008). Measurement Error and Reliability Testing: Application to Rehabilitation. Int. J. Ther. Rehabil. 15, 422–427. doi:10.12968/ijtr.2008.15.10.31210

CrossRef Full Text | Google Scholar

Birchak, J. R., Gardner, C. G., Hipp, J. E., and Victor, J. M. (19941974). High Dielectric Constant Microwave Probes for Sensing Soil Moisture. Proc. IEEE 62, 93–98.

Google Scholar

Bland, J. M., and Altman, D. G. (1999). Measuring Agreement in Method Comparison Studies. Stat. Methods Med. Res. 8, 135–160. doi:10.1191/096228099673819272

PubMed Abstract | CrossRef Full Text | Google Scholar

Blumberg, B., Cooper, D. R., and Schindler, P. S. (2005). Business Research Methods. Berkshire: McGrawHill Education.

Google Scholar

Boeker, E. (2021). Forschungsdaten und die Blockchain. Available at: https://www.forschungsdaten.info/themen/speichern-und-rechnen/forschungsdaten-und-die-blockchain/(Accessed July 28, 2021).

Google Scholar

Brovelli, A., and Cassiani, G. (2008). Effective Permittivity of Porous media: A Critical Analysis of the Complex Refractive index Model. Geophys. Prospecting 56 (5), 715–727. doi:10.1111/j.1365-2478.2008.00724.x

CrossRef Full Text | Google Scholar

Brown, A. W., Kaiser, K. A., and Allison, D. B. (20182018). Issues with Data and Analyses: Errors, Underlying Themes, and Potential Solutions. Proc. Natl. Acad. Sci. USA 115 (11), 2563–2570. doi:10.1073/pnas.1708279115

PubMed Abstract | CrossRef Full Text | Google Scholar

Bush, T. (2012). “Authenticity in Research: Reliability, Validity and Triangulation,” in Research Methods in Educational Leadership and Management. Editors A. Briggs, M. Coleman, and M. Morrison (Thousand Oaks, CA: SAGE Publications Ltd). doi:10.4135/9781473957695.n6

CrossRef Full Text | Google Scholar

Cai, L., and Zhu, Y. (2015). The Challenges of Data Quality and Data Quality Assessment in the Big Data Era. Codata 14, 2. doi:10.5334/dsj-2015-002

CrossRef Full Text | Google Scholar

Castello, C. C., Sanyal, J., Rossiter, J., Hensley, Z., and New, J. R. (2014). Sensor Data Management, Validation, Correction, and Provenance for Building Technologies, Proceedings of the ASHRAE Annual Conference and ASHRAE Transactions. Available at: http://web.eecs.utk.edu/∼jnew1/publications/2014_ASHRAE_provDMS_sensorDVC.p.df (Accessed July 28, 2021).

Google Scholar

Chakrabartty, S. N. (2013). Best Split-Half and Maximum Reliability. IOSR J. Res. Method Education 3 (1), 1–8.

Google Scholar

Chang, P.-C., Lin, Y.-K., and Chiang, Y.-M. (2019). System Reliability Estimation and Sensitivity Analysis for Multi-State Manufacturing Network with Joint Buffers--A Simulation Approach. Reliability Eng. Syst. Saf. 188, 103–109. doi:10.1016/j.ress.2019.03.024

CrossRef Full Text | Google Scholar

Cho, S. (2012). A Study for Detection of Drift in Sensor Measurements. in Electronic Thesis and Dissertation Repository, 903. Available at: https://ir.lib.uwo.ca/etd/903 (Accessed July 28, 2021).

Google Scholar

Corradini, C. (2014). Soil Moisture in the Development of Hydrological Processes and its Determination at Different Spatial Scales. J. Hydrol. 516, 1–5. doi:10.1016/j.jhydrol.2014.02.051

CrossRef Full Text | Google Scholar

Creswell, J. W. (2013). Qualitative Inquiry and Research Design: Choosing Among Five Approaches. Thousand Oaks, CA: Sage.

Google Scholar

Crosetto, M., Tarantola, S., and Saltelli, A. (2000). Sensitivity and Uncertainty Analysis in Spatial Modelling Based on GIS. Agric. Ecosyst. Environ. 81, 71–79. doi:10.1016/S0167-8809(00)00169-9

CrossRef Full Text | Google Scholar

Dawreaa, A. A., Zytnerb, R. G., and Donald, J. (2019). An Improved Method to Measure In Situ Water Content in a Landfill Using GPR, CSCE ANNUAL Conference, Laval (Greater Montreal), June 12-15. Available at: https://csce.ca/elf/apps/CONFERENCEVIEWER/conferences/2019/pdfs/PaperPDFversion_12_0405075523.pdf (Accessed July 20, 2021).

Google Scholar

Dekkers, O. M., Elm, E. v., Algra, A., Romijn, J. A., and Vandenbroucke, J. P. (2010). How to Assess the External Validity of Therapeutic Trials: a Conceptual Approach. Int. J. Epidemiol. 39 (1), 89–94. doi:10.1093/ije/dyp174

CrossRef Full Text | Google Scholar

Devillis, R. E. (2006). Scale Development: Theory and Application. Applied Social Science Research Method Series, 26. Newbury Park: SAGE Publishers Inc.

Google Scholar

Diffbot Technologies Corp (2021). Data Provenance, Menlo Park/CA. Available at: https://blog.diffbot.com/knowledge-graph-glossary/data-provenance/(Accessed February 1, 2021).

Google Scholar

Dobson, M., Ulaby, F., Hallikainen, M., and El-Rayes, M. (1985). Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sensing GE-23, 35–46. doi:10.1109/TGRS.1985.289498

CrossRef Full Text | Google Scholar

Domholdt, E. (2005). Physical Therapy Research. Principles and Applications. Philadelphia: WB Saunders Company.

Google Scholar

Du, E., Zhao, L., Zou, D., Li, R., Wang, Z., Wu, X., et al. (2020). Soil Moisture Calibration Equations for Active Layer GPR Detection-A Case Study Specially for the Qinghai-Tibet Plateau Permafrost Regions. Remote Sensing 12, 605. doi:10.3390/rs12040605

CrossRef Full Text | Google Scholar

EU (2021). Data Validation in Business Statistics. Available at: https://ec.europa.eu/eurostat/documents/54610/7779382/Data-validation-in-business-statistics.pdf (Accessed February 1, 2021).

Google Scholar

Fegraus, E., Andelman, S., Jones, M., and Schildhauer, M. (2005). Maximizing the Value of Ecological Data with Structured Metadata: An Introduction to Ecological Metadata Language (EML) and Principles for Metadata Creation. Bull. Ecol. Soc. America 86. doi:10.1890/0012-9623(2005)86[158:mtvoed]2.0.co;2

CrossRef Full Text | Google Scholar

Fugazza, C., Pepe, M., Oggioni, A., Tagliolato, P., and Carrara, P. (2018). Raising Semantics-Awareness in Geospatial Metadata Management. Ijgi 7 (9), 370. doi:10.3390/ijgi7090370

CrossRef Full Text | Google Scholar

Glavic, B., and Dittrich, K. (2007). “Data Provenance: A Categorization of Existing Approaches,” in Datenbanksysteme in Business, Technologie und Web (BTW)/12. Fachtagung des GI-Fachbereichs "Datenbanken und Informationssysteme" (DBIS), 07.-09.03.2007 in Aachen. Editors A. Kemper, H. Schöning, T. Rose, M. Jarke, T. Seidl, C. Quixet al. (Bonn, 227–241. doi:10.5167/uzh-24450

CrossRef Full Text | Google Scholar

Gordon, F. R. (2018). Identifying Validity in Qualitative Research: A Literature Review. Available at: https://pdfs.semanticscholar.org/ac9c/b9f0b26ab67329b84934b2a4b52b5922329c.pdf (Accessed July 31, 2020).

Google Scholar

Gordon, S., and Habermann, T. (2018). The Influence of Community Recommendations on Metadata Completeness. Ecol. Inform. 43, 38–51. doi:10.1016/j.ecoinf.2017.09.005

CrossRef Full Text | Google Scholar

Graeves, R. J., Lesmes, D. P., and LeeToksoez, J. M. M. N. (1996). Velocity Variations and Water Content Estimated from Multi-Offset Ground-Penetrating Radar. Geophysics 61, 683–695.

Google Scholar

Guenther, R. S. (2003). MODS: The Metadata Object Description Schema. Portal: Libraries and the Academy 3, 137–150. doi:10.1353/pla.2003.0006

CrossRef Full Text | Google Scholar

Heuvelink, G. B. M., and Pebesma, E. J. (2002). “Is the Ordinary Kriging Variance a Proper Measure of Interpolation Error?” in Proceedings of the Fifth International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences. Editors G. Hunter, and K. Lowell (Melbourne: RMIT University), 179–186.

Google Scholar

Hider, P. (2019). Metadata Standards. Cambridge University Press. doi:10.29085/9781783302253.009

CrossRef Full Text | Google Scholar

Huisman, J. A., Hubbard, S. S., Redman, J. D., and Annan, A. P. (2003). Measuring Soil Water Content with Ground Penetrating Radar: A Review. Vadose Zone J. 2, 476–491. doi:10.2136/vzj2018.03.0052

CrossRef Full Text | Google Scholar

ICOS (2021). Instruction on Soil Meteorological Measurements. Available at: http://www.icos-etc.eu/icos/documents/instructions/soilmet (Accessed May 21, 2021).

Google Scholar

Iso 5725-1, (1994). Accuracy (Trueness and Precision) of Measurement Methods and Results — Part 1: General Principles and Definitions. Available at: https://www.iso.org/obp/ui/#iso:std:iso:5725:-1:ed-1:v1:en (Accessed July 31, 2020).

Google Scholar

Jacobsen, A., de Miranda Azevedo, R., Juty, N., Batista, D., Coles, S., Cornet, R., et al. (2020). FAIR Principles: Interpretations and Implementation Considerations. Data Intellegence 2, 10–29. doi:10.1162/dint_r_00024

CrossRef Full Text | Google Scholar

Kennedy, J., and Kent, E. (2014). A Review of Uncertainty in In Situ Measurements and Data Sets of Sea-Surface Temperature, 52. doi:10.1002/2013rg000434

CrossRef Full Text | Google Scholar

Kent, E. C., Woodruff, S. D., and Berry, D. I. (2007). Metadata from WMO Publication No. 47 and an Assessment of Voluntary Observing Ship Observation Heights in ICOADS. J. Atmos. Oceanic Technology 24, 214–234. doi:10.1175/JTECH1949.1

CrossRef Full Text | Google Scholar

Kimberlin, C. L., and Winterstein, A. G. (2008). Validity and Reliability of Measurement Instruments Used in Research. Am. J. health-system Pharm. AJHP : official J. Am. Soc. Health-System Pharm. 65, 2276–2284. doi:10.2146/ajhp070364

CrossRef Full Text | Google Scholar

Klotz, D., Herrnegger, M., and Schulz, K. (2017). Symbolic Regression for the Estimation of Transfer Functions of Hydrological Models. Water Resour. Res. 53, 9402–9423. doi:10.1002/2017WR021253

CrossRef Full Text | Google Scholar

Krishnamurty, G. B., Kasovia‐Schmitt, P., and Ostroff, D. J. (1995). Statistics: An Interactive Text for the Health and Life Sciences. Boston: Jones & Bartlett.

Google Scholar

Lamprecht, A.-L., García, L., Kuzak, M., Martínez, C., Arcila, R., Martin Del Pico, E., et al. (2020). Towards FAIR Principles for Research Software. Ds 3 (1), 37–59. doi:10.3233/DS-190026

CrossRef Full Text | Google Scholar

Ledieu, J., De Ridder, P., De Clerck, P., and Dautrebande, S. (1986). A Method of Measuring Soil Moisture by Time-Domain Reflectometry. J. Hydrol. 88 (3–4), 319–328. doi:10.1016/0022-1694(86)90097-1

CrossRef Full Text | Google Scholar

Lo, S. K., Xu, X., Chiam, Y. K., and Lu, Q. (2017). “Evaluating Suitability of Applying Blockchain,” in Proceedings of 2017 22nd International Conference on Engineering of Complex Computer Systems (ICECCS) (IEEE), 158–161. doi:10.1109/ICECCS.2017.26

CrossRef Full Text | Google Scholar

Méndez, E. (2006). Dublin Core, Metadatos Y Vocabularios. El Profesional de la Informacion 15, 84–86. doi:10.3145/epi.2006.mar.01

CrossRef Full Text | Google Scholar

Menditto, A., Patriarca, M., and Magnusson, B. (2006). Understanding the Meaning of Accuracy, Trueness and Precision. Accred Qual. Assur. 12, 45–47. doi:10.1007/s00769-006-0191-z

CrossRef Full Text | Google Scholar

Minasny, B., and Mc Bratney, A. B. (2002). Uncertainty Analysis for Pedotransfer Functions. Eur. J. Soil Sci. 53, 417–429. doi:10.1046/j.1365-2389.2002.00452.x

CrossRef Full Text | Google Scholar

Minasny, B., McBratney, A. B., and Bristow, K. L. (1999). Comparison of Different Approaches to the Development of Pedotransfer Functions for Water-Retention Curves. Geoderma 93 (3–4), 225–253. doi:10.1016/S0016-7061(99)00061-0

CrossRef Full Text | Google Scholar

Mohajan, H. K. (2017). Two Criteria for Good Measurements in Research: Validity and Reliability. Ashu- Es 17, 59–82. doi:10.26458/1746

CrossRef Full Text | Google Scholar

Mons, B., Schultes, E., Liu, F., and Jacobsen, A. (2020). The FAIR Principles: First Generation Implementation Choices and Challenges. Data Intellegence 2 (1-2), 1–9. doi:10.1162/dint_e_00023

CrossRef Full Text | Google Scholar

Montenij, L. J., Buhre, W. F., Jansen, J. R., Kruitwagen, C. L., and de Waal, E. E. (2016). Methodology of Method Comparison Studies Evaluating the Validity of Cardiac Output Monitors: a Stepwise Approach and Checklist. Br. J. Anaesth. 116 (6), 750–758. doi:10.1093/bja/aew094

PubMed Abstract | CrossRef Full Text | Google Scholar

Noble, H., and Smith, J. (2015). Issues of Validity and Reliability in Qualitative Research. Evid. Based Nurs. 18. doi:10.1136/eb-2015-102054

PubMed Abstract | CrossRef Full Text | Google Scholar

Ochsner, T. E., Cosh, M. H., Cuenca, R. H., Dorigo, W. A., Draper, C. S., Hagimoto, Y., et al. (2013). State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. America J. 77, 1888–1919. doi:10.2136/sssaj2013.03.0093

CrossRef Full Text | Google Scholar

Pepin, S., Livingston, N. J., and Hook, W. R. (1995). Temperature-Dependent Measurement Errors in Time Domain Reflectometry Determinations of Soil Water. Soil Sci. Soc. America J. 59, 38–43. doi:10.2136/sssaj1995.03615995005900010006x

CrossRef Full Text | Google Scholar

Prabhakar, S., and Cheng, R. (2009). “Data Uncertainty Management in Sensor Networks,” in Encyclopedia of Database Systems. Editors L. LIU, and M. T. ÖZSU (Boston, MA: Springer). doi:10.1007/978-0-387-39940-9_115

CrossRef Full Text | Google Scholar

Ramachandran, A., and Kantacioglu, M. (2017). Using Blockchain and Smart Contracts for Secure Data Provenance Management. Available at: https://arxiv.org/pdf/1709.10000v1.pdf (Accessed July 28, 2021).

Google Scholar

Ranstam, J. (2008). Methodological Note: Accuracy, Precision, and Validity. Acta Radiol. 49 (1), 105–106. doi:10.1080/02841850701772706

PubMed Abstract | CrossRef Full Text | Google Scholar

Robson, C., and Sussex, A. (2011). Real World Research: A Resource for Users of Social Research Methods in Applied Settings. 2nd Ed. John Wiley & Sons.

Google Scholar

Román Dobarco, M., Cousin, I., Le Bas, C., and Martin, M. P. (2019). Pedotransfer Functions for Predicting Available Water Capacity in French Soils, Their Applicability Domain and Associated Uncertainty. Geoderma 336, 81–95. doi:10.1016/j.geoderma.2018.08.022

CrossRef Full Text | Google Scholar

Roth, C. H., Malicki, M. A., and Plagge, R. (1992). Empirical Evaluation of the Relationship between Soil Dielectric Constant and Volumetric Water Content as the Basis for Calibrating Soil Moisture Measurements by TDR. J. Soil Sci. 43, 1–13. doi:10.1111/j.1365-2389.1992.tb00115.x

CrossRef Full Text | Google Scholar

Roth, K., Schulin, R., Flühler, H., and Attinger, W. (1990). Calibration of Time Domain Reflectometry for Water Content Measurement Using a Composite Dielectric Approach. Water Resour. Res. 26, 2267–2273. doi:10.1029/WR026i010p02267

CrossRef Full Text | Google Scholar

Saunders, M., Lewis, P., and Thornhill, A. (2009). Research Methods for Business Students. 5th Ed. Harlow: Pearson Education.

Google Scholar

Schoen, J. (1996). “Physical Properties of Rocks: Fundamentals and Principles of Petrophysics,”. Handbook of Geophysical Exploration Series. Editors K. Helbig, and S. Treitel (Oxford, New York, Tokyo: Elsevier), 18.

Google Scholar

Schröter, I., Paasche, H., Dietrich, P., and Wollschläger, U. (2015). Estimation of Catchment-Scale Soil Moisture Patterns Based on Terrain Data and Sparse TDR Measurements Using a Fuzzy C-Means Clustering Approach. Vadose Zone J. 14, vzj2015010008–16. doi:10.2136/vzj2015.01.0008

CrossRef Full Text | Google Scholar

Schröter, I., Paasche, H., Doktor, D., Xu, X., Dietrich, P., and Wollschläger, U. (2017). Estimating Soil Moisture Patterns with Remote Sensing and Terrain Data at the Small Catchment Scale. Vadose Zone J. 16, vzj2017010012. doi:10.2136/vzj2017.01.0012

CrossRef Full Text | Google Scholar

Siepmann, T., Spieth, P. M., Kubasch, A. S., Penzlin, A. I., Illigens, B. M.-W., and Barlinn, K. (2016). Randomized Controlled Trials – a Matter of Design. Ndt 12, 1341–1349. doi:10.2147/NDT.S101938

CrossRef Full Text | Google Scholar

Steelman, C. M., and Endres, A. L. (2011). Comparison of Petrophysical Relationships for Soil Moisture Estimation Using GPR Ground Waves. Vadose Zone J. 10, 270–285. doi:10.2136/vzj2010.0040

CrossRef Full Text | Google Scholar

Stokes, P. (2016). Can Blockchain Be Applied to Research Data Management? Available at: https://researchdata.jiscinvolve.org/wp/2016/11/14/can-blockchain-be-applied-to-research-data-management/(Accessed July 28, 2021).

Google Scholar

Swanson, E. (2014). Validity, Reliability, and the Questionable Role of Psychometrics in Plastic Surgery. Plast. Reconstr. Surg. Glob. Open 2 (6), e161. doi:10.1097/GOX.0000000000000103

PubMed Abstract | CrossRef Full Text | Google Scholar

Teh, H. Y., Kempa-LiehrWang, A. W. K. I. K., and Wang, K. I.-K. (2020). Sensor Data Quality: a Systematic Review. J. Big Data 7, 11. doi:10.1186/s40537-020-0285-1

CrossRef Full Text | Google Scholar

Thatcher, R. W. (2010). Validity and Reliability of Quantitative Electroencephalography. J. Neurotherapy 14, 122–152. doi:10.1080/10874201003773500

CrossRef Full Text | Google Scholar

Thigpen, N., Kappenman, E., and Keil, A. (2017). Assessing the Internal Consistency of the Event‐Related Potential: An Example Analysis. Psychophysiology 54, 123–138. doi:10.1111/psyp.12629

PubMed Abstract | CrossRef Full Text | Google Scholar

Topp, G. C., Davis, J. L., and Annan, A. P. (1980). Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resour. Res. 16 (3), 574–582. doi:10.1029/WR016i003p00574

CrossRef Full Text | Google Scholar

Trajković, G. (2008). “Measurement: Accuracy and Precision, Reliability and Validity,” in Encyclopedia of Public Health. Editor W. Kirch (Dordrecht: Springer). doi:10.1007/978-1-4020-5614-7_2081

CrossRef Full Text | Google Scholar

Twycross, A., and Shields, L. (2004). Validity and Reliability - What's it All about? Paediatric Nurs. 16 (10), 36. doi:10.7748/paed.16.10.36.s22

CrossRef Full Text | Google Scholar

UCLA (2020). What Does Cronbach's Alpha Mean? Statistical Consulting: Institute for Digital Research & Education. Available at: https://stats.idre.ucla.edu/spss/faq/what-does-cronbachs-alpha-mean/(Accessed June 3, 2020).

Google Scholar

Van Iersel, M. W., Chappell, M., and Lea-Cox, J. D. (2013). Sensors for Improved Efficiency of Irrigation in Greenhouse and nursery Production. hortte 23, 735–746. doi:10.21273/HORTTECH.23.6.735

CrossRef Full Text | Google Scholar

Van Looy, K., Bouma, J., Herbst, M., Koestel, J., Minasny, B., Mishra, U., et al. (2017). Pedotransfer Functions in Earth System Science: Challenges and Perspectives. Rev. Geophys. 55, 1199–1256. doi:10.1002/2017RG000581

CrossRef Full Text | Google Scholar

Wang, F., Niedermayr, C. V., and Liu, P. (2014). Metadata Based Management and Sharing of Distributed Biomedical Data. Ijmso 9 (1), 42–57. doi:10.1504/IJMSO.2014.059126

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, G., Gertner, G. Z., Fang, S., and Anderson, A. B. (2005). A Methodology for Spatial Uncertainty Analysis of Remote Sensing and GIS Products. Photogramm Eng. Remote Sensing 71, 1423–1432. doi:10.14358/PERS.71.12.1423

CrossRef Full Text | Google Scholar

Ware, J. E., and Gandek, B. (1998). Methods for Testing Data Quality, Scaling Assumptions, and Reliability. J. Clin. Epidemiol. 51 (11), 945–952. doi:10.1016/S0895-4356(98)00085-7

CrossRef Full Text | Google Scholar

Weast, R. C. (1987). Handbook of Physics and Chemistry. 67th ed. BocaRaton, FL, USA: CRC Press, 1983–1984.

Google Scholar

Wharton, R. P., Hazen, G. A., Rau, R. N., and Best, D. L. (1980). Electro-magnetic Propagation Logging: Advances in Technique and Interpretation. Casper, Wyoming: SPE Rocky Mountain Regional Meeting. May 1980, No. 9267. doi:10.2118/9041-MS

CrossRef Full Text | Google Scholar

Wieczorek, J., Bloom, D., Guralnick, R., Blum, S., Döring, M., Giovanni, R., et al. (2012). Darwin Core: An Evolving Community-Developed Biodiversity Data Standard. PLOS ONE 7 (1), e29715. doi:10.1371/journal.pone.0029715

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilkinson, M. D., Dumontier, M., Aalbersberg, I. J., Appleton, G., Axton, M., Baak, A., et al. (2016). The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 3, 160018. doi:10.1038/sdata.2016.18

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, L. G., Everett, G. L., and Cullen, S. J. (1996). Vadose Zone Characterisation and Monitoring. London: Lewis Publishers.

Google Scholar

Zahid, M., El Zohbi, J., Viktor, E., Rechid, D., Schuck-Zöller, S., Keup-Thiel, E., et al. (2020). “Evaluation of Climate Services: Enabling Users to Assess the Quality of Multi-Model Climate Projections and Derived Products,” in Handbook of Climate Services. Climate Change Management. Editors W. Leal Filho, and D. Jacob (Cham: Springer), 183–201. doi:10.1007/978-3-030-36875-3_10

CrossRef Full Text | Google Scholar

Zhang, D., and Zhou, G. (2016). Estimation of Soil Moisture from Optical and Thermal Remote Sensing: A Review. Sensors 16 (8), 1308. doi:10.3390/s16081308

PubMed Abstract | CrossRef Full Text | Google Scholar

Zilioli, M., Lanucara, S., Oggioni, A., Fugazza, C., and Carrara, P. (2019b). Fostering Data Sharing in Multidisciplinary Research Communities: A Case Study in the Geospatial Domain. Data Sci. J. 18, 15. doi:10.5334/dsj-2019-015

CrossRef Full Text | Google Scholar

Zilioli, M., Oggioni, A., Tagliolato, P., Pugnetti, A., and Carrara, P. (2019a). Feeding Essential Biodiversity Variables (EBVs): Actual and Potential Contributions from LTER-Italy. Nc 34, 477–503. doi:10.3897/natureconservation.34.30735

CrossRef Full Text | Google Scholar