Construction and application of the carbon peak model for Chinese industries --based on Markal-Macro model

Industrial carbon peaking is a critical pathway toward achieving sustainable development. Given that industrial sectors account for nearly 70% of China’s total carbon emissions, conducting simulation studies on industrial carbon peaking holds significant practical importance. Unlike regional carbon peaking models, industrial carbon peaking models face distinct challenges due to the substantial influence of market dynamics. In this study, we focus on three key objectives: (1) reducing carbon emissions from energy consumption, (2) minimizing process-related carbon emissions, and (3) optimizing industrial profitability. We propose an innovative industrial carbon peaking simulation model, developed by adapting the Markal-Macro framework. Using the iron and steel industry as a case study, we establish five distinct scenarios to simulate carbon peaking trajectories. Our analysis incorporates data on energy consumption, employment, product output, and other key indicators. To enhance computational efficiency, we integrate genetic algorithms with the penalty function method. The results indicate that under the baseline scenario, China’s iron and steel industry could achieve carbon peaking by 2027, with emissions reaching approximately 2.04 billion tonnes of CO₂. Based on these findings, we provide targeted policy recommendations for carbon peaking in the iron and steel sector. These recommendations address energy structure optimization, clean energy adoption, and technological advancements, aligning with China’s 14th Five-Year Plan objectives and long-term sustainable development goals.

1 Introduction

In September 2020, China officially declared its carbon peaking and carbon neutrality timeline at the United Nations General Assembly. In August 2024, the General Office of the State Council issued the Work Plan for Accelerating the Establishment of a Dual Carbon Emission Control System, integrating carbon emission targets and associated requirements into national strategy. This initiative aims to establish comprehensive policies and management mechanisms for regional carbon assessments and industry-level carbon control while ensuring effective alignment with the national carbon emissions trading market, thereby providing a robust institutional foundation for achieving the dual carbon goals. At the industry level, key energy-intensive sectors have been actively implementing various carbon peaking and trading initiatives. In August 2022, the Ministry of Industry and Information Technology (MIIT), the National Development and Reform Commission (NDRC), and the Ministry of Ecology and Environment (MEE) jointly issued the Implementation Plan for Industrial Sector Carbon Peaking, followed by the Implementation Plan for Carbon Peaking in the Non-Ferrous Metal Industry in November. Similarly, in November 2022, MIIT, the Ministry of Housing and Urban-Rural Development (MOHURD), and two other ministries jointly issued the Implementation Plan for Carbon Peaking in the Building Materials Industry. While these industry-specific carbon peaking plans outline concrete targets, key implementation tasks, and supporting measures, they lack scientific simulations and calculations of carbon peaking trajectories, as well as scenario analyses and optimal pathway discussions necessary for an effective industry-wide transition.

In 2023, the European Council voted to pass the EU Carbon Border Adjustment Mechanism, which requires exported products to meet low-carbon standards, forcing Chinese industries to accelerate carbon reduction and peak carbon research. In 2025, the National Development and Reform Commission and other departments will issue a notice on the construction of zero carbon parks, promoting the low-carbon transformation of high energy consuming industries, and research on industry carbon peak will become an important support for policy implementation. Carbon peaking at the industry level is undoubtedly multifaceted systemic undertaking, involving not only adjustments in the energy utilization framework and manufacturing procedures but also broader concerns related to market dynamics, such as industry product prices, raw material costs, and energy price fluctuations. In October 2023, the NDRC issued the National Carbon Peaking Pilot Construction Plan, which introduced 26 regional and 14 industrial park-level reference indicators for carbon peaking. While this multi-indicator approach offers simplicity and high operational efficiency, it lacks a systematic perspective and fails to account for interactions between core metrics. From a methodological standpoint, model-based simulation approaches act as a key mechanism for studying carbon peaking goals and execution routes. These approaches provide theoretical guidance and practical applications to assist governments, industries, and enterprises in developing scientifically informed carbon peaking action plans.

Obviously, conducting research on industry carbon peaking has important practical significance. On the one hand, research on industry carbon peaking can support the implementation of Chinese national “dual carbon” strategy. Industry carbon peak research can accurately calculate the peak time and peak path of industry emissions, providing scientific basis for the country to formulate phased and industry-specific carbon peak policies. On the other hand, research on industry carbon peaking can help promote the green and low-carbon transformation of industries and respond to international green trade rules. By simulating and calculating the industry’s peak path, the quantitative indicators for industry peak are clarified, and corresponding policy measures are formulated, such as the construction of industry zero carbon parks, direct supply of industry green electricity, etc., in order to reduce industry carbon emissions and enhance international “low-carbon” competitiveness.

Existing research on carbon peaking pathways for high-emission industries in China covers industrial, building, power, logistics, and mining sectors, as well as sub-sectors such as cement, non-ferrous metals, and ICT. Given that industrial domains constitute around 70% of China’s total carbon emissions, they have become a focal point of research. However, significant variations in carbon peaking timelines exist across energy-intensive sectors, such as heavy chemicals, manufacturing, and the power and mining industries. For instance, Zhang et al. (2017) found that China’s Industrial Carbon Emission Intensity (ICEI) is strongly driven by investment intensity, while Fang et al. (2022) showed that non-energy-intensive sectors such as agriculture, construction, and transportation could peak before 2030, whereas the power and mining sectors may lag beyond 2030. Regional studies further reveal heterogeneity within industries. Guo et al. (2023) examined Henan Province and found that steel and cement could peak before 2025, while the power sector may not peak until 2033. Similarly, Dai et al. (2024) highlighted significant provincial differences in carbon peaking timelines for the construction industry, with economically developed provinces (e.g., Shandong, Guangdong) achieving earlier peaks than central and western provinces.

A consensus in the academic community suggests that most industries in China can achieve carbon peaking between 2030 and 2040 through policy interventions and technological advancements. However, the choice of transition pathways and policy intensity directly influence the peaking timeline and peak emissions level. In the industrial sector, strong policy scenarios (e.g., energy efficiency improvements and structural optimization) could enable carbon peaking as early as 2025 (Zhang et al., 2017), while baseline scenario might delay the peak beyond 2035. The construction and logistics sectors, if coupled with breakthroughs in low-carbon technologies, could peak before 2030 (Guo et al., 2023; Chen and Wang, 2024). However, energy-intensive industries such as power and mining face substantial challenges. Gao et al. (2023) suggested that the power sector must reduce coal-fired power’s share below 50% to peak by 2030, while Zhou et al. (2025) emphasized that the ICT sector must leverage digital technologies for emissions reduction or risk delaying its peak until 2033. Research also highlights regional coordination and technological innovation as key bottlenecks, as western provinces struggle with heavy industrial reliance (Tan et al., 2024) and slow technology diffusion (Guo et al., 2023), necessitating differentiated policy support. Future studies should further integrate multi-scale data and cross-sector collaboration to support the systematic achievement of China’s dual carbon targets.

In terms of methodological approaches, most existing studies follow a “drivers decomposition—scenario simulation—pathway optimization” framework, with innovation mainly focused on model integration and uncertainty analysis. In the drivers decomposition stage, factor decomposition models (e.g., LMDI, STIRPAT) are widely used to quantify the contributions of economic, technological, and policy variables. For example, Li J. et al. (2020) applied Generalized Divisia Index (GDI) analysis to show that 81% of carbon emissions in the construction sector were driven by GDP growth. In the scenario simulation stage, methods such as dynamic Monte Carlo simulations, machine learning (e.g., RF-WOA-RBF), and system dynamics models have gained prominence. Chen and Wang (2024) combined random forest and whale optimization neural networks to predict carbon emission trends in logistics and identified technological breakthrough (TB) scenarios as optimal pathways. Wen and Diao (2022) built an electricity supply-demand system dynamics model incorporating CCUS technology to simulate China’s three-stage carbon neutrality transition.

Currently, carbon peaking modeling approaches are categorized into three primary types:

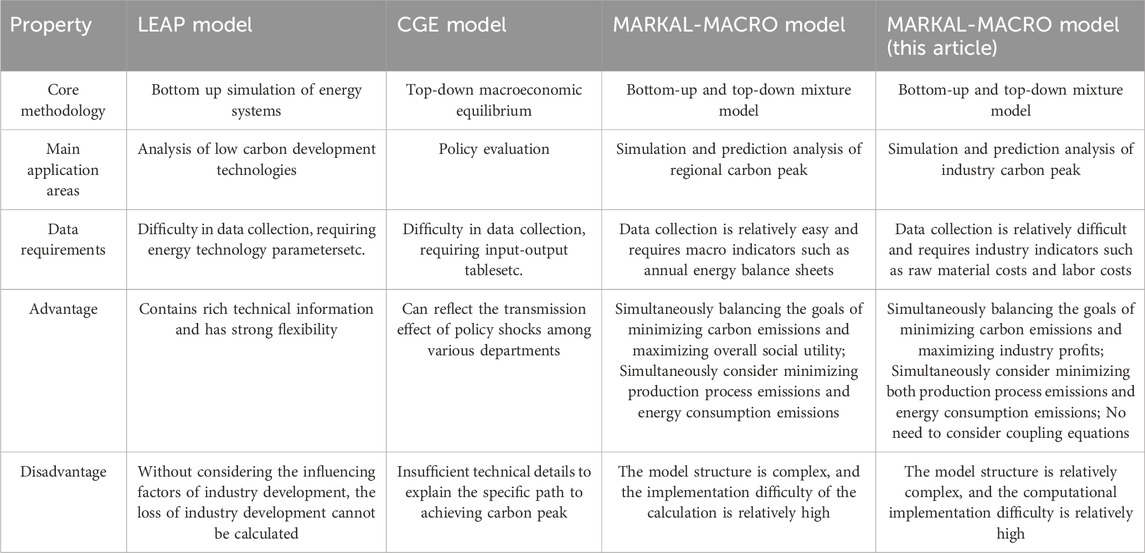
Firstly, Top-down macroeconomic models (e.g., CGE models), which assess policy shocks across sectors but lack detailed pathway analysis (Zhang and Chen, 2022; Niu and Liu, 2023). Secondly, Bottom-up technology-rich models (e.g., LEAP models), which provide high technical resolution but do not account for economic trade-offs (Du et al., 2022; Sun et al., 2023; Zhou et al., 2023). Thirdly, hybrid models, such as MARKAL-MACRO, which integrate both economic and technological perspectives, enabling detailed simulation of industry- and regional-level carbon peaking scenarios (Wei Y. et al., 2022; Ma and Chen, 2017; Cai et al., 2022). However, despite their advantages, hybrid models remain computationally complex, requiring advanced optimization techniques.

Existing hybrid modeling studies have made important contributions. However, they have two major limitations: (1) they fail to simultaneously model emissions from energy use and production processes, and (2) they lack the MARKAL-MACRO model’s ability to optimize both carbon minimization and overall societal utility maximization. Shen et al. (2025) addressed these gaps by developing a multi-objective nonlinear programming model for regional carbon peaking, yet their approach remains unsuitable for industry-level analysis due to significant differences between regional and industry-specific carbon peaking objectives.

The main contributions in this paper include: firstly, we distinguish from the regional utility maximisation objective function and innovatively construct the industry profit maximisation objective function, which in turn constructs the Markal-Macro model of the industry carbon peak. Second, for the purpose of improving the computational efficiency, we introduce genetic algorithm on the basis of penalty function method, which avoids the drawbacks of difficult to find analytical solution and slow convergence.

2 Materials and methods

2.1 Model design

The MARKAL-MACRO model is a representative of hybrid models, formed by coupling the MARKAL model with the MACRO model. It mainly consists of three modules: the MARKAL model, the MACRO model, and the coupling equations.

Building upon the industry energy-carbon model proposed by Wang et al. (2024), this study assesses industry carbon emissions from two perspectives: energy use and the production process. A novel multi-objective MARKAL-MACRO model is developed, incorporating three optimization objectives: the reduction of carbon emissions from energy consumption, the minimization of carbon emissions associated with production processes, and the maximization of industry profits.

In this framework, the MARKAL model is structured as a multi-objective dynamic linear programming model, encompassing two objective functions: (1) the minimization of carbon emissions from energy consumption, and (2) the reduction of carbon emissions from the production process. In contrast, the MACRO model is formulated as a linear industry profit model, designed to optimize industry profits throughout the planning horizon.

2.1.1 MARKAL model specification

The MARKAL model in this study integrates two objective functions: the minimization of total energy consumption and the reduction of carbon emissions from the production process.

2.1.1.1 Objective 1: minimization of total industry energy consumption

In alignment with China’s dual carbon strategy, the carbon peaking target is simulated by maximizing the minimization function of total energy consumption over the period from 2022 to 2030. Accordingly, the industry’s objective function is defined to minimize the total energy consumption, measured in standard coal equivalent, from coal, oil, gas, and thermal power generation. The mathematical formulation is given as Equation 1:

$\underset{t}{\max }\left(\min \sum {2.46\times \mu }_{ik}{X}_{itk}\right)(1)$

In this formulation, ${\mathrm{X}}_{\text{itk}}$ denotes the standard coal conversion coefficient for energy type i in industry k, where i = 1,2,3,4 correspond to coal, oil, gas, and electricity, respectively. ${\mathrm{\mu }}_{\text{ik}}$ denotes the conversion factor for converting the ith energy source of the kth industry to standard coal, the exact value of which is shown in Table 1.

Table 1

Table 1. Carbon emission parameters for coal, oil, gas, and electricity.

The 2024–2025 Energy Conservation and Carbon Reduction Action Plan, issued by the State Council of China in 2024, stresses the strict and rational control of coal consumption, the optimization of oil and gas consumption structures, and the vigorous promotion of non-fossil energy consumption. These measures are recognized as essential tasks to actively and prudently advance the carbon peaking target and intensify energy conservation and carbon reduction efforts. Thus, from the perspective of energy consumption types, two constraints are established to achieve the goal of minimizing carbon emissions from energy consumption, namely: the share of coal, oil, gas, primary electricity and other energy sources in total energy consumption; and the proportion of thermal power in the structure of overall power generation. The constraints on the consumption share of each energy product are as Equations 2, 3:

${\left(X_i\right)}_{\mathit{min}}\le X_{it}\le {\left(X_i\right)}_{\mathit{max}},i=1,2,3(2)$

${\left(\frac{X_4}{X_5}\right)}_{\mathit{min}}\le {\left(\frac{X_4}{X_5}\right)}_t\le {\left(\frac{X_4}{X_5}\right)}_{\mathit{max}}(3)$

Where ${\mathrm{X}}_{\mathrm{i}}$ denotes the ith type of energy consumption, and i = 1, 2, 3, 4, 5 donates the total amount of coal, oil, gas, thermal power, and electricity consumption, respectively. The upper limit value of the proportion of thermal power in total electricity consumption refers to the actual value of the proportion of thermal power in the overall power generation structure nationwide in 2022, which is 66.55%. Taking into account the relevant indicator requirements proposed in the official policy documents “Action Plan for Carbon Peak before2030¹” and “Special Action Plan for Energy Conservation and Carbon Reduction in the Steel Industry (2024–2030)²”, we have set the lower limit of the proportion of thermal power in the overall electricity consumption of the steel industry at 50%.

2.1.1.2 Objective 2: minimize carbon emissions from industry production processes

Similarly, the industry’s production process carbon emissions mainly come from CO2 and additional greenhouse gas emissions generated during the processing and manufacturing stages of raw materials. The production process carbon emission minimization target is as Equation 4:

$\underset{t}{\max }\left(\min {\phi }_k{Q}_{kt}\right)(4)$

Where ${\mathrm{Q}}_{\text{kt}}$ is the output of the main products of the kth industry in year t; ${\mathrm{\phi }}_{\mathrm{k}}$ represents the carbon dioxide emission factor of the main products of the kth industry (here, the main products of the iron and steel industry are recorded as crude steel).

For the production process carbon emission minimization target, the constraints are set as product output constraints in the industry, which are expressed as Equation 5:

${\left(Q_k\right)}_{\mathit{min}}\le Q_{kt}\le {\left(Q_k\right)}_{\mathit{max}}(5)$

Where ${\mathrm{Q}}_{\text{kt}}$ is the main product output of the kth industry in year t, and ${\left({\mathrm{Q}}_{\mathrm{k}}\right)}_{\min },{\left({\mathrm{Q}}_{\mathrm{k}}\right)}_{\max }$, respectively, represents the lower and upper limits of the product output of the kth industry.

2.1.2 Industry MACRO model setting

When constructing the industry carbon peak multi-objective optimization model, the dual needs of carbon emission reduction and economic benefits need to be fully considered. Industry profit maximization reflects the need for enterprises to maintain economic vitality and market competitiveness while pursuing environmental protection and carbon emission control. This objective aims to ensure that the industry is able to maintain or even improve its profitability in the context of achieving carbon peaking by means of measures including optimizing production processes, improving resource utilization efficiency and reducing costs. Using the industry profit maximization objective as part of the optimization model helps to balance the correlation between carbon emission reduction and economic development, and promotes the industry’s development in a greener, more efficient and sustainable direction. The specific industry profit maximization objective function is set as follows:

${\max }_{\mathrm{t}}\left({IP}_{kt}\right)={\max }_{\mathrm{t}}\left({OV}_{kt}-{IC}_{kt}\right)(6)$

Where ${IP}_{kt}$ refers to the industry profit, ${\mathrm{O}V}_{kt}$ refers to the output value, ${IC}_{kt}$ refers to the intermediate inputs, k = 1,2 represents the iron and steel and non-ferrous industries respectively, and t donates to the year. The calculation process of ${\mathrm{O}V}_{kt}$ and ${IC}_{kt}$ is as Equations 7–12.

${OV}_{kt}=Q_{kt}\times P_{kt}(7)$

${IC}_{kt}={RME}_{kt}+{EE}_{kt}+{LC}_{kt}+{DE}_{kt}(8)$

${RME}_{kt}={\alpha Q}_{kt}\times {RMP}_{kt}(9)$

${EE}_{kt}=P_1{X}_1+P_2{X}_2+P_3{X}_3+P_4{X}_4(10)$

${LC}_{kt}={NOE}_{kt}\times {AS}_{kt}(11)$

${DE}_{kt}={FAI}_{kt}\times {DR}_{kt}(12)$

Where ${\mathrm{Q}}_{\text{kt}}$ refers to the total output of the main products of the whole steel industry (Considering that crude steel is an upstream product of the steel industry and its carbon emissions are similar to steel, crude steel production here is used as the output of the steel industry), which is an endogenous variable; ${\mathrm{P}}_{\text{kt}}$ refers to the unit price of the main products of the industry, and the range of price intervals needs to be given in the process of calculation; ${\text{RME}}_{\text{kt}}$ refers to the expenditure on raw materials (iron ore, scrap), ${\text{EE}}_{\text{kt}}$ refers to the expenditure on energy costs (metallurgical coal), ${\text{LC}}_{\text{kt}}$ refers to the expenditure on manpower, ${\text{DE}}_{\text{kt}}$ refers to depreciation expenses. $\alpha$ refers to the proportional relationship between the output of major products and the use of raw materials in an industry, i.e., the output ratio, and ${\text{RMP}}_{\text{kt}}$ refers to the price per unit of raw materials. ${\mathrm{X}}_1$ is the consumption of coal, ${\mathrm{X}}_2$ is the consumption of oil, ${\mathrm{X}}_3$ is the consumption of natural gas, and ${\mathrm{X}}_4$ is the consumption of primary electricity, and ${\mathrm{P}}_{\mathrm{i}}$ is the cost of energy consumption per unit of energy, with i = 1,2,3,4 representing coal, oil, gas, and electricity, respectively. ${\text{NOE}}_{\text{kt}}$ refers to the number of persons employed by enterprises of size above the industry, ${\text{AS}}_{\text{kt}}$ refers to the average salary of the industry, and ${\text{FAI}}_{\text{kt}}$ refers to the investment in fixed assets, ${\text{DR}}_{\text{kt}}$ refers to the depreciation rate.

For the industry profit maximization objective function, the constraints are set as follows: First, considering that the steel industry is the fundamental industry of the Chinese economy and is dominated by state-owned enterprises, if the entire industry incurs losses, it may lead to supply chain disruptions, posing a threat to national economic security and industrial chain stability. Therefore, we set the industry profit as non-negative. Second, the production function constraints, with reference to the C-D production function, for the equation constraints (Equations 13, 14):

${IP}_{kt}\ge 0(13)$

$Q_{kt}=A\times {\left({FAI}_{kt}\right)}^{\alpha }\times {\left({NOE}_{kt}\right)}^{\beta }\times {\left(E_{kt}\right)}^{\gamma }(14)$

Where ${\mathrm{Q}}_{\text{kt}}$ refers to the industry’s main product output, A refers to technological progress, ${\text{FAI}}_{\text{kt}}$ refers to the industry’s investment in fixed assets, ${\text{NOE}}_{\text{kt}}$ refers to the quantity of people employed in the industry’s enterprises above the scale, and ${\mathrm{E}}_{\text{kt}}$ refers to the industry’s total energy consumption, which is the value of the standard coal (including X1, X2, X3, and X4). $\mathrm{\alpha }$, $\mathrm{\beta }$, and $\mathrm{\gamma }$ are the elasticity coefficients of the investment, manpower, and energy consumption, respectively, for the t th year.

The reason for not setting coupled equations for the MARKAL-MACRO model of the industry here is mainly because the expression of the MACRO model of the industry already contains the relevant variables in the MARKAL model, so there is no need to set coupled equations for the variables of the two models, which in turn reduces the complexity of the MARKAL-MACRO model of the industry. Generally speaking, if a coupled equation is set, it is usually regarded as a strict equality constraint in the optimization solution of the model. Therefore, whether it is solved by penalty function method or genetic algorithm, it will increase the difficulty of finding the optimal value. In order to clearly demonstrate the differences between the model constructed in this article and other models, we compared these models in Table 2.

Table 2

Table 2. Comparison of differences in major carbon peaking simulation methods.

2.2 Simulation scenario setup and data description

2.2.1 Data description and preprocessing

This study uses the steel industry as a case example for simulation calculations. The steel industry encompasses both the black metal mining and the black metal smelting and rolling sectors. Therefore, the total energy consumption of the steel industry is the sum of the energy consumption from these two sub-sectors, with data derived from the National Bureau of Statistics of China. The industry’s product output, total fixed asset value of large-scale industrial enterprises, fixed asset investment, and average employment figures are all collected from the National Bureau of Statistics. Product price data are sourced from China Economic Net, while the ratio between major product output and raw material consumption is derived from Zhiyan Consulting. Average wage data are referenced from the China Steel Industry Yearbook and China Steel Network. Prices of raw materials and fuels are obtained from the Wind Database, and energy consumption per unit of product is based on the Industrial Key Areas Energy Efficiency Benchmarking and Baseline Levels (2023 Edition).

Calculate the usage of raw material iron ore and fuel metallurgical coal based on the production of crude steel, the main product of the steel industry, and the ratio of crude steel to raw material and fuel usage; According to the usage ratio of crude steel to iron ore, scrap steel, and metallurgical coal released by Zhiyan Consulting, the output ratio of crude steel to iron ore, scrap steel, and metallurgical coal can be obtained as follows: “Crude steel: iron ore: scrap steel: metallurgical coal = 1:1.1795:0.3487:0.5641″, which means that producing one ton of crude steel requires 1.1795 tons of iron ore, 0.3487 tons of scrap steel, and 0.5641 tons of metallurgical coal; Based on this proportional relationship and the crude steel production over the years, the usage of iron ore, scrap steel, and metallurgical coal over the years can be calculated.

The expenditure on raw materials in the steel industry is obtained by multiplying and adding the calculated usage of iron ore and scrap steel, as well as their respective prices; The energy cost is obtained by multiplying the calculated metallurgical coal usage and its price; The labor cost is calculated based on the average number of employed people and their average wages in the steel industry; The depreciation cost is calculated based on the total original value of fixed assets of industrial enterprises above designated size in the steel industry (in billions of yuan) and the depreciation rate, which is set at 5.2% according to above relevant data source.

2.2.2 Simulation scenario setup

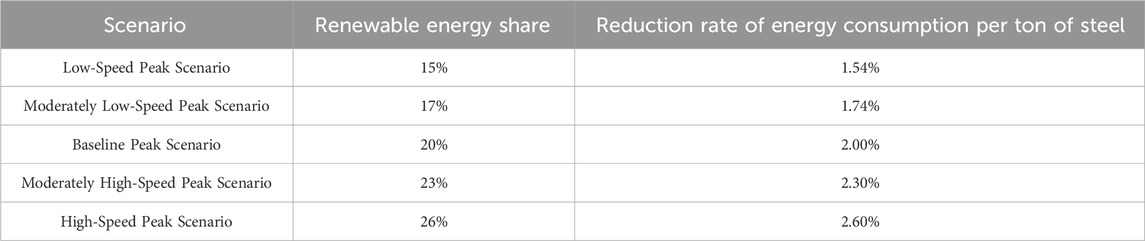
In multi-objective optimization, constraints serve to filter potential solutions, while scenario settings guide the orientation and extent of the optimization process, directly affecting the selection of solving tactics and the efficacy of the final solution. Scenario settings not only determine the parameters and boundaries concerning the problem but also incorporate the decision-makers’ preferences and priorities, which in turn affect the choice of the final solution. On the basis of the target indicators outlined in current policy documents, this study selects the renewable energy share and energy consumption reduction per ton of steel as key indicators for the simulation scenario setup. The renewable energy share reflects the degree of energy structure decarbonization in the steel industry. As an energy-intensive sector, the steel industry’s carbon emissions primarily stem from the use of fossil fuels. Increasing the proportion of renewable energy can significantly reduce carbon emission intensity during the production process and is a key pathway to achieving carbon peaking. The decrease in energy consumption per ton of steel reflects the industry’s potential for energy efficiency improvements. Through technological advancements, process optimization, and equipment upgrades, reducing energy consumption per ton of steel can directly decrease total energy consumption, thereby lowering carbon emissions. These scenario indicators not only quantify the technical feasibility of the steel industry’s low-carbon transition but also provide clear guidelines for policy formulation.

On the basis of a review of current literature, five scenario types are established. The baseline carbon peak scenario adopts the national target for renewable energy share, while the energy consumption reduction per ton of steel is derived from the 2024–2025 Energy Conservation and Carbon Reduction Action Plan and the Steel Industry Energy Conservation and Carbon Reduction Action Plan. Based on relevant policy targets, the slow carbon peak scenario and slower carbon peak scenario are set by reducing the baseline scenario data by 30% and 15%, respectively. Conversely, the fast carbon peak scenario and faster carbon peak scenario are set by increasing the baseline scenario data by 30% and 15%, respectively. The specific results are shown in Table 3.

Table 3

Table 3. Table of five simulated scenarios.

2.3 Optimization algorithm

Given that the MARKAL-MACRO model developed in this study is a multi-objective dynamic model, we initially employ the Sequential Unconstrained Minimization Technique (SUMT) to convert the multi-objective dynamic optimization problem into a single-objective dynamic optimization problem. The specific computational steps for the penalty function can be referenced in Shen et al. (2025). In order to improve the computational efficiency of SUMT, we introduce genetic algorithm (GA) in the optimization process. The advantages of GA over other commonly used optimization algorithms such as particle swarm optimization (PSO) and firefly optimization (FA) are: firstly, GA has global search capability and diversity preservation. PSO relies on individual and group historical optimal solutions, which can easily lead to local optima. FA searches through brightness attraction mechanism, but may lack diversity due to “excessive clustering”. Secondly, GA has a high tolerance for nonlinearity and discontinuity in the objective function or constraints. The optimization effect of PSO and FA on non smooth and multimodal functions is not as stable as that of GA. Thirdly, GA is usually less sensitive to parameter changes than PSO/FA. PSO is susceptible to the influence of “particle stagnation”; FA may cause search direction deviation when the target space is uneven.

After the penalty function transformation, the resulting optimization problem involves five endogenous variables and requires year-by-year computations. This leads to relatively low computational efficiency and high sensitivity to parameters, which may cause issues such as gradient explosion, resulting in solutions that exceed constraint conditions. To address these challenges, we employ the Genetic Algorithm to optimize the penalty function. The key steps of the Genetic Algorithm are outlined in Table 4. It should be noted that due to the analytical nature of the penalty function method, it takes a long time to solve. Our experience shows that simulating a scenario using the penalty function alone takes nearly 30 min, while using genetic algorithms only takes 2 min, greatly improving computational efficiency.

Table 4

Table 4. Genetic algorithm steps.

3 Results and validation anlysis

3.1 Results discussion

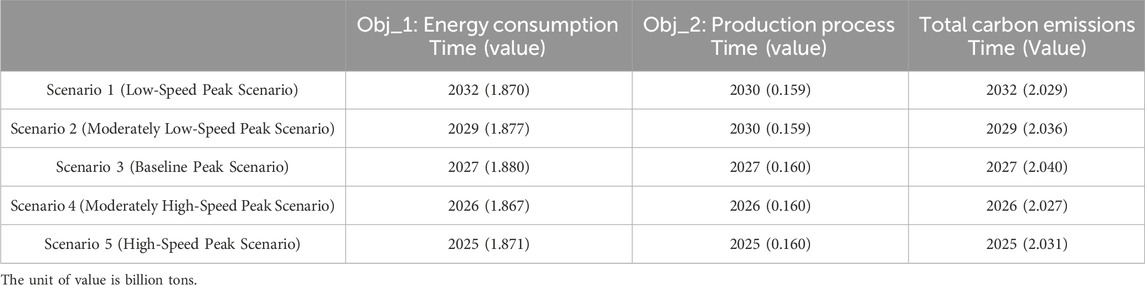
We simulated the carbon peaking pathway for China’s steel industry from 2024 to 2035 under different scenario settings. The carbon peak time and peak value are shown in Table 5. The primary findings suggest that emission and energy consumption levels align closely with the respective scenario assumptions, validating the internal consistency of the model. Particularly, as scenario constraints tighten, the steel industry’s carbon peaking timeline accelerates. The peak carbon emission years for the five scenarios are 2032, 2029, 2027, 2026 and 2025 respectively, as shown in Figure 1.

Table 5

Table 5. Carbon peak time and peak value of China’s steel industry under different scenarios.

Figure 1

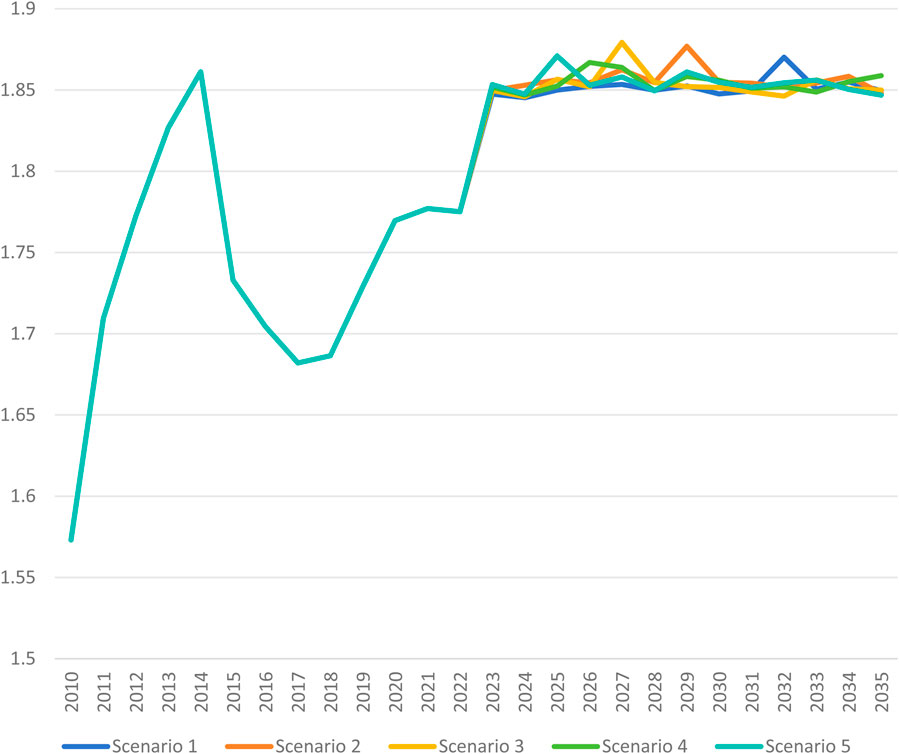
Figure 1. Simulation results of peak carbon emissions from energy consumption in China’s steel industry under 5 scenarios (unit: billion tons).

For Objective 1 (Energy Consumption), the peak years for energy consumption under the five scenarios are 2032, 2029, 2027, 2026, and 2025, respectively. These findings indicate that as constraints on the carbon peaking process become more stringent, the timeline for peak energy consumption advances. Scenario 3, serving as the baseline scenario, projects that the steel industry will reach its peak in 2027, with carbon emissions from energy consumption reaching 1.88 billion tons in that year.

For Objective 2 (Production Process), the peak years are 2030, 2030, 2027, 2026, and 2025 respectively, as shown in Figure 2. Meanwhile, industry production levels exhibit slight fluctuations between 2024 and 2035 but tend to stabilize over time. The fluctuations in the subsequent simulation years may be attributed to uncertainties in industry production levels, economic structural adjustments, and changes in energy consumption patterns across different sectors.

Figure 2

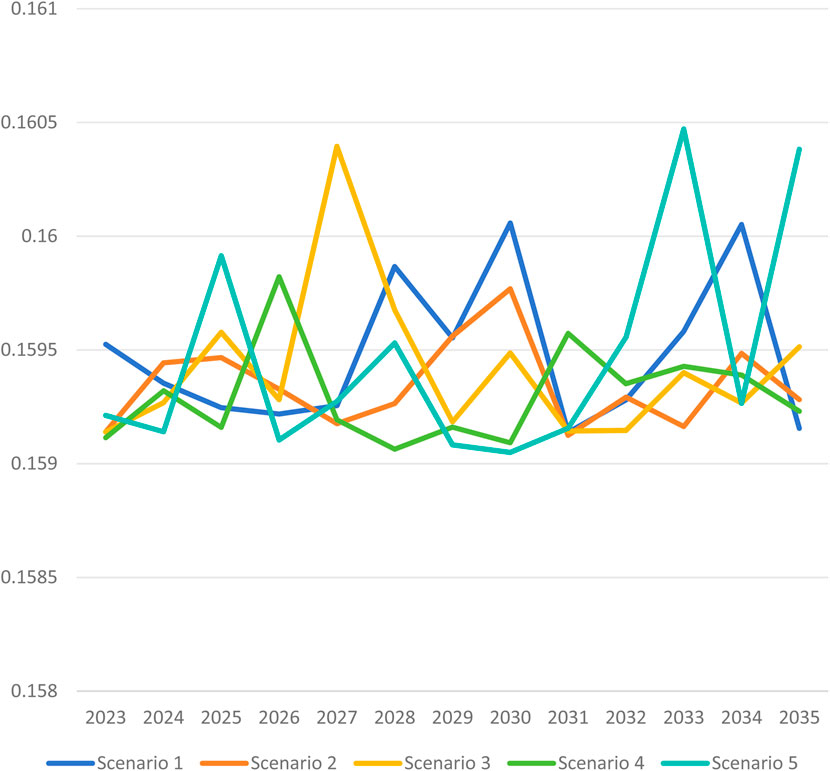
Figure 2. Simulation results of peak carbon emissions from production process in China’s steel industry under 5 scenarios (unit: billion tons).

For Total Emissions, the peak years mirror those of energy consumption, occurring in 2032, 2029, 2027, 2026 and 2025 respectively, as shown in Figure 3. This consistency can be attributed to the dominant role of energy consumption emissions in contributing to the total emissions. Under scenario 3 (baseline), the peak occurs in 2027, with energy consumption-related emissions at 1.88 billion tons, production process emissions at 160 million tons, and total emissions reaching 2.04 billion tons. Additionally, the peak emission values across the five scenarios are 2.029, 2.036, 2.040, 2.027, and 2.031 billion tons, respectively. These values highlight the potential and effectiveness of emission control under varying levels of constraint intensities. Collectively, these results emphasize the significance of a coordinated approach between energy consumption and the production process in the formulation of carbon peaking policies, aiming to achieve more effective emission reduction outcomes.

Figure 3

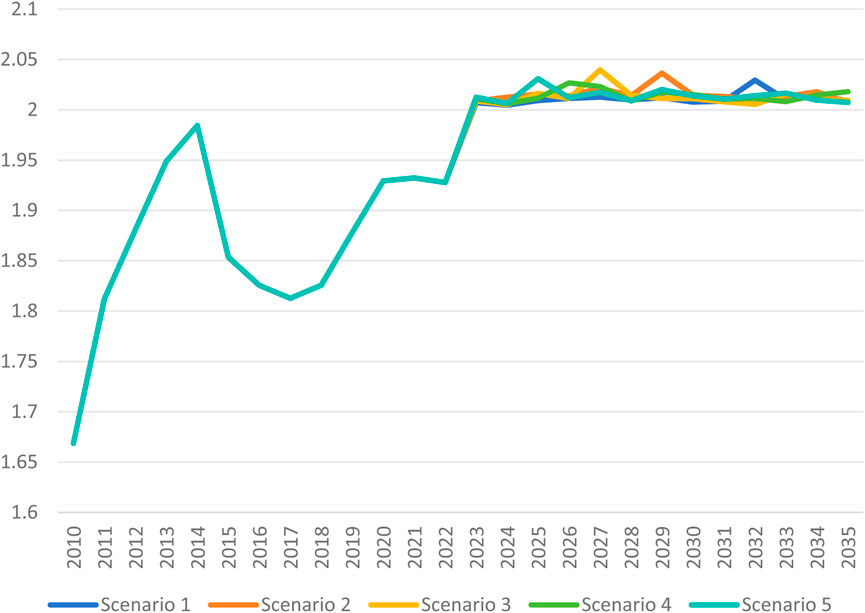
Figure 3. Simulation results of peak carbon emissions in China’s steel industry under 5 scenarios (unit: billion tons).

3.2 Results validation analysis

We verify and analyze the results from the following three aspects. Firstly, from the perspective of comparing the results with those of other literature, conduct a validation analysis of the results. Secondly, analyze the stability of the model results from the perspective of optimizing the sensitivity of algorithm parameters. Thirdly, from the perspective of sensitivity of model parameters, some representative parameters were selected to conduct stability analysis on the model results.

Our simulation results have a certain level of reliability. Firstly, from the historical data of carbon emissions of the steel industry, our simulation calculation results have a certain degree of reliability. The highest point of historical carbon emissions data in China’s steel industry occurred in 2014, with emissions of 1.985 billion tons (as shown in Figure 3). Considering that the production of China’s steel industry was in a period of rapid growth in 2014 and could not reach its peak, our simulated peak of 2.04 billion tons has a certain degree of reliability. Secondly, compared with other relevant literature, our results have a certain level of reliability. Pan et al. (2023) found that under the baseline scenario, China’s steel industry is expected to reach its peak in 2025, with carbon emissions of 1.904 billion tons [23]. According to the research by Wei YM. et al. (2022), the peak of China’s steel industry is between 1.93 billion tons and 20 billion tons, with a peak time around 2023 [24]. Since China has not yet announced the carbon peak time for the steel industry, we believe that the peak time will not be earlier than 2025. However, based on historical emission data, the peak should be higher than 1.985 billion tons. Therefore, compared with the research of Pan et al. (2023) and Wei YM. et al. (2022), our research results are relatively more reliable.

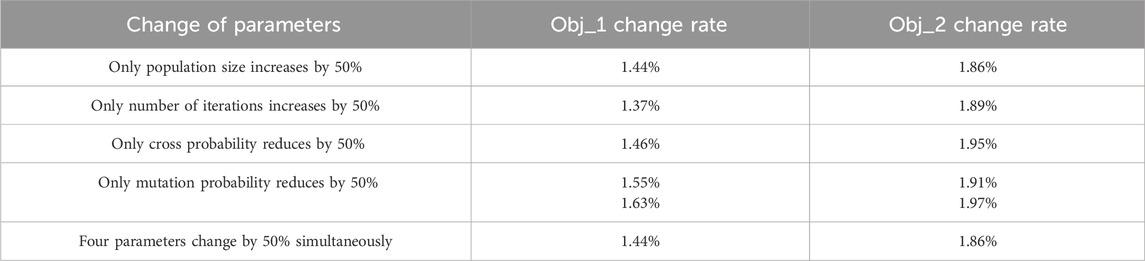
In order to evaluate the robustness of the model results, we conducted sensitivity analysis on the algorithm parameters. Consider the rate of change in the simulation results of objective 1 and objective 2 when the population size, iteration number, crossover probability, and mutation probability change by 50%. The sensitivity analysis results are shown in Table 6. From Table 6, it can be seen that when the four parameters are individually changed by 50%, the simulation results of objective 1 and objective 2 show relative robustness, with a change rate of less than 2%. When all four parameters are changed by 50% simultaneously, the transformation rate of the simulation results for objective 1 and objective 2 is greater than that when all four parameters are changed by 50% individually, but still controlled within 2%, indicating the robustness of the genetic algorithm results. It should be noted that there are two reasons why we only conducted sensitivity analysis on unilateral directional changes of parameters: firstly, in the initial selection process of each parameter, we considered both empirical values from literature and our own test values. Secondly, based on the results of our testing, we have preliminarily identified some unreasonable intervals for each parameter. Therefore, when conducting parameter sensitivity analysis, we only consider the analysis of changes in reasonable intervals.

Table 6

Table 6. Results of sensitivity analysis of parameters of GA.

Considering the strong volatility of actual energy prices, we have chosen energy price fluctuations of ±20% and ±70% to conduct sensitivity analysis on the generation process emissions, energy consumption emissions, and total emissions of the steel industry. Considering that technological progress is relatively slow and will be reflected in the depreciation rate of the industry, we have set depreciation rates of 8% and 10% based on a depreciation rate of 5.2% to conduct sensitivity analysis on the emissions from the steel industry’s generation process, energy consumption, and total emissions. The results are shown in Table 7. From the table, it can be seen that firstly, the changes in depreciation rates of 8% and 10% have little impact on the model results, and the change rates of each result are within ±2%. Secondly, when energy prices fluctuate by ±20%, the impact on the model results is not significant, and the rate of change for each result is within ±5%; But when the energy results fluctuate by ±70%, the changes in the model results are very obvious, with simulation results for each year changing at a rate between 40% and 70%. When there is a significant change in energy prices, the peak simulation results of the steel industry will also undergo increased changes.

Table 7

Table 7. Results of sensitivity analysis of main parameters of Markal-Macro model.

4 Conclusion and policy recommendations

The study yields the following key findings. First, under China’s ″30–60″carbon peaking and neutrality targets, the steel industry can achieve peak carbon emissions before 2030 in four of the five scenarios, with the exception of scenario 1. Notably, under the high-speed peak scenario, the industry can reach peak emissions as early as 2025. In the low-speed peak scenario, it means that the steel industry cannot meet the government’s peak requirements. The reason is that in scenario 1, the proportion of renewable energy reflecting changes in the industry’s energy structure is relatively low, and the reduction rate of energy consumption per ton of steel reflecting the industry’s production technology level is too slow. In this scenario, the pressure for enterprises to change is relatively small, but the cost of energy consumption and carbon emissions increases. In the scenario of high-speed peak, the steel industry can achieve rapid peak due to the high proportion of renewable energy that reflects changes in the industry’s energy structure. At the same time, rapid technological innovation in the industry leads to a faster reduction in energy consumption per ton of steel. In this scenario, companies face greater pressure to change, but reducing energy and carbon emission costs will be beneficial for enhancing their competitiveness. Second, in the baseline scenario (scenario 3), the peak emissions level is approximately 2.04 billion tons, highlighting the significant impact of policy constraints on emissions control. Third, simulation results indicate that the speed of carbon peaking is primarily driven by the growth rate of energy consumption, emphasizing the crucial role of energy structure transformation and energy efficiency improvements in achieving carbon peaking. In contrast, emissions from the production process account for a relatively smaller proportion of total emissions.

In light of the empirical evidence, the following policy interventions are recommended.

First, scenario 3 should be adopted as the optimal carbon peaking pathway for China’s steel industry. Under this scenario, the share of renewable energy in the steel industry reaches 20%, while the yearly reduction rate of energy consumption per ton of steel is 2%.

Second, optimizing the energy structure and increasing the share of renewable energy is crucial. The government should encourage steel enterprises to intensify research and investment in clean energy technologies like hydrogen, wind, and solar power, and promote the demonstration and application of hydrogen-based steelmaking. Fiscal subsidies, tax incentives, and other policy measures should be introduced to support the transition toward renewable energy. Additionally, renewable energy infrastructure should be improved to ensure a stable supply of clean energy. By optimizing the energy structure, carbon emissions from energy consumption can be effectively reduced, providing critical support for the steel industry’s carbon peaking efforts.

Third, promote energy efficiency improvement, reduce energy consumption per ton of steel, and ensure that the annual reduction rate of energy consumption per ton of steel is 2%. It is recommended that industry enterprises achieve the goal of reducing energy consumption per ton of steel by 2% annually through specific measures such as technological transformation, equipment upgrading, and process optimization. Compared with the 1.54% reduction in energy consumption per ton of steel in the Low-speed peak scenario (Scenario 1), a 2% reduction in energy consumption per ton of steel in the baseline peak scenario (Scenario 3) can result in an additional emission reduction of 8.648 million tons; On the contrary, compared with the High-speed peak scenario (Scenario 5), Scenario 3 loses 11.28 million tons of opportunity emission reduction.

Fourth, strengthen emission reduction in the production process and promote low-carbon technologies. Specifically, it includes several aspects. On the one hand, it emphasizes the research and application of low-carbon technologies, such as carbon capture, utilization, and storage (CCUS), electric furnace steelmaking, and other technologies. On the other hand, we attach great importance to the research and application of digital and intelligent technologies in the industry, and utilize technologies such as the Internet of Things, big data, and artificial intelligence to establish an intelligent control system for the steel production process, optimize the production process, and reduce carbon emissions in the production process.

Fifth, improve the carbon market mechanism and strengthen carbon emission constraints. According to the document “Work Plan for the National Carbon Emission Trading Market to Cover the Cement, Steel, and Electrolytic Aluminum Industries” released by the Chinese Ministry of Ecology and Environment, the steel industry will enter the carbon trading market by 2025. Through market-oriented means, the total quota of the steel industry can be controlled, promoting emissions reduction in the steel industry. Specific measures include the design of carbon quota allocation in the steel industry and the participation of enterprises in carbon emission trading.

Sixth, based on regional differences, the transfer of the steel industry and the reduction of labor costs are beneficial to improving the overall profit level and competitiveness of the steel industry in the context of carbon peak. The steel industry requires a large amount of labor force. Due to the significant difference in economic development between developed areas along the southeast coast of China and underdeveloped areas in the west, in the context of the steel industry’s upcoming participation in carbon market trading, achieving regional transfer of the steel industry can reduce labor costs, offset the additional costs brought by carbon trading for enterprises, and thereby improve the overall profit level of enterprises, which is conducive to enhancing their competitiveness.

There are two limitations of our work. Firstly, the lack and interpolation of industry raw data will to some extent affect the accuracy of model simulation results. In China, there is a certain degree of error in the official historical statistics of energy data related to carbon emissions. For example, there are significant differences in the historical statistics of energy consumption between the national and provincial levels in China. Although the system was adjusted in 2015, the differences still exist (Li B. et al., 2020). For the data related to carbon peak in the industry, due to the fact that data statistics at the industry level are more difficult than at the macro level, there are certain deficiencies in data such as raw material statistics and energy cost statistics. Adopting interpolation methods will affect the final results to a certain extent. Secondly, in terms of optimization algorithms, other algorithms such as FA and PSOA can be introduced for more comparisons in the future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

QY: Writing – original draft. CZ: Writing – original draft, Conceptualization, Data curation. XC: Conceptualization, Formal Analysis, Writing – original draft. PJ: Data curation, Writing – original draft. JS: Conceptualization, Data curation, Methodology, Supervision, Writing – original draft, Writing – review and editing. HJ: Conceptualization, Data curation, Formal Analysis, Methodology, Project administration, Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This paper is funded by the Research on the Multi-Objective Path Optimization Technique of Carbon Peak Carbon Neutrality in Sub-regions and Years Based on the Synergy of Energy-Industry-Economy of the Science and Technology Project of Big Data Center of State Grid Corporation of China (Contract No. SGSJ0000NYJS2400040).

Conflict of interest

Authors QY, CZ, XC, and PJ were employed by Big Data Center of State Grid Corporation of China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The “Action Plan for Peaking Carbon Emissions before 2030” requires that the proportion of non-fossil energy consumption in China reach around 25% by 2030.

²The “Special Action Plan for Energy Conservation and Carbon Reduction in the Steel Industry (2024–2030)” proposes that by 2030, the energy efficiency of major energy consuming equipment in the steel industry should reach the international advanced level, and the proportion of short process electric furnace steelmaking should be increased to over 15%.

References

Cai, B., Lyu, C., Dong, J., Wang, X., Zheng, Y., Li, X., et al. (2022). Research methods for carbon peak pathways in key industries/fields. Res. Environ. Sci. 35 (02), 320–328. doi:10.13198/j.issn.1001-6929.2021.11.05

CrossRef Full Text | Google Scholar

Chen, T., and Wang, M. (2024). Deep learning-based carbon emission forecasting and peak carbon pathways in China's logistics industry. Sustainability 16 (5), 1826. doi:10.3390/su16051826

CrossRef Full Text | Google Scholar

Dai, C., Tan, Y., Cao, S., Liao, H., Pu, J., Huang, H., et al. (2024). Analysis and short-term peak forecasting of the driving factors of carbon emissions in the construction industry at the provincial level in China. Energies 17 (16), 4101. doi:10.3390/en17164101

CrossRef Full Text | Google Scholar

Du, H., Zhao, L., Liu, C., Qiu, K., and Li, H. (2022). Carbon peak prediction and uncertainty analysis of main urban areas based on LEAP model and KAYA model. J. Ecol. Rural Environ. 38 (08), 983–991. doi:10.19741/j.issn.1673-4831.2022.0205

CrossRef Full Text | Google Scholar

Fang, K., Li, C., Tang, Y., He, J., and Song, J. (2022). China's pathways to peak carbon emissions: new insights from various industrial sectors. Appl. Energy 306, 118039. doi:10.1016/j.apenergy.2021.118039

CrossRef Full Text | Google Scholar

Gao, G., Wen, Y., Wang, L., and Xu, R. (2023). Research on carbon peak in urban agglomerations based on influencing factors of carbon emissions. Econ. Manag. 45 (02), 39–58. doi:10.19616/j.cnki.bmj.2023.02.003

CrossRef Full Text | Google Scholar

Guo, Y., Hou, Z., Fang, Y., Wang, Q., Huang, L., Luo, J., et al. (2023). Forecasting and scenario analysis of carbon emissions in key industries: a case study in Henan Province, China. Energies 16 (20), 7103. doi:10.3390/en16207103

CrossRef Full Text | Google Scholar

Li, J., Guo, J., and Gao, S. (2020a). Current status, problems and challenges of national carbon emission accounting. Dev. Res. (06), 9–14.

Google Scholar

Li, B., Han, S., Wang, Y., and Li, J. (2020b). Feasibility assessment of the carbon emissions peak in China's construction industry: factor decomposition and peak forecast. Sci. Total Environ. 706, 135716. doi:10.1016/j.scitotenv.2019.135716

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, D., and Chen, W. (2017). Carbon emission peak pathways based on China's TIMES model. J. Tsinghua Univ. Nat. Sci. Ed. 57 (10), 1070–1075. doi:10.16511/j.cnki.qhdxxb.2017.25.047

CrossRef Full Text | Google Scholar

Niu, H., and Liu, Z. (2023). Multi-objective collaborative evolution prediction of China's manufacturing structure under the background of carbon peak. Systems Engineering-Theory & Practice. doi:10.14120/j.cnki.cn11-5057/f.2023.09.0059-10

CrossRef Full Text | Google Scholar

Pan, C., Wang, B., Hou, X., Gu, Y., Xing, Y., Liu, Y., et al. (2023). Research on the carbon peak pathway of China's iron and steel industry based on the LMDI-STIRPAT model. Chin. J. Eng. 45 (06), 1034–1044. doi:10.13374/j.issn2095-9389.2022.04.25.002

CrossRef Full Text | Google Scholar

Shen, L., Yuan, Q., He, Q., Jiang, P., Ji, H., and Shi, J. (2025). Simulation and pathway selection for China's carbon peak: a multi-objective nonlinear dynamic optimization approach. Sustainability 17, 154. doi:10.3390/su17010154

CrossRef Full Text | Google Scholar

Sun, L., Zhou, Y., and Wu, H. (2023). Low-carbon transition pathways for the steel industry: an empirical analysis based on the LEAP-LCA coupling model. J. Iron Steel Res.

Google Scholar

Tan, J., Zhang, S., Zhang, Y., and Wang, B. (2024). Differential quantitative analysis of carbon emission efficiency of Gansu manufacturing industry in 2030. Sustainability 16 (5), 2007. doi:10.3390/su16052007

CrossRef Full Text | Google Scholar

Wang, Y., Ji, H., Wang, S., and Shi, J. (2024). Research on carbon emissions estimation in key industries based on the electricity–energy–carbon model: a case study of Henan Province. Energies 17, 2933. doi:10.3390/en17122933

CrossRef Full Text | Google Scholar

Wei, Y., Yu, B., Tang, B., Liu, L., Liao, H., Chen, J., et al. (2022a). Optimization methods for China's carbon peak and carbon neutrality pathways. J. Beijing Inst. Technol. Soc. Sci. Ed. 24 (04), 3–12. doi:10.15918/j.jbitss1009-3370.2022.1164

CrossRef Full Text | Google Scholar

Wei, Y., Yu, B., Tang, B., Liu, L., Liao, H., Chen, J., et al. (2022b). Timetable and roadmap for China's carbon peak and carbon neutrality. J. Beijing Inst. Technol. Soc. Sci. Ed. 24 (04), 13–26. doi:10.15918/j.jbitss1009-3370.2022.1165

CrossRef Full Text | Google Scholar

Wen, L., and Diao, P. (2022). Simulation study on carbon emission of China's electricity supply and demand under the dual-carbon target. J. Clean. Prod. 379, 134654. doi:10.1016/j.jclepro.2022.134654

CrossRef Full Text | Google Scholar

Zhang, Q., and Chen, X. (2022). Sequential prediction of carbon peak in China's industrial sector: based on a multi-sector dynamic CGE model. Syst. Eng. - Theory and Pract.

Google Scholar

Zhang, X., Zhao, X., Jiang, Z., and Shao, S. (2017). How to achieve the 2030 CO2 emission-reduction targets for China's industrial sector: retrospective decomposition and prospective trajectories. Glob. Environ. Change 44, 83–97. doi:10.1016/j.gloenvcha.2017.03.003

CrossRef Full Text | Google Scholar

Zhou, T., Zheng, H., and Ma, J. (2023). Research on renewable energy penetration rate and carbon peak threshold of power systems. China Electr. Power.

Google Scholar

Zhou, K., Zhang, S., and Yang, J. (2025). Carbon reduction scenarios and potential analysis of China's information and communications technology industry. J. Environ. Manag. 375, 124248. doi:10.1016/j.jenvman.2025.124248

PubMed Abstract | CrossRef Full Text | Google Scholar