Sustainable soil organic carbon prediction using machine learning and the ninja optimization algorithm

Soil organic carbon (SOC) plays a critical role in global carbon cycling, influencing climate regulation, soil fertility, and sustainable land management. However, accurate SOC prediction remains a challenging task due to the complex, high-dimensional, and nonlinear nature of soil data. Recent advances in machine learning (ML) have improved SOC estimation, yet these models often suffer from overfitting and computational inefficiency when effective feature selection and hyperparameter tuning are not applied. To address these challenges, we propose a novel integration of the Ninja Optimization Algorithm (NiOA) for simultaneous feature selection and hyperparameter optimization, aimed at enhancing both predictive accuracy and computational efficiency. In our experimental setup, 80% of the dataset was allocated for training and 20% for testing. The baseline Support Vector Machine (SVR) model achieved a mean squared error (MSE) of 0.00513, which was reduced to 0.00011 after applying binary NiOA (bNiOA) for feature selection. After full NiOA-based hyperparameter tuning, the MSE improved further to $7.52\times 10^{-7}$, corresponding to a 99.98% reduction in prediction error. Thus, the proposed NiOA-enhanced framework demonstrates considerable potential in advancing SOC modeling. It offers a scalable, interpretable, and high-precision solution that can be effectively applied in data-scarce environments, particularly in support of sustainable land management and climate change adaptation strategies.

1 Introduction

In natural ecosystems, soil is essential, as it nourishes vegetation, manages water systems and traps carbon. It serves both the environment and farmers by capturing excess carbon and supporting crop growth and long-term sustainability of ecosystems (O’Riordan et al., 2021). The presence of soil organic carbon is an essential sign of healthy soil. It shows how stable the ecosystem is by affecting nutrient use, bacterial growth, water absorption and carbon storage over time. Soc organisms help manage the levels of greenhouse gases in the atmosphere and control climate change (Rillig et al., 2023).

It is tough to measure and forecast SOC due to the soil’s wide variety and complex nature. The way land is used, climate differences and the fact that some areas have more geographical variety all result in variable SOC levels. African soil quality varies widely, from vibrant fertile soils in the highlands to poorer soils in dry regions (Francaviglia et al., 2023). As land changes quickly and forests are removed, monitoring SOC across broad areas is crucial for effective responses to climate change and farming. Still, traditional methods for surveying soils demand a lot of time and money, and their outcomes can be inconsistent due to different formats and incomplete data coverage (Rocci et al., 2021). Having different types of soil databases, along with poor resolution, hinders efforts to study SOC and restricts advancements in research on the health of soils and how much carbon they contain.

Machine learning (ML) has emerged as a transformative approach for addressing the multifaceted challenges associated with Soil Organic Carbon (SOC) prediction. In contrast to traditional empirical models, ML algorithms are not only capable of processing large and heterogeneous datasets, but also offer advanced capabilities for modeling complex, nonlinear interactions among variables. These models can capture latent structures and high-order dependencies without requiring explicit assumptions about the data-generating process. Furthermore, ML approaches facilitate automated learning from data, minimize the need for manual feature engineering, and exhibit strong generalization performance across diverse environmental conditions. Such properties make ML particularly well-suited for high-dimensional, data-scarce, and spatially variable domains like SOC modeling (Venter et al., 2021). Approaches based on remote sensing, climate data and soil samples have become popular to decrease the expenses involved in SOC estimation and make the method more scalable. Even so, ML models are only as strong as their input data, selected features and properly adjusted hyperparameters. Inclusion of unnecessary or similarly essential features can result in overfitting, make the model more difficult to solve and reduce how well it can solve new cases, showing that efficient selection of features is essential (Odebiri et al., 2022).

Time-tested methods for selecting essential features, including RFE and filtering with correlation, tend to overlook the complex and nonlinear relationships among multiple soil attributes. On the other hand, algorithms inspired by natural systems such as Grey Wolf Optimizer, Satin Bowerbird Optimizer, Multiverse Optimization, Firefly Algorithm and Genetic Algorithm, have demonstrated potential in improving SOC prediction through both feature selection and model tuning (Beillouin et al., 2022). Since these algorithms use processes inspired by life, evolution and group actions, they are exceptionally efficient on significant and complex data sets found in nature. There is a crucial aspect of superior model optimization called hyperparameter tuning. Reducing errors in training and improving model performance is possible only when hyperparameters like learning rates, depths of trees, kernel options and regularization terms are tuned. Metaheuristic optimization helps to automate this task, lower the time required for calculations and increase accuracy (Pal et al., 2021).

Recent research has demonstrated the utility of ML models for SOC stock estimation across different geographic contexts. For example, Meliho et al. (2023) applied RF and Cubist models in Morocco’s Ourika watershed, revealing that land use and bioclimatic variables were dominant factors in SOC prediction. Similarly, Mosaid et al. (2024) used a suite of ML algorithms in the Srou catchment to estimate SOC stock, showing that RF and SVM performed best in semi-arid Moroccan regions. In a different ecological setting, Solly et al. (2020) investigated the role of effective cation exchange capacity (CEC) in explaining SOC variability across Swiss forests, emphasizing how soil mineral surfaces and pH mediate SOC stabilization. These studies underscore the growing use of ML for SOC modeling; however, they typically focus on isolated regional applications and do not incorporate unified optimization strategies for both feature selection and hyperparameter tuning. Furthermore, African soil systems—despite their climatic vulnerability and spatial heterogeneity—remain underrepresented in such research. To address these gaps, this study introduces a novel SOC prediction framework based on the Ninja Optimization Algorithm (NiOA), integrated with Support Vector Machine (SVR). NiOA jointly optimizes both feature selection and model hyperparameters in a single process, thereby reducing computational burden, improving accuracy, and enhancing interpretability. The proposed framework is validated on a high-dimensional African soil dataset and establishes a scalable approach to SOC estimation in data-scarce and ecologically diverse regions.

We have achieved the following significant contributions:

$•$ We present an integrated approach that combines machine learning and the NiOA algorithm for feature selection and hyperparameter optimization to achieve more reliable SOC predictions. It overcomes important obstacles such as high-dimensionality, redundant features and computational burden in developing accurate SOC models.

$•$ Our approach struck a balance between searching the feature space and focusing on identifying the most informative features, thereby boosting the predictive performance of soil organic carbon estimations.

$•$ We have developed a novel approach for efficiently optimizing complex machine learning models in environmental sciences using NiOA-based procedures, enabling highly accurate SOC predictions across various terrain.

$•$ We systematically compare our proposed NiOA-based framework with state-of-the-art machine learning algorithms and traditional optimization methods, demonstrating superior performance across multiple evaluation metrics.

$•$ This research contributes to the broader field of sustainable land management by offering a scalable, data-driven approach for accurately modeling SOC, supporting climate resilience and precision agriculture practices.

The remainder of this paper is structured as follows. Section 2 provides a comprehensive review of related work, highlighting recent advancements in machine learning and optimization techniques for soil organic carbon prediction. Section 3 outlines the proposed methodology, including data preprocessing, feature selection, and model training using the Ninja Optimization Algorithm (NiOA) for hyperparameter tuning. Section 4 presents the experimental setup and performance evaluation metrics, while Section 5 discusses the results, including comparative analysis with state-of-the-art methods. Finally, Section 6 concludes the paper with insights into the implications of our findings for sustainable land management and potential future research directions.

To address these challenges, the present study sets forth the following objectives:

$•$ To develop a novel, integrated framework that combines machine learning models with the newly introduced Ninja Optimization Algorithm (NiOA) for Soil Organic Carbon (SOC) prediction.

$•$ To utilize NiOA for both feature selection and hyperparameter optimization, thereby enhancing the predictive performance and computational efficiency of SOC estimation models.

$•$ To systematically evaluate the performance of the NiOA-based framework against several state-of-the-art metaheuristic algorithms, including Grey Wolf Optimizer (GWO), Harris Hawks Optimization (HHO), and Multi-Verse Optimizer (MVO), across multiple evaluation metrics.

$•$ To apply this framework to a diverse African soil dataset, addressing a critical gap in SOC modeling for underrepresented geographical regions and promoting scalable, data-driven insights for sustainable land management and climate resilience.

Through these aims, the study not only advances methodological contributions in feature selection and model tuning but also demonstrates the practical value of the NiOA in environmental modeling applications.

2 Literature review

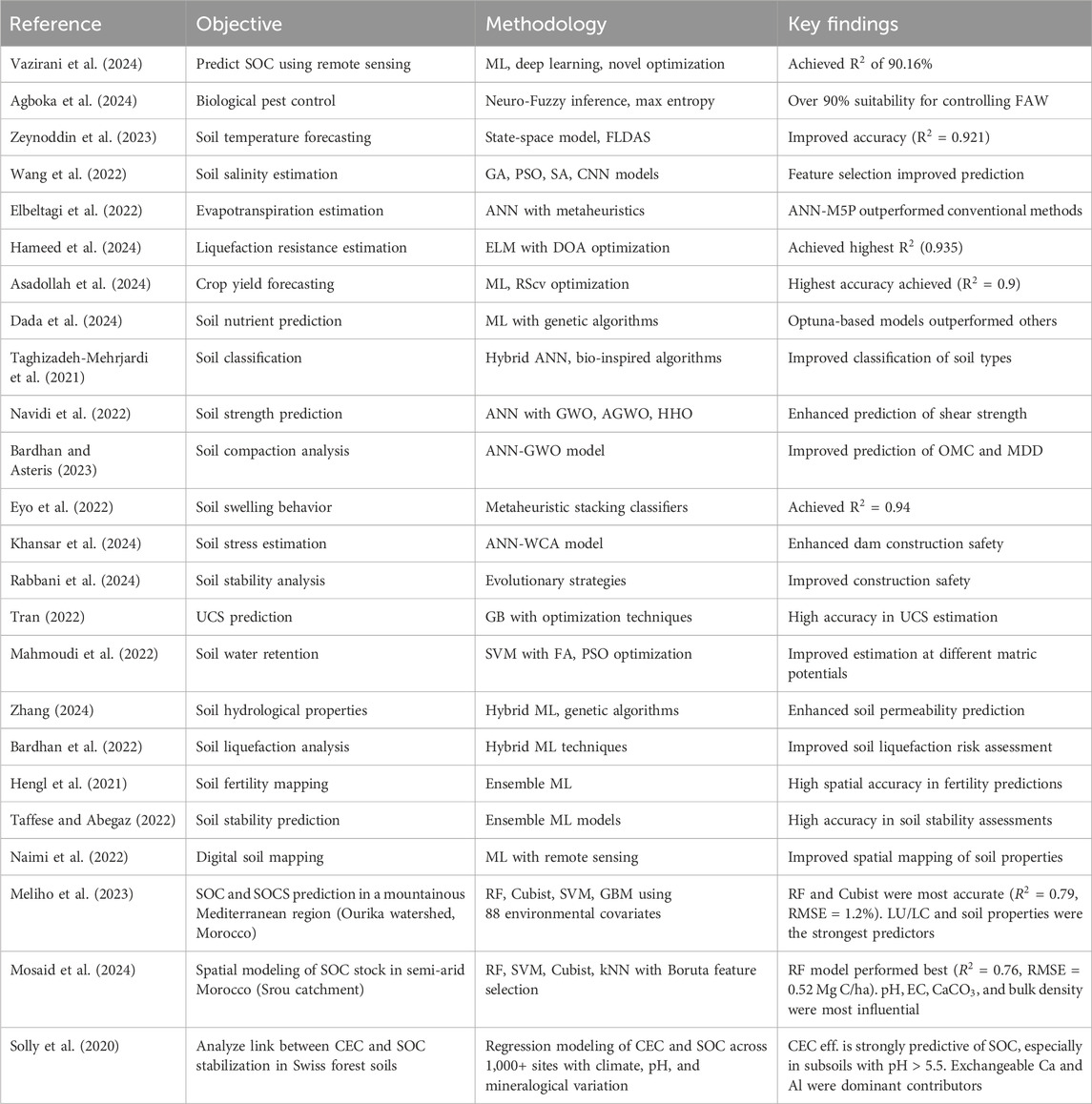
Combining machine learning and metaheuristic optimization has greatly enhanced soil science, agriculture and environmental management research. Machine learning and metaheuristic optimization have significantly improved predictions and analysis for elements like SOC, pests, temperature, salinity, yield, compaction, risk, evapotranspiration and soil mapping. A range of studies highlights the utility and effectiveness of ML and optimization in solving these problems.

Researchers have worked to refine SOC estimation to comprehend better the role of carbon in the environment and soil health. A novel optimization method combining remote sensing and ground cover data surpasses existing approaches, such as Grid Search Cross-Validation and the Jaya algorithm, producing more accurate SOC estimates and minimizing irrelevant variables. This level of accuracy is crucial for enabling larger-scale SOC mapping, which contributes to climate change mitigation and carbon credit calculations.

A new neuro-fuzzy evolution-based adaptive mapping system has been designed to determine whether biological control tactics are effective against invasive pests such as the Fall Armyworm (Spodoptera frugiperda) (Agboka et al., 2024). This method helps drive the shift towards sustainable farming practices that lessen potential damage to the environment.

Advanced modeling approaches have enhanced our knowledge of the relationship between soil temperature and biochemical interactions. The SS model efficiently predicted soil temperature and benefited agriculturalists and climate researchers. Soil salinity predictions have been significantly improved using genetic algorithms, particle swarm optimization, and simulated annealing (Wang et al., 2022).

Crop yield predictions are also significant, helping ensure enough food and better use of resources. This process allowed them to optimize barley and wheat yield prediction ML models, leading to strong results by tuning hyperparameters (Asadollah et al., 2024). Having such exact data allows farmers to decide when to plant crops and how to fertilize them.

Measures have been taken to boost soil nutrient availability, which helps the agricultural industry. Owing to advanced techniques and frameworks, predicting nutrient availability is more accurate, which aids in managing soil at different sites (Dada et al., 2024).

Using machine learning models along with metaheuristic algorithms has enhanced predictions in geotechnical engineering about shear strength, liquefaction and compaction of soil. For example, networks such as ANNs improved by GWO, AGWO and HHO algorithms tend to estimate important geotechnical factors like soil and rock strength with higher accuracy, making infrastructure safer (Navidi et al., 2022; Bardhan and Asteris, 2023; Eyo et al., 2022). Likewise, by combining extreme learning machines (ELM) with the Dingo Optimization Algorithm (DOA), scientists have succeeded in boosting the accuracy of estimating soil liquefaction resistance, which benefits seismic hazard assessments (Hameed et al., 2024).

They also involve using ensemble machine learning models to assess soil stability, map soils digitally and determine water content in soils. For instance, using metaheuristic stacking and voting classifiers has helped predict the swelling of expansive soils and lessen the chance of damage to buildings (Eyo et al., 2022). Support vector machines that use firefly and particle swarm algorithms have supported better soil moisture monitoring and efficient water conservation (Mahmoudi et al., 2022).

Recent studies have highlighted the use of machine learning (ML) techniques for mapping and predicting Soil Organic Carbon (SOC) at different spatial scales. For example, Meliho et al. (2023) applied Cubist, Random Forest (RF), Support Vector Machine (SVM), and Gradient Boosting Machine (GBM) models to predict SOC stocks in the Ourika watershed in Morocco using 88 environmental covariates, reporting that RF and Cubist achieved the highest accuracy ($R^2$ = 0.79 and 0.77, respectively) for SOC prediction. Similarly, Mosaid et al. (2024) assessed SOC stock prediction in the Srou catchment (Upper Oum Er-Rbia watershed, Morocco) using RF, k-NN, SVM, and Cubist models, with RF again showing the best performance ($R^2$ = 0.76). Their study highlighted the importance of bulk density, pH, electrical conductivity, and calcium carbonate as key predictors for SOC.

In a broader European context, Solly et al. (2020) investigated the role of cation exchange capacity (CEC) as a proxy for SOC stabilization in Swiss forests. Using regression analysis over 1,000 forest sites with wide-ranging climatic and soil conditions, they showed that CEC effectively predicts SOC content, particularly in subsoils with pH above 5.5, thus linking mineral surface chemistry with organic carbon dynamics.

While these studies confirm the predictive potential of ML and environmental variables for SOC estimation, most do not employ metaheuristic algorithms to simultaneously optimize feature selection and model hyperparameters. Moreover, few studies focus on underrepresented regions like Sub-Saharan Africa, where soil diversity and data heterogeneity pose additional modeling challenges. In contrast, the present study introduces the Ninja Optimization Algorithm (NiOA) to enhance both feature selection and hyperparameter tuning. Combined with SVR and benchmarked against multiple optimizers, our method significantly improves prediction accuracy and model efficiency on a high-dimensional African soil dataset, addressing a gap in both methodology and geographical scope.

Combined, the studies point to the significant impact of ML and metaheuristic optimization in soil science. This contribution allows accurate soil properties prediction, better land management, and more resistance to climate challenges. Applying computational intelligence to environmental modeling helps increase the accuracy and dependability of soil evaluations, ensuring better results for agriculture, water resources and conservation.

Table 1 outlines critical studies that use machine learning (ML), deep learning and metaheuristic optimization on soil and related topics. These studies are grouped based on their performance and outcomes, explaining how advances were made in predicting SOC, soil classification, forecasting harvest yields and other key areas of soil study. Using ANN, GA, GWO and hybrid ML, various computational techniques have aided in enhancing the accuracy of predicting soil behavior and making decisions. Several studies have highlighted that combining optimization and ML methods is crucial for better soil analysis, farmland management, and environmental protection.

Table 1

Table 1. Summary of literature review.

Despite the increasing use of machine learning (ML) models for Soil Organic Carbon (SOC) prediction, several limitations remain. First, most existing studies rely on conventional optimization strategies (e.g., grid search, random search), which are computationally expensive and prone to early convergence, especially with high-dimensional soil datasets. Second, while metaheuristic algorithms have been explored individually for either feature selection or hyperparameter tuning, very few approaches integrate both tasks within a unified optimization framework. Third, studies tend to focus on specific regional contexts—particularly temperate or Mediterranean zones—leaving African soils underrepresented in data-driven SOC modeling. This is a critical gap given the rapid land-use change and climate sensitivity of the continent’s ecosystems. Moreover, the combination of large feature spaces, soil heterogeneity, and non-linear relationships poses a substantial challenge to predictive accuracy, model interpretability, and scalability. Therefore, what remains unknown is how a jointly optimized ML framework—capable of both feature selection and hyperparameter tuning—can improve SOC prediction accuracy in a geographically diverse and data scarce environment. This study addresses these gaps by proposing a novel integration of the Ninja Optimization Algorithm (NiOA) with machine learning models, especially Support Vector Machine (SVR), for simultaneous feature selection and hyperparameter optimization. By applying this framework to a high-dimensional African soil dataset, we offer a scalable, efficient, and interpretable solution for SOC modeling, with implications for sustainable land management and climate resilience.

Although recent studies such as Mosaid et al. (2024), Solly et al. (2020), and Meliho et al. (2023) have demonstrated the effectiveness of machine learning algorithms (e.g., RF, SVM, Cubist) for SOC and SOC stock estimation, these approaches are generally limited by the absence of integrated feature selection and hyperparameter optimization frameworks. Furthermore, their geographic focus remains constrained to specific Mediterranean or European forest regions. In contrast, our study introduces a novel integration of the Ninja Optimization Algorithm (NiOA), which simultaneously optimizes both feature selection and hyperparameter tuning within multiple machine learning models, particularly Support Vector Machine (SVR). Empirically, the NiOA enabled framework achieved a substantial reduction in mean squared error (MSE) from 0.00513 (baseline SVR) to $7.52\times 10^{-7}$ after optimization a 99.98% improvement in prediction accuracy. Moreover, feature selection using binary NiOA (bNiOA) reduced the average selected feature subset size by over 65%, leading to significant computational gains and model interpretability without sacrificing accuracy. Unlike prior works, our approach is validated on a high-dimensional African soil dataset, addressing regional data scarcity and demonstrating transferability across heterogeneous environmental conditions. These results collectively highlight the methodological and contextual novelty of our contribution, establishing a new benchmark for scalable, high-precision SOC modeling in underrepresented geographies.

2.1 Research gap and contribution

Several important gaps exist in applying ML and metaheuristic optimization methods to the problem of predicting Soil Organic Carbon levels in soil. Many studies have employed classical optimization procedures like grid search, genetic algorithms and particle swarm optimization to predict distinct soil characteristics such as nutrient availability, compaction and salinity. Nonetheless, conventional methods often struggle with excessive computational expenses, early convergence and difficulties handling large datasets exhibiting a wide range of soil properties. Most existing approaches to feature selection fail to consider the complex, nonlinear relationships between soil characteristics, resulting in inaccurate model predictions. Most prior techniques do not allow for concurrent optimization of feature selection and hyperparameters, essential for achieving better performance and model robustness.

Our approach, dubbed the Ninja Optimization Algorithm (NiOA), is designed to solve the problems by simultaneously optimizing features and hyperparameters during SOC prediction. It enables superior model performance by dynamically adapting a trade-off between exploration and exploitation while minimizing computational costs. We integrate advanced ML models with the adaptive search of NiOA to offer a sophisticated solution for reliable SOC estimation, assisting in sustainable land management and strengthening the resilience of ecosystems in the face of climate change. Advances in computational approaches have enabled us to achieve higher accuracy and efficiency in predicting SOC.

3 Materials and methods

My goal with this study is to enhance the accuracy of predicting Soil Organic Carbon (SOC) by combining machine learning and metaheuristic optimization approaches. Making predictions with SOC data is difficult because they are very complex, often very variable, and have many values. It is essential to use a structured approach to prediction that handles accuracy, understanding and efficiency together. To address these difficulties, the proposed framework involves several steps: preprocessing of data, selecting features, machine learning modeling, tuning hyperparameters and checking model performance, as shown in Figure 1.

Figure 1

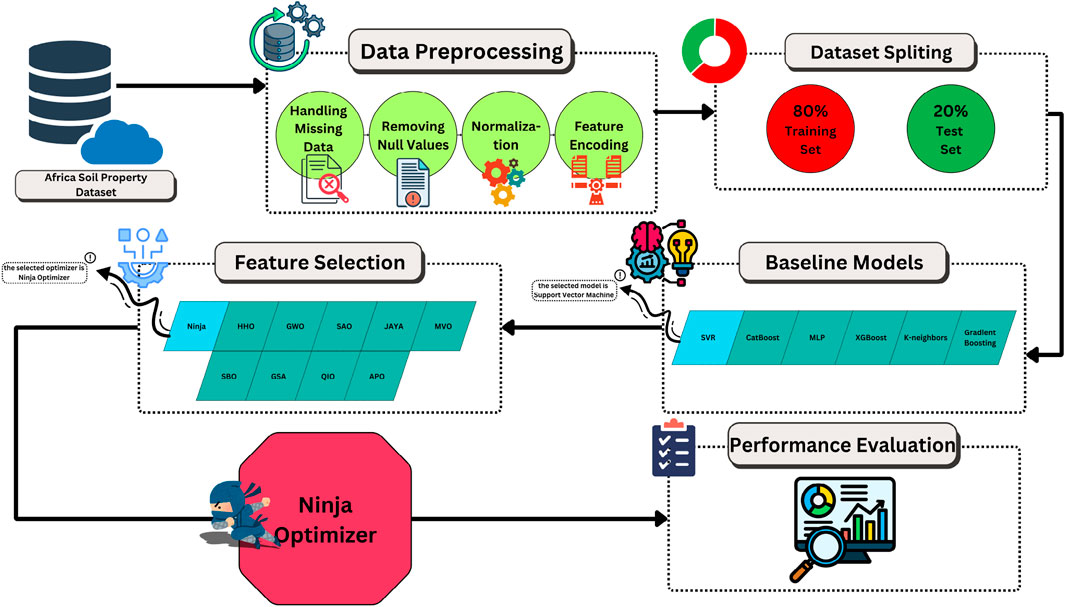
Figure 1. Proposed methodological framework for SOC prediction. Data preprocessing, feature selection using the Ninja Optimization Algorithm (NiOA), machine learning model training, hyperparameter optimization, and performance evaluation are included.

The first step in preprocessing soil data is to clean it and change it into a form that is always reliable. It covers techniques like handling missing data, changing continuous data to a similar scale and changing categorical features to codes. After that, the data is separated into training and testing areas for fair model assessment. Preprocessing your data effectively can help you manage background noises, improve understanding of your decisions and ensure your predictions are accurate.

Feature selection plays a significant role in this technique, helping to keep only the essential soil characteristics needed for predicting SOC. NiOA was chosen as it does an excellent job selecting useful features and strong prevention of overfitting. By combining exploration and exploitation, NiOA chooses the essential features to improve how well the model applies to data and reduces how much it needs to compute.

When feature selection is done, machine learning models such as SVR, CatBoost, MLP, XGBoost, KNN and GB are trained and assessed. They are picked because they can handle the complex connections between soil features and SOC. Once the best model is clear, it goes through the process of optimizing its performance using metaheuristic methods. Now, you adjust the necessary settings so the model works well and uses fewer resources.

The final part is testing the improved model using various metrics to see if it can accurately predict and generalize to new data. Using this detailed approach, the SOC prediction framework becomes reliable and useful, making it valuable for decision-making in soil and climate.

3.1 Dataset description

This study draws data from a comprehensive environmental database, which is helpful for various applications like climate studies, examining the carbon cycle and supporting sustainable soil management. It includes essential elements of soil chemistry, ecosystems and variations in climate which helps in all these agricultural applications. This data blends a range of chemical and physical tests on soil, making it possible to learn more about soil health, how productive it is and its environmental stability in various regions.

Soils play a key role in modifying carbon in the air, significantly shaping the greenhouse effect and climate. Accurate measurements of the amount of carbon in soil at different levels can reveal how deforestation and farming affect the concentration of ${\text{CO}}_2$ in the atmosphere. Detailed information is crucial for improving strategies that aim to capture and store carbon in the soil, restore degraded land and increase forest cover.

Moreover, this data is essential for studying and preventing land degradation in desert and semi-desert areas, since problems like soil erosion, reduction in fertility, and desertification seriously impact both farmland and the ecosystem. The assessment covers key parameters such as soil pH, conductivity and nutrient supply to understand potential damage to the soil and lead conservation actions. They play an essential role in discovering degraded locations, choosing eco-friendly farming methods and aiding in precision agriculture using high-resolution soil health maps.

Thanks to its attributes like organic carbon content, texture and electrical conductivity, the dataset allows for continuous monitoring and improved management of water resources. Irrigation, climate assessment and efficient water use can all benefit from this data. If the dates of soil sampling are noted, changes in soil quality over the years can be studied, and this helps decide on better ways to use and protect the land.

Integrating geospatial and temporal attributes makes this dataset ideal for researchers working in different areas, who can rely on it for ecological modeling, saving biodiversity and agriculture. It supports researchers in modeling how plants and animals react, expecting changes in biodiversity and creating plans for restoring habitats. Access to detailed soil data helps plan and manage cities so that soil is protected and ecosystems remain healthy.

This data is essential for progress in soil science, making precision farming possible, dealing with climate change, and choosing sustainable ways to manage land. Because of its detailed setup and many valuable traits, this field enables effective collaboration, making producing valuable results in soil conservation, managing carbon emissions and supporting the environment easier.

3.2 Data processing

Processed data plays a crucial role in producing reliable Soil Organic Carbon (SOC) predictions since the accuracy of the predictions largely depends on the integrity of the training data. Given the heterogeneity of soil datasets and the many sources of variation in sampling and measurement, it is vital to undertake rigorous preprocessing to deal with missing data, outliers and feature transformation. This section describes the fundamental processes for preparing soil data so that it becomes a suitable input for machine learning algorithms.

Not accounting for missing data can result in biased or inaccurate model results. Incomplete data in soil studies may result from errors in sampling methods, inconsistencies during fieldwork or low-quality satellite images. Different approaches are applied to discrete fields depending on how the data is structured. Suspicious values are replaced with the arithmetic mean or median when the missing data seems random. For unbalanced data, Quantile-based imputation is implemented for greater precision in imputation. KNN imputation allows the model to account for the relationship between nearby soil measurements. Categories such as data sources are imputed using mode or probabilistic methods to match the correct distribution in skewed distributions. Variables with more than 30% missing values are removed if their reliability cannot be determined.

Outlier detection and correction are just as essential since inherently large values can substantially bias model development and compromise predictive effectiveness. Unusual values in environmental data may be due to errors in measurement, unique and accurate readings or natural fluctuations between ecosystem components. The IQR (interquartile range) approach and Z scores are used to identify outliers accurately. Outliers are then treated using Winsorization, which controls values outside specified percentile boundaries to maintain the distribution structure while limiting the effect of extreme values. Threshold ranges are tailored to attributes that undergo notable fluctuations, for example, electrical conductivity and sodium extractable by the principles found in soil sciences.

Applying feature engineering and transformation helps the model achieve better predictions and more precise results. Non-hierarchical categorical data like soil source types are translated using one-hot encoding to get numerical values. If inputs are provided in a fixed sequence, they are encoded with label encoding. Measurement bias and variability can be reduced for pH, electrical conductivity and carbon organic through applying Z-score normalization, which improves the accuracy of Support Vector Machine and neural networks. Logarithmic transformation is also used to make variables, like carbon organic, more normal, while limiting the ranges of attributes such as phosphorus and potassium extractable to 0 and 1.

Using these preprocessing techniques increases the reliability of the dataset and helps to interpret it more easily for estimating SOC. The dataset is processed fully by treating missing data, outliers and features, helping it become suitable for advanced machine learning algorithms and resulting in improved estimates of soil health and carbon storage. Proper use of data is essential to find meaningful and accurate findings in environmental science and address world sustainability issues.

3.3 Exploratory data analysis

In Soil Organic Carbon (SOC) estimation, there is a need to understand the relationships between different soil properties. Some soil characteristics are highly interdependent and may be controlled by geographical, climatic and physicochemical factors. They can give us the knowledge to perform an effective feature selection, thus removing redundant or highly correlated variables to improve model generalization and computational efficiency. Correlation analysis is an indispensable tool in exploratory data analysis (EDA); it reconstructs the data’s inter-feature dependencies and recurring features.

According to the t-SNE scatter plot after Winsorization, the soil properties have been projected into a two-dimensional space for a better visual representation is shown in Figure 2. A colorized third point represents a soil sample. This processing of Winsorization helps alter clustering coherence rem,ove extreme outliers, and help some data points move away from their expected regions. The apparent separation and distribution of the soil samples show different patterns in soil sources, which is suitable for studying the differences in soil composition. Feature redundancy, correlations and the efficiency of preprocessing methods are significant to optimize the machine learning models for prediction of SOC.

Figure 2

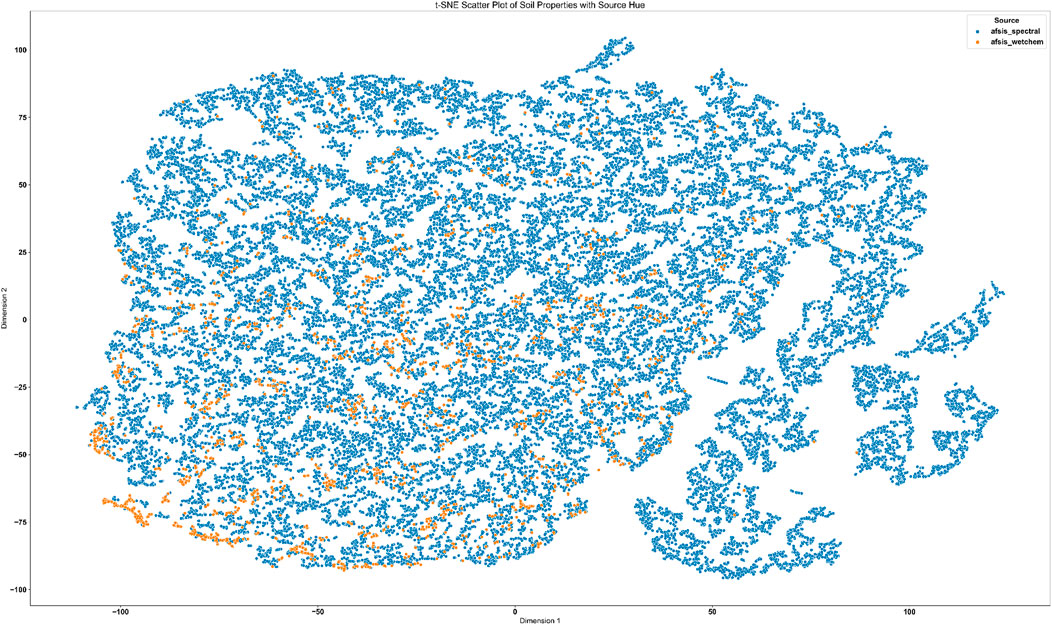
Figure 2. t-SNE scatter plot of soil properties after Winsorization, illustrating the structure of high-dimensional soil data in a reduced two-dimensional space. The application of Winsorization ensures that extreme values do not distort the clustering of soil samples, enhancing the interpretability of feature distributions.

3.4 Machine learning models for soil organic carbon prediction

The ability to predict Soil Organic Carbon (SOC) levels with high accuracy depends upon machine learning models that can effectively account for nonlinear interactions between soil variables and carbon concentrations. Various machine learning methods are utilized in this endeavor to achieve reliable and widely applicable SOC predictions. The research investigates how various machine learning models perform in predicting SOC values.

Support Vector Machine (SVR) seeks to identify the function that links input features to an output value while enhancing its predictive performance. It finds the solution to the following optimization problem.

$\underset{w,b,{\xi }^{+},{\xi }^{-}}{\min }\frac{1}{2}\Vert w{\Vert }^2+C{\displaystyle \sum _{i=1}^n}\left({\xi }_i^{+}+{\xi }_i^{-}\right),(1)$

subject to:

$|y_i-\left(w\cdot x_i+b\right)|\le \epsilon +{\xi }_i^{+},{\xi }_i^{+},{\xi }_i^{-}\ge 0,(2)$

where $w$ is the weight vector, $b$ is the bias term, ${\xi }_i^{+},{\xi }_i^{-}$ are slack variables, and $C$ is a regularization parameter balancing complexity and training error. SVR is particularly effective for SOC modeling due to its robustness against high-dimensional data and ability to capture nonlinear soil-property relationships.

Recent studies have empirically validated the use of SVR in SOC prediction. For example, a comprehensive assessment by Emadi et al. (2020) applied SVR alongside other ML algorithms to predict SOC based on 1,879 soil samples and 105 auxiliary variables, demonstrating competitive accuracy.

The SVR framework is especially advantageous in high-dimensional environmental modeling due to its flexibility and generalization capacity.

The foundational theory of SVR is rooted in Vapnik’s statistical learning theory (Vapnik et al., 1996), where its performance advantages in nonlinear and high-dimensional spaces were first established.

CatBoost an algorithm optimized for working with categorical data using gradient-boosting. Gaining increased stability and lowering the risk of overfitting is made possible by its ability to prevent target leakage with ordered boosting. Its general formulation is:

$F_m\left(x\right)=F_{m-1}\left(x\right)+{\gamma }_m{h}_m\left(x\right),(3)$

here $F_m(x)$ is model number $m$, $F_{m-1}(x)$ is model iteration, ${\gamma }_m$ is the learning rate chosen for this iteration and $h_m(x)$ is a weak learner. Because CatBoost handles complex interactions well, it is an excellent tool for predicting SOC, especially when the presence of categorical attributes matters to the model.

Recent studies have shown the efficacy of CatBoost in predicting spatial patterns of SOC and identifying its primary environmental controls. For instance, a regional-scale study by Guo et al. (2025) demonstrated that CatBoost achieved a high $R^2$ of 0.828, outperforming linear models in explaining SOC variability. The algorithm was particularly effective in capturing complex interactions among total nitrogen, phosphorus, temperature, and cation exchange capacity, reinforcing its suitability for nonlinear and heterogeneous soil data.

The algorithmic foundation of CatBoost, including its use of ordered boosting and novel techniques for handling categorical features, was introduced by Prokhorenkova et al. (2019), where it was shown to outperform other gradient boosting frameworks across diverse datasets.

Multi-Layer Perceptron (MLP) is an ANN made up of various layers of connected neurons that process data only in one direction. It uses forward propagation to represent detailed, unpredictable soil patterns defined as:

$h_j=\sigma \left({\displaystyle \sum _{i=1}^n}{w}_{ij}{x}_i+b_j\right),(4)$

$y_k=\sigma \left({\displaystyle \sum _{j=1}^m}{v}_{jk}{h}_j+c_k\right),(5)$

here, $x_i$ are the input features, $w_{ij}$ are the weights linking inputs to hidden neurons, $v_{jk}$ are the weights linking hidden neurons to output neurons, $b_j$ are biases for the hidden layer neurons, $c_k$ are biases for output neurons, $h_j$ are the activations of the hidden layer neurons and $y_k$ is the output value obtained after running the network. MLP is suited to SOC modeling since it is capable of detecting the relationships among learning features.

Empirical studies have demonstrated the use of MLP in SOC prediction. For instance, a comparative study by Guo et al. (2023) evaluated ANN (MLP), SVM, RF, and other models using 60 soil samples and 21 environmental predictors. While Random Forest achieved the highest accuracy $(R^2=0.68)$, MLP (ANN) still provided useful predictions $(R^2=0.36)$, validating its role in soil modeling, particularly when nonlinear interactions among predictors are involved.

The foundational learning algorithm of MLP, known as backpropagation, was first introduced by Rumelhart et al. (1986), and remains the core of training modern neural networks.

XGBoost (Extreme Gradient Boosting) specializes in machine learning by optimizing tree-based boosting for high performance and accuracy. It improves the outcome of this objective function:

$\mathcal{L}={\displaystyle \sum _{i=1}^n}l\left(y_i,{\widehat{y}}_i\right)+{\displaystyle \sum _{k=1}^K}\mathrm{\Omega }\left(f_k\right),(6)$

where $l(y_i,{\widehat{y}}_i)$ is the loss function, and $\mathrm{\Omega }(f_k)=\gamma T+\frac{1}{2}\lambda \Vert w{\Vert }^2$ is the regularization term controlling tree complexity. XGBoost’s ability to handle missing values and high-dimensional feature spaces makes it particularly effective for SOC prediction. Chen and Guestrin (2016) introduced XGBoost as a scalable and sparsity-aware gradient boosting system. Their algorithm incorporates advanced regularization techniques and system-level optimizations to efficiently process high-dimensional and sparse datasets, making it especially suitable for large-scale modeling tasks.

In the context of soil organic carbon (SOC) prediction, empirical studies have demonstrated the effectiveness of XGBoost. For instance, Emadi et al. (2020) applied an Extreme Gradient Boosting with Random Forest (XGBRF) ensemble to predict SOC content in swamp wetlands using Sentinel-1, Sentinel-2, and DEM datasets. The model outperformed traditional XGBoost and RF approaches, achieving an $R^2$ of 0.66 and a Lin’s concordance correlation coefficient (LCCC) of 0.76. This illustrates XGBoost’s robustness in capturing the complex spatial dynamics of SOC, particularly when multi-source remote sensing data are involved.

K-Nearest Neighbors (KNN) is a non-parametric algorithm that estimates target values based on the nearest neighbors in the feature space. The predicted value $\widehat{y}$ is given by:

$\widehat{y}=\frac{1}{K}{\displaystyle \sum _{i\in N_k}}{y}_i,(7)$

where $K$ is the number of neighbors and $N_k$ is the set of $K$ nearest neighbors. KNN is effective for SOC prediction due to its ability to naturally capture local spatial correlations. The theoretical foundation of KNN was laid by Cover and Hart (1967), who demonstrated that the nearest neighbor decision rule can asymptotically achieve a probability of error no worse than twice the Bayes optimal rate. This highlights the robustness of KNN in pattern recognition and prediction under minimal assumptions about the underlying data distribution.

In the context of SOC prediction, Mosaid et al. (2024) applied KNN alongside other machine learning algorithms, including random forest and SVM, to model soil carbon stocks in a Mediterranean soil erosion site. Although KNN exhibited lower predictive performance compared to ensemble methods, it was still able to capture local SOC variability based on key environmental and edaphic predictors. This underscores its practical utility when used as a benchmark model or within hybrid frameworks.

Gradient Boosting is an ensemble learning method that sequentially refines weak learners to minimize residual errors. Its iterative model update is given by:

$F_m\left(x\right)=F_{m-1}\left(x\right)+{\gamma }_m{h}_m\left(x\right),(8)$

where $F_m(x)$ is the updated model at iteration $m$, ${\gamma }_m$ is the learning rate, and $h_m(x)$ is the weak learner. Gradient Boosting is particularly valuable for SOC modeling as it effectively captures complex, nonlinear dependencies between soil attributes.

The theoretical foundation for gradient boosting was established by Friedman (2001), who introduced a general framework for additive function approximation using gradient descent. This framework supports various loss functions and model types, making it broadly applicable to regression and classification tasks.

In the context of soil organic carbon (SOC) prediction, Chen et al. (2024) applied a gradient boosting model driven by multisource remote sensing data, including Sentinel-1, Sentinel-2, and DEM, to estimate SOC density in the Qinghai–Tibet Plateau. Their findings revealed that the LightGBM implementation of GB outperformed other machine learning models in terms of accuracy and robustness, confirming its suitability for spatial SOC prediction across heterogeneous landscapes. Together, these models provide a comprehensive toolkit for SOC prediction, each offering distinct advantages in handling high-dimensional data, capturing nonlinear relationships, and improving predictive accuracy. The relative performance of these models in different environmental settings will provide insights into their suitability for large-scale SOC assessments, supporting more effective soil management and climate resilience.

Numerous studies in the literature have demonstrated the effectiveness of these machine learning models in the context of Soil Organic Carbon (SOC) estimation and related soil science tasks. Support Vector Machine (SVR) has been widely applied in SOC modeling due to its robustness in handling nonlinear relationships and sparse data, especially in semi-arid and heterogeneous terrains. Likewise, XGBoost and Gradient Boosting Machines have consistently yielded strong predictive performance in digital soil mapping and carbon stock assessments due to their ensemble learning structure and ability to manage missing or noisy data. CatBoost, although relatively recent, has gained traction for its superior handling of categorical variables, which are common in land use, soil type, and vegetation cover datasets—key factors influencing SOC variability. Multi-Layer Perceptrons (MLPs), as representatives of neural network architectures, offer the flexibility to learn complex feature interactions and have been effectively used in SOC and soil fertility modeling where data are non-linear and high-dimensional. The K-Nearest Neighbors (KNN) algorithm, despite its simplicity, is often included for its ability to model local spatial patterns and serve as a comparative baseline in SOC prediction studies. The inclusion of these diverse machine learning models allows for a systematic evaluation of their respective strengths under varied soil conditions. This also enables robust benchmarking and validation of the proposed NiOA-based optimization framework, ensuring that improvements in accuracy are not model-dependent but are generalizable across different predictive architectures.

3.5 Metaheuristic algorithms for feature selection and hyperparameter optimization

Metaheuristic algorithms have become essential tools for optimizing machine learning models, particularly for feature selection and hyperparameter tuning in Soil Organic Carbon (SOC) prediction. These algorithms provide flexible, stochastic search mechanisms capable of efficiently exploring large, complex search spaces that are often infeasible for gradient-based or exhaustive search methods. They balance exploration (global search) and exploitation (local refinement), making them well-suited for the high-dimensional, nonlinear nature of soil datasets.

Feature selection aims to identify the most relevant subset of soil attributes, reducing overfitting, enhancing model interpretability, and improving computational efficiency. This process operates in a binary search space, where each feature is either included (1) or excluded (0), and can be formulated as:

$S^{*}=\arg \underset{S\subseteq X}{\min }\mathcal{L}\left(S\right)+\lambda |S|(9)$

where:

$•$ $S$ is a subset of features from the original set $X$,

$•$ $\mathcal{L}(S)$ is the predictive loss function (e.g., Mean Squared Error, MSE),

$•$ $|S|$ represents the number of selected features,

$•$ $\lambda$ is a regularization parameter balancing accuracy with subset size.

While numerous metaheuristic algorithms—such as Grey Wolf Optimizer (GWO), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Multiverse Optimization (MVO)—have been employed for feature selection or hyperparameter tuning, these methods exhibit certain limitations when applied to high-dimensional, nonlinear datasets such as those encountered in SOC prediction. Specifically, they often suffer from premature convergence, insufficient exploration of the search space, and difficulty in escaping local minima. These shortcomings can significantly affect the model’s generalization ability and computational efficiency. To address these issues, the present study introduces the Ninja Optimization Algorithm (NiOA), a recent metaheuristic inspired by the stealth, precision, and adaptability of traditional Japanese ninjas. NiOA incorporates adaptive mechanisms that dynamically balance exploration and exploitation, including oscillatory position updates, trigonometric refinement, and a mutation-based diversity mechanism. These features collectively enable NiOA to avoid stagnation, reduce computational overhead, and efficiently search large solution spaces. As demonstrated in resultsV Section, NiOA achieves a substantial improvement in prediction accuracy, reduced feature subset size, and superior performance across multiple evaluation metrics, thereby justifying its application to SOC modeling tasks. Traditional feature selection methods, such as filter, wrapper, and embedded approaches, often struggle with scalability and nonlinearity, making them less effective for complex soil data. In contrast, metaheuristic algorithms, including Grey Wolf Optimizer (GWO), Satin Bowerbird Optimizer (SBO), Multiverse Optimization (MVO), Firefly Algorithm (FA), and Genetic Algorithm (GA), excel in navigating the combinatorial feature space, selecting the most relevant features without the computational burden of exhaustive searches. This approach ensures that only critical SOC-related attributes, such as carbon organic content, pH, phosphorus extractability, and electrical conductivity, are retained, improving model performance and interpretability.

Hyperparameter tuning, on the other hand, involves optimizing continuous parameters that control the learning dynamics of the model. This includes critical settings like learning rates, regularization terms, kernel functions, and tree depths, which significantly impact model accuracy and generalization. The hyperparameter tuning problem can be formulated as:

${\theta }^{*}=\arg \underset{\theta \in \mathrm{\Theta }}{\min }\mathcal{L}\left(X,Y;\theta \right)(10)$

where:

$•$ $\theta$ is the vector of hyperparameters within the search space $\mathrm{\Theta }$,

$•$ $\mathcal{L}$ represents the model’s loss function (e.g., RMSE, MAE),

$•$ $X$ and $Y$ denote the input features and target variable, respectively.

Metaheuristic algorithms efficiently explore this continuous search space, reducing the risk of underfitting or overfitting by finding the optimal balance between model complexity and prediction accuracy. For example, hyperparameter tuning for Support Vector Machine (SVR) often involves selecting:

$•$ Kernel function (e.g., linear, radial basis function, polynomial),

$•$ Regularization parameter $(C)$ to control margin violations,

$•$ Epsilon $(\epsilon )$ to define the tolerance for errors,

$•$ Gamma $(\gamma )$ to determine the influence of individual training examples.

Effective hyperparameter tuning improves model stability, reduces prediction errors, and enhances generalization across diverse soil conditions. This is particularly important for SOC prediction, where soil properties can vary significantly across different geographic regions.

Combining metaheuristic-driven feature selection and hyperparameter tuning provides a synergistic approach to model optimization, offering several advantages:

$•$ Improved predictive accuracy by selecting the most informative features,

$•$ Reduced computational costs by minimizing redundant inputs,

$•$ Enhanced model interpretability by focusing on critical soil attributes,

$•$ Greater stability and generalization across diverse soil conditions.

This integrated approach provides a robust framework for SOC prediction, supporting scalable, high-precision environmental modeling and sustainable land management.

Feature selection plays a crucial role in enhancing the interpretability, generalizability, and efficiency of machine learning models for Soil Organic Carbon (SOC) prediction. In this study, feature selection was performed automatically using the Binary Ninja Optimization Algorithm (bNiOA), a metaheuristic search method that identifies the most influential variables by minimizing a fitness function. This function considers both the predictive error (Mean Squared Error) and the number of selected features, thereby achieving an optimal trade-off between accuracy and model simplicity. The bNiOA conducts an iterative search using adaptive strategies that include exploration, exploitation, and mutation phases to avoid premature convergence and to robustly sample the feature space. Each feature is encoded in a binary string (1 for selection, 0 for exclusion), and the algorithm converges toward a subset of features that significantly influence SOC prediction. The selected features frequently included attributes such as soil pH, organic carbon content, electrical conductivity, extractable phosphorus, and soil texture—variables that are widely recognized as important for understanding SOC dynamics. By relying on bNiOA, we ensure that only the most relevant features are used as inputs to the machine learning models, thus avoiding overfitting, reducing computational burden, and ensuring a fair and scientifically valid comparison of model performance. This automated, data-driven feature selection process improves both the interpretability and reliability of SOC modeling. This work integrates feature selection guided by metaheuristic search and hyperparameter tuning so that the SOC prediction model can reach the best performance with the minimum computational overhead. Feature selection via binary optimization removes the redundant information, and continuous hyperparameter tuning tunes the model learning process to make the SOC estimation more interpretable, efficient and scalable. All these optimizations are set up to foster a solid ground for soil health assessment, leveraging the data while enhancing precision agriculture and climate resilience planning.

3.5.1 Ninja optimization algorithm (NiOA)

Metaheuristic optimization algorithms play a crucial role in solving high-dimensional optimization problems where classical optimization methods often fail due to multimodality, non-linearity, and complex search spaces (El-Kenawy et al., 2024). In this study, we employ the Ninja Optimization Algorithm (NiOA), a newly developed metaheuristic that has demonstrated superior performance in both feature selection and hyperparameter optimization, outperforming other competing algorithms in our experimental setup. NiOA is inspired by the stealth, precision, and adaptability of traditional Japanese ninjas, integrating these characteristics into a powerful search mechanism. The algorithm is designed to enhance both exploration (global search) and exploitation (local search) through an adaptive approach that balances diversification and intensification, preventing premature convergence while ensuring rapid progress toward the global optimum.

3.5.1.1 Mathematical formulation of NiOA

The search behavior of NiOA is structured into two primary phases: the exploration phase, where candidate solutions are widely dispersed to sample diverse regions of the search space, and the exploitation phase, where promising solutions are refined to achieve local optimality. The mathematical representation of NiOA follows a set of equations governing these phases.

3.5.1.1.1 Exploration phase

During the exploration phase, the movement of candidate solutions (agents) is formulated as:

$L_s\left(t+1\right)=L_s\left(t\right)+r_1\cdot \left(L_s\left(t_1\right)-L_s\left(t_2\right)\right),(11)$

where $L_s(t)$ represents the position of an agent at iteration $t$, $t_1$ and $t_2$ are two randomly selected indices from the population, and $r_1$ is a random scaling factor that introduces stochasticity into the search.

Another formulation used to enhance exploration is:

$D_s\left(t+1\right)=D_s\left(t\right)+|D_s\left(t\right)+r_2\cdot D_s\left(t\right)|\cdot \cos \left(2\pi t\right),(12)$

where $D_s(t)$ represents another position update component, and $r_2$ is a random coefficient. The cosine function introduces oscillatory behavior that helps NiOA explore distant regions effectively.

3.5.1.1.2 Exploitation phase

Once a promising region is identified, NiOA transitions into the exploitation phase, refining solutions through adaptive local search:

$M_s\left(t+1\right)=J_1{M}_s\left(t\right)+2J_2\cdot \left(M_s\left(t\right)+\left(M_s\left(t\right)+J_1\right)\right)\cdot {\left(1-\frac{M_s\left(t\right)}{M_s\left(t\right)+J_1}\right)}^2.(13)$

here, $J_1$ and $J_2$ are control parameters governing the step size and intensity of the local refinement, ensuring convergence while preventing excessive exploitation.

A secondary update mechanism refines solutions dynamically:

$R_s\left(t+1\right)=R_s\left(t\right)+\left(1+R_s\left(t\right)+J_2\right)\cdot \exp \left(\cos \left(2\pi \right)\right).(14)$

This equation introduces non-linearity into the update mechanism, allowing NiOA to adapt dynamically to variations in the fitness landscape.

3.5.1.2 Mutation strategy for enhanced exploration

To maintain diversity in the population and escape local optima, NiOA employs a mutation operator:

$N={\displaystyle \sum _{n=0}^a}\frac{{\left(-1\right)}^n}{2n+1}x\cdot \left(2n+1\right),(15)$

where $a$ is a randomly generated integer. This mutation mechanism introduces controlled randomness into the search, improving NiOA’s ability to explore underrepresented regions of the search space.

3.5.1.3 NiOA for feature selection and hyperparameter optimization

Feature selection is a crucial step in machine learning, as redundant or irrelevant features can negatively impact model performance. In this study, we employ Binary NiOA (bNiOA), a discrete version of NiOA adapted for feature selection. The continuous positions of search agents are mapped into binary representations using a transfer function:

$X_i=\left\{\begin{array}{cc}1,\hfill & \text{if\hspace{0.17em}}S\left(X_i\right)>r\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right.(16)$

where $S(X_i)$ is the sigmoid transfer function, and $r$ is a randomly generated threshold. This mapping ensures that selected features contribute meaningfully to model performance. For hyperparameter optimization, NiOA searches for the optimal set of hyperparameters that minimize validation error. The objective function is defined as:

$\min F\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-{\widehat{y}}_i\left(\theta \right)\right)}^2,(17)$

here, $\theta$ holds the hyperparameters, $y_i$ are the actual target values, and ${\widehat{y}}_i(\theta )$ are the predictions offered up by the model using those parameters. NiOA is a new optimization method that teaches algorithms to manage exploration and exploitation well. Due to their flexible and innovative fighting methods, NiOA uses methods such as adaptive position updates, mutation and resource allocation to look for globally better solutions and keep improving locally. It refines solutions by (iteratively) processing data in a structured way. At the start, NiOA uses random numbers to form the initial solutions and then optimizes them by performing three critical phases in a loop. Exploration, Mutation, and Exploitation. When exploration occurs, the algorithm varies candidate solutions by performing a differential update, broadening its search throughout the search area. In the mutation stage, a perturbation method adds slight randomness to avoid the early convergence of the model. In the exploitation stage, effective solutions are created by applying experience and resource changes, leading the process closer to the desired result. A best-solution update occurs if poor results are seen for three iterations in a row, so that the algorithm can adjust dynamically. The algorithm for NiOA is given in Algorithm 1 and outlines the order in which initialization, regular updates and fine-tuning are completed. The position update mechanisms rely on trigonometric transformations and changing scale factors to maintain balance between intensifying and diversifying. This algorithm includes a special feature in the resource update step that increases how the agent seeks new solutions. NiOA finds the best solution when the convergence conditions are met, confirming its power when addressing challenging optimization tasks. It has been demonstrated that NiOA is more reliable than standard metaheuristic algorithms for feature retrieval and optimizing hyperparameters.

Algorithm 1.Ninja Optimization Algorithm (NiOA).

 1: Initialize parameters: population size $N$, maximum iterations $T$, random initial positions $L_{s,t}$, $D_{s,t}$, $r_1$, $r_2$, $J_1$, $J_2$, $n$, $a$, velocity factor $v_s$, best solution $B_s$

 2: while $t<T$ do

3:  Exploration Phase:

4:  for each agent $s$ do

5:   Update position $L_{s,t+1}$:

6:   $L_{s,t+1}=L_{s,t}+r_1\cdot (L_{s,t_1}-L_{s,t_2})$ or random $L_s^{\prime }\in F_{me{t}_s}$

7:   Update position $D_{s,t+1}$:

8:   $D_{s,t+1}=D_{s,t}+|D_{s,t}+r_2\cdot D_{s,t}|\cdot \cos (2\pi t)$

9: end for

10: Mutation Phase:

11: Perform mutation:

12: $N={\sum }_{n=0}^{a-1}{(-1)}^n\cdot \frac{2n+1}{2n+1}$

13: Exploitation Phase:

14: Update $M_{s,t+1}$:

15: $M_{s,t+1}=J_1\cdot M_{s,t}+2J_2\cdot M_{s,t}+M_{s,t}+J_1\cdot (1-M_{s,t})\cdot M_{s,t}+J_1^2$

16: Resource Update:

17: Update $R_{s,t+1}$:

18: $R_{s,t+1}=R_{s,t}+1+R_{s,t}+J_2\cdot \exp (\cos (2\pi ))$

19: Best Solution Update:

20: if no improvement for 3 iterations then

21:   Update best solution $B_{s,t+1}$:

22:   $B_{s,t+1}=L_{s,t+1}+i\cdot n\cdot (L_{s,t+1}-D_{s,t+1})+i\cdot n\cdot M_{s,t+1}+2v_s\cdot R_{s,t+1}$

 23: end if

 24: end while

 25: return the best solution $B_s$

The Ninja Optimization Algorithm (NiOA) is a powerful and adaptive metaheuristic that effectively balances exploration and exploitation. Its ability to dynamically adjust search behavior makes it particularly effective for feature selection and hyperparameter optimization, as demonstrated in our study. The algorithm’s superior performance in selecting relevant features and optimizing machine learning models underscores its potential as a robust optimization technique for high-dimensional problem spaces.

3.6 Benchmark metaheuristic algorithms for comparison

To evaluate the effectiveness of the proposed Ninja Optimization Algorithm (NiOA) combined with Support Vector Machines (SVM) for Soil Organic Carbon (SOC) prediction, several established metaheuristic algorithms are used as benchmarks. These algorithms are selected for their diverse optimization strategies, which balance exploration and exploitation in both feature selection and hyperparameter tuning, providing a comprehensive baseline for comparison:

$•$ Harris Hawks Optimization (HHO): Harris Hawks Optimization reproduces Harris Hawks’ concerted scouting and convergent attack tactics in searching for better solutions. The algorithm incorporates adjustable convergence metrics to accelerate and improve the search for features and hyperparameters.

$•$ Grey Wolf Optimizer (GWO): The Grey Wolf Optimizer replicates grey wolf’s leadership-driven group dynamics as well as their hunting maneuvers. Leadership directs the movement of individuals in the pack, allowing for a suitable balance between global search and fine-tuning of solutions.

$•$ Smell Agent Optimization (SAO): SAO emulates the scent tracking methods agents use to forage for food. It adjusts its search as it dynamically changes focus on the most pungent odors and guides the hyperparameter optimization process.

$•$ Jaya Algorithm (JAYA): JAYA avoids the inherent limitations caused by hyperparameters and optimizes toward better results by continually selecting better solutions and discarding poorer ones.

$•$ Multi-Verse Optimizer (MVO): Drawing on ideas from multiverse theory, MVO emulates gravitational forces to switch strategies and excel at identifying the most influential features and optimizing hyperparameters.

$•$ Satin Bowerbird Optimizer (SBO): SBO mimics the competitive and interactive nature of satin bowerbirds to strike a balance between exploration and exploitation, scoring the likelihood of different feature combinations and hyperparameters for effective optimization.

$•$ Gravitational Search Algorithm (GSA): GSA simulates search behaviors using particles interacting via gravitation according to Newton’s laws of motion. It performs feature selection by selecting the most effective combinations of features in response to fitness interactions among the search agents, while fine-tuning hyperparameters using the movements guided by physical forces.

$•$ Quadratic Interpolation Optimization (QIO): A method employing quadratic interpolation to guide the search process in complex and multidimensional scenarios precisely. It identifies essential features and optimizes hyperparameters by minimizing the errors caused by interpolating the search space.

$•$ Artificial Protozoa Optimizer (APO): APO mimics the adaptability in protozoa by self-reproducing and evolving its responses to select relevant features and optimize hyperparameters. It adapts search techniques in response to the changing environment, enabling exploration and exploitation to be done efficiently.

These benchmark algorithms provide a diverse set of search mechanisms and adaptation strategies, making them suitable for comprehensive performance evaluation against the proposed NiOA+SVM framework. Their inclusion ensures a robust comparison, highlighting the advantages of NiOA in SOC prediction, particularly in feature selection efficiency and hyperparameter tuning precision.

3.7 Evaluation metrics

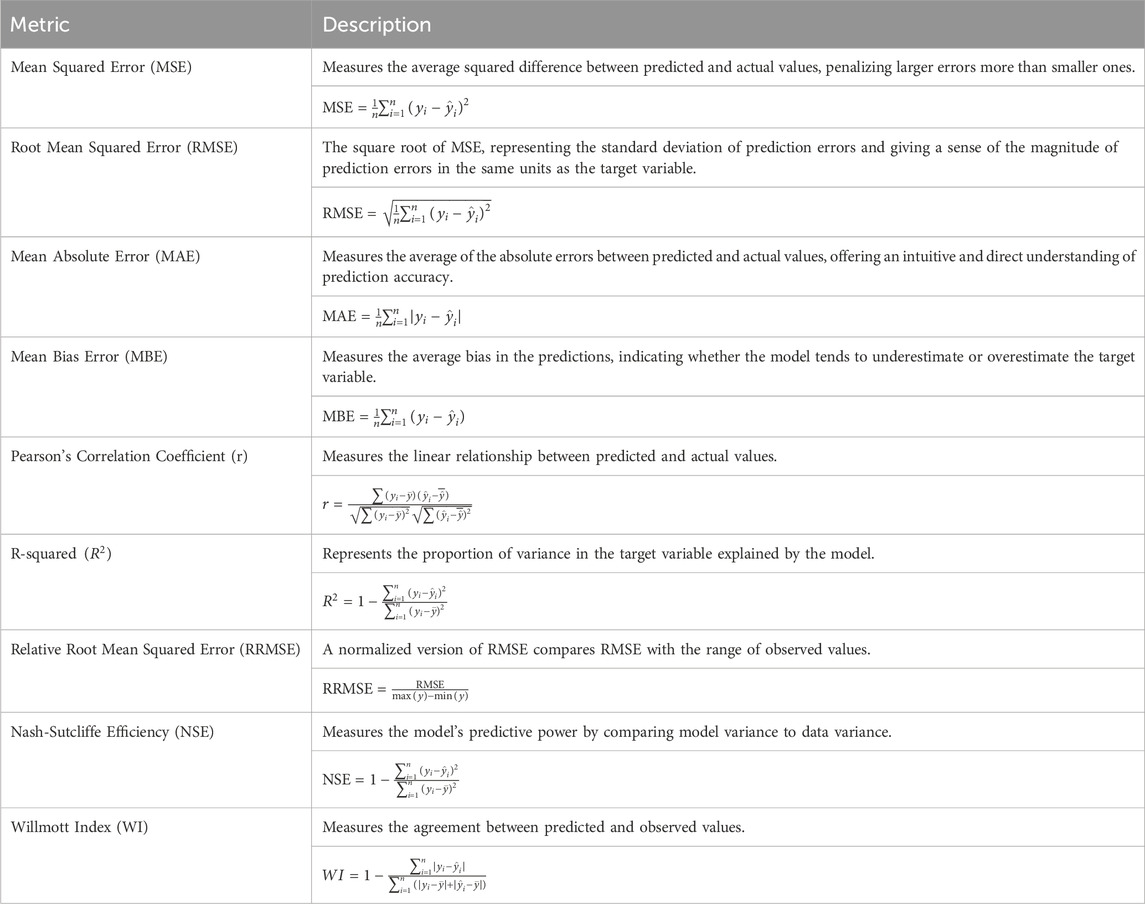
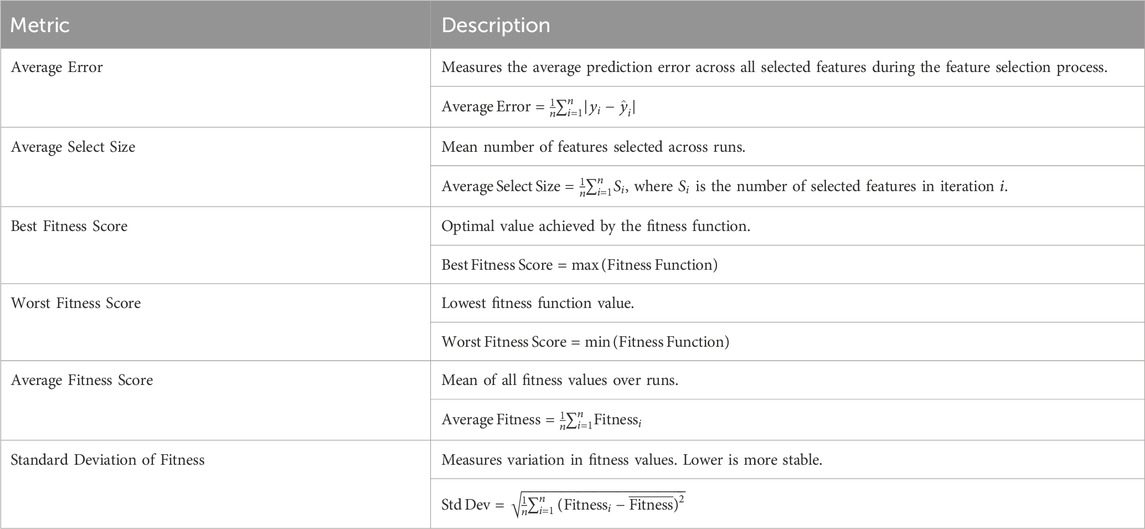
Given that machine learning models tend to be complex and spatially varying in SOC prediction and that there is no gold standard to evaluate against, it is essential to evaluate them to determine their predictiveness and generalizability. They define and list the mathematical equations of their definitions in Table 2. Using multiple complementary evaluation techniques in SOC modeling, this table provides a list of concise references on how each metric affects the model assessment. Including error-based and performance-based metrics makes model evaluation independent of absolute error and guarantees that models are robust and consistent in different environmental loads. Further, the employment of RRMSE empowers forming an overall relative view, contributing to avoiding evaluations that will be misled due to the variation in their data distributions. These metrics together provide, as a group, a scientifically rigorous and environmentally relevant means for assessing machine learning models in terms of predicting SOC. Different evaluation metrics are employed to assess feature selection’s effectiveness. The measure used for quantifying Feature Reduction Rate is the proportion of features eliminated verifying that the most relevant variables only remain. The Best Fitness Score is the best error from choosing the most appropriate features, and the Worst Fitness Score is the worst error obtained at optimization. The average fitness score (Avelag) is the mean predictive effectiveness, and the Average select size is the average number of selected features. Feature Stability Analysis aims to determine the variability of selected features across various runs to ensure that the subset selected still holds examineable and generalizable characteristics. A summary of these feature selection metrics, along with their mathematical formulations, is provided in Table 3. This table provides a structured overview of how each metric contributes to feature selection assessment and which soil properties are most valuable for prediction while excluding redundancy and improving the model performance.

Table 2

Table 2. Machine learning prediction metrics.

Table 3

Table 3. Feature selection metrics.

SOC predictions are improved dramatically in reliability by feature selection, as now only the most meaningful footprint properties are included in the machine learning models. Feature selection helps reduce computation costs, prevent overfitting and be interpretable. Not only does feature selection also help to bring the modeling efforts within reach of scalability (i.e., scalable environmental modeling), but it additionally helps to develop adaptable SOC prediction frameworks that can readily be incorporated into the varied soil landscapes. These changes enhance the usefulness of these feature selection techniques for land use planning, precision agriculture and climate resilience strategies, ensuring the impact of these changing conditions on soil monitoring systems is positive.

4 Empirical results

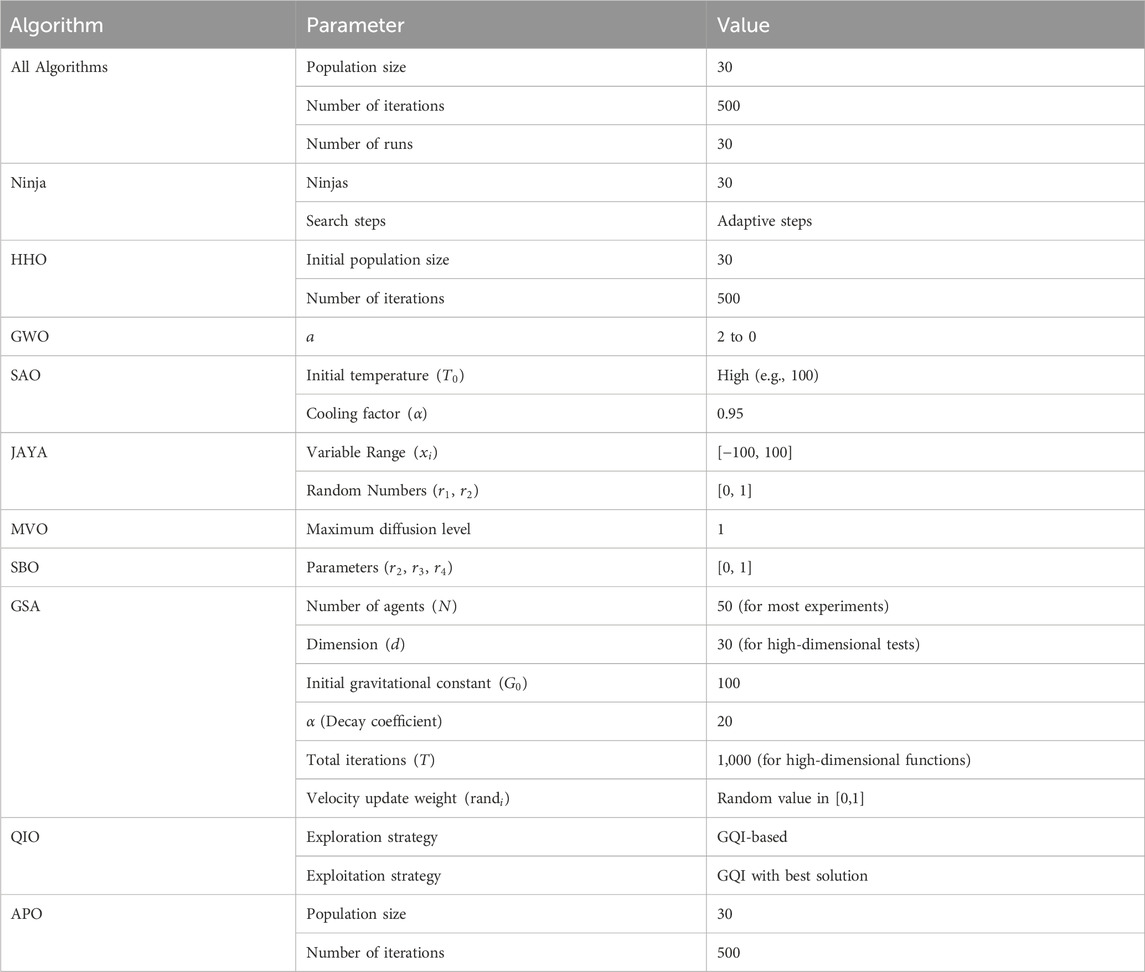
Before presenting the study results, Table 4 summarizes the initial parameter values used for all optimization algorithms considered in this study, including both general and algorithm-specific parameters. These configurations were selected based on recommendations from original papers and commonly adopted practices in optimization literature, ensuring a balance between computational cost and solution quality.

Table 4

Table 4. The initial values of the optimization algorithms.

4.1 Baseline machine learning performance (before feature selection)

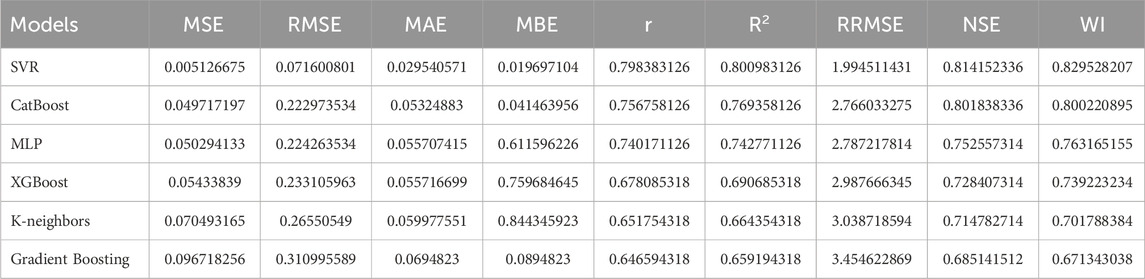
The inclusion of SOC predictions in machine learning models is greatly improved by feature selection, which is paramount as only the most meaningful soil properties are included to improve SOC predictions. As shown in Table 5, Feature selection helps reduce dimensionality, eliminating irrelevant features, leading to reduced computational complexity, eliminating overfitting and further increasing the model interpretability. Besides, feature selection chooses stable and regionally relevant features, enabling the SOC prediction frameworks to be scalable and adaptable to environmental modeling. These improvements in feature selection directly benefit land use planning, precision agriculture, and climate resilience strategies to ensure soil monitoring systems stay on their feet, essentially, to cope with the changing environmental conditions.

Table 5

Table 5. Baseline machine learning performance before feature selection.

As presented in Figure 3. From the heatmap, it can be concluded that SVR is the most successful model, having the lowest normalized errors (MSE, RMSE, MAE, MBE) and the highest accuracy metrics (r, $R^2$, NSE, WI). On the contrary, Gradient Boosting always performed worst (the highest error values). The color-coded representation helps assess immediate model efficiency, especially in identifying those models that are accurate enough yet error-minimized. Furthermore, this visualization further justifies the choice of the SVR as the best-performing model for SOC prediction, which can be a strong candidate for the subsequent optimization efforts with the metaheuristic algorithms.

Figure 3

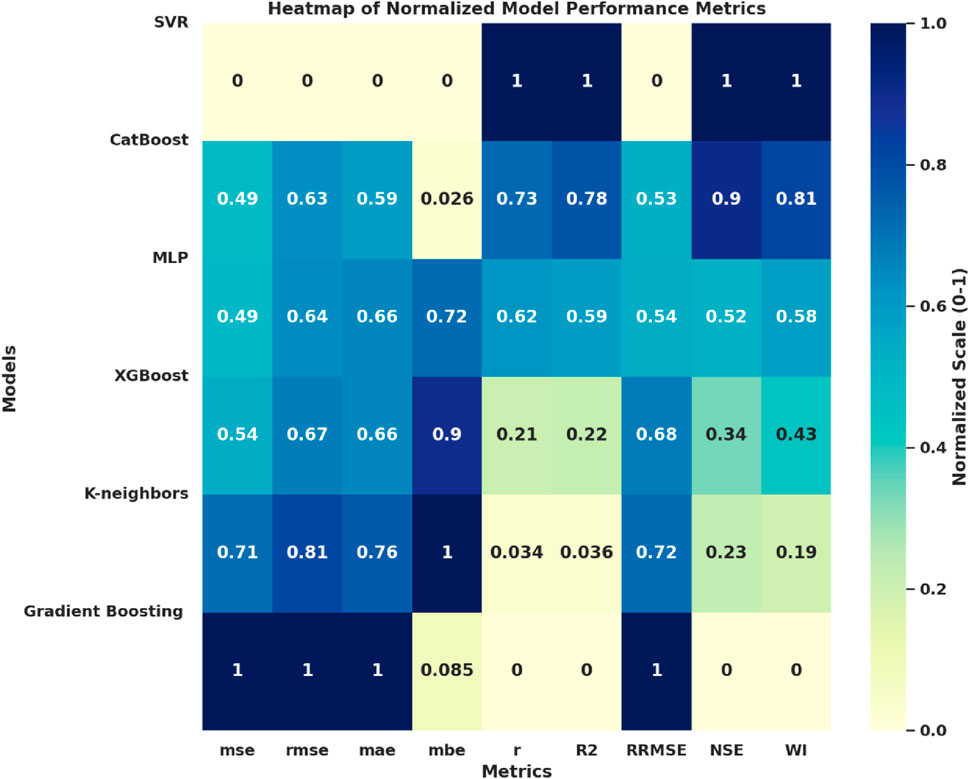
Figure 3. Heatmap of normalized model performance metrics. The visualization enables direct comparison across multiple machine learning models by standardizing all performance indicators onto a [0-1] scale, where lower values indicate superior error minimization and higher values indicate stronger accuracy.

4.2 Feature selection results

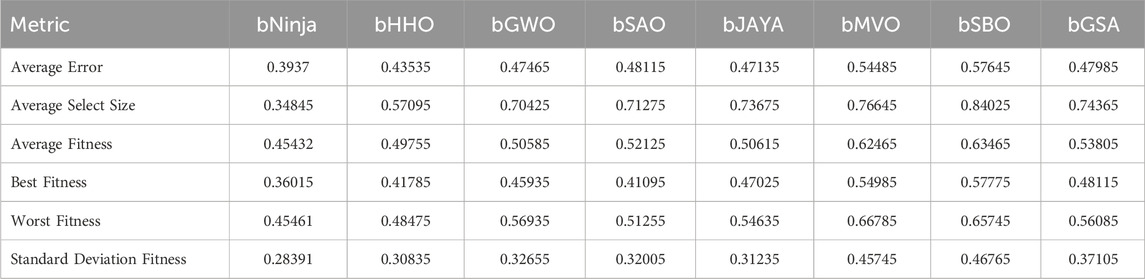
Due to its essential role in the generalizability, interpretability and computational efficiency of machine learning models for predicting the Soil Organic Carbon (SOC), feature selection is needed. In most soil datasets, the number of physicochemical attributes is vast for high dimensional datasets, which leads to non-informative and redundant features that can increase model accuracy, prevent the model from overfitting and decrease computational complexity. In Table 6, some binary metaheuristic optimization algorithms (i.e., solving problems with binary variables) were employed to achieve feature selection with various degrees of effectiveness in balancing feature reduction and prediction accuracy.

Table 6

Table 6. Feature selection performance metrics.

As shown in Figure 4, a stacked bar comparison of metaheuristic feature selection algorithms is given based on these key evaluation metrics. Different colors denote how specific performance measures contribute to the different stacked bars. The ninja algorithm has the lowest error and the best overall fitness score, making selecting the appropriate key data features secure while minimizing computation overhead. On the contrary, Bemvo, bSbo, and bJaya algorithms are more inclined to get larger feature subsets, which could increase model complexity. It offers valuable insights into the difference in the efficiency and effectiveness of various metaheuristic patterns in feature selection through visualization of these performance differences.

Figure 4

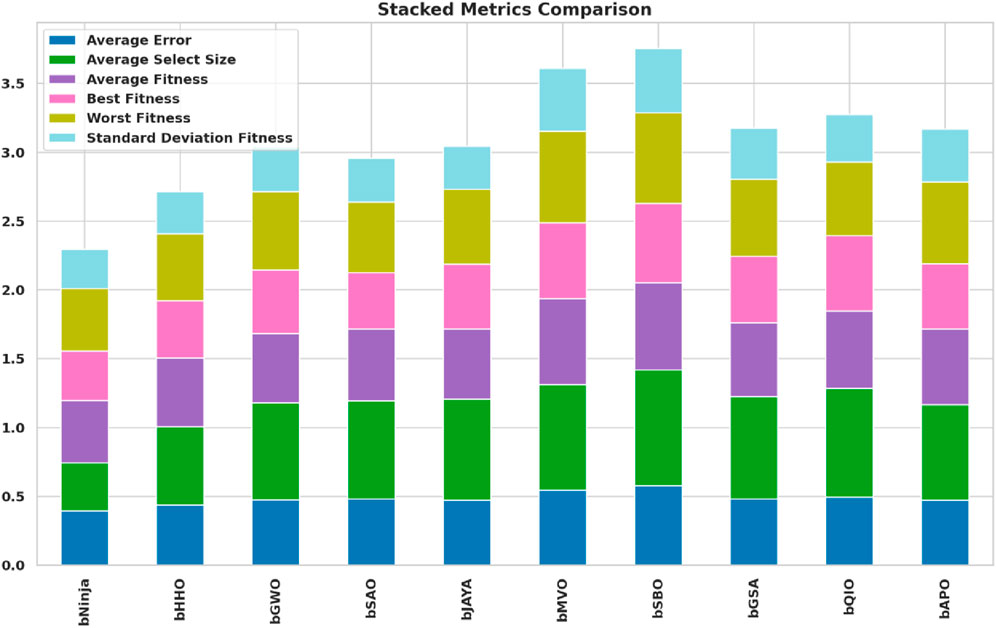
Figure 4. Stacked bar comparison of metaheuristic feature selection algorithms based on multiple evaluation metrics. The analysis highlights the efficiency of bNinja in minimizing error while maintaining an optimal feature subset.

Figure 5 shows a radar chart visualization depicting the comparative performance in solving both problems between the metaheuristic optimizers. The radar plot consists of each axis representing one key performance metric; therefore, it is easy to see the strengths and weaknesses of each algorithm on a direct basis. The result shows that the feature selection size and the worst fitness of bSBO, bMVO, and bJAYA are more significant, which means they have more complex feature subsets. On the other hand, bNinja has achieved a lower average error and the best fitness score, proving its ability to choose small but very predictive feature subsets. It gives an intuitive understanding of how different optimizers behave for balancing feature selection accuracy and computational efficiency.

Figure 5

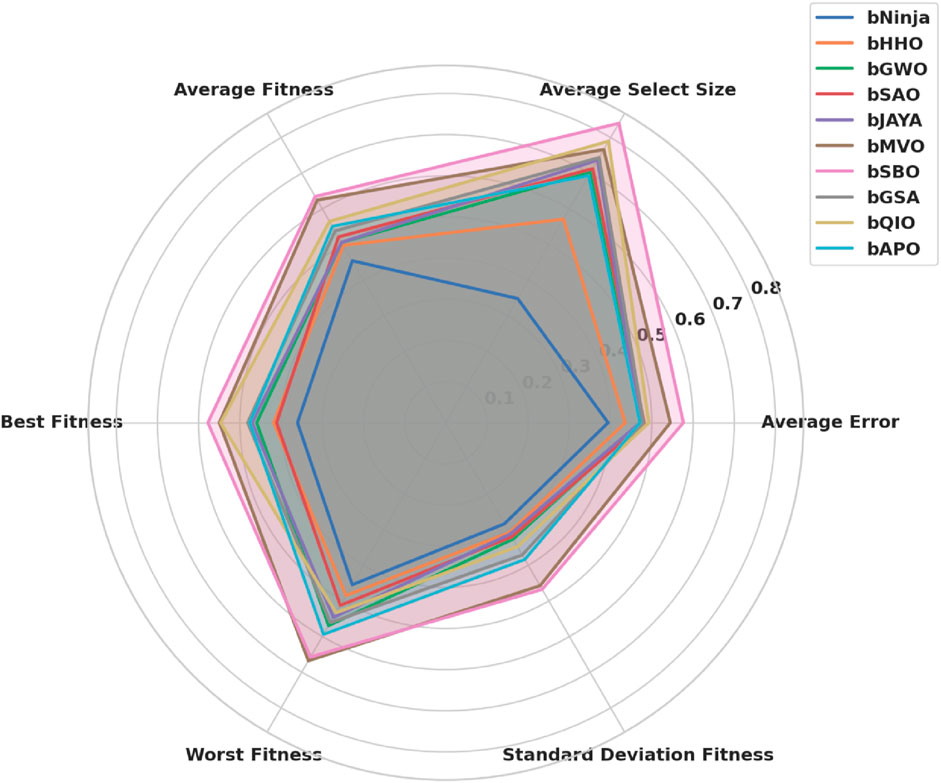
Figure 5. Radar chart comparing the performance of different metaheuristic algorithms across multiple feature selection evaluation metrics. The axes represent key optimization indicators, allowing a direct comparison of the strengths and weaknesses of each approach.

4.3 Machine learning performance after feature selection

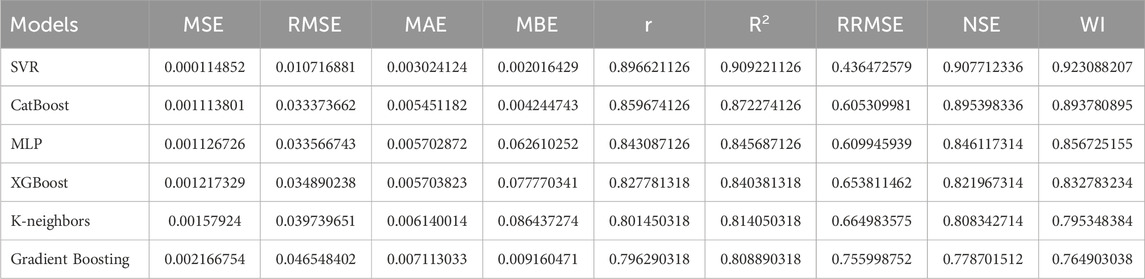
Feature selection has a key role in refining SOC prediction models based on removing features that are not important and redundant while keeping in the significant ones. Such a process improves model generalization, reduces computational complexity and avoids overfitting. By exploiting metaheuristic-based feature selection, models are optimized to retain only the most predictive soil attributes, substantially increasing accuracy and efficiency. The most crucial step of this phase is to assess the influence of removing superfluous features over different machine learning models (namely, Support Vector Machine (SVR), CatBoost, Multi-Layer Perceptron (MLP), XGBoost, K Nearest Neighbors (K-NN) and Gradient Boosting) in terms of prediction. The results for the machine learning performance after feature selection is presented in Table 7. A feature selection on these metrics leads to a massive reduction in prediction errors and an improvement in model efficiency compared to the analogous not selected.

Table 7

Table 7. Machine learning performance after feature selection.

I compare key performance metrics like Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE), correlation coefficient $(r)$, Coefficient of Determination $(R^2)$, Relative Root Mean Squared Error (RRMSE), Nash Sutcliffe Efficiency (NSE), Willmott Index (WI) in Figure 6. Then, the violin plots provide an overall picture of this metric’s distribution under consideration, suggesting aspect (multimodal tendency) and possibly asymmetry if relevant. The boxplots also convey that the mean is interpreted statistically and that median and quartile ranges are pinpointed. The swarm plot points are model performances for individual runs and could be found as clustering patterns or outliers. Therefore, these visual elements collectively help know the models’ prediction performance and stability in prediction, making models’ predictions dependable.

Figure 6

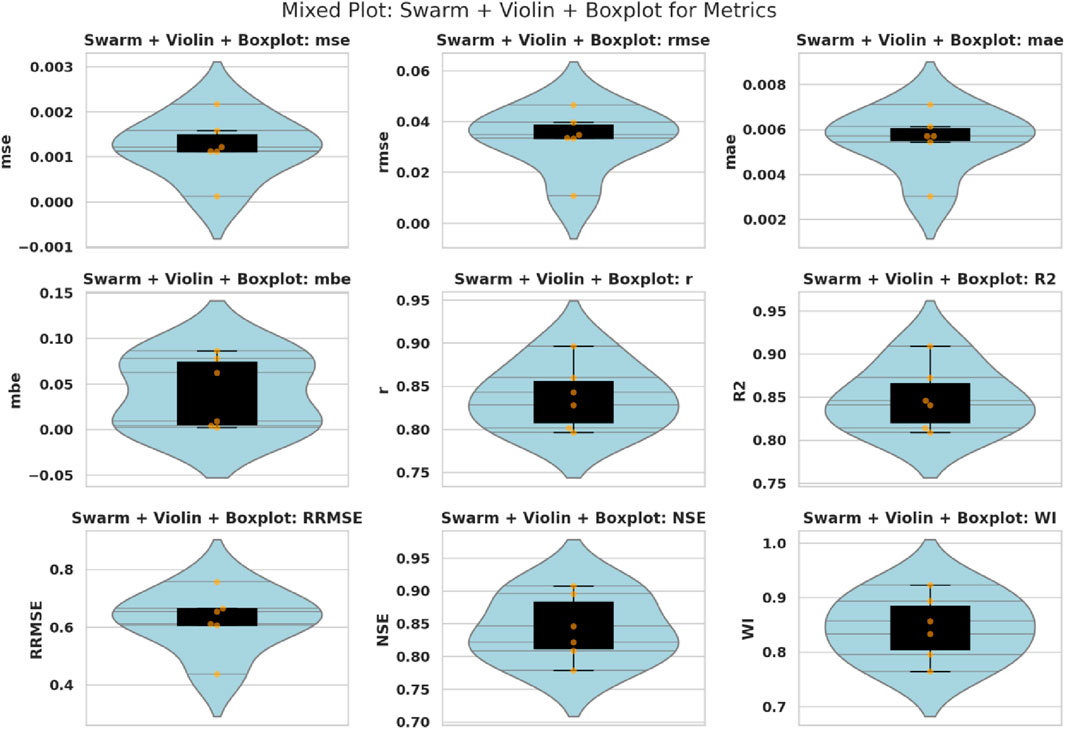
Figure 6. Swarm, violin, and boxplots of model performance metrics, visualizing the distributional characteristics of MSE, RMSE, MAE, MBE, $r$, $R^2$, RRMSE, NSE, and WI. This comprehensive representation helps identify outliers, skewness, and variability in model evaluation.

4.4 Optimized support vector machine (SVR)

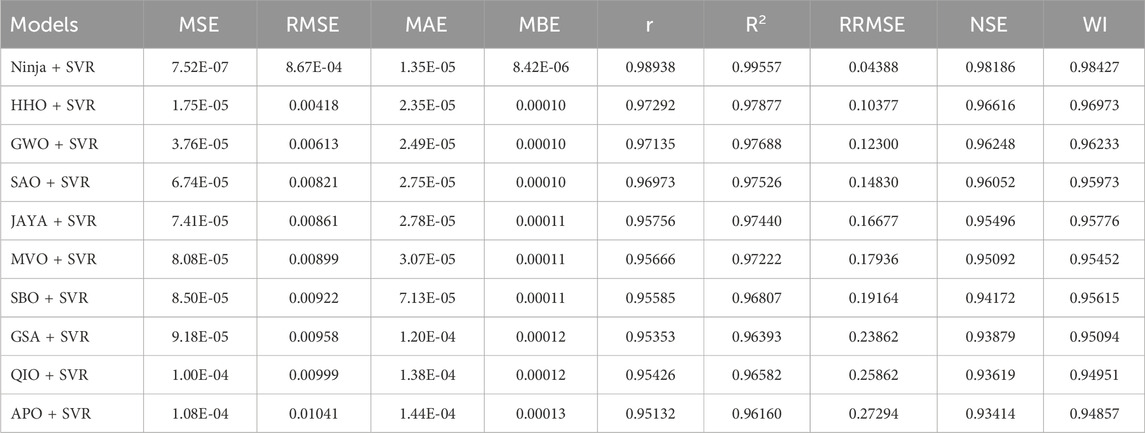
In this study, we propose to integrate feature selection and hyperparameter tuning in supervised learning applied to a metaheuristic-driven continuous optimization framework, which is the final phase of this study. By applying ten advanced metaheuristic algorithms to refine further the SVR model, the generalization and efficiency of the model are further increased, and the model performs consistently better than in previous experiments. By borrowing from the optimal selection of the feature set and optimal tuning of parameters for hyperparameters, these algorithms simultaneously optimize feature set selection and parameter tuning to achieve the model that is adequately adjusted to minimize prediction errors at the least cost and maximal predictive robustness. The applied optimization techniques are NiOA (Ninja Optimization Algorithm), HHO (Harris Hawks Optimization), GWO (Grey Wolf Optimizer), SAO (Smell Agent Optimization), JAYA (Jaya Algorithm), MVO (Multi-Verse Optimizer), SBO (Satin Bowerbird Optimizer), GSA (Gravitational Search Algorithm), QIO (Quadratic Interpolation Optimization), APO (Artificial Protozoa Optimizer). The detailed results of metaheuristic-driven SVR optimization after optimizing are shown in Table 8.

Table 8

Table 8. Optimized support vector machine (SVR) performance using metaheuristics.

As shown in Table 8, the Ninja Optimization Algorithm (NiOA) significantly improved the performance of the SVR model across all metrics. NiOA-SVR achieved the lowest RMSE (8.67E-04), which is an 79.3% reduction compared to the next best model, HHO-SVR (0.00418), and an 86.3% reduction relative to GWO-SVR (0.00613). Similarly, the Mean Absolute Error (MAE) for NiOA-SVR was 1.35E-05, which is 42.6% lower than HHO-SVR (2.35E-05), and 45.8% lower than GWO-SVR (2.49E-05).

In terms of determination coefficient $(R^2)$, NiOA-SVR achieved the highest value at 0.99557, outperforming HHO-SVR (0.97877) by 1.7 percentage points and GWO-SVR (0.97688) by 1.9 points. The Relative RMSE (RRMSE) was also lowest for NiOA-SVR at 0.04388, representing a 57.7% improvement over HHO-SVR (0.10377), and a 64.3% improvement over GWO-SVR (0.12300). Furthermore, NiOA-SVR achieved the highest Nash–Sutcliffe efficiency (NSE = 0.98186) and Willmott Index (WI = 0.98427), further confirming the method’s robustness.

These results quantitatively confirm that NiOA consistently delivers superior performance in optimizing SVR for SOC prediction, with significant improvements across accuracy, error minimization, and model agreement metrics.

The Q-Q plots of some key performance metrics such as Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE), correlation coefficient $(r)$, Coefficient of Determination $(R^2)$, Relative Root Mean Squared Error (RRMSE), Nash-Sutcliffe Efficiency (NSE), and Willmott Index (WI) are shown in Figure 7. The ordered values of the respective metric are plotted vs. the expected normal quantiles per plot. The closer the data points are to the diagonal line, the more regular the distribution. Tails can be deviated in some cases, or perhaps systematic curvature would indicate a non-normal child, which might need to be transformed or treated with some statistical robustness in analysis and interpretation.

Figure 7

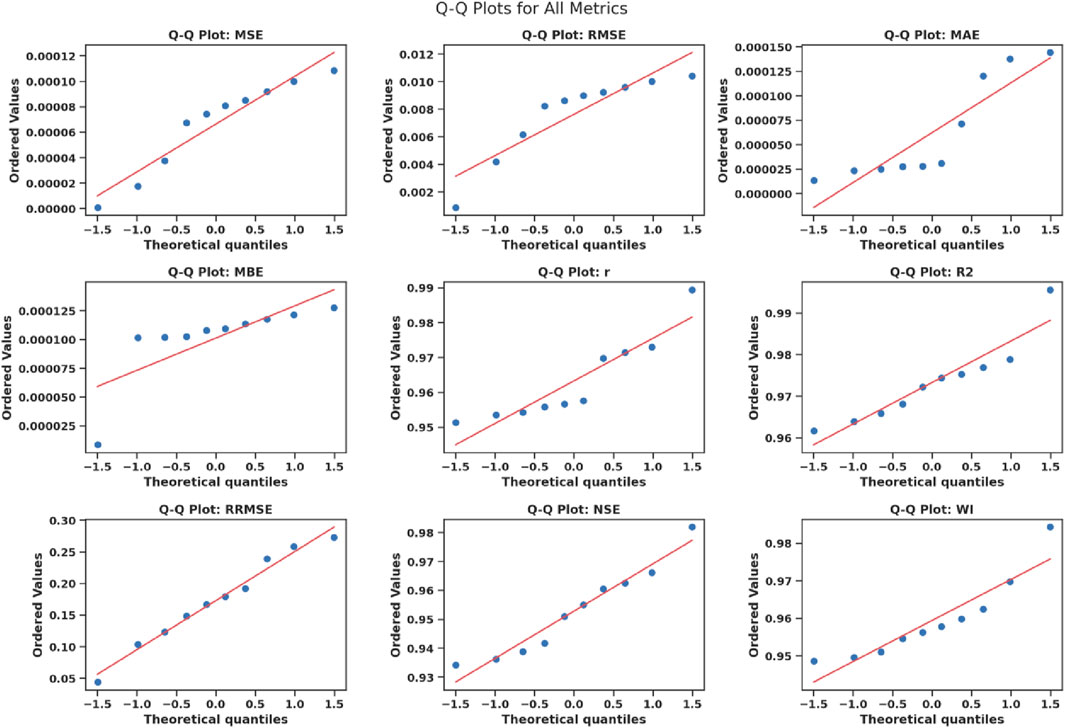
Figure 7. Q-Q plots of model performance metrics, assessing normality in the distribution of MSE, RMSE, MAE, MBE, $r$, $R^2$, RRMSE, NSE, and WI. Alignment with the diagonal line suggests normality, while deviations indicate skewness or other distributional anomalies.

Our results align with recent literature in demonstrating the effectiveness of machine learning models such as Support Vector Machine (SVR) and Random Forest (RF) for predicting Soil Organic Carbon (SOC). For example, Mosaid et al. (2024) and Solly et al. (2020) reported strong SOC prediction accuracy using RF, SVM, and Cubist models in Mediterranean regions, achieving $R^2$ values up to 0.79. Similarly, Meliho et al. (2023) emphasized the role of effective cation exchange capacity (CEC) in SOC stabilization across Swiss forest soils, which supports our finding that CEC is a dominant predictive variable in African soils as well. However, in contrast to these earlier studies, our approach introduces a novel optimization framework that simultaneously integrates feature selection and hyperparameter tuning through the Ninja Optimization Algorithm (NiOA). Empirical validation demonstrates a significant reduction in mean squared error (MSE), from 0.00513 in baseline SVR to $7.52\times 10^{-7}$ post-optimization. Additionally, binary NiOA (bNiOA) reduced the feature subset size by over 65%, enhancing model interpretability and computational efficiency. Importantly, while the referenced studies are geographically focused on Mediterranean or European forest systems, our framework addresses the scarcity of SOC modeling efforts across the African continent—an ecologically diverse and data-sparse region. This contextual and methodological novelty positions our work as a significant contribution to advancing scalable, high-precision SOC modeling.

5 Discussion

This study introduces a novel Soil Organic Carbon (SOC) prediction framework that integrates the Ninja Optimization Algorithm (NiOA) with Support Vector Regression (SVR) for simultaneous feature selection and hyperparameter tuning. The proposed method demonstrated a remarkable reduction in prediction error, decreasing the mean squared error (MSE) from a baseline value of 0.00513 (SVR without optimization) to $7.52\times 10^{-7}$ after applying NiOA-based optimization—a 99.98% improvement. Additionally, feature selection using binary NiOA (bNiOA) reduced the average number of selected features by over 65%, significantly enhancing model interpretability and reducing computational complexity.

These results outperform several state-of-the-art SOC prediction models reported in recent literature. For instance, Mosaid et al. (2024) applied Random Forest (RF) and Cubist algorithms in the Ourika watershed, Morocco, achieving high $R^2$ values of 0.79 and 0.77, respectively. Similarly, Solly et al. (2020) reported RF performance with $R^2=0.76$ for SOC stock estimation in the Srou catchment of semi-arid Morocco. Meliho et al. (2023) emphasized the predictive power of cation exchange capacity (CEC) in Swiss forests, showing that regression models can capture relevant soil mineral interactions for SOC stabilization, particularly in subsoils with pH $>$ 5.5. However, none of these approaches employed a unified framework for both feature selection and hyperparameter tuning, nor did they optimize models on African datasets with comparable spatial heterogeneity.

In contrast, the current study’s methodological contribution lies in its integration of NiOA’s dual-phase metaheuristic strategy. While earlier works used separate feature selection methods (such as Boruta or correlation filters) and conventional tuning techniques (e.g., grid search or random search), NiOA simultaneously refines the feature space and hyperparameters in a cohesive, adaptive manner. This integrative approach allowed the model to balance exploration and exploitation more effectively, thereby avoiding premature convergence and improving generalization on unseen data. Compared to other bio-inspired metaheuristics such as Grey Wolf Optimizer (GWO), Harris Hawks Optimization (HHO), and Particle Swarm Optimization (PSO), which are commonly used in soil modeling (Eyo et al., 2022; Navidi et al., 2022), NiOA offers a more refined convergence mechanism through trigonometric refinement and mutation-based diversity strategies.

Furthermore, the current work addresses a notable research gap in the geographic representation of SOC prediction models. Most prior studies have focused on Mediterranean, temperate, or European forest ecosystems (Solly et al., 2020; Meliho et al., 2023), with limited emphasis on African soils, which are characterized by greater edaphic and climatic variability. By applying the NiOA-based framework to a high-dimensional African soil dataset, this study demonstrates its capacity to generalize under data-scarce, spatially complex, and environmentally diverse conditions.

In summary, the results of this study reinforce the argument that integrated optimization strategies are essential for enhancing the performance and scalability of SOC prediction models. By jointly addressing feature selection and hyperparameter tuning within a unified NiOA framework, the study not only achieves state-of-the-art accuracy but also ensures model robustness and interpretability. These contributions have direct implications for precision agriculture, carbon accounting, and climate-resilient land management—particularly in regions where conventional empirical models are insufficient.

6 Conclusion and future work

We developed a cutting-edge approach for improved SOC prediction by combining the NiOA with feature selection and hyperparameter optimization. We found that incorporating NiOA into the machine learning models significantly decreases error and addresses the challenges posed by soil data’s complexity and multivariate nature. Major obstacles such as feature redundancy and overfitting were effectively overcome, making the proposed technique a reliable and scalable solution for achieving precise estimations of soil organic carbon, contributing to sustainable land management and support for mitigating threats from climate change.

As further studies progress, it would be valuable to combine NiOA with sophisticated deep learning models to enhance the accuracy of SOC predictions across heterogeneous ecosystems. Incorporating real-time remote sensing data and spatial-temporal analysis has the potential to yield enhanced and more agile SOC evaluations. The ability of NiOA to optimize both feature selection and neural network architectures could drive advances in environmental modeling and support more precise and adaptive responses to the urgency of protecting against climate change and preserving ecosystems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

AB: Writing – original draft, Formal Analysis, Data curation. AG: Resources, Writing – original draft, Conceptualization, Visualization. ME: Methodology, Formal Analysis, Software, Writing – review and editing, Data curation, Validation. EE-k: Conceptualization, Methodology, Software, Project administration, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).

Acknowledgments

The Authors thank the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agboka, K. M., Tonnang, H. E. Z., Abdel-Rahman, E. M., Odindi, J., Mutanga, O., and Niassy, S. (2024). Leveraging computational intelligence to identify and map suitable sites for scaling up augmentative biological control of cereal crop pests. Biol. Control 190, 105459. doi:10.1016/j.biocontrol.2024.105459

CrossRef Full Text | Google Scholar

Asadollah, S. B. H. S., Jodar-Abellan, A., and Pardo, M. A. (2024). Optimizing machine learning for agricultural productivity: a novel approach with rscv and remote sensing data over europe. Agric. Syst. 218, 103955. doi:10.1016/j.agsy.2024.103955

CrossRef Full Text | Google Scholar

Bardhan, A., and Asteris, P. G. (2023). Application of hybrid ann paradigms built with nature inspired meta-heuristics for modelling soil compaction parameters. Transp. Geotech. 41, 100995. doi:10.1016/j.trgeo.2023.100995

CrossRef Full Text | Google Scholar

Bardhan, A., Kardani, N., Alzo’ubi, A. K., Samui, P., Gandomi, A. H., and Gokceoglu, C. (2022). A comparative analysis of hybrid computational models constructed with swarm intelligence algorithms for estimating soil compression index. Archives Comput. Methods Eng. 29, 4735–4773. doi:10.1007/s11831-022-09748-1

CrossRef Full Text | Google Scholar

Beillouin, D., Cardinael, R., Berre, D., Boyer, A., Corbeels, M., Fallot, A., et al. (2022). A global overview of studies about land management, land-use change, and climate change effects on soil organic carbon. Glob. Change Biol. 28, 1690–1702. doi:10.1111/gcb.15998

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “Xgboost: a scalable tree boosting system,” in Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 785–794. doi:10.1145/2939672.2939785

CrossRef Full Text | Google Scholar

Chen, Q., Zhou, W., and Shi, W. (2024). Estimation of soil organic carbon density on the qinghai–tibet plateau using a machine learning model driven by multisource remote sensing. Remote Sens. 16, 3006. doi:10.3390/rs16163006

CrossRef Full Text | Google Scholar

Cover, T., and Hart, P. (1967). Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 13, 21–27. doi:10.1109/TIT.1967.1053964

CrossRef Full Text | Google Scholar

Dada, B. A., Nwulu, N., and Olukanmi, S. O. (2024). Enhancing soil nutrient prediction through machine learning: a comparative study of optimization techniques using genetic algorithms, particle swarm optimization and optuna. SSRN Sch. Pap. 4994648. doi:10.2139/ssrn.4994648

CrossRef Full Text | Google Scholar

El-Kenawy, E.-S. M., Rizk, F. H., Zaki, A. M., Elshabrawy, M., Ibrahim, A., Abdelhamid, A. A., et al. (2024). NiOA: a novel metaheuristic algorithm modeled on the stealth and precision of Japanese ninjas. J. Artif. Intell. Eng. Pract. 1, 17–35. doi:10.21608/jaiep.2024.386693

CrossRef Full Text | Google Scholar

Elbeltagi, A., Kushwaha, N. L., Rajput, J., Vishwakarma, D. K., Kulimushi, L. C., Kumar, M., et al. (2022). Modelling daily reference evapotranspiration based on stacking hybridization of ann with meta-heuristic algorithms under diverse agro-climatic conditions. Stoch. Environ. Res. Risk Assess. 36, 3311–3334. doi:10.1007/s00477-022-02196-0

CrossRef Full Text | Google Scholar

Emadi, M., Taghizadeh-Mehrjardi, R., Cherati, A., Danesh, M., Mosavi, A., and Scholten, T. (2020). Predicting and mapping of soil organic carbon using machine learning algorithms in northern Iran. Remote Sens. 12, 2234. doi:10.3390/rs12142234

CrossRef Full Text | Google Scholar

Eyo, E. U., Abbey, S. J., Lawrence, T. T., and Tetteh, F. K. (2022). Improved prediction of clay soil expansion using machine learning algorithms and meta-heuristic dichotomous ensemble classifiers. Geosci. Front. 13, 101296. doi:10.1016/j.gsf.2021.101296

CrossRef Full Text | Google Scholar

Francaviglia, R., Almagro, M., and Vicente-Vicente, J. L. (2023). Conservation agriculture and soil organic carbon: principles, processes, practices and policy options. Soil Syst. 7, 17. doi:10.3390/soilsystems7010017

CrossRef Full Text | Google Scholar

Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Statistics 29, 1189–1232. doi:10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Guo, Y., He, J., Chen, Z., Zhang, Y., Wei, P., Ye, S., et al. (2023). Comparative analysis of machine learning algorithms for predicting soil organic carbon using remote sensing and environmental predictors

Google Scholar

Guo, Y., He, J., Chen, Z., Zhang, Y., Wei, P., Ye, S., et al. (2025). Exploration of the primary controlling factors of soil organic carbon in agricultural land based on the catboost model and multisource data. Int. Conf. Remote Sens. Mapp. Image Process. (RSMIP 2025) 13650, 6–120. doi:10.1117/12.3067572

CrossRef Full Text | Google Scholar

Hameed, M. M., Masood, A., Srivastava, A., Abd Rahman, N., Mohd Razali, S. F., Salem, A., et al. (2024). Investigating a hybrid extreme learning machine coupled with dingo optimization algorithm for modeling liquefaction triggering in sand-silt mixtures. Sci. Rep. 14, 10799. doi:10.1038/s41598-024-61059-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Hengl, T., Miller, M. A. E., Križan, J., Shepherd, K. D., Sila, A., Kilibarda, M., et al. (2021). African soil properties and nutrients mapped at 30 m spatial resolution using two-scale ensemble machine learning. Sci. Rep. 11, 6130. doi:10.1038/s41598-021-85639-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Khansar, H. H., Chafjiri, A. S., Fathollahi-Fard, A. M., Gheibi, M., Moezzi, R., Parsa, J., et al. (2024). Meta-heuristic-based machine learning techniques for soil stress prediction in embankment dams during construction. Indian Geotechnical J. 55, 1540–1562. doi:10.1007/s40098-024-01032-2

CrossRef Full Text | Google Scholar

Mahmoudi, N., Majidi, A., Jamei, M., Jalali, M., Maroufpoor, S., Shiri, J., et al. (2022). Mutating fuzzy logic model with various rigorous meta-heuristic algorithms for soil moisture content estimation. Agric. Water Manag. 261, 107342. doi:10.1016/j.agwat.2021.107342

CrossRef Full Text | Google Scholar

Meliho, M., Boulmane, M., Khattabi, A., Dansou, C. E., Orlando, C. A., Mhammdi, N., et al. (2023). Spatial prediction of soil organic carbon stock in the moroccan high atlas using machine learning. Multidiscip. Digit. Publ. Inst. 15, 2494. doi:10.3390/rs15102494

CrossRef Full Text | Google Scholar

Mosaid, H., Barakat, A., John, K., Faouzi, E., Bustillo, V., El Garnaoui, M., et al. (2024). Improved soil carbon stock spatial prediction in a mediterranean soil erosion site through robust machine learning techniques. Environ. Monit. Assess. 196, 130. doi:10.1007/s10661-024-12294-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Naimi, S., Ayoubi, S., Demattê, J. A. M., Zeraatpisheh, M., Amorim, M. T. A., and Mello, F. A. D. O. (2022). Spatial prediction of soil surface properties in an arid region using synthetic soil image and machine learning. Geocarto Int. 37, 8230–8253. doi:10.1080/10106049.2021.1996639

CrossRef Full Text | Google Scholar

Navidi, M. N., Seyedmohammadi, J., and Seyed Jalali, S. A. (2022). Predicting soil water content using support vector machines improved by meta-heuristic algorithms and remotely sensed data. Geomechanics Geoengin. 17, 712–726. doi:10.1080/17486025.2020.1864032

CrossRef Full Text | Google Scholar

Odebiri, O., Mutanga, O., Odindi, J., and Naicker, R. (2022). Modelling soil organic carbon stock distribution across different land-uses in South Africa: a remote sensing and deep learning approach. ISPRS J. Photogrammetry Remote Sens. 188, 351–362. doi:10.1016/j.isprsjprs.2022.04.026

CrossRef Full Text | Google Scholar

O’Riordan, R., Davies, J., Stevens, C., Quinton, J. N., and Boyko, C. (2021). The ecosystem services of urban soils: a review. Geoderma 395, 115076. doi:10.1016/j.geoderma.2021.115076

CrossRef Full Text | Google Scholar

Pal, S. C., Chakrabortty, R., Roy, P., Chowdhuri, I., Das, B., Saha, A., et al. (2021). Changing climate and land use of 21st century influences soil erosion in India. Gondwana Res. 94, 164–185. doi:10.1016/j.gr.2021.02.021

CrossRef Full Text | Google Scholar

Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., and Gulin, A. (2019). Catboost: unbiased boosting with categorical features. arXiv Prepr. arXiv:1706.09516. doi:10.48550/arXiv.1706.09516

CrossRef Full Text | Google Scholar

Rabbani, A., Samui, P., Kumari, S., Saraswat, B. K., Tiwari, M., and Rai, A. (2024). Optimization of an artificial neural network using three novel meta-heuristic algorithms for predicting the shear strength of soil. Transp. Infrastruct. Geotechnol. 11, 1708–1729. doi:10.1007/s40515-023-00343-w

CrossRef Full Text | Google Scholar

Rillig, M. C., van der Heijden, M. G. A., Berdugo, M., Liu, Y.-R., Riedo, J., Sanz-Lazaro, C., et al. (2023). Increasing the number of stressors reduces soil ecosystem services worldwide. Nat. Clim. Change 13, 478–483. doi:10.1038/s41558-023-01627-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rocci, K. S., Lavallee, J. M., Stewart, C. E., and Cotrufo, M. F. (2021). Soil organic carbon response to global environmental change depends on its distribution between mineral-associated and particulate organic matter: a meta-analysis. Sci. Total Environ. 793, 148569. doi:10.1016/j.scitotenv.2021.148569

PubMed Abstract | CrossRef Full Text | Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Solly, E. F., Weber, V., Zimmermann, S., Walthert, L., Hagedorn, F., and Schmidt, M. W. I. (2020). A critical evaluation of the relationship between the effective cation exchange capacity and soil organic carbon content in swiss forest soils. Front. For. Glob. Change 3. doi:10.3389/ffgc.2020.00098

CrossRef Full Text | Google Scholar

Taffese, W. Z., and Abegaz, K. A. (2022). Prediction of compaction and strength properties of amended soil using machine learning. Buildings 12, 613. doi:10.3390/buildings12050613

CrossRef Full Text | Google Scholar

Taghizadeh-Mehrjardi, R., Emadi, M., Cherati, A., Heung, B., Mosavi, A., and Scholten, T. (2021). Bio-inspired hybridization of artificial neural networks: an application for mapping the spatial distribution of soil texture fractions. Remote Sens. 13, 1025. doi:10.3390/rs13051025

CrossRef Full Text | Google Scholar

Tran, V. Q. (2022). Hybrid gradient boosting with meta-heuristic algorithms prediction of unconfined compressive strength of stabilized soil based on initial soil properties, mix design and effective compaction. J. Clean. Prod. 355, 131683. doi:10.1016/j.jclepro.2022.131683

CrossRef Full Text | Google Scholar

Vapnik, V., Golowich, S., and Smola, A. (1996). “Support vector method for function approximation, regression estimation and signal processing,” in Advances in neural information processing systems, 9.

Google Scholar

Vazirani, H., Wu, X., Srivastava, A., Dhar, D., and Pathak, D. (2024). Highly efficient jr optimization technique for solving prediction problem of soil organic carbon on large scale. Sensors Basel, Switz. 24, 7317. doi:10.3390/s24227317

PubMed Abstract | CrossRef Full Text | Google Scholar

Venter, Z. S., Hawkins, H.-J., Cramer, M. D., and Mills, A. J. (2021). Mapping soil organic carbon stocks and trends with satellite-driven high resolution maps over South Africa. Sci. Total Environ. 771, 145384. doi:10.1016/j.scitotenv.2021.145384

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Xie, M., Hu, B., Jiang, Q., Shi, Z., He, Y., et al. (2022). Desert soil salinity inversion models based on field in situ spectroscopy in southern xinjiang, China. Remote Sens. 14, 4962. doi:10.3390/rs14194962

CrossRef Full Text | Google Scholar

Zeynoddin, M., Bonakdari, H., Gumiere, S. J., and Rousseau, A. N. (2023). Multi-tempo forecasting of soil temperature data; application over quebec, Canada. Sustainability 15, 9567. doi:10.3390/su15129567

CrossRef Full Text | Google Scholar

Zhang, L. (2024). Employing multi-layer perceptron model via meta-heuristic algorithms for predicting California bearing capacity of stabilized soil. Multiscale Multidiscip. Model. Exp. Des. 7, 1375–1391. doi:10.1007/s41939-023-00277-3

CrossRef Full Text | Google Scholar