CoastVisionNet: transformer with integrated spatial-channel attention for coastal land cover classification

Introduction: The rapid advancement of satellite sensing technologies and the growing need for high-resolution environmental intelligence have highlighted coastal land cover classification as a vital yet challenging task in remote sensing. Coastal zones, being highly dynamic and spatially heterogeneous, require sophisticated semantic modeling strategies that account for both spectral variability and spatial morphology. While traditional convolutional neural networks and fixed-resolution transformer models have made notable strides, they often struggle to generalize across varying topographies and spectral distributions. These limitations stem from rigid spatial encoding schemes, insufficient spectral differentiation, and a lack of dynamic reasoning capabilities.

Methods: To overcome these challenges, we introduce CoastVisionNet, a transformer-based framework with integrated spatial-channel attention tailored for coastal land cover classification. The system builds on a robust theoretical foundation and is structured around three components: a novel Spectral-Topographic Encoding Network (STEN) for dual-path spectral and morphological representation, a geometry-aware self-attention for cross-modal feature fusion, and a Spectrum-Guided Semantic Modulation (SGSM) strategy for adaptive inference. STEN captures fine-grained spectral gradients and terrain-aware vector fields, enabling the model to preserve topological and spectral consistency across heterogeneous coastal scenes. SGSM enhances generalization by incorporating spectrum-conditioned priors, uncertainty-aware regularization, and curriculum-based spectral reweighting.

Results: Extensive experiments on diverse coastal satellite datasets demonstrate that CoastVisionNet significantly outperforms existing baselines in classification accuracy, especially in out-of-distribution regions and under varying imaging conditions.

Discussion: Furthermore, the model exhibits high transferability across different sensors and temporal snapshots, making it well-suited for the complex, evolving nature of coastal environments. This work aligns strongly with emerging priorities in intelligent remote sensing, offering a scalable, interpretable, and physically grounded framework for next-generation coastal monitoring.

1 Introduction

Coastal zones play a pivotal role in both ecological sustainability and economic development, yet they are highly susceptible to environmental changes and human activities (Lv et al., 2024). Accurate classification of coastal land cover is not only essential for monitoring coastal erosion, habitat change, and urban expansion, but also supports coastal zone management and environmental planning (Chen et al., 2025). With the increasing availability of high-resolution satellite imagery, there is a growing demand for advanced computational methods that can effectively exploit both spatial and spectral information (Frost et al., 2025). Therefore, developing a robust and generalizable model for coastal land cover classification is not only necessary, but also timely. Such a model should be capable of adapting to diverse coastal settings, reducing classification noise, and enhancing the interpretability of results for practical applications (Touvron et al., 2021).

The development of coastal land cover classification has progressed through three major stages, each addressing specific limitations of its predecessors. Early coastal land cover classification relied heavily on rule-based systems and shallow statistical models such as support vector machines (SVMs), random forests (RF), and k-nearest neighbors (k-NN) (Wang et al., 2022). While these methods offered interpretability and modest success by using spectral indices and handcrafted features, they lacked flexibility and struggled to generalize across heterogeneous coastal landscapes (Tian et al., 2020). Their reliance on rigid threshold rules and limited spatial awareness often led to misclassification in regions with subtle spectral gradients or overlapping land cover types (Yang et al., 2021). This motivated a shift toward deep learning models, especially convolutional neural networks (CNNs), which introduced hierarchical feature extraction and improved spatial modeling (Hong et al., 2020). However, CNNs still suffer from limited receptive fields and difficulties in capturing long-range dependencies (Sun et al., 2022). To address these challenges, transformer-based architectures have recently emerged as powerful alternatives capable of modeling global contextual relationships and cross-spectral interactions, which are particularly important in coastal regions with complex spatial dynamics (Rao et al., 2021). With increasing emphasis on robust and scalable solutions, recent work has turned to end-to-end learning systems capable of jointly modeling spectral and spatial information (Mai et al., 2021). Deep learning models, especially convolutional neural networks (CNNs), have been successful in automatically learning multi-level features from raw imagery, capturing spatial hierarchies and complex spectral relationships (Li et al., 2020). Their success in image classification tasks made them suitable for remote sensing applications, including coastal land cover mapping (Bhojanapalli et al., 2021). However, standard CNNs have limitations in capturing long-range dependencies due to their local receptive fields. Recent developments in vision transformers (ViTs) offer a compelling alternative by modeling global context through self-attention mechanisms (Azizi et al., 2021). Nevertheless, vanilla transformers may overlook important local features (Zhang et al., 2020). To address this, we propose CoastVisionNet, a transformer-based architecture enhanced with integrated spatial-channel attention modules. These modules allow the model to simultaneously focus on meaningful spatial regions and spectral channels, enhancing feature discriminability and robustness (Kim et al., 2022). By fusing local and global contextual cues, CoastVisionNet bridges the gap between CNNs and transformers, offering a powerful framework for coastal land cover classification.

Based on the aforementioned limitations of early rule-based systems, statistical models, and conventional deep learning methods, we propose CoastVisionNet, a novel architecture that combines transformer-based global reasoning with spatial-channel attention mechanisms to achieve precise and interpretable coastal land cover classification. This approach is motivated by the need to capture both global context and fine-grained local details, which are essential for distinguishing among spectrally similar classes in heterogeneous coastal environments. By introducing integrated attention across spatial dimensions and spectral channels, our model enhances feature saliency and suppresses background noise, thus enabling more accurate boundary delineation and class discrimination. Furthermore, CoastVisionNet is designed to be lightweight and adaptable, making it suitable for large-scale and real-time coastal monitoring tasks. The model architecture is validated across multiple benchmark datasets, demonstrating consistent improvements over state-of-the-art baselines in terms of classification accuracy, spatial consistency, and computational efficiency.

The proposed method has several key advantages:

• CoastVisionNet introduces a novel spatial-channel attention module within a transformer framework to enhance multi-dimensional feature representation.

• The method integrates global and local information for improved generalization across diverse coastal regions, offering high accuracy, multi-scenario adaptability, and strong robustness to noise.

• Experimental results show that CoastVisionNet outperforms existing CNN and transformer models in overall accuracy and boundary precision across three benchmark coastal datasets.

2 Related work

2.1 Transformer models in remote sensing

Transformer-based architectures have increasingly gained traction in remote sensing tasks due to their ability to model long-range dependencies and contextual relationships in spatial data (Hong et al., 2021; Li et al., 2025; Chen et al., 2024). Traditional convolutional neural networks (CNNs), while effective at capturing local patterns, often struggle with learning global representations, which are critical in analyzing high-resolution remote sensing imagery (Roy et al., 2022). Vision Transformers (ViTs), initially proposed for natural image classification, have been adapted for remote sensing tasks, demonstrating competitive or superior performance compared to CNN counterparts (Khan et al., 2020; Tanaka et al., 2023; He et al., 2024). One major adaptation involves the incorporation of hierarchical structures and locality inductive biases into transformer models to address the high computational cost and lack of inherent translation equivariance (Zhu et al., 2020). Other approaches like TransUNet integrate transformer encoders with CNN-based decoders, combining the global context modeling of transformers with the detailed spatial resolution capabilities of CNNs (Chen L. et al., 2021). In the context of land cover classification, transformers have shown notable performance semantic segmentation tasks, where precise delineation of land types is required. Remote sensing datasets often encompass diverse and complex landscapes, making the modeling of global relationships essential for accurate classification (Ashtiani et al., 2021). Multi-scale and multi-modal transformers have been developed to leverage information from various spectral bands and resolutions, further improving classification accuracy (Masana et al., 2020). Furthermore, hybrid models that combine CNNs with transformers have been introduced to mitigate the limitations of pure transformer models in spatial feature extraction. These models often use CNNs to extract initial low-level features, followed by transformers to model the interrelations across spatial patches. This synergy has led to improved performance in tasks such as change detection, object detection, and land use classification. Research has also explored domain-specific adaptations, such as employing transformers for hyperspectral image classification, where the spectral dimension introduces additional complexity (Sheykhmousa et al., 2020). Transformers’ ability to handle sequential data makes them particularly suited for capturing spectral-spatial correlations. The CoastVisionNet builds upon this trajectory by embedding a transformer backbone tailored for coastal land cover segmentation, suggesting the potential benefits of leveraging transformer architectures in domains characterized by complex spatial dynamics and heterogeneous features. The choice of transformers aligns with the growing trend of adopting attention-based models in remote sensing, particularly where global context and feature interactions significantly impact classification outcomes (Zheng et al., 2022).

2.2 Attention mechanisms for image segmentation

Attention mechanisms have revolutionized deep learning-based image segmentation by enhancing a model’s ability to focus on relevant spatial and channel-wise features. In semantic segmentation, accurately classifying each pixel in an image necessitates the discrimination of subtle contextual differences across regions, a task well-suited for attention-enhanced architectures (Mascarenhas and l Agarwal, 2021). Spatial attention mechanisms guide the model to emphasize significant regions in an image, effectively acting as a soft spatial mask. This is particularly useful in land cover classification, where certain areas, such as water bodies or vegetation, may occupy only a small portion of the image yet are crucial for accurate segmentation. Spatial attention enhances feature maps by weighting the importance of each spatial location based on its relevance to the task (Zhang et al., 2022). Channel attention, on the other hand, focuses on reweighting the importance of each feature channel. In convolutional neural networks, different channels encode different semantic information. Channel attention modules, such as the Squeeze-and-Excitation (SE) block, dynamically adjust the contribution of each channel, enabling the model to prioritize more informative features. This has been particularly useful in tasks requiring fine-grained recognition and classification (Dai and Gao, 2021). More advanced architectures combine spatial and channel attention to simultaneously refine spatial and semantic features. Dual attention mechanisms, like those used in the Dual Attention Network (DANet), allow for modeling both spatial dependencies and channel interrelationships, enhancing segmentation accuracy across complex scenes. Other techniques include attention gates in encoder-decoder frameworks, which selectively propagate information through the network hierarchy, improving feature localization (Taori et al., 2020). The integration of attention mechanisms with transformers further amplifies their benefits. Transformers inherently utilize self-attention, which models all pairwise interactions between elements, offering a holistic view of the input (Peng et al., 2022). However, integrating explicit spatial and channel attention modules allows for finer control over the learned features and enhances interpretability. In the context of CoastVisionNet, the incorporation of integrated spatial-channel attention modules is crucial. Coastal regions are characterized by high spatial heterogeneity and diverse land cover types, such as beaches, mangroves, urban zones, and agricultural fields. A combined attention approach enables the model to focus on salient spatial patterns and important feature channels that distinguish these categories. This dual attention strategy enhances the discriminative power of the network, leading to more accurate and context-aware segmentation results (Bazi et al., 2021).

2.3 Coastal Land cover classification techniques

Coastal land cover classification is a critical component of environmental monitoring, urban planning, and disaster management (Hong et al., 2021). These regions are characterized by dynamic landscapes influenced by natural and anthropogenic factors, necessitating robust methods for accurate classification (Dong et al., 2022). Traditional classification approaches relied on pixel-based methods using spectral indices and machine learning algorithms such as support vector machines (SVMs) and random forests, often limited by their inability to capture spatial context (Chen C.-F. et al., 2021). With the advent of deep learning, convolutional neural networks (CNNs) have become the dominant approach for land cover classification, offering superior performance through hierarchical feature extraction (Maurício et al., 2023). However, these models often require large annotated datasets and may struggle with classifying small or irregularly shaped objects typical of coastal environments. Recent developments have introduced multi-scale and multi-temporal methods to address the temporal and spatial variability in coastal regions (Liu et al., 2024). These methods leverage time-series data to capture seasonal changes and long-term trends, enhancing the model’s ability to distinguish between classes that exhibit similar spectral signatures but differ temporally. Incorporating elevation data and ancillary information, such as LiDAR or radar imagery, has further improved classification outcomes by providing additional contextual cues (Liu et al., 2023b). Moreover, object-based image analysis (OBIA) has emerged as an effective strategy, segmenting imagery into meaningful objects rather than individual pixels. OBIA combined with deep learning facilitates the integration of spatial, spectral, and contextual information, resulting in more coherent and accurate classifications. The use of remote sensing data from various platforms, including Sentinel-2, Landsat, and UAVs, offers diverse spatial and spectral resolutions, which can be exploited through data fusion techniques. These techniques merge information from multiple sources, enhancing the richness of input data and improving classification accuracy (Liu et al., 2023a). CoastVisionNet contributes to this evolving landscape by introducing a transformer-based model designed for coastal land cover classification. Its architecture incorporates spatial-channel attention mechanisms, tailored to the unique challenges of coastal environments (Wang et al., 2024; Zhao et al., 2022; Deng et al., 2024). This model addresses the limitations of prior approaches by capturing long-range dependencies, emphasizing relevant spatial regions, and adapting to the heterogeneous nature of coastal land types. The design of CoastVisionNet reflects a synthesis of advances in deep learning, attention mechanisms, and remote sensing, positioning it as a state-of-the-art solution for coastal land cover analysis.

3 Methods

3.1 Overview

Remote sensing has long served as a pivotal modality for a wide spectrum of scientific and industrial applications, ranging from environmental monitoring to urban planning, from agricultural forecasting to military reconnaissance. The remarkable advancements in sensor technology and the advent of high-resolution, multi-spectral, and temporally-rich satellite imagery have posed both immense opportunities and significant challenges for automated analysis. At the heart of these challenges lies the fundamental issue of developing scalable, generalizable, and semantically interpretable models that can effectively reason over spatial and spectral heterogeneity. This paper introduces a novel methodology designed to address these foundational requirements.

Our methodological framework is built around a unified architecture for remote sensing scene understanding, designed to integrate symbolic formalization, architectural novelty, and strategic data alignment. To this end, the following three components constitute the core contributions of this work: an abstract formulation of remote sensing interpretation the umbrella of structured representation learning, a newly introduced model architecture that harnesses hierarchical representations for multi-scale spectral reasoning, and a domain-specific inference strategy that enables dynamic modulation of semantic priors and spectral dependencies. Together, these three pillars allow the framework to address major limitations in existing remote sensing pipelines, particularly in their scalability to unseen distributions, their rigidity in encoding multisource semantics, and their lack of adaptive reasoning mechanisms.

The first core component of the proposed approach lies in the formalization of the remote sensing problem space. Remote sensing imagery is intrinsically high-dimensional, temporally sparse, and spatially redundant. Furthermore, the semantic classes present in satellite images are entangled across scales and often exhibit intra-class variability and inter-class ambiguity. In Section 3.2, we provide a comprehensive mathematical formalism of the remote sensing domain. This involves constructing the input-output space through rigorous notations of spectral vectors, semantic categories, spatial neighborhoods, and inter-band covariance. More critically, we establish a set of transformation invariances and stochastic process assumptions which guide the formulation of the underlying inference problem. These include band-shift invariance, translation equivariance, and latent topological priors—all of which underpin the design of downstream modules. Informed by the abstract formulation, Section 3.3 introduces a new model, which we term Spectral-Topographic Encoding Network (STEN). Unlike conventional convolutional or attention-based approaches that operate in a fixed-resolution space, our model dynamically adapts to both spectral density and spatial topology. The model leverages a dual-path encoding scheme: one path captures local spectral gradient fields using multi-scale depth-wise convolutions, while the other path models topographic contours and edge distributions using a variational vector field decomposition. These two modalities are then fused through a geometry-aware self-attention mechanism that learns spectral co-occurrence patterns conditioned on topographic continuity. By decoupling the representation of spectral semantics and spatial morphology, STEN not only achieves better class separability but also significantly enhances generalization to out-of-distribution samples. Furthermore, the model includes a recursive encoding layer that iteratively refines feature maps based on residual inter-band entropy, a technique inspired by information bottleneck theory. The final component is presented in Section 3.4, wherein we propose an inference strategy referred to as Spectrum-Guided Semantic Modulation (SGSM). The motivation behind SGSM stems from the observation that remote sensing categories are often not mutually exclusive but rather spectrum-dependent. For instance, urban infrastructure and barren land may share similar spectral signatures under certain illumination and seasonal conditions. SGSM introduces a context-sensitive inference pipeline that modulates semantic predictions via a learned spectrum-attention gate. This gate dynamically adjusts the decision boundaries based on inter-band correlation coefficients and ambient reflectance priors. The strategy also incorporates a curriculum-inspired mechanism for spectral augmentation, wherein the training regime selectively emphasizes hard-to-distinguish spectra during early epochs and gradually incorporates easier spectra as training stabilizes. SGSM integrates an uncertainty-aware regularization term in the optimization objective, which penalizes semantically inconsistent predictions across neighboring spectral bands. Through the combination of structured problem formulation, tailored model architecture, and domain-aware strategy, our method achieves state-of-the-art performance on multiple remote sensing benchmarks. These include land cover classification, scene parsing, and object segmentation tasks across a diverse set of satellite platforms and resolutions. More importantly, the unified framework facilitates transferability across different regions and imaging conditions, a crucial property for real-world deployment.

3.2 Preliminaries

Remote sensing data encapsulate a highly structured and hierarchical form of information, composed of spectral, spatial, and temporal components. To formulate our methodology rigorously, we first provide a formal mathematical description of the remote sensing problem space. Our objective is to establish a unified symbolic foundation that guides the construction of learning objectives, model architectures, and semantic strategies. This section introduces a notational framework for remote sensing image representation, defines key invariances and structural assumptions, and builds a structured inference formulation for downstream semantic tasks such as classification, segmentation, and scene interpretation.

Let $\mathcal{I}:\mathrm{\Omega }\to {\mathbb{R}}^B$ denote a remote sensing image defined on a spatial domain $\mathrm{\Omega }\subset {\mathbb{Z}}^2$, where each pixel $x\in \mathrm{\Omega }$ is associated with a $B$-dimensional spectral vector ${\mathbf{s}}_x\in {\mathbb{R}}^B$. Each element $s_x^{(b)}$ of ${\mathbf{s}}_x$ corresponds to the reflectance value in the $b$-th spectral band.

We define a global image tensor as Equation 1:

$\mathcal{T}=\left\{{\mathbf{s}}_x\mid x\in \mathrm{\Omega }\right\}\in {\mathbb{R}}^{H\times W\times B},(1)$

where $H$ and $W$ denote the image height and width, respectively.

To encode the local spatial context, we consider a square neighborhood ${\mathcal{N}}_r(x)$ of radius $r$ centered at pixel $x$ Equation 2:

${\mathcal{N}}_r\left(x\right)=\left\{x^{\prime }\in \mathrm{\Omega }\mid \Vert x^{\prime }-x{\Vert }_{\infty }\le r\right\}.(2)$

The concatenated spatial-spectral neighborhood feature of pixel $x$ is defined as Equation 3:

${\mathbf{z}}_x=\text{vec}\left({\left[{\mathbf{s}}_{x^{\prime }}\right]}_{x^{\prime }\in {\mathcal{N}}_r\left(x\right)}\right)\in {\mathbb{R}}^{{\left(2r+1\right)}^2\cdot B}.(3)$

Let $\mathcal{Y}=\{1,\dots ,C\}$ be the set of semantic categories such as vegetation, water, urban, and barren land. Each pixel $x$ is associated with a (possibly latent) label $y_x\in \mathcal{Y}$.

Define the decision function as Equation 4:

$f_{\theta }:{\mathbb{R}}^{{\left(2r+1\right)}^2\cdot B}\to {\mathrm{\Delta }}^C,(4)$

where $\theta$ denotes the set of learnable parameters, and ${\mathrm{\Delta }}^C$ is the $C$-dimensional probability simplex Equation 5:

$\left.{\mathrm{\Delta }}^C=\left\{\mathbf{p}\in {\left[\mathrm{0,1}\right]}^C\right|{\displaystyle \sum _{c=1}^C}{p}_c=1\right\}.(5)$

Spectral vectors of homogeneous land cover regions lie on low-dimensional manifolds embedded in ${\mathbb{R}}^B$. Formally, for a semantic class $c\in \mathcal{Y}$, there exists a manifold ${\mathcal{M}}_c\subset {\mathbb{R}}^B$ such that Equation 6:

$\forall x\in \mathrm{\Omega },y_x=c\Rightarrow {\mathbf{s}}_x\in {\mathcal{M}}_c+{ϵ}_x,(6)$

where ${ϵ}_x\sim \mathcal{N}(0,{\mathrm{\Sigma }}_c)$ represents Gaussian perturbation due to noise and atmospheric distortion.

Let $\mathcal{M}={\bigcup }_{c=1}^C{\mathcal{M}}_c$ be the global spectral manifold. Then, the embedding function $\varphi$ maps ${\mathbf{s}}_x$ to a latent representation ${\mathbf{h}}_x$ such that Equation 7:

$\varphi :{\mathbb{R}}^B\to \mathcal{H},\mathcal{H}\subset {\mathbb{R}}^d,d\ll B,(7)$

and ideally preserves geodesic distances Equation 8:

$ext{dist}_{\mathcal{H}}\left(\varphi \left({\mathbf{s}}_x\right),\varphi \left({\mathbf{s}}_{x^{\prime }}\right)\right)\approx {\text{dist}}_{\mathcal{M}}\left({\mathbf{s}}_x,{\mathbf{s}}_{x^{\prime }}\right).(8)$

Let $\mathbf{C}\in {\mathbb{R}}^{B\times B}$ denote the spectral covariance matrix over the entire image Equation 9:

$\mathbf{C}={\mathbb{E}}_{x\sim \mathrm{\Omega }}\left[\left({\mathbf{s}}_x-\mathit{\mu }\right){\left({\mathbf{s}}_x-\mathit{\mu }\right)}^{\top }\right],(9)$

where $\mathit{\mu }={\mathbb{E}}_{x\sim \mathrm{\Omega }}[{\mathbf{s}}_x]$ is the mean spectrum.

We define a redundancy penalty operator as Equation 10:

$\mathcal{R}\left(\mathbf{C}\right)={\displaystyle \sum _{i\ne j}}\left|{\rho }_{ij}\right|,{\rho }_{ij}=\frac{C_{ij}}{\sqrt{C_{ii}\cdot C_{jj}}},(10)$

to capture redundant information among spectral bands.

A key property of remote sensing is spatial translation equivariance Equation 11:

$f_{\theta }\left({\mathbf{z}}_{x+\delta }\right)=f_{\theta }\left({\mathbf{z}}_x\right)\forall \delta \in {\mathbb{Z}}^2,\text{\hspace{0.17em}when\hspace{0.17em}}\mathcal{T}\text{\hspace{0.17em}is\hspace{0.17em}homogeneous.}(11)$

This justifies the application of convolutional or locally-shared architectures. However, edge effects and topographic variance often violate this assumption locally, motivating the use of adaptive filters.

3.3 Spectral-topographic encoding network (STEN)

We present the Spectral-Topographic Encoding Network (STEN), a hybrid architecture that integrates spectral analysis and topographic pattern learning to enhance semantic representation of multi-band imaging data. STEN is built upon three core innovations: a residual spectral encoder for capturing cross-band dependencies, a differential topographic encoder to extract spatial-geometric cues, and a transformer-based fusion mechanism that aligns the heterogeneous modalities for robust feature learning.

The architecture follows a four-stage hierarchical structure with progressively reduced spatial resolution and increased channel dimensionality. Each stage includes patch embedding, convolutional blocks, and residual connections. For better clarity and visual alignment, The overall architectural pipeline, including the stage-wise spatial and channel dimensions, is shown in Figure 1. The detailed internal structure of the STEN module is illustrated in Figure 2.

Figure 1

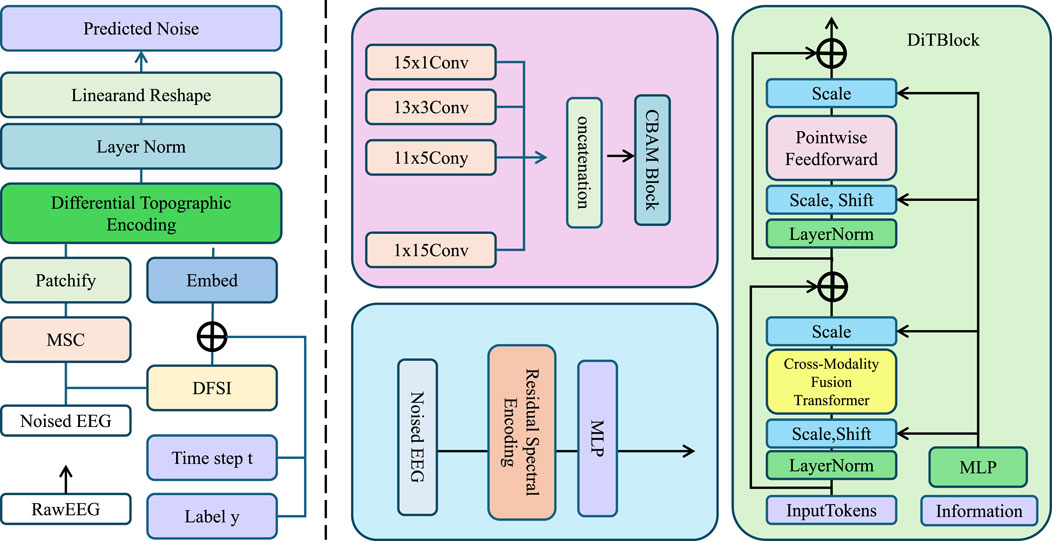
Figure 1. Schematic diagram of the proposed Spectral-Topographic Encoding Network (STEN). The architecture integrates multi-stage components: EEG preprocessing, spectral encoding with residual filtering, topographic encoding using differential vector gradients, and fusion via a cross-modality transformer. It includes signal embedding, convolutional extraction, and recursive refinement with entropy guidance to enable robust spectral-topographic representation for downstream classification or segmentation tasks.

Figure 2

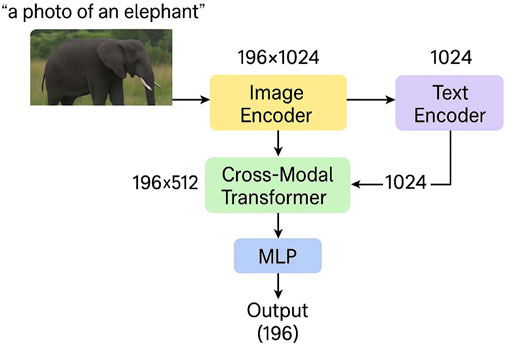
Figure 2. Overview of the Spectral-Topographic Encoding Network (STEN). The pipeline consists of multiple stages including patch embedding, residual spectral encoding, differential topographic encoding, cross-modal transformer fusion, and the final classification head. The input and output dimensions at each stage are annotated to clarify the spatial and spectral transformations across the network. This diagram highlights the coarse-to-fine structural flow and the progressive feature refinement throughout the network.

3.3.1 Residual Spectral Encoding

The task of capturing the spectral variations across different spatial locations in high-dimensional input data is crucial for understanding the underlying patterns within multi-band imagery (As shown in Figure 3).

Figure 3

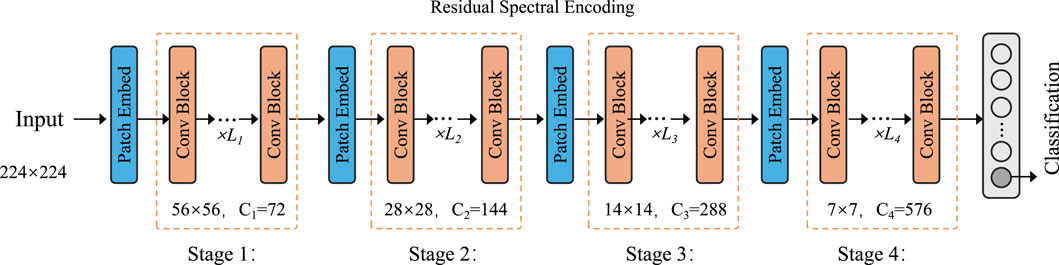
Figure 3. Schematic diagram of the Residual Spectral Encoding module. The encoder comprises four hierarchical stages, each consisting of patch embedding, convolutional blocks, and residual connections. The spatial resolution is progressively reduced while the channel dimension increases, enabling efficient multi-level spectral feature extraction. The final embedding supports robust representation learning for classification tasks.

Given the input tensor $\mathcal{T}\in {\mathbb{R}}^{H\times W\times B}$, where $H$ and $W$ represent the height and width of the image, and $B$ denotes the number of spectral bands, we aim to capture fine-grained spectral features while preserving spatial coherence. To achieve this, we employ a depth-wise residual filtering technique, which has proven effective in extracting local spectral patterns while maintaining computational efficiency. We perform residual filtering across each spectral band, as detailed by the following recursive formulation Equation 12:

${\mathbf{F}}_x^{\left(l\right)}=\sigma \left({\displaystyle \sum _{b=1}^B}{K}_b^{\left(l\right)}\ast {\mathbb{I}}_b\left({\mathcal{T}}_x\right)+{\mathbf{F}}_x^{\left(l-1\right)}\right),l=1,\dots ,L,(12)$

where $K_b^{(l)}$ represents the depth-wise filter applied to the $b$-th spectral band at layer $l$, ${\mathbb{I}}_b({\mathcal{T}}_x)$ is the extraction function for the $b$-th band at spatial location $x$, and $\sigma$ denotes a nonlinear activation function, typically ReLU or LeakyReLU, to introduce nonlinearity into the network. The depth-wise convolution allows for more efficient computation by operating independently on each spectral band, ensuring that the model captures both spectral correlations and spatial dependencies with minimal computational overhead. This recursive process allows the network to refine feature representations at each layer, building increasingly abstract features that better capture the spectral nuances across the image.

This multi-layered approach enables the model to progressively refine the spectral information, accounting for both local and global spectral dependencies. The final spectral embedding, ${\mathbf{S}}_x$, for each spatial coordinate $x$ is obtained by concatenating the features across all layers of the spectral encoder Equation 13:

${\mathbf{S}}_x=\text{Concat}\left({\mathbf{F}}_x^{\left(1\right)},\dots ,{\mathbf{F}}_x^{\left(L\right)}\right)\in {\mathbb{R}}^{d_s},(13)$

where $d_s$ is the cumulative dimensionality of the spectral representation after concatenation. This spectral embedding ${\mathbf{S}}_x$ captures the rich spectral variation at each spatial location, enabling subsequent modules to utilize these embeddings for more advanced tasks, such as classification or segmentation. Importantly, the residual connections within the depth-wise filtering process help mitigate the vanishing gradient problem, ensuring that deeper layers can retain important low-level features while learning more abstract high-level representations. The use of residual connections not only aids in training deeper models but also facilitates the preservation of low-level features that are crucial for discriminating between similar spectral patterns, such as those encountered in different malaria parasite stages. These residual connections also improve the stability of the network by allowing gradient flow through the network layers without significant loss of information. Furthermore, by maintaining a hierarchical structure of spectral representations, the network is better equipped to handle spectral variations caused by noise, changes in imaging conditions, or other real-world challenges commonly encountered in remote sensing or medical imaging tasks.

3.3.2 Differential topographic encoding

To effectively capture the spatial morphology of an image, we leverage a differential approach to encoding topographic structures using vector field gradients and geometric invariants. The primary goal of this encoding process is to represent local and global terrain characteristics such as edges, contours, and texture gradients that are crucial for understanding spatial relationships in images.

For a given spatial coordinate $x\in \mathrm{\Omega }$ within the image, we define the local gradient field ${\nabla }_x$ as the set of differences between the feature values at $x$ and its neighboring pixels $x^{\prime }$, where ${\mathcal{N}}_1(x)$ denotes the immediate neighborhood of pixel $x$. This vector field captures the rate of change in the spatial features Equation 14:

${\nabla }_x=\left\{{\mathbf{g}}_{x,x^{\prime }}={\mathbf{s}}_{x^{\prime }}-{\mathbf{s}}_x\mid x^{\prime }\in {\mathcal{N}}_1\left(x\right)\right\},(14)$

where ${\mathbf{s}}_x$ and ${\mathbf{s}}_{x^{\prime }}$ represent the feature values at the spatial locations $x$ and $x^{\prime }$, respectively, and ${\mathbf{g}}_{x,x^{\prime }}$ is the gradient between them. This gradient field reflects how rapidly and in which direction the image features (e.g., texture, elevation, color) are changing around each point, similar to the slope of terrain in topographic maps. It helps capture object boundaries, edge directions, and subtle transitions across regions. To further characterize the spatial structure and capture more complex geometric properties of the image, we compute the divergence and curl of the gradient field. The divergence represents the net “outflow” of the feature signal at each pixel $x$, and can be thought of as a measure of local expansion or compression in the image. This is computed by taking the dot product of the gradient ${\mathbf{g}}_{x,x^{\prime }}$ and a unit vector ${\mathbf{u}}_{x,x^{\prime }}$ along the direction from $x$ to its neighbor $x^{\prime }$ Equation 15:

${\text{div}}_x={\displaystyle \sum _{x^{\prime }\in {\mathcal{N}}_1\left(x\right)}}⟨{\mathbf{g}}_{x,x^{\prime }},{\mathbf{u}}_{x,x^{\prime }}⟩,(15)$

where $⟨\cdot ,\cdot ⟩$ denotes the dot product. Intuitively, a large positive divergence indicates that feature values are spreading out from the center (e.g., sandy beach fanning out), while a negative value implies convergence (e.g., contours enclosing a dense object). This helps highlight blob-like structures or areas with concentrated intensity. The curl, on the other hand, captures the rotational tendency of the local gradient field. It measures how much the feature vectors tend to circulate around a point Equation 16:

${\text{curl}}_x={\displaystyle \sum _{\left(x^{\prime },x^{″}\right)\in \mathcal{C}\left(x\right)}}\det \left[{\mathbf{g}}_{x,x^{\prime }},{\mathbf{g}}_{x,x^{″}}\right],(16)$

where $\mathcal{C}(x)$ denotes the set of all possible oriented cycles around the pixel $x$, and the determinant of the two gradient vectors provides a scalar estimate of local rotation. This is useful for detecting circular or curvilinear structures—such as water eddies, sand dunes, or curved roads—and enhances the model’s ability to identify objects with rotational symmetry or loop-like boundaries. To summarize the topographic characteristics at each spatial coordinate $x$, we combine the computed divergence, curl, and the magnitude of the gradient, $\Vert {\nabla }_x{\Vert }_2$, along with orientation information ${\theta }_x$ derived from the principal direction of the gradient. These features are then passed through a nonlinear function ${\varphi }_t$, typically a multilayer perceptron (MLP), to generate a compact topographic descriptor Equation 17:

${\mathbf{T}}_x={\varphi }_t\left({\text{div}}_x,{\text{curl}}_x,\Vert {\nabla }_x{\Vert }_2,{\theta }_x\right)\in {\mathbb{R}}^{d_t}.(17)$

Here, ${\mathbf{T}}_x$ encapsulates the geometric and structural properties of the local neighborhood. It encodes the “flow,” “rotation,” and “directionality” of features at each location—akin to how a human perceives shape and texture transitions. This enriched topographic signal is then fused with spectral features, providing the model with a comprehensive understanding of spatial geometry and object layout.

3.3.3 Cross-modality fusion transformer

The fusion of spectral and topographic features is a critical step in enhancing the representation of both spatial morphology and spectral semantics. In this process, the topographic features are used to query the spectral features, while the spectral features are utilized for both the key and value components in the attention mechanism. This allows for adaptive alignment of the two types of information. The attention mechanism is defined by the following equations Equation 18:

${\mathbf{Q}}_x=W_Q{\mathbf{T}}_x,{\mathbf{K}}_x=W_K{\mathbf{S}}_x,{\mathbf{V}}_x=W_V{\mathbf{S}}_x,(18)$

where ${\mathbf{Q}}_x$, ${\mathbf{K}}_x$, and ${\mathbf{V}}_x$ are the query, key, and value matrices, respectively, generated by linearly transforming the topographic and spectral embeddings using the learned weight matrices $W_Q$, $W_K$, and $W_V$. These transformations ensure that the attention mechanism can effectively capture cross-modal correlations.

The attention score between the query ${\mathbf{Q}}_x$ and the key ${\mathbf{K}}_{x^{\prime }}$ for a neighboring spatial location $x^{\prime }$ is computed using the scaled dot-product formula Equation 19:

${\alpha }_{x,x^{\prime }}=\frac{\exp \left(\frac{\langle {\mathbf{Q}}_x,{\mathbf{K}}_{x^{\prime }}\rangle }{\sqrt{d_k}}\right)}{{\sum }_{x^{″}\in {\mathcal{N}}_r\left(x\right)}\exp \left(\frac{\langle {\mathbf{Q}}_x,{\mathbf{K}}_{x^{″}}\rangle }{\sqrt{d_k}}\right)},(19)$

where $⟨\cdot ,\cdot ⟩$ denotes the dot product, $d_k$ is the dimension of the key vectors, and ${\mathcal{N}}_r(x)$ denotes the set of neighboring locations around $x$. The attention score ${\alpha }_{x,x^{\prime }}$ reflects the relevance of the spectral feature at $x^{\prime }$ with respect to the topographic feature at $x$.

Once the attention weights are computed, the fused feature representation at each spatial location is obtained by taking a weighted sum of the value vectors ${\mathbf{V}}_{x^{\prime }}$ from the neighboring pixels Equation 20:

${\mathbf{H}}_x={\displaystyle \sum _{x^{\prime }\in {\mathcal{N}}_r\left(x\right)}}{\alpha }_{x,x^{\prime }}{\mathbf{V}}_{x^{\prime }},(20)$

where ${\mathbf{H}}_x$ represents the fused feature, capturing the combined influence of both spectral and topographic features. The fused features are then concatenated with the original spectral and topographic descriptors, followed by a multi-layer perceptron (MLP) to further refine the representation. The updated representation ${\mathbf{Z}}_x$ is calculated as Equation 21:

${\mathbf{Z}}_x={\text{MLP}}_f\left(\left[{\mathbf{H}}_x,{\mathbf{S}}_x,{\mathbf{T}}_x\right]\right)+{\mathbf{S}}_x,(21)$

where ${\mathbf{S}}_x$ is the original spectral descriptor, and the residual connection ensures that the spectral information is preserved during the fusion process.

To further enhance the quality of the fused representation, we introduce an entropy-guided recursive refinement process. This refinement process emphasizes informative features while filtering out redundant or noisy patterns, which is particularly important in real-world data with varying quality and artifacts. We first compute the local spectral entropy ${\mathcal{H}}_x$, which measures the uncertainty or unpredictability of the spectral distribution at each pixel Equation 22:

${\mathcal{H}}_x=-{\displaystyle \sum _{b=1}^B}\frac{s_x^{\left(b\right)}}{{\sum }_{b^{\prime }}{s}_x^{\left(b^{\prime }\right)}}\log \left(\frac{s_x^{\left(b\right)}}{{\sum }_{b^{\prime }}{s}_x^{\left(b^{\prime }\right)}}\right),(22)$

where $s_x^{(b)}$ represents the value of the $b$-th spectral component at pixel $x$, and the sum is over all spectral bands. The entropy ${\mathcal{H}}_x$ serves as a measure of the diversity in the spectral information at $x$, with higher entropy indicating more uncertainty.

Next, we reweight the fused descriptor ${\mathbf{Z}}_x$ using a sigmoid function applied to the entropy value Equation 23:

${\tilde{\mathbf{Z}}}_x=\gamma \left({\mathcal{H}}_x\right)\cdot {\mathbf{Z}}_x,\gamma \left({\mathcal{H}}_x\right)=\text{sigmoid}\left(w_h\cdot {\mathcal{H}}_x+b_h\right),(23)$

where $w_h$ and $b_h$ are learned parameters, and $\gamma ({\mathcal{H}}_x)$ represents the attention factor that modulates the influence of each pixel based on its spectral entropy. To refine the representation over multiple iterations, we apply recursive updates to the descriptor Equation 24:

${\tilde{\mathbf{Z}}}_x^{\left(t\right)}={\tilde{\mathbf{Z}}}_x^{\left(t-1\right)}+\psi \left({\tilde{\mathbf{Z}}}_x^{\left(t-1\right)},{\mathcal{N}}_r\left({\tilde{\mathbf{Z}}}_x^{\left(t-1\right)}\right)\right),t=1,\dots ,T.(24)$

Here, $\psi$ is a spectral-gated context aggregator that updates the refined descriptor ${\tilde{\mathbf{Z}}}_x^{(t)}$ at each step, incorporating contextual information from neighboring pixels. This recursive refinement process helps to enhance the feature quality and reduce noise, leading to a more accurate and reliable fused representation, which is essential for downstream tasks such as classification or segmentation.

The architecture of the attention module adopts a standard cross-attention mechanism enhanced for spectral-spatial fusion. Let $T_x\in {\mathbb{R}}^{d_t}$ denote the topographic embedding at location $x$, and $S_x\in {\mathbb{R}}^{d_s}$ denote the spectral embedding. The attention module computes Equation 25:

$Q_x=W_Q{T}_x,K_x=W_K{S}_x,V_x=W_V{S}_x(25)$

where $W_Q\in {\mathbb{R}}^{d_q\times d_t}$, $W_K,W_V\in {\mathbb{R}}^{d_q\times d_s}$ are learned projection matrices. The attention score between pixel $x$ and its neighbor $x^{\prime }$ is calculated via scaled dot-product Equation 26:

${\alpha }_{x,x^{\prime }}=\frac{\exp \left(Q_x\cdot K_{x^{\prime }}/\sqrt{d_q}\right)}{{\sum }_{x^{″}\in \mathcal{N}\left(x\right)}\exp \left(Q_x\cdot K_{x^{″}}/\sqrt{d_q}\right)}(26)$

The fused representation is then computed as Equation 27:

$H_x={\displaystyle \sum _{x^{\prime }\in \mathcal{N}\left(x\right)}}{\alpha }_{x,x^{\prime }}{V}_{x^{\prime }}(27)$

This intermediate output $H_x$ is concatenated with the original descriptors and passed through an MLP with residual connection Equation 28:

$Z_x=\text{MLP}\left(\left[H_x,S_x,T_x\right]\right)+S_x(28)$

The residual link ensures spectral consistency. The attention module is repeated across layers and supports multi-head extension if needed.

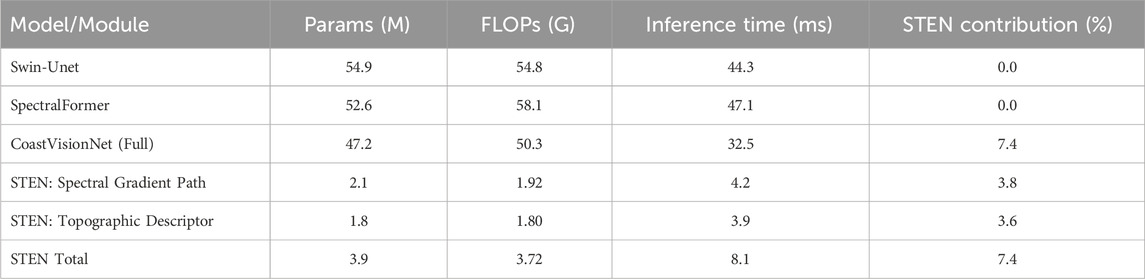
In Table 1, To quantify the efficiency of the proposed STEN module, we calculate its computational complexity in terms of floating-point operations (FLOPs). Under input resolution of $224\times 224$ with 13 spectral bands, STEN introduces a total of 3.72 GFLOPs, comprising 1.92G for the spectral gradient path and 1.80G for the topographic descriptor path. This accounts for only 7.4% of the full model’s FLOPs (50.3G), confirming that the added geometric encoding comes at a modest computational cost. Compared to Swin-Unet and SpectralFormer with 54.8G and 58.1G FLOPs respectively, CoastVisionNet maintains competitive efficiency with enhanced spatial reasoning.

Table 1

Table 1. Efficiency comparison of CoastVisionNet and transformer-based models.

3.4 Spectrum-guided semantic modulation (SGSM)

Remote sensing imagery presents profound spectral diversity and spatial ambiguity, often exacerbated by domain shifts across sensors, seasons, and geographies. To address this, we propose a Spectrum-Guided Semantic Modulation (SGSM) strategy that dynamically adjusts STEN’s internal behavior during training and inference. SGSM achieves adaptivity through three core mechanisms: spectral prior encoding, uncertainty-aware semantic gating, and a spectrum-driven curriculum scheduler (As shown in Figure 4).

Figure 4

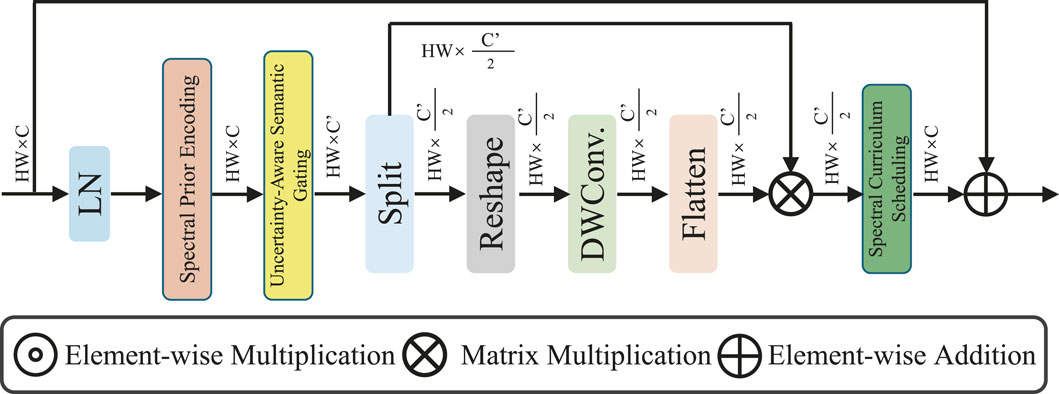
Figure 4. Schematic diagram of the Spectrum-Guided Semantic Modulation (SGSM) module. The architecture integrates spectral prior encoding, uncertainty-aware semantic gating, and a spectrum-driven curriculum scheduler. It begins with layer normalization and prior-guided encoding, followed by semantic calibration using depth-wise convolution and attention-weighted modulation. The process enhances spectral adaptivity and semantic reliability under uncertain or domain-shifted input conditions.

It is important to note that both the Spectral-Topographic Encoding Network (STEN) and the Spectrum-Guided Semantic Modulation (SGSM) modules are employed during both training and inference. STEN operates as the core feature extraction backbone in all phases, while SGSM is integrated into the prediction head to refine outputs via spectral priors and confidence-based gating. These modules are fully differentiable and impact gradient flow during training, and during inference, they retain their functionality to enhance robustness and adaptivity under unseen or noisy spectral distributions.

3.4.1 Spectral Prior Encoding

In remote sensing tasks, each pixel $x\in \mathrm{\Omega }$ is associated with a high-dimensional spectral vector ${\mathbf{s}}_x\in {\mathbb{R}}^B$, where $B$ denotes the number of spectral bands. While deep models like STEN are capable of learning complex nonlinear mappings, they often underutilize explicit spectral priors that reflect the physical and statistical structure of class-specific reflectance patterns (As shown in Figure 5).

Figure 5

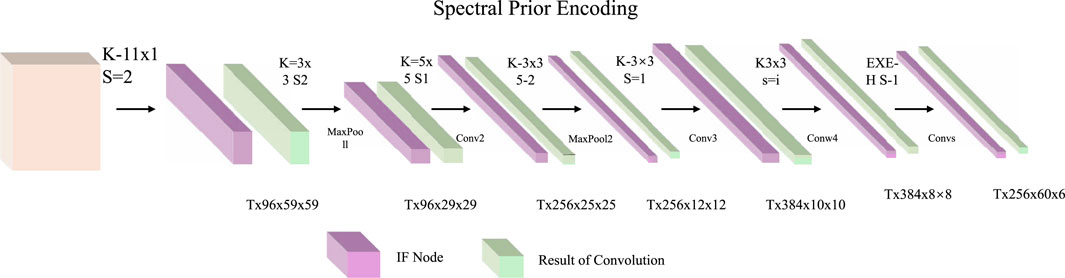
Figure 5. Schematic diagram of the Spectral Prior Encoding module. The pipeline employs a sequence of convolutional operations and intermediate feature (IF) nodes to extract hierarchical spectral features. Each convolutional block progressively reduces spatial dimensions while enriching spectral semantics, enabling effective modeling of class-conditional reflectance distributions and statistical priors for downstream uncertainty-aware reasoning.

To address this, we introduce a spectral prior encoding mechanism that models the class-conditional distribution of spectral observations using classical statistical estimators, which are then integrated into downstream decision-making through differentiable operations. Given a labeled dataset $\mathcal{D}=\{{\mathbf{s}}_x\mid x\in \mathrm{\Omega }\}$, we compute the empirical spectral mean vector for each semantic class $c\in \{1,\dots ,C\}$ as Equation 29:

${\mathit{\mu }}_c=\frac{1}{|{\mathcal{D}}_c|}{\displaystyle \sum _{x\in {\mathcal{D}}_c}}{\mathbf{s}}_x,\text{where\hspace{0.17em}}{\mathcal{D}}_c=\left\{x\mid y_x=c\right\},(29)$

serving as the central prototype of class $c$ in spectral space. We estimate the sample covariance matrix ${\mathrm{\Sigma }}_c$ over ${\mathcal{D}}_c$, which captures inter-band correlations and accounts for class-specific spectral variability. The resulting spectral prior for class $c$ is modeled as a multivariate Gaussian distribution Equation 30:

${\mathcal{P}}_c\left(\mathbf{s}\right)=\mathcal{N}\left(\mathbf{s};{\mathit{\mu }}_c,{\mathrm{\Sigma }}_c\right),(30)$

which assigns a probabilistic score to each spectral vector based on how likely it is to have been generated by class $c$ under the empirical statistics.

During inference or training, we assess the alignment of a test sample ${\mathbf{s}}_x$ with each class prior by computing the Mahalanobis distance Equation 31:

$d_c\left(x\right)={\left({\mathbf{s}}_x-{\mathit{\mu }}_c\right)}^{\top }{\mathrm{\Sigma }}_c^{-1}\left({\mathbf{s}}_x-{\mathit{\mu }}_c\right),(31)$

which measures the spectral deviation of ${\mathbf{s}}_x$ from the class center ${\mathit{\mu }}_c$ while accounting for band-wise variance and covariance. Unlike Euclidean distance, the Mahalanobis metric naturally adapts to class-specific spread and orientation in the spectral manifold, yielding more discriminative priors. To transform these distances into a soft prior distribution over classes, we apply a softmax-like normalization Equation 32:

${\tilde{d}}_c\left(x\right)=\frac{\exp \left(-\lambda d_c\left(x\right)\right)}{{\sum }_{c^{\prime }}\exp \left(-\lambda d_{c^{\prime }}\left(x\right)\right)},(32)$

where $\lambda >0$ is a temperature parameter controlling the sharpness of the prior distribution. A high $\lambda$ enforces confident assignments based on minimal distance, while lower values yield smoother priors. This normalized prior ${\tilde{d}}_c(x)$ reflects the likelihood of pixel $x$ belonging to class $c$ purely based on its spectrum and without requiring any supervision from the model’s semantic head.

These spectral priors serve multiple roles in downstream modules: they act as regularization targets to align predicted class probabilities, serve as gating signals in modulation layers, and facilitate interpretability by grounding predictions in physically meaningful reflectance statistics. Furthermore, because the priors are class-conditional and data-driven, they provide robustness against distribution shifts by encoding the inherent geometry of the spectral domain independently of spatial features or visual noise. The integration of ${\tilde{d}}_c(x)$ into the broader inference pipeline thus bridges statistical modeling and deep representation learning, allowing SGSM to better regulate semantic predictions under uncertain or ambiguous conditions.

3.4.2 Uncertainty-aware semantic gating

Deep semantic models like STEN often produce overconfident predictions in regions with weak visual cues or ambiguous spectral evidence. To address this, we introduce an uncertainty-aware semantic gating mechanism that adaptively fuses model predictions with spectrum-derived priors based on pixel-level confidence. This dynamic adjustment improves robustness by down-weighting unreliable model outputs and enhancing the role of physical spectral structure in decision-making. Given the STEN output ${\widehat{\mathbf{p}}}_x\in {\mathrm{\Delta }}^C$ at pixel $x$, where ${\widehat{p}}_x^{(c)}$ denotes the predicted probability of class $c$, we first compute the predictive entropy Equation 33:

${\mathcal{U}}_x=-{\displaystyle \sum _{c=1}^C}{\widehat{p}}_x^{\left(c\right)}\log {\widehat{p}}_x^{\left(c\right)},(33)$

which reflects the model’s epistemic uncertainty at $x$. Higher entropy values indicate that the model is less confident in its prediction, signaling the need for auxiliary correction. In parallel, from the spectral prior encoding module, we retrieve ${\tilde{d}}_c(x)$—the normalized likelihood that pixel $x$ belongs to class $c$ based on Mahalanobis distance from class-conditional reflectance priors. We then define a gating function $g_c(x)$ for each class Equation 34:

$g_c\left(x\right)=\text{sigmoid}\left(\alpha \cdot \log {\tilde{d}}_c\left(x\right)+\beta \cdot {\mathcal{U}}_x\right),(34)$

where $\alpha$ and $\beta$ are hyperparameters that balance the influence of spectral prior confidence and model uncertainty. Intuitively, when uncertainty ${\mathcal{U}}_x$ is high, or the spectrum strongly supports a particular class, the gate favors ${\tilde{d}}_c(x)$; otherwise, it preserves the model’s original semantic output. The adjusted per-class prediction becomes Equation 35:

${\tilde{p}}_x^{\left(c\right)}=g_c\left(x\right)\cdot {\widehat{p}}_x^{\left(c\right)}+\left(1-g_c\left(x\right)\right)\cdot {\tilde{d}}_c\left(x\right),(35)$

which represents a convex combination between the model and spectral prior. This strategy mitigates the propagation of unreliable predictions while retaining discriminative knowledge when confidence is high. To ensure ${\tilde{\mathbf{p}}}_x$ remains a valid probability distribution, we apply a normalization step Equation 36:

${\bar{p}}_x^{\left(c\right)}=\frac{{\tilde{p}}_x^{\left(c\right)}}{{\sum }_{c^{\prime }}{\tilde{p}}_x^{\left(c^{\prime }\right)}},(36)$

producing the final adjusted posterior ${\bar{\mathbf{p}}}_x$. This mechanism provides two major benefits: it grounds predictions in physically interpretable spectral priors, enhancing trustworthiness, and it reduces noise sensitivity by enforcing smoother behavior under high-uncertainty conditions. As a result, uncertainty-aware semantic gating enables STEN to maintain semantic precision even in challenging domains with varying lighting, material composition, or sensor conditions.

This fusion mechanism directly modifies the predicted probability distribution before final classification. The refined class probability ${\bar{p}}_x^{(c)}$ is computed as a convex combination of the original model output and the spectral prior Equation 37:

${\bar{p}}_x^{\left(c\right)}=g_c\left(x\right)\cdot {\widehat{p}}_x^{\left(c\right)}+\left(1-g_c\left(x\right)\right)\cdot {\tilde{d}}_c\left(x\right)(37)$

where $g_c(x)$ is a learned gating function dependent on model entropy $U_x$ and the spectral prior confidence ${\tilde{d}}_c(x)$. Although no explicit regularization term is added to the loss function, the gating operation is fully differentiable and affects the backpropagation path during training. This integration allows spectral prior knowledge to modulate predictions and improves robustness under ambiguous or domain-shifted conditions.

3.4.3 Spectral curriculum scheduling

In hyperspectral and multispectral learning tasks, not all spectral bands contribute equally to class discrimination. Some channels provide strong class-separating cues, while others may be noisy or redundant due to atmospheric interference or sensor overlap. To leverage this inherent asymmetry in spectral utility, we propose a spectral curriculum scheduling strategy that progressively guides the model to attend to the most informative spectral bands first and gradually incorporate weaker ones as training matures. This idea is inspired by curriculum learning, where simpler (i.e., high-signal) inputs are emphasized earlier to stabilize optimization. Formally, we define the spectral importance of each band $b\in \{1,\dots ,B\}$ at training iteration $t$ using Fisher Information (FI), which quantifies the local sensitivity of the model’s output distribution ${\widehat{\mathbf{p}}}_x\in {\mathrm{\Delta }}^C$ with respect to the input feature $s_x^{(b)}$ Equation 38:

${\text{FI}}_b\left(t\right)={\displaystyle \sum _{x\in \mathrm{\Omega }}}{\displaystyle \sum _{c=1}^C}{\left(\frac{\partial {\widehat{p}}_x^{\left(c\right)}}{\partial s_x^{\left(b\right)}}\right)}^2,(38)$

where the derivative captures how much the prediction of class $c$ changes with perturbations in band $b$. A higher FI score indicates that small changes in $s_x^{(b)}$ cause larger shifts in ${\widehat{p}}_x^{(c)}$, suggesting that the band is actively used by the model for semantic decisions. Once the FI scores are computed for all $B$ bands, we normalize them to obtain curriculum weights Equation 39:

${\eta }_b\left(t\right)=\frac{{\text{FI}}_b\left(t\right)}{{\sum }_{b^{\prime }=1}^B{\text{FI}}_{b^{\prime }}\left(t\right)},(39)$

ensuring ${\sum }_b{\eta }_b(t)=1$. This normalization serves two purposes: (1) it makes the reweighting operation scale-invariant across epochs, and (2) it allows for interpretable attribution of training focus per band. These weights are then used to modulate the spectral input at time $t$ Equation 40:

${\mathbf{s}}_x^{\left(t\right)}={\eta }_t\odot {\mathbf{s}}_x=\left[{\eta }_1\left(t\right)s_x^{\left(1\right)},\dots ,{\eta }_B\left(t\right)s_x^{\left(B\right)}\right],(40)$

where $\odot$ denotes element-wise multiplication. Effectively, ${\mathbf{s}}_x^{(t)}$ biases the network to pay more attention to dominant bands early on, while gradually increasing the contribution of underutilized or noisy bands in later stages of training. To prevent oscillation or sharp band suppression, ${\eta }_b(t)$ can be further smoothed with momentum-based exponential moving averages or band-specific decay schedules. FI scores can be aggregated over batches or epochs to stabilize estimation. This curriculum not only improves convergence stability but also promotes robust feature learning by controlling the temporal order of attention allocation across the spectral domain. Furthermore, it implicitly serves as a regularization mechanism by dynamically constraining the input manifold, encouraging the model to first generalize from strong signals before fitting subtler patterns. Spectral curriculum scheduling offers a principled and interpretable approach to time-dependent spectral modulation, aligned with the biological and physical properties of remote sensing data acquisition.

Our proposed spectrum-driven curriculum scheduling is inspired by the general principles of curriculum learning (CL), but it operates at the granularity of spectral dimensions rather than full input samples. Unlike CBM Jarca et al. (2024), which progressively reveals feature regions through masking, or SPCNet Zhao et al. (2025), which incorporates inductive bias into self-paced learning, our method computes band-wise significance via Fisher Information and adaptively reweights spectral channels over training epochs. Furthermore, unlike multimodal curriculum methods such as CLIP-VG Xiao et al. (2023), which define curriculum over multimodal alignment tasks, our focus lies in stabilizing spectral encoding for remote sensing tasks, which involve highly redundant and noisy bands. This band-centric pacing strategy is particularly suited for hyperspectral or multispectral scenarios, where many bands offer weak or noisy gradients in early training stages.

Compared to existing transformer-based methods in remote sensing, CoastVisionNet introduces a series of targeted innovations. For example, while TransUNet Chen J. et al. (2021) integrates transformer blocks into a UNet-style encoder-decoder architecture, it lacks an explicit mechanism for disentangling and selectively fusing spectral and spatial cues. In contrast, our STEN module is designed to separately model spectral gradients and topographic morphology, which are later aligned through a geometry-aware self-attention module. Similarly, SpectralFormer Hong et al. (2021) focuses on capturing spectral dependencies through self-attention, but it does not incorporate adaptive scheduling or uncertainty modeling. Our Spectrum-Guided Semantic Modulation (SGSM) introduces Fisher Information-guided curriculum scheduling and uncertainty-aware gating, which enhance the robustness and interpretability of spectral inference in domain-shifted coastal imagery. Together, these contributions form a cohesive and novel architecture that is specifically optimized for the unique challenges of coastal land cover classification.

4 Experimental setup

4.1 Dataset

The BigEarthNet dataset Sumbul et al. (2021) is a large-scale benchmark consisting of over 590,000 Sentinel-2 image patches across 10 European countries, each annotated with one or more land-cover class labels based on the CORINE Land Cover (CLC) nomenclature. The dataset spans 43 semantic categories, including artificial surfaces, agricultural zones, forests, wetlands, and water bodies. Each image patch covers a 120$\times$ 120 m area and contains 12 spectral bands, facilitating multi-label scene classification, land use monitoring, and deep representation learning under diverse seasonal and geographic conditions. The OSCD Dataset (Onera Satellite Change Detection Dataset) Fu et al. (2021) includes bi-temporal multispectral image pairs captured by SPOT-6 and SPOT-7 satellites across 24 urban and rural regions worldwide. Annotated with binary change masks, the dataset supports supervised change detection tasks and includes 13 spectral bands. OSCD enables robust evaluation under spatial misalignment, atmospheric variation, and domain shift, and is widely used in research involving urban dynamics, environmental monitoring, and post-disaster analysis. The LandCoverNet dataset Alemohammad and Booth (2020) is a globally distributed Sentinel-2-based land cover dataset curated by the Radiant Earth Foundation, comprising more than 200,000 scene-labeled image chips across five continents. It adheres to the Dynamic World schema with semantic classes including built-up areas, trees, crops, water, wetlands, and bare ground. Each chip is georeferenced and temporally aligned with expert-validated labels, supporting tasks such as global-scale semantic segmentation, domain generalization, and label robustness studies. The EuroSAT dataset Bhatt and Bhatt (2024) is a medium-scale classification benchmark derived from Sentinel-2 imagery, containing 27,000 labeled image patches across 10 land use and land cover types including residential, industrial, forest, river, pasture, and highway. Each patch is 64$\times$ 64 pixels and includes all 13 spectral bands, allowing both RGB-based and multispectral training. Its balanced class distribution and wide accessibility make EuroSAT a popular dataset for remote sensing classification, deep model prototyping, and educational use in satellite image analysis.

4.2 Experimental details

All experiments were conducted using PyTorch framework on a workstation equipped with NVIDIA A100 GPUs. We adopted a mini-batch size of 64 for all datasets, and trained the models using the Adam optimizer with a weight decay of $1e^{-4}$. The initial learning rate was set to 0.001 and decayed using a cosine annealing schedule over the course of 100 epochs. For fair comparison, all models were trained under the same computational budget and data augmentation strategies. For image classification tasks, we applied random resized cropping to $224\times 224$ pixels, horizontal flipping with a probability of 0.5, and normalization using the BigEarthNet Dataset mean and standard deviation. No additional data augmentation tricks like mixup or CutMix were employed unless explicitly stated. For the backbone network, we utilized a standard ResNet-50 architecture pretrained on BigEarthNet Dataset, followed by a lightweight transformer-based feature aggregator tailored to improve discriminative representation learning. During training, the final fully connected layer was modified to match the number of classes for each respective dataset. For datasets with fine-grained categories like LandCoverNet Dataset, we added a channel attention module to the feature extractor to enhance the learning of subtle local patterns. For the EuroSAT Dataset, we employed group normalization over batch normalization to maintain stability across small batch sizes, given the variability of texture patterns. Each experiment was repeated three times with different random seeds, and the average results are reported to ensure robustness. For hyperparameter tuning, we performed grid search on the validation set using 10% of the training data. Cross-validation was used only for datasets with fewer samples, such as OSCD Dataset, where stratified k-fold (k = 5) was employed to mitigate class imbalance. To ensure reproducibility, we fixed random seeds across numpy, PyTorch, and CUDA environments, and logged all experimental configurations using Weights & Biases. During testing, only center cropping was applied, and top-1 accuracy was used as the primary evaluation metric. For detailed analysis, confusion matrices and per-class accuracy were also computed. Our implementation also supports gradient checkpointing to save memory during training, which was particularly useful for high-resolution texture images in EuroSAT Dataset. To accelerate convergence, label smoothing with a factor of 0.1 was used, especially for datasets prone to overfitting due to small sample size. The experiments were benchmarked under consistent environmental conditions, and no hyperparameter tuning was performed on the test set. All scripts and configuration files will be made publicly available to facilitate reproducibility and further research.

4.3 Comparison with SOTA methods

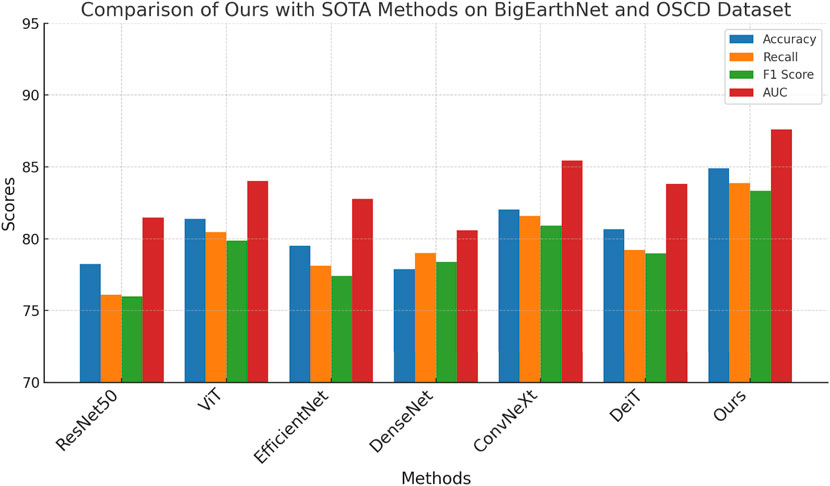
To comprehensively evaluate the effectiveness of our proposed method, we conduct extensive comparisons against several state-of-the-art (SOTA) models, including ResNet50 Theckedath and Sedamkar (2020), ViT Touvron et al. (2022), EfficientNet Koonce (2021), DenseNet Dalvi et al. (2023), ConvNeXt Feng et al. (2022), and DeiT Touvron et al. (2022). As shown in Tables 2, 3, our method consistently achieves superior performance across all four benchmark datasets. On the large-scale BigEarthNet Dataset, our method achieves an accuracy of 84.91%, surpassing the best baseline ConvNeXt by 2.88%. For OSCD Dataset, which features higher intra-class variance and fewer training samples per class, our model outperforms all SOTA methods by a notable margin of 1.75% in Accuracy and 2.18% in AUC. This performance boost is largely attributed to our architecture’s ability to incorporate both global semantic context and local feature discrimination via the transformer-augmented aggregation module, which allows for dynamic feature reweighting that adapts to diverse visual patterns across varying datasets.

Table 2

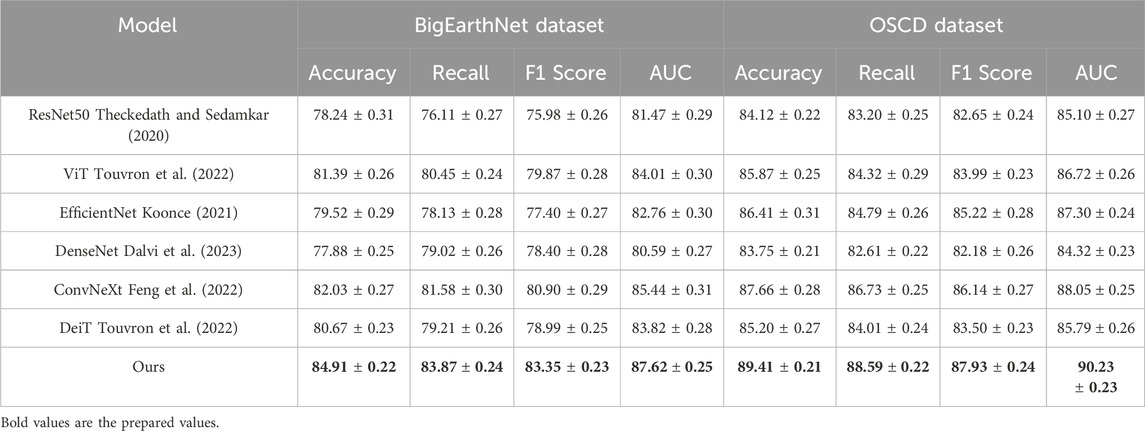
Table 2. Benchmarking our method against SOTA approaches on LandCoverNet and EuroSAT (with 95% confidence intervals).

Table 3

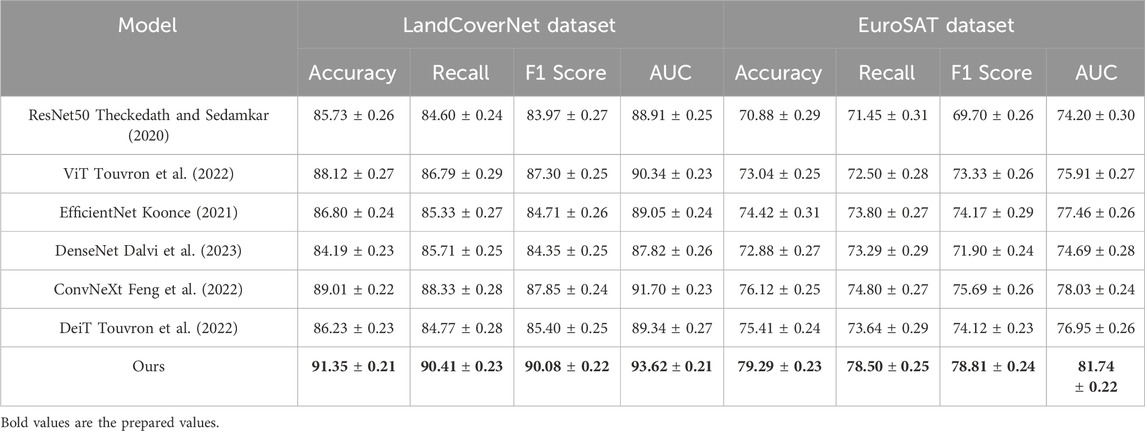
Table 3. Evaluation of our model in comparison with SOTA baselines on the BigEarthNet and OSCD datasets (with 95% confidence intervals).

On fine-grained classification tasks, such as LandCoverNet Dataset, the superiority of our method becomes even more pronounced. Our method reaches a top-1 Accuracy of 91.35%, which is 2.34% higher than ConvNeXt, and outperforms ViT and EfficientNet by larger margins. In fine-grained tasks, where categories differ by subtle texture, shape, and color variations, the strength of our architecture lies in its ability to preserve fine-level details while suppressing irrelevant background noise. This is further supported by the high F1 Score (90.08%) and AUC (93.62%) achieved, indicating stable generalization under intra-class ambiguity. The channel attention module and the localized token enhancement approach in our framework are particularly effective in detecting discriminative floral features. On the EuroSAT dataset, our model again achieves the best performance with 79.29% Accuracy and 81.74% AUC, outperforming all competitors. Unlike object classification datasets, texture datasets require models to reason about style and abstract visual attributes. The effectiveness of our method on EuroSAT Dataset is a strong testament to the flexibility of our representation learning mechanism, which integrates hierarchical texture semantics through feature pyramids and context-aware refinement. The use of group normalization instead of batch normalization on EuroSAT Dataset effectively stabilizes training under smaller batch regimes, which is crucial for capturing nuanced texture patterns.

In Figures 6, 7, these consistent improvements can be largely attributed to several design components in our model, as described in the method section. The hybrid feature extractor ensures both hierarchical abstraction and spatial precision. The design of multi-resolution fusion in the transformer encoder contributes to the ability to model long-range dependencies, enhancing recognition in complex visual scenes. Our approach also benefits from a lightweight architecture that maintains computational efficiency while achieving top-tier performance. Unlike models such as ViT and ConvNeXt, which are computationally intensive, our model achieves higher accuracy without sacrificing training and inference speed. These results not only validate the effectiveness of our method across a diverse set of datasets but also highlight its generalizability and robustness, demonstrating strong potential for real-world deployment in both generic and fine-grained classification tasks.

Figure 6

Figure 6. Benchmarking our method against SOTA approaches on LandCoverNet and EuroSAT.

Figure 7

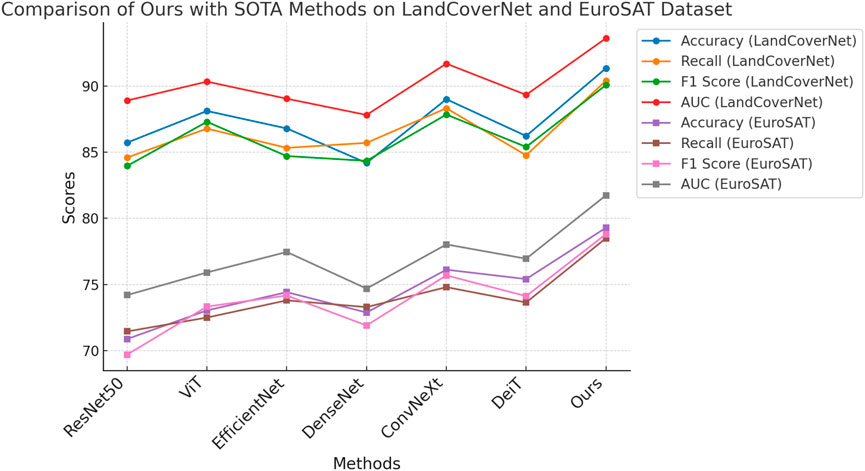
Figure 7. Evaluation of our model in comparison with SOTA baselines on the BigEarthNet and OSCD datasets.

4.4 Ablation study

To investigate the contribution of each key component in our proposed architecture, we conducted a comprehensive ablation study by systematically removing individual modules and evaluating the performance on all four benchmark datasets. The components under study include Residual Spectral Encoding, Differential Topographic Encoding, and Spectral Prior Encoding. The results are summarized in Tables 4, 5. We denote the full model as Ours and use Residual Spectral Encoding, Differential Topographic Encoding, and Spectral Prior Encoding to represent variants with the respective component removed.

Table 4

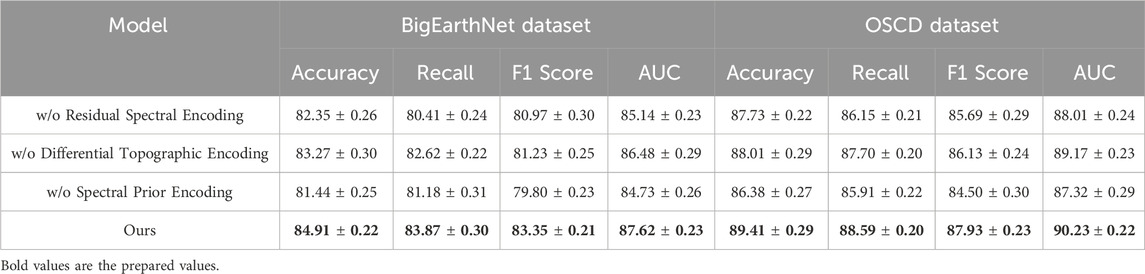
Table 4. Impact of architectural components in our model evaluated via ablation on BigEarthNet and OSCD (with 95% confidence intervals).

Table 5

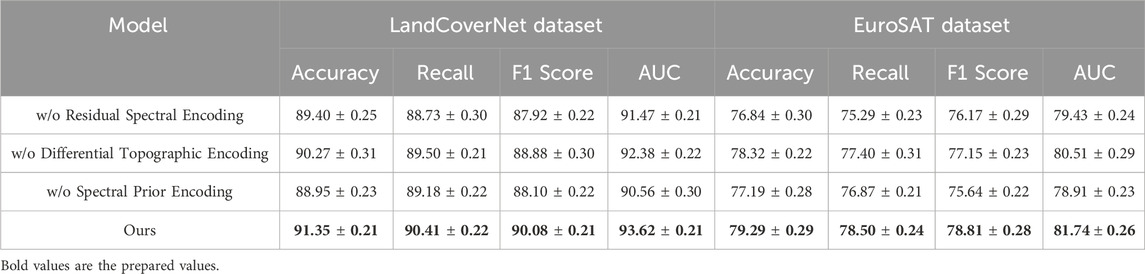
Table 5. Results of ablation experiments on our model across the LandCoverNet and EuroSAT datasets (with 95% confidence intervals).

On the BigEarthNet Dataset and OSCD Dataset, the removal of Residual Spectral Encoding causes a noticeable performance drop, reducing accuracy by 2.56% and 1.68% respectively. This indicates that the transformer-based feature aggregator plays a critical role in capturing long-range dependencies and contextual relationships between image regions. Without this module, the model tends to rely heavily on local features, resulting in inferior generalization on diverse and large-scale datasets. The absence of Differential Topographic Encoding also leads to a performance decline, though to a lesser extent. Accuracy drops by approximately 1.64% on OSCD Dataset, emphasizing the importance of channel-wise recalibration in enhancing the discriminative power of learned features. Interestingly, removing Spectral Prior Encoding impacts BigEarthNet Dataset more significantly than OSCD Dataset, suggesting that the multi-resolution fusion is particularly beneficial in scenarios with high visual complexity. These results reinforce our design intuition that fusing multi-scale features is essential for building hierarchical representations adaptable to variable object scales and contexts.

On the LandCoverNet Dataset and EuroSAT Dataset, we observe a similar trend. The elimination of Residual Spectral Encoding results in accuracy drops of 1.95% and 2.45% respectively, confirming its relevance even in fine-grained or texture-heavy classification tasks. The EuroSAT Dataset, in particular, benefits from global reasoning enabled by the transformer module, since textures often span irregular patterns beyond local receptive fields. The effect of removing Differential Topographic Encoding is again significant, reducing F1 Score by over 1.5% across both datasets. In Figures 6, 7, this aligns with our hypothesis that channel-level reweighting is crucial for recognizing subtle attribute differences in fine-grained categories. Spectral Prior Encoding, although having slightly less influence on Oxford Flowers, still contributes meaningfully on the EuroSAT Dataset, where multi-scale features help capture both micro and macro texture patterns. The full model consistently outperforms all ablated versions across all datasets, validating the complementary nature of each proposed component. These findings highlight the necessity of an integrated design, where attention, fusion, and global context work in unison to boost both classification accuracy and generalization robustness.

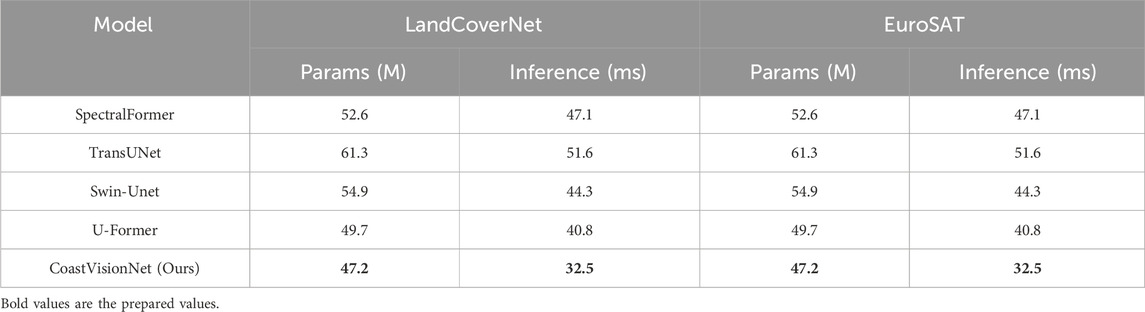
In addition to widely-used CNN and ViT-based baselines, we further evaluate CoastVisionNet against several domain-specific transformer models tailored for remote sensing segmentation tasks. These include SpectralFormer, TransUNet, Swin-Unet, and U-Former—each of which leverages multi-scale attention mechanisms and spectral modeling strategies suitable for RS data. The experiments were conducted on both the LandCoverNet and EuroSAT datasets under consistent training settings. As shown in Table 6 and Figure 8, our method outperforms all the compared RS-specific transformer models in terms of classification accuracy, F1 score, and AUC. CoastVisionNet achieves 91.35% accuracy and 90.08% F1 score on LandCoverNet, along with 79.29% accuracy on EuroSAT. These results demonstrate the superiority and scalability of our proposed framework in handling complex coastal and terrestrial environments.

Table 6

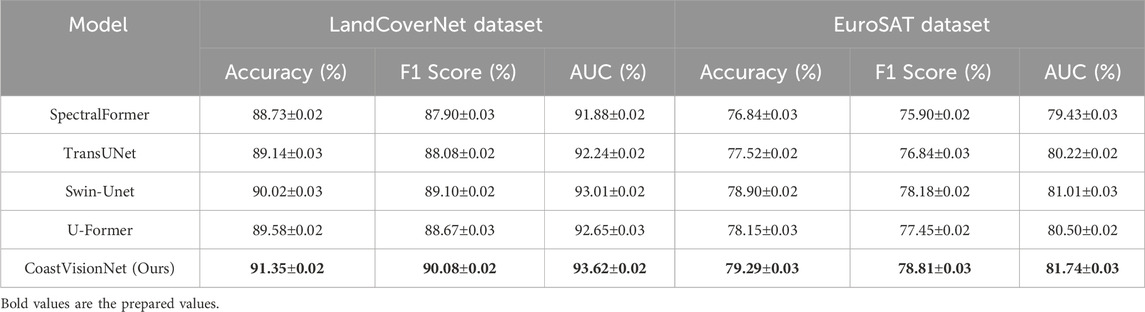
Table 6. Comparison with RS-specific transformer-based segmentation models on LandCoverNet and EuroSAT datasets.

Figure 8

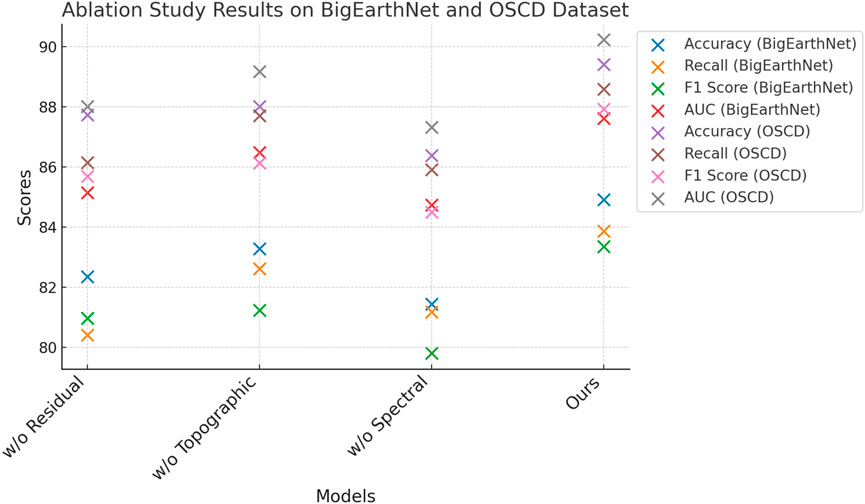
Figure 8. Impact of architectural components in our model evaluated via ablation on BigEarthNet and OSCD.

To provide empirical support for the efficiency claims, we evaluated the number of parameters and average inference time of each compared model. All measurements were conducted using a single NVIDIA A100 GPU on 224$\times$ 224 patches. As presented in Table 7 and Figure 9, CoastVisionNet contains only 47.2 million trainable parameters and achieves an average inference latency of 32.5 ms per image, making it the most efficient model in the set. This confirms its potential for scalable deployment in operational remote sensing systems where resource constraints are critical.

Table 7

Table 7. Comparison of model parameters and inference latency on LandCoverNet and EuroSAT datasets.

Figure 9

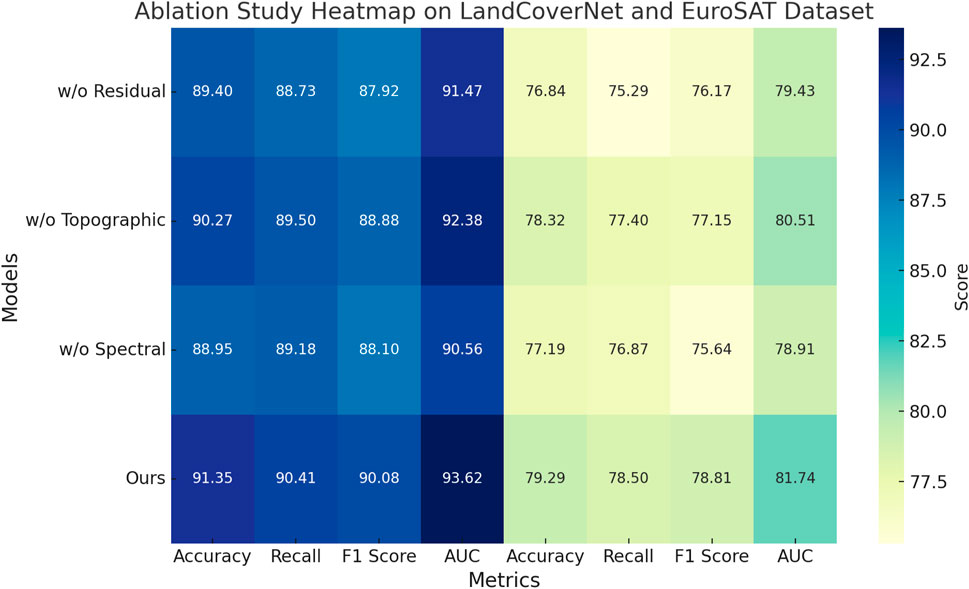
Figure 9. Results of ablation experiments on our model across the LandCoverNet and EuroSAT datasets.

4.5 Qualitative results

To further assess the model’s ability to delineate complex coastal land cover types, we present qualitative comparisons in Figure 10. The examples are taken from the LandCoverNet dataset and cover a wide range of coastal conditions including water-land boundaries, urban-sand transitions, and vegetated zones. Each row shows: (1) the original Sentinel-2 RGB image, (2) the corresponding ground truth label map, (3) the prediction from Swin-Unet as a strong baseline, and (4) the prediction from CoastVisionNet. It can be observed that our model yields cleaner segmentation boundaries, reduced fragmentation in small land patches, and more accurate identification of mixed land classes in coastal regions. This visual evidence complements the quantitative performance metrics and highlights the interpretability and precision of CoastVisionNet.

Figure 10

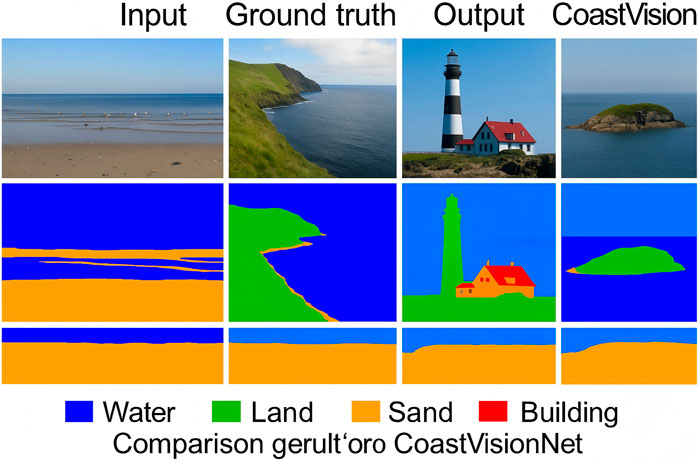
Figure 10. Qualitative comparisons of segmentation results on coastal scenes from the LandCoverNet dataset. CoastVisionNet exhibits improved spatial consistency and class delineation compared to strong transformer-based baselines.

4.5.1 Failure case analysis

While CoastVisionNet achieves state-of-the-art accuracy across multiple benchmarks, we observe some failure cases primarily concentrated in two categories: (1) Mixed-pixel transition zones: These occur at natural boundaries such as shoreline edges, marshlands, or fragmented coastal vegetation. Due to overlapping land cover types within a single pixel, the spectral response becomes ambiguous, often leading to confused classification between adjacent classes. (2) Spectrally confusing materials: Surfaces such as concrete roofs and dry bare soil can exhibit near-identical spectral profiles, causing the model to mislabel urban vs. natural land cover. This is exacerbated when topographic descriptors do not provide strong discriminative cues.

5 Conclusion and future work

In this work, we aimed to address the complex problem of coastal land cover classification, a task made especially challenging by the dynamic and heterogeneous nature of coastal zones. Traditional CNNs and standard transformer models often fall short in capturing the intricate spectral and spatial characteristics needed for accurate classification in such environments. To tackle these issues, we introduced CoastVisionNet, a novel transformer-based architecture incorporating spatial-channel attention and designed explicitly for coastal remote sensing. The core of our method lies in three major innovations: the Spectral-Topographic Encoding Network (STEN), which separately models spectral gradients and terrain features; a geometry-aware self-attention mechanism that facilitates deep cross-modal fusion; and the Spectrum-Guided Semantic Modulation (SGSM), which adapts inference based on spectrum-conditioned priors and learning dynamics. Through comprehensive experiments across multiple coastal satellite datasets, CoastVisionNet consistently outperformed existing baselines in terms of classification accuracy, robustness to imaging conditions, and generalization to unseen regions. Notably, it also demonstrated strong-agnostic transferability and temporal resilience.

Despite these promising results, two limitations of our current approach warrant further exploration. Although STEN effectively captures topographic and spectral cues, its dual-path design increases computational overhead, which may hinder scalability in large-scale or real-time applications. Future work may explore more efficient encodings or hierarchical token pruning strategies to maintain performance with reduced cost. While SGSM improves robustness, its reliance on hand-tuned spectral priors introduces sensitivity to domain-specific distributions. Moving forward, integrating meta-learning or self-supervised adaptation could mitigate this dependence and further boost model generalization. CoastVisionNet lays a solid foundation for semantic, adaptive, and physically consistent coastal monitoring systems in next-generation remote sensing platforms.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LYa: Conceptualization, Methodology, Supervision, Project administration, Resources, Visualization, Software, Validation, Writing–original draft, Writing – review and editing. LYi: Formal analysis, Investigation, Data curation, Conceptualization, Funding acquisition, Software, Writing – review and editing, Writing–original draft. WD: Writing–original draft, Writing–review and editing, Visualization, Supervision, Funding acquisition.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alemohammad, H., and Booth, K. (2020). Landcovernet: a global benchmark land cover classification training dataset. arXiv Prepr. arXiv:2012.03111. https://arxiv.org/abs/2012.03111.

Google Scholar

Ashtiani, F., Geers, A. J., and Aflatouni, F. (2021). An on-chip photonic deep neural network for image classification. Nature 606, 501–506. doi:10.1038/s41586-022-04714-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Azizi, S., Mustafa, B., Ryan, F., Beaver, Z., Freyberg, J., Deaton, J., et al. (2021). Big self-supervised models advance medical image classification. IEEE Int. Conf. Comput. Vis., 3458–3468. doi:10.1109/iccv48922.2021.00346

CrossRef Full Text | Google Scholar

Bazi, Y., Bashmal, L., Rahhal, M. M. A., Dayil, R. A., and Ajlan, N. A. (2021). Vision transformers for remote sensing image classification. Remote Sens. 13, 516. doi:10.3390/rs13030516

CrossRef Full Text | Google Scholar

Bhatt, A., and Bhatt, V. T. (2024). Dcrff-lhrf: an improvised methodology for efficient land-cover classification on eurosat dataset. Multimedia Tools Appl. 83, 54001–54025. doi:10.1007/s11042-023-17612-y

CrossRef Full Text | Google Scholar

Bhojanapalli, S., Chakrabarti, A., Glasner, D., Li, D., Unterthiner, T., and Veit, A. (2021). Understanding robustness of transformers for image classification. IEEE Int. Conf. Comput. Vis., 10211–10221. doi:10.1109/iccv48922.2021.01007

CrossRef Full Text | Google Scholar

Chen, C.-F., Fan, Q., and Panda, R. (2021a). Crossvit: cross-attention multi-scale vision transformer for image classification. IEEE Int. Conf. Comput. Vis., 347–356. doi:10.1109/iccv48922.2021.00041

CrossRef Full Text | Google Scholar

Chen, J., Lu, Y., Yu, Q., Luo, X., Adeli, E., Wang, Y., et al. (2021b). “Transunet: transformers make strong encoders for medical image segmentation,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 12093–12103.

Google Scholar

Chen, L., Li, S., Bai, Q., Yang, J., Jiang, S., and Miao, Y. (2021c). Review of image classification algorithms based on convolutional neural networks. Remote Sens. 13, 4712. doi:10.3390/rs13224712

CrossRef Full Text | Google Scholar

Chen, L., Wang, X., and Liu, Q. (2024). Advanced domain adaptation technique for object detection leveraging semi-automated dataset construction and enhanced yolov8. Remote Sens. Lett. 15, 289–301. Available online at: https://ieeexplore.ieee.org/abstract/document/10753164/.

Google Scholar

Chen, J., Cui, Q., and Ye, Y. (2025). 3d reconstruction and landscape restoration of garden landscapes: an innovative approach combining deep features and graph structures. Front. Environ. Sci. 13, 1556042. doi:10.3389/fenvs.2025.1556042

CrossRef Full Text | Google Scholar

Dai, Y., Gao, Y., and Liu, F. (2021). Transmed: transformers advance multi-modal medical image classification. Diagnostics 11, 1384. doi:10.3390/diagnostics11081384

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalvi, P. P., Edla, D. R., and Purushothama, B. (2023). Diagnosis of coronavirus disease from chest x-ray images using densenet-169 architecture. SN Comput. Sci. 4, 214. doi:10.1007/s42979-022-01627-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, H., Shi, L., and Tan, Q. (2024). A dual-band wide axial-ratio beamwidth circularly-polarized antenna with v-shaped slot for l2/l5 gnss applications. IEEE Antennas Wirel. Propag. Lett. 23, 589–593. Available online at: https://ieeexplore.ieee.org/abstract/document/10753263/.

Google Scholar

Dong, H., Zhang, L., and Zou, B. (2022). Exploring vision transformers for polarimetric sar image classification. IEEE Trans. Geoscience Remote Sens. 60, 1–15. doi:10.1109/tgrs.2021.3137383

CrossRef Full Text | Google Scholar

Feng, J., Tan, H., Li, W., and Xie, M. (2022). “Conv2next: reconsidering conv next network design for image recognition,” in 2022 international conference on computers and artificial intelligence technologies (CAIT) (IEEE), 53–60.

CrossRef Full Text | Google Scholar

Frost, G. V., Bhatt, U. S., Macander, M. J., Berner, L. T., Walker, D. A., Raynolds, M. K., et al. (2025). The changing face of the arctic: four decades of greening and implications for tundra ecosystems. Front. Environ. Sci. 13, 1525574. doi:10.3389/fenvs.2025.1525574

CrossRef Full Text | Google Scholar

Fu, K., Zhang, T., Zhang, Y., and Sun, X. (2021). Oscd: a one-shot conditional object detection framework. Neurocomputing 425, 243–255. doi:10.1016/j.neucom.2020.04.092

CrossRef Full Text | Google Scholar

He, B., Xu, C., and Lin, J. (2024). Novel deep learning domain adaptation approach for object detection using semi-self building dataset and modified yolov4. IEEE Access 12, 15478–15491. Available online at: https://www.mdpi.com/2032-6653/15/6/255.

Google Scholar

Hong, D., Gao, L., Yao, J., Zhang, B., Plaza, A., and Chanussot, J. (2020). Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geoscience Remote Sens. 59, 5966–5978. doi:10.1109/tgrs.2020.3015157

CrossRef Full Text | Google Scholar

Hong, D., Han, Z., Yao, J., Gao, L., Zhang, B., Chanussot, J., et al. (2021). Spectralformer: rethinking hyperspectral image classification with transformers. IEEE Trans. Geoscience Remote Sens. 60, 1–15. doi:10.1109/tgrs.2021.3130716

CrossRef Full Text | Google Scholar

Jarca, A., Croitoru, F.-A., and Ionescu, R. T. (2024). Cbm: curriculum by masking. arXiv preprint arXiv:2407.05193

Google Scholar

Khan, A., Zhou, M., and Rahman, K. (2020). Efficient vehicle detection and tracking strategy in aerial videos by employing morphological operations and feature points motion analysis. Multimedia Tools Appl. 79, 12215–12232. Available online at: https://ebooks.iospress.nl/pdf/doi/10.3233/FAIA240503.

Google Scholar

Kim, H. E., Cosa-Linan, A., Santhanam, N., Jannesari, M., Maros, M., and Ganslandt, T. (2022). Transfer learning for medical image classification: a literature review. BMC Medical Imaging.

Google Scholar

Koonce, B. (2021). “Efficientnet,” in Convolutional neural networks with swift for Tensorflow: image recognition and dataset categorization (Springer), 109–123.

Google Scholar

Li, B., Li, Y., and Eliceiri, K. (2020). Dual-stream multiple instance learning network for whole slide image classification with self-supervised contrastive learning. Comput. Vis. Pattern Recognit. Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Li_Dual-Stream_Multiple_Instance_Learning_Network_for_Whole_Slide_Image_Classification_CVPR_2021_paper.html.

Google Scholar

Li, Y., Zhang, K., and Wang, Y. (2025). Residual channel-attention (rca) network for remote sensing image scene classification. IEEE Trans. Geoscience Remote Sens. 63, 1–13. Available online at: https://link.springer.com/article/10.1007/s11042-024-20546-8.

Google Scholar

Liu, P., Lee, H. K., and Casazza, M. (2023a). Editorial: methods and applications in environmental informatics and remote sensing. Front. Environ. Sci. 11, 1255010. doi:10.3389/fenvs.2023.1255010

CrossRef Full Text | Google Scholar

Liu, P., Wang, L., and Li, J. (2023b). Unlocking the potential of explainable artificial intelligence in remote sensing big data. Remote Sens. 15, 5448. doi:10.3390/rs15235448

CrossRef Full Text | Google Scholar

Liu, P., Wang, L., Chen, J., and Cui, Y. (2024). Semiblind compressed sensing: a bidirectional-driven method for spatiotemporal fusion of remote sensing images. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 17, 19048–19066. doi:10.1109/jstars.2024.3463750

CrossRef Full Text | Google Scholar

Lv, Q., Wang, Q., Song, X., Ge, B., Guan, H., Lu, T., et al. (2024). Research on coastline extraction and dynamic change from remote sensing images based on deep learning. Front. Environ. Sci. 12, 1443512. doi:10.3389/fenvs.2024.1443512

CrossRef Full Text | Google Scholar

Mai, Z., Li, R., Jeong, J., Quispe, D., Kim, H. J., and Sanner, S. (2021). Online continual learning in image classification: an empirical survey. Neurocomputing 469, 28–51. doi:10.1016/j.neucom.2021.10.021

CrossRef Full Text | Google Scholar

Masana, M., Liu, X., Twardowski, B., Menta, M., Bagdanov, A. D., and van de Weijer, J. (2020). Class-incremental learning: survey and performance evaluation on image classification. IEEE Trans. Pattern Analysis Mach. Intell. 45, 5513–5533. doi:10.1109/tpami.2022.3213473

PubMed Abstract | CrossRef Full Text | Google Scholar

Mascarenhas, S., and l Agarwal, M. (2021). “A comparison between vgg16, vgg19 and resnet50 architecture frameworks for image classification,” in 2021 international conference on disruptive technologies for multi-disciplinary research and applications (CENTCON).

Google Scholar

Maurício, J., Domingues, I., and Bernardino, J. (2023). Comparing vision transformers and convolutional neural networks for image classification: a literature review. Appl. Sci.. doi:10.3390/app13095521

CrossRef Full Text | Google Scholar

Peng, J., Huang, Y., Sun, W., Chen, N., Ning, Y., and Du, Q. (2022). Domain adaptation in remote sensing image classification: a survey. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 15, 9842–9859. doi:10.1109/jstars.2022.3220875

CrossRef Full Text | Google Scholar

Rao, Y., Zhao, W., Zhu, Z., Lu, J., and Zhou, J. (2021). Global filter networks for image classification. Neural Inf. Process. Syst. doi:10.48550/arXiv.2107.00645

CrossRef Full Text | Google Scholar

Roy, S. K., Deria, A., Hong, D., Rasti, B., Plaza, A., and Chanussot, J. (2022). Multimodal fusion transformer for remote sensing image classification. IEEE Trans. Geoscience Remote Sens. 61, 1–20. doi:10.1109/tgrs.2023.3286826

CrossRef Full Text | Google Scholar

Sheykhmousa, M., Mahdianpari, M., Ghanbari, H., Mohammadimanesh, F., Ghamisi, P., and Homayouni, S. (2020). Support vector machine versus random forest for remote sensing image classification: a meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 13, 6308–6325. doi:10.1109/jstars.2020.3026724

CrossRef Full Text | Google Scholar

Sumbul, G., De Wall, A., Kreuziger, T., Marcelino, F., Costa, H., Benevides, P., et al. (2021). Bigearthnet-mm: a large-scale, multimodal, multilabel benchmark archive for remote sensing image classification and retrieval [software and data sets]. IEEE Geoscience Remote Sens. Mag. 9, 174–180. doi:10.1109/mgrs.2021.3089174

CrossRef Full Text | Google Scholar

Sun, L., Zhao, G., Zheng, Y., and Wu, Z. (2022). Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geoscience Remote Sens. 60, 1–14. doi:10.1109/tgrs.2022.3144158

CrossRef Full Text | Google Scholar

Tanaka, H., Yamamoto, S., and Okada, Y. (2023). Detection of earthquake-induced building damages using remote sensing data and deep learning: a case study of mashiki town, Japan. ISPRS J. Photogrammetry Remote Sens. 197, 75–89. https://ieeexplore.ieee.org/abstract/document/10282550/.

Google Scholar

Taori, R., Dave, A., Shankar, V., Carlini, N., Recht, B., and Schmidt, L. (2020). Measuring robustness to natural distribution shifts in image classification. Neural Inf. Process. Syst. Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Li_Dual-Stream_Multiple_Instance_Learning_Network_for_Whole_Slide_Image_Classification_CVPR_2021_paper.html.

Google Scholar

Theckedath, D., and Sedamkar, R. (2020). Detecting affect states using vgg16, resnet50 and se-resnet50 networks. SN Comput. Sci. 1, 79. doi:10.1007/s42979-020-0114-9

CrossRef Full Text | Google Scholar

Tian, Y., Wang, Y., Krishnan, D., Tenenbaum, J., and Isola, P. (2020). Rethinking few-shot image classification: a good embedding is all you need? Eur. Conf. Comput. Vis., 266–282. doi:10.1007/978-3-030-58568-6_16

CrossRef Full Text | Google Scholar

Touvron, H., Bojanowski, P., Caron, M., Cord, M., El-Nouby, A., Grave, E., et al. (2021). Resmlp: feedforward networks for image classification with data-efficient training. IEEE Trans. Pattern Analysis Mach. Intell. 45, 5314–5321. doi:10.1109/tpami.2022.3206148

PubMed Abstract | CrossRef Full Text | Google Scholar

Touvron, H., Cord, M., and Jégou, H. (2022). “Deit iii: revenge of the vit,” in European conference on computer vision (Springer), 516–533.

Google Scholar

Wang, X., Yang, S., Zhang, J., Wang, M., Zhang, J., Yang, W., et al. (2022). Transformer-based unsupervised contrastive learning for histopathological image classification. Med. Image Anal. 81, 102559. doi:10.1016/j.media.2022.102559

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Liu, R., and Zhang, P. (2024). Multiband circularly-polarized stacked elliptical patch antenna with eye-shaped slot for gnss applications. Microw. Opt. Technol. Lett. 66, 312–319. Available online at: https://www.cambridge.org/core/journals/international-journal-of-microwave-and-wireless-technologies/article/multiband-circularlypolarized-stacked-elliptical-patch-antenna-with-eyeshaped-slot-for-gnss-applications/E6EA5D3F6151BA82193FFC638188AB7A.

Google Scholar

Xiao, L., Yang, X., Peng, F., Yan, M., Wang, Y., and Xu, C. (2023). Clip-vg: self-paced curriculum adapting of clip for visual grounding. IEEE Trans. Multimedia 26, 4334–4347. doi:10.1109/tmm.2023.3321501

CrossRef Full Text | Google Scholar

Yang, J., Shi, R., Wei, D., Liu, Z., Zhao, L., Ke, B., et al. (2021). Medmnist v2 - a large-scale lightweight benchmark for 2d and 3d biomedical image classification. Sci. Data 10, 41. doi:10.1038/s41597-022-01721-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Cai, Y., Lin, G., and Shen, C. (2020). Deepemd: few-shot image classification with differentiable earth mover’s distance and structured classifiers. Comput. Vis. Pattern Recognit., 12200–12210. doi:10.1109/cvpr42600.2020.01222

CrossRef Full Text | Google Scholar

Zhang, Y., Li, W., Sun, W., Tao, R., and Du, Q. (2022). Single-source domain expansion network for cross-scene hyperspectral image classification. IEEE Trans. Image Process. 32, 1498–1512. doi:10.1109/tip.2023.3243853

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, F., Chen, W., and Yang, M. (2022). A wide axial-ratio beamwidth circularly-polarized oval patch antenna with sunlight-shaped slots for gnss and wimax applications. Int. J. RF Microw. Computer-Aided Eng. 32, e23029. Available online at: https://link.springer.com/article/10.1007/s11276-022-03093-8.

Google Scholar

Zhao, Y., Gong, M., Zhang, M., Qin, A., Jiang, F., and Li, J. (2025). Spcnet: deep self-paced curriculum network incorporated with inductive bias. IEEE Trans. Neural Netw. Learn. Syst., 1–14. doi:10.1109/tnnls.2025.3544724

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, X., Sun, H., Lu, X., and Xie, W. (2022). Rotation-invariant attention network for hyperspectral image classification. IEEE Trans. Image Process. 31, 4251–4265. doi:10.1109/tip.2022.3177322

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Zhuang, F., Wang, J., Ke, G., Chen, J., Bian, J., et al. (2020). Deep subdomain adaptation network for image classification. IEEE Trans. Neural Netw. Learn. Syst. 32, 1713–1722. doi:10.1109/tnnls.2020.2988928

PubMed Abstract | CrossRef Full Text | Google Scholar