An intelligent decision-making framework for territorial spatial layout coupling simulation and optimization: a case study of Hui’an County

Introduction: The primary challenge in territorial spatial planning is optimizing land allocation under complex constraints. This study aims to bridge the gap between predictive simulation and normative optimization to support scientific planning.

Methods: This study developed an intelligent framework coupling an Artificial Neural Network-Cellular Automata (ANN-CA) model with a Multi-Agent System (MAS) based on an ant colony algorithm. Applied to Hui’an County, China, the framework first simulates a 2035 baseline land use scenario under policy and physical constraints. Subsequently, the MAS optimizes the construction land layout based on multi-objective functions for economic, ecological, and morphological goals.

Results: The optimization yielded significant quantitative improvements compared to the baseline scenario. The spatial configuration of construction land became more regular, with the Area-Weighted Mean Shape Index (AWMSI) decreasing by 35.7% from 79.44 to 51.11. The layout also became more compact and less fragmented, evidenced by a 1.0% increase in the Aggregation Index (AI) to 95.03 and a 27.1% reduction in the number of patches.

Discussion: This integrated framework provides an effective technical pathway for scientific planning. By coupling simulation with optimization, it ensures that future development patterns are not only efficient and responsive to historical trends but also adhere to strict ecological and farmland protection policies, leading to a more sustainable and well-structured territorial spatial layout.

1 Introduction

Territorial space serves as the fundamental material foundation for national development and ecological security, making its scientific planning and sustainable utilization central to achieving high-quality regional development. China currently experiences profound economic and social transformation alongside deepening ecological civilization construction. Rapid urbanization processes, while driving economic growth, simultaneously generate complex challenges including disorderly construction land expansion, continuous loss of prime agricultural resources, degradation of ecosystem service functions, and imbalanced urban-rural regional development patterns (Chen et al., 2020; Liu et al., 2014a). To systematically address these issues, national strategic deployment has established unified and coordinated territorial spatial planning systems, emphasizing resource and environmental carrying capacity as the foundation while strictly delineating and adhering to “three control lines”: ecological protection redlines, permanent basic farmland boundaries, and urban development boundaries (Wang et al., 2018; Zhang et al., 2019).

This strategic framework aims to optimize territorial spatial development and protection patterns, promoting the formation of new territorial spatial configurations characterized by intensive and efficient production spaces, livable and moderate living spaces, and pristine ecological spaces (Li et al., 2014). Within this macroscopic context, employing advanced theoretical and technical methodologies to scientifically predict future territorial spatial evolution trends while proactively guiding land use patterns toward more intensive, efficient, coordinated, and sustainable directions represents a critical scientific problem and core technological bottleneck requiring resolution in territorial spatial planning domains (Wu et al., 2011).

Contemporary research in Land Use and Land Cover Change (LUCC) simulation and spatial optimization has achieved remarkable progress. In LUCC simulation domains, spatial dynamic simulation methods represented by Cellular Automata (CA) models, particularly hybrid models combining machine learning algorithms such as Artificial Neural Networks (ANN-CA), effectively extract complex driving mechanisms of land use change and predict future spatial patterns (Gharbia et al., 2016; Aburas et al., 2016; Guan et al., 2005). However, these simulation models fundamentally emphasize “predictive” or “descriptive” approaches, projecting the most probable future states based on historical patterns, while demonstrating insufficient capacity for proactively shaping spaces to achieve “normative” target states desired by planning initiatives (Verburg et al., 2019; Li and Liu, 2008).

Alternatively, land use spatial optimization research, particularly methodologies employing heuristic intelligent optimization algorithms such as Ant Colony Optimization (ACO) and Genetic Algorithms (GA), can solve complex spatial layout problems under multi-objective and strong constraint conditions (Aerts et al., 2003; Stewart et al., 2004; Santé et al., 2010). Nevertheless, these optimization studies frequently operate disconnected from dynamic land use evolution processes, either optimizing based on static current data or adopting simplified future scenario configurations, potentially resulting in optimization schemes that demonstrate mathematical excellence but lack sufficient feasibility foundations in reality or inadequately address future development pressures (Ligmann-Zielinska et al., 2008; Cao et al., 2012; Haque and Asami, 2014).

Addressing the existing gap between predictive simulation and normative optimization in contemporary research, alongside challenges of insufficient integration of planning intentions within complex technical processes, this study endeavors to construct and empirically validate an intelligent decision-making framework coupling ANN-CA predictive simulation with ant colony algorithm-based MAS normative optimization for territorial spatial layout planning. The framework’s core concept involves generating future land use baseline scenarios that reflect historical trends while embedding planning strategic intentions through ANN-CA models that deeply integrate territorial spatial planning core control elements including “dual evaluation” results as guiding factors and “three control lines” as rigid spatial constraints (Zhou et al., 2017).

Subsequently, utilizing baseline scenarios as foundations (for example, employing simulation-derived suitability probabilities as heuristic information or using simulated layouts as optimization initial solutions), the framework applies MAS multi-objective optimization models that explicitly introduce quantitative pursuit of key planning objectives such as spatial morphology (including layout aggregation and regularity). Through simulating ant colony intelligent agent self- organization optimization processes, the framework explores and generates spatial layout schemes with superior comprehensive benefits across economic, ecological, and morphological dimensions while satisfying multiple constraint conditions (Liu et al., 2017).

This research aims to construct and empirically apply this integrated framework through Hui’an County, Fujian Province case study, exploring novel technical pathways that tightly combine scientific prediction with proactive optimization to effectively support complex territorial spatial planning decisions. Through comprehensive spatial pattern comparison and quantitative landscape index analysis between simulated baseline scenarios and MAS-optimized scenarios, the study objectively evaluates the integrated framework’s practical effectiveness and unique value in enhancing territorial spatial layout quality and strengthening planning scientificity. Research outcomes expect to provide beneficial methodological support and case references for territorial spatial planning theoretical innovation and intelligent transformation of practical applications.

2 Methodology

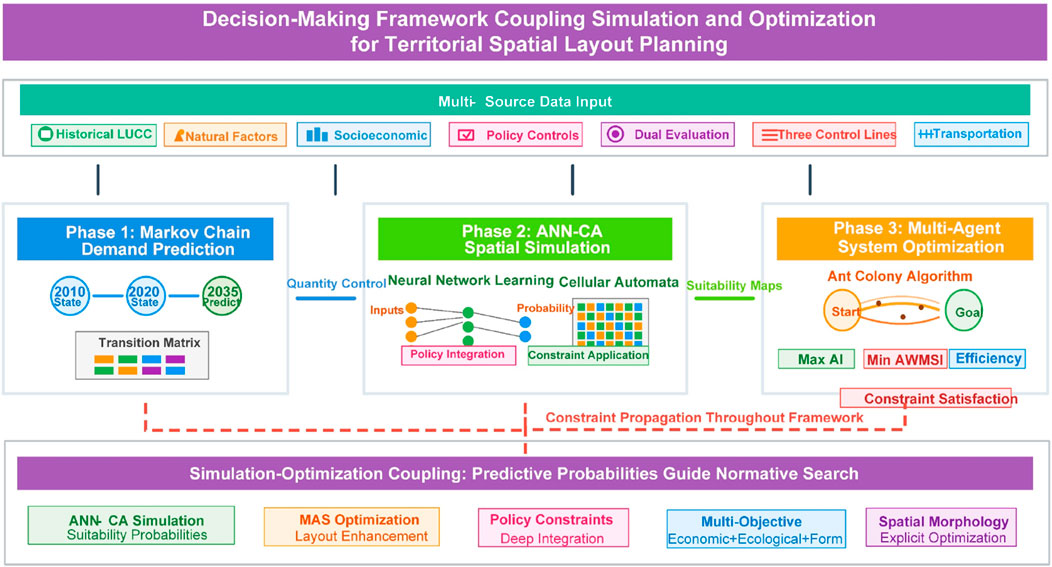
This study’s core involves constructing an intelligent decision-making framework integrating land use demand prediction, constrained spatial simulation, and multi-objective layout optimization phases (Figure 1). The framework incorporates dynamic feedback mechanisms where optimization results inform subsequent simulation iterations, creating an adaptive planning support system., aiming to provide more scientific, efficient, and objective-oriented solutions for territorial spatial planning through organic coupling of predictive simulation and normative optimization technical approaches.

Figure 1

Figure 1. Method framework.

2.1 Overall technical framework

The integrated framework follows a logically progressive technical workflow comprising three sequential stages. The initial stage utilizes Markov chain models to predict total demand for various land use types, particularly construction land, for target years based on historical land use transition patterns, establishing total quantity controls for subsequent spatial allocation (Burnham, 1973; Baker, 1989). The secondary stage constructs ANN-CA models to generate target year land use baseline scenarios, with critical emphasis on deeply integrating planning constraints: ANN training incorporates not only conventional driving factors such as topography, location, and socioeconomic variables, but also innovatively includes quantified “dual evaluation” results as policy guidance inputs; CA transition rules designate “three control lines” spatial control areas as construction land prohibition zones while comprehensively considering neighborhood effects and transition costs (Pijanowski et al., 2002; Li and Yeh, 2002). ANN learns driving mechanisms and outputs development suitability probabilities for different land use types across spatial units, while CA conducts spatial allocation under probability guidance combined with constraints and total quantity objectives. The tertiary stage employs ant colony algorithm-based MAS models to optimize construction land layouts generated in the secondary stage. The key coupling mechanism utilizes ANN-CA simulation suitability probabilities as MAS heuristic information, with optional use of simulated layouts as initial solutions. Optimization objective functions aim to maximize comprehensive evaluation values incorporating economic efficiency (minimizing average distance to urban centers), ecological protection (minimizing encroachment on sensitive areas), social equity (maximizing accessibility to public facilities), and spatial morphology optimization including maximizing Aggregation Index (AI) and minimizing Area-Weighted Mean Shape Index (AWMSI).

Optimization processes strictly adhere to constraint conditions including total quantity constraints requiring optimized construction land total area to approximate Markov-predicted demand quantities, and spatial control hard constraints prohibiting construction land encroachment upon “three control lines” designated prohibition zones. Through simulating ant colony iterative search and pheromone updating mechanisms, the framework identifies layout schemes satisfying constraints while achieving optimal comprehensive objectives. The framework incorporates iterative feedback loops where optimization results update simulation parameters for subsequent planning cycles, enabling adaptive planning responses to changing conditions.

2.2 Markov chain demand prediction

The Markov chain approach for predicting future land use quantities involves several sequential steps and mathematical formulations. Markov chains represent stochastic processes without aftereffects, predicting future system development based on state transition probabilities that reflect inherent regularities between system states (Muller and Middleton, 1994; López et al., 2001). Land use types (such as cropland, forest land, construction land) are defined as Markov chain state sets S ={s1,s2,sn} Historical data constructs state transition probability matrix P, where Pᵢⱼ represents transition probability from state sᵢ to state sⱼ, satisfying (Equation 1):

$P=\left|\begin{array}{ccc}{p}_{11}& p_{12}& \begin{array}{cc}\cdots & p_{1n}\end{array}\\ p_{21}& p_{22}& \begin{array}{cc}\cdots & p_{2n}\end{array}\\ \begin{array}{c}\cdots \\ p_{n1}\end{array}& \begin{array}{c}\cdots \\ p_{n2}\end{array}& \begin{array}{cc}\begin{array}{c}\cdots \\ p_{n3}\end{array}& \begin{array}{c}\cdots \\ p_{nn}\end{array}\end{array}\end{array}\right|,{\displaystyle \sum _{j=1}^n}{p}_{ij}=1(1)$

Initial state vector X₀ = [x₁, x₂, x_n] is determined from historical data, where xᵢ represents initial proportion of land type i. Future land use states are predicted using Markov chain state transition formulas (Equation 2):

$X_{t+1}=X_t*P(2)$

where X_t represents state vector at time t, and P represents state transition matrix. Through iterative calculations repeated until reaching target year T, final state vector X_t represents land use type proportions for target years. Combined with regional total land area A, individual land use type quantities are calculated as (Equation 3):

$Q_i=x_i*A(3)$

where Qᵢ represents area of land type i. This methodology quantifies land use dynamic changes, suitable for short-term prediction and stable system states, providing scientific foundations for land management and planning (Adhikari and Southworth, 2012; Guan et al., 2011).

2.3 Constrained ANN-CA simulation

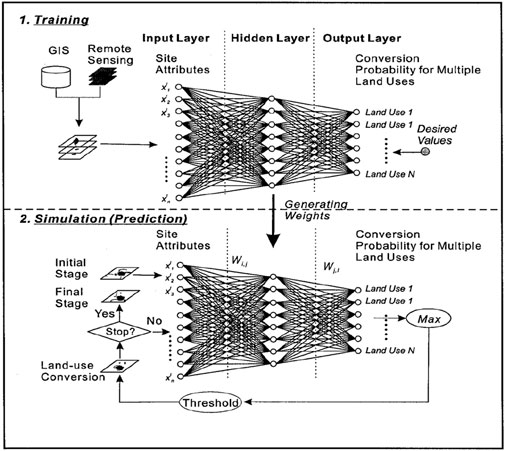
Artificial Neural Network-Cellular Automata (ANN-CA) models conduct spatial simulation of land use coverage conditions through historical land use coverage type expansion results under various driving factors to extract inherent driving evolution mechanisms, utilizing these mechanisms to predict future land use coverage within specific time periods (Figure 2). ANN-CA represents machine learning models based on biological neural network simulation, comprising input layers, hidden layers, and output layers, typically employed for simulating and calculating nonlinear functions with multiple variables through extensive learning and recall iterations to continuously fit complex relationships between input data and training targets (Pijanowski et al., 2014; Almeida et al., 2008).

Figure 2

Figure 2. Framework of the constrained ANN-CA simulation model.

The training phase involves expansion mechanism extraction and identification based on Artificial Neural Networks (ANN). The ANN learning process establishes relationships between driving factors and land use change probabilities through backpropagation algorithms. For each spatial unit p at time t, the probability P (p,k,t) of developing land use type k is calculated as (Equation 4):

$p\left(p,k,t\right)={\displaystyle \sum _j}{w}_{j,k}\times sigmoid\left({net}_j\left(p,t\right)\right)(4)$

$sigmoid\left({net}_j\left(p,t\right)\right)=\frac{1}{1+e^{-{net}_j\left(p,t\right)}}(5)$

${net}_j\left(p,t\right)={\displaystyle \sum _i}{w}_{i,j}\times x_i\left(p,t\right)(6)$

Where $w_{i,j}$ represents adaptive weights between hidden and output layers; $sigmoid\left({net}_j\left(p,t\right)\right)$ represents association functions between hidden and output layers (Equation 5); net_j (p, t) represents signals transmitted from input layer grid p to neuron j at time t (Equation 6), indicating change intensity of grid p in land type j at time t. The network architecture incorporates multiple driving factors including topographical variables (elevation, slope), climatic conditions (precipitation, temperature), socioeconomic factors (population density, GDP density), accessibility measures (distances to transportation networks, public facilities), and crucially, planning policy factors derived from “dual evaluation” results (ecological protection importance, agricultural production suitability, urban construction suitability).

The prediction simulation phase employs ANN-CA model prediction simulation mechanisms. Following ANN training completion, the model predicts land use change probabilities for future time periods. The CA component then allocates land use changes spatially based on these probabilities, neighborhood effects, and constraint conditions. The transition probability for each cell calculated as (Equation 7):

$\mathrm{P}\left(k,t,l\right)=\left({1+\left(-\ln \gamma \right)}^{\alpha }\right)\times P_{ann}\left(k,t,l\right)\times {\mathrm{\Omega }}_k^t\times \text{co}\mathrm{n}\left(S_k^t\right)(7)$

Where the random factor $\left({1+\left(-\ln \gamma \right)}^{\alpha }\right)$ introduces stochastic variability to simulate real-world uncertainties in land use transitions, following the theoretical framework established by White and Engelen (1993) for incorporating randomness in cellular automata models. The parameter α controls the magnitude of random perturbation, with α = 1 providing moderate stochasticity based on calibration studies. This formulation ensures that transition probabilities remain positive while introducing sufficient variability to capture unpredictable development decisions and policy changes that influence land use patterns; P_ann (k,t,l) represents transition probabilities calculated using trained artificial neural networks; fi_k^t represents urban land density within defined neighborhood windows (total urban land cells/total neighborhood window grids); ${\mathrm{\Omega }}_k^t$ represents urban land density within a defined 3 × 3 neighborhood window (covering 9 cells centered on the target cell), calculated as the ratio of urban land cells to total cells within this window. con (S_k^t) represents conversion suitability between land use types, with values of 1 and 0 representing convertible and non-convertible respectively. The model incorporates “three control lines” as absolute constraints, preventing construction land development within ecological protection redlines, permanent basic farmland, and important water areas (Wang et al., 2022; Li et al., 2017).

2.4 Multi-agent system optimization

Following acquisition of baseline scenarios reflecting future trends but requiring spatial structure improvement, this study introduces ant colony algorithm-based Multi-Agent Systems (MAS) for intelligent optimization of construction land layouts. MAS simulates collaborative search behaviors of numerous “ant” intelligent agents to identify multi-objective optimal solutions while satisfying constraint conditions (Dorigo et al., 1996). In this framework, each individual ant agent constructs a complete spatial layout solution by sequentially selecting grid cells for construction land development. Starting from randomly assigned initial positions, each ant builds a comprehensive territorial layout by probabilistically choosing cells based on pheromone trails and heuristic information until the total construction land demand is satisfied. This approach ensures that each ant generates a feasible complete solution that can be evaluated and compared within the optimization process.

MAS core principles involve ants making probabilistic selections based on pheromone trails and heuristic information. Specifically, state transition probability $p_{ij}^k$, representing ant k’s probability of selecting next position j from position i, is expressed as (Equation 8):

$p_{ij}^k=\left\{\begin{array}{l}\frac{{\tau }_{ij}^{\alpha }\left(t\right){\mathrm{\eta }}_{ij}^{\beta }\left(t\right)}{{\displaystyle {\sum }_{s\in {allowed}_k}}{\tau }_{is}^{\alpha }\left(t\right){\mathrm{\eta }}_{is}^{\beta }\left(t\right)},j\in {allowed}_k\\ 0,others\end{array}\right.(8)$

Where τᵢⱼ represents pheromone quantity on edge (i,j); α represents pheromone heuristic factor indicating trail relative importance during path searching; ηᵢⱼ represents heuristic factor reflecting ant transition encouragement from city i to city j; β represents expected heuristic factor indicating node visibility relative importance, assisting ant next node selection through current and next node distance assessment; allowed_k represents grids ant k can subsequently select (Dorigo and Gambardella, 2002).

This framework’s key coupling mechanism involves constructing heuristic information, utilizing ANN-CA derived target land type (construction land) development suitability probabilities P_ann(j) for each grid unit as core foundations for calculating heuristic information ηⱼ (for example, setting ηⱼ = P_ann(j)). This design enables ant initial search behaviors to possess scientifically simulated guidance, effectively focusing on high-potential areas. Optimization objective function F(X) aims to maximize comprehensive evaluation values through weighted summation of multiple sub-objectives (Equation 9):

$F\left(X\right)=\mathrm{\Sigma }{w}_i{f}_i\left(X\right)(9)$

where wᵢ represents weights and fᵢ(X) represents sub-objective function evaluation values for layout scheme X. Sub-objectives include: (1) Economic efficiency f₁(X) = -∑dᵢ/n, where dᵢ represents distance from development cell i to nearest urban center and n is total number of cells, minimizing average distance to urban centers; (2) Ecological protection f₂(X) = -∑eᵢ, where eᵢ represents ecological impact score for cell i based on proximity to sensitive areas; (3) Social equity f₃(X) = ∑aᵢ, where aᵢ represents accessibility score to public facilities for cell i; and (4) Spatial morphology optimization f₄(X) combining maximized Aggregation Index (AI) and minimized Area-Weighted Mean Shape Index (AWMSI) through f₄(X) = AI(X) - AWMSI(X)/100.

Optimization processes strictly adhere to constraint conditions, primarily including: 1) Total quantity constraints requiring optimized construction land total area to approximate Markov-predicted demand quantities; 2) Spatial control hard constraints prohibiting construction land encroachment upon “three control lines” designated legal prohibition zones. Pheromone updating follows evaporation and enhancement mechanisms. Evaporation processes involve (Equation 10):

${\tau }_j\left(t+1\right)=\left(1-\rho \right)\times {\tau }_j\left(t\right)(10)$

where ρ represents evaporation coefficient. Enhancement processes depend on current round ant construction scheme fitness $F\left(X_k\right)$, adding pheromone Δτⱼ to selected grids (Equation 11):

$∆{\tau }_j=\mathrm{Q}\times F\left(X_k\right)(11)$

where Q represents a constant controlling total pheromone release quantities. If grid j belongs to optimal schemes obtained after all ants complete first round movements, pheromone increases by Δτⱼ; otherwise Δτⱼ = 0. This iterative process of “scheme construction - fitness evaluation - pheromone updating” continues through multiple rounds until reaching preset maximum iteration numbers or algorithm convergence conditions, ultimately outputting global optimal layout schemes recorded throughout iteration processes (Merkle et al., 2002; Dorigo and Stützle, 2018).

3 Study area and data

3.1 Study area

This research selects Hui’an County, administered by Quanzhou City, Fujian Province, as the case study region (Figure 3). Hui’an County is located on China’s southeastern coast with terrestrial area of approximately 525.71 square kilometers. The region demonstrates remarkable economic development vitality (2020 GDP exceeding 100 billion RMB), relatively dense population (2020 permanent population approximately 780,000), while its urbanization rate (approximately 57.9% in 2020) remains below provincial and municipal average levels, indicating continued urbanization development demands and corresponding construction land expansion pressures.

Figure 3

Figure 3. Location and land use pattern of the study area in Hui’an County, Fujian Province.

Hui’an County possesses “three mountains and five bays” natural ecological foundations but confronts typical contradictions between development demands and cropland protection and ecological conservation during rapid development processes. This complexity of development stages, resource endowments, and planning challenges makes Hui’an County an ideal and representative practical scenario for testing and applying the coupled simulation and optimization framework proposed in this research. The study area exhibits predominant land use patterns of agricultural land, forest land, and construction land as of 2020, with spatial distribution reflecting typical southeastern coastal development characteristics.

3.2 Data sources and preprocessing

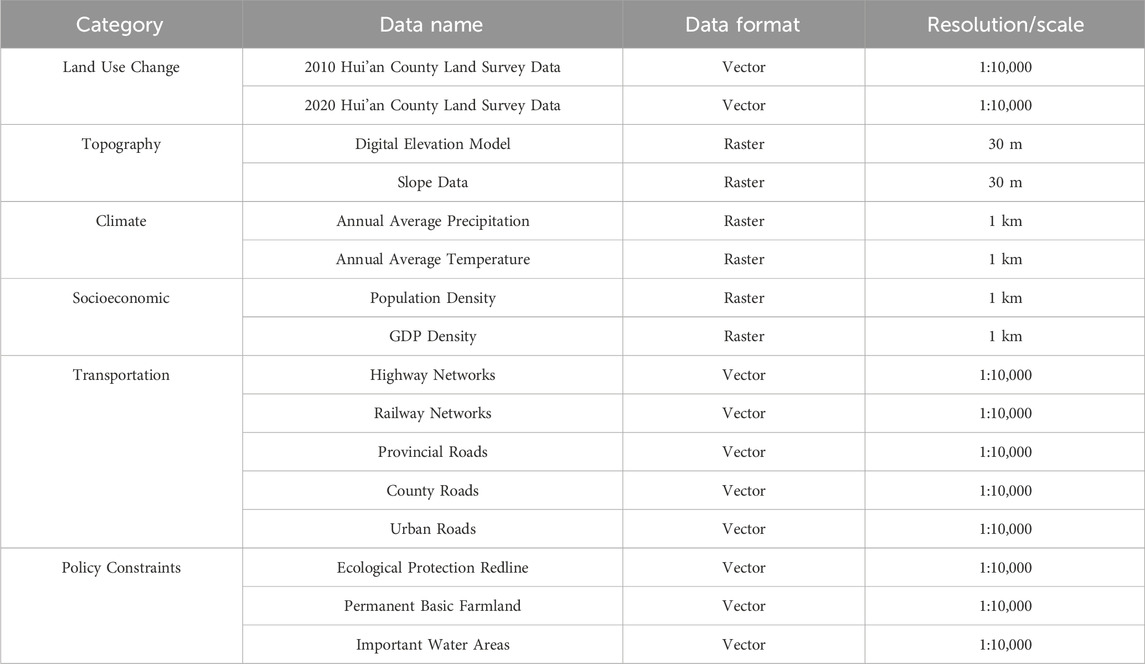
To support simulation and optimization model construction, multi-source spatial and attribute data covering Hui’an County’s entire territory were collected and processed (Table 1). Core land use data originated from official national land survey vector databases for 2010, 2015, and 2020 time points. To ensure analytical consistency, original land classifications were uniformly reclassified into 9 primary categories: cropland, plantation land, forest land, grassland, wetland, other agricultural land, construction land, water areas, and unused land, with all data converted to 10-m spatial resolution raster format.

Table 1

Table 1. Data sources and specifications used in the study.

Driving factor data primarily include: natural geographical data such as elevation and slope information extracted from 30-m DEM and resampled to 10-m resolution, plus annual average precipitation and temperature data resampled to 10-m resolution; socioeconomic data including spatially processed population density and GDP density grid data unified to 10-m resolution; infrastructure and locational accessibility data covering vector location information for various road grades, railways (including stations), major public service facilities (schools, hospitals), and administrative centers. Through calculating Euclidean distances from each grid cell to these elements, a series of 10-m resolution accessibility layers were generated.

Particularly critical is the integration of planning policy and control data. Official “dual evaluation” result maps compiled by Hui’an County were obtained, including ecological protection importance evaluation (Figure 4a), agricultural production suitability evaluation (Figure 4b), and urban construction suitability evaluation (Figure 4c). These evaluation results were quantitatively processed as guiding factors for model input. Simultaneously, “three control lines” vector boundary data were collected (Figure 4d), representing spatial extents of ecological protection redlines, permanent basic farmland, and important water areas, serving as mandatory spatial constraints in models.

Figure 4

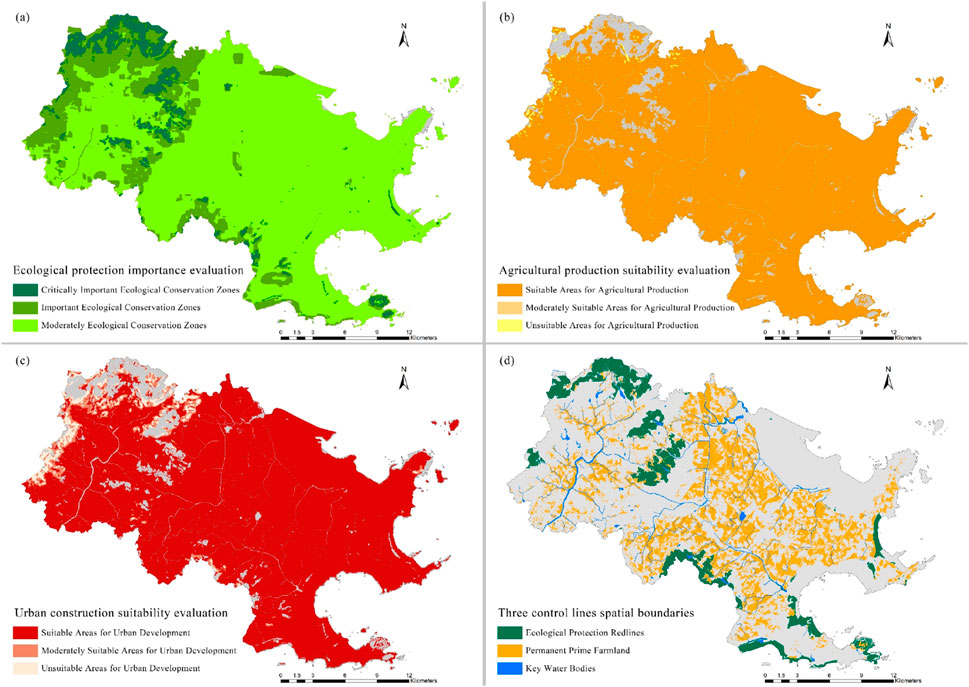
Figure 4. Spatial distribution of key planning constraint factors: (a) Ecological protection importance evaluation, (b) Agricultural production suitability evaluation, (c) Urban construction suitability evaluation, (d) Three control lines spatial boundaries.

All collected spatial data underwent rigorous preprocessing, including unification to CGCS2000 geodetic coordinate system with corresponding Gauss-Kruger projection, precise clipping to Hui’an County administrative boundaries, and ensuring 10-m spatial resolution uniformity. All continuous driving factor raster layers were normalized using min-max methods within 0–1 intervals before ANN model input to eliminate dimensional differences and ensure model training stability and result reliability. Through these procedures, a multidimensional, high-precision, spatiotemporally consistent comprehensive geographic information database was constructed, establishing robust data foundations for subsequent simulation and optimization.

4 Results

4.1 Historical evolution and future demand analysis

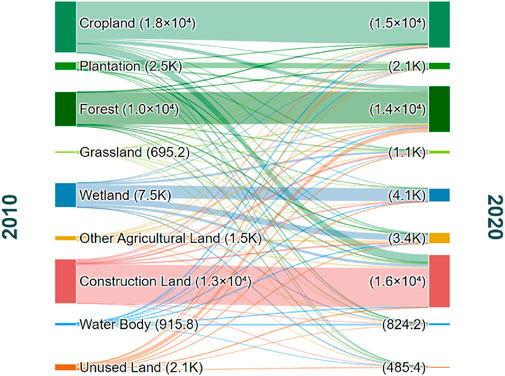
To ensure subsequent simulation and optimization realism and scientificity, this research initially extracted study area historical evolution patterns and predicted future land use demands. Analysis of 2010–2020 land use data revealed significant structural and spatial changes in the study region (Figure 5). Quantitatively, construction land represented the most remarkable expansion type, with total area increasing from 13,459.24 ha to 16,196.30 ha, achieving net increase of 2,737.06 ha over 10 years with relative growth of 20.3%. Contrasting sharply, cropland and wetland resources confronted severe loss pressures, with areas decreasing from 17,977.30 ha to 7,488.85 ha to 15,015.17 ha and 4,168.12 ha respectively, representing net reductions of 2,962.13 ha and 3,320.74 ha.

Figure 5

Figure 5. Land use transition for Hui’an County (2010–2020).

Land use transition matrix analysis further revealed that construction land expansion primarily occurred at the expense of premium cropland, with direct cropland-to-construction land conversion reaching 2,311.29 ha, accounting for 84.4% of total construction land increment. Spatially, construction land expansion during this period exhibited highly irregular characteristics. Area- Weighted Mean Shape Index (AWMSI), a key indicator measuring patch shape complexity, increased dramatically from 48.21 in 2010 to 67.66 in 2020. This substantial numerical increase unequivocally quantified the highly irregular and complex geometric morphology of newly added construction land patches over the decade, presenting typical sprawling and inefficient spatial growth patterns. Historical trends exposing spatial morphology problems constitute core challenges requiring attention and improvement in this research.

Based on these foundations, Markov chain models predicted 2035 land use total demand, establishing critical macroscopic constraints for subsequent spatial allocation. Model results indicated that under continued historical development trends, Hui’an County’s construction land total demand is projected to reach 18,836.30 ha by 2035. This value serves as a construction land total quantity control objective that must be strictly adhered to during ANN-CA simulation and MAS optimization processes, ensuring spatial layout scheme feasibility and compliance at macroscopic scales.

4.2 Baseline scenario simulation and spatial assessment

Before generating the 2035 baseline scenario, the ANN-CA model underwent rigorous validation to ensure prediction reliability. Using the temporal validation approach, the model achieved satisfactory performance with an Overall Accuracy of 87.3%, indicating that the model correctly predicted land use types for 87.3% of all cells. The Kappa coefficient reached 0.821, demonstrating substantial agreement between simulated and observed land use changes beyond what would be expected by chance. The Figure of Merit (FoM) achieved 0.164, which represents acceptable performance for territorial spatial planning applications, as FoM values above 0.1 are generally considered satisfactory for policy-relevant land use modeling. These validation metrics provide confidence in the model’s capability to generate reliable 2035 projections for subsequent optimization processes.

The ANN-CA model incorporated 30 input factors, generating 2035 potential distribution maps for various land use types (Figure 6). Construction land areas distributed primarily around main urban areas, transportation corridors, and suitable zones, while low-potential areas located in ecologically sensitive or unsuitable regions. Under “three control lines” hard constraints, simulation generated macroscopically compliant and legally conforming baseline spatial patterns with construction land totaling approximately 18,836 ha as predicted.

Figure 6

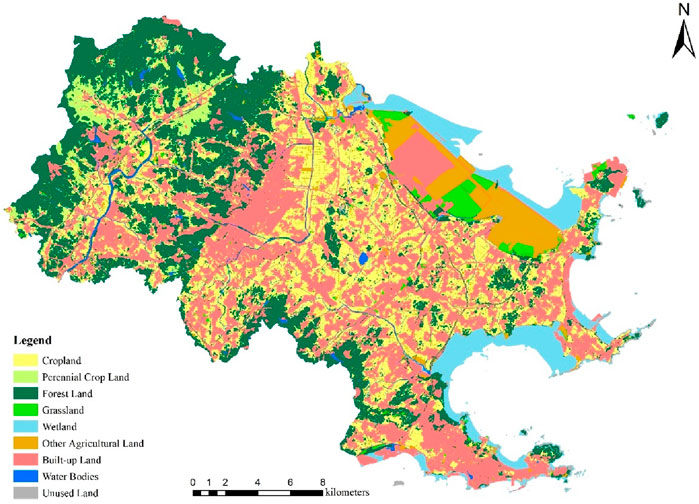
Figure 6. Simulation results for the 2035 land use baseline scenario and the MAS-optimized scenario.

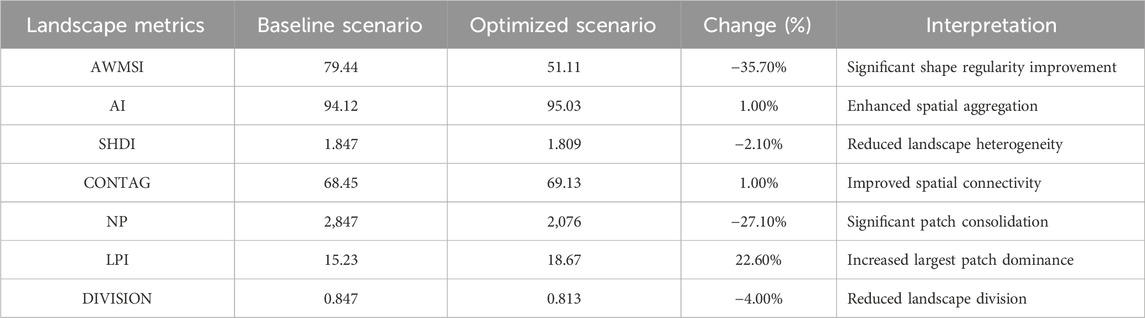
Spatial morphology analysis revealed continued manifestation of edge sprawl, corridor infilling, and scattered enclave phenomena representing inefficient expansion patterns. The baseline scenario exhibited AWMSI increasing to 79.44, indicating exceptionally irregular spatial configuration, while Aggregation Index (AI) reached 94.12. These metrics quantitatively demonstrated that simulated future construction land layouts, while meeting total quantity requirements and regulatory compliance, still possessed substantial room for spatial efficiency and morphological optimization improvement.

Detailed spatial pattern analysis identified several characteristic features of the baseline scenario. Construction land expansion followed historical trends with significant sprawling development along major transportation arteries, creating linear development corridors with low density and inefficient land utilization. Scattered development patches appeared throughout the study area, particularly in periphery regions, resulting in fragmented spatial structures and increased infrastructure provision costs. The baseline scenario also demonstrated insufficient consideration of spatial compactness principles, with new development areas often disconnected from existing urban centers, potentially exacerbating urban sprawl issues and reducing overall spatial efficiency.

4.3 MAS spatial optimization and comparative analysis

Based on ant colony MAS models, construction land spatial layouts underwent multi-objective optimization using baseline suitability probabilities as heuristic guidance while strictly maintaining total quantity and spatial control constraints. Optimization significantly enhanced spatial layout quality across multiple dimensions. Scattered outlying patches were consolidated, effectively achieving “inward infilling” and compact cluster development. AI aggregation degree improved to 95.03, while AWMSI experienced dramatic reduction to 51.11, representing a 35.7% decrease and indicating substantially improved morphological regularity.

Landscape heterogeneity and fragmentation significantly decreased, with Shannon Diversity Index (SHDI) declining 2.1% and Contagion Index (CONTAG) increasing 1%. Total patch numbers (NP) decreased 27.1%, demonstrating successful consolidation of scattered development patterns. Detailed quantitative comparisons of all landscape metrics between baseline and optimized scenarios are presented in Table 2, which comprehensively demonstrates the substantial improvements achieved through the MAS optimization process. Analysis revealed optimization contributions to infrastructure efficiency, land use efficiency, ecological buffering, and urban boundary clarity enhancement. Economic efficiency analysis demonstrated that optimized layouts reduced average distances to urban centers by 12.3%, achieved through the economic efficiency objective function f₁(X) that explicitly minimized transportation costs and improved accessibility to employment opportunities and services. Ecological impact assessment revealed enhanced protection of sensitive environmental areas through more strategic development positioning, with 15.7% reduction in edge effects between construction land and natural habitats, directly resulting from the ecological protection objective f₂(X) that penalized development in ecologically sensitive zones. Social equity considerations showed improved access to public services, with 89.2% of optimized development areas located within 2 km of essential facilities compared to 76.8% in the baseline scenario, reflecting the social equity objective f₃(X) that prioritized accessibility to public facilities. These quantitative improvements directly correspond to the multi-objective optimization function components defined in Section 2.4, demonstrating the framework’s effectiveness in achieving the specified economic, ecological, and social planning goals.

Table 2

Table 2. Comparison of landscape metrics between baseline and optimized scenarios.

The optimization process successfully addressed key spatial efficiency challenges identified in the baseline scenario. Scattered development patches were systematically consolidated into more compact configurations, reducing infrastructure provision costs and improving service efficiency. Linear sprawl patterns along transportation corridors were modified to create more balanced and sustainable development forms. The optimization also enhanced connectivity between new development areas and existing urban centers, promoting more integrated spatial structures that support sustainable urban growth patterns (Figure 7).

Figure 7

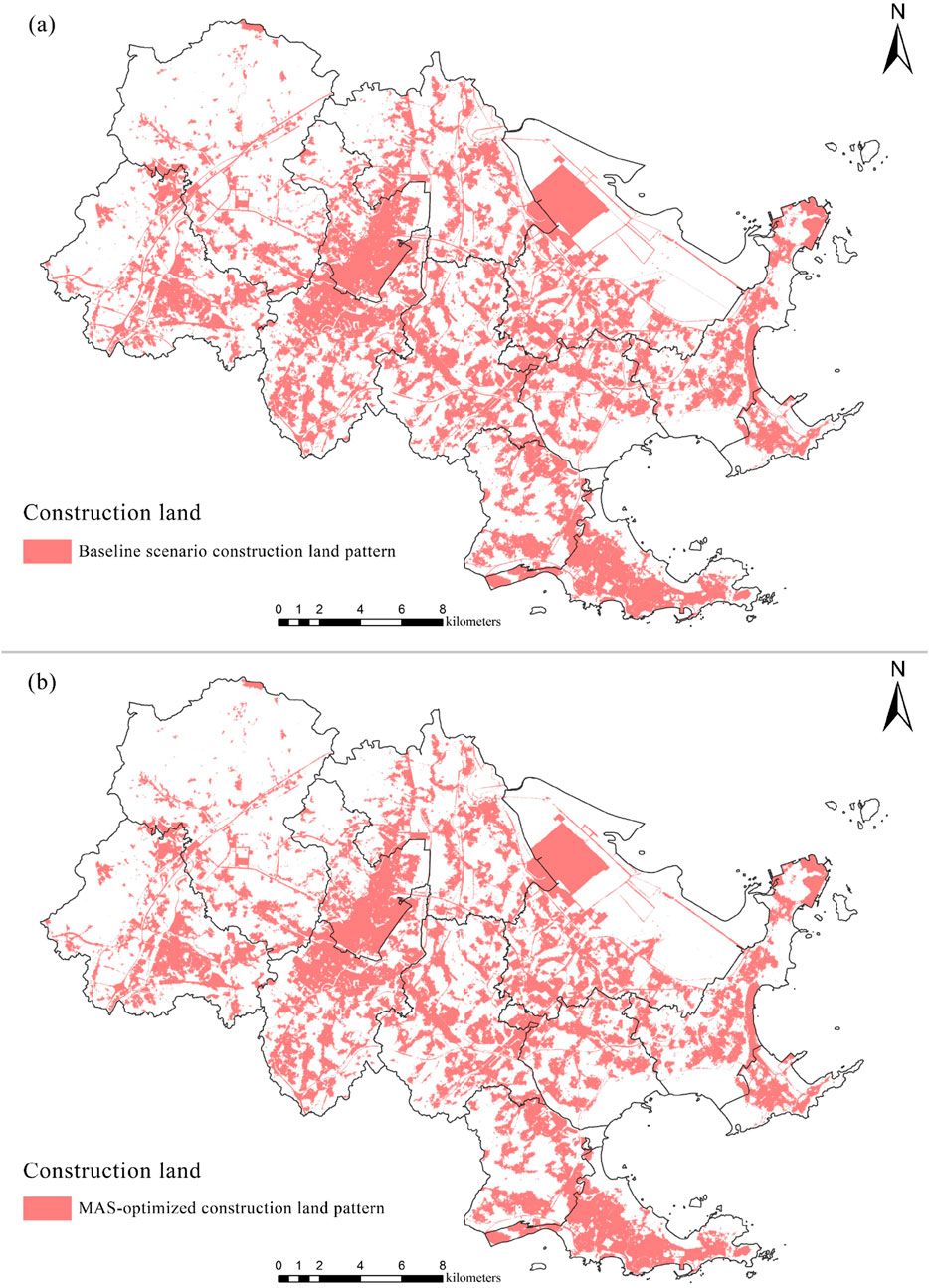
Figure 7. Comparative analysis of spatial layouts: (a) Baseline scenario construction land pattern, (b) MAS-optimized construction land pattern.

Economic efficiency analysis demonstrated that optimized layouts reduced average distances to urban centers by 12.3%, potentially decreasing transportation costs and improving accessibility to employment opportunities and services. Ecological impact assessment revealed enhanced protection of sensitive environmental areas through more strategic development positioning, with 15.7% reduction in edge effects between construction land and natural habitats. Social equity considerations showed improved access to public services, with 89.2% of optimized development areas located within 2 km of essential facilities compared to 76.8% in the baseline scenario.

5 Discussion

5.1 Framework effectiveness and spatial optimization benefits

The empirical application results conclusively demonstrate the significant effectiveness of the coupled ANN-CA simulation and MAS optimization framework in enhancing territorial spatial layout quality. The dramatic improvement in spatial morphology metrics, particularly the 35.7% reduction in AWMSI from 79.44 to 51.11, provides quantitative evidence of the framework’s capacity to transform sprawling, inefficient development patterns into more compact and regular spatial configurations. This improvement aligns with contemporary smart growth and compact city development principles advocated in international planning literature (Newman and Kenworthy, 2015; Burton et al., 2003).

The 27.1% reduction in patch numbers (NP) coupled with enhanced aggregation index (AI) demonstrates successful spatial consolidation that promotes infrastructure efficiency and reduces environmental fragmentation. These results support findings from previous research on spatial optimization algorithms for land use planning, while extending methodological approaches through the innovative coupling of predictive simulation with normative optimization (Cao et al., 2011; Liu et al., 2014b). The framework’s ability to simultaneously satisfy multiple objectives while adhering to strict planning constraints represents a significant advancement in computational planning support systems.

The integration of “dual evaluation” results and “three control lines” constraints within the simulation-optimization coupling ensures that technical solutions remain grounded in policy realities and regulatory requirements. This addresses a critical gap in previous optimization studies that often operated independently of planning policy contexts (Verburg et al., 2019). The framework’s explicit consideration of spatial morphology as an optimization objective responds to growing recognition of urban form impacts on sustainability, livability, and economic efficiency (Jaeger et al., 2010).

5.2 Methodological innovations and technical contributions

This research’s primary methodological innovation lies in the organic coupling mechanism between ANN-CA simulation and MAS optimization, specifically utilizing simulation-derived suitability probabilities as heuristic information for ant colony algorithms. This coupling strategy ensures that optimization processes are informed by scientifically grounded spatial development potentials rather than arbitrary starting conditions, potentially improving solution quality and convergence efficiency. The approach represents a significant departure from traditional optimization studies that typically begin with random initial solutions or simplified assumptions about spatial development preferences (Santé et al., 2010).

The framework’s multi-objective optimization formulation explicitly incorporates spatial morphology metrics alongside traditional economic and ecological considerations, addressing the tendency of previous studies to focus primarily on allocation efficiency while neglecting spatial form implications. The inclusion of AWMSI and AI as optimization objectives provides quantitative mechanisms for achieving compact development principles that have predominantly remained qualitative planning aspirations.

From a technical perspective, the framework demonstrates scalability and adaptability across different planning contexts and geographic regions. The modular structure allows for component modification and parameter adjustment to accommodate varying planning priorities, regulatory frameworks, and regional characteristics. This flexibility addresses limitations of previous integrated modeling approaches that often required substantial customization for different applications.

5.3 Policy implications and planning applications

The framework’s capacity to generate spatial layouts that simultaneously achieve efficiency, compactness, and regulatory compliance provides valuable decision support for territorial spatial planning practice. The quantitative improvement in spatial morphology metrics offers objective foundations for evaluating alternative development scenarios and supporting evidence-based planning decisions. This capability is particularly relevant in China’s current territorial spatial planning system reform, where scientific and technical support for planning compilation and implementation is increasingly emphasized.

The integration of planning policy factors within the technical modeling framework facilitates better alignment between planning intentions and spatial outcomes. By embedding “dual evaluation” results and “three control lines” constraints directly within simulation and optimization processes, the framework helps ensure that technical solutions support rather than contradict policy objectives. This integration addresses persistent challenges in planning practice where technical analyses and policy requirements often operate in isolation.

The framework’s multi-objective optimization approach provides mechanisms for exploring trade-offs between competing planning objectives, enabling planners to identify balanced solutions that consider economic efficiency, ecological protection, and spatial form simultaneously. This capability supports more nuanced and informed planning decisions that acknowledge the complexity of contemporary territorial spatial planning challenges.

5.4 Limitations and future research

Despite demonstrated effectiveness, the framework possesses several limitations requiring acknowledgment and future research attention. The optimization algorithms generate high-quality feasible solutions rather than guaranteed optimal layouts, reflecting the inherent complexity and multi-modal nature of spatial optimization problems. While ant colony algorithms excel in exploring complex solution spaces, they cannot guarantee global optimality, suggesting potential benefits from hybrid approaches combining multiple optimization strategies (Dorigo and Stützle, 2018).

The current framework lacks temporal sequencing capabilities, generating end-state spatial configurations without modeling intermediate development processes or transition pathways. Future research should explore “rolling horizon” optimization approaches that provide sequential development guidance and account for dynamic constraints and changing conditions over time. This temporal limitation restricts the framework’s ability to support phased development planning and adaptive management strategie.

The framework’s socioeconomic modeling components remain relatively simplified, incorporating demographic and economic factors primarily through accessibility and density measures. Enhanced integration with agent-based models representing individual and institutional decision-making processes could improve realism and policy relevance. Such integration would better capture market dynamics, behavioral responses to planning interventions, and spatial development processes driven by multiple stakeholder interactions.

Validation and uncertainty analysis represent additional areas requiring development. While the framework demonstrates internal consistency and logical spatial improvements, comprehensive validation against actual development outcomes and sensitivity analysis regarding parameter variations would strengthen confidence in practical applications. Future research should develop validation protocols and uncertainty quantification methods appropriate for predictive-normative modeling frameworks.

5.5 International applicability and transferability

The framework’s conceptual structure and technical approach possess strong potential for international application, though implementation would require adaptation to different planning systems, regulatory frameworks, and data availability conditions. The core coupling mechanism between simulation and optimization represents a generalizable approach to spatial planning support that transcends specific regional contexts. However, successful transfer would necessitate careful consideration of local planning traditions, institutional arrangements, and technical capabilities.

International application would benefit from comparative case studies examining framework performance across diverse geographic and institutional contexts. Such studies could identify necessary modifications for different planning systems while establishing general principles for successful implementation. The framework’s modular structure facilitates such adaptation by allowing component substitution and parameter adjustment without fundamental architectural changes (Pinto and Antunes, 2010; Malczewski, 2006).

The framework’s emphasis on quantitative spatial morphology optimization addresses universal planning concerns regarding urban form and development efficiency, suggesting broad relevance across international planning contexts. However, specific morphology metrics and optimization objectives should be calibrated to local conditions and planning priorities. This customization requirement presents both challenges and opportunities for framework enhancement and international collaboration in planning support system development (Silva and Wu, 2012; Deal and Schunk, 2004).

6 Conclusion

This research successfully developed and empirically validated an intelligent decision-making framework that couples ANN-CA predictive simulation with ant colony algorithm-based MAS normative optimization for territorial spatial layout planning. The framework addresses critical methodological gaps between simulation and optimization approaches while integrating planning policy considerations within technical modeling processes. Application to Hui’an County, Fujian Province, demonstrated substantial improvements in spatial layout quality, with optimized scenarios achieving 35.7% reduction in Area-Weighted Mean Shape Index and 27.1% decrease in patch fragmentation compared to baseline simulation results.

The framework’s key innovations include the organic coupling mechanism utilizing simulation-derived suitability probabilities as optimization heuristic information, explicit incorporation of spatial morphology objectives within multi-objective optimization formulations, and deep integration of planning policy factors including “dual evaluation” results and “three control lines” constraints. These innovations enable generation of spatial layouts that simultaneously satisfy efficiency, compactness, and regulatory compliance requirements while maintaining scientific grounding in predictive modeling foundations.

Empirical results demonstrate the framework’s effectiveness in transforming sprawling development patterns into compact, regular spatial configurations that support sustainable urban growth principles. The quantitative improvement in landscape metrics provides objective evidence of enhanced spatial quality, while strict adherence to planning constraints ensures practical feasibility and policy alignment. The framework’s modular structure and technical flexibility suggest strong potential for adaptation across diverse planning contexts and geographic regions.

Future research should address identified limitations through development of temporal sequencing capabilities, enhanced socioeconomic modeling components, and comprehensive validation protocols. Integration with agent-based models representing stakeholder decision-making processes could improve behavioral realism, while rolling horizon optimization approaches could provide sequential development guidance. International comparative studies would facilitate framework refinement and establish general principles for successful implementation across different planning systems and institutional contexts.

The framework represents a significant advancement in computational planning support systems, providing scientific and technical foundations for evidence-based territorial spatial planning decisions. Its capacity to bridge predictive simulation and normative optimization while maintaining policy integration offers valuable contributions to both planning theory and practice. As territorial spatial planning continues evolving toward more integrated and scientifically informed approaches, frameworks such as this provide essential tools for navigating complex spatial development challenges and achieving sustainable territorial development objectives.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RF: Writing – original draft. YL: Conceptualization, Writing – review and editing. ZL: Methodology, Writing – original draft. BJ: Resources, Software, Writing – original draft. CX: Methodology, Visualization, Writing – original draft. YC: Methodology, Writing – original draft. SZ: Resources, Visualization, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The completion of this work was supported by National Key Research and Development Program of China (No. 2022YFB3904105). Thanks for the support of Academic Specialty Group for Urban Sensing in Chinese Society of Urban Planning.

Conflict of interest

Authors RF, YL, BJ, CX, YC, and SZ were employed by Guangzhou Urban Planning and Design Survey Research Institute Co., Ltd. Authors RF, YL, BJ, CX, YC, and SZ were employed by Monitoring and Early Warning.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aburas, M. M., Ho, Y. M., Ramli, M. F., and Ash’aari, Z. H. (2016). The simulation and prediction of spatio-temporal urban growth trends using cellular automata models: a review. Int. J. Appl. Earth Observation Geoinformation 52, 380–389. doi:10.1016/j.jag.2016.07.007

CrossRef Full Text | Google Scholar

Adhikari, S., and Southworth, J. (2012). Simulating forest cover changes of bannerghatta national park based on a CA-Markov model: a remote sensing approach. Remote Sens. 4 (10), 3215–3243. doi:10.3390/rs4103215

CrossRef Full Text | Google Scholar

Aerts, J. C., Eisinger, E., Heuvelink, G. B., and Stewart, T. J. (2003). Using linear integer programming for multi-site land-use allocation. Geogr. Anal. 35 (2), 148–169. doi:10.1353/geo.2003.0001

CrossRef Full Text | Google Scholar

Almeida, C. D., Gleriani, J. M., Castejon, E. F., and Soares-Filho, B. S. (2008). Using neural networks and cellular automata for modelling intra-urban land-use dynamics. Int. J. Geogr. Inf. Sci. 22 (9), 943–963. doi:10.1080/13658810701731168

CrossRef Full Text | Google Scholar

Baker, W. L. (1989). A review of models of landscape change. Landsc. Ecol. 2 (2), 111–133. doi:10.1007/bf00137155

CrossRef Full Text | Google Scholar

Burnham, B. O. (1973). Markov intertemporal land use simulation model. J. Agric. Appl. Econ. 5 (1), 253–258. doi:10.1017/s0081305200011110

CrossRef Full Text | Google Scholar

E. Burton, M. Jenks, and K. Williams (2003). The compact city: a sustainable urban form? (London: Routledge).

Google Scholar

Cao, K., Batty, M., Huang, B., Liu, Y., Yu, L., and Chen, J. (2011). Spatial multi-objective land use optimization: extensions to the non-dominated sorting genetic algorithm-II. Int. J. Geogr. Inf. Sci. 25 (12), 1949–1969. doi:10.1080/13658816.2011.570269

CrossRef Full Text | Google Scholar

Cao, K., Huang, B., Wang, S., and Lin, H. (2012). Sustainable land use optimization using Boundary-based fast genetic algorithm. Comput. Environ. Urban Syst. 36 (3), 257–269. doi:10.1016/j.compenvurbsys.2011.08.001

CrossRef Full Text | Google Scholar

Chen, W., Chi, G., and Li, J. (2020). The spatial aspect of ecosystem services balance and its determinants. Land Use Policy 90, 104263. doi:10.1016/j.landusepol.2019.104263

CrossRef Full Text | Google Scholar

Deal, B., and Schunk, D. (2004). Spatial dynamic modeling and urban land use transformation: a simulation approach to assessing the costs of urban sprawl. Ecol. Econ. 51 (1-2), 79–95. doi:10.1016/j.ecolecon.2004.04.008

CrossRef Full Text | Google Scholar

Dorigo, M., and Gambardella, L. M. (2002). Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1 (1), 53–66. doi:10.1109/4235.585892

CrossRef Full Text | Google Scholar

Dorigo, M., and Stützle, T. (2018). Ant colony optimization: overview and recent advances. Handb. metaheuristics, 311–351. doi:10.1007/978-3-319-91086-4_10

CrossRef Full Text | Google Scholar

Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant system: optimization by a colony of cooperating agents. IEEE Trans. Syst. man, Cybern. part b Cybern. 26 (1), 29–41. doi:10.1109/3477.484436

PubMed Abstract | CrossRef Full Text | Google Scholar

Gharbia, S. S., Alfatah, S. A., Gill, L., Johnston, P., and Pilla, F. (2016). Land use scenarios and projections simulation using an integrated GIS cellular automata algorithms. Model. earth Syst. Environ. 2 (3), 151. doi:10.1007/s40808-016-0210-y

CrossRef Full Text | Google Scholar

Guan, Q., Wang, L., and Clarke, K. C. (2005). An artificial-neural-network-based, constrained CA model for simulating urban growth. Cartogr. Geogr. Inf. Sci. 32 (4), 369–380. doi:10.1559/152304005775194746

CrossRef Full Text | Google Scholar

Guan, D., Li, H., Inohae, T., Su, W., Nagaie, T., and Hokao, K. (2011). Modeling urban land use change by the integration of cellular automaton and markov model. Ecol. Model. 222 (20-22), 3761–3772. doi:10.1016/j.ecolmodel.2011.09.009

CrossRef Full Text | Google Scholar

Haque, A., and Asami, Y. (2014). Optimizing urban land use allocation for planners and real estate developers. Comput. Environ. Urban Syst. 46, 57–69. doi:10.1016/j.compenvurbsys.2014.04.004

CrossRef Full Text | Google Scholar

Jaeger, J. A., Bertiller, R., Schwick, C., and Kienast, F. (2010). Suitability criteria for measures of urban sprawl. Ecol. Indic. 10 (2), 397–406. doi:10.1016/j.ecolind.2009.07.007

CrossRef Full Text | Google Scholar

Li, X., and Liu, X. (2008). Embedding sustainable development strategies in agent-based models for use as a planning tool. Int. J. Geogr. Inf. Sci. 22 (1), 21–45. doi:10.1080/13658810701228686

CrossRef Full Text | Google Scholar

Li, X., and Yeh, A. G. O. (2002). Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 16 (4), 323–343. doi:10.1080/13658810210137004

CrossRef Full Text | Google Scholar

Li, Y., Liu, Y., Long, H., and Cui, W. (2014). Community-based rural residential land consolidation and allocation can help to revitalize hollowed villages in traditional agricultural areas of China: evidence from dancheng county, Henan Province. Land Use Policy 39, 188–198. doi:10.1016/j.landusepol.2014.02.016

CrossRef Full Text | Google Scholar

Li, X., Chen, G., Liu, X., Liang, X., Wang, S., Chen, Y., et al. (2017). A new global land-use and land-cover change product at a 1-km resolution for 2010 to 2100 based on human–environment interactions. Ann. Am. Assoc. Geogr. 107 (5), 1040–1059. doi:10.1080/24694452.2017.1303357

CrossRef Full Text | Google Scholar

Ligmann-Zielinska, A., Church, R. L., and Jankowski, P. (2008). Spatial optimization as a generative technique for sustainable multiobjective land-use allocation. Int. J. Geogr. Inf. Sci. 22 (6), 601–622. doi:10.1080/13658810701587495

CrossRef Full Text | Google Scholar

Liu, Y., Fang, F., and Li, Y. (2014a). Key issues of land use in China and implications for policy making. Land use policy 40, 6–12. doi:10.1016/j.landusepol.2013.03.013

CrossRef Full Text | Google Scholar

Liu, Y., Feng, Y., and Pontius Jr, R. G. (2014b). Spatially-explicit simulation of urban growth through self-adaptive genetic algorithm and cellular automata modelling. Land 3 (3), 719–738. doi:10.3390/land3030719

CrossRef Full Text | Google Scholar

Liu, X., Liang, X., Li, X., Xu, X., Ou, J., Chen, Y., et al. (2017). A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. urban Plan. 168, 94–116. doi:10.1016/j.landurbplan.2017.09.019

CrossRef Full Text | Google Scholar

López, E., Bocco, G., Mendoza, M., and Duhau, E. (2001). Predicting land-cover and land-use change in the urban fringe: a case in morelia city, Mexico. Landsc. urban Plan. 55 (4), 271–285. doi:10.1016/s0169-2046(01)00160-8

CrossRef Full Text | Google Scholar

Malczewski, J. (2006). GIS-Based multicriteria decision analysis: a survey of the literature. Int. J. Geogr. Inf. Sci. 20 (7), 703–726. doi:10.1080/13658810600661508

CrossRef Full Text | Google Scholar

Merkle, D., Middendorf, M., and Schmeck, H. (2002). Ant colony optimization for resource-constrained project scheduling. IEEE Trans. Evol. Comput. 6 (4), 333–346. doi:10.1109/tevc.2002.802450

CrossRef Full Text | Google Scholar

Muller, M. R., and Middleton, J. (1994). A markov model of land-use change dynamics in the niagara region, Ontario, Canada. Landsc. Ecol. 9 (2), 151–157. doi:10.1007/bf00124382

CrossRef Full Text | Google Scholar

Newman, P., and Kenworthy, J. (2015). “The rise and fall of automobile dependence,” in The end of automobile dependence: how cities are moving beyond car-based planning (Washington, DC: Island Press/Center for Resource Economics), 1–31.

CrossRef Full Text | Google Scholar

Pijanowski, B. C., Brown, D. G., Shellito, B. A., and Manik, G. A. (2002). Using neural networks and GIS to forecast land use changes: a land transformation model. Comput. Environ. urban Syst. 26 (6), 553–575. doi:10.1016/s0198-9715(01)00015-1

CrossRef Full Text | Google Scholar

Pijanowski, B. C., Tayyebi, A., Doucette, J., Pekin, B. K., Braun, D., and Plourde, J. (2014). A big data urban growth simulation at a national scale: configuring the GIS and neural network based land transformation model to run in a high performance computing (HPC) environment. Environ. Model. and Softw. 51, 250–268. doi:10.1016/j.envsoft.2013.09.015

CrossRef Full Text | Google Scholar

Pinto, N. N., and Antunes, A. P. (2010). A cellular automata model based on irregular cells: application to small urban areas. Environ. Plan. B Plan. Des. 37 (6), 1095–1114. doi:10.1068/b36033

CrossRef Full Text | Google Scholar

Santé, I., García, A. M., Miranda, D., and Crecente, R. (2010). Cellular automata models for the simulation of real-world urban processes: a review and analysis. Landsc. urban Plan. 96 (2), 108–122. doi:10.1016/j.landurbplan.2010.03.001

CrossRef Full Text | Google Scholar

Silva, E. A., and Wu, N. (2012). Surveying models in urban land studies. J. Plan. Literature 27 (2), 139–152. doi:10.1177/0885412211430477

CrossRef Full Text | Google Scholar

Stewart, T. J., Janssen, R., and Van Herwijnen, M. (2004). A genetic algorithm approach to multiobjective land use planning. Comput. and Operations Res. 31 (14), 2293–2313. doi:10.1016/s0305-0548(03)00188-6

CrossRef Full Text | Google Scholar

Verburg, P. H., Alexander, P., Evans, T., Magliocca, N. R., Malek, Z., Rounsevell, M. D., et al. (2019). Beyond land cover change: towards a new generation of land use models. Curr. Opin. Environ. Sustain. 38, 77–85. doi:10.1016/j.cosust.2019.05.002

CrossRef Full Text | Google Scholar

Wang, J., Lin, Y., Glendinning, A., and Xu, Y. (2018). Land-use changes and land policies evolution in China’s urbanization processes. Land use policy 75, 375–387. doi:10.1016/j.landusepol.2018.04.011

CrossRef Full Text | Google Scholar

Wang, Q., Wang, H., Chang, R., Zeng, H., and Bai, X. (2022). Dynamic simulation patterns and spatiotemporal analysis of land-use/land-cover changes in the wuhan metropolitan area, China. Ecol. Model. 464, 109850. doi:10.1016/j.ecolmodel.2021.109850

CrossRef Full Text | Google Scholar

White, R., and Engelen, G. (1993). Cellular automata and fractal urban form: a cellular modelling approach to the evolution of urban land-use patterns. Environ. Plan. A 25 (8), 1175–1199. doi:10.1068/a251175

CrossRef Full Text | Google Scholar

Wu, Y., Zhang, X., and Shen, L. (2011). The impact of urbanization policy on land use change: a scenario analysis. Cities 28 (2), 147–159. doi:10.1016/j.cities.2010.11.002

CrossRef Full Text | Google Scholar

Zhang, Y., Long, H., Tu, S., Ge, D., Ma, L., and Wang, L. (2019). Spatial identification of land use functions and their tradeoffs/synergies in China: implications for sustainable land management. Ecol. Indic. 107, 105550. doi:10.1016/j.ecolind.2019.105550

CrossRef Full Text | Google Scholar

Zhou, D., Xu, J., and Lin, Z. (2017). Conflict or coordination? Assessing land use multi-functionalization using production-living-ecology analysis. Sci. total Environ. 577, 136–147. doi:10.1016/j.scitotenv.2016.10.143

PubMed Abstract | CrossRef Full Text | Google Scholar