Spatial-temporal distribution prediction of transmission corridor wildfire risk based on ARIMA-DBN

This study proposes a predictive model for assessing the spatiotemporal risk of wildfire occurrence in transmission corridors, with an emphasis on the role of meteorological factors in short-term wildfire dynamics. A comprehensive set of 17 factors across four categories is considered. Following factor selection via the Random Forest (RF) algorithm, the predictive model is constructed using the key subset of wildfire factors. The Auto Regressive Integrated Moving Average (ARIMA) and Generalized Autoregressive Conditional Heteroskedasticity (GARCH) algorithms are employed to predict dynamic meteorological factor data, while the Dynamic Bayesian Network (DBN) is used to explore the interrelationships among wildfire factors across different time periods. The result shows that the DBN-based wildfire risk assessment model at a 3-day time scale achieves a high accuracy of 86.39%; when utilizing meteorological data predicted by ARIMA-GARCH, the wildfire risk prediction model still reaches an accuracy of 79.64%. Additionally, wildfire risk distribution maps for typical high-risk periods in Guangdong Province are generated using the model, revealing that 80.00%, 100.00%, 70.00%, and 72.72% of actual fire points, respectively, fall within high-risk and very high-risk areas, demonstrating the model's ability to provide accurate short-term predictions. This model offers significant value for decision-making in wildfire management, particularly for policymakers, grid operators, and fire management teams, enhancing the efficiency of risk mitigation efforts in critical transmission corridors.

1 Introduction

Due to the reverse distribution of energy resources and load centers in China, long-distance, high-capacity transmission technologies are crucial to meet power supply demands in load centers (Chen et al., 2020). However, the increasing frequency of extreme weather events, such as prolonged droughts and high temperatures due to global warming, has led to more frequent wildfires. These wildfires near transmission corridors can severely disrupt grid reliability (Trakas and Hatziargyriou, 2018; Zhou et al., 2022). For example, in 2023, the transmission corridors under the jurisdiction of China Southern Power Grid Co., Ltd. issued over 4,000 wildfire warnings, resulting in 78 transmission line trips. As wildfires become one of the most severe natural disasters affecting both production and daily life, it is crucial for predicting and issuing timely warnings for wildfires in transmission corridors (Shu et al., 2023; Liu et al., 2022).

Extensive research has focused on assessing wildfire risk in transmission corridors. Early models primarily used meteorological inputs, such as fire danger indices, to predict regional wildfire risks (França et al., 2014; Ziccardi et al., 2019). However, these methods often suffer from low spatial resolution due to the limited number of meteorological stations, making them more suitable for large-scale regional risk assessments rather than the fine-scale predictions for transmission corridors. Later studies improved prediction accuracy by incorporating factors like vegetational and meteorological factors. For example, State Grid, the largest power companies in China, evaluate wildfire risks by using the factors including historical fire density and vegetation types, whereas China Southern Power Grid additionally incorporate the factor of fuel load. To further enhance evaluation accuracy, Lu et al. (2017) introduced precipitation and the locations of industrial and agricultural fires to assess hazard risks to transmission lines. However, these models still suffer from bias due to the reliance on subjective expert weights. Data-driven approaches, such as neural networks (Zhou et al., 2014; de Vasconcelos et al., 2001), multivariate logistic regression (Oliveira et al., 2012; Mallinis et al., 2019; Wang, 2023), and Naïve Bayes Networks (Chen et al., 2021; Xiang et al., 2022), have shown promise in reducing expert bias by leveraging historical data to identify patterns. However, these models typically assume that influencing factors are mutually independent and rely on adjusting the non-linear weights of each factor to improve model performance through data fitting. Moreover, these studies commonly employ annual average meteorological data to assess wildfire risk over extended periods, neglecting the influence of short-term meteorological variations. Achieving dynamic prediction of wildfire risk remains challenging.

To address these limitations, this study proposes an innovative ARIMA-DBN model for predicting wildfire risks in transmission corridors. By integrating time-series forecasting with probabilistic factor relationships, the proposed model captures both temporal dynamics and interdependencies among various factors. Specifically, the Autoregressive Integrated Moving Average (ARIMA) component is employed to forecast meteorological factors, thereby addressing the temporal dynamics of short-term meteorological variations that were previously overlooked. The Dynamic Bayesian Network (DBN) component models the probabilistic relationships among these factors, offering a more comprehensive approach to wildfire risk prediction.

2 Study area

Guangdong Province was selected as the study area, focusing on transmission corridors of 110 kV and above. The region is characterized by mountainous and hilly terrain, with a subtropical monsoon climate that promotes vegetation growth. The forest coverage rate has reached 58.7%, with oil-rich, fast-growing species like eucalyptus and pine widely distributed in the northern and hilly areas. These species, which account for 58.5% of wildfire combustibles, provide ample fuel for the spread of wildfires. Additionally, the region experiences significant seasonal drought from October to April, particularly from February to April, when surface vegetation is dry and strong winter winds exacerbate wildfire risks (Qin et al., 2013). Studies show that during the peak wildfire period in February, the forest fire danger level often reaches the highest grade in northern Guangdong, such as Qingyuan and Shaoguan, which directly increases the risk of transmission line failures (Li et al., 2024).

Guangdong's permanent population is about 127.8 million, with a dense population distribution and rich folk activities, such as those in the Chaoshan region. This has led to frequent agricultural and sacrificial activities, including spring plowing, burning, and Qingming Festival ancestor worship, which easily ignite surrounding vegetation in hilly areas. Such human fire sources account for over 60% of wildfires along transmission corridors, becoming a significant driving factor for the high incidence of wildfires.

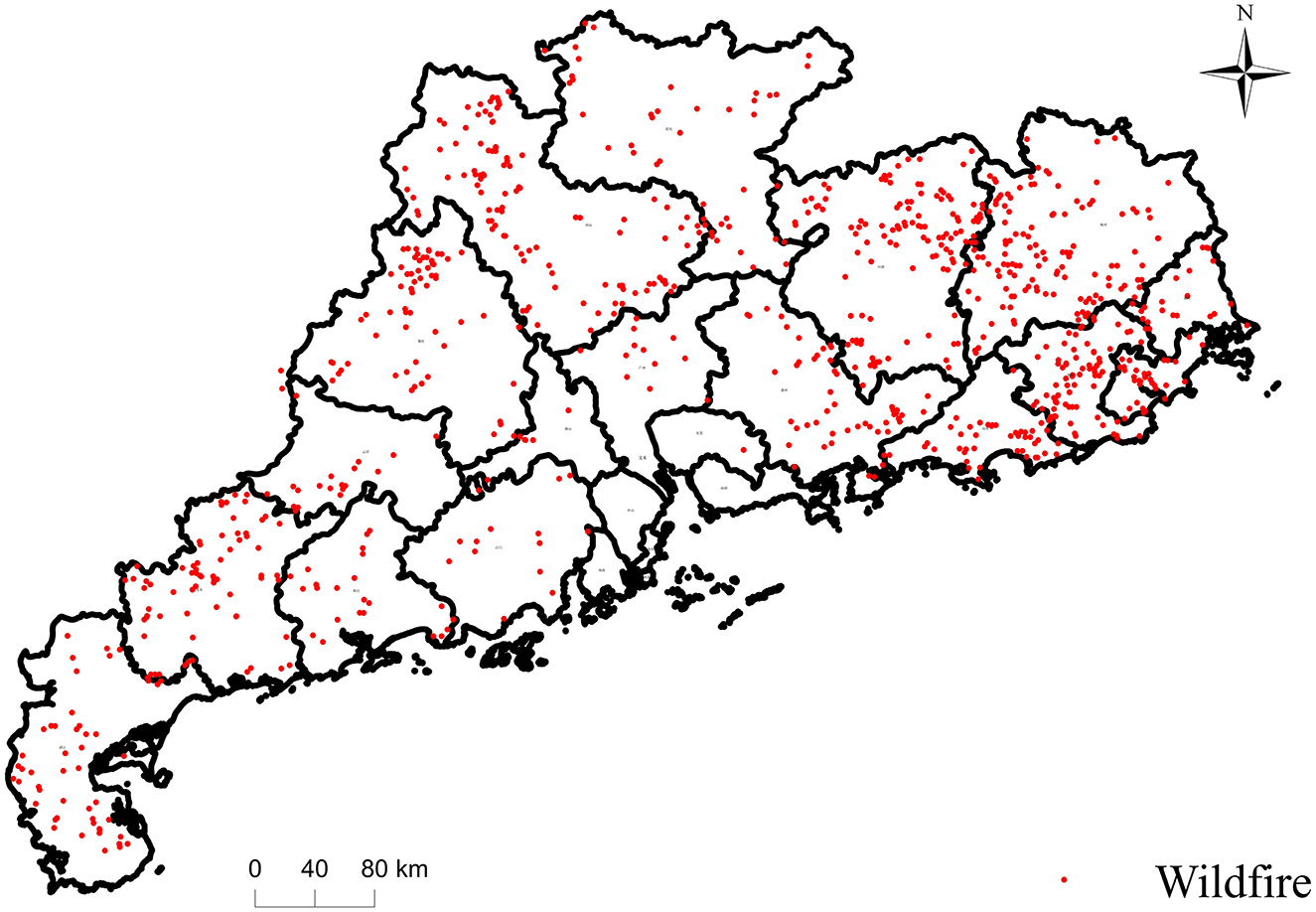
More importantly, as a core province for national electricity load, Guangdong has the densest 110 kV and above transmission network, particularly the lines extending from the Pearl River Delta to northern mountainous areas, such as the “West-to-East Power Transmission” channels. These lines pass through continuous hills and forest areas, forming high-risk zones. Wildfires that cause line tripping may result in regional power outages, significantly impacting sensitive loads such as manufacturing industries and data centers. From 2018 to 2023, 3,584 wildfires were recorded within 3 kilometers of 110 kV and above transmission corridors in Guangdong, as shown in Figure 1 (only geographical positions of wildfire are displayed, omitting line details due to confidentiality).

Figure 1

Figure 1. Wildfires distribution in Guangdong Province during 2018 to 2023.

In conclusion, Guangdong's high forest coverage rate, seasonal fire risk climate, human-induced fire risks, and the strategic importance of its dense power grid make it an ideal area for studying wildfire risks in transmission corridors.

3 Methods

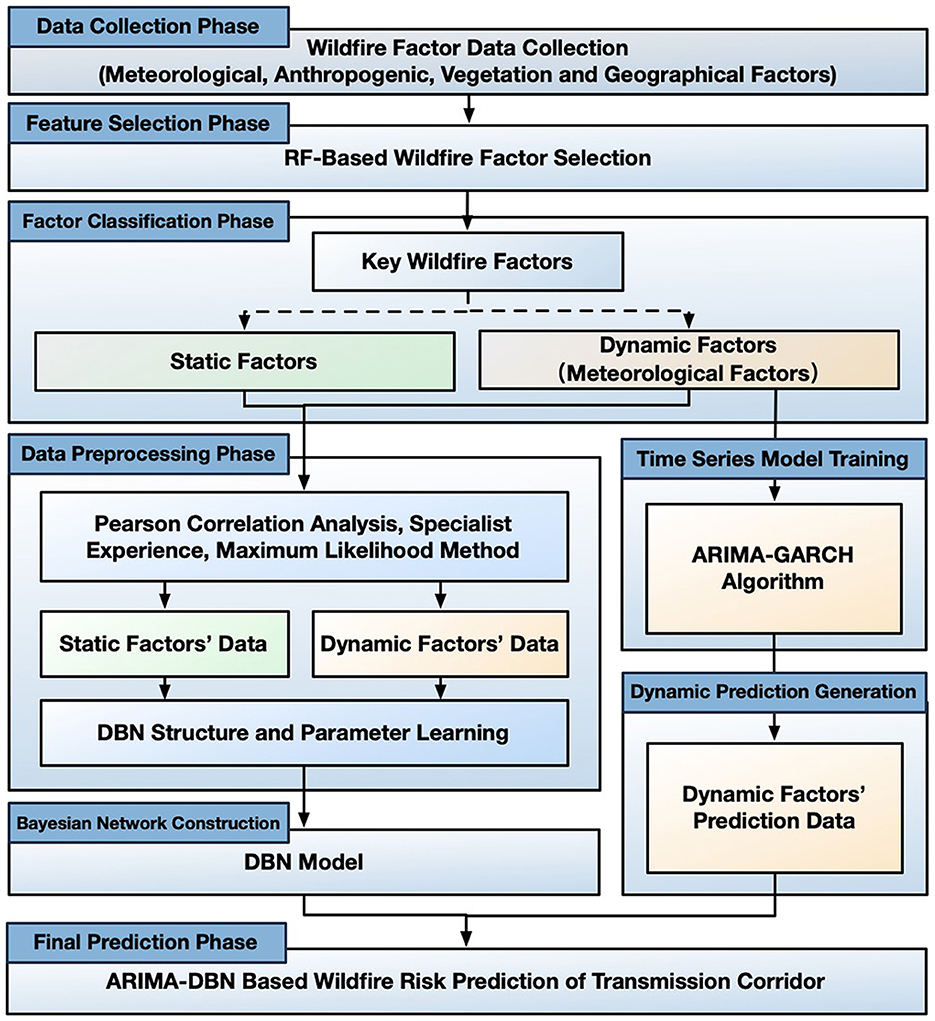
To predict the spatiotemporal distribution of wildfire risk in transmission corridors, this study proposes an ARIMA-DBN-based model framework. First, wildfire alarm data and relevant Wildfire Factor Data within the target region's transmission corridor are collected, integrating expert knowledge. Next, the RF algorithm is used to assess the contribution of each Wildfire Factor to the wildfire risk, selecting key factors for the subsequent DBN model. The structure of the DBN is determined through correlation analysis and expert-driven causal analysis. Time-varying meteorological data are predicted by using an ARIMA-GARCH algorithm. Finally, the predicted meteorological data from ARIMA, along with other static factors, are input into the DBN model to forecast short-term wildfire risk in the transmission corridor. The technical flowchart is shown in Figure 2.

Figure 2

Figure 2. Technical flowchart of ARIMA-DBN-Based wildfire risk prediction model.

3.1 Wildfire factor data collection and pre-processing

The occurrence of wildfires is influenced by both dynamic and static factors. Dynamic factors, such as meteorological conditions, exhibit temporal fluctuations that significantly impact wildfire risk. Both the Forest and Urban departments use meteorological factors to predict fire risk. Temperature, precipitation, and humidity affect flammability by altering vegetation moisture, whereas wind speed accelerates drying and promotes ignition. Therefore, the average value of consecutive dry days, temperature, precipitation, humidity, and wind speed were used to capture the impact of dynamic meteorological changes on wildfire risk over time.

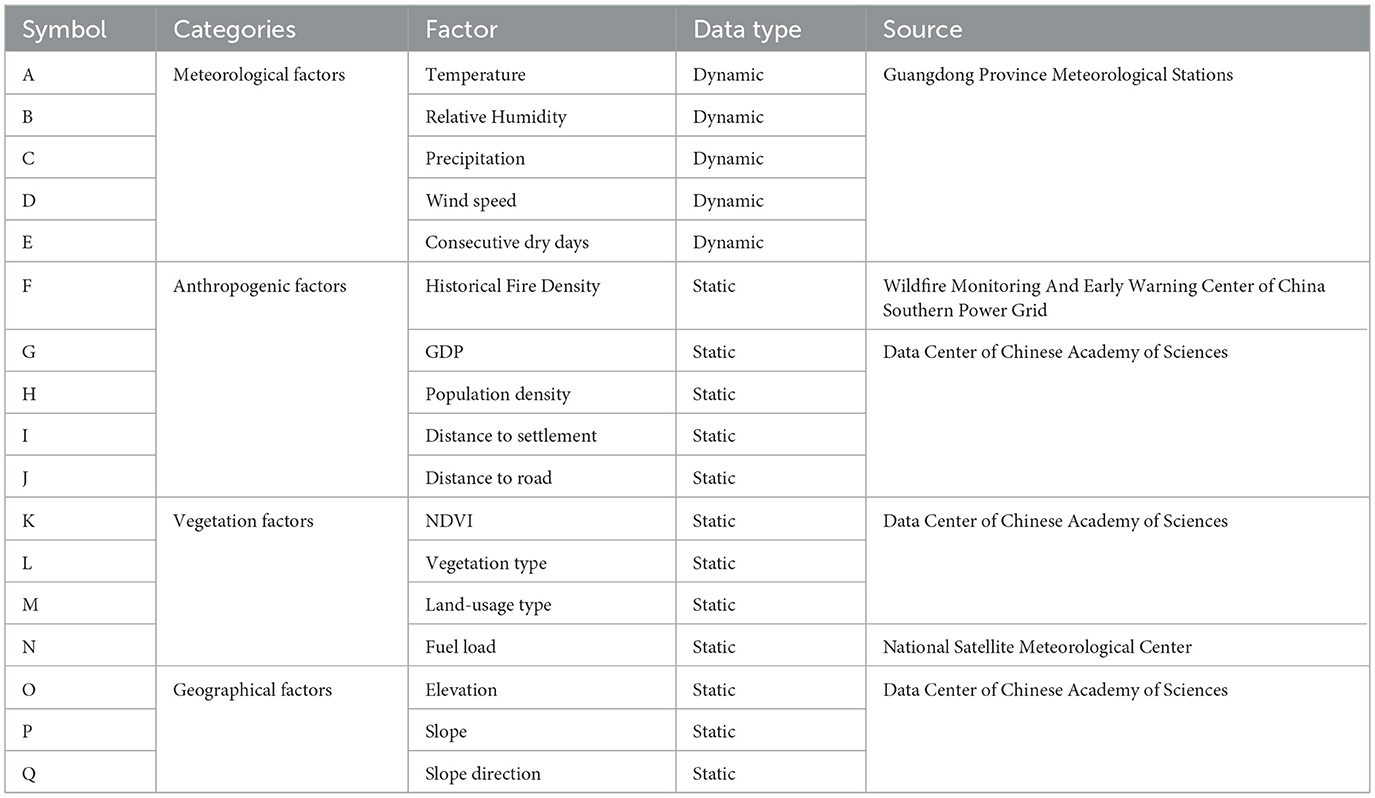
Static factors, by contrast, remain relatively constant over short time periods. These factors can be categorized into three main types: Anthropogenic, vegetation, and geographic (Prestemon and Butry, 2005; Albertson et al., 2019; Faivre et al., 2014; Kalabokidis et al., 2007; Costafreda-Aumedes et al., 2017). Human activities, such as ancestral rituals and slash-and-burn agriculture, contribute to wildfire occurrence Anthropogenic factor such as distance to road, distance to settlement, population density, GDP, and historical fire density were selected to represent human influences. Vegetation factors, being the primary fuel for wildfires, directly affect the ease of fire spread and the likelihood of wildfire occurrence. Key vegetation-related factors include land-usage type, vegetation type, Normalized Difference Vegetation Index (NDVI), and fuel load. In terms of geographic factors, elevation, slope, and aspect not only influence vegetation distribution but also affect human activity intensity, making them key topographic features for assessing wildfire risk.

Wildfire occurrence data from 2010 to 2023 were obtained from the Wildfire Monitoring and Early Warning Center of China Southern Power Grid. Data from 2010 to 2017 were used to calculate historical fire density, while data from 2018 to 2023 were used for model training and validation. Meteorological data were sourced from the Guangdong Provincial Meteorological Station and spatially interpolated using Kriging. The consecutive dry days variable was derived from precipitation data. Geographic data, including population density, GDP, settlement locations, road networks, vegetation types, NDVI, and land use types, were obtained from the Chinese Academy of Sciences' Resource and Environmental Science Data Center (https://www.resdc.cn). Proximity to settlements and roads was calculated using raster-based Euclidean distance computations. A summary of all wildfire-related factors and their data sources is provided in Table 1.

Table 1

Table 1. Wildfire factors in transmission corridor.

For spatial analysis, the study area was divided into 0.05° × 0.05° grids. Wildfire occurrences within each grid were calculated for specific time intervals. Grids containing one or more fire events were classified as “Fire Samples.” “Non-Fire Samples” were defined as grids with no recorded fire events during the same time intervals and located at least 3 kilometers away from any Fire Samples, ensuring they represent spatially independent non-fire scenarios. To address potential sample imbalance, the number of Non-Fire Samples was adjusted to maintain a ratio of 1:1 relative to Fire Samples through stratified random sampling, which helps avoid model bias caused by uneven sample distribution and enhances the reliability of model training.

To improve computational efficiency and stability in the DBN, continuous data of key wildfire factors were discretized based on the differences between Fire and Non-Fire samples. Discretization thresholds were determined by analyzing the frequency distributions of factors across Fire Samples and Non-Fire Samples (Supplementary Table 1). Given the temporal variability of wildfire events and influencing factors, the impact of time scales on model performance was evaluated. Dynamic datasets (D30, D15, D10, D7, and D3) were created using time scales of 30, 15, 10, 7, and 3 days, respectively, to address the needs of power utilities for differentiated short-to-medium-term wildfire prevention and control. Wildfire data as well as the related factors data from 2018 to 2023 were partitioned into intervals, generating time-series datasets for Fire and Non-Fire samples.

Considering excessive factors would increase model complexity and computational costs, leading to potential accuracy loss, the RF (França et al., 2014) feature selection algorithm, which is an ensemble model based on decision trees, was used to evaluate factor importance by calculating their contribution to wildfire occurrence across all trees. The DBN model was then constructed solely based on the factor subset with high contribution to wildfire events.

3.2 ARIMA-GARCH based meteorological factor prediction

Meteorological factors exhibit distinct temporal variations and are influenced by local climate. These factors often demonstrate strong autocorrelation and cyclical fluctuations. Therefore, this study employs the ARIMA model to capture the autocorrelation and trend characteristics inherent in the time series data of meteorological factors, enabling short-term forecasting. However, the residuals of the ARIMA model may still exhibit conditional heteroscedasticity. To address this, the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) algorithm is introduced to model the residuals. This approach uncovers volatility and other significant dynamics, thereby enhancing the forecasting accuracy.

3.2.1 Basic principles of ARIMA

The ARIMA model is a widely used statistical tool for time series forecasting, particularly effective for non-stationary data with temporal dependencies (Jatinder et al., 2023). It combines three key components: Autoregressive (AR), Integrated (I), and Moving Average (MA), which together capture the underlying patterns and trends in time series data.

The AR component describes the relationship between the current observation and its past values. It uses historical data to predict future values, and is expressed as:

$\begin{array}{ll}{y}_t={\phi }_1{y}_{t-1}+{\phi }_2{y}_{t-2}+\cdots +{\phi }_p{y}_{t-p}+{\epsilon }_t& (1)\end{array}$

where y_t represents the current observation, φ_i are the autoregressive coefficients, ε_t is the residual, and p denotes the order of the AR component.

The Integrated component is used to transform a non-stationary time series into a stationary one. Stationarity is an essential assumption for time series modeling, where the mean and variance of the series remain constant over time. The differencing operation aims to eliminate trend components from the series, and is expressed as:

$\begin{array}{ll}{\nabla }^d{y}_t={{(1-B)}^{d}y}_t& (2)\end{array}$

where B is the backshift operator, and d is the order of differencing.

The MA component models the relationship between the current observation and past residuals. It adjusts the series by taking a weighted average of past residuals.

$\begin{array}{ll}{y}_t={\theta }_1{\epsilon }_{t-1}+{\theta }_2{\epsilon }_{t-2}+\cdots +{\theta }_q{\epsilon }_{t-q}+{\epsilon }_t& (3)\end{array}$

where θ_i are the coefficients for the moving average terms, ε_t is the residual, and q denotes the order of the MA component.

By combining these components, the ARIMA model is able to account for trends, seasonal effects, and autocorrelation. The differencing process is used to achieve stationarity, followed by the AR and MA components to model internal dependencies and forecast future values.

$\begin{array}{ll}(1-{\displaystyle \sum _{i=1}^p{\phi }_i{B}^i}){(1-B)}^d{y}_t=(1+{\displaystyle \sum _{j=1}^q{\theta }_j{B}^j}){\epsilon }_t& (4)\end{array}$

3.2.2 Basic principles of GARCH

The GARCH model is a statistical method used to model conditional heteroscedasticity in time series data. Unlike traditional regression models, which assume constant variance for residuals, the GARCH model assumes that the conditional variance is time-varying and dependent on past residuals and past conditional variances (Paraskev, 2017).

The basic form of the GARCH model is expressed as:

$\begin{array}{ll}{\epsilon }_t=z_t\sqrt{h_t}& (5)\end{array}$

$\begin{array}{ll}{h}_t={\alpha }_0+{\displaystyle \sum _{i=1}^q}{\alpha }_i{z}_{t-i}^2+{\displaystyle \sum _{j=1}^p}{\beta }_j{h}_{t-j}& (6)\end{array}$

where z_t is standard residuals, h_t is conditional variance, α_i and β_j are the model parameters to be estimated, and p and q represent the order of the autoregressive and moving average terms, respectively.

One of the key advantages of the GARCH model is its ability to capture the phenomenon of volatility clustering, where periods of high volatility tend to be followed by other high-volatility periods, and periods of low volatility are followed by low-volatility periods. This feature is particularly relevant in modeling meteorological data, where the volatility of various factors often exhibits temporal dependencies.

3.2.3 ARIMA-GARCH model development steps

To develop the ARIMA model for the meteorological factors, observational data from meteorological stations in Guangdong Province covering the period from 2018 to 2023 were utilized. The original dataset, which contained hourly records of temperature, precipitation, humidity, and wind speed, was first examined. It was found that precipitation was frequently recorded as 0 mm for many time intervals. This pattern resulted in non-stationarity of the series and the absence of continuous dynamic patterns, thereby rendering it unsuitable for traditional time series modeling. To address this issue, the precipitation data were aggregated into daily precipitation sequences so that the stability of the time series could be improved.

As stationarity, defined as constant mean and variance over time, is a prerequisite for time series analysis, the original meteorological data were checked and found to exhibit significant fluctuations and trends. Therefore, transformations were applied to achieve stationarity. In particular, a first-order differencing operation was performed on each time series, and stationary sequences were thereby obtained.

Subsequently, ARIMA (p, d, q) models were constructed for each meteorological factor. The determination of model order was carried out in the following sequence. First, maximum values for p_max and q_max for the AR and MA components were identified through the autocorrelation function (ACF) and partial autocorrelation function (PACF) tests. Then, the Bayesian Information Criterion (BIC) (Burnham and Anderson, 2004) was employed as the evaluation metric. For each (p, q) combination, the BIC value was calculated and compared, and the combination yielding the minimum BIC value was selected as the optimal model order. The BIC, which is widely accepted for balancing model complexity and goodness of fit, is defined as:

$\begin{array}{ll}BIC=kln(n)-2ln(L)& (7)\end{array}$

where k is the number of model parameters, n is the sample size, and L is the likelihood function.

Once the model order and parameters had been determined, the residuals were subjected to a white noise test in order to assess the adequacy of model fitting. If the residuals were confirmed to be white noise, it was inferred that no autocorrelation remained in the sequence, indicating that the ARIMA model had successfully extracted the useful information for forecasting purposes. If, however, the residuals exhibited autocorrelation, the presence of autoregressive heteroscedasticity was implied.

In such cases, the residuals from the ARIMA model were further modeled using a GARCH approach so that the volatility characteristics could be more accurately captured. Through this procedure, the short-term forecasting models were refined, and the accuracy of meteorological predictions was thereby enhanced.

3.3 DBN based wildfire risk assessment

3.3.1 Basic principles of DBN

Bayesian Networks (BNs), introduced by Pearl et al. in the 1980s (Marcot Bruce and Penman Trent, 2019), are graphical probabilistic models wherein each node represents a random variable, and the edges signify dependencies between these variables. Each node has a conditional probability distribution, which quantifies the likelihood of the node's state given its parent nodes. Assuming the parent set of node X is Pa(X), the conditional probability distribution of node X is given by:

$\begin{array}{ll}P(X|Pa(X))& (8)\end{array}$

The joint probability distribution of a BN can be expressed using the chain rule:

$\begin{array}{ll}P(X_1,X_2,\cdots ,X_n)={\displaystyle \prod _{i=1}^n}P(X_i|Pa(X_i))& (9)\end{array}$

While traditional BNs are effective for modeling static systems, they are less suited for capturing dynamic processes that evolve over time. To address this limitation, Dynamic Bayesian Networks (DBNs) were developed as an extension of BNs. A DBN incorporates a time dimension, enabling the modeling of system states that change over time and the representation of dependencies across different time points.

A typical DBN consists of two main components: the initial BN and the transition network. At each time step, the DBN uses the conditional probability P(X_t|X_t−1) to describe the transition from the state at time t−1 to the state at time t. The system state can be expressed as:

$\begin{array}{ll}P(X_t|X_{t-1},Pa(X))& (10)\end{array}$

The joint probability distribution for the entire DBN can be written as the product of joint distributions across time points:

$\begin{array}{ll}P(X_1,X_2,\cdots ,X_T)=P(X_1){\displaystyle \prod _{i=2}^T}P(X_t|X_{t-1},Pa(X_i^t))& (11)\end{array}$

where X_t represents the random variables at time t, and T is the total number of time steps. This equation demonstrates that a DBN can effectively capture temporal dependencies within a sequence through its recursive structure.

To simplify dynamic model inference, DBNs often assume two key properties: the First-order Markov Property, in which the state of a variable at time t depends only on its state at the previous time step t−1, and the Time-invariant Transition Probabilities, where is the transition probabilities remain constant over time, unaffected by shifts in the time series (Nima, 2015).

3.3.2 Network structure and parameter learning

During the construction of a DBN, network structure learning and parameter learning are the two key steps. The goal of network structure learning is to determine the structure of the BN at each time point and define the dependencies between different time points. In this study, a correlation analysis is first performed on the data of every two wildfire factors. If a correlation is found between two factors, they are connected in the BN structure. The direction of the edges is then determined by analyzing the causal relationship between the factors, based on expert knowledge.

Given that the occurrence of wildfires in transmission corridors is primarily influenced by dynamic changes in meteorological factors, and that meteorological data from the distant past has minimal impact on the likelihood of a wildfire at a specific time, the DBN model is constructed by considering only two adjacent time slices. This approach extends the static BN model along the time axis. Dynamic factors are connected by directed arrows, reflecting their causal relationships within the time series.

The parameters of the DBN nodes are defined by their Conditional Probability Tables (CPTs), which characterize the probabilistic dependencies among wildfire factors. Under the condition of complete observational data in the historical wildfire dataset, the CPTs of network nodes are estimated using the maximum likelihood estimation (MLE) method (Yang and Baoding, 2022).

4 Results

4.1 Key wildfire factors selection

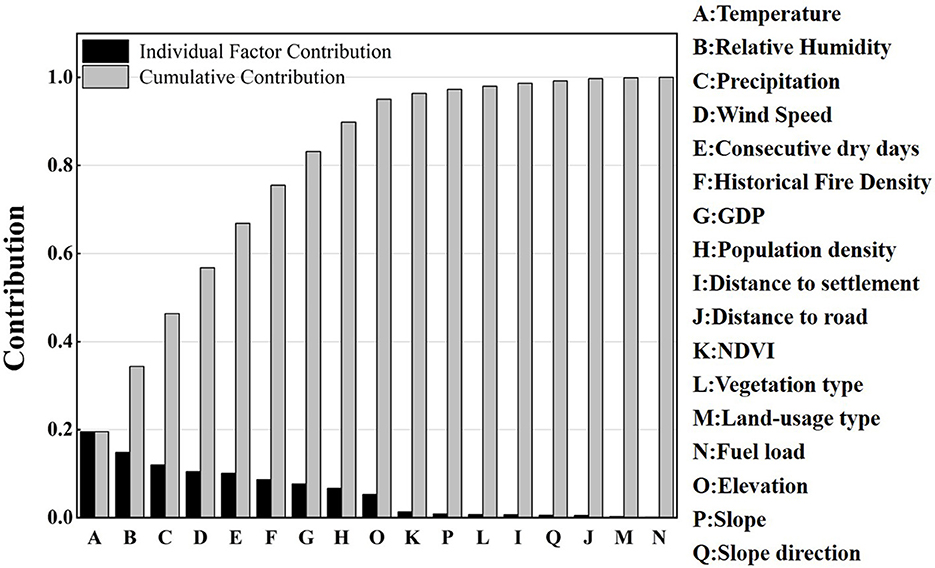
By using the RF algorithm, the importance of wildfire factors was evaluated. The contribution ranking and cumulative contribution of factors are shown in Figure 3. The analysis revealed that meteorological factors were the most significant contributors to wildfire occurrences, a finding that aligns with previous studies. For instance Yu et al. (2025) highlights the importance of precipitation and humidity in driving wildfires in Taiwan province, while (Liu et al., 2024) emphasizes the role of meteorological variables like sunshine duration and relative humidity in influencing wildfire risk in Southwest China. These findings further underscore the central role of climatic conditions in shaping wildfire events. Beyond meteorological factors, factors such as historical fire density, GDP, population density, and elevation also had notable impacts on wildfire risk. The cumulative contribution of the top nine factors accounts for 95.07% of the total contribution, whereas vegetation and geographical factors exhibited relatively lower contributions.

Figure 3

Figure 3. Contribution ranking and cumulative contribution of wildfire factors.

This pattern arises because this study focuses on short-term wildfire risk. Meteorological conditions directly influence vegetation flammability, making them the primary driver of wildfire events. Furthermore, as a highly populated province in China, Guangdong experiences frequent human activities, with the majority of wildfires being caused by human ignition, whether intentional or accidental. Therefore, factors related to human activity, such as population density and GDP, correlate strongly with wildfire spatial patterns. Furthermore, Guangdong exhibits relatively minor variations in terrain and elevation, while its subtropical climate ensures that vegetation remains green throughout the year. As a result, topographic and vegetation factors show limited spatial variation, thus having a reduced impact on differentiating wildfire risk across the region. Given the high cumulative contribution of the nine most significant factors, they were selected for the construction of the DBN model.

4.2 Performance of ARIMA-GARCH forecasts

The time series data of the meteorological factors were first transformed into stationary series by using differencing. And the stationarity was then tested using the Augmented Dickey-Fuller (ADF) test (Torbjorn, 2014), as shown in Supplementary Table 2. It shows that the ADF test statistics for all meteorological factors were below the critical values at the 1%, 5%, and 10% significance levels, indicating that the differenced series data is stationary with over 99% confidence. The developed ARIMA models for temperature, precipitation, humidity, wind speed, and consecutive dry days are shown in Equations 12–16.

$\begin{array}{ll}{y}_{t\text{\_}T}=-0.007+0.5576·y_{t-1}+{\epsilon }_t-0.3860·{\epsilon }_{t-1}& (12)\end{array}$

$\begin{array}{r}{y}_{t\text{\_}P}=0.0128-0.2878y_{t-1}+0.0593y_{t-2}\\ +{\epsilon }_t-0.6422{\epsilon }_{t-1}-0.2939{\epsilon }_{t-2}& (13)\end{array}$

$\begin{array}{ll}{y}_{t\text{\_}H}=0.0017+0.6137y_{t-1}+{\epsilon }_t-0.4706{\epsilon }_{t-1}& (14)\end{array}$

$\begin{array}{r}{y}_{t\text{\_}W}=0.0011-0.3925y_{t-1}+0.5473y_{t-2}\\ +{\epsilon }_t-0.0224{\epsilon }_{t-1}-0.9976{\epsilon }_{t-2}& (15)\end{array}$

$\begin{array}{ll}{y}_{t\text{\_}C}=-0.0031-0.0256y_{t-1}+0.0081y_{t-2}+{\epsilon }_t-0.9171{\epsilon }_{t-1}& (16)\end{array}$

Thermal factors, such as temperature and humidity, exhibit strong autoregressive persistence, with coefficients of 0.5576 and 0.6137, respectively, indicating that current values are heavily influenced by their immediate past. This persistence reflects the inertia inherent in atmospheric conditions, where changes are gradual. Precipitation processes, including both precipitation and consecutive dry days, are dominated by significant negative moving average effects. Precipitation is strongly suppressed in the days following a major rainfall event due to moisture depletion, as reflected by the negative MA coefficients of −0.6422 and −0.2939. Similarly, consecutive dry days is primarily driven by a very strong negative MA effect of −0.9171, where a precipitation event immediately resets the dry spell count. Wind speed displays an oscillatory pattern in its autoregressive structure, with an initial negative response at y_t−1 and a positive response at y_t−2, alongside a pronounced delayed negative moving average effect at ε_t−2.

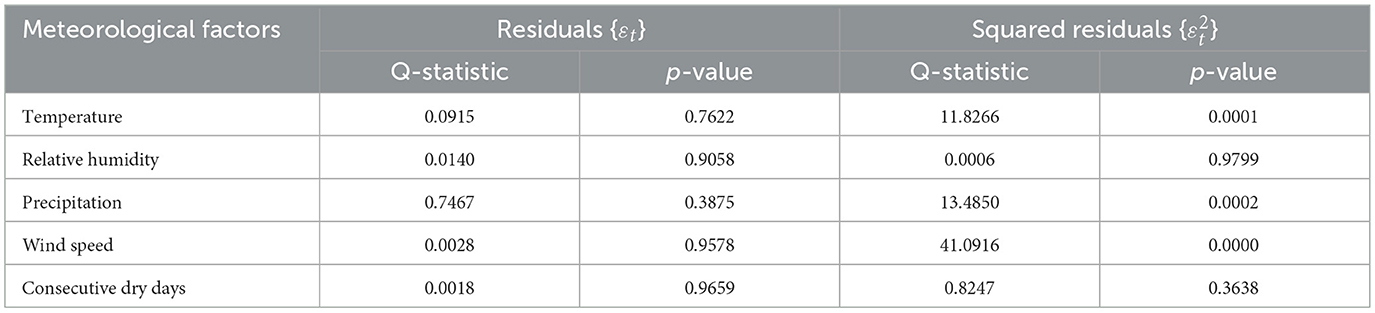
To assess the applicability of the ARIMA models, the Q-statistic was applied to test the residuals {ε_t} and squared residuals {${\epsilon }_t^2$} for white noise. The results are presented in Table 2.

Table 2

Table 2. Q-statistic for the ARIMA models.

The results indicate that the p-values of the residuals {ε_t} for all the meteorological factors are >0.05, suggesting that the residuals are white noise at the 95% confidence level, indicating no autocorrelation in the series. However, the p-values of the squared residuals {${\epsilon }_t^2$} for temperature, humidity, and wind speed are < 0.05, indicating potential autoregressive heteroscedasticity in these residuals. To further explore this issue, the Autoregressive Conditional Heteroskedasticity-Lagrange Multiplier (ARCH-LM) test was applied to the residuals of these models (Supplementary Table 3), confirming the presence of heteroscedasticity. This heteroscedasticity can be attributed to the physical characteristics of temperature, humidity, and wind speed. Specifically, temperature tends to show persistence with extreme values, where previous temperature anomalies can influence the current state, leading to volatility clustering. Similarly, humidity is similarly affected by weather systems, often resulting in extended periods of high or low levels. Wind speed, influenced by turbulent energy cascade processes, can also show clustering, especially during strong wind events such as typhoons. In contrast, precipitation and consecutive dry days are more discrete and independent, lacking such persistence, which explains their lack of heteroscedasticity.

To address this heteroscedasticity, the GARCH was used to model the standard residuals of temperature, humidity, and wind speed, were derived as shown in Equations 17–19.

$\begin{array}{ll}{h}_{t\text{\_}T}=0.1007+0.2384z_{t-1}^2+0.7616h_{t-1}& (17)\end{array}$

$\begin{array}{ll}{h}_{t\text{\_}H}=4.7743+0.3534z_{t-1}^2+0.6466h_{t-1}& (18)\end{array}$

$\begin{array}{ll}{h}_{t\text{\_}W}=0.7290-0.2116z_{t-1}^2+0.7884h_{t-1}& (19)\end{array}$

Temperature exhibits strong persistence (α + β ≈ 1), indicating that temperature fluctuations have long-lasting inertia, with larger deviations in temperature leading to increased volatility in subsequent periods. Humidity, on the other hand, demonstrates a strong short-term response to shocks (α = 0.35), meaning that significant fluctuations tend to persist for a longer duration. Wind speed shows a unique negative shock absorption characteristic (α = −0.21), suggesting that an increase in past volatility may lead to a decrease in current wind speed. Additionally, the high volatility persistence (β = 0.79) indicates that strong wind events are followed by prolonged periods of high wind speeds.

The Q-statistic test showed that the residuals {ε_t} and squared residuals {${\epsilon }_t^2$} of the three ARIMA-GARCH models passed the white noise test (Table 3). This indicates that the residuals do not exhibit autocorrelation, and the GARCH model effectively captures the conditional heteroscedasticity in the residuals. Therefore, the ARIMA-GARCH models for temperature, humidity, and wind speed can be effectively used for wildfire risk forecasting.

Table 3

Table 3. Q-test for the ARIMA-GARCH models.

The one-step prediction method was used to forecast the meteorological factor sequences, with the results shown in Figure 4. The predicted values of the models are generally consistent with the actual values. However, there are still some deviations at nodes with larger fluctuations, especially in temperature, relative humidity, and wind speed.

Figure 4

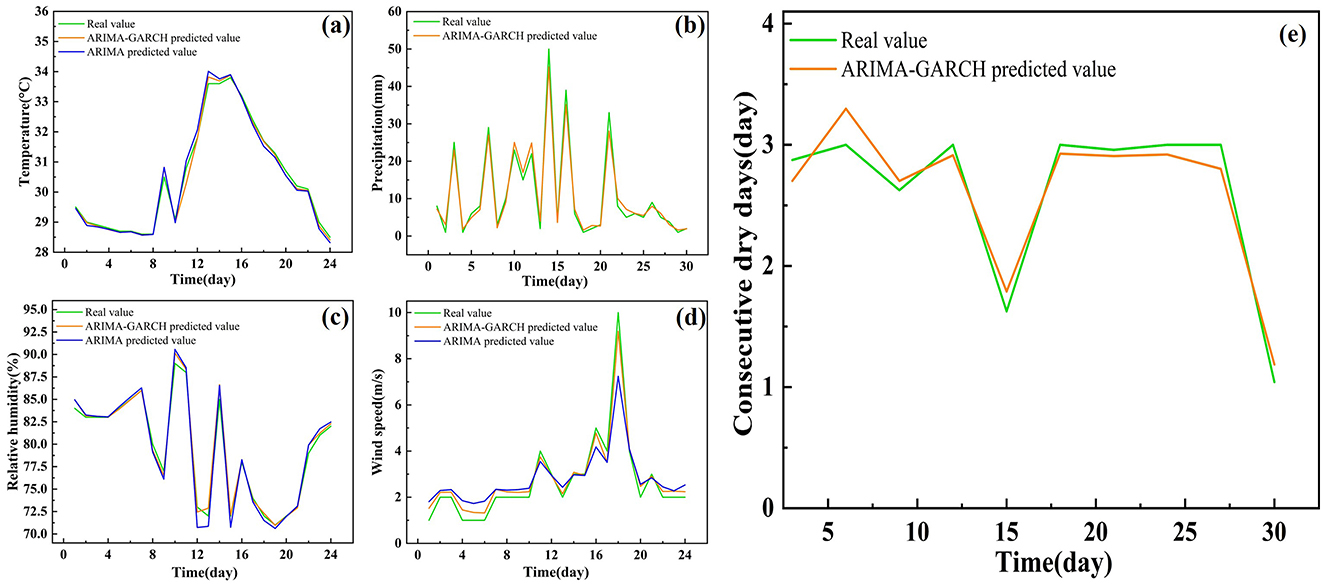
Figure 4. The prediction results of meteorological factors by using ARIMA-GARCH models, (a) Temperature; (b) Precipitation; (c) Relative humidity; (d) Wind speed; (e) Consecutive dry days.

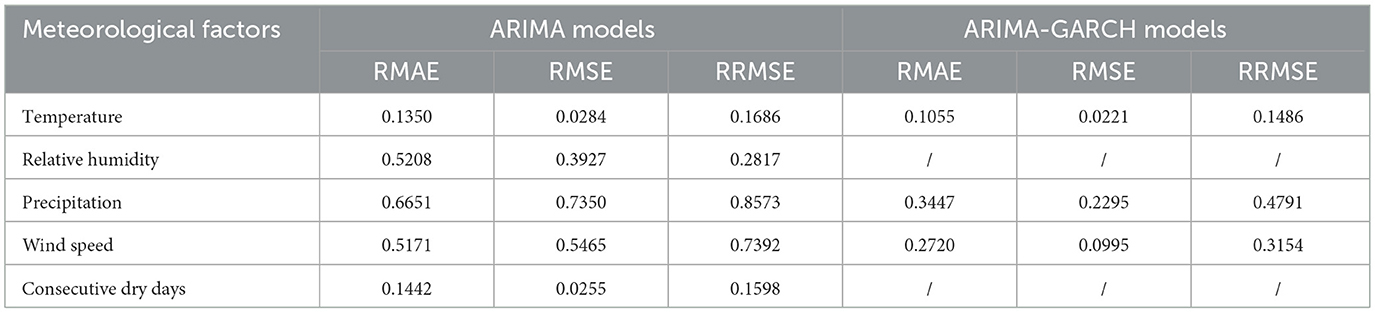
To further analyze the model's performance, the Mean Absolute Error (RMAE), Root Mean Square Error (RMSE), and Root Mean Square Relative Error (RRMSE) were calculated. The results, presented in Table 4, demonstrate that the ARIMA model provides good prediction accuracy. And for temperature, relative humidity, and wind speed, the ARIMA-GARCH mixed model further improved the accuracy by effectively capturing the heteroscedasticity, resulting in more precise predictions.

Table 4

Table 4. Error analysis of ARIMA and ARIMA-GARCH models.

4.3 DBN wildfire risk assessment

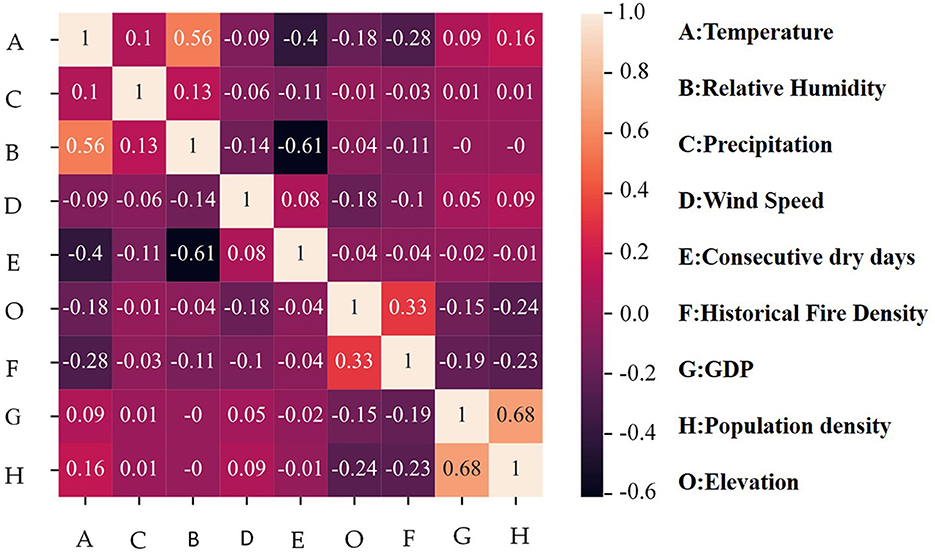
To explore the interdependencies among wildfire factors, Pearson correlation analysis was first conducted on the corresponding data. The resulting correlation heatmap is presented in Figure 5.

Figure 5

Figure 5. Interrelationships of wildfire factors.

According to correlation theory, a correlation coefficient exceeding an absolute value of 0.1 signifies a significant relationship between two factors (Xiang et al., 2022). In this study, higher altitudes are associated with lower temperatures, and human populations typically inhabit lower elevation areas. As a result, a significant negative correlation is observed between altitude and both population density and temperature. The correlation coefficients are −0.24 and −0.18, respectively. On the other hand, Guangdong Province, as a populous and economically developed region with strict fire regulations in urban areas, experiences wildfires primarily in sparsely populated regions. While population density decreases with altitude, the positive correlation between altitude and wildfire density likely reflects the prevalence of anthropogenic fire use (e.g., in upland agriculture or forest fringe settlements) and less effective suppression in remote highland areas. Consequently, the correlation coefficient between population density and historical wildfire density is −0.23. The coupled relationship between altitude, population density, and historical wildfire density results in a positive correlation of 0.33 between altitude and historical wildfire density.

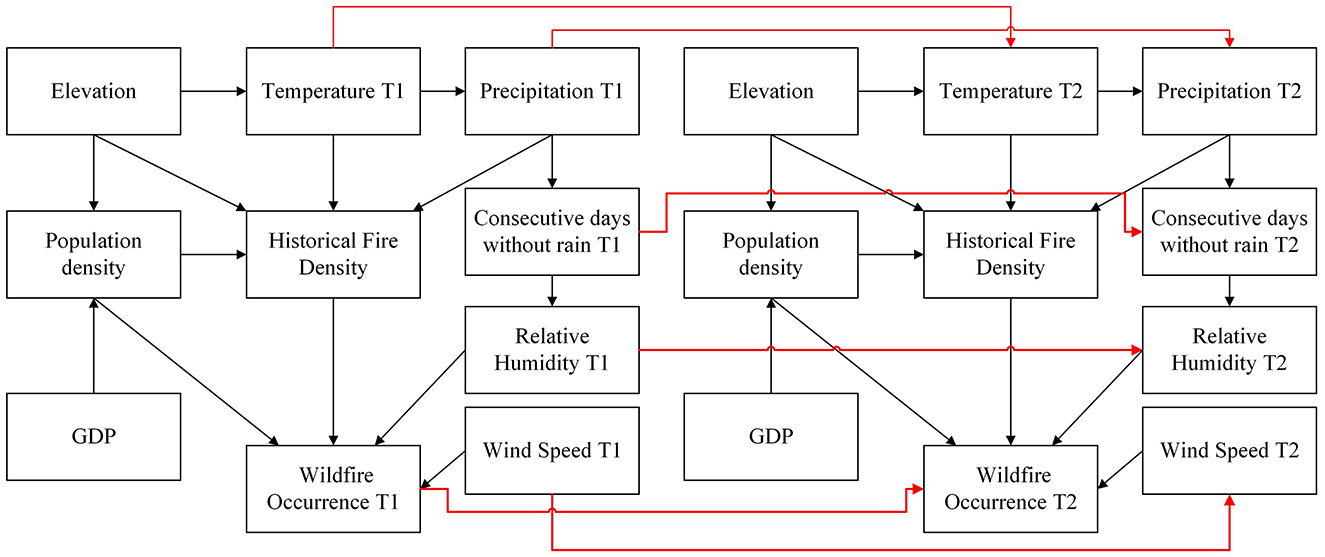
Based on this analysis, the wildfire factors are first connected using directed arrows according to their causal relationships, forming a static BN structure. Considering the first-order Markov assumption and operational constraints in wildfire response, only two adjacent time slices were used for the DBN structure, as shown in Figure 6. In this model, wildfire events exhibit spatiotemporal clustering under specific solar terms due to folk activities, and therefore, the wildfire event nodes of adjacent time slices are linked by directed edges. Additionally, meteorological data, as dynamic variables, interact to jointly influence wildfire occurrences, necessitating directed edges to connect the meteorological factors. Other static factors, however, do not require connections across time slices.

Figure 6

Figure 6. Network structure of DBN for wildfire risk prediction.

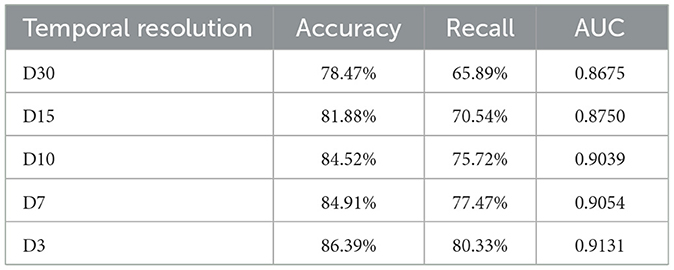
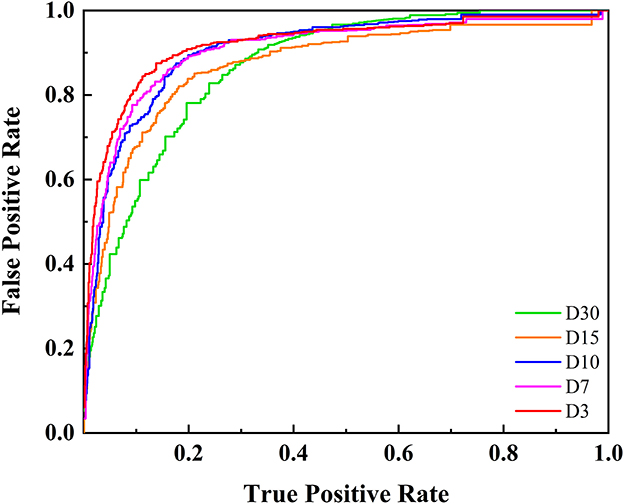
After establishing the DBN's structure, the CPTs for the network nodes were estimated using MLE with datasets D30, D15, D10, D7, and D3. Based on these CPTs, the DBN models for wildfire risk prediction in transmission corridors were constructed. The models were then trained and tested by using a 5-fold cross-validation method. The confusion matrix, ROC curve, and AUC value were used to evaluate the models' generalization ability, as presented in Table 5 and Figure 7.

Table 5

Table 5. Performance of DBN models with different temporal resolution.

Figure 7

Figure 7. ROC of DBN models with different temporal resolution.

The results indicate that the accuracy of wildfire prediction models improves significantly as the temporal resolution decreases. This improvement is primarily due to the stronger influence of meteorological factors on short-term wildfire risk assessment. As the temporal resolution decreases, the forecasted meteorological data becomes more accurate, allowing for a more precise reflection of real-time wildfire risk. Although finer temporal resolutions could further refine predictions, practical operational constraints, such as the 48–72 h response window for strategies like drone deployment and load shifting, limit the relevance of finer resolutions for guiding differentiated maintenance and risk mitigation strategies. Therefore, subsequent research was conducted with a temporal resolution of 3 days, which balances both predictive accuracy and operational feasibility.

4.4 Impact of individual wildfire factors

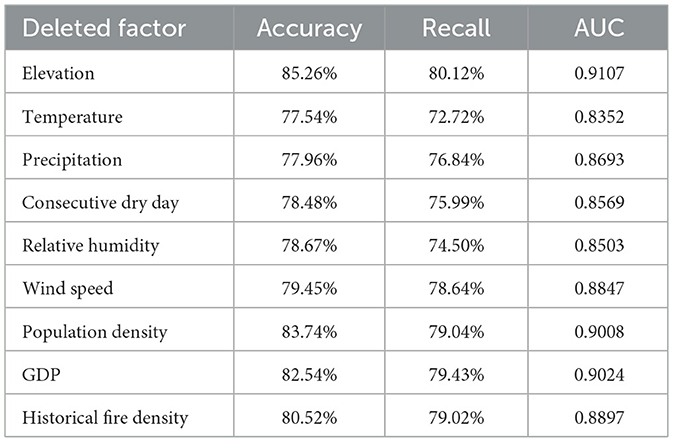
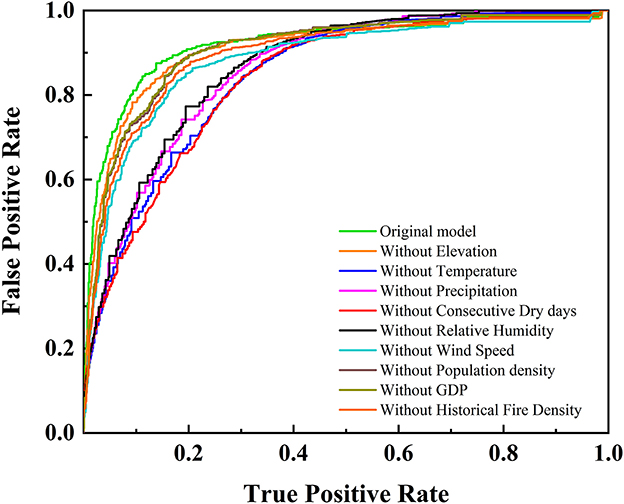
To further investigate the impact of different wildfire factors on wildfire risk, a series of modeling experiments by sequentially removing each factor from the DBN model was conducted. In cases where a factor has both parent and child nodes, deleting this factor results in a direct connection between the parent and child nodes. For example, temperature influences precipitation, which in turn affects the number of consecutive dry days. If the precipitation node is eliminated, temperature will directly affect the number of consecutive dry days in the model. The performance of the DBN models with deleted wildfire factors is presented in Table 6 and Figure 8.

Table 6

Table 6. Performance of DBN models with deleted wildfire factors.

Figure 8

Figure 8. ROC of DBN models without individual wildfire factor.

The analysis reveals that meteorological factors exert the most significant impact on model performance, with temperature being the most influential. After deleting the temperature node, the accuracy of the DBN model drops to 77.54%, and the recall rate decreases to 72.72%, which is significantly lower than the baseline model performance that includes temperature.

In contrast, the influence of population density and GDP on model performance is relatively minor. This may be attributed to the inclusion of historical fire density as a key wildfire risk factor in the model. Historical fire density partially reflects human activity and fire usage patterns within a region, thus mitigating the influence of socio-economic factors, such as population density and GDP, on wildfire risk. As a result, when historical fire density is included, the contribution of population density and GDP may be partially diminished, leading to a weaker independent effect of these factors on the model's prediction.

4.5 Impact of predicted meteorological data

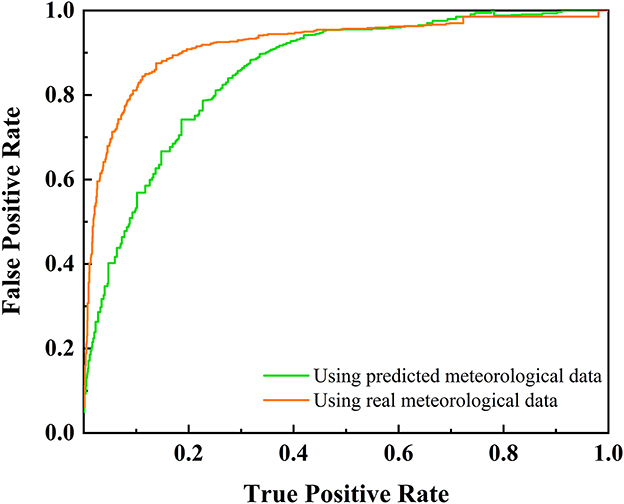
To investigate the effect of predicted meteorological data on the DBN model, meteorological factors with a 3-day temporal resolution were incorporated along with other static wildfire risk factors as inputs for training the model. The resulting ROC curve for the wildfire prediction model is shown in Figure 9.

Figure 9

Figure 9. ROC of DBN models by using predicted meteorological data.

After incorporating predicted meteorological data, the model's AUC value decreased from 0.9131 to 0.8693. And the accuracy and recall rates dropped to 79.64% and 75.41%, respectively. This reduction in performance can be attributed to the introduction of new errors by using predicted meteorological data. Nevertheless, the ARIMA-DBN model continued to exhibit acceptable performance for wildfire risk prediction, despite the reduced accuracy.

4.6 Application of ARIMA-DBN model

In the practical application of the model, real-time meteorological observations from weather stations were first used to predict the meteorological factors for the next 3 days by using the ARIMA-GARCH model. Subsequently, Kriging spatial interpolation was employed to interpolate the meteorological predictions from each station onto a spatial grid, covering the study area and generating spatially continuous predicted results. These forecasts serve as input for the pre-constructed DBN wildfire risk prediction model, enabling the prediction of future wildfire occurrence risks along the transmission corridor. The model's output is classified into different wildfire risk levels based on predefined thresholds and is spatially visualized through the ArcGIS platform. The resulting risk distribution maps offer clear, spatialized decision support for power grid operation and maintenance departments, facilitating targeted wildfire prevention and emergency preparedness efforts.

To validate the model's predictive capability, wildfire risk predictions in Guangdong Province were performed for two specific periods in 2023 and 2024: Period 1, from January 15 to January 17, and Period 2, from April 5 to April 8. The wildfire occurrence probabilities were then classified into four risk levels—Low, Moderate, High, and Very High risk—using 25%, 50%, and 75% thresholds based on the probabilities derived from the DBN model, as shown in Figures 10.

Figure 10

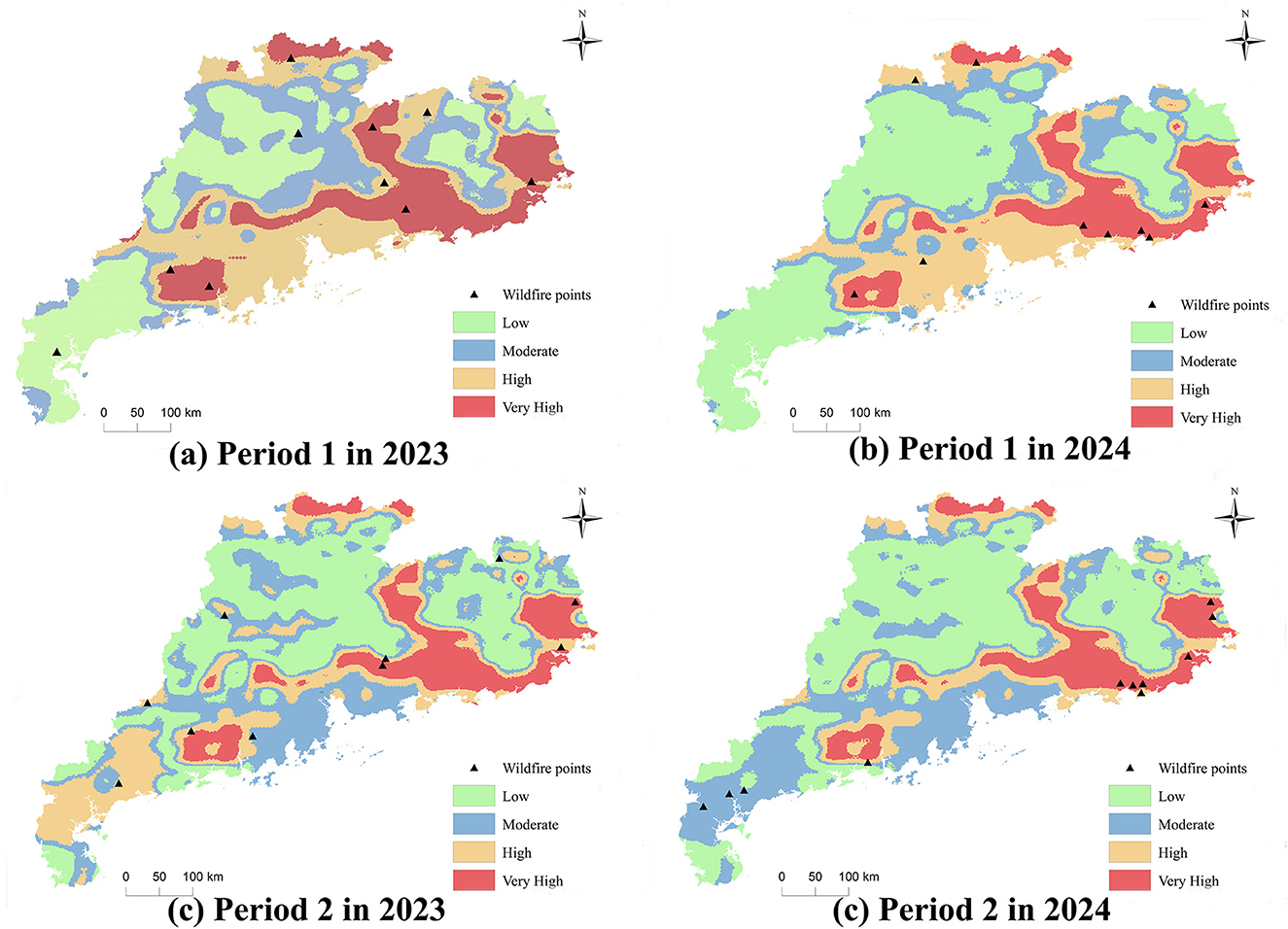
Figure 10. Typical wildfire risk distribution maps for Guangdong Province, (a) Period 1 in 2023; (b) Period 1 in 2024; (c) Period 2 in 2023; (d) Period 2 in 2024.

The risk distribution map illustrates that meteorological factors significantly influence the fire risk distribution across different periods. In general, the eastern, northern, and northeastern to western parts of the Pearl River Delta in Guangdong Province are identified as high-risk wildfire areas. The high-risk nature of these regions primarily results from low rainfall during the autumn and winter months, leading to prolonged drought conditions, which increases vegetation dryness and wildfire likelihood. Additionally, the predominantly mountainous and hilly terrain in these areas—such as in Raoping—facilitates the spread of wildfires toward ecologically sensitive regions like water source forests and core ecological zones, especially in the presence of strong winds.

The high-risk areas also include regions such as Heyuan, Shanwei, Jieyang, Shantou, Chaozhou, and Meizhou. While economically underdeveloped compared to the Pearl River Delta, these areas have rich cultural traditions and are more prone to fire hazards due to activities like firecracker lighting and paper money burning, particularly during the Spring Festival and Qingming Festival. The influx of migrant workers returning home during these periods further increases the fire risk, with common sources of ignition such as discarded cigarette butts. Additionally, high population density, regulatory gaps, and delayed social customs contribute to vulnerabilities in wildfire prevention, leading to sustained high wildfire risks.

Statistical analysis of wildfire alerts from the local power company, correlated with wildfire risk levels, is summarized in Supplementary Table 4. The proportion of wildfires occurring in high-risk and very high-risk areas during four time periods was 80%, 100%, 70%, and 72.72%, respectively. These results provide preliminary evidence of the model's effectiveness in identifying high-risk wildfire zones in Guangdong Province.

4.7 Discussion

This study focuses on Guangdong Province and presents a wildfire risk predictive model for transmission corridors based on ARIMA-DBN. In the factor analysis, meteorological factors (such as precipitation and humidity) were found to play a dominant role in short-term wildfire risk prediction, with a cumulative contribution rate exceeding 50%. This finding is highly consistent with conclusions from studies conducted in East Asia (Yu et al., 2025; Liu et al., 2024), highlighting the direct regulatory mechanism of climate conditions on vegetation flammability. In particular, in subtropical and humid regions such as Guangdong, fluctuations in meteorological conditions can quickly alter surface fuel dryness, thereby triggering wildfire events.

The significant impact of human activity factors reflects the regional characteristics of Guangdong. As a densely populated province, more than 90% of wildfires in Guangdong are caused by human activities, such as sacrifices, agricultural practices, which sharply contrasts with temperate regions where natural fires dominate. On the other hand, the relatively low contribution of terrain and vegetation factors can be attributed to the weak spatial heterogeneity: Guangdong has a generally limited elevation range (average altitude < 500 meters), and the evergreen vegetation coverage throughout the year reduces the seasonal variation in fuel load.

Given the key role of meteorological factors in wildfire risk, the accurate forecasting of meteorological data becomes central to assessing risk distribution. The results show that temperature and humidity exhibit strong persistence, reflecting the thermal inertia of the atmospheric system, while the negative moving average effect of precipitation supports the self-regulation process of the “rain-drought” mechanism. These characteristics, however, limit the applicability of the traditional ARIMA model for forecasting meteorological fluctuations. To address this issue, the GARCH model was introduced, which, by capturing the volatility clustering of temperature and wind speed, effectively enhanced the representation of meteorological data volatility. Although the use of the ARIMA-GARCH model led to a 6.74% decrease in the DBN model's accuracy and a 4.92% drop in recall, the overall performance remained within an acceptable range.

Based on the model, the power grid can effectively identify high-risk wildfire areas and accurately locate transmission lines and towers within these areas. This allows for the implementation of a differentiated inspection resource strategy (Arab et al., 2021; Vazquez et al., 2022). For high-risk areas, inspection frequencies should be increased, employing drones for frequent surveillance and scanning of key transmission lines. Additionally, dynamic adjustments to transmission loads can be made, and emergency response plans can be developed to address potential circuit breaker issues in critical lines during wildfires. The power grid should also collaborate closely with local forestry, meteorological, and emergency management departments, ensuring timely transmission of wildfire risk forecast data to forestry fire prevention stations and fire brigades for coordinated control measures.

It is important to note that the model is based on historical wildfire data from the transmission corridors in Guangdong Province. Therefore, its construction and prediction results are influenced by regional factors such as climate, vegetation, terrain, and human activity. Variations in these factors across different regions can significantly affect wildfire occurrence and spread, thus influencing the model's performance. As a result, the direct application of this model to other regions may require adjustments to account for local conditions.

For application in other regions, the framework outlined in this study can serve as a reference. Initially, historical wildfire data for the target region should be collected and processed, followed by tailored feature selection based on the region's climate, vegetation, and terrain. Additionally, the ARIMA-based dynamic forecasting model and DBN structure should be redesigned and optimized according to the specific conditions of the target area. Such adjustments will improve the model's accuracy and practicality in various regions. Future research will focus on expanding the model's applicability, particularly by validating its performance in different regions. Cross-regional comparative studies will provide opportunities to refine the model and explore its broader applicability on a global scale.

5 Conclusions

To overcome the limitations of existing methods in predicting the wildfire risk distribution in transmission corridors, a spatiotemporal distribution prediction method based on the ARIMA-DBN framework is proposed.

(1) The ARIMA model alone was sufficient for accurately predicting precipitation and consecutive non-rainy days. However, for temperature, humidity, and wind speed, the residuals from the ARIMA models exhibited conditional heteroskedasticity, necessitating the incorporation of GARCH models for improved residual fitting.

(2) As the temporal resolution was refined, the DBNs' model performance improved, as the improved accuracy of the meteorological data. It achieved an accuracy of 86.39% and a recall of 80.33% with a 3-day temporal resolution.

(3) The ARIMA-DBN framework was demonstrated to enable spatiotemporal wildfire risk prediction for transmission corridors. By using the prediction of meteorological data, the accuracy of ARIMA-DBN decreased to 79.64% due to the propagation of meteorological prediction errors, retaining a robust predictive capability.

(4) This integrated approach provides a scalable solution for short-term wildfire risk prediction and can support proactive management of transmission corridors in fire-prone regions. While dominating wildfire factors may differ, the BDN structure proposed here may not be directly applicable to other regions. However, the technical framework can help identify appropriate wildfire factors and network structures tailored to specific regions.

Data availability statement

The datasets presented in this article are not readily available because they can only be used for wildfire risk studies in Guangdong Province. Requests to access the datasets should be directed to emhvdV9ka3lAMTYzLmNvbQ==.

Author contributions

EZ: Writing – original draft. LW: Writing – review & editing. HW: Data curation, Conceptualization, Writing – review & editing, Investigation. ZW: Project administration, Formal analysis, Writing – review & editing, Methodology, Supervision. RW: Writing – review & editing, Resources, Visualization, Validation.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

We thank China Southern Power Grid Corporation Science and technology projects GDKJXM20222559.

Conflict of interest

EZ, HW, and RW were employed by Electric Power Research Institute of Guangdong Power Grid Co., Ltd. LW and ZW were employed by Guangdong Power Grid Co., Ltd.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2025.1637263/full#supplementary-material

References

Albertson, K., Aylen, J., Cavan, G., and McMorrow, J. (2019). Forecasting the outbreak of moorland wildfires in the English Peak District. J. Environ. Manag. 90, 2642–2651. doi: 10.1016/j.jenvman.2009.02.011

PubMed Abstract | Crossref Full Text | Google Scholar

Arab, A., Khodaei, A., Eskandarpour, R., Thompson, M. P., and Wei, Y. (2021). Three lines of defense for wildfire risk management in electric power grids: a review. IEEE Access 9, 61577–61593. doi: 10.1109/ACCESS.2021.3074477

Crossref Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2004). Multimodel inference understanding AIC and BIC in model selection. Sociol. Methods Res. 33, 261–304. doi: 10.1177/0049124104268644

Crossref Full Text | Google Scholar

Chen, G., Liang, Z., Dong, Y., et al. (2020). Analysis and reflection on the marketization construction of electric power with chinese characteristics based on energy transformation. Proc. CSEE 40, 369–378. doi: 10.13334/j.0258-8013.pcsee.191382

Crossref Full Text | Google Scholar

Chen, W., Zhou, Y., Zhou, E., Xiang, Z., Zhou, W., and Lu, J. (2021). Wildfire risk assessment of transmission-line corridors based on naïve bayes network and remote sensing data. Sensors 21:634. doi: 10.3390/s21020634

PubMed Abstract | Crossref Full Text | Google Scholar

Costafreda-Aumedes, S., Comas, C., and Vega-Garcia, C. V. (2017). Human-caused fire occurrence modelling in perspective: a review. Int. J. Wildland Fire 26, 983–998. doi: 10.1071/WF17026

Crossref Full Text | Google Scholar

de Vasconcelos, M. J. P., Silva, S., Tome, M., Alvim, M., and Pereira, J. M. C. (2001). Spatial prediction of fire ignition probabilities: comparing logistic regression and neural networks. Photogrammetr. Eng. Remote Sens. 67, 73–81. doi: 10.1016/S0031-0182(00)00158-9

Crossref Full Text | Google Scholar

Faivre, N., Goulden, M. L., Randerson, J. T., and Jin, Y. (2014). Controls on the spatial pattern of wildfire ignitions in Southern California. Int. J. Wildland Fire 23, 799–811. doi: 10.1071/WF13136

Crossref Full Text | Google Scholar

França, G. B., Oliveira, A. N. D., Paiva, C. M., Peres, L. D. F., Silva, M. B. D., and Oliveira, L. M. T. D. (2014). A fire-risk-breakdown system for electrical power lines in the North of Brazil. J. Appl. Meteorol. Climatol. 53, 813–823. doi: 10.1175/JAMC-D-13-086.1

Crossref Full Text | Google Scholar

Jatinder, K., Singh, P. K., and Sarbjit, S. (2023). Autoregressive models in environmental forecasting time series: a theoretical and application review. Environ. Sci. Pollut. Res. 30:19617–19641. doi: 10.1007/s11356-023-25148-9

PubMed Abstract | Crossref Full Text | Google Scholar

Kalabokidis, K. D., Koutsias, N., Konstantinidis, P., and Vasilakos, C. (2007). Multivariate analysis of landscape wildfire dynamics in a Mediterranean ecosystem of Greece. Area 39, 392–402. doi: 10.1111/j.1475-4762.2007.00756.x

Crossref Full Text | Google Scholar

Li, J., Liu, Y., Wang, J., Chen, C., Huang, D., Shao, Y., et al. (2024). Prediction of forest-fire occurrence in Eastern China utilizing deep learning and spatial analysis. Forests 15:1672. doi: 10.3390/f15091672

Crossref Full Text | Google Scholar

Liu, J., Wang, Y., Lu, Y., Zhao, P., Wang, S., Luo, Y., et al. (2024). Application of remote sensing and explainable artificial intelligence (XAI) for wildfire occurrence mapping in the mountainous region of Southwest China. Remote Sens. 16:3602. doi: 10.3390/rs16193602

Crossref Full Text | Google Scholar

Liu, S., Lu, J., Zhou, E., Huang, Y., Wei, R., and Chen, W. (2022). Refined wildfire monitoring and alarming technology for overhead transmission lines. Guangdong Electric Power 35, 99–106. doi: 10.3969/j.issn.1007-290X.2022.006.011

Crossref Full Text | Google Scholar

Lu, J., Liu, Y., Xu, X., Yang, L., Zhang, G., and He, L. (2017). Prediction and early warning technology of wildfire nearby overhead transmission lines. High Voltage Eng. 43, 314–320. doi: 10.13336/j.1003-6520.hve.20161227041

Crossref Full Text | Google Scholar

Mallinis, G., Petrila, M., Mitsopoulos, I., Lorent, A., Neagu, S., Apostol, B., et al. (2019). Geospatial patterns and drivers of forest fire occurrence in Romania. Appl. Spatial Anal. Policy 12, 773–795. doi: 10.1007/s12061-018-9269-3

Crossref Full Text | Google Scholar

Marcot Bruce, G., and Penman Trent, D. (2019). Advances in Bayesian network modelling: integration of modelling technologies. Environ. Modell. Softw. 111, 386–393. doi: 10.1016/j.envsoft.2018.09.016

Crossref Full Text | Google Scholar

Nima, K. (2015). Application of dynamic Bayesian network to risk analysis of domino effects in chemical infrastructures. Reliab. Eng. Syst. Saf. 138, 263–272. doi: 10.1016/j.ress.2015.02.007

Crossref Full Text | Google Scholar

Oliveira, S., Oehler, F., San-Miguel-Ayanz, J., Camia, A., and Pereira, J. M. (2012). Modeling spatial patterns of fire occurrence in Mediterranean Europe using multiple regression and random forest. For. Ecol. Manag. 275, 117–129. doi: 10.1016/j.foreco.2012.03.003

Crossref Full Text | Google Scholar

Paraskev, K. (2017). Volatility estimation for Bitcoin: a comparison of GARCH models. Econ. Lett. 158, 3–6. doi: 10.1016/j.econlet.2017.06.023

Crossref Full Text | Google Scholar

Prestemon, J. P., and Butry, D. T. (2005). Time to burn: modeling wildland arson as an autoregressive crime function. Am. J. Agric. Econ. 87, 756–770. doi: 10.1111/j.1467-8276.2005.00760.x

Crossref Full Text | Google Scholar

Qin, X., Li, Z., Yan, H., and Zhan, Z. (2013). Characterising vegetative biomass burning in China using MODIS data. Int. J. Wildland Fire 23, 69–77. doi: 10.1071/WF12163

Crossref Full Text | Google Scholar

Shu, S., Chen, Y., Cao, S., Zhang, B., Fang, C., and Xu, J. (2023). Monitoring and alarm method for wildfires near transmission lines with multi-doppler weather radars. IET Gen. Transm. Distrib. 17, 2055–2069. doi: 10.1049/gtd2.12790

Crossref Full Text | Google Scholar

Torbjorn, L. (2014). Statistical analysis of temperature data sampled at Station-M in the Norwegian Sea. J. Mar. Syst. 130:31–45. doi: 10.1016/j.jmarsys.2013.09.009

Crossref Full Text | Google Scholar

Trakas, D. N., and Hatziargyriou, N. D. (2018). Optimal distribution system operation for enhancing resilience against wildfires. IEEE Trans. Power Syst. 33, 2260–2271. doi: 10.1109/TPWRS.2017.2733224

Crossref Full Text | Google Scholar

Vazquez, D. A. Z., Qiu, F., Fan, N., and Sharp, K. (2022). Wildfire mitigation plans in power systems: a literature review. IEEE Trans. Power Syst. 37, 3540–3551. doi: 10.1109/TPWRS.2022.3142086

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Z. (2023). Research on feature selection methods based on random forest. Tenicki Vjesnik-Technical Gazette 30, 623–633. doi: 10.17559/TV-20220823104912

Crossref Full Text | Google Scholar

Xiang, K., Zhou, Y., Lu, J., Liu, H., Huang, Y., and Zhou, E. (2022). A spatial assessment of wildfire risk for transmission-line corridor based on a weighted Naïve Bayes model. Front. Energy Res. 10:829934. doi: 10.3389/fenrg.2022.829934

Crossref Full Text | Google Scholar

Yang, L., and Baoding, L. (2022). Estimating unknown parameters in uncertain differential equation by maximum likelihood estimation. Soft Comput. 26, 2773–2780. doi: 10.1007/s00500-022-06766-w

Crossref Full Text | Google Scholar

Yu, H. W., Simon Wang, S.-Y., and Liu W, Y. (2025). Do fireweather conditions significantly affect wildfires in subtropical forests in Taiwan? J. Appl. Meteorol. Climatol. 64, 165–184. doi: 10.1175/JAMC-D-24-0031.1

Crossref Full Text | Google Scholar

Zhou, E., Gong, B., Liu, S., Xiang, Z., Shi, X., Huang, D., et al (2022). Statistics and analysis on tripping fault of overhead transmission lines caused by mountain fires in China Southern power crids. Guangdong Electric Power 35, 80–86. doi: 10.3969/j.issn.1007-290X.2022.004.010

Crossref Full Text | Google Scholar

Zhou, J., Ma, W., and Miao, J. (2014). Fire risk assessment of transmission line based on BP neural network. Int. J. Smart Home 8, 119–130. doi: 10.14257/ijsh.2014.8.3.11

Crossref Full Text | Google Scholar

Ziccardi, L. G., Yanai, A. M., Fearnside, P. M., Thiersch, C. R., and Ferreira-Filho, P. J. (2019). Forest fire risk indices and zoning of hazardous areas in Sorocaba, Sao Paulo state, Brazil. J. For. Res. 31, 581–590. doi: 10.1007/s11676-019-00889-x

Crossref Full Text | Google Scholar