Optimization method of electric vehicle energy system based on machine learning

Introduction: To enhance energy management in electric vehicles (EVs), this study proposes an optimization model based on reinforcement learning.

Methods: The model integrates gated recurrent units (GRU) with double deep Q-networks (DDQN) to improve time-series data processing and action value estimation.

Results: Results show that the model achieves the lowest estimation bias (0.017 in training, 0.018 in testing) and the highest cumulative reward (97.1) among all compared methods. In real-world highway scenarios, it records the lowest total energy consumption at 14.2 kWh, achieving a range of 503 km and an energy efficiency of 87.6%.

Discussion: These findings suggest that the proposed model offers a more efficient and reliable solution for EV energy optimization with strong application potential.

1 Introduction

As the electric vehicle (EV) technology rapidly develops, the role of EV energy management systems in improving vehicle range and optimizing energy utilization efficiency is gradually increasing (Demircali and Koroglu, 2022; Wang X. et al., 2022). The sustainable development of EVs is not only facing issues of battery life and energy efficiency, but also constrained by the scarcity of rare metal resources, especially the extensive use of key materials such as neodymium, which poses challenges to the environment and supply chain. The recycling efficiency and sustainable utilization have become important directions for future technological optimization. By constructing intelligent optimization models, strategic support can be provided for battery recycling, resource allocation, and other related areas. In addition, the environmental advantages of EVs can only be truly realized when their power source is renewable energy (such as hydro, wind, solar). If the electricity used relies on fossil fuels, its overall carbon emissions may not necessarily be better than traditional internal combustion engine vehicles. Therefore, while constructing an energy efficiency optimization model, it is necessary to consider it uniformly within the renewable energy system (Skrúcaný et al., 2018). Efficient energy management not only extends battery life, but also significantly cut down the total energy consumption of vehicles, thereby promoting the widespread application of EVs. However, the energy system of EVs involves various dynamic and complex energy flows, including power batteries, electric motor drive systems, onboard electronic devices, and charging systems. This makes traditional optimization methods inefficient and inflexible in dealing with multi-objective and multi-constraint conditions (Venkatasatish and Dhanamjayulu, 2022; Tang et al., 2022). In the last few years, reinforcement learning (RL) has gradually become a critical research direction for optimizing energy management systems in EVs due to its advantages in dynamic decision-making and strategy optimization (Yang et al., 2023). Among them, Deep Q-Network (DQN) and Double Deep Q-Network (DDQN) have shown good performance in handling high-dimensional state spaces and complex decision tasks. However, traditional Q-network structures often struggle to capture long-term dependencies when dealing with time dependent energy management tasks, resulting in limited accuracy and stability of decision-making. Based on this, a new model combining Gated Recurrent Unit (GRU) and DDQN is proposed to further enhance the processing capability of the model for time series data and the accuracy of action value estimation. The innovation of the research lies in utilizing GRU’s gating mechanism to effectively capture time-dependent features, to enhance the model’s understanding and predictive ability of dynamic energy system states. At the same time, adding DDQN can reduce the bias of action value estimation, thereby improving the decision stability and reliability of the model.

2 Related works

The energy optimization problem of EVs usually refers to how to reasonably allocate and manage the resources of EVs in charging, energy consumption, and range, to maximize the operating efficiency of the system, reduce energy loss, lower costs, and improve user satisfaction. Currently, many experts have utilized various multi-objective optimization algorithms to address the energy optimization issue of EVs. Sadeghi D et al. designed a power sharing technology that combines EVs and hybrid renewable energy systems. The issue was addressed by means of two case studies, in which the multi-objective particle swarm optimization algorithm and the multi-objective crow search algorithm were respectively adopted. The experiment findings denoted that the introduction of EVs significantly reduced the total cost of the system and improved the life cycle cost and power supply probability loss index (Sadeghi et al., 2022). Mu et al. proposed a sustainable reverse logistics network optimization method for the recycling of retired new energy vehicle power batteries. The methodology employed in this study involved the construction of a dynamic reverse logistics network model, encompassing six levels and three dimensions: economy, environment, and society. The model’s resolution was achieved through the implementation of a multi-objective combination optimisation model. The research results indicated that dynamic reverse logistics networks had better performance compared to static networks, and the changes in cooperation costs had a greater impact on the transaction volume and network costs between third parties and cooperative enterprises (Mu et al., 2023). Mahato et al. proposed an optimization method for EV charging scheduling. Firstly, the demand variation of EVs and available charging stations were simulated by an on-board self-organizing network model. A novel load scheduling algorithm based on combining Jaya and multiverse optimization algorithms was then used for scheduling optimization. The research results indicated that the combined algorithm outperformed traditional methods in terms of charging cost, adaptability, power consumption, and user convenience (Mahato et al., 2024). In addition to battery-only EVs, RL has also been applied to hybrid energy systems. For instance, Fu et al. proposed a deep RL-based energy management strategy for fuel cell/battery/supercapacitor EVs, which improved adaptability under complex conditions (Fu et al., 2022). Furthermore, Wu et al. reviewed EV–transportation–grid integration, highlighting challenges in multi-agent coordination and energy scheduling across domains (Wu et al., 2023). These studies illustrate the growing complexity and scale of RL applications in EV energy systems.

As a common RL algorithm, DQN can combine deep learning and Q-learning to solve traditional Q-learning problems in high-dimensional state spaces. Currently, many scholars use DQN and its optimization models to solve various complex problems. Cao et al. proposed a path planning method for introducing unmanned aerial and underwater vehicles into ocean sensor networks. Firstly, a 2D scene model was established, and the entry point of the unmanned aerial vehicle was optimized through traversal search algorithm. The performance differences between the cross domain mode and underwater mode of the unmanned aerial vehicle were compared. Path planning was optimized using DDQN algorithm in 3D scene models. The research results showed that the DDQN algorithm saved 60.94% of time and 20.26% of energy, and performed well in path planning (Cao et al., 2024). Xiao et al. proposed a multi-energy microgrid optimization scheduling method grounded on improved DQN to solve the challenges posed by complex energy trading mechanisms and multi-energy coupling decision-making processes. Firstly, by introducing an improved Kriging agent to enhance the GRU-temporal convolutional network model, an equivalent model of the external interaction environment was constructed for each multi-energy microgrid. Next, the traditional greedy strategy was replaced by an improved k-cross sampling strategy. The experiment findings denoted that the improved method outperformed traditional DQN in terms of convergence, stability, energy management, and operational efficiency (Xiao et al., 2023). Oroojlooyjadid et al. designed an improved DQN algorithm to optimize decision-making in beer games. This algorithm did not require assumptions about costs or other conditions, and could quickly adapt to different agent settings through transfer learning. When working with teammates who use benchmark inventory strategies, the algorithm could achieve near optimal order quantities. Sensitivity analysis showed that the model was robust to cost changes, and transfer learning reduced training time by an order of magnitude (Oroojlooyjadid et al., 2022).

In summary, although various optimization methods have been applied to EV energy management systems, there are still some shortcomings. Firstly, many studies have not fully utilized the characteristics of time series data, which limits the adaptability of models in dynamic energy management systems. Secondly, traditional RL algorithms often face issues such as slow convergence speed and large deviation in action value estimation in energy optimization tasks with multiple objectives and constraints, which can affect the accuracy of decision-making. Based on this, the study combines GRU and DDQN to enhance the processing capability of time series data and the accuracy of action value estimation, aiming to achieve efficient optimization of EV energy management systems. While existing hybrid RL models (e.g., DDPG-based, actor-critic, or prioritized replay extensions) have been widely applied to EV-related optimization problems, they often lack the ability to capture long-range temporal dependencies or suffer from value overestimation. By integrating GRU for temporal sequence modeling and DDQN for value stabilization, the proposed Gated Recurrent Unit-Double Deep Q-Network (GRU-DDQN) framework achieves a tighter coupling of state modeling and decision reliability, providing a novel solution path in this domain.

3 Construction of optimization model for EV energy system based on RL

Based on the deficiencies identified in existing research—such as poor adaptability to time-dependent energy flows and large estimation bias in complex environments—this section aims to construct a more effective EV energy optimization framework. Building upon the identified problems, the following methodology outlines the system model and algorithmic improvements. To enhance the energy utilization efficiency and lifespan of EV energy systems, the study firstly conducted a systematic analysis of each energy module of EVs and established an optimization objective function for the EV energy system. Secondly, a solution model was built by combining GRU and DDQN, which enables the objective function to obtain the optimal solution and achieve energy optimization utilization.

3.1 Construction of energy system model for electric vehicles

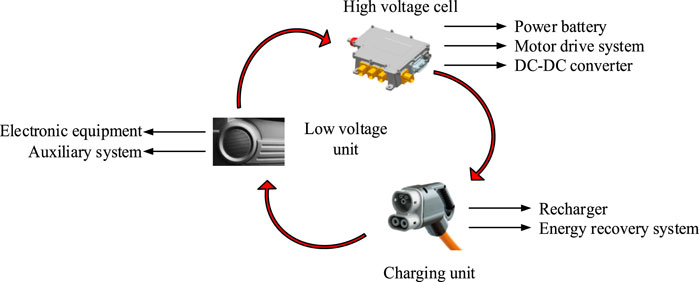
To comprehensively understand and enhance the energy management system of EVs, the study first conducted a systematic analysis and modeling of each energy module of the vehicle, dividing it into three categories: high-voltage units, low-voltage units, and charging units. The energy composition structure of the entire EV is shown in Figure 1.

Figure 1

Figure 1. Energy composition and structure diagram of electric vehicles.

In Figure 1, the high-voltage unit mainly includes a power battery and an electric motor drive system. The power battery constitutes the core of the energy system. Its principal functions include the storage and supply of electrical energy, while the electric motor serves to convert electrical energy into mechanical energy, thereby enabling the vehicle to move. Low-voltage units cover in vehicle electronic devices and auxiliary systems, such as lighting systems, information and entertainment systems, etc. The charging unit is responsible for the charging process of the battery, transmitting the electrical energy from the external power source to the power battery through the charger, ensuring that the battery can continuously supply electrical energy during driving (Omoniwa et al., 2022; Li et al., 2022). The energy flow between energy modules during vehicle operation is shown in Figure 2.

Figure 2

Figure 2. Energy flow diagram of electric vehicles.

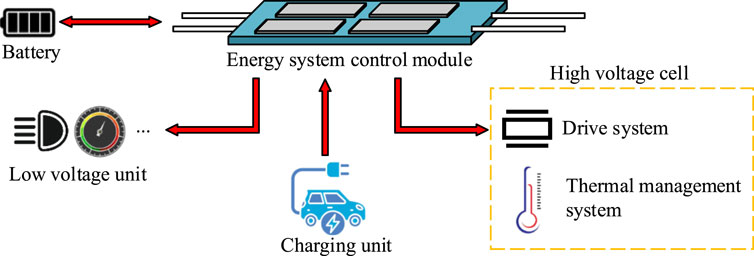
In Figure 2, the power battery in the energy system supplies electrical energy to the electric motor drive system, which subsequently converts this electrical energy into mechanical energy, thereby driving the vehicle. At the same time, through DC-DC converters, the high-voltage unit converts some of the electrical energy into low-voltage electrical energy, which is supplied to the onboard electronic devices and auxiliary systems of the low-voltage unit. During the braking process, the energy recovery system converts mechanical energy into electrical energy, which is fed back to the power battery to further optimize energy utilization efficiency. To enable the energy system to accurately identify the current system state and perform corresponding correct feedback, environmental models and computational models were respectively built as the interaction objects of the energy system. Firstly, a linear temperature dependent model was used to describe the relationship between battery capacity and temperature variation, as shown in Equation 1 (Peng et al., 2022; Jin et al., 2023).

$C\left(T\right)=C_0\left(1-\alpha \left(T-T_{ref}\right)\right)(1)$

In Equation 1, $C\left(T\right)$ represents the battery capacity at a temperature of $T$, $C_0$ represents the battery capacity at a reference temperature of $T_{ref}$, and $\alpha$ represents the temperature influence coefficient, which can reflect the degree of influence of temperature changes on battery capacity. Secondly, a calculation model is established for driving power, utilizing the motion state parameters of the vehicle, as shown in Equation 2.

$P_{drive}=\left(F_{drive}+F_{rolling}+F_{aero}\right)·v(2)$

In Equation 2, $P_{drive}$ represents the driving power, measured in kilowatts (kW). $F_{drive}$, $F_{rolling}$, and $F_{aero}$ are vehicle traction force, rolling resistance, and air resistance, respectively, all measured in Newtons (N). $v$ represents the vehicle speed, measured in m/s. In the design of EV systems, air resistance is the main energy loss factor during high-speed driving, and its optimization is particularly important. Saeed et al. pointed out that body structure design can significantly improve the aerodynamic performance of the entire vehicle, thereby enhancing its energy efficiency (Chen X. et al., 2022). The specific calculation formula for $F_{drive}$ is shown in Equation 3.

$F_{drive}=m·a(3)$

In Equation 3, $m$ represents the vehicle mass, measured in kg. $a$ denotes the acceleration of the vehicle, measured in m/s². The specific calculation formula for $F_{rolling}$ is shown in Equation 4.

$F_{rolling}=C_r·m·g(4)$

In Equation 4, $C_r$ is the rolling resistance coefficient, $g$ is the gravitational acceleration, taken as 9.81 m/s². The calculation method for $F_{aero}$ is indicated in Equation 5.

$F_{aero}=\frac{1}{2}·\rho ·C_d·A·v^2(5)$

In Equation 5, $C_d$ refers to the air resistance coefficient, $\rho$ stands for the air density, measured in kg/m³, and $A$ is the front surface area of the vehicle, measured in m². By comprehensively considering traction, rolling resistance, and air resistance, the driving power calculation model can more comprehensively reflect the energy demand of the vehicle in different operating states, supporting more efficient energy allocation and management. Finally, batteries generate heat during the charging and discharging process, so proper thermal management is needed to maintain battery performance and extend battery life. A heat generation and dissipation calculation model for batteries was constructed using a model based on thermal conduction and convective heat transfer. The calculation formula for heat generation is shown in Equation 6 (Ullah et al., 2023).

$Q_{gen}=I^{2}R(6)$

In Equation 6, $Q_{gen}$ represents the heat generated by the battery during the charging and discharging process, measured in watts (W). $I$ denotes current, measured in amperes (A). $I$ represents battery resistance, measured in ohms (Ω). The calculation formula for heat dissipation is shown in Equation 7.

$Q_{cool}=h{A}^{\prime }\left(T-T_{ambient}\right)(7)$

In Equation 7, $Q_{cool}$ represents the heat dissipated through the heat dissipation system, measured in W. $h$ represents the convective heat transfer coefficient, measured in W/m²°C. $A^{\prime }$ means the heat dissipation area, measured in m². $T$ and $T_{ambient}$ respectively represent battery temperature and ambient temperature, both in degrees Celsius (°C). After constructing the environmental interaction model and calculation model of the energy system, the study further selected driving energy consumption, thermal management energy consumption, low-voltage unit energy consumption, and battery capacity change caused by battery temperature changes as the main components of total energy consumption, and built an optimization objective function for the EV energy system, as shown in Equation 8.

$\min E_{total}\left(t_1,t_2\right)=\min \left(E_{drive}\left(t_1,t_2\right)+E_{thermal}\left(t_1,t_2\right)+E_{low}\left(t_1,t_2\right)+\Delta C\left(T\right)\right)(8)$

In Equation 8, $\left(t_1,t_2\right)$ represents a certain period of travel time, while $E_{total}$, $E_{drive}$, $E_{thermal}$, and $E_{low}$ represent total energy consumption, drive system energy consumption, thermal management energy consumption, and low-voltage unit energy consumption, respectively. $\Delta C\left(T\right)$ represents the change in battery capacity caused by changes in battery temperature. By minimizing total energy consumption, the goal is to raise the energy utilization efficiency of EVs, extend vehicle range, and reduce energy demand, thereby achieving a more environmentally friendly and economical energy management solution. Equations 1–8 in the text are mainly derived from the fundamental theories of vehicle dynamics and thermodynamics. The driving power model refers to the coupling relationship between classical traction, rolling resistance, and air resistance, while the heat generation and dissipation model is constructed based on Joule heating and Newton’s cooling law. In addition, the team has previously conducted relevant experiments on temperature control equipment and battery energy consumption modeling for small pure EVs, providing data and modeling basis for research. In terms of software and models, this article uses Python language and TensorFlow deep learning framework to implement GRU-DDQN optimized structure. The data used comes from the Applanix EV public database. The experiment was run on a workstation equipped with Intel i9-12900K, NVIDIA RTX 3090, and 64 GB memory, ensuring the stability and reproducibility of the training process.

3.2 Design of optimization algorithm for electric vehicle energy system based on GRU-DDQN

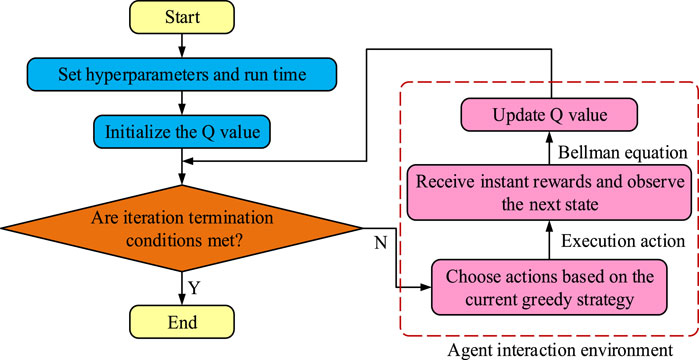
After completing the construction of the optimization objective function for the energy system of EVs, the next step is to design an efficient and adaptable solving algorithm to achieve the optimization of the objective function. The Q-learning algorithm in RL was chosen as the basic framework for the study, and its advantages in dynamic decision-making and strategy optimization were utilized to address the complex requirements of energy management systems. The operation of this algorithm is denoted in Figure 3.

Figure 3

Figure 3. Q Running flow diagram of the learning algorithm.

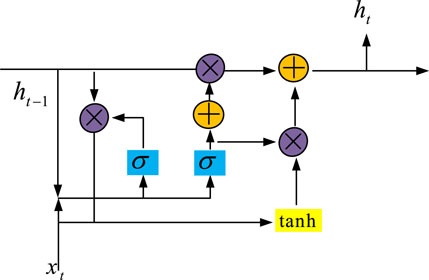
The Q-learning algorithm depicted in Figure 3 is a model-free RL algorithm. The fundamental premise of this algorithm is to guide the decision-making of the agent by learning the state-action value function. However, as the state and action space expands, the size of the Q-value table grows exponentially, leading to a sharp increase in storage and computational costs for traditional Q-learning algorithms. In addition, Q-learning is difficult to effectively capture long-term dependencies when facing sequence data with temporal dependencies, which affects the accuracy and stability of decision-making (Shi et al., 2024). To surmount the aforementioned challenges, the study initially introduced GRU to enhance the model’s capacity to process time series data. The GRU’s neural structure is illustrated in Figure 4.

Figure 4

Figure 4. Structural diagram of the GRU neurons.

In Figure 4, the neural structure of GRU principally comprises two gates, namely, the updating gate and the reset gate. The function of the updating gate is to determine the extent to which information from the previous hidden state (PHS) is to be retained in the current one. In contrast, the reset gate serves to determine the extent to which information from the PHS is to be forgotten, thereby generating new candidate hidden states (CHSs). The calculation formula for updating the door activation value is shown in Equation 9 (Chen Q. et al., 2022; Wang Z. et al., 2022; Mehdi et al., 2022).

$z_t=\sigma \left(W_z·x_t+U_z·h_{t-1}+b_t\right)(9)$

In Equation 9, $z_t$ represents the activation value of the update gate, ranging from 0 to 1. $b_t$ represents the bias vector of the update gate. $W_z$ and $U_z$ denote the weight matrices of the input $x_t$ and the PHS $h_{t-1}$ in the update gate, respectively. $\sigma$ expresses the Sigmoid activation function. The calculation formula for resetting the door is shown in Equation 10.

$r_t=\sigma \left(W_r·x_t+U_r·h_{t-1}+b_r\right)(10)$

In Equation 9, $r_t$ represents the activation value of the reset gate, which also ranges from 0 to 1. $b_r$ represents the bias vector of the updating gate. $W_r$ and $U_r$ indicate the weight matrices of the reset gate for the input $x_t$ and the PHS $h_{t-1}$, respectively. The calculation formula for CHSs is shown in Equation 11.

${\stackrel{\sim }{h}}_t=\tanh \left(W_h·x_t+U_h·\left(r_t·h_{t-1}\right)+b_h\right)(11)$

In Equation 11, ${\stackrel{\sim }{h}}_t$ represents the CHS. $\tanh$ stands for hyperbolic tangent activation function. $W_h$ and $U_h$ mean the weight matrices of the input $x_t$ and the PHS $h_{t-1}$ in the CHSs, respectively. $b_h$ represents the bias vector of CHSs. The final current hidden state balances the contributions of the PHS and CHSs through $z_t$, as shown in Equation 12.

$h_t=\left(1-z_t\right)·h_{t-1}+z_t·{\stackrel{\sim }{h}}_t(12)$

In Equation 12, $h_t$ means the current hidden state. After introducing GRU to enhance the processing capability of time series data, further research is conducted on introducing DDQN to raise the accuracy of action value estimation and the stability of decision-making. Compared to Long Short-Term Memory (LSTM) networks, GRUs have a simpler architecture with fewer trainable parameters, enabling faster convergence and reduced computational overhead. In EV energy systems, where real-time performance and low-latency decision-making are crucial, GRUs are well-suited for embedded deployment. Moreover, while attention mechanisms offer strong global context modeling, they typically require larger memory and computational resources, making them less practical for short-term sequence modeling in vehicle control scenarios. Therefore, GRU was selected to achieve a balance between temporal modeling capability and inference efficiency in EV energy optimization tasks. The update process of the two Q networks is shown in Figure 5.

Figure 5

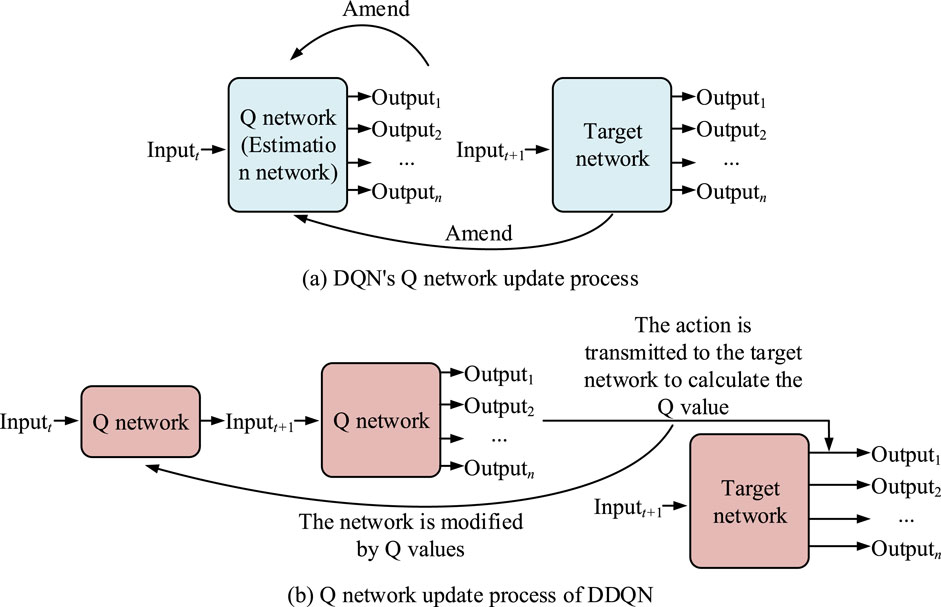
Figure 5. Flow diagram of Q network updates for DQN and DDQN. (a) DQN’s Q network update process; (b) Q network update process of DDQN.

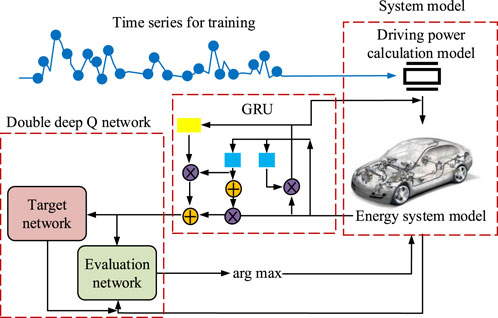
In Figure 5a, DQN only utilizes the same network to choose and assess actions during training, which often leads to overestimation of Q and affects the optimization effect of the strategy. To address this issue, DDQN in Figure 5b introduces two independent neural networks. One online network is applied to choose the optimal action, while the other target network is applied to assess the actual value of the action. This separation mechanism can not only reduce the deviation of Q values, but also improve the decision-making reliability of the algorithm in complex environments. Finally, a Gated Recurrent Unit-Double Deep Q-Network (GRU-DDQN)-based optimization algorithm model for EV energy systems was constructed, as shown in Figure 6.

Figure 6

Figure 6. GRU-DDQN structure diagram.

In Figure 6, firstly, the data input module is responsible for collecting and organizing real-time status information of the EV energy system. Then, the GRU feature extraction module is applied to process time series data and extract deep feature representations that are helpful for decision-making, thereby raising the model’s ability to process time-dependent data. Next, the DDQN decision module receives feature vectors from GRU and uses online and target networks to select the optimal action and evaluate the action value, respectively. In the decision-making process, the experience replay buffer plays a crucial role in storing experience data. This data is generated during the interaction between the agent and the environment, and is subsequently selected at random to disrupt the correlation between data and enhance the stability and efficiency of training. The action execution module adjusts the energy allocation strategy in the EV energy system in real-time based on the output of the DDQN decision module. At the same time, the reward calculation module calculates real-time rewards based on system feedback, guiding the agent’s learning process. Through a reasonable reward mechanism, it guides the agent to optimize strategies towards the goal of reducing total energy consumption. Finally, the optimization objectives and strategy update module define and minimize the total energy consumption of the vehicle during the driving cycle.

4 Results

To assess the effect of the GRU-DDQN EV energy system optimization algorithm, multiple experimental evaluations were conducted on standard datasets and actual tasks. Firstly, a benchmark performance comparison analysis was conducted with several mainstream energy optimization algorithms. Secondly, the algorithm was applied to practical EV energy management scenarios and its optimization effect was evaluated under different operating conditions.

4.1 Benchmark performance testing

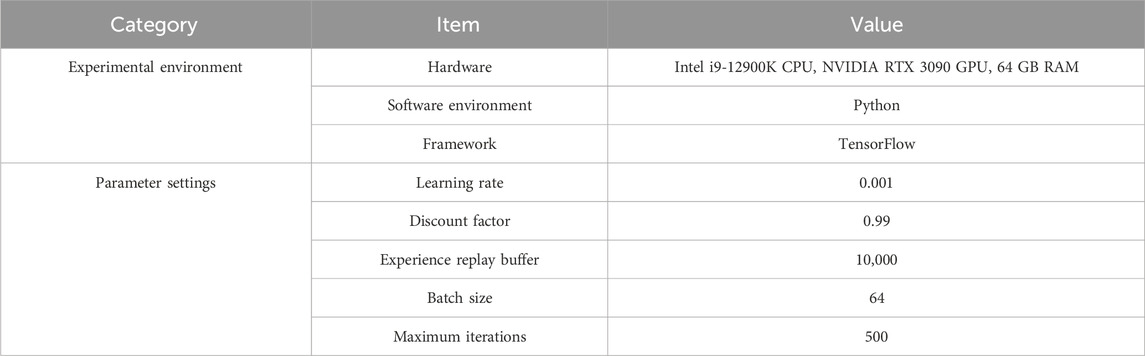
To validate the effect of the GRU-DDQN algorithm in optimizing EV energy systems, an experimental platform was constructed and experiments were conducted on standard datasets and real-world scenarios. All experiments were carried out within a Python environment and run using the TensorFlow deep learning framework. The experimental equipment was a workstation with Intel i9-12900K CPU, NVIDIA RTX 3090 GPU, and 64 GB memory. The Applanix EV public energy dataset was selected as the experimental dataset. The Applanix EV dataset contained 50,000 labeled samples, which were preprocessed through missing value elimination, normalization, and label remapping. The dataset was then categorized into four real-world driving conditions: urban (12,500 samples), highway (13,000), complex (12,000), and cold environment (12,500). Each category included time-stamped energy consumption, velocity, and temperature data aligned with system states. The experimental environment and key parameter settings are denoted in Table 1.

Table 1

Table 1. Experimental setup and model parameters.

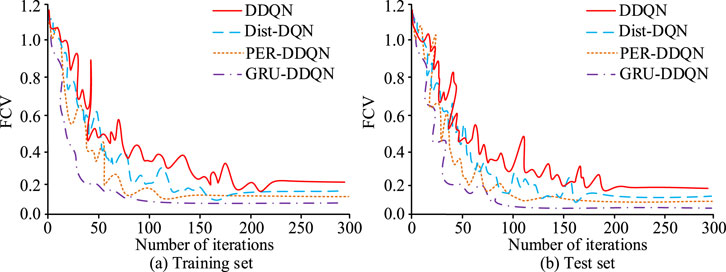
According to Table 1, this study set the learning rate of the model to 0.001, discount factor to 0.99, experience replay buffer size to 10,000, batch size to 64, and maximum iteration count to 500. DDQN, Distributed Deep Q-Network (Dist-DQN) based on distributed value estimation, and Double Deep Q-Network with Prioritized Experience Replay (PER-DDQN) were selected as comparison models to test the Final Converged Value (FCV) of the four models, as shown in Figure 7.

Figure 7

Figure 7. FCV values of different algorithms in both datasets. (a) Training set; (b) Test set.

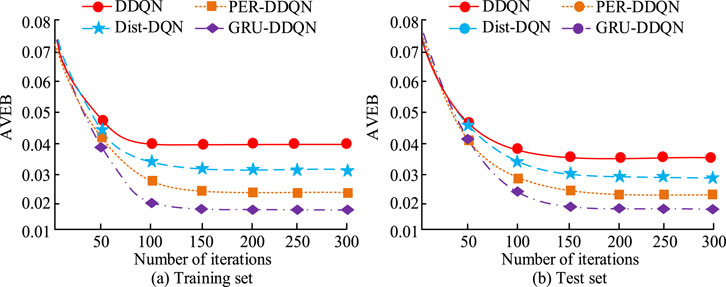
In Figure 7a, GRU-DDQN exhibited a faster convergence speed compared to the other three algorithms, reaching a stable state after approximately 78 iterations, with an FCV of 0.08. In contrast, DDQN had the slowest convergence speed, with a total of 223 iterations to reach stability, and the FCV was 0.26. The FCVs of Dist-DQN and PER-DDQN were between DDQN and GRU-DDQN, with better convergence speed and optimization effect than DDQN, but slightly inferior to GRU-DDQN. Similarly, in Figure 7b, the FCVs of DDQN, Dist-DQN, PER-DDQN, and GRU-DDQN when iterating to a stable state in the training set were 0.19, 0.16, 0.09, and 0.04. Further testing the errors of the four models in estimating action value resulted in the Action Value Estimation Bias (AVEB) of each model in different datasets, as shown in Figure 8.

Figure 8

Figure 8. AVEB values of different algorithms in both datasets. (a) Training set; (b) Test set.

Figure 8 shows the AVEB changes of DDQN, Dist-DQN, PER-DDQN, and GRU-DDQN in the training and testing sets. In Figure 8a, GRU-DDQN performed the best in the training set, with its AVEB value first iterating to stability and finally reaching 0.017. Dist-DQN and PER-DDQN performed second, with final AVEB values stabilizing at 0.035 and 0.024, respectively. The AVEB value of DDQN remained consistently high, eventually stabilizing at 0.043, indicating a significant bias in its action value estimation. Figure 8b showcases the performance of four models in the test set, with an overall trend consistent with the training set. The AVEB values at which DDQN, Dist-DQN, PER-DDQN, and GRU-DDQN reach stability were 0.036, 0.031, 0.024, and 0.018, respectively. The cumulative reward (CR) values of four models were compared in different datasets, as shown in Figure 9.

Figure 9

Figure 9. CR values of different algorithms in both datasets. (a) Training set; (b) Test set.

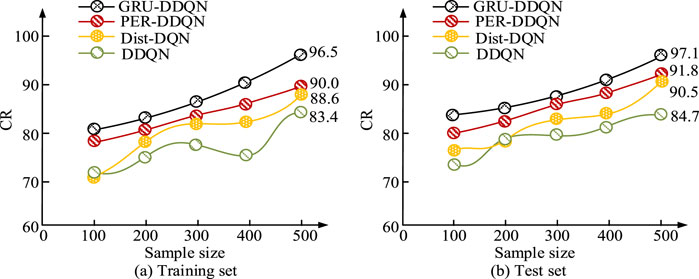
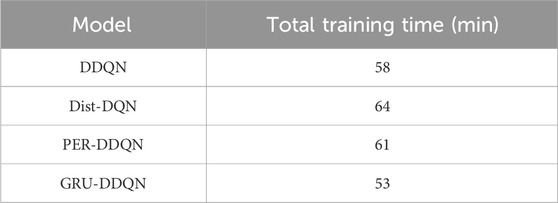
In the training set of Figure 9a, GRU-DDQN consistently had the highest CR value, increasing from 80.2 to 96.5, demonstrating good reward accumulation ability. The highest CR values for PER-DDQN, Dist-DQN, and DDQN were 90.0, 88.6, and 83.4, respectively. In the test set of Figure 9b, GRU-DDQN also performed the best, with a stable increase in CR value from 84.7 to 97.1, PER-DDQN and Dist-DQN increasing to 91.8 and 90.5, respectively, while DDQN remained the lowest at only 84.7. The comparison of total training time for different models is shown in Table 2.

Table 2

Table 2. Model training time comparison on identical hardware.

As shown in Table 2, GRU-DDQN achieved the shortest training time (53 min) among all models, indicating its improved convergence efficiency despite the more complex architecture. This highlights the framework’s practical advantage for real-time or large-scale deployment.

4.2 Application effect analysis

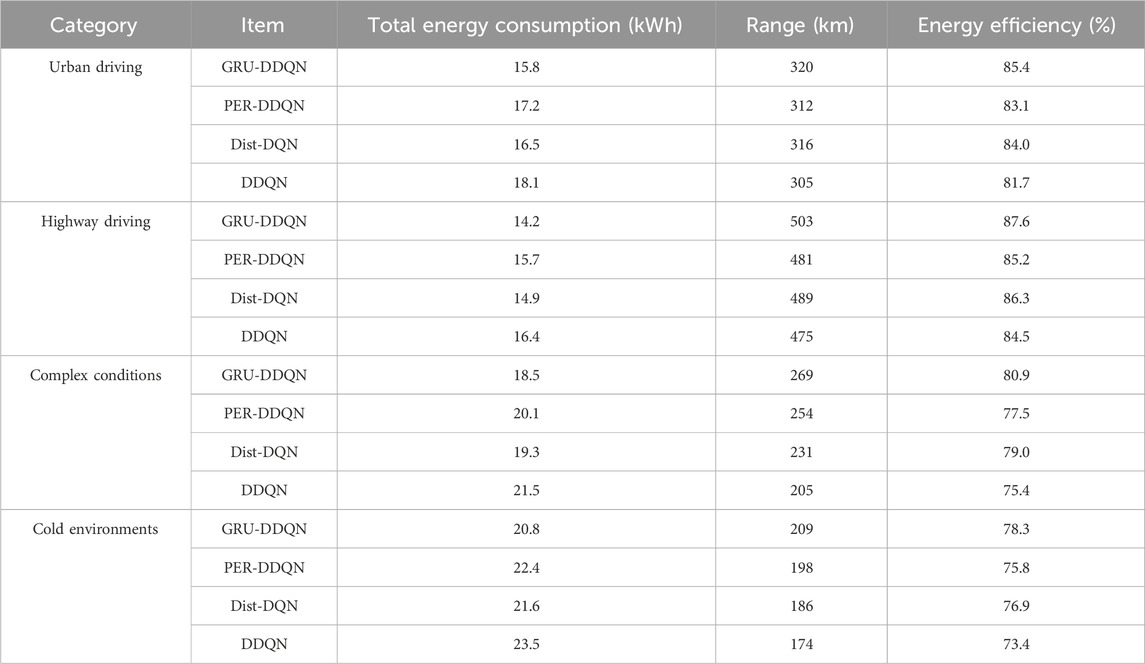
To assess the effectveness of the GRU-DDQN model in practical EV energy system optimization tasks, the study first collected and preprocessed energy data of EVs under different actual operating scenarios. Subsequently, these data were divided into four categories: urban road driving, highway driving, complex condition driving, and low-temperature environment driving, each scenario containing different speed changes, energy consumption, and temperature characteristics. Using the preprocessed dataset, the performance of the GRU-DDQN model and other comparative algorithms in actual energy optimization tasks was tested. Key indicators such as total energy consumption, range, and energy utilization rate of different algorithms in various scenarios were recorded, as denoted in Table 3.

Table 3

Table 3. Comparison of the optimization effects of the four models in real scenarios.

Table 3 shows the optimization effects of four models, GRU-DDQN, PER-DDQN, Dist-DQN, and DDQN, in four types of actual driving scenarios. In urban road driving scenarios, the total energy consumption of GRU-DDQN was 15.8 kWh, the range was 320 km, and the energy utilization efficiency was 85.4%. Compared with PER-DDQN and Dist-DQN, the energy consumption was reduced by 1.4 kWh and 0.7 kWh, respectively. In highway driving scenarios, GRU-DDQN still performed the best, with a total energy consumption of 14.2 kWh, a range of up to 503 km, and an energy utilization efficiency of 87.6%. Under complex operating conditions, the energy consumption of GRU-DDQN was 18.5 kWh, and the energy utilization efficiency was 80.9%. In low-temperature driving scenarios, the optimization effect of various indicators of GRU-DDQN was also the best. Overall, GRU-DDQN had the lowest total energy consumption, longest range, and highest energy utilization efficiency in all scenarios, outperforming the other three algorithms. City road driving, highway driving, complex conditions driving and low temperature environment driving were denoted as categories 1, 2, 3, and 4, and the mean optimization time (MOT) and mean decision time (MDT) of the four models in the four environments were tested, as shown in Figure 10.

Figure 10

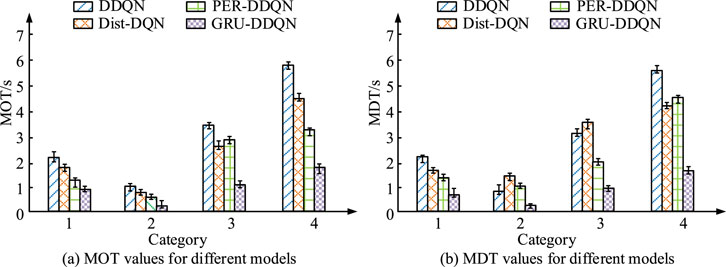
Figure 10. MOT and MDT values for the different models. (a) MOT values for different models; (b) MDT values for different models.

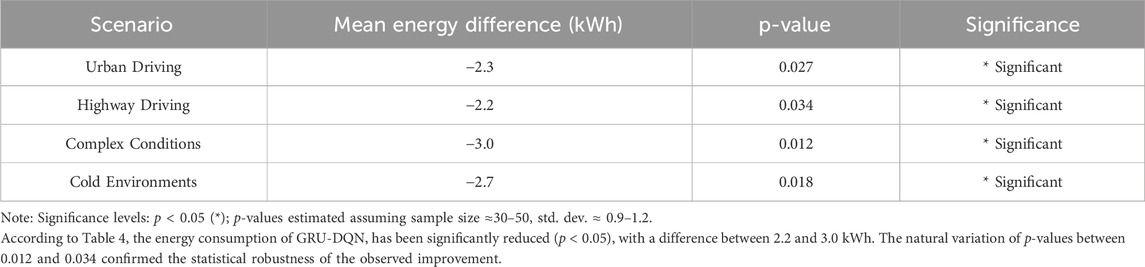
In Figure 10a, there were significant differences in MOT performance among different models under the four environmental categories. In all four environments, the MOT value of the GRU-DDQN model was the smallest. When the environment type was a highway driving environment, the MOT value of the GRU-DDQN model was as low as 0.2 s. Similarly, in Figure 10b, the GRU-DDQN model also had the smallest MDT value in the highway driving environment, as low as 0.3 s. Overall, the GRU-DDQN model performed the best in both MOT and MDT metrics, indicating significant advantages in optimization efficiency and decision efficiency. To assess whether the observed energy savings are statistically meaningful, independent-sample t-tests were conducted comparing GRU-DDQN with DDQN under four typical driving scenarios, as shown in Table 4.

Table 4

Table 4. Statistical significance test of total energy consumption across algorithms.

5 Conclusion

To enhance the energy utilization effectiveness of contemporary EV energy management systems and curtail their aggregate energy consumption, a novel GRU-DDQN energy management system optimization model was formulated. In benchmark performance testing, GRU-DDQN performed the best in FCV, AVEB, and CR values in both datasets. The FCV and AVEB values were as low as 0.04 and 0.017, indicating that the model had faster convergence speed and better accuracy in estimating action value. The CR value of the GRU-DDQN model in the test set could steadily increase to 97.1, far higher than PER-DDQN’s 91.8, Dist-DQN’s 90.5, and DDQN’s 84.7. In practical applications, GRU-DDQN could achieve optimal performance under highway driving conditions, with a total energy consumption of 14.2 kWh, a range of up to 503 km, and an energy utilization efficiency of 87.6%. Even under low-temperature driving conditions, the performance optimization results of GRU-DDQN were the best, with a total energy consumption as low as 20.8 kWh, which was reduced by 1.6 kWh, 0.8 kWh, and 2.7 kWh compared to PER-DDQN, Dist-DQN, and DDQN, respectively. Finally, GRU-DDQN also performed the best in MOT and MDT under four driving conditions, as low as 0.2 s and 0.3 s, respectively. Overall, the GRU-DDQN model exhibits high energy utilization efficiency and decision stability.

6 Limitations and future directions

However, the composition of energy management systems in real environments is diverse and complex, so subsequent research needs to consider different optimization objective functions to expand the adaptability of the model in more practical scenarios. In addition, with the continuous deepening of machine learning methods in the fields of transportation and energy systems, future research can further expand their application in the full lifecycle management of EVs. For example, combining multi-objective tasks such as path planning, energy consumption prediction, remaining life modeling, and retired battery resource recycling scheduling, a more intelligent energy control strategy can be achieved through end-to-end optimization. To further expand the adaptability of this method in complex scenarios, future research can combine meta learning and transfer learning to enhance the model’s generalization ability in multiple operating conditions and vehicle models. Self-supervised and unsupervised learning mechanisms are also introduced to reduce the dependence on labeled data and enhance the system’s ability to self-identify abnormal energy consumption behaviors. In addition, drawing on the data-driven adaptive optimization strategy proposed by Marinković et al. (2024), the clustering based state abstraction method can be embedded into the GRU-DDQN structure in the future to further enhance its decision-making efficiency and reliability in high-dimensional state spaces. The GRU-DDQN model constructed by the research has the potential to extend towards multidimensional energy consumption optimization, intelligent scheduling, and carbon emission modeling, providing theoretical basis and methodological support for building a green and efficient electric travel system. Additionally, to promote practical deployment, future work should explore the model’s scalability across heterogeneous EV fleets and varying battery chemistries. This includes adapting the GRU-DDQN framework to different battery types (e.g., NMC, LFP, solid-state), drive train architectures, and control parameters. Integrating transfer learning or meta-learning could help enhance generalization, enabling the model to adapt across diverse EV platforms without extensive retraining.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HR: Methodology, Project administration, Conceptualization, Funding acquisition, Writing – review and editing, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The research is supported by University-level project: Shanghai Jianqiao University Project Name: Research on temperature characteristics and temperature control devices of pure electric vehicle batteries (No. SJQ20014).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, Q., Kang, W., Ma, R., Liu, G., and Chang, L. (2024). DDQN path planning for unmanned aerial underwater vehicle (UAUV) in underwater acoustic sensor network. Wirel. Netw. 30 (6), 5655–5667. doi:10.1007/s11276-023-03300-0

CrossRef Full Text | Google Scholar

Chen, Q., Zhao, W., Li, L., Wang, C., and Chen, F. (2022). ES-DQN: a learning method for vehicle intelligent speed control strategy under uncertain cut-in scenario. IEEE Trans. Veh. Technol. 71 (3), 2472–2484. doi:10.1109/tvt.2022.3143840

CrossRef Full Text | Google Scholar

Chen, X., Wang, J., Zhao, K., and Yang, L. (2022). Electric vehicles body frame structure design method: an approach to design electric vehicle body structure based on battery arrangement. Proc. Institution Mech. Eng. Part D J. Automob. Eng. 236 (9), 2025–2042. doi:10.1177/09544070211052957

CrossRef Full Text | Google Scholar

Demircali, A., and Koroglu, S. (2022). Modular energy management system with jaya algorithm for hybrid energy storage in electric vehicles. Int. J. Energy Res. 46 (15), 21497–21510. doi:10.1002/er.7848

CrossRef Full Text | Google Scholar

Fu, Z., Wang, H., Tao, F., Ji, B., Dong, Y., and Song, S. (2022). Energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles using deep reinforcement learning with action trimming. IEEE Trans. Veh. Technol. 71 (7), 7171–7185. doi:10.1109/tvt.2022.3168870

CrossRef Full Text | Google Scholar

Jin, J., Mao, S., and Xu, Y. (2023). Optimal priority rule-enhanced deep reinforcement learning for charging scheduling in an electric vehicle battery swapping station. IEEE Trans. Smart Grid 14 (6), 4581–4593. doi:10.1109/tsg.2023.3250505

CrossRef Full Text | Google Scholar

Li, S., Hu, W., Cao, D., Zhang, Z., Huang, Q., Chen, Z., et al. (2022). A multiagent deep reinforcement learning based approach for the optimization of transformer life using coordinated electric vehicles. IEEE Trans. Industrial Inf. 18 (11), 7639–7652. doi:10.1109/tii.2021.3139650

CrossRef Full Text | Google Scholar

Mahato, D., Aharwal, V. K., and Sinha, A. (2024). Multi-objective optimisation model and hybrid optimization algorithm for electric vehicle charge scheduling. J. Exp. and Theor. Artif. Intell. 36 (8), 1645–1667. doi:10.1080/0952813x.2023.2165719

CrossRef Full Text | Google Scholar

Marinković, D., Dezső, G., and Milojević, S. (2024). Application of machine learning during maintenance and exploitation of electric vehicles. Adv. Eng. Lett. 3, 132–140. doi:10.46793/adeletters.2024.3.3.5

CrossRef Full Text | Google Scholar

Mehdi, G., Hooman, H., Liu, Y., Peyman, S., Raza, A., Jalili, A., et al. (2022). Data mining techniques for web mining: a survey. Artif. Intell. Appl. 1 (1), 3–10. doi:10.47852/bonviewaia2202290

CrossRef Full Text | Google Scholar

Mu, N., Wang, Y., Chen, Z. S., Xin, P., Deveci, M., and Pedrycz, W. (2023). Multi-objective combinatorial optimization analysis of the recycling of retired new energy electric vehicle power batteries in a sustainable dynamic reverse logistics network. Environ. Sci. Pollut. Res. 30 (16), 47580–47601. doi:10.1007/s11356-023-25573-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Omoniwa, B., Galkin, B., and Dusparic, I. (2022). Optimizing energy efficiency in UAV-Assisted networks using deep reinforcement learning. IEEE Wirel. Commun. Lett. 11 (8), 1590–1594. doi:10.1109/lwc.2022.3167568

CrossRef Full Text | Google Scholar

Oroojlooyjadid, A., Nazari, M. R., Snyder, L. V., and Takáč, M. (2022). A deep q-network for the beer game: deep reinforcement learning for inventory optimization. Manuf. and Serv. Operations Manag. 24 (1), 285–304. doi:10.1287/msom.2020.0939

CrossRef Full Text | Google Scholar

Peng, J., Fan, Y., Yin, G., and Jiang, R. (2022). Collaborative optimization of energy management strategy and adaptive cruise control based on deep reinforcement learning. IEEE Trans. Transp. Electrification 9 (1), 34–44. doi:10.1109/tte.2022.3177572

CrossRef Full Text | Google Scholar

Sadeghi, D., Amiri, N., Marzband, M., Abusorrah, A., and Sedraoui, K. (2022). Optimal sizing of hybrid renewable energy systems by considering power sharing and electric vehicles. Int. J. Energy Res. 46 (6), 8288–8312. doi:10.1002/er.7729

CrossRef Full Text | Google Scholar

Shi, P., Zhang, J., Hai, B., and Zhou, D. (2024). Research on dueling double deep Q network algorithm based on single-step momentum update. Transp. Res. Rec. 2678 (7), 288–300. doi:10.1177/03611981231205877

CrossRef Full Text | Google Scholar

Skrúcaný, T., Milojević, S., Semanova, S., Čechovič, T., Figlus, T., Synák, F., et al. (2018). The energy efficiency of electric energy as a traction used in transport. Trans. Technic Tech. 14 (2), 9–14. doi:10.2478/ttt-2018-0005

CrossRef Full Text | Google Scholar

Tang, X., Chen, J., Yang, K., Toyoda, M., Liu, T., and Hu, X. (2022). Visual detection and deep reinforcement learning-based car following and energy management for hybrid electric vehicles. IEEE Trans. Transp. Electrification 8 (2), 2501–2515. doi:10.1109/tte.2022.3141780

CrossRef Full Text | Google Scholar

Ullah, I., Liu, K., Yamamoto, T., Shafiullah, M., and Jamal, A. (2023). Grey wolf optimizer-based machine learning algorithm to predict electric vehicle charging duration time. Transp. Lett. 15 (8), 889–906. doi:10.1080/19427867.2022.2111902

CrossRef Full Text | Google Scholar

Venkatasatish, R., and Dhanamjayulu, C. (2022). Reinforcement learning based energy management systems and hydrogen refuelling stations for fuel cell electric vehicles: an overview. Int. J. Hydrogen Energy 47 (64), 27646–27670. doi:10.1016/j.ijhydene.2022.06.088

CrossRef Full Text | Google Scholar

Wang X., X., Wang, R., Shu, G. Q., Tian, H., and Zhang, X. (2022). Energy management strategy for hybrid electric vehicle integrated with waste heat recovery system based on deep reinforcement learning. Sci. China Technol. Sci. 65 (3), 713–725. doi:10.1007/s11431-021-1921-0

CrossRef Full Text | Google Scholar

Wang, Z., Lu, J., Chen, C., Ma, J., and Liao, X. (2022). Investigating the multi-objective optimization of quality and efficiency using deep reinforcement learning. Appl. Intell. 52 (11), 12873–12887. doi:10.1007/s10489-022-03326-5

CrossRef Full Text | Google Scholar

Wu, G., Yi, C., Xiao, H., Wu, Q., Zeng, L., Yan, Q., et al. (2023). Multi-objective optimization of integrated energy systems considering renewable energy uncertainty and electric vehicles. IEEE Trans. Smart Grid 14 (6), 4322–4332. doi:10.1109/tsg.2023.3250722

CrossRef Full Text | Google Scholar

Xiao, H., Pu, X., Pei, W., Ma, L., and Ma, T. (2023). A novel energy management method for networked multi-energy microgrids based on improved DQN. IEEE Trans. Smart Grid 14 (6), 4912–4926. doi:10.1109/tsg.2023.3261979

CrossRef Full Text | Google Scholar

Yang, N., Han, L., Liu, R., Wei, Z., Liu, H., and Xiang, C. (2023). Multiobjective intelligent energy management for hybrid electric vehicles based on multiagent reinforcement learning. IEEE Trans. Transp. Electrification 9 (3), 4294–4305. doi:10.1109/tte.2023.3236324

CrossRef Full Text | Google Scholar