- Department of Information and Communication Technology, Adani University, Ahmedabad, Gujarat, India
Quantum cryptography has emerged as a radical research field aimed at mitigating various security threats in modern communication systems. The integration of Quantum Machine Learning (QML) protocols plays a crucial role in enhancing security measures, addressing previously inaccessible threats, and improving cryptographic efficiency. Key research areas in quantum cryptography include Quantum Key Distribution (QKD), eavesdropping detection, QSDC, security analysis of QKD protocols, post-quantum cryptography, Quantum Network Security & Intrusion Detection, Quantum-secure communication beyond QKD, quantum random number generation, Quantum Secure Multi-Party Computation (QSMPC), Quantum Homomorphic Encryption (QHE), and privacy-preserving computation. QML algorithms improve the key generation of QKD, by improving quantum state selection and reducing measurements. This also allows them to increase efficiency because it identifies trends in errors and applies corrections, making quantum cryptography a more dependable option. With intelligent processing machine learning is excellent at handling complex, high-dimensional data-this may provide a viable strategy for enhancing QKD performance and increasingly real-world secure quantum communication networks. This review will explore current research gaps and future developments in QKD, security analysis of QKD protocols, and eavesdropping detection by leveraging various QML algorithms.
1 Introduction
Beyond the constraints of classical encryption, the field of quantum cryptography (QC) provides a revolutionary method of secure communication. Despite traditional cryptography methods, QC protocols offer verifiable security assurances by utilizing the concepts of quantum mechanics (Goyal, 2024). Quantum teleportation (QT), quantum secret sharing (QSS), quantum secure direct communication (QSDC), and quantum key distribution (QKD) represent the four fundamental branches of quantum cryptography protocols. Unlike QKD, which is primarily concerned with the secure negotiation of cryptographic keys, QSDC introduces a novel communication paradigm that provides a comprehensive, confidential, and near-instantaneous solution by transmitting actual messages directly over a quantum channel. By eliminating the need for cryptographic keys for encryption and decryption, QSDC ensures secure communication (Pan et al., 2024). Quantum private communication is a practical application for quantum mechanics. It enables secure communication against traditional approaches and advanced technologies such as quantum computers. There are several types of Cryptographic tasks, such as quantum private inquiry and quantum digital signatures control communication. The most basic one is quantum key distribution (QKD) (Liu et al., 2022). The QKD system utilizes physics principles rather than the computational complexity of mathematics problems to enable the provably safe exchange of cryptographic keys against eavesdropping. This fact helps make sure anyone attempting to access the key exchange process may be identified, ensuring the highest level of security possible. Quantum Random Number Generation (QRNG) improves cryptographic solutions by producing real random numbers needed for key-setting and growth processes, among other areas (Gowda et al., 2025). For quantum key generation, random numbers are used. Various protocols used in QKD include BB84 protocols, E91 protocol, CV-QKD protocol, Measurement-Device-Independent QKD (MDI-QKD), Twin-Field QKD Protocol etc. QML is a rapidly evolving field, which is formed by integrating standard machine learning with the concepts of quantum computing. It uses machine learning methods to further research on quantum computing and strives to revolutionize machine learning by utilizing the unique capabilities of quantum physics (Qi et al., 2024). QML plays a significant role in improving the Quantum cryptography research landscape. Various QML algorithms like quantum-inspired feature maps and kernel-based classifiers, Real-time protocol prediction for quantum key distribution, Applications of artificial neural networks in quantum key distribution, Dimensionality reduction using quantum algorithms, Hybrid quantum-classical convolutional neural networks, Kernal-based QML, quantum neural networks with machine learning principles, Quantum convoluted neural networks (QCNN), Quantum Particle Swarm Optimization (QPSO) improves QKD, Random number generation, side channel attack mitigation, Adaptive protocols, post-quantum cryptography, anomaly detection essential for quantum-safe communication and data protection techniques. The rapid growth of developments of QML algorithms to maximize the efficiency of Quantum cryptography research like QKD, eavesdropping detection, and security analysis of QKD protocols is demonstrated in Figure 1a, which represents the number of articles published in this field from 1990 to 2025 as per research data collected google scholar and web of science. Figure 1b illustrates key aspects of both QML and Quantum Cryptography (QC), highlighting how advancements in quantum mechanics and computing enhance classical cryptography and machine learning, leading to the evolution of quantum cryptography and QML. As shown in the figure, integrating QML with quantum cryptography enhances security, optimizes cryptographic processes, and improves vulnerability detection.
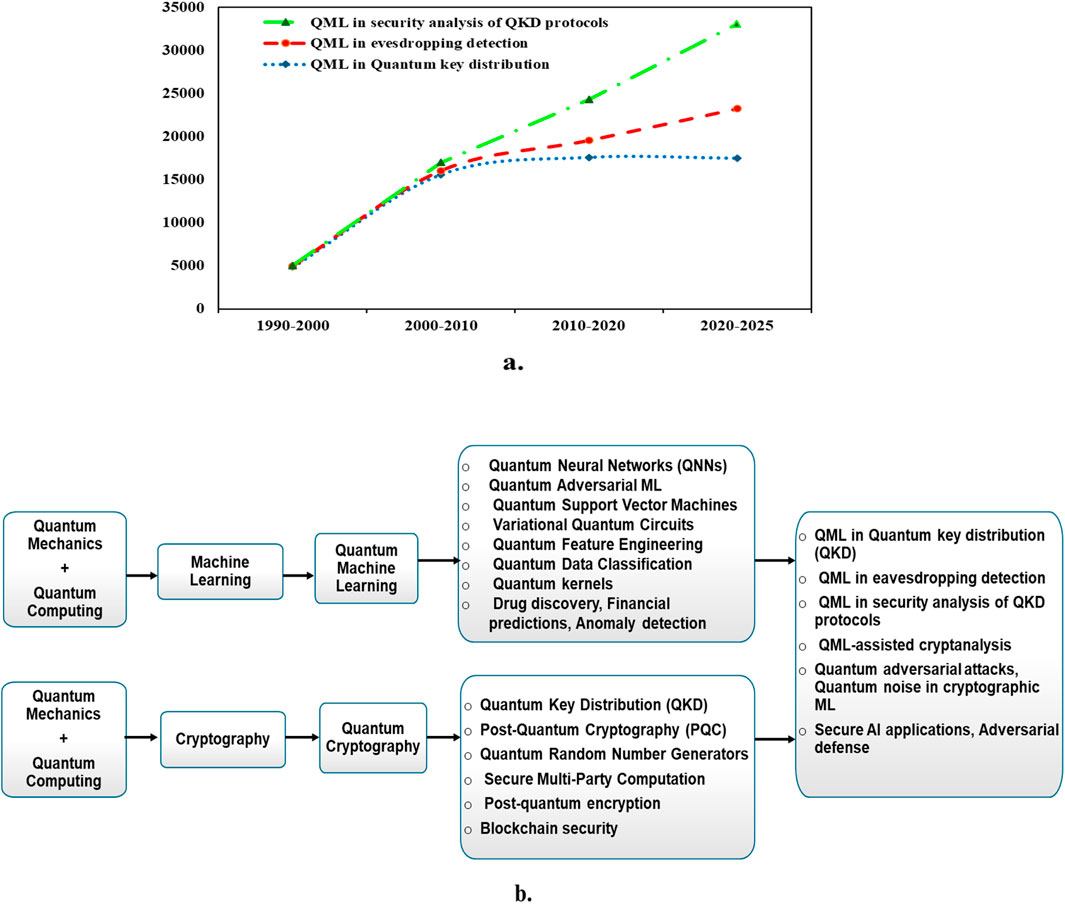
Figure 1. The integration of QML into QKD research has facilitated the resolution of more complex problems within the quantum cryptography community. As illustrated in (a) research on eavesdropping detection and security analysis of QKD protocols has significantly increased after 2010, reflecting a growing focus on more robust and intelligent cryptographic applications. (b) Illustrates how advancements in quantum mechanics and quantum computing have contributed to the development of quantum cryptography (QC) and quantum machine learning (QML). Various technologies associated with these verticals are highlighted, paving the way for intelligent, adaptive, and secure quantum communication systems. (a) Quantum cryptography research landscape represents the number of articles published in Quantum cryptography research. (b) Quantum machine learning in augmenting quantum cryptography.
The rest of the article explores the fundamental aspects of quantum cryptography, the role of QML in Quantum cryptography, and three major research areas: quantum key distribution, eavesdropping detection, and the security analysis of QKD protocols with advancements in QML algorithms. Additionally, it highlights current research gaps and future developments in the domain in detail.
2 Quantum cryptography
Quantum cryptography utilizes quantum mechanics to develop secure communication systems that differ from conventional methods. Quantum cryptography’s security depends on physics principles, unlike traditional encryption, which relies on the computational complexity of certain mathematical problems. Quantum cryptography utilizes quantum physics principles to ensure secure communication. Quantum Encryption employs quantum states to encrypt data directly, along with the prominent QKD application for secure key exchange. Random numbers are essential for generating keys in QKD. As a result, both QKD and random number generation play a crucial role in the landscape of quantum cryptography. This includes advanced protocols like Quantum Secure Direct Communication and Quantum Homomorphic Encryption (Goyal, 2024). The two primary categories of Quantum Key Distribution Protocols (QKDPs) are Continuous Variable (CV) and Discrete Variable (DV) QKDPs. Discrete Variable QKDPs generate discrete outcomes by employing the polarization of a single photon or the spin of an electron for key distribution. Discrete Variable QKDPs, which employ a single proton to store information, CV-QKDPs use light, which has the advantage of being easier to create coherent light. Single photons are used in DV protocols, whereas homodyne or heterodyne detection techniques are used in CV protocols. Some examples of Discrete Variable QKDPs include BB84, E91, B92, and SARG04 protocols. Some protocols like the Coherent-One-Way (COW) protocol, Differential-Phase-Shift (DPS) protocol, and Round-Robin Differential Phase Shift (RRDPS) protocol are Distributed Phase Reference QKDPs. Continuous Variable QKDPs also include some protocols based on source state, squeezed state of light, two-state protocol, and coherent states for discrete modulation. Super-Dense Coding (SDC) also known as the “Ping-Pong” Protocol and LM05 Protocol are examples of two-way protocol (Nwaga and Nwagwughiagwu, 2024). Some of the experimental implementations of quantum cryptography include Fiber-Based QKD Systems, Free-Space Quantum Communication, Integrated Quantum Photonics, Quantum Repeaters, Satellite-Based Quantum Communication, and Quantum Cryptographic Networks (Goyal, 2024). Recent advancements in quantum cryptography include the Semi-Quantum Private Comparison (SQPC) protocol based on Bell states, without quantum entanglement swapping. This enhances the performance of quantum cryptography against various attacks, making it particularly effective for noisy quantum channels (Geng et al., 2024). Gong et al. (2024c) discuss the Novel semi-quantum private comparison protocol with Bell states in which any quantum state is not required to prepare and measure for classical users and it also excludes unitary operation on received quantum particles. This novel approach is also secure against external and internal attacks. Another recent revaluation in quantum cryptography protocols includes Mode-pairing quantum key distribution based on wavelength division multiplexing in multi-user networks developed by Cui et al. (2024) which includes the performance of MP-QKD for multiple users with integration of WDM (wavelength division multiplexing). This analysis is essential for asymmetric network channels to find many applications in quantum communication networks. Multi-party semi-quantum private comparison (MQPC) protocols developed by Gong et al. (2023) represent an advancement in quantum cryptography in which the use of decoherence-free states (DFS) against collective noise multiparty can communicate in the presence of collective-dephasing noise and collective-rotation noise which affects the integrity of quantum communication.
3 Quantum machine learning in augmenting quantum cryptography
With the integration of quantum computing into classical machine learning, QML emerges as a powerful approach to enhance computational performance. Various classical machine learning algorithms, including supervised and unsupervised learning, benefit from quantum principles, leading to improved efficiency and scalability. Unsupervised learning, particularly in processing large real-time data, has gained popularity with the development of quantum generative models. Several variants of Generative Adversarial Networks (GANs) with advanced computing capabilities have been introduced. Recently, a hybrid quantum-classical Generative Adversarial Network (GAN) has been developed for image generation, leveraging QML to overcome quantum hardware constraints (Zhou et al., 2023). With the advancement of artificial intelligence and machine learning, traditional optimization techniques struggle to handle complex, nonlinear, and systemic problems. Advanced algorithms such as ant colony optimization, bat optimization, simulated annealing, genetic optimization, fruit fly optimization, particle swarm optimization (PSO), and the gravitational search method, combined with effective preprocessing techniques, offer more robust solutions. Among these, PSO, a nature-inspired metaheuristic algorithm, stands out due to its fewer control parameters, faster search rate, and lower computational complexity. It has proven highly effective in addressing various engineering and AI optimization challenges, particularly in identifying optimal solutions across a wide range of applications (Gong C. et al., 2024; She et al., 2025) discuss quantum-classical hybrid neural network model—St-HQCNN which can be used in quantum-enhanced cryptographic security, anomaly detection, and QKD protocols optimization (Gong L. et al., 2024). discusses the Quantum K-Nearest Neighbor (QKNN) classification algorithm, utilizing a divide-and-conquer strategy, which offers several advantages in QKD, including eavesdropping detection, error and noise reduction, and improved scalability. The advancement of QKD includes a proposed strategy for measurement-free mediated semi-quantum key distribution (MSQKD) using single-particle states. This approach enables two classical users to establish a secret key with the assistance of a third party, enhancing security and scalability while eliminating the need for a quantum detector (Zhou et al., 2024). The Multi-Party Semi-Quantum Private Comparison (SQPC) protocol, utilizing d-dimensional single-particle states, enables the secure comparison of private data sizes with the assistance of a quantum third party. It is well-suited for multi-user and large-scale quantum cloud applications (Gong et al., 2025). An MSQPC protocol is constructed using d-dimensional SPSs to securely determine the size relationship between classical participants’ private data. This protocol relies on unitary operations and a pre-shared key, while entanglement swapping remains optional (Gong et al., 2025). Two prominent fields of quantum technology, QML and quantum cryptography (QC) hold immense potential for future advancements. While research at the intersection of QML and QC is still in its early stages, the outlook is promising as both areas continue to evolve. The integration of QML and QC could pave the way for more secure communication systems in the quantum era, as hardware capabilities and practical applications progress.
3.1 Prospects and constraints of quantum machine learning in QKD, eavesdropping detection and security analysis of QKD protocols
QKD is a fundamental aspect of quantum cryptography, and integrating QML with QKD can significantly enhance the performance of quantum cryptographic systems. Once keys are successfully generated in QKD, detecting eavesdropping becomes a critical step in ensuring the security of quantum communication channels. Strengthening QKD protocols remains a vital frontier, representing the convergence of quantum communication and quantum computing.
The Table 1 provides a summary of recent QML protocols applied in QKD, highlighting current research gaps and potential future directions.
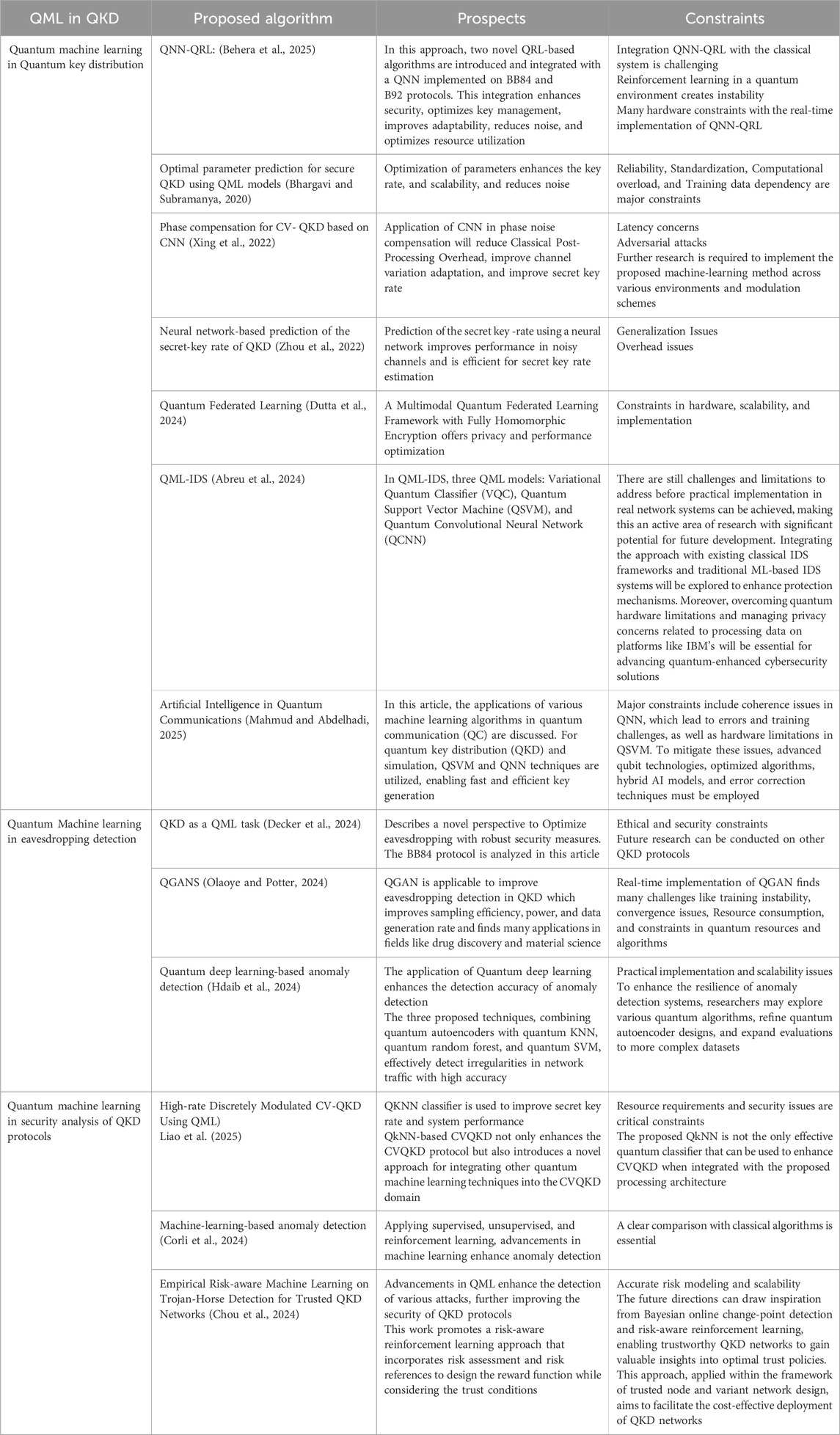
Table 1. Recent advancements in QML algorithms for QKD highlight current research gaps and future directions.
4 Discussion
This article discusses advancements in QML for quantum cryptography, especially with a focus on QKD, eavesdropping detection, and security analysis. Recent studies are reviewed, and their prospects and constraints are summarized in a tabular format. Key research gaps include optimization challenges due to the lack of dedicated QML models, practical implementation and real-time testing limitations, hybrid quantum-classical tradeoffs, scalability issues, hardware constraints, security and robustness concerns, quantum memory and data loading difficulties, data encoding challenges, and computational overhead. Future research directions include optimizing model design to enhance security and robustness. Hybrid quantum-classical Generative Adversarial Networks (GANs) help overcome hardware constraints by requiring fewer Qubits and enabling parallel processing. Unsupervised learning minimizes resource usage, reduces noise, lowers computational overhead, and facilitates adaptive quantum encoding and compression—critical for real-time problem analysis. Additionally, advanced optimization algorithms such as ant colony optimization, bat optimization, simulated annealing, genetic optimization, fruit fly optimization, particle swarm optimization (PSO), and the gravitational search method, when combined with effective preprocessing techniques, offer more robust and efficient solutions. Additionally, QSDC protocols are well-suited for a wide range of cryptographic applications, and several advanced protocols extending beyond QSDC have been developed. Unlike the QKD family of protocols, which focuses solely on secret key negotiation, QSDC enables secure communication without requiring cryptographic keys for encryption and decryption.
Author contributions
KP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. AV: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Visualization, Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abreu, D., Rothenberg, C. E., and Abelém, A. (2024). “QML-IDS: quantum machine learning intrusion detection system,” in 2024 IEEE Symposium on Computers and communications (ISCC) (IEEE), 1–6.
Behera, B. K., Al-Kuwari, S., and Farouk, A. (2025). QNN-QRL: quantum neural network integrated with quantum reinforcement learning for quantum key distribution. arXiv Prepr. arXiv:2501.18188. doi:10.48550/arXiv.2501.18188
Bhargavi, K., and Subramanya, K. N. (2020). “Optimal parameter prediction for secure quantum key distribution using quantum machine learning models,” in Quantum cryptography and the future of cyber security, (IGI global), 44–69.
Chou, H., Vu, T. X., Maity, I., Garces-Socarras, L. M., Gonzalez-Rios, J. L., Merlano-Duncan, J. C., et al. (2024). Empirical risk-aware machine learning on trojan-horse detection for trusted quantum key distribution networks. arXiv Prepr. arXiv:2401.14622. doi:10.48550/arXiv.2401.14622
Corli, S., Moro, L., Dragoni, D., Dispenza, M., and Prati, E. (2024). Quantum machine learning algorithms for anomaly detection: a Survey. arXiv Prepr. arXiv:2408.11047. doi:10.48550/arXiv.2408.11047
Cui, W., Yang, C., Huang, G., and Jiao, R. (2024). Mode-pairing quantum key distribution based on wavelength division multiplexing in multi-user networks. Phys. Scr 99, 085112. doi:10.1088/1402-4896/ad5f61
Decker, T., Gallezot, M., Kerstan, S. F., Paesano, A., Ginter, A., and Wormsbecher, W. (2024). QKD as a quantum machine learning task. arXiv preprint arXiv:2410.01904. doi:10.48550/arXiv.2410.01904
Dutta, S., Karanth, P. P., Xavier, P. M., de Freitas, I. L., Innan, N., Yahia, S. B., et al. (2024). Federated learning with quantum computing and fully homomorphic encryption: a novel computing paradigm Shift in privacy-preserving ML. arXiv Prepr. arXiv:2409.11430. doi:10.48550/arXiv.2409.11430
Geng, M.-J., Li, X., and Ye, T.-Y. (2024). Semiquantum private comparison based on Bell states without quantum measurements from the classical user. Laser Phys. Lett. 21, 105205. doi:10.1088/1612-202x/ad72de
Gong, C., Zhou, N., Xia, S., and Huang, S. (2024a). Quantum particle swarm optimization algorithm based on diversity migration strategy. Future Gener. comput. Syst. 157, 445–458. doi:10.1016/J.FUTURE.2024.04.008
Gong, L., Chen, Z., Qin, L., and Huang, J. (2023). Robust multi-party semi-quantum private comparison protocols with decoherence-free states against collective noises. Adv. Quantum Technol. 6, 2300097. doi:10.1002/qute.202300097
Gong, L., Ding, W., Li, Z., Wang, Y., and Zhou, N. (2024b). Quantum k-nearest neighbor classification algorithm via a divide-and-conquer strategy. Adv. Quantum Technol. 7, 2300221. doi:10.1002/qute.202300221
Gong, L.-H., Li, M.-L., Cao, H., and Wang, B. (2024c). Novel semi-quantum private comparison protocol with Bell states. Laser Phys. Lett. 21, 055209. doi:10.1088/1612-202x/ad3a54
Gong, L.-H., Liu, Y.-Y., Huang, J.-H., and Wang, Y.-Z. (2025). Multi-party semi-quantum private comparison protocol of size relation based on d-dimensional single-particle states. Chin. J. Phys. 94, 471–486. doi:10.1016/j.cjph.2025.02.005
Gowda, D., Pandiya, D. K., Katkoori, A. K., and Jakkani, A. K. (2025). “Quantum cryptography and machine learning: enhancing security in AI systems,” in Advancing cyber security through quantum cryptography (United States: IGI Global), 137–174. doi:10.4018/979-8-3693-5961-7.ch006
Goyal, R. (2024). Quantum cryptography: secure communication beyond classical limits. J. Quantum Sci. Technol. 1, 1–5. doi:10.36676/jqst.v1.i1.01
Hdaib, M., Rajasegarar, S., and Pan, L. (2024). Quantum deep learning-based anomaly detection for enhanced network security. Quantum Mach. Intell. 6, 26. doi:10.1007/s42484-024-00163-2
Liao, Q., Liu, J., Huang, A., Huang, L., Fei, Z., and Fu, X. (2025). High-rate discretely modulated continuous-variable quantum key distribution using quantum machine learning. Chaos Solit. Fractals 196, 116331. doi:10.1016/J.CHAOS.2025.116331
Liu, W.-B., Li, C.-L., Liu, Z.-P., Zhou, M.-G., Yin, H.-L., and Chen, Z.-B. (2022). Theoretical development of discrete-modulated continuous-variable quantum key distribution. Front. Quantum Sci. Technol. 1, 985276. doi:10.3389/frqst.2022.985276
Mahmud, I., and Abdelhadi, A. (2025). Artificial intelligence in quantum communications: a comprehensive Survey. Authorea Prepr. doi:10.36227/techrxiv.173749978.88367470/v1
Nwaga, P. C., and Nwagwughiagwu, S. (2024). Exploring the significance of quantum cryptography in future network security protocols. World J. Adv. Res. Rev. 24, 817–833. doi:10.30574/wjarr.2024.24.3.3733
Pan, D., Long, G.-L., Yin, L., Sheng, Y.-B., Ruan, D., Ng, S. X., et al. (2024). The evolution of quantum secure direct communication: on the road to the qinternet. IEEE Commun. Surv. & Tutorials 26, 1898–1949. doi:10.1109/comst.2024.3367535
Qi, J., Yang, C.-H., Chen, S. Y.-C., and Chen, P.-Y. (2024). Quantum machine learning: an Interplay between quantum computing and machine learning. arXiv Prepr. arXiv:2411.09403.
She, T., Shao, H., Deng, X., and Jiang, Y. (2025). Design and analysis of a novel quantum-classical hybrid neural network for environmental sound classification. Appl. Acoust. 231, 110527. doi:10.1016/j.apacoust.2024.110527
Xing, Z., Li, X., Ruan, X., Luo, Y., and Zhang, H. (2022). Phase compensation for continuous variable quantum key distribution based on convolutional neural network. Photonics 9, 463. doi:10.3390/photonics9070463
Zhou, M.-G., Liu, Z.-P., Liu, W.-B., Li, C.-L., Bai, J.-L., Xue, Y.-R., et al. (2022). Neural network-based prediction of the secret-key rate of quantum key distribution. Sci. Rep. 12, 8879. doi:10.1038/s41598-022-12647-x
Zhou, N.-R., Zhang, T.-F., Xie, X.-W., and Wu, J.-Y. (2023). Hybrid quantum–classical generative adversarial networks for image generation via learning discrete distribution. Signal Process Image Commun. 110, 116891. doi:10.1016/j.image.2022.116891
Keywords: quantum cryptography (QC), quantum machine learning (QML), quantum key distribution (QKD), quantum convoluted neural networks (QCNN), quantum support vector machine (QSVM), eavesdropping detection, quantum secure direct communication (QSDC)
Citation: Purohit K and Vyas AK (2025) Quantum key distribution through quantum machine learning: a research review. Front. Quantum Sci. Technol. 4:1575498. doi: 10.3389/frqst.2025.1575498
Received: 12 February 2025; Accepted: 23 April 2025;
Published: 02 May 2025.
Edited by:
Qin Liao, Hunan University, ChinaReviewed by:
Nanrun Zhou, Shanghai University of Engineering Sciences, ChinaCopyright © 2025 Purohit and Vyas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Krupa Purohit, a3J1cGEuZGF2ZTI0QGdtYWlsLmNvbQ==
 Krupa Purohit
Krupa Purohit Ajay Kumar Vyas
Ajay Kumar Vyas