- 1DISI, University of Trento, Trento, Italy
- 2TIM-SKIL, Trento, Italy
- 3Department of Computer Science, KU Leuven, Leuven, Belgium
When faced with large or complex decision problems, human decision makers (DM) can make costly mistakes, due to inherent limitations of their memory, attention, and knowledge. Preference elicitation tools assist the decision maker in overcoming these limitations. They do so by interactively learning the DM’s preferences through appropriately chosen queries and suggesting high-quality outcomes based on the preference estimates. Most state-of-the-art techniques, however, fail in constructive settings, where the goal is to synthesize a custom or entirely novel configuration rather than choosing the best option among a given set of candidates. Many wide-spread problems are constructive in nature: customizing composite goods such as cars and computers, bundling products, recommending touristic travel plans, designing apartments, buildings, or urban layouts, etc. In these settings, the full set of outcomes is humongous and can not be explicitly enumerated, and the solution must be synthesized via constrained optimization. In this article, we describe recent approaches especially designed for constructive problems, outlining the underlying ideas and their differences as well as their limitations. In presenting them, we especially focus on novel issues that the constructive setting brings forth, such as how to deal with sparsity of the DM’s preferences, how to properly frame the interaction, and how to achieve efficient synthesis of custom instances.
1. Introduction
Consider a tourist planning her upcoming trip to Italy. She has to solve a decision problem involving several decision variables: what cities to visit and in what order, how to travel from one city to the next, how long to stay and what activities to enjoy at each location, etc. This is a very complex decision problem. The set of potential travel plans is naturally delimited by hard requirements, such as maximum duration and budget, while the tourist’s preferences define a ranking between feasible alternatives. Analogous decision problems occur in many day-to-day activities: configuring one’s next car (product configuration (Sabin and Weigel, 1998)), planning the working shifts of employees (scheduling (Ernst et al., 2004)), designing a pleasant and functional arrangement of furniture pieces (layout synthesis (Harada et al., 1995)), and many others.
All these tasks boil down to identifying a structured configuration consisting of several interrelated variables, where the space of configurations is delimited by hard constraints and the ranking among feasible alternatives is determined by the user’s preferences. When faced with such decision problems, human decision makers (DM) often fail to choose an optimal, or even satisfactory, outcome, for several reasons (Boutilier, 2002; Pigozzi et al., 2016). The space of alternatives is simply too large to search directly. Furthermore, the relationships between variables and the hard constraints impose an additional burden on the DM’s limited knowledge, memory, and attention.
Computational aids can assist human DMs in identifying good quality solutions. Preference elicitation approaches (Boutilier, 2002; Pigozzi et al., 2016) involve interactively learning the DM’s preferences, which are unobserved, and using them to suggest progressively better recommendations until a satisfactory one is found. However, existing approaches are typically conceived for identifying the most preferred solution from a given collections of candidates (e.g., movies, books), and they are not directly applicable to constructive preference elicitation problems, which involve “synthesizing” the structured configuration from basic components given feasibility constraints and (an estimate of) the user’s preferences. Bayesian approaches (Guo and Sanner, 2010; Viappiani and Boutilier, 2010) rely on expensive routines to compute the expected informativity of candidate queries (Chajewska et al., 2000) and cannot scale to large configuration scenarios. Regret-based elicitation strategies (Boutilier et al., 2006; Braziunas and Boutilier, 2007) assume perfect feedback from the user and cannot handle the occasional inconsistencies which are to be expected when dealing with human DMs. Finally, standard recommendation techniques such as collaborative filtering (Koren and Bell, 2015) cannot be straightforwardly applied in this context, as it will rarely be the case that two users choose the very same configuration.
In this article, we survey a general framework specifically designed for constructive preference elicitation. As in standard preference elicitation, our framework revolves around making informative queries to the user and collecting preference feedback, but it integrates structured-output ideas and efficient constrained optimization techniques to deal with combinatorial search spaces. The proposed framework offers the following key advantages. First, queries and recommendations are synthesized on-the-fly via constrained optimization. This avoids having to enumerate the space of alternatives and enables to seamlessly handle both preferences and hard constraints. In addition, our formulation is very general: it accommodates fully combinatorial applications like personnel timetabling, and hybrid ones involving also continuous variables, like layout synthesis. Second, the learning loop employs structured-output ideas to efficiently deal with the large number of alternatives. In contrast to regret-based approaches, it is robust against inconsistencies in the user’s feedback. Third, our framework can be adapted to different kinds of interaction, depending on the specific application. In this article, we will discuss pairwise ranking queries (e.g., “do you prefer a to b?”), improvement queries (“please improve a, even a little”), and example critiques (“why do/don’t you like a?”). Improvement critiques are more appropriate in tasks like layout synthesis or other design applications, where configurations can be easily modified by the user via manipulation, while ranking queries work fine in other tasks. Example critiques can in principle be combined with either of the previous.
We showcase the feasibility of our framework by surveying three concrete implementations. The first one is a setwise generalization of max-margin learning (SetMargin or SM for short) (Teso et al., 2016). It relies on setwise ranking queries, an extension of pairwise ranking queries to small collections of alternatives, for increased flexibility. The query selection strategy aims at selecting an informative, diverse set of high-quality query configurations. The core optimization step can be cast as a mixed-integer linear problem and solved directly with any efficient off-the-shelf solver. A major feature of SM is its ability to handle sparsity in the user’s preferences. In many cases, the DM will have strong preferences on some components, while being largely indifferent to the others. Contrary to existing approaches, SM employs a sparsifying regularizer that can effectively exploit this phenomenon.
The second implementation is an application of Coactive Learning, a recently introduced online preference learning framework (Shivaswamy and Joachims, 2012) designed for learning from implicit feedback (e.g., click counts). In coactive interaction, the recommender presents a single candidate recommendation and the user modifies it (even slightly) to better fit her preferences. Here, we show that this paradigm can be naturally adapted to constructive preference elicitation. Coactive interaction is especially well suited to problems where explicit manipulative feedback is easy to obtain, for instance, layout synthesis. Notably, the theoretical convergence guarantees of Coactive Learning still hold in the constructive setting.
The third algorithm, the Critiquing Preference Perceptron (CPP) (Teso et al., 2017a), combines coactive interaction and example critiquing. CPP stems from the observation that, during the elicitation procedure, the DM may realize that they care about some aspect of the configuration that they previously deemed irrelevant (Slovic, 1995; Lichtenstein and Slovic, 2006). Contrary to other methods, CPP is designed to dynamically adapt to these newly discovered preference criteria. To this end, it couples improvement queries with example critiques, i.e., “why do you prefer a over b?” questions, to acquire the missing preference criteria. The critiques are only requested at specific iterations, to minimize the user effort. We include a theoretical analysis of the CPP algorithm, derived from Shivaswamy and Joachims (2015), that elucidates the convergence properties of the algorithm.
While stemming from the same framework, the three approaches offer complementary advantages. SetMargin is designed to handle constructive recommendation problems where the user preference criteria are fixed, but sparse, as is usually the case for non-expert DMs. On the other hand, PP and CPP are suited for design problems, where manipulative interaction is more natural. Furthermore, CPP supports cases where the preference criteria may change during the elicitation process, as often happens while the DM is exploring the catalog of options (Chen and Pu, 2012). All algorithms are extensively validated on synthetic and realistic constructive tasks, most of which are too large to be tackled with standard elicitation procedures. Our evaluation shows that SM, PP, and CPP can easily solve problems much larger than previously possible, while still performing as well or better than state-of-the-art competitors. Please note that, while SM and CPP have previously been presented in Teso et al. (2016) and Teso et al. (2017a), the application of PP to layout synthesis is a novel contribution of this article.
While constructive preference elicitation bears some resemblance to active learning and configurator technologies, we stress that there are significant differences between these tasks. Active learning approaches (Settles, 2012) aim at learning an accurate model of some system by interacting with an external oracle (human or otherwise). Supervision is obtained via membership queries, e.g., questions like “what is the label of instance x?” Each label comes at a cost, and therefore interaction is kept at a minimum. The main differences with preference elicitation are that membership queries ask for labels rather than preferences, and that the query selection strategies used in active learning ignore the quirks of interacting with non-expert human DMs. For instance, uncertainty sampling selects examples close to the separation margin (Kremer et al., 2014). Examples chosen this way may be arbitrarily similar to each other or uninteresting, and therefore difficult to evaluate for the DM.
Product configurator systems (Sabin and Weigel, 1998; Felfernig et al., 2014) guide the user in searching for a good configuration. While sharing the same goal of constructive preference elicitation, configurators typically do not include a learning component. They iteratively ask the user to restrict the potential values that a component can take, thus progressively trimming away irrelevant regions from the search space. Component-based interaction has its advantages, and it is not impossible to integrate it in preference elicitation. However, in this article, we will focus on more customary interaction protocols, like pairwise comparison queries.
This article is structured as follows. Section 2 overviews some prerequisite background on preference learning and structured-output prediction. Section 3 introduces our constructive preference elicitation framework and some basic learning methods. We proceed by detailing three implementations of the general framework: the SetMargin algorithm, which makes use of setwise choice queries (in Section 4), the Preference Perceptron, a Coactive Learning approach based on improvement queries (Sec. 5), and the Critiquing Perceptron, which also exploits example critiques (Sec. 6). We conclude by discussing some open issues in Section 7.
2. Background
In this section, we overview some prerequisite literature on preference and structured prediction, starting from our notation. We indicate scalars and tuples x in italics, column vectors x in bold, and sets χ in calligraphic letters. Important scalar constants N, M, T are upper-case. The inner product between vectors is written as , the Euclidean norm as , and the norm as . Finally, we abbreviate the set {1, …, n} as [n]. Table 1 summarizes the most frequently used symbols.
2.1. Preferences
Modeling and eliciting preferences is a long standing interest in AI (Domshlak et al., 2011; Pigozzi et al., 2016) and related fields like decision theory, psychology, and econometrics (Von Neumann and Morgenstern, 1947; Slovic et al., 1977; Kahneman and Tversky, 1979). The first and probably most critical issue is how to appropriately represent preferences. There exist various alternative representations, which differ in terms of expressiveness and compactness. In addition, the choice of representation heavily impacts the computational complexity of query answering, e.g., selecting a candidate recommendation to present to the user.
The most general way to represent the preferences of a DM over a set of choices 𝒴 is to employ a binary preference relation ≽ ⊆𝒴×𝒴. The statement y ≽ y′ reads “y is at least as good as y′.” The relation ≽ induces a partial preorder over the outcomes in 𝒴. This, in turn, can be used to reason over the preferences, e.g., to answer ordering queries like “is y better than y′?” or dominance queries like “which are the most preferred outcomes?” Being able to answer these queries is a critical component of decision support systems. However, this encoding becomes impractical when the set 𝒴 contains more than a handful of outcomes: an arbitrary preference relation over c choices requires c2 parameters. Eliciting this many parameters becomes infeasible even for moderate values of c.
It is customary to introduce additional assumptions on the relation ≽ to represent the DM preferences more compactly and make the elicitation task more tractable. The basic assumption of multi-attribute decision theory (Keeney and Raiffa, 1976) is that the options y ∈ 𝒴 are composed of multiple attributes yi and can therefore be mapped to points in a multi-dimensional space. In this case, the options can be represented as tuples y = (y1, …, yN), where N is the number of attributes and each yi takes values in some domain 𝒴i. The set of all possible outcomes can be seen as the Cartesian product of the attributes domains 𝒴 = 𝒴1×, …, ×𝒴N. Under this assumption, graphical model representations (such as conditional preference networks) and utility functions can be employed.
Conditional preference networks—CP-nets for short—(Boutilier et al., 2004; Allen, 2015) represent a multi-attribute preference relation with a directed graph. The graph encodes the conditional preferential independences between attributes. Each node of a CP-net represents an attribute yi, whose parents are all the attributes that impact the user preferences with respect to yi. Each node is then associated with a conditional preference table (CPT) that encodes how preferable each possible value of yi is given the value of the parent nodes. In this way, CP-nets compactly represent the structure of a preference relation and can be used to efficiently answer dominance queries (when the network is acyclic). One major problem of CP-nets is that they require complete preference information to properly represent a preference relation over a domain 𝒴. If a CPT is incomplete, configurations included in the uncovered cases of the CPT are not represented by the CP-net and cannot be reasoned over, not even approximately. Obtaining complete preference information, however, is infeasible when the outcome domain 𝒴 has more than a dozen attributes.
Contrarily to CP-nets, utility functions can encode an (approximate) preference model over the full domain 𝒴, and thus they can work with partial utility information. By reasoning with utility functions, we can provide recommendations of increasing quality as the estimated utility model improves throughout the elicitation process, as will be discussed Section 2.2. A utility function is a mapping u : from outcomes y ∈ 𝒴 to utility values . The utility values provide a numerical estimate of the preferability of a configuration and are meant to mimic the (qualitative) preferences encoded by ≽: for all configurations y, y′ ∈ 𝒴, u(y) ≥ u(y′) if and only if y ≽ y′. Utility functions offer varying degrees of expressivity and ease of manipulation. Additive independent utilities are the simplest (and least expressive) class of utility functions. They work based on the assumption that the overall utility of a configuration y can be decomposed into n independent subutilities, one for each attribute yi:
Here, the subutilities ui depend exclusively on the i-th attribute. Under additive independence, utility elicitation is especially convenient, as each attributes provides an independent contribution to the overall utility and thus the corresponding subutility may be elicited separately from other attributes. Once all the subutilities have been elicited, answering dominance queries is also quite convenient, by selecting for each attribute the value maximizing the corresponding subutility.
One problem with additive independent models is that attributes are typically interrelated, especially in the structured setting. This entails that the utility can not be broken down into independent, per-attribute components. A much less restrictive structural assumption is the generalized additive independence (GAI) (Fishburn, 1967). Given M attribute subsets I1, …, IM ⊆ [N], a GAI utility has the form:
where is a partial outcome on the attributes Ik. A GAI utility is a combination of M subutilities, each one dependent only on the attributes in Ik. The subsets Ik may, however, overlap. This model is very general and includes the linear functions over arbitrary feature spaces used in structured-output prediction tasks (see Section 2.3), which are the natural choice for our constructive preference elicitation scenario.
As a final remark, we note that the preferences of human DMs exhibit specific structure, which must be dealt with while designing the elicitation mechanism. First, in domains with many attributes, users often exhibit strong preferences on a few selected aspects of the candidate configurations (e.g., fuel consumption or trunk size for a car) while being indifferent about others (e.g., top speed, wheel covers). This entails that human preferences are sparse. For linear and GAI utilities, this translates into most of the subutilities ui(⋅) being close to zero. Second, human DMs are unaware of most of their preference criteria and tend to discover or refine them while browsing the available options (Chen and Pu, 2012). In other words, the subutilities deemed relevant may change during elicitation. Models that do not account for this fact may fail to learn accurate representations of the user’s preferences and may end up providing suboptimal recommendations.
2.2. Preference Elicitation
Preference elicitation is the process of interactively learning a model of the DM’s preferences, with the goal of providing a high-quality recommendation with the least cognitive effort. The difficult part is that decision makers have trouble stating their preferences upfront and may not even be fully aware of them (Lichtenstein and Slovic, 2006; Pigozzi et al., 2016). Elicitation strategies focus on asking suitably chosen queries to the DM, and learning from the obtained feedback; see below for more details. The number of questions should be kept low, not to overload or annoy the user. The key insight here is that even partial preference information is often enough to suggest satisfactory recommendations, avoiding the need for eliciting all of the DM’s preferences (Viappiani and Boutilier, 2011).
The elicitation process proceeds iteratively for some reasonable number of iterations T, which depends on the task at hand. Let u* : 𝒴 → ℝ denote the true, unobserved utility function of the DM. The algorithm maintains an internal estimate ut of the true utility, where t ∈ [T] is the iteration index. At each iteration, the algorithm selects a query Qt to be posed to the user, typically by exploiting the current estimate ut and potentially additional information (e.g., Bayesian methods (Guo and Sanner, 2010; Viappiani and Boutilier, 2010) maintain a full probability distribution over the space of candidate utility functions, and use it extensively during query selection). For instance, in pairwise ranking queries the algorithm chooses two configurations y and y′ and asks the DM which one is better. The DM’s feedback is then used (possibly along with all the feedback received so far) to compute a new estimate ut+1 of the utility function. An algorithmic template of this procedure is listed in Algorithm 1. A preference elicitation algorithm also provides a recommendation yt at each iteration t. Typically, the highest utility configuration yt = argmaxy∈𝒴 ut(y) is recommended. In some cases, as in Coactive Learning (see below) the query Qt and the recommendation yt coincide. The elicitation procedure terminates when the user is satisfied with the recommendation yt or after a finite number T of steps, after which, the best configuration according to the final estimate uT is provided as final recommendation. Notice that to effectively deal with human users, the algorithm should be robust to occasional inconsistencies in DM feedback.
There exist many types of queries, like lotteries, pairwise or setwise rankings, improvements, which all share the goal of being easy to answer to and as informative as possible. Queries involving comparisons and rankings have come to be predominant in the literature with respect to quantitative evaluations. Indeed, users are typically more confident in providing qualitative judgments like “I prefer configuration y over y′” than in specifying how much they prefer y over y′ (Conitzer, 2009; Carson and Louviere, 2011). In this article, we experiment with three different types of feedback:
• Choice set feedback: the DM is queried with a set of candidate solutions (typically two to five) and asked to pick the best one, according to her preferences. This type of feedback is usually deemed to be the best trade-off between informativeness and user cognitive effort (Guo and Sanner, 2010; Viappiani and Boutilier, 2010). Larger sets of alternatives can be more informative, at the cost of a potentially higher cognitive cost for the user, as detailed in Section 4.
• Coactive feedback: this was recently proposed by Shivaswamy and Joachims (2015) as an alternative to comparative feedback. It is a type of manipulative feedback, where the system provides a single recommendation and the user is asked to (slightly) improve it to better match her preferences. Shivaswamy and Joachims (2015) argue that coactive feedback is often implicitly attainable from the user interaction with a system. However, we also suggest that explicit coactive interaction comes handy in constructive decision tasks, such as design or planning, as discussed in Section 5.
• Example critiquing: a “critique” is, broadly speaking, a sort of explanation about why the user may like or dislike a certain configuration. Many types of critiquing-based system, or conversational recommenders, have been devised (McGinty and Reilly, 2011; Chen and Pu, 2012), but they usually boil down to employing the user critiques to refine the recommended objects by imposing more constraints on their attributes, and do not use them to learn an explicit model of the user’s preferences. In our Critiquing Perceptron, detailed in Section 6, we instead employ a specific type of critiques that allows us to improve the underlying utility model by expanding the set of relevant features for the user.
Finally, the performance of a preference elicitation algorithm is measured via the quality of the recommendations yt it delivers. Recommendation quality is measured with the regret (or utility loss):
that is, the difference in true utility between the best possible configuration y* and the recommended one yt. Depending on the type of interaction, however, different definitions of regret may be used. In some cases, we are also interested in the average regret: , indicating the overall performance of the system throughout the elicitation process. These measures will be used in our theoretical and empirical analyses.
2.3. Structured-Output Prediction
Ordinary supervised learning algorithms predict one or more categorical or continuous output labels. When the output labels are structures—such as sequences, trees, graphs, and other composite objects—ordinary supervised methods cannot be applied. Structured-output prediction refers to a class of techniques explicitly designed to predict such objects (Tsochantaridis et al., 2005; Bakir et al., 2007; Joachims et al., 2009b).
Let 𝒳 and 𝒴 be the set of input and output structures, respectively. In structured-output prediction, the goal is to learn a function f : 𝒳 → 𝒴mapping inputs x ∈ 𝒳 to their corresponding output y ∈ 𝒴. The function f is defined in terms of a numerical scoring function F :𝒳 × 𝒴 → ℝ that evaluates the “compatibility” F(x, y) of an input–output pair. Given an input x, prediction amounts to searching for the most compatible output y by solving the following inference problem:
As is common in the structured-output prediction literature (Joachims et al., 2009b), we will restrict ourselves to linear scoring function of the form F(x, y) = 〈w, ϕ(x, y)〉defined over some joint feature representation ϕ(x, y) of the input–output pair. The weight vector w ∈ ℝM is a parameter controlling the importance of the various features and is learned from data. In this section, we will cover two learning algorithms most closely related to our contribution: the structured-output support vector machine (SSVM) (Tsochantaridis et al., 2004) and the Structured Perceptron (SP) (Collins, 2002).
The SSVM is an offline learning approach, but serves as a basis for our interactive preference elicitation schemes. Given a dataset of examples 𝒟 = {(xi, yi)}, SSVMs learn a weight vector w that scores correct input–output pairs higher than all incorrect ones, that is for all examples (xi, yi) ∈ 𝒟 and all incorrect outputs y ∈ 𝒴, y ≠ yi. Here, μ(yi, y) is a structured loss that captures how bad it would be to predict the “wrong” output y in place of the correct one yi and is application dependent. The slacks ∈i take care of possible inconsistencies in the dataset. As in other max-margin approaches (Joachims, 2002), learning aims at maximizing the separation margin between correct and incorrect predictions while minimizing slack variables and is cast as a quadratic programming (QP) problem. The resulting QP includes a potentially exponential number of large margin constraints (namely, one for each example in 𝒟 and candidate output in 𝒴), and therefore can not be solved directly. However, since only a small subset of constraints is usually active, the QP can be solved via constraint generation strategies. Please see Joachims et al. (2009a,b) for a more detailed description, and Shah et al. (2015) and Osokin et al. (2016) for some recent developments.
Contrary to the SSVM, the Structured Perceptron is an online learning algorithm. The training algorithm is straightforward. The procedure involves iteratively inferring the best prediction for the current example using equation (2), and then adjusting the weights whenever the predicted label does not match the true one. More formally, at each iteration t, the SP receives an input structure xt and predicts the corresponding structured label yt. Next, it compares the true label with the predicted one and computes an updated weight estimate using a simple Perceptron update, that is . Despite its simplicity, the SP comes with solid theoretical guarantees (Collins, 2002) (so long as the dataset is linearly separable) and works well in practice. An advantage of SP with respect to max-margin formulations is that the update rule is trivial to compute, at the cost of a less robust handling of inconsistencies in the data.
A major advantage of structured-output prediction approaches is that inference and learning are reasonably decoupled. So long as the inference problem (equation (2)) can be solved, learning in SSVMs and the SP is guaranteed to work. This allows to encode arbitrary inference problems using arbitrary modeling frameworks, e.g., constraint programming in our case, to solve various constructive applications, as shown in the next sections.
3. Constructive Preference Elicitation
Constructive preference elicitation (CPE) extends standard preference elicitation to settings where the configurations to be recommended are structured object, e.g., car or PC configurations, travel plans, layouts, etc. Our framework mixes ideas from structured-output prediction and constraint satisfaction (and optimization) to the standard PE approach, as follows.
As in multi-attribute preference elicitation (see Section 2.1), in our framework the candidate structures y ∈ 𝒴 are defined by N attributes y = (y1, …, yN) ∈𝒴1×, …, × 𝒴N. The attributes represent the low-level components of the configuration. For instance, in a car configuration scenario, they may encode the choice of engine, tires, body color, etc. The DM’s preferences are over features ϕ(y) of the configuration, which may include both simple attributes (“is the color red?”) and more complex statements (“is the gas consumption low?”). The rationale is that non-domain experts usually do have no preferences on the particular engine or tires, but rather care about speed and gas consumption, which are functions of the individual attributes. The user’s utility function is assumed to be a linear combination of the features, i.e., u*(y) = 〈w*, ϕ(y)〉. This representation is analogous to the one used in structured-output prediction (see Section 2.3) and it is expressive enough to encode various real-world constructive problems, as shown by our experiments. The only difference with respect to the standard formulation of structured-output learning is that here the input x is missing. Indeed, the goal of CPE in general is to synthesize an optimal configuration from scratch, rather than predicting the best (structured) output for a given input. There are actually applications in which we want to generalize a learned preference vector to several instances of the same problem. In these cases, the preference model can be trivially extended including an input object x representing given contextual information about the current task. In layout synthesis, for instance, after learning an interior designer’s preferences over a certain house, we may want to apply the same learned preferences to another house with a different shape. The shape of the house could therefore be given as an input context x to our model, to generalize the learned weights over different contexts. In this article, we omit the context for notational simplicity, but all algorithms can be straightforwardly applied in the presence of contextual information: it suffices to add the contextual component x to the feature map (as in structured-output models) and drop the stopping criterion, as the learning task and satisfactory recommendations change with different contexts.
The CPE framework follows closely Algorithm 1. At each iteration, a query is presented to the DM, and the feedback received is used to update the weights. The update step (line 10) depends on the actual algorithm. With SSVM, feedback is turned into additional constraints and the updated parameters wt+1 are learned from the entire dataset 𝒟t+1. Pairwise ranking queries, for instance, generate feedback in the form of binary preferences , which are turned into pairwise ranking constraints . Other interaction protocols can be dealt with similarly, e.g., improvements and example critiques (see Sections 5 and 6). In SP, weights are updated according to the latest feedback Ft only. For pairwise preference queries, the update rule is simply .
Given an estimate wt, choosing a single recommendation yt is analogous to performing structured inference (equation (2)). Choosing the query set Qt depends on the specific query strategy used (e.g., pairwise, choice set, improvement), recalling that the goal is to select queries that are easy to answer and convey as much information as possible. Leaving the specifics to Sections 4 and 5, here we merely note that, just like inference, query selection in structured domains can be interpreted as a constrained optimization problem. The complexity of this problem depends on the type of variables (Boolean, integer, or continuous) and the type of features and hard constraints (linear, quadratic, etc.). The CPE framework is generic and can be combined with any optimization technology which is suitable for the type of problem at hand. In this article, we focus on scenarios where numeric features and constraints are linear in the attributes. Inference and query selection in this case can be cast as (mixed) integer linear programs (MILP). Despite being NP-hard in the general case, off-the-shelf solvers do optimize practical MILP instances very efficiently, as shown by our experiments on a number of relevant application scenarios.
In the following, we describe three CPE algorithms which rely on different forms of interaction with the DM. Setwise max-margin (Sec. 4) is conceived for comparative feedback in the form of preferences within a choice set of candidates. Coactive Learning (Sec. 5) employs manipulative feedback in the form of (slight) user improvements over a candidate configuration. Coactive Critiquing (Sec. 6) extends Coactive Learning by further requiring explanations for the DM feedback when deemed needed to incorporate it into the model.
4. Setwise Max-Margin
SetMargin (or SM) (Teso et al., 2016) is an implementation of our CPE framework which generalizes the max-margin principle to sets to recommend both high-quality and maximally diverse configurations to the DM.
During interaction, the algorithm builds K ≥ 2 configurations and presents them to the user, asking for her most preferred one. Here, K is a small constant, usually 2–5. When K = 2, queries reduce to pairwise comparisons. Larger values of K can increase the potential informativeness of interaction: the user has more options to choose from, and her choice induces K − 1 pairwise ranking constraints. Of course, if K is too large the user may have trouble picking the absolutely best option. The value of K should be chosen to trade-off between these two aspects in an application specific manner. There are two caveats, however. If the query configurations are too similar, they may look undistinguishable to the DM, who may not know what to answer. Furthermore, low-quality or random configurations may be difficult to evaluate for the user. Both issues may lead to potentially uninformative or inconsistent answers. To avoid them, SM is explicitly designed to select K query configurations that are diverse between each other, and that have high utility with respect to the current preference estimates.
In SM the features ϕ(⋅) are restricted to be 0–1 only, a common choice in preference elicitation (Guo and Sanner, 2010; Viappiani and Boutilier, 2010). The set of feasible configurations 𝒴 is implicitly defined by hard constraints. This setup is rather general, and naturally allows to encode both arithmetical and logical constraints. Categorical features can be handled by using a one-hot encoding, while numerical attributes that depend linearly on the categorical ones can be dealt with too. In addition, SM assumes without loss of generality that the preference weights wi are non-negative. User dislikes can be encoded by adding negated features to ϕ(⋅), if needed. We refer the reader to Teso et al. (2016) for a more extensive discussion.
4.1. The Algorithm
As can be seen from the pseudo-code listed in Algorithm 2, the SM algorithm follows the standard preference elicitation loop (Algorithm 1). At each iteration t, SM selects K query configurations based solely on the collected feedback 𝒟t. The configurations are chosen to be diverse and high-quality, to facilitate acquiring preferences from the user, while inconsistencies in the user preferences are handled by the mathematical formulation, as discussed later on. The DM is invited to select her most preferred configuration among the K alternatives. Her choice implicitly defines K − 1 ranking constraints:1 for every configuration that was not chosen, SM extracts a pairwise preference and adds it to 𝒟t, obtaining 𝒟t+1. The algorithm terminates when the user is satisfied with the suggested configuration or the maximum number of iterations is reached.
The SM query selection strategy encourages diversity and high-quality of the query set by employing max-margin ideas, as follows. The algorithm jointly learns a set of K weight vectors, each representing a candidate utility function, and a set of K candidate configurations, one for each weight vector. The weights and configurations are mutually constrained so that (i) each configuration has high utility with respect to the corresponding weight vector, therefore encouraging their subjective quality, and (ii) each configuration has low utility with respect to the other weight vectors, to encourage diversity. All weight vectors are further required to be consistent with the feedback acquired so far (modulo inconsistencies in the data).
More formally, let 𝒟t be the set of pairwise ranking constraints collected so far. The user preference models are represented by K weight vectors . Each wi is chosen as to provide the largest possible separation margin for the pairs in 𝒟t, i.e., for all i ∈ [K] and pairwise ranking the utility difference should be as large as possible. Non-separable pairs are dealt with through slack variables ε, as customary. The query configurations are chosen to be high-quality and diverse: each is required to have maximal utility with respect to the associated weights wi and large separation from the other configurations , ∀j ≠ i. The latter constraint is implemented by requiring the difference in utility to be at least as large as the margin. A visualization for K = 2 can be found in Figure 1.
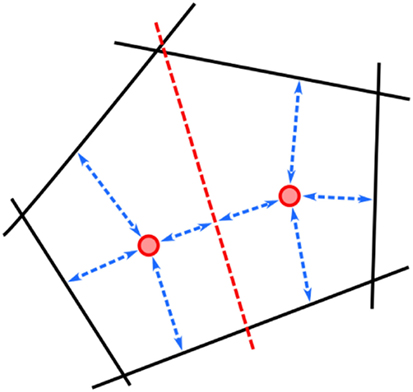
Figure 1. Setwise max-margin optimization. The red points are weight vectors w1 and w2; the black lines correspond to preference constraints 𝒟t, and the red line corresponds to the hyperplane . The arrows represent the separation margins.
The previous discussion leads directly to the quadratic version of the SM optimization problem over the non-negative margin μ and the variables {wi}, {yi}, and {εi}:
The w⊤ and w⊥ refer to the minimum and maximum attainable weights and can be arbitrary non-negative vectors. We refer to this optimization problem as OP1.
The objective has four parts. The first part drives the maximization of the margin μ. The second minimizes the total sum of the ranking errors {εi}. The third one introduces an ℓ1 regularizer encouraging sparsity in the learned weights. It copes with the common scenario in which the user has strong preferences about some attributes, but is indifferent to most of them. The ℓ1 penalty is frequently used to improve the sparsity of learned models (Tibshirani, 1996; Zhang and Huang, 2008; Hensinger et al., 2010), with consequent gains in generalization ability and efficiency. The fourth part encourages the configurations to have high utility with respect to the associated weight vector. The hyperparameters α, β, γ ≥ 0 modulate the contribution of the various parts. Constraint 4 enforces consistency of the learned weights with respect to the collected user feedback through a ranking loss. Ranking mistakes are absorbed by the slack variables {εi}. Constraint 5 enforces the generated configurations to be as diverse as possible with respect to the corresponding weight vectors. Finally, Constraint 6 ensures that all variables lie in the corresponding feasible sets.
Unfortunately, Constraint 5 renders OP1 a mixed-integer quadratic optimization problem, and therefore difficult to solve directly. However, so long as the weights are non-negative (as assumed by SM), it is possible to linearize it, obtaining a (tight) mixed-integer linear approximation [please see Teso et al. (2016) for the details]. The MILP formulation, which we refer to as OP2, can be readily solved by off-the-shelf MILP solvers, and in practice it performs as well or better than state-of-the-art Bayesian approaches, while scaling to much larger configuration problems.
4.2. Empirical Evaluation
We implemented SM using Python, leveraging Gurobi 6.5.0 for solving OP2.2 SM was compared against three state-of-the-art Bayesian approaches: (1) the Bayesian approach of Guo and Sanner (2010), which selects queries according to an efficient heuristic approximation of the Value of Information (VOI) criterion (namely the restricted informed VOI or rivoi) (2) the Bayesian framework of Viappiani and Boutilier (2010) using Monte Carlo methods (with 50,000 particles) for Bayesian inference and asking K-way choice queries selected using a greedy optimization of Expected Utility of a Selection (a tight approximation of EVOI, hereafter just called eus); (3) Query Iteration (referred as qi below), also from Viappiani and Boutilier (2010), an even faster query selection method based on sampling sets of utility vectors.
Following the experimental protocol in Guo and Sanner (2010) and Viappiani and Boutilier (2010), we simulated 20 users in each experiment. Their true preferences w* were drawn at random from each of two different distributions: (1) a normal distribution with mean 25 and SD , (2) a sparse versions of the normal distribution where 80% of the weights are set to zero, simulating sparsity in the user’s preferences. We set a maximum budget of 100 iterations for all methods for simplicity. As in Guo and Sanner (2010), user responses were simulated using the Bradley–Terry model (Bradley and Terry, 1952) extended to support indifference. More formally, the probability that a simulated user prefers configuration y over y′ was defined as 1/(1 + exp(−λ(u*(y) − u*(y′)))), while the probability of her being indifferent was defined as exp(−λ2|u*(y) − u*(y′)|). The parameters λ1 and λ2 were set to one for all simulations. Finally, SetMargin was instructed to update the hyperparameters α, β, and γ every 5 iterations by minimizing the ranking loss over 𝒟 via cross-validation. α was selected from {20, 10, 5, 1}, while β and γ were taken from {10, 1, 0.1, 0.001}.
In the first experiment, we evaluated the behavior of the proposed method on artificial problems of increasing size. Each problem includes r categorical attributes, each taking values in [r], and no hard constraints. As an example, for r = 3 the feasible space 𝒴 is [3] × [3] × [3], for r = 4 it is [4] × [4] × [4] × [4], and so on. The cardinality of 𝒴 is rr, which for r ≥ 4 is much larger than the datasets typically used in the Bayesian preference elicitation literature. As such, this dataset represents a good testbed for comparing the scalability of the various methods. The problem space was encoded in SM with MILP constraints, while the other methods require all datasets to be explicitly grounded.
We report the regret and cumulative runtime of all algorithms, for K = 2 and r = 3, 4, in Figures 2 and 3. The curves are averaged over the 20 users; the shaded area represents the SD. For the dense weight distribution (Figure 2), SM performs comparably to the Bayesian competitors, but at a fraction of the computational cost. For sparse weight distribution (Figure 3) SM, in addition to being substantially faster on each iteration, requires less queries to reach optimal solutions. This is an expected result as the sparsification norm in our formulation (‖w‖1) enforces sparsity in the learned weights, while none of the other approaches is designed to do this.
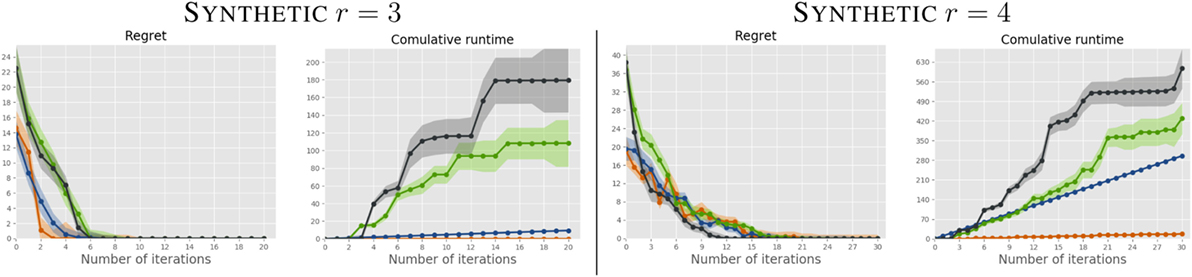
Figure 2. Comparison between SM (orange), riVOI (blue), qi (green), and eus (gray) on the r = 3 (left) and r = 4 (right) synthetic problems on users with dense preferences. Best viewed in color.
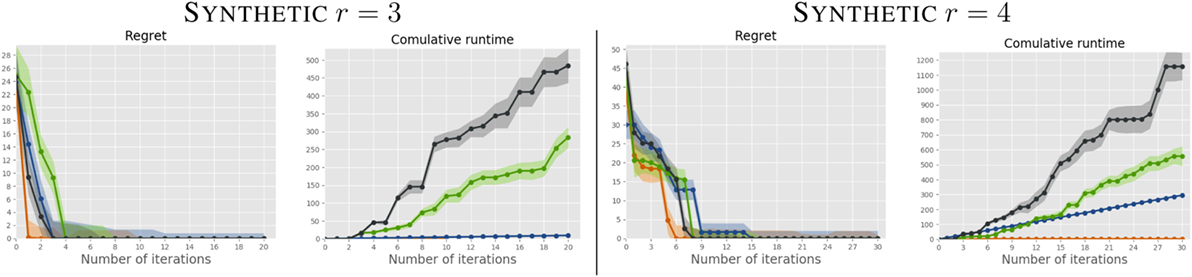
Figure 3. Comparison between SM (orange) and the Bayesian competitors on users with sparse preferences.
In a second experiment, we ran SetMargin on a realistic PC recommendation problem. Here, PC configurations are defined by eight attributes: type (laptop, desktop, or tower), manufacturer (8 choices), CPU model (37), monitor size (8), RAM amount (10), storage (10) size, and price. The latter is a linear combination of the other attributes, as it can be well approximated by the sum of the price of the components plus a bias due to branding. Interactions between attributes are modeled as 16 Horn clauses (e.g., a certain manufacturer implies a set of possible CPUs) and encoded as MILP constraints. The search space 𝒴 includes hundreds of thousands of candidate configurations and is far beyond reach of standard preference elicitation approaches.
Figure 4 reports results of SetMargin with K = 2, 3, 4 using the sparse uniform distribution, the more complex of the sparse ones, dense distributions being unrealistic in this scenario. To evaluate the effect of the query set size K, the curves are plotted both against the iteration index (which is independent of K) and the number of acquired constraints |𝒟| (which depends on K). Overall, between 50 and 70 queries on average are needed to find a solution which is only 10% worse than the optimal one, out of the more than 700,000 thousands available. Note that a vendor may ensure a considerably smaller number of queries by cleverly constraining the feasible configuration space; since our primary aim is benchmarking, we chose not to pursue this direction further. Please see Teso et al. (2016) for a more detailed discussion.
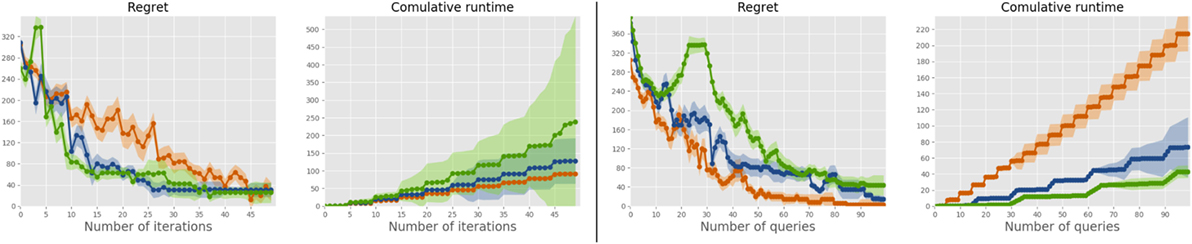
Figure 4. Results for SetMargin for K = 2 (red), K = 3 (blue), and K = 4 (green) on the PC dataset for the sparse uniform distribution. Regret and time are plotted against number of iterations (left) and number of acquired constraints (right).
5. Coactive Learning
Coactive Learning (Shivaswamy and Joachims, 2015) is an online structured prediction framework for learning utility functions through user interaction. In this case, user interaction is done via coactive feedback: the algorithm presents a single configuration to the user, who is asked to produce a slightly improved version of that object.
The Coactive Learning framework can be readily applied to constructive preference elicitation tasks. Query selection here boils down to suggesting the currently best solution, which is obtained by solving structured inference (equation (4)). To apply Coactive Learning to constructive problems, it suffices to define an appropriate inference procedure based on constraint optimization. The improved solution received as feedback from the user is then combined with the presented solution into a pairwise preference.
The coactive protocol is well suited for tasks where the user is actively involved in shaping the final recommended object. Coactive interaction can be seen as a form of “cooperation” between the system and the user to achieve the shared goal of producing a good recommendation. This is especially useful when considering large configuration tasks like the ones addressed in the CPE framework, provided that manipulation is sufficiently natural in the application at hand (as in design tasks) and that the user is willing to stand the required cognitive effort. The rest of this section outlines a particular Coactive Learning algorithm, the Preference Perceptron, and details our experiments on a prototypical layout synthesis problem. To the best of our knowledge, using Coactive Learning for solving a constructive design problem has never been proposed before and represents an original contribution of this article.
5.1. The Algorithm
The Coactive Learning paradigm encompasses a variety of different algorithms. Perhaps the simplest (but quite effective) algorithm is the Preference Perceptron (PP) (Shivaswamy and Joachims, 2015), a generalization of the Structured Perceptron (Collins, 2002) (see Sec. 2.3) where the supervision is provided by weak user feedback, i.e., pairwise ranking constraints. Algorithm 3 show a slightly simplified version of the PP.3 The algorithm first initializes the weights w1 to a reasonable guess and then performs T iterations, interacting with the user to learn a better estimate of the user weights. The initial weights may be chosen to be either all zero (a safe, unbiased choice) or estimated offline from data collected during past interaction with other users, as is usually done when bootstrapping recommender systems. A smart initialization speeds up the learning process and reduces the cognitive effort on the user side. At each iteration t ∈ [T], the algorithm solves an inference problem to obtain a configuration yt that is optimal with respect to the current weight estimate wt (line 4). The object yt is presented to the user, who then replies with an improved version . The improvement implicitly defines the ranking pair , which is exploited to learn a better estimate wt+1 of the user weights. The PP computes the new weights wt+1 using a structured perceptron update (line 8).

Algorithm 3. The Preference Perceptron algorithm (Shivaswamy and Joachims, 2015).
Coactive Learning assumes that the DM is α-informative: given any recommendation yt, she will provide an improvement whose true utility is larger than that of yt by at least a fraction α of the regret, modulo a slack term ξt. More, formally, a user if α-informative if she satisfies:
for all possible recommendation yt. Here, α ∈ (0,1] and are constants. Note that this formulation is very general and can represent feedback of any quality, given appropriate values of α and 𝒳t.
Shivaswamy and Joachims (2015) provide a theoretical framework to analyze the behavior of Coactive Learning algorithms under the above assumption. As mentioned in Section 2.2, preference elicitation algorithms are usually evaluated by means of their attained regret or average regret (equation (1)). From a theoretical perspective, Coactive Learning algorithms aim specifically at minimizing the average regret . The main theorem of Shivaswamy and Joachims (2015) provides an upper bound on the average regret incurred by the configurations suggested by PP, which holds for all α-informative users, regardless of their actual preferences w*. More specifically, the theorem is the following:
theorem 1 (Shivaswamy and Joachims, 2015). For an α-informative user with preference vector w* and bounded feature vector ‖ϕ(y)‖ ≤ R, the average regret incurred by the PP algorithm after T iterations is upper bounded by
The proof can be found on Shivaswamy and Joachims (2015). The above bound tells us that the average regret decreases as , and therefore that, given enough iterations T, the algorithm eventually converges to a true optimal solution.
5.2. Empirical Evaluation
We apply Coactive Learning to the task of automated, preference-based layout synthesis. Layout synthesis refers the task of creating new “layouts,” i.e., arrangements of objects in space, subject to feasibility constraints. This is customary in interior and architectural design, urban planning, and other tasks involving the placement of objects in some constrained space (Merrell et al., 2011; Yu et al., 2011; Yeh et al., 2012). We argue that many of these tasks are intrinsically “preference-driven,” meaning that the final result should reflect the customer or designer taste. They are also quite involved from an optimization perspective, given the combination of (partially unknown) continuous and discrete, soft and hard constraints. Layout synthesis can be readily cast as a constructive preference elicitation problem, and coactive feedback seems like a natural choice in this domain. For instance, a designer would take advantage of the learning system to speed her work up, while still being able to use her expertise to incrementally reshape the layout to her taste. We tested coactive learning based CPE on furniture arrangement, a prototypical layout synthesis task in which the goal is to arrange furniture in a room. We focused on a table arrangement problem, in which layouts y ∈ 𝒴 consist in the coordinates of the tables in the room and their sizes. We assumed the size and the shape of the room and the position of the entrance doors to be given in advance. The feature vectors include formulas encoding high-level properties of the layouts, for instance, the maximum and minimum distance between the tables. See Table 2 for a summary of the encoding.
We first performed a quantitative evaluation to show quality of recommendations and computational cost of CPE in this domain. We simulated 20 users by randomly sampling their true preference models w* from a standardized normal distribution. Improvements were generated according to the α-informativeness assumption, with α = 0.2. The top row of Figure 5 shows the median of the average regret over all users (left plot) and the corresponding median cumulative inference time (right plot), for problems of increasing complexity (i.e., increasing number of tables). The results show that the average regret decreases quite rapidly, reaching a value of 0.04 in around 50 iterations in all problems. Computational complexity, on the other hand, grows substantially with the problem size, making real-time interaction with exact inference infeasible for the larger problems. The bottom row of Figure 5 compares median average regret (left) and cumulative time (right) of exact inference with the ones obtained setting a cutoff to the underlying solver and reporting the best solution found so far, for different cutoff values. The results indicate a clear trade-off between the inference time and performance loss, with linear cumulative time achieved at the cost of a slight to moderate degradation of solution quality. We briefly discuss some alternative ways to speed up inference in the conclusion of the article.
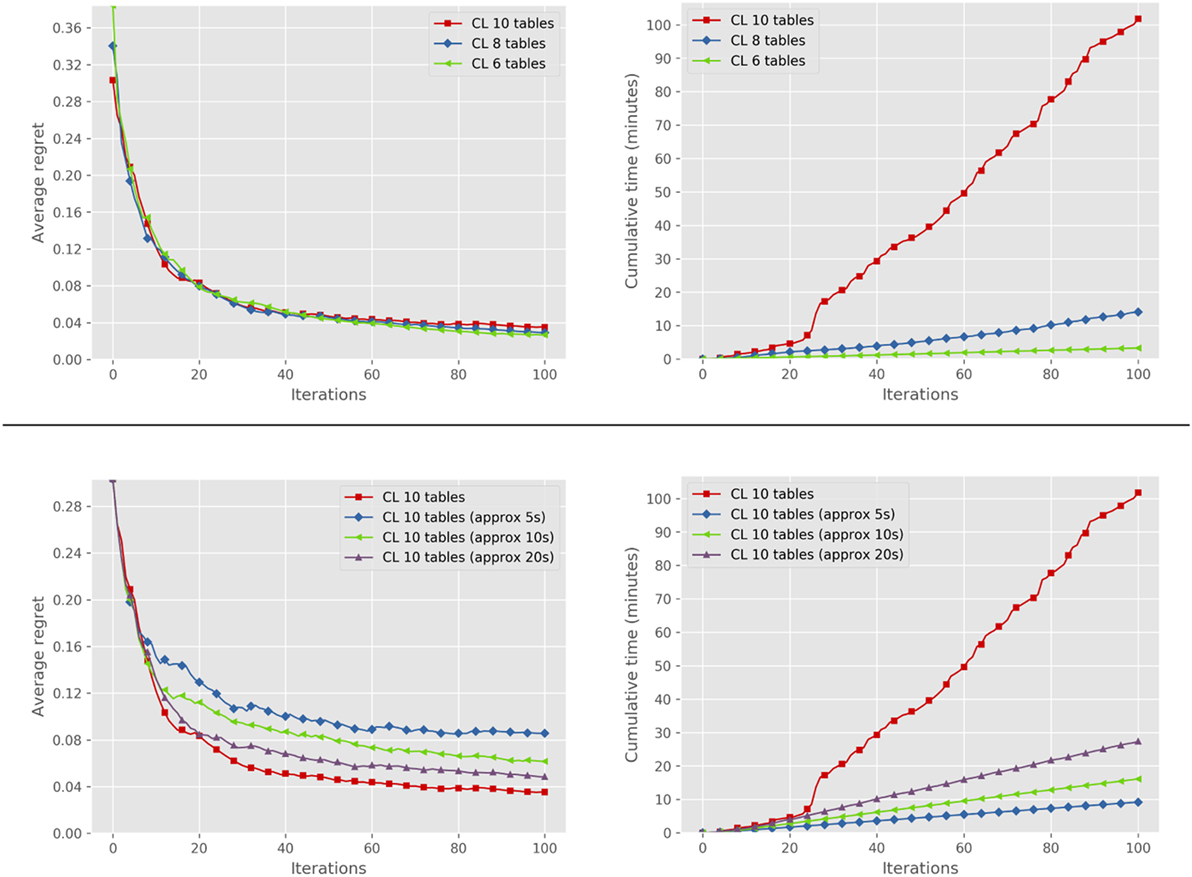
Figure 5. Comparison of median average regret (left) and median cumulative time (right) of the system in the furniture arrangement setting with exact inference on 6, 8, and 10 tables (top); exact and approximate inference on 10 tables (bottom). Best viewed in color.
We also made a qualitative experiment by simulating two prototypical cases, a user interested in arranging tables in a café and another one who needs to furnish an office. A typical table arrangement in a café is made by tightly packed small tables, usually along the walls to make more space for the people standing by the bar. An office, instead, contains mostly desks, distributed around the room in an ordered way. The two user prototypes were sampled according to the above criteria. We simulated the interaction of the system with these users and we collected all the recommended configurations. Figure 6 shows three snapshots of the recommendations produced by the algorithm. The initial configuration produced by the algorithm was random in both cases, as no prior information was given to the algorithm. After few iterations, in the intermediate stage, the algorithm started predicting interesting patterns. In the cafe, the algorithm chose mostly small tables and it started placing them along the walls of the room. In the office case, instead, some order started to appear by the intermediate stage but the type of tables were still not right. In the final step, the algorithm produced recommendations matching the desiderata of the users. This experiment shows that the learning algorithm is able to adapt to very different types of users reaching high-quality recommendations.
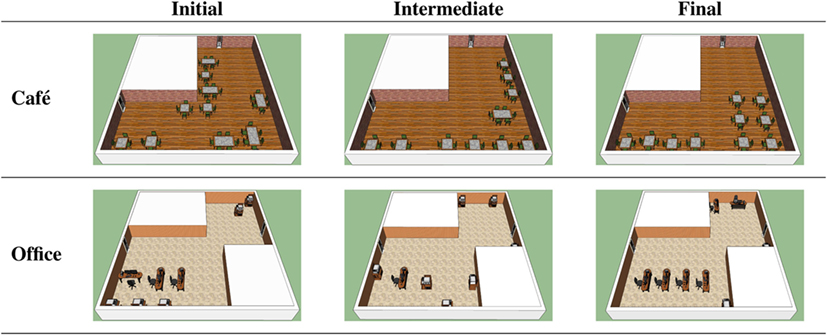
Figure 6. Two use cases of our system. The images are 3D renderings of configurations recommended by our system when interacting with users whose goal is to furnish a cafe (top) and an office (bottom). Horizontally, the figures show different stages of the elicitation process. In the cafe, 1 × 1 and 1 × 2 tables are seen as dining tables of different sizes, whereas in the office 1 × 2 tables represent desks while 1 × 1 tables contain utilities such as printers. Best viewed in colors.
6. Coactive Critiquing
Different users reason with different sets of preference criteria (i.e., features). This is especially true in complex recommendation tasks where features can be arbitrary combinations of basic attributes. Selecting only relevant features for a user is critical in this setting. It improves the quality of the learned models that can focus on learning the weights of the relevant features, and substantially speeds up computational time for both inference and learning. One possible approach is the one employed in the SM algorithm (Section 4), in which many different features are defined and then a sparsifying regularization is introduced to select only the relevant ones (Teso et al., 2016). A possible alternative consists of discovering relevant features by interacting with the DM. Asking the user to pre-specify the whole set of relevant features in advance is infeasible for most human DMs. However, querying the user about the reason for a certain feedback, especially a manipulative one, can be more feasible: it is well known that DMs become aware of their preference criteria during the elicitation process, when confronted with concrete examples (Chen and Pu, 2012). In this section, we describe Coactive Critiquing (Teso et al., 2017a), which combines manipulative feedback as in coactive learning with occasional requests for critiques explaining the given feedback. Critiques are user-issued explanations about pairwise preferences, answering a query of the type “why is y better than y′?”
In the following we formalize the notion of critique used in this setting, we describe the Critiquing Perceptron algorithm, highlight its theoretical convergence properties, and evaluate it on different constructive problems.
6.1. The Algorithm
The Critiquing (Preference) Perceptron algorithm is an extension of the Preference Perceptron (Algorithm 3) that performs feature elicitation via user critiques when needed. More precisely, the Critiquing Perceptron asks a critique to the user when, for some iteration t, the pair produces a ranking constraint that is inconsistent with all the previously collected ones. The user replies with a critique ρ that is a formula “explaining” the improvement , i.e., such that . Intuitively, such a formula may be elicited using a simple web form or even from raw text (e.g., reviews).
Algorithm 4 shows the pseudo-code of the Critiquing Preference Perceptron algorithm (CPP). As in PP (Algorithm 3), CPP keeps an estimate wt of the weight vector of the utility function. In addition, CPP keeps a feature map ϕt which gets updated each time the user provides a critique. At each iteration t, CPP produces the recommendation yt maximizing the utility estimate 〈wt, ϕt(y)〉. When the user replies with an improvement , CPP adds it to a dataset 𝒟 which is then used to check whether a critique is needed. The NeedCritique procedure checks whether the dataset 𝒟 is separable, i.e., whether all the improvements are representable with the current set of features.4 If the dataset is not separable, then the user is queried for a critique. Upon receiving a critique ρ from the user, CPP concatenates ρ to the feature vector and appends an additional weight to the weight vector. After that, the weight vector is updated using the pair as usual.
The CPP algorithm comes with theoretical guarantees which are similar to the ones of PP, with an additional term due to the uncertainty in the set of relevant features. We assume the user reasons with a true utility function u*(y) = 〈w*, ϕ*(y)〉, where w* is the true unknown parameter vector of the user and ϕ* is the true unknown vector of relevant features for the user. Let the initial set of features of CPP (ϕ1) be missing some of the features ϕ*. By working on a smaller feature space than the one used by the user, the Critiquing Perceptron “misses-out” some of the utility information provided by the improvements, so the utility gain of each weight update is smaller than that of a normal Preference Perceptron. More precisely, the amount of missing utility gain is quantified as5:
This discrepancy ζt between the true feature vector and the less informed one used by CPP decreases as more critiques are collected. Assuming the user is α-informative (equation (7)), CPP enjoys the following regret upper bound.
theorem 2. For an α-informative user with true preference vector w* and bounded length feature vector ‖ϕ*(y)‖ ≤ R, the average regret incurred by Critiquing Preference Perceptron after T iterations is upper bounded by
where the additional term reflects the utility gain which is lost throughout the iterations because of the missing features. The proof is provided in Teso et al. (2017a) and is based on the one of the Preference Perceptron (Shivaswamy and Joachims, 2015) but considering only the current subset of elicited features.
Crucially, CPP is guaranteed to eventually converge to an optimal solution as the standard PP algorithm. Moreover, in our experiments, we found that CPP is also able to converge without the need of eliciting the complete feature vector of the user.
6.2. Empirical Evaluation
We evaluated the CPP algorithm over two constructive settings, a synthetic task and a travel plan recommendation problem. All experiments were run by sampling 20 complete user weight vectors from a standardized normal distribution and simulating their behavior according to these vectors. Improvements were simulated using the α-informative feedback model as in Coactive Learning (Section 5). Critiques were simulated by selecting the most discriminative feature for a given pair , accounting for some noise in the selection. Please refer to Teso et al. (2017a) for a complete description of the experimental setup.
The first experimental setting we considered is a synthetic constructive problem, in which configurations are represented by all points in a 100 × 100 lattice (104 feasible configurations). Features are represented as rectangles inside the lattice, and 50 of them were sampled uniformly at random. The corresponding formula in the feature vector ϕ is an indicator function (ϕ(y) = {–1,1}) of whether the point corresponding to the configuration y is included in the rectangle. A positive weight wi associated with a feature ϕi corresponds to a preference of the user for points inside the corresponding rectangle, whereas a negative weight corresponds to the user disliking points inside the rectangle.
The synthetic setting was used for two experiments. We first tested the performance of our formulation for the function NeedCritique, which, as said, consists in querying the user for a critique when the current feature space cannot represent all the ranking pairs in 𝒟. This strategy was compared against a random strategy consisting in asking critique queries at random iterations, according to a binomial distribution with p ∈ {0.25, 0.5, 0.75, 1}. The left plots of Figure 7 show the regret (top) and the acquired features (bottom) of CPP using the different possible criteria for NeedCritique. The results show that the separability criterion is a good trade-off, performing almost as well as asking a critique at each iteration, while asking for roughly 25% less critiques. We employed this criterion in all the following experiments.
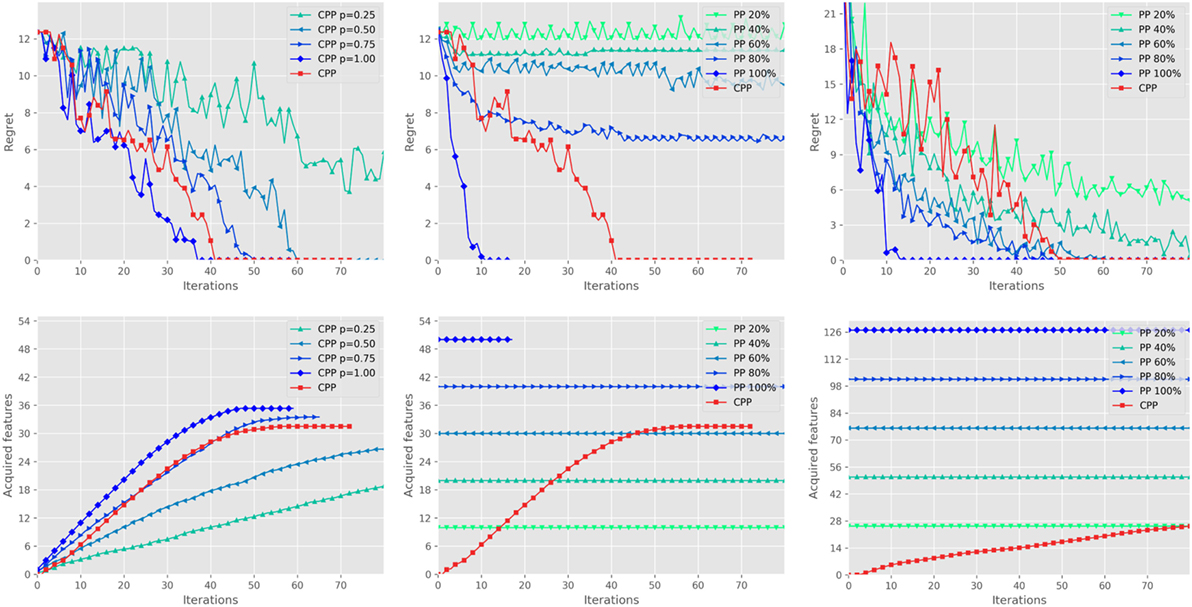
Figure 7. Left: Comparison of CPP for different choices of NeedCritique procedure; median utility loss at the top, average number of acquired features at the bottom. Middle: Comparison between CPP and PP on the synthetic problem. Right: Comparison between CPP and PP on the trip planning problem. Best viewed in color.
In the second experiment, we compared CPP to PP. CPP started with 2 randomly selected user features and acquired the others throughout the elicitation process, whereas PPp started with a fixed percentage p% of (randomly selected) user features and did not acquire more. The middle plots in Figure 7 report the regret and the acquired features of CPP and PPp, with p ∈ {20, 40, …, 100}. The plots show that PP100 clearly converges much faster than all other settings, which was expected given that it uses all the user features. CPP also converges, albeit in a few more iterations, while PP does not converge at all if not provided with the entire set of features. Notice that CPP manages to converge to an optimal solution by eliciting only roughly 60% of the user features.
The same experimental setting was used for a more realistic (and complicated) scenario consisting of an interactive travel plan problem. A trip is represented as a sequence of time slots, each one fillable with some activity in some city or by traveling between cities. The algorithm is in charge or recommending a trip y between a subset of the cities, along with the activities planned for each time-slot in each city. A subset of activities is available in each city. The trip has a maximum of usable time-slots. In our experiments, the trip length was fixed to 10. User features include, e.g., the time spent in each city and the time spent doing each activity, the number of visited cities, etc. The total number of acquirable features is 92. As for the synthetic experiment, we ran CPP and PPp, averaging the results over 20 randomly selected users. The results are shown in the right plots of Figure 7. Even in this complex scenario CPP outperforms PP40 and is competitive against the much more informed PP60 and PP80, by converging in roughly the same amount of iterations. This experiment shows that CPP is very effective despite using a fraction of the user information. Indeed, it ends up using less than 20% of the acquirable user features, even less of PP20 and PP40 that fail to converge after 100 iterations.
7. Conclusion and Open Issues
In this article, we introduced a general framework for constructive preference elicitation. It targets structured prediction problems over several interrelated variables where the set of feasible configurations is defined by hard constraints and the ranking between alternatives is determined by the user’s preferences. The latter are estimated by interactively making queries to the user. Our framework combines ideas from the preference elicitation, online learning, and structured-output prediction literatures for estimating the DM’s preferences and employs efficient constraint solvers for synthesizing the queries and recommended configurations on-the-fly. The framework is very general and allows to deal with substantially different applications and interaction protocols.
We showcased the flexibility of our framework by presenting three implementations tailored to different kinds of constructive applications: (1) SM, an elicitation algorithm that employs setwise choice queries. It leverages max-margin techniques to select diverse, high-quality query configurations to maximize the informativeness of queries. Furthermore, it uses a sparsifying norm to natively handle sparsity in the user’s preferences, which is very common in practice. (2) PP, a approach taken straight from the Coactive Learning literature (Shivaswamy and Joachims, 2015), originally intended for click data. Here, we show how it can be applied to solve constructive preference elicitation problems. Contrary to most PE methods, it uses improvement queries, which are especially suited for applications where manipulative interaction is most natural, such as layout synthesis and similar design problems. Furthermore, its theoretical guarantees keep holding in the constructive case. (3) CPP, a theoretically sound approach that extends PP to cases where the user’s preference criteria change over time. By allowing the user to explain the reasons behind her choices, CPP dynamically adjusts the feature space to better represent the target user’s preferences. The results of our empirical analysis show that our algorithms perform comparably or better than state-of-the-art Bayesian methods, but scale to constructive problems beyond the reach of non-constructive approaches.
Of course, these approaches are not without flaws. The first major limitation is still efficiency. Our experiments show that current constraint programming solvers can deal with relatively large synthesis and query selection problems. However, there is a limit to the size of problems that can be solved in real-time. This is especially true when dealing with non-linear constraints (e.g., to reason over areas or angles in layout synthesis problems). One way to surpass this limitation is to infer partial structures rather than complete ones and interact with the user over those. The drawback is that partial configurations may convey less information than full ones. How to appropriately solve this issue is an open research question.
A second issue is related to the interaction protocol itself. If the candidate configurations are too large, the DM may have trouble understanding them entirely or telling them apart, compromising the reliability of the feedback (Ortega and Stocker, 2016). Intriguingly, this limitation can also be solved by working with partial configurations. More generally, constructive preference elicitation calls for innovative interaction mechanisms, possibly combined with Bayesian optimization approaches (Brochu et al., 2010) to synthesize maximally informative partial queries.
The correct identification of relevant features is another critical aspect. Automatically identifying the subset of relevant features by sparsification strategies, as in SetMargin, cannot scale to complex combinations of basic attributes. Querying users for explanations, as in Coactive Critiquing, should be done sparingly not to annoy them too early. Learning critiques from user feedback is a promising direction to complement critiquing and alleviate the burden on the user.
Finally, a key ingredient which allows recommender systems to reduce the cost of user modeling is recommendation propagation between users. Standard collaborative filtering approaches cannot be straightforwardly applied in the constructive setting, as configurations are synthesized from scratch and will rarely be identical for different users. However, similarity-based approaches can be adapted to this setting by, e.g., defining similarity between users in terms of similarity between their learned utility models. Promising results have been obtained by extending the SetMargin algorithm along these lines (Teso et al., 2017b).
Author Contributions
PD implemented the CL and CC approaches, contributed to their design, and ran the corresponding experiments. ST implemented the SM algorithm, ran the SM experiments, and contributed to the design of the CL and CC approaches. AP contributed to the design of the different algorithms and supervised the experimental validations. All authors contributed to writing the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
PD is a fellow of TIM-SKIL Trento and is supported by a TIM scholarship. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. [694980] SYNTH: Synthesising Inductive Data Models).
Footnotes
- ^The algorithm presented in Teso et al. (2016) uses a slightly different strategy, where the user is asked to rank the set of alternatives, and pairwise preference constraints are generated from this ranking. This variant is simpler and has similar performance in practice.
- ^The full experimental setup is available at: https://github.com/stefanoteso/setmargin.
- ^The original formulation included contextual information xt in the inference procedure. This is still possible in our CPE formulation, as previously explained, but we prefer to drop this term throughout the article for the sake of readability.
- ^It could also be the case that the dataset is non-separable because of an occasionally inconsistent (noisy) feedback from the user (e.g., a ≻b ≻a). Allowing the user to manipulate an object to provide an improvement should minimize the risk of such inconsistencies. Nonetheless, the algorithm works also in the presence of inconsistent feedback, at the cost of an increase of the number of critiques elicited.
- ^Here, the vector ϕt is projected into the same space of w* by including “zero” features 0(y) = 0 in place of all the not yet elicited features.
References
Allen, T. E. (2015). “Cp-nets: from theory to practice,” in International Conference on Algorithmic Decision Theory (Lexington, KY: Springer), 555–560.
Bakir, G. H., Hofmann, T., Schölkopf, B., Smola, A. J., Taskar, B., and Vishwanathan, S. V. N. (2007). Predicting Structured Data. Cambridge, MA: MIT Press.
Boutilier, C. (2002). “A POMDP formulation of preference elicitation problems,” in Eighteenth National Conference on Artificial Intelligence Organization, American Association for Artificial Intelligence, 239–246.
Boutilier, C., Brafman, R. I., Domshlak, C., Hoos, H. H., and Poole, D. (2004). Cp-nets: a tool for representing and reasoning with conditional ceteris paribus preference statements. J. Artif. Intell. Res. 21, 135–191.
Boutilier, C., Patrascu, R., Poupart, P., and Schuurmans, D. (2006). Constraint-based optimization and utility elicitation using the minimax decision criterion. Artif. Intell. 170, 686–713. doi: 10.1016/j.artint.2006.02.003
Bradley, R. A., and Terry, M. E. (1952). Rank analysis of incomplete block designs: I. The method of paired comparisons. Biometrika 39, 324–345. doi:10.1093/biomet/39.3-4.324
Braziunas, D., and Boutilier, C. (2007). “Minimax regret based elicitation of generalized additive utilities,” in Proceedings of the Twenty-Third Conference on Uncertainty in Artificial Intelligence (UAI-07) (Vancouver), 25–32.
Brochu, E., Cora, V. M., and de Freitas, N. (2010). A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. Eprint arXiv:1012.2599, arXiv.org.
Carson, R. T., and Louviere, J. J. (2011). A common nomenclature for stated preference elicitation approaches. Environ. Res. Econ. 49, 539–559. doi:10.1007/s10640-010-9450-x
Chajewska, U., Koller, D., and Parr, R. (2000). “Making rational decisions using adaptive utility elicitation,” in Proceedings of AAAI’00, Austin, 363–369.
Chen, L., and Pu, P. (2012). Critiquing-based recommenders: survey and emerging trends. User Model. User-adapt. Interact. 22, 125–150. doi:10.1007/s11257-011-9108-6
Collins, M. (2002). “Discriminative training methods for hidden Markov models: theory and experiments with perceptron algorithms,” in Proceedings of the ACL-02 Conference on Empirical Methods in Natural Language Processing, Association for Computational Linguistics, 10, 1–8.
Conitzer, V. (2009). Eliciting single-peaked preferences using comparison queries. J. Artif. Intell. Res. 35, 161–191.
Domshlak, C., Hüllermeier, E., Kaci, S., and Prade, H. (2011). Preferences in AI: an overview. Artif. Intell. 175, 1037–1052. doi:10.1016/j.artint.2011.03.004
Ernst, A. T., Jiang, H., Krishnamoorthy, M., Owens, B., and Sier, D. (2004). An annotated bibliography of personnel scheduling and rostering. Ann. Oper. Res. 127, 21–144. doi:10.1023/B:ANOR.0000019087.46656.e2
Felfernig, A., Hotz, L., Bagley, C., and Tiihonen, J. (2014). Knowledge-Based Configuration: From Research to Business Cases. Newnes. Waltham, MA: Morgan Kaufmann.
Fishburn, P. C. (1967). Interdependence and additivity in multivariate, unidimensional expected utility theory. Int. Econ. Rev. 8, 335–342. doi:10.2307/2525541
Guo, S., and Sanner, S. (2010). “Real-time multiattribute Bayesian preference elicitation with pairwise comparison queries,” in International Conference on Artificial Intelligence and Statistics, 289–296.
Harada, M., Witkin, A., and Baraff, D. (1995). “Interactive physically-based manipulation of discrete/continuous models,” in Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques (Los Angeles, CA: ACM), 199–208.
Hensinger, E., Flaounas, I. N., and Cristianini, N. (2010). “Learning the preferences of news readers with SVM and lasso ranking,” in IFIP International Conference on Artificial Intelligence Applications and Innovations (Larnaca: Springer), 179–186.
Joachims, T. (2002). “Optimizing search engines using clickthrough data,” in Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, 133–142.
Joachims, T., Finley, T., and Yu, C.-N. J. (2009a). Cutting-plane training of structural SVMs. Mach. Learn. 77, 27–59. doi:10.1007/s10994-009-5108-8
Joachims, T., Hofmann, T., Yue, Y., and Yu, C.-N. (2009b). Predicting structured objects with support vector machines. Commun. ACM 52, 97–104. doi:10.1145/1592761.1592783
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291. doi:10.2307/1914185
Keeney, R. L., and Raiffa, H. (1976). Decisions with Multiple Objectives: Preferences and Value Tradeoffs, IEEE. doi:10.1109/TSMC.1979.4310245
Koren, Y., and Bell, R. (2015). “Advances in collaborative filtering,” in Recommender Systems Handbook (Springer), 77–118.
Kremer, J., Steenstrup Pedersen, K., and Igel, C. (2014). Active learning with support vector machines. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 4, 313–326.
Lichtenstein, S., and Slovic, P. (2006). The Construction of Preference. Cambridge University Press.
McGinty, L., and Reilly, J. (2011). “On the evolution of critiquing recommenders,” in Recommender Systems Handbook, eds F. Ricci, L. Rokach, B. Shapira, and P. Kantor (Boston, MA: Springer), 419–453.
Merrell, P., Schkufza, E., Li, Z., Agrawala, M., and Koltun, V. (2011). “Interactive furniture layout using interior design guidelines,” in ACM Transactions on Graphics (TOG), Vol. 30 (ACM), 87.
Ortega, P. A., and Stocker, A. A. (2016). “Human decision-making under limited time,” in Advances in Neural Information Processing Systems, 100–108.
Osokin, A., Alayrac, J.-B., Lukasewitz, I., Dokania, P., and Lacoste-Julien, S. (2016). “Minding the gaps for block Frank-Wolfe optimization of structured SVMs,” in Proceedings of the 33rd International Conference on Machine Learning, Vol. 48, eds M. F. Balcan and K. Q. Weinberger (New York, NY: PMLR), 593–602.
Pigozzi, G., Tsoukiàs, A., and Viappiani, P. (2016). Preferences in artificial intelligence. Ann. Math. Artif. Intell. 77, 361–401. doi:10.1007/s10472-015-9475-5
Sabin, D., and Weigel, R. (1998). Product configuration frameworks-a survey. IEEE Intell. Syst. Appl. 13, 42–49. doi:10.1109/5254.708432
Settles, B. (2012). Active learning. Synth. Lect. Artif. Intell. Mach. Learn. 6, 1–114. doi:10.2200/S00429ED1V01Y201207AIM018
Shah, N., Kolmogorov, V., and Lampert, C. H. (2015). “A multi-plane block-coordinate Frank-Wolfe algorithm for training structural SVMs with a costly max-oracle,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA.
Shivaswamy, P., and Joachims, T. (2012). “Online structured prediction via coactive learning,” in Proceedings of the 29th International Conference on International Conference on Machine Learning, 1431–1438.
Slovic, P. (1995). The construction of preference. Am. Psychol. 50, 364. doi:10.1037/0003-066X.50.5.364
Slovic, P., Fischhoff, B., and Lichtenstein, S. (1977). Behavioral decision theory. Annu. Rev. Psychol. 28, 1–39. doi:10.1146/annurev.ps.28.020177.000245
Teso, S., Dragone, P., and Passerini, A. (2017a). “Coactive critiquing: elicitation of preferences and features,” in Thirty-First AAAI Conference on Artificial Intelligence, 2639–2645.
Teso, S., Passerini, A., and Viappiani, P. (2017b). “Constructive preference elicitation for multiple users with setwise max-margin,” in International Conference on Algorithmic Decision Theory, 3–17.
Teso, S., Passerini, A., and Viappiani, P. (2016). “Constructive preference elicitation by setwise max-margin learning,” in Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, 2067–2073.
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B Methodol. 58, 267–288.
Tsochantaridis, I., Hofmann, T., Joachims, T., and Altun, Y. (2004). “Support vector machine learning for interdependent and structured output spaces,” in Proceedings of the Twenty-First International Conference on Machine Learning (Banff: ACM), 104.
Tsochantaridis, I., Joachims, T., Hofmann, T., and Altun, Y. (2005). Large margin methods for structured and interdependent output variables. J. Artif. Intell. Res. 6, 1453–1484.
Viappiani, P., and Boutilier, C. (2010). “Optimal Bayesian recommendation sets and myopically optimal choice query sets,” in Advances in Neural Information Processing Systems, 2352–2360.
Viappiani, P., and Boutilier, C. (2011). “Recommendation sets and choice queries: there is no exploration/exploitation tradeoff!,” in Twenty-Fifth AAAI Conference on Artificial Intelligence.
Von Neumann, J., and Morgenstern, O. (1947). Theory of Games and Economic Behavior. Princeton University Press.
Yeh, Y.-T., Yang, L., Watson, M., Goodman, N. D., and Hanrahan, P. (2012). Synthesizing open worlds with constraints using locally annealed reversible jump MCMC. ACM Trans. Graphics 31, 56. doi:10.1145/2185520.2185552
Yu, L. F., Yeung, S. K., Tang, C. K., Terzopoulos, D., Chan, T. F., and Osher, S. J. (2011). “Make it home: automatic optimization of furniture arrangement,” in ACM Transactions on Graphics (TOG)-Proceedings of ACM SIGGRAPH 2011, Vol. 30 (New York, NY: ACM), 86.
Keywords: structured-output prediction, preference elicitation, recommendation systems, configuration systems, layout synthesis
Citation: Dragone P, Teso S and Passerini A (2018) Constructive Preference Elicitation. Front. Robot. AI 4:71. doi: 10.3389/frobt.2017.00071
Received: 12 October 2017; Accepted: 08 December 2017;
Published: 08 January 2018
Edited by:
Fabrizio Riguzzi, University of Ferrara, ItalyReviewed by:
Nicola Di Mauro, Università degli studi di Bari Aldo Moro, ItalyAline Paes, Federal Fluminense University, Brazil
Copyright: © 2018 Dragone, Teso and Passerini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Passerini, YW5kcmVhLnBhc3NlcmluaUB1bml0bi5pdA==
 Paolo Dragone
Paolo Dragone Stefano Teso
Stefano Teso Andrea Passerini
Andrea Passerini



