Abstract
Unmanned surface vehicles (USVs), as a type of marine robotic systems, are widely used in various applications such as maritime surveillance, environmental monitoring, and cargo transportation. This article addresses the trajectory tracking control issue for an USV subject to model uncertainties and actuator faults. A logarithm barrier Lyapunov functions based predefined tracking control scheme is proposed to regulate the position error of the USV into predefined performance region. Then, to ensure the predefined transient and steady state tracking performance of the USV in the presence of actuator faults, we propose an adaptive fuzzy fault-tolerant controller to address the actuator faults. Additionally, to deal with the uncertainties arising from the USV system model, fuzzy logic systems are utilized to estimate the unknown hydrodynamic parameters. Based on the Lyapunov stability criterion, it can be demonstrated that all the closed-loop signals are bounded. Finally, the validity of the developed control scheme is demonstrated from simulation results.
1 Introduction
Motivated by their substantial commercial and military importance, unmanned surface vehicles (USVs) have become a focal point in the domains of control theory and engineering (Su et al., 2025b; Shan et al., 2024; Ye et al., 2024; Martinsen et al., 2020; Berman et al. 2020; Wang W. et al., 2024). The commercial worth is manifested in areas such as ocean data acquisition, resource prospecting and construction, as well as bathymetric and environmental assessments (Su et al., 2022b). The military utilizations encompass intelligence gathering, surveillance activities, reconnaissance missions, countermine operations, and submarine hunting (Wen et al., 2022). In general, a dynamic positioning system pertains to the control mechanism of an USV operating in a fully actuated, low-velocity mode (Gao and Li 2024). Its objective is to uphold the USV’s position and orientation at a stationary location or a designated point along its intended path (Gao et al., 2023). The purpose of path-following control is to guide an USV along a prescribed trajectory, often functioning in an underpowered state, navigating it independently through the designated course while maintaining an optimal velocity profile (Wei et al., 2023). Trajectory tracking entails an USV adhering to a precise spatial and temporal path with stringent timing constraints, holding immense importance in marine operations for ensuring safe navigation, minimizing emissions, and conserving energy (Zhang et al., 2024c; Su et al., 2025a). In contrast to path-following, in addition to the steering control algorithm, a defined velocity regulation is now required (Shan et al., 2023).
Currently, a multitude of difficult problems pertain to the control of trajectory tracking for underpowered USVs, with two of these challenges being tackled in this paper. The primary concern revolves around tracking efficacy. Swift and precise trajectory tracking is indispensable for the progression of autonomous capabilities in marine settings and the operational excellence of USVs, particularly in the occurrence of faults (Hu et al., 2016). Relying on the premise of an accurate dynamical representation of the USV, convergence to zero of the tracking deviations was ensured in (Jiang 2002). Accounting for modeling inaccuracies or external disruptions, the boundedness of closed-loop signals was upheld in (Yang et al., 2014; Park et al., 2017). Although adjustable, the predefined values cannot be set for either the convergence rate of the tracking errors or the extent of the residual set, as they are contingent upon uncertain system parameters. The motion control of surface vehicles, particularly focusing on user-specified transient and steady-state performance, was highlighted in (Dai et al., 2016; He et al., 2019; Wang G. et al., 2024). Assurance was given that the tracking errors would enter a predetermined zone at a specified speed. However, because of the exponential convergence performance, the closed-loop errors ultimately approach and settle within the residual set over an indefinite period. In practice, precise trajectory tracking must invariably be accomplished within a specific time and resist the occurrence of failures (Zhang and Yang 2020a). Fortunately, the fault-tolerant prescribed performance control is an effective method. The authors in (Zhang and Yang 2020b) firstly develop a new fault-tolerant prescribed tracking control method for unknown Euler–Lagrange systems, where a novel fault compensation strategy is proposed to ensure the prescribed tracking accuracy and time even if facing the actuator failures. In Zhang et al. (2024a), a challenging fault-tolerant prescribed performance control problem is solved for wheeled mobile robots by designing a novel mixed-gain adaption technology. The work in Wu et al. (2024) develops a novel finite-time prescribed performance control for stochastic systems subject to actuator faults.
As the complexity of modern USVs continues to rise, faults have become virtually unavoidable, potentially causing a decline in performance, system instability, or, in the worst-case scenario, catastrophic accidents (Hao et al., 2021; Andreotti et al., 2024; Wu et al., 2025). Among all potential fault types, actuator faults pose a particularly grave threat, as they can directly alter the behavior of the system through erroneous actuator actions (Li 2019). Motivated by these observations, a fault-tolerant trajectory tracking for an USV to counteract actuator faults was developed in (Wan et al., 2022). The authors in Liu et al. (2024) proposed a leader-following fault-tolerant tracking control method for multiple USVs. In Li et al. (2024), the problem of fuzzy adaptive tracking control for USVs subject to actuator faults has been addressed. To realize the predefined transient performance tracking, an event-based intelligent fault-tolerant control approach was developed in (Su et al., 2022a).
Driven by these observations, this article investigates the adaptive predefined performance trajectory tracking control issue for an USV in the presence of actuator faults. The main contributions of the article are summarized as follows: (1) By fusing the fuzzy logic system into adaptive mechanism, an adaptive fuzzy tracking strategy is developed for an uncertain USV system. The proposed control laws for kinematics and kinetics of the USV can accommodate significant model uncertainties. In this article, we dispense with the assumption concerning the availability of precise or partial information on the dynamic model parameters of the USV; (2) by designing the intermediate control laws in surge and yaw in the kinetic layer design, an adaptive fault-tolerant controller is proposed to address actuator faults and create controllers that do not rely on any prior information about the unknown system parameters or actuator malfunctions; (3) a position error constraint mechanism is employed to solve the underactuation of the USV. By managing the shifted tracking variable, the proposed method allows the user to predetermine both the convergence time and the control precision.
2 System description and preliminaries
2.1 System model
From Xu et al. (2024b), the USV model with kinematics and kinetics is given bywhere and are the displacement in surge and sway, and is the yaw angel; and are the linear speeds in surge and sway, and is the yaw rate; , , and represent the USV’s inertia; , , and denote the damping terms; and are the surge force and yaw moment; , , and are the external disturbances.
2.2 Actuator faults
In practice, it is preferable for the controlled USV to possess fault resistance. The paper considers the following actuator failures aswhere and denote the designed control laws, acting as the actuator inputs; and are the multiplicative faults; and are the additive faults. When and , the USV’s actuators are fault-free.
2.3 Problem statement
The article concentrates on the trajectory tracking control issue for the USV in a desired reference . We define the following coordinate transformations aswhere is the position error; and are surge and sway displacement errors; is a barrier function to manage the control coefficient in sway , and is a design parameter with ; and are the surge and yaw speed errors.
To continue, we introduce the following assumptions.
Assumption 1. The unknown constants , , , and are bounded. Then, there are unknown constants , , , , , satisfying , , , and .
Assumption 2. The given reference trajectory and its first and second derivative are bounded.
Assumption 3. Zhang et al. (2024c) The sway speed is passive-bounded.
Assumption 4. The disturbance terms , , and are bounded.
3 Tracking control design
3.1 Kinematics design
Based on Equation 1, and differentiating in Equation 3, we havewhere and . For the sake of ensuring the controllability of the dynamics Equation 4, we attempt to constrain such that , where is a design parameter. Note from the definition of and that . Thus, can be ensured by constraining . Then, the variable in the form of logarithm-type barrier function is used.
Based on the prearranged time and the prescribed accuracy , we employ the constraint function in Zhang et al. (2024c) described aswithin which the design parameter is the specified steady-state control accuracy; is a constant and should meet ; are the designed constants.Subsequently, utilizing the aforementioned constraint mechanism for the position error, the shifted error is defined asThen, we employed the following Lyapunov function to manage the shifted position error
Based on Equation 4, the time derivative of in Equation 8 iswhere and .
Next, the virtual surge speed signal can be proposed aswhere is a design parameter.
By invoking Equation 10 into Equation 9, one has
By differentiating in Equation 3, we getwhere and .
Define the following Lyapunov function as
Based on Equation 12, differentiating in Equation 13 gives that
Design the virtual yaw rate control law aswhere is a design parameter.
By substituting Equation 15 into Equation 14, one obtains that
3.2 Kinetics design
Due to the unknown fault parameters, we defineand , , , and are the estimates of , , , and , respectively. and .
By differentiating and in Equation 3, it yields thatwhere nd are disturbance terms. and are residual terms about derivatives of the virtual control laws and . The symbol is the derivative calculation.
Select the following Lyapunov function aswhere are the designed positive definite matrixes; , , and are the positive constants; .
From Equations 17, 18 differentiating in Equation 19 results inwhere and are unknown nonlinearities since , are the uncertain parameters. Therefore, from Du et al. (2022); Su et al. (2024a), for given parameters , there are the fuzzy logic systems such thatwhere are the ideal weights; are the fuzzy basic functions; is the number of fuzzy rules.
Design the following control laws aswhere , , , and are positive constants to be designed.
Design the following adaptive laws aswhere , and are positive constants to be designed.
3.3 Stability analysis
3.3.1 Theorem 1
With the virtual control laws Equations 10, 15, actual control laws (Equations 24, 25), and adaptive laws Equations 26–31, the USV control system (1) under Assumptions 1 and 2 has two properties:
1) The position error can be managed into the prescribed area within the predefined time .
2) All closed-loop signals are bounded.
From Equations 24, 25, and Lemma 5 in (Liang et al., 2021), one can getBased on the Young’s inequality, one haswhere and are bounded due to the bundedness of disturbances.
By invoking Equations 21–25, Eqautions 26–32, and Equations 33, 34 into Equation 20, we haveEmploying the inequality gives
Using the Young’s inequality Su et al. (2024b); Teng et al. (2024a); Xu Y. et al. (2024); Li et al. (2025), we haveBy substituting Equation 36 and Equation 37 into Equation 35, it follows thatDesign the total Lyapunov function asFrom Equations 11, 16, 38, the time derivative of iswhere , , , and .
Then, Equation 40 can be further written aswhere and .
Integrating both sides of Equation 41, we haveTherefore, closed-loop signals , , , , , , , , , and are both bounded.
Because is met, and smoothly and momtonically reduces from to on . on . Then, the position error can be managed into the prescribed area within the predefined time .
4 Simulation verification
The validity of presented control method is demonstrated by the numerical simulation.
The system parameters are chosen as , , , , , . The reference trajectory is selected as . The disturbances are set as , , and The initial conditions are chosen as , , , , , .
It is assumed that the actuators in surge and yaw simultaneously undergo multiplicative faults and additive faults at s, such that
The adjusting parameters are given by , , , , , , , , and . The control objective is that the position error can be managed into the prescribed area within the predefined time 10s.
Fault-tolerance performance: To show the advantage and effectiveness of the proposed fault-tolerant control method, a comparison between the classical prescribed performance tracking control method in (Zhang et al., 2024c) and our method is proposed. In order to ensure the fairness of the comparison, all design parameters are the same. The tracking performance is described in Figure 1, from which it is observable that the control performance is well guaranteed even subject to faults based on our method. Figure 2 describes that the position error can be regulated into the prescribed area within the predefined time 10s under our method. Although the performance constraint cannot be violated by using the method (Zhang et al., 2024c), the steady-state tracking accuracy is lower than that our method since actuator failures occur 30 s later. Figure 3 shows that the errors of surge speed and yaw rate approach zero. Figure 4 shows that the speed curves in surge, sway, and yaw. Figures 5, 6 show that the control inputs and outputs of the surge and yaw actuators. The parameter adaptive laws are shown in Figure 7. From Figures 2–7, it can be observed that closed-loop signal are bounded.
FIGURE 1

Tracking control performance.
FIGURE 2
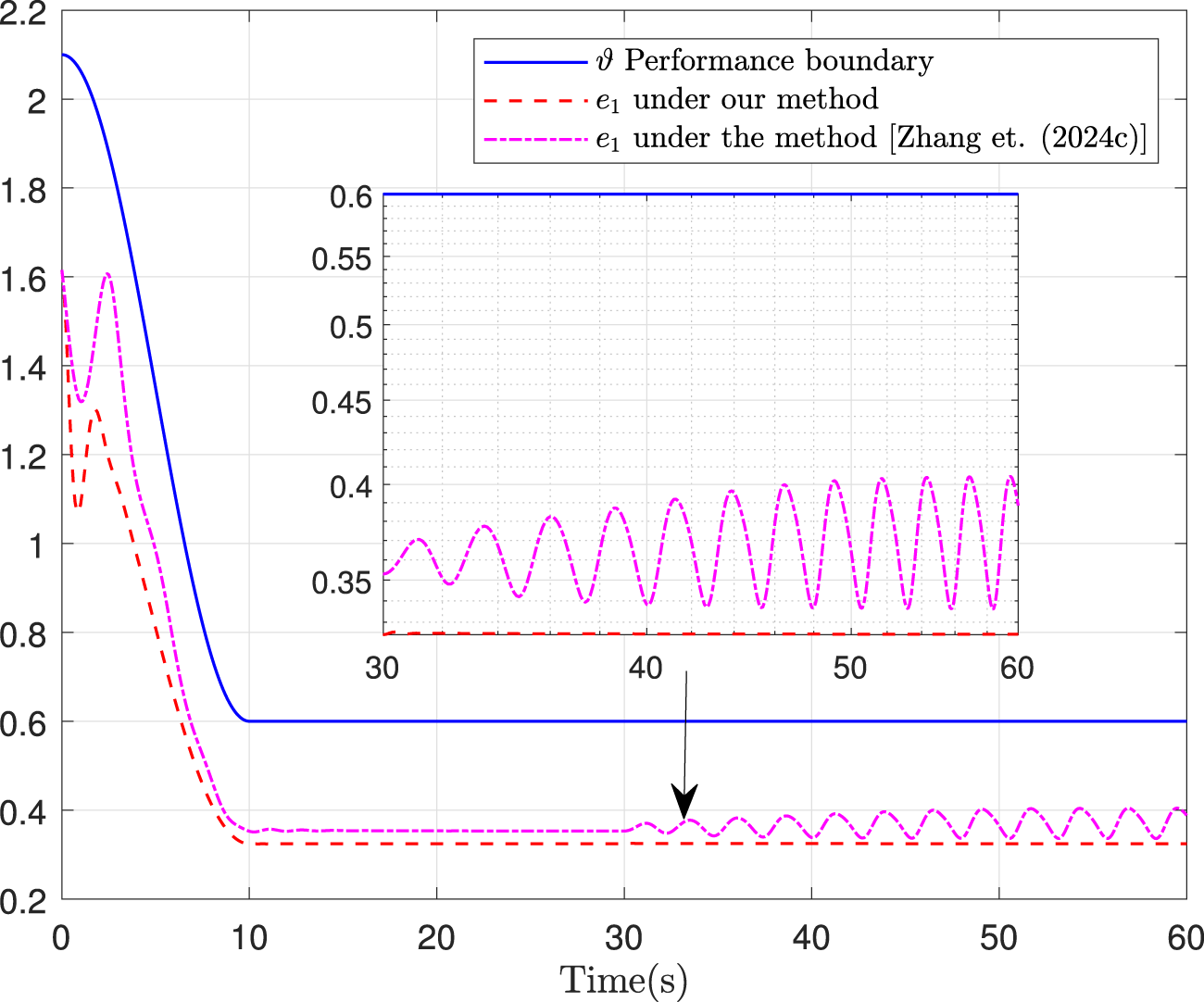
Position error.
FIGURE 3

Speed errors in surge and yaw.
FIGURE 4
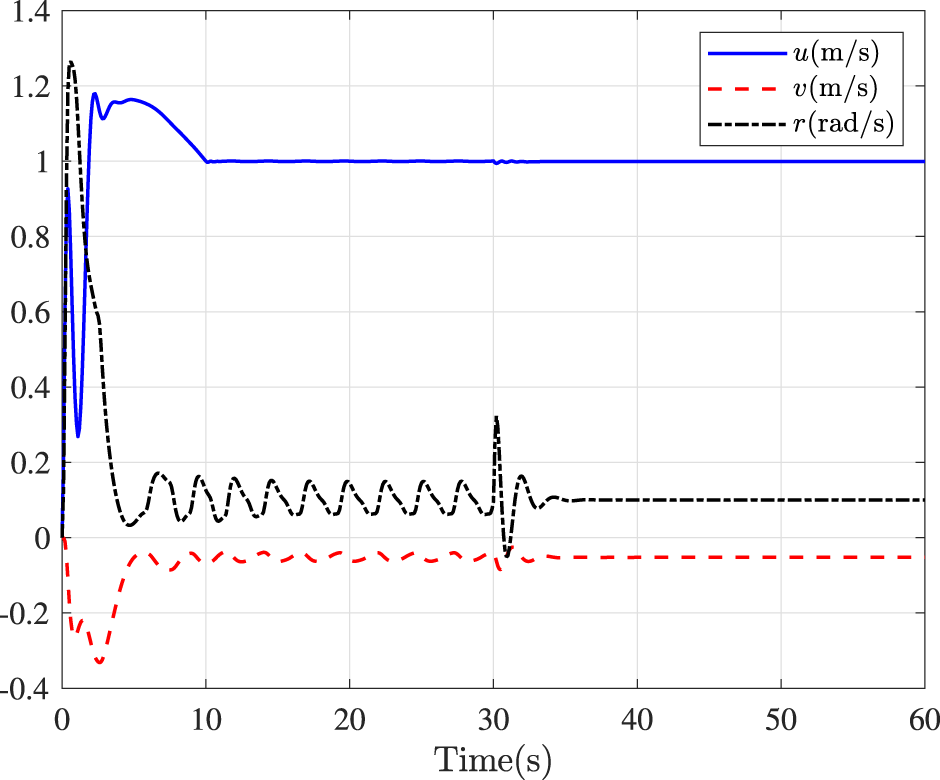
Linear speeds and yaw rate.
FIGURE 5
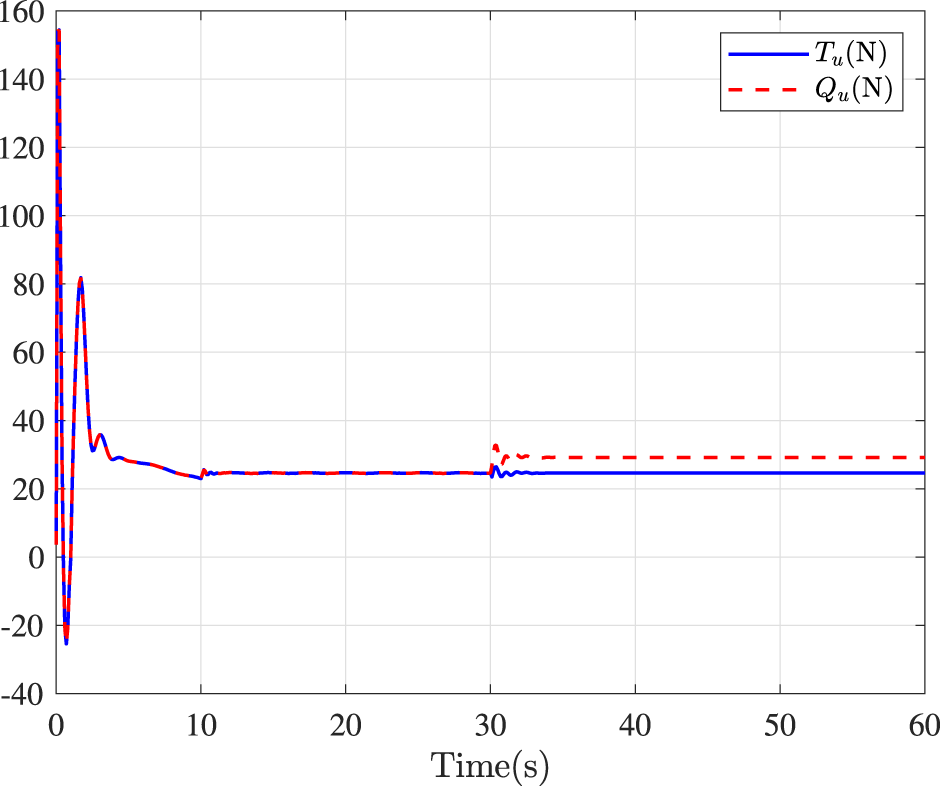
Control inputs in surge.
FIGURE 6
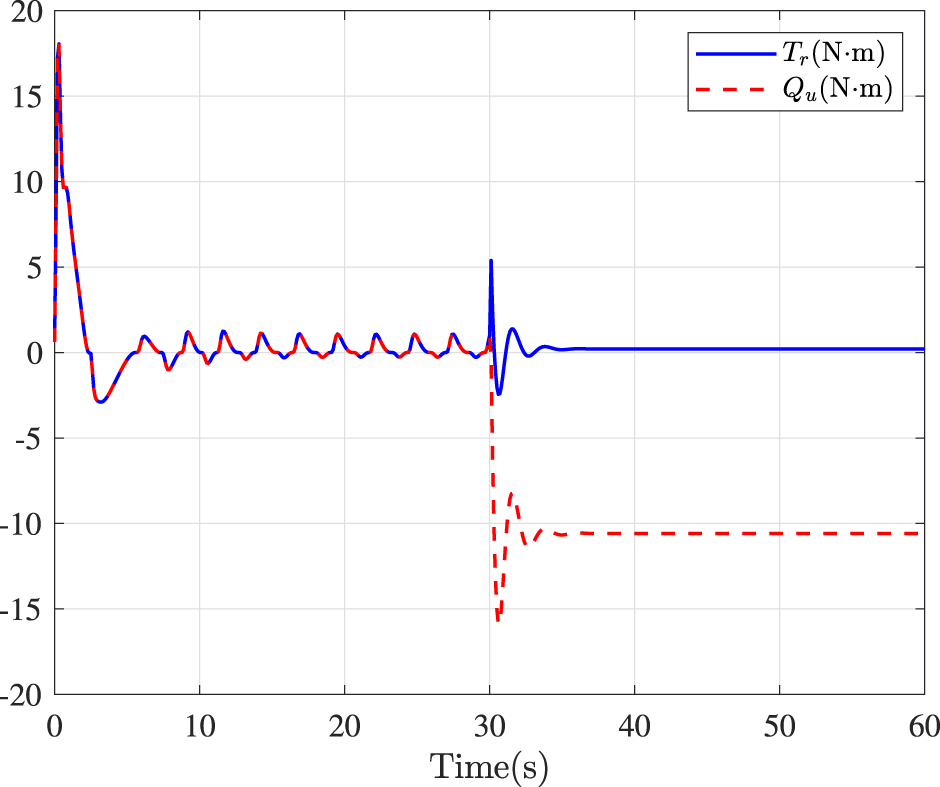
Control inputs in yaw.
FIGURE 7
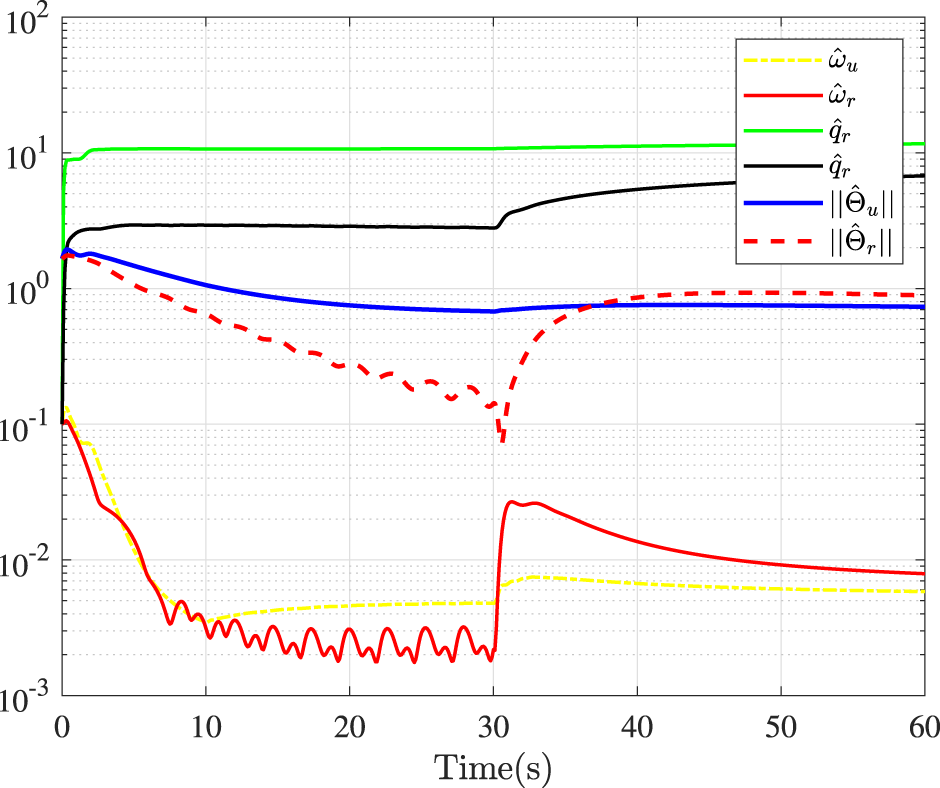
Adaptive parameters.
Robustness Test: In order to demonstrate the robustness of the developed control strategy against actual disturbances, the ocean disturbances resulting from waves, winds, and currents are considered from a simulation testing. In simulation, the ocean disturbances are mimicked as a Gaussian random process. Specifically, a second-order bandstop filter is employed to mimic the high-frequency wave motion and a first-order transfer function is used to denote the slow-varying disturbance resulting from wave drift, ocean currents, and winds in the yaw channel. Thus, the disturbance terms are shown as , , and , where and denote the high-frequency wave motion and the slow-varying environmental disturbances, respectively. For comprehensive details, please see the result in Zhang and Yang (2018). The following trajectory is selected as . The control parameters in simulation are the same as the previous simulation. Figure 8 describes that the trajectory tracking task is achieved with the presented control method. Figure 9 describes that the position error can be regulated into the prescribed area within the predefined time 10s under our method. Since the actual disturbances are considered in this test, the control performance is slightly reduced, which is acceptable.
FIGURE 8
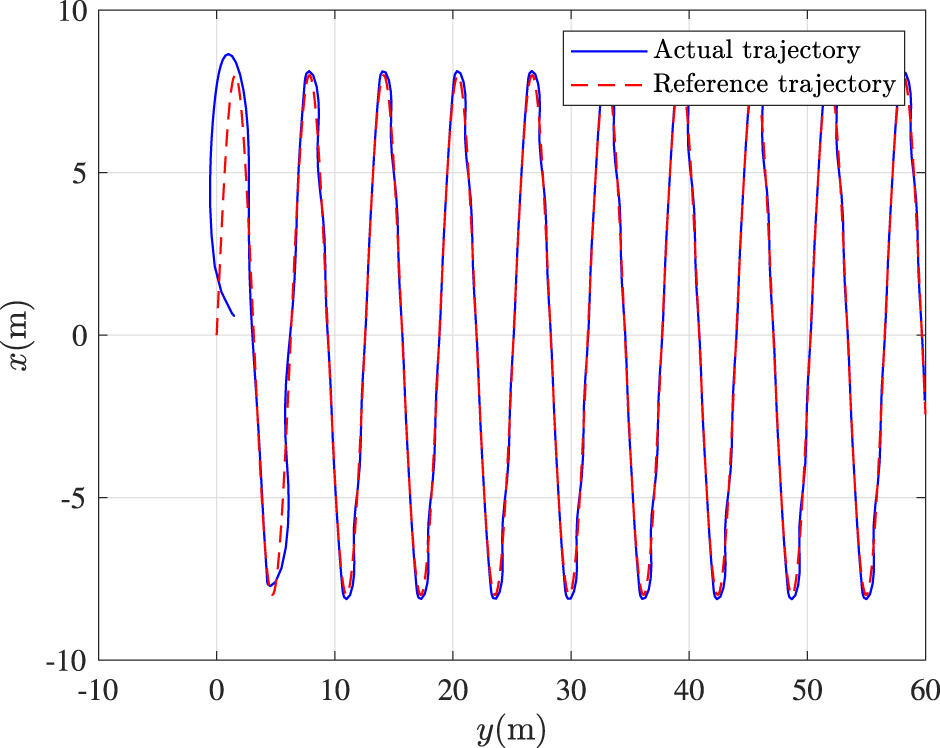
Tracking control performance under actual ocean disturbances.
FIGURE 9
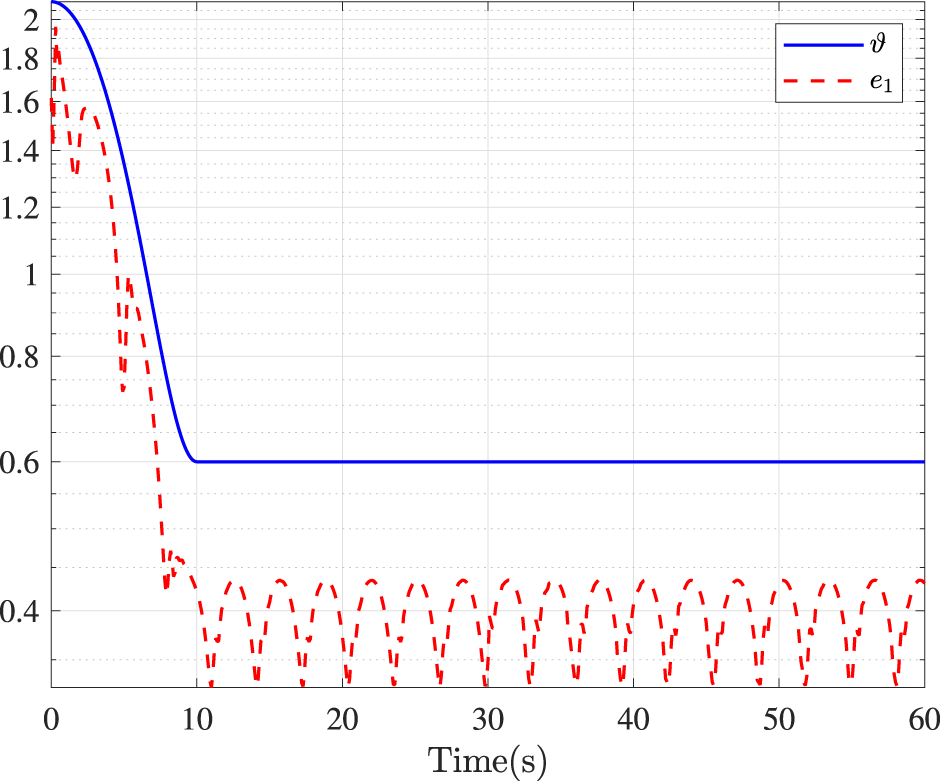
Position error under actual ocean disturbances.
5 Conclusion
This article has investigated the fuzzy adaptive fuzzy predefined performance tracking control issue for the USV subject to actuator faults. By integrating the logarithm barrier Lyapunov functions with adaptive control strategy, the position error is managed into predefined performance region and closed-loop signals are all bounded. Moreover, the proposed adaptive fault-tolerant controller can realize desired control performance even with actuator faults. Future work will focus on the security control problem of the USV with cyber attacks (Teng et al., 2025; Teng et al., 2024b). Considering that all the closed-loop signals are semiglobally uniformly ultimately bounded in this paper, future work also will devote to realize a globally stable result (Zhang et al., 2024b).
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
YB: Methodology, Validation, Writing – original draft. JG: Conceptualization, Funding acquisition, Visualization, Writing – review and editing. PP: Investigation, Resources, Software, Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
Authors JG and PP were employed by company China State Shipbuilding Corporation Limited.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Andreotti A. Caiazzo B. Lui D. G. Petrillo A. Santini S. (2024). Asymptotic voltage restoration in islanded microgrids via an adaptive asynchronous event-triggered finite-time fault-tolerant control. Sustain. Energy, Grids Netw.39, 101406. 10.1016/j.segan.2024.101406
2
Berman I. Zereik E. Kapitonov A. Bonsignorio F. Khassanov A. Oripova A. et al (2020). Trustable environmental monitoring by means of sensors networks on swarming autonomous marine vessels and distributed ledger technology. Front. Robotics AI7, 70. 10.3389/frobt.2020.00070
3
Dai S.-L. Wang M. Wang C. (2016). Neural learning control of marine surface vessels with guaranteed transient tracking performance. IEEE Trans. Industrial Electron.63, 1717–1727. 10.1109/TIE.2015.2504553
4
Du P. Peng X. Li Z. Li L. Zhong W. (2022). Performance-guaranteed adaptive self-healing control for wastewater treatment processes. J. Process Control116, 147–158. 10.1016/j.jprocont.2022.06.004
5
Gao X. Li T. (2024). Dynamic positioning control for marine crafts: a survey and recent advances. J. Mar. Sci. Eng.12, 362. 10.3390/jmse12030362
6
Gao X. Long Y. Li T. Hu X. Chen C. L. P. Sun F. (2023). Optimal fuzzy output feedback control for dynamic positioning of vessels with finite-time disturbance rejection under thruster saturations. IEEE Trans. Fuzzy Syst.31, 3447–3458. 10.1109/TFUZZ.2023.3257200
7
Hao L.-Y. Zhang Y.-Q. Li H. (2021). Fault-tolerant control via integral sliding mode output feedback for unmanned marine vehicles. Appl. Math. Comput.401, 126078. 10.1016/j.amc.2021.126078
8
He S. Dai S.-L. Luo F. (2019). Asymptotic trajectory tracking control with guaranteed transient behavior for msv with uncertain dynamics and external disturbances. IEEE Trans. Industrial Electron.66, 3712–3720. 10.1109/TIE.2018.2842720
9
Hu C. Wang R. Yan F. Chen N. (2016). Robust composite nonlinear feedback path-following control for underactuated surface vessels with desired-heading amendment. IEEE Trans. Industrial Electron.63, 6386–6394. 10.1109/TIE.2016.2573240
10
Jiang Z.-P. (2002). Global tracking control of underactuated ships by lyapunov’s direct method. Automatica38, 301–309. 10.1016/S0005-1098(01)00199-6
11
Li K. Feng K. Li Y. (2024). Fuzzy adaptive fault-tolerant formation control for usvs with intermittent actuator faults. IEEE Trans. Intelligent Veh.9, 4445–4455. 10.1109/TIV.2024.3358351
12
Li Y.-X. (2019). Finite time command filtered adaptive fault tolerant control for a class of uncertain nonlinear systems. Automatica106, 117–123. 10.1016/j.automatica.2019.04.022
13
Li Z. An T. Dong B. Yuan X. (2025). Event-triggered v2v communication-based cooperative adaptive tracking control for nonlinear vehicle platoon systems with unknown lag time. Nonlinear Dyn.113, 519–532. 10.1007/s11071-024-10155-3
14
Liang H. Guo X. Pan Y. Huang T. (2021). Event-triggered fuzzy bipartite tracking control for network systems based on distributed reduced-order observers. IEEE Trans. Fuzzy Syst.29, 1601–1614. 10.1109/TFUZZ.2020.2982618
15
Liu C. Xia Z. Tian Y. Patton R. J. (2024). Defense and tolerance technique against attacks and faults on leader-following multi-usvs. IEEE Trans. Intelligent Transp. Syst.25, 5450–5461. 10.1109/TITS.2023.3330570
16
Martinsen A. B. Lekkas A. M. Gros S. Glomsrud J. A. Pedersen T. A. (2020). Reinforcement learning-based tracking control of usvs in varying operational conditions. Front. Robotics AI7, 32. 10.3389/frobt.2020.00032
17
Park B. S. Kwon J.-W. Kim H. (2017). Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica77, 353–359. 10.1016/j.automatica.2016.11.024
18
Shan Q. Liu W. Li T. Zhang H. (2024). A topology reconfiguration strategy for containment control of the multi-usv system based on algebraic connectivity. IEEE Trans. Industrial Electron., 1–11doi. 10.1109/TIE.2024.3472272
19
Shan Q. Wang X. Li T. Chen C. P. (2023). Finite-time control for usv path tracking under input saturation with random disturbances. Appl. Ocean Res.138, 103628. 10.1016/j.apor.2023.103628
20
Su Y. Liang H. Pan Y. Chen D. (2022a). Event-triggered adaptive fuzzy fault-tolerant control for autonomous underwater vehicles with prescribed tracking performance. Int. J. Syst. Sci.53, 1353–1366. 10.1080/00207721.2021.2002462
21
Su Y. Shan Q. Li T. Chen C. L. P. (2024a). Variable separation-based fuzzy optimal control for multiagent systems in nonstrict-feedback form. IEEE Trans. Fuzzy Syst.32, 547–561. 10.1109/TFUZZ.2023.3302293
22
Su Y. Shan Q. Li T. Zhang H. (2024b). Prescribed-time optimal resilient consensus control for nonlinear uncertain multiagent systems. IEEE Trans. Syst. Man, Cybern. Syst.54, 6127–6140. 10.1109/TSMC.2024.3417186
23
Su Y. Teng F. Li T. Liang H. Chen C. L. P. (2025a). Fuzzy-based optimal control for an underactuated surface vessel with user-specified performance. IEEE Trans. Intelligent Transp. Syst., 1–15doi. 10.1109/TITS.2025.3526758
24
Su Y. Teng F. Li T. Sun Q. (2025b). Adaptive prescribed-time tracking control for an unmanned surface vehicle considering motor-driven propellers. IEEE Trans. Industrial Inf.21, 1665–1673. 10.1109/TII.2024.3485795
25
Su Y. Xue H. Liang H. Chen D. (2022b). Singularity avoidance adaptive output-feedback fixed-time consensus control for multiple autonomous underwater vehicles subject to nonlinearities. Int. J. Robust Nonlinear Control32, 4401–4421. 10.1002/rnc.6038
26
Teng F. Ban Z. Li T. Sun Q. Li Y. (2024a). A privacy-preserving distributed economic dispatch method for integrated port microgrid and computing power network. IEEE Trans. Industrial Inf.20, 10103–10112. 10.1109/TII.2024.3393569
27
Teng F. Zhang X. Li T. Shan Q. Philip Chen C. L. Li Y. (2025). Distributed resilient energy management for seaport microgrid against stealthy attacks with limited security defense resource. IEEE Trans. Cybern.55, 917–926. 10.1109/TCYB.2024.3514693
28
Teng F. Zhang Y. Yang T. Li T. Xiao Y. Li Y. (2024b). Distributed optimal energy management for we-energy considering operation security. IEEE Trans. Netw. Sci. Eng.11, 225–235. 10.1109/TNSE.2023.3295079
29
Wan L. Cao Y. Sun Y. Qin H. (2022). Fault-tolerant trajectory tracking control for unmanned surface vehicle with actuator faults based on a fast fixed-time system. ISA Trans.130, 79–91. 10.1016/j.isatra.2022.04.013
30
Wang G. Zuo Z. Li P. (2024a). Distributed control in uncertain nonlinear multiagent systems under event-triggered communication and general directed graphs. IEEE Trans. Signal Inf. Process. over Netw.10, 599–609. 10.1109/TSIPN.2024.3422878
31
Wang W. Shan Q. Li T. Chen C. L. P. Wang Y. (2024b). Finite-time-prescribed performance-based platoon formation control for unmanned surface vehicles using event-triggered extended state observer. IEEE Trans. Veh. Technol.73, 18460–18471. 10.1109/TVT.2024.3432742
32
Wei J. Zhang J. Liu Z. Qu J. Sui B. Zhang Y. (2023). Path-following and obstacle-avoidance control of usv based on finite-distance convergence. J. Mar. Sci. Eng.12, 34. 10.3390/jmse12010034
33
Wen G. Fang X. Zhou J. Zhou J. (2022). Robust formation tracking of multiple autonomous surface vessels with individual objectives: a noncooperative game-based approach. Control Eng. Pract.119, 104975. 10.1016/j.conengprac.2021.104975
34
Wu Y. Hu L. Chen Q. Zhang Y. Wu L. (2025). Dynamic event-triggered fault-tolerant control for nonaffine systems with asymmetric error constraint. Fuzzy Sets Syst.499, 109180. 10.1016/j.fss.2024.109180
35
Wu Y. Hu L. Liu L. Zhang Y. Zhang Y. (2024). Finite time prescribed performance control for stochastic systems with asymmetric error constraint and actuator faults. Commun. Nonlinear Sci. Numer. Simul.139, 108290. 10.1016/j.cnsns.2024.108290
36
Xu Y. Liang H. Li T. Long Y. Cheng Y. Wang D. (2024a). Adaptive fuzzy resilient control of nonlinear multiagent systems under dos attacks: a dynamic event-triggered method. IEEE Trans. Fuzzy Syst.32, 3568–3580. 10.1109/TFUZZ.2024.3376402
37
Xu Z. He S. Zhou W. Li Y. Xiang J. (2024b). Path following control with sideslip reduction for underactuated unmanned surface vehicles. IEEE Trans. Industrial Electron.71, 11039–11047. 10.1109/TIE.2023.3340191
38
Yang Y. Du J. Liu H. Guo C. Abraham A. (2014). A trajectory tracking robust controller of surface vessels with disturbance uncertainties. IEEE Trans. Control Syst. Technol.22, 1511–1518. 10.1109/TCST.2013.2281936
39
Ye P. Yu R. Shan Q. (2024). Distributed neuroadaptive formation control for aerial base station-assisted hovercraft systems with mixed disturbances. J. Mar. Sci. Eng.12, 1946. 10.3390/jmse12111946
40
Zhang J.-X. Ding J. Chai T. (2024a). Fault-tolerant prescribed performance control of wheeled mobile robots: a mixed-gain adaption approach. IEEE Trans. Automatic Control69, 5500–5507. 10.1109/TAC.2024.3365726
41
Zhang J.-X. Song J.-G. Shi P. (2024b). Decentralized robust global prescribed performance control of unknown interconnected nonlinear systems. IEEE Trans. Industrial Electron.71, 14701–14711. 10.1109/TIE.2024.3370953
42
Zhang J.-X. Yang G.-H. (2018). Fault-tolerant leader-follower formation control of marine surface vessels with unknown dynamics and actuator faults. Int. J. Robust Nonlinear Control28, 4188–4208. 10.1002/rnc.4228
43
Zhang J.-X. Yang G.-H. (2020a). Fault-tolerant fixed-time trajectory tracking control of autonomous surface vessels with specified accuracy. IEEE Trans. Industrial Electron.67, 4889–4899. 10.1109/TIE.2019.2931242
44
Zhang J.-X. Yang G.-H. (2020b). Fault-tolerant output-constrained control of unknown euler–Lagrange systems with prescribed tracking accuracy. Automatica111, 108606. 10.1016/j.automatica.2019.108606
45
Zhang J.-X. Yang T. Chai T. (2024c). Neural network control of underactuated surface vehicles with prescribed trajectory tracking performance. IEEE Trans. Neural Netw. Learn. Syst.35, 8026–8039. 10.1109/TNNLS.2022.3223666
Summary
Keywords
unmanned surface vehicles (USVs), actuator faults, trajectory tracking, fault-tolerant control, fuzzy adaptive control
Citation
Bao Y, Gao J and Peng P (2025) Fuzzy adaptive fault-tolerant control for an unmanned surface vehicle with prescribed tracking performance. Front. Robot. AI 12:1576171. doi: 10.3389/frobt.2025.1576171
Received
13 February 2025
Accepted
25 March 2025
Published
09 April 2025
Volume
12 - 2025
Edited by
Farah Bouakrif, University of Jijel, Algeria
Reviewed by
Jin-Xi Zhang, Northeastern University, China
Yang Wu, Tianjin University of Commerce, China
Updates
Copyright
© 2025 Bao, Gao and Peng.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ji Gao, jigao1234@126.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.