- 1School of Mechanical and Materials Engineering, Indian Institute of Technology Mandi, Mandi, India
- 2Centre for Artificial Intelligence and Robotics, Indian Institute of Technology Mandi, Mandi, India
- 3School of Computing and Electrical Engineering, Indian Institute of Technology Mandi, Mandi, India
This paper presents a robust vision-based motion planning framework for dual-arm manipulators that introduces a novel three-way force equilibrium with velocity-dependent stabilization. The framework combines an improved Artificial Potential Field (iAPF) for linear velocity control with a Proportional-Derivative (PD) controller for angular velocity, creating a hybrid twist command for precise manipulation. A priority-based state machine enables human-like asymmetric dual-arm manipulation. Lyapunov stability analysis proves the asymptotic convergence to desired configurations. The method introduces a computationally efficient continuous distance calculation between links based on line segment configurations, enabling real-time collision monitoring. Experimental validation integrates a real-time vision system using YOLOv8 OBB that achieves 20 frames per second with 0.99/0.97 detection accuracy for bolts/nuts. Comparative tests against traditional APF methods demonstrate that the proposed approach provides stabilized motion planning with smoother trajectories and optimized spatial separation, effectively preventing inter-arm collisions during industrial component sorting.
1 Introduction
The increasing demand for industrial automation is driven by the need to enhance production speed, accuracy, and efficiency. Robots are increasingly replacing human workers to address challenges like fatigue and maintain consistent performance over extended periods (Liu et al., 2022). Despite challenges with human workers, bi-manual operations offer significant value through component recognition and manipulation. Humans instinctively understand unfamiliar objects by material, shape, size, and color, enabling effective planning for separation or assembly tasks. Integrating these capabilities into robotics is crucial for upgrading industrial automation through: i) HRC - Human robot collaboration where humans and robots collaboratively enhance process efficiency ii) robots with capabilities that mimic human intelligence and dexterity. A dual-arm system with efficient inter-arm collision avoidance and vision perception provides a robust solution matching human-like manipulations, essential for industrial component handling in warehouse management, assembly lines, and manufacturing.
In general, dual-arm manipulators offer improved dexterity and faster task completion compared to single arm manipulators. However, these advantages require careful consideration of movements to avoid inter-arm collisions while maintaining efficiency (Smith et al., 2012). Categories of dual-arm manipulators include the following: i) non-coordinated manipulations, where manipulators move independently executing different tasks, and ii) coordinated manipulations, involving combined movements with spatial and temporal synchronization in shared workspace. Coordinated manipulations further divide into symmetric (mirror movements with equal force distribution) and asymmetric (complementary movements with different force distributions) (Makris, 2021). Although more challenging, asymmetric manipulations enable a wider range of complex tasks that require coordinated actions. Integration with real-time vision and inter-arm collision awareness enhances robustness for industrial manufacturing assembly and warehouse management applications.
The planning of dual-arm movements addresses coordination through two primary approaches: path planning and motion planning. Path planning generates geometric trajectories avoiding obstacles and self-collisions, prioritizing spatial relationships without timing information. Motion planning extends this by incorporating velocity profiles, acceleration constraints, and dynamic considerations, creating time-parametrized trajectories (Abbas et al., 2023). The selection between these approaches depends on application requirements, with industrial manipulation tasks often benefiting from motion planning’s ability to manage the temporal aspects of coordination between manipulators. In addition Tang et al. (2012) provides a comprehensive review of robot motion planning approaches, categorizing and analyzing the research evolution from 1980 to 2010. They systematically compared conventional approaches like Bug Algorithms Lumelsky and Stepanov (1987), Roadmap Asano et al. (1985); Aurenhammer (1991); Canny (1989), Cell Decomposition, Potential Fields Khatib, (1986), and Mathematical Programming with heuristic methods (Neural Networks, Genetic Algorithms, Fuzzy Logic, etc.), demonstrating the field’s evolution from conventional methods in the 1980s to predominantly heuristic approaches by the 2000s. Their analysis includes quantitative comparisons of implementation frequency for each approach and identifies future research directions for integrating perception, sensing, and motion planning system provides useful insights for research directions.
2 Related work
Numerous studies enhanced dual-arm motion planning for industrial manipulation. Robust inter-arm collision avoidance improved collaborative motion by enabling safe execution of coordinated tasks. This capability required continuous awareness of relative link configurations, maintaining safe distances while maximizing shared workspace utilization. Real-time collision monitoring provided the foundation for effective dual-arm coordination in dynamic environments.
This literature review categorizes dual-arm manipulation research into three key areas: (i) collision detection methodologies (both geometric and alternative approaches), (ii) artificial potential field methods (ranging from classical formulations to specialized variants), and (iii) temporal coordination strategies. This organization traces the field’s evolution while revealing challenges in real-time adaptation and asymmetric manipulation challenges that suggest the potential value of extending APF approaches with improved force equilibrium mechanisms.
Effective dual-arm manipulation requires robust collision detection to prevent inter-arm collisions while maintaining operational efficiency. Researchers have developed various approaches, from geometric primitives to advanced mathematical frameworks, to address this fundamental challenge. Lumelsky (1985) introduced a parameter-based algorithm for minimum distance calculation between line segments in n-dimensional space. Using parameters t and u (range [0,1] for points inside segments), they established a framework handling all geometric configurations. The method first calculates minimum distance between infinite lines by minimizing a quadratic function, then verifies if these points lie within actual segments. By using parameter values to identify relevant endpoints, computational complexity reduces to 5n+12 multiplications and 8n+1 additions. However, it provides only discrete collision detection without continuous distance metrics, limiting its application in modern control approaches requiring gradient information for smooth motion planning. Furthermore, Chang et al. (1990) proposed collision detection approach uses minimum distance functions defined by Euclidean norms to determine collision risk between robot arms. Their method modeled robot links as cylinders with hemispheres and end-effector as spheres, then calculates distances between these primitives in three scenarios: line segment to line segment, line segment to point, and point to point. Lee and Moradi (2001) proposed a hierarchical geometric collision detection algorithm for dual-arms using: bounding boxes, joint-joint distance thresholds, perpendicular distance calculations, and cross-product methods. Despite a 30
Apart from the geometric approaches, researchers explored alternative methods for collision detection for dual-arm collaboration. Feng et al. (2020) introduced a graph-based network approach for multi-robot collision detection where robots are represented as vertices with edges connecting interacting robots. It focuses on maintaining network connectivity through local and global edge management methods, using algebraic connectivity measures and market-based algorithms. Limitations include computational demands from continuous eigenvalue calculation, potential delays in link decisions, and the focus on network connectivity potentially overlooking actual collisions, which may compromise safety. Jamisola and Roberts (2015); Jamisola et al. (2015) presented a transformation-based approach to multi-manipulator kinematics that focuses on relative motion between end-effectors while providing a mathematical framework for coordinate transformations relevant to absolute motion control. They express individual manipulator Jacobians with rotation and wrench transformation matrices to ensure coordinate consistency across the system. Their analysis shows that positional errors increase significantly at higher angular velocities when transformation matrices are incomplete, emphasizing the need for rigorous mathematical formulations when multiple manipulators share a workspace. This approach complements geometric collision detection by providing insight into how manipulator kinematics must be properly transformed between reference frames for accurate motion planning. Fei et al. (2004) presented a dual-arm collision avoidance approach using configuration space (C-Space) representation. The methodology identifies collision regions through reachable manifold and contact manifold concepts, then applies the A* algorithm on discretized grids to find optimal paths. Path optimization is incorporated through scan rules. While innovative for its time, the approach has limitations: it relies on static geometric planning rather than continuous adaptation, uses discretized boundaries that may limit motion smoothness, and lacks mechanisms for maintaining optimal arm configurations during complex movements. Schmidt and Wang (2014) implemented collision avoidance using Kinect depth sensors that process images by removing backgrounds and converting obstacles to 3-D point clouds with efficient bounding box representation. Their system calculates minimum distances between robot and obstacles, enabling three strategies: warnings, stops, or path modification through vector decomposition. This methodology provided valuable insights for our vision perception conceptualization, particularly in how sensor data can be transformed into actionable spatial information for real-time goal attraction with collision avoidance in robot-robot collaborative environments.
Physics-inspired potential field approaches offer an intuitive framework for robot motion planning by simulating attractive and repulsive forces. Beginning with Khatib’s foundational work Khatib (1986), these methods have evolved to address limitations like local minima while accommodating increasingly complex manipulation tasks. Khatib (1986) pioneered the Artificial Potential Field (APF) method, transforming discrete path planning into a continuous optimization problem. The robot is treated as a particle moving in a force field where an attractive force proportional to goal distance pulls the robot toward the target, while repulsive forces decaying quadratically with proximity push it away from obstacles. The robot follows the negative gradient of this composite potential function, implementing steepest descent optimization in configuration space. A key limitation is that APF can suffer from local minima in cluttered environments due to the superposition of attractive and repulsive forces. Subsequent research by Volpe and Khosla (1987), Volpe and Khosla (1990) refined the original APF concept, by introducing n-ellipse representation that varies with distance. The n-elliptical iso-potential contours address the fundamental limitations in obstacle avoidance. Their innovative approach seamlessly transitioned from rectangular contours near obstacles
Furthermore, enhanced APF with specialized variants, such as D-APF(Dynamic Artificial Potential Field) Jayaweera and Hanoun (2020) for UAV path planning using exponential attractive and repulsive potential fields for moving target tracking and obstacle avoidance. It prioritizes vertical over horizontal motion, favoring altitude changes for obstacle avoidance. Combined forces generate smooth trajectories converted to velocity waypoints for PX4 autopilot, with separate PD-based orientation control. The force separation into vertical/horizontal components adds complexity and may cause oscillations during rapid directional changes, and the approach struggles with complex or closely spaced obstacles where vertical avoidance is insufficient. D-APF demonstrates potential field method evolution for aerial navigation, though dual-arm manipulation presents unique challenges requiring careful force field design. Sun et al. (2022) used APF in a hybrid approach with their mobile dual-arm system combined with RRT (Rapidly Exploring Random Tree)-based motion planning for base navigation along with integrated vision and impedance control. Wang et al. (2018) developed an optimized APF with velocity feedforward and simplified collision detection for redundant manipulators. Li et al. (2024a) and Li et al. (2024b) introduced an attractive potential field rotation method for local minima avoidance and develop a smooth attractive function
Beyond spatial collision avoidance, successful dual-arm manipulation demands sophisticated temporal coordination to synchronize movements and optimize task execution. Researchers have developed various frameworks to address this critical dimension of collaborative robotic systems. Montaño and Suárez (2016) proposed a temporal coordination approach for multiple robots using Discretized Coordination Space (DCS) where robots adjust timing along fixed paths. It builds a Collision-free Coordination Curve using state diagrams with wall-follower or impact heuristics to select motion directions. The computational complexity increases exponentially with robot numbers (
Furthermore, for effective object handling in real-time operation, precise detection of required components is an important aspect. Object detection has evolved from traditional computer vision techniques like SIFT, SURF, and BRIEF -which require manual feature extraction and parameter tuning O’Mahony et al. (2019) to more advanced CNN methods that automatically learn relevant features (Alzubaidi et al., 2021). For handling industrial components, an accurate pose estimation is crucial. K et al. (2024) presented a classical approach for bolt handling using k-mean clustering and chamfer matching, offering simple implementation without training data but limited by sensor quality and lighting conditions. S. K et al. (2024) employed DeeplabV3P with classical techniques for estimating and sorting bolt size. Instance segmentation provides both classification and precise localization with clean edge masks (Sharma et al., 2022). Mask R-CNN He et al. (2017), built on Faster R-CNN Ren (2015) which uses region proposal networks instead of selective search Girshick (2015); Girshick et al. (2014) adds a parallel branch for segmentation masks. Detectron2 Wu et al. (2019), successor to Detectron Girshick et al. (2018) and maskrcnn-benchmark Massa and Girshick (2018), incorporates Mask R-CNN and RetinaNet with focal loss. For real-time inference on CPU machines, Ultralytics’ YOLOv8 and YOLOv11 Jocher et al. (2023); Jocher and Qiu (2024) offer faster performance through single-pass architecture, lightweight backbones, anchor-free detection, and efficient feature pyramids. YOLOv8’s oriented bounding boxes capability avoids computationally expensive instance segmentation.
Our improved Artificial Potential Field (iAPF) approach addresses key limitations identified across existing methodologies as shown Table 1. While geometric approaches like Lumelsky (1985) and Chang et al. (1990) provide precise collision detection, they lack continuous distance metrics for smooth motion planning. Traditional APF methods by Khatib (1986) offer intuitive frameworks but suffer from local minima, particularly in cluttered environments. Prior coordination strategies like Montaño and Suárez (2016), discretized coordination space and Malvido Fresnillo et al. (2023), master-slave paradigm lack dynamic adaptability to changing environments. iAPF overcomes these limitations through a novel three-way force equilibrium that balances goal attraction, obstacle repulsion, and home-seeking behavior. Unlike Byrne et al. (2015) and Byrne et al. (2013) approach, which showed slower convergence despite higher success rates, our method achieves real-time performance without sacrificing stability. Where Li et al. (2024a) and Li et al. (2024b) rotating repulsive fields work well for single arms, our approach extends to dual-arm coordination with a priority-based state transition mechanism that enables truly asymmetric dual-arm manipulation without oscillations or deadlocks. By addressing the need for continuous adaptation rather than pre-planned trajectories, iAPF motion planning along with real-time 20 frames per second (FPS) inference provides a robust solution for collaborative robot tasks in dynamic industrial environments like manufacturing, warehouse management and assembly line fields. Our novel iAPF methodology addresses these limitations through the following key contributions.
1. Case-Specific Analytical Inter-Arm Distance - Algorithm employing closed-form vector solutions for parallel, intersecting, and skew link configurations with epsilon-based numerical stability handling.
2. Hybrid Linear-Angular Control Framework - iAPF-derived linear velocity control coupled with independent PD (Proportional Derivative)-regulated angular velocity, creating a dual-control system with proven Lyapunov stability for exponential
3. 4-DoF Vision-Based Pose Estimation - Real-time component detection (20 FPS) with oriented bounding box analysis providing position and yaw for precise grasp planning.
4. State-Conditional Kinodynamic Control - Velocity damping coefficients and task-specific z-axis constraints adaptively modulated based on operational phase (targeting, gripping, transport).
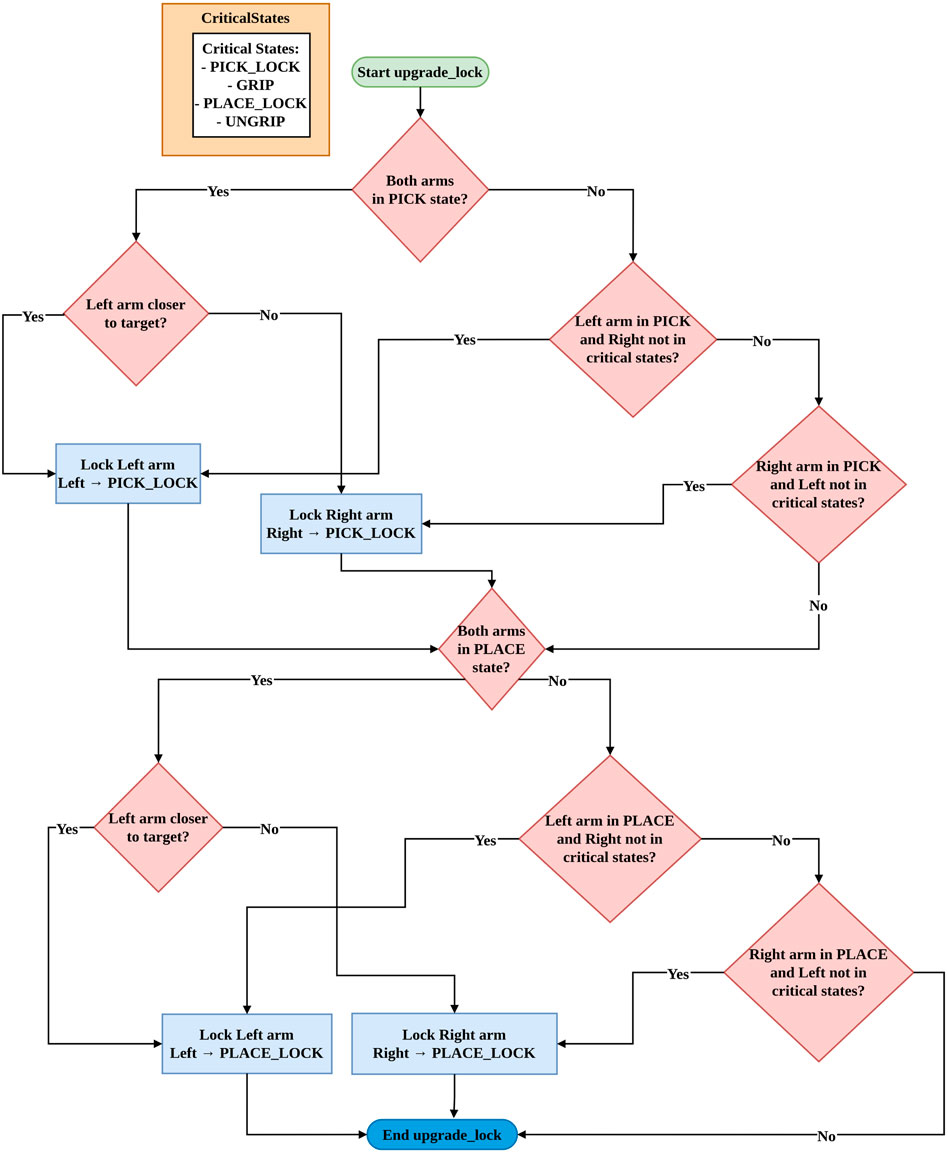
5. Priority-Based Dual-Arm Task Allocation - Hierarchical state machine with comparative-distance-based resource locking for deadlock-free simultaneous manipulation in shared workspaces.
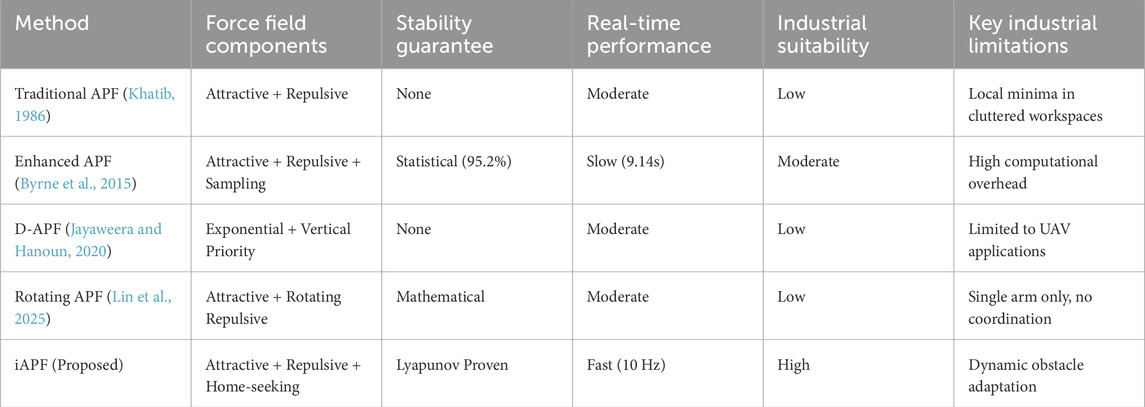
Table 1. Comparative analysis of the proposed iAPF with traditional and existing APF variants for industrial dual-arm manipulation.
This paper is organized as follows: Section 1 introduces the motivation and significance of asymmetric bi-manual manipulations in industrial automation. Section 2 provides a systematic review of relevant literature, highlighting the advantages of our proposed method. Section 3 presents the proposed methodology for establishing inter-arm collision avoidance in dual-arm motion planning, incorporating real-time vision and providing theoretical proofs for the potential field formulations. Section 4 describes the experimental setup, including the hardware used and the required transformation of frames. Section 5 presents a comparative analysis between the proposed iAPF and traditional APF methods, highlighting the advantages of our approach, and showcases the deep learning model’s performance metrics. Finally, Section 6 summarizes the key findings, presents the conclusions, and discusses potential future research directions.
3 Methodology
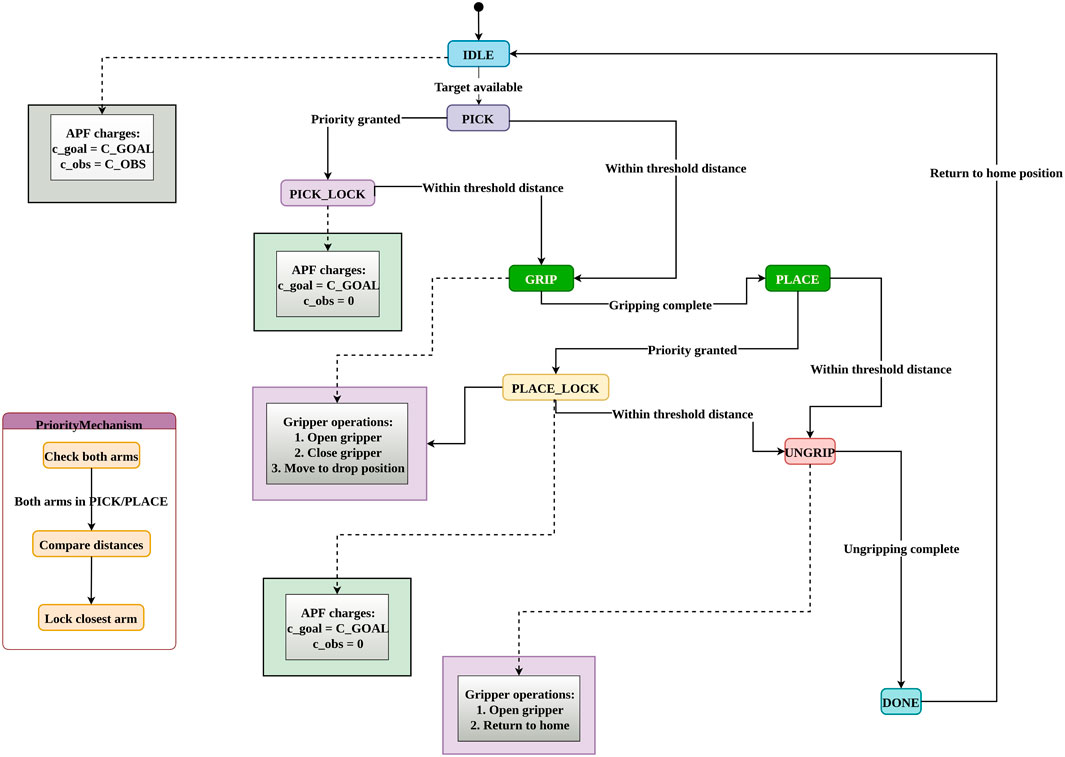
The proposed overall methodology as shown in Figure 1 integrates four key components: (1) minimum distance calculation between inter-arm links using geometric classification, (2) vision-based pose estimation for industrial components, (3) three-way force equilibrium combining attractive, repulsive, and home-seeking forces with velocity-dependent stabilization and (4) state-based asymmetric coordination for dual-arm manipulation with priority locking. Together, these components enable collision-free, coordinated manipulation in shared workspaces.
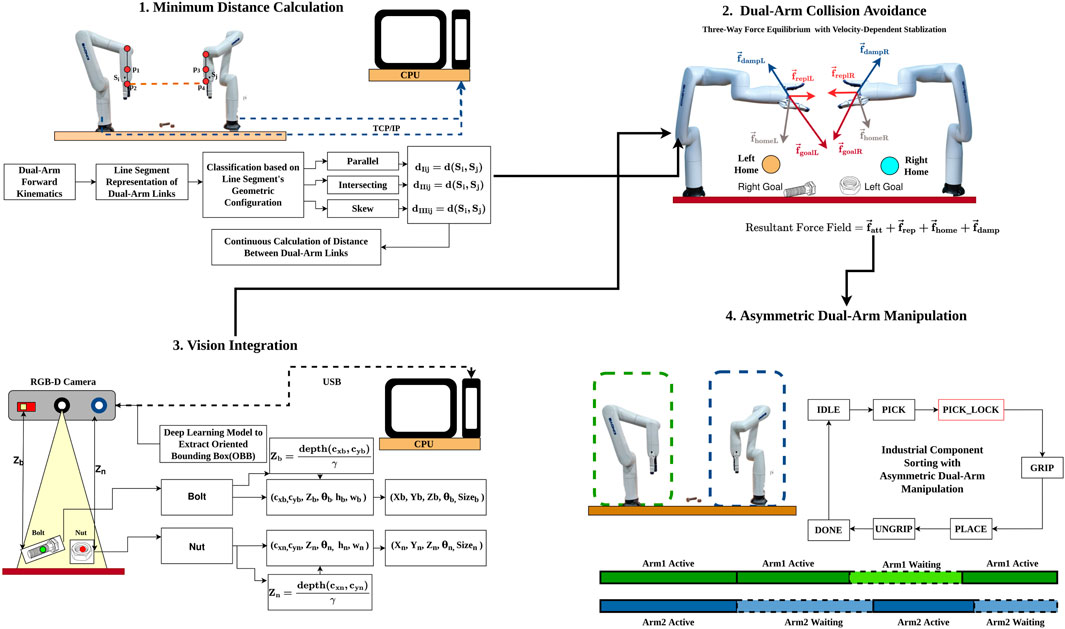
Figure 1. The Proposed Overall Methodology of iAPF framework for Asymmetric Dual-Arm Manipulation with Real-Time Inter-Arm Collision Avoidance.
3.1 Minimum distance calculation between inter-arm links using geometric classification
We modeled each robotic arm link as a line segment in 3-D space using Equation 1 and Equation 2 as given in Equation 3 using D-H parameters shown in Figure 2 enabling efficient minimum distance calculation between inter-arm links through geometric classification as parallel, intersecting, or skew configurations.
Where
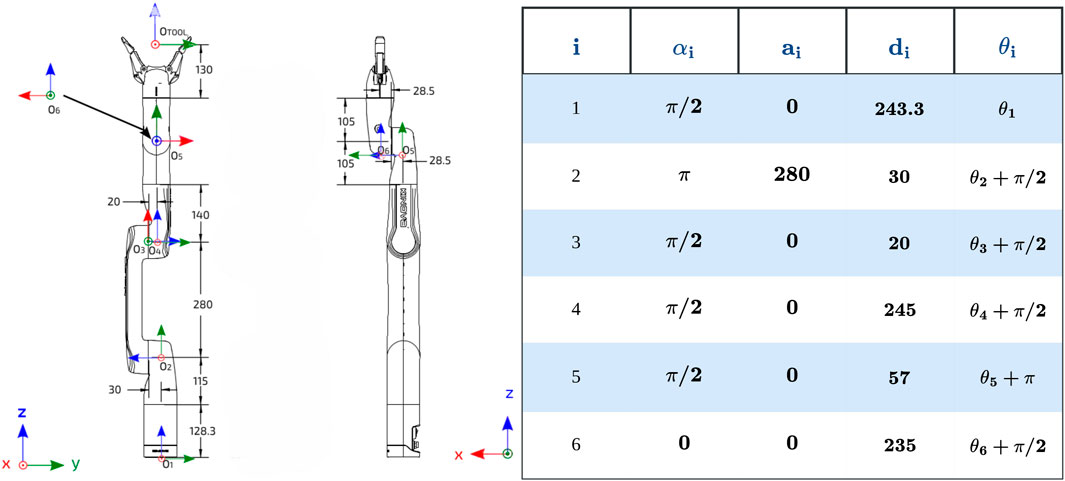
Figure 2. Kinova Gen3 lite with link frames with modified DH parameters for forward kinematics computation.
Theorem 1. (Segment Properties). Every line segment
The segment between two bounding points
For segments
Theorem 2. (Angle Invariance). The angle
Theorem 3. (Configuration Completeness). Every pair of line segments falls exactly into one of:
1. Intersecting
2. Parallel
3. Skew
Theorem 4. (Metric Space Properties). The function
The distance function
For all
The distance between a line segment on the left arm
where,
The minimum distance between any pair of links in the dual-arm system is determined based on their geometric configuration, one of three cases: parallel, intersecting, or skew as in Figure 3. The method of distance calculation varies depending on the specific geometric configuration. A systematic formulation for finding the minimum distance between dual-arm links in 3-D space has been developed. Further the proposed method for calculating minimum distance is verified as shown in Figure 4. Example Distance Calculation between various cases of line segments are shown in Supplementary Material in Supplementary Figure S9.
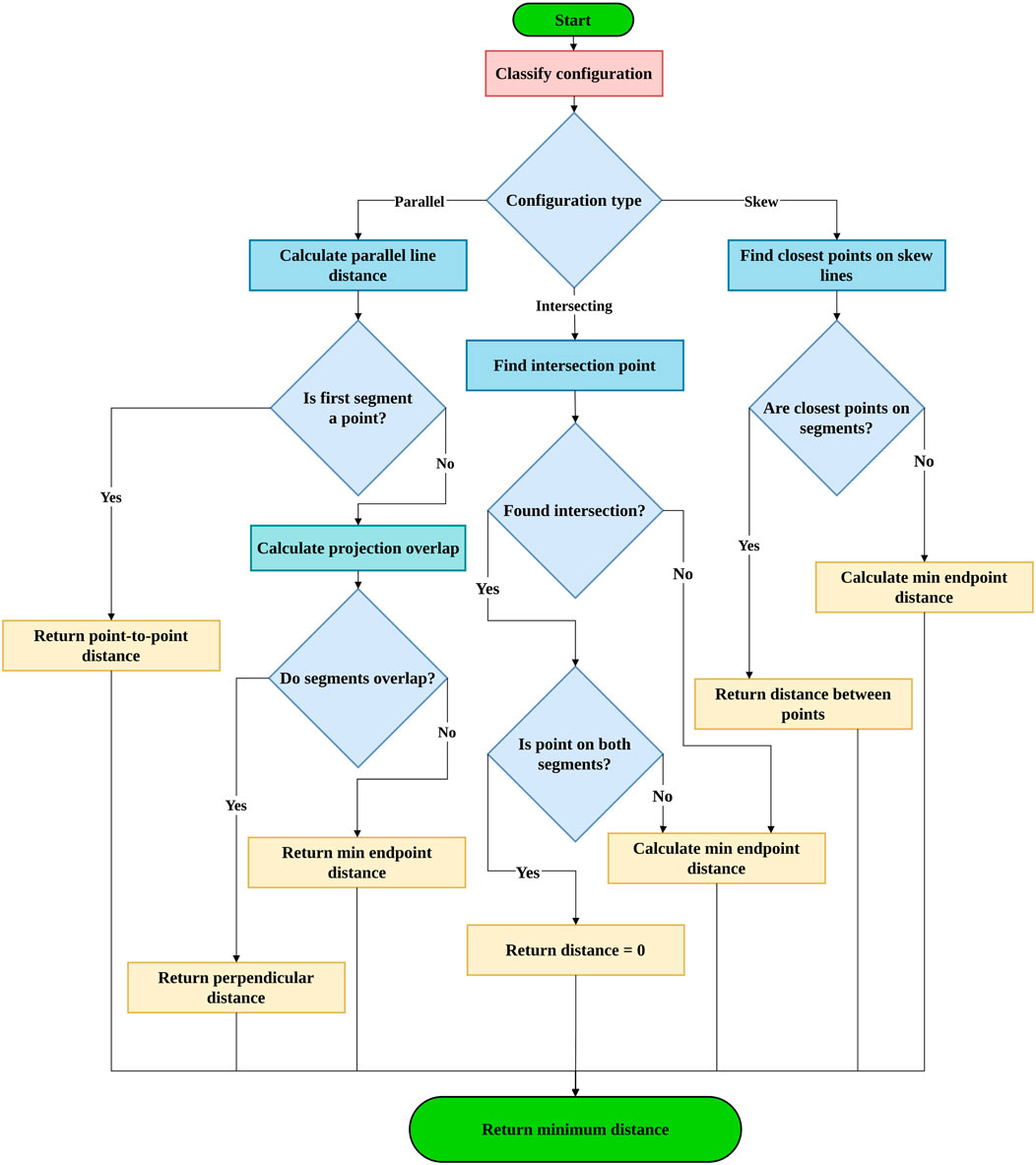
Figure 3. Procedure to compute minimum distance between inter-arm robot links modeled as line segments in 3-D space according to geometric configurations.
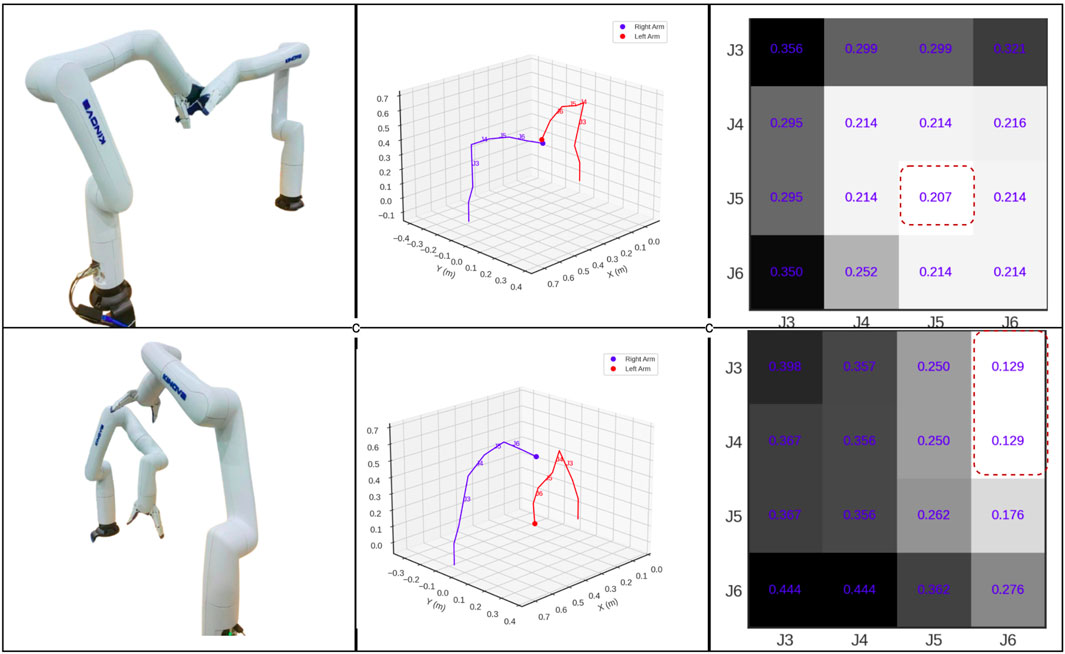
Figure 4. Visualization of real-time minimum distance(m) calculation for Dual-Arm Links (block with more bright and red dotted lines indicates the minimum distance).
3.2 Vision-based pose estimation of industrial components
Real-time asymmetric dual-arm manipulation requires rapid inference of object information within the system’s workspace. Prioritizing inference speed for effective real-time object handling, we selected the YOLOv8 OBB model for object detection, which achieved 20 frames per second on our hardware configuration while maintaining high detection accuracy. The systematic evaluation of various models used on our custom data as shown in Table 2.

Table 2. Systematic evaluation of models on our custom dataset (nut/bolt) for suitable selection of model.
3.2.1 Data collection and labeling
Data collection and data labeling as shown in Figure 5, are crucial steps in preparing meaningful information to train deep learning models. We carefully prepared our dataset, incorporating diverse real-world conditions, including varying backgrounds (cluttered workspaces, different table surfaces), lighting, and object ages (new and old). To enhance the model’s robustness against false positives, we employed a strategic negative mining technique by adding a background/reference class. This class included objects visually similar to the target objects (bolts, nuts) and images of the empty workspace on the table. Our dataset, comprising 1,230 images, divided into training, validation, and testing sets of 1120, 80, and 30 images, respectively. Furthermore, we used data augmentation techniques of the Ultralytics training framework, increasing the dataset size tenfold. As a result, we achieved a prediction rate of 20 frames per second during model deployment, crucial for real-time applications. The system operates under controlled workspace assumptions where only target components are present, eliminating occlusion challenges typical in structured industrial sorting environments.

Figure 5. Data Collection (top row) and (b) Data Labeling of nuts (blue border) and bolts (red border) (bottom row).
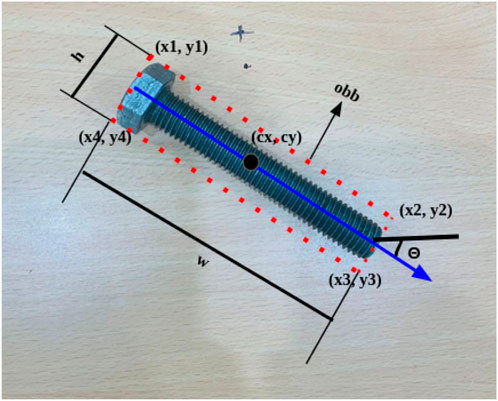
After detecting objects (nuts and bolts) globally from an RGB-D camera, further inferred object centroids (
Where [K] is camera intrinsic parameter matrix of Intel Realsense2 D415,
We further estimate its size using the width
The final feature information of industrial components (nut/bolt) in real world coordinates are:
3.3 Improved artificial potential field (iAPF) framework for dual-arm motion planning
Considering the robot position
where,
where
The home-seeking force represents a novel integration to traditional APF, providing exponential attraction towards the home position of the manipulator.
where,
where,
The carefully designed force fields are crucial for achieving successful asymmetric bi-manual manipulation. The exponential goal attraction force field Equation 12, significantly enhances convergence speed and facilitates smooth transitions near the goal, essential for achieving precise pick-and-place operations. The inverse-distance repulsive force Equation 13, effectively prevents collisions between manipulators by exerting a repulsive force that scales inversely with the distance between them, ensuring robust collision avoidance while minimizing unnecessary interference. The exponential home-seeking force Equation 14, counteracts excessive arm extension, particularly in scenarios where strong repulsive forces arise due to near-goal conflicts. By encouraging the arms to return to a more neutral position, it maintains system stability and facilitates balanced convergence. Furthermore, the velocity-dependent damping force Equation 15, plays a crucial role in stabilizing the system by dissipating energy, effectively reducing the oscillatory behaviors that may arise during arm interactions, ensuring smooth and controlled trajectories.
The resultant force with damping is given by Equation 16:
From the visual perception module described in Section 3.2, the feature information obtained in Cartesian coordinates, as defined in Equation 11, provides the position and orientation of the goal.
3.3.1 iAPF based linear velocities
Considering the position of objects obtained from the vision module Equation 11, the generation of force fields is initiated to guide the manipulators to their respective target positions. In the absence of object detection, the target position for each manipulator defaults to its home position. The linear velocities of manipulators are determined as follows:
where,
Considering the manipulator’s end-effector position as
The gradient
where,
In the pre-priority state, when robots start to move towards goal, the Lyapunov function is selected as:
where
The time trajectory of
At the pick-lock state (
Making obstacle charge
Substituting these conditions, we get:
The time trajectory at
Simplifying, we have:
For
The stability analysis demonstrates, dual-arm iAPF control achieves coordinated manipulation through two key phases. Initially, both manipulators move under complete force set (attractive, repulsive, home-seeking) with Lyapunov function
3.3.2 PD controller based angular velocities
Considering the orientation of objects obtained from the vision module, the current end-effector orientation for each manipulator is obtained through real-time forward kinematics of the dual-arm system, providing the basis for orientation control.
The current orientation of the end-effector is given by:
The desired orientation, obtained from visual perception given by:
The corresponding rotation matrix is represented as:
The error rotation matrix is given by:
The error rotation matrix
The PD control law for orientation control of manipulator given by:
Where
4 Experimental setup
The experimental setup for demonstrating asymmetric dual-arm manipulation is established with reference frames as shown in Figure 9. The system comprises two 6-DOF Kinova Gen3 Lite arms mounted on a fixed table, with an overhead Realsense2 D415 camera providing a global view of the workspace. Processing is handled by an Intel Nuc9I7Qnx with 32 GB RAM, which connects to the manipulators via TCP/IP sockets using a specific communication protocol, while the camera interfaces through USB. The Kinova-Kortex Python API is used for manipulator control, and the ROS-Noetic framework facilitates publishing and subscribing to the vision module’s inference data.
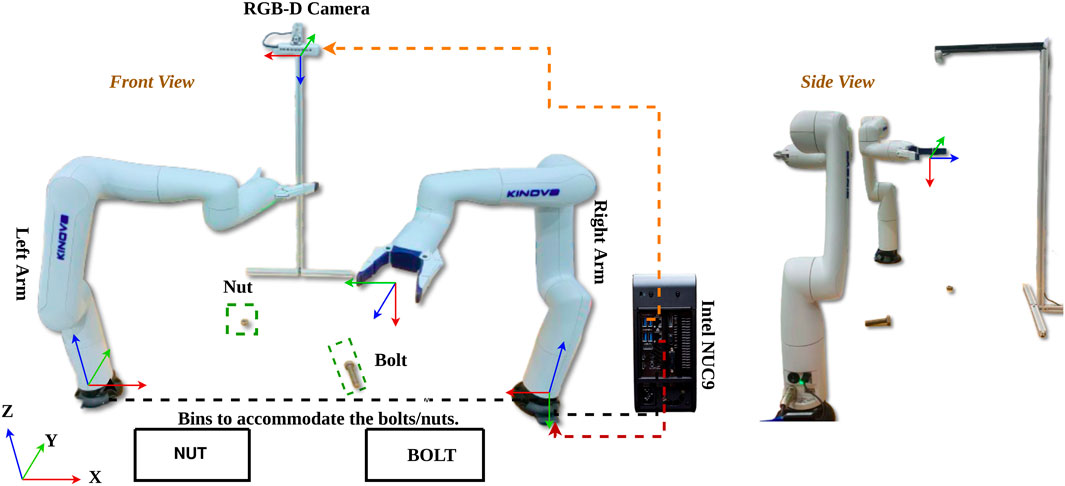
Figure 9. Experiment setup to demonstrate the iAPF based motion planning for dul-arm asymmetric manipulations.
Individual forward kinematics, as given by Equation 4, provide the position and orientation of each manipulator’s end-effector with respect to its respective base frame. Furthermore,
The further pose from Equation 11, is transformed to the left arm’s base as Equation 19:
where
The rotation angle
The gripper angle
This ensures proper alignment between the gripper and nut/bolt for grasping.
Both linear velocities (from iAPF) and angular velocities (from PD control) for both arms are initially calculated in left base frame using Equation 17 and Equation 18. Subsequently, the right arm velocities (both linear and angular) are transformed from left base frame to right base frame using
Where
5 Results and discussion
To validate the proposed system for asymmetric dual-arm manipulation framework for sorting industrial components, created challenging scenarios by placing nuts and bolts in close proximity, deliberately inducing goal conflicts between the manipulators. This setup rigorously tests the framework’s collision avoidance capabilities, priority-based state transitions, and the effectiveness of exponential attractive home-seeking forces in maintaining stable coordination during sorting tasks.
The performance metrics for the bolt and nut detection classes demonstrate superior discrimination capabilities compared to the reference class. Bolts achieve 0.99 detection accuracy and nuts achieve 0.97 detection accuracy, with minimal inter-class confusion of 0.02. The F1 score reaches 0.89 at a confidence threshold of 0.120, while precision achieves 1.00 at 0.808. Recall maintains 1.00 at low confidence thresholds, indicating robust detection even under varying conditions. These metrics validate the model’s effectiveness in discriminating between nuts and bolts while successfully handling the reference class for false positive reduction. The final deployment results are as shown in Deep Learning Model Metrics and Real-Time Vision Update Experiment Figures are shown in Supplementary Figures S1-S8.
The proposed iAPF, incorporating three distinct force fields, effectively addressed near-goal conflict scenarios, as demonstrated in Figure 10. The implementation of three force fields: exponential goal attraction, inverse-distance other-arm repulsion, and home exponential attraction, demonstrates superior control over dual-arm trajectories, effectively mitigating inter-arm collision. The transition point shows deliberate stop and stable movement of the arms during collision possible scenarios and maintains better spatial separation throughout their movements. The exponential home attraction force acts as a regulator, preventing excessive arm extension in scenarios where near-goal conflicts result in strong repulsive forces. The establishment of a three-way force equilibrium results in more predictable and controlled motion paths. The home force establishes natural boundaries for arm movements, maintaining optimal manipulator poses and preventing over-extension. Particularly, how the trajectories exhibit smoother curves with minimal oscillations, as the arms move toward goals, the exponential home attraction scales with distance, providing graduated control that keeps configurations within safe operating ranges. This makes the system more robust against kinematic singularities while ensuring efficient task completion.
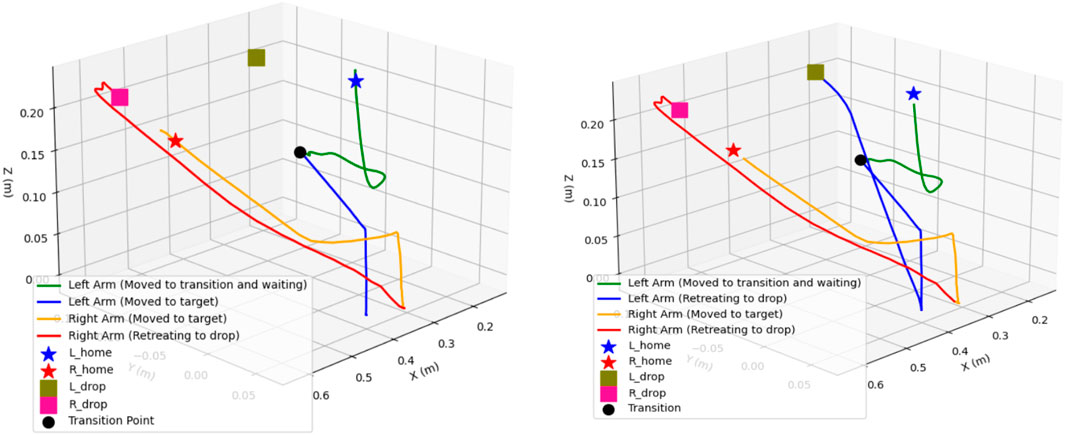
Figure 10. Dual-arm end effectors’ trajectories with exponential attraction, inverse distance and exponential home-seeking attraction force fields. [Both arms initiate movement from their home positions towards their respective target locations. Due to distance priority, the right arm reaches its target first, picks up the object, and then retreats to its designated drop point. While the right arm is performing these actions, the left arm remains at the transition point. Once the right arm has move away by picking the object, the left arm begins its movement towards its target. The second plot illustrates the complete trajectories of both arms].
In traditional attractive-repulsive APF, as shown in Figure 11 without home attraction, the system exhibits inherent instabilities near goal regions. While the arms successfully navigate to their target locations, the trajectories demonstrate less controlled movements with larger sweeping motions and more aggressive approaches. The fundamental issue lies in the force imbalance - as both arms approach their respective goals simultaneously, the attractive forces dominate while the inter-arm distance decreases, causing a sudden spike in repulsive forces. This force antagonism leads to oscillatory behaviors and potential over-extension of the arms. Without a stabilizing home force, the arms can reach configurations near kinematic singularities with no natural mechanism to recover optimal poses. The problem is particularly pronounced when both arms operate in close proximity, where the rapid transition between attraction-dominated and repulsion-dominated states can lead to unstable motion patterns.
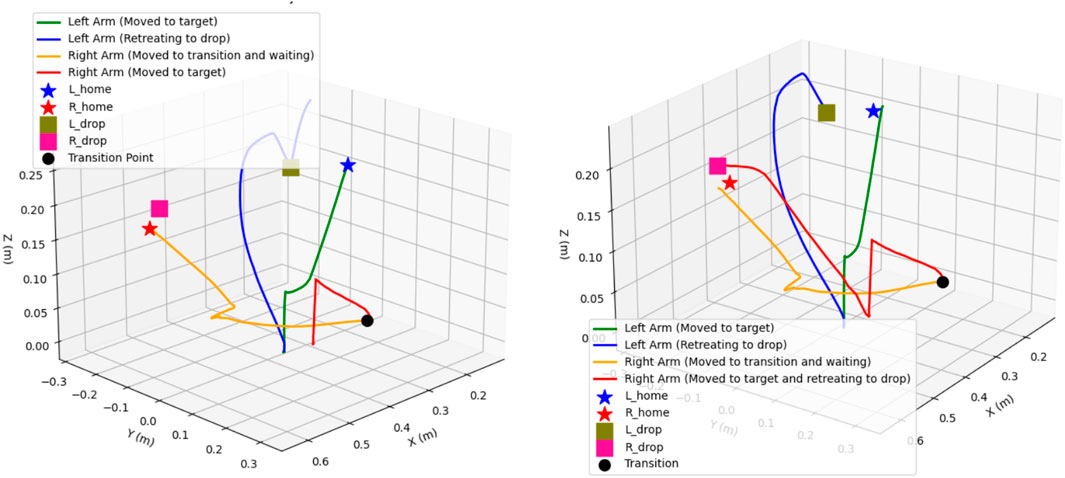
Figure 11. Dual-arm end effectors’ trajectories with exponential attraction, inverse distance repulsion without exponential home-seeking attraction force fields. [Both arms initiate movement from their home positions towards their respective target locations. Due to distance priority, the left arm reaches its target first, picks up the object, and then retreats to its designated drop point. While right arm remains at the transition point. Once the left arm has move away by picking the object, the right arm begins its movement towards it target. The second plot illustrates the complete trajectories of both arms].
Observing Figures 12a, 13a, 10, represents attractive and repulsive force trends for our iAPF which represents three-way force equilibrium: Both arms exhibit controlled convergence to home positions with initial attractive forces of
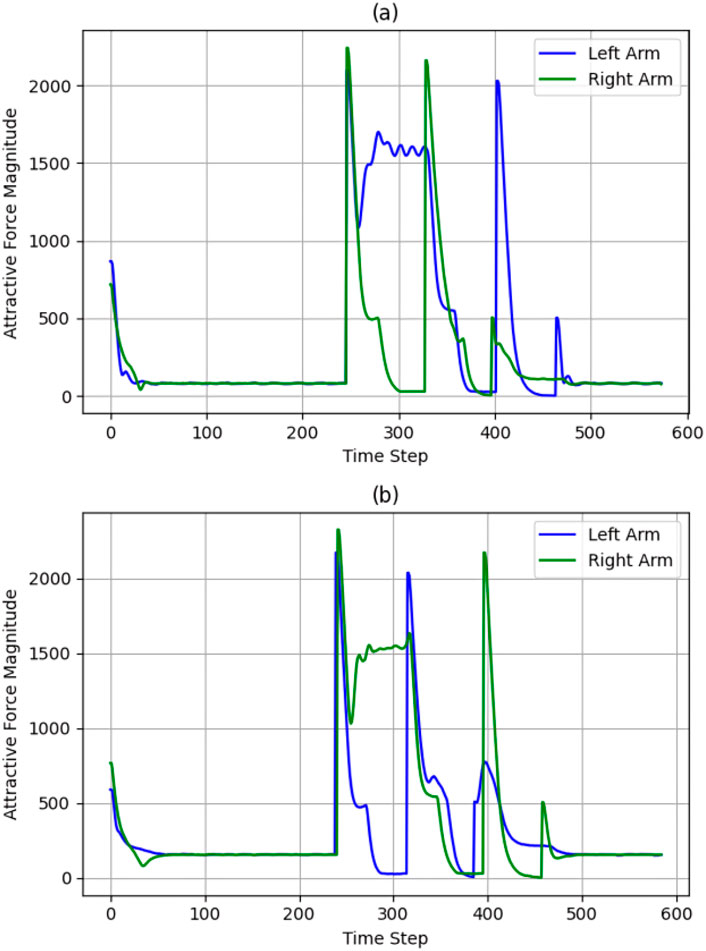
Figure 12. Convergence of attractive forces for both cases (a) with exponential home (b) without exponential home.
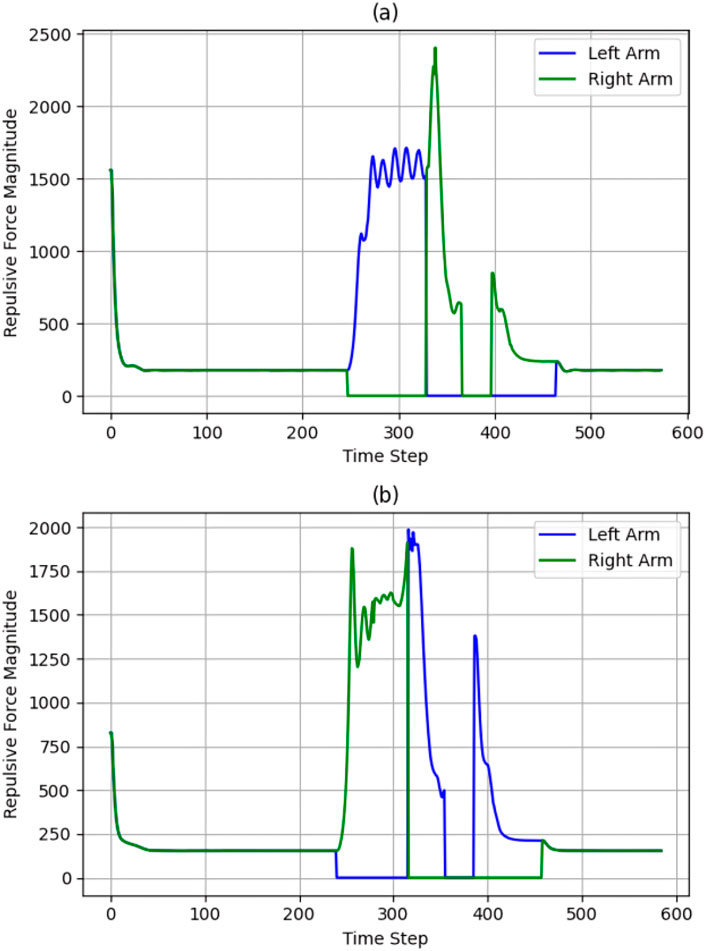
Figure 13. Convergence of Repulsive forces for both cases Forces (a) with exponential home (b) without exponential home.
Observing Figures 12b, 13b, 11, analyzing the second row sub-plots represents attractive and repulsive force trends for traditional attractive-repulsive APF which represents two-way force equilibrium: Both arms show initial convergence to home position with
The convergence behaviors depicted in Figures 14, 15, illustrate the interplay of two parallel control systems. Position trajectories are governed by the APF framework, while orientation trajectories are controlled by a PD controller. Figure 14 demonstrates smooth convergence, attributed to the inclusion of the three-way force equilibrium that effectively mitigates oscillations and prevents excessive arm extension. Notably, orientation convergence is independently controlled and effectively synchronized with position convergence. But in Figure 15 shows that without home attraction, position trajectories oscillate due to force antagonism between pure attraction-repulsion, while orientation still achieves convergence with PD control but experiences coupling effects from less stable positional behavior. This separation of position and orientation control allows for independent tuning of linear and angular responses while maintaining overall system stability. The sequential illustration of experiments for explaining two cases are shown in Figures 16, 17.
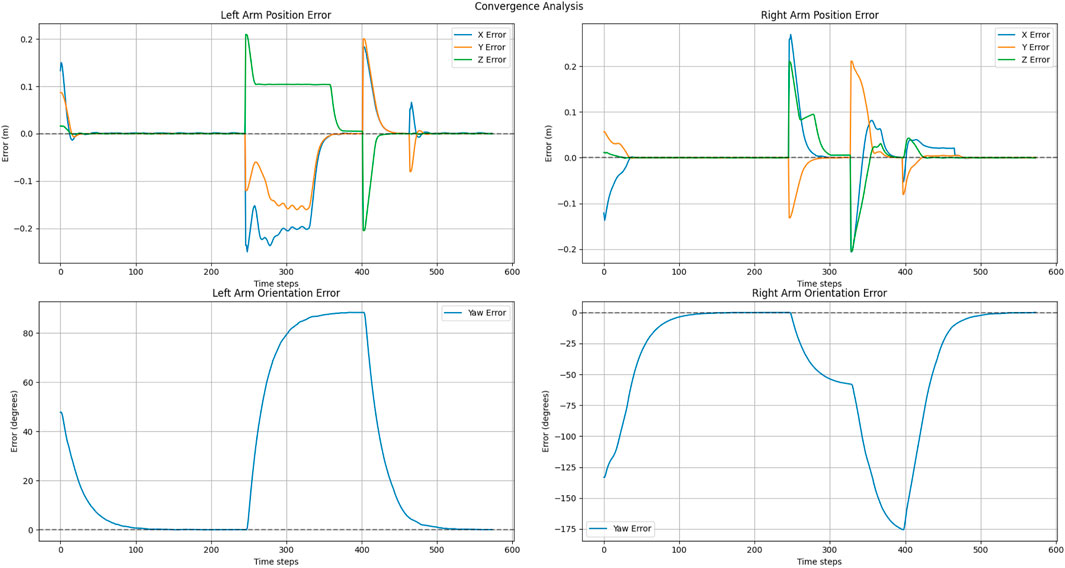
Figure 14. Position and orientation convergence in exponential goal attraction, exponential home attraction and inverse distance repulsion.
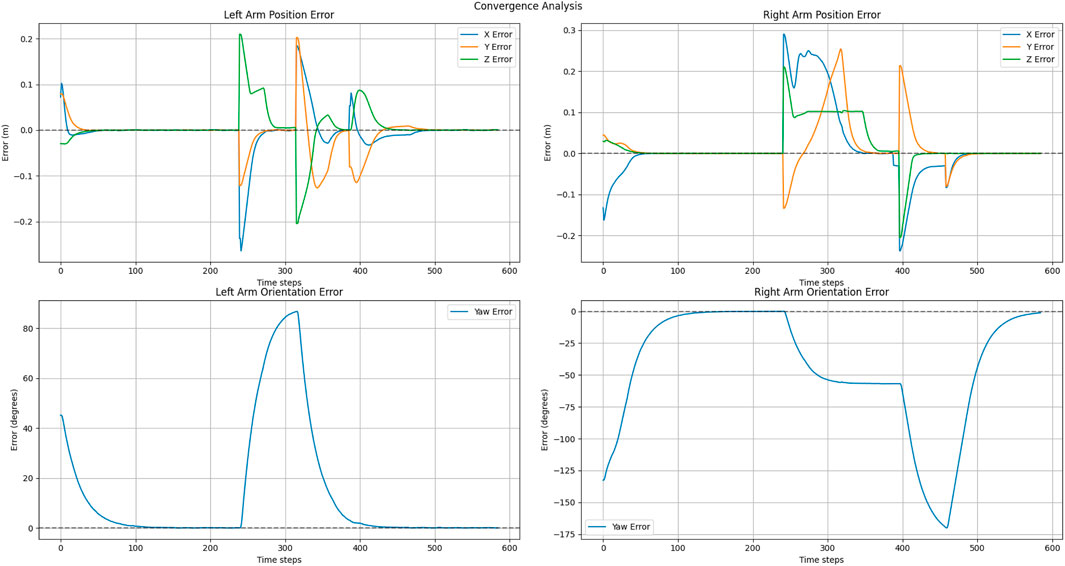
Figure 15. Position and orientation convergence in exponential goal attraction, without exponential home attraction and inverse distance repulsion.

Figure 16. Sequential Illustration of Asymmetric Dual-Arm Manipulation at Near Goal Conflict situation with Clear Spatial Separation between Arms [at t = 6.25 left arm gets priority due to the proximity, t = 8.33 left arm picking the object while right arm waiting at safe transition point, t = 15.66 right arm picks the object and t = 16.32 left arm drops the object and right arm at t = 22.50.] - With Three-way Force Equilibrium.

Figure 17. Sequential Illustration of Asymmetric Dual-Arm Manipulation at Near Goal Conflict situation with Close Proximity Movement of Dual-Arm [at t = 7.33 left arm gets priority due proximity with goal, while right arm move far away from left arm due to spike in repulsion, t = 14 arms are near collision situation.] - Without Three-Way Force Equilibrium.
6 Conclusion
In this paper, we presented a comprehensive framework for dual-arm asymmetric manipulation with inter-arm collision avoidance for handling industrial components. Our approach introduces a computationally efficient collision detection method that represents manipulator links as line segments in 3-D space, enabling real-time distance monitoring through analytical solutions for parallel, intersecting, and skew configurations. The integration of YOLOv8 OBB-based object detection achieves robust real-time perception at 20 frames per second with oriented bounding boxes, demonstrating high accuracy of 0.99 and 0.97 for bolt and nut detection respectively along with components size estimation. The improved Artificial Potential Field (iAPF) framework implements a novel three-way force equilibrium through exponential attractive, inverse-square repulsive, and exponential home-seeking forces, significantly enhancing trajectory stability and reducing oscillations compared to traditional APF approaches. Our hybrid twist control scheme combines iAPF-generated linear velocities with PD-controlled angular velocities, with proven stability through Lyapunov analysis and enabling precise asymmetric manipulation through a priority-based state machine. Experimental validation demonstrates the framework’s effectiveness in handling challenging scenarios, including close-proximity object sorting and goal conflicts between manipulators, while maintaining safe separation distances. This integrated approach provides a promising foundation for deploying collaborative dual-arm systems in industrial settings where reliable, efficient, and safe manipulation of industrial components is essential. The proposed framework assumes a controlled workspace free from external dynamic obstacles, focusing primarily on inter-arm collision avoidance. The vision system is currently limited to pre-trained component classes (nuts/bolts), though it remains adaptable through retraining for new object types.
Future work will extend the present framework to handle external dynamic environments through: i) real-time external obstacle detection using RGB-D depth sensing to detect unknown objects in the workspace, ii) adaptive repulsive force field generation that incorporates external obstacles into the existing iAPF framework. This progression will enable deployment in unstructured manufacturing environments while maintaining the proven stability and collision avoidance capabilities demonstrated in this work. Potential applications include automated assembly of industrial components, transitioning from absolute motion to relative motion control during assembly phase, with integrated size matching and precise alignment capabilities.
Data availability statement
The datasets and codes generated/analyzed for this study can be found in the Dual-Arm-Manipulation, https://github.com/suryarobotcontrol/Dual-Arm-Manipulation.git.
Ethics statement
Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
SS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. DP: Conceptualization, Methodology, Software, Writing – original draft, Writing – review and editing. BN: Conceptualization, Methodology, Software, Writing – original draft, Writing – review and editing. AS: Conceptualization, Methodology, Resources, Supervision, Validation, Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
We would like to express our gratitude to Ravi Kiran Akumalla, Research Scholar in the Modeling & Intelligent Control Lab, IIT Mandi, for his contribution to the Lyapunov stability proof. We also extend our appreciation to Nandini, a research intern at the Centre for Artificial Intelligence and Robotics (CAIR), IIT Mandi, for her contribution to custom data preparation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that Generative AI was used in the creation of this manuscript. We have used Claude Anthropic for English Sentence Formation, Punctuation Checking of our original text.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2025.1604506/full#supplementary-material
References
Abbas, M., Narayan, J., and Dwivedy, S. K. (2023). A systematic review on cooperative dual-arm manipulators: modeling, planning, control, and vision strategies. Int. J. Intelligent Robotics Appl. 7, 683–707. doi:10.1007/s41315-023-00292-0
Alzubaidi, L., Zhang, J., Humaidi, A. J., Al-Dujaili, A., Duan, Y., Al-Shamma, O., et al. (2021). Review of deep learning: concepts, cnn architectures, challenges, applications, future directions. J. big Data 8, 53–74. doi:10.1186/s40537-021-00444-8
Asano, T., Asano, T., Guibas, L., Hershberger, J., and Imai, H. (1985). “Visibility-polygon search and euclidean shortest paths,” in 26th annual symposium on foundations of computer science (SFCS 1985) (IEEE), 155–164.
Aurenhammer, F. (1991). Voronoi diagrams—a survey of a fundamental geometric data structure. ACM Comput. Surv. (CSUR) 23, 345–405. doi:10.1145/116873.116880
Basile, F., Caccavale, F., Chiacchio, P., Coppola, J., and Curatella, C. (2012). Task-oriented motion planning for multi-arm robotic systems. Robotics Computer-Integrated Manuf. 28, 569–582. doi:10.1016/j.rcim.2012.02.007
Byrne, S., Naeem, W., and Ferguson, S. (2013). “An intelligent configuration-sampling based local motion planner for robotic manipulators,” in 9th international workshop on robot motion and control, 147–153. doi:10.1109/RoMoCo.2013.6614600
Byrne, S., Naeem, W., and Ferguson, S. (2015). Improved apf strategies for dual-arm local motion planning. Trans. Inst. Meas. Control 37, 73–90. doi:10.1177/0142331214532002
Canny, J. (1989). On computability of fine motion plans. Proc. 1989 Int. Conf. Robotics Automation 1, 177–182. doi:10.1109/ROBOT.1989.99986
Chang, C., Chung, M. J., and Bien, Z. (1990). Collision-free motion planning for two articulated robot arms using minimum distance functions. Robotica 8, 137–144. doi:10.1017/s0263574700007712
Chuang, J.-h., Lin, C.-c., and Chou, T.-h. (2006). “An alternate priority planning algorithm for dual-arm systems,” in 2006 IEEE international symposium on industrial Electronics, 4, 3084–3089. doi:10.1109/ISIE.2006.296108
Fei, Y., Fuqiang, D., and Xifang, Z. (2004). Collision-free motion planning of dual-arm reconfigurable robots. Robotics Computer-Integrated Manuf. 20, 351–357. doi:10.1016/j.rcim.2004.01.002
Feng, Z., Hu, G., Sun, Y., and Soon, J. (2020). An overview of collaborative robotic manipulation in multi-robot systems. Annu. Rev. Control 49, 113–127. doi:10.1016/j.arcontrol.2020.02.002
Gallier, J. (2011). Geometric methods and applications: for computer science and engineering, 38. Springer Science and Business Media.
Girshick, R. (2015). Fast r-cnn. arXiv Prepr. arXiv:1504.08083, 1440–1448. doi:10.1109/iccv.2015.169
Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014). “Rich feature hierarchies for accurate object detection and semantic segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 580–587.
Girshick, R., Radosavovic, I., Gkioxari, G., Dollár, P., and He, K. (2018). Detectron. Available online at: https://github.com/facebookresearch/detectron.
He, K., Gkioxari, G., Dollár, P., and Girshick, R. (2017). “Mask r-cnn,” in Proceedings of the IEEE international conference on computer vision, 2961–2969.
Jamisola, R. S., and Roberts, R. G. (2015). A more compact expression of relative jacobian based on individual manipulator jacobians. Robotics Aut. Syst. 63, 158–164. doi:10.1016/j.robot.2014.08.011
Jamisola, R. S., Kormushev, P., Caldwell, D. G., and Ibikunle, F. (2015). “Modular relative jacobian for dual-arms and the wrench transformation matrix,” in 2015 IEEE 7th international conference on Cybernetics and intelligent systems (CIS) and IEEE conference on robotics, Automation and Mechatronics RAM (NY, United States: IEEE), 181–186.
Jayaweera, H. M., and Hanoun, S. (2020). A dynamic artificial potential field (d-apf) uav path planning technique for following ground moving targets. IEEE Access 8, 192760–192776. doi:10.1109/ACCESS.2020.3032929
K, S. P. S., Shukla, A., and S, S. (2024). “Automated vision-based bolt handling for industrial applications using a manipulator,” in 2024 12th international conference on control, Mechatronics and automation (ICCMA), 193–198. doi:10.1109/ICCMA63715.2024.10843915
Ketchel, J. S., and Larochelle, P. M. (2008). Self-collision detection in spatial closed chains. J. Mech. Des. 130, 092305. doi:10.1115/1.2965363
Khatib, O. (1986). Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robotics Res. 5, 90–98. doi:10.1177/027836498600500106
Larsen, E., Gottschalk, S., Lin, M., and Manocha, D. (2000). “Fast distance queries with rectangular swept sphere volumes,” in Proceedings 2000 ICRA. Millennium conference. IEEE international conference on robotics and automation. Symposia Proceedings (Cat. No.00CH37065), 4, 3719–3726. doi:10.1109/ROBOT.2000.845311
Lee, S., and Moradi, H. (2001). A real-time dual-arm collision avoidance algorithm for assembly. J. Robotic Syst. 18, 477–486. doi:10.1002/rob.1038
Li, Y., Ji, Y., Zhang, L., and Wang, G. (2024a). “Path planning method and control of mobile robot with uncertain dynamics based on improved artificial potential fields,” in 2024 IEEE 14th international conference on CYBER Technology in automation, control, and intelligent systems (CYBER), 523–528. doi:10.1109/CYBER63482.2024.10748726
Li, Y., Song, H., Ji, Y., and Zhang, L. (2024b). Path planning method and control of mobile robot with uncertain dynamics based on improved artificial potential field and its application in health monitoring. Mathematics 12, 2965. doi:10.3390/math12192965
Lin, H.-I., Shodiq, M. A. F., and Hsieh, M. F. (2025). Robot path planning based on three-dimensional artificial potential field. Eng. Appl. Artif. Intell. 144, 110127. doi:10.1016/j.engappai.2025.110127
Liu, Z., Liu, Q., Xu, W., Wang, L., and Zhou, Z. (2022). Robot learning towards smart robotic manufacturing: a review. Robotics Computer-Integrated Manuf. 77, 102360. doi:10.1016/j.rcim.2022.102360
Lumelsky, V. J. (1985). On fast computation of distance between line segments. Inf. Process. Lett. 21, 55–61. doi:10.1016/0020-0190(85)90032-8
Lumelsky, V. J., and Stepanov, A. A. (1987). Path-planning strategies for a point mobile automaton moving amidst unknown obstacles of arbitrary shape. Algorithmica 2, 403–430. doi:10.1007/bf01840369
O’MahonyN.CampbellS.CarvalhoA.HarapanahalliS.VelascoG.KrpalkovaL. (2019). “Deep learning vs. traditional computer vision,” in Science and information conference. (Heidelberg, Germany: Springer), 128–144.
Makris, S. (2021). Cooperative manipulation—the case of dual arm robots. Cham: Springer International Publishing, 123–132. doi:10.1007/978-3-030-51591-1_5
Malvido Fresnillo, P., Vasudevan, S., Mohammed, W. M., Martinez Lastra, J. L., and Perez Garcia, J. A. (2023). Extending the motion planning framework—moveit with advanced manipulation functions for industrial applications. Robotics Computer-Integrated Manuf. 83, 102559. doi:10.1016/j.rcim.2023.102559
Massa, F., and Girshick, R. (2018). Maskrcnn-benchmark: fast, modular reference implementation of instance segmentation and object detection algorithms in PyTorch. Available online at: https://github.com/facebookresearch/maskrcnn-benchmark.
Montaño, A., and Suárez, R. (2016). Coordination of several robots based on temporal synchronization. Robotics Computer-Integrated Manuf. 42, 73–85. doi:10.1016/j.rcim.2016.05.008
Pottmann, H., Wallner, J., Pottmann, H., and Wallner, J. (2001). Computational line geometry, 6. Springer.
Ren, S. (2015). Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural. Inf. Process. Syst. 28.
Rescsanski, S., Hebert, R., Haghighi, A., Tang, J., and Imani, F. (2025). Towards intelligent cooperative robotics in additive manufacturing: Past, present, and future. Robotics Computer-Integrated Manuf. 93, 102925. doi:10.1016/j.rcim.2024.102925
S. K, S. P., Shukla, A., Pandya, N., and Jha, S. S. (2024). “Automated vision-based bolt sorting by manipulator for industrial applications,” in 2024 IEEE 20th international conference on automation science and Engineering (CASE), 3602–3607. doi:10.1109/CASE59546.2024.10711806
Schmidt, B., and Wang, L. (2014). Depth camera based collision avoidance via active robot control. J. Manuf. Syst. 33, 711–718. doi:10.1016/j.jmsy.2014.04.004
Sharma, R., Saqib, M., Lin, C.-T., and Blumenstein, M. (2022). A survey on object instance segmentation. SN Comput. Sci. 3, 499. doi:10.1007/s42979-022-01407-3
Shin, Y., and Bien, Z. (1989). Collision–free trajectory planning for two robot arms. Robotica 7, 205–212. doi:10.1017/s0263574700006068
Smith, C., Karayiannidis, Y., Nalpantidis, L., Gratal, X., Qi, P., Dimarogonas, D. V., et al. (2012). Dual arm manipulation—a survey. Robotics Aut. Syst. 60, 1340–1353. doi:10.1016/j.robot.2012.07.005
Sun, F., Chen, Y., Wu, Y., Li, L., and Ren, X. (2022). Motion planning and cooperative manipulation for mobile robots with dual arms. IEEE Trans. Emerg. Top. Comput. Intell. 6, 1345–1356. doi:10.1109/TETCI.2022.3146387
Tang, S. H., Khaksar, W., Ismail, N., and Ariffin, M. (2012). A review on robot motion planning approaches. Pertanika J. Sci. Technol. 20, 15–29.
Volpe, R., and Khosla, P. (1987). “Artificial potentials with elliptical isopotential contours for obstacle avoidance,” in 26th IEEE conference on decision and control, 26, 180–185. doi:10.1109/CDC.1987.272738
Volpe, R., and Khosla, P. (1990). Manipulator control with superquadric artificial potential functions: theory and experiments. IEEE Trans. Syst. Man, Cybern. 20, 1423–1436. doi:10.1109/21.61211
Wang, W., Zhu, M., Wang, X., He, S., He, J., and Xu, Z. (2018). An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. Int. J. Adv. Robotic Syst. 15, 172988141879956. doi:10.1177/1729881418799562
Wu, Y., Kirillov, A., Massa, F., Lo, W.-Y., and Girshick, R. (2019). Detectron2. Available online at: https://github.com/facebookresearch/detectron2.
Keywords: collision avoidance, motion planning, improved artificial potential field, dual-arm manipulators, industrial automation
Citation: Surya Prakash SK, Prajapati D, Narula B and Shukla A (2025) iAPF: an improved artificial potential field framework for asymmetric dual-arm manipulation with real-time inter-arm collision avoidance. Front. Robot. AI 12:1604506. doi: 10.3389/frobt.2025.1604506
Received: 02 April 2025; Accepted: 15 September 2025;
Published: 28 October 2025.
Edited by:
Rajkumar Muthusamy, Dubai Future Foundation, United Arab EmiratesReviewed by:
Ruthber Rodriguez Serrezuela, Corporación Universitaria del Huila, ColombiaZhongpan Zhu, University of Shanghai for Science and Technology, China
Copyright © 2025 Surya Prakash, Prajapati, Narula and Shukla. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. K. Surya Prakash, cy5zdXJ5YTE3NTRAZ21haWwuY29t; Amit Shukla, YW1pdHNodWtsYUBpaXRtYW5kaS5hYy5pbg==
 S. K. Surya Prakash
S. K. Surya Prakash Darshankumar Prajapati
Darshankumar Prajapati Bhuvan Narula
Bhuvan Narula Amit Shukla
Amit Shukla