Heterogeneity, transient, and persistent technical efficiency: implications for African agrifood systems

This study departs from conventional estimation of technical efficiency by distinguishing between transient and persistent technical efficiency while accounting for heterogeneity to gain insights for transforming agri-food systems in Africa. A four-error component stochastic frontier model with a translog specification, assuming a half-normal distribution, is applied to panel data comprising 980 observations from 49 countries between 2000 and 2019. Our results show that output is significantly explained by land, labor, and capital. In addition, technological innovation, represented by log (t), consistently emerges as a significant driver of output. The heterogeneity analysis reveals that Cameroon, Ghana, South Africa, Egypt, Cote d'Ivoire, Nigeria, Malawi, and Benin exhibit significantly higher output levels. Persistent technical inefficiency is dominant, with significant heterogeneity in agricultural output. Specific interventions to address persistent technical inefficiency in the agrifood system should include strengthening value chains and farm credit markets, stabilizing land reform policies, promoting the adoption of modern technology, and improving governance. Human capital development through training and education could help mitigate transient technical inefficiency. We conclude that a viable strategy for the transformation of agrifood systems in Africa is to clearly differentiate between short-term (transient) and long-term (persistent) policies, tailored to the unique characteristics (heterogeneity) of each country or region. Therefore, the results are crucial given the ongoing implementation of the Comprehensive Africa Agriculture Development Programme and Agenda 2063.

1 Introduction

Agrifood systems (AFS) are defined as coordinated actors and activities involved in the food value chain from field to fork (Govaerts et al., 2021). In a broader sense, these include knowledge, institutions, practices, infrastructure, production, transportation, processing, distribution, marketing, disposal, and consumption. Recently, AFS have received growing research interest throughout the world. For example, the theme for the 32^nd International Conference of Agricultural Economists held in India was “transformation toward sustainable agrifood systems.” A year prior to this, the African Association of Agricultural Economists, along with the Agricultural Economics Association of South Africa, held a joint conference in Durban under the theme “Through Crisis: Building Resilient Agrifood Systems in Africa.” The main reason for the growing attention on AFS is that traditional ways of food production and consumption have produced the climate change crisis, while poverty, hunger, and food and nutrition insecurity continue to grow unabated.

The concept of efficiency was first introduced in the early 1950s by Debreu (1951) and Koopmans (1951). It was further refined by Farrell (1957), who described efficiency as the degree to which the decision-making unit uses input to produce output. Using the non-parametric data envelopment analysis (DEA) approach, which permits multiple inputs and outputs, this researcher also identified two types of efficiency, namely, technical and allocative efficiencies. The former refers to the ability of a firm to obtain maximum output from a given set of inputs, while the latter reflects the ability of a firm to use the inputs in optimal proportions, given their respective prices and the production technology (Coelli et al., 2005). The combination of technical efficiency (TE) and allocative efficiency (AE) yields economic efficiency (EE). After a decade, Aigner et al. (1977) developed a regression-based stochastic frontier analysis (SFA) to estimate efficiency, and these two methods have remained the most commonly used for efficiency analysis. However, the main concern in efficiency analysis within the context of transforming the AFS revolves around a strong emphasis on mix efficiency, short-term (transient) and long-term (persistent) efficiencies (O'Donnell, 2012; Bokusheva et al., 2023). But the study pays attention to transient and persistent technical efficiency.

Extensive literature has been published on the analysis of efficiency in agriculture on a global scale. This includes several reviews (Batiese, 1992; Bravo-Ureta and Pinheiro, 1993; Thiam et al., 2001) and meta-analyses (Bravo-Ureta et al., 2007; Iliyasu et al., 2014; Ogundari and Brümmer, 2011). Within the context of Africa, Thiam et al. (2001) relies on only two studies from the continent, while Bravo-Ureta et al. (2007) considers 14 studies but fails to shed light on agricultural efficiency for the different regions. Ogundari and Brümmer (2011) is restricted to a single African nation. Notwithstanding these drawbacks, the review by Ogundari (2014) remains the most comprehensive examination of agricultural efficiency in Africa and its regions. One of the main findings of this study is that agricultural efficiency estimates derived in different parts of the continent vary according to the methodology applied, type of dataset, geographic location, and study timeframe. Although these reviews have laid a solid foundation for efficiency analysis, they remain silent on transient and persistent technical efficiency and the determinants thereof. However, Berisso and Heshmati (2020) and Adom and Adams (2020) are the few existing studies on transient and persistent technical efficiency. Although both apply SFA on a panel dataset, they are different in terms of study area and remain silent on implications for the transformation of AFS. Our study aims to examine transient and persistent technical efficiency in African agriculture using the four-error component stochastic model, famously known as the Generalized True Random-Effects (GTRE) model, applied to panel data from 49 countries over 19 years. Although we cover the same number of African nations as Adom and Adams (2020), our study extends the time frame by 3 years, providing more recent estimates and allowing the identification of variables that were not previously explored. In addition, this study applies the Bayesian Generalized True Random-Effects (BGTRE) model, incorporating African regional dummy variables as shifters of the production frontier, to draw implications for the transformation of AFS. Classifying technical efficiency into transient and persistent allows for the development of more targeted policies aimed at improving agricultural productivity as part of the broader effort to transform AFS in Africa. The study has one main research question: Is the agriculture sector in Africa transiently or persistently inefficient? The remaining sections are organized as follows. The method, which includes an estimation procedure and data, is discussed in Section 2. The results are presented in Section 3, followed by the conclusion and policy implications in Section 4, and the bibliography in Section 5.

2 Methodology

2.1 Data information and model

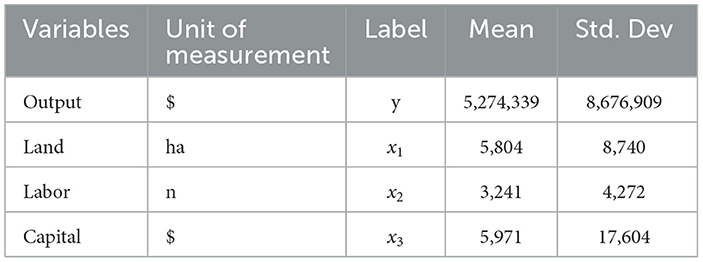
The study considers panel data of 49 countries in Africa from 2000 to 2019. The minute details of data sources, variable information, individual countries, and regions are discussed in Myeki et al. (2022, 2023). However, the overall summary of variables is presented in Table 1 below. It is clear from the table that the study consisted of a single output, the gross value of agricultural output from crops, livestock, and aquaculture, $1,000 at constant 2015 prices. Three input variables were considered: land, labor, and capital. Land is the quality of adjusted agricultural area measured per 1,000 hectares of “rainfed equivalent cropland.” Labor is the number of economically active adults (male and female) who are employed in agriculture, measured per 1,000 persons. While capital is the net capital stock measured in $1,000, taking 2015 as the base. Compared to 2000 to 2004, output grew by an average of 19% in 2005 to 2009, followed by 41% and 61% in subsequent periods. Land grew at an average of 9%, 21%, and 34% over the reported periods, respectively. For labor, the average growth was 11%, 17% and 24% while capital had 19%, 47%, and 83%, respectively. Much of the growth in both output and inputs happened during 2015 to 2019. As can be seen in Table 1, the gross output averaged $5,274,339 (Std. dev = 9,676,909), ranging from 30 024 in Sao Tome and Principe in 2015 to 5,930,633 in Nigeria in 2019. The summary of inputs shows that land averaged 5,808 hectares (8,740) with a range from 37.39 ha in Djibouti in 2006 to 62,459 ha in Nigeria in 2019. On average, 3,241 people were employed in agriculture, ranging from 11.33 in Sao Tome and Principe in 2002 to 21,298 in Nigeria in 2011. On the other hand, capital had an average of 5,971 (17,604) with a range from 4.83 in Djibouti in 2000 to 188,491 in Nigeria in 2019.

Table 1

Table 1. The summary of input-output variables for the study.

It employs the GTRE model by Colombi et al. (2014), Kumbhakar et al. (2014), and Tsionas and Kumbhakar (2014) to estimate transient and persistent inefficiency in the agricultural sector for the continent. The model is expressed as follows:

$\begin{array}{ll}{y}_{it}={\alpha }_0+f(x_{it},t;\beta )+{\mu }_i-{\eta }_i+v_{it}-u_{it},& (1)\end{array}$

where y_it is the dependent variable defined as the logarithm for agricultural output of nation i in period t, α₀ is the intercept, f(x_it, t; β) is the production technology, including a time trend t to account for technological change, x_it is a vector of inputs (in logs), and β is a vector of unknown parameters to be estimated. Additionally, the μ_i represents time-invariant firm-specific latent (unobserved) heterogeneity, η_i denotes the persistent (time-invariant) technical inefficiency, u_it captures transient (time-varying) technical inefficiency, and v_it is a random noise term. The composite error term for the model described in Equation (1) is ε_it = μ_i−h_i+v_it−u_it with ${\mu }_i~\text{N}(0,{\sigma }_{\mu }^2)$; $v_{it}~\text{N}(0,{\sigma }_v^2)$; ${\eta }_i~{\text{N}}^{+}(0,{\sigma }_{\eta }^2)$, and; $u_{it}~{\text{N}}^{+}(0,{\sigma }_u^2)$. Numerous stochastic frontier models are embedded in the GTRE model defined in Equation (1). For instance, dropping both μ_i and η_i leads to a “pooled” model proposed by Aigner et al. (1977), described as follows:

$\begin{array}{ll}{y}_{it}={\alpha }_0+f(x_{it},t;\beta )+v_{it}-u_{it}& (2)\end{array}$

The v_it is a random variable assumed to be identically and independently distributed iid with zero mean and variance ${\sigma }_v^2(v_{it}~\text{N}(0,{\sigma }_v^2))$, assumed to capture the effect of random noise; and u_it is the time-varying non-negative half-normal inefficiency random variable, which is assumed to be iid with zero mean and variance ${\sigma }_u^2(u_{it}~{\text{N}}^{+}(0,{\sigma }_u^2))$. Discarding η_i and u_it from the same model, described by Equation (1), yields the standard panel stochastic frontier model with random effects (RE) developed by Pitt and Lee (1981), expressed in Equation (3). The error specification of this equation is ε_it = v_it−h_i, distributed as $v_{it}~\text{N}(0,{\sigma }_v^2)$ and ${\mu }_i~{\text{N}}^{+}(0,{\sigma }_{\mu }^2)$

$\begin{array}{ll}{y}_{it}={\alpha }_0+f(x_{it},t;\beta )+{\mu }_{it}-v_{it}& (3)\end{array}$

On the other hand, removing η_i alone from Equation (1) leads to Greene (2005a,b)'s true random effect (TRE) model in Equation 4, depending on whether μ_i is correlated with the error term (${\mu }_i~{\text{N}}^{+}(0,{\sigma }_{\mu }^2)$, $v_{it}~\text{N}(0,{\sigma }_v^2)$ and; $u_{it}~{\text{N}}^{+}(0,{\sigma }_u^2)$

$\begin{array}{ll}{y}_{it}={\alpha }_0+f(x_{it},t;\beta )+{\mu }_i+v_{it}-u_{it}& (4)\end{array}$

The study adopted an approach of Filippini and Hunt (2015) and Alberini and Filippini (2018) where the GTRE model and three traditional models described in Equations (2–4) are estimated separately and compared to each other for robustness. Moreover, we also employed the translog functional form based on log-likelihood ratio test results (see Table 2), leading to rejection of the Cobb-Douglass functional form. Thus, the final model is expressed as follows:

$\begin{array}{ll}ln{y}_{it}=\alpha +{\displaystyle \sum _{j=1}^3}{\beta }_{j}ln{x}_{jt}+\frac{1}{2}{\displaystyle \sum _{j=1}^3}{\displaystyle \sum _{k=1}^3}{\beta }_{jk}ln{x}_{jt}ln{x}_{kt}+{\mu }_i-{\eta }_i+v_{it}-u_{it},& (5)\end{array}$

where ln y_it represents the agricultural output of individual nation i in period t while α₀ is the intercept. x_jt represents the three key inputs used to derive agricultural output, and they include land, labor, and capital. β_jt is a vector of unknown parameters to be estimated. The μ_i represents time-invariant firm-specific latent (unobserved) heterogeneity, η_i denotes the persistent (time-invariant) technical inefficiency, u_it captures transient (time-varying) technical inefficiency, and v_it is a random noise term. Models described in Equations (1–5) were implemented using STATA 17 software.

Table 2

Table 2. The summary of diagnostic test for the study.

For confirmatory purposes, we also estimated the GTRE model using Bayesian SFA analysis, where the different sub-regions of Africa were used as shifters of efficiency. Although extended to include panel data analysis by Koop (1994), the Bayesian framework is novel to Van den Broeck et al. (1994). The advantages of the framework include the ability to minimize the loss associated with an estimation error; permit probability statements about unknown parameters, hypotheses, and models; provide exact finite-sample results for most estimation problems; and allow for the ease of incorporating restrictions that allow for a formal treatment of parameters and model uncertainty. Let θ = (θ₁, …, θ_k) denote the unknown parameters of the GTRE model to be estimates p(θ)≡p(β, σ_w, σ_h, σ_v, σ_u) denotes the probability density function (pdf) of prior information for parameters while L(y, X∣θ) is the likelihood function. The posterior distribution follows from Bayes's theorem as follows:

$\begin{array}{ll}p(\theta \mid y,\text{X})\propto L(y,\text{X}\mid \theta )p(\theta ),& (6)\end{array}$

where p(θ∣y, X) is the posterior pdf and ∝ denotes “is proportional to.” Put simply, the posterior pdf is proportional to the likelihood function multiplied by the prior pdf. Thus, the posterior distribution includes all the information on the parameters contained in the prior and the data. The prior pdf p(θ) can be non-informative or informative. The complex models that do not allow inference by analytical methods, implementing the Bayesian approach, require the use of iterative Markov Chain Monte Carlo (MCMC) algorithms such as the Metropolis-Hastings and Gibbs Sampling, which focus on sampling from the conditional distribution for blocks of the parameter vector. The Gibbs Sampler algorithm used by Koop et al. (1992) is particularly useful for problems involving latent variables, such as SFA models, and is commonly used in the literature. The researcher can write their own MCMC algorithms or just specify the model but use the Bayesian inference using Gibbs Sampling (BUGS) software, such as WinBUGS or JAGS, to handle the MCMC sampling. In our study, we used JAGS in R through the “APEAR” package to implement the final BGTRE model, which is expressed below.

$\begin{array}{l}\ln y_{it}=\alpha +{\displaystyle \sum _{j=1}^3{\beta }_j}\ln x_{jt}+\frac{1}{2}{\displaystyle \sum _{j=1}^3{\displaystyle \sum _{k=1}^3{\beta }_{jk}}}\ln x_{jt}\ln x_{kt}\\ +{\displaystyle \sum _{i=1}^4{\beta }_l}{D}_l+{\mu }_i-{\eta }_i+v_{it}-u_{it},& (7)\end{array}$

where i = 1,...., n denotes the i-th country, and t = 1. x_jt is a vector of j-th used inputs normalized by the means. The three inputs used in agricultural output are land, labor, and capital. D_l(l = 1, 2, 3) are regional dummy variables, denoting East Africa, North Africa, West Africa, and Southern Africa, all of which were included for the comparisons for regional performance in terms of transient and persistent technical inefficiency. The α and β are unknown parameters to be estimated. Again, the μ_i represents time-invariant firm-specific latent (unobserved) heterogeneity, η_i denotes the persistent (time-invariant) technical inefficiency, u_it captures transient (time-varying) technical inefficiency, and v_it is a random noise term. We also computed partial output elasticities with respect to inputs with the purpose of examining the sensitivity of output change when a change in inputs occurs. The equation to derive partial elasticities is as follows:

$\begin{array}{ll}{E}_j=\frac{\partial ln{y}_{it}}{\partial ln{x}_{jt}}={\widehat{\beta }}_j+{\widehat{\beta }}_{jj}ln{x}_{jt}+{\displaystyle \sum _{k=1}^3}{\widehat{\beta }}_{jk}ln{x}_{kt},& (8)\end{array}$

where ${\widehat{\beta }}_j,{\widehat{\beta }}_{jj}$ and ${\widehat{\beta }}_{jk}$ are the parameters of the BGTRE model estimated in Equation (7). The returns to scale for this model are computed by summing up the partial output elasticities with respect to inputs, as follows:

$\begin{array}{ll}\text{RTS}={\displaystyle \sum _{j=1}^3}{E}_j& (9)\end{array}$

3 Empirical findings

3.1 Summary of diagnostic tests

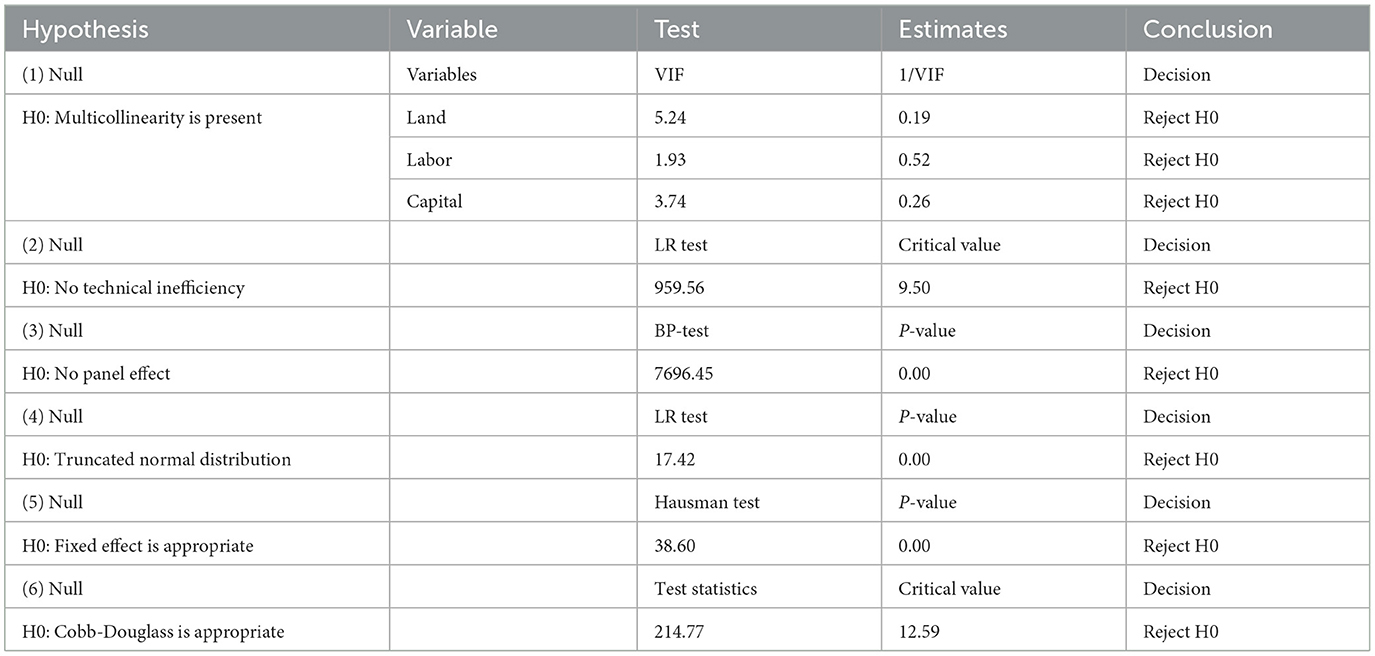
A series of diagnostic tests were performed to ascertain the most appropriate models, and the results are shown in Table 2. Our first null hypothesis was concerned with testing for the presence of multicollinearity. Since the Variance Inflation Factor (VIF) for the three variables is <10, the null hypothesis is rejected, implying that the independent variables are independent of one another. Using the log-likelihood ratio (LR) test, the findings (test statistic = 959.96; critical = 9.50 and df = 1) show that the null hypothesis stating that inefficiency is not present was rejected, thus indicating the presence of inefficiency and the fact that we cannot use the ordinary least squares. Additionally, the panel effect was found to be significant across the dataset, indicating that heterogeneity is significant. This also suggests that we cannot use the pooled model. The assumption of truncated normal distribution for the inefficiency term was rejected using the Breusch-Pagan (BP) test, which suggests that a half-normal distribution is appropriate. This result implies that we could not test if inefficiency varies over time because such a test requires a truncated normal distribution.

Moreover, testing between fixed and random effects models using the Hausman test showed a p-value of zero, indicating that random effects were appropriate. The results in Table 2 further reveal that the translog stochastic frontier model is preferred over the Cobb-Douglas functional form. Although not presented in the table, we also found that variables were stationary while using the Hadri-LM test. Next, we present the results for the translog stochastic frontier models.

3.2 Estimates of translog stochastic frontier model

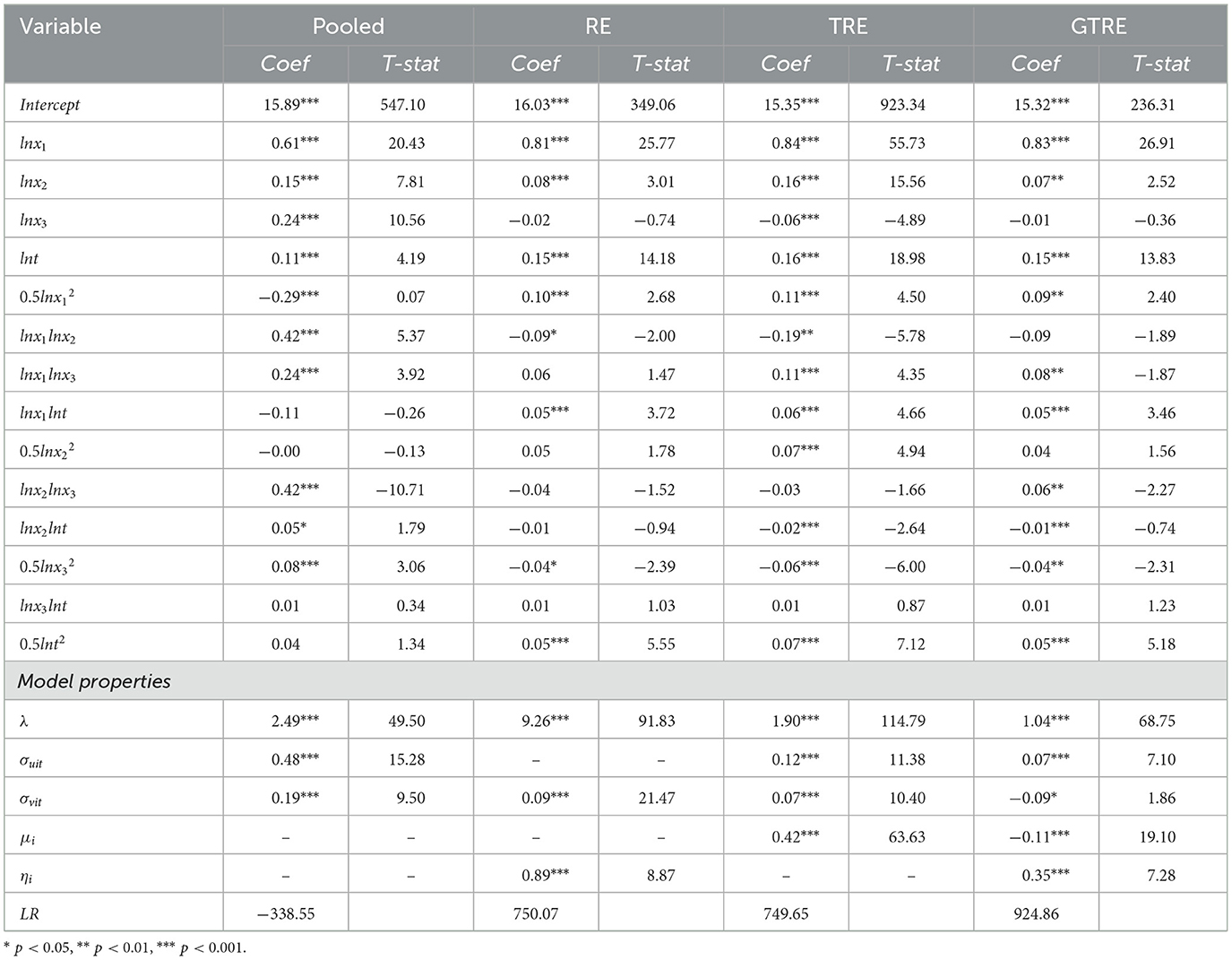
Table 3 presents the parameter estimates for pooled, RE, TRE, and GTRE models. The first three models are nested in the latter. Nonetheless, the coefficient lnt is positive for all estimated models, indicating that agriculture in Africa has experienced technological progress over the study period. The findings suggest that Africa is on the right track in terms of adopting technology to improve agricultural efficiency and productivity. The variables land, labor, and capital are all significant at the 1% level for the pooled and TRE models. This finding was expected because improvement on: (i) land through the application of better fertilizer, (ii) labor through training and education, and (iii) capital through investment in farm machinery and equipment are all highly likely to improve efficiency. Surprisingly, the coefficient for variable capital for RE and GTRE is negative and insignificant, indicating a lack of empirical evidence for the relationship between output and capital for the two models. The coefficient for η is 0.35% and significant in GTRE, suggesting that persistent inefficiency is dominant compared to transient inefficiency (0.07%). This implies that over the study period, agriculture in Africa had an average persistent technical efficiency of 65% and a transient technical efficiency of 93%. The heterogeneity and persistent inefficiency are significant, indicating that the GTRE model is appropriate.

Table 3

Table 3. Summary of translog stochastic production models (N = 980).

3.3 Estimates of Bayesian stochastic frontier model

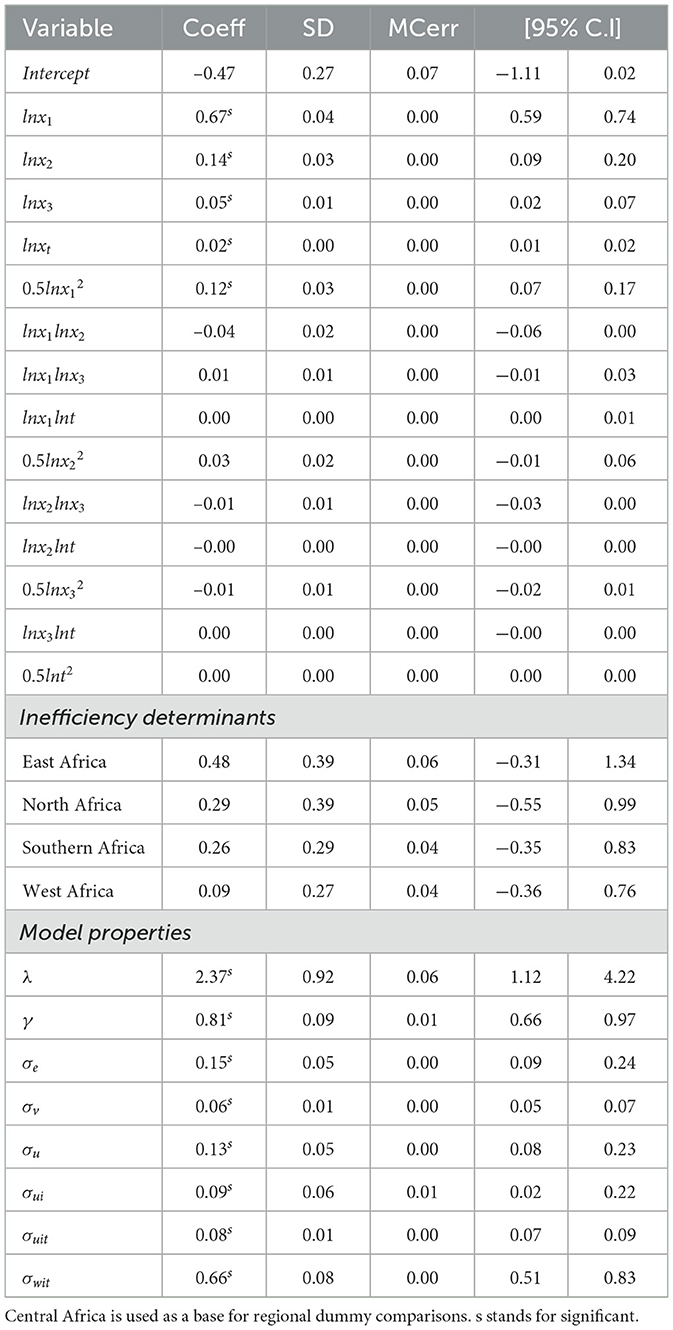
The estimates for the Bayesian stochastic frontier model with translog specification are shown in Table 4. The Gibbs sampler was run for one chain, with a burn-in of 200,000 iterations, 10,000 retained draws, and a thinning to every 40th draw in order to reduce the level of autocorrelation of the chain. This table clearly shows that a percentage increase in any of the inputs leads to an increase in agricultural productivity in Africa. For instance, with each unit increase in agricultural land allocated in Africa, output increases by 0.67%, and this increase falls within the 95% posterior probability interval (0.60%, 0.74%). A unit increase in labor leads to a 0.14% increase in output. In addition, this increase falls in a 0.09% to 0.20% interval with 95% posterior probability. On the other hand, the coefficient for t is 0.02 and positive, indicating technological progress over the study period. These findings are significant, as shown by the same sign for the values of the confidence interval. However, the agricultural output has been more responsive to changes in land compared to labor. On the other hand, a unit increase in capital is associated with a 0.04% increase in output, and this falls in the 0.02% to 0.07% interval with 95% posterior probability. These findings correspond to those discussed earlier in Table 2 and suggest that production behaves well and meets the monotonicity assumption. The results also imply that countries can continue to increase their input levels until any increase in input yields no additional output. The results further reveal that the Monte Carlo (MC) error is lower than the corresponding posterior standard deviation, suggesting convergence of the model and accuracy of estimates. However, if evidence of significance was present, the result would suggest that East Africa is 0.47% more productive compared to Central Africa, while North Africa, Southern Africa, and West Africa are more productive by 0.29%, 0.26%, and 0.10%, respectively. The coefficient for gamma (γ) is significant and positive, indicating that 0.81% of the variation in agricultural output among the African nations is attributed to the variations in technical efficiency. The value of lambda (λ), gives information about the inefficiency level of the agriculture sector. Put in simple terms, it shows by how much an African country has fallen short of the total output. Similarly to Table 2, the persistent technical inefficiency (σ_ui) is dominant at 0.10%, while transient inefficiency (σ_uit) was at 0.08%.

Table 4

Table 4. Bayesian estimates of translog stochastic frontier (N = 980).

With respect to the results of Equation (9), the value of returns to scale for BGTRE is 0.86, indicating that agricultural production in Africa achieved a decreasing return to scale over the study period. This value is slightly higher by 0.07 compared to that of the GTRE model at 0.79. It suggests that the proportion of output is less than the desired increased inputs during the production process. We found that agricultural output is more responsive to land and labor use. More details of elasticity estimates for each country are presented in Appendix Table 6.

3.4 Estimates of inefficiency and heterogeneity

In this section, we present the results for various efficiencies, beginning with those models discussed in Table 3. The pooled model yielded an average efficiency (transient efficiency) score of 0.69%, ranging from 0.22% to 0.93%, while RE had an average (persistent efficiency) score of 0.50% with a range from 0.17% to 0.98%. The TRE model produced an average efficiency score of 0.89, implying room for improving efficiency by 11% without changing the input and current technology. The main model (GTRE) yielded averages of 0.73% and 0.93% for persistent and transient efficiencies, respectively, leading to an overall average efficiency score of 0.68%. This suggests that persistent efficiency has less contribution to the overall efficiency of the agricultural sector in Africa over the study period (see Figure 1). The efficiency estimates of the Bayesian stochastic frontier reveal an overall average efficiency of 0.84%, ranging from 0.52% to 0.91%. However, there is a slight difference between transient and persistent efficiency, showing that transient efficiency dominates by 1%. Nonetheless, further details of efficiency scores obtained from BGTRE for each sampled African nation over the study period are presented in Appendix Table 5. The results for heterogeneity in Appendix Table 7 show that Cameroon, Ghana, South Africa, Egypt, Cote d'Ivoire, Nigeria, Malawi, and Benin have significantly large agricultural outputs. On the other hand, Libya, Niger, Cape Verde, Sao Tome, and Principe, Comoros, Equatorial Guinea and Djibouti had significantly low agricultural output.

Figure 1

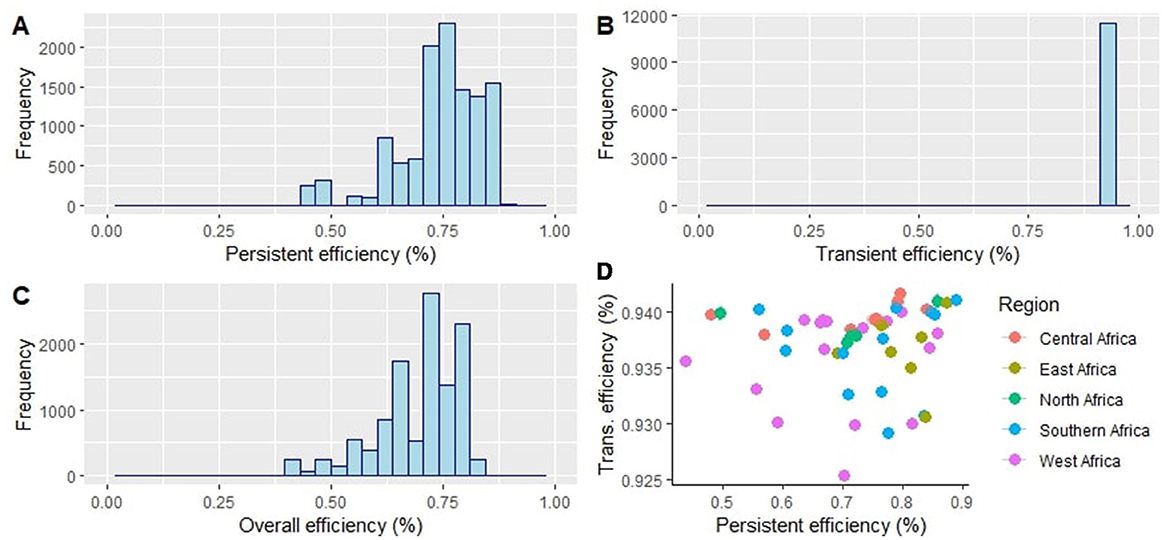
Figure 1. Efficiency score from GTRE model depicted in four panels. (A–C) Depict persistent, transient and overall efficiency for the continent while (D) shows persistent efficiency for African regions.

4 Discussion and implications for African agrifood systems

The study aimed to examine heterogeneity and transient and persistent technical inefficiency to draw lessons for the transformation of AFS in Africa. The main finding to emerge from the study is that persistent inefficiency was dominant in agriculture on the continent. This was also evident for most of the sampled countries. These findings correspond to Adom and Adams (2020) reporting that persistent technical inefficiency constrained the overall efficiency of the sector on the continent for 49 nations from 1990 to 2016. It suggests that the remaining inefficiency is driven by short-term (transient) agrifood system inefficiency. Moreover, country or regional characteristics (such as resource endowments, infrastructure, value chains, and institutions) appear to influence the transformation and efficiency of AFS.

Another important finding is that both GTRE and BGTRE have consistently shown progress in resolving transient technical inefficiency for the continent over the study period. These findings corroborate Myeki et al. (2022), who established that short-term (transient) technical efficiency was the main driver of productivity in Africa for the first 16 years of the 21st century while using the DEA method on panel data from 49 countries to derive Fare-Primont TFP estimates. The finding implies that investment in education and training in conjunction with technology innovation could increase the resilience and sustainability of agrifood systems in the face of shocks such as COVID-19, pest infestations, trade restrictions, changing diets and customer preferences, wars, and extreme weather events.

The results for the coefficient on both land and labor for the same models (GTRE and BGTRE) match those of Singvejsakul et al. (2021), who employ the Bayesian stochastic frontier to analyze agriculture productivity and efficiency in four Asian countries over a period of 29 years. However, this finding suggests that part of the effort to transform AFS should involve a coordinated reform, prioritizing the relationship between land, labor, and food systems. Nonetheless, the returns to scale of 0.79 in Table 2 and 0.86 in Table 3 are contrary to the value obtained by Pisulewski and Marzec (2019) at 1.16, exhibiting increasing returns to scale in Polish farmers. However, they are almost similar to Berisso (2019) who report a value of 0.71 while studying heterogeneity, persistent and transient efficiency for cereal farms in Ethiopia. A possible explanation for this result could be the law of diminishing returns. However, taken together, these have serious implications for the transformation of agrifood systems in the African continent.

5 Conclusion

In view of the ongoing effort to transform AFS in Africa by increasing productive efficiency in agriculture as one possible strategy, the study was designed to estimate both transient and persistent technical efficiency for policy guidance. Balanced panel data from 49 countries were applied using a four-error component stochastic frontier model with a translog specification. The heterogeneity results show that Cameroon, Ghana, South Africa, Egypt, Cote d'Ivoire, Nigeria, Malawi, and Benin have significantly large agricultural outputs. Regarding the nature of technical inefficiency in African agriculture, our findings demonstrate the predominance of long-term (persistent), which appears to stem from country- or region-specific structural challenges. This leads to our first policy recommendation: the continent must develop a long-term strategy for comprehensive agricultural transformation that takes into account country-specific characteristics to improve persistent efficiency. This plan could include, among other things, vertical integration, agro-processing, and infrastructure development. The study also discovered a small room for improvement in transient efficiency, which can be addressed by focusing on managerial issues, extension service programs, and training to enhance the adoption of modern technologies.

Given that land and labor are more responsive to increases in output, a comprehensive and stable land reform policy, along with adherence to decent work standards, is crucial for the transformation of AFS in Africa. These policy measures are likely to enhance productivity, promote economic growth, and strengthen food security across the continent. Future studies should expand the time frame of our study and focus on/(in)efficiency.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LM: Conceptualization, Data curation, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. NM: Writing – review & editing. YB: Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The publication fee for this research was co-funded by both North West University and the University of the Free State.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2025.1505465/full#supplementary-material

References

Adom, P. K., and Adams, S. (2020). Decomposition of technical efficiency in agricultural production in Africa into transient and persistent technical efficiency under heterogeneous technologies. World Dev. 129:104907. doi: 10.1016/j.worlddev.2020.104907

Crossref Full Text | Google Scholar

Aigner, D., Lovell, C. K., and Schmidt, P. (1977). Formulation and estimation of stochastic frontier production function models. J. Econom. 6, 21–37. doi: 10.1016/0304-4076(77)90052-5

Crossref Full Text | Google Scholar

Alberini, A., and Filippini, M. (2018). Transient and persistent energy efficiency in the US residential sector: evidence from household-level data. Energy Effic. 11, 589–601. doi: 10.1007/s12053-017-9599-z

Crossref Full Text | Google Scholar

Batiese, G. E. (1992). Frontier production functions and technical efficiency: a survey of empirical applications in agricultural economics. Agric. Econ. 7, 185–208. doi: 10.1111/j.1574-0862.1992.tb00213.x

Crossref Full Text | Google Scholar

Berisso, O. (2019). “Analysis of factors affecting persistent and transient inefficiency of Ethiopia's smallholder cereal farming,” in Efficiency, Equity and Well-Being in Selected African Countries, 199–228. doi: 10.1007/978-3-030-11419-0_10

Crossref Full Text | Google Scholar

Berisso, O., and Heshmati, A. (2020). Farm-heterogeneity and persistent and transient productive efficiencies in Ethiopia's smallholder cereal farming. IZA J. Dev. Migr. 11:18. doi: 10.2478/izajodm-2020-0018

Crossref Full Text | Google Scholar

Bokusheva, R., Čechura, L., and Kumbhakar, S. C. (2023). Estimating persistent and transient technical efficiency and their determinants in the presence of heterogeneity and endogeneity. J. Agric. Econ. 74, 450–472. doi: 10.1111/1477-9552.12512

Crossref Full Text | Google Scholar

Bravo-Ureta, B. E., and Pinheiro, A. E. (1993). Efficiency analysis of developing country agriculture: a review of the frontier function literature. Agric. Resour. Econ. Rev. 22, 88–101. doi: 10.1017/S1068280500000320

Crossref Full Text | Google Scholar

Bravo-Ureta, B. E., Solís, D., Moreira López, V. H., Maripani, J. F., Thiam, A., and Rivas, T. (2007). Technical efficiency in farming: a meta-regression analysis. J. Product. Anal. 27, 57–72. doi: 10.1007/s11123-006-0025-3

Crossref Full Text | Google Scholar

Coelli, T. J., Prasada Rao, D., O'Donnell, C. J., and Battese, G. E. (2005). “Stochastic frontier analysis,” in An Introduction to Efficiency and Productivity Analysis, 241–261.

Google Scholar

Colombi, R., Kumbhakar, S. C., Martini, G., and Vittadini, G. (2014). Closed-skew normality in stochastic frontiers with individual effects and long/short-run efficiency. J. Product. Anal. 42, 123–136. doi: 10.1007/s11123-014-0386-y

Crossref Full Text | Google Scholar

Debreu, G. (1951). The coefficient of resource utilization. Econometrica 19, 273–292. doi: 10.2307/1906814

Crossref Full Text | Google Scholar

Farrell, M. J. (1957). The measurement of productive efficiency. J. R. Stat. Soc. 120, 253–281. doi: 10.2307/2343100

Crossref Full Text | Google Scholar

Filippini, M., and Hunt, L. C. (2015). Measurement of energy efficiency based on economic foundations. Energy Econ. 52, S5–S16. doi: 10.1016/j.eneco.2015.08.023

Crossref Full Text | Google Scholar

Govaerts, B., Negra, C., Camacho Villa, T. C., Chavez Suarez, X., Espinosa, A. D., Fonteyne, S., et al. (2021). One cgiar and the integrated agri-food systems initiative: from short-termism to transformation of the world's food systems. PLoS ONE 16:e0252832. doi: 10.1371/journal.pone.0252832

PubMed Abstract | Crossref Full Text | Google Scholar

Greene, W. (2005a). Fixed and random effects in stochastic frontier models. J. Product. Anal. 23, 7–32. doi: 10.1007/s11123-004-8545-1

Crossref Full Text | Google Scholar

Greene, W. (2005b). Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 126, 269–303. doi: 10.1016/j.jeconom.2004.05.003

Crossref Full Text | Google Scholar

Iliyasu, A., Mohamed, Z. A., Ismail, M. M., and Abdullah, A. M. (2014). A meta-analysis of technical efficiency in aquaculture. J. Appl. Aquac. 26, 329–339. doi: 10.1080/10454438.2014.959829

Crossref Full Text | Google Scholar

Koop, G. (1994). Recent progress in applied Bayesian econometrics. J. Econ. Surv. 8, 1–34. doi: 10.1111/j.1467-6419.1994.tb00173.x

Crossref Full Text | Google Scholar

Koop, G., Steel, M. F., and Osiewalski, J. (1992). Posterior analysis of stochastic frontier models using gibbs sampling. Working Paper 92–45 31, Universidad Carlos III de Madrid, Madrid.

Google Scholar

Koopmans, T. C. (1951). Efficient allocation of resources. Econometrica 19, 455–465. doi: 10.2307/1907467

Crossref Full Text | Google Scholar

Kumbhakar, S. C., Lien, G., and Hardaker, J. B. (2014). Technical efficiency in competing panel data models: a study of Norwegian grain farming. J. Product. Anal. 41, 321–337. doi: 10.1007/s11123-012-0303-1

Crossref Full Text | Google Scholar

Myeki, L. W., Bahta, Y. T., and Matthews, N. (2022). Exploring the growth of agricultural productivity in Africa: a färe-primont index approach. Agriculture 12:1236. doi: 10.3390/agriculture12081236

Crossref Full Text | Google Scholar

Myeki, L. W., Matthews, N., and Bahta, Y. T. (2023). Decomposition of green agriculture productivity for policy in Africa: an application of global Malmquist-Luenberger index. Sustainability 15:1645. doi: 10.3390/su15021645

Crossref Full Text | Google Scholar

O'Donnell, C. J. (2012). An aggregate quantity framework for measuring and decomposing productivity change. J. Product. Anal. 38, 255–272. doi: 10.1007/s11123-012-0275-1

Crossref Full Text | Google Scholar

Ogundari, K. (2014). The paradigm of agricultural efficiency and its implication on food security in Africa: what does meta-analysis reveal? World Dev. 64, 690–702. doi: 10.1016/j.worlddev.2014.07.005

Crossref Full Text | Google Scholar

Ogundari, K., and Brümmer, B. (2011). Technical efficiency of Nigerian agriculture: a meta-regression analysis. Outlook Agric. 40, 171–180. doi: 10.5367/oa.2011.0038

Crossref Full Text | Google Scholar

Pisulewski, A., and Marzec, J. (2019). Heterogeneity, transient and persistent technical efficiency of polish crop farms. Spanish J. Agric. Res. 17:6. doi: 10.5424/sjar/2019171-13926

Crossref Full Text | Google Scholar

Pitt, M. M., and Lee, L.-F. (1981). The measurement and sources of technical inefficiency in the Indonesian weaving industry. J. Dev. Econ. 9, 43–64. doi: 10.1016/0304-3878(81)90004-3

Crossref Full Text | Google Scholar

Singvejsakul, J., Intapan, C., Chaiboonsri, C., and Permsiri, R. (2021). Bayesian stochastic frontier analysis of agricultural productivity efficiency in CLMV. J. Phys. 1936:012006. doi: 10.1088/1742-6596/1936/1/012006

Crossref Full Text | Google Scholar

Thiam, A., Bravo-Ureta, B. E., and Rivas, T. E. (2001). Technical efficiency in developing country agriculture: a meta-analysis. Agric. Econ. 25, 235–243. doi: 10.1111/j.1574-0862.2001.tb00204.x

Crossref Full Text | Google Scholar

Tsionas, E. G., and Kumbhakar, S. C. (2014). Firm heterogeneity, persistent and transient technical inefficiency: a generalized true random-effects model. J. Appl. Econ. 29, 110–132. doi: 10.1002/jae.2300

Crossref Full Text | Google Scholar

Van den Broeck, J., Koop, G., Osiewalski, J., and Steel, M. F. (1994). Stochastic frontier models: a Bayesian perspective. J. Econom. 61, 273–303. doi: 10.1016/0304-4076(94)90087-6

Crossref Full Text | Google Scholar