- 1Southern Power Grid Research Institute Co., Ltd., Guangzhou, China
- 2Power Dispatch Control Center of Guangdong Power Grid Co., Ltd., Guangzhou, China
With the increase in the integration of renewable sources, the home energy management system (HEMS) has become a promising approach to improve grid energy efficiency and relieve network stress. In this context, this paper proposes an optimization dispatching strategy for HEMS to reduce total cost with full consideration of uncertainties, while ensuring the users’ comfort. Firstly, a HEMS dispatching model is constructed to reasonably schedule the start/stop time of the dispatchable appliances and energy storage system to minimize the total cost for home users. Besides, this dispatching strategy also controls the switching time of temperature-controlled load such as air conditioning to reduce the energy consumption while maintaining the indoor temperature in a comfortable level. Then, the optimal dispatching problem of HEMS is modeled as a Markov decision process (MDP) and solved by a deep reinforcement learning algorithm called deep deterministic policy gradient. The example results verify the effectiveness and superiority of the proposed method. The energy cost can be effectively reduced by 21.9% at least compared with other benchmarks and the indoor temperature can be well maintained.
1 Introduction
1.1 Background
The rapid increase in population growth and energy consumption has brought about many environmental problems such as global warming (Weil et al., 2023) and energy crisis (Hafeez et al., 2020a). Among all energy consumption, household energy consumption is an important component (Zhang et al., 2023). To optimize the energy structure of households and reduce energy consumption, energy consuming equipment such as rooftop photovoltaics (PV), heat pumps, electric vehicle (EV), and batteries have been widely promoted. With the rapid increase in the number of distributed PV (Li et al., 2024) and EVs (Yin and Qin, 2022), home energy system management (HEMS) has become the most important aspect of achieving demand-side energy management in smart grids (Hafeez et al., 2021; Huy et al., 2023). The HEMS can make decisions for demand response based on current electricity prices, predicted photovoltaic output, user preferences, and device characteristics, achieving intelligent scheduling of home equipment and reducing electricity costs (Kikusato et al., 2019; Gomes et al., 2023). The HEMS is a key component in achieving zero-energy homes and has the potential for widespread application in residential distribution systems. The scheduling strategies used in HEMS mainly include real-time energy allocation, day ahead scheduling, and closed-loop energy management. Among them, day ahead scheduling can reduce computational complexity and improve computational efficiency, which is widely accepted and applied (Ren et al., 2024).
1.2 Related works
There are lots of related work have been conducted based on HEMS. Liu et al. in (Liu et al., 2022) proposes a HEMS for residential users that incorporates the uncertainty of data-driven results to achieve the best trade-off between electricity cost and the preference level. Tostada-Veliz et al. in (Tostado-Véliz et al., 2022) develops a HEMS that includes three novel demand response routines focused on peak clipping and demand flattening strategies. Chakir et al. in (Chakir et al., 2022) propose a management system for a future household equipped with controllable electric loads and an electric vehicle equipped with a PV–Wind–Battery hybrid renewable system connected to the national grid. However, these studies only consider the dispatch strategy of single type of load, which may not in line with real usage scenarios. In the real home energy system, there are multi-types of loads, such as dispatchable load and non-dispatchable load, all these types loads should be considered in the constructed system. To this end, Rehman et al. in (ur Rehman et al., 2022) proposed a holistic method to optimize the use of different types of home appliances according to the prosumers preferences and defined schedule. Dorahaki et al. in (Dorahaki et al., 2022) presents develop a behavioral home energy management model based on time-driven prospect theory incorporating energy storage devices, distributed energy resources, and smart flexible home appliances, which considers the dispatch of different types of appliances. Nezhad et al. in (Esmaeel Nezhad et al., 2021) proposes a new model for the self-scheduling problem using a home energy management system (HEMS), considering the presence of different types of loads, such as an air conditioner and EV. When temperature-controlled load such as air conditioner contained in the HEMS, the users’ comfort should be considered in the dispatch strategy. Song et al. in (Song et al., 2022) presents an intelligent HEMS with three adjustable strategies to maximize economic benefits and consumers’ comfort. Youssef et al. in (Youssef et al., 2024) proposes strategies that are evaluated in terms of consumer comfort, and cost, with waiting time used to assess user comfort. Once the users’ comfort is taken into account, the single objective optimization will change into a multi-objective optimization. It is difficult and important to balance performance of different objectives to obtain the optimal dispatch strategy in the multi-objective optimization. To this end, several studies (Ullah et al., 2021; Alzahrani et al., 2023) are proposed for tackling this problem.
Then, how to obtain the optimal dispatch strategy of the HEMS is a crucial problem (Xiong et al., 2024). Normally, the optimization-based methods such as stochastic programming method (SP) (Hussain et al., 2023) and robust optimization method (RO) (Wang et al., 2024) are utilized to solve the optimization problem of HEMS. Tostado et al. in (Tostado-Véliz et al., 2023a) develops a novel SP-based home energy management model considering negawatt trading. Kim et al. in (Kim et al., 2023) proposes an SP-based algorithm to reduce computation time while preserving the stochastic properties of generated scenarios based on the Wasserstein-1 distance. Nevertheless, the SP-based method requires both vast computational ability and accurate distribution of random variables that may not be realized in practice (Xiong et al., 2023a). In this context, the RO-based methods are widely applied. Tostado et al. in (Tostado-Véliz et al., 2023b) proposes a fully robust home energy management model, which accounts for all the inherent uncertainties that may arise in domestic installations. Wang et al. in (Wang et al., 2024) proposes a multi-objective two-stage robust optimization to address the inherent uncertainty of DES, aiming to concurrently realize energy savings, carbon emission reduction, and load smoothing. However, the optimization results calculated by RO method are usually conservative and utilize only one dispatch solution to deal with all uncertainties of whole dispatch period. To this end, the learning-based methods have been utilized to solve this problem (Hafeez et al., 2020b; Ben Slama and Mahmoud, 2023; Ren et al., 2024).
To bridge these gaps, this paper proposes an optimized scheduling model for home energy management to minimize the electricity cost with consideration of users’ comfort. Then, a novel deep reinforcement learning (DRL) based algorithm is utilized to deal with the uncertainties. The main contributions of this paper are summarized as follows:
1) This paper develops an optimized scheduling model for home energy management to schedule both interruptible load and uninterruptible load, which takes consideration of time-of-use price and users’ comfort. Different from the Refs. (Chakir et al., 2022; Tostado-Véliz et al., 2022), The optimized strategy for scheduling multi types of loads based on the time-of-use electricity price and real-time energy storage system charging status, which can reduce user electricity costs while ensuring users’ comfort.
2) The optimization problem of the HEMS is modeled as a Markov decision process (MDP) and then solved by deep deterministic policy gradient (DDPG) algorithm. Moreover, compared with the optimization-based methods in Refs. (Hussain et al., 2023; Wang et al., 2024; Xiong et al., 2024), the applied DDPG method can achieve fast decision making since the learned policy can be generalized to other situations without resolving the optimization model after the agent is trained.
The following sections are organized: The proposed system is described in detail in Section 2. The mathematical modeling and optimization algorithm are discussed in Section 3. Section 4 presents and analyzes the simulation results obtained for the proposed system. The paper concludes in Section 5.
2 System model
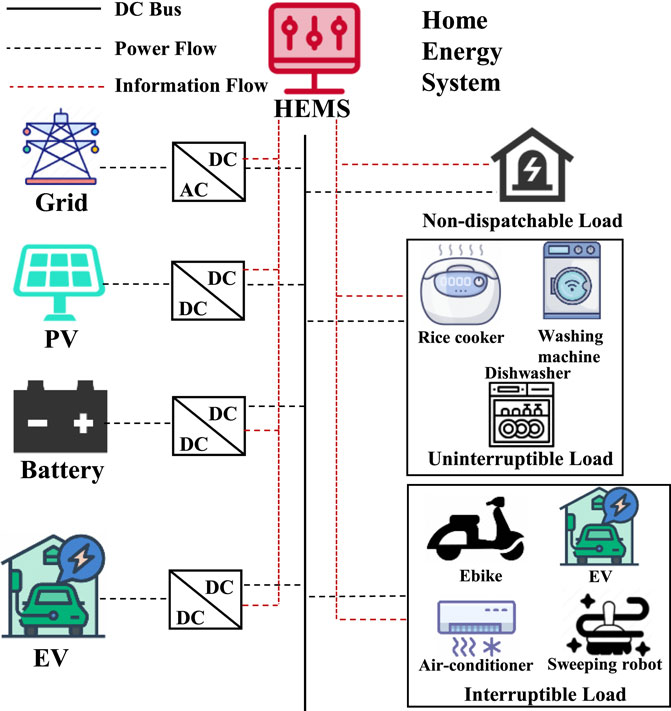
The modelled HEMS architecture is shown in Figure 1. It can be obtained that the constructed system includes HEMS, PV, energy storage and different types of loads. Note that the load can be divided into dispatchable load and non-dispatchable load. Besides, the dispatchable can be further divided into interruptible load and uninterruptible load, which are specifically shown in the Figure 1. The HEMS updates electricity prices, weather, and other information in real time. The HEMS controller is the core component of the entire system, which collects information from upper-level suppliers such as daily electricity prices and household load usage preferences, and calculates the most economical scheduling strategy based on various constraints. In this paper, the HEMS is modelled as a DRL agent for improving the control efficiency.
2.1 PV model
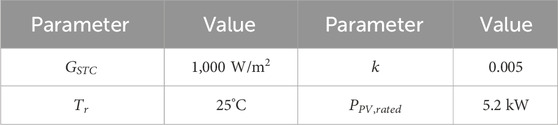
To construct the model of PV, temperature and light radiation intensity are the key factors for determining the output of PV (Xiong et al., 2023b). These factors can be represented in the following model:
where
2.2 Load model
The household electricity load can be divided into dispatchable load, non-dispatchable load, and temperature-controlled load based on the degree of controllability (Hafeez et al., 2020c).
2.2.1 Non-dispatchable load
The non-dispatchable load refers to a load does not adjust operating power or operating time, such as lighting fixtures, televisions, etc. Thus, the non-dispatchable load does not participate in scheduling, but is directly incorporated into the total energy consumption as an important load.
2.2.2 Dispatchable load
Dispatchable load refers to the load with certain elasticity time, which can participate in system dispatching, such as sweeping robots, dryers and other equipment. Dispatchable load can only be started and stopped within the specified operation time, and all other times are closed. The specific constraints are as follows:
where
Furthermore, the dispatchable load can be divided into interruptible load and uninterruptible load. The interruptible load can be modelled as:
where the subscript in represents interruptible flexible loads;
The mathematical model for uninterruptible flexible loads is:
where the subscript un represents uninterruptible loads; τ is the time node. Eq. 4 indicates that if device i starts working at time τ+1, it must continue working for at least
2.2.3 Temperature-controlled load
Temperature-controlled load refers to household equipment with indirect energy storage characteristics, such as air conditioning. The comfort index for residents in this paper is indoor temperature, so the following constraints need to be met (Dongdong, 2020):
where
Due to changes in outdoor temperature, it is not possible to directly set the rated operating time of the air conditioner. Its thermo-dynamic model and working time model can be expressed as:
where
2.3 Battery model
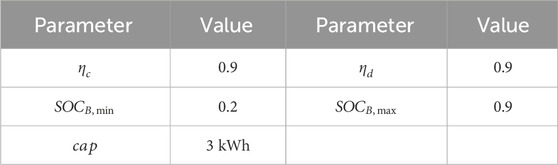
Energy storage devices participate in scheduling through charging and discharging, balancing power fluctuations and improving system flexibility. This article reflects the remaining capacity of energy storage devices through the State of Charge (SOC), which can be expressed as:
where
2.4 Problem formulation
To meet the power balance needs of household residents and the demand for excess photovoltaic power grid, HEMS needs to interact with the power grid for energy exchange, which can be expressed as:
where
This paper aims to minimize the total cost with consideration of comfort, so the optimization objective can be formulated as:
Where
3 Applied deep reinforcement learning algorithm
In this paper, a novel DRL algorithm called deep deterministic policy gradient (DDPG) is applied to solve the optimization problem for improving the solving efficiency (Shi et al., 2023).
3.1 Formulate the optimization problem as an MDP
When applying the DRL algorithm, the optimization problem should first be modeled as a Markov Decision Process (MDP), which can be expressed as follows:
State set S: the state set is composed of the state of agent at each time-step t, which can be represents
where
Action set A: the action set is composed of the action of agent at each time-step t, which can be represents
where
Reward function R: The reward at time t
Transition Probability P: once the current information (such as
3.2 Applied the DDPG algorithm to solve the MDP
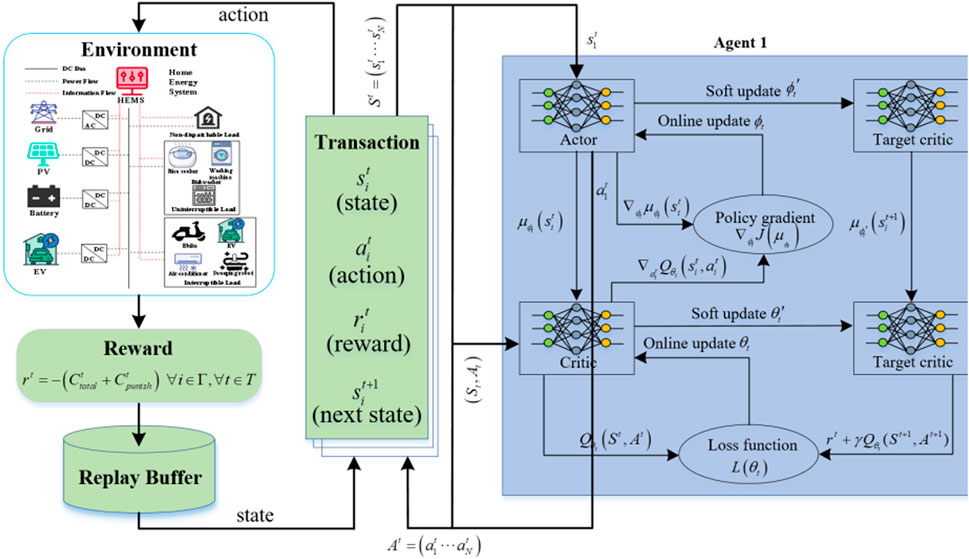
Then, the modeled MDP can be solved by proposed DDPG algorithm to obtain the optimal dispatch strategy, which is illustrated in Figure 2. The DDPG algorithm, as an advanced deep reinforcement learning algorithm, is very suitable for solving complex multidimensional optimization problems in continuous action spaces (Zheng et al., 2023). In the DDPG algorithm, the policy function maps the state to the expected output, while the critical function maps the state and action to the expected maximum output Rt, which maximizes the action value function Qπ(st, at). The calculation formula for the action value function Qπ(st, at) is as follows:
The DDPG algorithm is based on the actor critic framework, which consists of two main parts (actor network and critic network), with each part containing two networks (i.e., the main network and the target network). The actor network adjusts the value of the parameters θμ in the policy function μ(s|θμ) by fitting the current state to the corresponding actions. The critic network is used to adjust the value of the parameters θQ in the action-value function Q (s,a|θQ).
The parameters θQ in the critic network are updated by minimizing the value of the loss function ✓(θQ), which is expressed as follows:
where
In the actor network, the parameters θμ are updated through the policy gradient function as follows:
where ρ represents the discount factor; β represents the specific strategy corresponding to the current policy π.
In order to improve the stability and reliability of the learning process of the DDPG algorithm, two different target networks are added to the actor network and the critic network, respectively. They are the target actor network μ' (s|θμ') and the target critic network Q' (s, a|θQ'). In each iteration, the weight factors (θμ' and θQ') will be soft updated according to the following formulas:
where τ represents the soft update coefficient, and τ<< 1.
The specific training process of the proposed algorithm is described in Algorithm 1, which is shown as below:
Algorithm 1.Training procedures of proposed DDPG method.
1: Input: states of agent
2: Output: action of agent
3: Initialize: the weights of actor and critic networks
4: for episode = 1 to max episode do
5: Initialize Environment
6: for time step = 1 to max step do
7: Select action
8: Execute the actions and obtain the reward
9: Store the transition pair
10: end for
11: If time step >= update step do
12: Sample a mini-batch transition from the replay buffer.
13: Minimize the loss function to update the weights of critic network
14: Update the weights of actor network
15: Update the weights of target networks based on Eq. 22.
16: end if
17: end for
4 Cased study
4.1 Case setting
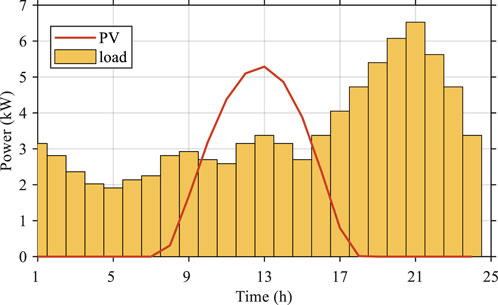
To verify the effectiveness of the proposed method, a smart home energy system is constructed. The simulation period is set as 1 day with 24 h from 00:00–24:00. There are six dispatchable devices in the home, which are shown in the Table 3. Note that the superscript “*” in the first column of Table 1 indicates the household appliance is an uninterrupted load. The PV generation and non-dispatchable load are shown in the Figure 3. The capacity of battery is 3 kWh, while the charging/discharging efficiency is 0.95. The minimum and maximum of the state of charge
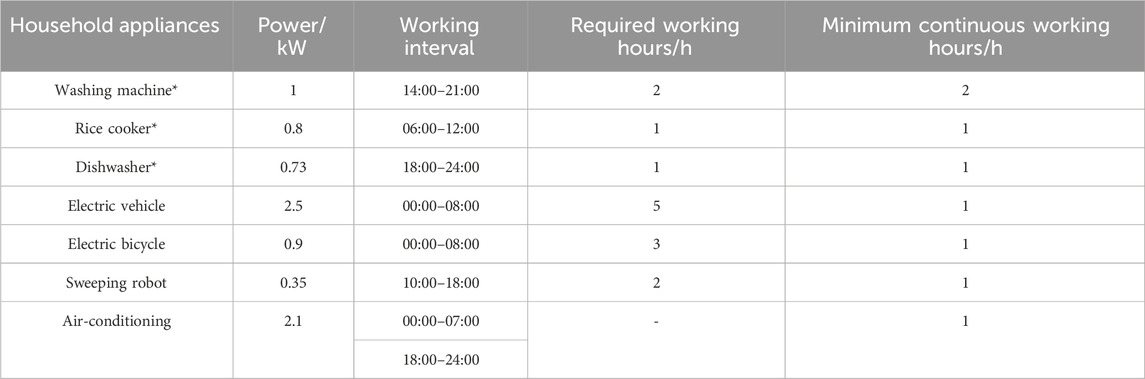
Table 3. Parameters of dispatchable load (WU et al., 2019).
4.2 Optimization results obtained by the applied DDPG method
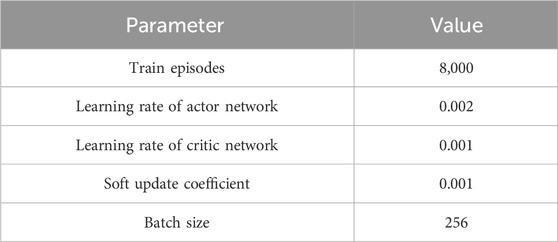
To obtain the optimal dispatch strategy of HEMS, the DDPG algorithm is applied. The hyper-parameters of the agent are set as the Table 4 shown. The total training episodes is 8,000 for ensuring convergence of agent. Besides, the learning rate of actor and critic network are set as 0.002 and 0.001 for ensuring the exploring ability and decision-making ability, respectively. The soft update coefficient and batch size are set as 0.001 and 256 to stable the training process.
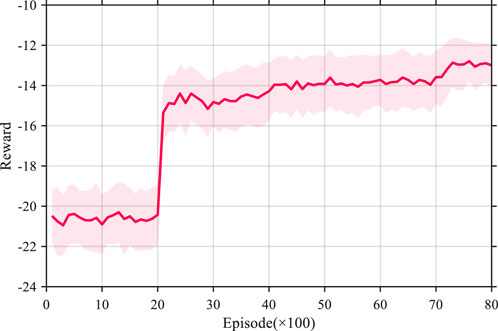
At each episode, the agent gets current state from the constructed home energy system, and then give the decided action back. The changes of reward of the applied DRL method during the whole training episodes is illustrated in the Figure 4. It can be obtained that the reward stays in a low range with an average value −21 in the first 2000 episodes, which indicates that the agent cannot finds the optimal policy for HMS dispatching. Then, the reward rises gradually to −14 and then converges to −13 after the ceaseless interaction between agents and environment, which means the agent can obtain better strategy for dispatching the system.
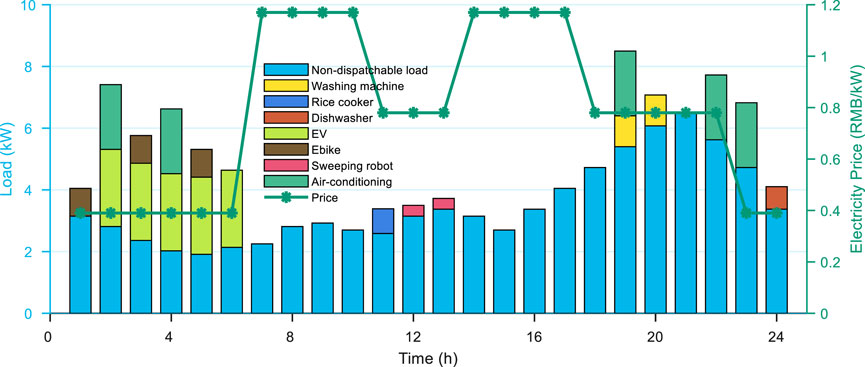
After the agent is well-trained, the optimal energy management strategy for HES can be obtained. The results of the dispatch optimization for devices are presented in Figure 5. The needs of non-dispatchable devices are satisfied first. Then, the dispatchable devices should be dispatch with consideration of the real-time electricity price and permitted working interval of each device. It can be observed that all the uninterruptable devices are scheduled at a relatively low price point for saving the total cost. For example, the work time-point of washing machine is scheduled at 19:00 and 20:00 caused by the low price. Thus, the dispatch strategy of the uninterruptible devices is quite reasonable.
Furthermore, the interruptible devices can be dispatchable at discontinuous time-point, whose dispatch strategy can be more flexible. When dispatching the interruptible devices, the system cost should be the first and only consider factor. It can be obtained that the EV and Ebike are scheduled to charge during the 00:00–06:00 cause the lower electricity price. Therefore, both the interruptible and uninterruptible devices can be reasonably scheduled after the agent is well-trained, which means that the proposed method can effectively realize the HEM optimal operation.
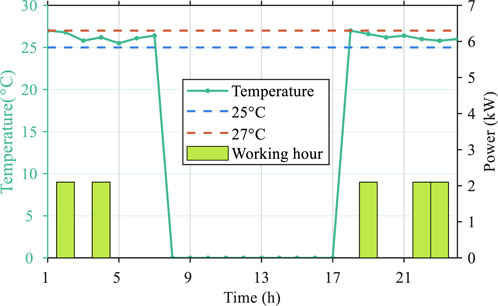
When dispatching the air-conditioning device, the comfort factor should be taken into account. The indoor temperature changes like a non-linear process when the air-conditioning working. Thus, the air-conditioning does not need to working continuous with consideration of cost saving. The dispatching result of air-conditioning and the indoor temperature are shown in Figure 6. Note that the comfort constraint only set between 00:00–07:00 and 18:00–24:00. It can be obtained that the air-conditioning is scheduled to work at 5 hours for keep the indoor temperature between 25°C–27°C. As the temperature curve shows, the indoor temperature always stays between 25°C and 27°C, which indicates the comfort constraint can be well limited.
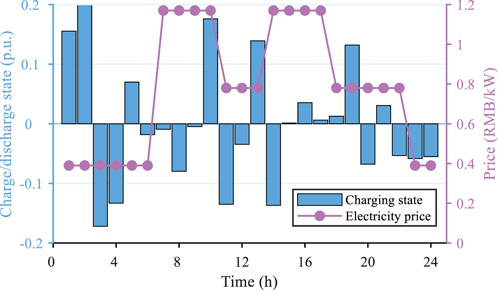
Generally, the energy storage device can store electricity during lower electricity price periods and release it during higher prices to reduce system costs. Thus, an energy storage device is equipped in the paper. The SOC curve of the applied energy storage device is illustrated in Figure 7. It can be found that the energy storage device charging when electricity price is low and discharging when the price is high, which can effectively reduce the system cost. Hence, the results effectively demonstrate that the proposed approach can efficiently schedule the energy storage device in real-time to reduce the operating cost after the agent is well-trained.
4.3 Comparison results with other benchmarks
The above results have verified the effectiveness of the proposed method. To further verify the effectiveness and progressiveness of the proposed method, the proposed method is separately compared with the optimization method based on stochastic programming (SP) and the optimization method based on deterministic optimization (DO) (Alzahrani et al., 2023). The difference between SP and DO is that DO only consider optimization problems in deterministic scenarios, which does not consider uncertainties of PV and loads.
The optimization results of the three algorithms are shown in Table 5. Compared to traditional optimization methods, the proposed method can better cope with the uncertainty of PV output and load demand to achieve better optimization results. It can be obtained that the proposed method can achieve the lowest total cost compared with other two method, which the total operation cost can be reduced by 21.9% at least. The proposed method can reasonably schedule the different types of appliances for reducing the cost of purchasing electricity and improving revenue from selling electricity. Besides, the proposed can maintain the highest comfort for the home users by reasonably dispatching the switching time of air-conditioning. The DO method solves the modelled optimization problem under deterministic conditions, and the final cancelled optimization effect is not significantly different from the optimization effect of the proposed method. This also fully demonstrates the effectiveness of the proposed method. However, the DO method cannot address the issue of output uncertainty and is not applicable to actual operating conditions. Therefore, the proposed method is more suitable for optimizing the operation of the HES in uncertain environments.
5 Conclusion
This paper proposes an optimized scheduling model for home energy management to minimize costs of household users with consideration of comfort of user. To enhance solution efficiency, a novel DRL-based algorithm call DDPG is applied to solve the optimization problem. Firstly, the results show that the proposed method can effectively dispatch both interruptible and uninterruptible loads, so the total cost of household user is obviously reduced while maintain high comfort. The optimal dispatch problem of HEMS is modeled as a MDP and solved by DDPG algorithm. The agent has converged after 8,000 episodes training, which means that the proposed DRL method can obtain the optimal policy for dispatching the HEMS. In the future work, the multi-agent deep reinforcement learning algorithm will be used to improve the efficiency of model training and decision making.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
TP: Conceptualization, Software, Writing–original draft. ZZ: Conceptualization, Data curation, Formal Analysis, Writing–review and editing. HL: Conceptualization, Investigation, Methodology, Software, Writing–original draft. CL: Investigation, Methodology, Project administration, Resources, Writing–original draft. XJ: Conceptualization, Methodology, Writing–review and editing. ZM: Conceptualization, Methodology, Supervision, Writing–review and editing. XC: Conceptualization, Investigation, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Southern Power Grid Corporation Technology Project under Grant 036000KK52222004 (GDKJXM20222117).
Conflict of interest
Authors TP, HL, and XJ were employed by Southern Power Grid Research Institute Co., Ltd. Authors ZZ, CL, ZM, and XC were employed by Power Dispatch Control Center of Guangdong Power Grid Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alzahrani, A., Rahman, M. U., Hafeez, G., Rukh, G., Ali, S., Murawwat, S., et al. (2023). A strategy for multi-objective energy optimization in smart grid considering renewable energy and batteries energy storage system. IEEE Access 11, 33872–33886. doi:10.1109/access.2023.3263264
Ben Slama, S., and Mahmoud, M. (2023). A deep learning model for intelligent home energy management system using renewable energy. Eng. Appl. Artif. Intell. 123, 106388. doi:10.1016/j.engappai.2023.106388
Chakir, A., Abid, M., Tabaa, M., and Hachimi, H. (2022). Demand-side management strategy in a smart home using electric vehicle and hybrid renewable energy system. Energy Rep. 8, 383–393. doi:10.1016/j.egyr.2022.07.018
Dongdong, Y. G. M. Z. Z. L. L. (2020). Home energy management strategy for Co-scheduling of electric vehicle and energy storage device. Proc. CSU-EPSA 32, 25–33.
Dorahaki, S., Rashidinejad, M., Fatemi Ardestani, S. F., Abdollahi, A., and Salehizadeh, M. R. (2022). A home energy management model considering energy storage and smart flexible appliances: a modified time-driven prospect theory approach. J. Energy Storage 48, 104049. doi:10.1016/j.est.2022.104049
Esmaeel Nezhad, A., Rahimnejad, A., and Gadsden, S. A. (2021). Home energy management system for smart buildings with inverter-based air conditioning system. Int. J. Electr. Power & Energy Syst., 133. doi:10.1016/j.ijepes.2021.107230
Gomes, I. L. R., Ruano, M. G., and Ruano, A. E. (2023). MILP-based model predictive control for home energy management systems: a real case study in Algarve, Portugal. Energy Build. 281, 112774. doi:10.1016/j.enbuild.2023.112774
Hafeez, G., Alimgeer, K. S., and Khan, I. (2020b). Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid. Appl. Energy 269, 114915. doi:10.1016/j.apenergy.2020.114915
Hafeez, G., Alimgeer, K. S., Wadud, Z., Khan, I., Usman, M., Qazi, A. B., et al. (2020a). An innovative optimization strategy for efficient energy management with day-ahead demand response signal and energy consumption forecasting in smart grid using artificial neural network. IEEE Access 8, 84415–84433. doi:10.1109/access.2020.2989316
Hafeez, G., Khan, I., Jan, S., Shah, I. A., Khan, F. A., and Derhab, A. (2021). A novel hybrid load forecasting framework with intelligent feature engineering and optimization algorithm in smart grid. Appl. Energy 299, 117178. doi:10.1016/j.apenergy.2021.117178
Hafeez, G., Wadud, Z., Khan, I. U., Khan, I., Shafiq, Z., Usman, M., et al. (2020c). Efficient energy management of IoT-enabled smart homes under price-based demand response program in smart grid. Sensors 20 (11), 3155. doi:10.3390/s20113155
Hussain, S., Imran Azim, M., Lai, C., and Eicker, U. (2023). Multi-stage optimization for energy management and trading for smart homes considering operational constraints of a distribution network. Energy Build. 301, 113722. doi:10.1016/j.enbuild.2023.113722
Huy, T. H. B., Truong Dinh, H., Ngoc Vo, D., and Kim, D. (2023). Real-time energy scheduling for home energy management systems with an energy storage system and electric vehicle based on a supervised-learning-based strategy. Energy Convers. Manag. 292, 117340. doi:10.1016/j.enconman.2023.117340
Kikusato, H., Mori, K., Yoshizawa, S., Fujimoto, Y., Asano, H., Hayashi, Y., et al. (2019). Electric vehicle charge–discharge management for utilization of photovoltaic by coordination between home and grid energy management systems. IEEE Trans. Smart Grid 10 (3), 3186–3197. doi:10.1109/tsg.2018.2820026
Kim, M., Park, T., Jeong, J., and Kim, H. (2023). Stochastic optimization of home energy management system using clustered quantile scenario reduction. Appl. Energy 349, 121555. doi:10.1016/j.apenergy.2023.121555
Li, B., Lei, C., Zhang, W., Olawoore, V. S., and Shuai, Y. (2024). Numerical model study on influences of photovoltaic plants on local microclimate. Renew. Energy 221, 119551. doi:10.1016/j.renene.2023.119551
Liu, Y., Ma, J., Xing, X., Liu, X., and Wang, W. (2022). A home energy management system incorporating data-driven uncertainty-aware user preference. Appl. Energy 326, 119911. doi:10.1016/j.apenergy.2022.119911
Ren, K., Liu, J., Wu, Z., Liu, X., Nie, Y., and Xu, H. (2024). A data-driven DRL-based home energy management system optimization framework considering uncertain household parameters. Appl. Energy 355, 122258. doi:10.1016/j.apenergy.2023.122258
Shi, L., Lao, W., Wu, F., Lee, K. Y., Li, Y., and Lin, K. (2023). DDPG-based load frequency control for power systems with renewable energy by DFIM pumped storage hydro unit. Renew. Energy 218, 119274. doi:10.1016/j.renene.2023.119274
Song, Z., Guan, X., and Cheng, M. (2022). Multi-objective optimization strategy for home energy management system including PV and battery energy storage. Energy Rep. 8, 5396–5411. doi:10.1016/j.egyr.2022.04.023
Tostado-Véliz, M., Arévalo, P., Kamel, S., Zawbaa, H. M., and Jurado, F. (2022). Home energy management system considering effective demand response strategies and uncertainties. Energy Rep. 8, 5256–5271. doi:10.1016/j.egyr.2022.04.006
Tostado-Véliz, M., Hasanien, H. M., Turky, R. A., Rezaee Jordehi, A., Mansouri, S. A., and Jurado, F. (2023b). A fully robust home energy management model considering real time price and on-board vehicle batteries. J. Energy Storage 72, 108531. doi:10.1016/j.est.2023.108531
Tostado-Véliz, M., Rezaee Jordehi, A., Hasanien, H. M., Turky, R. A., and Jurado, F. (2023a). A novel stochastic home energy management system considering negawatt trading. Sustain. Cities Soc. 97, 104757. doi:10.1016/j.scs.2023.104757
Ullah, K., Hafeez, G., Khan, I., Jan, S., and Javaid, N. (2021). A multi-objective energy optimization in smart grid with high penetration of renewable energy sources. Appl. Energy 299, 117104. doi:10.1016/j.apenergy.2021.117104
ur Rehman, U., Yaqoob, K., and Adil Khan, M. (2022). Optimal power management framework for smart homes using electric vehicles and energy storage. Int. J. Electr. Power & Energy Syst. 134, 107358. doi:10.1016/j.ijepes.2021.107358
Wang, G., Zhou, Y., Lin, Z., Zhu, S., Qiu, R., Chen, Y., et al. (2024). Robust energy management through aggregation of flexible resources in multi-home micro energy hub. Appl. Energy 357, 122471. doi:10.1016/j.apenergy.2023.122471
Weil, C., Bibri, S. E., Longchamp, R., Golay, F., and Alahi, A. (2023). Urban digital twin challenges: a systematic review and perspectives for sustainable smart cities. Sustain. Cities Soc. 99, 104862. doi:10.1016/j.scs.2023.104862
Wu, H. W. C., Zuo, Y., Chen, Y., and Liu, K. (2019). Home energy system optimization based on time-of-use price and real-time control strategy of battery. Power Syst. Prot. Control 47 (19), 23–30.
Xiong, B., Wei, F., Wang, Y., Xia, K., Su, F., Fang, Y., et al. (2024). Hybrid robust-stochastic optimal scheduling for multi-objective home energy management with the consideration of uncertainties. Energy 290, 130047. doi:10.1016/j.energy.2023.130047
Xiong, K., Cao, D., Zhang, G., Chen, Z., and Hu, W. (2023a). Coordinated volt/VAR control for photovoltaic inverters: a soft actor-critic enhanced droop control approach. Int. J. Electr. Power & Energy Syst. 149, 109019. doi:10.1016/j.ijepes.2023.109019
Xiong, K., Hu, W., Cao, D., Li, S., Zhang, G., Liu, W., et al. (2023b). Coordinated energy management strategy for multi-energy hub with thermo-electrochemical effect based power-to-ammonia: a multi-agent deep reinforcement learning enabled approach. Renew. Energy 214, 216–232. doi:10.1016/j.renene.2023.05.067
Yin, W., and Qin, X. (2022). Cooperative optimization strategy for large-scale electric vehicle charging and discharging. Energy 258, 124969. doi:10.1016/j.energy.2022.124969
Youssef, H., Kamel, S., Hassan, M. H., Yu, J., and Safaraliev, M. (2024). A smart home energy management approach incorporating an enhanced northern goshawk optimizer to enhance user comfort, minimize costs, and promote efficient energy consumption. Int. J. Hydrogen Energy 49, 644–658. doi:10.1016/j.ijhydene.2023.10.174
Zhang, F., Chan, A. P. C., and Li, D. (2023). Developing smart buildings to reduce indoor risks for safety and health of the elderly: a systematic and bibliometric analysis. Saf. Sci. 168, 106310. doi:10.1016/j.ssci.2023.106310
Keywords: home energy management system, dispatchable load, optimal dispatching strategy, users’ comfort, deep reinforcement learning
Citation: Pan T, Zhu Z, Luo H, Li C, Jin X, Meng Z and Cai X (2024) Home energy management strategy to schedule multiple types of loads and energy storage device with consideration of user comfort: a deep reinforcement learning based approach. Front. Therm. Eng. 4:1391602. doi: 10.3389/fther.2024.1391602
Received: 26 February 2024; Accepted: 13 May 2024;
Published: 05 June 2024.
Edited by:
Dibyendu Roy, Durham University, United KingdomReviewed by:
Ghulam Hafeez, University of Engineering and Technology, Mardan, PakistanMrinal Bhowmik, Durham University, United Kingdom
Sk Arafat Zaman, Indian Institute of Engineering Science and Technology, India
Copyright © 2024 Pan, Zhu, Luo, Li, Jin, Meng and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tingzhe Pan, bmFud2FuZ3NvdXRoZXJuQDE2My5jb20=
 Tingzhe Pan
Tingzhe Pan Zean Zhu2
Zean Zhu2