Phy-ChemNODE: an end-to-end physics-constrained autoencoder-NeuralODE framework for learning stiff chemical kinetics of hydrocarbon fuels

Predictive computational fluid dynamics (CFD) simulations of reacting flows in energy conversion systems are accompanied by a major computational bottleneck of solving a stiff system of coupled ordinary differential equations (ODEs) associated with detailed fuel chemistry. This issue is exacerbated with the complexity of fuel chemistry as the number of reactive scalars and chemical reactions increase. In this work, a physics-constrained Autoencoder (AE)-NeuralODE framework, termed as PhyChemNODE, is developed for data-driven modeling and temporal emulation of stiff chemical kinetics for complex hydrocarbon fuels, wherein a non-linear AE is employed for dimensionality reduction of the thermochemical state and the NODE learns temporal dynamics of the system in the low-dimensional latent space obtained from the AE. Both the AE and NODE are trained together in an end-to-end manner. We further enhance the approach by incorporating elemental mass conservation constraints directly into the loss function during model training. This ensures that total mass as well as individual elemental species masses are conserved in an a-posteriori manner. Demonstration studies are performed for methane combustion kinetics (32 species, 266 chemical reactions) over a wide thermodynamic and composition space at high pressure. Effects of various model hyperparameters, such as relative weighting of different terms in the loss function and dimensionality of the AE latent space, on the accuracy of Phy-ChemNODE are assessed. The physics-based constraints are shown to improve both training efficiency and physical consistency of the data-driven model. Further, a-posteriori autoregressive inference tests demonstrate that Phy-ChemNODE leads to reduced temporal stiffness in the latent space, and achieves 1-3 orders of magnitude speedup relative to the detailed kinetic mechanism depending on the type of ODE solver (implicit or explicit) used for numerical integration, while ensuring prediction fidelity.

1 Introduction

Computational fluid dynamics (CFD) modeling of reacting flows, such as those encountered in gas turbine and internal combustion engines, are computationally demanding owing to the complex interactions among multiple physico-chemical phenomena and the need to resolve a wide range of spatiotemporal scales governing the evolution of a large number of reactive scalars (chemical species). In particular, modeling of detailed chemical kinetics presents a major bottleneck, which is governed by a stiff system of coupled ordinary differential equations (ODEs) and characterized by high condition number of the corresponding chemical Jacobian matrix (Shampine, 1993). In addition, as the complexity of fuel chemistry increases, the dimensionality and stiffness of the ODE system also become more prohibitive (Lu and Law, 2009). To address these computational challenges, kinetic model reduction is typically performed (Lu and Law, 2005; Jones and Rigopoulos, 2005; Valorani et al., 2006; Maas and Pope, 1992), but it often leads to less reliable description of chemical kinetics.

In this context, data-driven machine learning (ML) techniques (Dana, 1987; Wold et al., 1987) have been extensively explored in an effort to emulate chemical kinetics and accelerate detailed finite-rate chemistry computations. Some of these approaches reduce the dimensionality of the reaction system via linear projection onto an appropriate basis typically identified through Principal Component Analysis (PCA). Artificial neural network (ANNs) are, then, employed for regression of the PC source terms and transport coefficients (Owoyele et al., 2017; Kumar et al., 2023). On the other hand, ANN-based approaches have also been used for predicting chemical source terms directly from the thermochemical state (Christo et al., 1996; Blasco et al., 1998; Sen et al., 2010; Ranade et al., 2019; Wan et al., 2020). More recently, novel deep learning architectures have been explored to capture the temporal evolution of chemical kinetics and combustion simulations, such as Deep Operator Network (DeepONet) (Kumar and Echekki, 2024) and Fourier Neural Operator (FNO) (Zhang et al., 2024).

Despite the potential benefits of employing ML methods, When they are trained in an a-priori or offline setting and then coupled with a numerical solver, predicted solutions may diverge or become unstable. Due to the non-linearity of the combustion process, even minor predictive errors can escalate into significant discrepancies in the temporal evolution of thermochemical state due to error accumulation. To handle this issue, an alternative and more robust data-driven technique for chemical source term computations based on neural ordinary differential equations (NeuralODEs, NODEs) (Chen et al., 2018) was developed by the authors, known as ChemNODE (Owoyele and Pal, 2021). It combines the chemical source term predictions with ODE integration in an a-posteriori learning paradigm, where the source terms predicted by the neural network are passed to the ODE solver for time integration, and the neural network weights are optimized to minimize the loss computed between the predicted and ground truth thermochemical states (comprised of species mass fractions and thermodynamic variables). A key advantage of this approach is that NODEs learn continuous-time dynamics which can be integrated using existing ODE solvers. This ensures that the predicted thermochemical state, even after a long-time horizon, remains adherent to the ground truth solution trajectory. For relatively large chemical kinetic mechanisms, the coupling of a non-linear autoencoder (AE) to perform dimensionality reduction and a NODE to evolve the dynamics in the lower-dimensional latent space has shown promise (Vijayarangan et al., 2024). A similar approach has also been pursued in the field of astro-chemistry (Sun Tang and Turk, 2022; Maes et al., 2024).

Another major limitation of traditional black-box ML techniques applied to the modeling of chemical kinetics is that they do not inherently incorporate conservation laws, which can adversely impact simulation accuracy and hinder the integration of ML surrogate models with multidimensional CFD solvers. With the advent of scientific machine learning, the practice of combining domain science-specific constraints to embed physics into neural network training has emerged lately (Raissi et al., 2019). This is achieved through regularization of the loss function, in which physical laws are embedded in the learning process as soft constraints (Kumar Tadbhagya et al., 2023; Almeldein and Van Dam, 2023; Kumar et al., 2025; Weng et al., 2025; Kercher and Votsmeier, 2025). This has been shown to improve model accuracy and generalization, especially in scenarios where traditional methods struggle with noisy data and high-dimensional problems governed by parameterized differential equations. Another way to enforce conservation laws is by enforcing a hard constraint in the neural network architecture through constraint layers (Sturm and Wexler, 2022; Mohan et al., 2023).

In light of the above discussion, the overarching goal of the present work is to demonstrate an end-to-end physics-constrained AE-NODE framework called Phy-ChemNODE for data-driven modeling and temporal emulation of stiff chemical kinetics for hydrocarbon fuels. Unlike previous work (Vijayarangan et al., 2024; Sun Tang and Turk, 2022; Maes et al., 2024), the present study demonstrates that this integrated approach improves physical consistency of the resulting data-driven model with mass conservation laws and accelerates training convergence, while simultaneously reducing temporal stiffness of the chemical kinetic system. The remainder of the paper is organized as follows: the Phy-ChemNODE framework is first outlined along with details of the physics-constrained formulation and training methodology in Sections 2, 3, respectively. Subsequently, results from a-posteriori proof-of-concept studies are discussed in Section 4. Finally, the Conclusions section summarizes the major findings and directions for future work.

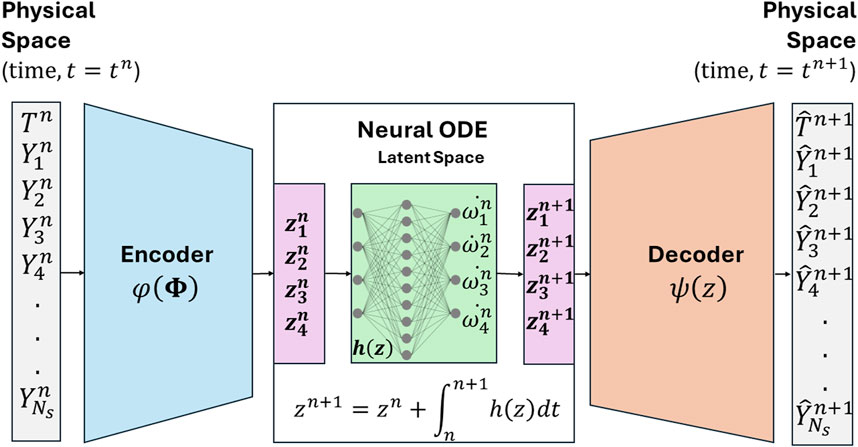
2 Physics-constrained autoencoder-NODE (Phy-ChemNODE) framework for stiff chemical kinetics emulation

In combustion CFD simulations, it is a common numerical approach to decouple finite-rate chemistry from transport using operator splitting. Chemistry is solved (independently from advective and diffusive transport) within each computational grid cell considered as a homogeneous reactor, which is equivalent to solving a system of stiff ODEs. The temporal evolution of $N_s$ reactive scalars (chemical species) can be defined by:

$\frac{d{Y}_k}{dt}=\frac{\dot{{\omega }_k}}{\rho },k=\mathrm{1,2,3},\dots ,N_s(1)$

where $Y_k$ is the mass fraction of $k^{th}$ species ($N_s$ being the total number of species), $\dot{{\omega }_k}$ is the corresponding chemical source term computed using law of mass action, and $\rho$ refers to mixture density. The temporal evolution of temperature (T) is governed by a similar ODE defined as follows:

$\frac{dT}{dt}=-\frac{{\sum }_{k=1}^{N_s}{h}_k\dot{{\omega }_k}}{\rho {\mathrm{c}}_p},k=\mathrm{1,2,3},\dots ,N_s(2)$

where $h_k$ and ${\mathrm{c}}_p$ refer to the enthalpy of $k^{th}$ species and mixture-averaged constant pressure specific heat, respectively. To calculate the source terms, one needs to account for several elementary reactions involving production and consumption of multiple species. As the chemical mechanism becomes larger, the number of chemical species and elementary reactions also increase (Lu and Law, 2009). This leads to prohibitive computational costs since all chemical time scales must be fully resolved. In the NODE-based data-driven framework (Owoyele and Pal, 2021), the expensive physics-based computation of chemical source terms is replaced by a neural network, which can be described as Equation 3 below:

$\frac{d\mathrm{\Phi }}{dt}=f\left(\mathrm{\Phi },t;\mathrm{\Theta }\right)(3)$

where $\mathrm{\Phi }=[T,Y_1,Y_2,\dots ,Y_{Ns}]$ is the vector of thermochemical state (temperature and species mass fractions), and $f(\mathrm{\Phi },t;\mathrm{\Theta })$ is a feedforward neural network parameterized by weights $\mathrm{\Theta }$. For larger chemical mechanisms, $\mathrm{\Phi }$ increases in dimensionality and stiffness. To address the high dimensionality, a non-linear AE is coupled with the NODE for dimensionality reduction, so that the NODE learns the temporal evolution of the dynamical system in a reduced-order latent space obtained from the non-linear projection of the AE. A schematic of the coupled AE-NODE data-driven modeling framework is shown in Figure 1. The model training process is posed as an optimization problem of determining the optimal parameters of the encoder $(\phi )$, NODE $(h(z))$, and the decoder $(\psi )$ networks in an end-to-end manner, that minimizes the loss function defined as:

$L_{\mathit{Phy-ChemNODE}}={\lambda }_{\mathit{rec}}{L}_{\mathit{rec}}+L_{\mathit{data}}+{\lambda }_z{L}_z+{\displaystyle \sum _{j=1}^{N_{el}}}{\lambda }_{el-j}{L}_{el-j}(4)$

where the reconstruction loss $L_{\mathit{rec}}=\text{L}(\mathrm{\Phi },\tilde{\mathrm{\Phi }})$ measures the loss between ground truth $(\mathrm{\Phi })$ and corresponding encoder-decoder mapping ($\tilde{\mathrm{\Phi }}=\psi (\phi (\mathrm{\Phi }))$, the data loss $L_{\mathit{data}}=\text{L}(\mathrm{\Phi },\widehat{\mathrm{\Phi }})$ measures the loss between ground truth and encoder + NODE + decoder prediction $(\widehat{\mathrm{\Phi }})$, and the latent loss $L_z=L(\bar{z},z)$ measures the loss between encoder mapping of ground truth ($\bar{z}$ = $\phi (\mathrm{\Phi })$) and encoder + NODE prediction. Each loss term is chosen to be in mean absolute error (MAE) form. It is noted that the loss terms $L_{\mathit{rec}}$ and $L_z$ ensure that the encoder and decoder mappings are bijective or unique. The loss function also contains elemental mass conservation constraints (Kumar Tadbhagya et al., 2023; Kumar et al., 2025), defined in Equation 5 below:

$L_{el-j}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{k=1}^{N_s}}\frac{N_j^k{W}_j|Y_{k,i}-{\widehat{Y}}_{k,i}|}{W_k}(5)$

where $L_{el-j}$ refers to the loss associated with mass conservation of element $j$ (in the chemical system with a total of $N_{el}$ elements). ${\widehat{Y}}_{k,i}$ and $Y_{k,i}$ correspond to the AE + NODE predicted and ground truth mass fractions of $k^{th}$ species, respectively. $W_j$ is the atomic mass of element $j$, $N_j^k$ is the number of atoms of element $j$ in $k^{th}$ species, $W_k$ is the molecular weight of $k^{th}$ species, and $N$ is the number of training data points. Lastly, the weights ${\lambda }_{\mathit{rec}}$, ${\lambda }_z$, and ${\lambda }_{el-j}$ in Equation 4 balance the contributions from the different loss terms.

Figure 1

Figure 1. Schematic of the coupled AE-NODE framework.

3 Proof-of-concept study

For proof-of-concept demonstration of Phy-ChemNODE, an autoigniting methane-oxygen (${\text{CH}}_4$-${\text{O}}_2$) zero-dimensional (0D) homogeneous reactor is considered, at a constant pressure of 20 atm that corresponds to practical high-pressure isobaric operating conditions for stationary gas turbine engines. The detailed chemical mechanism (Gregory et al., 2016) consists of 32 species and 266 chemical reactions. The ground truth data for model training is generated using Cantera (Goodwin et al., 2009), which solves the coupled ODE system (Equations 1, 2) with detailed chemistry. The thermodynamic and composition space chosen for data generation comprises 9 equispaced initial temperatures in the range $T_i$ = [1600 K, 2000 K] and 11 equivalence ratios within $\varphi =[1.0,1.5]$ resulting in a total of 99 initial conditions. Each of these initial conditions is integrated to chemical equilibrium. Ground truth data is generated by selecting time instants such that the change in any of the thermochemical scalars (species mass fractions or temperature) between two successive time instants is greater than 1% of their corresponding overall ranges of variation, and then downsampling 200 points from the selected time instants. A $70\%,20\%,10\%$ random split (based on initial conditions) is used to obtain the training, validation, and test datasets, respectively. The AE-NODE model is initialized with the same initial conditions (during training) as the physics-based simulations. The input to the encoder is the vector $\mathrm{\Phi }$ containing the temperature and species mass fractions, which is scaled using the maximum and minimum of the training data, respectively, and the output is a vector in the latent space $(z)$. The decoder has the same dense architecture as the encoder, with an input size equal to the latent dimension $(dim(z)=4)$ (chosen based on a sensitivity study discussed in Section 4) and the output size equal to the physical space vector $(dim(\mathrm{\Phi })=33)$. Both the encoder and decoder have 5 hidden layers with 64 neurons each and Exponential Linear Unit (ELU) activation function. The NODE has the same input and output dimensions as the latent space $(dim(z)=4)$, and a 4 hidden-layer dense network with 64 neurons in each hidden layer and ELU activation function, to model the chemical source terms in the lower-dimensional latent space. The output layers for the encoder, NODE, and the decoder are considered to be linear. The above discussed AE-NODE architecture was finalized based on multiple ablation studies, targeting a good balance between dimensionality reduction and overall model accuracy. Although more exhaustive hyperparameter optimization can be performed to further optimize the number of latent variables, it is out of scope of the current work.

The forward pass through the NODE requires time integration, for which a 4th order explicit Runge-Kutta (RK) solver is used. Once the time integration is completed, the temporal trajectories are mapped back to physical space and the loss is computed using Equation 4. The gradients for updating the neural network parameters are calculated using backward adjoint automatic differentiation and ADAM optimizer with exponential learning rate decay (every 200 epochs) is used. The model is trained for 10000 epochs. To ensure that all the loss terms are of similar magnitude, ${\lambda }_{\mathit{rec}}=5.0$ is used. Further, ${\lambda }_z=0.05$ and ${\lambda }_{el-H}={\lambda }_{el-C}={\lambda }_{el-O}=0.5$ are chosen based on a hyperparameter sweep (discussed in Section 4). The training framework was implemented in Julia programming language using Flux.jl (Innes et al., 2018) library and the model was trained on 2 AMD EPYC 7713 64-core processors for a walltime of 96 h.

4 Results and discussion

To determine the optimal weighting of terms in the loss function and the latent space dimensionality, hyperparameter studies were carried out. Figure 2a compares the loss terms computed on the validation set (post training) corresponding to different ${\lambda }_z$ values for ${\lambda }_{\mathit{rec}}=5,{\lambda }_{el-j}=0.5$, and fixed size of the latent space (dim$(z)=4$), and Figure 2b shows a similar comparison for varying size of the latent space (dim$(z)$) with ${\lambda }_{\mathit{rec}}=5$, ${\lambda }_z=0.05$, and ${\lambda }_{el-j}=0.5$. Moreover, to assess the impact of adding elemental mass conservation constraints to the training loss function, Figure 2c compares the decay of data loss (during training) between the cases trained with $({\lambda }_{\mathit{ele-j}}=0.5)$ and without elemental mass constraints $({\lambda }_{\mathit{ele-j}}=0)$ on the validation set. It can be clearly seen that incorporating the soft constraints in the loss function results in lower loss for the same number of epochs, thereby enabling more efficient model training and faster training convergence.

Figure 2

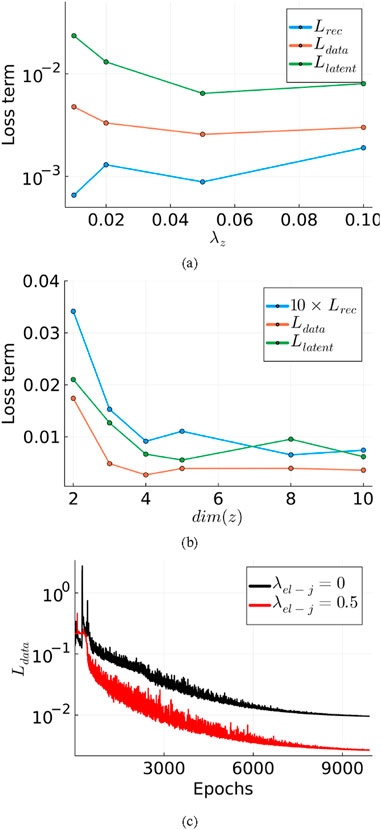
Figure 2. Comparison of loss terms (computed on validation set) across hyperparameter experiments: (a) varying ${\lambda }_z$, (b) varying latent space size $(dim(z))$, and (c) data loss $(L_{\mathit{data}})$ evolution with $({\lambda }_{el-j}=0.5)$ and without $({\lambda }_{el-j}=0)$ elemental mass constraints.

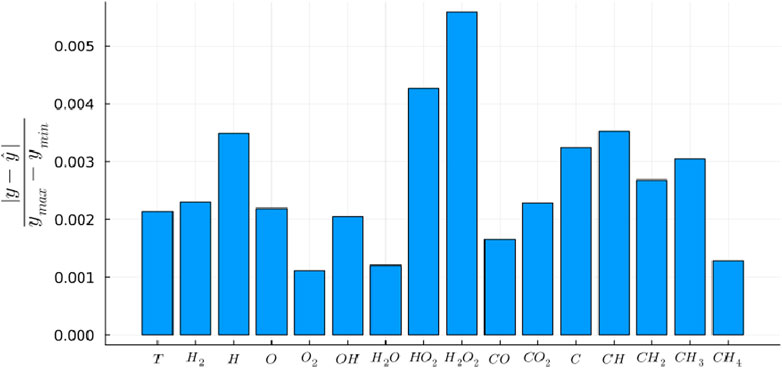
The trained Phy-ChemNODE model is then deployed for predicting the temporal evolution of thermochemical scalars in a-posteriori autoregressive tests. Figure 3 plots the temporal evolution of temperature and a subset of species mass fractions (${\text{CH}}_4$, CO, ${\text{CO}}_2$, OH, and ${\text{O}}_2$) for an initial condition (corresponding to $T_0=1600$K) in the training set $(\varphi =1.0)$ and test set $(\varphi =1.1)$, where ground truth data is indicated by solid lines and the predicted Phy-ChemNODE solutions are shown in markers. Overall, great agreement can be observed between the predictions and ground truth data. Figure 4 shows the temporal evolution of a few intermediate species for another set of initial conditions in the training set ($T_0=1650$K, $\varphi =1.0$) and the test set ($T_0=1700$K$,\varphi =1.05$), again demonstrating high accuracy. As further quantification of the accuracy of Phy-ChemNODE framework, Figure 5 shows the test set MAEs for a subset of the thermochemical scalars including both major and minor species, scaled by their corresponding data ranges, indicating that Phy-ChemNODE performs extremely well in capturing the temporal dynamics.

Figure 3

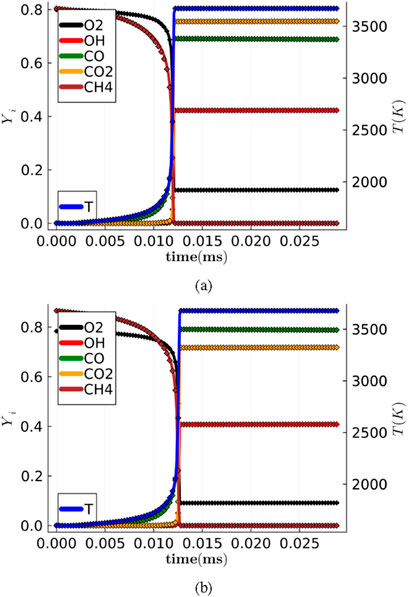
Figure 3. Temporal evolution of temperature $(T)$ and mass fractions of ${\text{CH}}_4$, CO, ${\text{CO}}_2$, OH, and ${\text{O}}_2$ corresponding to initial conditions in (a) training set ($T_i=1600$K, $\varphi =1.0$) and (b) test set ($T_i=1600$K, $\varphi =1.1$). The mass fractions of ${\text{CH}}_4$, ${\text{CO}}_2$ and OH are scaled by 4, and that of CO by 3 for ease of plotting. Solid lines denote ground truth and markers denote Phy-ChemNODE predictions.

Figure 4

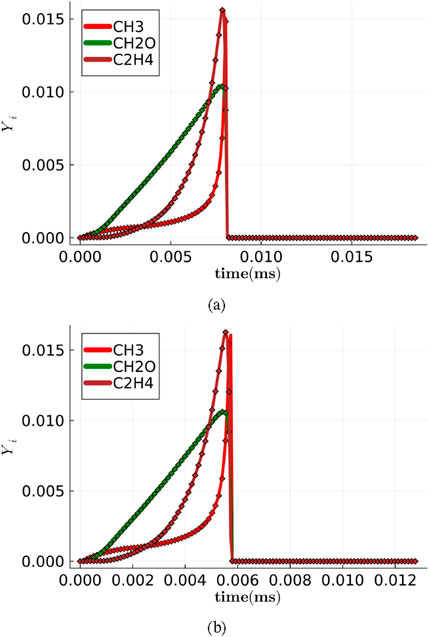
Figure 4. Temporal evolution of intermediate species (${\text{CH}}_3$, ${\text{CH}}_2$O and ${\text{C}}_2{\text{H}}_4$) corresponding to initial conditions in (a) training set $(T_i=1650$K, $\varphi =1.0$) and (b) test set $(T_i=1700$K, $\varphi =1.05$). Solid lines denote ground truth and markers denote Phy-ChemNODE predictions.

Figure 5

Figure 5. Scaled test set MAEs for prediction of temperature $(T)$ and a few species mass fractions.

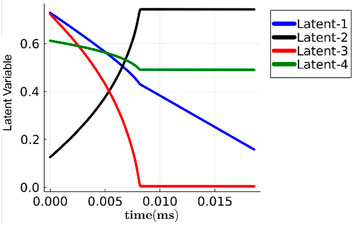
Based on inference on an Intel i7-1165G7 workstation with 16 cores, Phy-ChemNODE yields speedups of 6x and 860x over the full chemical mechanism in terms of overall simulation walltime, when deployed with implicit (backward differentiation formula (BDF)) and explicit (RK45) solvers, respectively. Figure 6 plots the latent space temporal dynamics corresponding to the initial conditions of $T_0=1650$K, $\varphi =1.0$. It is evident that the evolution of latent variables is much smoother than that of thermochemical scalars in the physical space earlier shown in Figure 4a. This indicates that the coupled AE-NODE approach significantly reduces the temporal stiffness of the chemical kinetic system. Similar stiffness reduction in the latent space was also observed by Nair et al. (2025) in case of AE-NODE models of advection-dominated dynamical systems. Lastly, Figure 7 shows the predicted temporal evolution of C, H, and O mass fractions from autoregressive tests corresponding to certain initial conditions from the training and test sets. Evidently, the model trained with elemental mass constraints in the loss function (Phy-ChemNODE/PCNODE) conserves the elemental mass fractions during deployment much better than the MAE-trained case without constraints.

Figure 6

Figure 6. Temporal evoluiton of latent space variables corresponding to $T_i=1650$K, $\varphi =1.0$.

Figure 7

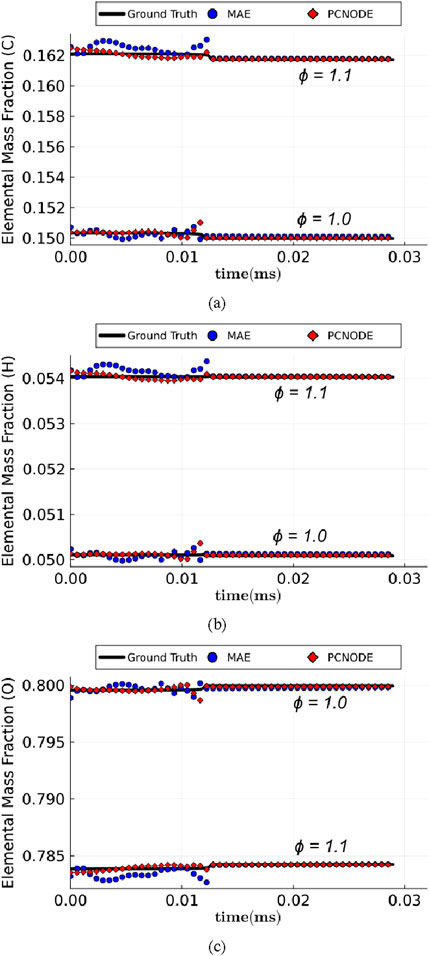
Figure 7. Temporal evolution of mass fractions of: (a) C, (b) H, and (c) O elements corresponding to initial conditions in the training ($T_0=1600$K, $\varphi =1.0$) and test ($T_0=1600$K, $\varphi =1.1$) sets.

In future studies, multiple avenues for further extension of the Phy-ChemNODE framework will be pursued. These include: (a) efficient scaling of the training workflow to wider ranges of thermodynamic conditions (including multiple pressures), larger kinetic mechanisms, and multicomponent fuels; (b) integration of Phy-ChemNODE with CFD solvers and demonstration of accelerated multidimensional reacting flow simulations on modern high-performance computing (HPC) platforms; (c) demonstration for constant-volume combustion; (d) incorporation of uncertainty quantification; and (e) exploration of training methodologies to enhance model out-of-distribution generalizability.

5 Conclusion

In this work, an end-to-end physics-constrained AE-NODE framework (PhyChemNODE) was introduced for accelerated temporal emulation of stiff chemical kinetics targeting complex hydrocarbon fuel combustion. The deep learning approach employed a non-linear AE for dimensionality reduction of the thermochemical state and utilized a NODE to learn temporal dynamics of the kinetic system in the low-dimensional latent space obtained from the AE. In addition, elemental mass conservation constraints were included in the loss function during training of the data-driven model to ensure that total mass and mass of each elemental species are conserved. Proof-of-concept studies were performed for homogeneous autoignition of a methane-oxygen mixture over a range of composition and thermodynamic conditions at high pressure. The results showed that the physics-based constraints not only improve physical consistency of the resulting data-driven model, but also enhance training efficiency. In addition, Phy-ChemNODE achieved 6–860$\times$ speedup relative to the detailed chemical mechanism depending on the type of ODE solver (implicit or explicit) used for numerical integration during autoregressive inference tests. Temporal evolution of the latent variables was visualized and it was found that the coupled AE-NODE approach leads to reduced temporal stiffness of the chemical kinetic system. In future work, Phy-ChemNODE will be further scaled to larger kinetic mechanisms and wider ranges of thermodynamic conditions (including pressure), and demonstrated for multidimensional combustion CFD simulations. In addition, uncertainty quantification techniques will be incorporated and training methodologies will be explored to enhance out-of-distribution generalizability.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TK: Data curation, Methodology, Conceptualization, Validation, Investigation, Software, Formal Analysis, Writing – original draft. AK: Software, Investigation, Methodology, Writing – original draft, Formal Analysis, Data curation. PP: Methodology, Supervision, Conceptualization, Investigation, Writing – original draft, Resources, Funding acquisition, Project administration.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The research work was funded by the U.S. DOE Fossil Energy and Carbon Management (FECM) office through the Technology Commercialization Fund (TCF) program.

Acknowledgments

The authors would like to acknowledge the computing core hours available through the Improv cluster provided by the Laboratory Computing Resource Center (LCRC) at Argonne National Laboratory. The contents of this manuscript have been presented at the Machine Learning and the Physical Sciences Workshop organized as part of the 38th conference on Neural Information Processing Systems (NeurIPS) in 2024 (Kumar et al., 2024).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Licenses and Permissions

The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (Argonne). Argonne, a U.S. Department of Energy (DOE) Office of Science laboratory, is operated under Contract No. DEAC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government.

References

Almeldein, A., and Van Dam, N. (2023). Accelerating chemical kinetics calculations with physics informed neural networks. J. Eng. Gas Turbines Power 145 (9), 091008. doi:10.1115/1.4062654

CrossRef Full Text | Google Scholar

Blasco, J. A., Fueyo, N., Dopazo, C., and Ballester, J. (1998). Modelling the temporal evolution of a reduced combustion chemical system with an artificial neural network. Combust. Flame 113 (1), 38–52. doi:10.1016/s0010-2180(97)00211-3

CrossRef Full Text | Google Scholar

Chen, R. T. Q., Rubanova, Y., Bettencourt, J., and Duvenaud, D. K. (2018). Neural ordinary differential equations. Adv. neural Inf. Process. Syst. 31.

Google Scholar

Christo, F. C., Masri, A. R., Nebot, E. M., and Pope, S. B. (1996). An integrated PDF/neural network approach for simulating turbulent reacting systems. Symposium Int. Combust. 26 (1), 43–48. doi:10.1016/s0082-0784(96)80198-6

CrossRef Full Text | Google Scholar

Dana, H. B. (1987). “Modular learning in neural networks,” in Proceedings of the sixth national conference on artificial intelligence - volume 1, AAAI’87 (AAAI Press), 279–284.

Google Scholar

Goodwin, D. G., Moffat, H. K., and Speth, R. L. (2009). Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes caltech, 124. CA: Pasadena.

Google Scholar

Gregory, P. S., Tao, Y., and Wang, H. (2016). Foundational fuel chemistry model version 1.0 (ffcm-1).

Google Scholar

Innes, M., Saba, E., Fischer, K., Gandhi, D., Rudilosso, M. C., Joy, N. M., et al. (2018). Fashionable modelling with flux. CoRR, 01457. abs/1811.

Google Scholar

Jones, W. P., and Rigopoulos, S. (2005). Rate-controlled constrained equilibrium: formulation and application to nonpremixed laminar flames. Combust. Flame 142 (3), 223–234. doi:10.1016/j.combustflame.2005.03.008

CrossRef Full Text | Google Scholar

Kercher, T., and Votsmeier, M. (2025). Machine learning surrogate models for mechanistic kinetics: embedding atomic balance and positivity. J. Phys. Chem. Lett. 16 (19). doi:10.1021/acs.jpclett.5c00602

CrossRef Full Text | Google Scholar

Kumar, A., and Echekki, T. (2024). Combustion chemistry acceleration with DeepONets. Fuel 365, 131212. doi:10.1016/j.fuel.2024.131212

CrossRef Full Text | Google Scholar

Kumar, A., Rieth, M., Owoyele, O., Chen, J. H., and Echekki, T. (2023a). Acceleration of turbulent combustion dns via principal component transport. Combust. Flame 255, 112903. doi:10.1016/j.combustflame.2023.112903

CrossRef Full Text | Google Scholar

Kumar, T., Kumar, A., and Pal, P. (2023b). “A physics-constrained neuralODE approach for robust learning of stiff chemical kinetics,” in NeurIPS machine learning and the physical sciences workshop.

Google Scholar

Kumar, T., Kumar, A., and Pal, P. (2024). “A physics-informed autoencoder-neuralODE framework (Phy-ChemNODE) for learning complex fuel combustion kinetics,” in NeurIPS machine learning and the physical sciences workshop.

Google Scholar

Kumar, T., Kumar, A., and Pal, P. (2025). A physics-constrained neural ordinary differential equations approach for robust learning of stiff chemical kinetics. Combust. Theory Model. 29 (2), 332–347. doi:10.1080/13647830.2025.2478266

CrossRef Full Text | Google Scholar

Lu, T., and Law, C. K. (2005). A directed relation graph method for mechanism reduction. Proc. Combust. Inst. 30 (1), 1333–1341. doi:10.1016/j.proci.2004.08.145

CrossRef Full Text | Google Scholar

Lu, T., and Law, C. K. (2009). Toward accommodating realistic fuel chemistry in large-scale computations. Prog. Energy Combust. Sci. 35 (2), 192–215. doi:10.1016/j.pecs.2008.10.002

CrossRef Full Text | Google Scholar

Maas, U., and Pope, S. B. (1992). Simplifying chemical kinetics: intrinsic low-dimensional manifolds in composition space. Combust. Flame 88 (3), 239–264. doi:10.1016/0010-2180(92)90034-m

CrossRef Full Text | Google Scholar

Maes, S., De Ceuster, F., Sande, M. V. de, and Decin, L. (2024). MACE: a machine-learning approach to chemistry emulation. Astrophysical J. 969 (79), 79. doi:10.3847/1538-4357/ad47a1

CrossRef Full Text | Google Scholar

Mohan, A. T., Lubbers, N., Chertkov, M., and Livescu, D. (2023). Embedding hard physical constraints in neural network coarse-graining of three-dimensional turbulence. Phys. Rev. Fluids 8, 014604. doi:10.1103/physrevfluids.8.014604

CrossRef Full Text | Google Scholar

Nair, A. S., Barwey, S., Pal, P., MacArt, J. F., Arcomano, T., and Maulik, R. (2025). Understanding latent timescales in neural ordinary differential equation models of advection-dominated dynamical systems. Phys. D: Nonlinear Phenom. 476, 134650. doi:10.1016/j.physd.2025.134650

CrossRef Full Text | Google Scholar

Owoyele, O., and Pal, P. (2021). ChemNODE: a neural ordinary differential equations framework for efficient chemical kinetic solvers. Energy AI 7, 100118. doi:10.1016/j.egyai.2021.100118

CrossRef Full Text | Google Scholar

Owoyele, O., and Echekki, T. (2017). Toward computationally efficient combustion DNS with complex fuels via principal component transport. Combust. Theory Model. 21 (4), 770–798. doi:10.1080/13647830.2017.1296976

CrossRef Full Text | Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

Ranade, R., Alqahtani, S., Farooq, A., and Echekki, T. (2019). An ann based hybrid chemistry framework for complex fuels. Fuel 241, 625–636. doi:10.1016/j.fuel.2018.12.082

CrossRef Full Text | Google Scholar

Sen, B. A, Hawkes, E. R., and Menon, S. (2010). Large eddy simulation of extinction and reignition with artificial neural networks based chemical kinetics. Combust. Flame 157 (3), 566–578. doi:10.1016/j.combustflame.2009.11.006

CrossRef Full Text | Google Scholar

Shampine, L. F. (1993). Ill-conditioned matrices and the integration of stiff ODEs. J. Comput. Appl. Math. 48 (3), 279–292. doi:10.1016/0377-0427(93)90025-7

CrossRef Full Text | Google Scholar

Sturm, P. O., and Wexler, A. S. (2022). Conservation laws in a neural network architecture: enforcing the atom balance of a julia-based photochemical model (v0.2.0). Geosci. Model Dev. 15 (8), 3417–3431. doi:10.5194/gmd-15-3417-2022

CrossRef Full Text | Google Scholar

Sun Tang, K., and Turk, M. (2022). “Reduced order model for chemical kinetics: a case study with primordial chemical network,” in ICML workshop on machine learning for astrophysics.

Google Scholar

Valorani, M., Creta, F., Goussis, D. A., Lee, J. C., and Habib, N. N. (2006). An automatic procedure for the simplification of chemical kinetic mechanisms based on CSP. Combust. Flame 146 (1), 29–51. doi:10.1016/j.combustflame.2006.03.011

CrossRef Full Text | Google Scholar

Vijayarangan, V., Uranakara, H. A., Barwey, S., Malpica Galassi, R., Rafi Malik, M., Valorani, M., et al. (2024). A data-driven reduced-order model for stiff chemical kinetics using dynamics-informed training. Energy AI 15, 100325. doi:10.1016/j.egyai.2023.100325

CrossRef Full Text | Google Scholar

Wan, K., Barnaud, C., Vervisch, L., and Domingo, P. (2020). Chemistry reduction using machine learning trained from non-premixed micro-mixing modeling: application to dns of a syngas turbulent oxy-flame with side-wall effects. Combust. Flame 220, 119–129. doi:10.1016/j.combustflame.2020.06.008

CrossRef Full Text | Google Scholar

Weng, Y., Han, Li, Zhang, H., Chen, Z. X., and Zhou, D. (2025). Extended fourier neural operators to learn stiff kinetics under unseen conditions. Combust. Flame 272, 113847. doi:10.1016/j.combustflame.2024.113847

CrossRef Full Text | Google Scholar

Wold, S., Esbensen, K., and Paul, G. (1987). Principal component analysis. Chemom. Intelligent Laboratory Syst. 2 (1), 37–52. doi:10.1016/0169-7439(87)80084-9

CrossRef Full Text | Google Scholar

Zhang, H., Weng, Y., Zhao, Z., and Zhou, D. (2024). Learning transient evolution of multidimensional reacting flows by multiscale fourier neural operators. Proc. Combust. Inst. 40, 105714. doi:10.1016/j.proci.2024.105714

CrossRef Full Text | Google Scholar