- 1Departamento de Geofísica, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, São Paulo, Brazil
- 2Universidade Federal do Pampa, Campus Caçapava do Sul, Caçapava do Sul, Brazil
- 3Coordenação de Geofísica, Observatório Nacional, Rio de Janeiro, Brazil
The Earth's rotation can change as a result of several internal and external processes, each of which is at a different timescale. Here, we present some possible connections between the Earth's rotation variations and the geomagnetic reversal frequency rates over the past 120 Myr. In addition, we show the possible relationship between the geomagnetic field reversal frequency and the δ18O oscillations. Because the latter reflects the glacial and interglacial periods, we hypothesize that it can be used as a possible indicator to explain the length of day (LOD) variations and consequently the reversal field frequency over the past 510 Myr. Therefore, our analysis suggests that the relationships between the geomagnetic reversal frequency rates and the Earth's rotation changes during the Phanerozoic. However, more reversal data are required for periods before the Kiaman Reverse Superchon (KRS) to strengthen the perspective of using the geomagnetic reversal data as a marker for the LOD variations through geological times.
Introduction
The Earth's rotation can be understood through internal and external processes that act upon the planet. External processes include: gravitational interactions with the Moon, the Sun and the planets; orbital and rotation axis variations; and position of the solar system relative to the galactic spiral arms. Internal processes include: the redistribution of densities in the mantle because of the lithospheric plate subduction and mantle convection; distribution of continents; variations caused by glacial and interglacial periods (e.g., Lambeck, 1980; Hide and Dickey, 1991; Gross, 2007).
The variations in Earth's rotation can be studied using the principle of conservation of angular momentum for the Earth system. The solid Earth rotation varies as a result of the applied external torques, internal mass redistribution and transfer of angular momentum between the solid Earth and its fluids (Gross, 2007). Regarding the fluids, hydrodynamic and magneto hydrodynamic torques strongly act at the solid and fluid parts of planet Earth (e.g., Hide et al., 2000). Rotation variations are often expressed as length of day (LOD) variations, which have been observed at decadal timescale and are considered a result of the angular momentum transfer from the outer core zonal flow to the mantle (e.g., Holme and De Viron, 2005, 2013; Holme, 2007). Large LOD variations over decadal time scales arise from the exchange of angular momentum between the solid mantle and the fluid core (Holme, 1998).
The main geomagnetic field is generated in the Earth's liquid metallic outer core. Driven by buoyancy forces from the action of gravity on density heterogeneities, the core motions are strongly affected by Coriolis forces because of the Earth's rotation and geometry of the coupling surfaces (e.g., Lambeck, 1980; Hide and Dickey, 1991; Hide et al., 2000; Miyagoshi and Hamano, 2013). A link between the decadal geomagnetic field and LOD variations has been treated (e.g., Yoshida and Hamano, 1995; Dumberry and Bloxham, 2006); however, the relationship between the geomagnetic field and LOD variations has not been explored for the geological timescale. Geomagnetic field reversals are the most important field features that have been observed throughout the geological timescales. The Earth's magnetic field irregularly reverses, and the reversal frequencies are highly variable: there are periods with high reversal frequencies and periods of remarkable stability, i.e., the superchrons (e.g., Merrill et al., 1998). The reason for this apparent discrepancy in reversal frequencies remains in debate, and the variations in Earth's rotation can play an important role during the geological times.
Here, we present some possible connections between the Earth's rotation variations and the geomagnetic reversal frequency rates over the past 120 Myr. In addition, we show the possible relationship between the geomagnetic field reversal frequency and δ18O oscillations. Because the latter reflects the glacial and interglacial periods, we hypothesize that it can be used as a possible indicator to explain LOD variations and consequently the reversal field frequency over the past 510 Myr. In this case, we suggest that the superchrons can be the Earth's internal markers for LOD oscillations through the Phanerozoic.
Magnetic Field Reversal Frequency and the Earth's Rotation Variations
The field reversal rate changes can be obtained based on the geomagnetic polarity time scale (GPTS), which is well constrained for the 0–160 Ma period using high-resolution sea-floor magnetic anomalies. For the period prior to 160 Ma, the GPTS is obtained from lower-resolution, paleomagnetic measurements in sedimentary and igneous rock records (Ogg, 1995). The current GPTS database spans approximately the past 540 Ma and indicates periods of high and low reversal rates according to Pavlov and Gallet (2005) (see Figures 1, 2). For the past 540 Ma, three periods without reversals are observed at approximately 125-83 Ma (the Cretaceous Normal Superchron—CNS), at approximately 314-267 Ma (the Kiaman Reverse Superchon—KRS) and at approximately 482-463 Ma (the Moyero Reversal Superchron—MRS), although some reversals may have occurred within these intervals (e.g., Ogg, 1995; Granot et al., 2012). High-frequency reversal periods have been determined before and after the CNS and KRS.
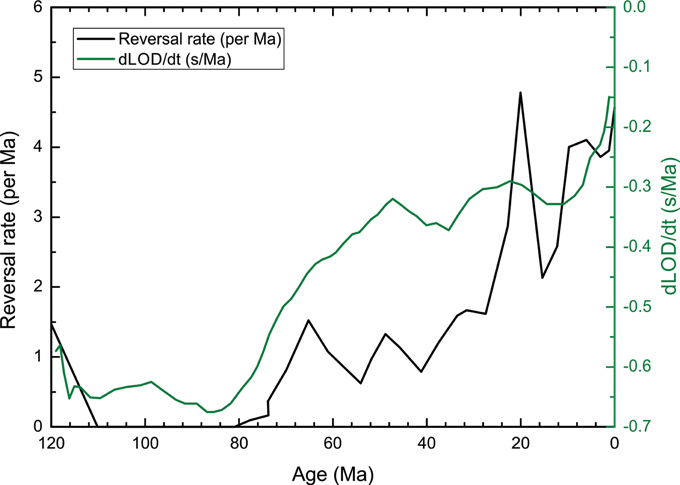
Figure 1. Geomagnetic reversal rates over the past 120 Ma period, which were calculated according to Pavlov and Gallet (2005) and compared with the LOD time derivative variations from Greff-Lefftz (2011).
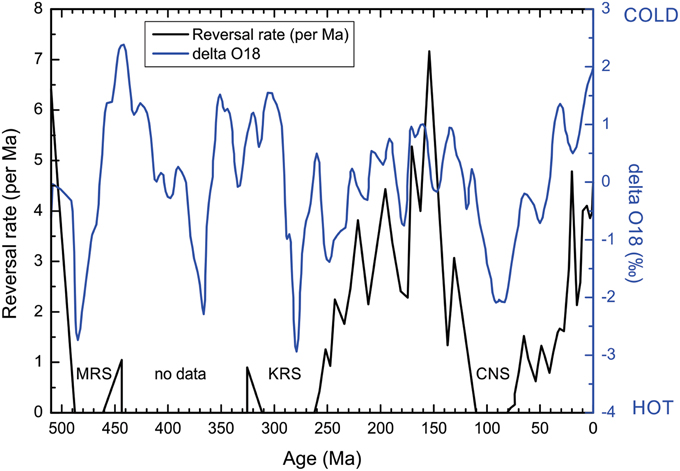
Figure 2. Geomagnetic field reversal rates over the past 510 Myr from Pavlov and Gallet (2005) compared with the δ18O (delta O18) variations from Veizer et al. (2000) and Price et al. (2013).
Each external or internal cause for rotation change acts at a certain timescale (Lambeck, 1980). Creer (1975) suggested that there might be a connection between changes in the predominant geomagnetic polarity reversals and Earth rotation variations, which were obtained from coral growth data. Greff-Lefftz (2011) constructed a 120 Ma model for the length of day (LOD) variations, where the change components are attributed to mantle density heterogeneities (i.e., upwelling domes and sinking plates) and viscoelasto-gravitational deformations according to Ricard et al. (1993) and Rouby et al. (2010). In that work, the LOD perturbation was estimated as 0.4 μs per year, which is an order of magnitude smaller than the effects of the last glaciation. Figure 1 shows the LOD time derivative from Greff-Lefftz (2011) and the geomagnetic reversal rates for the past 120 Ma. The two curves are similar from ~80 Ma until the present, although between approximately 115 and 80 Ma, which coincides with the CNS, the LOD variation and reversal rates (Figure 1) are approximately constant. Prior to approximately 115 Ma, both the LOD and reversal rate variations show a similar trend, which can be ascertained by the strong correlation (r = +0.82) between both curves (Figure 1). In addition, both phenomena vary at the identical timescale (i.e., at Ma), which indicates that the geomagnetic field reversals “instantaneously respond” to the LOD changes. These observations clearly suggest a possible direct connection between the LOD variations and an internal process in the Earth's core (geodynamo).
Comparison with δ18O Data
At a Phanerozoic time scale, the variations of the Earth's rotation can be a result of glacial isostatic adjustment (GIA) (e.g., Wu and Peltier, 1984; Nakada and Okuno, 2003; Martinec and Hagedoorn, 2014). The glacial-interglacial transitions induce variations in sea level and temperature. The δ18O values for the Phanerozoic calcitic and phosphatic shells from all continents (Veizer et al., 1999, 2000) have been used as a proxy for sea level and temperature variations (Miller et al., 2005; Shaviv, 2005; Müller et al., 2008; Price et al., 2013; Shaviv et al., 2014). A correlation between the sea level and the rotation caused by glacial-interglacial transitions can follow from the Earth's angular momentum conservation, when large displaced water masses induce changes in the inertia tensor, which consequently causes variations in rotation. The geomagnetic field responds to the rotation changes because one of the main forces in the geodynamo dynamical equation (Navier-Stokes) is the Coriolis force.
Figure 2 shows a comparison between the Phanerozoic geomagnetic reversal frequency variation and δ18O values. The δ18O curve is adapted from Veizer et al. (2000) and Price et al. (2013). The curve shows detrended running averages with steps of 10 Myr and windows of 20 Myr. The reversal frequency curve was linearly interpolated with an interval of 10 Myr. The data were divided into three time intervals: 0–120 Ma, 120–270 Ma and 270–510 Ma. The first time interval is shown in Figure 1. The second interval is a continuation of the first interval, for which many reversal frequency data are available. The third interval has little available geomagnetic reversal data. The computed correlation coefficients between the reversal frequency rate and δ18O variations are +0.79 and +0.72 for the 0–120 Ma and 120–270 Ma intervals, respectively. In these cases, the correlations between both curves indicate a similar trend, and both CNS and KRS superchrons coincide with temperature maxima values from δ18O values. These temperature maxima correspond to the inertia momentum maxima and rotation minima during the Phanerozoic. For both intervals (0–120 and 120–270 Ma), the statistical significance of the calculated correlation coefficients was tested using Student's test. The results indicate that the calculated correlation coefficients are reliable considering the 95% confidence level. For the 270–510 Ma interval, the correlation coefficient is −0.26, and the significance test indicates that the 95% confidence level has not been reached. This result may have been strongly affected by the lack of reversals data. This is not an evident clue for the relation between the geomagnetic field reversal rate (consequently, LOD variations) and δ18O oscillations for this time interval.
Final Remarks
The LOD variations over the past 120 Myr show a close relationship with the geomagnetic field reversal frequency. This relationship is ascertained by strong similarities between both curves with a correlation coefficient of +0.82. Because geomagnetic field variations can be an “instantaneous direct response” of the LOD oscillations, they can be used as a marker for other phenomena. According to the LOD modeling, it causes perturbations in the Earth's rotation that are approximately one order of magnitude smaller than those caused by the last glaciation. If this assumption is correct, the glacial-interglacial transitions directly affect the LOD variations. In this case, the reversal frequency rate can be used to compare with climatic proxies such as δ18O data.
The comparison between δ18O and the geomagnetic reversal frequency presents similar trends during 0–120 Ma and 120–270 Ma. For these two periods, the CNS and KRS superchrons coincide with the temperature maxima, which correspond to the inertia momentum maxima and rotation minima. The MRS superchron also corresponds to a temperature maxima, although the correlation between the two curves is low due to scarcity of data. These rotation variations (LOD) can occur because of the hydrodynamic changes (water and ice mass displacements) on the Earth's surface. These hydrodynamic variations consequently reflect the observed glacial and interglacial transitions during the 510 Ma period. There is a fourth Phanerozoic temperature maximum, where reversal data are scarce, that could correspond to a Devonian Superchron.
Therefore, our analysis suggests relationships between the geomagnetic reversal frequency rates and the Earth's rotation changes during the Phanerozoic. However, more reversal data are required for periods before the KRS to strengthen the perspective of using geomagnetic reversal data as a marker for LOD variations through geological times.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
IP is thankful for a CNPq Research Fellowship; GH is thankful for CNPq (454609/2014-0) and CAPES (AUXPE 2043/2014) grants. We would like to thank the Instituto de Astronomia, Geofísica e Ciências Atmosféricas of the Universidade de São Paulo (IAG/USP) the Universidade Federal do Pampa and the Coordenação de Geofísica of the Observatório Nacional (COGE/ON) for the institutional support.
References
Creer, K. M. (1975). “On a tentative correlation between changes in geomagnetic polarity bias and reversal frequency and the earth's rotation through Phanerozoic time” in Growth Rhythms and the History of the Earth's Rotation, eds G. D. Rosenbeg and S. K. Runcorn (London: John Wiley and Sons), 559.
Dumberry, M., and Bloxham, J. (2006). Azimuthal flows in the Earth's core and changes in length of day at millennial timescales. Geophys. J. Int. 165, 32–46. doi: 10.1111/j.1365-246X.2006.02903.x
Granot, R., Dyment, J., and Gallet, Y. (2012). Geomagnetic field variability during the Cretaceous Normal Superchron. Nat. Geosci. 5, 220–223. doi: 10.1038/ngeo1404
Greff-Lefftz, M. (2011). Length of day variations due to mantle dynamics at geological timescale. Geophys. J. Int. 187, 595–612. doi: 10.1111/j.1365-246X.2011.05169.x
Gross, R. S. (2007). “Earth rotation variations—long period,” in Treatise on Geophysics, Vol. 3, Geodesy, eds G. Schubert and T. Herring (Amsterdam: Elsevier), 239–294.
Hide, R., Boggs, D. H., and Dickey, J. O. (2000). Angular momentum fluctuations within the Earth's liquid core and torsional oscillations of the core–mantle system. Geophys. J. Int. 143, 777–786. doi: 10.1046/j.0956-540X.2000.01283.x
Hide, R., and Dickey, J. O. (1991). Earth's variable rotation. Science 253, 629–637. doi: 10.1126/science.253.5020.629
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Holme, R. (1998). Electromagnetic core–mantle coupling—I. Explaining decadal changes in the length of day. Geophys. J. Int. 132, 167–180. doi: 10.1046/j.1365-246x.1998.00424.x
Holme, R. (2007). “Large-scale flow in the Core,” in Treatise on Geophysics, Vol. 8, Core Dynamics, eds G. Schubert and P. Olson (Amsterdam: Elsevier), 107–131.
Holme, R., and De Viron, O. (2005). Geomagnetic jerks and a high-resolution length-of-day profile for core studies. Geophys. J. Int. 160, 435–439. doi: 10.1111/j.1365-246X.2004.02510.x
Holme, R., and De Viron, O. (2013). Characterization and implications of intradecadal variations in length of day. Nature 499, 202–204. doi: 10.1038/nature12282
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Martinec, Z., and Hagedoorn, J. (2014). The rotational feedback on linear momentum balance in glacial isostatic adjustment. Geophys. J. Int. 199, 1823–1846. doi: 10.1093/gji/ggu369
Merrill, R. T., McElhinny, M. W., and McFadden, P. L. (1998). The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle, Vol. 63 (International Geophysics Series.) Amsterdam: Elsevier; Academic Press.
Miller, K. G., Kominz, M. A., Browning, J. V., Wright, J. D., Mountain, G. S., Katz, M. E., et al. (2005). The phanerozoic record of global sea-level change. Science 310, 1293–1298. doi: 10.1126/science.1116412
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Miyagoshi, T., and Hamano, Y. (2013). Magnetic field variation caused by rotational speed change in a magnetohydrodynamic dynamo. Phys. Rev. Lett. 111, 124501. doi: 10.1103/PhysRevLett.111.124501
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Müller, R. D., Sdrolias, M, Gaina, C., Steinberger, B., and Heihe, B. (2008). Long-term sea-level fluctuations driven by ocean basin dynamics. Science 319, 1357–1362. doi: 10.1126/science.1151540
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Nakada, M., and Okuno, J. (2003). Perturbations on the Earth's rotation and their implications for the present day mass balance of both polar ice caps. Geophys. J. Int. 152, 124–138. doi: 10.1046/j.1365-246X.2003.01831.x
Ogg, J. (1995). “Magnetic polarity time scale of the Phanerozoic,” in AGU Reference Shelf, Vol. 1, Global Earth Physics: A Handbook of Physical Constants, ed T. J. Ahrens (Washington, DC: AGU), 240–270.
Pavlov, V., and Gallet, Y. (2005). A third superchron during the Early Paleozoic. Episodes 28, 78–84.
Price, G. D., Twitchett, R. J., Wheeley, J. R., and Buono, G. (2013). Isotopic evidence for long term warmth in the Mesozoic. Nat. Sci. Rep. 3, 1438. doi: 10.1038/srep01438
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Ricard, Y., Richards, M., Lithgow-Bertelloni, C., and Le Stunff, Y. (1993). A geodynamic model of mantle density heterogeneity. J. Geophys. Res. B98, 21895–21909. doi: 10.1029/93JB02216
Rouby, H., Greff-Lefftz, M., and Besse, J. (2010). Mantle dynamics, geoid, inertia and TPW since 120 Myr. Earth Planet. Sci. Lett. 292, 301–311. doi: 10.1016/j.epsl.2010.01.033
Shaviv, N. J. (2005). On climate response to changes in the cosmic ray flux and radiative budget. J. Geophys. Res. 110, A08105. doi: 10.1029/2004JA010866
Shaviv, N. J., Prokoph, A., and Veizer, J. (2014). Is the solar system's galactic motion imprinted in the phanerozoic climate? Sci. Rep. 4, 6150. doi: 10.1038/srep06150
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Veizer, J., Ala, D., Azmy, K., Bruckschen, P., Buhl, D., Bruhn, F., et al. (1999). 87Sr, 86Sr, d13C and d18O evolution of Phanerozoic seawater. Chem. Geol. 161, 59–88. doi: 10.1016/S0009-2541(99)00081-9
Veizer, J., Godderis, Y., and François, L. M. (2000). Evidence for decoupling of atmospheric CO2 and global climate during the Phanerozoic eon. Nature 408, 698–701. doi: 10.1038/35047044
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Wu, P., and Peltier, W. R. (1984). Pleistocence deglaciation and the Earth's rotation: a new analysis. Geophys. J. R. Astr. Soc. 76, 753–791. doi: 10.1111/j.1365-246X.1984.tb01920.x
Keywords: geomagnetic field reversals, Earth's rotation variation, length of day, Earth's temperature variation, Phanerozoic
Citation: Pacca IG, Frigo E and Hartmann GA (2015) Possible relationship between the Earth's rotation variations and geomagnetic field reversals over the past 510 Myr. Front. Earth Sci. 3:14. doi: 10.3389/feart.2015.00014
Received: 18 December 2014; Accepted: 23 March 2015;
Published: 09 April 2015.
Edited by:
Eric Font, University of Lisbon, PortugalReviewed by:
Oscar Pueyo Anchuela, Universidad de Zaragoza, SpainRamon Egli, Central Institute for Meteorology and Geodynamics, Australia
Copyright © 2015 Pacca, Frigo and Hartmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Igor G. Pacca, Departamento de Geofísica, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, Rua do Matão, 1226, Cidade Universitária, São Paulo 05508-090, BrazilaWdwYWNjYUB1c3AuYnI=
 Igor G. Pacca
Igor G. Pacca Everton Frigo
Everton Frigo Gelvam A. Hartmann
Gelvam A. Hartmann