- Earthquake Research Institute, University of Tokyo, Tokyo, Japan
Temporal changes of seismic properties, such as velocity, attenuation, anisotropy, and scattering properties, have been inferred by active methods for decades and more recently by passive methods. In particular, passive methods are capable of monitoring seismic properties because they do not require earthquakes but rely on continuously excited signals in the ocean, for example, a collection of continuous monitoring of seismic velocities has revealed that the susceptibility of velocity changes to stress perturbations are highly variable. These variations can be translated to variability of third-order elastic moduli, elastic moduli arising by considering finite deformation. The third-order elastic moduli are shown by theoretical studies to be a good indicator of granular properties of rocks and, in general, as to how fluids interact with solid rocks. Advancement of theoretical and observational studies will gain more insights into the nature of third-order elastic moduli, which will eventually become yet another parameters to characterize the properties of rocks.
The Earth deforms by various processes including earthquakes, volcanic activity, and tidal attractions. Numerous studies have revealed, through laboratory measurements, that stress changes change seismic velocities and anisotropy of rocks (e.g., Birch, 1960, 1961; Nur and Simmons, 1969). Also, Seismic velocities around active faults are significantly lower due to an intensive cracking (e.g., Li et al., 1990). This indicates that cracks generated by faulting alter the seismic properties. Monitoring seismic properties can therefore gain insights into the mechanics of the deformation of the Earth.
Time-lapse seismic monitoring has been widely conducted with temporary deployment of a number of seismometers and artificial seismic sources (e.g., Greaves and Fulp, 1987; Lumley, 2001; Nishimura et al., 2005). While this approach is capable of detecting time-lapse changes of fine structure, it is not always suitable to continuously monitor seismic properties for two reasons. First, campaigns with artificial seismic sources are usually discrete in time so that high temporal resolution cannot be gained. Second, artificial sources are not strong enough to image deep and extensive areas. To circumvent the first pitfall, that is poor temporal resolution, instruments that continuously emit precisely controlled waves are devised to monitor Earth's interior (e.g., Ikuta et al., 2002; Yamaoka et al., 2014). These instruments are, however, usually too expensive to extract seismic velocity changes in high spatial resolution by deploying a large number of instruments.
Natural earthquakes have more energy than artificial sources so that the former have more potential to probe the seismic structure at depth. For an ideal distribution of earthquakes, we would enable us to monitor seismic velocity changes through time-lapse tomography (Patanè et al., 2006). However, distribution of earthquakes is usually not ideal, making the detection of subtle velocity changes difficult. Using earthquake doublets sharing more or less the same focal mechanism and hypocenter can circumvent the problem because the difference of waveforms of the two earthquakes comes from the structural changes along the ray path between the hypocenter and station (e.g., Poupinet et al., 1984; Sawazaki et al., 2015). Unfortunately, however, this technique can be applied in limited cases because earthquake doublets cannot be found everywhere.
With this background, a technique to derive seismic structure and its temporal changes from random signals such as seismic codas, or ambient noise, has rapidly been emerging in last decade or so. Snieder et al. (2002) coined the term seismic interferometry referring to this method. The idea is that given the incidence of mutually uncorrelated waves with azimuthally isotropic power, cross-correlating observed signals at two stations yields wavefield as if the source is at one station and the receiver is at the other. Seismic interferometry has an advantage over conventional methods in that random signals, in particular ocean hums in frequencies lower than ~1 Hz and anthropogenic noise in those frequencies higher than ~1 Hz (e.g., Bonnefoy-Claudet et al., 2006), are generated continuously in time, so that it is capable of monitoring seismic structure in high temporal resolution.
The idea of seismic interferometry itself was coined decades ago (Aki, 1957; Claerbout, 1968), but it was only around the turn of the century that the technique started to be widely applied to real materials. Weaver and Lobkis (2001) and Snieder et al. (2002) first applied this technique in materials in laboratory scale using acoustic waves. Campillo and Paul (2003) and Shapiro and Campillo (2004) first successfully extracted surface wave propagation between two stations with seismic coda and ambient noise, respectively. Subsequently, Shapiro et al. (2005) succeeded in delineating spatial variations of group velocities of surface waves to demonstrate that ambient seismic noise is capable of imaging Earth's interior in high spatial resolution. Imaging Earth's interior with ambient seismic signals has been prevailing since then in local (e.g., Brenguier et al., 2007; Nagaoka et al., 2012), regional (e.g., Shapiro et al., 2005; Lin et al., 2007; Nishida et al., 2008), and global (e.g., Nishida et al., 2009; Poli et al., 2012) scales.
As the generation of seismic ambient noise is continuous in time, temporal changes of seismic velocities of Earth's interior can be inferred by examining time-lapse seismic wavefield extracted from ambient seismic noise. Studies have shown that seismic interferometry can detect even tiny velocity changes of < 0.1 % due to stress and strain changes by earthquakes (e.g., Brenguier et al., 2008a; Chen et al., 2010), volcanic activity (e.g., Brenguier et al., 2008b), or tidal attractions (Takano et al., 2014; Hillers et al., 2015). There is another advantage of using random signals to infer temporal changes of seismic velocity. Theoretical and experimental considerations show that if the noise distribution does not change too much in time, velocity changes are measured in a robust way even with a non-isotropic distribution of noise incidence when the retrieval of Green's function is difficult (Hadziioannou et al., 2009; Froment et al., 2010; Weaver et al., 2011).
There are many studies to detect subtle changes in seismic velocities, but there are still issues to be solved to enhance our understanding of seismic velocity changes. These include (1) locating seismic velocity changes, (2) locating changes of scattering properties, and (3) understanding the cause of velocity changes. Recent studies succeeded in delineating horizontal or depth-averaged distribution of velocity changes by mapping travel time changes of each station pair onto the horizontal plane. However, locating velocity changes in three dimensions is not straightforward. Taking advantages that correlograms at larger lag time samples wider areas due to scattering (e.g., Pacheco and Snieder, 2005), Obermann et al. (2013) developed a method to estimate the depth variations of velocity changes from time-lapse correlograms. Obermann et al. (2014) applied the method to the 2008 Wenchuan earthquake.
Time-lapse correlograms are not only sensitive to velocity changes but also sensitive to mechanical changes, such as crack generation, manifested by scattering properties. When the scattering properties such as location or intensity of scatterers change, time-lapse collerograms are represented by docorrelation with respect to the reference correlogram. Larose et al. (2010) and Rossetto et al. (2011) developed a method to delineate the spatial distribution of changes in scattering intensities in two dimensions. Obermann et al. (2014) applied the method to the 2008 Wenchuan earthquake. A method to locate changes in scattering properties in three dimensional halfspace has not been developed yet.
While it is obvious that not only permanent and static stress changes but also transient and dynamic stress changes play substantial roles in observed velocity changes. For example, Rubinstein and Beroza (2004) and Brenguier et al. (2008b) observed a sudden coseismic velocity drops followed by gradual recovery associated with the 1989 Loma Prieta and 2004 Parkfield earthquakes, respectively. The coseismic velocity drops they observed are due to a combination of permanent deformation and damage generated by dynamic stress perturbation, while the slow velocity recovery is due to the healing of cracks generated by the dynamic perturbation due to the earthquake. However, the contribution of static and dynamic stress changes to velocity changes is not straightforward. Brenguier et al. (2014) found that the seismic velocity changes at a frequency range between 1 and 10 km, most sensitive to the first ~10 km, associated with the 2011 Tohoku-oki, Japan, earthquake, do not correlate well with static nor dynamic stress changes. They also found that the velocity changes do not correlated well with shallow seismic velocities, although larger velocity drops tend to be observed in volcanic areas. This observations demonstrate that the dynamic stress perturbation contributes to seismic velocity changes in a complicated manner.
In a general elastic medium, the strain energy E is given by (e.g., Brugger, 1964; Johnson and Rasolofosaon, 1996)
where eij is the ij component of the strain tensor and Cijkl and Cijklmn denote the components of the second-order and third-order elastic tensor, respectively. Note that Einstein's summation convention on repeated indices is assumed. The strain energy for an isotropic medium is simplified as (Murnaghan, 1951)
where λ and μ represent the second-order elastic constants or Lamé's constants and l, m, and n denote the third-order elastic constants. I1, I2, and I3 are strain invariants given by
The contribution of finite strain is in the last three terms of Equation (2).
In the absence of damages due to dynamic stress perturbation, the seismic velocity Vij, where i and j denote the direction of wave propagation and particle displacements, respectively, of an initially isotropic body subjected to a triaxial strain ei is given by Hughes and Kelly (1953); Egle and Bray (1976)
where ρ0 is the initial density. Note that V11 corresponds to the P-wave velocity and and V12 and V13 corresponds to S-wave velocity.
When an isotropic strain, where e1 = e2 = e3 = θ∕3 with volumetric strain given by θ, is considered, Equations (6–8) is rewritten by
where VP and VS denote P- and S-wave velocities, respectively. Sensitivity of P- and S-wave velocities to volumetric strain is given with an approximation of infinitesimal θ by
Laboratory measurements show that the third-order elastic constants typically range between −10 and −1000 times of rigidity μ (e.g., Winker and McGowan, 2004; D'Angelo et al., 2008), so that the susceptibility of P- and S-wave velocities to volumetric strain changes is comparable with roughly between −500 and −5/strain. These values are translated to the susceptibility to volumetric stress changes as between −200 and −2 × 10−10/Pa in a Poisson solid, a solid with λ = μ with a rigidity of 30 GPa.
Since coseismic velocity changes may involve an effect of damages to the rock induced by dynamic stress perturbation, slower deformation such as tidal deformation is better to delineate the third-order elastic parameters. Velocity perturbation due to deformation induced by tides has long been measured by active methods (e.g., DeFazio et al., 1973; Reasenberg and Aki, 1974; Yamamura et al., 2003) and more recently by passive methods (Takano et al., 2014; Hillers et al., 2015). The sensitivity of the velocity changes ranges between −10−6 and −10−10/Pa, implying that the third-order elastic moduli are more variable than those inferred from laboratory experiments.
A few previous studies (e.g., Tsai, 2011; Sawazaki et al., 2015) tried to constrain the third-order elastic moduli from observed seismic velocity changes. While the values they obtained are consistent with those derived from laboratory experiments, to my knowledge, no studies have ever given a physical interpretation of the obtained moduli. What is then the physics behind the stress sensitivity of seismic velocity? Previous studies include those by Guyer and Johnson (1999) and Norris (2007). Among them, I here refer Norris (2007) to give a brief overview of a possible physical background on what is behind the stress sensitivity of seismic velocity. Inspired by laboratory measurements that granular materials such as rocks have larger third-order elastic constants (e.g., Norris, 1998), Norris (2007) developed a theoretical framework in which each spherical grains of radius R is in contact with a neighboring grain by a region of radius a (Figure 1). In this framework, the ratio of third-order elastic moduli to the second-order elastic moduli, or Lamé's constants for isotropic solids, is of the order of (R∕a)2, implying that rocks with low confining pressure, or those with less packing, exhibit larger velocity susceptibility to stress perturbation. This conjecture is consistent with observations that the 2011 Tohoku-oki earthquake induced large seismic velocity drops at the first few hundred meters from the surface (e.g., Nakata and Snieder, 2011; Takagi and Okada, 2012; Sawazaki et al., 2015). Norris (2007) pointed out that a fluid-solid composite system yields a non-zero velocity sensitivity to stress perturbations but combining theoretical considerations with observations is tedious.
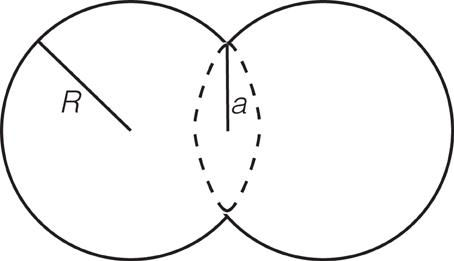
Figure 1. A shematic view of two spherical grains of radius R are in contact by an area of radius a.
In summary, monitoring changes of seismic properties, such as velocity, attenuation, and scattering properties, either by active and passive methods is a powerful tool to gain more insights into the mechanics of seismic and volcanic phenomena. Furthermore, third-order elastic moduli inferred through the susceptibility of seismic velocity changes to stress perturbation has a potential to yet another parameters to characterize the property of the Earth in terms of, for example, granularity, grain contacts, and fluid inclusion in the crust. Further studies both from theoretical and observational aspects are necessary to understand what the third-order elastic moduli indicate.
Funding
This study is supported by Grants-in-Aid for Young Scientists (B) 25800244.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Reviews by two referees significantly improved the manuscript.
References
Aki, K. (1957). Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull. Earthq. Res. Inst. Univ. Tokyo 35, 415–456.
Birch, F. (1960). The velocity of compressional waves in rocks to 10 kilobars: part 1. J. Geophys. Res. 65, 1083–1102. doi: 10.1029/JZ065i004p01083
Birch, F. (1961). The velocity of compressional waves in rocks to 10 kilobars: part 2. J. Geophys. Res. 66, 2199–2224. doi: 10.1029/JZ066i007p02199
Bonnefoy-Claudet, S., Cotton, F., and Bard, P. -Y. (2006). The nature of noise wakefield and its applications for site effects studies: a literature review. Earth-Sci. Rev. 79, 205–227. doi: 10.1016/j.earscirev.2006.07.004
Brenguier, F., Shapiro, N. M., Campillo, M., Nercessian, A., and Ferrazzini, V. (2007). 3-D surface wave tomography of the Piton de la Fournaise volcano using seismic noise correlations. Geophys. Res. Lett. 34, L02305. doi: 10.1029/2006GL028586
Brenguier, F., Campillo, M., Hadziioannou, C., Shapiro, N. M., Nadeau, R. M., and Larose, E. (2008a). Postseismic relaxation along the San Andreas fault at Parafield from continuous seismological observations. Science 321, 1478–1481. doi: 10.1126/science.1160943
Brenguier, F., Shapiro, N. M., Campillo, M., Ferrazzini, V., Duputel, Z., Coutant, O., et al. (2008b). Towards forecasting volcanic eruptions using seismic noise. Nat. Geosci. 1, 126–130. doi: 10.1038/ngeo104
Brenguier, F., Campillo, M., Takeda, T., Aoki, Y., Shapiro, N. M., Briand, X., et al. (2014). Mapping pressurized volcanic fluids from induced crustal seismic velocity drops. Science 345, 80–82. doi: 10.1126/science.1254073
Brugger, K. (1964). Thermodynamic definition of higher order elastic coefficients. Phys. Rev. 133, A1611–A1612. doi: 10.1103/physrev.133.a1611
Campillo, M., and Paul, A. (2003). Long-range correlations in the diffuse seismic coda. Science 299, 547–549. doi: 10.1126/science.1078551
Chen, J. H., Froment, B., Liu, Q. Y., and Campillo, M. (2010). Distribution of seismic wave speed changes associated with the 12 May 2008 Mw 7.9 Wenchuan earthquake. Geophys. Res. Lett. 37, L18302. doi: 10.1029/2010GL044582
Claerbout, J. F. (1968). Synthesis of a layered medium from its acoustic transmission response. Geophysics 33, 264–269. doi: 10.1190/1.1439927
D'Angelo, R. M., Winkler, K. W., and Johnson, D. L. (2008). Three wave mixing test of hyper elasticity in highly nonlinear solids: Sedimentary rocks. J. Acoust. Soc. Am. 123, 622–639. doi: 10.1121/1.2821968
DeFazio, T. L., Aki, K., and Alba, K. (1973). Solid earth tide and observed change in the in situ seismic velocity. J. Geophys. Res. 78, 1319–1322. doi: 10.1029/JB078i008p01319
Egle, D. M., and Bray, D. E. (1976). Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 60, 741–744. doi: 10.1121/1.381146
Froment, B., Campillo, M., Roux, P., Gouédard, P., Verdel, A., and Weaver, R. L. (2010). Estimation of the effect of nonisotropically distributed energy on the apparent arrival time in correlations. Geophysics 75, SA85–SA93. doi: 10.1190/1.3483102
Greaves, R. J., and Fulp, T. J. (1987). Three-dimensional seismic monitoring of an enhanced oil recovery process. Geophysics 52, 1175–1187. doi: 10.1190/1.1442381
Hadziioannou, C., Larose, E., Coutant, O., Roux, P., and Campillo, M. (2009) Stability of monitoring weak changes in multiply scattering media with ambient noise correlation: Laboratory experiments. J. Acoust. Soc. Am. 125, 3688–3695. doi: 10.1121/1.3125345
Hillers, G., Retailleau, L., Campillo, M., Inbal, A., Ampuero, J. P., and Nishimura, T. (2015). In situ observations of velocity changes in response to tidal deformation from analysis of the high-frequency ambient wakefield. J. Geophys. Res. 120, 210–225. doi: 10.1002/2014JB011318
Hughes, D. S., and Kelly, J. L. (1953). Second-order elastic deformation of solids. Phys. Rev. 92, 1145–1149. doi: 10.1103/PhysRev.92.1145
Ikuta, R., Yamaoka, K., Miyakawa, K., Kunitomo, T., and Kumazawa, M. (2002). Continuous monitoring of propagation velocity of seismic wave using ACROSS. Geophys. Res. Lett. 29, 1627. doi: 10.1029/2001GL013974
Johnson, P. A., and Rasolofosaon, P. N. J. (1996). Nonlinear elasticity and stress-induced anisotropy in rock. J. Geophys. Res. 101, 3113–3124. doi: 10.1029/95JB02880
Larose, E., Planes, T., Rosetto, V., and Margerin, L. (2010). Locating a small change in a multiple scattering environment. Appl. Phys. Lett. 96, 204101. doi: 10.1063/1.3431269
Li, Y. G., Leary, P., Aki, K., and Malin, P. (1990). Seismic trapped modes in the Oroville and San Andreas fault zones. Science 249, 763–766. doi: 10.1126/science.249.4970.763
Lin, F. C., Ritzwoller, M. H., Townend, J., Bannister, S., and Savage, M. K. (2007). Ambient noise Rayleigh wave tomography of New Zealand. Geophys. J. Int. 170, 649–666. doi: 10.1111/j.1365-246X.2007.03414.x
Lumley, D. E. (2001). Time-lapses seismic reservoir monitoring. Geophysics 66, 50–53. doi: 10.1190/1.1444921
Nagaoka, Y., NIshida, K., Aoki, Y., Takeo, M., and Ohminato, T. (2012). Seismic imaging of magma chamber beneath an active volcano. Earth Planet. Sci. Lett. 333–334, 1–8. doi: 10.1016/j.epsl.2012.03.034
Nakata, N., and Snieder, R. (2011). Near-surface weakening in Japan after the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 38, L17302. doi: 10.1029/2011GL048800
Nishida, K., Kawakatsu, H., and Obara, K. (2008). Three-dimensional crustal S velocity structure in Japan using microseismic data recorded by Hi-net tiltmeters. J. Geophys. Res. 113, B10302. doi: 10.1029/2007JB005395
Nishida, K., Montagner, J. P., and Kawakatsu, H. (2009). Global surface wave tomography using seismic hum. Science 326, 112. doi: 10.1126/science.1176389
Nishimura, T., Tanaka, S., Yamawaki, T., Yamamoto, H., Sano, T., Sato, M., et al. (2005). Temporal changes in seismic velocity of the crust around Irate volcano, Japan, as inferred from analyses of repeated active seismic experiment data from 1998 to 2003. Earth Planet. Space 57, 491–505. doi: 10.1186/BF03352583
Norris, A. N. (1998). “Finite-amplitude waves in solids,” in Nonlinear Acoustics, eds M. F. Hamilton and D. T. Blackstock (New York, NY: Academic Press), 263–277.
Norris, A. (2007). “Small-on-large theory with applications to granular materials and fluid/solid systems,” in Waves in Nonlinear Pre-stressed Materials, CISM Course and Lecture, Vol. 495, eds M. Destrade and G. Saccomandi (Vienna; New York, NY: Springer), 27–62.
Nur, A., and Simmons, G. (1969). Stress-induced velocity anisotropy in rocks: an experimental study. J. Geophys. Res., 74, 6667–6674. doi: 10.1029/JB074i027p06667
Obermann, A., Planès, T., Larose, E., Sens-Schönfelder, C., and Campillo, M. (2013). Depth sensitivity of seismic coda waves to velocity perturbations in an elastic heterogeneous medium. Geophys. J. Int. 194, 372–382. doi: 10.1093/gji/ggt043
Obermann, A., Froment, B., Campillo, M., Larose, E., Planès, T., Valette, B., et al. (2014). Seismic noise correlations to image structural and mechanical changes associated with the Mw 7.9 2008 Wenchuan earthquake. J. Geophys. Res. 119, 3155–3168. doi: 10.1002/2013JB010932
Pacheco, C., and Snieder, R. (2005). Time-lapse travel time change of multiply scattered acoustic waves. J. Acoust. Soc. Am. 118, 1300–1310. doi: 10.1121/1.2000827
Patanè, D., Barberi, G., Cocina, O., de Gori, P., and Chiarabba, C. (2006). Time-resolved seismic tomography detects magma intrusions at Mount Etna. Science 313, 821–823. doi: 10.1126/science.1127724
Poli, P., Campillo, M., Pedersen, H., and LAPNET Working Group. (2012). Body-wave imaging of Earth's mantle discontinuities from ambient seismic noise. Science 338, 1063–1065. doi: 10.1126/science.1228194
Poupinet, G., Ellsworth, W. L., and Frechet, J. (1984). Monitoring velocity variations in the crust using earthquake doublets: an application to the Calaveras fault, California. J. Geophys. Res. 89, 5719–5731. doi: 10.1029/JB089iB07p05719
Reasenberg, P., and Aki, K. (1974). A precise, continuous measurement of seismic velocity for monitoring in situ stress. J. Geophys. Res. 79, 399–406. doi: 10.1029/JB079i002p00399
Rossetto, V., Margerin, L., Planès, T., and Larose, É. (2011). Locating a weak change using diffuse waves: theoretical approach and inversion procedure. J. Appl. Phys. 109, 034903. doi: 10.1063/1.3544503
Rubinstein, J. L., and Beroza, G. C. (2004). Evidence for widespread nonlinear strong ground motion in the Mw 6.9 Loma Prieta earthquake. Bull. Seismol. Soc. Am. 94, 1595–1608. doi: 10.1785/012004009
Sawazaki, K., Kimura, H., Shiomi, K., Uchida, N., Takagi, R., and Snieder, R. (2015). Depth-dependence of seismic velocity change associated with the 2011 Tohoku earthquake, Japan, revealed from repeating earthquake analysis and finite-difference wave propagation simulation. Geophys. J. Int. 201, 741–763. doi: 10.1093/gji/ggv014
Shapiro, N. M., and Campillo, M. (2004). Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett. 31, L07614. doi: 10.1029/2004GL019491
Shapiro, N. M., Campillo, M., Stehly, L., and Ritzwoller, M. H. (2005). High-resolution surface-wave tomography from ambient seismic noise. Science 307, 1615–1618. doi: 10.1126/science.1108339
Snieder, R., Grêt, A., Douma, H., and Scales, J. (2002). Coda wave interferometry for estimating nonlinear behavior in seismic velocity. Science 295, 2253–2255. doi: 10.1126/science.1070015
Takagi, R., and Okada, T. (2012). Temporal change in shear velocity and polarization anisotropy related to the 2011 M9.0 Tohoku-Oki earthquake examined using KiK-net vertical array data. Geophys. Res. Lett. 39, L09310. doi: 10.1029/2012gl051342
Takano, T., Nishimura, T., Nakahara, H., Ohta, Y., and Tanaka, S. (2014). Seismic velocity changes caused by the Earth tide: ambient noise correlation analyses of small-array data. Geophys. Res. Lett. 41, 6131–6136. doi: 10.1002/2014GL060690
Tsai, V. C. (2011). A model for seasonal changes in GPS positions and seismic wave speeds due to thermoelastic and hydrologic variations. J. Geophys. Res. 116, B04404. doi: 10.1029/2010jb008156
Weaver, R. L., Hadziioannou, C., Larose, E., and Campillo, M. (2011). On the precision of noise correlation interferometry. Geophys. J. Int. 185, 1384–1392. doi: 10.1111/j.1365-246X.2011.05015.x
Weaver, R. L., and Lobkis, O. I. (2001). Ultrasonics without a source: thermal fluctuation correlations at MHz frequencies. Phys. Rev. Lett. 87, 134301. doi: 10.1103/PhysRevLett.87.134301
Winker, K. W., and McGowan, L. (2004). Nonlinear acoustoelastic constants of dry and saturated rocks. J. Geophys. Res. 109, B10204. doi: 10.1029/2004JB003262
Yamamura, K., Sano, O., Utada, H., Takei, Y., Nakao, S., and Fukao, Y. (2003). Long-term observation of in situ seismic velocity and attenuation. J. Geophys. Res. 108, 2317. doi: 10.1029/2002JB002005
Keywords: seismic interferometry, third-order elasticity, continuous monitoring, stress change, granular materials
Citation: Aoki Y (2015) Monitoring temporal changes of seismic properties. Front. Earth Sci. 3:42. doi: 10.3389/feart.2015.00042
Received: 24 March 2015; Accepted: 16 July 2015;
Published: 29 July 2015.
Edited by:
Sonja Leonie Philipp, Georg-August-University of Göttingen, GermanyReviewed by:
Maurizio Battaglia, US Geological Survey, USAAgust Gudmundsson, Royal Holloway University of London, UK
Copyright © 2015 Aoki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yosuke Aoki, Earthquake Research Institute, University of Tokyo, 1-1 Yayoi 1, Bunkyo-ku, Tokyo 113-0032, Japan,eWFva2lAZXJpLnUtdG9reW8uYWMuanA=
 Yosuke Aoki
Yosuke Aoki