- 1Department of Mineral Sciences, National Museum of Natural History, Smithsonian Institution, Washington, DC, USA
- 2Department of Earth Sciences, ETH-Zurich, Institute for Geochemistry and Petrology, Zurich, Switzerland
- 3Formerly affiliated with the Department of Earth and Planetary Science, University of California, Berkeley, Berkeley, CA, USA
- 4Department of Earth Sciences, University of Geneva, Geneva, Switzerland
- 5Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland
The transition from viscous to brittle behavior in magmas plays a decisive role in determining the style of volcanic eruptions. While this transition has been determined for one- or two-phase systems, it remains poorly constrained for natural magmas containing silicic melt, crystals, and gas bubbles. Here, we present new experimental results on shear-induced fracturing of three-phase magmas obtained at high-temperature (673–1023 K) and high-pressure (200 MPa) conditions over a wide range of strain-rates (5·10−6 s−1–4·10−3 s−1). During the experiments bubbles are deformed (i.e., capillary number is in excess of 1) enough to coalesce and generate a porous network that potentially leads to outgassing. A physical relationship is proposed that quantifies the critical stress required for magmas to fail as a function of both crystal (0.24–0.65) and bubble volume fractions (0.09–0.12). The presented results demonstrate efficient outgassing for low crystal fraction (< 0.44), whereas high crystal fractions (>0.44) promote gas bubble entrapment and inhibit outgassing. The failure of bubble-free, crystal-bearing systems is enhanced by the presence of bubbles that lower the critical failure stress in a regime of efficient outgassing, while the failure stress is increased if bubbles remain trapped within the crystal framework. These contrasting behaviors have direct impact on the style of volcanic eruptions. During magma ascent, efficient outgassing reduces the potential for an explosive eruption and favors brittle behavior, contributing to maintain low overpressures in an active volcanic system resulting in effusion or rheological flow blockage of magma at depth. Conversely, magmas with high crystallinity experience limited loss of exsolved gas, permitting the achievement of larger overpressures prior to a potential sudden transition to brittle behavior, which could result in an explosive volcanic eruption.
Introduction
Volcanic eruptive styles are strongly dependent on the dynamics of magma flow and the modalities of degassing (e.g., Papale, 1999). The most critical parameter defining the physical properties of magmas is viscosity. The measured flow resistance of the macroscopic magmatic suspension is the bulk or apparent viscosity (ηapp), defined as the ratio of the bulk stresses and strain-rates. The apparent viscosity is a measure of magma's capacity to dissipate the applied stress during flow. However, when stress accumulates more rapidly than can be viscously dissipated by the system, magmas experience a rheological transition into brittle behavior where viscous flow is not permitted and, thus, viscosity becomes unimportant. Linear viscoelastic theory provides mechanical models for the prediction of the isothermal transition from liquid (viscous) to glassy (Hookean) behavior (Dingwell and Webb, 1990). This implies that melts are viscoelastic media and, thus, their response to an external disturbance (i.e., stress) can be elastic or viscous, depending on the timescale or frequency competition between relaxation and external applied disturbance (Maxwell, 1867). This infers that a melt can experience: (i) a “brittle failure” in the Hookean regime, or (ii) a “ductile failure” in the viscous regime. Applying stress-strain curves, Ranalli (1995) pointed out the difference between brittle failure, characterized by sudden vertical drop of stress (theoretically to zero), and ductile failure, evidenced by a progressive evolution of stress (from its ideal constant value with increasing strain) by either increasing (strain hardening) or decreasing stress (strain softening) with increasing strain. The viscous to brittle transition (VBT) in magmas is determined by the stress accumulated in the magma relative to a critical threshold characteristic for brittle behavior (Dingwell and Webb, 1990). Such a threshold is function of the magmatic properties and textures (Cordonnier et al., 2012a). In order to define the viscous and brittle regimes in chemical and physical space and to determine if the conditions for failure are encountered during magma ascent, a quantitative understanding of the failure of multiphase magmas, containing both crystals and gas bubbles, is required. Experimental (e.g., Smith et al., 2009) and theoretical approaches (e.g., Dingwell, 1996; Gonnermann and Manga, 2003) provided preliminary insights into the dynamics of the VBT in magmas. Cordonnier et al. (2012b) constrained the VBT of bubble-free and crystal-bearing systems, suggesting that stress localization in the silicic melt phase lowers the bulk stress required to rupture magmas. Under this assumption, the melt always breaks at the same value of critical stress, and the local stress required to rupture the melt remains the same as the bulk stress required to rupture crystal-free melts. Additionally, the experiments of Cordonnier et al. (2012b) exhibited shear-induced fractures that healed over relatively short timescales, confirming the possibility for cyclic fracture-healing processes, representing a potential source of volcanic tremors (Tuffen et al., 2003).
To date, only a few studies on magma rheology have accounted for the simultaneous presence of crystals and bubbles. Bagdassarov et al. (1994) determined the rheology of three-phase mixtures over a restricted range of temperatures, crystal and bubble contents, limiting the possibility of using their results to calibrate rheological models for three-phase magmas. Avard and Whittington (2011) and Vona et al. (2013) conducted high-temperature compression tests on rock samples with variable crystal contents (28–59 vol.%) and connected pressurized gas-free porosity (5–40 vol.%). The rheological results from these two studies reveal that the presence of vesicles allows the application of large deformation and, for similar strain-rates, strongly reduces the bulk stress. Achieving the brittle stress threshold consequently requires rather high values of strain-rate (>10−4 s−1) at 800°C (i.e., ηmelt > 1010 Pa·s). Recently, Pistone et al. (2012) conducted deformation experiments over a wide range of crystallinity (24–65 vol.%) and a limited range of bubble content (9–12 vol.%), and demonstrated that the effect of pores/vesicles (i.e., not pressurized “fossil” bubbles) in natural volcanic rock samples cannot directly be compared with the behavior of bubbles (i.e., gas-pressurized pockets in the melt phase) in natural magmas. The addition of relatively small bubble volume fractions to crystal-bearing suspensions “lubricate” the entire system during deformation and significantly decrease magma viscosity (Pistone et al., 2012, 2013).
The original work of Pistone et al. (2012) provided a detailed rheological and microstructural analysis of multiphase magmas in the viscous regime prior to the brittle failure. In this contribution we explore the brittle failure of the same magmatic systems and constrain the effect of crystals and gas bubbles on the VBT in multiphase high-viscosity haplogranitic magmas.
Experimental and Analytical Methods
Experimental Strategy
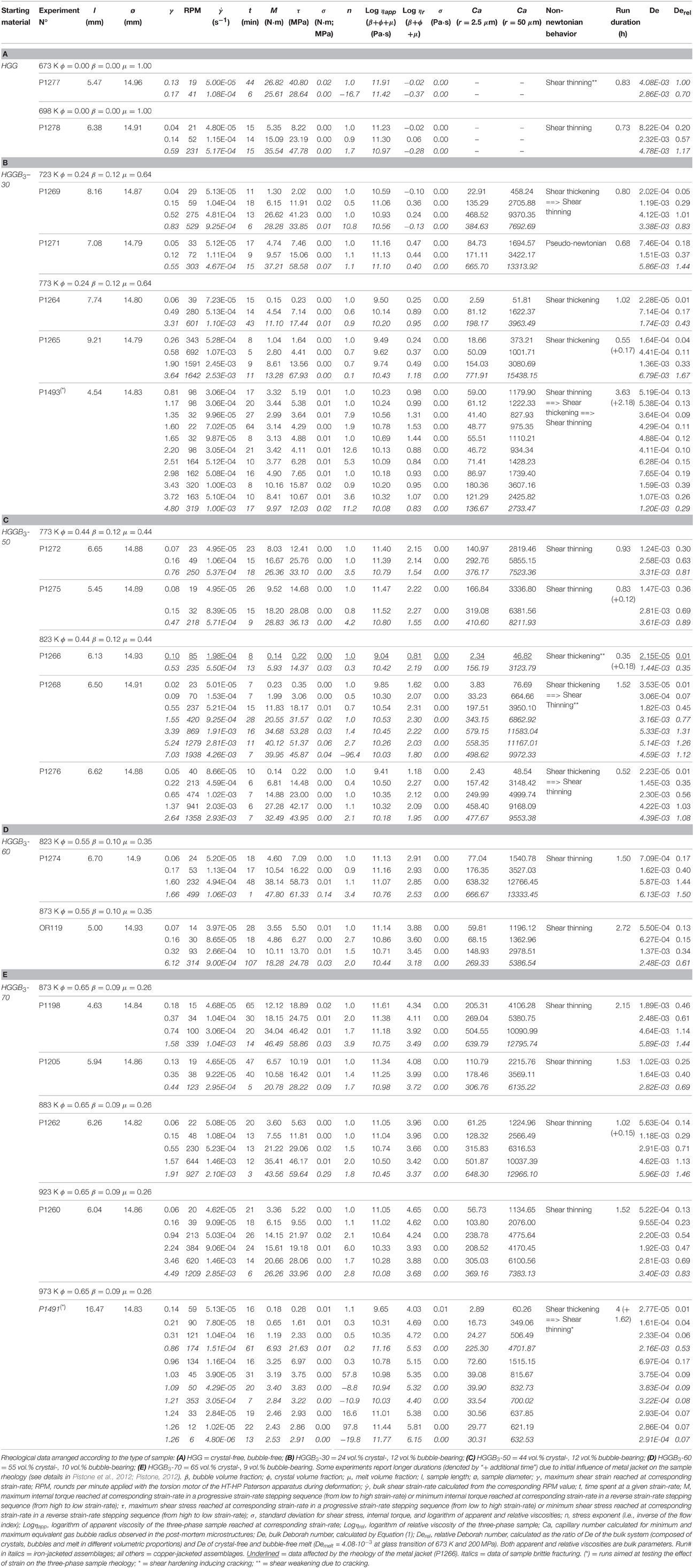
Seventeen torsion experiments on synthetic hydrous (H2O = 2.26 ± 0.04 wt.%) haplogranitic glasses (HGGB3; Pistone et al., 2012) containing quartz crystals (crystal fraction, ϕ = 0.24–0.65) and CO2-rich gas bubbles (bubble fraction, β = 0.09–0.12) were performed using a HT-HP Paterson-type apparatus (Paterson and Olgaard, 2000). Experiments were conducted under isothermal (673–1023 K) and isobaric (200 MPa) conditions, and run at constant shear strain-rate (), over a range relevant for volcanic processes ( 5·10−6 s−1−4·10−3 s−1). Experiments were performed under a stepping method, where the is increased to a higher value once a constant value of stress (τ) is achieved after a reasonable amount of accumulated strain (γ). Rheological curves of the experiments performed in this study are reported in Pistone et al. (2012).
In the range of temperature and pressure conditions used for the experiments, the expected CO2-rich bubble/silicate melt viscosity ratio is between 1.02·10−16 at 673 K and 8.48·10−10 at 1023 K (Table 1) for the experiments here conducted at 200 MPa (Table 2). The viscosity of haplogranitic melt was determined between 673 and 773 K, and extrapolated to higher temperatures (823–1023 K) using a Vogel-Fulcher-Tamman type equation (A = −6.55; B = 11185.2 J; C = 67.3 K). The discrepancy between our fit results and the predictions by the model of Giordano et al. (2008), may find its explanation by correcting the parameter A (which is temperature- and composition-independent; Giordano et al., 2008) for the H2O content and pressure effects highlighted by the studies of Ardia et al. (2008, 2014) and Pistone et al. (2012). Although the study of Russell et al. (2003) evidences that the constant A should be restricted to ±1 log units and establishes the high-temperature viscosity limits for melts at 10−3.5-10−5.5 Pa·s, there is no pressure effect on melt viscosity (e.g., Scarfe et al., 1987) included in their model. The values of CO2-rich bubble viscosity at experimental temperature and pressure conditions are estimated from the NIST (National Institute of Standards and Technology) database. Table 1 lists the values of melt and CO2-gas bubble viscosities (ηmelt and ηCO2), bubble-melt interfacial tension (Γ; Bagdassarov et al., 2000) and the viscosity gas/melt ratio at the experimental conditions of this study.
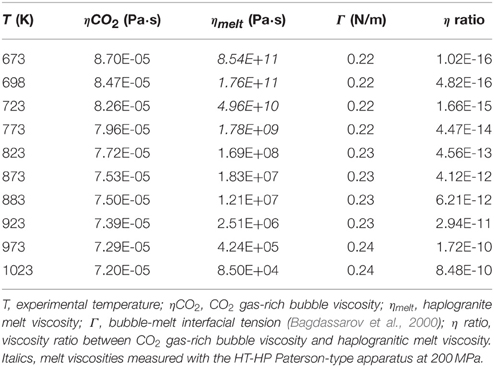
Table 1. Viscosities of CO2 gas-rich bubbles and haplogranitic melt and their viscosity contrast at different temperatures at 200 MPa.
We investigated four different crystal volume fractions (0.24, 0.44, 0.55, and 0.65±0.02) with similar bubble volume fraction (0.09–0.12 ± 0.02). Experimental conditions are reported in Table 2. Experiments were additionally performed on bubble- and crystal-free silicate melts (Table 2) to establish the reference conditions for brittle onset and determine the effect of different volumetric proportions of crystals on the VBT at similar contents of gas bubbles. Capillary numbers were calculated from the measured minimum and maximum gas bubble equivalent radii in the post-mortem microstructures. Details of the preparation and synthesis of the starting materials are reported in Pistone et al. (2012) and Pistone (2012).
X-ray Tomography and Analysis
Run products were imaged by Synchrotron-based X-ray Tomographic Microscopy (SRXTM). Cylindrical cores of 2 mm outer diameter and 2–4 mm length were drilled from the outer portions of deformed and cracked samples, where the torsional deformation is highest. Cylinders are isotropic in the scan plane and, thus, represent the best geometry to capture maximum volume (Ketcham and Carlson, 2001). SRXTM provided high-resolution volumetric (3D) information in a non-destructive manner. Tomographic data were acquired at the TOMCAT (TOmographic Microscopy and Coherent rAdiology experimenTs; Stampanoni et al., 2006) beamline at the Swiss Light Source (Paul Scherrer Institute, Villigen, Switzerland). Specimens were mounted on a carbon fiber rod and rotated 180° during acquisition. Between 2000 and 3000 raw projections were acquired for each scan. The energy was set to 20 keV and the exposure time to 100 ms. The acquired images consist of 2048 × 2048 pixels with a 10x magnification, resulting in an isotropic voxel size of 0.74 μm. Tomographic reconstructions were performed using a highly optimized algorithm based on Fourier methods (Marone and Stampanoni, 2012). ImageJ 1.43s software was used to process the raw tomographic slices (i.e., removal of background noise, and adjustment of brightness/contrast) and to generate image stacks. The 3D visualization and analysis of gas bubbles were performed using Avizo® Fire (Visualization Sciences Group) software. Quartz crystals were not selected for the 3D rendering visualization because of their low-density contrast (i.e., low-grayscale contrast) with respect to the silicate glass matrix. Given the poor contrast between quartz and glass in the experimental charges analyzed by SRXTM, we refer to the studies of Pistone et al. (2012, 2013) where SEM-BSE images are presented, revealing the relationships between all phases (glass, crystals, and bubbles) in three-phase samples affected by brittle failure.
Results
Rheology
Figure 1 displays stress (τ) vs. strain (γ) diagrams of typical experiments for low and high crystallinity as well as the relative viscosity (ηrel) vs. strain rate () diagram for typical experiments. ηrel is the ratio between ηapp and ηmelt under identical melt composition, H2O content in the melt, pressure, temperature, applied τ, and . All runs reveal a first elastic phase of near linear τ increase with γ, followed by a yielding stage and viscous flow at constant τ (Figures 1A,B). Experiments were stopped once a significant drop of τ was measured. Post-experiment visual analysis confirmed that this drop is clearly associated to macroscopic sample brittle failure (as defined above; Ranalli, 1995) during shear deformation.
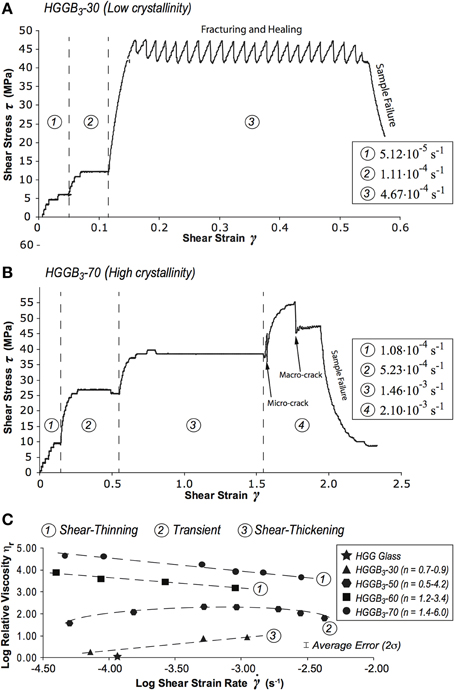
Figure 1. Shear stress (τ) vs. strain (γ) diagrams for (A) low crystallinity (run P1271; ϕ = 0.24; β = 0.12) and (B) high crystallinity (run P1262; ϕ = 0.65; β = 0.09). (C) Logarithm of relative viscosity (ηrel = ratio between the apparent viscosity of the system composed of crystals, bubbles and melt, and the melt viscosity under identical chemical and physical conditions) vs. logarithm of diagram for representative experiments (from Pistone et al., 2012, modified) showing: shear-thinning (ϕ > 0.44), shear-thickening (ϕ < 0.44), and transient rheological behavior (ϕ = 0.44), with corresponding range of stress exponent (n) values (as reported in Table 2).
In crystal-poor (ϕ < 0.44 and β = 0.12) systems, the maximum value of τ reached prior to fracture is 47 MPa (Figure 1A). Fracturing starts at = 4.67·10−4 s−1 and is evidenced by shear stress oscillations of about 8 MPa for a total γ of 0.4. We interpret these data as continuous partial fracturing and healing of the samples, prior to the complete failure of the sample, resulting in the catastrophic drop of the τ applied to the sample during deformation (Figure 1A).
In crystal-rich (ϕ > 0.44 and β = 0.09–0.1) systems, the maximum τ prior to sample fracturing is about 60 MPa at = 2.10·10−3 s−1 (Figure 1B). In the final phases of the experiments, a τ drop of about 10 MPa occurs, with limited hardening just prior to complete failure of the sample (Figure 1B).
Two -dependent non-Newtonian behaviors were observed in the experiments (Figure 1C): (i) shear-thickening (increase of ηrel with increasing ) at low crystallinity (ϕ < 0.44), and (ii) shear-thinning (decrease of ηrel with increasing ) at high crystallinity (ϕ > 0.44). At intermediate crystallinity (ϕ = 0.44) a transient behavior from shear-thickening to shear-thinning is observed. Previous experiments revealed that the impact of on magma rheology tends to be more important than the effect of γ when deformation rate is rapidly changed during experiments (Okumura et al., 2006, 2008, 2010; inset in Figure 1A). Indeed, our rheological results show that no τ variations were observed with increasing γ at constant applied (i.e., absence of shear-weakening or shear-hardening after an accumulated γ > 0.5 for any ), even when the strain-rate stepping experiments were performed for different total durations (i.e., different total γ; Table 2). Additional tests were performed to assess the relative contribution of γ and on the rheological behavior of three-phase magmas (see runs P1491 and P1493; Table 2), which confirmed the absence of a strong γ dependent behavior (e.g., thixotropy or rheopectic behavior). Strain-rate changes result in variations of ηrel of about 1 order of magnitude (Figure 1C). Instead, with increasing γ, there is no appreciable variation of viscosity in our experimental setup (Figures 1A,B). This does not exclude that a certain amount of strain (γ > 1) is required to produce the microstructures observed after the shear deformation experiments (Shields et al., 2014). However, Shields et al. (2014), using the same material as in this study (b12x24Ω5 and b12x24Ω10 in (Shields et al., 2014) = HGGB3-30 in Table 2), found that the effect of γ on the evolution of τ and ηapp is rheologically not as impacting as the effect of , which induces changes in ηapp of several orders of magnitude (Figure 1C; Table 2).
Three-dimensional Microstructures
3D textural analyses reveal that shear fractures are arranged at different angles relative to the shear plane, depending on the degree of crystallinity of the sample and the amount of strain localization during deformation. To establish the mechanisms leading to the formation of fractures in our experiments, it is important to consider that, in the simple shear configuration here applied, the maximum compressive stress is at 45° from the shear plane (see principal stress configuration in Figure 2C).

Figure 2. Synchrotron-based X-ray tomographic microscopy virtual slices (whose positions in the 3D space are highlighted by the green planes reported in the reference frame) and corresponding 3D microstructural renderings of three representative samples. (A,B) P1271 with an inset from sample P1269 (HGGB3-30; low crystallinity); (C,D) P1268 (HGGB3-50; intermediate crystallinity). In (A) and (C) black objects are bubbles and fractures, the dark gray area is silicic glass and light gray objects are quartz crystals. In (B) the principal stress configuration imposed during torsion experiments of multiphase samples is indicated. In (B) and (D), bubbles and fractures are highlighted by yellow color. White arrows indicate macroscopic fractures in the samples; in (D) the macroscopic fracture plane is marked with brown color. (E) Non-fractured sample portion at high crystallinity (HGGB3-60, run OR119) exhibiting highly deformed bubbles within the shear band and the presence of fractured crystals (indicated by yellow arrows and shown in the inset image from the same sample provided as Movie 1/Presentation 1 ZIP) due to intensive particle collisions during deformation.
At low crystallinity (Figures 2A,B), fractures at high angle (80°) from the shear plane (35° from the maximum compressive stress) propagate through both, the melt phase and the gas bubbles. The propagation of fractures through gas bubbles is highlighted by the occurrence of angular features at the rim of the bubbles (inset Figure 2A). We interpret these uncommon bubble shapes as the result of possible migration of gas through the open crack once a fracture crosses the bubbles, without gas bubble healing (i.e., pore compaction after gas migrates into the fracture).
At intermediate crystallinity (Figures 2C,D), fractures at 45° from the shear plane (90° from the maximum compressive stress) pass through the melt phase and continue within the crystals (insets 1–2 in Figure 2C). Crystals show size reduction due to intense mutual interaction and stress concentration ultimately leading to their fracture (Forien et al., 2011), even before macroscopic sample failure occurs (Figure 2E). Microfractures are present between crystal fragments (inset 2 in Figure 2C). Gas bubbles are strongly deformed in melt-enriched shear bands where deformation is localized (inset 3 in Figures 2C,E).
Discussion
Empirical Quantification of the Viscous to Brittle Transition (VBT) in Three-phase Magmas
The VBT in multiphase magmas is evaluated here applying the failure criterion proposed by Cordonnier et al. (2012b). This criterion is based on the Deborah number (De), the dimensionless ratio between the Maxwell relaxation time of magmas and the deformation timescale (i.e., characteristic time of flow = ):
where, ηapp is the apparent viscosity of a system composed of crystals, bubbles, and melt, and G∞ is the elastic shear modulus at infinite frequency of the melt phase (1010±0.5 Pa; Dingwell and Webb, 1989). The presence of crystals amplifies the τ applied to the melt phase (Cordonnier et al., 2012b). Thus, the critical stress required for failure (τc) is lower than the τ required to fracture the melt alone (τcmelt) (Cordonnier et al., 2012b). The relationship between τc and τcmeltcan be written as Cordonnier et al. (2012b):
where, , with ϕm corresponding to the maximum packing fraction (0.6–0.93, depending on the degree of particle polydispersity of the system; Costa, 2005, and references therein). The crystal shape adopted in this study (average aspect ratio of 2 ± 0.2) is close enough to a spherical shape and, for congruence with the model of Cordonnier et al. (2012b), we thus use ϕm = 0.74. Combining Equations (1) and (2), the critical Deborah number (Dec) required for magma to cross the VBT can be written as:
where, Decmelt is the Dec for the pure silicate melts (Decmelt = 10−2; Cordonnier et al., 2012a). In a three-phase system, Dec should additionally vary as function of the bubble content. Bubbles can either behave as “rigid” (capillary number, Ca = 1) or deformable objects (Ca > 1; Manga et al., 1998). The capillary number, Ca, is the product of the bubble relaxation time (λ) and the local strain-rate applied to a single bubble ():
where, ηmelt is the melt viscosity, τlocal is the local stress applied on the single bubble, rb is the bubble radius (for spherical bubbles) and equivalent bubble radius (for sheared bubbles), Γ is the bubble-melt interfacial tension. Considering the bulk (lower than the maximum reached in shear bands at high crystallinity or gas-rich regions at low crystal content, where deformation localizes) and typical values of bubble radii from the starting materials (2.5-50 ± 0.3 μm), all experiments were performed at Ca > 1 (Table 1), thus, bubbles behave as deformable objects. Consequently, the presence of bubbles tends to decrease magma ηapp and results in an amplification of or τlocal required for failure (Equation 1). This finally implies that, at identical ϕ, the τc required for failure should be lower than that for bubble-free systems.
For Ca > 1, the recorded total γ is expected to mostly localize in the deformable bubbles. For rb ≤ rc (crystal size/radius), ϕ and the associated stress localization between crystals would increase τlocal and consequently Ca. The resulting effect would be an increased stress localization into the gas phase. However, when the crystal network becomes competent between ϕc (minimum crystal fraction at which crystal-crystal interaction starts to be dominant, which corresponds to 0.44 in our experiments) and ϕm, gas bubbles will switch from freely deforming objects that undergo large deformation (i.e., within shear bands) to locked spheres within the crystal network where shear deformation has not been concentrated yet. During deformation bubbles first act as a weak phase reducing the magmatic strength. However, the increase of the ϕ (i.e., ϕc < ϕ < [ϕc + (ϕm−ϕc)/2]) will increase the bubble/melt fraction ratio (β/μ; i.e., relative increase of β), further localize strain into the bubble phase (e.g., generation of high-strain shear bands), and globally increases the impact of gas bubbles on the overall rheology. The VBT is delayed and higher τ are required to rupture the sample. When the crystal network becomes strongly competent and connected, bubbles can no longer be significantly strained (i.e., [ϕc + (ϕm−ϕc)]/2 < ϕ < ϕm), and the bubble effect results much less impacting on the overall magma rheology. Considering the competition between stress localization in gas bubbles and crystal interlocking effects, we found that the critical Deborah number can be expressed as:
where, the second term on the right side of Equation (5), , becomes negligible when bubbles are removed from the sheared system via coalescence and subsequent outgassing, β is defined as:
and f is an empirical fitting parameter representing the “internal friction” of the crystal network (i.e., particle-particle interaction), and ranges from 0 at ϕ ≤ 0.44 to 0.62 at ϕ = 0.65 for magmas containing quartz or corundum crystals as experimentally explored in this study and that of Cordonnier et al. (2012b). Based on this empirical approach, Equation (5) can be applied to a large range of ϕ (0 to ϕm) and a range of β up to 0.20 for multiphase magmatic systems.
The VBT in Shear-thickening and Shear-thinning Magmas
Figure 3 synthesizes our observations and the impact of gas bubbles on the VBT of multiphase systems. In our experiments we distinguish two rheological fields. The first one (ϕ < 0.4; green field in Figure 3A) shows that bubbles may connect upon deformation and outgas, generating an increase in magma ηapp (i.e., shear-thickening regime). The second one (ϕ > 0.5; purple field in in Figure 3A) reveals that bubble connectivity is hindered by the crystal network resulting in suppression of lowering of the bulk viscosity of the magma. In between these two contrasting regimes a transition zone exists where the β/μ produces a strong contribution of the bubble phase even at β = 0.1 and where the VBT is strongly delayed.
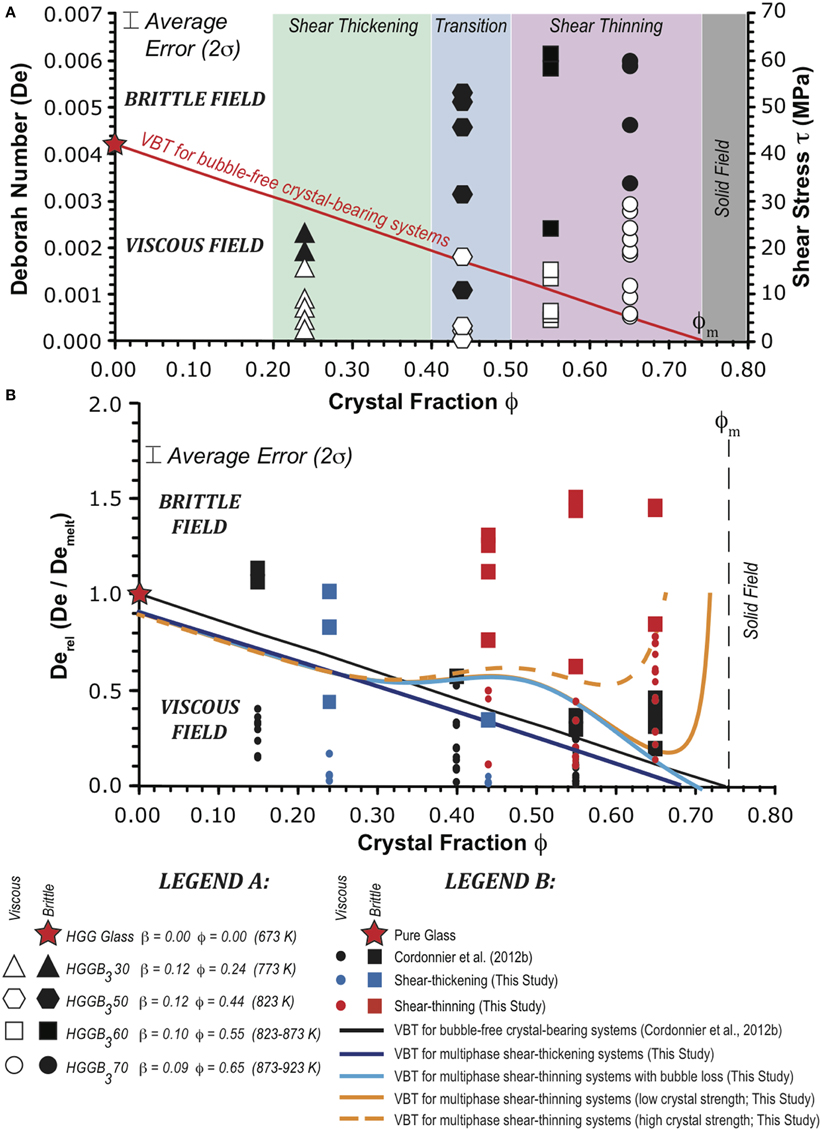
Figure 3. (A) Deborah number (left) and shear stress (τ, right) vs. crystal fraction (ϕ; and corresponding bubble fraction, β) for representative experiments showing: shear-thickening (ϕ < 0.44) and shear-thinning rheology (ϕ > 0.44). The VBT for bubble-free crystal-bearing systems is calculated with Equation (3). (B) Relative Deborah number (Derel, ratio of Deborah numbers of a multiphase magma [Debulk] and a pure melt [Demelt], respectively) vs. ϕ for experiments from this study and Cordonnier et al. (2012b). Experiments with reverse strain-rate stepping (from high to low) are not reported here (see Table 2). All experimental data for the viscous and brittle regimes reported here are based on the peak shear stress at a specified applied constant strain-rate prior to brittle failure and normalized with Demelt from this study. This diagram shows all the possible VBTs linking low crystallinity (where outgassing dominates) and high crystallinity (where shear banding is dominant), estimated using Equation (5) from this study. ϕm denotes the maximum packing fraction. See the text for further details.
For ϕ < 0.4 the τ required for fracturing bubble- and crystal-bearing magmas decreases with increasing ϕ, similarly to bubble-free systems (Figure 3A). However, differently from crystals that concentrate the τ in the melt phase, gas bubbles are the loci of high shear deformation and, thus, the VBT should be shifted to higher values of De. However, our experiments also infer a significant outgassing (i.e., decrease of β). The increase of leads to an increase of the bubble eccentricity (Rust and Manga, 2002), favors connectivity and ultimately outgassing (Okumura et al., 2006, 2008, 2010) that, in turn, lowers the VBT. As β is reduced in the system and the effect of bubbles becomes less pronounced, the entire rheology and the “swinging” VBT follow a trend close to that typical for bubble-free systems (Figure 3A).
Conversely, for 0.4 > ϕ > 0.5 a transition occurs and bubbles are not easily outgassed from the system. The τ required for fracturing bubble-bearing and crystal-rich magmas increases with increasing ϕ of the magma (Figure 3A). Moreover, the expected VBT is higher than the VBT for bubble-free systems established by Cordonnier et al. (2012b). This inversion of the relationship between the τc and magma crystallinity can be reconciled with microscopic processes (Figures 2C,D). Once ϕ reaches about 0.4-0.5, shear-thinning behavior is observed because local dilation and compaction are required for magmas to flow at such high crystallinity (Rutter et al., 2006; Caricchi et al., 2007; Pistone et al., 2012). When the ϕ increases at constant β, the β/μ increases leading to a relative bubble enrichment in the melt phase. Melt- and bubble-enriched shear bands are characterized by a local viscosity significantly lower than that of the surrounding crystals and, thus, accommodate most of the applied deformation. Such strain accommodation within the shear bands results in a decrease of τlocal and local of the melt phase, shifting the VBT to higher bulk τ. Therefore, the critical τ required to fracture such magmas increases with increasing ϕ, as long as ϕ < ϕm (Figure 3A).
Finally for ϕ > 0.5, the effect of shear-induced outgassing vanishes and the VBT criterion is a mixture between the stress localization in the melt and the crystal network strength. In such a case, the overall rheology is controlled by the crystallinity of the magmatic system. Gas bubbles as the weakest phases become the focus of stress localization within melt-enriched shear bands.
Our VBT model for multiphase magmatic systems has the potential to correlate magma crystallinity, bubble volume fraction, and critical stress required for fracturing in a single relationship, as reported in Equation (5). This model is able to unify in a single equation the opposite strain-rate dependent rheologies (shear-thickening and shear-thinning) and, thus, quantify the VBT over the entire range of crystallinity (ϕ ≤ ϕm) and bubble content (β ≤ 0.2). Figure 3B displays four different VBTs calculated using Equation (5): (i) VBT for multiphase shear-thickening systems where the strength of the unconnected (i.e., not competent) crystal network is negligible (blue line); (ii) VBT for multiphase shear-thinning systems that experience outgassing within large shear bands and where the term describing the bubble effect is negligible (marine blue line); (iii) VBT for multiphase shear-thinning systems displaying low crystal interaction and corresponding to the crystal characteristics reported by Cordonnier et al. (2012b; i.e., continuous orange line), and (iv) VBT for multiphase shear-thinning systems displaying high crystal friction as observed in this study (i.e., dashed orange line). In case of gas escape (related to a decrease of β) during deformation, the VBT shifts to Dec values similar to those typical for bubble-free crystal-bearing systems (blue line in Figure 3B). The release of gas increases the relative effect of crystals on sample rheology and consequent brittle failure. In such a case, sample fracturing requires lower values of τ (as well as Dec) in presence of crystals that amplify the τlocal applied to the melt phase (marine blue line in Figure 3B). Conversely, at constant β in the case of no outgassing, the VBT occurs at higher Dec values than those typical for bubble-free, crystal-bearing systems (orange line in Figure 3B) since gas bubbles largely accommodate the applied deformation and stress, and lower the τlocal of the melt. The related shear-thinning effect is more pronounced in presence of gas bubbles; thereby, higher values of τ (as well as Dec) are expected to lead to magma fracturing.
Insights into Natural Systems
The experimental observations obtained in this study and, more specifically, the different VBTs between low-crystallinity and high-crystallinity samples have profound implications for the dynamics of magma ascent and eruption. Ascending magmas, affected by significant outgassing during flow in a volcanic conduit, become more viscous and are fated to break earlier at depth. Particularly at low crystallinity (ϕ < 0.4), magma breakage is controlled by gas removal through bubble coalescence and formation of gas planes. The gas permeability increases in gas-enriched planes, where deformation is accommodated (with 1.5–100-fold increase in local ; Wright and Weinberg, 2009). Once the gas escapes, plane healing produces a sudden local increase of viscosity forcing the system to accommodate deformation to regions that are still relatively bubble-rich (Okumura et al., 2010; Caricchi et al., 2011). Outgassing, which is mostly favored by increasing in our experiments (Figure 1A), produces a decrease of the β in the magma and, thus, a decrease of the VBT to lower τ (Figure 3B). Fracturing enhances further release of gas (e.g., Castro et al., 2012) and gas-filled cracks connected to the periphery of the system favor the arrest of magma at depth (Tuffen et al., 2003) and its “viscous death” (Pistone et al., 2013). Further potential explosions of gas-poor stagnant magmas may be driven by influx of new volatile-rich magma (e.g., Rust and Cashman, 2007). Outgassing will lead to a more effusive eruption since a large part of the magmatic overpressure will be released.
Conversely, when gas is trapped in the crystal framework of high crystallinity systems (ϕ > 0.5), magma can be potentially more viscous and sustain large amount of stress and deformation (Pistone et al., 2012, 2013). This could have two major consequences: (1) for plug flow types (i.e., a volcanic conduit with a constant velocity profile to depth), the VBT may occur at shallower depths and, thus, the fragmentation level for crystal-rich magmas may be shallower than previously estimated; (2) the differential stress reached prior to rupture by a highly crystallized bubble-bearing magma may be higher than that achievable for a bubble-free system displaying an equivalent crystallinity. These highly crystallized bubble-bearing magmas are typical of lava domes (Sparks, 1997) and our findings may constrain why catastrophic explosions often accompany dome extrusions during periods of lower gas fluxes.
Most volcanoes of intermediate to silicic magma compositions exhibit repeatedly both effusive and explosive behavior during the same event. Their evolution can rarely be accurately predicted but has profound impact for the surrounding populations. Typical magmas that are characterized by this eruption duality (effusive vs. explosive style) are generally andesites to dacites with 40–50 vol.% crystals. Typically, the evolution of a single eruptive event changes from explosive to effusive with decreasing eruptive intensity. However, the opposite evolution is also not uncommon; for example, the Lascar Volcano (Matthews et al., 1997) is a typical representative of the latter case showing the switch from effusive to explosive behavior. The volcano started with a low volume effusion of a lava dome in 1984, accompanied by vigorous outgassing on and around the dome. Unexpectedly, the volcano produced a very high-intensity explosive eruption in April 1993, which might be attributed to the increased strength of the crystallizing dome requesting a much larger overpressure to fail. This behavior is supported by our rheological observations and underlines the urgent requirement to establish rigorous relationship between physical properties (i.e., rheology) of magmas and their eruption dynamics. Passive volcanic degassing in well-monitored active volcanoes may potentially be used to evaluate the strength of magmas at depth, the potential build-up of stress, and, finally, the likelihood of the system to enter into a brittle/explosive state. The link between the VBT in multiphase magmas and eruptive style of volcanoes is essential to “predict” the physical behavior of volcanoes, particularly of those characterized by both effusive and explosive volcanic activity (e.g., Mt St Helens, US; Montserrat, Lesser Antilles, West Indies; Santiaguito, Guatemala; Unzen, Japan). The transient switch from effusive to explosive eruptions highlights the problem that lava effusion can suddenly change to very hazardous explosive activity after several years of constant eruption behavior.
Conclusions
In this study we have determined the VBT in high-viscosity (> 105 Pa·s) silica-rich, three-phase magmas, containing both crystals (24–65 vol.%; average aspect ratio of 2) and gas bubbles (9–12 vol.%), deformed at high-temperature (673–1023 K) and high-pressure conditions (200 MPa) under variable range of strain-rates (5·10−6 s−1−4·10−3 s−1). Based on the experimental results, we propose an empirical equation describing the VBT as a function of crystallinity and the strain-rate-dependent rheology (shear-thickening in crystal-poor systems and shear-thinning in crystal-rich magmas). The transient behavior from shear-thickening to shear-thinning occurs at crystallinity (ϕ = 0.4–0.5) and bubble volume fractions (β ≤ 0.2) that are typical for magmas associated with dome forming volcanic systems and may account for the frequently observed sudden transition from effusive to explosive activity during these eruptions. This study offers an explanation why certain volcanoes displaying initial lava effusion and high intensity gas emission over prolonged durations, suddenly change to very hazardous explosive activity. Defining the VBT in volatile-rich magmas at intermediate crystallinity and correlating it to the switch of eruption style from non-explosive to explosive and vice versa is a central topic in future experimental investigations targeting the behavior of intermediate composition volcanic systems.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
SNF (Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung) grants 200020-120221 and 200020-132878 supported this research. BC acknowledges the Marie Curie International Outgoing Fellowships for Career Development RHEA-254407 grant. We acknowledge: R. Hoffmann (ETH-Zurich), L. Arbaret and R. Champallier (CNRS-Orleans) for their support in the laboratory; P. Modregger for his support at the TOMCAT beamline (SLS, PSI, Villigen); Alberto Luisoni AG (Switzerland) and Nabaltec AG (Germany) for supplying quartz crystals and APYRAL 60CD used in the starting materials. We thank J.K. Russell and Y. Lavallée for the helpful comments on an earlier version of the manuscript. We thank the Editor and the three reviewers for their helpful comments. In memoriam to Luigi Burlini.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/feart.2015.00071
Movie 1/Presentation 1 ZIP. Non-fractured sample portion at high crystallinity (HGGB3-60, run OR119) showing strain partitioning within the microstructural domain: highly deformed bubbles within the shear band and presence of fractured crystals due to intensive particle collisions during deformation in the less deformed sample regions (as inferred by the bubble shape; Pistone et al., 2012).
References
Ardia, P., Di Muro, A., Giordano, D., Massare, D., Sanchez-Valle, C., and Schmidt, M. W. (2014). Densification mechanisms of haplogranite glasses as a function of water content and pressure based on density and Raman data. Geochim. Cosmochim. Acta 138, 158–180. doi: 10.1016/j.gca.2014.03.022
Ardia, P., Giordano, D., and Schmidt, M. W. (2008). A model for the viscosity of rhyolite as a function of H2O-content and pressure: a calibration based on centrifuge piston cylinder experiments. Geochim. Cosmochim. Acta 72, 6013–6123. doi: 10.1016/j.gca.2008.08.025
Avard, G., and Whittington, A. G. (2011). Rheology of arc dacite lavas: experimental determination at low strain rates. Bull. Volcanol. 74, 1039–1056. doi: 10.1007/s00445-012-0584-2
Bagdassarov, N. S., Dingwell, D. B., and Webb, S. L. (1994). Viscoelasticity of crystal-bearing and bubble-bearing rhyolite melts. Phys. Earth Planet. Inter. 83, 83–99. doi: 10.1016/0031-9201(94)90066-3
Bagdassarov, N. S., Dorfman, A., and Dingwell, D. B. (2000). Effect of alkalis, phosphorus, and water on the surface tension of haplogranite melt. Am. Mineral. 85, 33–40. doi: 10.2138/am-2000-0105
Caricchi, L., Burlini, L., Ulmer, P., Gerya, T., Vassalli, M., and Papale, P. (2007). Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics. Earth Planet Sci. Lett. 264, 402–419, doi: 10.1016/j.epsl.2007.09.032
Caricchi, L., Pommier, A., Pistone, M., Castro, J., Burgisser, A., and Perugini, D. (2011). Strain-induced magma degassing: insights from simple-shear experiments on bubble bearing melts. Bull. Volcanol. 73, 1245–1257. doi: 10.1007/s00445-011-0471-2
Castro, J. M., Cordonnier, B., Tuffen, H., Tobin, M. J., Puskar, L., Martin, M. C., et al. (2012). The role of melt-fracture degassing in defusing explosive rhyolite eruptions at Volcán Chaitén. Earth Planet. Sci. Lett. 333–334, 63–69. doi: 10.1016/j.epsl.2012.04.024
Cordonnier, B., Caricchi, L., Pistone, M., Castro, J., Hess, K.-U., Manga, M., et al. (2012b). The viscous-brittle transition of crystal-bearing silicic melt: direct observation of magma rupture and healing. Geology 40, 611–614. doi: 10.1130/G3914.1
Cordonnier, B., Schmalholz, S. M., Hess, K.-U., and Dingwell, D. B. (2012a). Viscous heating in silicate melts: an experimental and numerical comparison. J. Geophys. Res. 117. doi: 10.1029/2010jb007982
Costa, A. (2005). Viscosity of high crystal content melts: dependence on solid fraction. Geophys. Res. Lett. 32:L22308. doi: 10.1029/2005GL024303
Dingwell, D. B. (1996). Volcanic dilemma: flow or blow? Science 273, 1054–1055. doi: 10.1126/science.273.5278.1054
Dingwell, D. B., and Webb, S. L. (1989). Structural relaxation in silicate melts and non-newtonian melt rheology in geologic processes. Phys. Chem. Miner. 16, 508–516. doi: 10.1007/BF00197020
Dingwell, D. B., and Webb, S. L. (1990). Relaxation in silicate melts. Eur. J. Mineral. 2, 427–449. doi: 10.1127/ejm/2/4/0427
Forien, M., Arbaret, L., Burgisser, A., and Champallier, R. (2011). Experimental constrains on shear-induced crystal breakage in magmas. J. Geophys. Res. 116:B08217. doi: 10.1029/2010JB008026
Giordano, D., Russell, J. K., and Dingwell, D. B. (2008). Viscosity of magmatic liquids: a model, Earth Planet. Sci. Lett. 271, 123–134. doi: 10.1016/j.epsl.2008.03.038
Gonnermann, H. M., and Manga, M. (2003). Explosive volcanism may not be an inevitable consequence of magma fragmentation. Nature 426, 432–435. doi: 10.1038/nature02138
Ketcham, R. A., and Carlson, W. D. (2001). Acquisition, optimization and interpretation of X-ray computed tomographic imagery: applications to the geosciences. Comput. Geosci. 27, 381–400. doi: 10.1016/S0098-3004(00)00116-3
Manga, M., Castro, J., Cashman, K. V., and Loewenberg, M. (1998). Rheology of bubble-bearing magmas. J. Volcanol. Geother. Res. 87, 15–28. doi: 10.1016/S0377-0273(98)00091-2
Marone, F., and Stampanoni, M. (2012). Regridding reconstruction algorithm for real-time tomographic imaging. J. Synchrotron Radiat. 19, 1029–1037. doi: 10.1107/S0909049512032864
Matthews, S. J., Gardeweg, M. C., and Sparks, R. S. J. (1997). The 1984 to 1996 cyclic activity of Lascar Volcano, northern Chile: cycles of dome growth, dome subsidence, degassing and explosive eruptions. Bull. Volcanol. 59, 72–82. doi: 10.1007/s004450050176
Maxwell, J. C. (1867). On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. A 157, 49–88. doi: 10.1098/rstl.1867.0004
Okumura, S., Nakamura, M., Nakano, T., Uesugi, K., and Tsuchiyama, A. (2010). Shear deformation experiments on vesicular rhyolite: implications for brittle fracturing, degassing, and compaction of magmas in volcanic conduits. J. Geophys. Res. 115, B06201. doi: 10.1029/2009JB006904
Okumura, S., Nakamura, M., and Tsuchiyama, A. (2006). Shear-induced bubble coalescence in rhyolitic melts with low vesicularity. Geophys. Res. Lett. 33, L20316. doi: 10.1029/2006GL027347
Okumura, S., Nakamura, M., Tsuchiyama, A., Nakano, T., and Uesugi, K. (2008). Evolution of bubble microstructure in sheared rhyolite: formation of a channel-like bubble network. J. Geophys. Res. 113, B07208. doi: 10.1029/2007JB005362
Papale, P. (1999). Strain-induced magma fragmentation in explosive eruptions. Nature 397, 425–428. doi: 10.1038/17109
Paterson, M. S., and Olgaard, D. L. (2000). Rock deformation tests to large shear strains in torsion. J. Struct. Geol. 22, 1341–1358. doi: 10.1016/S0191-8141(00)00042-0
Pistone, M. (2012). Physical Properties of Crystal- and Bubble-Bearing Magmas. Dissertation ETH No. 20698, ETH – Zurich, Switzerland, 442.
Pistone, M., Caricchi, L., Ulmer, P., Burlini, L., Ardia, P., Reusser, E., et al. (2012). Deformation experiments of bubble- and crystal-bearing magmas: rheological and microstructural analysis. J. Geophys. Res. 117:B05208. doi: 10.1029/2011jb008986
Pistone, M., Caricchi, L., Ulmer, P., Burlini, L., Reusser, E., and Ardia, P. (2013). Rheology of volatile-bearing crystal mushes: mobilization vs. viscous death. Chem. Geol. 345, 16–39. doi: 10.1016/j.chemgeo.2013.02.007
Russell, J. K., Giordano, D., and Dingwell, D. B. (2003). High-temperature limits on viscosity of non-Arrhenian silicate melts. Am. Mineral. 8, 1390–1394.
Rust, A. C., and Cashman, K. V. (2007). Multiple origins of obsidian pyroclasts and implications for changes in the dynamics of the 1300 B.P. eruption of Newberry Volcano, USA. Bull. Volcanol. 69, 825–845. doi: 10.1007/s00445-006-0111-4
Rust, A. C., and Manga, M. (2002). Orientation and deformation of bubbles in shear flows. J. Colloid Interface Sci. 249, 476–480. doi: 10.1006/jcis.2002.8292
Rutter, E. H., Brodie, K. H., and Irving, D. H. (2006). Flow of synthetic, wet, partially molten “granite” under undrained conditions: an experimental study. J. Geophys. Res. 111:B06407. doi: 10.1029/2005JB004257
Scarfe, C. M., Mysen, B. O., and Virgo, D. (1987). “Pressure dependence of the viscosity of silicate melts,” in Magmatic Processes: Physicochemical Principles, ed B. O. Mysen (University Park, PA: Geochemical Society), 59–68.
Shields, J., Mader, H. M., Pistone, M., Caricchi, L., Floess, D., and Putlitz, B. (2014). Strain-induced outgassing of three-phase magmas during simple shear. J. Geophys. Res. 119, 6936–6957. doi: 10.1002/2014jb011111
Smith, R., Sammonds, P., and Kilburn, C. R. J. (2009). Fracturing of volcanic systems: experimental insights into pre-eruptive conditions. Earth Planet. Sci. Lett. 280, 211–219. doi: 10.1016/j.epsl.2009.01.032
Sparks, R. S. J. (1997). Causes and consequences of pressurization in lava dome eruptions. Earth Planet. Sci. Lett. 150, 177–189. doi: 10.1016/S0012-821X(97)00109-X
Stampanoni, M., Groso, A., Isenegger, A., Mikuljan, G., Chen, Q., Bertrand, A., et al. (2006). “Trends in synchrotron-based tomographic imaging: the SLS experience,” in Proceedings of SPIE Developments in X-ray tomography V, Vol. 6318, ed U. Bonse (San Diego, CA). Available online at: http://spie.org/Publications/Proceedings/Paper/10.1117/12.679497
Tuffen, H., Dingwell, D. B., and Pinkerton, H. (2003). Repeated fracture and healing of silicic magma generate flow banding and earthquakes? Geology 31, 1089–1092. doi: 10.1130/G19777.1
Vona, A., Romano, C., Giordano, D., and Russell, J. K. (2013). The multiphase rheology of magmas from Monte Nuovo (Campi Flegrei, Italy). Chem. Geol. 346, 213–227. doi: 10.1016/j.chemgeo.2012.10.005
Keywords: magma, bubbles, crystals, viscous flow, brittle fracture, outgassing, shear banding, volcanic eruption style
Citation: Pistone M, Cordonnier B, Caricchi L, Ulmer P and Marone F (2015) The Viscous to Brittle Transition in Crystal- and Bubble-Bearing Magmas. Front. Earth Sci. 3:71. doi: 10.3389/feart.2015.00071
Received: 06 June 2015; Accepted: 30 October 2015;
Published: 24 November 2015.
Edited by:
Antonio Costa, Istituto Nazionale di Geofisica e Vulcanologia, ItalyReviewed by:
Eisuke Fujita, National Research Institute for Earth Science and Disaster Prevention, JapanDiego Perugini, University of Perugia, Italy
Copyright © 2015 Pistone, Cordonnier, Caricchi, Ulmer and Marone. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mattia Pistone, cGlzdG9uZW1Ac2kuZWR1
 Mattia Pistone
Mattia Pistone Benoît Cordonnier
Benoît Cordonnier Luca Caricchi
Luca Caricchi Peter Ulmer
Peter Ulmer Federica Marone
Federica Marone