- 1Department of Geology, University of Illinois—Urbana-Champaign, Urbana, IL, United States
- 2Department of Geology, State University of New York at Buffalo, Buffalo, NY, United States
- 3Earthquake Research Institute, University of Tokyo, Tokyo, Japan
Quantifying the eruption potential of a restless volcano requires the ability to model parameters such as overpressure and calculate the host rock stress state as the system evolves. A critical challenge is developing a model-data fusion framework to take advantage of observational data and provide updates of the volcanic system through time. The Ensemble Kalman Filter (EnKF) uses a Monte Carlo approach to assimilate volcanic monitoring data and update models of volcanic unrest, providing time-varying estimates of overpressure and stress. Although the EnKF has been proven effective to forecast volcanic deformation using synthetic InSAR and GPS data, until now, it has not been applied to assimilate data from an active volcanic system. In this investigation, the EnKF is used to provide a “hindcast” of the 2009 explosive eruption of Kerinci volcano, Indonesia. A two-sources analytical model is used to simulate the surface deformation of Kerinci volcano observed by InSAR time-series data and to predict the system evolution. A deep, deflating dike-like source reproduces the subsiding signal on the flanks of the volcano, and a shallow spherical McTigue source reproduces the central uplift. EnKF predicted parameters are used in finite element models to calculate the host-rock stress state prior to the 2009 eruption. Mohr-Coulomb failure models reveal that the host rock around the shallow magma reservoir is trending toward tensile failure prior to 2009, which may be the catalyst for the 2009 eruption. Our results illustrate that the EnKF shows significant promise for future applications to forecasting the eruption potential of restless volcanoes and hind-cast the triggering mechanisms of observed eruptions.
Introduction
Volcanic unrest observations including surface deformation, seismicity, gas emissions, or fumarole activity may or may not indicate that a system is trending toward eruption (Biggs et al., 2014). Understanding the dynamics of the underlying magma reservoirs is crucial for volcanologists to link volcanic unrest signals to eruption potential. A key challenge is to take full advantage of monitoring data to update and optimize dynamic models of the magma storage systems (Mogi, 1958; McTigue, 1987; Yang et al., 1988; Battaglia et al., 2003; Currenti et al., 2007; Nooner and Chadwick, 2009; Cianetti et al., 2012; Gregg et al., 2012, 2013; Newman et al., 2012; Ronchin et al., 2013; Cannavò et al., 2015; Parks et al., 2015). Model-data fusion techniques are necessary to provide statistically robust estimations of volcano evolution during periods of unrest. Classically, volcanic activity has been evaluated using static inversions (Battaglia et al., 2003; Newman et al., 2012; Parks et al., 2015), finite element model (FEM) optimizations (Hickey et al., 2015), model-data comparison (Le Mével et al., 2016). Most inversion techniques provide an important snap shot into the state of volcanic unrest, but are limited in their forecasting ability. Fewer studies use time-evolving inversions from the InSAR data, which successfully provide a quantitative model to explain the dynamics of the magma storage system (e.g., Pagli et al., 2012). However, this approach is limited to regions where SAR data is widely available and consistent and continuous acquisitions are guaranteed. Furthermore, this method requires separated steps to determine the chamber geometry and the time-dependent loading, which requires that the storage geometry is relatively stable. More recently, Kalman filter statistical data assimilation approaches such as the Extended Kalman Filter (EKF) (Schmidt, 1966; Julier et al., 2000) and unscented Kalman filter (UKF) (Fournier et al., 2009) have been used to provide temporal models of volcanic evolution. However, EKF and UKF are computationally expensive and intractable for use with FEMs.
The Monte Carlo based Ensemble Kalman Filter (EnKF) successfully circumvents linearization issues and computational costs inherent to other Kalman filter approaches (Evensen, 1994). The EnKF has been widely applied and has proven effective for multi-data stream data assimilation in hydrology, physical oceanography, and climatology (vanLeeuwen and Evensen, 1996; Allen et al., 2003; Bertino et al., 2003; Evensen, 2003; Lisaeter et al., 2007; Skjervheim et al., 2007; Wilson et al., 2010). Gregg and Pettijohn (2016) first applied the EnKF in volcanology by conducting a series of 2D elliptical magma chamber tests to assimilate synthetic InSAR (Interferometric Synthetic Aperture Radar) and/or GPS data into a thermomechanical FEM. Zhan and Gregg (2017) further establishes a 3D EnKF workflow to update a Mogi source (Mogi, 1958) using synthetic data and illustrates that the EnKF is a robust method even where data are limited. Bato et al. (2017) provides an additional synthetic test of the EnKF to track the migration of magma between two sources based on synthetic InSAR and/or GNSS data. Although these three synthetic tests indicate great potential, until now the EnKF has not been utilized to analyze volcano deformation from a natural system.
In this study, the EnKF is used to assimilate InSAR time series data (Chaussard and Amelung, 2012; Chaussard et al., 2013) from Kerinci volcano in Indonesia to investigate the surface deformation associated with the evolution of an upper crustal magma storage system leading up to its 2009 eruption. Kerinci volcano, located in Central Sumatra along the Sunda (Indonesia) Arc (Figure 1), has had 32 confirmed eruptions (VEI = 1–2) since 1838, and three recent eruptions, including the 2009/04/01–2009/06/19 eruption, the 2016/03/31–2016/08/09 eruption, and the 2016/11/15–2016/11/21 eruption (Global Volcanism Program, 2009), but also has more than 50,000 people living within 20 km distance around it. Previously analyzed 2007–2011 InSAR time series data from the ALOS-1 satellite (Chaussard and Amelung, 2012; Chaussard et al., 2013) provide an excellent opportunity to test the application of the EnKF in tracking the dynamics of a shallow magma storage system before and after an eruption. We apply a two-step EnKF analysis with a two-source magma storage system which models a deflating, dike-like spheroid feeding an inflating shallow, spherical magma chamber. InSAR data are assimilated as they would have become available if distributed in semi-real time following acquisition and provide model parameter updates. Finally, best-fit model parameters are used to calculate the predicted stress state of the system leading up to the 2009 eruption.
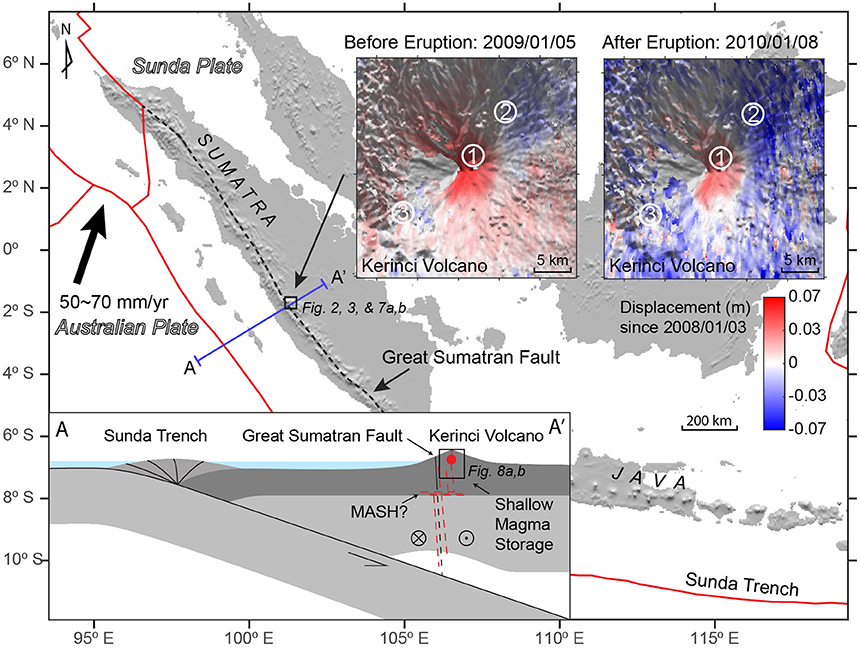
Figure 1. Location and tectonic setting of Kerinci volcano. More than 10% of active volcanoes on the Earth are distributed along the Sunda arc (McCaffrey, 2009), due to subduction of the Australian Plate beneath the Sunda Plate. The oblique subduction results in the right lateral Great Sumatran Fault, which is the northeastern boundary of the forearc plate (McCaffrey, 2009). Blue-red color maps show the InSAR time series data at 2009/1/5 and 2010/1/8. The numbers in the circles indicate locations used in Figure 4. The left bottom insert is a sketch section (not to scale) showing the tectonic setting of the Kerinci volcano and the box highlights that the shallow magma chamber may be fed by dikes associated with the Great Sumatran Fault as magma may take the advantage of the pre-existing fractures to ascend from depth (Chaussard and Amelung, 2012; Muksin et al., 2013). The geometry of the magmatic system illustrates the dike and reservoir model used to explain the InSAR data.
Methods
InSAR Data
SAR data were acquired between 2008/1 and 2011/11 by the Japanese Space Exploration Agency ALOS-1 satellite (Chaussard and Amelung, 2012; Chaussard et al., 2013). The displacement time series with 14 epochs is calculated using the small baseline subset (SBAS) from the InSAR data (Chaussard and Amelung, 2012; Chaussard et al., 2013) (Figure 1). To reduce the random atmospheric noise (Hanssen, 2001; Li et al., 2005), we filter the time series data spatially with a low pass median filter. The InSAR time-series dataset with a 15-m resolution contains more than 150,000 pixels for each time slice when we set the study area as a 6 by 6 km square centered on the volcano. It is therefore computationally prohibitive to assimilate data from the entire InSAR database. A QuadTree algorithm based on root-mean-square-error of the displacement values is applied to reduce the number of samples for each epoch of InSAR data from ~150,000 to ~800 (Jónsson et al., 2002; Simons et al., 2002; Lohman and Simons, 2005; Zhan and Gregg, 2017; Figure 2A; Figure S1), further reducing the short wavelength random atmospheric noise.
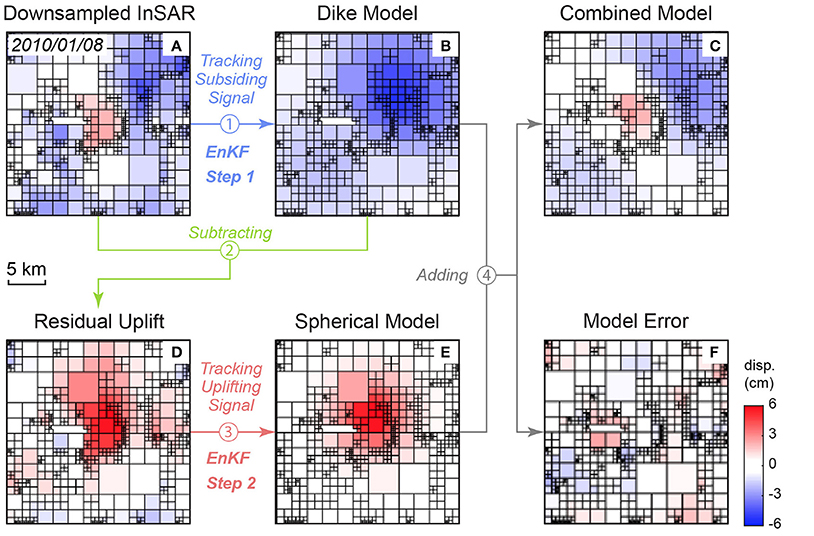
Figure 2. Workflow of the two-step data assimilation with the downsampled InSAR data. (A) Downsampled InSAR, (B), Dike model, (C) combined model, (D) residual uplift, (E) spherical model, (F) model error.
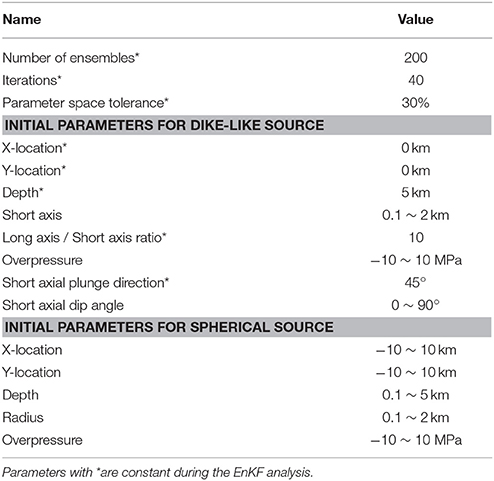
We use the EnKF data assimilation method to find the best-fit storage model for the Kerinci volcano. The EnKF uses a Markov chain of Monte Carlo (MCMC) approach to estimate the covariance matrix in the Kalman filter. The EnKF overcomes the limitations of the Kalman Filter and EKF methods, such as computational expense, storage issues, and poor performance with highly nonlinear problems (Evensen, 2009). We follow the EnKF analysis scheme described by Zhan and Gregg (2017) to obtain the magma storage models. The initial ensemble of models is constructed according to the initial guess of the parameters (Table 1), based on which the forecast ensemble is obtained. At time tk when new data (InSAR time series data) is available, an EnKF analysis is conducted to update the model parameters and change the trajectory of the model. The updated model parameters are then used to create a new forecast ensemble, which will be assimilated at tk+1 when another epoch of InSAR time series data is available. Effectively, the EnKF provides a temporal inversion that captures the system's dynamics through time. The final output of the EnKF can be used to investigate the system state at the time of the last observation, and can be propagated forward in time to provide a system forecast. The EnKF dynamic inversion strategy has proved robust, even when the InSAR data have a topographic shadow masking the flank of the volcano edifice (Zhan and Gregg, 2017). The ensemble parameters in this implementation of the EnKF analysis is chosen based on previous synthetic tests (Zhan and Gregg, 2017; Table 1).
Magma Storage Model
The InSAR time series reveals uplift entered at the summit of the volcano and two subsiding areas located on the NE and SW flanks. To simulate both the uplift and subsidence signals, we combine an inflating spherical source with a deflating dike-like source located at an angle beneath the chamber to form an upper crustal magma storage system (Gudmundsson, 2006; Chaussard et al., 2013) beneath Kerinci (Figure 1) and calculate the elastic response of the country rock (Table 2). The deformation pattern can also be created by other sources. For example, the two-peak pattern of the subsiding signal can be approximated using two deflating sills beneath the NE and SW side of the volcano edifice. However, it is unlikely that three magma sources would develop so close to each other while remaining separate and stable thermally. On the contrast, the single deflating dike-like source at depth feeding a shallow magma reservoir is more reasonable.
We use McTigue's analytical approach (McTigue, 1987) to produce the displacement at the center due to a shallow inflating sphere. We reproduce the two-peak subsidence with a deflating near vertical oblate spheroid (Yang et al., 1988; Dzurisin, 2006), with a high ratio of its long and short axes (~10), acting as a dike-like source. The center of the Kerinci volcano is located on the dilatational Siulak segment of the Great Sumatra Fault (Bellier and Sébrier, 1994; Sieh and Natawidjaja, 2000). Therefore, we assume a near vertical, NW-SE striking dike-like source guided by the preexisting stress field of the Great Sumatra Fault (Pasquare and Tibaldi, 2003; Gudmundsson, 2006; Tibaldi, 2015).
Two-Step Data Assimilation
Tracking both the upper spherical and lower dike-like source introduces too many parameters for the EnKF to obtain unique solutions. Thus, a two-step EnKF analysis is used to track the two sources separately. First, the EnKF estimates the subsidence generated by a deflating dike using the Yang et al.'s model (Yang et al., 1988) (Figure 2B; Figure S2). During this step, the uplift signal is masked from the InSAR data, and is treated as missing data. The Yang et al.'s model (Yang et al., 1988) requires eight independent parameters beside the Young's Modulus and Poisson's ratio, including the x, y, and z coordinates, long, and short axis, plunging direction and dipping angle, the overpressure of the spheroid. As many parameters may cause strong non-uniqueness during the EnKF analysis (Zhan and Gregg, 2017), we assume that the location of the center of the dike is 5 km beneath the summit of the volcano, and it is striking NW-SE aligned with the Great Sumatran Fault system (Table 1). The residual displacement is calculated by subtracting the predicted subsidence from the corresponding InSAR data time step (Figure 2D; Figure S3). At the second step, the EnKF analysis (initial parameters listed in Table 1) tracks the inflating spherical source using the McTigue's model (Figure 2E; Figure S4) to reproduce the uplift signal in the residual displacement obtained from Step 1. A combination of both the deeper deflating dike-like spheroid model and the shallower inflating spherical model produces a modeled displacement, which closely matches the observed pattern of central uplift and flank subsidence (Figure 2C; Figure S5). Finally, the two models are combined to produce the total displacement. The misfit is the difference between the modeled displacement from the combined model and the measured displacement from the InSAR time series (Figure 2F; Figure S6).
Stress and Coulomb Failure Calculation
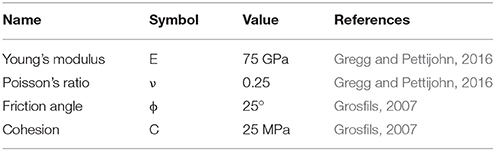
To calculate the stress field of the country rock around the magma storage, we follow the benchmarked strategy of Zhan and Gregg (2017). Elastic FEMs are established with the parameters estimated by the two-step EnKF analysis and then solved for by COMSOL5.2. The maximum and minimum principle stresses at the top of the chamber are calculated for failure determination. The application of the Coulomb failure criterion follows the same strategy as previous studies (Grosfils, 2007; Gregg et al., 2012; Table 2).
Results
Volcanic Deformation
Down-sampled InSAR time series data (Figures 3A,D) reveal two deformation signals at Kerinci Volcano, an uplifting signal centered on the summit and a subsiding signal on the NE and SW flanks. Both signals are consistent in temporal and spatial domains, suggesting they are not associated with atmospheric delay and should be treated as deformation (Figures 3, 4). Prior to the April 2009 eruption, the volcano experienced a continuous uplift at a maximum rate of ~4 cm/yr (Figure 4a), while the NE and SW flanks subsided at a much lower rate of <1 cm/yr (Figures 4b,c). At the time of the eruption, the center and flanks of the volcano went through a rapid subsidence (Figures 3A,D, 4), reflecting withdrawal of magma from the storage system. After the eruption, central uplift recommenced while deformation of the NE and SW flanks ceased (Figure 4). The deformation centered on the summit has a short wavelength, indicating a shallow source, while a deep source is more likely to create a long wavelength subsidence deformation signal. The symmetrical shape of the central uplift strongly suggests an inflating spherical source, while the two-peak pattern of the subsidence suggests a deflating dike-liked source.
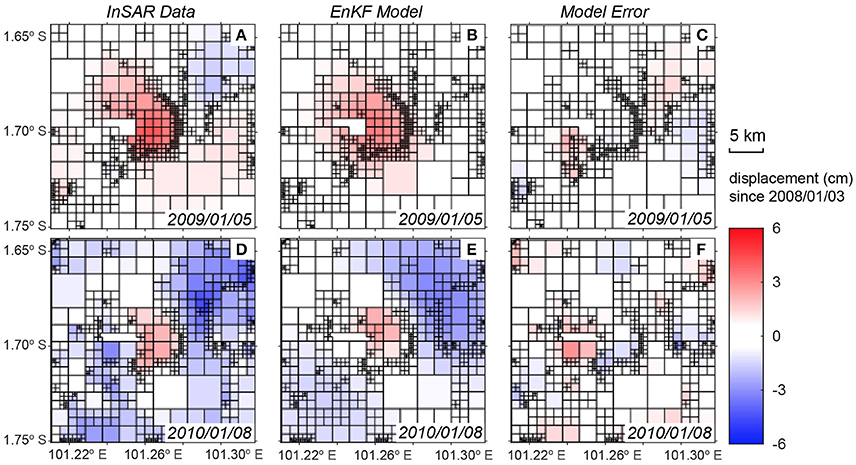
Figure 3. Comparison between the QuadTree down-sampled InSAR time series (A,D) and the EnKF data assimilation results (B,E), before (top row) and after (bottom row) the 2009 eruption. (B,E) show the best fit two-sources model obtained from the EnKF data assimilation and (C,F) show the misfit between the EnKF prediction and the InSAR data.
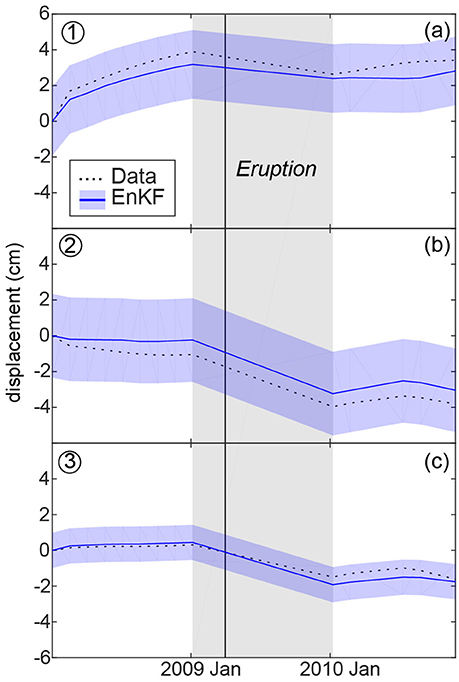
Figure 4. 2008–2011 displacement measured by the InSAR time series (dash line) compared to the displacement produced by the best fit combined EnKF model (full line and filled blue area). The numbers at the left-top corners correspond to the sampling locations shown on Figure 1. (a) Is the center of the volcano and (b,c) are the flanks. The blue shaded regions show the standard deviations of the ensembles. The black solid line indicates the time of the 2009/1/11 eruption of Kerinci, and the gray shaded region highlights the gap in SAR acquisitions.
A two-step data assimilation approach (Figure 2) is implemented to track the surface deformation created by a shallow, inflating spherical source (McTigue, 1987) and a deeper, deflating dike-like (oblate spheroid) source (Yang et al., 1988). The two-sources model reproduces both the observed central uplift signal and the subsidence signal on the flank (Figure 3E). Model errors are <1 cm in most regions and are <0.5 cm at the center of the volcano (Figures 3C,F). A comparison of the deformation time-series and the model predictions confirms that the two-step model is able to track the observed deformation within uncertainty (Figure 4). We further calculate the L2 norm of the displacement to illustrate the total misfit between the forecast models and the data. The L2 norm error estimation is the sum of the square of the differences between the model values and the measurement values, which also considers the size of the quad created during QuadTree down-sampling. Normalized L2 norms of both the spherical source and tilted dike-like source decrease through time as more InSAR data are assimilated (Figure 5). The L2 norm of the spherical source is overall significantly lower than for the tilted dike-like source, indicating that the spherical chamber model reproduces more accurately the uplift at the center of the volcano compared to the flank subsidence. The L2 norms of the spherical source decreases rapidly after several InSAR assimilations and become static until the eruption (Figure 5B). The low displacement errors (Figures 3, 4) and observed convergence in the L2 norms (Figure 5) suggest that the two-sources combination of a shallower inflating chamber and a deeper deflating dike-like source is a good representation of the storage system at Kerinci and their volume changes due to the magma transport explains the deformation associated with the 2009 eruption.
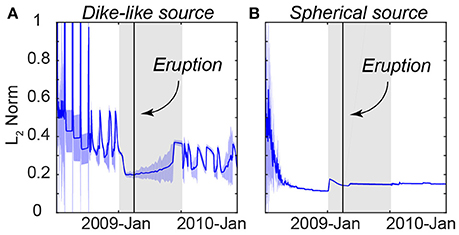
Figure 5. Normalized L2 norm comparing the misfit between the EnKF data assimilation results and the InSAR data. (A) L2 norm for the first step EnKF, which uses a dike-like source to track the subsiding signal. (B) L2 norm for the second step of the EnKF, which uses McTigue's model (McTigue, 1987) of an inflating spherical source to track the uplifting signal. The blue solid lines and the blue shaded regions are the mean and standard deviations respectively of the L2 norms of the 200 models in the ensembles.
Magma Source Parameters
The EnKF provides evolving estimates of the model parameters for the dike-like spheroid and shallow spherical chamber as new SAR observations are assimilated (Figure 6; the detailed values of the parameter estimation are listed in the Supplementary Tables 1, 2). We focus on EnKF's predictions of the evolution of over-pressurization and volume of the shallow chamber to investigate eruption precursors. The negative overpressure of the dike-like source is consistent with deflation of this deep source, but its rapid change is suspicious (Figure 6e). It is difficult to constrain the depth of the center of the dike-like spheroid with the InSAR subsiding signal alone. To constrain the depth of the dike, we conduct a series of tests to model the deflating signal. Results indicate that a dike deeper than 7 km cannot produce the deformation signal revealed by the InSAR data (Figure S7). Alternatively, a dike shallower than 3 km may overlap with the inflating magma chamber. As such, the depth to the center of the dike should be in a range of 3–7 km. Therefore, we assume the dike center is at a depth of 5 km. Furthermore, a 2-km uncertainty in the depth will not affect the result significantly for a near vertical dike. Due to the uncertainty in the deeper deflating source, this study instead focuses on the host rock stress evolution surrounding the shallow inflation source.
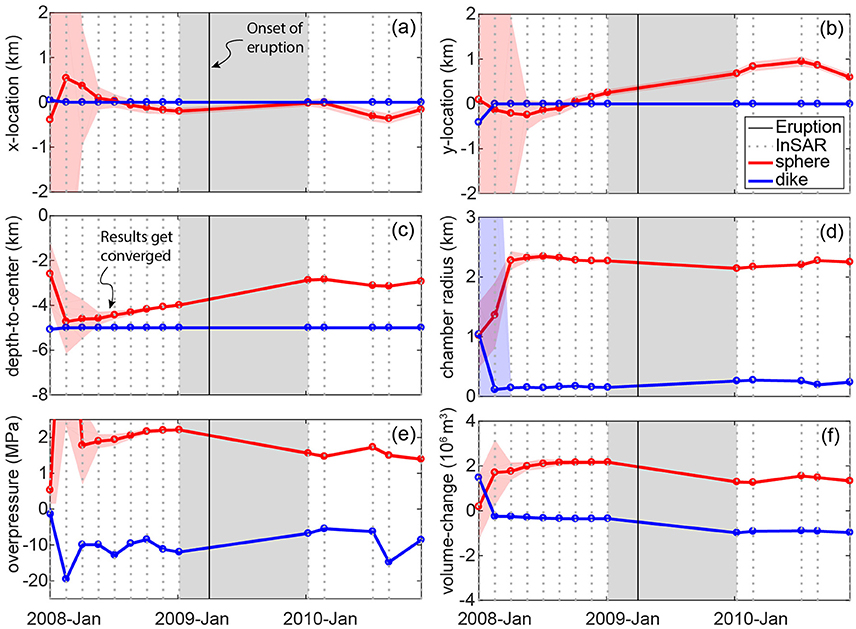
Figure 6. EnKF parameter estimations for the spherical (red lines) and dike-shaped (blue lines) sources. The EnKF predictions start to converge after several three epochs of InSAR time series data are assimilated. The x- and y-location in (a) and (b) are the horizontal distances between the deformation sources and the center of the volcano. (c) Is the depth to the center of the source. (d,e,f) Are the radius, overpressure and volume change of the source. The colored solid lines and shaded areas indicate the ensemble means and standard deviations respectively. The colored circle symbols indicate the estimated parameters of the best-fit model from each ensemble at each time step. The black dashed lines indicate time steps when InSAR data were assimilated. Notice the upper and lower part of (e) have different scales of the Y-axis.
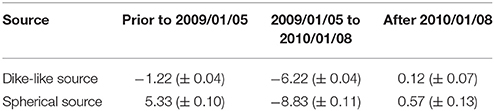
The second step of the data assimilation estimates the evolution of the shallow inflating source. The model converges after two to three time steps (05/2008–07/2008), when the standard deviation of the parameters and the L2 norms of the model significantly decrease (Figures 5B, 6). After the model parameters stabilize at July 2008, the EnKF estimates that the shallow inflating source shoaled from 4.43 (±0.19) km to 3.99 (±0.05) km (depth-to-center) beneath the summit prior to the eruption, and after the eruption the shallow source migrated northward 0.46 (±0.2) km and shoaled to ~1.12 (±0.1) km depth (Figures 6a–c). While this outcome provides a robust estimation of the migration of the pressure source, the variation through the time likely indicates magma migration in the magma storage system (through dikes or conduits), rather than the movement of a void chamber. However, the spherical chamber model provides a first-order approximation of the deformation source location through time. The EnKF predicts that the radius of the shallow chamber is 2.27 (±0.01) km (Figure 6d), which is likely too large given its shallow depth (see Supplemental Tables). However, trade-offs exists between overpressure and radius due to the non-uniqueness of the analytical model (Zhan and Gregg, 2017). To account for the non-uniqueness of the model, overpressure and radius are combined to calculate the volume evolution (Figure 6f). The volume of the shallow chamber increases at a rate of 5.33 (±0.10) × 105 (±0.04) m3/yr (Table 3) throughout the pre-eruptive time period, reaching its maximum just prior to the eruption. The volume of the dike-like source decreases [1.22 (±0.04) × 105 m3/yr] during the same time period (Figure 6f). During the eruption period, both sources experience substantial deflation resulting in a strong subsiding signal observed in the InSAR data (Figure 1). After the eruption, the deeper source returns to a steady state, while the shallower chamber continues to inflate at a much smaller rate [0.57 (±0.15) × 105 m3/yr] than prior to the eruption. Given that the shape of the post-eruption inflation curve does not mimic a typical viscoelastic roll-off, it likely indicates a slow recharge stage of the next eruption cycle which culminated in the 2016 eruption.
Discussion
Magmatic System Evolution at Kerinci
Based on the converged parameter estimation and the displacement agreement between the EnKF predictions and InSAR observations, we propose that the upper crustal magma transport-storage system of Kerinci is comprised of a shallow, spherical chamber at a depth of ~4 km connected by a dike system below to a possible lower crustal reservoir (Figures 1, 8a,b). The dike-like source may have developed aligned with the Great Sumatran Fault (Pasquare and Tibaldi, 2003; Gudmundsson, 2006; Tibaldi, 2015). Alternatively, other source combinations can also create the displacement pattern shown by the InSAR, such as inflating and deflating sills, and connected chambers. However, to model the two-peak pattern of the subsiding signal without an inclined feeder dike, at least two deflating chambers or sills would need to flank either side of the central inflating source, which is unlikely. Additionally, the preexisting faults beneath the volcano may provide an ideal path for magma transport (Tibaldi, 2015).
The coincident volume changes of the dike-like source and the chamber imply magma migration between these sources. Prior to the 2009 eruption, the volume of the shallow chamber continuously increased indicating possible magma injection (Mogi, 1958; Lister and Kerr, 1991) and/or differentiation (Tait et al., 1989). In the meantime, the volume of the dike-like spheroid decreased (Figure 6f), indicating that the dike-like source may only act as a pathway for magma to ascent from a lower reservoir (e.g., MASH zone; Hildreth and Moorbath, 1988), as suggested by seismic tomography (Koulakov et al., 2007; Collings et al., 2012). Following the eruption, the volumes of both the dike-like spheroid and the chamber decrease drastically, but because of the lack of data in the first months after the eruption, we cannot determine how fast this subsidence occurred. The volume loss is most likely related to the erupting steam-, ash-, and cinder-bearing plumes recorded in April 2009 (Global Volcanism Program, 2009). The total volume loss of the two-sources system is ~1.6 × 106 m3, which is consistent with volume estimates for the April 2009 eruption (VEI = 1) (Global Volcanism Program, 2009).
Although the misfits between the surface displacement model and the InSAR data are small (Figure 3), some locations show higher misfits (up to 1.5 cm), especially in the subsiding areas to the SW. The minimal misfit at the volcano center confirms that the model accurately captures the parameters of the shallower spherical chamber. On the other hand, the misfit in the subsiding areas suggests a bias that could be due to lithospheric heterogenesis (Zhan et al., 2016) or could be associated with atmospheric noise in the data. We focus our discussion on the dynamics of the shallower chamber, as it is better constrained and the eruption is largely controlled by overpressure and failure of the rock surrounding it.
Overpressure and Stress Evolution Prior to the 2009 Eruption
A central paradigm in volcanology is that eruption is triggered when the overpressure within an expanding magma chamber exceeds the strength of the surrounding rock. Unfortunately, analytical models such as Mogi (1958) and McTigue (1987) are limited in their ability to provide reliable overpressure predictions, because the calculations are inherently non-unique. As previously discussed, this non-uniqueness makes it difficult for the EnKF to reconcile estimations of radius and overpressure. The magma system parameters estimated by the EnKF are used in combination with a series of FEMs with different combinations of radius and overpressure to predict the stress field of the country rock prior to and directly following the 2009 eruption. Calculations of stress evolution are focused at the top of the magma chamber where confining pressures are lowest and tensile failure is most likely (Grosfils, 2007). Additionally, the 2009 eruption fed from a central vent further indicating failure at the top of the magma reservoir.
We utilize the benchmarked COMSOL FEM approach for a pressurized sphere in 3D (Del Negro et al., 2009; Gregg et al., 2012; Zhan and Gregg, 2017) to perform a series of tests for magma chamber radius values of 100–2,500 m and their corresponding overpressures (Figure 7). Of particular interest is whether the magma chamber is in a stable configuration or in a state of tensile failure, potentially indicating imminent eruption.
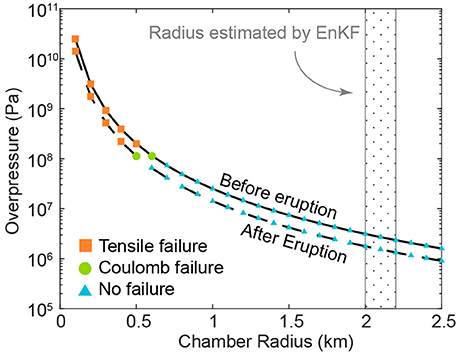
Figure 7. The relationship between the assumed overpressure of the chamber and its corresponding radius before (solid line) and after (dashed line) the 2009 eruption of Kerinci Volcano. The overpressure and the radius cannot be uniquely determined due to the nature of the deformation source. Colored symbols indicate that the type of the failure predicted at the top of the magma chamber is controlled by the combination of the overpressure and the radius. Blue triangles indicate a stress state where no failure is calculated. Green circles indicate a situation where only Coulomb failure is predicted. The orange squares indicate a stress state in which tensile failure is predicted. Figure 8 provides an illustration of this approach.
Figure 7 illustrates the tradeoff between overpressure and radius required to produce the same surface deformation given the optimal EnKF magma chamber depth-to-center estimation. Model configurations that result in either tensile failure or Mohr-Coulomb failure are shown. The most striking outcome of these tests is the clear correlation between chamber radius and failure. As the radius increases, the minimum principal stresses also increase, while the maximum shear stresses are significantly reduced due to decreasing overpressure (Figures 7, 8c,d). This indicates that systems with smaller magma chamber radii are more likely to fail, given the same volume change. This finding has been previously indicated by other researchers (Grosfils, 2007; Gregg et al., 2012) and further indicates the need for an independent assessment of magma reservoir size.
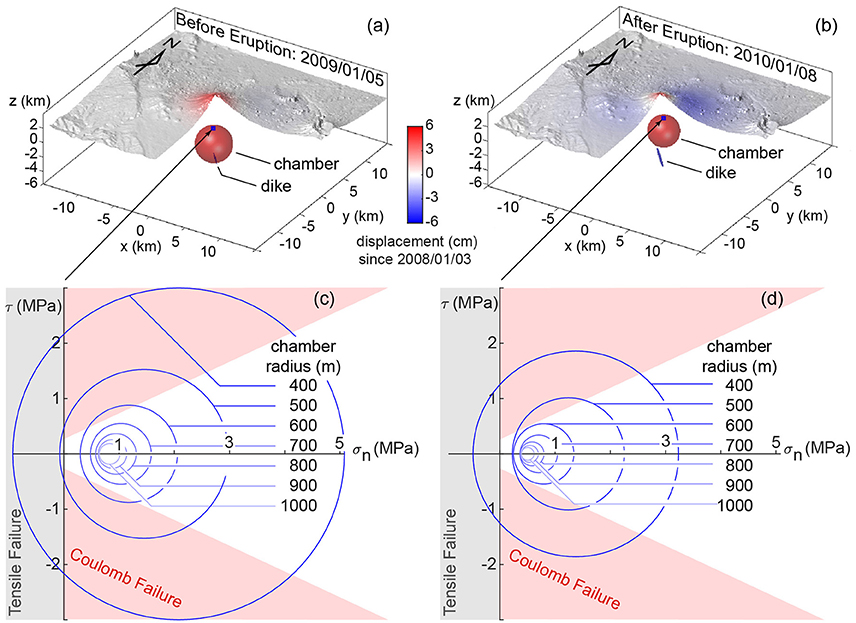
Figure 8. 3D illustrations of the best fit models estimated by EnKF before (a) and after (b) the 2009 eruption. (c,d) Show the estimated Mohr's circle for the country rock (Grosfils, 2007; Gregg et al., 2012) directly above the top of the spherical chamber. The predicted stress is sensitive to the radius size, which tradeoffs with the depth of the top of the chamber. Red shaded regions in (c,d) shows the Coulomb-failure envelop (C = 25 MPa, ϕ = 25° after Grosfils, 2007). The gray shaded region (σn < 0) indicates when the system is in tension. Tensile failure may indicate dike initiation away from the magma chamber and immanent eruption.
The predicted overpressure prior to the eruption is at least two times higher than during and after the eruption (Figure 7) due to the depressurization of the system during the eruption. The models predict that a magma chamber with a radius of 500 m will experience tensile failure (Figure 8c), potentially leading to an eruption. The model also predicts no tensile failure after the eruption if the chamber size is not greatly reduced (Figure 8d); the total estimated volume loss of the chamber is <1%. Similarly, Mohr-Coulomb failure calculated in the host rock prior to eruption is more extensive than after the eruption (Figures 7, 8); however, while failure is predicted in both instances, the orientation and mode of failure may not be optimal for catalyzing eruption (Grosfils, 2007). Due to the non-uniqueness issue, radius estimates may be unreasonably large (Figure 6) and an analysis of the system's stress state assuming a variety of radii-overpressure combinations is necessary to investigate the possibility of an eruption. Future work using data assimilation with displacement and seismicity data may provide stronger constraints on the stress evolution, helping to decipher the dynamics of the magma storage system.
The L2 norm evolution provides additional insights to aid eruption prediction. Since the EnKF analysis updates the model based on the previous time steps, a sudden increase of the L2 norm (Figure 5B) means that the pre-eruption model is no longer able to reproduce the observed deformation, suggesting a sudden change of the magma storage system. Volume change due to magma withdrawal, opening of fractures and dikes (Lister and Kerr, 1991), and alterations of country rock's rheology due to temperature evolution (Annen and Sparks, 2002) could explain this change. Some of these transitions may occur just prior to eruptions and are captured by InSAR and/or GPS. Therefore, the L2 norms provides useful information for characterization of unrest.
Near Real-Time Data Assimilation with InSAR Data
The advantage of SAR observations is that they offer a high spatial resolution, which provides a broad view of the region surrounding the magma system. The EnKF analysis is able to efficiently track surface deformation from the down-sampled InSAR time series of Kerinci (Figure 3). Prior to the 2009 eruption, the InSAR-ALOS time-series repeat interval is 46 days, providing observations of continuous uplift. The models become unconstrained just prior to and immediately following the eruption (gray shaded area in Figure 5) due to the gap in acquisitions. As EnKF is able to update deformation models in near real-time, getting access to SAR data in near-real time could lead to usage of these data to provide early warning of eruption. Additionally, higher temporal repeatability of the SAR systems could lead to improved constraints of the magmatic systems worldwide and of their temporal evolution.
In this EnKF study, 200 models are used in the forecasting ensembles adding up to more than 1,000 iterations. However, the computational expense is <3 min to finish the calculation on a workstation (3.2 GHz Intel Core i5). Although the EnKF is slightly longer than other inversion techniques (e.g., Pagli et al., 2012), it provides huge flexibility for incorporating a wide range of observations from deformation to seismicity, and from heat flow to geochemistry. The primary limitation of this study is the analytical models used. The analytical approach is ideal for decreasing the computational expense of calculating a large population of ensembles; however the models are oversimplified. In the future, more realistic physics-based models and FEMs will take the place of the analytical models to allow researchers to explore more realistic deformation based on other geophysical observations from tomography, gravity, and/or magnetotellurics. Coupling solid mechanics with the fluid dynamics (Le Mével et al., 2016), the evolution of the magma storage systems will be closely related to the magma flux inferred from geological records, instead of the enigmatic and oversimplified overpressure. In the case of a finite element approach, the computational expense is far more significant and a supercomputer is necessary to conduct the Monte Carlo suites for the data assimilation. Future efforts are necessary to optimize the EnKF approach for the use of more sophisticated and computationally expensive models (Gregg and Pettijohn, 2016).
Conclusion
A two-step EnKF data assimilation provides a shallow chamber connect to a deep dike-like source as the most likely model to explain the surface displacement around the 2009 eruption of the Kerinci volcano revealed by the InSAR data. The Yang et al. (1988) model is used to mimic a deep, deflating dike-like source, which can explain the subsiding signal on the flanks of the volcano. At the meantime, a shallow spherical source (McTigue, 1987) is built to reproduce the central uplift. The parameters with highest likelihood are applied to reconstruct the stresses around the magma chamber utilizing a benchmarked FEM. The stress model suggests that the shallow magma reservoir is most likely to fail prior to 2009, which may explain the eruption. Our results illustrate the great potential of the EnKF data assimilation as a technique to explore the dynamic evolution of the magma storage system, giving insight into the eruption forecasting of restless volcanoes.
Author Contributions
YZ and PG conceived the study and YZ wrote the paper with input from all authors. EC and YA contributed to the InSAR data set.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to acknowledge helpful discussions with Dr. F. Amelung, J. Albright, Dr. J. C. Pettijohn, Dr. J. Freymeuller, Dr. Z. Lu, Dr. L. Liu, Dr. J. Biggs, Dr. G. Hou and the UIUC Dynamics Group. We would also like to thank Dr. V. Acocella, Dr. Z. Lu, Dr. A. Tibaldi, and Dr. C. Pagli for their comments which greatly improved our manuscript. Development of Ensemble Kalman Filter approach for modeling active volcanic unrests using InSAR data is funded by NASA (13-ESI13-0034).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2017.00108/full#supplementary-material
References
Allen, J. I., Eknes, M., and Evensen, G. (2003). An Ensemble Kalman Filter with a complex marine ecosystem model: hindcasting phytoplankton in the Cretan Sea. Ann. Geophys. 21, 399–411. doi: 10.5194/angeo-21-399-2003
Annen, C., and Sparks, R. S. J. (2002). Effects of repetitive emplacement of basaltic intrusions on thermal evolution and melt generation in the crust. Earth Planet. Sci. Lett. 203, 937–955. doi: 10.1016/S0012-821X(02)00929-9
Bato, M. G., Pinel, V., and Yan, Y. (2017). Assimilation of Deformation data for eruption forecasting: potentiality assessment based on synthetic cases. Front. Earth Sci. 5:48. doi: 10.3389/feart.2017.00048
Battaglia, M., Segall, P., Murray, J., Cervelli, P., and Langbein, J. (2003). The mechanics of unrest at Long Valley caldera, California: 1. Modeling the geometry of the source using GPS, leveling and two-color EDM data. J. Volcanol. Geotherm. Res. 127, 195–217. doi: 10.1016/S0377-0273(03)00170-7
Bellier, O., and Sébrier, M. (1994). Relationship between tectonism and volcanism along the Great Sumatran fault zone deduced by SPOT image analyses. Tectonophysics 233, 215–231. doi: 10.1016/0040-1951(94)90242-9
Bertino, L., Evensen, G., and Wackernagel, H. (2003). Sequential data assimilation techniques in oceanography. Int. Stat. Rev. 71, 223–241. doi: 10.1111/j.1751-5823.2003.tb00194.x
Biggs, J., Ebmeier, S. K., Aspinall, W. P., Lu, Z., Pritchard, M. E., Sparks, R. S. J., et al. (2014). Global link between deformation and volcanic eruption quantified by satellite imagery. Nat. Commun. 5, 3471. doi: 10.1038/ncomms4471
Cannavò, F., Camacho, A. G., González, P. J., Mattia, M., Puglisi, G., and Fernández, J. (2015). Real time tracking of magmatic intrusions by means of ground deformation modeling during volcanic crises. Sci. Rep. 5:109070. doi: 10.1038/srep10970
Chaussard, E., Amelung, F., and Aoki, Y. (2013). Characterization of open and closed volcanic systems in Indonesia and Mexico using InSAR time series: INSAR TIME SERIES IN INDONESIA AND MEXICO. J. Geophys. Res. Solid Earth 118, 3957–3969. doi: 10.1002/jgrb.50288
Chaussard, E., and Amelung, F. (2012). Precursory inflation of shallow magma reservoirs at west Sunda volcanoes detected by InSAR: InSAR SURVEY OF WEST SUNDA VOLCANOES. Geophys. Res. Lett. 39:L21311. doi: 10.1029/2012GL053817
Cianetti, S., Giunchi, C., and Casarotti, E. (2012). Volcanic deformation and flank instability due to magmatic sources and frictional rheology: the case of Mount Etna. Geophys. J. Int. 191, 939–953. doi: 10.1111/j.1365-246X.2012.05689.x
Collings, R., Lange, D., Rietbrock, A., Tilmann, F., Natawidjaja, D., Suwargadi, B., et al. (2012). Structure and seismogenic properties of the Mentawai segment of the Sumatra subduction zone revealed by local earthquake traveltime tomography. J. Geophys. Res. Solid Earth 117, B01312. doi: 10.1029/2011JB008469
Currenti, G., Del Negro, C., and Ganci, G. (2007). Modelling of ground deformation and gravity fields using finite element method: an application to Etna volcano. Geophys. J. Int. 169, 775–786. doi: 10.1111/j.1365-246X.2007.03380.x
Del Negro, C., Currenti, G., and Scandura, D. (2009). Temperature-dependent viscoelastic modeling of ground deformation: application to Etna volcano during the 1993–1997 inflation period. Phys. Earth Planet. Inter. 172, 299–309. doi: 10.1016/j.pepi.2008.10.019
Dzurisin, D. (2006). Volcano Deformation. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-540-49302-0 (Accessed August 25, 2015).
Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 99, 10143–10162. doi: 10.1029/94JC00572
Evensen, G. (2003). The Ensemble Kalman Filter: theoretical formulation and practical implementation. Ocean Dyn. 53, 343–367. doi: 10.1007/s10236-003-0036-9
Evensen, G. (2009). Data Assimilation. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-642-03711-5 (Accessed August 25, 2015).
Fournier, T., Freymueller, J., and Cervelli, P. (2009). Tracking magma volume recovery at Okmok volcano using GPS and an unscented Kalman filter. J. Geophys. Res. Solid Earth 114, B02405. doi: 10.1029/2008JB005837
Global Volcanism Program (2009). “Report on Kerinci (Indonesia),” in Bulletin of the Global Volcanism Network, ed R. Wunderman (Smithsonian Institution). doi: 10.5479/si.GVP.BGVN200912-261170
Gregg, P. M., and Pettijohn, J. C. (2016). A multi-data stream assimilation framework for the assessment of volcanic unrest. J. Volcanol. Geotherm. Res. 309, 63–77. doi: 10.1016/j.jvolgeores.2015.11.008
Gregg, P. M., de Silva, S. L., and Grosfils, E. B. (2013). Thermomechanics of shallow magma chamber pressurization: implications for the assessment of ground deformation data at active volcanoes. Earth Planet. Sci. Lett. 384, 100–108. doi: 10.1016/j.epsl.2013.09.040
Gregg, P. M., de Silva, S. L., Grosfils, E. B., and Parmigiani, J. P. (2012). Catastrophic caldera-forming eruptions: Thermomechanics and implications for eruption triggering and maximum caldera dimensions on Earth. J. Volcanol. Geotherm. Res. 241–242, 1–12. doi: 10.1016/j.jvolgeores.2012.06.009
Grosfils, E. B. (2007). Magma reservoir failure on the terrestrial planets: assessing the importance of gravitational loading in simple elastic models. J. Volcanol. Geotherm. Res. 166, 47–75. doi: 10.1016/j.jvolgeores.2007.06.007
Gudmundsson, A. (2006). How local stresses control magma-chamber ruptures, dyke injections, and eruptions in composite volcanoes. Earth Sci. Rev. 79, 1–31. doi: 10.1016/j.earscirev.2006.06.006
Hanssen, R. F. (2001). Radar Interferometry: Data Interpretation and Error Analysis. Springer Science & Business Media. Available online at: http://www.springer.com/us/book/9780792369455
Hickey, J., Gottsmann, J., and Mothes, P. (2015). Estimating volcanic deformation source parameters with a finite element inversion: the 2001-2002 unrest at Cotopaxi volcano, Ecuador. J. Geophys. Res. Solid Earth 120, 1473–1486. doi: 10.1002/2014JB011731
Hildreth, W., and Moorbath, S. (1988). Crustal contributions to arc magmatism in the Andes of Central Chile. Contrib. Mineral. Petrol. 98, 455–489. doi: 10.1007/BF00372365
Jónsson, S., Zebker, H., Segall, P., and Amelung, F. (2002). Fault slip distribution of the 1999 Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 92, 1377–1389. doi: 10.1785/0120000922
Julier, S., Uhlmann, J., and Durrant-Whyte, H. F. (2000). A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 45, 477–482. doi: 10.1109/9.847726
Koulakov, I., Bohm, M., Asch, G., Lühr, B.-G., Manzanares, A., Brotopuspito, K. S., et al. (2007). P and S velocity structure of the crust and the upper mantle beneath central Java from local tomography inversion. J. Geophys. Res. 112:B08310. doi: 10.1029/2006JB004712
Le Mével, H., Gregg, P. M., and Feigl, K. L. (2016). Magma injection into a long-lived reservoir to explain geodetically measured uplift: Application to the 2007–2014 unrest episode at Laguna del Maule volcanic field, Chile. J. Geophys. Res. Solid Earth 121, 6092–6108. doi: 10.1002/2016JB013066
Li, Z., Muller, J.-P., Cross, P., and Fielding, E. J. (2005). Interferometric synthetic aperture radar (InSAR) atmospheric correction: GPS, Moderate Resolution Imaging Spectroradiometer (MODIS), and InSAR integration. J. Geophys. Res. Solid Earth 110, B03410. doi: 10.1029/2004JB003446
Lisaeter, K. A., Evensen, G., and Laxon, S. (2007). Assimilating synthetic CryoSat sea ice thickness in a coupled ice-ocean model. J. Geophys. Res. Oceans 112, C07023. doi: 10.1029/2006JC003786
Lister, J. R., and Kerr, R. C. (1991). Fluid-mechanical models of crack propagation and their application to magma transport in dykes. J. Geophys. Res. Solid Earth 96, 10049–10077. doi: 10.1029/91JB00600
Lohman, R. B., and Simons, M. (2005). Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosystems 6:Q01007. doi: 10.1029/2004GC000841
McCaffrey, R. (2009). The tectonic framework of the sumatran subduction zone. Annu. Rev. Earth Planet. Sci. 37, 345–366. doi: 10.1146/annurev.earth.031208.100212
McTigue, D. F. (1987). Elastic stress and deformation near a finite spherical magma body: resolution of the point source paradox. J. Geophys. Res. 92:12931. doi: 10.1029/JB092iB12p12931
Mogi, K. (1958). Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull. Earthq. Res. Inst. Univ. Tokyo 36, 99–134.
Muksin, U., Bauer, K., and Haberland, C. (2013). Seismic Vp and Vp/Vs structure of the geothermal area around Tarutung (North Sumatra, Indonesia) derived from local earthquake tomography. J. Volcanol. Geotherm. Res. 260, 27–42. doi: 10.1016/j.jvolgeores.2013.04.012
Newman, A. V., Stiros, S., Feng, L., Psimoulis, P., Moschas, F., Saltogianni, V., et al. (2012). Recent geodetic unrest at Santorini Caldera, Greece. Geophys. Res. Lett. 39, L06309. doi: 10.1029/2012GL051286
Nooner, S. L., and Chadwick, W. W. (2009). Volcanic inflation measured in the caldera of axial seamount: implications for magma supply and future eruptions. Geochem. Geophys. Geosystems 10, Q02002. doi: 10.1029/2008GC002315
Pagli, C., Wright, T. J., Ebinger, C. J., Yun, S.-H., Cann, J. R., Barnie, T., et al. (2012). Shallow axial magma chamber at the slow-spreading erta ale ridge. Nat. Geosci. 5, 284–288. doi: 10.1038/ngeo1414
Parks, M. M., Moore, J. D. P., Papanikolaou, X., Biggs, J., Mather, T. A., Pyle, D. M., et al. (2015). From quiescence to unrest: 20years of satellite geodetic measurements at Santorini volcano, Greece. J. Geophys. Res. Solid Earth 120, 1309–1328. doi: 10.1002/2014JB011540
Pasquare, F. A., and Tibaldi, A. (2003). Do transcurrent faults guide volcano growth? The case of NW Bicol Volcanic Arc, Luzon, Philippines. Terra Nova 15, 204–212. doi: 10.1046/j.1365-3121.2003.00484.x
Ronchin, E., Masterlark, T., Molist, J. M., Saunders, S., and Tao, W. (2013). Solid modeling techniques to build 3D finite element models of volcanic systems: an example from the Rabaul Caldera system, Papua New Guinea. Comput. Geosci. 52, 325–333. doi: 10.1016/j.cageo.2012.09.025
Schmidt, S. F. (1966). “Application of state-space methods to navigation problems,” in Advances in Control Systems, ed C. T. Leondes (Elsevier), 293–340. Available online at: http://www.sciencedirect.com/science/article/pii/B9781483167169500114 (Accessed July 21, 2016).
Sieh, K., and Natawidjaja, D. (2000). Neotectonics of the Sumatran fault, Indonesia. J. Geophys. Res. Solid Earth 105, 28295–28326. doi: 10.1029/2000JB900120
Simons, M., Fialko, Y., and Rivera, L. (2002). Coseismic deformation from the 1999 Mw 7.1 Hector Mine, California, earthquake as inferred from InSAR and GPS Observations. Bull. Seismol. Soc. Am. 92, 1390–1402. doi: 10.1785/0120000933
Skjervheim, J.-A., Evensen, G., Aanonsen, S. I., Ruud, B. O., and Johansen, T.-A. (2007). Incorporating 4D seismic data in reservoir simulation models using ensemble kalman filter. SPE J. 12, 282–292. doi: 10.2118/95789-PA
Tait, S., Jaupart, C., and Vergniolle, S. (1989). Pressure, gas content and eruption periodicity of a shallow, crystallising magma chamber. Earth Planet. Sci. Lett. 92, 107–123. doi: 10.1016/0012-821X(89)90025-3
Tibaldi, A. (2015). Structure of volcano plumbing systems: a review of multi-parametric effects. J. Volcanol. Geotherm. Res. 298, 85–135. doi: 10.1016/j.jvolgeores.2015.03.023
vanLeeuwen, P. J., and Evensen, G. (1996). Data assimilation and inverse methods in terms of a probabilistic formulation. Mon. Weather Rev. 124, 2898–2913. doi: 10.1175/1520-0493(1996)124<2898:DAAIMI>2.0.CO;2
Wilson, G. W., Oezkan-Haller, H. T., and Holman, R. A. (2010). Data assimilation and bathymetric inversion in a two-dimensional horizontal surf zone model. J. Geophys. Res. Oceans 115, C12057. doi: 10.1029/2010JC006286
Yang, X.-M., Davis, P. M., and Dieterich, J. H. (1988). Deformation from inflation of a dipping finite prolate spheroid in an elastic half-space as a model for volcanic stressing. J. Geophys. Res. Solid Earth 93, 4249–4257. doi: 10.1029/JB093iB05p04249
Zhan, Y., and Gregg, P. M. (2017). Data assimilation strategies for volcano geodesy. J. Volcanol. Geotherm. Res. 344, 13–25. doi: 10.1016/j.jvolgeores.2017.02.015
Keywords: ensemble kalman filter, InSAR, magma storage, eruption, kerinci volcano
Citation: Zhan Y, Gregg PM, Chaussard E and Aoki Y (2017) Sequential Assimilation of Volcanic Monitoring Data to Quantify Eruption Potential: Application to Kerinci Volcano, Sumatra. Front. Earth Sci. 5:108. doi: 10.3389/feart.2017.00108
Received: 28 September 2017; Accepted: 05 December 2017;
Published: 19 December 2017.
Edited by:
Zhong Lu, Southern Methodist University, United StatesReviewed by:
Alessandro Tibaldi, Università Degli Studi di Milano Bicocca, ItalyCarolina Pagli, University of Pisa, Italy
Copyright © 2017 Zhan, Gregg, Chaussard and Aoki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Zhan, eWFuemhhbjNAaWxsaW5vaXMuZWR1
 Yan Zhan
Yan Zhan Patricia M. Gregg
Patricia M. Gregg Estelle Chaussard2
Estelle Chaussard2 Yosuke Aoki
Yosuke Aoki