Unraveling InSAR Observed Antarctic Ice-Shelf Flexure Using 2-D Elastic and Viscoelastic Modeling

1. Introduction

Grounding zones form the junction between grounded ice-sheets and floating ice-shelves. They link the ice-sheets with the global ocean and are vulnerable to change (Gudmundsson, 2013). Oscillation of ocean tides causes the ice in this region to bend which strongly influences temporal variations in ice-mass discharge and affects the location of the grounding line, where the ice body comes in direct contact with the ocean water. Understanding these short-term processes is necessary to estimate the transmission of longitudinal stress gradients across the grounding line, which in turn are important for calculating long-term ice-sheet mass balance and predicting future sea-level rise with confidence.

Since Goldstein et al. (1993) successfully observed glacier motion from space at the Rutford Ice Stream, Antarctica, interferometric synthetic aperture radar (InSAR) has become a widely used tool in glaciology. This method determines surface displacement with centimeter accuracy and has been applied to measure temporal and spatial variations of ice-flow velocities (Mouginot et al., 2014; Minchew et al., 2017). In the grounding zone, satellite interferometry can identify horizontal ice flow and vertical tidal deflection. The phase contribution of steady horizontal ice flow can be removed by differencing the 2 InSAR signals (Rignot, 1996), leaving only vertical deflection due to ocean tides. These 2 InSAR pairs can be a triple or quadruple image combination of 3 or 4 coherent SAR images. This space-borne measurement is known as double-differential InSAR (DInSAR).

While DInSAR is often used to delineate the grounding line (Rignot et al., 2011) the flexure pattern also contains additional information on ice-shelf thickness, material properties and ocean tides at the snapshots of SAR data acquisition. In combination with numerical modeling of grounding-zone flexure, DInSAR has been used to estimate ice-thickness distribution (Schmeltz et al., 2002; Marsh et al., 2014). Additionally, grounding-line retreat over time can be monitored (Rignot, 1998; Sykes et al., 2009; Rignot et al., 2014) as an indicator for the onset of marine ice-sheet instability (Weertman, 1974; Schoof, 2007; Durand et al., 2009). The main difficulty interpreting DInSAR is that images originate from a combination of several snapshots in time and do not display the vertical displacement for a single tidal amplitude (Rignot et al., 2000). The derived flexure pattern is a combination of multiple separate states of the tidal oscillation. Theoretical considerations of tidal flexure indicate that grounding-line curvature complicates the bending pattern (Rabus and Lang, 2002). A 1-D beam model may therefore be representative of grounding-line profiles across straight and seaward protrusions (convex sections), but fails to predict the vertical deflection within landward embayments (concave sections) at the same spatial scale. This is a particular problem as a large portion of ice is discharged through fjord-type embayments around Antarctica.

In this manuscript, we carefully address the complex interpretation of double-differential imagery and explore the uncertainty of some of the applications outlined above. We achieve this as follows: First we introduce the study area, the available data set and methods used for the analysis. Second we derive a suite of ice-thickness distributions across the Southern McMurdo Ice Shelf (SMIS) and adjust two tide models with information stored in DInSAR. Third we numerically model the ice-shelf bending using two different types of materials to describe the behavior of ice. We then compare the model solutions to nine double-differential TerraSAR-X interferograms and make a statement about the applicability of both numerical models.

2. Study Area and Observations

2.1. The Southern McMurdo Ice Shelf, Antarctica

The study area is a small and almost stagnant ice shelf in the western Ross Sea region (78°15′S, 167°7′E, Figure 1). The main ice inflow into the SMIS originates from the accumulation areas on the slopes of White Island, but is less than 10 m yr⁻¹. The grounding zone has a variety of configurations like embayments and protrusions and is supported locally by an ice rise. A dedicated field-survey was conducted in the ice-shelf grounding zone during the 2014/15 Antarctic season, where we collected tidal flexure measurements concurrent with satellite data acquisitions.

FIGURE 1

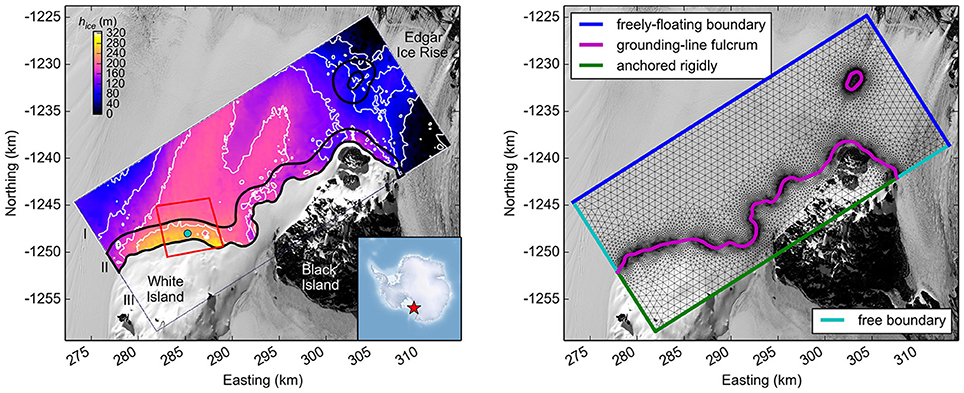
Figure 1. (Left) Ice-thickness distribution at the Southern McMurdo Ice Shelf: White contours show 5 m freeboard intervals based on CryoSat-2 radar altimetry, corresponding to a change in ice thickness of 46.7 m. Note (in yellows) the relatively thick ice south of White Island and (in black) zero ice thickness in areas with changing surface types. The red box delineates the area of GPR measurements for field validation. The black line encloses the grounding-zone area between the grounding line (upstream) and the hydrostatic line (downstream). Surface classification in (I) freely-floating area, (II) grounding-zone area, and (III) grounded ice is based on double-differential InSAR. The blue dot is placed at the firn core drillsite within the grounding-zone area. The red star in the insert marks the location of the study area in the western Ross Sea region. (Right) The model domain, finite-element mesh and boundary conditions. The map background is a contrast-stretched Landsat 8 panchromatic imagery. The geographic projection is Antarctic Polar Stereographic with easting and northing coordinates shown in kilometers.

2.2. Data Set and Processing

2.2.1. Satellite Data

The TerraSAR-X satellite operates in an 11 day repeat pass polar orbit. Its SAR antenna (X-band 3.1 cm at 9.6 GHz) provides high-quality radar images with up to 3 m spatial resolution and a scene size of 30 × 50 km in StripMap imaging mode. We derived 9 DInSAR images from 12 TerraSAR-X scenes between October and December 2014 and calculated surface displacement caused by vertical ice deformation using the Gamma software package (Werner et al., 2000). Figures in the Supplementary Material (Figures S1–S3, top middle panels) show examples for relative differential interferograms with each color cycle (fringe) corresponding to about 2.2 cm vertical displacement. The grounding and hydrostatic line, at which the ice oscillates with the full tidal amplitude, were determined from these interferograms and placed at the inward and seaward limits of tidal fringes to ensure that all floating data is included in the analysis. To determine ice thickness, we derived a Digital Elevation Model (DEM) from 5 years (2011–2015) of CryoSat-2 baseline-C data (section 3). As the satellite's radar altimeter has been shown to be sensitive to changes in surface type (Chuter and Bamber, 2015), we filter each track by a moving window of 9 consecutive measurements and remove the samples outside 1 standard deviation of the running mean. Additionally we used the latest global combined gravity field model EIGEN-6C4 (Förste et al., 2014) which is a result of the GRACE and GOCE satellite missions.

All data were reprojected and resampled onto a 50 m regular Antarctic Polar Stereographic grid. We define easting in positive x-direction, northing in y-direction and depth below surface in z-direction of a Cartesian coordinate system (Figure 1).

2.2.2. Field Data

We measured ice thickness in the south of White Island with a 25 MHz pulseEKKO Pro Ground Penetrating Radar (GPR). Six tiltmeters along a transect across the grounding zone were used to derive the rheological parameters for ice in a previous study (Wild et al., 2017). We also installed a number of GPS receivers to record horizontal and vertical ice movement due to tidal bending processes (Rack et al., 2017). Here we use 75 d of GPS data from the freely-floating part of the ice shelf to correct for the Inverse Barometric Effect (IBE, Padman et al., 2003b). Atmospheric pressure data originates from a nearby weather station at Scott Base on Ross Island (linear distance ≈50 km), which correlates well (R of +0.998) where it overlaps with our 64 d barometric record at SMIS. Two tide models are used to predict the tidal oscillation at SMIS: (1) the circum-Antarctic tide simulation model CATS2008a_opt (CATS) developed by Padman et al. (2008), which is corrected for the deformation of the Earth's crust due to the water load by using TPXO6.2 load tide model (Egbert and Erofeeva, 2002); (2) the t_tide prediction (Pawlowicz et al., 2002) of a previously IBE corrected GPS record from the freely-floating area of the SMIS. We restrict the analysis to these 2 records, as other global or regional Antarctic tide models include the SMIS into their land mask.

3. Ice Thickness From Freeboard

Our GPR data set only covers parts of the SMIS with an atypical straight grounding line. In order to investigate any presumed 2-D control of grounding-line shape on tidal flexure, we derive ice thickness from freeboard to cover areas with grounding-line configurations that are more representative for the Antarctic coastline. We classify the study area into 3 categories: (I) the freely-floating area bordered by the hydrostatic line which is determined by the seaward limit of tidal flexure from DInSAR (Fricker and Padman, 2006, accuracy within one sixth of a fringe), (II) the ice-shelf grounding zone between the hydrostatic line and the landward limit of tidal fringes (Rignot, 1996) and (III) the grounded portion fully resting on land (Figure 1). We define the location of these regions a priori from 9 DInSAR images.

At first, ice thickness distribution on the freely-floating ice shelf is derived from CryoSat-2 measurements and hydrostatic equilibrium principles. The CryoSat-2 DEM is translated from surface elevations to freeboard by assuming that the mean sea level underneath the ice shelf corresponds to the geoid model. We neglect changes in sea-level height due to mean dynamic topography as they are not directly measurable on the ice-shelf surface (Griggs and Bamber, 2011). The relation between freeboard z_s and ice thickness H is:

$\begin{array}{ll}H=(z_s-\Delta z)\frac{{\rho }_{sw}}{{\rho }_{sw}-\stackrel{-}{\rho }},& (1)\end{array}$

and is determined by the firn correction factor Δz, the density of sea water ρ_sw = 1, 027 kg m⁻³ and the mean density $\stackrel{-}{\rho }$ of the ice column. For a solid iceberg Δz is zero and mean density is equal to the density of pure ice ρ_ice = 917 kg m⁻³; however, the iceberg relation needs to be modified for an ice shelf with a layer of firn at its surface. We use a firn core and GPR measurements to estimate the correction Δz and find that accumulation and ice thickness both increase non-linearly toward the grounding line. The principles of hydrostatic equilibrium also break down in the grounding zone (Bindschadler et al., 2011). We use 3 methods to provide lower and upper limits of ice thickness in this area: (1) a constant extrapolation of the freely-floating ice thickness across the grounding zone, (2) a scaled extrapolation of the freely-floating ice thickness across the grounding zone guided by GPR measurements in our field area and (3) directly from freeboard in the grounding zone with Δz = 5.9 m. Compared to the GPR data these 3 methods produce errors of −7.4 ± 13.2 m, 2.4 ± 8.9 m and 0.0 ± 12.4 m, respectively. Here we use method (3) which corresponds to a percentage ice-thickness error of ±5.6 %, with the largest errors along the grounding line, where the hydrostatic equilibrium assumption breaks down.

4. Tidal Forcing

Tidal load and atmospheric pressure variability both influence ice-shelf surface elevation. An increase of 1 hPa in atmospheric pressure causes an isostatic response of −1 cm on the freely-floating ice shelf (Padman et al., 2003b). This signal is known as the Inverse Barometric Effect (IBE) and needs to be accounted for when predicting tidal amplitudes accurately. Even after the IBE correction, the 2 tidal forcings do not perfectly match the DInSAR observed tidal amplitudes on the freely-floating ice shelf. These IBE corrected misfits are up to 14.6 cm for the CATS and 10.3 cm for the t_tide record (Table 1), making a direct comparison of the gradient of the modeled and satellite-observed flexure pattern meaningless. It is therefore desirable to derive a tidal forcing for the finite-element simulations that reproduces the DInSAR observations on the freely-floating ice shelf. This new tidal forcing must preserve the phase information about the tidal constituents gained from harmonic analysis of GPS data, and require minimal data intervention. We calculate the 9 original misfits, μ, between the double-differential tidal predictions and the DInSAR observations. These misfits result from the combination of individual offsets, θ, between the modeled and observed tides at each SAR data acquisition. The system is solved for all 9 double-differential interferograms simultaneously by finding the least-squares combination of offsets that result in zero net misfit. A continuous adjustment function is interpolated between these discrete offsets using a cubic spline function and then added to the tidal prediction (Figure 2). This adjustment corresponds to 2.1 ± 2.3 cm for the CATS tide model and 0.4 ± 2.3 cm for the t_tide prediction (Table 2).

TABLE 1

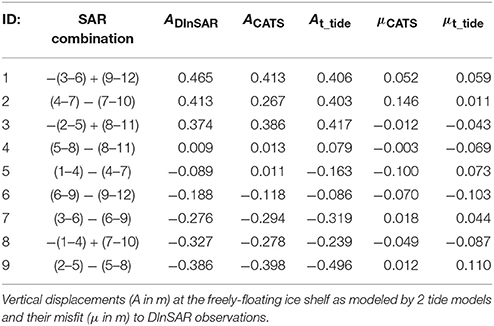
Table 1. SAR combinations of 12 images (see Table 2) used to generate 9 double-differential interferograms.

FIGURE 2

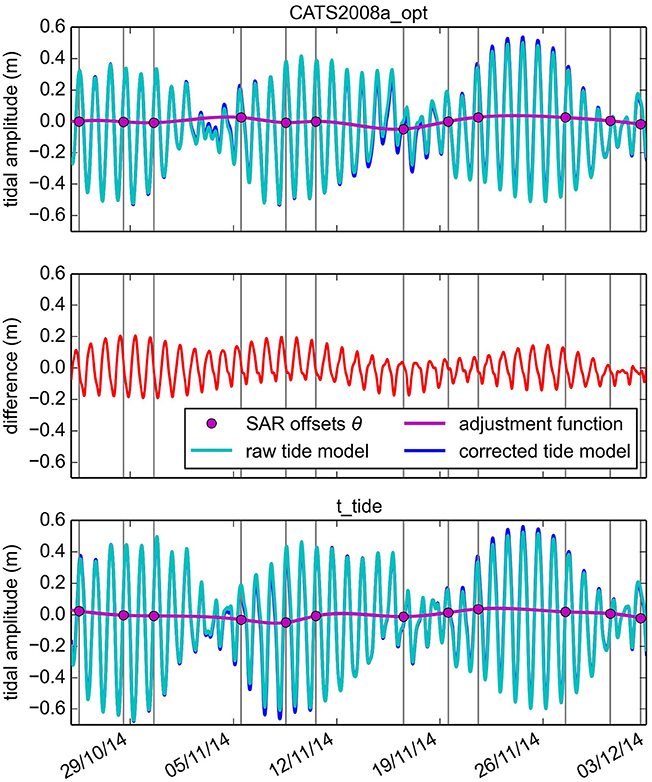
Figure 2. The tidal oscillation as predicted by (Top) a regional tide model of the circum-Antarctic ocean and (Bottom) a harmonic analysis of GPS data from the freely-floating area. The raw model forecasts are both adjusted to match DInSAR observations using a least-squares fitting technique as explained in section 4. The (Center) red line shows the differences between the adjusted tide predictions. Gray vertical lines coincide with times of SAR data acquisitions. Values for the prevailing tidal amplitudes and their adjustment at these times are given in Table 2.

TABLE 2

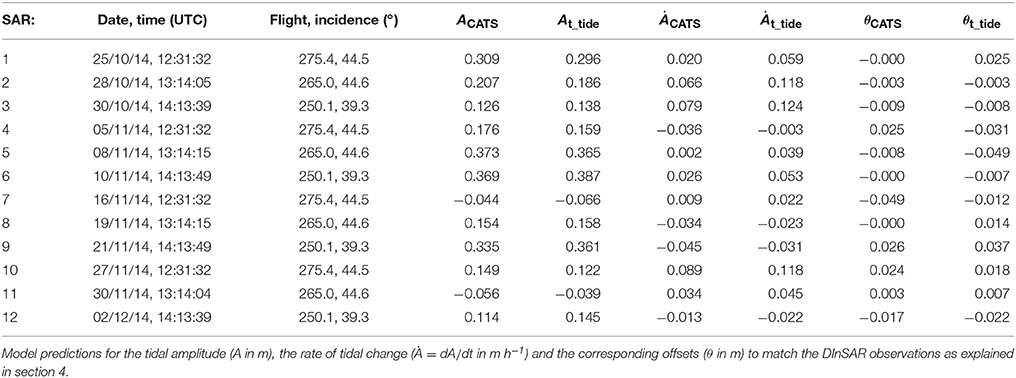
Table 2. SAR images used in this study and the prevailing satellite geometries at times of data acquisition (the flight direction is from North, the incidence angle is from the surface normal).

Although both tide models now perfectly match the DInSAR observations on the freely-floating area, they differ in the timing of the applied tidal forcing. Harmonic analysis of our GPS data suggests that the phase of the CATS model is leading the t_tide model (Wild et al., 2017). This is reflected in the temporal evolution of the difference between the tide records (red curve in Figure 2), which varies by ±8.8 cm. Similarly, the absolute tidal range of the CATS record (1.07 m) is smaller than for the t_tide record (1.24 m). This implies that the tides within the t_tide data set are changing more rapidly (0.166 m h⁻¹) than expected from the CATS record (0.136 m h⁻¹).

5. Numerical Modeling of Tidal Ice-Shelf Flexure

The vertical displacement of an ice shelf due to ocean tides is described by 2 finite-element models. Both models are separated at the grounding line into grounded and floating portions. The grounded part is resting on an elastically deforming bed expressed by a series of springs, the floating portion experiences the hydrostatic pressure from the ocean underneath. First we introduce the well-known elastic theory (Holdsworth, 1969; Vaughan, 1995; Schmeltz et al., 2002) as formulated by Walker et al. (2013):

$\begin{array}{ll}kw+{\nabla }^2(D{\nabla }^{2}w)=q,& (2)\end{array}$

where w(t) is the vertical deflection of the neutral layer in a plate, ∇² is the Laplace operator in 2-D space and k = 5 MPa m⁻¹ a spring constant of the foundation which is zero for the floating part. The applied tidal force q(t) is defined by:

$\begin{array}{ll}q={\rho }_{sw}g(A(t)-w),& (3)\end{array}$

with g = 9.81 m s⁻² the gravitational acceleration and A(t) the tidal amplitude given by the adjusted tide records. The resistance offered by the ice shelf while undergoing tidal bending is given by Love (1906, p. 443):

$\begin{array}{ll}D=\frac{E{H}^3}{12(1-{\lambda }^2)},& (4)\end{array}$

where E = 1.6 GPa is the Young's modulus for ice, H(x, y) the ice thickness distribution and λ = 0.4 the Poisson's ratio. We compare the elastic model with the more realistic viscoelastic approach developed by Walker et al. (2013):

$\begin{array}{ll}\frac{\partial }{\partial t}(kw+{\nabla }^2(D{\nabla }^{2}w))+\frac{Ek}{2\nu (1-{\lambda }^2)}w=\frac{\partial }{\partial t}q+\frac{E}{2\nu (1-{\lambda }^2)}q,& (5)\end{array}$

where the rheological parameters E = 1.6 GPa and the value for viscosity ν = 50.1 TPa s are predetermined from tiltmeter data (Wild et al., 2017). We implement the following boundary conditions for both models (Figure 1): the upstream boundary of the model domain of the grounded portion is anchored rigidly (w = 0, ∇²w = 0), the downstream boundary of the freely-floating ice shelf is equal to the tidal oscillation (w = A(t), ∇w = 0) and the grounding line is represented by a fulcrum (w = 0). Both models are implemented in the finite-element software COMSOL Multiphysics. The models are discretized in space using a mesh of 44,853 triangular elements leading to an average mesh size of 585 m and numerically integrated with a fully implicit time stepping method (backward differentiation formula). Strict time steps are taken by the MUMPS numerical solver to minimize errors induced by the temporal discretization.

These numerical models of tidal flexure calculate vertical displacements w(x, y) for the neutral layer half-way down the ice column. Here, longitudinal stresses are generally zero and neither compressional (δ_x, δ_y < 0) nor tensional strains (δ_x, δ_y > 0) are present. Tidal flexure, in turn, is generally measured on the surface of ice shelves using either in-situ data from GPS (Vaughan, 1994), and tiltmeters (Smith, 1991; Reeh et al., 2003), or SAR imagery (Rignot et al., 2011). A direct comparison between model solutions and any surface observation is thus spuriously assuming that displacement at the surface is the same as at the neutral layer (Schmeltz et al., 2002; Reeh et al., 2003; Han and Lee, 2014). We build on earlier work by Rack et al. (2017) but assume that curvature is directly proportional to the bending moment, because the slope of the neutral layer is small compared with the flexural length scale. This approximation allows us to integrate the horizontal surface strain components, δ_x and δ_y, to yield a straightforward equation for the additional horizontal motion (Be, hereafter “bending effect”):

$\begin{array}{ll}\begin{array}{c}{\displaystyle {\int }_x}{\delta }_{x}dx=B{e}_x=\frac{H}{2}{w}_x^{\prime }\\ {\displaystyle {\int }_y}{\delta }_{y}dy=B{e}_y=\frac{H}{2}{w}_y^{\prime }.\end{array}& (6)\end{array}$

Here, H/2 is the distance to the neutral layer to be in accordance with classic Euler–Bernoulli beam theory and $w_x^{\prime }$ and $w_y^{\prime }$ are the first spatial derivatives of vertical deflection of the neutral layer. As SAR sensors are sensitive to displacement in line of sight (look direction), we rotate the coordinate system from longitude/latitude to radar look direction for each SAR image (satellite imaging geometries are given in Table 2). This converts the horizontal components Be_x and Be_y to apparent vertical motion as captured with DInSAR. We then add this component onto all model output for vertical deflection of the neutral layer to match the observations seen with DInSAR.

6. Results

We now compare the satellite observations to the model solutions. First, we assess any control of curved grounding lines on tidal flexure. Second, we investigate differences between elastic and viscoelastic models. Third, we analyze the quality of the tide models and their potential to affect our flexure model results.

6.1. Two-Dimensional Controls on Tidal Flexure

The overall model performance is characterized by the standard deviation of the differences between the DInSAR observations of vertical displacement and the flexure model output. A relatively large standard deviation originates from a poor model fit.

The elastic model (Equation 2) is forced only by the value of the net tidal amplitude. The misfit between the elastic model and the DInSAR is generally within 1 fringe in the grounding zone with a mean standard deviation of 2.19 cm (Figure 3) Areas where the standard deviation exceeds this value are evidence of ice heterogeneity, e.g., the Ross Ice-Shelf Shear Zone or around the Edgar Ice Rise. The viscoelastic model, in turn, incorporates the time derivative of the tidal forcing (Equation 5). It therefore captures the different behavior between the smoothly oscillating CATS record and the more rapidly changing t_tide model. The viscoelastic CATS model matches our satellite data set better than the viscoelastic t_tide model as the standard deviation is smaller within the grounding zone (mean standard deviations of 2.24 and 2.62 cm, respectively, Figure 4).

FIGURE 3

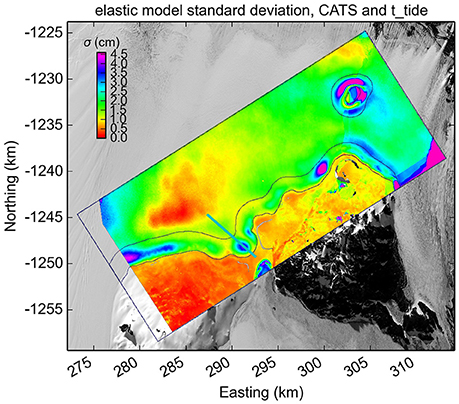
Figure 3. Pixel-based standard deviation between the elastic model solution for 9 DInSAR observations. The blue line shows the location of the elastic transects shown in Figure 5.

FIGURE 4

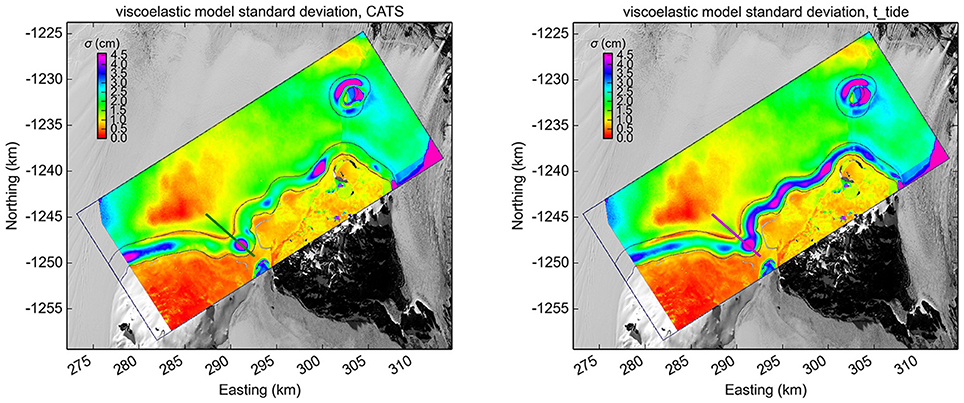
Figure 4. Pixel based standard deviation between the viscoelastic model solutions for 9 DInSAR observations, (Left) using the adjusted CATS tide model and (Right) the adjusted t_tide forecast. The green and magenta lines show the location of the viscoelastic transects shown in Figure 5 for the CATS and t_tide predictions, respectively.

All combinations of flexure and tide models fit equally well along straight parts of the grounding line and seaward protrusions but exhibit the largest standard deviations at locations within landward embayments of the grounding line. Changing λ has a negligible effect within embayments with best results for λ = 0.4, as defined initially. Varying ice thickness within the specified bounds (section 3) produces the same pattern in variation of standard deviation, but of larger magnitude. We therefore restrict further analysis to the ice thickness map of Figure 1 that assumes hydrostatic equilibrium in the grounding zone as it presents the overall smallest standard deviation.

To further investigate model performance within embayments we define a transect across the grounding zone. This profile begins on the grounded ice, then runs through the peak error located within the embayment between White and Black Island and ends on the freely-floating part of the SMIS. We perform 1-D elastic and viscoelastic simulations using the same ice thickness, forcings and corrections as for the 2-D simulations. These flexure curves act as “control runs” for 2-D effects as they are not influenced by the shape of the grounding line (Figure 5).

FIGURE 5

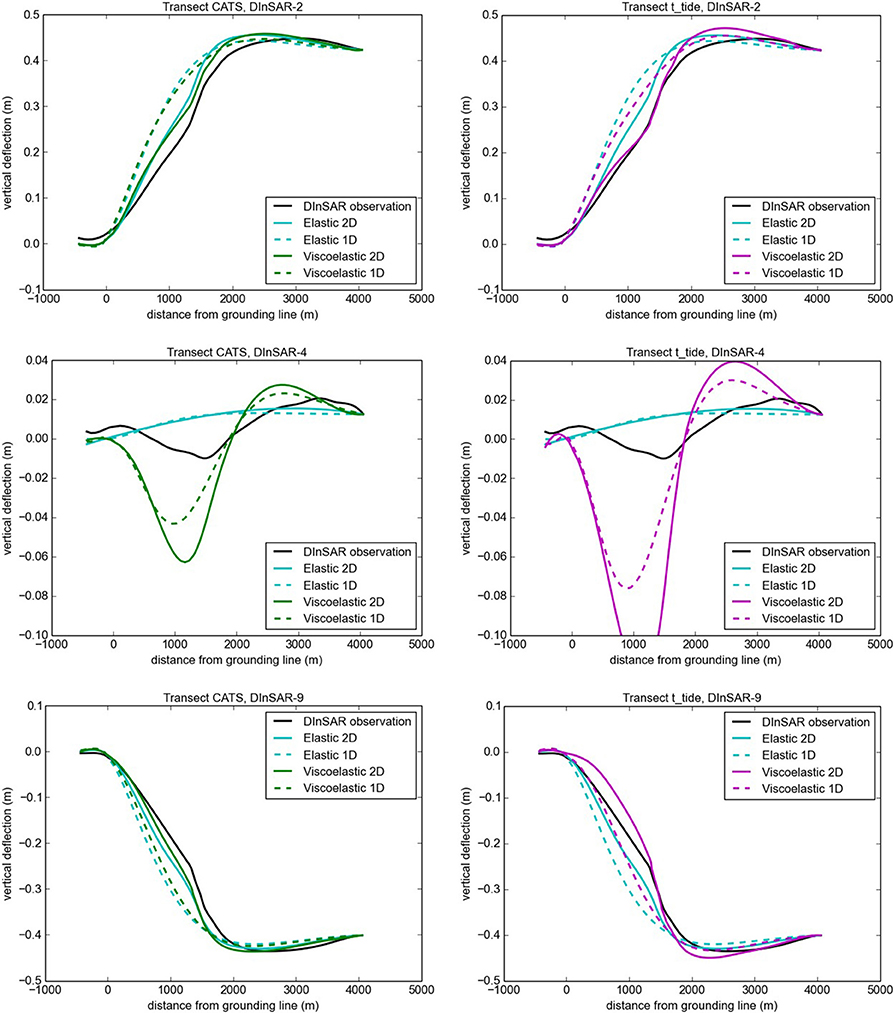
Figure 5. Transects as shown in Figure 4, (Left) using the CATS forcing and (Right) the t_tide model. Ice-shelf flexure curves for (Top) a positive net tidal amplitude, (Center) almost zero net tidal amplitude and (Bottom) a negative net tidal amplitude. The black lines show the highly-accurate DInSAR observations, solid lines originate from transects through 2-D model results and dashed lines from 1-D simulations along this transect.

6.2. Tide-Model Quality

As ice is a viscoelastic material (Reeh et al., 2000, 2003; Gudmundsson, 2011), a viscoelastic model should generally improve the elastic model fit. However, our analysis reveals that in the case of an inaccurate tide model elastic theory is preferable overall to describe the DInSAR observations, due to its simplicity.

The differences between the elastic and viscoelastic models are largest around relatively small tidal amplitudes, when tides are steeply rising or falling. This is expected as the rate of tidal change has a strong impact on the viscoelastic model (Wild et al., 2017). To investigate the effect of tidal conditions during SAR data acquisition we more closely examine three individual DInSAR combinations.

DInSAR-2 results in a relatively large net displacement (41.3 cm, Table 1), although all 3 SAR images are acquired at relatively small tidal amplitudes (SAR 4-7-10 in Table 2). For this reason, the viscoelastic model is expected to largely improve the elastic fit (Wild et al., 2017). This is supported by the viscoelastic model using the adjusted t_tide record which almost perfectly reproduces the DInSAR observation (Figure 5, top and Figure S1). Here, only a small misfit to the t_tide forecast (1.1 cm, Table 1) results in a good match with DInSAR. The CATS forecast, in turn, shows a large misfit (14.6 cm, Table 1). This misfit introduces uncertainty in the rate of change of the tide increasing the error in the viscoelastic model. In this case there is no obvious improvement over the elastic model.

DInSAR-4 features the smallest net tidal displacement (0.9 cm, Table 1), with SAR data acquisitions during one large and two relatively small tidal amplitudes when the rate of tidal changes are high (SAR 5-8-11 in Table 2). Viscoelastic effects are therefore most likely to be observed in this DInSAR measurement. Nevertheless, the elastic model at first seems preferable across the SMIS (Figure S2). As the net tidal displacement is positive, the elastic solution is characterized by seaward upward bending. In contrast, the viscoelastic model reproduces the general s-shaped flexure curve as observed with DInSAR (Figure 5, center). Although this pattern is captured by the viscoelastic models, its amplitude is overestimated and worsens from the 1-D control runs to the 2-D simulations. Here, the CATS forcing required the least net adjustment (−0.3 cm) whereas the t_tide record was heavily modified (−6.9 cm) to match the DInSAR observation. The effects of this adjustment are evident (Figure 5, center).

DInSAR-9 features the largest negative net displacement (−38.6 cm) and is a combination of two large and one small tidal displacement (SAR 2-5-8 in Table 2). SAR images 2 and 8 are both acquired during steeply rising and falling tides, respectively. In this case, the CATS forecast requires a much smaller overall tidal adjustment (1.2 cm) than t_tide (11.0 cm). Since there is almost no adjustment for the CATS model, it is expected that there will be a good fit (Figure 5, bottom and Figure S3).

We rationalize that the theoretical superiority of the viscoelastic model over elastic approximation is only valid, when the tide model output requires minimal adjustment. For net adjustments (i.e., misfits μ) smaller than ≈1.5 cm, the viscoelastic model outputs result in a smaller root-mean-square-error in the grounding-zone areas than elastic model output (Figure 6). Differences between the two flexure models are increasing for larger net adjustments (>4.0 cm) and the viscoelastic model performance becomes more variable.

FIGURE 6

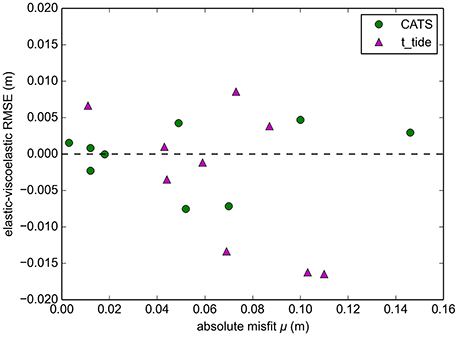
Figure 6. The difference between elastic and viscoelastic root-mean-square-errors within the grounding-zone areas as a function of the net adjustment (misfits) of the utilized tide model. A positive difference corresponds to an improvement of viscoelastic theory over the elastic approximation.

7. Discussion

7.1. Evaluation of Tide Models

In order to directly compare satellite measurements to model solutions, tidal forcings need to perfectly match the observed vertical displacements on the freely-floating part of an ice-shelf. Centimeter-scale adjustments are currently necessary which not only modify the tidal amplitudes at times of SAR data acquisitions, but also alter the rate of tidal change. As the viscoelastic model incorporates the time derivative of the tidal forcing, it captures the adverse consequences of this adjustment. The elastic model in turn, is only dependent on the prevailing tidal amplitude and ignores any information on the tidal stage. Therefore, the elastic modeling approach performs better with an inaccurate tidal forcing when directly compared to DInSAR measurements. Despite this, the viscoelastic model is preferable when the tidal forcing does not require significant adjustment (<1.5 cm).

Inaccuracies in the tidal forcing can be a consequence of (1) the quality of the tide model, (2) the IBE correction, or (3) a combination of both. Current Antarctic tide models are estimated to be accurate within a root-mean-square deviation of 10 cm around the Ross Sea (Padman et al., 2002). These errors are a result of insufficient bathymetric measurements underneath ice shelves, inaccuracies in grounding-line locations and the scarcity of tide-model assimilation data around Antarctica (King and Padman, 2005). The IBE correction reduces the standard deviation of the residual error for the CATS prediction from 7.9 to 5.8 cm and from 8.9 to 7.0 cm for the t_tide prediction over a 75 d period of GPS data. However, this correction is developed for long time-scales and freely-floating ice shelves far away from the grounding line and shear margins (Padman et al., 2003b). The shallow sea under the SMIS is likely to alter the ocean's response to pressure fluctuations, because coastal effects cannot be excluded. Harmonic analysis of these residual errors shows: (1) the CATS model only captures diurnal (O1, K1, NO1, J1) and semi-diurnal (S2, N2, M2, L2) tidal constituents within centimeter accuracy, (2) the t_tide forecast reproduces these short-period components down to millimeter accuracy, but only captures the amplitudes of the long-period signals (MM, MSF) to within centimeters.

Even a perfect tide model can theoretically only match DInSAR measurements within its own accuracy. Rignot et al. (2011) obtained a detectable InSAR signal above noise within less than 1 cm vertical deflection. We therefore consider the DInSAR measurement as the absolute truth as it is one to two orders of magnitude more accurate than the CATS tide model (Rack et al., 2017). DInSAR-4, using the adjusted CATS forcing, appears to be a special case in that the net displacement is almost zero. Although the s-shaped bending pattern was generally captured by viscoelastic models, its magnitude was overestimated leading to smaller errors with the elastic approach. Despite the larger errors, the viscoelastic model better represents the physics of ice-shelf flexure. The larger errors, in turn, are probably due to tide model inaccuracies and/or consequences of ice heterogeneity across the SMIS.

A logical step further is to perform a similar analysis for a suite of tide models. Han and Lee (2014) investigated two global tide models: TPXO7.1 (Egbert and Erofeeva, 2002) and FES2004 (Lyard et al., 2006), and two regional Antarctic tide models: CATS2008a (Padman et al., 2002, 2008) and Ross_Inv (Padman et al., 2003a). The authors used linear regression analysis and found that Ross_Inv performed best when compared to DInSAR data on the freely-floating portion of the Campbell Glacier Tongue. Unfortunately, these tide models do not include the SMIS.

7.2. Variability in Ice Rheology

In this study, it is assumed that variation in flexural rigidity is only a function of ice thickness distribution. Ice is an inhomogeneous material which experiences spatial variations in its rheological properties. Similarly, ice stiffness and viscosity are affected by the thermal regime of the ice shelf, with ice temperature at the base equal to the freezing point of seawater and surface conditions varying with surface climate and ice dynamics (Cuffey and Paterson, 2010). Larour et al. (2005) used a map of surface velocity from Radarsat-1 interferometry to derive rigidity and ice viscosity variation over the Ronne Ice Shelf, although the observed stiffness variability is larger than expected from surface temperatures alone. Additionally, density variations with depth and crevassing can lead to large changes in ice rheology (Rosier et al., 2017). These reduce the ice stiffness and explain why modeled standard deviations in the grounding zone increase toward the east, where advection of basal crevasses originating from the Ross Ice-Shelf Shear Zone is expected. Basal crevassing is also expected around the Edgar Ice Rise, but our derived ice thickness is likely underestimated there (Figure 1, left panel), which further complicates the interpretation of modeled standard deviations in this area.

7.3. Uncertainties in Ice Thickness

Our freeboard to thickness conversion neglects effects of basal refreezing under the ice shelf which may alter the resulting freeboard. Marine ice is present in the western and southern parts of the SMIS (Fitzsimons et al., 2012), but wasn't detected within the area of our field survey. The model domain does include surface ablation areas and we may therefore overestimate ice thickness in areas of blue ice. Similarly, basal crevassing has been observed around the ice rise (Clifford, 2006) and toward the shear zone with the Ross Ice Shelf (Ryan, 2016). Ice fracture reduces the effective ice thickness in these areas and may cause the high standard deviations of model misfits.

7.4. Two-Dimensional Controls During Small Tidal Deflections

Along straight sections and seaward protrusions of the grounding line, 1-D simulations of tidal flexure yield very similar results to 2-D flexure models (not shown here). In contrast, 2-D simulations largely improve the match to DInSAR within landward embayments, especially for large net displacements (Figure 5, top and bottom panels). For small tidal displacements the 1-D model seems to perform better at first, but fails to reproduce the flexure pattern as observed with DInSAR (Figure 5, center panels). Therefore, a viscoelastic model is necessary to describe the physics of ice-shelf flexure for small tidal displacements. We notice that the value of viscosity has a larger effect in 2-D models than in 1-D models, where the floating ice within the embayment is supported by the surrounding ice. Along our transect this is most distinctly noticeable within 1.5 km of the grounding line and for small tidal deflections (Figure 5, center panels). Additionally, all our viscoelastic models overestimate the s-shaped flexure curve as measured with DInSAR. This points to a slightly higher value for ice viscosity than the one we derived from tiltmeter data earlier (Wild et al., 2017).

8. Conclusion

Here we show that tidal flexure patterns in grounding zones observed using DInSAR can be reproduced within a few centimeters using finite-element modeling. We find that model misfits are generally largest within landward embayments of the grounding line, where the support of neighboring ice dampens the vertical flexure. When comparing an elastic and a viscoelastic model, we find that the quality of input data is crucial in determining which model should be used. Viscoelastic models are superior, particularly in landward embayments or when tidal amplitudes are low. Unfortunately they are also much more sensitive to errors in tidal forcing, as they rely on the rate of change of the tide. Here we use two tide models, validated by GPS data and find that centimeter-scale adjustments are necessary to match DInSAR observations on the SMIS. These adjustments fail to correct for any errors in the rate of tidal change, which impacts the output from viscoelastic models. A logical further step is to investigate the performance of various tide models to force grounding-zone flexure in areas where a suite of tide models are available.

It is worth mentioning that our 75 d record of high-resolution GPS measurements improves the CATS forecast for short-period tidal constituents but is too short to sufficiently capture long-period tidal components. A longer time series of GPS measurements (>1 year) is necessary to extract the tidal constituents to develop a tide model matching DInSAR accuracy. This finding underlines the need for ongoing, long-term field observations to support the full interpretation of DInSAR measurements – an inevitable tool in grounding zone glaciology.

Author Contributions

OM and WR contributed to initial ideas and methodological developments. CW undertook the numerical modeling of ice-shelf flexure and wrote this manuscript. WR processed the TerraSAR-X data. All authors contributed to the discussion of the results and approved the final manuscript.

Funding

All authors of this study are partially supported by the Past Antarctic Climate and Future Implications program (contract CX05X1001). Additionally, OM is supported by the Marsden Fund Council (14-UOC-056).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer, HP, and handling Editor declared their shared affiliation.

Acknowledgments

We thank Antarctica New Zealand as well as the Scott Base staff for all their support of the event K053 during the 2014/15 Antarctic field season. The German Aerospace Agency (DLR) for providing TerraSAR-X data and the European Space Agency for making CryoSat-2 data available. We acknowledge the National Institute of Water and Atmospheric Research (NIWA) for weather station data at Scott Base and the Norwegian Polar Institute's Quantarctica package. We also thank D. Price for fieldwork and assistance with CryoSat-2 data, M. Ryan for fieldwork and processing of our GPR measurements, M. King for GPS data processing, H. Purdie and S. Rosier for useful discussions and L. Padman for insights in the CATS2008a tide model. We acknowledge the excellent comments of our three reviewers and the editor.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2018.00028/full#supplementary-material

References

Bindschadler, R., Choi, H., Wichlacz, A., Bingham, R., Bohlander, J., Brunt, K., et al. (2011). Getting around Antarctica: new high-resolution mappings of the grounded and freely-floating boundaries of the Antarctic ice sheet created for the International Polar Year. Cryosphere 5, 569–588. doi: 10.5194/tc-5-569-2011

CrossRef Full Text | Google Scholar

Chuter, S. J., and Bamber, J. L. (2015). Antarctic ice shelf thickness from CryoSat-2 radar altimetry. Geophys. Res. Lett. 42, 721–729. doi: 10.1002/2015GL066515

CrossRef Full Text | Google Scholar

Clifford, A. E. (2006). Physiography, Flow Characteristics and Vulnerablity of the Southern McMurdo Ice Shelf, Antarctica, Master's thesis, University of Otago.

Cuffey, K. M., and Paterson, W. S. B. (2010). The Physics of Glaciers. Oxford, UK: Elsevier.

Google Scholar

Durand, G., Gagliardini, O., de Fleurian, B., Zwinger, T., and Le Meur, E. (2009). Marine ice sheet dynamics: hysteresis and neutral equilibrium. J. Geophys. Res. Earth Surf. 114:F03009. doi: 10.1029/2008JF001170

CrossRef Full Text | Google Scholar

Egbert, G. D., and Erofeeva, S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmos. Oceanic Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

CrossRef Full Text | Google Scholar

Fitzsimons, S., Mager, S., Frew, R., Clifford, A., and Wilson, G. (2012). Formation of ice-shelf moraines by accretion of sea water and marine sediment at the southern margin of the McMurdo Ice Shelf, Antarctica. Ann. Glaciol. 53, 211–220. doi: 10.3189/2012AoG60A155

CrossRef Full Text | Google Scholar

Förste, C., Bruinsma, S., Abrikosov, O., Flechtner, F., Marty, J. C., Lemoine, J. M., et al. (2014). “EIGEN-6C4: the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse,” in Paper Presented at 5th GOCE User Workshop (Paris), 25–28.

Fricker, H. A., and Padman, L. (2006). Ice-shelf grounding-zone structure from ICESat laser altimetry. Geophys. Res. Lett. 33:l15502. doi: 10.1029/2006GL026907

CrossRef Full Text | Google Scholar

Goldstein, R. M., Engelhardt, H., Kamb, B., and Frolich, R. M. (1993). Satellite radar interferometry for monitoring ice-sheet motion: application to an Antarctic ice stream. Science 262, 1525–1530. doi: 10.1126/science.262.5139.1525

PubMed Abstract | CrossRef Full Text | Google Scholar

Griggs, J. A., and Bamber, J. L. (2011). Antarctic ice-shelf thickness from satellite radar altimetry. J. Glaciol. 57, 485–498. doi: 10.3189/002214311796905659

CrossRef Full Text | Google Scholar

Gudmundsson, G. H. (2011). Ice-stream response to ocean tides and the form of the basal sliding law. Cryosphere 5, 259–270. doi: 10.5194/tc-5-259-2011

CrossRef Full Text | Google Scholar

Gudmundsson, G. H. (2013). Ice-shelf buttressing and the stability of marine ice sheets. Cryosphere 7, 647–655. doi: 10.5194/tc-7-647-2013

CrossRef Full Text | Google Scholar

Han, H., and Lee, H. (2014). Tide deflection of Campbell Glacier Tongue, Antarctica, analyzed by double-differential SAR interferometry and finite element method. Remote Sens. Environ. 141, 201–213. doi: 10.1016/j.rse.2013.11.002

CrossRef Full Text | Google Scholar

Holdsworth, G. (1969). Flexure of a floating ice tongue. J. Glaciol. 8, 385–397. doi: 10.1017/S0022143000026976

CrossRef Full Text | Google Scholar

King, M. A., and Padman, L. (2005). Accuracy assessment of ocean tide models around Antarctica. Geophys. Res. Lett. 32:L23608. doi: 10.1029/2005GL023901

CrossRef Full Text | Google Scholar

Larour, E., Rignot, E., Joughin, I., and Aubry, D. (2005). Rheology of the Ronne Ice Shelf, Antarctica, inferred from satellite radar interferometry data using an inverse control method. Geophys. Res. Lett. 32:L05503. doi: 10.1029/2004GL021693

CrossRef Full Text | Google Scholar

Love, A. E. H. (1906). A Treatise on the Mathematical Theory of Elasticity. London: Cambridge University Press.

Google Scholar

Lyard, F., Lefevre, F., Letellier, T., and Francis, O. (2006). Modelling the global ocean tides: modern insights from FES2004. Ocean Dyn. 56, 394–415. doi: 10.1007/s10236-006-0086-x

CrossRef Full Text | Google Scholar

Marsh, O. J., Rack, W., Golledge, N. R., Lawson, W., and Floricioiu, D. (2014). Grounding-zone ice thickness from InSAR: inverse modelling of tidal elastic bending. J. Glaciol. 60, 526–536. doi: 10.3189/2014JoG13J033

CrossRef Full Text | Google Scholar

Minchew, B. M., Simons, M., Riel, B., and Milillo, P. (2017). Tidally induced variations in vertical and horizontal motion on Rutford Ice Stream, West Antarctica, inferred from remotely sensed observations. J. Geophys. Res. Earth Surf. 122, 167–190. doi: 10.1002/2016JF003971

CrossRef Full Text | Google Scholar

Mouginot, J., Rignot, E., and Scheuchl, B. (2014). Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophys. Res. Lett. 41, 1576–1584. doi: 10.1002/2013GL059069

CrossRef Full Text | Google Scholar

Padman, L., Erofeeva, S. Y., and Fricker, H. A. (2008). Improving Antarctic tide models by assimilation of ICESat laser altimetry over ice shelves. Geophys. Res. Lett. 35:L22504. doi: 10.1029/2008GL035592

CrossRef Full Text | Google Scholar

Padman, L., Erofeeva, S. Y., and Joughin, I. (2003a). Tides of the Ross Sea and Ross Ice Shelf cavity. Antarct. Sci. 15, 31–40. doi: 10.1017/S0954102003001032

CrossRef Full Text | Google Scholar

Padman, L., Fricker, H. A., Coleman, R., Howard, S., and Erofeeva, L. (2002). A new tide model for the Antarctic ice shelves and seas. Ann. Glaciol. 34, 247–254. doi: 10.3189/172756402781817752

CrossRef Full Text | Google Scholar

Padman, L., King, M., Goring, D., Corr, H., and Coleman, R. (2003b). Ice-shelf elevation changes due to atmospheric pressure variations. J. Glaciol. 49, 521–526. doi: 10.3189/172756503781830386

CrossRef Full Text | Google Scholar

Pawlowicz, R., Beardsley, B., and Lentz, S. (2002). Classical tidal-harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Gesosci. 28, 929–937. doi: 10.1016/S0098-3004(02)00013-4

CrossRef Full Text | Google Scholar

Rabus, B. T., and Lang, O. (2002). On the representation of ice-shelf grounding zones in SAR interferograms. J. Glaciol. 48, 345–356. doi: 10.3189/172756502781831197

CrossRef Full Text | Google Scholar

Rack, W., King, M. A., Marsh, O. J., Wild, C. T., and Floricioiu, D. (2017). Analysis of ice shelf flexure and its InSAR representation in the grounding zone of the Southern McMurdo Ice Shelf. Cryosphere 11, 2481–2490. doi: 10.5194/tc-11-2481-2017

CrossRef Full Text | Google Scholar

Reeh, N., Christensen, E. L., Mayer, C., and Olesen, O. B. (2003). Tidal bending of glaciers: a linear viscoelastic approach. Ann. Glaciol. 37, 83–89. doi: 10.3189/172756403781815663

CrossRef Full Text | Google Scholar

Reeh, N., Mayer, C., Olesen, O. B., Christensen, E. L., and Thomsen, H. H. (2000). Tidal movement of Nioghalvfjerdsfjorden glacier, northeast Greenland: observations and modelling. Ann. Glaciol. 31, 111–117. doi: 10.3189/172756400781820408

CrossRef Full Text | Google Scholar

Rignot, E. (1996). Tidal motion, ice velocity and melt rate of Petermann Gletscher, Greenland, measured from radar interferometry. J. Glaciol. 42, 476–485. doi: 10.1017/S0022143000003464

CrossRef Full Text | Google Scholar

Rignot, E. (1998). Hinge-line migration of Petermann Gletscher, north Greenland, detected using satellite-radar interferometry. J. Glaciol. 44, 469–476. doi: 10.1017/S0022143000001994

CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H., and Scheuchl, B. (2014). Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011. Geophys. Res. Lett. 41, 3502–3509. doi: 10.1002/2014GL060140

CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., and Scheuchl, B. (2011). Antarctic grounding line mapping from differential satellite radar interferometry. Geophys. Res. Lett. 38:L10504. doi: 10.1029/2011GL047109

CrossRef Full Text | Google Scholar

Rignot, E., Padman, L., MacAyeal, D. R., and Schmeltz, M. (2000). Observation of ocean tides below the Filchner and Ronne Ice Shelves, Antarctica, using synthetic aperture radar interferometry: comparison with tide model predictions. J. Geophys. Res. Oceans 105, 19615–19630. doi: 10.1029/1999JC000011

CrossRef Full Text | Google Scholar

Rosier, S. H. R., Marsh, O. J., Rack, W., Gudmundsson, G. H., Wild, C. T., and Ryan, M. (2017). On the interpretation of ice-shelf flexure measurements. J. Glaciol. 63, 783–791. doi: 10.1017/jog.2017.44

CrossRef Full Text | Google Scholar

Ryan, M. R. (2016). Characteristics of the Ross and Southern McMurdo Ice Shelves as Revealed From Ground-Based Radar Surveys, Master's Thesis, University of Canterbury.

Schmeltz, M., Rignot, E., and MacAyeal, D. (2002). Tidal flexure along ice-sheet margins: comparison of InSAR with an elastic-plate model. Ann. Glaciol. 34, 202–208. doi: 10.3189/172756402781818049

CrossRef Full Text | Google Scholar

Schoof, C. (2007). Ice-sheet grounding line dynamics: steady states, stability, and hysteresis. J. Geophys. Res. Earth 112:F03S28. doi: 10.1029/2006JF000664

CrossRef Full Text | Google Scholar

Smith, A. M. (1991). The use of tiltmeters to study the dynamics of Antarctic ice-shelf grounding lines. J. Glaciol. 37, 51–58. doi: 10.1017/S0022143000042799

CrossRef Full Text | Google Scholar

Sykes, H. J., Murray, T., and Luckman, A. (2009). The location of the grounding zone of Evans Ice Stream, Antarctica, investigated using SAR interferometry and modelling. Ann. Glaciol. 50, 35–40. doi: 10.3189/172756409789624292

CrossRef Full Text | Google Scholar

Vaughan, D. G. (1994). Investigating tidal flexure on an ice shelf using kinematic GPS. Ann. Glaciol. 20, 372–376. doi: 10.3189/172756494794587375

CrossRef Full Text | Google Scholar

Vaughan, D. G. (1995). Tidal flexure at ice-shelf margins. J. Geophys. Res. Solid Earth 100, 6213–6224. doi: 10.1029/94JB02467

CrossRef Full Text | Google Scholar

Walker, R. T., Parizek, B. R., Alley, R. B., Anandakrishnan, S., Riverman, K. L., and Christianson, K. (2013). Ice-shelf tidal flexure and subglacial pressure variations. Earth Planet. Sci. Lett. 361, 422–428. doi: 10.1016/j.epsl.2012.11.008

CrossRef Full Text | Google Scholar

Weertman, J. (1974). Stability of the junction of an Ice Sheet and an Ice Shelf, J. Glaciol. 13, 3–11. doi: 10.1017/S0022143000023327

CrossRef Full Text | Google Scholar

Werner, C., Wegmüller, U., Strozzi, T., and Wiesmann, A. (2000). “Gamma SAR and interferometric processing software,” in Proceedings of the ERS-envisat Symposium, Vol. 1620 (Gothenburg), 1620.

Google Scholar

Wild, C. T., Marsh, O. J., and Rack, W. (2017). Viscosity and elasticity: a model intercomparison of ice-shelf bending in an Antarctic grounding zone. J. Glaciol. 63, 573–580. doi: 10.1017/jog.2017.15

CrossRef Full Text | Google Scholar