- 1Laboratoire Magmas et Volcans, Université Clermont Auvergne–CNRS–IRD, OPGC, Aubière, France
- 2Lunar and Planetary Institute, Universities Space Research Association, Houston, TX, United States
Basaltic shield volcanoes most commonly form as intraplate volcanic ocean islands that arise from the ocean floor and continue to grow above the sea water level to form gigantic volcanic edifices. The volcanic edifice evolution and the internal stress distribution may be influenced by the water load of the surrounding ocean. We therefore investigate how the presence of an ocean affects the internal stress of a volcanic edifice and thus magma propagation by means of axisymmetric elastic models of a volcanic edifice overlying an elastic lithosphere. We designed a volcanic edifice featuring a height of ~6,000 m and a radius of ~ 60 km which was build up either instantaneously or incrementally, i.e., by emplacing new layers of equal volumes on top of each other. The latter was done in a way that the resulting stress and edifice geometry from one step served as the initial condition of the subsequent step. Thus, each new deposit was emplaced on an already deformed and stressed model layer. The ocean load was simulated using a boundary condition at the surface of the model. For the instantaneous volcano growth scenario, different water levels were investigated, while for the incrementally growing volcano the water level was fixed to 4,000 m. We employed both half-space and flexural models and compared the deformation of the volcanic edifice, as well as its internal stress orientation and magnitude with and without applying an ocean load. Our results show major differences in the resulting state of stress between an instantaneous and an incrementally built volcanic edifice. Further, our results imply that stress orientations and types of potential magma intrusions within the volcano as well are influenced by the loading effect of an ocean. Ocean loading reduces the effective load magnitude of an edifice via a buoyancy effect, reducing edifice stress magnitudes and substrate subsidence. Ocean loading also adds vertical compression to edifices; in half-space models, this addition reinforces the existing principal stress orientations and increases the differential stress, whereas in flexural models, ocean loading reduces the differential stress and favors re-orientation of principal stresses within the edifices. Our results therefore provide new insights into the state of stress and deformation within the edifices of basaltic ocean island volcanoes with significant implications for magma ascent and eruption and edifice construction.
Introduction
Basaltic ocean island shield volcanoes are the largest volcanic edifices on Earth. While these islands develop over millions of years as a result of continuous volcanic hot spot activity [e.g., La Réunion: ~5 Ma (Gillot et al., 1994), Galapagos Islands ~4 Ma (Bailey, 1976), Hawaiian Islands: ~5.1 Ma (Clague and Dalrymple, 1987)], individual volcanic centers that build those islands have a shorter lifespan [e.g., Piton de la Fournaise at La Réunion: ~530 ka (Gillot et al., 1994), and Mauna Kea at Hawaii: ~700 ka (Frey et al., 1990)]. Growth mechanisms include both magmatic intrusions that generate dike and sill complexes (Walker, 1993, 1999) and volcanic eruptions characterized by lava flow emplacement and pyroclastic or volcanoclastic material deposition (Walker, 1973, 2000). The contribution of magmatic intrusions to the growth and therefore overall volume of a volcanic edifice can be significant: for instance, at Ko'olau Volcano (O'ahu Island, HI, USA) sill complexes may be responsible for at least half of the height of the edifice (Annen et al., 2001). As a basaltic volcano grows, the increasing gravitational load causes a flexure of the underlying lithosphere (McNutt and Menard, 1978; McGovern, 2007), generating horizontal compressional stresses within the volcanic edifice and clamping the propagation of magmas toward the surface and promoting the formation of sills (McGovern and Solomon, 1998; Pinel and Jaupart, 2004; McGovern, 2007; Menand et al., 2010; Galgana et al., 2011). The accumulation of magma within the volcanic edifice leads to the formation of magmatic reservoirs (Annen, 2011; Menand et al., 2011), wherein pressure can then build up to generate eruptions at the surface (Tait et al., 1989; McLeod and Tait, 1999; Pinel et al., 2010; Becerril et al., 2013). These eruptions are the result of magma propagation through the volcanic edifice, which is largely controlled by the internal state of stress in response to structural controls (Fiske and Jackson, 1972; Carracedo, 1994; Rubin, 1995; Acocella and Neri, 2009; Bagnardi et al., 2013; Chestler and Grosfils, 2013; Tibaldi, 2015), the mechanical layering (Gudmundsson, 2005; Kavanagh et al., 2006; Maccaferri et al., 2011), and pre-existing fractures (Gaffney et al., 2007; Le Corvec et al., 2013).
Volcanic edifices are often modeled as instantaneous volume (referred subsequently as instantaneous volcano; van Wyk de Vries and Matela, 1998; Pinel and Jaupart, 2003; Casagli et al., 2009; Galgana et al., 2011), while in fact they grow incrementally over time (referred subsequently as incremental volcano; McGovern and Solomon, 1993, 1998; Apuani et al., 2005; Musiol et al., 2016). Stresses within instantaneously-formed and incrementally-grown volcanoes are significantly different. While instantaneously-formed edifices show high differential stresses in the upper parts of the volcano and low differential stresses in the lower parts, incrementally-grown edifices show low differential stresses in in upper and lower parts of the volcano, separated by a zone of high differential stresses (McGovern and Solomon, 1993). Over the course of their life, basaltic ocean island volcanoes rose from the bottom of the ocean and emerged to form the islands that we observe today. Previous research has shown that ocean loading alters the state of stress within the lithosphere at near-shore plate boundaries (Luttrell and Sandwell, 2010) and influences volcanic eruptive activity (McNutt, 1999), and that glacial cycles can cause pressure changes in the mantle that yet affect the melt production at mid-oceanic ridges (Crowley et al., 2015). Here, we investigate the role of ocean loading on the growth of basaltic ocean island volcanoes and suggest that edifice internal stresses and magma propagation pathways may in fact be biased by ocean loads.
In the following, we present finite element models of both instantaneously- and incrementally grown volcanic edifices and show the effect of the presence or absence of ocean load on their internal stresses. Furthermore, we illustrate scenarios incorporating or ignoring lithospheric flexure. We provide the amount of displacement and the favored type of magmatic intrusion (dyke or sill) within the edifice as calculated from the edifice internal state of stress and we discuss the implications of our models for tackling edifice internal stresses and magma propagation at basaltic ocean island volcanoes.
Methodology
In this study, we use finite element models (FEMs) to investigate the effect of ocean load on the vertical deformation and the state of stress within a basaltic ocean island volcano. We develop axisymmetric elastic models of a volcanic edifice overlying an elastic lithosphere following the work of Galgana et al. (2011) and using the COMSOL Multiphysics software. All our models have similar physical parameters (Table 1) and are loaded gravitationally with body forces and initial lithostatic stresses (Table 2, no ocean load). The boundary condition applied at the base of the lithosphere balance the loading of the lithostatically-prestressed lithosphere (–g.ρlith.Tl) and simulates buoyant restoring forces (g. ρasth.w) in response to the lithosphere subsidence within a denser asthenosphere (Table 2; Watts, 2001). In our models, we adopt the convention that extension is positive while compression is negative.
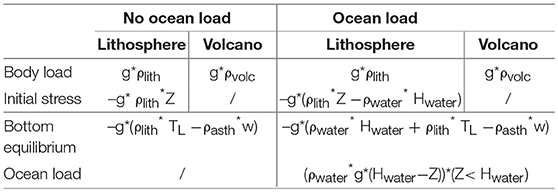
Table 2. Boundary conditions of the initial finite element models (FEM), where w is the vertical displacement, g is the Earth's gravitational acceleration; ρlith, ρasth and ρwater are the lithosphere, asthenosphere and water densities, respectively, Hwater is the water height, TL is the thickness of the lithosphere, Z represents the depth of any point of the initial geometry (negative downward)..
By developing and testing different model scenarios, we investigate or account for: 1- a half-space configuration vs. the flexure of the lithosphere below the edifice, 2- instantaneous volcano existence vs. incremental volcano evolution, and 3- the presence (or absence) of ocean load.
Half-Space vs. Flexural Models
In order to understand the role of flexure on edifice internal stresses, two sets of models were developed (1) half-space models, where the domain underlying the volcanic edifice is considered as infinite (TL = 1,000 km), and (2) flexural models where the thickness of the domain (TL = 30 km) represents an average elastic thickness of the oceanic lithosphere (Figure 1; Watts and ten Brink, 1989; Wessel, 1993).
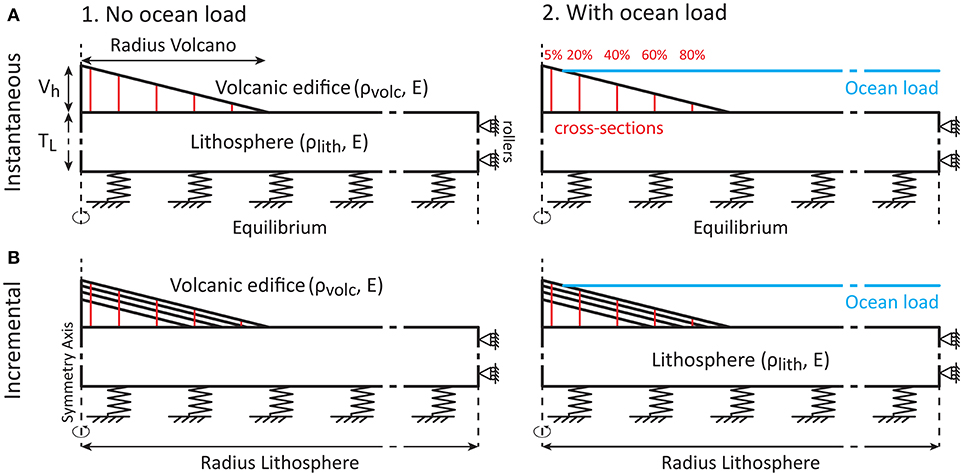
Figure 1. Boundary conditions for the different axisymmetric finite element models (FEMs) used in this study. Initially, models are composed of an elastic lithosphere and an elastic volcanic edifice with or without an ocean load, with buoyant restoring forces applied at the base of the model and rollers applied to the right margin to constrain horizontal movements. Models are tested for a half-space geometry where TL = 1,000 km, and a flexure geometry where TL = 30 km. We studied two types of edifice growth: (A) an instantaneously-formed volcanic edifice, and (B) an incrementally-grown volcanic edifice consisting of layers of equal volumes as the initial edifice. In the models taking into account an ocean load, the ocean level varies from 1,000 to 7,000 m in instantaneously-formed volcano models (A2), while it stays constant at 4,000 m in incrementally-grown volcano models (B2). Cross-sections were created at 5, 20, 40, 60, and 80% of the resulting length of the volcanic edifice away from the symmetry axis (Table S3). These cross-sections are used to plot the differential stress and the type of magmatic intrusions within the edifice (cf. Figures 3, 5, 7).
Instantaneous Edifice Existence vs. Incremental Edifice Growth
Following the work of McGovern and Solomon (1993, 1998), we reconstruct the volcanic edifice (a) as if it was existing instantaneously, and (b) as if it was building up incrementally, assuming a constant magma supply rate over time. For the latter case, we start with an initial edifice of height Vh = 3,000 m and radius Vr = 30,000 m (Figure 1) and then we subsequently emplace seven new layers, each of them featuring the same volume as the initial edifice (representing a constant magma flux rate). The lithospheric and edifice internal stresses, as well as the deformed geometry that result from one step, serve as the initial conditions before the emplacement of the subsequent layer. For each new layer, we apply two bottom boundary conditions (Table 3); the first one in order to compensate for the imported geometry and the second one in order to act as the buoyant response of the asthenosphere to the load of the new layer. To be computationally efficient and keep run-times less than 1 day long, a maximum of seven increments were performed for any incrementally-grown edifice. The instantaneously-formed volcanoes were built to match the final volumes of their counterpart incrementally-grown volcano model (bold values in Tables S1,S2).

Table 3. Boundary conditions of the subsequent FEMs, where wn is the vertical displacement in the nth model.
Ocean Load
In order to understand the effect of the ocean on a growing volcanic edifice, two kinds of models were developed and tested in combination with the half-space and flexural models (section Half-Space vs. Flexural Models) and the two distinct edifice growth scenarios (section Instantaneous Edifice Existence vs. Incremental Edifice Growth). For the scenario of instantaneously-formed volcanoes, we tested eight different ocean levels (from 0 to 7km) in order to study the effect of different amounts of oceanic load on a volcano of constant height. For the scenario of incrementally-grown volcanoes, the ocean level was set to either 0 or 4,000 m [similar to the mean depth of the ocean floor worldwide (Sverdrup et al., 1942; Vezzi et al., 2005)] in order to study the rise and emergence of a basaltic ocean island volcano. The ocean load was simulated as a boundary load at the surface of the model, and taken into account in buoyant restoring forces (Bottom equilibrium in Tables 2, 3).
Limitations
In order to focus our interest on the mechanical response of a volcanic edifice to the presence of an ocean load, we made a series of simplifications. First, the growth of volcanic islands is also affected by the process of gravitational spreading, usually facilitated by basal sediments units (Borgia et al., 1992; Le Corvec and Walter, 2009; McGovern and Morgan, 2009; Byrne et al., 2013; McGovern et al., 2015; Musiol et al., 2016). However, not all volcanic edifices are subject to decollement-based gravitational spreading [e.g., the volcanoes of the Canary Islands (Carracedo, 1994; Mitchell et al., 2002)]; therefore in order to focus on the flexural response and the ocean load effect, we neglect the effect of gravitational spreading in our models. Second, the development of magma reservoirs is known to influence the surrounding state of stress and the type of magma intrusions (Chestler and Grosfils, 2013; Le Corvec et al., 2015); however the influence of the magma reservoirs is localized compared to the scale of an edifice as modeled in this study. Finally, we limit our models to the elastic rheology, the viscoelastic response of the asthenosphere (McGovern and Solomon, 1993, 1998; Musiol et al., 2016) and the hot cumulates within the volcanic edifice (Clague and Denlinger, 1994) are neglected. These behaviors will be integrated in future work. As we show in the following section, although our models are simplified, important information can be extracted that helps in understanding real volcano behavior.
Results
In the following, we first present the vertical displacements observed at the surface of the models (Figure 2). For our incrementally-grown volcano models, the final vertical displacement corresponds to the cumulative vertical displacements of all successive steps. Then we describe the state of stress within the volcanic edifice along cross sections by means of the differential stress (Δσ = σ1 – σ3). The cross sections were created at 5, 20, 40, 60, and 80% of the length of the volcanic edifice away from the symmetry axis (red lines in Figure 1). The initial 5% cross-section was chosen to avoid the stress orientation degeneracy at the symmetric axis (i.e., r = 0 km). Pathways of magmatic intrusions are defined by the orientation of the minimum compressional stress (σ3; Rubin, 1995). Sills, angular dikes and circumferential dikes are formed when σ3 is in the r-z plane (with r being the radial (horizontal) distance from the symmetry axis, z corresponds to the vertical coordinates); sills are sub-horizontal intrusions, and are defined for angles ≤ 20° between σ3 and the z-axis (cf. dark blue color in Figures 3–8), angular dikes are defined for angles >20° and < 70° (cf. light blue in Figures 3–8), finally circumferential dikes are sub vertical intrusions, and are defined for angles of ≥70° (cf. green color in Figures 3–8). Radial dikes are formed when σ3 is the “out of plane” stress, perpendicular to the r-z plane (cf. red color in Figures 3–8).
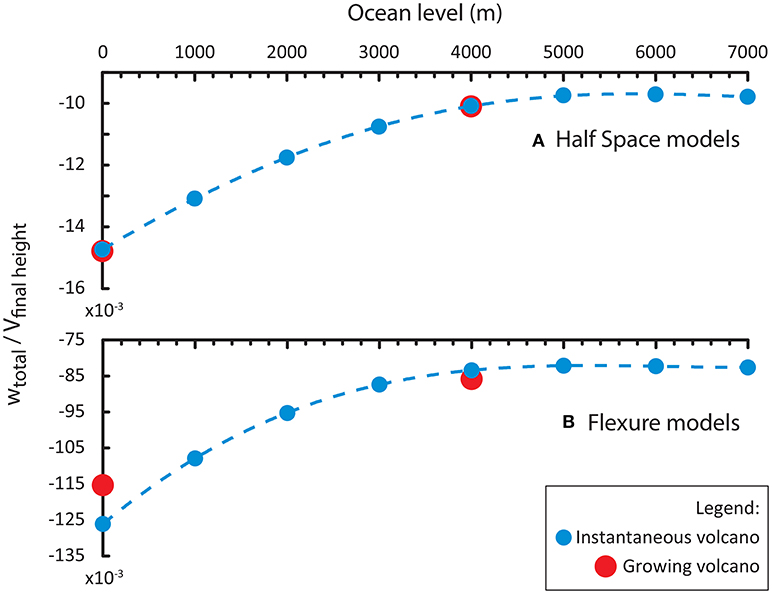
Figure 2. Ratios between the vertical displacements at summit of the volcanic edifice (w) and its the final height (Vh) for instantaneously-formed (blue) and incrementally-grown (red) volcano models. Different sea levels are displayed for instantaneously-formed volcano models (0, 3,000, 5,000, and 7,000 m), and for incrementally-grown volcano models (0 or 4,000 m). Results for half-space models are shown in the upper panel (A) while results for flexural models are shown in the lower panel (B).
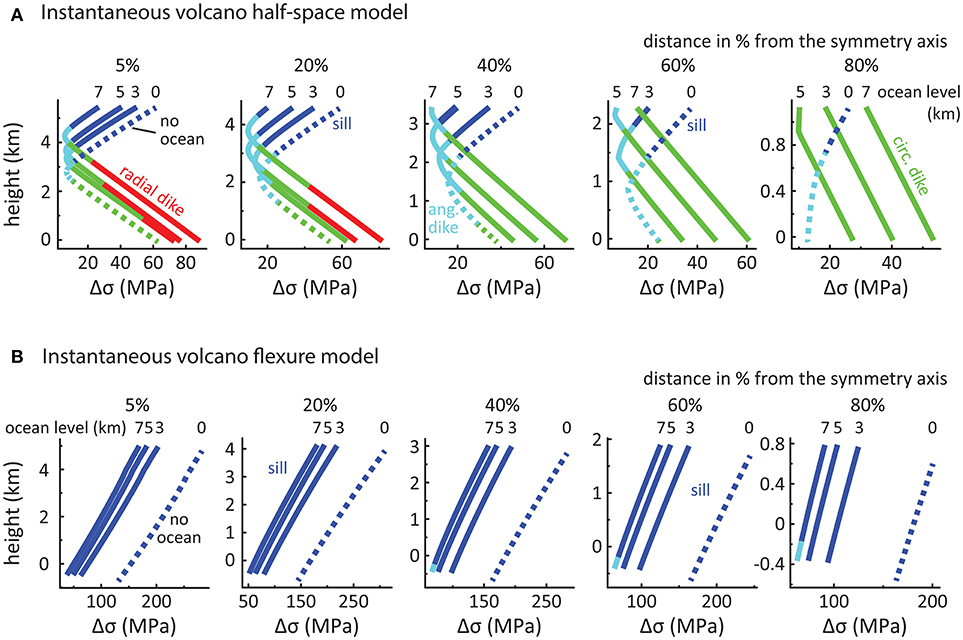
Figure 3. Differential stress magnitudes, and magmatic intrusion types predicted from principal stress orientations along the internal cross-sections for instantaneously-formed volcanoes in (A) half-space and (B) flexure models. Dashed lines represent the model without an ocean load. Solid lines represent models taking into account different ocean loads (with the sea levels in km given above each line). Dark blue color represents sill intrusion ([0°-20°] between σ3 and the z-axis), light blue color represents angular dike intrusion [(20°-70°) between σ3 and the z-axis], green color represents circumferential dike intrusion ([70°-90°] between σ3 and the z-axis), and red color represents radial dike intrusion.
Vertical Displacements
Instantaneous Volcano
For an instantaneous volcano, the vertical displacements we observe differ significantly between half-space and flexural models. We compare the ratio between the vertical displacements and the final height of the volcanic edifice (Figure 2 and Tables S1,S2). Without an ocean load, the displacement ratio in the half-space model reaches ~0.15 × 10−3 (blue color at 0 m sea level in Figure 2A), while in the flexural model the displacement ratio is about two orders of magnitude higher and reaches ~123 × 10−3 (blue color at 0 m sea level in Figure 2B). In the presence of an ocean load, we observe decreasing vertical displacements with increasing sea levels (blue dotted lines in Figures 2A,B). This tendency is valid until a certain water level threshold is reached at ~5,500 m after which the vertical displacements slowly increase again.
Incremental Volcano
We obtain quasi-identical vertical displacements for incrementally-grown volcanoes and the equivalent instantaneously-formed volcano simulations when applying half-space models without the effect of ocean loading and also for incrementally-grown volcanoes and the analogous instantaneous volcano modeled in half-space with an oceanic load (red dots at 0 and 4,000 m ocean level in Figures 2A, and Tables S1,S2). For flexural models, we observe slightly lower vertical displacements for the incrementally-grown volcano without an ocean load as compared to the analogous instantaneous volcano, but slightly more displacements from models with the presence of an ocean load (red dots at 0 and 4,000 m seal level in Figures 2B, and Tables S1,S2).
State of Stress and Magmatic Intrusions
Instantaneous Volcano
Instantaneous volcano half-space models
A volcanic edifice that is instantaneously-formed in a half-space model and is not affected by an ocean load shows a curved state of stress, i.e., high Δσ in the upper and lower parts of the edifice, separated by a zone of low Δσ in most part of the edifice (cf. dotted lines from 5 to 60% in Figures 3A, 4A and Figure S1.1). At the tip of the edifice (cf. dotted line at 80% in Figure 3A), the Δσ decreases from top to bottom. Below the summit (i.e., at 5% distance from the symmetry axis), the state of stress promotes circumferential dike intrusions and sill emplacement at the lower and upper parts of the edifice, respectively, separated by an intermediate zone of angular dike intrusion. Such state of stress becomes more prominent with increasing distance from the symmetry axis, replacing the deep zones prone to circumferential dikes and decreasing the vertical extent of sill emplacements (cf. cross-sections at 20–80% in Figure 3A).
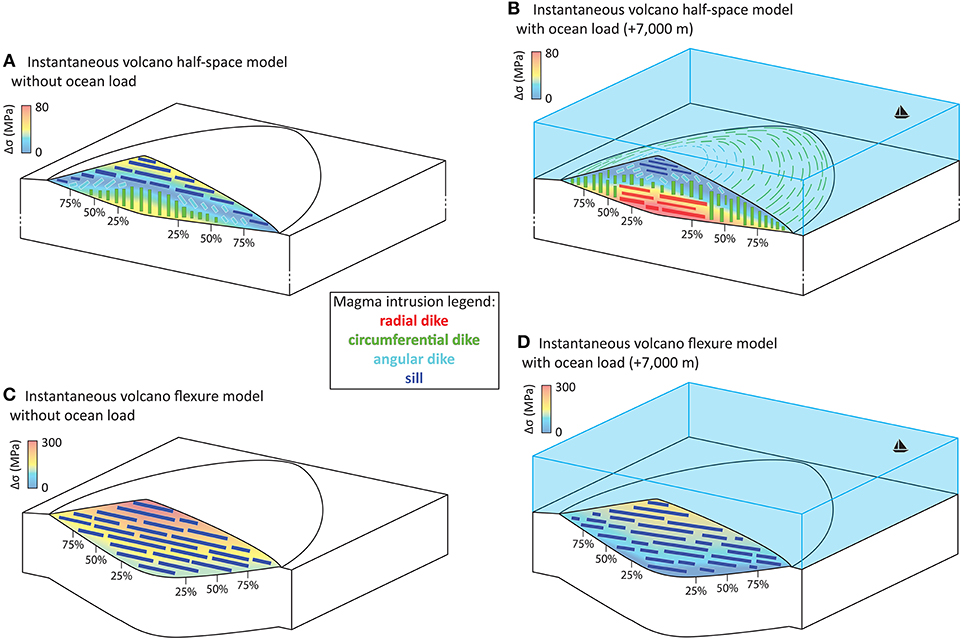
Figure 4. Sketch illustrating the state of stress and the type of magmatic intrusions within instantaneously-formed volcanoes in (A,B) half-space and (C,D) flexure models without an ocean load (A,C) and (B,D) with an ocean load (+7,000 m). Sill intrusions are presented by dark blue-colored bars, while angular, circumferential and radial dikes presented by light blue, green and red-colored bars (in cross-section) and lines (at the surface of the edifice). Background colors represent the amount of differential stress (Δσ; similar Δσ scales are applied for A,B; and for C,D).
We find that rising ocean levels decrease the amount of Δσ within the upper part of the volcanic edifice while at deeper levels of the edifice Δσ increases with increasing oceanic load (cf. solid lines in Figures 3A, 4B and Figures S1.2–4). In addition, the zone of low Δσ shifts upward within the edifice, which ultimately changes the curved state of stress into a linear one (e.g., the cross-section at 40% distance from the symmetry axis with an ocean level of 7 km in Figure 3A). At the highest water level (+7,000 m), we also observe that the magnitude of Δσ becomes larger at the surface of the lower flanks than the models with lower ocean load (cf., cross-sections 60 and 80% in Figures 3A, 4B and Figures S1.2–4). Furthermore, our results show that the type of magmatic intrusions is also affected when applying oceanic loading. We find that increasing the ocean load increases the fraction of the edifice that is subject to stress states favoring circumferential dike development. Furthermore, we find stress states that facilitate radial diking at the base of the volcanic flank near the summit and that the vertical extent of such conditions increases with increasing ocean levels (cf., e.g., the cross-sections at 5 and 20% distance from the symmetry axis with ocean levels of 3, 5, and 7 km in Figure 3A).
Instantaneous volcano flexure models
When ignoring oceanic load, a volcanic edifice instantaneously-formed on an elastic 30 km thick lithosphere shows increasing differential stresses Δσ from deeper to shallower levels within the volcanic edifice (dotted lines in Figures 3B, 4C and Figure S2.1). The state of stress promotes sill intrusions throughout the entire edifice (Figures 3B, 4C).
Increasing the ocean load causes the magnitude of Δσ to decrease without substantially changing the slope or shape of the Δσ (solid lines in Figures 3B, 4D and Figures S2.2–4). While Δσ decreases in magnitude, the stress orientations are not affected and continue to favor the formation of sills throughout the entire edifice, with the exception of small zones favoring angular dikes at the base of the outer flanks for an ocean level of 7,000 m (Figure 3B).
Incremental Volcano
Incremental volcano half-space models
When neglecting the loading effect of the ocean (dashed lines in Figures 5, 6A,B, and Figure S3), the initial volcanic edifice that is emplaced on a half-space shows essentially the same curved stress distribution as the corresponding instantaneous volcano model (dashed lines in Figure 3A in comparison with the dotted lines in step 1 of Figure 5). In the subsequent layers, the differential stress Δσ at the center of the edifice (i.e., at 5% distance from the symmetry axis) increases almost linearly with depth (first row of steps 3 to 7 in Figure 5), a pattern that becomes more curved toward the flanks (e.g., cross-section at 60% in step 3 in Figure 5). However, this curved differential stress gradient becomes more linear upon the emplacement of new layers [e.g., the curved dashed line at 60% distance from the symmetry axis (18 km) in step 1 of Figure 5 becomes the linear dashed line at a similar distance (40%) from the summit (~17.4 km) at deep levels within the edifice (0–1 km) in step 3 of Figure 5 upon the emplacement of two new layers (during step 2 and 3). The predominant type of magmatic intrusions (dikes or sills) that are likely to form within the edifice also changes in response to the emplacement of new layers. In the first stage, only angular, circumferential dikes (light blue and green) and sills (dark blue) can be formed (colored dashed lines in step 1 in Figure 5). Their occurrence decreases simultaneously with the increase of radial dikes in consequence of additional layer emplacement (red dashed lines in steps 2–7 in Figures 5, 6). The emplacement of angular and circumferential dikes is favored below the summit and in the deeper parts below the flanks (light blue and green dotted lines in steps 2–6 from 5 to 80% in Figures 5, 6) while radial dikes become predominant with edifice growth within the edifice (red dotted lines in steps 4–7 from 5 to 80% in Figure 5). While sill formation can be observed at the surface of the entire edifice, sills are more prominent near the surface of the outer parts of the edifice (dark blue dashed lines in steps 2–7 from 40 to 80% in Figures 5, 6).
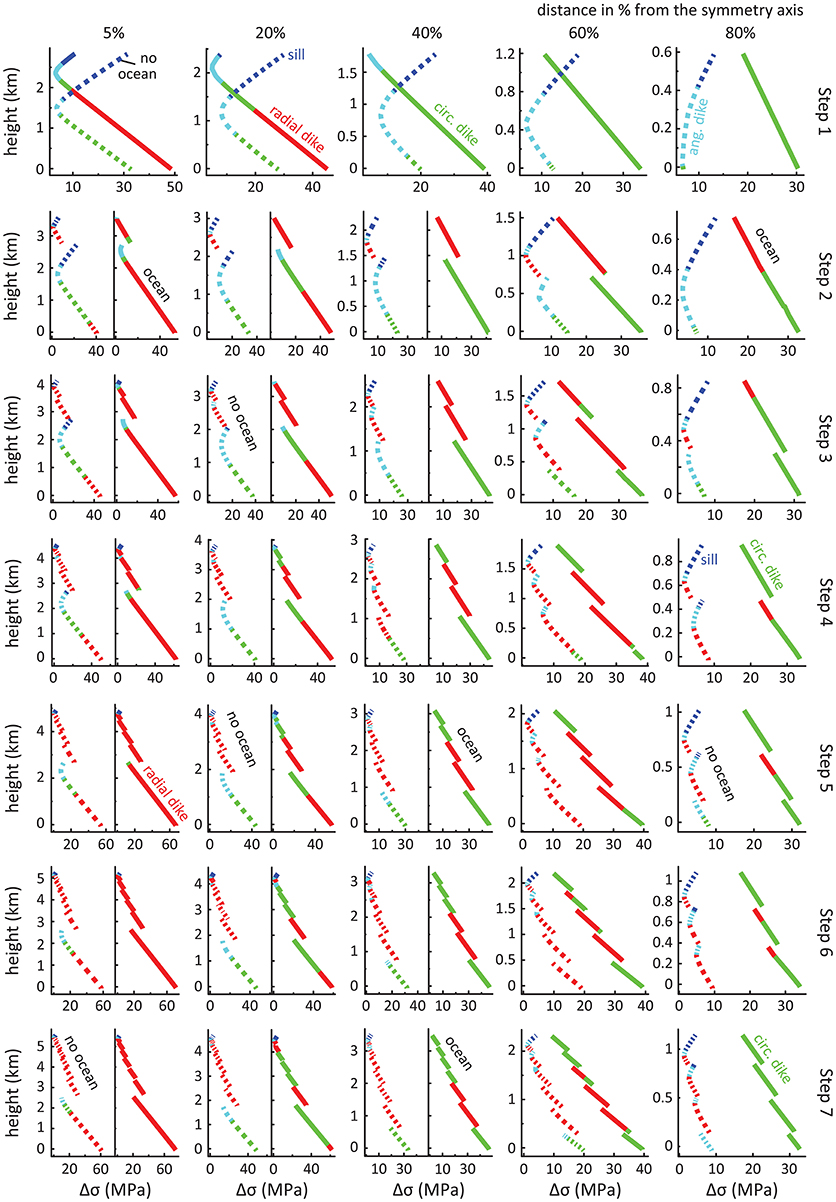
Figure 5. Differential stress magnitudes, and magmatic intrusion types predicted from principal stress orientations along the internal cross-sections for incrementally-grown volcanoes in half-space models with and without an ocean load (solid and dashed lines, respectively). Legend as in Figure 3.
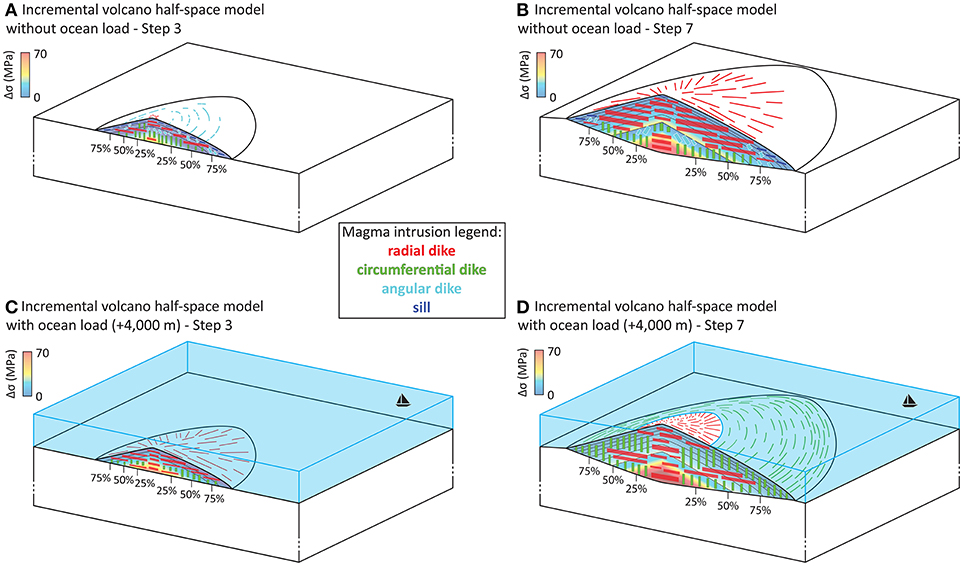
Figure 6. Sketch illustrating the state of stress and the type of magmatic intrusions within incrementally-grown volcanoes for half-space models. Steps 3 (A) and 7 (B) of the model without an ocean load. Steps 3 (C) and 7 (D) of the model with an ocean load (+4,000 m). Legend as in Figure 4.
When taking the effect of ocean loading into account (solid lines in Figures 5, 6C,D, and Figures S4), the initial volcanic edifice that is emplaced on a half-space (first row of Figure 5) again gives a similar edifice internal stress distribution to that obtained for the corresponding instantaneous volcano model (Figure 3B). In comparison to our simulations ignoring the oceanic loading, we observe lower differential stresses at the shallower parts of the edifice, and higher Δσ magnitudes at deeper levels of the edifice (solid lines from 5 to 60% in Step 1 in Figures 5, 6C,D, and Figures S4). However, we observe that at the tip of the flank the Δσ displays higher values along the entire cross-section than the model without an ocean load (solid line at 80% in Step 1 in Figure 5). As the volcano grows, we observe that the loading effect of an ocean results in a homogeneous linear increase of the differential stress (Δσ) within each layer from top to bottom and overall in the entire edifice (solid lines in Figure 5), and we observe that the magnitudes of Δσ are slightly higher near the summit than the models without an ocean (from 5 to 40% in Figure 5), while further within the flank the magnitudes of Δσ are much larger than for the model without an ocean load (solid lines at 60 and 80% in (Figure 5).
Magmatic intrusions are only slightly influenced by the growth of the edifice from the initial step promoting mostly circumferential and radial dikes (green and red solid lines in step 1 in Figure 5). Angular dikes and sills (light and dark blue) are restricted to the upper part of the flank near the summit of the volcano (from 5 to 40% in step 1 in Figure 5). As the volcano grows radial dikes (red) are favored throughout the entire volcanic edifice near the summit (at 5% from the symmetrical axis during steps 2–7 in Figure 5) and near the surface of the flanks in the first steps (red solid lines in steps 2–4 from 20 to 60% in Figure 5). In the subsequent steps, radial dikes are formed mostly within the edifice flanks (red solid lines in steps 4–7 from 20 to 60% in Figure 5). Finally, we observe that more circumferential dikes are dictated by the state of stress within the edifice's flanks when compared to the non-ocean load model as the volcano grows larger (green solid lines in steps 1–7 from 40 to 80% in Figures 5, 6).
Incremental volcano flexure models
We study the effect of an incrementally growing volcanic edifice on an elastic lithosphere by allowing lithospheric flexure (Figures 7, 8 and Figures S5–S6). When neglecting the effect of an ocean, the initial step is again similar to the instantaneously-formed volcano model (Figure 3B) with the magnitude of Δσ increasing from the base to the surface of the edifice (dotted lines in step 1 in Figures 7, 8 and Figure S5.1). As the edifice grows, we find that overall the magnitude of Δσ within each load increment increases with increasing edifice height, i.e., with the emplacement of subsequent layers, e.g., Δσmax in step 1 equals ~70 MPa while Δσmax in step 7 equals ~200 MPa (in Figures 7, 8 and Figure S5). However and more specifically, the magnitude of Δσ in each successive increment decreases compared to that of the previous layer, such that the lowest differential stresses are observed at shallow levels within the edifice, i.e., within the youngest, uppermost increment. The combination of these effects produces a characteristic “zig-zag” pattern of Δσ within the edifice [see also (McGovern et al., 2001)] at all distances from the symmetry axis (Figure 7). The characteristics described above occur regardless of the presence or absence of a water load as the volcano grows. We observe however that the ocean load influences the state of stress within the initial edifice (solid lines in step 1 in Figure 7), which produced a curved state of stress within the edifice (solid lines in step 1 from 5 to 40% in Figure 7). As in the instantaneously-formed volcano models (Figure 3B), the presence of an ocean results in a significant decrease of the differential stress Δσ, e.g., Δσmax in step 1 equals ~40 MPa vs. ~80 MPa for the model without an ocean load, while Δσmax in step 7 equals ~150 MPa vs. ~210 MPa (solid lines in Figure 7, 8 and Figure S6).
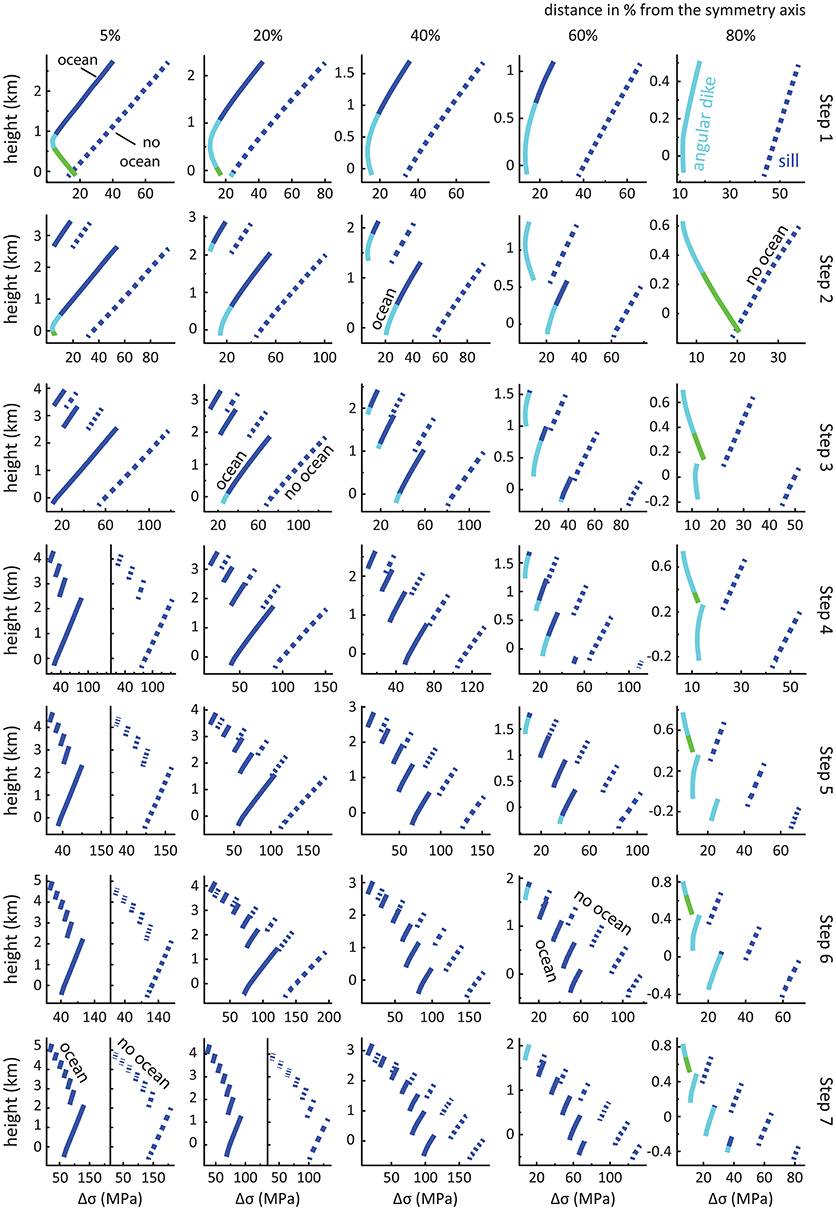
Figure 7. Differential stress magnitudes, and magmatic intrusion types predicted from principal stress orientations along the internal cross-sections for incrementally-grown volcanoes in flexure models with and without an ocean load (solid and dashed lines, respectively). Legend as in Figure 3.
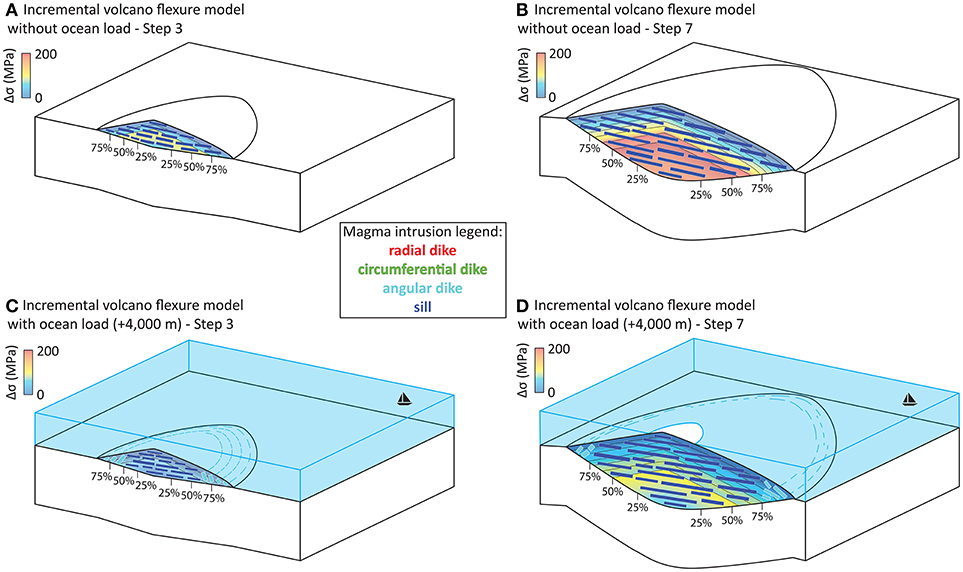
Figure 8. Sketch illustrating the state of stress and the type of magmatic intrusions within incrementally-grown volcanoes for flexure models. Steps 3 (A) and 7 (B) of the model without an ocean load. Steps 3 (C) and 7 (D) of the model with an ocean load (+4,000 m). Legend as in Figure 4.
Magmatic intrusions formed within a growing edifice without the presence of an ocean will only be sills (dark blue dashed lines in Figures 7, 8). When considering the ocean load, we observe that the proportion of the edifice with internal stresses promoting angular and circumferential dike intrusions increases (cf. light blue and green portions of solid lines in Figure 7). Circumferential dikes are favored in the base of the initial edifice below the summit (cf. green portions in step 1 from 5 to 20% in Figure 7), while the proportion of angular dike within the edifice increase away from the summit (cf. light blue portions of solid lines in steps 1–3 from 5 to 80% in Figures 7, 8). As the edifice grows, sill intrusions are favored closer to the summit (cf. cross-sections at 5 and 20% in steps 3–7 in Figure 7) while the proportion of angular dike decreases and becomes restricted at the extremities of the edifice (c.f. light blue solid lines in steps 1–7 at 80% in Figures 7, 8) with limited opportunities for circumferential dikes (e.g., green solid lines in steps 2–7 at 80% in Figure 7).
Discussion
Vertical Displacement
In our experiments, we observed that the increase of an ocean load decreases the subsidence of the volcanic edifice until the ocean depth level becomes greater than the original height of the edifice load (Figure 2). The decrease in subsidence is due to the buoyancy imparted to the volcanic rock by the pre-existing ocean water (Wessel and Keating, 1994; Kim and Wessel, 2010). For segments of the edifice deeper than the ocean level, volcanic rock replaces water, and therefore the net change in load felt by the lithosphere is proportional to the difference of rock and water densities. This reduction of load magnitude relative to the oceanless case reduces the vertical displacement and the magnitude of Δσ as seen in Figure 2 until the ocean greater than the total edifice height. No significant differences of the edifice vertical deformation are observed between instantaneously-formed and incrementally-grown volcanoes in a half-space model (blue and red circles, respectively in Figure 2A), nor in the oceanless flexure model (Figure 2B). However, we observe that in the flexural model subjected to an ocean load the vertical displacement is larger for the incrementally-grown volcanoes. This result likely stems from a reduced contribution of the growing edifice to local thickening (effective stiffening) of the lithosphere (see Figures 14 and Figure 19A of McGovern and Solomon, 1993) vs. that of the instantaneous edifice. The full height of the instantaneous edifice is present throughout the flexural response, whereas the growing edifice is shorter during early increments, and thus the response to those is not affected by as much effective stiffening, resulting in greater final displacements at the end of loading.
Volcanic Growth and Magma Intrusions
An important difference in the effects of ocean loads on half-space loads vs. flexural loads can be explained in terms of the stress tensor. For the half-space incremental loads (Figure 5, steps 2–7), the effect of the ocean load is to generally increase Δσ, while in contrast, for the flexural incremental loads (Figure 7, steps 2–7) the ocean load generally decreases Δσ. This phenomenon can be understood in terms of the orientation of the stress tensors in these edifices. For the half-space cases shown in Figure 5, σ1, the most compressive principal stress, is vertical. Thus, adding another component of vertical compressive load from an overlying ocean will reinforce this stress state, thereby driving Δσ higher. Conversely, the flexural loading case without an ocean is generally characterized by horizontal principal compression and vertical principal extension (σ1 horizontal and σ3 vertical, the “sill” stress state; see the dark blue dashed lines in Figure 7). Thus, the imposed vertical compression from the ocean will add to σ3, thereby reducing Δσ and in some cases reorienting the stress tensor such that σ3 is horizontal (the light blue and green solid lines in Figure 7).
The loads acting on the volcanic edifice and on the orientation of the state of stress will therefore influence volcanic edifices growth as a result of magmatic intrusions and/or eruptions (Annen et al., 2001; Pinel et al., 2010; Roman and Jaupart, 2014), where buoyant magma is propagating through the lithosphere, and finally through the volcanic edifice via self-induced fractures that form perpendicular to σ3 (Nakamura, 1977; Rubin, 1995). The flexural response of the lithosphere to the increasing gravitational load is dependent on the viscous flow of the underlying asthenosphere (Watts and Zhong, 2000). Therefore our models can be seen as temporal growth end-members such that instantaneously-formed volcanoes could represent the fastest growth rate of a volcanic edifice (Figures 3, 4), while incrementally-grown volcanoes the slowest growth rate (Figures 5–8). The behavior of the lithosphere depends on the geodynamic environment and is represented in our simulations using flexural models describing the simplest mechanical response of a lithosphere to a load (Figures 3B, 7), and the half-space models that enable us to take into account (1) the delayed mechanical response of the lithosphere due to a fast volcanic growth, and (2) the counteracting load of a plume, magmatic underplating and/or crustal accumulation (Figures 3A, 5; Wolfe et al., 1994; Michon et al., 2007; Klügel et al., 2015; Ramalho et al., 2017).
We show that the magmatic systems within volcanic edifices subject or not to flexural subsidence are highly different (Figures 3–8). In fact, the lithospheric flexure inhibits the vertical propagation of magmas as it generates horizontal compressive stresses within the edifice (McGovern and Solomon, 1993, 1998; Galgana et al., 2011). This will ultimately favor endogenous growth through sill-like magmatic intrusions (Francis et al., 1993). On the other hand, when volcanic edifices are not subjected to flexure, magmas are more able to propagate vertically and eventually erupt (Grosfils et al., 2013), favoring exogenous edifice growth through subaerial emplacement (Annen et al., 2001; Garcia and Davis, 2001).
The ocean load significantly increases the proportion of a volcanic edifice that is favorable to the development of radial dikes (c.f. red lines in Figures 5, 6). This especially applies to the early increments of the half-space, incremental case (Figure 5, Steps 1–3). However, as the edifice grows (Figure 5, Steps 4–7), the prominence of radial dike-favoring zones becomes less pronounced. In fact, the difference between models taking into account or ignoring the ocean load becomes negligible or might even turn into the opposite effect of predominant radial dike development as a result of lacking ocean load. This trend suggests that oceanic load can facilitate early-stage radial diking in incrementally-grown volcanic edifices. However, if the magma supply rate is low with respect to the relaxation time of the lithosphere, allowing for flexure to occur (Figures 7, 8), the presence of radial dikes is not predicted anywhere in the edifice regardless of the presence or absence of an ocean. This can be understood in terms of the substantial horizontal compression induced in edifices welded to a flexing lithosphere (e.g., McGovern and Solomon, 1993, 1998; McGovern et al., 2001). The compression results in stress states consistent with sill intrusions for most of the edifice (c.f. dark blue lines in Figure 7), although small portions at the lower parts of the flanks exhibit stress states that allow for angular diking and few occurrences of circumferential dikes (c.f. light blue and green lines in Figure 7). This horizontal compressional stresses increase will promote the formation of magmatic reservoirs by trapping intrusions within the edifice (Klügel et al., 2015; McGovern et al., 2015). The resulting oblate reservoirs or sill complexes can lead to the lateral migration of magmas into the edifice's flank; these magmas can ultimately reach zones favoring vertical propagation (Chestler and Grosfils, 2013) and ultimately promote lateral migration of volcanic activity (Maccaferri et al., 2017). Furthermore, the reduction in Δσ and increase in vertical compression experienced by a sub-ocean volcanic edifice subject to flexure (Figures 7, 8) will increase the likelihood that a stress perturbation of given magnitude (such as magma chamber inflation Chestler and Grosfils, 2013, regional stress fields, or local edifice deformation) can re-orient the principal stresses to achieve a state of horizontal principal extension consistent with magma ascent.
Applicability to Natural Volcanic Systems
Our models represent theoretical end-members that do not imitate the full reality of natural volcanic systems, which are known to be far more complex. Nonetheless, we will discuss similarities and differences between our results and several natural examples worldwide.
More common on continental basaltic volcanoes (Poland et al., 2008; Roman and Jaupart, 2014), the formation of radial dike systems on basaltic ocean island volcanoes, as observed on Fernandina (Galapagos; Chadwick and Howard, 1991), Fogo (Day et al., 1999) or Piton de la Fournaise (Michon et al., 2016) is explained by some authors by the behavior of the magmatic system and/or with its interaction with the volcanic edifice (Chestler and Grosfils, 2013; Corbi et al., 2015). However, the state of stress within an edifice subjected to flexural deformation inhibits radial intrusions to develop (Figures 3B, 4C,D, 7, 8). Here, we show that growing edifices lacking flexural deformation will tend to promote the formation of radial dike systems (Figures 3A, 4B, 5, 6) which can be applied at Piton de la Fournaise (Lénat, 2016) where the plume positive buoyancy contribute to the dynamic support of the load of La Réunion. Flexure can also be counteracted by magmatic intrusions at crustal levels that can lead to uplift deformation of the basaltic ocean island volcano allowing potential stress state rotation and the formation of radial dike intrusions in the upper part of the edifice (e.g., Fogo, Cape Verde; Klügel et al., 2015; Ramalho et al., 2017).
Hawaiian volcanoes are the typical example of volcanic edifice subjected to flexural deformation (Thurber and Gripp, 1988; Watts and ten Brink, 1989; Wessel, 1993; Pritchard et al., 2007). Geophysical data have provided information on the growth and contemporary magmatic processes occurring at these volcanoes (Hill and Zucca, 1987) and their structural interpretation defines the Hawaiian flanks to be composed of basaltic dikes overlaid by pillow lavas and subaerial flows and clastic deposits (Hill and Zucca, 1987). While recent formation of pillow lavas is linked to the subaerially erupted material traveling through lava tubes (Garcia and Davis, 2001), the formation of dikes in the flanks of a growing underwater edifice and their accompanying pillow lavas could correlate with the stress orientation favoring angular and circumferential dike formation in the flanks of the growing flexural model subjected to an ocean load (Figure 8C). As the volcanic edifice grows and the flexural response increases, compressional stresses will inhibit vertical magma propagation favoring sill intrusion and the development of accumulation zones or reservoir within the edifice (Figures 8D; Staudigel and Schmincke, 1984; Ryan, 1988; Pietruszka et al., 2015).
Our results also have implications for the outer flank submarine structure of basaltic ocean island volcanoes. Bathymetry data for Fernandina volcano (Galápagos Islands) reveal three focused offshore rift zones emanating from the southwest, west, and northwest submerged flanks (Geist et al., 2006). These workers attribute the rift zones to a rift-normal orientation of the least compressive stress σ3, arguing for a transition in stress states between low differential stress in and beneath the subaerial edifice (producing diffuse radial rift zones) and high differential stress in the outer flanks (producing strongly defined radial rift zones). Our results suggest an alternative scenario: incrementally grown ocean loaded edifices in a half-space configuration predict outer flank stress states with high Δσ and principal stress orientations consistent with radial diking (red solid lines in Figure 5), an effect that is particularly enhanced relative to oceanless models for early stages of growth (steps 2–4, with edifice dimensions comparable to those of Fernandina) and for the 60% flank position. Thus, radial dikes within the edifice, predicted by the stress states of Figure 5, could transport magmas from centrally located magma bodies to the locations of the rift zones, as inferred on petrological grounds by Geist et al. (2006). We note that such a scenario is not consistent with the stress states found for the flexural models (Figures 7, 8), suggesting that expected downward flexure at Fernandina is being counteracted by some mechanism. The inference of substantial crustal underplating at the western Galápagos based on analysis of bathymetry and gravity data provides such a mechanism (Mittelstaedt et al., 2014).
The presence of thick and dense fluid layers at other planetary bodies in the solar systems provides a final application for our analysis. The ~9 MPa surface atmospheric pressure on Venus can provide a stress-altering effect comparable to an ocean depth of about 1 km on Earth, helping to counteract the magma ascent-inhibiting effects of the large magnitude horizontal compressive stresses predicted for the very broad basaltic volcanic edifices on Venus (e.g., McGovern and Solomon, 1998). Further, worlds with substantial water oceans that envelop silicate cores, such as Jupiter's moon Europa, may exhibit silicate edifice-building volcanism at the surfaces of the cores. In the case of Europa, the total thickness of outer ice shell plus ocean may be as high as 100 km (Nimmo and Pappalardo, 2016), providing an immense vertical load on an edifice that could re-orient the principal stresses to enhance horizontal extension (and thus magma ascent) at a magnitude at least comparable to, and likely greater than, the effects shown in Figures 3–7. Thus, the mechanical effects of an icy planet ocean may facilitate eruption and edifice construction at the top of a silicate core, in turn enhancing delivery of heat and chemical energy to the subsurface ocean, with important implications for surface ice shell structure and astrobiological potential.
Conclusion
The growth of basaltic ocean island volcanoes is linked to their growth rate, the flexural response of their underlying lithosphere and the presence of an ocean. Specifically, these factors significantly influence a volcano's internal stress distribution and preferred pathways of magma propagation.
In this work, we show that vertical propagation of magmas is favored for a limited flexural response of the lithosphere, which can be caused by a balance between edifice growth (i.e., loading) and (a) mantle plume rise, magmatic underplating and/or crustal accumulation (pushing against the load), or (b) the presence of an ocean (pushing on the flanks). We translate predominant types of magmatic intrusions at volcanic ocean islands into edifice growth mechanisms: extrusive/exogenous growth is more like to occur within incrementally-grown edifices that are affected or not by the load of a water body, but where the stress signatures of lithospheric flexure are reduced (for the above described reasons). In addition, the transfer from extrusive/exogenous to intrusive/endogenous growth mechanisms at basaltic ocean island volcanoes is largely governed by the growth rate of the edifice (fast/instantaneous vs. slow/incremental). The application of these results to natural examples (e.g., Hawai'i, La Réunion, Galapagos) show that growing mechanisms can provide new explanation in understanding the formation of radial diking as well as potential submarine rift zone formations on the outer flanks of these edifices. Although we focus on ocean island volcanoes, our methods and findings can be applied to study active seamounts [e.g., Nishinoshima Volcano (Maeno et al., 2016)] or other volcanic phenomena in various environments, including extra-terrestrial volcanism. Future investigations should address and take into account the viscoelastic rheology of the mantle and its temporal response to flexural deformation, as well as edifice internal inelastic processes, such as the inelastic material response to magmatic intrusions (e.g., fracturing).
Author Contributions
NLC contributed to the conception and conduction of the modeling, and the writing of the manuscript. PJM contributed to the initial project idea, aspects of the modeling, and writing of the manuscript.
Funding
This work is produced as part of NASA Planetary Geology and Geophysics grant NX12AO49G, with additional support graciously provided by the Lunar and Planetary Institute/USRA and le LaboratoireMagmas et Volcans, Université Clermont Auvergne - CNRS - IRD, OPGC.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Nicole Richter for her help in improving the content of the manuscript. We are grateful for the insightful critiques provided by Marco Neri, Alessandro Tibaldi, associate editor Laura Becerril Carretero and chief editor Valerio Acocella. Data supporting this manuscript are available through the main author. This is LPI contribution 2111. This work represents LMV/ClerVolc contribution #291.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2018.00119/full#supplementary-material
References
Acocella, V., and Neri, M. (2009). Dike propagation in volcanic edifices: overview and possible developments. Tectonophysics. 471, 67–77. doi: 10.1016/j.tecto.2008.10.002
Annen, C. (2011). Implications of incremental emplacement of magma bodies for magma differentiation, thermal aureole dimensions and plutonism–volcanism relationships. Tectonophysics. 500, 3–10. doi: 10.1016/j.tecto.2009.04.010
Annen, C., Lénat, J. F., and Provost, A. (2001). The long-term growth of volcanic edifices: numerical modelling of the role of dyke intrusion and lava-flow emplacement. J. Volcanol. Geother. Res. 105, 263–289. doi: 10.1016/S0377-0273(00)00257-2
Apuani, T., Corazzato, C., Cancelli, A., and Tibaldi, A. (2005). Stability of a collapsing volcano (Stromboli, Italy): Limit equilibrium analysis and numerical modelling. J. Volcanol. Geother. Res. 144, 191–210. doi: 10.1016/j.jvolgeores.2004.11.028
Bagnardi, M., Amelung, F., and Poland, M. P. (2013). A new model for the growth of basaltic shields based on deformation of Fernandina volcano, Galápagos Islands. Earth Planet. Sci. Lett. 377–378, 358–366. doi: 10.1016/j.epsl.2013.07.016
Bailey, K. (1976). Potassium-argon ages from the Galápagos Islands. Science 192, 465–467. doi: 10.1126/science.192.4238.465
Becerril, L., Galindo, I., Gudmundsson, A., and Morales, J. M. (2013). Depth of origin of magma in eruptions. Sci. Rep. 3:2762. doi: 10.1038/srep02762
Borgia, A., Ferrari, L., and Pasquare, G. (1992). Importance of gravitational spreading in the tectonic and volcanic evolution of Mount Etna. Nature 357, 231–235. doi: 10.1038/357231a0
Byrne, P. K., Holohan, E. P., Kervyn, M. B., van Wyk de Vries, Troll, V. R., and Murray, J. B. (2013). A sagging-spreading continuum of large volcano structure. Geology 41, 339–342. doi: 10.1130/G33990.1
Carracedo, J. C. (1994). The Canary Islands: an example of structural control on the growth of large oceanic-island volcanoes. J. Volcanol. Geother. Res. 60, 225–241. doi: 10.1016/0377-0273(94)90053-1
Casagli, N., Tibaldi, A., Merri, A., Del Ventisette, C., Apuani, T., Guerri, L., et al. (2009). Deformation of Stromboli Volcano (Italy) during the 2007 eruption revealed by radar interferometry, numerical modelling and structural geological field data. J. Volcanol. Geother. Res. 182, 182–200. doi: 10.1016/j.jvolgeores.2009.01.002
Chadwick, W. W., and Howard, K. A. (1991). The pattern of circumferential and radial eruptive fissures on the volcanoes of Fernandina and Isabela islands, Galapagos. Bull. Volcanology 53, 259–275. doi: 10.1007/BF00414523
Chestler, S. R., and Grosfils, E. B. (2013). Using numerical modeling to explore the origin of intrusion patterns on Fernandina volcano, Galapagos Islands. Ecuador. Geophys. Res. Lett. 40, 4565–4569. doi: 10.1002/grl.50833
Clague, D. A., and Dalrymple, G. B. (1987). The Hawaiian-Emperor volcanic chain, Part 1: geologic evolution. USGS. Prof. Pap. 1350, 5–54.
Clague, D. A., and Denlinger, R. P. (1994). Role of olivine cumulates in destabilizing the flanks of Hawaiian volcanoes. Bull. Volcanol. 56, 425–434. doi: 10.1007/BF00302824
Corbi, F., Rivalta, E., Pinel, V., Maccaferri, F., Bagnardi, M., and Acocella, V. (2015). How caldera collapse shapes the shallow emplacement and transfer of magma in active volcanoes. Earth Planetary Sci. Lett. 431, 287–293. doi: 10.1016/j.epsl.2015.09.028
Crowley, J. W., Katz, R. F., Huybers, P., Langmuir, C. H., and Park, S. H. (2015). Glacial cycles drive variations in the production of oceanic crust. Science 347, 1237–1240. doi: 10.1126/science.1261508
Day, S. J., Heleno da Silva, S. I. N., and Fonseca, J. F. (1999). A past giant lateral collapse and present-day flank instability of Fogo, Cape Verde Islands. J. Volcanol. Geother. Res. 94, 191–218. doi: 10.1016/S0377-0273(99)00103-1
Fiske, R. S., and Jackson, E. D. (1972). Orientation and growth of hawaiian volcanic rifts: the effect of regional structure and gravitational stresses. Proc. R. Soc. Lond. Math. A. Phys. Sci. 329, 299–326.
Francis, P., Oppenheimer, C., and Stevenson, D. (1993). Endogenous growth of persistently active volcanoes. Nature 366:554. doi: 10.1038/366554a0
Frey, F. A., Wise, W. S., Garcia, M. O., West, H., Kwon, S. T., and Kennedy, A. (1990). Evolution of Mauna Kea Volcano, Hawaii: Petrologic and geochemical constraints on postshield volcanism. J. Geophys. Res. 95, 1271–1300. doi: 10.1029/JB095iB02p01271
Gaffney, E. S., Damjanac, B., and Valentine, G. A. (2007). Localization of volcanic activity: 2. Effects of pre-existing structure. Earth Planetary Sci. Lett. 263, 323–338. doi: 10.1016/j.epsl.2007.09.002
Galgana, G. A., McGovern, P. J., and Grosfils, E. B. (2011). Evolution of large Venusian volcanoes: insights from coupled models of lithospheric flexure and magma reservoir pressurization. J. Geophys. Res. 116:E03009. doi: 10.1029/2010JE003654
Garcia, M. O., and Davis, M. G. (2001). Submarine growth and internal structure of ocean island volcanoes based on submarine observations of Mauna Loa volcano, Hawaii. Geology 29, 163–166. doi: 10.1130/0091-7613(2001)029<0163:SGAISO>2.0.CO;2
Geist, D. J., Fornari, D. J., Kurz, M. D., Harpp, K. S., Soule, S. A., Koleszar, A. M., et al. (2006). Submarine Fernandina: Magmatism at the leading edge of the Galápagos hot spot. Geochem. Geophys. Geosyst. 7:Q12007. doi: 10.1029/2006GC001290
Gillot, P. Y., Lefèvre, C. J., and Nativel, P. E. (1994). Model for the structural evolution of the volcanoes of Réunion Island. Earth Planetary Sci. Lett. 122, 291–302. doi: 10.1016/0012-821X(94)90003-5
Grosfils, E. B., McGovern, P. J., Gregg, P. M., Galgana, G. A., Hurwitz, D. M, Chestler, S. R., et al. (2013). Elastic models of magma reservoir mechanics: a key tool for investigating planetary volcanism, Geol. Soc. Lond. Spec. 401, 239–267. doi: 10.1144/SP401.2
Gudmundsson, A. (2005). The effects of layering and local stresses in composite volcanoes on dyke emplacement and volcanic hazards. Compt. Rendus Geosci. 337, 1216–1222. doi: 10.1016/j.crte.2005.07.001
Hill, D. P., and Zucca, J. J. (1987). Geophysical constraints on the structure of Kilauea and Mauna Loa Volcanoes and some implications for seismomagmatic processes, U.S. Geol. Surv. Prof. Pap. 1350, 903–917.
Kavanagh, J. L., Menand, T., and Sparks, R. S. J. (2006). An experimental investigation of sill formation and propagation in layered elastic media. Earth Planetary Sci. Lett. 245, 799–813. doi: 10.1016/j.epsl.2006.03.025
Kim, S. S., and Wessel, P. (2010). Flexure modelling at seamounts with dense cores. Geophys. J. Int. 182, 583–598. doi: 10.1111/j.1365-246X.2010.04653.x
Klügel, A., Longpré, M. A., García-Cañada, L., and Stix, J. (2015). Deep intrusions, lateral magma transport and related uplift at ocean island volcanoes. Earth Planetary Sci. Lett. 431, 140–149. doi: 10.1016/j.epsl.2015.09.031
Le Corvec, N., McGovern, P. J., Grosfils, E. B., and Galgana, G. (2015). Effects of crustal-scale mechanical layering on magma chamber failure and magma propagation within the Venusian lithosphere. J. Geophys. Res. 120:1279–1297. doi: 10.1002/2015JE004814
Le Corvec, N., Menand, T., and Lindsay, J. (2013). Interaction of ascending magma with pre-existing crustal fractures in monogenetic basaltic volcanism: an experimental approach. J. Geophys. Res. 118, 968–984. doi: 10.1002/jgrb.50142
Le Corvec, N., and Walter, T. R. (2009). Volcano spreading and fault interaction influenced by rift zone intrusions: insights from analogue experiments analyzed with digital image correlation technique. J. Volcanol. Geothermal Res. 183, 170–182. doi: 10.1016/j.jvolgeores.2009.02.006
Lénat, J.-F. (2016). “Construction of La Réunion,” in Active Volcanoes of the Southwest Indian Ocean: Piton de la Fournaise and Karthala, eds P. Bachelery, J. F. Lenat, A. Di Muro, and L. Michon. (Berlin; Heidelberg: Springer Berlin Heidelberg), 31–44.
Luttrell, K., and Sandwell, D. (2010). Ocean loading effects on stress at near shore plate boundary fault systems. J. Geophys. Res. 115:B08411. doi: 10.1029/2009JB006541
Maccaferri, F., Bonafede, M., and Rivalta, E. (2011). A quantitative study of the mechanisms governing dike propagation, dike arrest and sill formation. J. Volcanol. Geother. Res. 208, 39–50. doi: 10.1016/j.jvolgeores.2011.09.001
Maccaferri, F., Richter, N., and Walter, T. R. (2017). The effect of giant lateral collapses on magma pathways and the location of volcanism. Nature Commun. 8:1097. doi: 10.1038/s41467-017-01256-2
Maeno, F., Nakada, S., and Kaneko, T. (2016). Morphological evolution of a new volcanic islet sustained by compound lava flows. Geology 44, 259–262. doi: 10.1130/G37461.1
McGovern, P. J. (2007). Flexural stresses beneath Hawaii: Implications for the October 15, 2006, earthquakes and magma ascent. Geophys. Res. Lett. 34:L23305. doi: 10.1029/2007GL031305
McGovern, P. J., Grosfils, E. B., Galgana, G. A., Morgan, J. K., Rumpf, M. E., Zimbelman, J. R., et al. (2015). Lithospheric flexure and volcano basal boundary conditions: keys to the structural evolution of large volcanic edifices on the terrestrial planets. Geol. Soc. Lond. Spec. Pub. 401, 219–237. doi: 10.1144/SP401.7
McGovern, P. J., and Morgan, J. K. (2009). Volcanic spreading and lateral variations in the structure of Olympus Mons, Mars. Geology. 37, 139–142. doi: 10.1130/G25180A.1
McGovern, P. J., and Solomon, S. C. (1993). State of stress, faulting, and eruption characteristics of large volcanoes on Mars. J. Geophys. Res. 98, 23553–23579. doi: 10.1029/93JE03093
McGovern, P. J., and Solomon, S. C. (1998). Growth of large volcanoes on Venus: Mechanical models and implications for structural evolution, J. Geophys. Res. 103, 11071–11101. doi: 10.1029/98JE01046
McGovern, P. J., Solomon, S. C., Head, J. W., Smith, D. E., Zuber, M. T., and Neumann, G. A. (2001). Extension and uplift at Alba Patera, Mars: Insights from MOLA observations and loading models, J. Geophys. Res. 106. 23769–23809. doi: 10.1029/2000JE001314
McLeod, P., and Tait, S. (1999). The growth of dykes from magma chambers. J. Volcanol. Geother. Res. 92, 231–245. doi: 10.1016/S0377-0273(99)00053-0
McNutt, M., and Menard, H. W. (1978). Lithospheric flexure and uplifted atolls, J. Geophys. Res. 83, 1206–1212. doi: 10.1029/JB083iB03p01206
McNutt, S. R. (1999). “Eruptions of pavlof volcano, alaska, and their possible modulation by ocean load and tectonic stresses: re-evaluation of the hypothesis based on new data from 1984-1998,” in Seismicity Patterns, their Statistical Significance and Physical Meaning, eds M. Wyss, K. Shimazaki, and A. Ito (Basel; Boston, MA; Berlin: Birkhäuser), 701–712.
Menand, T., Daniels, K. A., and Benghiat, P. (2010). Dyke propagation and sill formation in a compressive tectonic environment. J. Geophys. Res. 115:B08201. doi: 10.1029/2009JB006791
Menand, T., de Saint-Blanquat, M, and Annen, C. (2011). Emplacement of magma pulses and growth of magma bodies. Tectonophysics 500, 1–2. doi: 10.1016/j.tecto.2010.05.014
Michon, L., Ferrazzini, V., and Di Muro, A. (2016). “Magma Paths at Piton de la Fournaise Volcano,” in Active Volcanoes of the Southwest Indian Ocean: Piton de la Fournaise and Karthala, eds P. Bachelery, J. F. Lenat, A. Di Muro, and L. Michon (Berlin; Heidelberg: Springer Berlin Heidelberg), 91–106.
Michon, L., Saint-Ange, F., Bachelery, P., Villeneuve, N., and Staudacher, T. (2007). Role of the structural inheritance of the oceanic lithosphere in the magmato-tectonic evolution of Piton de la Fournaise volcano (La Réunion Island). J. Geophys. Res. 112: B04205. doi: 10.1029/2006JB004598
Mitchell, N. C., Masson, D. G., Watts, A. B., Gee, M. J. R., and Urgeles, R. (2002). The morphology of the submarine flanks of volcanic ocean islands: a comparative study of the Canary and Hawaiian hotspot islands. J. Volcanol. Geothermal Res. 115, 83–107. doi: 10.1016/S0377-0273(01)00310-9
Mittelstaedt, E., Soule, A. S., Harpp, K. S., and Fornari, D. (2014). “Variations in crustal thickness, plate rigidity, and volcanic processes throughout the northern galápagos volcanic province,” in The Galápagos: A Natural Laboratory for the Earth Sciences, eds K. S. Harpp, E. Mittelstaedt, N. D. W. d'Ozouville and Graham (Hoboken, NJ: American Geophysical Union, Geophysical Monograph 204), 263–284.
Musiol, S., Holohan, E. P., Cailleau, B., Platz, T., Dumke, A., van Gasselt, S., et al. (2016). Lithospheric flexure and gravity spreading of Olympus Mons volcano, Mars. J. Geophys. Res. 121, 255–272. doi: 10.1002/2015JE004896
Nakamura, K. (1977). Volcanoes as possible indicators of tectonic stress orientation - principle and proposal. J. Volcanol. Geother. Res. 2, 1–16. doi: 10.1016/0377-0273(77)90012-9
Nimmo, F., and Pappalardo, R. T. (2016). Ocean worlds in the outer solar system. J. Geophys. Res. 121, 1378–1399. doi: 10.1002/2016JE005081
Pietruszka, A. J., Heaton, D. E., Marske, J. P., and Garcia, M. O. (2015). Two magma bodies beneath the summit of Kilauea Volcano unveiled by isotopically distinct melt deliveries from the mantle. Earth Planetary Sci. Lett. 413, 90–100. doi: 10.1016/j.epsl.2014.12.040
Pinel, V., and Jaupart, C. (2003). Magma chamber behavior beneath a volcanic edifice. J. Geophys. Res. 108:2072. doi: 10.1029/2002JB001751
Pinel, V., and Jaupart, C. (2004). Magma storage and horizontal dyke injection beneath a volcanic edifice. Earth Planetary Sci. Lett. 221, 245–262. doi: 10.1016/S0012-821X(04)00076-7
Pinel, V., Jaupart, C., and Albino, F. (2010). On the relationship between cycles of eruptive activity and growth of a volcanic edifice. J. Volcanol. Geother. Res. 194, 150–164. doi: 10.1016/j.jvolgeores.2010.05.006
Poland, M., Moats, W., and Fink, J. (2008). A model for radial dike emplacement in composite cones based on observations from Summer Coon volcano, Colorado, U. S. A. Bull. Volcanol. 70, 861–875. doi: 10.1007/s00445-007-0175-9
Pritchard, M. E., Rubin, A. M., and Wolfe, C. J. (2007). Do flexural stresses explain the mantle fault zone beneath Kilauea volcano? Geophys. J. Int. 168, 419–430. doi: 10.1111/j.1365-246X.2006.03169.x
Ramalho, R. S., Helffrich, G., Madeira, J., Cosca, M., Thomas, C., Quartau, R. J., Ávila, S. P., et al. (2017). Emergence and evolution of Santa Maria Island (Azores)—The conundrum of uplifted islands revisited. GSA Bull. 129, 372–390. doi: 10.1130/B31538.1
Roman, A., and Jaupart, C. (2014). The impact of a volcanic edifice on intrusive and eruptive activity. Earth Planetary Sci. Lett. 408, 1–8. doi: 10.1016/j.epsl.2014.09.016
Rubin, A. M. (1995). Propagation of magma-filled cracks. Ann. Rev. Earth Planet. Sci. 23, 287–336. doi: 10.1146/annurev.ea.23.050195.001443
Ryan, M. P. (1988). The mechanics and three-dimensional internal structure of active magmatic systems: Kilauea Volcano, Hawaii. J. Geophys. Res. 93, 4213–4248. doi: 10.1029/JB093iB05p04213
Staudigel, H., and Schmincke, H. U. (1984). The Pliocene seamount series of La Palma/Canary Islands. J. Geophys. Res. 89, 11195–11215. doi: 10.1029/JB089iB13p11195
Sverdrup, H. U., Johnson, M. W., and Fleming, R. H. (1942). The Oceans: Their Physics, Chemistry, and General Biology. New York, NY: Prentice-Hall.
Tait, S., Jaupart, C., and Vergniolle, S. (1989). Pressure, gas content and eruption periodicity of a shallow, crystallising magma chamber. Earth Planetary Sci. Lett. 92, 107–123. doi: 10.1016/0012-821X(89)90025-3
Thurber, C. H., and Gripp, A. E. (1988). Flexure and seismicity beneath the south flank of Kilauea Volcano and tectonic implications. J. Geophys. Res. 93, 4271–4278. doi: 10.1029/JB093iB05p04271
Tibaldi, A. (2015). Structure of volcano plumbing systems: a review of multi-parametric effects. J. Volcanol. Geother. Res. 298, 85–135. doi: 10.1016/j.jvolgeores.2015.03.023
van Wyk de Vries, B., and Matela, R. (1998). Styles of volcano-induced deformation: numerical models of substratum flexure, spreading and extrusion. J. Volcanol. Geother. Res. 81, 1–18. doi: 10.1016/S0377-0273(97)00076-0
Vezzi, A., Campanaro, S. M., D'angelo, M., Simonato, F., Vitulo, N., Lauro, F., et al. (2005). Life at depth: Photobacterium profundum genome sequence and expression analysis. Science 307, 1459–1461. doi: 10.1126/science.1103341
Walker, G. P. L. (1973). Lengths of lava flows. Philos. Trans. R. Soc. Lond. 274, 107–118. doi: 10.1098/rsta.1973.0030
Walker, G. P. L. (1993). Basaltic-volcano systems. Geological Society, London, Special Publications, 76, 3–38. doi: 10.1144/GSL.SP.1993.076.01.01
Walker, G. P. L. (1999). Volcanic rift zones and their intrusion swarms, Journal of Volcanology and Geothermal Research, 94, 21–34. doi: 10.1016/S0377-0273(99)00096-7
Walker, G. P. L. (2000). “Basaltic volcanoes and volcanic systems,” in Encyclopedia of Volcanoes. eds H. Sigurdsson, B. F. Houghton, S. R. McNutt, H. Rymer, J. Stix (San Diego, CA: Academic Press), 283–289.
Watts, A. B. (2001). Isostasy and Flexure of the Lithosphere. Cambridge, UK: Cambridge Univercity Press.
Watts, A. B., and ten Brink, U. S. (1989). Crustal structure, flexure, and subsidence history of the Hawaiian Islands. J. Geophys. Res. 94, 10473–10500. doi: 10.1029/JB094iB08p10473
Watts, A. B., and Zhong, S. (2000). Observations of flexure and the rheology of oceanic lithosphere. Geophys. J. Int. 142, 855–875. doi: 10.1046/j.1365-246x.2000.00189.x
Wessel, P. (1993). A reexamination of the flexural deformation beneath the Hawaiian Islands. J. Geophys. Res. 98, 12177–12190. doi: 10.1029/93JB00523
Wessel, P., and Keating, B. H. (1994). Temporal variations of flexural deformation in Hawaii. J. Geophys. Res. 99, 2747–2756. doi: 10.1029/93JB02876
Keywords: basaltic ocean island volcano, magmatic system, finite element models, flexure, numerical modeling, volcano deformation
Citation: Le Corvec N and McGovern PJ (2018) The Effect of Ocean Loading on the Growth of Basaltic Ocean Island Volcanoes and Their Magmatic Plumbing System. Front. Earth Sci. 6:119. doi: 10.3389/feart.2018.00119
Received: 26 January 2018; Accepted: 30 July 2018;
Published: 07 September 2018.
Edited by:
Laura Becerril Carretero, Instituto de Ciencias de la Tierra Jaume Almera (ICTJA), SpainReviewed by:
Alessandro Tibaldi, Università degli studi di Milano Bicocca, ItalyMarco Neri, Istituto Nazionale di Geofisica e Vulcanologia (INGV), Italy
Copyright © 2018 Le Corvec and McGovern. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicolas Le Corvec, bmljb2xhcy5sZV9jb3J2ZWNAdWNhLmZy
 Nicolas Le Corvec
Nicolas Le Corvec Patrick J. McGovern
Patrick J. McGovern